SYGNAŁ
Jest to proces zmian w czasie pewnej wielkości fizycznej, dlatego tez za modele matematyczne sygnalu przyjmujemy
funkcje których argumentem jest czas t. Wyróżniamy rozne typy sygnałow –s. jednowymiarowe(mowy, zmiana
cisnienai względem czasu), dwuwymiarowe (nieruchomy obraz), trójwymiarowe(obraz zmienny w czasie-wideo).
Przetwarzaniu sygnałów z pojeciem sygnalu utożsamiac będziemy jego model matematyczny.
MODEL SYGNAŁU LOSOWEGO
Modelem losowym jest rzeczywisty lub zespolony proces stochastyczny (w szczególnym przypadku zmienna losowa),
model ten opisuje rzeczywistość dokładniej niż model deterministyczny (m.in. w przeciwieństwie do niego uwzględnia
szumy). W modelu losowym nie jesteśmy jesteśmy stanie określić wartości sygnalu w dowolnej chwili czasu, możemy
natomiast określić pewne prawdopodobieństwo wystapienia wartości osiaganych przez sygnał. Przykładowo dla
sygnalu sinusoid. Model deterministyczny:

)

2

sin(

)

(

ϕ

π

+

=

ft

A

t

x

model losowy:

)

(

)

2

sin(

)

(

t

n

t

f

A

t

x

+

+

=

ϕξ

ξ

π

ξ

SYGNAŁ LOSOWY NOSNIKEM INFORMACJI A DETERMINISTYCZNY NIE
Z punktu widzenia odbiorcy, sygnał przekazuje informacje jedynie wówczas ma dla odbiorcy charakter losowy, gdy
odbiorca nie jest w stanie przewidzieć zachowania i wartości sygnalu, a jedynie prognnozowac to z pewnym
prawdopodobieństwem. Ponieważ dla sygnału deterministycznego odbiorca może wyznaczyc jego wartość i parametry
w dowolnej chwili czasu

t to tez nie niesie on informacji.

ROZNICE MIEDZY S. CIĄGŁYM DYSKRETNYM I CYFROWYM(sygnał x w funkcji czasu t)
s. ciagłe SA ciągłymi funkcjami czasu, spełniającymi założenie tεR, xεR. S. dyskretne czas jest nie ciągły, nie
występują one w rzeczywistości spełniaja założenie tεZ, xεR. S. cyfrowe zarówno czas i wartośc sygnału SA nieciągłe
spełniaja założenie tεZ, xεZ (mogą przyjmowac tylko określone wartości)
PRZESTRZEŃ ZUPEŁNA
P.Z. nazywamy przestrzen metryczną, w której każdy ciąg Cauchyego ma granice i granica ta jest elementem
przestrzeni, oraz w której wszystkie wyniki operacji na jej elementach również naleza do tej przestrzeni. Przykładem
P.Z. z metryką euklidesową jest zbiór liczb rzeczywistych. R: ro(x,y)=|x-y|
PRZESTRZEN UNITARNA
P.U. zwiemy przestrzeń liniowa X, w którj określony jest iloczyn skalarny i unormowaną przez norme ||x||=sqrt(x,x),
xεX. Ponieważ iloczyn skalarny indukuje norme, a ta z kolei metryke, wiec przestrzeń unitarna jest zarazem
przestrzenią metryczną.
PRZESTRZEŃ HILBERTA
P.H. jest przestrzenią zupełną liniową (w przestrzeni liniowej zdefiniowane SA dwie operacje: dodawanie element.
Przestrzeni i mnożenie element. Przestrzeni przez stałą), unitarną (w P. unitarnej określony jest iloczyn skalarny i jest
ona unormowana przez norme ||x||=sqrt(x,x), xεX.) a skoro unitarną to również metryczną.
PRSTRZEŃ L²

P.L² jest przestrzenią metryczną i zupełną, znormalizowaną (dla przedziału (0,T) norma

dt

t

x

x

T

)

(

||

||

0

2

∫

=

dla

przedziału (-∞,∞) norma

dt

t

x

x

)

(

||

||

2

∫

∞

∞

−

=

, całkowalna w kwadracie(ale tylko L²(0,T)) (całka kwadratu jest

skończona), jest ona również P. sygnałow ciągłych.
MOMENT CENTRALNY R-TEGO RZEDU DLA S. DETERMINISTYCZNEGO CIĄGŁEGO

∫

−

=

R

r

x

r

x

dt

t

x

m

t

c

)

(

)

(

gdzie mx-moment zwykły r-tego rzędu określony wzorem

∫

=

R

r

r

x

dt

t

x

t

m

)

(

JAKIE OPERACJE NA ELEMENTACH P. DEFINIOWANE SA W PRZESTRZENI LINIOWEJ
W przestrzeni liniowej definiowane sa 2 operacje na elementach P. sa to: -dodawanie elementów przestrzeni(+) XxX-
>X -mnożenie elementów P. przez stałą(*) FxX->X; F- sigma ciało zbiór wszystkich liczb R lub Z.
JAKI ZBIÓR ELEMENTÓW P. może stanowić bazę p. (np. X^n). Z ilu elemen. Składa sie baza X^n.
Niech X^n będzie liniową przestrzenią n-wymiar. zbiór elemen. {xi:i=1...n}będący zbiorem liniowo niezależnym
nazywamy bazą przestrzeni. Z powyższego prosto wynika że baza przestrzeni X^n sklada sie z n elemen.
BAZA ORTOGONALNA I NIEORTOGONALNA
Baza O. od bazy N.O. rozni sie tym iz dla bazy O. rozwiazanie układu równań Aα=a jest duzo prostsze faktem iż
macierze A oraz A-¹ są w przypadku bazy O. macierz. Jednostkowyi, oraz tym że dla każdego elementu bazy O. norma
jest jednostkowa tj. ||xi||=1 dla i=1,2...n , oraz (xi,xj)=0, i≠j, i,j=1,2...n
WARUNEK ORTOGALNOSCI DLA 2 SYGNAŁÓW W P. SYGNAŁÓW
Dwa sygnały w przestrzeni sygnałów są O. jezeli ich iloczyn skalarny jest równy zeru czyli

2

2

2

||

||

||

||

||

||

0

)

,

(

y

x

y

x

y

x

y

x

+

=

+

=>

=

<=>

⊥

uogulnienie wzoru Pitagorasa na dowolna przestrzeń unitarną.

ZBIORY ORTOGONALNE ZUPEŁNE

1)Trygonometryczny szereg Fouriera- całkowany na odcinku L²(0,T)

...}

2

,

1

),...

2

sin(

2

,

2

cos(

2

,

1

{

=

n

t

T

n

T

t

T

n

T

T

π

π

2)zespolony szereg Fouriera - zbiór zupełny w L²(0,T)

...}

2

,

1

1

{

2

±

±

=

n

e

T

t

T

jn

π

3)szereg Shannona - zbiór zupełny w

przestrzeni dla sygnałów dolnoprzepustowych L²(-∞,∞)

...}

2

,

1

)),...

2

(

2

(

2

{

±

±

=

−

n

fm

n

t

fm

Sa

fm

π

4)funcje Haara

5)funkcje Walsha 6) wielomiany Lagrange’a

...}

2

,

1

),...

(

2

1

2

){

1

,

1

(

2

=

+

−

n

t

Pn

n

L

NORMA ELEMENTU PRZESTRZENI SYGNAŁÓW PODAC DEF.
Norma elementu przestrzeni to odwzorowanie elementu przestrzeni w zbiór liczb rzeczywistych dodatnich plus zero

})

0

{

||:

(||

∪

>

−

•

+

R

x

. Norma musi spełniac nastepujące aksjomaty:

1) jezeli ||x||=0 => x= (x jest elementem zerowym przestrzeni)
2) ||αx||=||α||||x||
3) ||x+y||≤||x||+||y||

przykładowa def: dla przestrzeni L²:

∑

∞

=

=

1

2

||

||

i

i

x

x

PROCEDURA GRAMMA-SCHMIDT’A
1) {xi:i=1...n} zb. Nieortog. 2) {yi:i=1...n} zb. Ortogon. 3) {zi:i=1...n} zb. Ortonor. P.G-S. słuzy do sprowadzenia bazy
nieortogonalnej do ortogonalnej. Przebiega ona następująco: 1) mamy baze nieortogonalną {x1...xn} 2) tworzymy na
jej podstawie baze ortogonalna {y1...yn} 3) na podstawie utworzonej bazy ortogonalnej tworzymy baze ortogonalną

{z1...zn}.. Procedura ta jest procedurą iteracyjną w której

k

n

k

k

k

n

n

z

z

x

x

y

∑

−
=

−

=

1

1

)

,

(

||

||

n

n

n

y

y

z

=

CZYM RÓZNIĄ SIE ALGORYTMY WYZNACZANIA DYSKRETNEJ REPREZENTACJI W PRZYPADKU
BAZY ORTOGONALNEJ I NIEORTOGONALNEJ
Przy wyznaczaniu dyskretnej reprezentacji sygnału otrzymujemy układ n skalarnych równań liniowych z
niewiadomymi αi; układ taki mozna zapisac w postaci macierzowej Aα=a. W przypadku bazy nieortogonalnej jego
zasadniczą wada jest fakt iz nalezy obliczyć wszystkie iloczyny skalarne po obu stronach powyzszgo wyrazenia, oraz
iż do rozwiaznia rownania α=A-¹a wymagane jest przeprowadzenie zmudnej operacji odwracania macierzy A. W
przypadku bazy ortogonalnej wygodnie jest zastosowac odpowiednią część procedury Gramma-Schmidt’a w wyniku
której z bazy ortogonalnej tworzona jest baza ortonormalna (czyli unormować ją) co z kolei sprawi iz zarówno macierz
A jak i A-¹ będą macierzami jednostkowymi a ostatecznie sprawi iz α=a i zatem ze αi=(x,xi) dla i=1...n.
DYSKRETNA REPREZENTACJA SYGNAŁÓW W KATEGORII P. SYGNAŁÓW

Jesli mamy ustaloną bazę {x1,x2...xn} oraz

∑

=

=

n

i

i

i

t

x

a

t

x

1

)

(

)

(

to ciąg α={α1...αn} jest dyskretną reprezentacja sygnału

przy danej bazie. Dla sygnału stochastycznego dyskretna reprezentacje mozna traktować jako odwzorowanie tego
sygnału w odpowiedni ciąg zmiennych losowych.
RÓśNICE MIĘDZY DYSKRETNĄ REPREZENTACJA SYGN. DETERMINIST. I SYG. LOSOWEGO
Dla syg. Losowego dyskretna reprezentacja jest odwzorowniem sygnału nie w zwykły ciag α={α1...αn} lecz w ciąg
odpowiednich zmiennych losowych (tzn. w przestrzen Γ^n lub Γ^∞)


TW. O RZUCIE ORTOGONALNYM
Niech X bedzie przestrzenią unitarna a X^n jej n-wymiar. podprzestrzenią rozpiętą na ortogonalnej bazie {xi; i=1...n}.

Jeżeli dla kazdego xεX istnieje jeden i tylko jeden element

n

x

x

∈

~

okreslony wzorem

i

n

i

i

x

x

x

x

∑

=

=

1

)

,

(

~

taki że dla

każdego

n

x

x

∈

~

gdzie

x

x

~

~

~

≠

zachodzi

||

~

~

||

||

~

||

x

x

x

x

−

<

−

oraz wektor

n

x

x

x

⊥

−

=

~

ε

to wówczas x

~ nazywamy nutem

ortogonalnym elementu x na przestrzeń X^n.

2

2

2

||

||

||

~

||

||

||

ε

+

=

n

x

x

TW. O NUCIE ORTOGONALNYM
TW. o N.O. zapewnia ze aproksymacja sygnałów przestrzeni X przez element podprzestrzeni X^n zostanie
przeprowadzona z możliwie najmniejszym błędem inaczej mówiąc rozstrzyga problem umożliwienia prostego i
efektywnego rozwiązania zagadnienia najlepszej aproksymacji.
OMÓWIC ZAGADNIENIE NAJLEPSZEJ APROKSYMACJI SYGNAŁÓW PRZESTRZENI X PRZEZ
ELEMENT PODPRZESTRZENI X^n
Element x nie należący do pp. X^n można reprezentować elementem

n

X

x

∈

~

jedynie z pewnym przybliżeniem.

Poszukiwanie najlepszegoprzyblizenia to treśc zagadnienia najlepszej aproksymacji które można sformółowac
następująco: niech X bedzie P. unitarną a X^n jej n-wymiar pp. Rozpiętą na bazie {xi; i=1...n}. Dla danego elementu

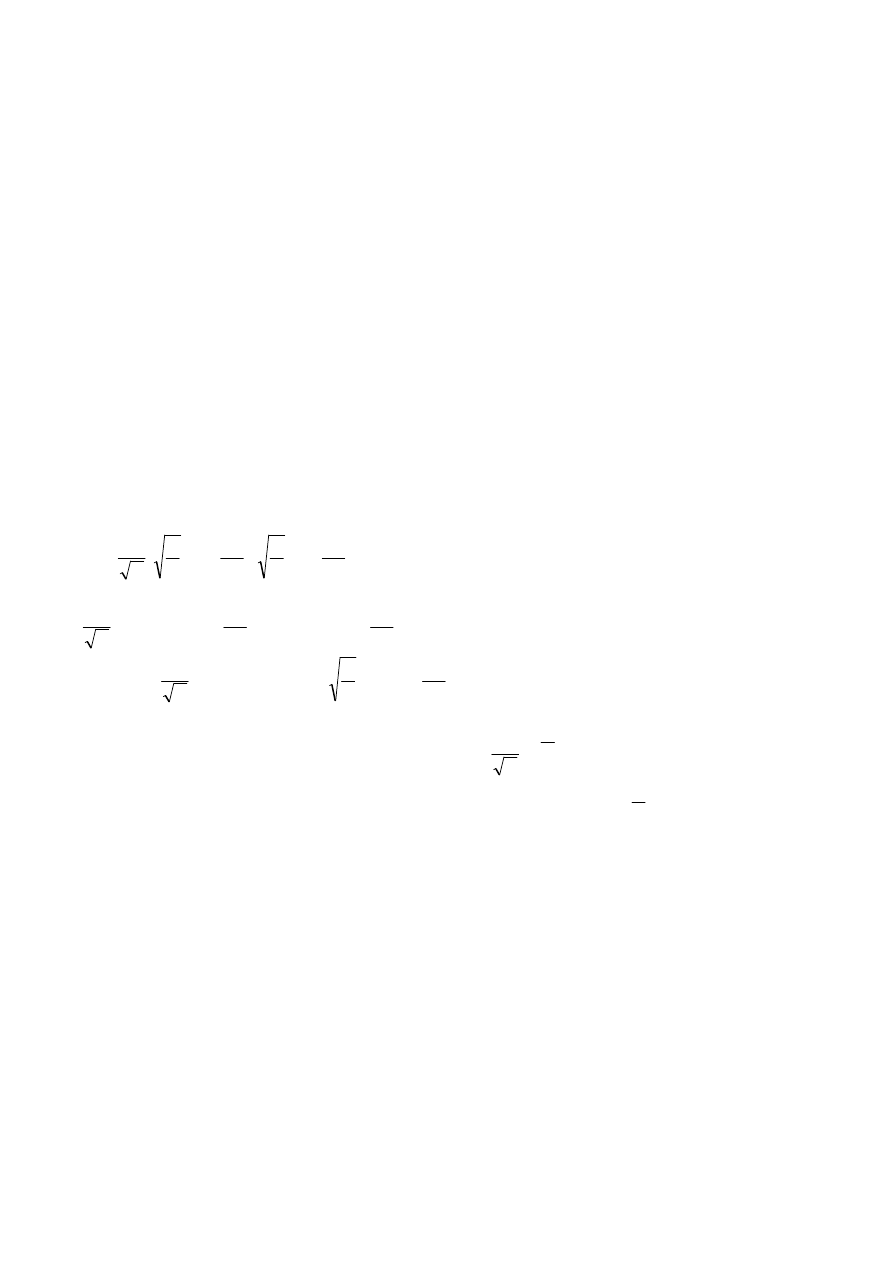
xεX-X^n należy znaleźć taki element

n

X

x

∈

~

dla którego norma elementu różnicowego

||

~

||

x

x

−

jest najmniejsza

(innymi słowy: dla którego zachodzi nierówność

||

~

~

||

||

~

||

x

x

x

x

−

<

−

dla każdego

n

X

x

∈

~

~

różnego od x

~ .

X^n=spon{x1...xn},

∑

=

=

=

n

i

n

ixi

x

x

1

~

α

,

∑

=

−

=

−

=

n

i

n

ixi

x

x

x

1

~

α

ε

WADY REPREZENTACJI S. Z P. X PRZEZ ELEMENT PP. X^n
1) wiele różnych S. może mieć tę sama reprezentację 2) nie wszystkie elementy przestrzeni X są dostatecznie dobrze
aproksymowane - błąd śr. kwadratowy ||ε|| wynikajacy z najlepszej aproksymacji moze być zaczny 4) reprezentacja
takiego wektora byłby wektor zerowy moc sygnału =0 a to bzdura

KOMBINACJA LINIOWA ELEMENTÓW PRZESTRZENI

Niech X bedzie P. liniową nad ciałem F i niech {xi; i=1...n}<X. Każdy element (wektor) o postaci

∑

=

=

n

i

ixi

x

1

α

gdzie

αiεF, i=1...n jest nazywany kombinacją liniową elementów xi.
ZBIÓR ELEMENTÓW LINIOWO NIEZALEśNYCH
Zbiór elementow {xi; i=1...n} P. liniowej X nad ciałem F nazywamy liniowo niezaleznym, a elementy tego zbioru

liniowo niezleżnymi, jeśli:

0

,

...

1

0

1

=

=

=>

=

∧

=

∑

i

n

i

ixi

n

i

α

α

gdzie  oznacza element zerowy przestrzeni X oraz αiεF,

i=1...n. Liniowa niezależność elementów xi oznacza ze żaden z tych elementow nie może być przedstawiony w postaci
kombinacji linowej pozostałych elementów.
DEF. S. OKRESOWEGO
S. nazywamy O. gdy jego wartości chwilowe powtarzaja sie w jednakowych odstepach czasu f(t)=f(t+nT), T≠0 gdzie T
jest okresem po którym występuja powtarzające sie elementy. Najmniejsy O. dodatni jeśli istnieje nazywamy O.
zasadniczym.
ORTOGONALNY, ZUPEŁNY TRYGONOMETRYCZNY SYGNAŁ SZEREGU FOURIERA W PRZESTRZ.
L²(0,T)

Zbiór funkcji

...}

2

,

1

:

2

sin

2

,

2

cos

2

,

1

{

=

n

t

T

n

T

t

T

n

T

T

π

π

jest zbiorem ortonormalnym zupełnym w przestrzeni

L²(0,T). Każdy sygnał x(t) należący do tej przestrzeni można zatem reprezentować szeregiem Fouriera

)

2

sin(

)

2

cos(

1

)

(

1

1

0

∑

∑

∞

=

∞

=

+

+

=

n

is

n

ic

t

T

i

t

T

i

T

t

x

π

α

π

α

α

dt

T

t

x

x

x

T

∫

=

=

0

0

0

1

)

(

)

,

(

α

dt

t

T

i

t

x

T

x

x

T

ic

ic

∫

=

=

0

)

2

cos(

)

(

2

)

,

(

π

α

ORTOGONALNY, ZUPEŁNY ZESPOLONY SYGNAŁ SZEREGU FOURIERA W PRZESTRZ. L²(0,T)

W przestrzeni L²(0,T) zbiorem ortonormalnym jest zbiór funkcji

}

2

,

1

,

0

:

1

{

2

±

±

=

n

e

T

t

T

jn

π

Zespolony szereg Fouriera

sygnału x(t) należącego do tej przestzeni ma wiec postac

∑

∞

−∞

=

=

n

t

jn

dt

Xne

t

x

0

)

(

ω

dt

e

t

x

T

x

T

t

jn

n

∫

−

=

0

0

)

(

1

ω

JAK WYZNACZA SIE WSPÓŁZYNNIKI FOURIERA DLACZEGO W PRZYPADKU BAZY ORTO
NORMALNEJ WYZNACZENIE ICH JEST ŁATWIEJSZE

Szereg Fouriera elementu X:

∑

=

=

n

i

ixi

x

1

α

tworzymy (•,xj), j=1...n.

∑

=

=

=

n

i

j

n

j

xj

xi

i

x

x

1

...

1

),

,

(

)

,

(

α

np dla j=1 (x,xj)=

α1(x1,x1)+ α2(x2,x1)+...+ αn(xn,x1) co z kolei prowadzi do układu równań który w postaci macieżowej można zapisać
jako Aα=a zatem α=A-¹a. W przypadku bazy ortonormalnej zarówno macierz A jak A-¹ sa jednakowe co elminuje
konieczność odwracania macierzy i znacznie upraszcza obliczenia.
CZY WIDMO SYGNAŁU FOURIERA JEST RZECZYWISTE CZY ZESPOLONE
Widmo sygnalu jest w ogólnym przypadku funkcja zespolona zmiennej f.
PODAĆ DEF FUNKCJI KOELACJI WZAJEMNEJ POMIEDZY DWOMA PROCESAMI
NIESTACJONARNYMI PODAC ZNACZENIE OZNACZEŃ
Rxy(τ)=(x,y)=calk(x(t)y(t+ τ)d τ)
CZY FUNKCJA KORELACJI WZAJEMNEJ DWUCH PROCESÓW JEST WIELKOŚCIA LOSOWĄ CZY
DETERMINISTYCZNĄ
Funkcja korelacji dwuch procesów jest wielkością deterministyczną
KIEDY FUNKCJA AUTOKORELACJI PROCESU JEST FUNKCJA TYLKO JEDNEGO CZASU
Wtedy gdy uklad jest słabo stacjonarny (stacjonarny w szerszym sensie). Wartość średnia mx procesów słabo
stacjonarnych jest stala afunkcja autokorelacji Rx zależy tylko od przesunięcia τ czyli mx(t1)=mx oraz Rx(t1,t1+
τ)=Rx(τ)

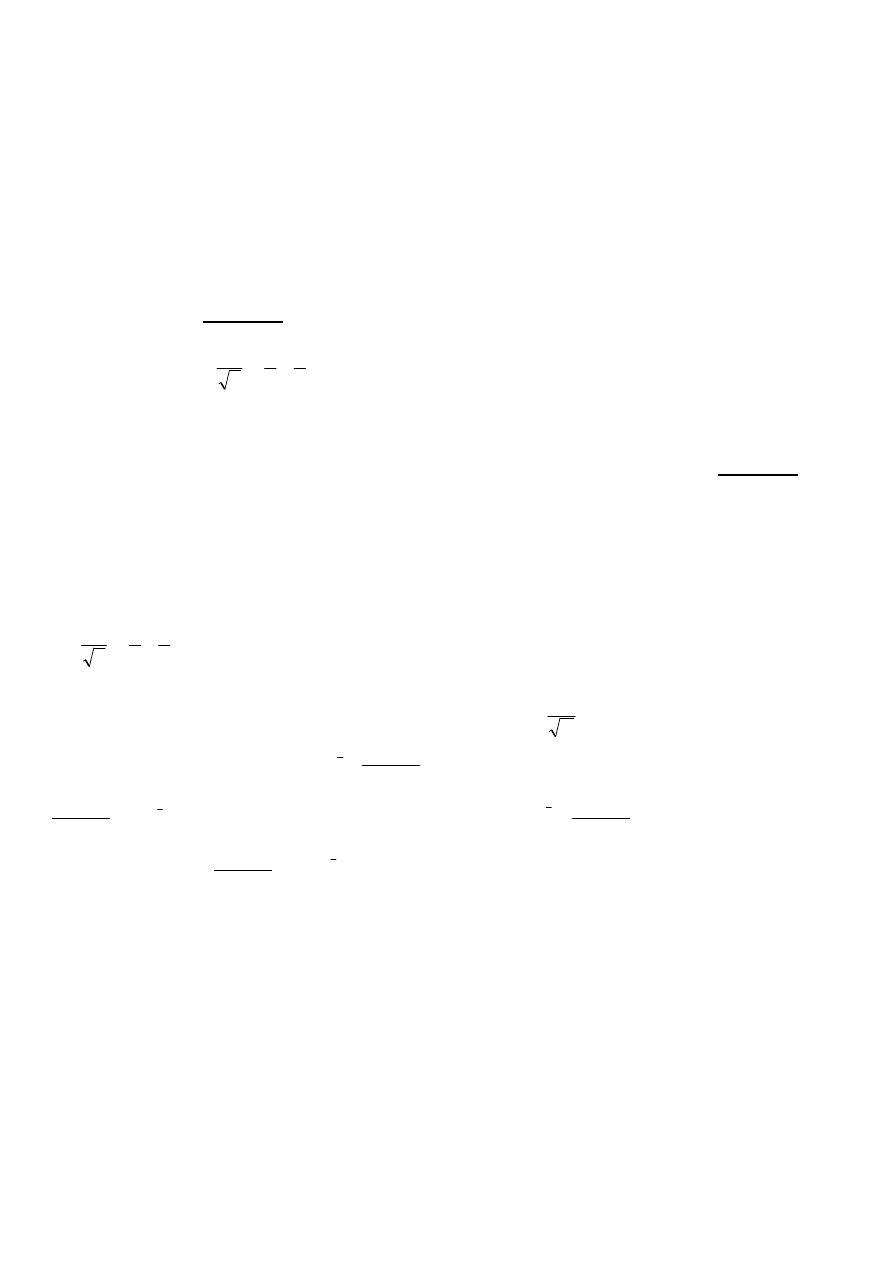
WŁASCIWOSCI FUNKCJI AUTOKORELACJI RZECZYWISTEGO PROCESU STACJONARNEGO. CZY
FUNK. AUTOKORELACJI JEST WIELKOSCIA DETERMINISTYCZNĄ CZY LOSOWA?
1) Jest funkcj. parzystą R(τ)=R(-τ) 2) ma makisimum w zerze |R(τ)|≤R(0), R(0)= τ² 3) funkcja autokorelacji procesu
jest wielkoscia deterministyczną



JAKIM WZOREM WYRAśA SIĘ TRANSFORMACJA FALKOWA, OMÓWIĆ
T.F jest funkcją dwóch zmiennych niezależnych i jest definiowana jako skalar. Wyraża się wzorem W(a,b)=(x,ψa,b) x-
analizowany sygnał. T.F. pozwala na przeniesienie sygnału z układu czas-wartość do układu czas-częstotliwość.
ZASADA NIEOZNACZONOŚCI
Z.N. w T.F. ma postać nastpującą: ponieważ każda falka odpowiada za pewien obszar płaszczyzny(okno czasowo-
częstotliwościowe), dobrze jest konstruować falki bardzo precyzyjnie okrelające czas i częstotliwość, o małym oknie
czasowo-częstotliwosciowym. W praktyce okazuje sie, iz okno to nie może być nieskończenie małe.z zasady
nieoznaczoności ∆t ∆f≥½

WYKRES Zjawisko to powoduje powstanie trójwymiarowych izolinii zamiast punktów.

TRANSFORMACJE CZASOWO-CZĘSTOTLIWOŚCIOWE W T.F.

Dla rodziny falek:

)

(

1

)

(

,

a

b

a

t

a

t

b

a

−

=

ψ

ψ

. a-wsp. skali, powoduje zmianę czasu trwania („rozciagniecie” lub

„sciaskanie”) falki, b-wsp. przesuniecia, zmienia położenie na osi czasu. t/a-przesunięcie w dziedzinie częstotliwości.
b/a-przesunięcie w dziedzinie czasu.
OKNO CZASOWO-CZĘSTOTLIWOSCIOWE W T.F.
Jest to pewien obszar czasu i częstotliwosci na plaszczyznie, za który odpowiada konkretna falka

WYKRES

T. CZASOWO-CZĘSTOTLIWOSCIOWYM PODDAJE SIE SYGNALY STACJONARNE CZY
NIESTACJONARNE
T.C-C. poddaje się sygnały niestacjonarne.
RÓśNICA MIĘDZY DYSKRETNĄ A CIĄGŁĄ T.F.
W(a,b)=(x,ψa,b) 1) dla ciagłej T.F. a,bεR; a≠0 2) dla dyskretnej T.F. a=2^(-m), b=n*a; m,nεZ.
POJECIE POŁOśENIA F. I ROZCIĄGLIWOŚCI F. W DZIEDZINI C. I C.
Położenie falki zależne jest od współczynnika przesunięcia b zaś rozciągliwość zależy od współ. Skali a, we wzorze

)

(

1

)

(

,

a

b

a

t

a

t

b

a

−

=

ψ

ψ

REALIZACJA PROCESU STOCHSTYCZNEGO

Dysponując falkową transformatą

Fouriera:

)}

(

{

)

(

ˆ

t

FT

f

ψ

ψ

=

)

(

)

(

ˆ

2

,

af

e

w

a

t

ft

j

b

a

ψ

ψ

π

−

=

możemy określić położenie i

rozciągłość falki: 1) Położenie na osi czasu:

dt

t

t

t

R

b

a

b

a

2

,

2

,

|

)

(

ˆ

|

||

ˆ

||

1

∫

=

ψ

ψ

2) Rozciągłość na osi czasu:

dt

t

t

t

R

b

a

b

a

t

2

,

2

2

,

2

|

)

(

ˆ

|

)

(

||

ˆ

||

1

∫

−

=

∆

ψ

ψ

1) 3)Położenie na osi częstotliwości:

df

f

f

f

R

b

a

b

a

2

,

2

,

|

)

(

ˆ

|

||

ˆ

||

1

∫

=

ψ

ψ

4) Rozciągłość

na osi częstotliwości:

df

f

f

f

R

b

a

b

a

f

2

,

2

2

,

2

|

)

(

ˆ

|

)

(

||

ˆ

||

1

∫

−

=

∆

ψ

ψ

REALIZACJA PROCESU STOCHASTYCZNEGO
P.S.->

)

(

|

)

,

(

t

x

t

x

const

=

=

ξ

ξ

<-realizacja P.S. Jeżeli ustalimy zadanie elementarne ξεS (przestrzeń propabilistyczna) to

mamy do czynienia z deterministyczną funkcją czasu, którą nazywamy R.P.S. Wszystkie realizacje razem wzięte
stanowią wartość procesu.
DEF. AUTOKOREL. SYG. DETERMINISTYCZNEGO

∫

+

=

τ

τ

τ

d

t

x

t

x

R

xx

)

(

)

(

)

(

PODOBIEŃSTWA I RÓśNICE MIĘDZY ZMIEN. LOSOWĄ A PROCES. STOCHAST.
Podstawowa różnica między Z.L. a P.S. jest taka ze P.S. jest funkcją dwóch zmiennych

)

,

(

ξ

t

x

, a Z.L. jest funkcja

jednej zmiennej

)

(

ξ

x

. Z.L. jest szczególnym przypadkiem P.S., gdy przyjmiemy t=const. P.S.->

)

(

|

)

,

(

ξ

ξ

x

t

x

const

t

=

=

<-

Z.L.
PROCES ERGODYCZNY
P. jest E. jeśli na podstawie jednej realizacji procesu z prawdopodobieństwem 1 mozna wyznaczyć wszystkie statystyki
tego P. Oznacza to że każda realizacja jest pełną reprezentacja P. Dla P-ów.E-cznych. Uśrednionych po zbiorze można
zastąpić uśrednieniem po czasie. P.E. jest P. stacjonarnym.
DEF. STATYSTYKI I-RZĘDU

S. I-rzędu 1)

dystrybuanta F(x,t)=Pr{x(t)≤x}, Pr-prawdopodobienstwo F(-∞,t)=0, F(t,∞,)=1, 2) gęstość prawdopoob.-

określa P. wystąpienia danego sygnału f(x,t)=(σF(x,t))/( σx)

3)wartość średnia ozn. η lub µ lub m(t), m(t)=E{x(t)} jest

to średnia ważona prawdopodobieństwa

x

d

t

x

xf

t

m

R

∫

=

)

,

(

)

(

DEF. STATYSTYKI II-RZĘDU

1) dystrybuanta F(x1,x2,t1,t2)=Pr(x(t1)≤x1, x(t2)≤x2) 2)gęst. prawdopod.

2

1

2

1

2

1

2

2

1

2

1

)

,

,

,

(

)

,

,

,

(

x

x

t

t

x

x

F

t

t

x

x

f

σ

σ

σ

=

3)funkcja autokowariancji C(t1,t2)= E{[x(t1)-m(t1)][x(t2)-m(t2)]} 4)wariancja σ^2= E{[x(t)-m(t)]^2} 5)widmowa

gęstość mocy-rozkład mocy w F. częstotliw. S(f1,f2)=FT{R(t1,t2)}=

2

1

)

2

2

1

1

(

2

2

^

2

1

)

,

(

dt

dt

e

t

t

R

t

f

t

f

j

R

+

−

∫

π

GĘSTOŚĆ PRAWDOPOD. PROCESU JEST WIELKOŚCIĄ ZDETERMINOWANĄ CZY LOSOWĄ?
WIDMO GĘSTOŚCI MOCY PROCESU LOSOW. JEST WIELK. ZDETERMINOW. CZY LOSOW.
DEF. DWUWYMIAROWEJ GĘST. PRAWDOPOD. PROCESU STOCHASTYCZ.

2

1

2

1

2

1

2

2

1

2

1

)

,

,

,

(

)

,

,

,

(

x

x

t

t

x

x

F

t

t

x

x

f

σ

σ

σ

=

DEF. DWUWYMIAROWEJ DYSTRYBUANTY PROCESU STOCHASTYCZ.
F(x1,x2,t1,t2)=Pr(x(t1)≤x1, x(t2)≤x2)
WŁASNOŚCI FUN. KORELACJI WZAJEMNEJ PROCESÓW LOSOWYCH RZECZYWIS.
Rxy(τ)=Ryx(-τ)
Rxy(τ)=0=> Ryx(τ)=0
Rxy(τ)=E{y(t)x(t+τ)}
JAKIE WARUNKI SPEŁNIA UKŁAD LINIOWY
Jeśli x1,2(t)-pobudzenia oraz a1,2-skalary oraz y(t)=L[x(t)], x(t)->L->y(t) to układ jest:

1)liniowy

y(t)=L{a1x1(t)+a2x2(t)}=a1L{x1(t)}+ a2L{x2(t)}

2)niezmienny w czasie x(t,τ1)= x(t,τ2)=> y(t,τ1)= y(t,τ2)

3)inercyjny

∫

∞

∞

−

−

=

)

(

)

(

)

(

α

α

h

t

x

t

y

AUTOKOWARIANCJA PROCESU CIĄGŁEGO(OGULNA I DLA P. STOCHASTYCZ.)
1) C(t1,t2)= E{[x(t1)-m(t1)] [x(t2)-m(t2)]} 2) C(t1,t2)=C(τ), t1=t, t2=t+τ, C(τ)= E{[x(t)-m(t)][x(t+τ)-m(t+τ)]}
DEF. WIELOWYMIAROW. DYSTRYBUANTY STOCHASTYCZNEGO (OZNACZENIA)
F(x1.....xn)=Pr(x(t1)≤x1......x(tn)≤xn)
W KATEGORIACH ZNANYCH SYGNAŁÓW ZDEFINIOWAĆ ZNANY CI WSPÓŁCZ. KORELACJI

||

||||

||

)

,

(

y

x

y

x

xy

=

α

inaczej

||

||||

||

)

,

)(

,

(

y

x

x

y

y

x

xy

=

α

przy czym 0≤|αxy|≤1, 0-są kompletnie niepodobne, 1-są takie same

DEF. KORELACJI WZAJEMNEJ MIĘDZY SYGNAŁAMI DETERMINISTYCZ.

Rxy(τ)=(x,y)=całka(x(t)y(t+τ)dτ),

∑

−

=

+

=

1

0

)

(

)

(

)

(

N

n

xy

k

n

y

n

x

n

R

Unormowana F. korelacji wzajemnej:

)

(

)

(

)

(

||

||||

||

)

(

)

(

τ

τ

τ

τ

yy

xx

xy

xy

xy

R

R

R

y

x

R

ro

=

=

POSTAĆ AUTOKOREL. PROCESU STACJONARNEGO
Ponieważ dla procesu stacjonarnego f(x1,x2,t,t+τ)=f(x1,x2,τ) oraz t1=t, t2=t+τ, to
R(t1,t2)=całkpoR(x1x2f(x1,x2,t1,t2)dx1dx2= całkpoR()x1x2f()x1,x2,τ)dx1dx2=R(τ)
ZALEśNOŚĆ MIĘDZY FUNKCJĄ AUTOKORELAC. PROCESU STACJONARNEGO A JEGO
WIDMOWĄ MOCĄ
S(f1,f2)=FT{e(t1,t2)}, Widmo gęstości mocy jest transformatą Fouriera F.A. sygnału o ograniczonej mocy średniej.
F.A. i widmo gęstości mocy stanowią parę transformat Fouriera w sensie granicznym.
WZAJEMNA WIDMOWA GĘSTOŚĆ MOCY

∫

∞

∞

−

−

=

=

τ

τ

τ

τ

d

e

R

R

FT

S

jw

xy

xy

xy

)

(

)}

(

{

DEF. WIDMOWEJ GĘSTOŚCI MOCY I JAKIE INFORMACJE O PROCESIE ZAWIERA
Widma gęstości mocy są wielkościami zdeterminowanymi. Widmowa gęstość mocy jest to rozkład mocy w funkcji

częstotliwości. S(f1,f2)=FT{e(t1,t2)}=

∫

+

−

2

^

2

1

)

2

2

1

1

(

2

)

2

,

1

(

R

t

f

t

f

j

dt

dt

e

t

t

R

π

Zawiera ona informacje o energii niesionej przez

poszczególne składowe.
CZY WIDMOWA GĘSTOŚĆ MOCY MOśE PRZYJMOWAĆ UUJEMNE WARTOŚCI
Nie, z def. S(f)≥0 - widmo gęstości mocy jest funkcją nieujemną. Sygnał zawsze niesie pewna energię (a zatem i moc)
wiekszą od zera.
CO POWODUJE śE WIDMOWA GĘSTOŚĆ MOCY JEST FUNKCJĄ RZECZYWISTĄ

Widmowa gęstość mocy jest F. czysto rzeczywistą, ponieważ lmS(f)=0. Z racji tego że F. autokorelacji sygnałów
rzeczywistych jest funkcją rzeczywistą, to i widmo gęstości mocy sygnałów rzeczywistych jest również funkcją
rzeczywistą.
ZALEśNOŚĆ MIĘDZY WIDMOWĄ GĘST. MOCY SYG. NE WE I WY UKŁADU LINIOWEGO.
Zakładając że Syy(f)-na wy, Sxx(f)-na we, i że H(f)- transmitancja częstotliwościowa
układu:Syy(f)=H(f)H(f)Sxx(f)=|H(f)|^2Sxx(f)
WŁAŚCIWOŚCI WIDM. GĘST. MOCY RZECZYWISTEGO PROC. STACJONAR.
1) czysto rzeczywista lmS(f)=0 2)jest parzysta S(f)=S(-f) 3)funkcja nieujemna S(f)≥0
DEF. WART.ŚREDNIEJ PROCESU I CZY JEST ONA F. CZASU
W.Ś. (oczekiwaną) m(t) nazyw. Nielosową F. czasu, której wartość w punkcie ti jest równa wartości oczekiwanej mi(t)
zmiennej losowej dla kazdej chwili czasu ti; gdy proces jest stacjonarny, to wartość średnia nie zależy od czasu
m(t)=E{x(t)}=całkpoR(xf(x,t)dx)
DEF. WARIANCJI I CZY JEST F. CZASU
Gdy P. jest stacjonarny to w takim wypadku wariancja procesu nie zależy od czasu.(σ^2=E{x^2(t)}). Def. wariancji
σ^2(t)=E{[x(t)-m(t)]^2}.
PROCES LOSOWY
P.L. (stochastyczny) to model sygnału L. jest on F. dwóch zmiennych - czasu i wyniku losowania. x(t,ξ)<-P.L.
PRZEKRÓJ P. STOCHAST. PO CZASIE
P.P.S.P.C. jest jednowymiarową zmienną losową.
DLA JAKIEGO PROCESU WARTOŚĆ ŚREDN. NIE JEST F. CZASU
Dla P. stacjonarnego
KIEDY WARIANCJA NIE ZALEśY OD CZASU
Dla P. stacjonarnego
WARIANCJA PROCESU WART. LOSOWA CZY DETERMINISTYCZNĄ
W.P. est wart. deterministy.
KIEDY P. JEST ŚCIŚLE STACJONAR. SŁABO, N-TEGO RZĘDU
P. jest Ś.S jeżeli przesunięcie punktu zerowego (obserwacji) nie oddziałuje na jego rozkłady prawdopodob. dowolnego
rzędu; dystrybuan. i gęstość nie zależą od czau.
P. jest S.S gdy wartość oczekiwana (średia) m(t)=m czyli nie zależy od czasu, oraz gdy F. autokorelacji jest F. jednej
zmiennej, czyli R(t1,t2)=R(t,t+τ)=R(τ)
P.S.n tego rzedu dla każdego ciagu t1...tn i kazdego przesunięcia τ wartości F. gęstości prawdopodobieństwa sygnłu i
sygnału przesuniętego względem niego o τ są sobie równe czyli: f1...n(x1...n,t1...tn)=f1...n(x1...n,t1-τ...tn-τ)
SZUM BIAŁY
S.B. jest przykładem S. losowego, który jest bardzo szybko zmienny. Jego F. autokorelacji jest delta Diraca (czyli nie
istniej powiaznie miedzy sąsiednimi w czasie próbkami), a jego widmowa gęstość mocy jest stała w funkcji
częstotliwo. Sygnał ten jest idealnie szerokopasmowy i nie daje sie on wytworzyć w układach fizycznych.
GAUSOWSKI SZUM BIALY
G.S.B. - GWN jest to szum bialy ktorego rozkład prawdopodobieństwa ma kształt krzywej gaussa, ma on równa
energie w całym paśmie częstotliwości.