P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

1 |

S t r o n a

METODA

PRZEMIESZCZEŃ

P

RZYKŁAD

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

2 |

S t r o n a

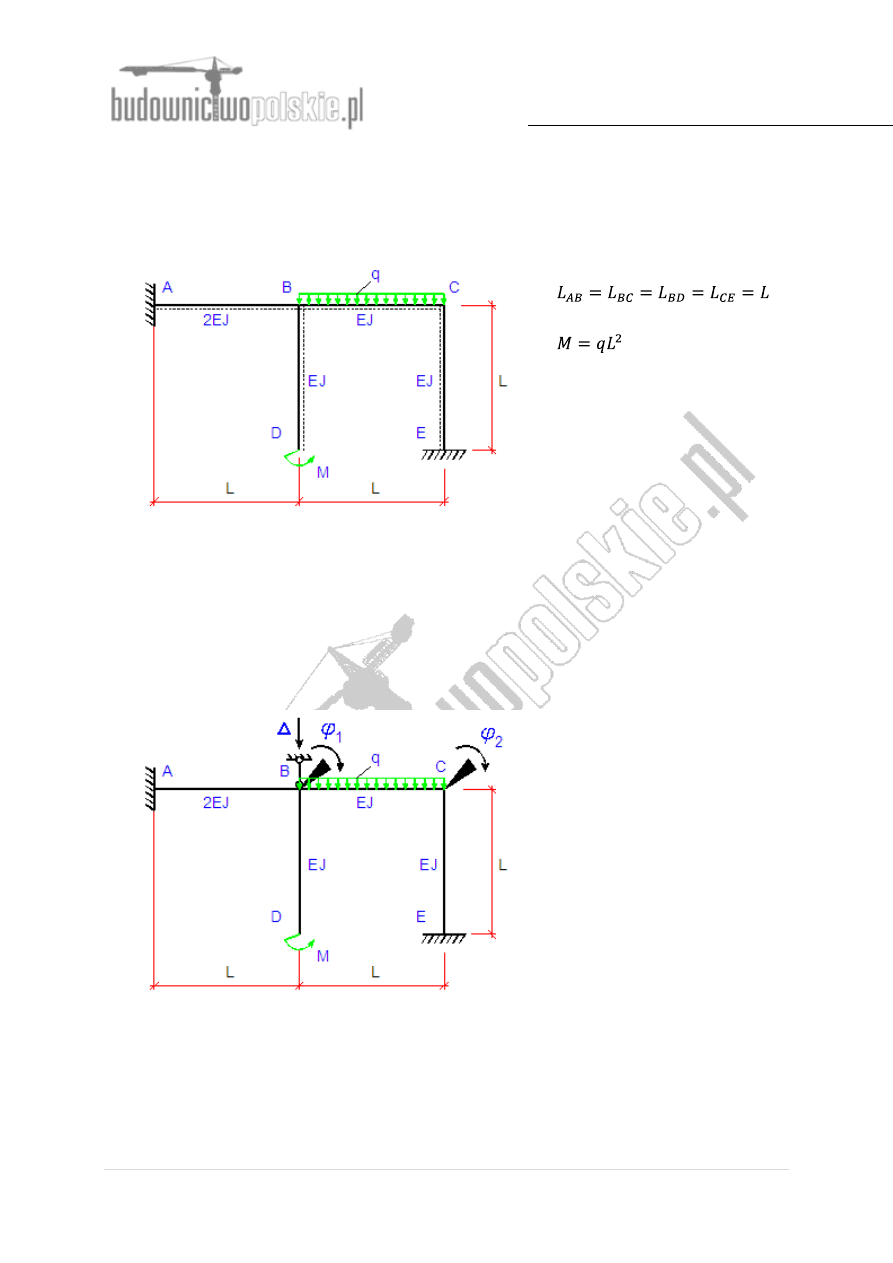
Rozwiązać ramę przy pomocy metody przemieszczeń

Rys.1 Schemat ramy

Rama przedstawiona na rys.1 jest układem trzykrotnie kinematycznie (geometrycznie)
niewyznaczalnym. Linią przerywaną zaznaczono „spody” prętów.

Przyjmujemy układ podstawowy (wprowadzamy fikcyjne więzy w węzłach doznających
przemieszczeń – blokujemy dwa obroty i jeden przesuw – rys.2):

Rys.2 Układ podstawowy

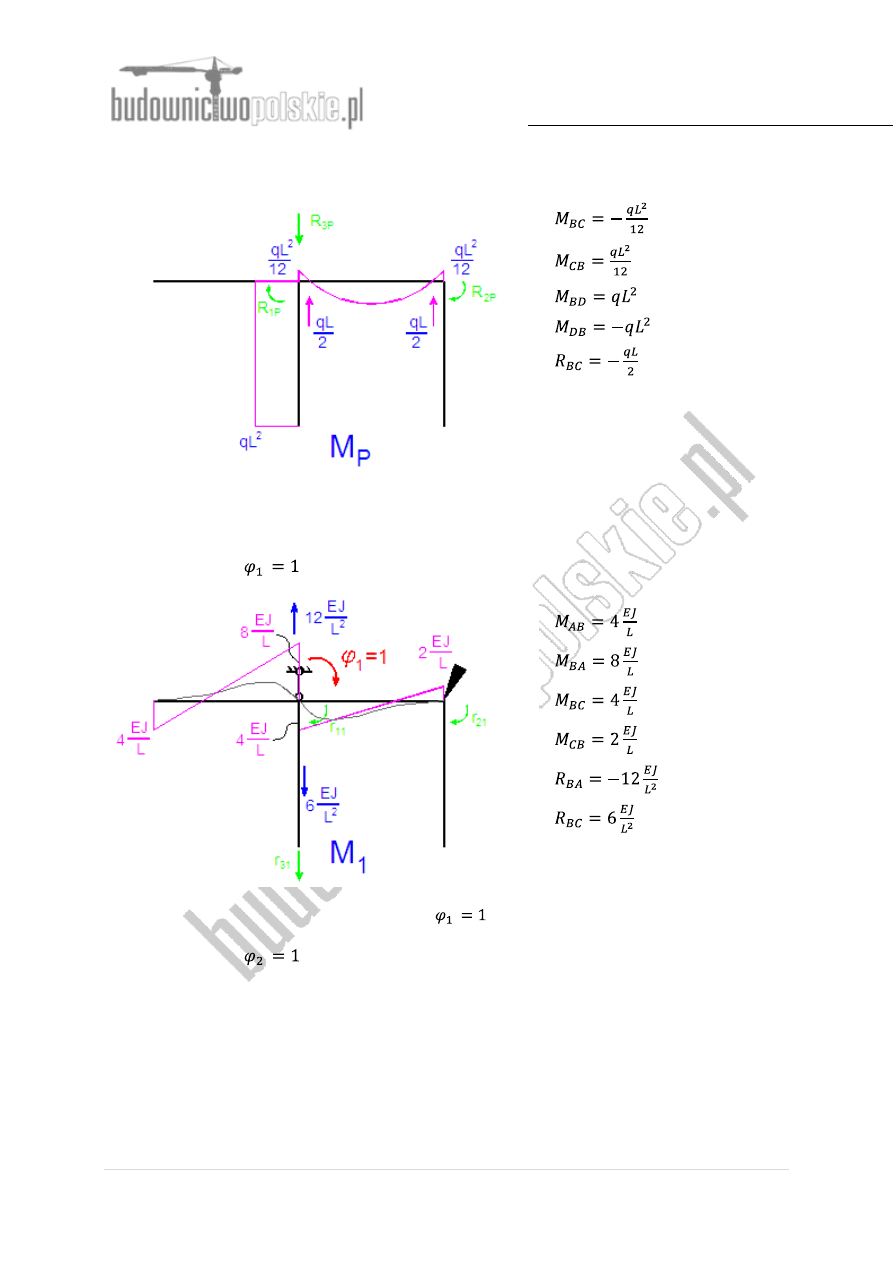
Stan od obciążenia zewnętrznego (wykres otrzymano na podstawie tabeli wartości momentów
brzegowych):

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

3 |

S t r o n a

Rys.3 Wykres momentów gnących dla układu podstawowego

Stan jednostkowy

(wymuszamy jednostkowe przemieszczenie kątowe węzła B):

Rys.4 Wykres momentów - stan jednostkowy

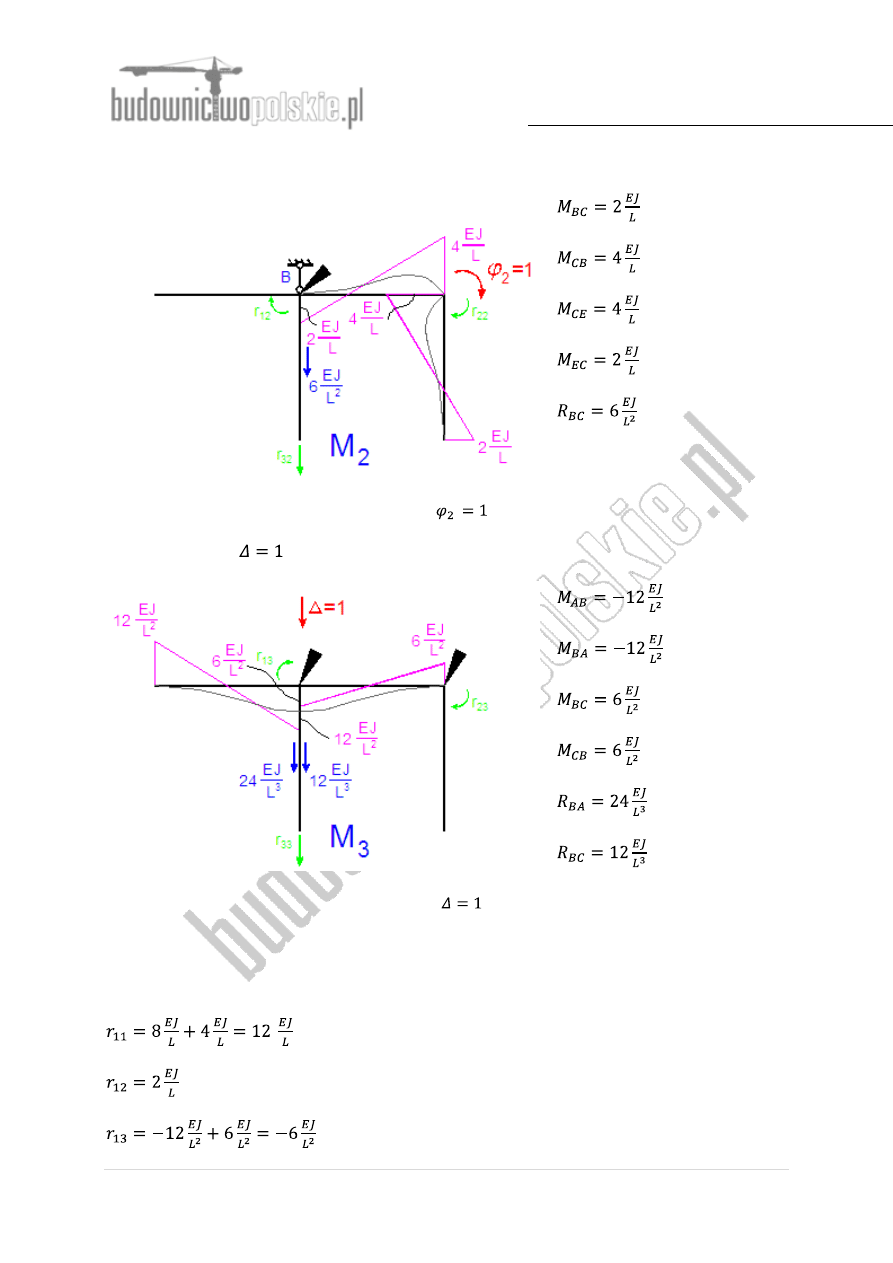
Stan jednostkowy

(wymuszamy jednostkowe przemieszczenie kątowe węzła C):

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

4 |

S t r o n a

Rys.5 Wykres momentów - stan jednostkowy

Stan jednostkowy

(wymuszamy jednostkowe przemieszczenie pionowe węzła B):

Rys.6 Wykres momentów - stan jednostkowy

Współczynniki (reakcje więzów fikcyjnych – na rysunkach oznaczone kolorem zielonym)
obliczamy sumując odpowiednie wartości momentów brzegowych i reakcji na kierunku
przemieszczeń (pierwszy indeks oznacza miejsce, drugi przyczynę):

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

5 |

S t r o n a

Układ równań kanonicznych metody przemieszczeń:

Rozwiązanie układu równań kanonicznych metody przemieszczeń:

Rzeczywiste siły przekrojowe:

- momenty węzłowe określimy korzystając z zasady superpozycji na podstawie wzoru:

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

6 |

S t r o n a

Wykres momentów gnących:

Rys.7 Wykres momentów gnących

Ekstremum:

- siły tnące (poprzeczne) obliczymy obciążając dodatkowo jednoprzęsłowe belki określonymi
wcześniej momentami:

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

7 |

S t r o n a

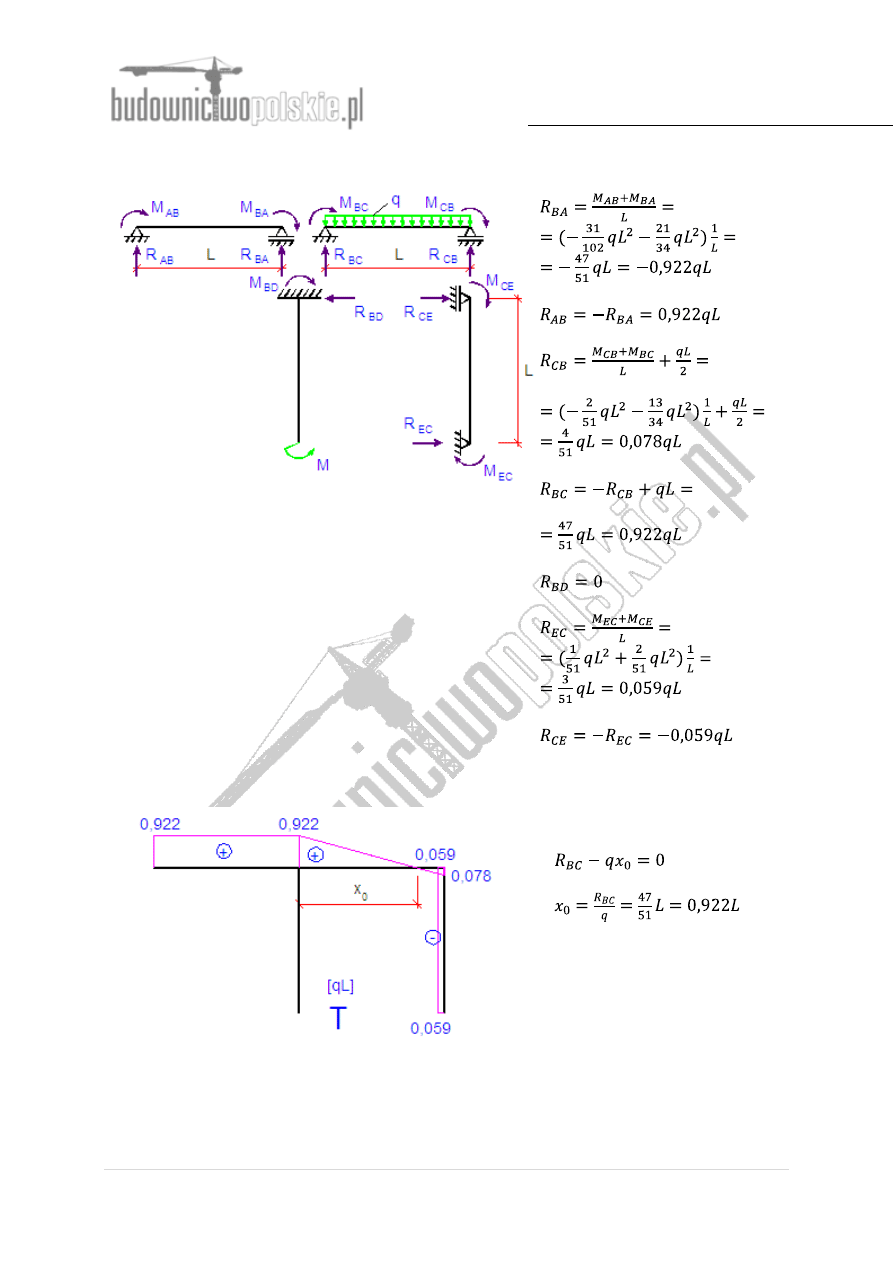
Rys.8 Rozkład momentów i reakcji dla belek jednoprzęsłowych

Wykres sił tnących:

Rys.9 Wykres sił tnących

Miejsce zerowe:

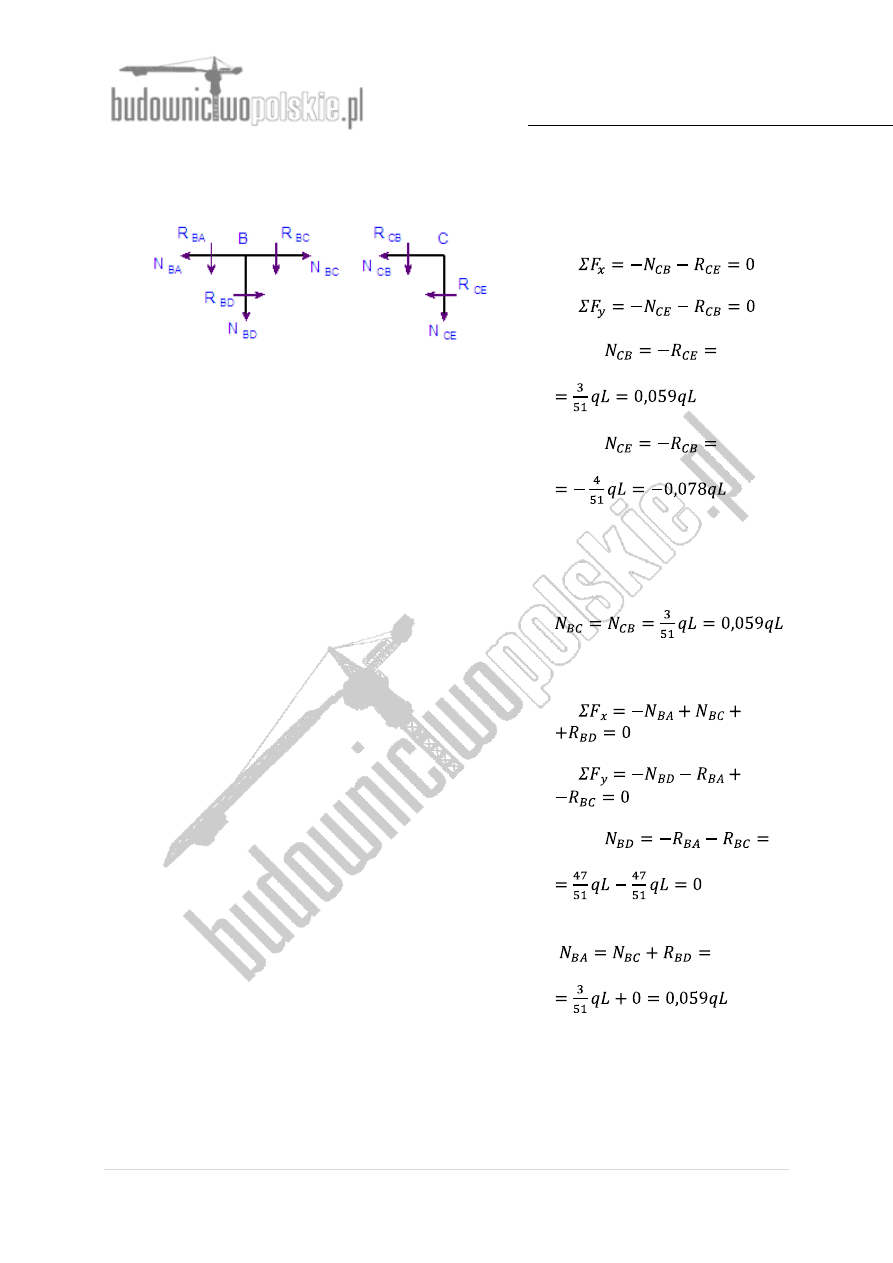
- siły normalne (podłużne) obliczymy wycinając węzły B i C obciążając je odpowiednio
siłami poprzecznymi:

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

8 |

S t r o n a

Rys.10 Rozkład sił tnących i normalnych w węzłach B i C

Węzeł C:

1)

2)

z 1)

z 2)

Na pręcie BC nie ma
obciążenia wzdłuż osi pręta
zatem:

Węzeł B:

3)

4)

z 4)

z 3)

P O M O C E N A U K O W E I D Y D A K T Y C Z N E

P

O R T A L U

B

U D O W N I C T W O P O L S K I E

.

P L

9 |

S t r o n a

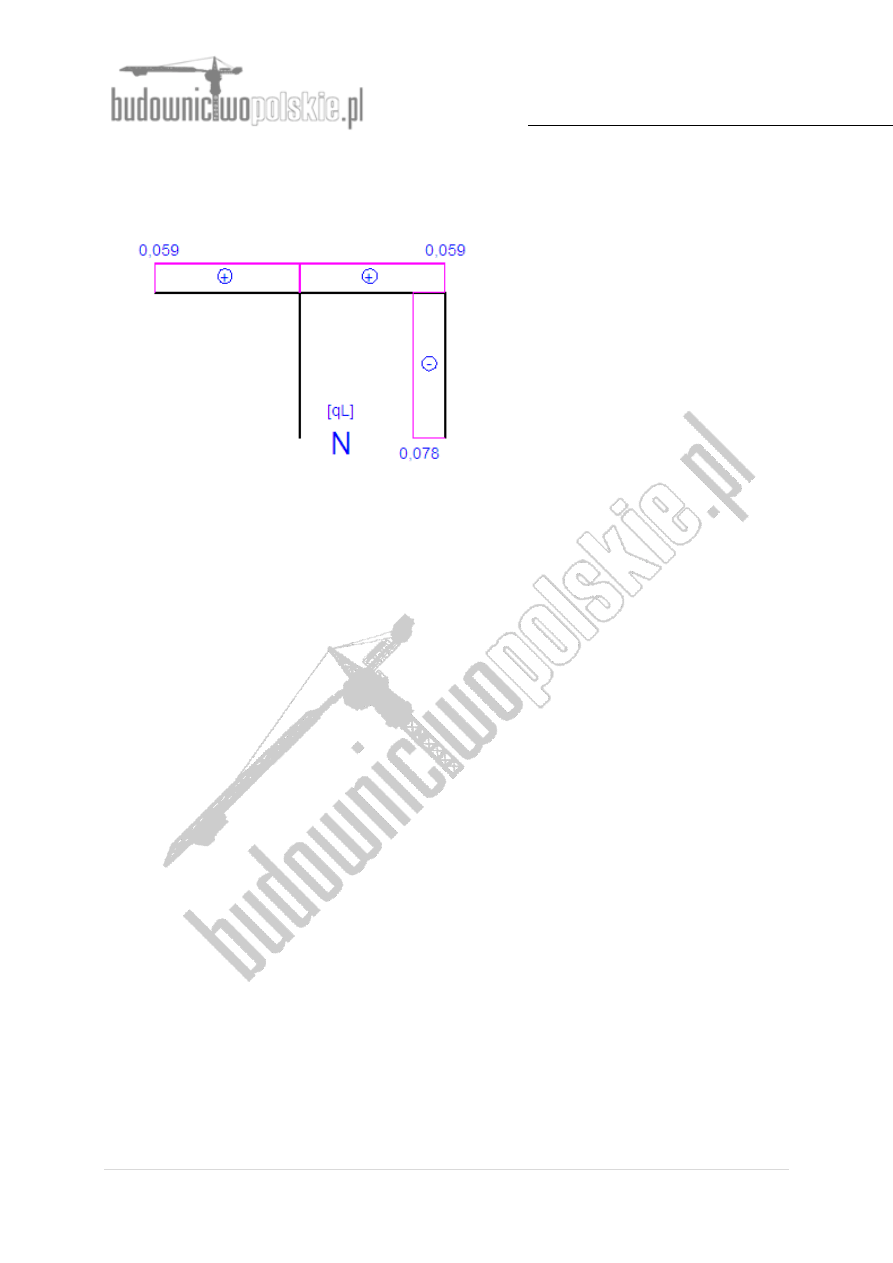
Wykres sił normalnych:

Rys.11 Wykres sił normalnych