Projekt Rama Metoda przemieszczeń Metor

www.gruparectan.com

Strona :1

UWAGA!!!: Projekt ma charakter edukacyjny, służy jedynie, jako wzorzec.

1. Metor

Dla danego uk

ładu wyznaczyć MTN metodą przemieszczeń

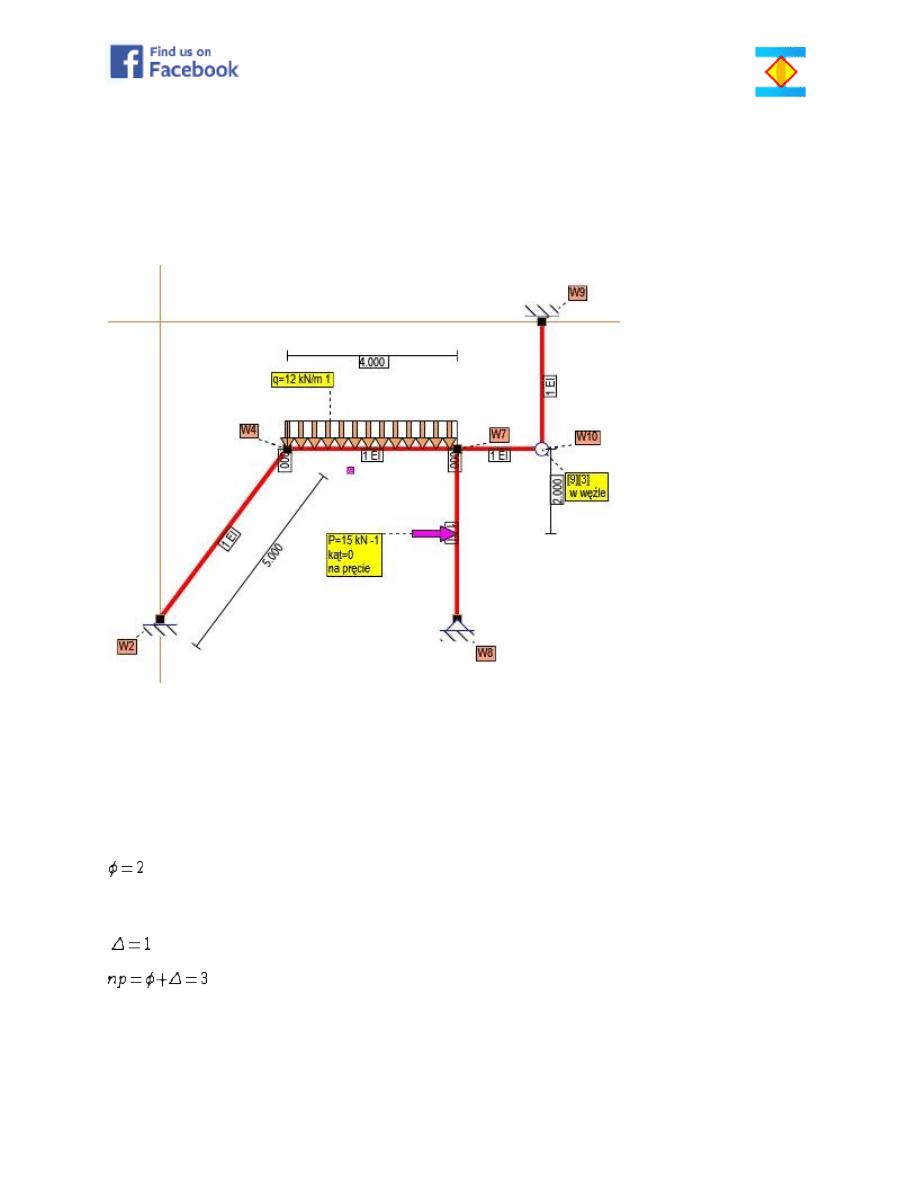
Rys. Schemat konstrukcji

.................................................................................................................................................................

2. Ustalenie stopnia kinematycznej niewyznaczalno

ści układu

ęzły o nieznanych obrotach :

Przemieszczenia nieznane :

ład jest : 3 krotnie kinematycznie niewyznaczalny

ϕ = węzły - podporowe - przeguby

/rectanbudownictwo

Strona :2

3. Przyj

ęcie układu podstawowego

Wsp

ółrzędne węzłów do obliczenia zależności kątowych łańcucha kinematycznego

ęzeł 2 x=[0.000]m , y=[7.000]m

ęzeł 4 x=[3.000]m , y=[3.000]m

ęzeł 7 x=[7.000]m , y=[3.000]m

ęzeł 8 x=[7.000]m , y=[7.000]m

ęzeł 9 x=[9.000]m , y=[0.000]m

ęzeł 10 x=[9.000]m , y=[3.000]m

.................................................................................................................................................................

ład równań kanonicznych

.................................................................................................................................................................

z uwagi na uog

ólnienie wzoru współczynniki wyrazów wolnych nazywać będziemy w dalszej części jako 'b'

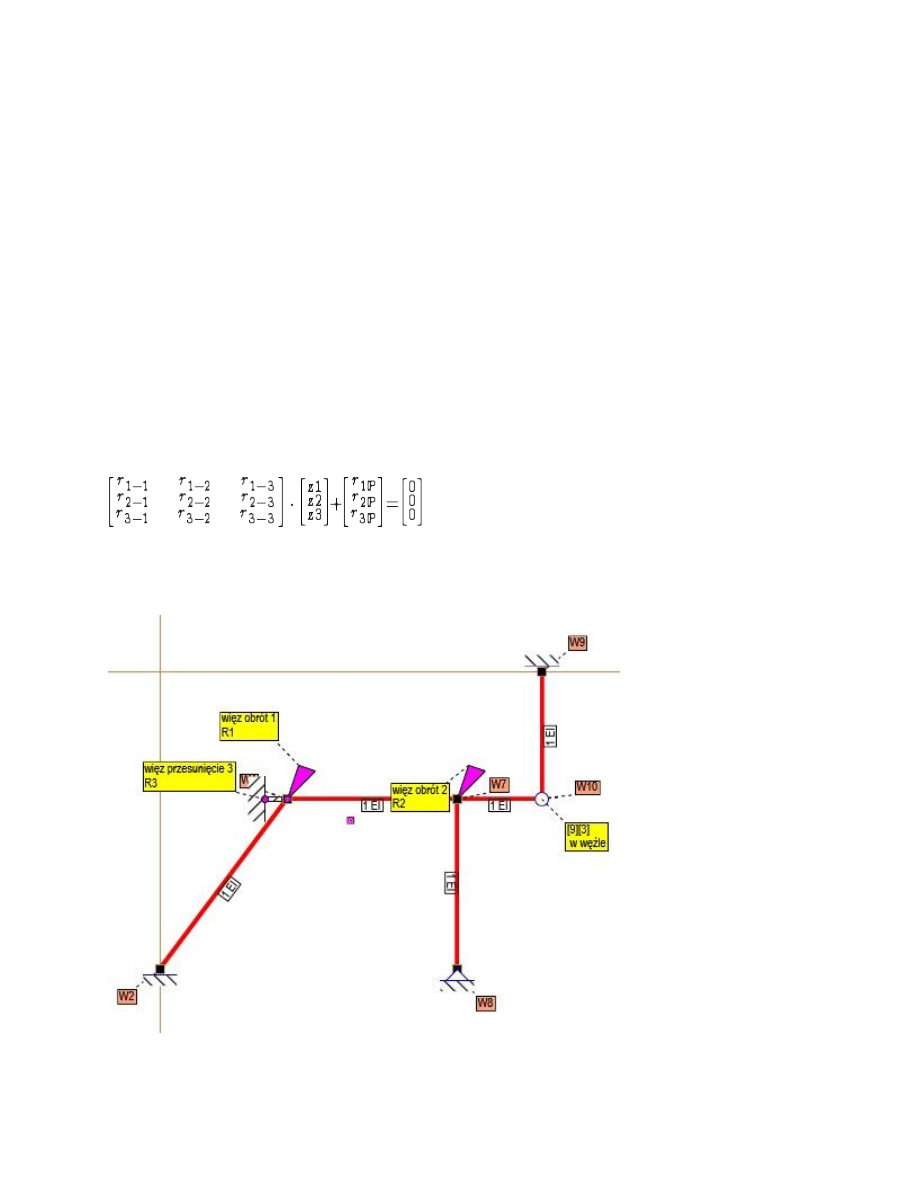
Rys. Układ podstawowy metody przemieszczeń

Strona :3

.................................................................................................................................................................

4. Obliczenie zale

żności kątowych obrotu cięciw prętów układu potrzebnych

do wyznaczenia macierzy sztywno

ści

Wystarczaj

ące do obliczeń łańcuchy kinematyczne

łańcuch : 2-4 : 4-7 : 7-8 :

łańcuch : 2-4 : 4-7 : 7-10 : 10-9 :

łańcuch : 8-7 : 7-10 : 10-9 :

łańcuch : 8-7 : 7-4 : 4-2 :

łańcuch : 9-10 : 10-7 : 7-8 :

Wybieram w

ęzeł przesuwany 4

Z węzłem tym powiązany jest pręt 7-8

Przyjmuję przesuw cięciwy pręta o Δ =1 jednostek

jest to wektor prostopadły do cięciwy pręta. Jego rzut na oś X ( lub oś Y w zależności od kierunku
przesunięcia) będzie miał wartość jednostkową. Wartość można obliczyć dzieląc wartość jednostkową
przez sin kąta pręta

węzeł powiązany z tym prętem przesunie się wtedy o wartość jednostkową

ąt obrotu cięciwy pręta wyniesie Ψ =0.25 jednostek

ęzeł przemieści się wtedy o dx= 1.000 dy= 0.000

Przyj

ęte przemieszczenie i kąt podstawiam do łańcuchów kinematycznych, jako wiadome

Obliczenia zaczynam od

łańcucha o najmniejszej liczbie niewiadomych - 9-10 : 10-7 : 7-8 :

.................................................................................................................................................................

Łańcuch obliczany : 9-10 : 10-7 : 7-8 :

Strona :4

Po obliczeniu r

ównania

.................................................................................................................................................................

Łańcuch obliczany : 8-7 : 7-4 : 4-2 :

Po obliczeniu r

ównania

Strona :5

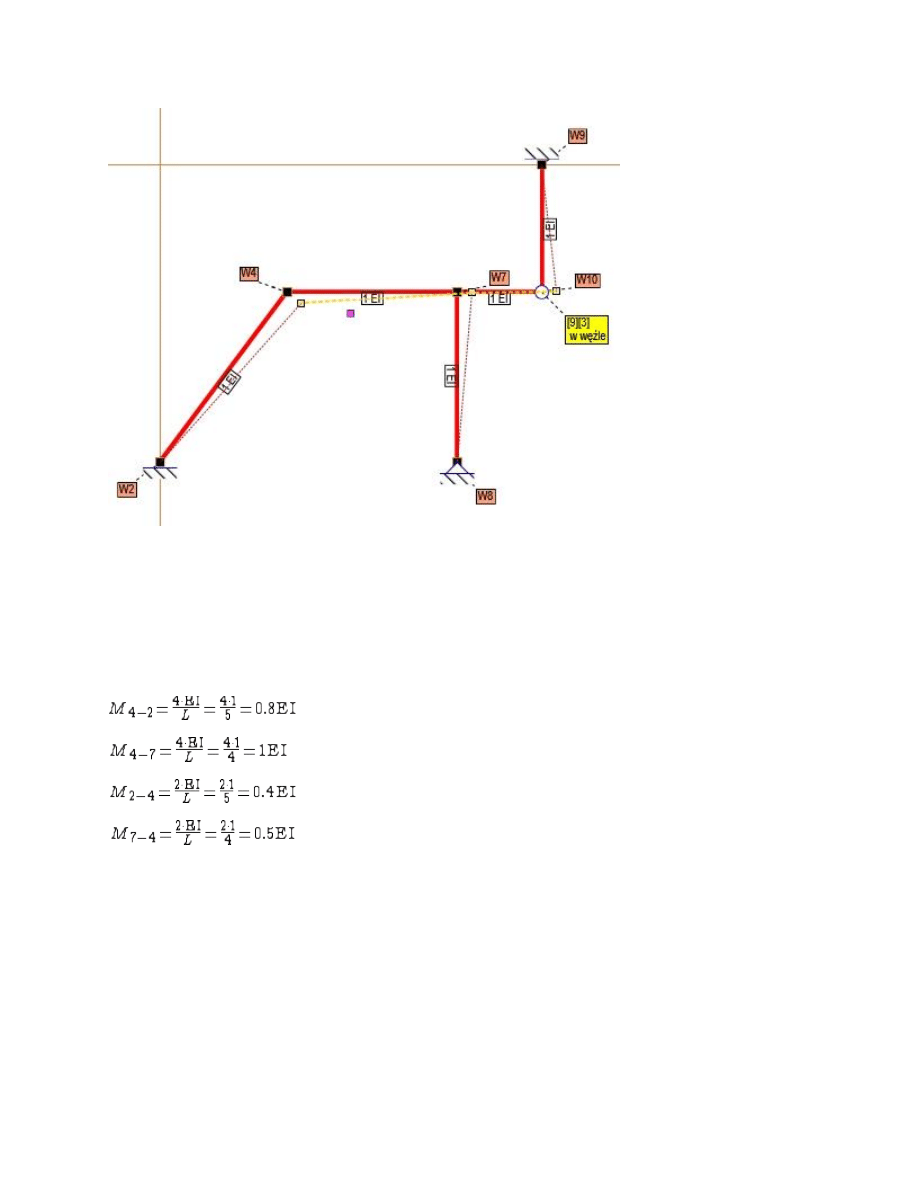
Rys. Łańcuch kinematyczny I

.................................................................................................................................................................

5. Stan z1

Strona :6

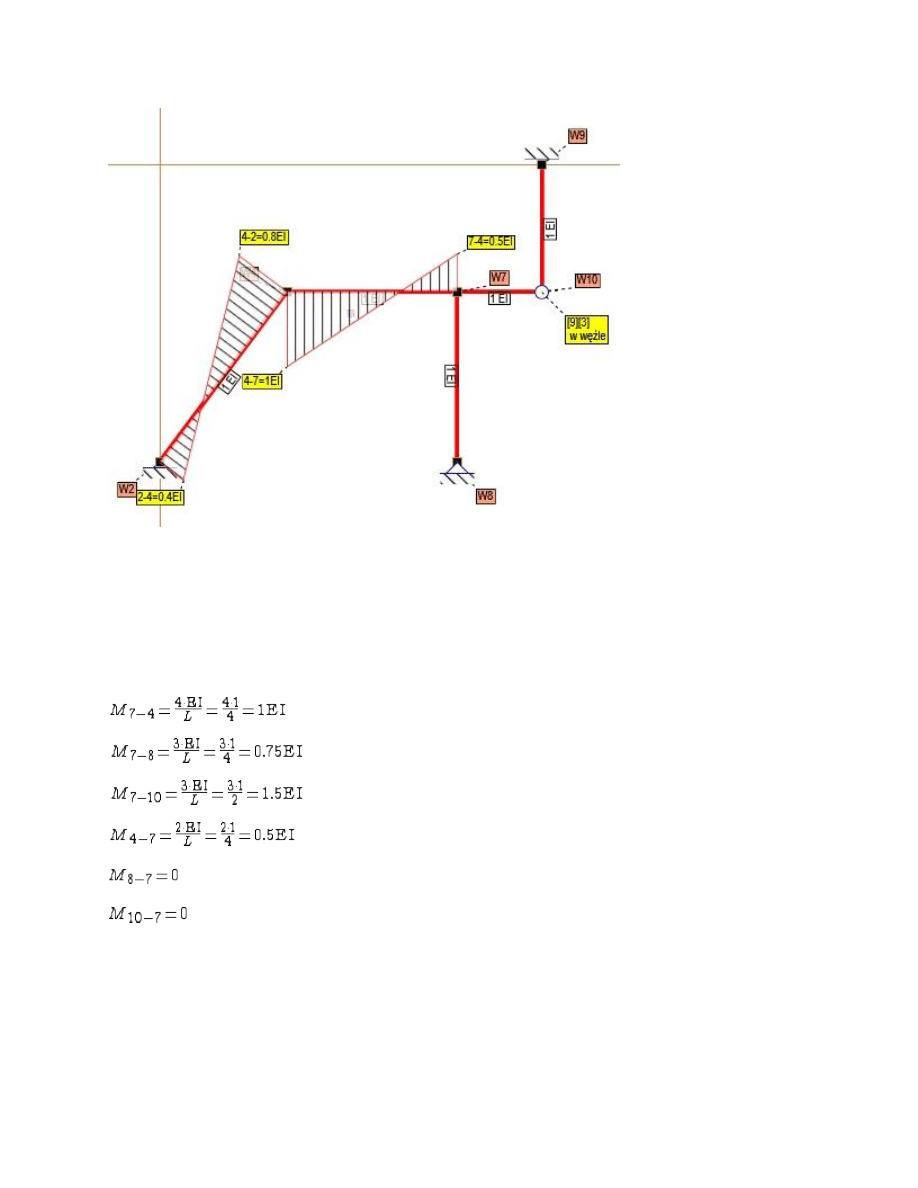
Rys. Stan z1

.................................................................................................................................................................

6. Stan z2

Strona :7

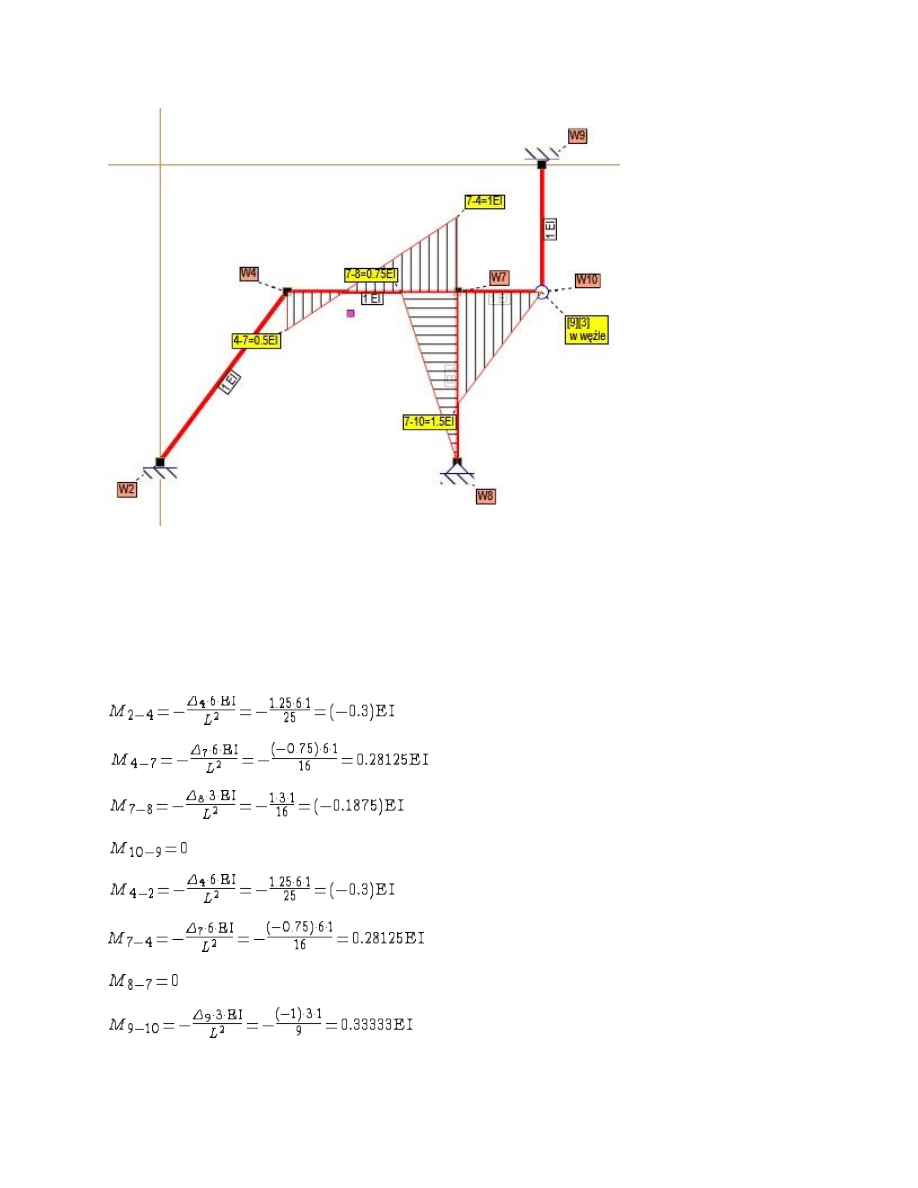
Rys. Stan z2

.................................................................................................................................................................

7. Stan z3

Strona :8

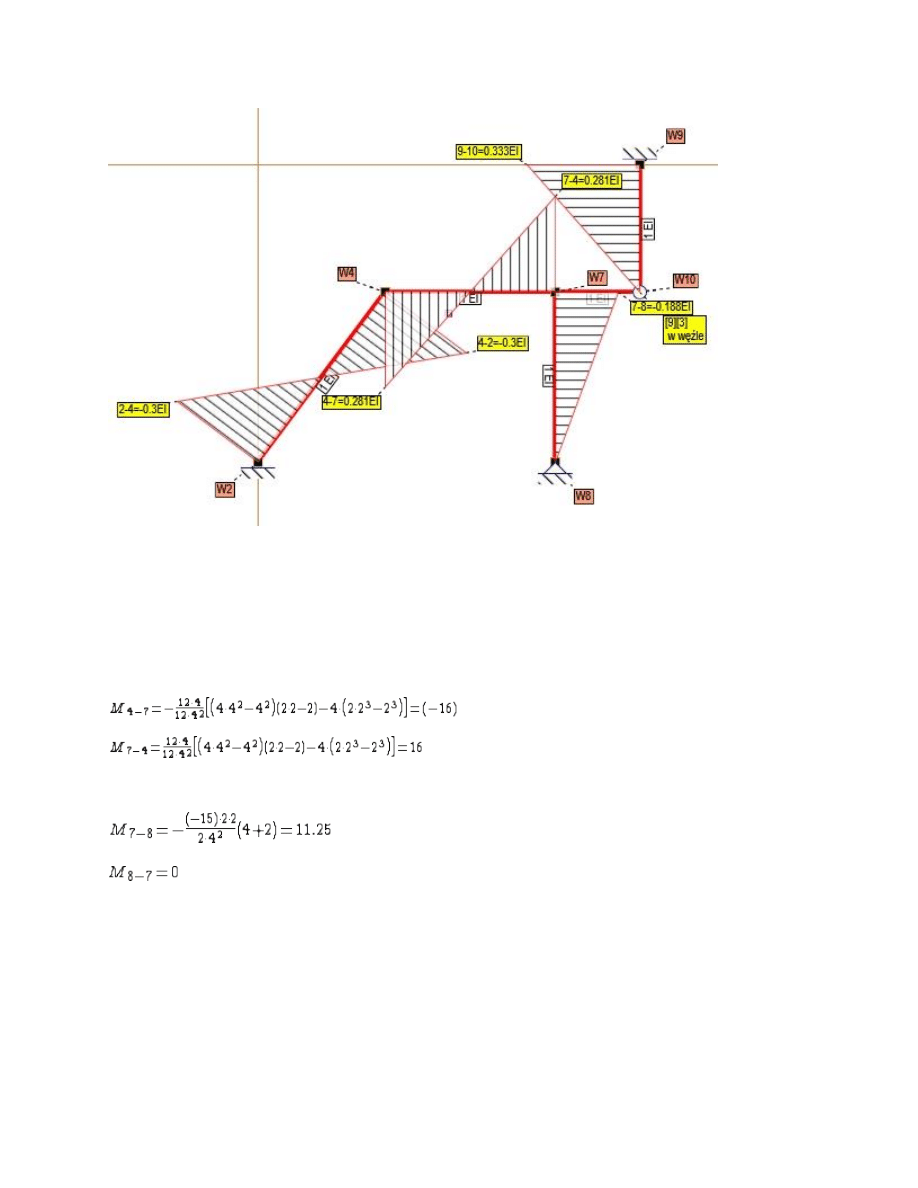
Rys. Stan z3

.................................................................................................................................................................

8. Stan P

q pr

ęt =4-7

P pr

ęt =7-8

Strona :9

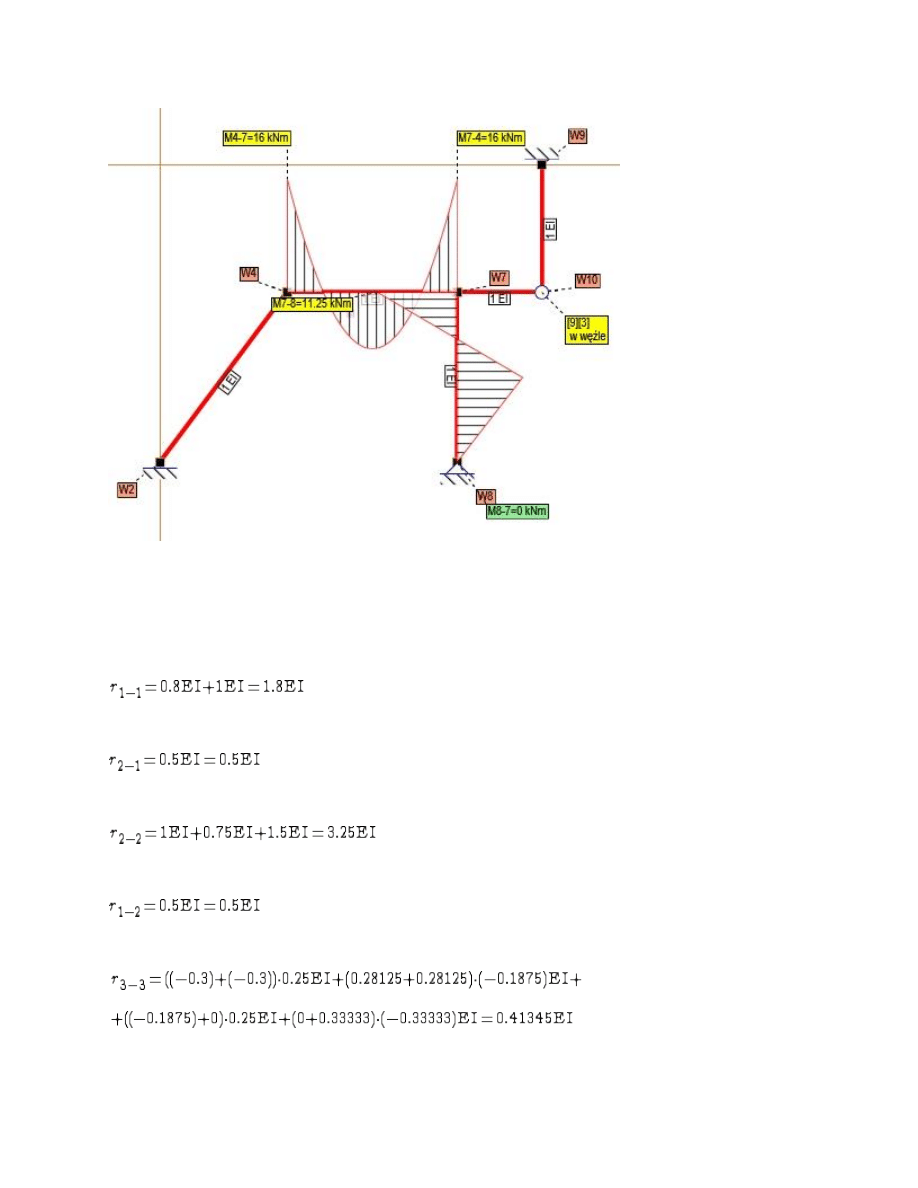
Rys. Stan P

.................................................................................................................................................................

9. Wsp

ółczynniki Macierzy Sztywności i Wyrazów Wolnych

.......................................................................................................................................... .......................

.................................................................................................................................................................

.............................................................................................................................................................. ...

.................................................................................................................................................................

Strona :10

.................................................................................................................................................................

Suma współczynników od przesunięcia jest pokazana ze znakiem przeciwnym. Tak podstawiane są do
macierzy. Składniki sumowania pokazane są ze znakami takimi jak na wykresach.

.................................................................................................................................................................

ład równań kanonicznych

.................................................................................................................................................................

Po rozwi

ązaniu układu otrzymano :

10. Obliczenie Moment

ów przywęzłowych

zgodnie ze wzorem :

Strona :11

.................................................................................................................................................................

Strona :12

................................................................................................................................................. ................

.................................................................................................................................................................

Strona :13

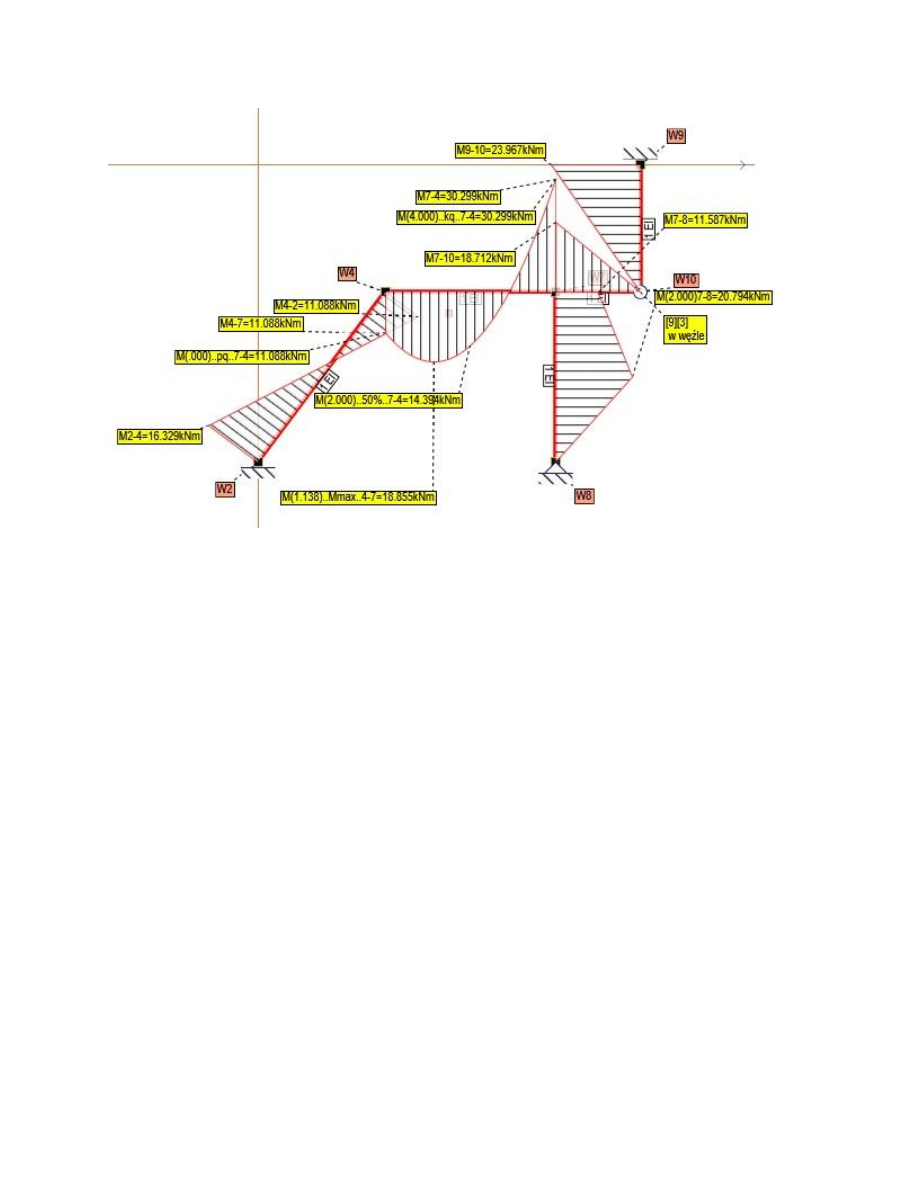
Rys. Wykres M

.................................................................................................................................................................

11. Obliczenie Si

ł Tnących

.................................................................................................................................................................

Strona :14

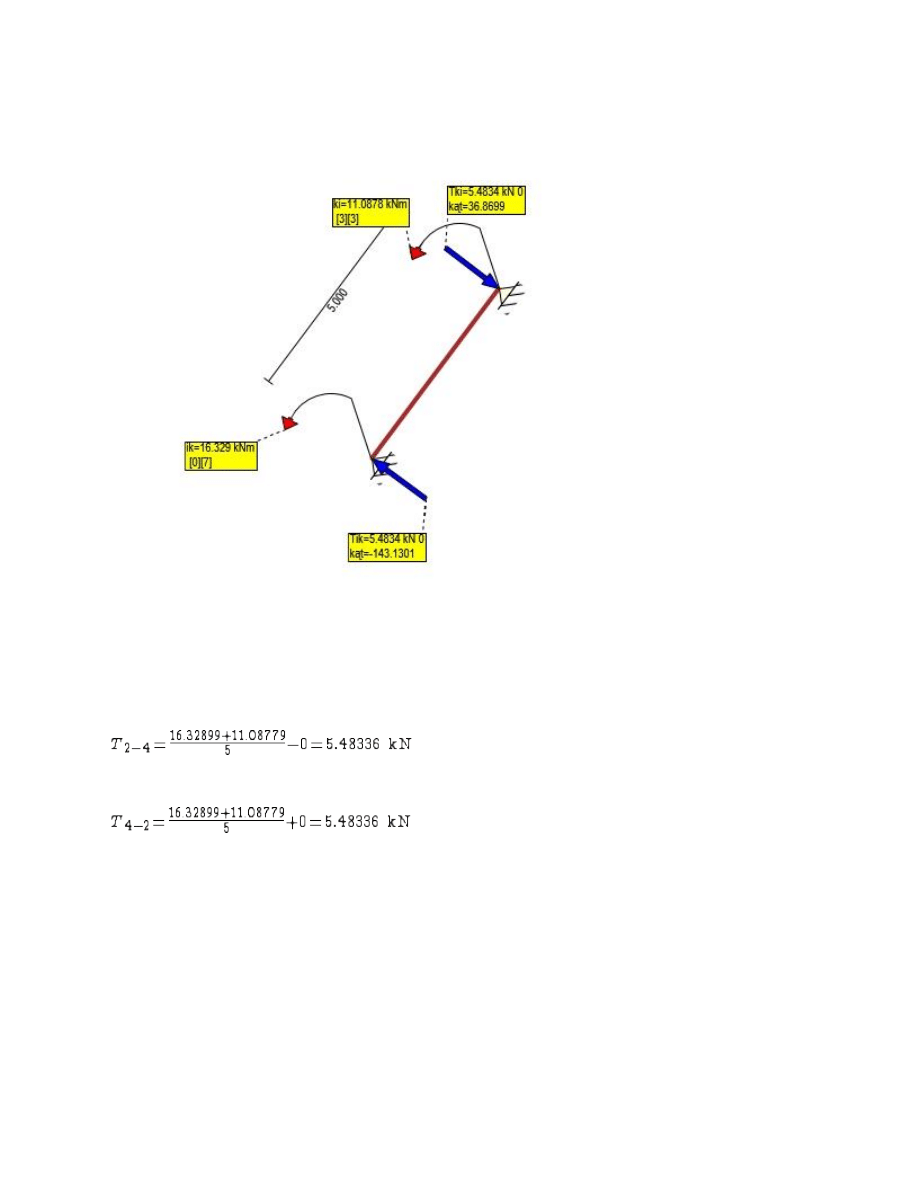
Rys. Siły Tnące 2-4

.................................................................................................................................................................

Strona :15

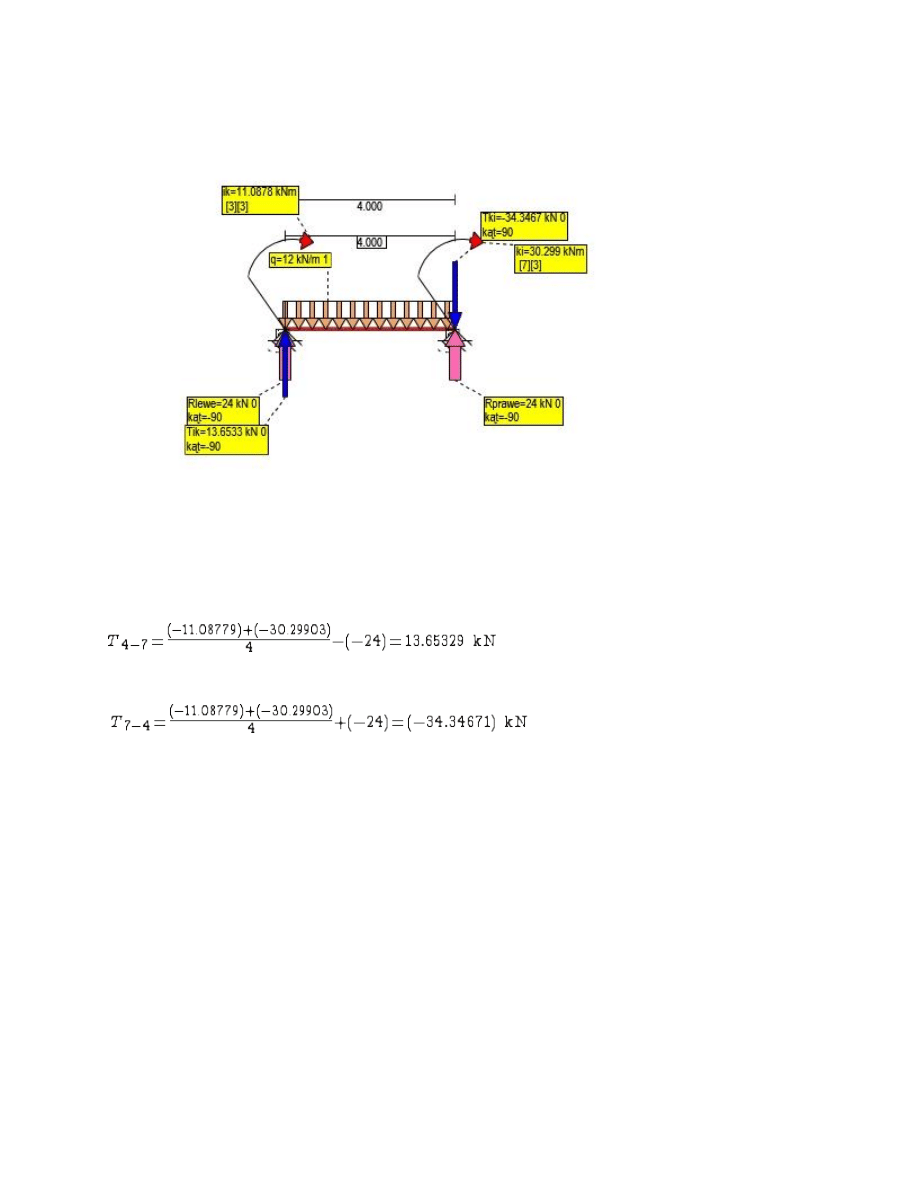
Rys. Siły Tnące 4-7

.................................................................................................................................................................

............................................................................................................................... ..................................

.................................................................................................................................................................

Strona :16

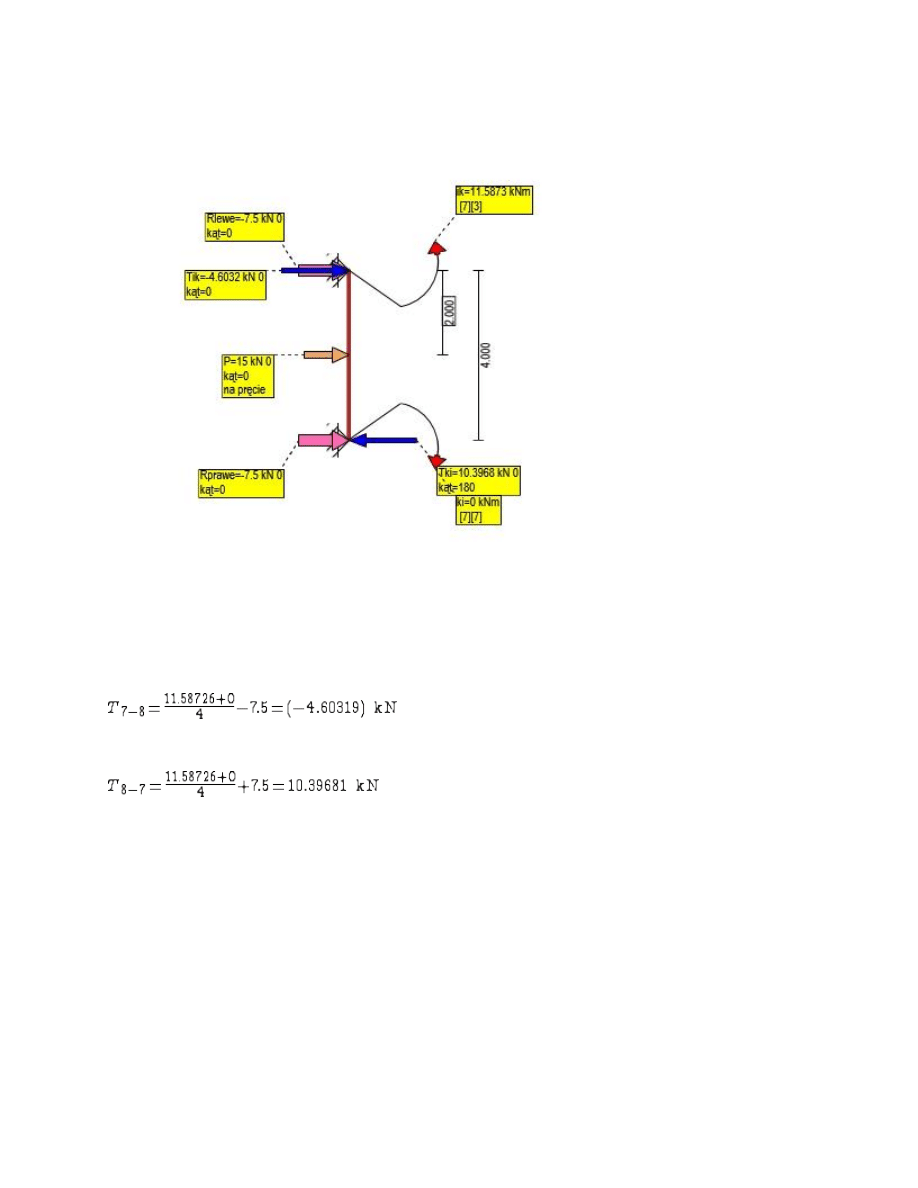
Rys. Siły Tnące 7-8

................................................................................................................................. ................................

.................................................................................................................................................................

....................................................................................................................................................... ..........

Strona :17

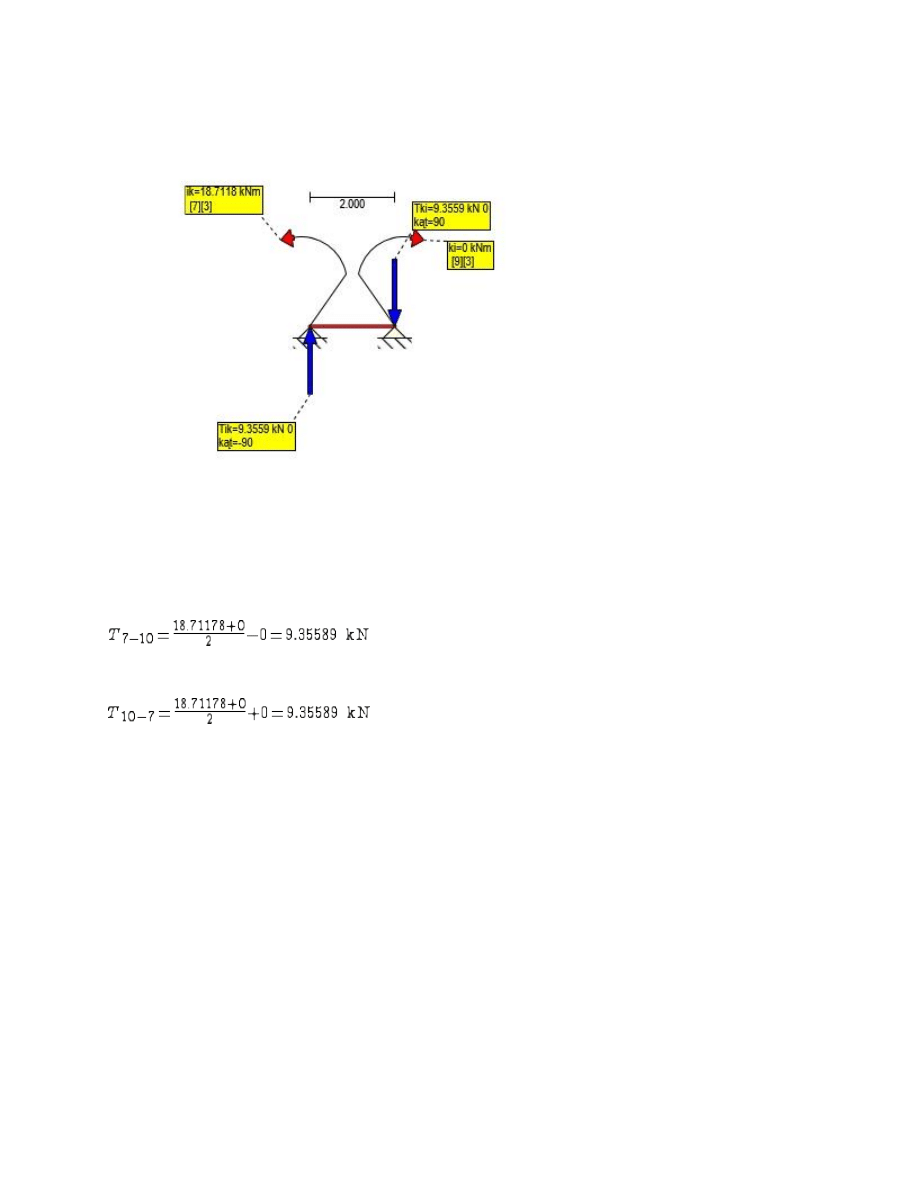
Rys. Siły Tnące 7-10

.................................................................................................................................................................

Strona :18

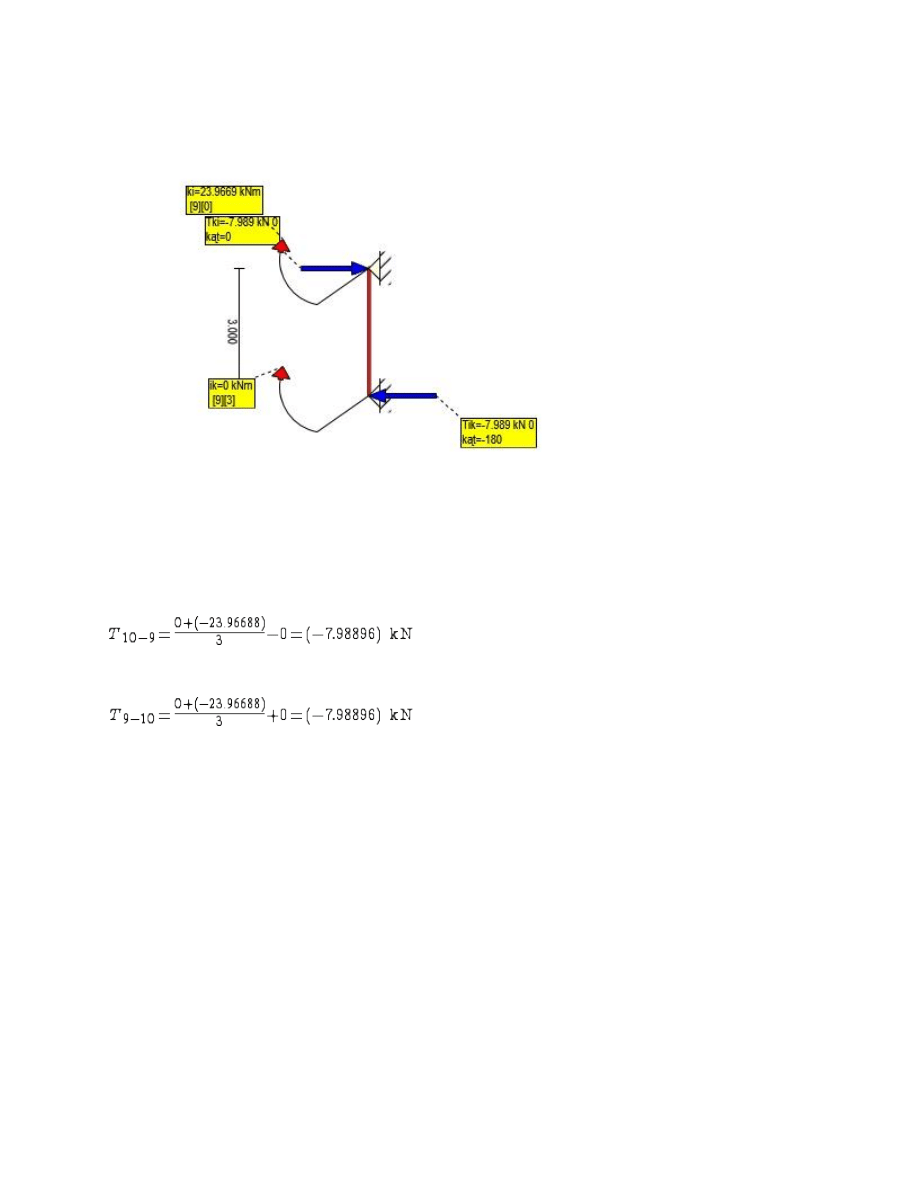
Rys. Siły Tnące 10-9

.................................................................................................................................................................

Strona :19

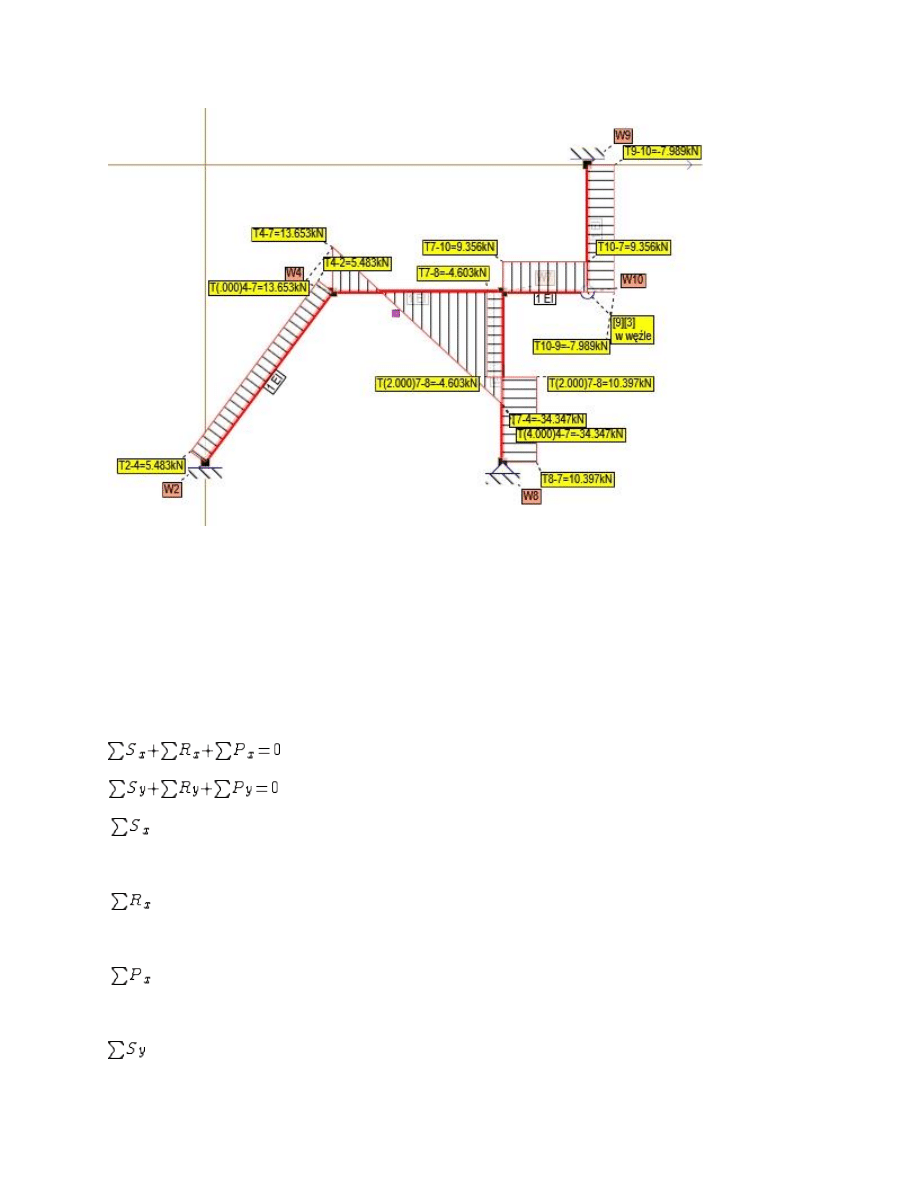
Rys. Wykres T

.................................................................................................................................................................

12. Obliczenie si

ł Normalnych

Aby W

ęzeł był w równowadze to suma jego składowych sił i reakcji rzutowana na oś X i oś Y musi być równa zero

to suma si

ł prętowych rzutowana na oś X w Węźle

to suma reakcji podporowych rzutowana na o

ś X w Węźle - jeżeli jest istnieje

to suma odzia

ływania zewnętrznego rzutowana na oś X w Węźle - jeżeli jest przyłożona

Strona :20

to suma si

ł prętowych rzutowana na oś Y w Węźle

to suma reakcji podporowych rzutowana na o

ś Y w Węźle - jeżeli jest istnieje

to suma odzia

ływania zewnętrznego rzutowana na oś Y w Węźle - jeżeli jest przyłożona

.................................................................................................................................................................

Obliczenia rozpoczynamy od W

ęzła, dla którego liczba niewiadomych sił w Prętach jest najmniejsza i wynosi

maksymalnie 2

W r

ównaniach dla uproszczenia zapisu szukane pręty przyjmiemy, jako A i B

.................................................................................................................................................................

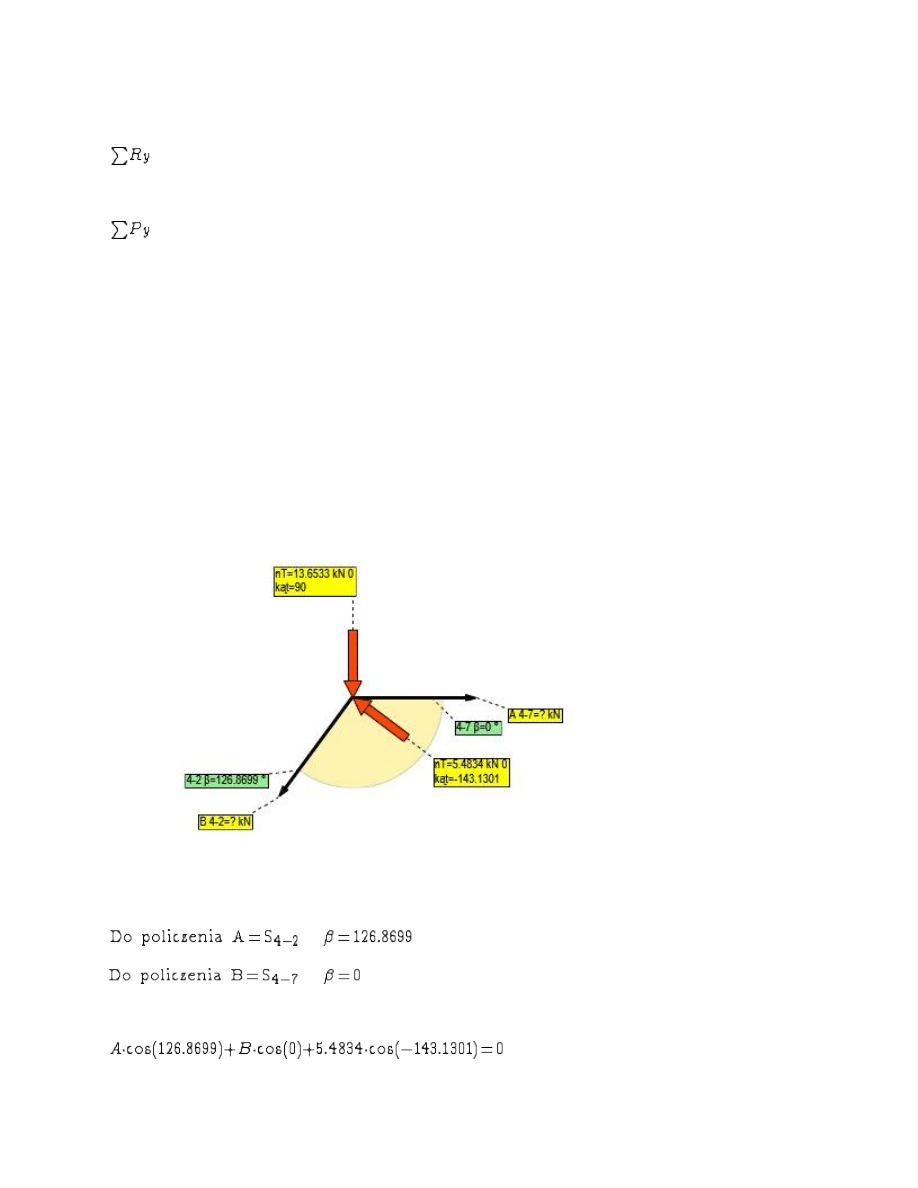
Wybrano W

ęzeł =4

Rzutowanie na o

ś X

Strona :21

Rzutowanie na o

ś Y

ład równań

.................................................................................................................................................................

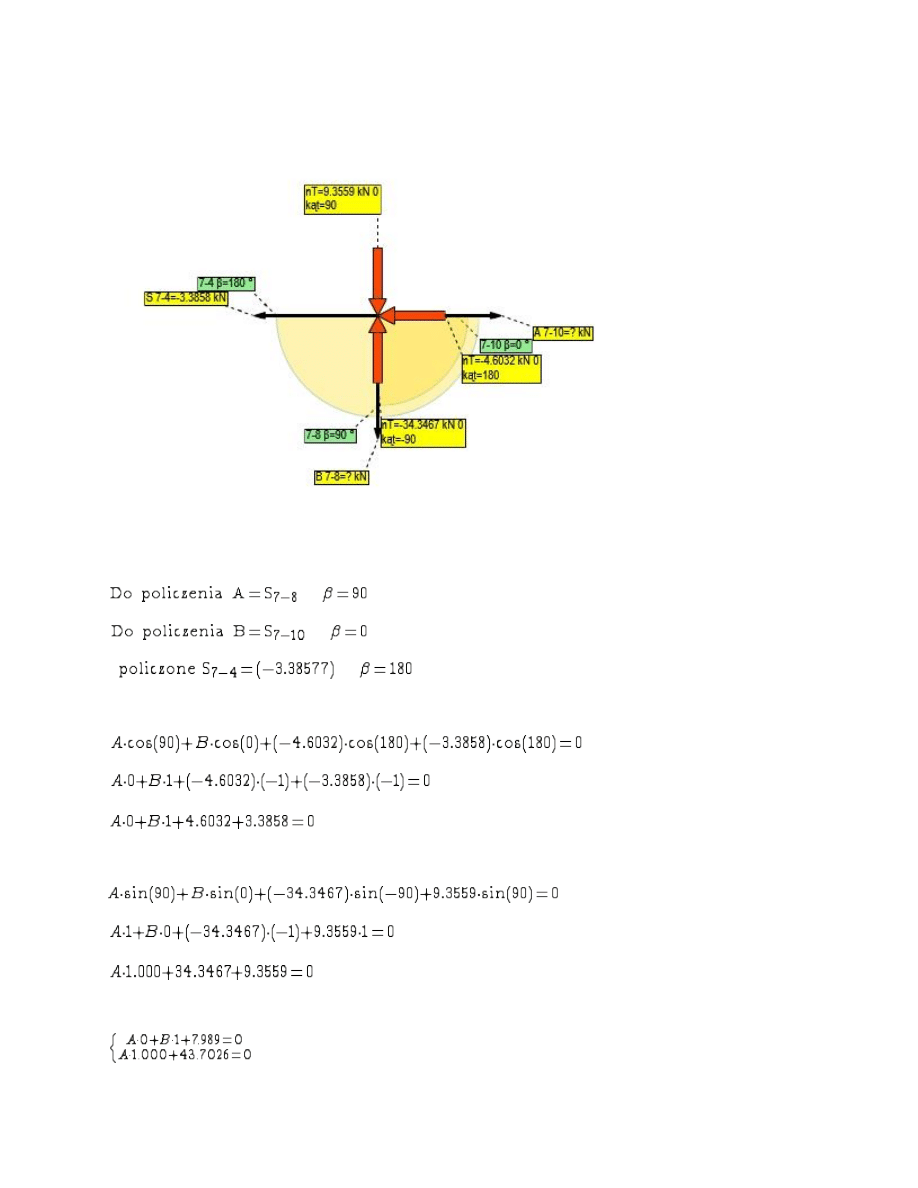
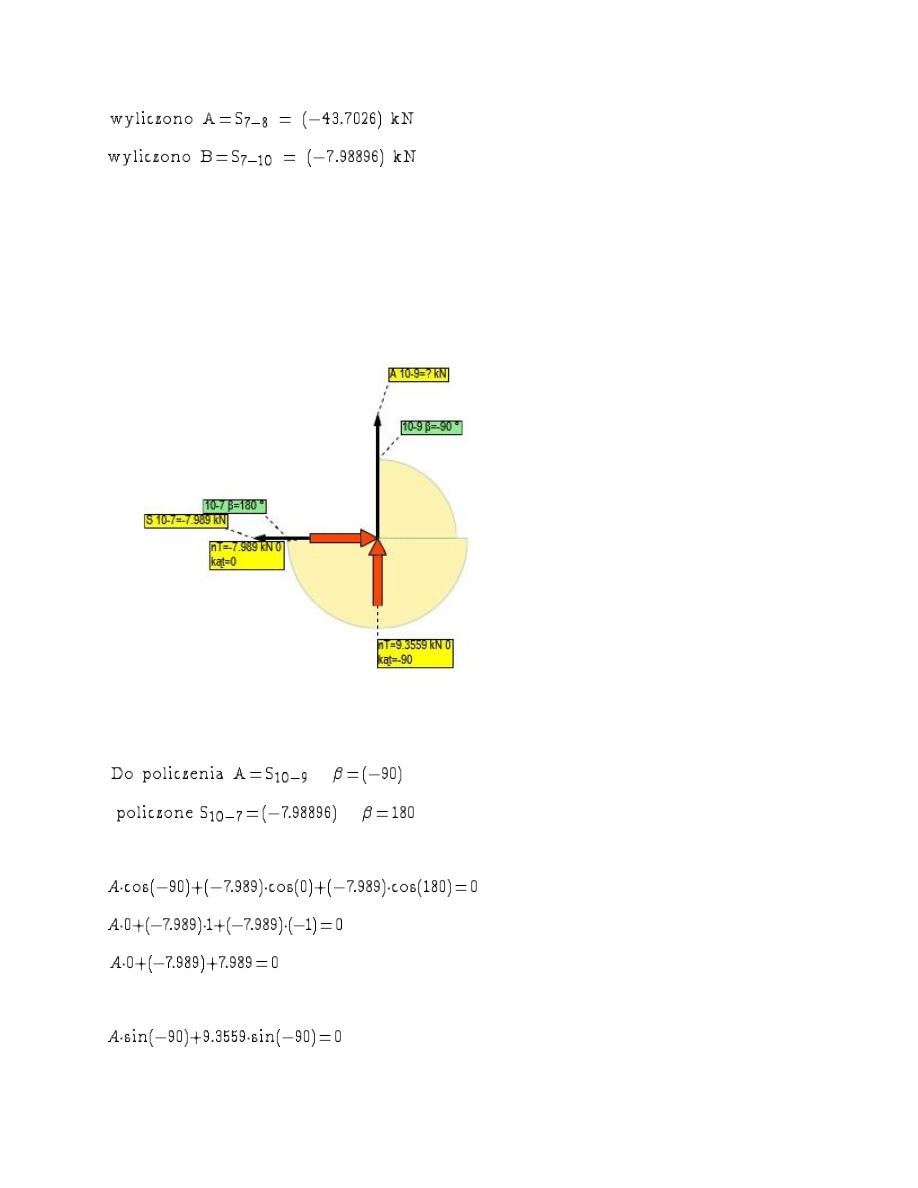
Wybrano W

ęzeł =7

Strona :22

Rzutowanie na o

ś X

Rzutowanie na o

ś Y

ład równań

Strona :23

.................................................................................................................................................................

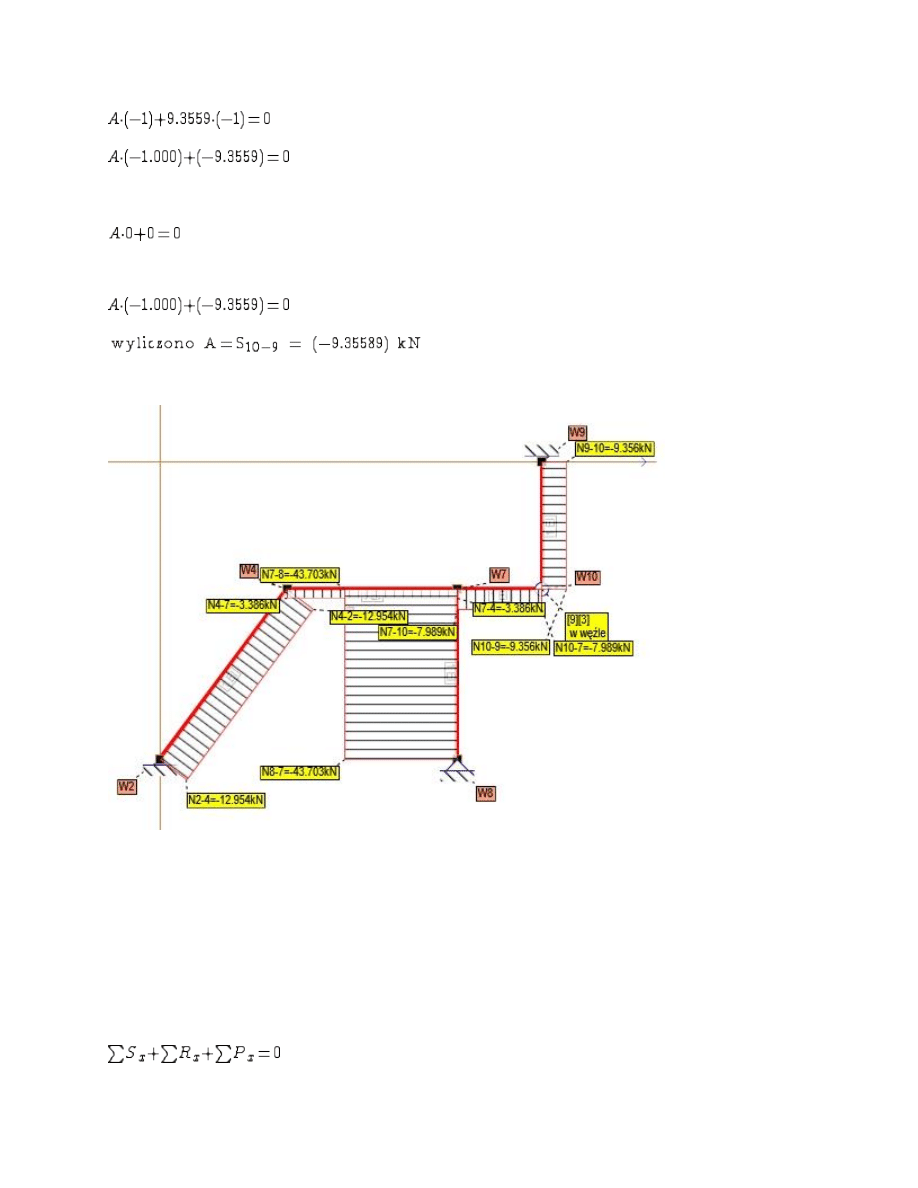
Wybrano W

ęzeł =10

Rzutowanie na o

ś X

Rzutowanie na o

ś Y

Strona :24

ównanie

lub r

ównanie

.................................................................................................................................................................

Rys. Wykres N

.................................................................................................................................................................

13. Obliczenie Reakcji Podporowych

Aby W

ęzeł był w równowadze to suma jego składowych sił i reakcji rzutowana na oś X i oś Y musi być równa zero

Strona :25

to suma si

ł prętowych rzutowana na oś X w Węźle

to suma reakcji podporowych rzutowana na o

ś X w Węźle - jeżeli jest istnieje

to suma odzia

ływania zewnętrznego rzutowana na oś X w Węźle - jeżeli jest przyłożona

to suma si

ł prętowych rzutowana na oś Y w Węźle

to suma reakcji podporowych rzutowana na o

ś Y w Węźle - jeżeli jest istnieje

to suma odzia

ływania zewnętrznego rzutowana na oś Y w Węźle - jeżeli jest przyłożona

..................................................................................................................................................... ............

W r

ównaniach dla uproszczenia zapisu szukane reakcje przyjmiemy, jako A i B

.................................................................................................................................................................

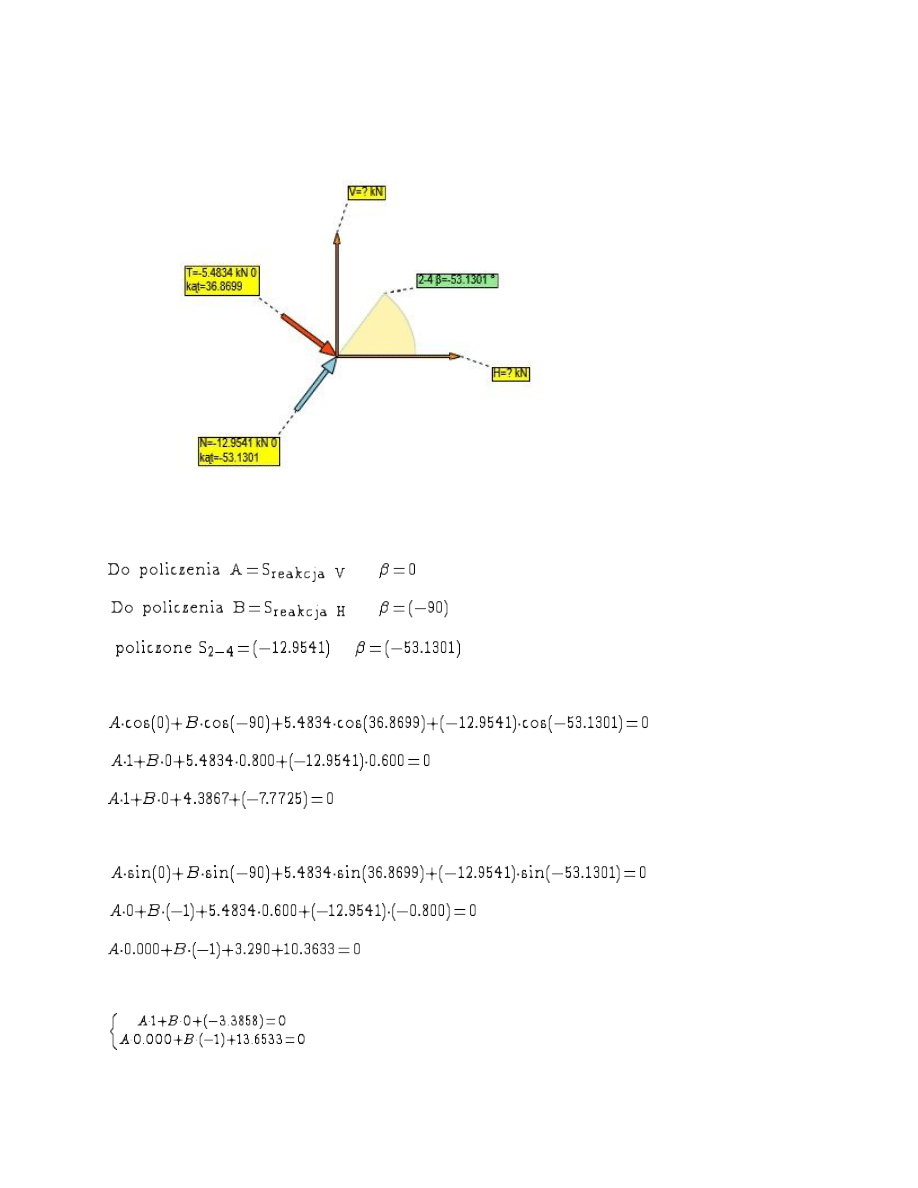
Wybrano W

ęzeł =2

Strona :26

Rzutowanie na o

ś X

Rzutowanie na o

ś Y

ład równań

Strona :27

.................................................................................................................................................................

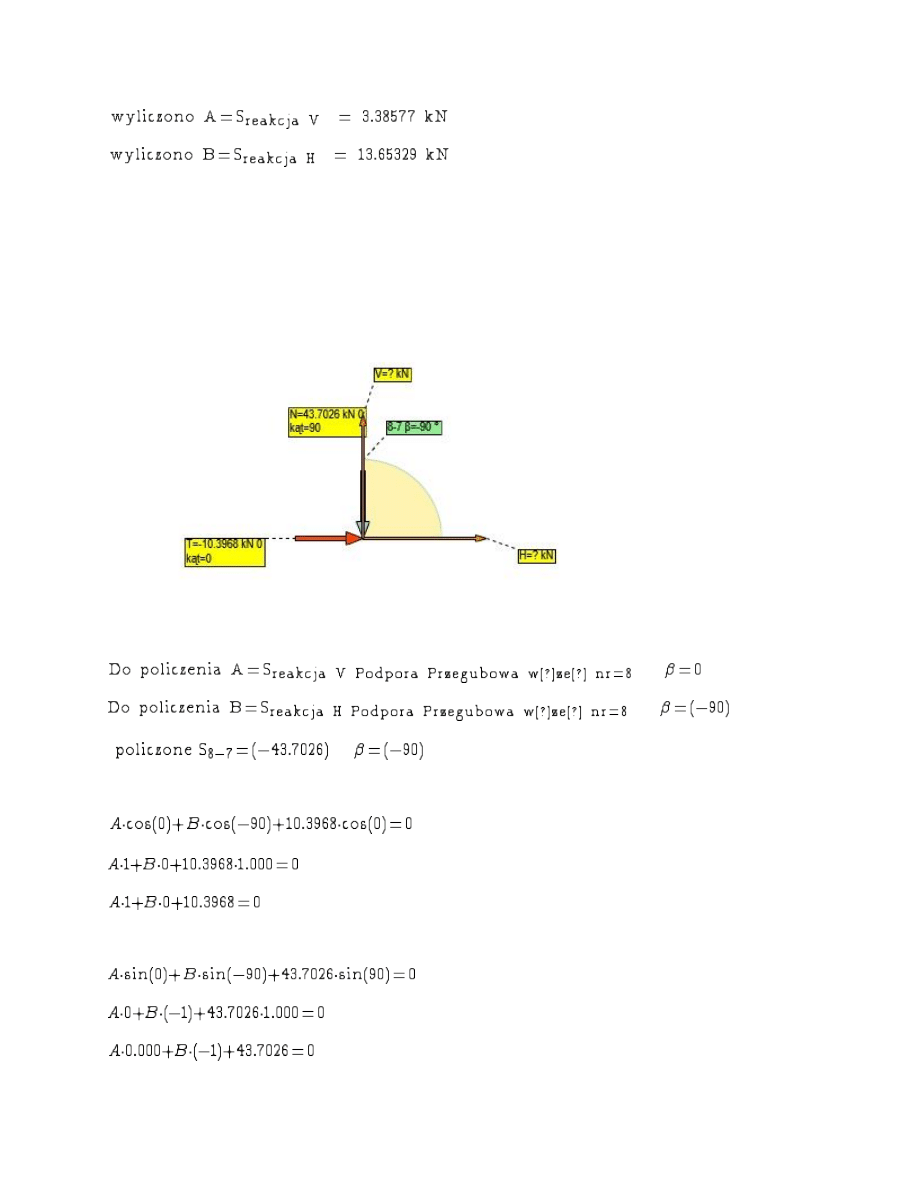
Wybrano W

ęzeł =8

Rzutowanie na o

ś X

Rzutowanie na o

ś Y

Strona :28

ład równań

.................................................................................................................................................................

Wybrano W

ęzeł =9

Rzutowanie na o

ś X

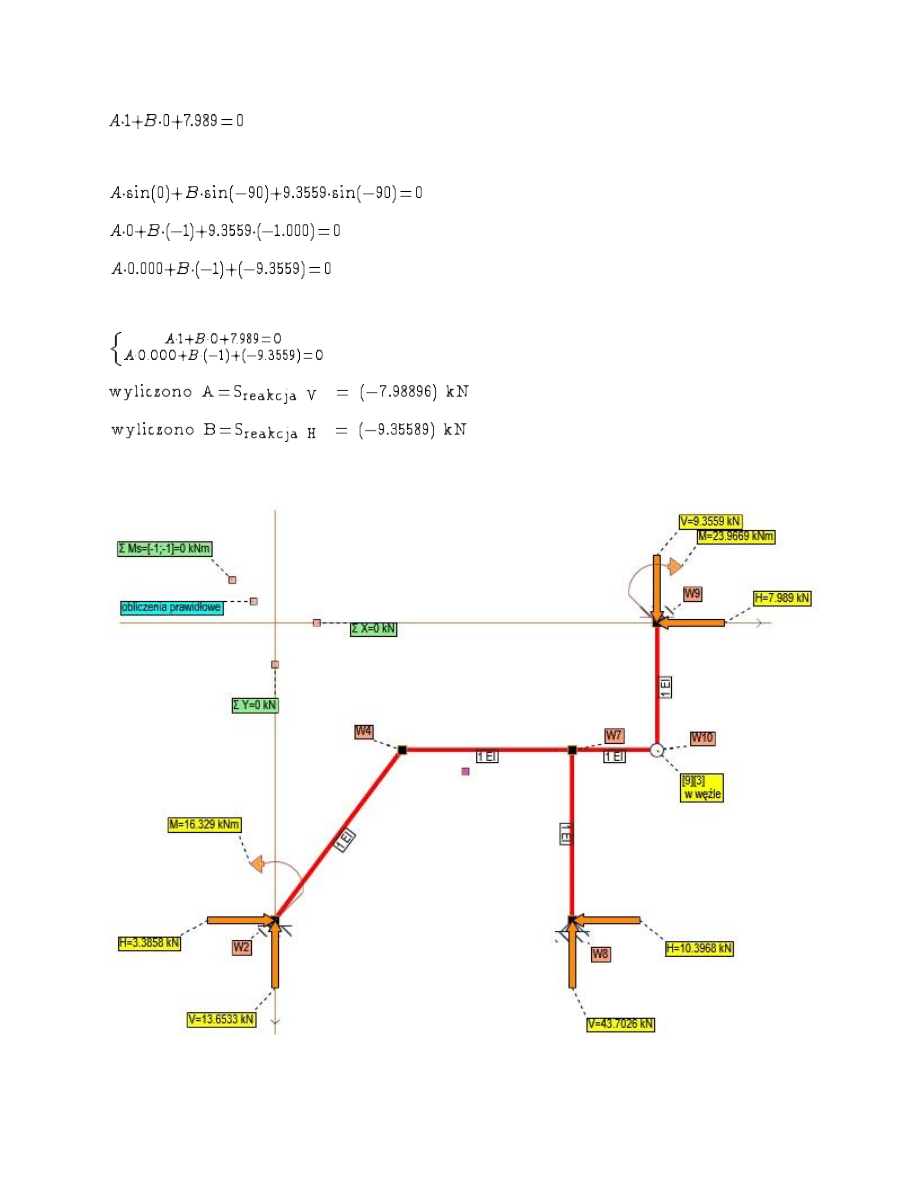
Strona :29

Rzutowanie na o

ś Y

ład równań

.................................................................................................................................................................

Strona :30

Rys. Reakcje podporowe

.................................................................................................................................................................

14. Sprawdzenie Reakcji Podporowych - Moment

Sprawdzenia poprawno

ści wyznaczenia reakcji podporowych dokonamy w punkcie [-1;-1] w naszym układzie XY

(Punkt musi by

ć tak dobrany, aby wszystkie siły i reakcje brały udział w obliczaniu Sumy Momentów )

W punkcie tym Suma Moment

ów od wszystkich sił i reakcji powinna wynosić M=0

suma wszystkich moment

ów od składowych reakcji i obciążeń siłowych w punkcie, w którym Moment = 0

15. Sprawdzenie Reakcji Podporowych Rzut X

Strona :31

16. Sprawdzenie Reakcji Podporowych Rzut Y

17. Ocena Wynik

ów Obliczeń

Z uwagi na spe

łnione warunki :

Ocena : obliczenia prawid

łowe

.................................................................................................................................................................

Wydruk Metor

www.gruparectan.com