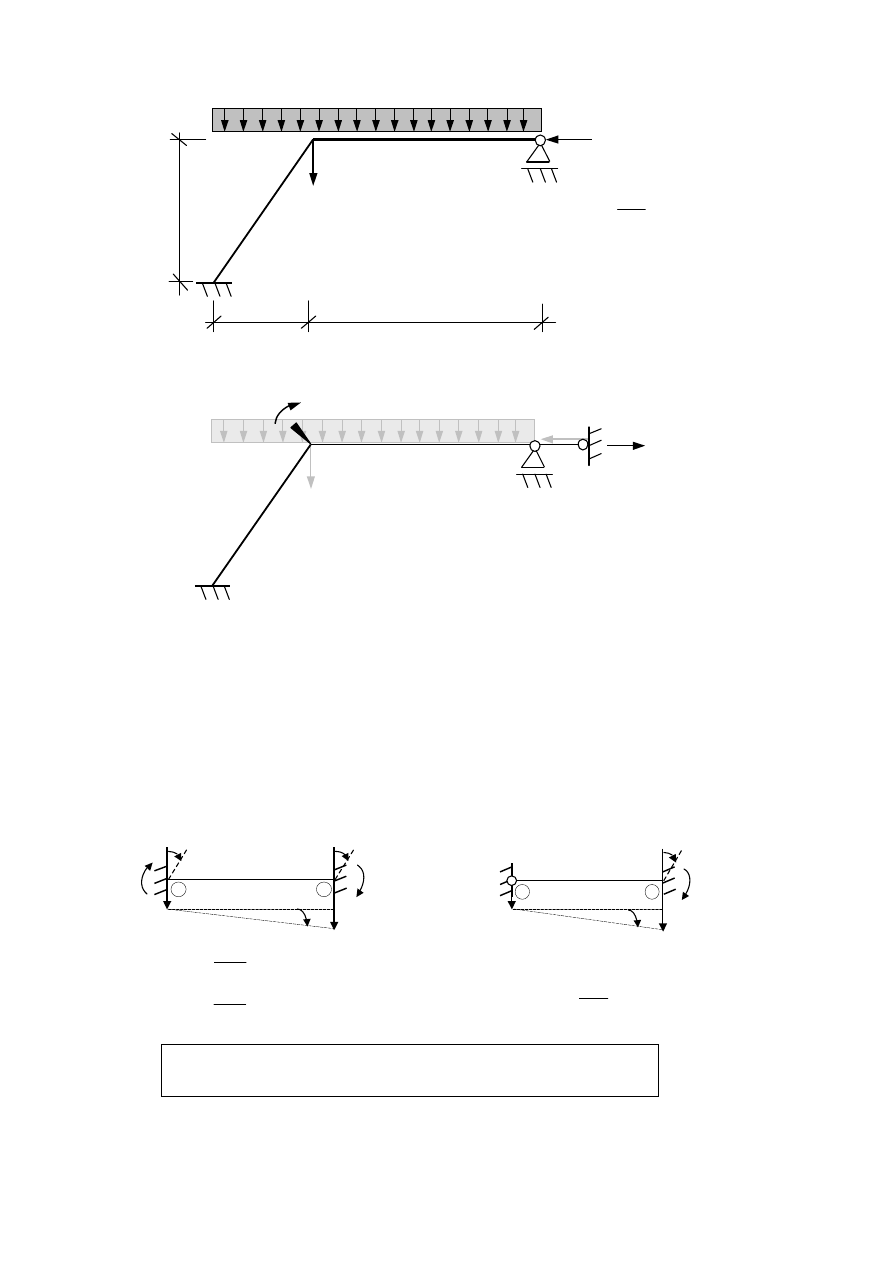
Schemat układu:
SKN=2
Układ podstawowy:
Układ równań kanonicznych metody przemieszczeń:
=
+
+
=
+
+
0
0
2
2
22
1
21
1
2
12
1
11
P
P
r
u
r
r
r
u
r
r
ϕ
ϕ
)
3
2
(
2
)
3
2
(
2
ik
k
i
ki
ik
k
i
ik
l
EI
M
l
EI
M
ψ
ϕ
ϕ
ψ
ϕ
ϕ
−
+
=
−
+
=
)
(
3
0
ik
k
ki
ik
l
EI
M
M
ψ
ϕ
−
=
=
reakcja w więzie i wywołana jednostkowym przemieszczeniem więzu
k
reakcja w więzie i wywołana obciążeniem zewnętrznym
−
ik
r
−
iP
r
obrót węzła 1
przemieszczenie poziome węzła 2
k
v
i
ϕ
k
ϕ
ik
ψ
i
v
i
k
l, EI
ik
M
ki
M
k
ϕ
ik
ψ
i
v
k
v
i
k
l, EI
ki
M
EI
EI
EI
EI
EI
EI
2
2
2
1
1
2
=
=
=
15kN
5kN
10kN/m
u
1
1
ϕ
0
2
1
1
EI
2
EI
−
2
u
−
1
ϕ
4
3
6
15kN
5kN
10kN/m
1
EI
2
EI
2
1
, u
ϕ
- niewiadome metody przemieszczeń
zasada znakowania momentów, kątów obrotu węzłów i cięciw:
zwrot prawoskrętny => wartość dodatnia
Wzory transformacyjne określają wartości momentów przęsłowych przywęzłowych M
ik
, M
ki
wywołanych obrotami i przemieszczeniami liniowymi (prostopadłymi do osi pręta) węzłow i oraz k :
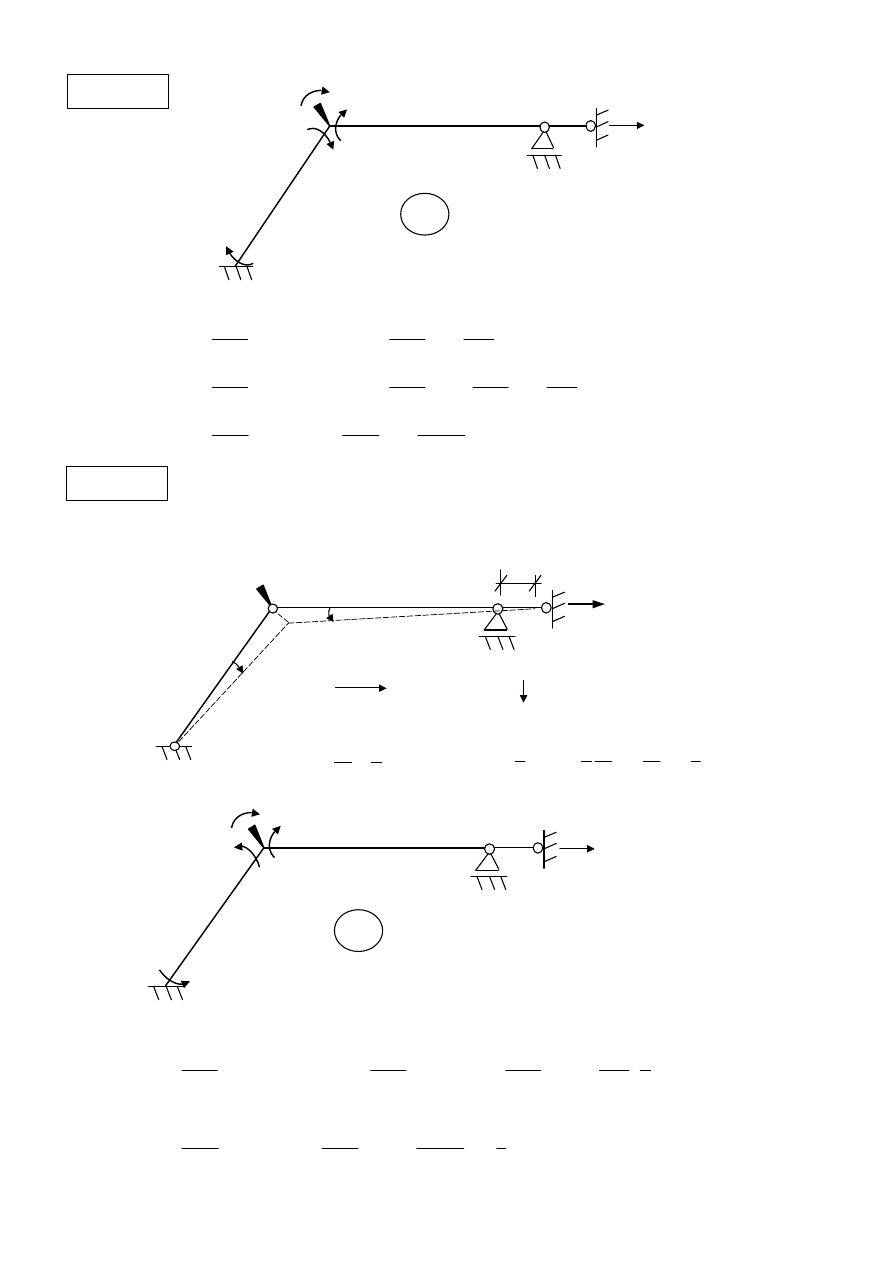
Stan
Stan u
2
=1
0 1 2
0 1 2
1
1
=
ϕ
8
1
8
4
2
1
6
3
0
6
3
2
2
01
12
12
01
−
=
−
=
−
=
−
=
=
+
u
u
ψ
ψ
ψ
ψ
0
2
1
0,3
EI
0.3
EI
0,125
EI
r
12
r
22
0,4
EI
0,8
EI
EI
0
2
1
r
11
r
21
4
1
4
0
4
2
01
2
01
=
=
=
+
u
u
ψ
ψ
u
2
= 1
1,0
01
ψ
12
ψ
0
2
1
0
0
0
0
2
=
=
⇒
=
ϕ
ψ
ik
u
0
1
0
=
=
ϕ
ϕ
( )
(
)
( )
( )
( )
EI
EI
l
EI
l
EI
M
EI
M
M
EI
EI
l
EI
l
EI
l
EI
M
125
,
0
8
1
6
2
3
3
)
(
3
3
,
0
3
,
0
4
1
5
6
6
3
2
)
3
2
(
2
12
2
12
1
2
2
12
2
01
2
10
01
1
01
1
01
1
0
1
2
01
=
−
⋅
⋅
−
=
−
=
−
=
−
=
=
−
=
⋅
−
=
−
=
⋅
−
=
⋅
−
+
=
ψ
ψ
ϕ
ψ
ψ
ψ
ϕ
ϕ
- momenty przęsłowe przywęzłowe:
- z równań łańcucha kinematycznego wyznaczamy kąty obrotów cięciw prętów
Ψ
ik
- momenty przęsłowe przywęzłowe:
M
(1)
( )
(
)
( )
(
)
( )
(
)
EI
EI
l
EI
l
EI
M
EI
EI
l
EI
l
EI
l
EI
M
EI
EI
l
EI
l
EI
M
=
⋅
=
=
−
=
=
=
=
=
−
+
=
=
=
=
−
+
=
6
2
3
3
3
8
,
0
5
4
4
2
2
3
2
2
4
,
0
5
2
2
3
2
2
1
2
121
1
2
1
12
1
1
1
1
01
0
1
1
1
10
1
1
01
1
0
1
1
01
ϕ
ψ
ϕ
ϕ
ϕ
ψ
ϕ
ϕ
ϕ
ψ
ϕ
ϕ
M
(2)
0,8
EI
EI
r
11
0
2
1
0,4
EI
r
21
1
0
2
0,3
EI
0.3
EI
0,125
EI
r
12
r
22
1
7,5
45
r
1P
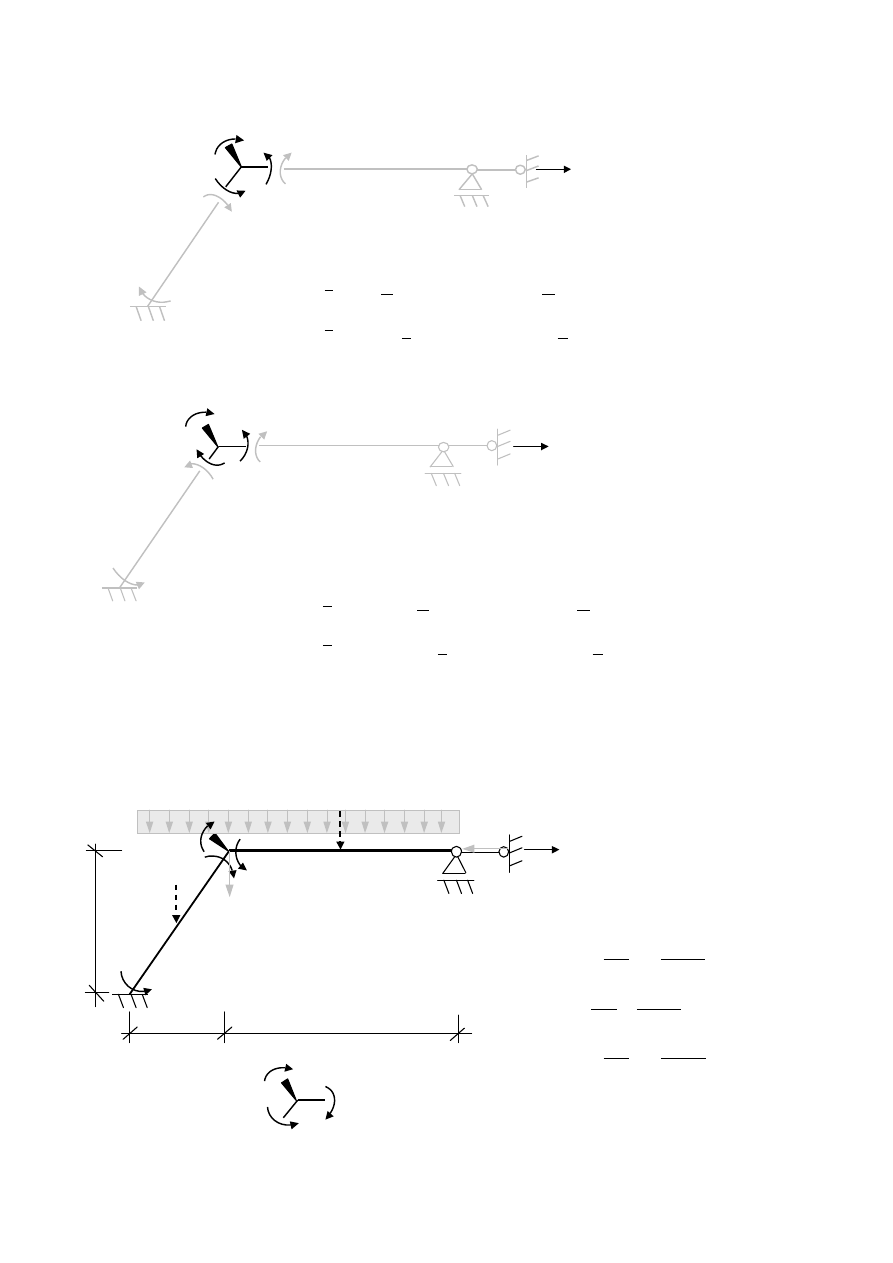
Wyznaczenie współczynników r
ik
układu równań kanonicznych:
- równowaga węzła 1 => r
11
=0,8EI +EI =1,8EI
- równanie pracy wirtualnej:
- równowaga węzła 1 => r
12
=0,125EI- 0,3EI =-0,175EI
r
12
= r
21
- równanie pracy wirtualnej:
EI
r
EI
EI
EI
r
EI
EI
EI
r
175
,
0
0
4
1
)
8
,
0
4
,
0
(
8
1
1
0
)
8
,
0
4
,
0
(
1
21
21
01
12
21
−
=
=
⋅
+
+
−
⋅
+
⋅
=
⋅
+
+
⋅
+
⋅
ψ
ψ
EI
r
EI
EI
EI
r
EI
EI
EI
r
1656
,
0
0
4
1
)
3
,
0
3
,
0
(
8
1
125
,
0
1
0
)
3
,
0
3
,
0
(
125
,
0
1
22
22
01
12
22
=
=
⋅
+
−
−
⋅
+
⋅
=
⋅
+
−
⋅
+
⋅
ψ
ψ
Wyznaczenie współczynników r
iP
układu równań kanonicznych:
- momenty przęsłowe przywęzłowe:
- równowaga węzła 1 =>
45
r
2P
r
1P
7,5
7,5
0
2
4
3
6
15kN
5kN
10kN/m
1
A
30kN
B
60kN
r
1P
=7,5-45=-37,5kNm
( )
( )
( )
kNm
ql
M
kNm
ql
M
kNm
ql
M
P
P
P
45
8
6
10
8
5
,
7
12
3
10
12
5
,
7
12
3
10
12
2
2
12
2
2
10
2
2
01
−
=
⋅
−
=
−
=
=
⋅
=
=
−
=
⋅
−
=
−
=

0 A
3 B
1 C
0
2
1
1,0
01
ψ
12
ψ
∆
A
∆
B
∆
C
B
A
x
y
=
−
⋅
+
⋅
−
=
−
⋅
−
⋅
0
625
,
45
1656
,
0
175
,
0
0
5
,
37
175
,
0
8
,
1
2
1
2
1
u
EI
EI
u
EI
EI
ϕ
ϕ
EI
EI
EI
W
EI
EI
EI
W
EI
EI
EI
EI
EI
W
6875
,
88
625
,
45
175
,
0
5
,
37
8
,
1
1944
,
14
1656
,
0
625
,
45
175
,
0
5
,
37
2675
,
0
1656
,
0
175
,
0
175
,
0
8
,
1
2
1
2
=
−
=
=
−
=
=
−
−
=
=
=
EI
u
EI
598
,
331
072
,
53
2
1
ϕ
- wyznaczenie r
2P
z równania pracy wirtualnej (stan sił - na rys. powyżej, stan przemieszczeń
wirtualnych - rys. poniżej):
kNm
r
r
P
P
625
,
45
0
1
5
4
3
15
8
3
60
8
3
30
8
1
45
2
2
−
=
=
⋅
−
⋅
+
⋅
+
⋅
+
−
⋅
−
przemieszczenia:
∆
A
,
∆
B
,
∆
C
,
∆
D
wyznaczamy z równań łańcucha kinematycznego
(znak dodatni oznacza przemieszczenia o zwrotach zgodnych z osiami układu współrzędnych.):
- stąd:
8
3
4
1
2
3
5
,
1
12
=
⋅
=
∆
∆
=
A
A
ψ
8
3
8
1
3
3
12
=
−
⋅
−
=
∆
∆
=
−
B
B
ψ
4
3
4
1
3
3
01
=
⋅
=
∆
∆
=
C
C
ψ
0
,
1
=
∆
D
Wyznaczenie rzeczywistych momentów przywęzłowych ze wzorów transformacyjnych:
(praca siły na odpowiadającym jej przemieszczeniu jest dodatnia, jeśli zwrot siły i
przemieszczenia jest taki sam):
RPW
0
5
15
6
10
3
10
)
(
1
01
10
01
12
12
2
=
∆
⋅
−
∆
⋅
+
∆
⋅
⋅
+
∆
⋅
⋅
+
⋅
+
+
⋅
+
⋅
D
C
B
A
P
P
P
P
M
M
M
r
ψ
ψ
(
)
( )
( )
(
)
( )
( )
(
)
( )
( )
kNm
EI
EI
EI
M
u
l
EI
M
l
EI
M
kNm
EI
EI
EI
M
u
l
EI
M
l
EI
M
kNm
EI
EI
EI
M
u
l
EI
M
l
EI
M
P
P
P
P
P
P
49,5218
49,5218
85,7506
=
−
+
=
=
+
+
⋅
=
+
−
=
−
=
+
⋅
−
=
=
+
⋅
−
=
+
−
+
=
−
=
−
⋅
−
=
=
+
⋅
−
=
+
−
+
=
45
8
598
,
331
072
,
53
6
6
8
2
3
3
5
,
7
4
598
,
331
3
072
,
53
2
5
2
4
3
2
2
3
2
2
5
,
7
4
598
,
331
3
072
,
53
5
2
4
3
2
3
2
2
12
2
1
12
12
1
2
12
10
2
1
10
01
0
1
1
10
01
2
1
01
01
1
0
1
01
ϕ
ψ
ϕ
ϕ
ψ
ϕ
ϕ
ϕ
ψ
ϕ
ϕ
Wyznaczenie niewiadomych układu równań kanonicznych:
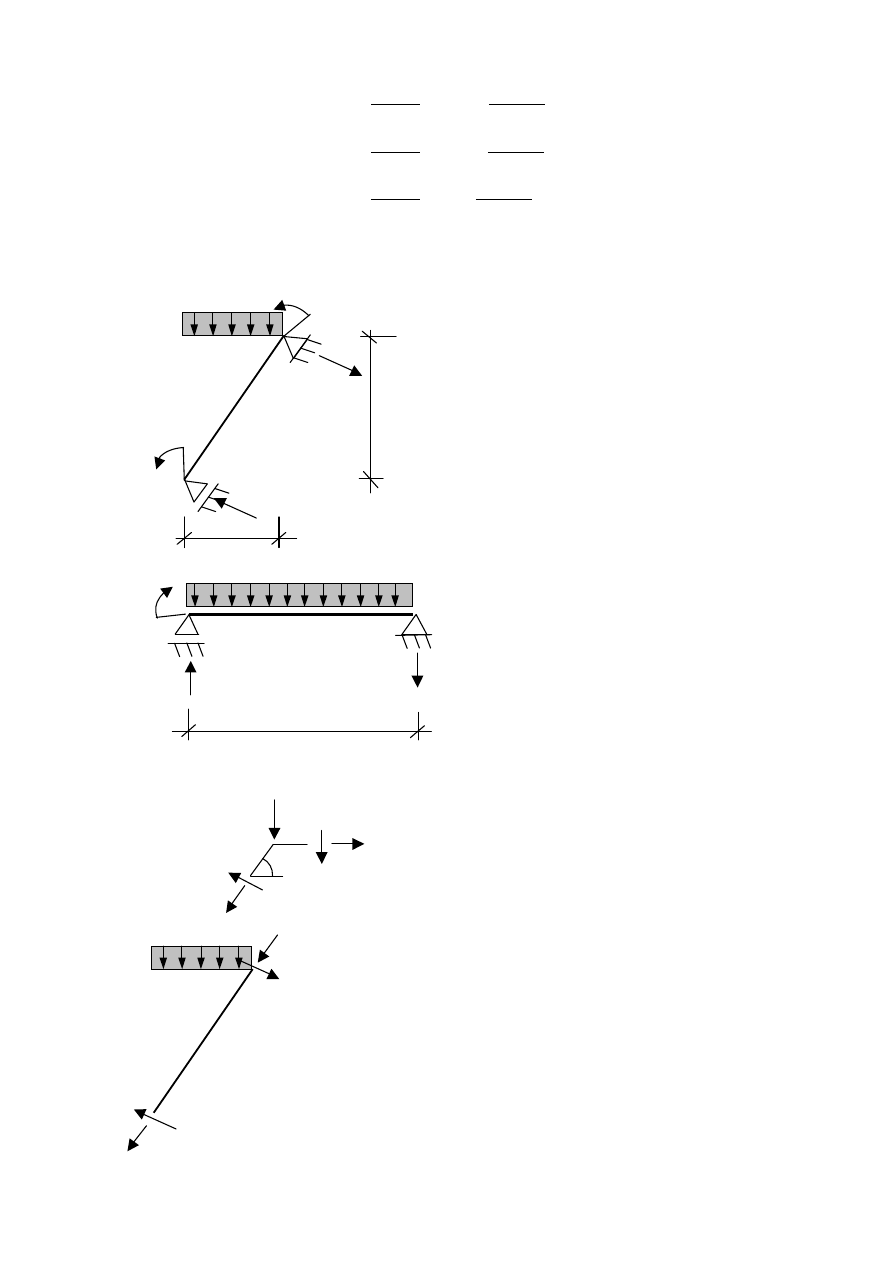
Wyznaczenie sił tnących w poszczególnych prętach:
każdy z prętów obliczamy jak belkę swobodnie podpartą, poddaną działaniu momentów podporowych i
obciążeniu w obrębie przęsła.
...lub korzystając z zasady superpozycji:
( )
( )
( )
(
)
( )
( )
( )
(
)
( )
( )
( )
kNm
EI
EI
EI
EI
M
M
u
M
M
kNm
EI
EI
EI
EI
M
M
u
M
M
kNm
EI
EI
EI
EI
M
M
u
M
M
P
P
P
49,5218
49,5218
85,7506
=
−
⋅
+
⋅
=
+
+
=
−
=
+
−
⋅
+
⋅
=
+
+
=
−
=
−
−
⋅
+
⋅
=
+
+
=
45
125
,
0
598
,
331
4
072
,
53
5
,
7
3
,
0
598
,
331
8
,
0
072
,
53
5
,
7
3
,
0
598
,
331
4
,
0
072
,
53
12
2
12
2
1
12
1
12
10
2
10
2
1
10
1
10
01
2
01
2
1
01
1
01
ϕ
ϕ
ϕ
Wyznaczenie sił normalnych w poszczególnych prętach: - na podstawie równań równowagi sił
działających na pręty i węzły.
10
kN/m
4
3
49,5218
kNm
85,7506
kNm
T
10
T
01
kN
T
T
M
0545
,
18
0
5
,
1
3
10
5
5218
,
49
7506
,
85
0
10
10
0
=
=
⋅
⋅
−
⋅
−
+
=
∑
0
1
10
kN/m
49,5218
kNm
6
2
EI
T
12
T
21
kN
T
T
M
7464
,
21
0
5218
,
49
3
6
10
6
0
12
12
2
=
=
+
⋅
⋅
−
⋅
=
∑
kN
T
T
M
2536
,
38
0
5218
,
49
3
6
10
6
0
21
21
1
−
=
=
+
⋅
⋅
+
⋅
=
∑
1
2
N
12
N
10
18,0545
kN
21,7464
kN
1
15
kN
α
kN
N
N
X
9918
,
4
0
cos
3921
,
32
sin
0545
,
18
0
12
12
−
=
=
+
−
=
∑
α
α
kN
T
T
M
0545
,
36
0
5
,
1
3
10
5218
,
49
7506
,
85
5
0
01
01
1
=
=
⋅
⋅
−
−
−
⋅
=
∑
10
kN/m
18.0545
kN
36.0545
kN
N
01
32.3921
kN
kN
N
N
Y
3921
,
32
0
sin
cos
0545
,
18
15
7464
,
21
0
10
10
−
=
=
+
−
+
=
∑
α
α
kN
N
N
X
3921
,
56
0
sin
3
10
3921
,
32
0
01
01
−
=
=
⋅
+
+
=
∑
α

Ostateczne wykresy:
Kontrola statyczna:
0
0003
,
0
6
2536
,
38
3
6
10
5
,
1
3
10
7506
,
85
5
0545
,
36
0
0
00002
,
0
sin
3921
,
56
cos
0545
,
36
2536
,
38
15
9
10
0
0
00014
,
0
cos
3921
,
56
sin
0545
,
36
9918
,
4
0
1
≅
−
=
⋅
−
⋅
⋅
+
⋅
⋅
−
−
⋅
=
≅
−
=
+
+
+
−
⋅
−
=
≅
−
=
+
−
−
=
∑
∑
∑
M
Y
X
α
α
α
α
Kontrola kinematyczna:
Wyszukiwarka
Podobne podstrony:
cwicz mechanika budowli metoda przemieszczen rama ugiecie
cwicz mechanika budowli metoda przemieszczen rama
metoda przemieszczen rama prosta
cwicz mechanika budowli metoda przemieszczen rama temperatura
cwicz mechanika budowli metoda przemieszczen rama osiadanie
Metoda przemieszczeń rama
Metoda przemieszczen Rama2, SGN=2
Projekt Rama Metoda przemieszczeń Metor
belka obroty i przesuwy metoda przemieszczeń
Linie wpływu Metoda przemieszczeń mmp belka lw
Metoda przemieszczeń
Metoda przemieszczen projekt4
Metoda sił rama temp montaz
Obliczanie ram metodą przemieszczeń wersja komputerowa
metoda przemieszczen0002
metoda przemieszczen0001
więcej podobnych podstron