Politechnika Pozna

ń

ska

►

Instytut Konstrukcji Budowlanych

►

Zakład Mechaniki Budowli

2007/08

Metoda przemieszcze

ń

www.ikb.poznan.pl/anita.kaczor

1

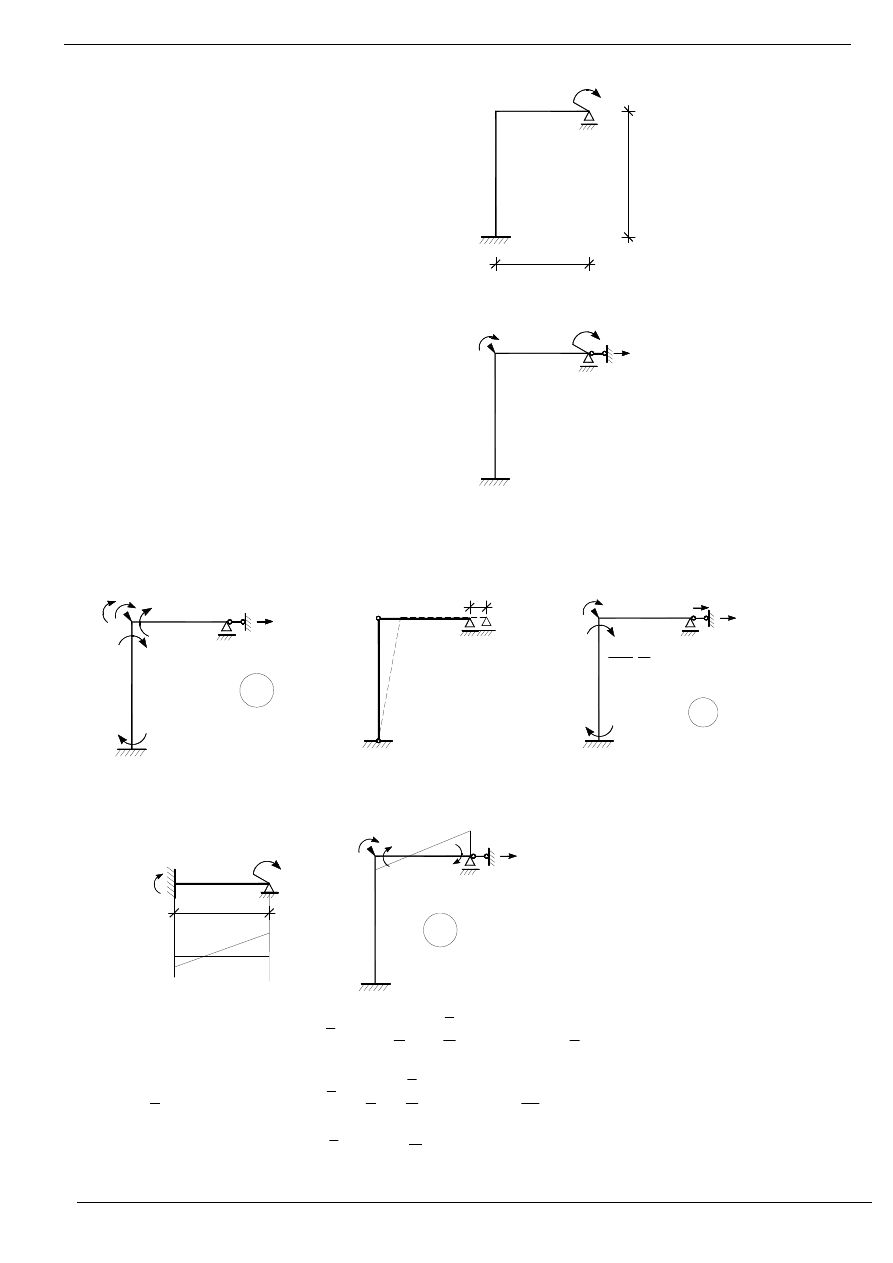
Wyznaczyć wykres momentów zginających
w ramie metodą przemieszczeń.
EJ = const.

UWAGA!
Proszę zwrócić uwagę na stan „P”!

Rozwiązanie:

SGN=2

Układ podstawowy:

Układ równań kanonicznych:







=

+

+

=

+

+

0

0

2

1

22

1

21

1

1

12

1

11

P

P

r

u

r

r

r

u

r

r

ϕ

ϕ

Stan

1

1

=

ϕ

:

Stan

1

2

=

u

:

Stan „P”:

EJ

r

2

11

=

EJ

r

EJ

EJ

r

8

3

0

4

1

2

1

22

21

−

=

⇒

=

⋅













+

+

⋅

1

EJ

r

8

3

12

−

=

EJ

r

EJ

r

16

3

0

4

1

8

3

2

22

22

=

⇒

=

⋅

⋅

−

⋅

1

kNm

r

P

5

1

=

(

)

0

0

10

5

2

12

2

=

⇒

=

⋅

+

+

⋅

P

P

r

r

1

ψ

3,0

10 kNm

4

,0

3EJ/3 = EJ

4EJ/4 = EJ

2EJ/4 = EJ/2

1

Μ

1

ϕ = 1

r

11

r

21

10 kNm

ϕ

1

u

2

Ψ

= 1/4

-6EJ

1

01

0

1

2

12

Ψ

= 0

2

u = 1

4

4

1

= -3EJ/8

-3EJ/8

r

22

12

r

M

2

M/2

M

ik

M

L

M

10

r

2P

r

1P

5

0

Μ

P

Politechnika Pozna

ń

ska

►

Instytut Konstrukcji Budowlanych

►

Zakład Mechaniki Budowli

2007/08

Metoda przemieszcze

ń

www.ikb.poznan.pl/anita.kaczor

2












−

=

−

=

⇒












=

⋅

+

⋅

−

=

+

⋅

−

⋅

EJ

u

EJ

u

EJ

EJ

u

EJ

EJ

8

4

0

16

3

8

3

0

5

8

3

2

2

1

2

1

2

1

ϕ

ϕ

ϕ

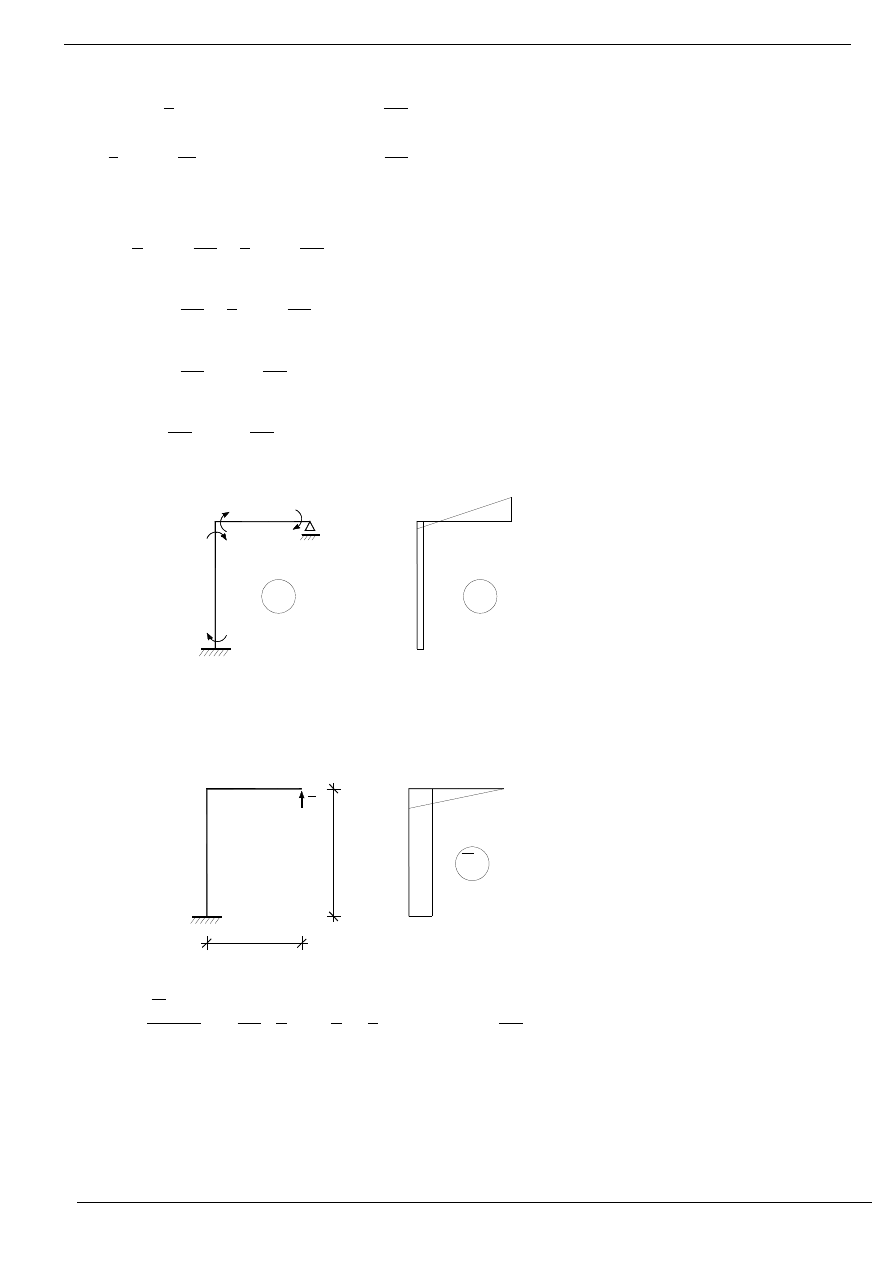
Ostateczny wykres momentów zginających:

kNm

EJ

EJ

EJ

EJ

M

n
01

0

,

1

0

8

8

3

4

2

1

=

+













−

⋅

−













−

⋅

=

kNm

EJ

EJ

EJ

EJ

M

n

10

0

,

1

0

8

8

3

4

−

=

+













−

⋅

−













−

⋅

=

kNm

EJ

EJ

EJ

M

n

12

0

,

1

5

8

0

4

=

+













−

⋅

+













−

⋅

=

kNm

EJ

EJ

M

n
21

0

,

10

10

8

0

4

0

=

+













−

⋅

+













−

⋅

=

Sprawdzenie kinematyczne:

EJ

EJ

dx

EJ

M

M

x

n

P

k

0

1

3

4

1

10

3

1

1

3

2

3

3

2

1

1

0

=













⋅

⋅

+

⋅













⋅

−

⋅

⋅

⋅

⋅

⋅

=

=

∑∫

ϕ

P

Μ

n

M

n

n

M

n

M

01

n

M

n

Μ

P

10

1

1

1

[kNm]

10

12

21

Μ

[kNm]

1

3

3

3

k

0

3,0

4

,0