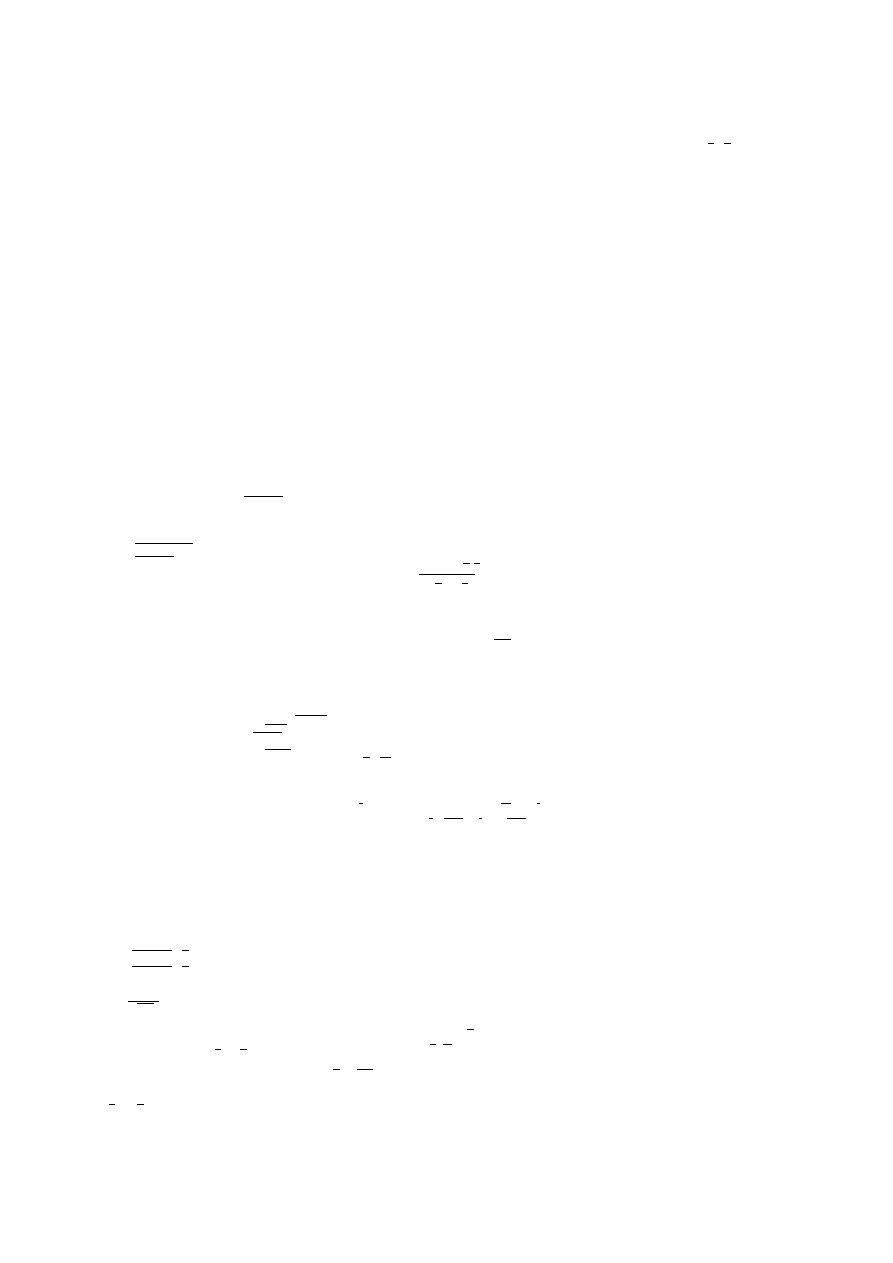
1. Własności przedziału.
Podział przedziału -
, punkty pośrednie-
, suma całkowa-
, ciąg podziałów
przedziału -
, maksymalna dł.
przedziału w n-tym podziale
2. Ciąg normalny.
Mówimy, że ciąg przedziałów jest normalnym witw gdy
3.Ciąg sum całkowych.
Zał.
,
;
4.Całka oznaczona.
Jeżeli dla każdego normalnego ciągu podziałów przedziału istnieje
skończona granica ciągu
niezależna od ciągu podziałów i
niezależna od wyboru punktów pośrednich to tą granicę nazywamy
. Jeżeli dla funkcji istnieje całka to mówimy, że funkcja jest
całkowalna w przedziale
5.Całka oznaczona w sensie Riemanna.
Jeżeli dla i jest całkowalna na przedziale , to
(pole pod wykresem)
gdzie
(uporządkowany układ równań)
6.Własnosci całek.
Tw.
,
Całka ze stałej to stała razy dł. przedziału
całkowania,
Tw. Jeżeli i jest całkowalna na prz. , to
Def. Niech funkcja
będzie całkowalna na przedziale ,
7. Tw. Newtona-Liebniza.
Jeżeli funkcja jest ciągła w przedziale to
, gdzie funkcja jest dowolna funkcją pierwotną funkcji
.
8.Całkowanie przez części.
Niech funkcja
i będą funkcjami kl.
w przedziale
wtedy
całka
9.Całkowanie przez podstawienie.
Jeżeli funkcja jest ciągła w zbiorze wartości funkcji
różniczkowalnej kl.
w przedziale
, to
10.Zast. całki oznaczonej.
dla
to
:
-objętość,
- pole
powierzchni bocznej
11.Dlugość łuku krzywej.
Jeżeli funkcje dla są kl.
w
to dł. łuku
krzywej zadanej równaniami parametrycznymi wyraża się wzorem
– dł. krzywej płaskiej , jeżeli
to
12.Całka niewłaściwa.
Niech funkcja
będzie określona w przedziale i całkowalna w
gdzie jest on zawarty w
. Punkt nazywamy osobliwym witw gdy
lub funkcja jest nieograniczona w pkt. . Jeżeli jest pkt.
osobliwym funkcji
w przedziale i istnieje granica skończona
, to tą granice nazywamy całką niewłaściwą z funkcji
na przedziale
i oznaczamy
13.Kryt. całkowe zbieżności szeregu
Jeżeli funkcja jest dodatnia i malejąca w przedziale i
, to
jest zbieżny witw, gdy całka
jest
zbieżna, czyli ma granicę skończoną.
14.Funkcja n-zmiennych.
15.Punkt skupienia zbioru.
Mówimy, że jest punktem skupienia zbioru,
, 2) Jeżeli każde otoczenie punktu zawiera co
najmniej jeden element zb.
różny od . Mówimy, że zb. jest domknięty
jeżeli wszystkie pkt. skupienia. Mówimy, że zb. jest otwarty jeżeli każdy
jego pkt. jest pkt. wewnętrznym. Zb. nazywamy obszarem jeśli jest zb.
otwartym i każde 2 pkt. tego zbioru można połączyć łamaną zawartą w
tym zb. Zb. domknięty i ograniczony nazywamy zb. zwartym.
16.Funkcja dwóch zmiennych.
Każdej parze przyporządkowuje 3
liczbę.
17.Definicja granicy funkcji Cauchy ’ego
.
18. Definicja granicy funkcji Heinego
.
19.Ciągłość funkcji w pkt.
Funkcja
jest ciągła w
z definicji gdy istnieje
,
i
20. Ciągłość funkcji w zbiorze.
Niech funkcja
będzie ciągła w zb. zwartym
wtedy istnieje
takie, że
jest wartością największą funkcji
w zb. i
jest wartością najmniejszą funkcji w zb. .
Funkcja ciągła w zb. zwartym jest ograniczona.
21.Pochodne cząstkowe I rzędu.
Pochodna- współczynnik zmiany długości,
- pochodna przy ustalonym y
- pochodna przy ustalonym x
22.Rózniczkowalność f. dwóch zmiennych.
Funkcja jest różniczkowalna w punkcie
z def. gdy zachodzi
Tw. Jeżeli pochodne cząstkowe są ciągłe w punkcie
to funkcja
jest różniczkowalna.
-
ogólny wzór,
– różniczka zupełna
23.Twierdzenie Schwarza.
Jeżeli pochodne mieszane są ciągłe to są równe.
24.Twierdzenie o gradiencie, gradient.
Gradient wyznacza kierunek najszybszego wzrostu funkcji.
25.Ekstrema f. dwóch zmiennych.
Mówimy, że funkcja określona w otoczeniu
posiada
ekstremum w
witw gdy istnieje otoczenie
takie, że
26. Ekstrema f. trzech zmiennych.
Mówimy, że funkcja określona w obszarze , gdzie
posiada w
max lokalne { min } witw gdy
istnieje kula o śr. w
i
takie, że
27.Def. Całka podwójna.
Prostokąt . Niech będzie
okreslona i ograniczona na prostokącie .
suma mnogościowa
;
-pole; suma algebraiczna
; Określenie prostokątow
podział prostkąta
Średnica podziału
; Pkt. pośrednie
; Suma całkowa
; ciąg podziałów
; Pola ciągu podziałów
; Pkt.
pośrednie ciągu podziałów
; ciag sum całkowych
; Jeżeli dla ciągu podziałów
to
mówimy, że ciag podziałów jest normalnym ciągiem podziałów. Jeżeli
norm. ciągu podziałów skończona
, niezależna od ciągu
podziałów i od wyboru pkt. pośrednich, to tą granicę nazywamy
28.Całki podwójne iterowane.
Niech
ciągła na prostokącie , wtedy istnieją całki iterowane
.
29.Def. całka potrójna.
Prostopadłościan .
Niech
będzie okreslona i ograniczona na prostopadłościanie
.
-podział prostopadłościanu
,
-objętość; pkt. pośrednie
; Suma całkowa
; średnica podziału
; ciąg
podziałów
; średnica ciągu podziału
; Jeżeli dla ciągu podziałów
to
mówimy, że ciag podziałów jest normalnym ciągiem podziałów; pkt.
pośrednie ciągu podziałów
; Jeżeli norm. ciągu
podziałów i dowolnego wyboru pkt. pośrednich skończona
,
niezależna od ciągu podziałów i od wyboru pkt. pośrednich, to tą granicę
nazywamy
30. Całki potrójne iterowane.
Jeżeli jest ciągła na prostopadłościanie , to istnieją całki
iterowane np.
31.Zast. całki potrójnej.
Niech obszar
będzie okr. obszar reg. ,
gdzie funkcje
są okr. i ciągłe na obszarze reg. , wtedy objętość
. Niech
,
obszar reg., funkcja jest kl.
w
i
są ograniczone, wtedy
pole płata pow.
32.Tw. o zmianie zmiennej.
Niech przekształcenie , odwzorowuje obszar
reg.
w obszar reg. . Niech w będzie określona funkcja
ograniczona i ciągła. Jeżeli 1)funkcje są kl.
w obszarze
obejmującym (brzeg); 2)jakobian przekszt.
w ;
3)przekształcenie jest różnowartościowe w to zachodzi wzór
,
33.Równanie R zwyczajne.
34.Co to jest problem początkowy Cauchy ’ego dla rów. R n-tego
rzędu.
Znaleźć rozwiązanie równania klasy
postaci
w
przedziale
, spełniające warunki początkowe:
,
.
35.Równanie R o zmiennych rozdzielonych.
Jeżeli jest ciągła w a , ciągła w , to
równanie
nazywamy równaniem różniczkowym o zm.
rozdzielonych. Przy powyższych zał. wzór przedst.
całkę ogólną równania
36.Równanie R jednorodne.
, funkcja ciągła w , ,
;
37.Równanie R liniowe I- rzędu.
ciągłe w
; Rozwiązaniem równania jednorodnego jest
przestrzeń liniowa(wektorowa) ; Rozwiązanie równania
niejednorodnego jest postaci
, gdzie
jest dowolnym rozw.
równania jednorodnego, a
jest pewnym rozw. równania
niejednorodnego (CSRN) ,
, gdzie
-(CORN), a -
(CORJ).
Tw.
.
Tw. Jeżeli jest ciągła w to wzór
,
,
, przedst.. całkę ogólną równania
, ponadto przez
każdy pkt. zb. przechodzi dokł. jedna całka równania
. Metoda uzmienniania stałych(wariacja zmiennych)
, np.
(1).
Tw. Jeżeli funkcje są ciągłe w , to wzór (1) przedstawia CORN
równania wyjściowego i ponadto przez każdy pkt. zb. przechodzi
dokł. jedna całka.
38.Równanie R Bernoulliego.
.
39.Równanie R zupełne.
,
są kl.
w pewnym obszarze
jednospójnym
.
gdy lewa str. jest
różniczką zupełną pewnej w , jest równanie różniczkowe
zupełne. jest całką ogólną równania
40.Warunek na zupełność (Schwarza).
Jeżeli funkcje są określone i kl.
, w prostokącie
, to równanie jest równaniem
różniczkowym zupełnym gdy spełniają warunek
.
41.Równanie R II- rzędu o stałych współczynnikach.
, są ciągłe w . Rozwiązaniem
jest
.