1
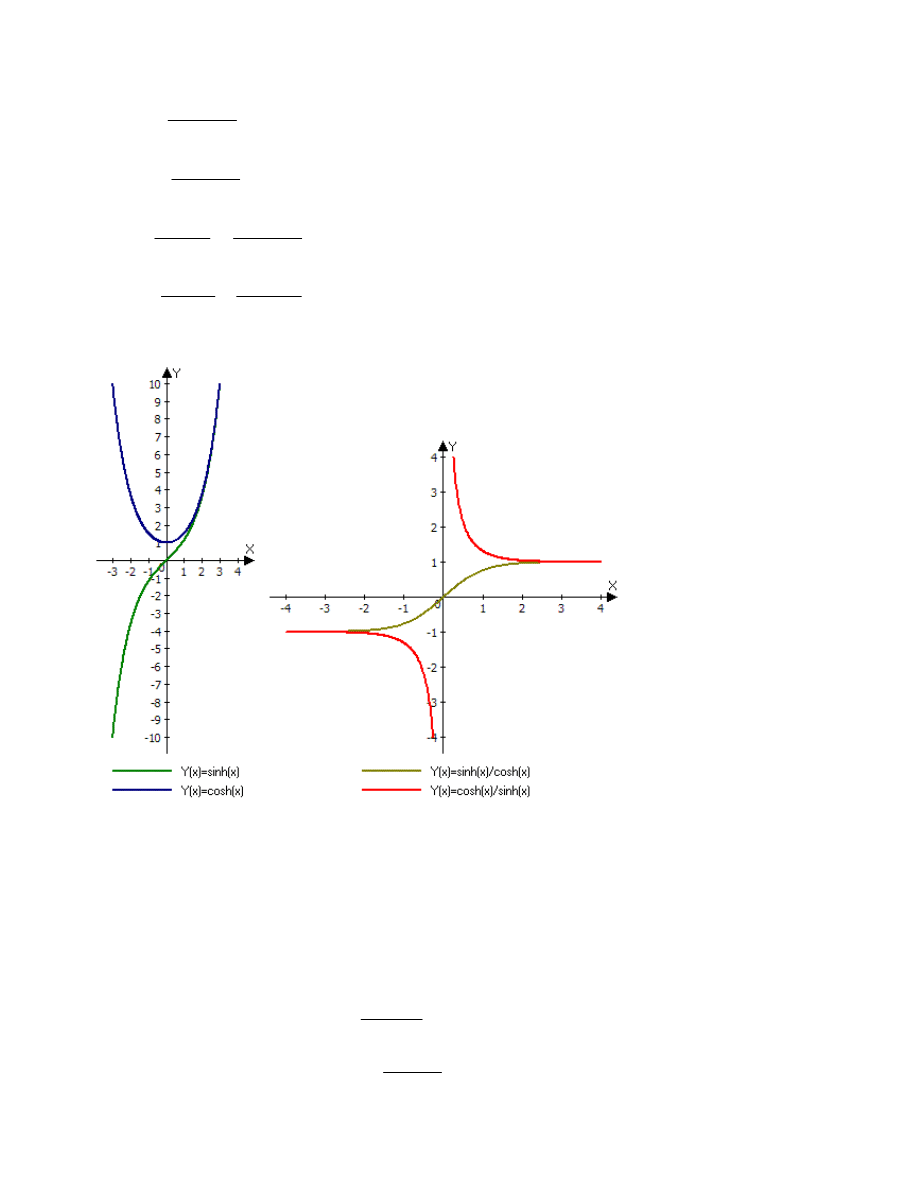
Funkcje hiperboliczne
x
x
x
x
x
x
x
x
e
e
e
e
x
x
tghx
e
e
x
e
e
x
−
−
−
−
+
−
=
=
+
=
−
=
cosh
sinh
:
2
:
cosh
2
:
sinh
,
gdzie
{ }
0
\
cosh
sinh
R
D
R
D
D
D
ctgh
tgh
=
=
=
=
x
x
x
x
e
e
e
e
x
x
ctghx
−
−
−
+
=
=
sinh
cosh
:
,
0
≠
x
Jedynka hiperboliczna
1
sinh
cosh
2
2
=
−
x
x
Inne wzory
x
x
x
x
x
x
cosh
sinh
2
2
sinh
sinh
cosh
2
cosh
2
2
⋅
=
+
=
(
)
(
)
x
x
x
x
sinh
cosh
cosh
sinh
=
′
=
′
(
)
(
)
x
ctghx
x
tghx
2
2
sinh
1
cosh
1
−
=
′
=
′

2
Nazwa (sinus hiperboliczny, …) wzi ła si st d, e funkcje
sinh
i
cosh
( )
( )
=
=
t
b
t
y
t
a
t
x
sinh
cosh
,
R
t
∈
które okre la hiperbol , bo
( )
( )
1
2
2
2
2
=
−
b
t
y
a
t
x
Wyszukiwarka
Podobne podstrony:
funkcje hiperboliczne
Funkcje hiperboliczne odwrotne
BANK CENTRALNY I JEGO FUNKCJE
Zaburzenia funkcji zwieraczy
Genetyka regulacja funkcji genow
BYT 2005 Pomiar funkcjonalnosci oprogramowania
Diagnoza Funkcjonalna
Insulinoterapia funkcjonalna
Postać kanoniczna funkcji kwadratowej
Wpływ choroby na funkcjonowanie rodziny
LAB PROCEDURY I FUNKCJE
STRUKTURA I FUNKCJONOWANIE GN
Hiperbilirubinemie J Radzięta
więcej podobnych podstron