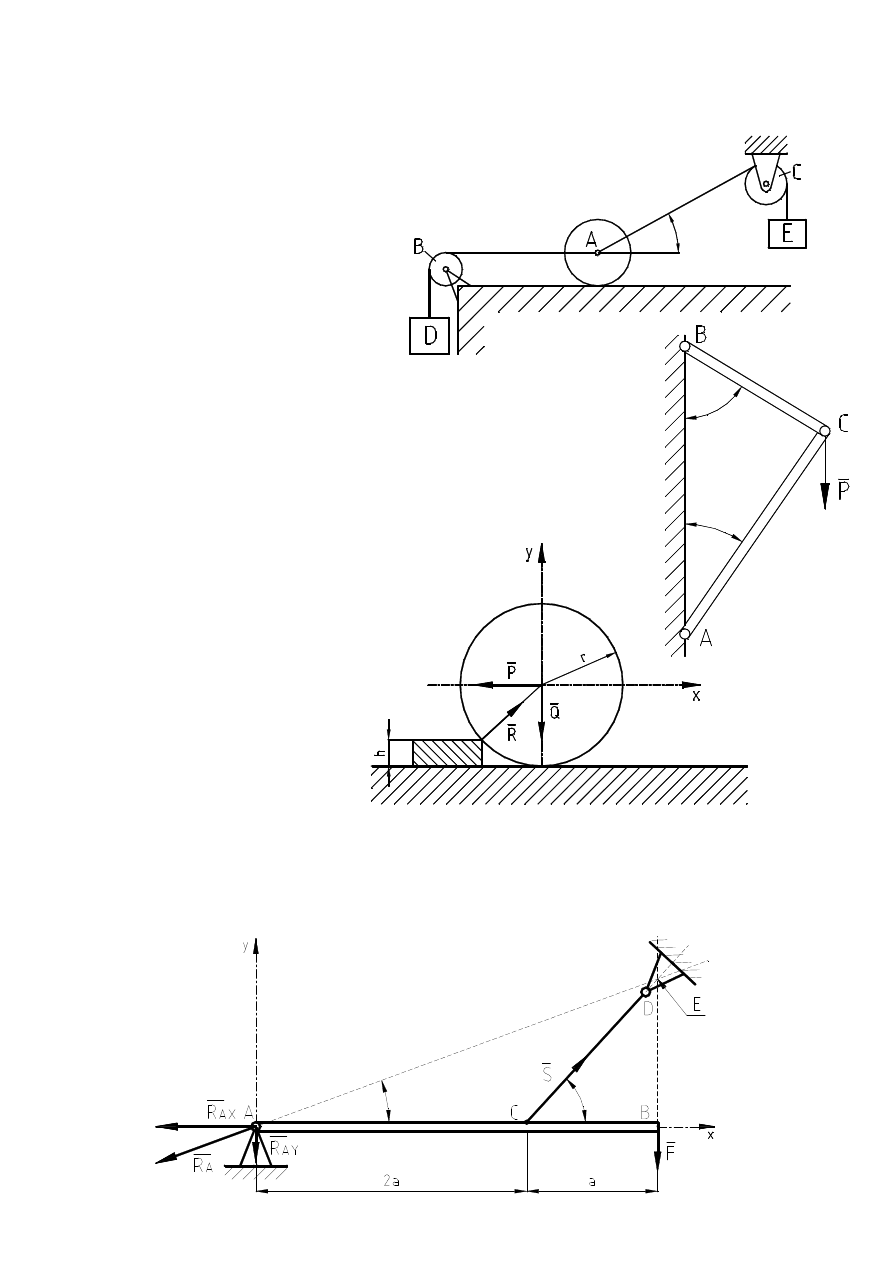
Zbieżny układ sił

1.

Walec (A) o ciężarze G=100 kN
znajduje

się

w

płaszczyźnie

poziomej. Obciążony jest ciałem
(D) o ciężarze P

1

=10 kN, za

pośrednictwem linki przerzuconej
przez blok (B), oraz ciałem (E) o
ciężarze P

2

=20 kN, poprzez linkę

przerzuconą

przez

blok

(C).

Wyznaczyć reakcję walca, oraz kąt

α

linki AC utrzymującej walec w

równowadze.

2.

Nieważki pręty AC i BC są połączone za pomocą przegubów ze
sobą w punkcie C, oraz z pionową ścianą w punktach A i B. Przegub
C został obciążony pionową siłą P=100 kN. Wyznaczyć siły reakcji
prętów na przegub C, jeżeli pręty tworzą ze ścianą kąty

α

=30

o

,

β

=60

o

.

3.

Walec o promieniu r i ciężarze
Q ma być przetoczony bez
poślizgu

przez

próg

o

wysokości h. Obliczyć wartość
poziomej siły P potrzebnej do
przetoczenia

walca,

oraz

reakcję progu R.

4.

Nieważka belka AB zamocowana przegubowo w punkcie A utrzymywana jest w
położeniu poziomym za pomocą linki przywiązanej do belki w punkcie C i tworzącej z
nią kąt

α

. Określić reakcję R

A

przegubu A, oraz siłę S napinającą linkę, jeżeli na końcu B

belki działa pionowa siła F. Dane: a=100 cm,

α

=45

o

, F=5 kN.

α

β

α

β

α

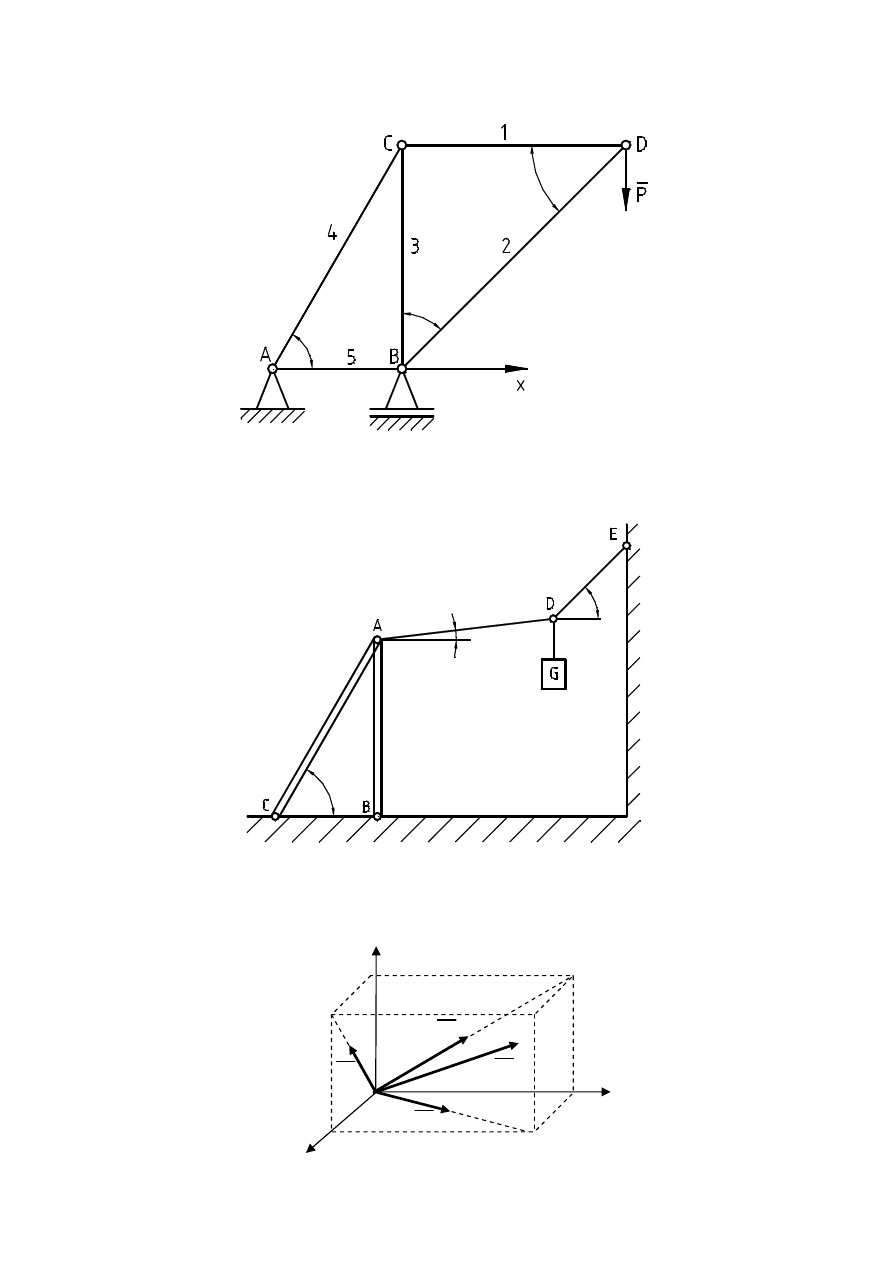
5.

Obliczyć siły wewnętrzne w prętach 1

÷

5 konstrukcji dźwigu, obciążonego w węźle D

siłą P=30 kN, dla zadanych wielkości kątów:

α

=45

o

,

β

=60

o

.

α

α

β

6.

Ciało o ciężarze G=518 N zawieszono w punkcie D za pomocą układu lin i prętów jak na
rysunku. Dla danych

α

=

π

/6,

β

=

π

/4,

γ

=

π

/3, wyznaczyć naciągi w linach i siły w prętach.

α=

30

°

β=

45

°

γ=6

0°

7.

Obliczyć wektor wypadkowy W trzech sił leżących na przekątnych ścian
prostopadłościanu o krawędziach a

×

b

×

c=6

×

8

×

9 (cm). Wartości sił wynoszą: P

1

=200 N,

P

2

=300 N, P

3

=400 N.

z

x

y

P

3

P

1

P

2

W

a

b

c