Przestrzenny dowolny układ sił 

 
 
 
Przykład 1 
 
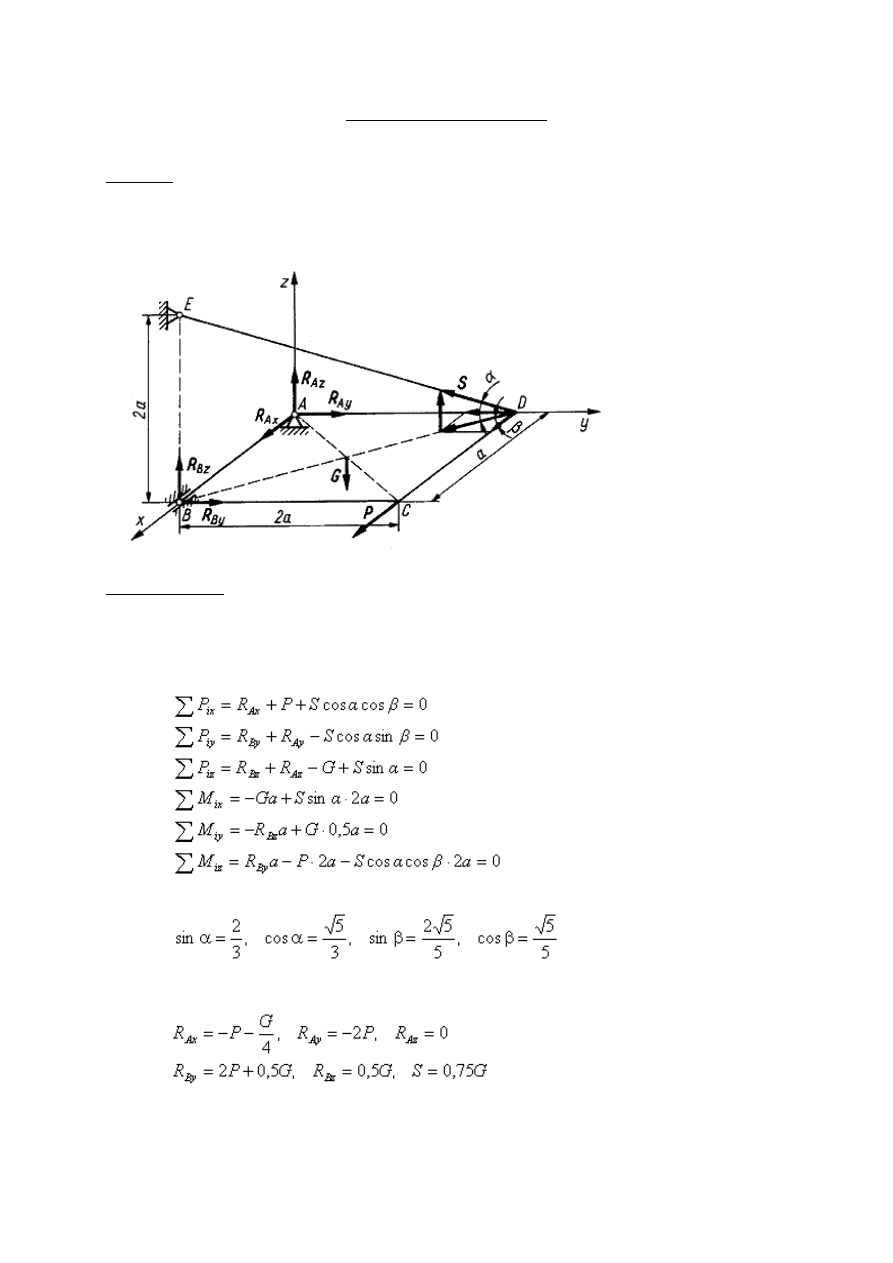
Prostokątna płyta ABCD o wymiarach a × 2a i ciężarze G została podparta na stałej podporze przegubowej w 
punkcie 

A i na przegubie walcowym w punkcie B oraz cięgnie DE. W punkcie C płytę obciążono dodatkowo siłą P. 

Obliczyć reakcje podpór i cięgna. Tarcie w przegubach należy pominąć.  
 

 

 
 
R o z w i ą z a n i e. 
 
Początek przestrzennego układu współrzędnych obrano w punkcie A. Reakcję w podporze A należy rozłożyć na 
trzy składowe R

Ax

, 

R

Ay 

i 

R

Az

. Reakcja w punkcie 

B jest prostopadła do osi Ax i należy ją rozłożyć na R

By 

i 

R

Bz

. Cięgno 

DE może być tylko rozciągane siłą S. W przyjętym układzie współrzędnych otrzymujemy następujące równania 
równowagi 
 

                  

 

 
gdzie 

                  

 

 
Z rozwiązania powyższego układu równań otrzymujemy odpowiedź 
 

                 

 

 
 
 
 

 

Przykład 2 
 
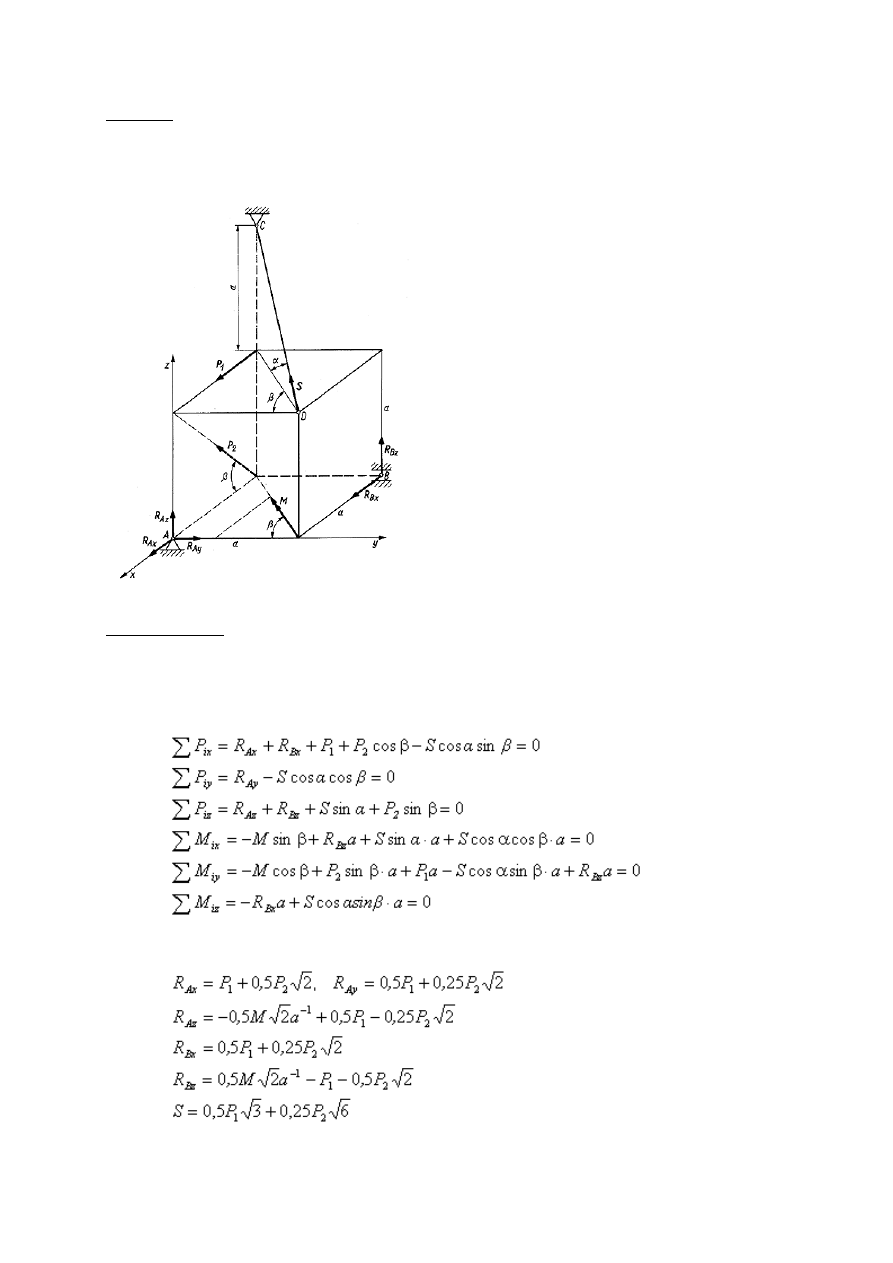
Ciało sztywne o kształcie sześcianu zostało podparte na stałej podporze przegubowej w punkcie A i przegubie 
walcowym (łożysko szyjne) w punkcie B oraz cięgnie CD. Obliczyć reakcje podpór i cięgna na ciało w przypadku, 
gdy działają na nie dwie siły P

1 

i 

P

2  

oraz moment 

M. Ciężar ciała oraz tarcie w przegubach należy pominąć. 

 

 

 
 
R o z w i ą z a n i e. 
 
Początek prostokątnego układu współrzędnych obrano w punkcie A stałej podpory przegubowej. Reakcje w tej 
podporze należy rozłożyć na trzy składowe R

Ax

, 

R

Ay 

i 

R

Az

. Reakcja w punkcie 

B jest prostopadła do osi A

y

 

i należy ją 

rozłożyć na dwie składowe R

Bx 

i 

R

Bz

. Cięgno CD może być tylko rozciągane siłą S. W przyjętym układzie 

współrzędnych otrzymujemy następujące równania równowagi 
 

                 

 

 
Po rozwiązaniu tego układu równań otrzymujemy