
Wojciech Wierzchowski
Podstawy fizyki jądrowej dla inżynierów
Materiały pomocnicze do wykładów
z podstaw fizyki
Wrocław 2008


Spis treści
Rozdział 1. Wstęp ............................................................................................................................................... 5
Rozdział 2. Budowa jądra atomowego .............................................................................................................. 7
2.1. Rozmiary jądra atomowego ....................................................................................................................... 9
2.2. Spin i moment magnetyczny jądra ........................................................................................................... 10
2.3. Energia wiązania jądra ........................................................................................................................... 11
2.4. Siły jądrowe ............................................................................................................................................. 13
Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze ........................................................................... 17
3.1. Reakcje jądrowe ...................................................................................................................................... 17
3.2. Bilans mas i energii w reakcjach jądrowych ........................................................................................... 18
3.3. Rozpady promieniotwórcze ..................................................................................................................... 21
3.4. Rodziny promieniotwórcze ...................................................................................................................... 24
Rozdział 4. Rozpady promieniotwórcze ......................................................................................................... 27
4.1. Rozpad α .................................................................................................................................................. 27
4.2. Charakterystyczne cechy rozpadu α ........................................................................................................ 28
4.3. Widma energetyczne cząstek α ................................................................................................................ 29
4.4. Warunki energetyczne i mechanizm rozpadu α ....................................................................................... 31
4.5. Rozpad β .................................................................................................................................................. 33
4.6. Wychwyt K ............................................................................................................................................... 35
4.7. Warunki energetyczne rozpadu β ............................................................................................................ 37
4.8. Widmo energetyczne cząstek β, hipoteza neutrino .................................................................................. 38
4.9. Właściwości neutrina .............................................................................................................................. 41
Rozdział 5. Sztuczna promieniotwórczość ..................................................................................................... 43
5.1. Uwagi na temat rozpadów β
–
i β
+
.......................................................................................................... 44
5.2. Transuranowce ........................................................................................................................................ 44
5.3. Promieniowanie γ .................................................................................................................................... 46
5.4. Konwersja wewnętrzna ............................................................................................................................ 47
Rozdział 6. Reakcje rozszczepienia jądra atomowego .................................................................................. 49
6.1. Reakcja rozszczepienia jądra .................................................................................................................. 52
6.2. Podział jądra pod wpływem bombardowania neutronami ...................................................................... 53
6.3. Przebieg reakcji podziału ........................................................................................................................ 54
6.4. Energia wydzielana w akcie podziału jądra ............................................................................................ 55

6.5. Fragmenty podziału ................................................................................................................................. 56
6.6. Promieniowanie neutronowe. Neutrony opóźnione ................................................................................. 57
6.7. Możliwość wykorzystania energii rozszczepienia .................................................................................... 58
Rozdział 7. Reaktory jądrowe ......................................................................................................................... 69
7.1. Typy reaktorów ........................................................................................................................................ 69
7.2. Reaktor PWR ........................................................................................................................................... 69
7.3. Reaktor BWR ........................................................................................................................................... 70
Rozdział 8. Reakcje syntezy termoądrowej ................................................................................................... 73
Literatura ........................................................................................................................................................... 77

Rozdział 1.
Wstęp
Jądrem atomowym nazywamy centralną część atomu o wymiarach liniowych rzędu
m
10
15
−
≈
i
R
(wymiary liniowe atomu są rzędu
m
10
10
−
≈
at
R
). W jądrze skupiony jest cały
dodatni ładunek atomu i praktycznie cała jego masa. Wszystkie jądra możemy podzielić na
stabilne i niestabilne. Jądra stabilne to takie, które pozostają dostatecznie długo
w niezmienionym stanie. Jądra niestabilne ulegają spontanicznym przemianom.
Najważniejszymi wielkościami charakteryzującymi jądra są:
1)
Liczba atomowa
Z (zwana także liczbą porządkową),
2)
Liczba masowa
A,
3)
Masa i energia wiązania,
4)
Promień jądra,
5)
Spin jądra,
6)
Moment magnetyczny.
Jądro charakteryzują jeszcze inne wielkości, takie jak elektryczny moment kwadrupolowy,
izospin, parzystość, ale tych wielkości nie rozpatruje się na podstawowym poziomie wiedzy
o jądrze.
Jądra niestabilne dodatkowo charakteryzujemy rodzajem przemiany (α
, β, γ itd.), okresem
połowicznego zaniku, stałą rozpadu, energią bombardujących cząstek itp.


Tabela 1. Liczby masowe i masy atomowe kilku wybranych pierwiastków w jma.
Jądro
A
M [jma]
He
4
2
4
4,002602
Li
7
3
7
6,941
Be
7
4
7
9,012182
N
14
7
14
14,00674
O
16
8
16
15,9994
Rozdział 2.
Budowa jądra atomowego
Zgodnie z protonowo-neutronową hipotezą w skład jądra wchodzą tylko protony i neutrony.
Protony i neutrony są jedynymi składnikami jądra atomowego. Samo jądro jako odrębny twór
zwane jest także nuklidem. Proton jest cząstką o ładunku
+1e. Neutron jest cząstką
elektrycznie obojętną. Ładunek jądra jest określony liczbą protonów w jądrze (a tym samym
liczbą elektronów powłokowych w obojętnym atomie). Liczbę protonów w jądrze nazywamy
liczbą atomową
Z. Liczba protonów w jądrze pokrywa się z numerem porządkowym
pierwiastka w układzie okresowym pierwiastków – stąd druga nazwa – liczba porządkowa
(w krajach zachodnich używa się określenia – liczba protonowa). Protony i neutrony mają
wspólną nazwę – nukleony.
Masa jądra jest jedną z najważniejszych wielkości charakteryzujących jądro. Masę jądra
wyznaczają masy protonów i neutronów. Sumę liczby protonów i neutronów w jądrze
nazywamy liczbą masową
A. W fizyce jądrowej masę jądra (a także masę atomu) wyrażamy
w jednostkach masy atomowej (jma). Za jednostkę masy atomowej przyjmujemy 1/12 masy
izotopu węgla C
12
6
kg
10
6603
,
1
)
C
(
12
1
jma
1
27
12
6
−
⋅
=
=
M
Masy protonu, neutronu i atomu wodoru wynoszą:
jma
007276
,
1
kg
10
6725
,
1
27
=
⋅
=
−
p
M
jma
008665
,
1
kg
10
6748
,
1
27
=
⋅
=
−
n
m
jma
007829
,
1
kg
10
6734
,
1
27
=
⋅
=
−
H
m
Przykłady mas atomowych kilku pierwiastków wyrażone w jma podano w tabeli 1.
Inna definicja liczby masowej: liczbą masową A nazywamy liczbę całkowitą najbliższą
masie atomowej jądra wyrażonej w jma.
Każde jądro opisujemy za pomocą symboli:
X
A
Z
, gdzie A – liczba masowa jest sumą
protonów i neutronów w jądrze, Z – liczba atomowa – podaje liczbę protonów w jądrze.
8
Rozdział 2. Budowa jądra atomowego
Liczba neutronów w jądrze wynosi N = A – Z
Często masę jądra lub innej cząstki wyrażamy w jednostkach energii. Zgodnie ze wzorem
Einsteina masie spoczynkowej
0
m odpowiada energia
2
0
c
m
E
=
. Jeżeli masę
0
m wyrazimy
w kilogramach, a prędkość świata w m/s, to otrzymamy energię wyrażoną w dżulach
2
2
16
0
2
8
0
s
m
10
9
)
kg
(
s
m
10
3
)
kg
(
)
(
⋅
⋅
=
⋅
⋅
=
m
m
J
E
a więc masie 1 kg odpowiada 9·10
16
dżuli energii. W obliczeniach jądrowych i atomowych
posługujemy się elektronowoltami
J
10
6
,
1
eV
1
19
−
⋅
=
stąd
eV
10
6
,
1
1
J
1
19
⋅
=
eV
10
62
.
5
)
kg
(
6
,
1
eV
10
10
9
)
kg
(
)
eV
(
35
0
19
16
0
⋅
⋅
=
⋅
⋅
=
m
m
E
Jednemu kilogramowi masy odpowiada energia równa
eV
10
62
,
5
35
⋅
. Masa spoczynkowa
elektronu odpowiada energii
MeV
511
,
0
kg
10
1
,
9
31
=
⋅
=
−
e
m
.
Jednostce masowej odpowiada następująca energia:
MeV
45
,
931
kg
10
6603
,
1
jma
1
27
=
⋅
=
−
Masy protonu i neutronu wynoszą:
MeV
2
,
938
kg
10
6725
,
1
27
=
⋅
=
−
p
m
MeV
5
,
939
kg
10
6748
,
1
27
=
⋅
=
−
n
m
Izotopami danego pierwiastka nazywamy różne odmiany tego samego pierwiastka
identyczne pod względem własności chemicznych, lecz różniące się masami atomowymi.
Rozdzielenie izotopów metodami chemicznymi jest niezmiernie trudne, prawie niemożliwe.
Izotopy danego pierwiastka mają tę samą liczbę protonów (liczbę Z), różnią się jednak liczbą
masową A. Wynika z tego, że izotopy różnią się liczbą neutronów w jądrze. Przykłady
izotopów:
H
1
1
, H
2
1
(lub D
2
1
), H
3
1
(lub T
3
1
) – wodór, deuter, tryt
He
3
2
, He
4
2
; K
39
19
, K
40
19
, K
41
19
Izobarami nazywamy jądra o tej samej liczbie masowej A, ale o różnych liczbach
atomowych Z. Przykłady izobarów:
H
3
1
i He
3
2
;
Sn
124
50
,
Te
124
52
,
Xe
124
54
Tak więc izobary mają jednakowe liczby masowe, lecz różne liczby protonów w jądrze
(liczby atomowe).

Rozdział 2. Budowa jądra atomowego
9
Izotonami nazywamy nuklidy o tej samej liczbie neutronów w jądrze, np.:
O
18
8
, F
19
9
i
Ne
20
10
; Mg
26
12
i Al
27
13
2.1. Rozmiary jądra atomowego
Oszacowany różnymi metodami doświadczalnymi promień jądra wynosi
)
f
(
3
/
1
0
A
r
R
=
;
m
10
fermi
1
f
1
15
−
=
=
(1)
gdzie:
f
)
5
,
1
—
2
,
1
(
m
10
)
5
,
1
—
2
,
1
(
15
0
=
⋅
=
−
r
– fenomenologiczny zasięg sił jądrowych,
natomiast
A jest liczbą masową. Przyjmuje się, że
m
10
4
,
1
15
0
−
⋅
=
r
.
Gęstość materii jądrowej ρ
j
możemy obliczyć ze wzoru:
3
45
3
27
3
0
3
m
10
)
4
,
1
(
π
3
4
kg
10
67
,
1
π
3
4
π
3
4
−
−
⋅
⋅
=
=
=
=
A
r
Am
R
Am
V
M
n
n
j
j
j
ρ
3
17
m
kg
10
4
,
1
⋅
=
j
ρ
gdzie:
M
j
–masa jądra, a
V
j
oznacza objętość jądra.
Porównując ρ
j
z gęstością atomową i przyjmując, że promień atomu jest 10
4
razy większy
od promienia jądra, możemy oszacować, że gęstość atomów:
3
5
3
3
4
17
m
kg
10
4
,
1
m
kg
)
10
(
10
4
,
1
⋅
=
⋅
=
at
ρ
Gęstość materii skondensowanej, np. wody, wynosi:
3
3
m
kg
10
=
ρ
Z przytoczonych oszacowań wynika, że gęstości jąder są bardzo duże w porównaniu
z gęstością atomów lub gęstością występujących na Ziemi cieczy lub ciał stałych.
Rys.1. Rozkład gęstości materii w jądrze atomowym;
R – promień jądra.

10
Rozdział 2. Budowa jądra atomowego
Rozkład gęstości materii i gęstości ładunku wewnątrz jąder jest jednorodny, analogicznie
jak gęstość cieczy jest stała i nie zależy od rozmiarów kropli. Gęstość materii jądrowej
j
ρ
maleje na powierzchni jądra (rys. 1).
2.2. Spin i moment magnetyczny jądra
Proton i neutron, podobnie jak elektron, mają swój własny moment pędu, czyli spin,
wywołany wirowaniem tych cząstek wokół własnej osi. Wartość spinu każdej z tych cząstek
wynosi:
ℏ
)
1
(
+
=
s
s
L
s
gdzie
s jest spinową liczbą kwantową, zwyczajowo zwaną spinem. Jej wartość wynosi
2
1
=
s
, dlatego potocznie mówimy, że spin protonu i neutronu jest połówkowy.
Moment magnetyczny jądra. Protonowi możemy przypisać (oczekiwany) moment
magnetyczny wynoszący:
p
p
j
m
e
2
ℏ
=
=
µ
µ
Ten oczekiwany moment magnetyczny nazywamy magnetonem jądrowym przez analogię do
magnetonu Bohra, który jest elementarnym momentem magnetycznym elektronu:
e
B
m
e
2
ℏ
=
µ
Ponieważ masa protonu jest 1836 razy większa od masy elektronu to magneton jądrowy jest
tyle razy mniejszy od magnetonu Bohra. Tymczasem wyznaczone momenty magnetyczne
protonu i neutronu wynoszą:
j
j
p
µ
µ
µ
79
,
2
7896
,
2
≈
=
j
j
n
µ
µ
µ
91
,
1
9128
,
1
−
≈
−
=
Tak więc moment magnetyczny protonu jest znacznie większy od oczekiwanego (magnetonu
jądrowego
j
µ
), a ujemny znak momentu magnetycznego neutronu wskazuje, że jest on
skierowany przeciwnie do momentu pędu (neutronu). W protonie, który ma ładunek dodatni,
moment pędu i moment magnetyczny mają ten sam zwrot.
Najbardziej nieoczekiwane jest jednak istnienie momentu magnetycznego neutronu.
Zwykle własności magnetyczne towarzyszą zjawiskom elektrycznym, lecz dotychczas nie
udało się wyznaczyć ładunku elektrycznego neutronu.
Jądra atomowe jako układy złożone z protonów i neutronów mają także spiny i momenty
magnetyczne związane ze spinami i momentami magnetycznymi nukleonów. Między spinem
jądra a jego liczbą masową występuje prosta zależność: jądra o parzystej liczbie masowej
mają spin całkowity (lub zero), a jądra o nieparzystej liczbie masowej mają spin połówkowy.
Rozdział 2. Budowa jądra atomowego
11
Wyniki pomiarów spinów i momentów magnetycznych nuklidów stabilnych
przedstawiono w tabeli 2.
Widzimy, że wśród jąder stabilnych przyroda preferuje kombinację parzystej liczby
protonów i parzystej liczby neutronów. Liczba kombinacji parzysta – nieparzysta
i nieparzysta – parzysta tworząca stabilne jądro jest prawie taka sama. Tylko cztery jądra
o kombinacji nieparzystej liczby protonów z nieparzystą liczbą neutronów są stabilne. Są to:
N
,
B
,
Li
,
H
14
7
10
5
6
3
2
1
.
Wartości spinów jąder nie przekraczają kilku jednostek. Świadczy to o tym, że spiny
nukleonów nie ustawiają się równolegle do siebie i nie dodają się algebraicznie. Gdyby tak
było, to spin jądra wynosiłby A/2. Mała wartość spinów jąder dowodzi, że spiny nukleonów
kompensują się, czyli że występuje tu zjawisko tzw. dwójkowania, a o spinie (i momencie
magnetycznym) jądra decyduje tylko niewielka liczba nukleonów. (Dwójkowanie polega na
tym, że spiny dwóch protonów ustawiają się parami antyrównolegle oraz spiny dwóch
neutronów też ustawiają się parami antyrównolegle).
2.3. Energia wiązania jądra
Znajomość dokładnej masy protonu i neutronu pozwala porównać masę jądra z sumą mas
wszystkich nukleonów, z jakich to jądro się składa. Okazuje się, że zawsze masa jądra jest
mniejsza od sumy mas protonów i neutronów będących składnikami tego jądra. To zjawisko
nazywa się defektem masy:
)
,
(
N
Z
M
Nm
Zm
j
n
p
>
+
Różnicę mas
)
,
(
)
(
N
Z
M
Nm
Zm
m
j
n
p
−
+
=
∆
nazywamy defektem (deficytem, niedoborem)
masy. Tak więc, gdy Z protonów i N neutronów łączy się, tworząc jądro, część masy zostaje
zamieniona na energię. Tę energię nazywamy energią wiązania
w
E :
2
2
))
,
(
(
)
(
c
N
Z
M
c
Nm
Zm
E
i
n
p
w
−
+
=
Całe wyrażenie ma wymiar energii zgodnie ze wzorem Einsteina przedstawiającym
równoważność masy i energii. Ta energia nosi nazwę energii wiązania jądra. Energia
wiązania jest to energia, jaka zostałaby wydzielona podczas budowania (zestawiania) jądra
z jego składników. Zestawianie jądra jest procesem egzoenergetycznym. Można powiedzieć
Tabela 2. Spiny i momenty magnetyczne nuklidów stabilnych.
A
Liczba
protonów
Liczba
neutronów
Spin s
j
Moment magnetyczny
µ
j
Liczba stabilnych
nuklidów
Parzyste
parzysta
parzysta
0
0
160
nieparzysta
nieparzysta
Całkowity
1, 2, 3 …
Dodatni
4
Nieparzyste
parzysta
nieparzysta
Połówkowy
1/2, 3/2, 5/2
Mały i ujemny
56
nieparzysta
parzysta
Połówkowy
1/2, 3/2, 5/2
Duży i dodatni
52
12
Rozdział 2. Budowa jądra atomowego
inaczej – aby jądro rozbić na jego składniki, należy mu dostarczyć energii równej co najmniej
energii wiązania. Rozbicie jądra jest więc procesem endoenergetycznym.
Energia wiązania jest bardzo duża – liczy się w milionach elektronowoltów. Każde jądro
ma swoją ściśle określoną energię wiązania, np.:
MeV
28
)
He
(
4
2
≅
w
E
MeV
128
)
O
(
16
8
≅
w
E
MeV
92
)
C
(
12
6
≅
w
E
MeV
272
)
S
(
32
16
≅
w
E
Energia wiązania jest miarą trwałości jądra. Jeżeli energia wiązania jest dodatnia, to jądro jest
stabilne i rozbicie go na składniki wymaga dostarczenia energii z zewnątrz. Jeżeli
w
E < 0, to
jądro jest niestabilne i rozpada się samorzutnie. Im większa jest energia wiązania, tym
stabilniejsze jest jądro.
Ś
rednia energia wiązania nukleonu w jądrze jest to energia wiązania przypadająca na jeden
nukleon:
A
E
w
=
ε
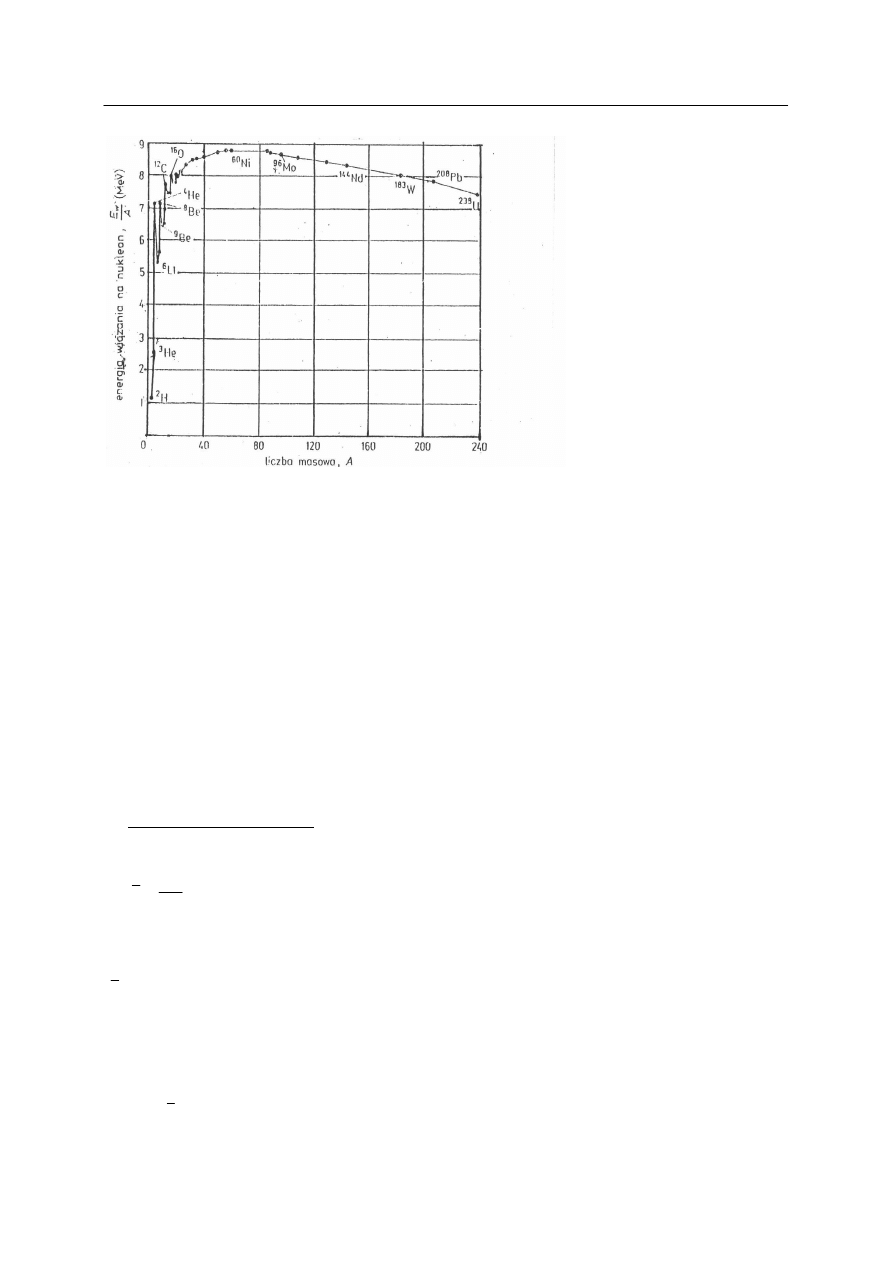
Zależność średniej energii wiązania od liczby nukleonów w jądrze (od liczby masowej A)
przedstawia rysunek 2. Widzimy, że wartość średniej energii wiązania szybko wzrasta od
0
=
ε
dla
A = 1 do 8 MeV dla A = 16, następnie osiąga maksimum 8.8 MeV dla A = 60
i następnie maleje do 7,6 MeV dla
A = 238 (dla ostatniego występującego w przyrodzie
pierwiastka
U
238
92
). Dla większości nuklidów średnia energia wiązania wynosi około 8 MeV.
W pierwszym przybliżeniu przyjmujemy, że średnia energia wiązania jest stała i wynosi
8 MeV
. Zależność energii wiązania
w
E od liczby nukleonów A można otrzymać ze wzoru:
A
E
w
ε
=
(2)
Z równania (2) wynika liniowa zależność między energią wiązania
E
w
i liczbą nuklidów
w jądrze
A.
Rys. 2. Średnia energia wiązania przypadająca na jeden nukleon w jądrze w zależności od liczby masowej A [1].
Rozdział 2. Budowa jądra atomowego
13
2.4. Siły jądrowe
Przyciągający charakter sił jądrowych. Protony w jądrze są gęsto upakowane i zgodnie
z prawem Coulomba działają między nimi siły elektrostatyczne (odpychające). Wiemy
jednak, że jądro jest bardzo trwałym układem nukleonów i tę dużą trwałość jądra można
wytłumaczyć tylko tym, że między nukleonami w jądrze działają duże siły przyciągające,
znacznie większe od elektrycznych sił odpychania. Przyciągający charakter sił jądrowych
wynika z tego, że zarówno energia wiązania, jak i średnia energia wiązania są dodatnie.
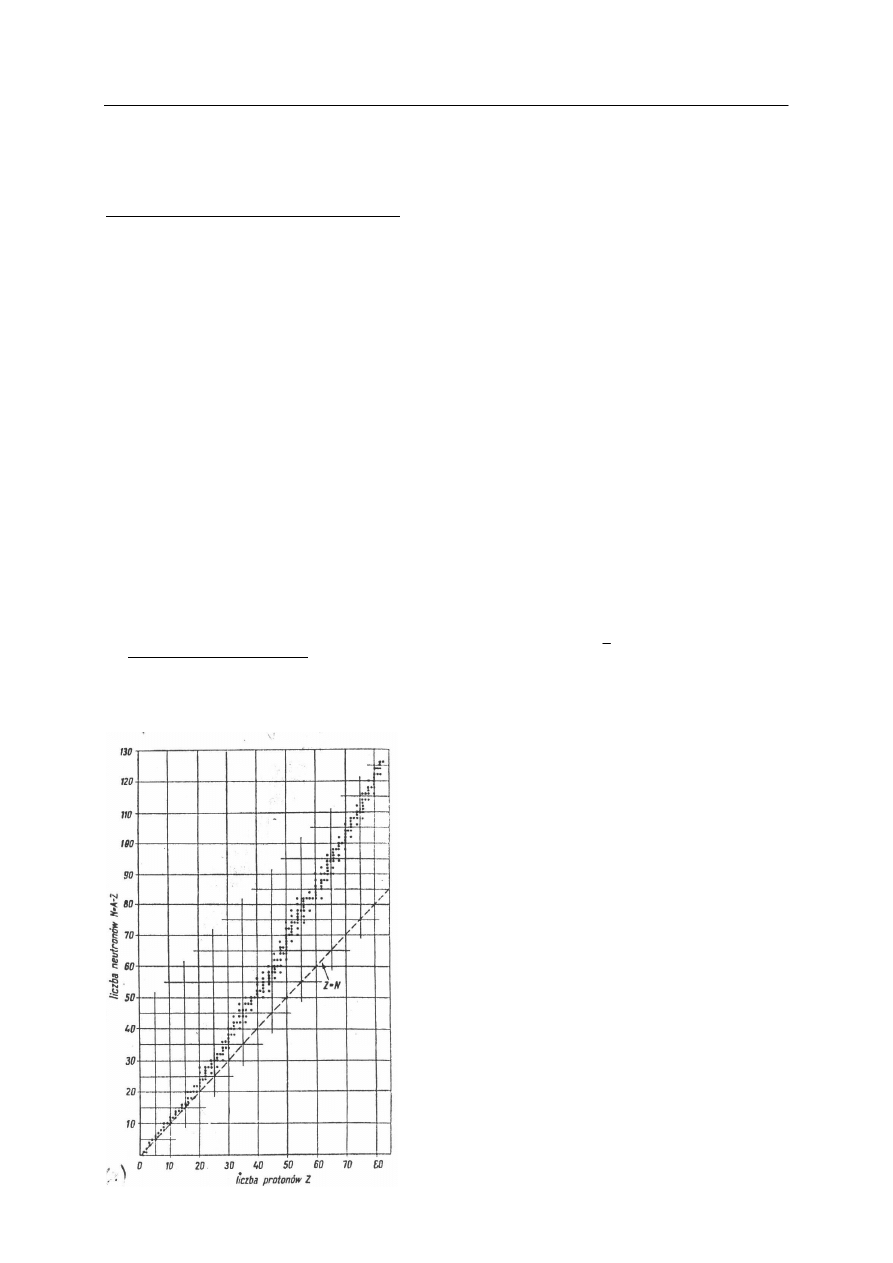
Ś
wiadczy o tym także zależność liczby neutronów
N od liczby protonów dla jąder stabilnych.
Dla lekkich jąder aż do
Z = 20 liczba neutronów jest równa liczbie protonów (z wyjątkiem
wodoru H
1
1
i izotopu helu He
3
2
). Dla cięższych jąder liczba neutronów przeważa nad
protonami. Stosunek
N/Z waha się od 1 do 1,6 dla
U
238
92
. Dla lekkich jąder do
Z = 20 wykres
N = f
(
Z), tzw. linia stabilności, jest linią prostą, a dla cięższych od Z = 20 i N = 20 krzywa
stabilności ulega zakrzywieniu (rys. 3). Wzrost udziału neutronów dla jąder o dużych
Z
można wyjaśnić tym, że należy skompensować rosnącą siłę odpychania elektrostatycznego
między coraz większą liczbą protonów w jądrze. Poszczególne własności sił jądrowych są
dostatecznie dobrze zbadane na drodze doświadczalnej. Dotychczas jednak nie udało się
znaleźć ogólnego prawa wyrażonego za pomocą jednego wzoru (jak na przykład prawo
Coulomba dla sił elektrostatycznych), które opisywałoby wszystkie własności sił jądrowych.
Brak takiego prawa nie pozwala na stworzenie jednolitej teorii jądra. W celu opisania
własności sił jądrowych stosuje się kilka modeli jądrowych, z których każdy odtwarza tylko
niektóre cechy budowy jądra oraz własności sił jądrowych i może być przydatny tylko do
opisu ograniczonego zakresu zjawisk zachodzących w jądrze.
Wielkość sił jądrowych. Duża wartość średniej energii wiązania
MeV
8
=
ε
(przypadającej
na jeden nukleon) mówi o tym, że siły jądrowe są bardzo duże; dwa nukleony (obiekty
mikroskopijne) o wymiarach rzędu 10
–12
cm mogą się przyciągać z siłą równą ciężarowi masy
około 10 ton.
Rys. 3. Liczba neutronów N w zależności od liczby
protonów Z dla trwałych nuklidów [2].
14
Rozdział 2. Budowa jądra atomowego
Zasięg sił jądrowych. Siły jądrowe są przyciągające na odległościach rzędu 1–2 fm (1 fm =
10
–15
m)
. Zasięg tych sił jest więc niewiele większy od promienia samego nukleonu i równy
ś
redniej odległości między nukleonami. Oznacza to, że każdy nukleon oddziałuje tylko
z nukleonami znajdującymi się najbliżej niego. Są to więc siły krótkiego zasięgu. Ich
działanie gwałtownie maleje, nawet do zera, dla odległości większych od 2·10
–15
m.
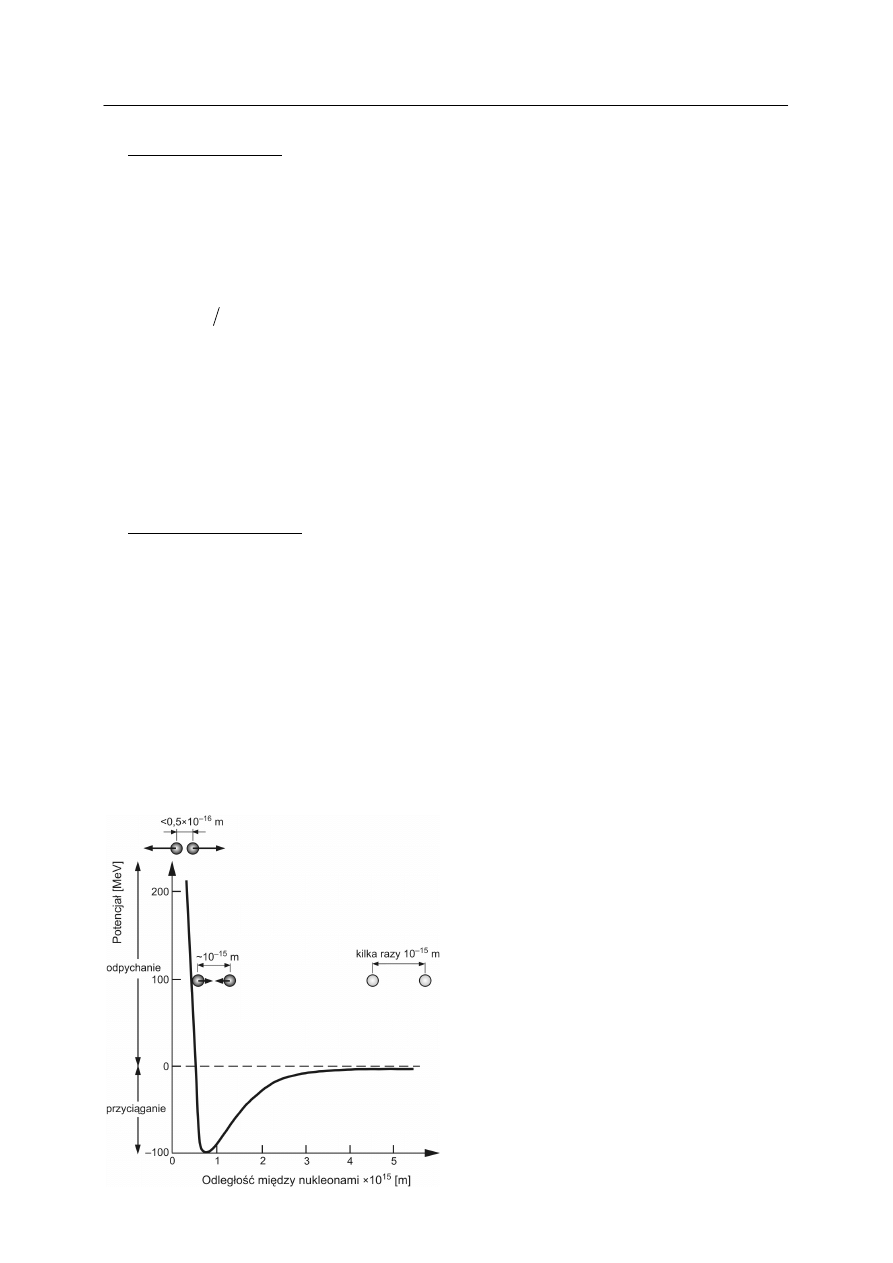
Na rysunku 4 przedstawiony jest potencjał sił jądrowych w zależności od odległości od
jądra. Dla odległości mniejszych od promienia jądra, potencjał sił jądrowych musi być
funkcją bardzo silnie malejącą, którą często przedstawia się za pomocą potencjału Yukawy
(
)
r
r
V
exp
~
α
−
dla
fm
2
–
1
4
,
0
≤
≤
r
, gdzie α
stała, a r to odległość od jądra. Przypuszcza
się, że na odległościach bardzo małych, mniejszych od 0,4–0,5 fm siły jądrowe są siłami
przyciągającymi (rys. 4). Może tak być dlatego, że:
a) jądro zajmuje pewien skończony
obszar w przestrzeni, a nukleony rozłożone są w nim na pewnych skończonych odległościach,
to znaczy, że począwszy od pewnych odległości między nukleonami, siła przyciągania
między nimi zamienia się na siłę odpychania;
b) gęstość materii jądrowej jest stała, jest ona
jednakowa dla różnych jąder, a zatem nie zależy od
A. Gdyby siły jądrowe miały
przyciągający charakter na każdej odległości, to gęstość materii jądrowej musiałaby rosnąć
wraz ze wzrostem
A, gdyż każdy nukleon znajdowałby się w zasięgu działania (przyciągania)
pozostałych nukleonów.
Właściwość wysycania. Ta właściwość oznacza, że oddziaływanie siłami jądrowymi na
inne cząstki zanika (wysyca się), gdy nukleon jest całkowicie otoczony innymi nukleonami.
Nukleon oddziałuje nie ze wszystkimi otaczającymi go nukleonami, nawet jeśli te sąsiednie
nukleony znajdują się w promieniu działania sił jądrowych. Siły jądrowe są jedynymi siłami
w przyrodzie mającymi własność wysycania. Wysycanie wynika z charakteru zależności
energii wiązania jąder od liczby masowej
A. Gdyby nie było zjawiska wysycania, to każdy
z
A nukleonów oddziaływałby z (A – 1) pozostałymi nukleonami. Wtedy energia wiązania
byłaby proporcjonalna do
A (A – 1), czyli do A
2
, a nie liniowo zależała od
A, zgodnie ze
wzorem (2). Tak więc w przypadku oddziaływań jądrowych nie można przedstawić sił
działających na dany nukleon jako sumy sił pomiędzy poszczególnymi nukleonami. Własność
wysycania jest analogiczna do własności wysycania wiązań chemicznych. Wiązanie między
atomami wodoru wysyca się dla dwóch atomów. Powstaje cząsteczka H
2
. Trzeci atom
wodoru, gdy znajdzie się w pobliżu, już nie wiąże się z cząsteczką H
2
.
Rys. 4. Zależność potencjału sił jądrowych od
odległości między nukleonami [1].

Rozdział 2. Budowa jądra atomowego
15
Spinowa zależność sił jądrowych. Na przykładzie deuteronu wiemy, że proton i neutron
tworzące jądro deuteru (jądro deuteru nazywamy deuteronem, a jądro trytu – trytonem) mają
spiny ustawione równolegle;
ℏ
1
=
D
S
. Takie jądro jest trwałe (istnieje w przyrodzie).
W przyrodzie nie ma natomiast deuteru, w którym spiny protonu i neutronu byłyby ustawione
antyrównolegle, czyli o spinie
S
D
= 0. Takiego jądra nie udało się otrzymać również
doświadczalnie. To oznacza, że nie może się związać proton z neutronem o spinach
ustawionych przeciwsobnie. Wynika stąd, że musi występować silna zależność sił jądrowych
od spinów nukleonów. Oznacza to, że siły jądrowe nie są siłami centralnymi. Zależą one nie
tylko od odległości między cząstkami, jak to ma miejsce w przypadku sił kulombowskich, ale
także od orientacji spinów tych cząstek.
Niezależność ładunkowa sił jądrowych. Siły jądrowe mają jeszcze jedną szczególną cechę.
Siły jądrowe między dwoma nukleonami nie zależą od tego, czy jeden czy obydwa nukleony
mają ładunek elektryczny, czy nie. Oddziaływanie neutronu z neutronem jest takie same jak
neutronu z protonem lub protonu z protonem.
Z punktu widzenia sił jądrowych proton i neutron są jednakowymi cząstkami. Ta własność
sił jądrowych nosi nazwę hipotezy o ładunkowej niezależności sił jądrowych.


Rozdział 3.
Reakcje jądrowe i rodziny promieniotwórcze
3.1. Reakcje jądrowe
Pod pojęciem reakcja jądrowa rozumiemy proces prowadzący do zmiany własności jądra lub
rodzaju jądra wywołany bombardowaniem tego jądra cząstkami. Pod pojęcie reakcji jądrowej
podciągamy także rozpady promieniotwórcze, ale rozpatrujemy je jako odrębną grupę
zjawisk. Wszystkie reakcje jądrowe podlegają następującym prawom.
1)
Prawo zachowania ładunku, które mówi, że we wszystkich reakcjach jądrowych
całkowity ładunek cząstek wchodzących w reakcję jest równy całkowitemu ładunkowi
produktów reakcji. Jest to prawo zachowania wskaźników dolnych (
X
A
Z
→
).
2)
Prawo zachowania nukleonów. Mówi ono, że liczba nukleonów przed reakcją jest
równa sumie nukleonów po reakcji. Jest to prawo zachowania wskaźników górnych (
X
A
Z
→
).
3)
Prawo zachowania pędu.
4)
Prawo zachowania spinu. Spin sumaryczny połówkowy cząstek wchodzących
w reakcję pozostaje połówkowy po reakcji, a spin sumaryczny całkowity pozostaje całkowity.
5)
Prawo zachowania masy – energii. Treść i komentarz do tego prawa przedstawiony jest
nieco dalej.
Pierwszą reakcję jądrową zawdzięczamy Rutherfordowi, który bombardował azot
N
14
7
cząstkami
α
4
2
o energii 7,68 MeV pochodzącymi z polonu
Po
214
82
. Otrzymał tlen i protony:
p
1
1
17
8
14
7
4
2
O
N
+
→
+
α
Skrócony zapis tej reakcji to
O
)
,
(
N
17
8
14
7
p
α
.
Typową reakcję jądrową zapisujemy symbolicznie w postaci:
Y
y
X
x
+
→
+
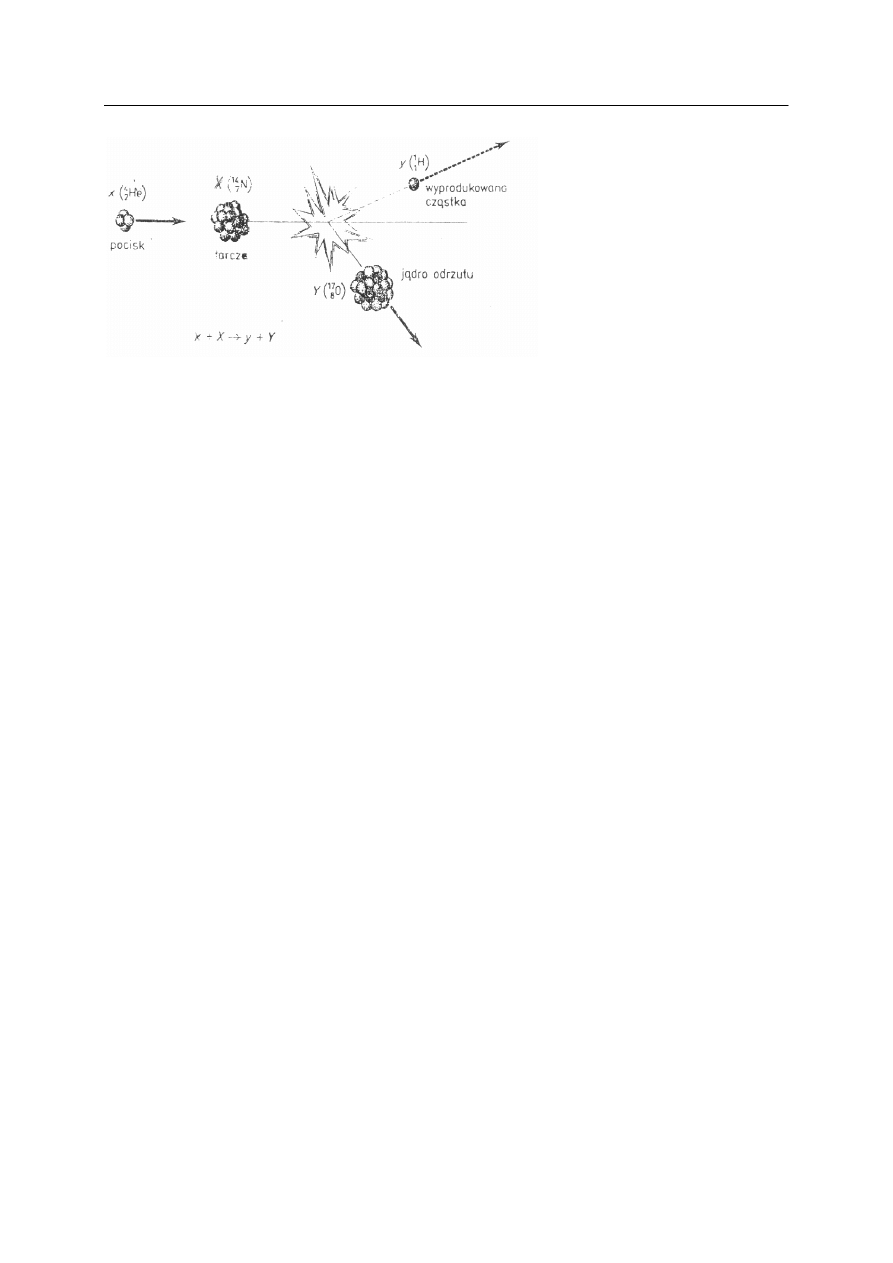
Na rys. 5 przedstawiono schematycznie przebieg reakcji jądrowej, podczas której jądro–
tarcza jest bombardowane jądrem–pociskiem.
Na rys. 5 x oznacza cząstkę bombardującą (pocisk), w reakcji Rutherforda He
4
2
, X –
jądro–tarczę, w reakcji Rutherforda N
14
7
, y – cząstkę–produkt (wylatującą z tarczy), w reakcji
Rutherforda
p
1
1
, Y – jądro odrzutu (produkt). W reakcji Rutherforda O
17
8
.
Przykłady innych reakcji jądrowych:
C
Be
12
6
1
0
4
2
9
4
+
→
+
n
α
C
)
,
(
Be
12
6
9
4
n
α
O
F
16
8
4
2
1
1
19
9
+
→
+
α
p
O
)
,
(
F
16
8
19
9
α
p
N
C
13
7
0
0
1
1
12
6
+
→
+
γ
p
N
)
,
(
C
13
7
12
6
γ
p
18
Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
C
N
12
6
4
2
2
1
14
7
+
→
+
α
d
C
)
,
(
N
12
6
14
7
α
d
+
Al
27
13
Si
28
14
1
0
2
1
+
→
n
d
Si
)
,
(
Al
28
14
27
13
n
d
Jako pocisków używa się jąder cięższych, np.
C
17
6
, a nawet takich jak
7
40
20
Ca
+
,
10
64
30
Zn
+
,
15
80
32
Kr
+
.
O wiele trudniej trafić w jądro cząstkami naładowanymi, zwłaszcza ciężkimi, ponieważ
mają one ten sam ładunek co jądro–tarcza i muszą mieć dużą energię kinetyczną, by pokonać
odpychanie kulombowskie i zbliżyć się na taką odległość, żeby mogła zajść reakcja jądrowa.
Niemniej jednak używamy takich pocisków, ponieważ umiemy przyśpieszać je do wysokich
energii; ponadto pozwalają one na dokonanie dużej liczby reakcji praktycznie niemożliwych
do przeprowadzenia, gdy cząstką bombardującą jest neutron czy kwant.
3.2. Bilans mas i energii w reakcjach jądrowych
W reakcjach jądrowych musi być spełniona zasada zachowania energii. Zasada ta mówi, że
w reakcjach jądrowych całkowita energia układu (włączając energię równoważną masie)
pozostaje stała. W reakcjach chemicznych prawo zachowania masy i zasada zachowania
energii występują osobno. W reakcjach jądrowych muszą występować razem. Prawo
zachowania masy i energii w reakcjach jądrowych należy stosować łącznie. Stosując te prawa
osobno stwierdzimy, że ani prawo zachowania masy, ani prawo zachowania energii nie są
spełnione.
Reakcja jądrowa zachodzi, gdy jądro jakiegoś pierwiastka zostało trafione cząstką o dużej
energii. Powstaje jądro-produkt i jakaś inna cząstka, też z pewną energią kinetyczną. Bilans
mas w reakcji jądrowej możemy zapisać następująco:
Y
y
X
x
M
m
M
m
+
→
+
x
m i
X
M
to masy spoczynkowe substratów reakcji (masy wejściowe),
y
m i
Y
M
to masy
spoczynkowe produktów reakcji (masy wyjściowe).
Bilans masy–energii napisany na podstawie prawa zachowania masy–energii jest
następujący:
Y
Y
y
y
X
X
x
x
T
c
M
T
c
m
T
c
M
T
c
m
+
+
+
=
+
+
+
2
2
2
2
(3)
Rys. 5. Schematyczne przedstawienie reakcji jądrowej [1].

Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
19
gdzie:
x
x
T
c
m
+
2
– całkowita energia pocisku,
X
X
T
c
M
+
2
– całkowita energia jądra–tarczy,
y
y
T
c
m
+
2
– całkowita energia cząstki wylatującej,
Y
Y
T
c
M
+
2
– całkowita energia
jądra–produktu (odrzutu);
2
2
2
2
,
,
,
c
M
c
m
c
M
c
m
Y
y
X
x
są energiami spoczynkowymi kolejno:
cząstki–pocisku, jądra- tarczy, cząstki nowej, jądra odrzutu;
Y
y
X
x
T
T
T
T
,
,
,
są energiami
kinetycznymi odpowiednio: cząstki-pocisku, jądra-tarczy, nowej cząstki i jądra odrzutu.
Zakładamy, że jądro–tarcza znajduje się w spoczynku
0
=
X
T
, wtedy równanie (3) ma
postać:
Y
Y
y
y
X
x
x
T
c
M
T
c
m
c
M
T
c
m
+
+
+
=
+
+
2
2
2
2
(4)
Zapisujemy to równanie następująco:
x
Y
y
y
y
x
x
T
T
T
c
M
m
M
m
−
+
=
+
−
+
)
(
)]
(
)
[(
2
Gdzie:
)
(
x
x
M
m
+
– masa wejściowa,
)
(
y
y
M
m
+
– masa wyjściowa,
)
(
Y
y
T
T
+
– energia
kinetyczna produktów reakcji,
x
T - energia kinetyczna pocisku.
Wprowadzamy pewną wielkość
Q, która podaje różnicę między energią kinetyczną
produktów reakcji a energią kinetyczną pocisku:
x
Y
y
T
T
T
Q
−
+
=
)
(
można też napisać:
2
)]
(
)
[(
)
(
c
M
m
M
m
T
T
T
Q
Y
y
X
x
x
Y
y
+
−
+
=
−
+
=
(5)
Wielkość
Q nosi nazwę energii reakcji lub „wartości Q”, przy czym można ją określić na
podstawie różnicy energii, jak i różnicy mas. Jeżeli
X
x
M
m
+
>
y
Y
m
M
+
to
Y
y
T
T
+
>
x
T
i wtedy
Q > 0. Jeżeli suma mas wejściowych jest większa od sumy mas wyjściowych, to
pewna część masy zostaje zamieniona na energię, zgodnie z relacją
Q
E
mc
∆
=
∆
=
∆
2
. Gdy
Q
O
>
, energia wydziela się, a reakcje, w których
O
Q
>
są reakcjami egzoenergetycznymi.
Reakcja egzoenergetyczna może przebiegać przy dowolnej energii cząstki padającej, jeżeli ta
energia wystarcza do pokonania bariery kulombowskiej (w przypadku cząstek
naładowanych). W reakcji jądrowej energia jest wydzielana w postaci energii kinetycznej
(ruchu) produktów reakcji. Energia reakcji może również wydzielać się w postaci energii
kwantów
γ
. Gdy
)
(
)
(
Y
y
X
x
M
m
M
m
+
<
+
, to
x
y
Y
T
T
T
<
+
, wtedy
O
Q
<
i masa końcowa jest
większa od początkowej. Pewna część masy jest utworzona kosztem energii kinetycznej.
Następuje przemiana energii w masę, zgodnie z wyrażeniem
2
/ c
E
m
∆
=
∆
. Ponieważ
O
Q
<
,
to energia musi być dostarczana z jakiegoś źródła zewnętrznego. Potrzebnej energii dostarcza
cząstka bombardująca w postaci swojej energii kinetycznej. Reakcja taka nazywa się
endoenergetyczną. Reakcja endoenergetyczna może zachodzić jedynie przy dostatecznie
dużej energii kinetycznej cząstki bombardującej:
=
x
T
|Q|
Y
T
+
.
Przykład 1: bombardujemy tarczę trytu deuteronami
n
d
1
0
4
2
3
1
2
1
He
T
+
→
+
Masy wejściowe wynoszą:
jma
5,030151
jma
016049
,
3
T
masa
jma
014102
,
2
masa
3
1
2
1
=
+
=
=
=
=
X
x
X
x
M
m
M
d
m

20
Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
Masy wyjściowe są następujące:
jma
5,011268
jma
002603
,
4
He
masa
jma
008665
,
1
masa
4
2
1
0
=
+
=
=
=
=
Y
y
Y
y
M
m
M
n
m
Różnica mas wynosi:
jma
018883
,
0
)
(
)
(
=
+
−
+
=
∆
Y
y
X
x
M
m
M
m
m
0
jma
0189
,
0
>
=
Q
MeV
6
,
17
MeV
16
,
931
0189
,
0
=
⋅
=
Q
Reakcja jest egzoenergetyczna i wyzwolona zostaje energia wynosząca 17,6 MeV. W tej
reakcji nadwyżka masy wejściowej została zamieniona na energię kinetyczną produktów
reakcji n
1
0
i
α
4
2
.
Przykład 2: reakcja Rutherforda
p
1
1
17
8
14
7
4
2
O
N
+
→
+
α
Masy wejściowe są następujące:
jma
010113
,
18
jma
007510
,
14
N
masa
jma
002603
,
4
masa
14
7
4
4
=
+
=
=
=
=
X
x
X
x
M
m
M
m
α
Masy wyjściowe:
jma
01262
,
18
jma
00450
,
17
O
masa
jma
00812
,
1
masa
17
8
1
1
=
+
=
=
=
=
Y
y
Y
y
M
m
M
p
m
Różnica mas wynosi:
jma
002507
,
0
)
(
)
(
−
=
+
−
+
=
∆
Y
y
X
x
M
m
M
m
m
0
<
∆
m
MeV
34
,
2
MeV
16
,
931
00251
,
0
jma
00251
,
0
−
=
⋅
−
=
−
=
∆
Q
Ujemna wartość bilansu masy-energii oznacza, że energia kinetyczna cząstki
α
musi w tej
reakcji przewyższać energię kinetyczną jądra tlenu i protonu (powstających z tej reakcji) o tę
właśnie wartość, aby reakcja doszła do skutku:
0
<
−
+
=
x
Y
y
T
T
T
Q
x
Y
y
T
T
T
<
+

Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
21
3.3. Rozpady promieniotwórcze
Rozpadem promieniotwórczym nazywamy zjawisko przemian zachodzących w jądrze,
w wyniku których następuje emitowanie cząstek na zewnątrz jądra. Okazuje się, że jądra
niektórych izotopów zarówno naturalnych, jak i otrzymanych sztucznie mogą spontanicznie
przekształcać się w inne jądra. Emitują one wówczas cząstki
α
, które są jądrami helu,
cząstki
β
, które są elektronami pochodzenia jądrowego, promieniowanie
γ
, które jest
promieniowaniem elektromagnetycznym, lub też mogą ulec spontanicznemu podziałowi na
dwie części o zbliżonych masach. Takie przemiany jąder w inne jądra nazywamy rozpadami
promieniotwórczymi. Każde jądro, które zmienia swoją strukturę wysyłając promieniowanie
γ
lub cząstki jądrowe, takie jak
α
i
β
, zwane jest jądrem promieniotwórczym.
W przyrodzie istnieją 272 stabilne jądra, tzn. nie ulegające rozpadowi promieniotwórczemu;
wszystkie inne są promieniotwórcze i nazywamy je radioizotopami.
Reguły przesunięć Soddy’ego i Fajansa:
1)
Rozpad
α
. Wysyłając cząstkę
α
jądro macierzyste M traci dwa protony i dwa neutrony.
W wyniku tej przemiany powstaje jądro pochodne P, które w porównaniu z jądrem
macierzystym ma liczbę atomową mniejszą o dwie, a liczbę masową mniejszą o cztery
jednostki
α
4
2
4
2
P
M
+
→
−
−
A
Z
A
Z
2)
Rozpad
β
–
. W przemianie
−
β
(beta minus) w jądrze macierzystym następuje przemiana
neutronu w proton z jednoczesną emisją elektronu. W wyniku przemiany
−
β
powstaje jądro
pochodne, które ma liczbę atomową Z większą o jednostkę w porównaniu z jądrem emiterem
(macierzystym), a liczba masowa nie ulega zmianie:
ν
β
+
+
→
+
−
P
M
1
0
1
A
Z
A
Z
gdzie
ν
oznacza antyneutrino. Jądro emiter i jądro pochodne są jądrami izobarycznymi.
3)
Rozpad
β
+
. W rozpadzie
+
β
(beta plus) w jądrze macierzystym następuje przemiana
protonu w neutron i cząstkę o masie równej masie elektronu i ładunku dodatnim o wartości
bezwzględnej równej ładunkowi elektronu. Taka cząstka nazywana jest pozytonem lub
pozytronem. W wyniku tej przemiany powstaje jądro pochodne, które ma liczbę atomową Z
mniejszą o jednostkę w porównaniu z jądrem emiterem, a liczba masowa nie zmienia się:
ν
β
+
+
→
−
+
P
M
1
0
1
A
Z
A
Z
gdzie
ν
oznacza neutrino. Jądro macierzyste i pochodne są izobarami.
4)
Wychwyt K. Jądro macierzyste wychwytuje swój własny elektron powłokowy,
najczęściej z powłoki K, rzadziej z L. W wyniku wychwytu K powstaje nowe jądro, które ma
liczbę atomową mniejszą o jeden, a liczba masowa nie zmienia się:
ν
+
→
+
−
−
P
M
1
0
1
A
Z
A
Z
e
Wychwyt K i rozpad
β
są równoważne pod względem skutków przemiany jądrowej. Symbol
e oznacza elektron powłokowy. Elektrony pochodzenia jądrowego przyjęto oznaczać
symbolem
β
, a elektrony powłokowe i swobodne symbolem e.
5)
Przemiana
γ
.
Jądro
macierzyste
emituje
foton
(kwant
promieniowania
elektromagnetycznego). Podczas tej reakcji ani liczba atomowa, ani masowa nie zmieniają
się. Przemiana
γ
zachodzi wtedy, gdy jądro macierzyste ze stanu wzbudzonego emituje
22
Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
kwant
γ
i przechodzi w stan energetycznie niższy, który może być stanem podstawowym.
Rozpad
γ
zapisujemy następująco:
γ
+
→
M
)
M
(
*
A
Z
A
Z
W tych procesach
ν
i
ν
oznaczają neutrino i antyneutrino – cząstki, o których więcej
powiemy później,
*
)
M
(
A
Z
oznacza jądro we wzbudzonym stanie energetycznym, które
emitując promieniowanie
γ
, wraca do stanu podstawowego lub innego stanu o niższej
energii.
6)
Podział spontaniczny jądra polega na tym, że ciężkie jądro macierzyste ulega
podziałowi na dwie (bardzo rzadko na trzy) części. Chodzi tu o podział spontaniczny
ciężkiego jądra:
n
A
Z
A
Z
A
Z
1
0
2
1
2
Y
Y
X
2
2
1
1
+
+
→
przy czym: A
1
+ A
2
= A + 2, Z
1
+ Z
2
= Z.
7)
Prawo rozpadu promieniotwórczego. Akt rozpadu promieniotwórczego jest zjawiskiem
typowo indywidualnym, niezależnym od rozpadu innych jąder preparatu, i jest procesem
statystycznym;
nie
można
przewidzieć,
kiedy
dany
atom
ulegnie
rozpadowi
promieniotwórczemu. W wyniku rozpadu promieniotwórczego maleje liczba atomów
pierwiastka macierzystego, przybywa zaś atomów pierwiastka pochodnego. Załóżmy, że
w chwili początkowej
0
=
t
liczba atomów wynosi N
0
. Po czasie t liczba atomów zmalała
i wynosi N. N jest liczbą atomów, które przeżyły czas t i nie rozpadły się w tym czasie.
Przez dN oznaczamy liczbę atomów rozpadających się w przedziale czasu dt. Ta liczba
atomów ulegających rozpadowi jest proporcjonalna do odstępu czasu dt i do liczby atomów
N jeszcze istniejących (po czasie t ):
t
N
N
d
d
λ
=
−
(6)
Znak minus jest po to, by zaznaczyć ubytek atomów. Współczynnik
λ
nosi nazwę stałej
rozpadu i charakteryzuje rodzaj rozpadającego się pierwiastka. Wyrażenie (6) przepisujemy
w postaci:
t
N
N
d
d
λ
−
=
(7)
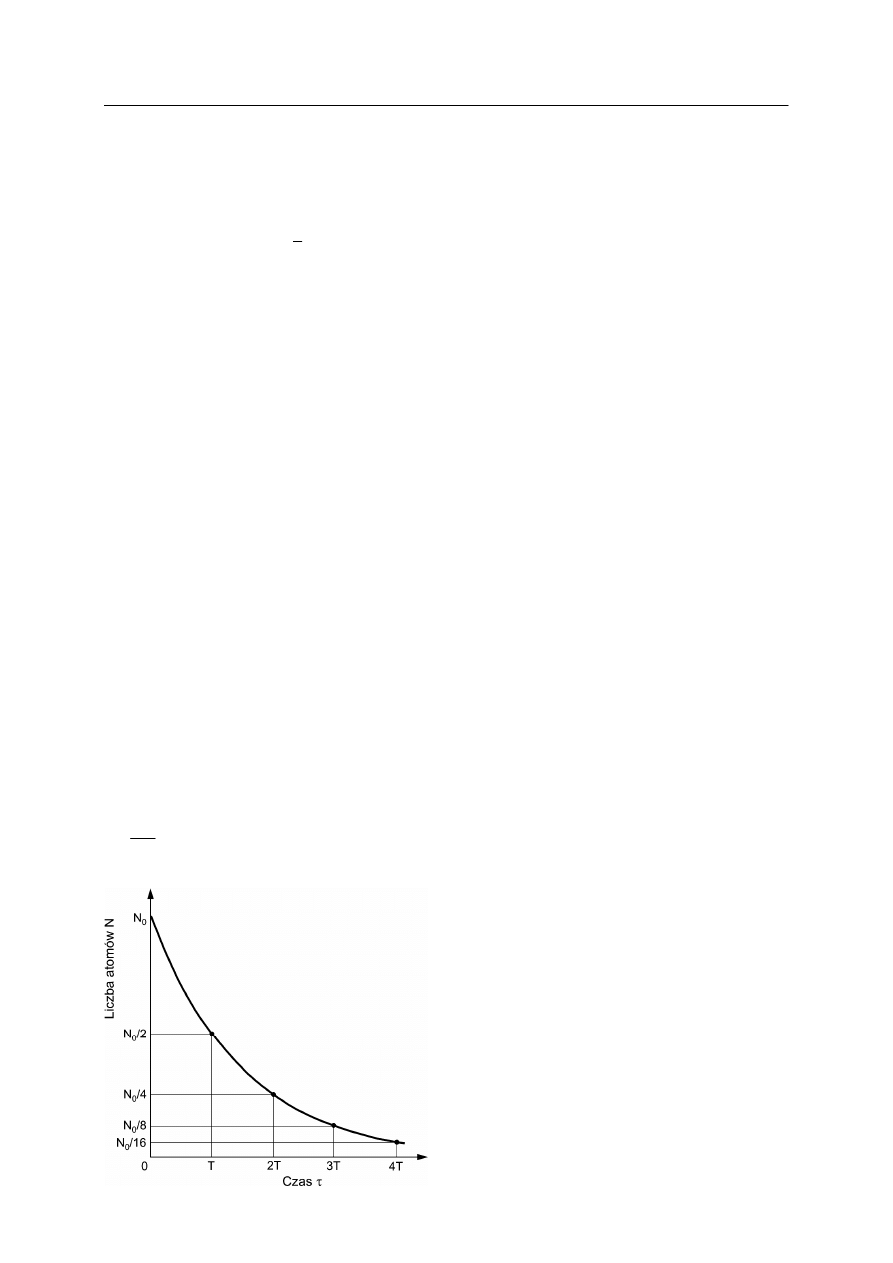
Rys. 6. Krzywa opisująca prawo rozpadu promie-
niotwórczego. Wykres obejmuje przedział czasu
odpowiadający czterem okresom połowicznego
rozpadu [11].

Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
23
i następnie całkujemy:
∫
∫
−
=
t
N
N
d
d
λ
C
t
N
+
−
=
λ
ln
Stałą całkowania C określamy z warunków początkowych: dla
0
,
0
N
N
t
=
=
, czyli
C
N
=
0
ln
stąd:
t
N
N
λ
−
=
−
0
ln
ln
t
N
N
λ
−
=
0
ln
t
e
N
N
λ
−
=
0
(8)
Równanie (8) jest podstawowym prawem rozpadu promieniotwórczego. Mówi ono, że liczba
rozpadających się jąder promieniotwórczych maleje w czasie wykładniczo (rys. 6).
Z prawa rozpadu promieniotwórczego (8) wynika, że taki rozpad może trwać
w nieskończoność, dlatego wprowadza się pojęcie czasu (okresu) połowicznego rozpadu
(zaniku) T
1/2
. Jest to czas, po którym ulegnie rozpadowi połowa atomów z początkowej liczby
0
N . Z definicji T
1/2
wynika, że po czasie t = T
1/2
N = N
0
/2. Podstawiamy to do wzoru (8)
i otrzymujemy N
0
/2 = N
0
exp(–
λ
T
1/2
). Stąd otrzymujemy: 1/2 = exp(–
λ
T
1/2
) lub –ln2 = –
λ
T
1/2
i ostatecznie T
1/2
= (ln2)/
λ
, czyli T
1/2
= 0,693/
λ
.
Okres połowicznego rozpadu dla różnych nuklidów zawiera się w bardzo szerokich
granicach od
s
10
7
−
do
11
10 lat.
Wprowadza się także pojęcie średniego czasu życia jądra. Każde jądro ma do dyspozycji
czas życia od 0 do
∞
i nie wiemy, które z nich i kiedy się rozpadnie. Średnim czasem życia
jądra promieniotwórczego nazywamy średnią arytmetyczną czasów życia wszystkich jąder
w próbce. Jeżeli w próbce jest
1
dN
jąder o czasie życia
1
t
,
2
dN
jąder o czasie życia
2
t
itd., to
ś
redni czas życia
τ
definiujemy jako:
…
…
+
+
+
⋅
+
⋅
=
2
1
2
2
1
1
d
d
d
d
N
N
t
N
t
N
τ
A w postaci całkowej jako:
0
0
0
0
d
d
d
0
N
N
t
N
N
t
N
∫
∫
∫
∞
∞
−
=
=
τ
(9)
Ponieważ
( )
t
N
N
λ
−
=
exp
0
stąd:
( )
t
t
N
N
d
exp
d
0
λ
λ
−
−
=
(10)

24
Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
Podstawiamy wyrażenie (10) do (9):
( )
( )
∫
∫
∞
∞
−
−
=
−
−
−
=
0
0
0
0
d
exp
d
exp
t
t
t
N
t
t
t
N
λ
λ
λ
λ
τ
W tablicach całek niewłaściwych znajdujemy:
( )
2
0
1
d
exp
λ
λ
=
−
∫
∞
t
t
t
Po podstawieniu otrzymujemy:
2
1
λ
λ
τ
⋅
=
, czyli
λ
τ
1
=
Zestawiamy:
λ
2
ln
2
1
=
T
;
λ
τ
1
=
Wystarczy znać jedną z trzech wielkości, żeby otrzymać dwie pozostałe.
3.4. Rodziny promieniotwórcze
Często się zdarza, że nuklidy powstające w wyniku rozpadu promieniotwórczego nie są
trwałe, lecz rozpadają się z inną stałą rozpadu niż substancja macierzysta. Mówimy wtedy
o sukcesywnym rozpadzie promieniotwórczym.
→
→
→
3
2
1
3
2
1
λ
λ
λ
Okazuje się, że większość pierwiastków promieniotwórczych występujących w przyrodzie
jest ze sobą powiązana genetycznie i wchodzi w skład trzech rodzin promieniotwórczych,
zwanych też szeregami albo łańcuchami promieniotwórczymi. Nazwy tych rodzin pochodzą
od pierwiastka zapoczątkowującego daną rodzinę lub od innego, leżącego blisko niego.
Pierwiastek stojący na czele rodziny jest pierwiastkiem najdłużej żyjącym spośród wszystkich
do niej należących. Każda rodzina kończy się trwałym izotopem, który już dalej się nie
rozpada. Rodziny są następujące:
Rodzina torowa. Rozpoczyna się od promieniotwórczego toru
Th
232
90
, który w wyniku
przemiany
α
przekształca się w promieniotwórczy
Ra
228
88
, ten z kolei ulega przemianie
β
,
dając
Ac
228
89
itd. Każdy następny produkt rozpadu ulega przemianie
α
lub
β
dając
pierwiastki wchodzące w skład rodziny. Rodzina kończy się trwałym izotopem ołowiu
Pb
208
82
.
Tor rozpoczynający łańcuch przemian jest w rodzinie torowej najdłużej żyjącym
pierwiastkiem z tej rodziny z okresem półrozpadu T
1/2
= 1,39·10
9
lat. Liczby masowe
pierwiastków tej rodziny można otrzymać z formuły (patrz Tabela 3):
n
A
4
=
,
52
58
→
=
n
Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
25
Rodzina uranowa. Rozpoczyna ją uran
U
238
92
z okresem półrozpadu T
1/2
= 4,51·10
9
lat,
a kończy trwały izotop ołowiu
Pb
206
82
. Liczby masowe pierwiastków z tej rodziny opisane są
formułą:
2
4
+
=
n
A
,
51
59
→
=
n
Rodzina aktyno-uranowa (aktynowa). Rozpoczyna się od uranu
U
235
92
z okresem
półrozpadu T
1/2
= 7,15·10
9
lat, a kończy ją trwały izotop ołowiu
.
Pb
207
82
Liczby masowe
pierwiastków wchodzących w skład tej rodziny określa formuła:
3
4
+
=
n
A
,
51
58
→
=
n
Okresy półrozpadu pierwiastków stojących na czele tych rodzin są rzędu wieku Ziemi
i można je spotkać w naturze.
Z tych rozważań wynika, że powinna istnieć też rodzina zawierająca pierwiastki, których
liczby masowe można by opisać formułą
1
4
+
=
n
A
. Rodzina taka istnieje, ale nie
w przyrodzie. Tworzą ją sztuczne izotopy promieniotwórcze, otrzymane na drodze reakcji
jądrowych. Na czele stoi neptun
Np
237
93
, stąd rodzina nosi nazwę rodziny neptunowej.
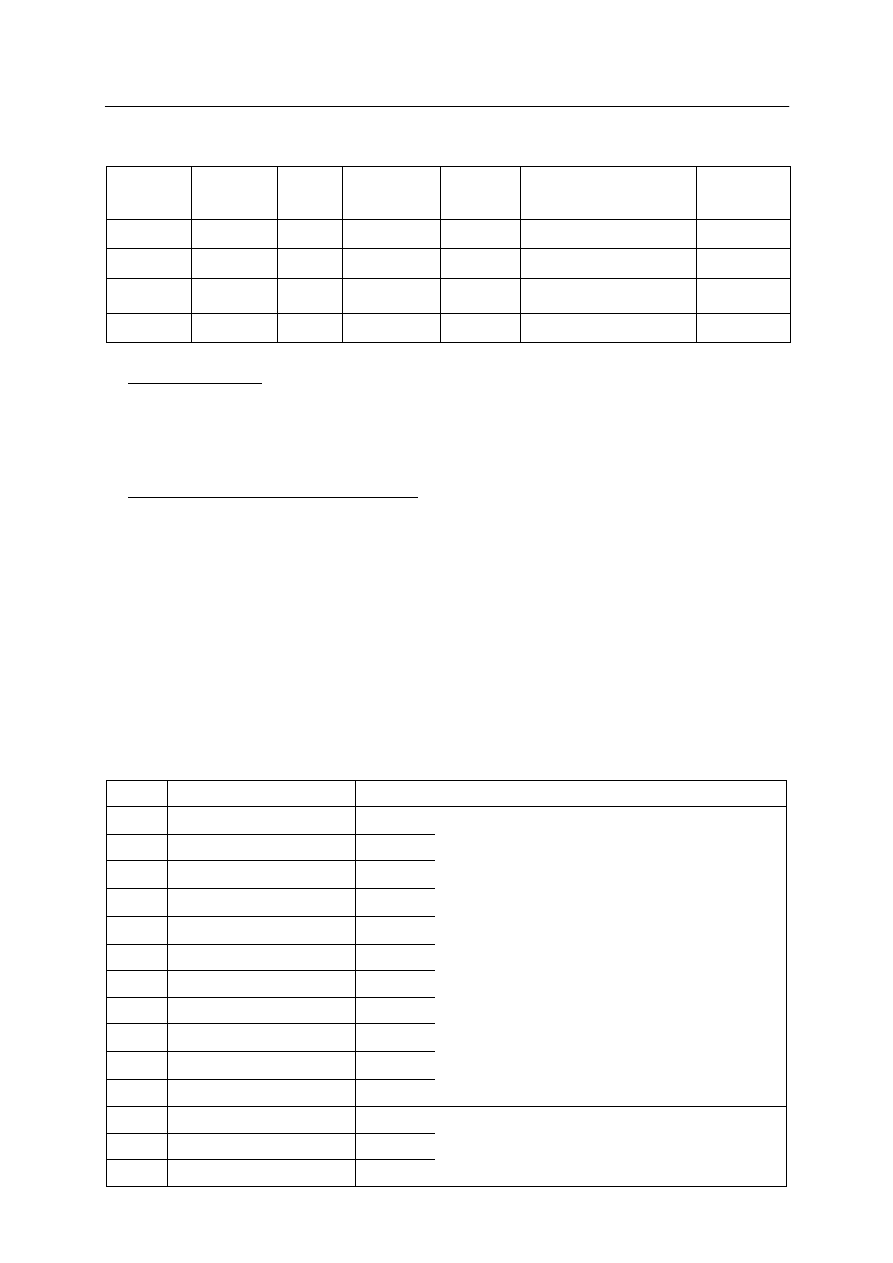
Tabela 3. Cztery szeregi promieniotwórcze.
Szereg
Jądro
początkowe
Liczba
masowa
n początkowe n końcowe
Czas połowicznego zaniku
jądra początkowego (lata)
Końcowe
jądro
stabilne
Torowy
Th
232
90
4n
58
52
1,39·10
10
Pb
208
82
Neptunowy
Np
237
93
4n + 1
59
52
2,20·10
6
Bi
209
83
Uranowo-
-radowy
U
238
92
4n + 2
59
51
4,51·10
9
Pb
206
82
Aktynowy
U
235
92
4n + 3
58
51
7,15·10
9
Pb
207
82
Tabela 4. Nuklidy, których okres połowicznego rozpadu jest porównywalny z wiekiem Ziemi.
Nuklid
Rodzaj nuklidu
Czas połowicznego rozpadu (lata)
40
K
β
–
, wychwyt elektronu
1,2·10
9
50
V
wychwyt elektronu
4,0·10
14
87
Rb
β
–
6,2·10
10
115
In
β
–
6,0·10
14
138
La
β
–
, wychwyt elektronu
1,0·10
11
142
Ce
α
5,0·10
15
Rozpad na stabilny nuklid pochodny
144
Nb
α
3,0·10
15
147
Sm
α
1,2·10
11
176
Lu
β
–
5,0·10
10
187
Re
β
–
4,0·10
12
192
Pt
α
1,0·10
15
232
Th
α
1,4·10
10
Dziesięć generacji promieniotwórczych
(kolejnych nuklidów pochodnych)
235
U
α
7,1·10
9
238
U
α
4,5·10
9

26
Rozdział 3. Reakcje jądrowe i rodziny promieniotwórcze
Warunkiem występowania rodziny w przyrodzie jest to, by czas półrozpadu pierwiastka
stojącego na czele rodziny był porównywalny z wiekiem Ziemi. Trzy rodziny występujące
w przyrodzie spełniają ten warunek. Czwarta rodzina go nie spełnia i nie występuje
w przyrodzie. Okres półrozpadu
Np
273
93
jest o trzy rzędy mniejszy od wieku Ziemi, więc na
Ziemi tej rodziny spotkać nie można.
Rodzinę neptunową rozpoczyna
Np
237
93
z okresem półrozpadu T
1/2
= 2,20·10
9
lat, a kończy
izotop bizmutu
Bi
209
83
. Liczby masowe pierwiastków z tej rodziny można otrzymać ze wzoru
1
4
+
⋅
=
n
A
,
52
59
→
=
n
Wszystkie pierwiastki wchodzące w skład rodzin promieniotwórczych mają liczby
masowe różniące się o wielokrotność czwórki. Jest tak dlatego, że podczas rozpadu
α
liczba
masowa maleje o cztery, a podczas rozpadu
β
nie ulega zmianie.
Poza omówionymi rodzinami promieniotwórczymi mamy szereg występujących
w przyrodzie izotopów, które nie zapoczątkowują dalszych rodzin, lecz bezpośrednio
przechodzą
w
izotopy
trwałe.
W
przyrodzie
istnieje
jedynie
14
nuklidów
promieniotwórczych, których czas połowicznego rozpadu jest tego samego rzędu lub dłuższy
niż wiek Ziemi (oszacowany na 4,5 mld lat). Rozpad 11 pierwszych nuklidów prowadzi
bezpośrednio do stabilnych nuklidów pochodnych, a rozpad trzech ostatnich prowadzi do
nuklidów, które są promieniotwórcze i tworzą rodziny (patrz tabela 4).

Rozdział 4.
Rozpady promieniotwórcze
4.1. Rozpad α
Emitując cząstkę
α
, jądro traci dwa protony i dwa neutrony. Powstaje nowe jądro, które ma
liczbę atomową mniejszą o 2, a liczbę masową o 4 jednostki:
P
M
4
2
4
−
−
+
→
A
Z
Z
A
Z
α
Cząstka
α
jest jądrem helu, czyli dwukrotnie zjonizowanym atomem helu.
Charakterystycznymi własnościami rozpadu
α
są okres połowicznego zaniku, energia
i zasięg cząstek
α
. Czas połowicznego rozpadu zawiera się w granicach od
s
10
7
−
do
15
10
lat, a energia od 4,0 do 8,8 MeV dla różnych izotopów. Zasięgiem cząstek
α
nazywamy
odległość przebytą przez cząstkę od źródła do chwili całkowitej utraty energii kinetycznej.
Zasięg zależy od energii; w powietrzu, w warunkach normalnych, zależność między
zasięgiem a energią przedstawia wzór:
2
/
3
318
,
0
α
T
R
=
;
α
T – energia cząstki
Powietrze wybrano jako standardowy ośrodek do badań cząstek
α
. Zasięg zależy
oczywiście od rodzaju ośrodka, ciśnienia, temperatury i wilgotności. Torami cząsteczek są
linie proste, które dopiero w końcu zasięgu załamują się nieco (rys. 7). Zasięg w powietrzu
nie przekracza 9 cm (z wyjątkiem cząstek dalekiego zasięgu). Cząstki
α
tracą energię
głównie na jonizację atomów ośrodka (mają bardzo silne własności jonizujące). Cząstka
α
pochodząca z
Po
214
82
o energii 7,68 MeV wytwarza w powietrzu na swojej drodze
5
10
2
,
2
⋅
par jonów (parą jonów nazywamy elektron i jon dodatni powstały w wyniku
Rys. 7. Zdjęcie cząstek
α
w komorze Wilsona. Źródłem cząstek
α
jest mieszanina
Bi
212
83
i
Po
212
84
. Torami
cząstek są linie proste. Widoczne są dwa różne zasięgi odpowiadające dwóm różnym energiom cząstek
α
[10].
28
Rozdział 4. Rozpady promieniotwórcze
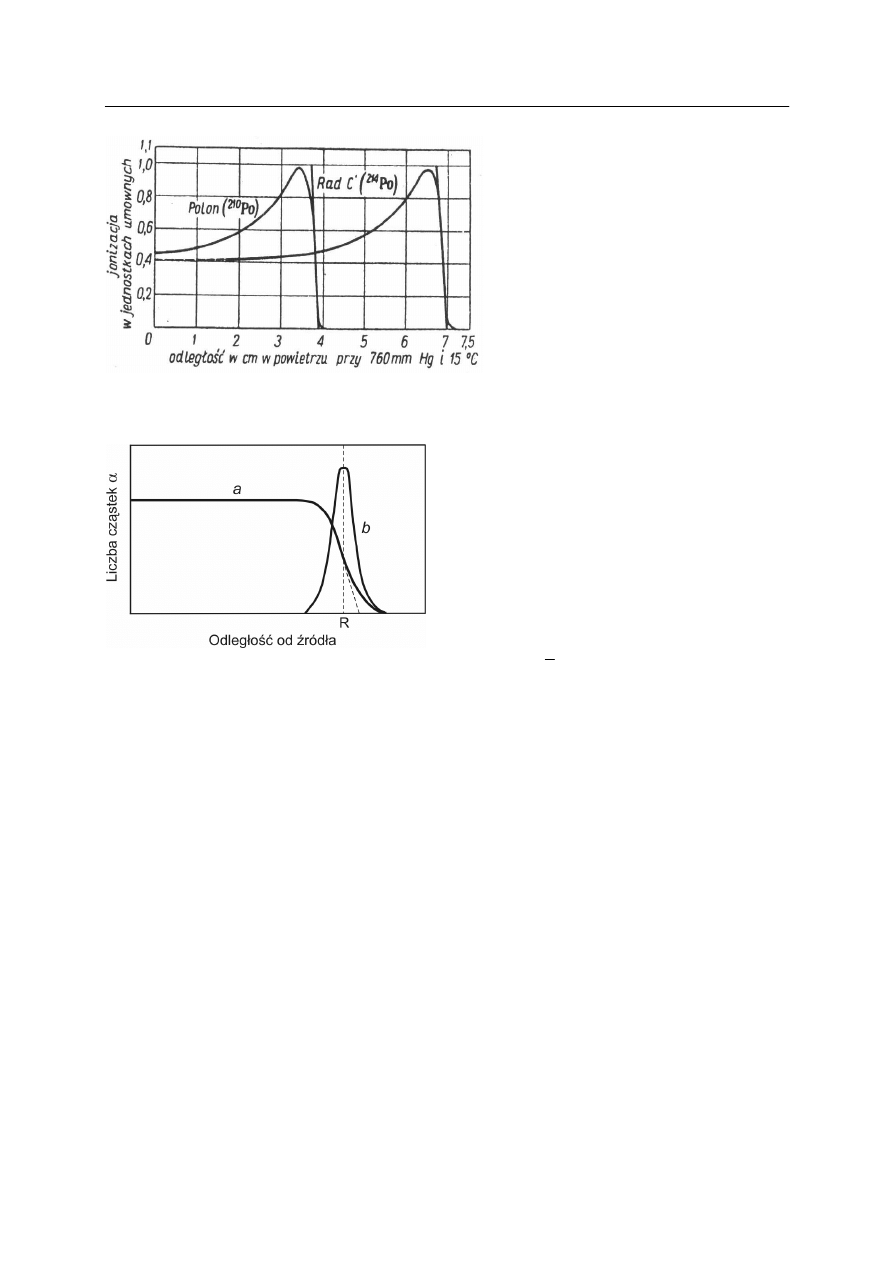
odłączenia elektronu od atomu). Zależność liczby jonów od odległości cząstki
α
od źródła
przedstawia rysunek 8.
Jonizacja rośnie w miarę oddalania się cząstki
α
od źródła. Ten wzrost tłumaczymy tak,
ż
e cząstka
α
, wytwarzając pary jonów, traci energię i maleje jej prędkość. Przy wolniejszym
ruchu zwiększa się czas przebywania cząstki w otoczeniu cząstek powietrza. Wtedy cząstka
może częściej oddziaływać z atomami ośrodka i tym samym zwiększa się
prawdopodobieństwo powstawania par jonów. W końcu przy małych energiach cząstka już
nie jonizuje, lecz tylko wzbudza atomy i w końcu wychwytuje elektrony. W rezultacie
powstaje obojętny atom helu.
Liczba cząstek
α
nie zmienia się wraz w miarę oddalania się od źródła, tzn. przez cały
czas liczba cząstek jest stała, dopiero pod koniec drogi (w okolicy zasięgu) obserwujemy
gwałtowny spadek liczby cząstek
α
do zera (rys. 9). Świadczy to o tym, że wszystkie cząstki
α
emitowane przez określony izotop mają zbliżone energie.
4.2. Charakterystyczne cechy rozpadu α
Przy porównywaniu zasięgu, energii, okresu półrozpadu (i stałej rozpadu) naturalnych
pierwiastków, które emitują cząstki
α
występują pewne prawidłowości:
1)
Zasięgi cząstek
α
z różnych izotopów zawierają się w granicach od 2,7 cm do 9 cm
(w powietrzu w warunkach normalnych). Wyjątek stanowią cząstki dalekiego zasięgu.
Rys. 8. Zależność jonizacji cząstek
α
od odległości od źródła [3].
Rys. 9. Zależność liczby cząstek
α
od zasięgu (krzywa a). Zasięg średni R określa położenie maksimum krzywej
różniczkowego zasięgu (krzywa b) [4].
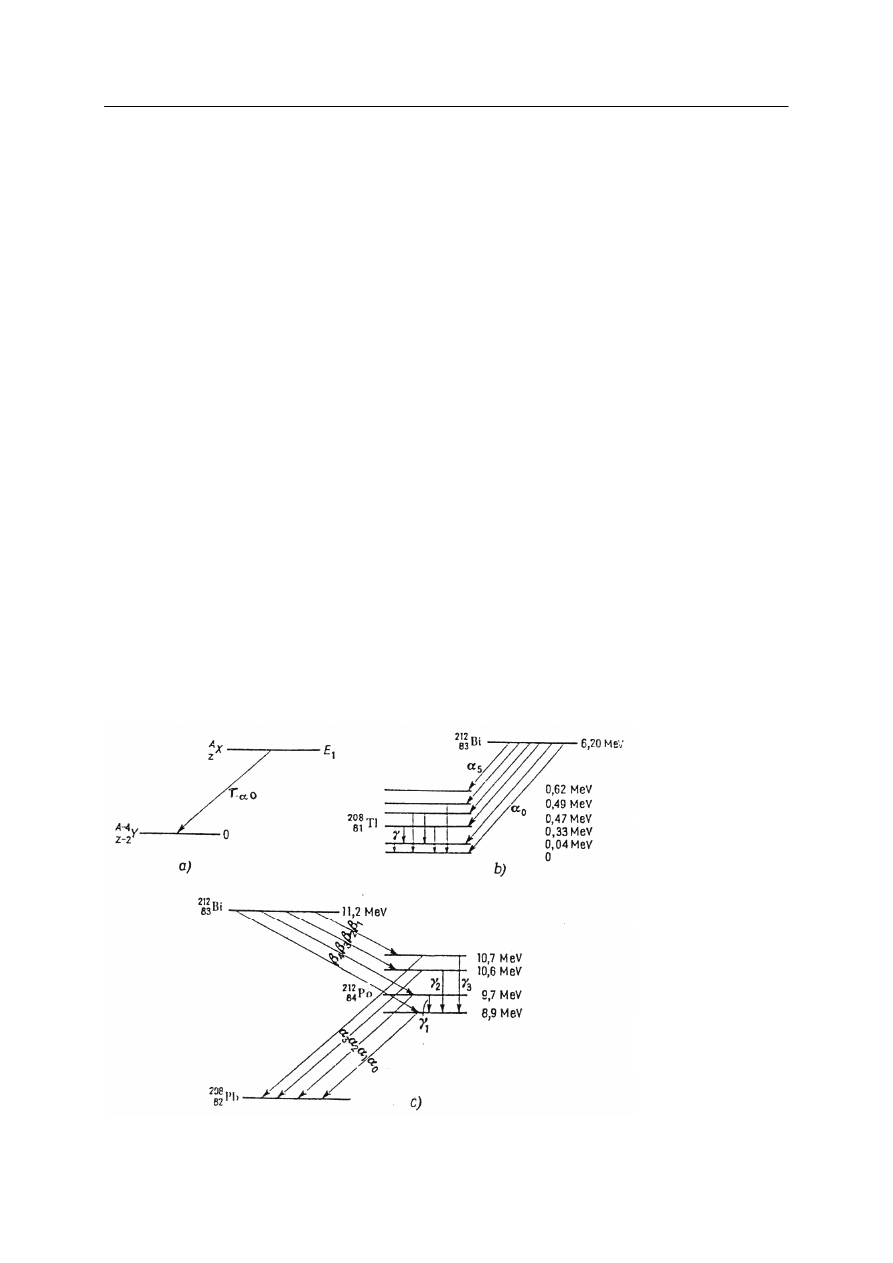
Rozdział 4. Rozpady promieniotwórcze
29
2)
Energie cząstek
α
zawierają się w granicach
MeV
8
,
8
MeV
0
,
4
≤
≤
α
T
, odpowiednio
dla
U
238
92
(zasięg
cm
7
,
2
=
R
) i dla
Po
212
84
(
cm
6
,
8
=
R
).
3)
Czas połowicznego rozpadu zawarty jest w granicach od T
1/2
= 4,5·10
9
lat (dla
U
238
92
)
do T
1/2
= 3·10
–7
s (dla
Po
212
84
).
4)
Stałe rozpadu zmieniają się w granicach od
1
10
s
10
54
,
1
−
−
⋅
=
λ
(dla
U
238
92
) do
1
6
s
10
31
,
2
−
⋅
=
λ
(dla
Po
212
84
).
5)
Najdłużej żyjące izotopy wysyłają cząstki
α
o najmniejszych energiach, a jądra krótko
ż
yjące wysyłają cząstki o największych energiach.
6)
Można przyjąć za regułę, że emiterami cząstek
α
są jądra ciężkie o ładunku
84
≥
Z
i liczbie masowej
208
≥
A
(cięższe od ołowiu) oraz, że energia cząstek
α
rośnie ze wzrostem
ładunku jądra.
7)
Energia emitowanych cząstek
α
zawarta jest w przedziale od około 4,0 MeV do około
9,0 MeV.
4.3. Widma energetyczne cząstek α
Widmo energetyczne cząstek
α
jest widmem liniowym, co oznacza, że dany izotop emituje
cząstki
α
o ściśle określonych energiach. Izotopy
α
-promieniotwórcze możemy podzielić na
trzy grupy.
1)
Izotopy, które wysyłają cząstki
α
tylko o jednej ściśle określonej energii (rys. 10a). Te
cząstki tworzą tzw. grupę główną o energii
0
T . Powstawanie liniowego widma można
przedstawić za pomocą poziomów energetycznych jądra emitera i jądra pochodnego. W tym
obrazie grupa główna
0
α
o energii
0
T powstaje wtedy, gdy jądro macierzyste znajduje się w
stanie podstawowym (o najniższej energii) i z tego stanu wysyła cząstkę
α
; jądro pochodne
także tworzy się w stanie podstawowym (rys. 10a). Stan podstawowy oznaczany jest przez 0.
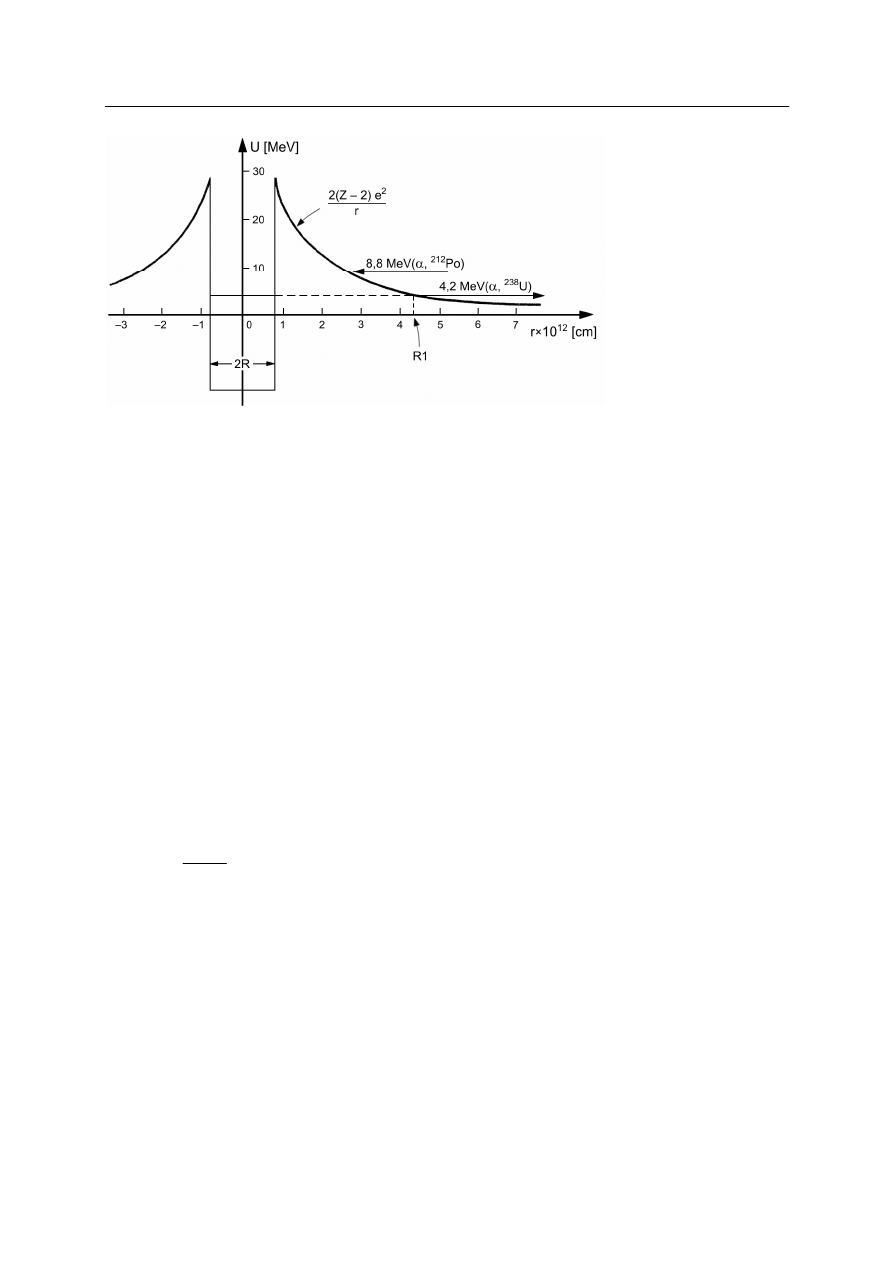
Rys. 10. Przykład prostego rozpadu
α
. Emitowana jest tylko jedna grupa cząstek
α
[5] – a. Schemat powstawania
subtelnej struktury widma energii cząstek
α
[6] – b. Schemat powstawania cząstek
α
dalekiego zasięgu ze stanu
wzbudzonego
Po
212
84
[6] – c.

30
Rozdział 4. Rozpady promieniotwórcze
2)
Izotopy, których widmo energetyczne cząstek
α
wykazuje subtelną strukturę. Oprócz
cząstek grupy głównej
0
α
, wysyłane są dwie lub więcej grup cząstek
α
o mniejszych
energiach, bardzo do siebie zbliżonych. W obrazie poziomów energetycznych widmo
powstaje także wówczas, gdy jądro emituje cząstki ze stanu podstawowego (0), a jądro
końcowe tworzy się w jednym ze stanów wzbudzonych. Właśnie wtedy powstaje subtelna
struktura widma cząstek
α
. Gdy jądro–emiter wysyła cząstki
α
ze stanu podstawowego,
a jądro pochodne tworzy się też w stanie podstawowym, powstaje grupa główna
0
α
(rys 10b).
Gdy przejście następuje ze stanu podstawowego jądra–emitera na któryś ze stanów
wzbudzonych jądra pochodnego, powstają grupy cząstek o energiach mniejszych
...
,
,
3
2
1
α
α
α
od grupy głównej
0
α
. Jądro końcowe przechodzi w stan podstawowy przez
emisję kwantów
...
,
,
3
2
1
γ
γ
γ
Suma energii emitowanego kwantu i cząstki
α
jest stała i wynosi
0
α
T :
n
n
E
T
T
E
T
T
E
T
T
γ
α
α
γ
α
α
γ
α
α
+
=
+
=
+
=
0
2
2
0
1
1
0
⋮
3)
Izotopy, których widmo cząstek
α
składa się z grupy głównej
0
α
i kilku grup cząstek
o dużo większej energii, wyraźnie przewyższającej energię cząstek grupy głównej. Różnica
energii jest zbyt duża, by ją można było zaliczyć do struktury subtelnej. Są to cząstki
długozasięgowe. Ślad po takiej cząstce widać na rysunku 11. Powstają one wtedy, gdy jądro–
emiter cząstek
α
utworzy się w stanie wzbudzonym (np. po uprzedniej emisji cząstki
β
)
i z takiego stanu emituje cząstki
α
, a jądro końcowe powstaje w stanie podstawowym
(rys. 10c). Jądro macierzyste może utworzyć się w stanie wzbudzonym jako jądro-produkt po
uprzednim rozpadzie promieniotwórczym innego jądra. Na przykład wskutek rozpadu
−
β
jądra
Bi
212
83
powstaje
Po
212
84
, przy czym może się ono utworzyć w stanie podstawowym lub
w jednym ze stanów wzbudzonych. Cząstki
α
emitowane ze stanu wzbudzonego są
cząstkami długozasięgowymi. Tylko dwa izotopy emitują długozasięgowe cząstki
α
. Są to
Po
212
84
i
Po
214
84
. Na przykład emisja
α
z
Po
212
84
jest następująca:
Grupa
]
MeV
[
α
T
%
0
α
8,947
~100
1
α
9,673
0,0034
2
α
10,570
0,0019
Rys. 11. Fotografia śladów cząstek
α
w komorze Wilsona.
Zarejestrowany został tor długozasięgowej cząstki
α
[4].

Rozdział 4. Rozpady promieniotwórcze
31
Cząstki długozasięgowe są emitowane niezwykle rzadko. Na kilkaset tysięcy rozpadów
dających cząstki o zwykłym zasięgu przypada jedna cząstka
α
długozasięgowa. Małe
natężenie cząstek długozasięgowych (~10
–5
) tłumaczymy tym, że jądro wzbudzone może
przejść do stanu podstawowego przez emisję kwantów
γ
lub cząstki
α
, jednakże
prawdopodobieństwo tego pierwszego procesu jest znacznie większe od prawdopodobieństwa
emisji cząstek
α
.
4.4. Warunki energetyczne i mechanizm rozpadu α
Jako przykład rozpadu
α
przytaczamy rozpad protaktynu
Pa
226
91
:
Ac
Pa
222
89
4
2
226
91
+
→
α
Obliczamy defekt masy i energię wiązania protaktynu 226 względem cząstki
α
i 222 Ac.
Defekt masy wynosi:
Pa
Ac
M
m
M
m
−
+
=
∆
)
(
α
jma
0280
,
226
Pa
masa
226
=
=
Pa
M
jma
0204
,
226
jma
0026
,
4
He
masa
jma
0178
,
222
Ac
masa
4
2
222
89
=
+
=
=
=
=
α
α
m
M
m
M
Ac
Ac
zatem
jma
0076
,
0
jma
0280
,
226
jma
0204
,
226
−
=
−
=
∆
m
eV
07
,
7
MeV
48
,
931
076
,
0
jma
076
,
0
2
−
=
⋅
−
=
−
=
∆
=
∆
mc
E
W
Ujemna energia wiązania oznacza, że jądro protaktynu
Pa
226
jest niestabilne na rozpad
α
i możliwa jest spontaniczna przemiana
α
.
Jeżeli energia wiązania jest ujemna, to dlaczego rozpad
α
nie zachodzi natychmiast?
Można oszacować oczekiwany czas rozpadu
α
przyjmując, że cząstka powstaje na jednym
brzegu jądra, a następnie przechodzi wzdłuż średnicy na drugi brzeg i stamtąd zostaje
wyrzucona. Na takie przejście drogi o promieniu R potrzebny jest czas:
v
R
=
τ
ponieważ
(
)
]
m
[
10
4
,
1
3
1
15
3
1
0
A
A
r
R
−
⋅
=
=
. Rozpadowi
α
ulegają ciężkie jądra
)
200
(
>
A
,
możemy więc przyjąć dla ułatwienia, że
200
=
A
oraz
[m/s]
10
2
7
⋅
=
v
– taką prędkość mają
cząstki
α
o energii
MeV
8
. Stąd mamy:
s
10
2
s
m
10
2
200
m
10
4
.
1
22
7
3
15
−
−
−
⋅
≈
⋅
⋅
=
τ
32
Rozdział 4. Rozpady promieniotwórcze
Po takim czasie powinien nastąpić rozpad
α
. Średni czas życia najkrócej żyjącego izotopu
to wielkość rzędu
s
10
7
−
, ale jest to i tak czas o 15 rzędów dłuższy od oczekiwanego,
a są przecież izotopy-emitery cząstek
α
, dla których czasy życia mają rząd miliardów
lat. Dlaczego więc rozpad
α
nie jest procesem natychmiastowym? Jaki jest mechanizm
rozpadu
α
?
Wyjaśnienie tego zagadnienia dała analiza wyników doświadczeń Rutherforda, który
bombardował jądra uranu 238 cząstkami
α
o energii 8,8 MeV pochodzącymi z
.
Po
212
84
Sam
uran 238 jest promieniotwórczy i wysyła cząstki
α
o energii 4,0 MeV. Rutherford ustalił, że
bombardujące cząstki
α
o energii 8,8 MeV są rozpraszane przez jądra
U
238
zgodnie
z prawem Coulomba. To znaczy, że rozpraszanie jest spowodowane kulombowskim
odpychaniem cząstki
α
przez dodatni ładunek jądra uranu. śadnego odchylenia
ś
wiadczącego o jądrowym charakterze oddziaływania cząstek
α
z jądrami uranu–tarczy nie
zaobserwowano. W szczególności nie stwierdzono wnikania cząstek
α
o energii ponad
8,0 MeV do jądra uranu 238. To oznacza, że dla odległości r większych od promienia jądra R
energię potencjalną cząstki
α
w polu elektrycznym jądra uranu można przedstawić wzorem:
r
Ze
r
U
0
2
4
2
)
(
πε
=
Na rysunku 12 przedstawiony jest schemat rozpraszania cząstek
α
przez jądra uranu
w doświadczeniu Rutherforda. W pierwszej fazie rozpraszania (zbliżanie się cząstki do jądra)
ma miejsce wzrost energii potencjalnej cząstki w polu elektrycznym jądra uranu zgodnie
z prawem Coulomba.
Energia ta rośnie od 0 dla
∞
=
r
do wartości co najmniej 8.8 MeV dla
R
r
=
(odległości
większej, równej promieniowi jądra), gdyż cząstki o takiej energii są rozpraszane przez jądra
uranu. Dla odległości mniejszych od promienia jądra (
R
r
<
) prawo Coulomba traci
znaczenie, bo rolę sił kulombowskich przejmują siły jądrowe, które są bardzo dużymi siłami
przyciągającymi. Przyciągający charakter sił jądrowych wewnątrz jądra (
R
r
<
) przejawia się
zmianą znaku krzywej energii potencjalnej. Krzywa ta staje się krzywą opadającą, a duża
wartość sił ujawnia się tym, że krzywa opada gwałtownie, niemal pionowo. W ten sposób
jądro otoczone zostało barierą potencjału o wysokości co najmniej 8,8 MeV dla
R
r
=
, dla
jądra uranu 238. Cząstki o takiej energii nie wnikają do jądra uranu i są przez nie rozpraszane.
Rys. 12. Zależność energii potencjalnej U cząstki
α
od odległości r od środka jądra (dla jądra
238
U; R
1
jest
punktem wyjścia cząstki o energii 4,2 MeV z jądra uranu [2].

Rozdział 4. Rozpady promieniotwórcze
33
W jądrze uranu cząstka o energii 4 MeV znajduje się w studni potencjał o wysokości
MeV
8
,
8
>
U
. Nic dziwnego więc, że rozpad
α
nie jest procesem natychmiastowym; wręcz
przeciwnie, należy się dziwić, że cząstka
α
wylatuje z jądra i że ten rozpad w ogóle
zachodzi. W fizyce klasycznej cząstka
α
może wejść do jądra tylko wtedy, gdy jej energia
jest większa od bariery potencjału i może wyjść z jądra też tylko wtedy, gdy ma energię
większą od bariery potencjału otaczającej jądro. Aby zrozumieć, jak cząstka
α
wydostaje się
z jądra, potrzebne jest zjawisko tunelowe. W tym zjawisku może ona przenikać przez barierę
potencjału dzięki efektowi tunelowemu nawet wtedy, gdy ma energię mniejszą od bariery
potencjału, przy czym pojawia się po drugiej stronie bariery (na zewnątrz jądra) z taką samą
energią, jaką miała w jądrze. Zjawisko tunelowe jest zjawiskiem kwantowym i nie ma swego
odpowiednika w fizyce klasycznej. Z punktu widzenia fizyki klasycznej cząstka
α
nigdy nie
opuściłaby jądra i nie byłoby rozpadu promieniotwórczego
α
. Proces tunelowy pozwala na
zignorowanie sił wiążących cząstkę
α
w jądrze i gdy ma ona energię mniejszą od bariery
potencjału może z określonym prawdopodobieństwem przez nią przejść. Cząstka w jądrze
porusza się między ściankami studni. Przy każdym uderzeniu o ściankę mamy określone
prawdopodobieństwo odbicia się od ścianki i określone prawdopodobieństwo przejścia przez
barierę i wyjścia na zewnątrz. Prawdopodobieństwo przeniknięcia przez barierę (zwane też
przepuszczalnością lub przeźroczystością bariery) określa się wzorem:
−
−
=
∫
1
d
)
(
2
2
exp
R
R
r
U
T
m
h
D
gdzie: R – promień jądra,
1
R
– punkt wyjścia cząstki z jądra, T – energia kinetyczna cząstki,
U – wysokość bariery potencjału. Te parametry przedstawione są na rysunku 12.
4.5. Rozpad β
Rozpadem
β
nazywamy spontaniczny proces przemiany jądra w jądro izobaryczne o ładunku
różniącym się od jądra macierzystego o
1
∓
=
∆
Z
, wywołany emisją elektronu, pozytronu lub
wychwytem
K. Jądra izobaryczne mają taką samą liczbę masową A lecz różnią się liczbą
protonów
Z.
Okresy połowicznego rozpadu izotopów ulegających rozpadowi
β
zawierają się
w granicach od
s
10
2
−
do
15
10
2
⋅
lat
. Energie wyzwalanych elektronów zawierają
się w granicach od 18 keV
do 16.6 MeV (chodzi tu o energię maksymalną). Istnieją 3 rodzaje
rozpadów
β
:
1)
Rozpad
−
β
, w którym jądro macierzyste wyrzuca elektron.
2)
Rozpad
+
β
polegający na emisji pozytronu (dodatniego elektronu) z jądra
macierzystego.
3)
Wychwyt
K – zjawisko, w którym elektron powłokowy jest wychwytywany przez jądro
macierzyste.
Jak zachodzi emisja elektronu i pozytronu z jądra, skoro w jądrze są tylko protony
i neutrony? Wyjaśnimy to zjawisko następująco: piszemy schemat rozpadu
−
β
ν
β
+
+
→
+
−
P
M
1
0
1
A
Z
A
Z
(11)
gdzie M i P są symbolami jądra macierzystego i pochodnego,
β
0
1
−
jest symbolem elektronu
jądrowego a
ν
jest antyneutrinem. W wyrażeniu (11) liczbą atomową jądra pochodnego jest

34
Rozdział 4. Rozpady promieniotwórcze
Z+1 a macierzystego Z, co oznacza, że jądro pochodne ma o jeden proton więcej niż
macierzyste, natomiast liczba masowa jądra macierzystego i pochodnego jest taka sama.
Liczba neutronów w jądrze macierzystym wynosi
Z
A
N
−
=
a w jądrze pochodnym:
1
1
)
(
)
1
(
−
=
−
−
=
+
−
=
N
Z
A
Z
A
N
'
a więc w jądrze pochodnym ubył jeden neutron i przybył jeden proton. Wyjaśnienie tego
zjawiska jest następujące: rozpad
−
β
(elektronowy) polega na tym, że wewnątrz jądra
następuje przemiana neutronu w proton z jednoczesną emisją elektronu i antyneutrina
(rys. 13). Taka przemiana zachodzi zgodnie ze schematem:
ν
β
+
+
→
−
0
1
1
1
1
0
p
n
(12)
Przykład rozpadu
−
β
:
ν
β
+
+
→
−
He
H
3
2
0
1
3
1
(
T
1/2
= 12,5 lat)
Rozpad
+
β
przedstawiamy następująco:
ν
β
+
+
→
−
+
P
M
1
0
1
A
Z
A
Z
(13)
gdzie M i P są, jak poprzednio, symbolami jądra macierzystego i pochodnego,
ν
jest
neutrinem,
β
0
1
+
jest symbolem pozytronu. W wyrażeniu (13) liczba atomowa jądra
końcowego wynosi
Z–1 a macierzystego Z, co oznacza, że jądro końcowe ma o jeden proton
mniej niż macierzyste, a liczby masowe obu jąder – początkowego i końcowego są takie
same. Liczba neutronów w jądrze macierzystym to:
Z
A
N
−
=
a w jądrze pochodnym:
1
1
)
(
)
1
(
+
=
+
−
=
−
−
=
N
Z
A
Z
A
N
'
Wniosek: w jądrze pochodnym ubył jeden proton i przybył jeden neutron. Rozpad
+
β
(pozytronowy) można interpretować jako zachodzący we wnętrzu jądra proces przemiany
protonu w neutron z jednoczesną emisją pozytronu i neutrina (rys. 13):
ν
β
+
+
→
+
0
1
1
0
1
1
n
p
(14)
Przykład rozpadu pozytronowego:
ν
β
+
+
→
+
B
C
11
5
0
1
11
6
(
T
1/2
= 20,4 min)
Rys. 13. Ilustracja rozpadów
β
: elektronowego (a),
pozytronowego (b) i wychwytu K (c) [6].

Rozdział 4. Rozpady promieniotwórcze
35
Przemiana protonu w neutron jest możliwa tylko w jądrze. Poza jądrem proton jest cząstką
trwałą. Natomiast neutron nie jest cząstką trwałą i poza jądrem neutron swobodny rozpada się
na proton, elektron i antyneutrino zgodnie ze schematem (12), z okresem półrozpadu
s
960
2
/
1
=
T
(13 min). Aby przekonać się, że rozpad neutronu jest możliwy a protonu nie jest,
obliczymy energię wiązania neutronu (względem protonu i elektronu) oraz energię wiązania
protonu (względem neutronu i pozytronu).
Masy protonu, neutronu i elektronu są:
kg
10
6725
,
1
27
−
⋅
=
p
m
kg
10
6748
,
1
27
−
⋅
=
n
m
kg
10
1
,
9
31
−
⋅
=
e
m
Defekt masy przy rozpadzie neutronu wynosi:
kg
10
4
,
1
)
(
30
−
⋅
−
=
−
+
=
∆
n
e
p
m
m
m
m
Energia wiązania wynosi:
MeV
7296
,
0
eV
10
64
,
5
10
4
,
1
35
30
,
−
=
⋅
⋅
⋅
−
=
−
n
w
E
Ta energia jest ujemna, a więc rozpad neutronu jest możliwy, tzn. możliwa jest spontaniczna
przemiana neutronu w proton. Proton może przechodzić w neutron tylko w jądrze atomowym.
Proton swobodny, poza jądrem, jest cząstką trwałą i nie może przechodzić w neutron.
Obliczymy energię wiązania protonu względem neutronu i pozytronu. Defekt masy wynosi:
kg
10
21
,
3
)
(
30
−
⋅
+
=
−
+
=
∆
p
e
n
m
m
m
m
Energia wiązania:
MeV
81
,
1
eV
10
64
,
5
10
21
,
3
35
30
,
+
=
⋅
⋅
⋅
+
=
−
p
w
E
Tutaj energia wiązania jest dodatnia, a zatem rozpad protonu na neutron i pozytron jest
niemożliwy. Taką energię należy dostarczyć protonowi, aby nastąpiła taka przemiana.
W jądrze, wskutek oddziaływania nukleonów z protonem, może on taką energię uzyskać
i ulec przemianie. Poza jądrem jest to niemożliwe, bo proton nie ma skąd czerpać tej energii.
4.6. Wychwyt K
Trzeci rodzaj promieniotwórczości
β
to wychwyt
K (rys. 13). Polega on na tym, że jądro
atomowe pochłania elektron powłokowy. Największe prawdopodobieństwo zaistnienia
wychwytu
K ma miejsce wtedy, gdy elektron zostaje wychwycony (porwany) z powłoki K –
stąd nazwa procesu „wychwyt K”. Obserwuje się też wychwyt elektronu z powłoki
L
(wychwyt
L), a nawet M, lecz jest on znacznie mniej prawdopodobny. Wychwyt K zachodzi
według schematu (rys. 13):
ν
+
→
+
−
−
P
M
1
0
1
A
Z
A
Z
e
(15)
Przykład wychwytu
K:
ν
+
→
+
−
Li
Be
7
3
0
1
7
4
e
(
T
1/2
= 54 dni)

36
Rozdział 4. Rozpady promieniotwórcze
Liczba protonów w jądrze końcowym jest o jeden mniejsza niż w macierzystym, przy
takiej samej liczbie masowej
A. Liczba neutronów w jądrze końcowym wynosi:
1
1
)
(
)
1
(
+
=
+
−
=
−
−
=
N
Z
A
Z
A
N
'
Gdzie
N jest liczbą neutronów w jądrze macierzystym,
Z
A
N
−
=
. A więc w jądrze
pochodnym ubył jeden proton, a przybył jeden neutron. Wychwyt
K można przedstawić
następująco – we wnętrzu jądra proton łączy się ze schwytanym elektronem i powstaje
neutron:
ν
+
→
+
−
n
p
e
1
0
1
1
0
1
Ś
ciągnięcie elektronu z powłoki
K pozostawia na niej puste miejsce. Elektrony spadają
z wyższych powłok na powłokę
K, powodując powstanie promieniowania rentgenowskiego
charakterystycznego dla jądra końcowego (rys. 14). Przejście elektronu na powłokę
K może
nastąpić bez wyświecenia promieni
X. Może wtedy dojść do przekazania energii przejścia
innemu elektronowi (rys. 14). Elektron ten opuszcza atom. Nazywa się on elektronem
Augera.
Zjawisko
to
może
również
towarzyszyć
zwykłemu
promieniowaniu
rentgenowskiemu, niekoniecznie tylko w wychwycie
K.
Czy w jądrze atomowym są elektrony? Pytanie to jest już nieaktualne, niemniej jednak
zdarzają się jeszcze niedowiarki, których trudno przekonać, że w jądrze nie ma i nie może być
elektronów. Spróbujemy więc oszacować energię elektronów w jądrze atomowym, gdyby
mogły one tam przebywać. Korzystamy z relacji nieoznaczoności Heisenberga w postaci:
h
x
p
≥
∆
∆
Dla elektronu w jądrze atomowym nieokreśloność położenia jest równa średnicy jądra:
m
10
4
,
1
15
3
−
⋅
=
=
∆
A
R
x
Stąd nieoznaczoność pędu:
15
3
10
4
,
1
−
⋅
=
∆
≥
∆
A
h
x
h
p
Rys. 14. Ilustracja emisji promieniowania charakterystycznego
X
lub elektronu Augera po wychwycie K.

Rozdział 4. Rozpady promieniotwórcze
37
Zakładamy, że
A = 125 (pierwiastek z okolicy środka układu okresowego)
m
125
4
.
1
10
Js
10
63
,
6
3
15
34
−
⋅
≥
∆
p
s
m
kg
10
47
,
9
5
4
,
1
10
63
,
6
20
19
−
−
⋅
=
⋅
⋅
≥
∆
p
Obliczamy energię, jaką miałby elektron w jądrze. Całkowita energia wynosi:
4
2
0
2
2
2
c
m
c
p
E
+
=
2
4
2
0
)
MeV
511
,
0
(
=
c
m
– ten człon pomijamy, emitowane cząstki
β
charakteryzują się dużą
energią, dochodzącą do kilkunastu MeV. Wobec tego
pc
E
=
to energia kinetyczna
elektronów
J
10
84
,
2
s
m
10
3
s
m
kg
10
4
,
9
11
8
20
−
−
⋅
=
⋅
⋅
⋅
=
=
T
E
MeV
178
eV
10
78
,
1
10
6
,
1
eV
10
84
,
2
8
19
11
=
⋅
=
⋅
⋅
=
−
−
T
ś
adna bariera potencjału nie utrzymałaby takich elektronów w jądrze. Porównanie tej
energii z energią cząstek
β
, wynoszącą kilkanaście MeV, jest wymowne.
4.7. Warunki energetyczne rozpadu β
Dla uproszczenia rozważań oznaczamy masę jądra macierzystego przez
M
j
(
Z, A), a masy
jąder pochodnych przez
M
j
(
Z – 1, A) lub M
j
(
Z+1, A).
Warunkiem, aby doszło do rozpadu
−
β
jest
e
j
j
m
A
Z
M
A
Z
M
+
+
>
)
,
1
(
)
,
(
(16)
Warunek na rozpad
+
β
ma postać:
e
at
at
m
A
Z
M
A
Z
M
2
)
,
1
(
)
,
(
+
−
>
(17)
a na wychwyt
K:
)
,
1
(
)
,
(
A
Z
M
A
Z
M
at
at
−
>
(18)
Jeżeli spełniony jest warunek (17), automatycznie spełniony jest warunek (18), dlatego
rozpad
+
β
i wychwyt
K często zachodzą równocześnie. Wychwyt K jest energetycznie
korzystniejszy niż emisja pozytronów, ale wychwyt
K zależy od tego, czy elektron zbliży się
(i wniknie) do jądra, a prawdopodobieństwo takiego zdarzenia jest małe. W rezultacie, gdy
dostępna energia przekroczy
2
0
2
c
m
, to emisja pozytronowa będzie zachodzić częściej niż
wychwyt
K. Warunek (18) jest warunkiem koniecznym, ale nie wystarczającym, żeby mógł
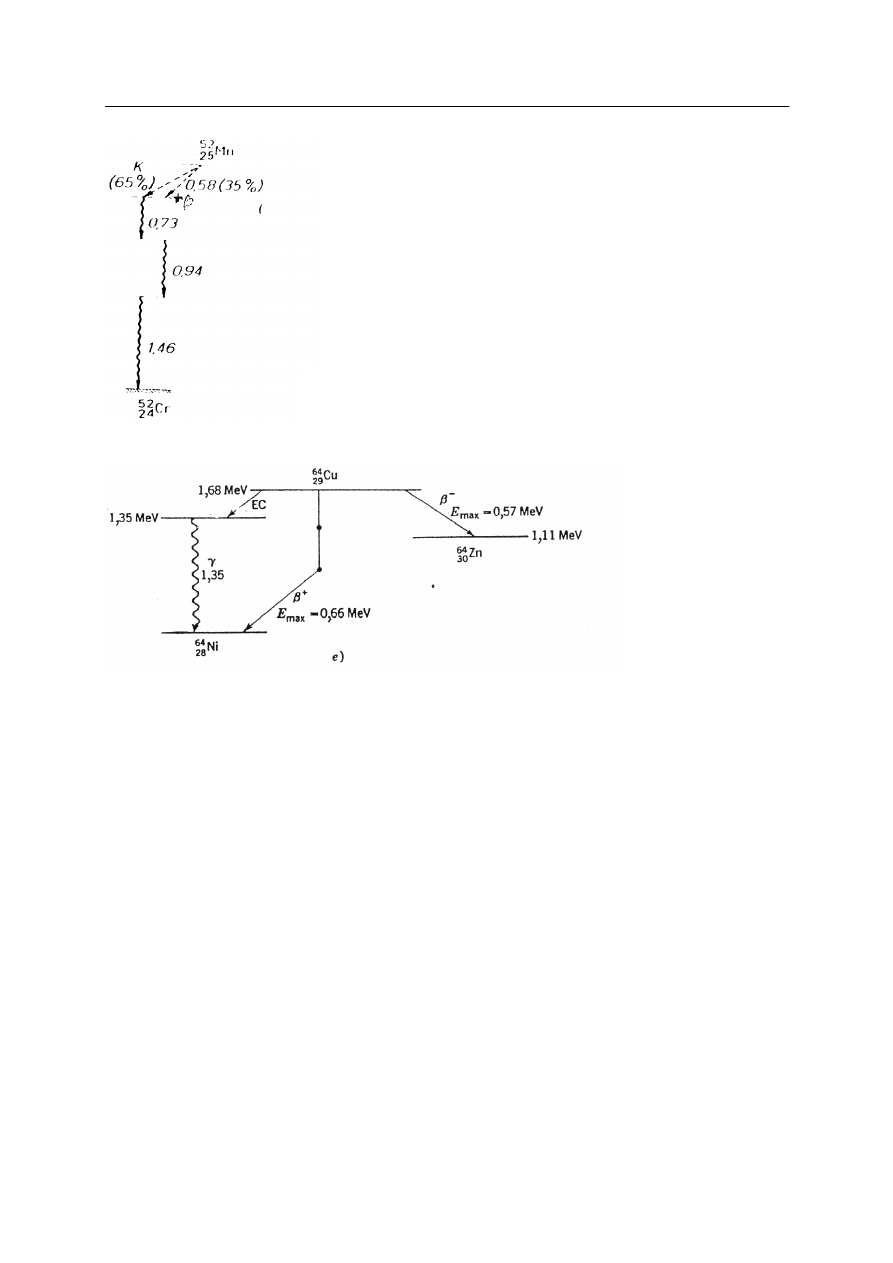
38
Rozdział 4. Rozpady promieniotwórcze
zajść wychwyt
K. Warunek ten może by spełniony a wychwyt K nie wystąpi. Jednak często
oba procesy (
+
β
i wychwyt
K) zachodzą równocześnie (rys. 15). Nie znaczy to, że w każde
jądro doznaje obu rozpadów na raz. W jednym jądrze może nastąpić tylko jeden z nich.
Na przykład
Mn
52
25
, który przekształca się w jądro
Cr
52
24
w 35% przechodzi przemianę
+
β
,
a w 65% przez wychwyt
K.
Zdarza się, że dla pewnych jąder mogą być spełnione wszystkie trzy warunki (16, 17, 18)
jednocześnie, tzn. dla pewnych jąder (
Z, A) spełniony jest warunek (16) w odniesieniu do
jądra izobarycznego (
Z+1, A), a warunek (17) w odniesieniu do jądra izobarycznego (Z–1, A),
wtedy jądro (
Z, A) ulega wszystkim trzem przemianom
β
. Przykładem może być izotop
Cu
64
29
, który w 40% rozpada się przez
−
β
, w 20% przez
+
β
w 40% ulega wychwytowi
K
(rys. 16).
4.8. Widmo energetyczne cząstek β, hipoteza neutrino
Najważniejszą własnością rozpadu
β
jest ciągły charakter widma energetycznego
emitowanych elektronów
−
β
i
+
β
. Oznacza to, że izotop-emiter cząstek
β
wysyła cząstki
o energiach bardzo małych aż do energii maksymalnej
max
β
T
, charakterystycznej dla tego
izotopu. Energia
max
β
T
jest w bardzo dobrym przybliżeniu równa energii rozpadu
β
, czyli
Rys. 16 Przykład jednoczesnego występowania trzech procesów
β
: rozpadów
β
–
,
β
+
i wychwytu K [8].
Rys. 15. Przykład jednoczesnego występowania dwóch procesów
β
: rozpadu
β
+
i wychwytu K [8].
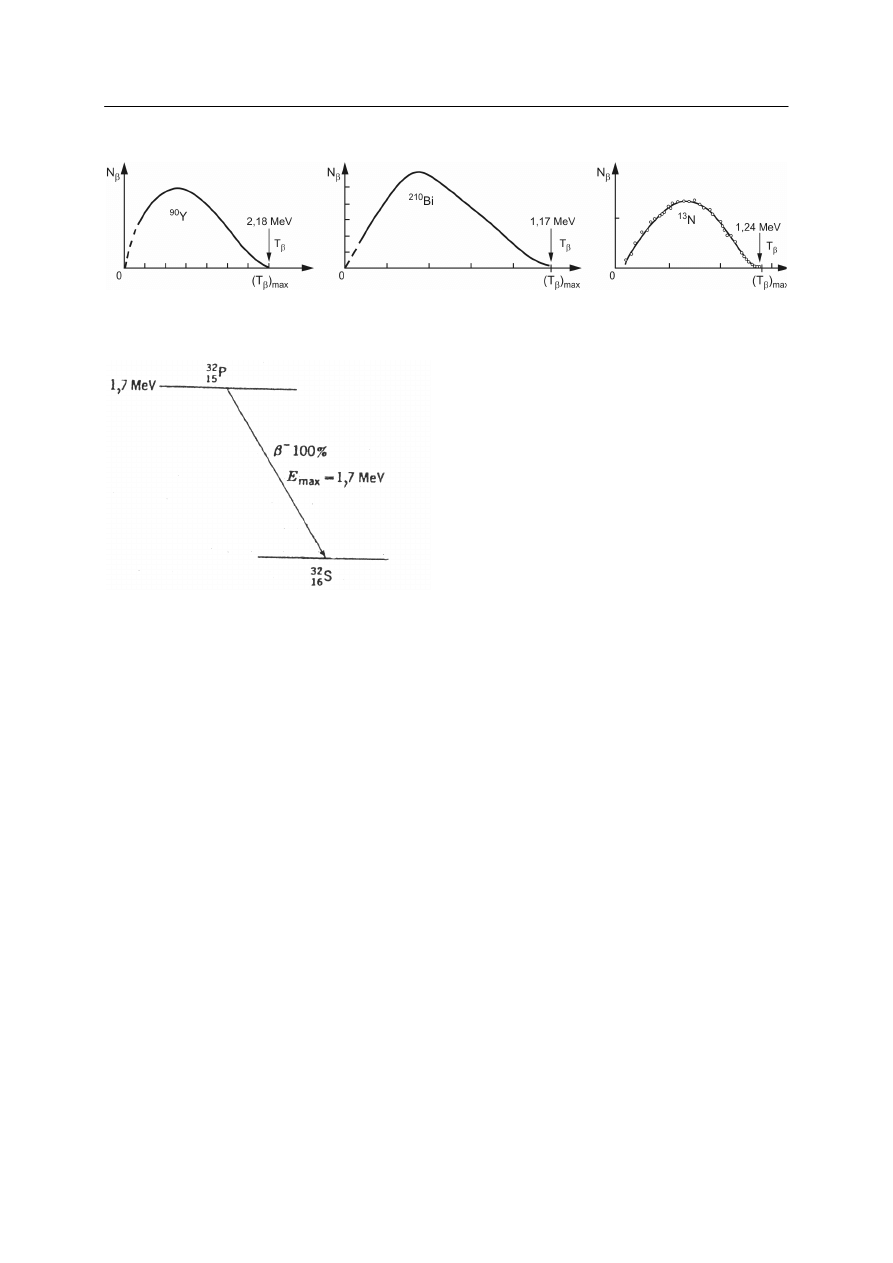
Rozdział 4. Rozpady promieniotwórcze
39
równa różnicy energii stanów podstawowych jądra macierzystego i końcowego. Jest to
energia, która wchodzi do bilansu mas i energii w każdym rozpadzie
β
. Przykłady widm
β
przedstawia rysunek 17, a schemat przejścia między izotopami rysunek 18.
Pauli zwrócił uwagę, że przy rozpadzie
β
nie zostaje spełnione prawo zachowania energii
i prawo zachowania spinu, jeżeli rozpad
β
zachodzi według schematu:
P
M
1
0
A
Z
A
Z
∓
+
→
±
β
(19)
czyli jeszcze przed wprowadzeniem i odkryciem neutrina.
Prawo zachowania energii jest spełnione tylko wtedy, gdy zostaje wyrzucona cząstka
β
o maksymalnej energii
max
β
T
. Energia ta jest w bardzo dobrym przybliżeniu równa energii
rozpadu
β
. Z kształtu widma energetycznego cząstek
β
wynika, że źródło wysyła elektrony
o energiach mniejszych od
max
β
T
(prawo zachowania energii nie jest spełnione). Brakującej
do bilansu energii nie może zabierać promieniowanie
γ
, które może towarzyszyć rozpadowi
β
. Widmo promieniowania
γ
jest liniowe, a musiałoby być widmem ciągłym, które byłoby
uzupełnieniem energii cząstek
β
do energii maksymalnej
max
β
T
β
β
γ
T
T
E
−
=
max
Znane są izotopy
β
promieniotwórcze, którym nie towarzyszy promieniowanie
γ
(rys.
18) i ich widmo energetyczne też jest ciągłe.
Jeżeli rozpad zachodzi według schematu (19), nie zostaje spełnione prawo zachowania
spinu. Jądro o parzystej liczbie masowej
A ma spin całkowity; natomiast dla jądra
o nieparzystej liczbie masowej
A spin jest połówkowy. Przy rozpadzie
β
liczba masowa
jądra początkowego i końcowego jest taka sama. Jeżeli spin jądra macierzystego był
całkowity, to nowe jądro też ma spin całkowity; jeśli był połówkowy, to po rozpadzie
β
pozostaje połówkowy. Po lewej stronie schematu rozpadu (19) mamy spin całkowity dla
Rys. 17. Przykłady widm energetycznych cząstek
β
, T
β
max
jest maksymalną energią cząstek
β
[3].
Rys. 18. Przykład rozpadu
β
, któremu nie towarzyszy
emisja promieniowania
γ
[8].

40
Rozdział 4. Rozpady promieniotwórcze
parzystego
A, po prawej zaś sumaryczny spin jest połówkowy (całkowity spin jądra
końcowego i połówkowy elektronu
β
)
1
1
2
1
+
→
Spin nie zostaje zachowany. Podobne rozważania można przeprowadzić dla
A
nieparzystego. Wtedy po lewej stronie schematu (19) będzie spin połówkowy, a po prawej
całkowity (połówkowy spin jądra pochodnego i połówkowy cząstki
β
):
2
1
2
1
2
1
+
→
Do podobnego wniosku dochodzimy po analizie spinów przemian neutronu w proton
i protonu w neutron zachodzących wewnątrz jądra:
2
1
2
1
2
1
0
1
1
1
1
0
+
→
+
→
−
β
p
n
2
1
2
1
2
1
0
1
1
0
1
1
+
→
+
→
+
β
n
p
Pauli wysunął hipotezę, że przy tym rozpadzie zostaje wyrzucona jakaś dodatkowa cząstka
o ładunku równym zero, która musi mieć spin połówkowy i masę spoczynkową równą zero.
Cząstka ta zabiera brakującą energię potrzebną do bilansu energii i pozwala na spełnienie
prawa zachowania spinu. Fermi nazwał tę cząstkę neutrinem. Neutrino zostało wykryte
w 1956 r., a więc prawo zachowania energii i spinu pozostało nienaruszone. Oznaczamy tę
cząstkę symbolem
ν
. Wobec tego, że cząstka ta nie ma masy spoczynkowej można ją opuścić
w bilansie mas i energii. Wiemy dzisiaj, że obok neutrina istnieje też antyneutrino
ν
.
Antyneutrino jest antycząstką neutrina. Uwzględniając neutrino i antyneutrino, rozpady
β
przedstawiamy następująco:
– Rozpad
−
β
ν
β
+
+
→
+
−
P
M
1
0
1
A
Z
A
Z
ν
β
+
+
→
−
p
n
1
1
0
1
1
0
– Rozpad
+
β
ν
β
+
+
→
−
+
P
M
1
0
1
A
Z
A
Z
ν
β
+
+
→
+
n
p
1
0
0
1
1
1
– Wychwyt K
ν
+
→
+
−
−
P
M
1
0
1
A
Z
A
Z
e
ν
+
→
+
−
n
p
e
1
0
1
1
0
1
Wprowadzenie neutrina wyjaśnia całkowicie teorię rozpadu
β
. Następuje rozpad na trzy
cząstki: jądro końcowe, cząstkę
β
i neutrino. Cząstki te mogą mieć różne energie, ponieważ
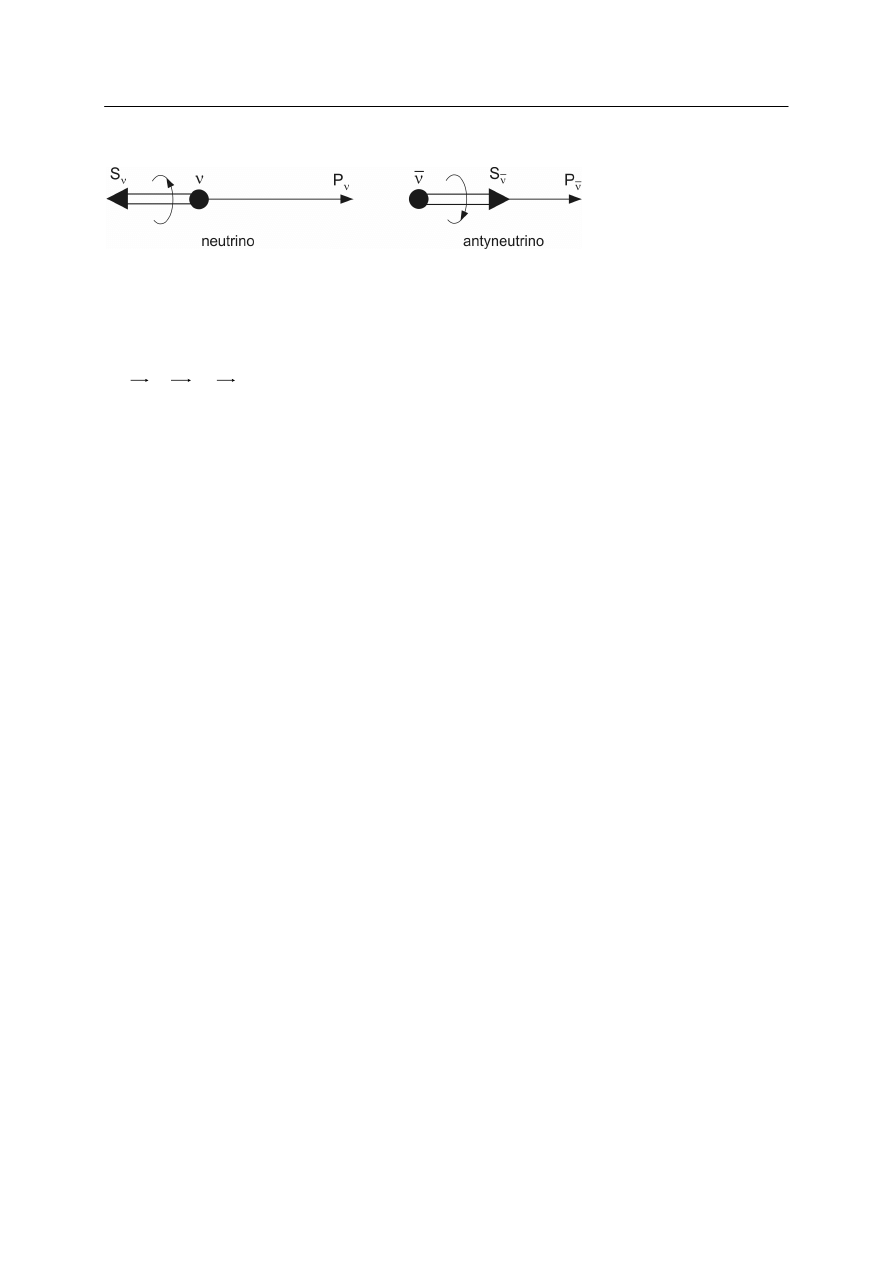
Rozdział 4. Rozpady promieniotwórcze
41
z zasady zachowania pędu wynika, że pęd wypadkowy po rozpadzie jest równy zero, a pęd
początkowy (jądra macierzystego) też jest równy zero:
0
=
+
+
ν
β
p
p
p
j
Pędy dodają się wektorowo, dając wypadkową wartość równą zero (cząstki mogą rozbiegać
się pod różnymi kątami).
4.9. Właściwości neutrina
Neutrino posiada następujące cechy:
1)
Brak ładunku elektrycznego,
2)
Masa spoczynkowa równa lub bliska zeru,
3)
Spin połówkowy,
4)
Podlega statystyce Fermiego–Diraca,
5)
Porusza się z prędkością światła,
6)
Jest cząstką bardzo przenikliwą, gdyż nie ma ładunku elektrycznego i momentu
magnetycznego, i dlatego nie oddziałuje z napotkanymi jądrami i elektronami. Gdyby
oddziaływała, musiałaby tracić energię, która ujawniłby się w postaci fotonów
γ
lub energii
kinetycznej odrzutu elektronów, i w ostatecznym wyniku przekształciłaby się w ciepło
mierzalne kalorymetrycznie,
7)
Neutrino od antyneutrina różni się skrętnością. Neutrinu przypisano symetrię śruby
lewoskrętnej. Przyjęto mianowicie, że kierunek pędu neutrina jest związany z kierunkiem
jego spinu, tak jak w śrubie lewoskrętnej kierunek obrotu związany jest kierunkiem przesuwu
ś
ruby (rys. 19). Tak więc w neutrinie kierunek i zwrot spinu jest jednoznacznie sprzężony
z kierunkiem pędu cząstki; podobnie jest i dla antyneutrina, lecz tam spin zorientowany jest
przeciwnie niż w neutrinie (symetria śruby prawoskrętnej).
Rys. 19. Ilustracja kierunku pędu i kierunku obrotu spinu neutrina i antyneutrina.


Rozdział 5.
Sztuczna promieniotwórczość
W wyniku reakcji jądrowej może powstać jądro końcowe, które jest promieniotwórcze. Jądro
takie nie jest więc jądrem trwałym – jest jądrem sztucznie promieniotwórczym. Pod
określeniem „sztuczna promieniotwórczość” rozumiemy to, że pierwiastek promieniotwórczy
powstaje wskutek reakcji jądrowej, czyli bombardowania cząstkami jakiegoś jądra. Jest to
promieniotwórczość wymuszona (lub wzbudzona).
Sztuczna promieniotwórczość została odkryta przez Irenę i Fryderyka Joliot w 1934 r.
Bombardowali oni aluminium cząstkami
α
i stwierdzili w próbce emisję pozytronów nawet
po przerwaniu bombardowania:
n
1
0
30
15
27
13
4
2
P
Al
+
→
+
α
Okazało się, że jądro końcowe P
30
15
jest
+
β
promieniotwórcze:
ν
β
+
+
→
+
0
1
30
14
30
15
Si
P
(
min
25
,
3
2
/
1
=
T
)
Trwałym izotopem fosforu jest
P
31
15
, który w przyrodzie występuje w 100%. Izotop
P
30
15
jest nowym izotopem, dotychczas nieznanym. W przyrodzie nie występują izotopy
+
β
promieniotwórcze.
Druga ich reakcja:
n
1
0
13
7
10
5
4
2
N
B
+
→
+
α
Izotop N
13
7
również okazał się
+
β
promieniotwórczy:
ν
β
+
+
→
+
0
1
13
6
13
7
C
N
(
min
14
2
/
1
=
T
)
Izotop
N
13
7
też jest nowym izotopem nie występującym w przyrodzie, gdzie spotkać można
tylko dwa izotopy azotu N
14
7
(99,63%) i N
15
7
(0,37%). Oba są izotopami trwałymi.
W ten sposób można otrzymać izotopy nie występujące w przyrodzie, jak i te, które
występują
–
zarówno
trwałe,
jak
i
promieniotwórcze.
Szczególnie
użyteczne
w przeprowadzaniu reakcji jądrowych są neutrony. Ze względu na brak ładunku mogą łatwo
przenikać do jądra i wywołać reakcję. Fermi poddał bombardowaniu neutronami niemal
wszystkie pierwiastki występujące w przyrodzie, uzyskując ich izotopy. Charakterystyczną
cechą tych reakcji było to, że te wszystkie izotopy ulegały przemianie
−
β
. W reakcjach tych
powstają izotopy, które mają o jeden neutron więcej w porównaniu z izotopami już
występującymi i naświetlanymi neutronami. Takie jądra z nadwyżką neutronów nie są trwałe
i ulegają przemianie zmierzającej do przywrócenia składu protonowo-neutronowego,
charakterystycznego dla jąder trwałych. Dla jąder z nadmiarem neutronów przemianą
prowadzącą do takiego składu jest przemiana
−
β
. Natomiast w reakcjach przeprowadzonych
przez małżonków Joliot-Curie, w wyniku bombardowania cząstkami
α
, w jądrze występował
nadmiar protonów. Przemianą prowadzącą do przywrócenia składu protonowo-neutronowego
występującego w jądrach trwałych jest przemiana
+
β
.
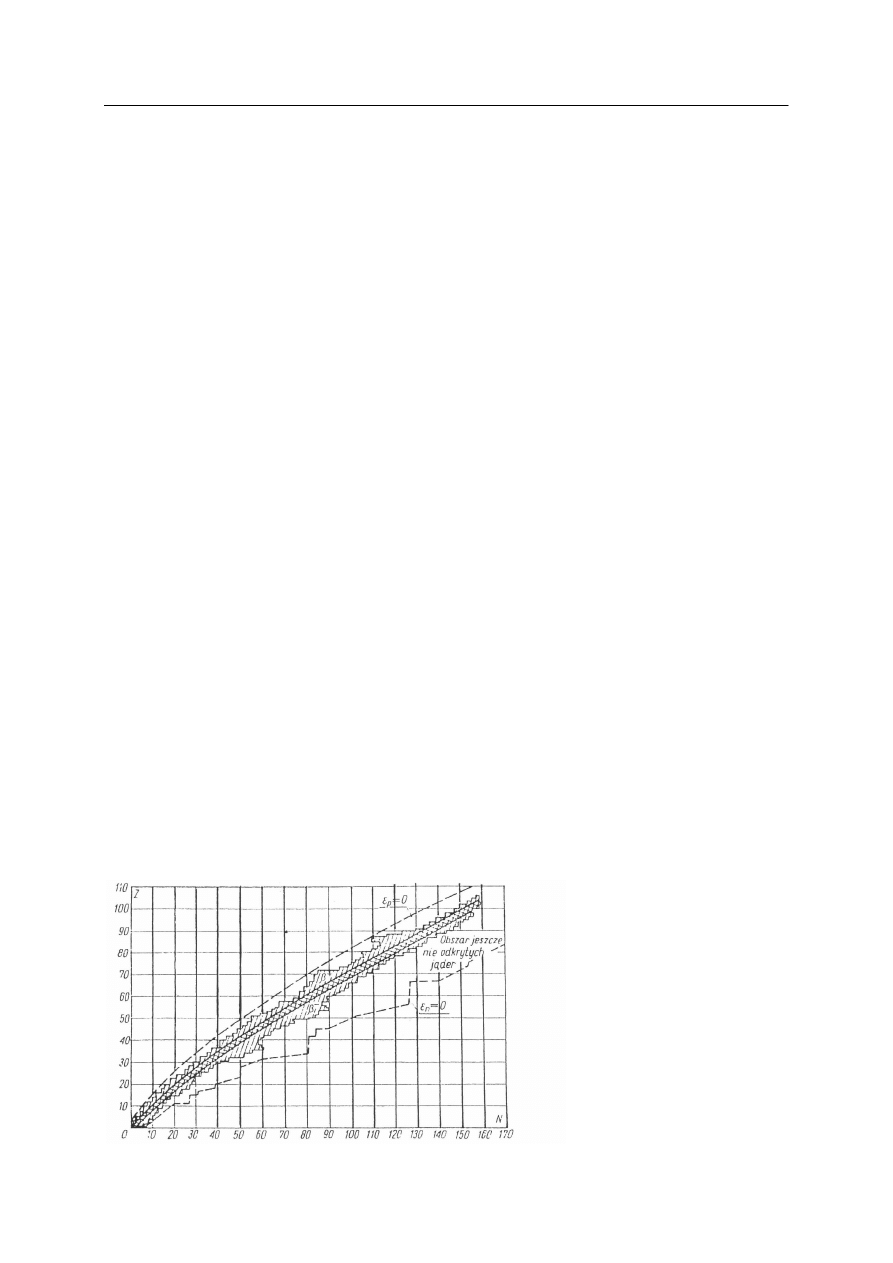
44
Rozdział 5. Sztuczna promieniotwórczość
5.1. Uwagi na temat rozpadów β
–
i β
+
Wszystkie izotopy, naturalne i sztuczne, możemy przedstawić na płaszczyźnie (Z, N)
(rys. 20).
Jądra trwałe tworzą tzw. ścieżkę stabilności. Jądra leżące na tej ścieżce nie ulegają
przemianom
β
. Jądra, które leżą poniżej ścieżki stabilności zawierają nadmiar neutronów
w porównaniu z jądrami ze ścieżki stabilności i wszystkie są
−
β
promieniotwórcze. Jądra
leżące powyżej ścieżki stabilności zawierają nadmiar protonów (niedobór neutronów)
jądrami wszystkie ulegają rozpadowi
+
β
. Można stąd wnioskować, że jądra trwałe ze ścieżki
stabilności mają określony skład protonowo-neutronowy, charakterystyczny dla tych jąder.
Natomiast jądra nietrwałe (spoza ścieżki stabilności) „starają się wejść na ścieżkę stabilności”
i przez rozpad
−
β
i
+
β
, uzyskać skład protonowo-neutronowy jąder leżących na tej ścieżce.
Gdy w jądrze jest nadmiar neutronów, przemiana
−
β
powoduje wzrost liczby porządkowej
jądra Z o jedynkę, a więc zwiększenie liczby protonów o jedynkę przy jednoczesnym
zmniejszeniu o jedynkę liczby neutronów w jądrze. Jeśli nietrwałe jądro zawiera nadmiar
protonów zachodzi przemiana
+
β
, gdyż powoduje ona zmniejszenie liczby protonów
o jedynkę i wzrost liczby neutronów o jedynkę. Tak więc jądra z nadmiarem neutronów
w porównaniu z jądrami ze ścieżki stabilności będą ulegały rozpadowi
−
β
, a jądra
z nadmiarem protonów (lub niedoborem neutronów) rozpadowi
+
β
.
5.2. Transuranowce
Fermi zwrócił uwagę na to, że gdyby ostatni naturalny pierwiastek (występujący
w przyrodzie) z układu okresowego
U
238
92
poddać bombardowaniu neutronami, to zaistniałaby
możliwość otrzymania izotopu
U
239
92
, który zawierałby nadmiarowy neutron. Izotop ten
mógłby ulec przemianie
−
β
i powstałby nuklid pochodny o liczbie atomowej Z+1, czyli
Z = 93. W ten sposób można by otrzymać pierwiastki leżące w układzie okresowym za
uranem (nie występujące w przyrodzie). Otrzymane w ten sposób pierwiastki nazwano
transuranowcami. Poniżej zostały przedstawione przykłady reakcji jądrowych w wyniku
których otrzymuje się transuranowce:
Rys. 20. Ścieżka stabilności jąder nie ulegających rozpadowi
β
[6].

Rozdział 5. Sztuczna promieniotwórczość
45
– Neptun
Np
239
93
γ
+
→
+
U
U
239
92
1
0
238
92
n
Pu
Np
U
239
94
0
1
239
93
0
1
239
92
+
→
+
→
−
−
β
β
– Pluton
Pu
238
94
n
d
1
0
238
93
2
1
238
92
2
Np
U
⋅
+
→
+
Pu
Np
238
94
0
1
238
93
+
→
−
β
– Ameryk
Am
241
95
γ
+
→
+
Pu
Pu
240
94
1
0
239
94
n
Am
Pu
241
95
0
1
1
0
240
94
+
→
+
−
β
n
– Kiur
Cm
242
96
n
1
0
242
96
4
2
239
94
Cm
Pu
+
→
+
α
– Berkel
Bk
243
97
n
1
0
243
97
4
2
241
95
2
Bk
Am
⋅
+
→
+
α
– Kaliforn
Cf
245
98
n
1
0
245
98
4
2
242
96
Cf
Cm
+
→
+
α
– Einstein
Es
246
99
n
1
0
246
99
14
7
238
92
6
Es
N
U
⋅
+
→
+
(energia
MeV
100
N
14
7
≈
T
)
– Ferm
Fm
250
100
n
1
0
250
100
16
8
238
92
4
Fm
O
U
⋅
+
→
+
(energia
MeV
180
O
16
8
≈
T
)
(Es i Fm pierwszy raz otrzymano w odpadach radioaktywnych po wybuchu termojądrowym
na atolu Bikini).
– Mendelew
Md
256
101
n
1
0
256
101
4
2
253
99
Md
Es
+
→
+
α
– Nobel
Nb
253
102
n
1
0
253
102
12
6
246
96
5
Nb
C
Cm
⋅
+
→
+
– Lorens
Lw
253
103
n
1
0
253
103
10
5
250
98
7
Lw
B
Cf
⋅
+
→
+
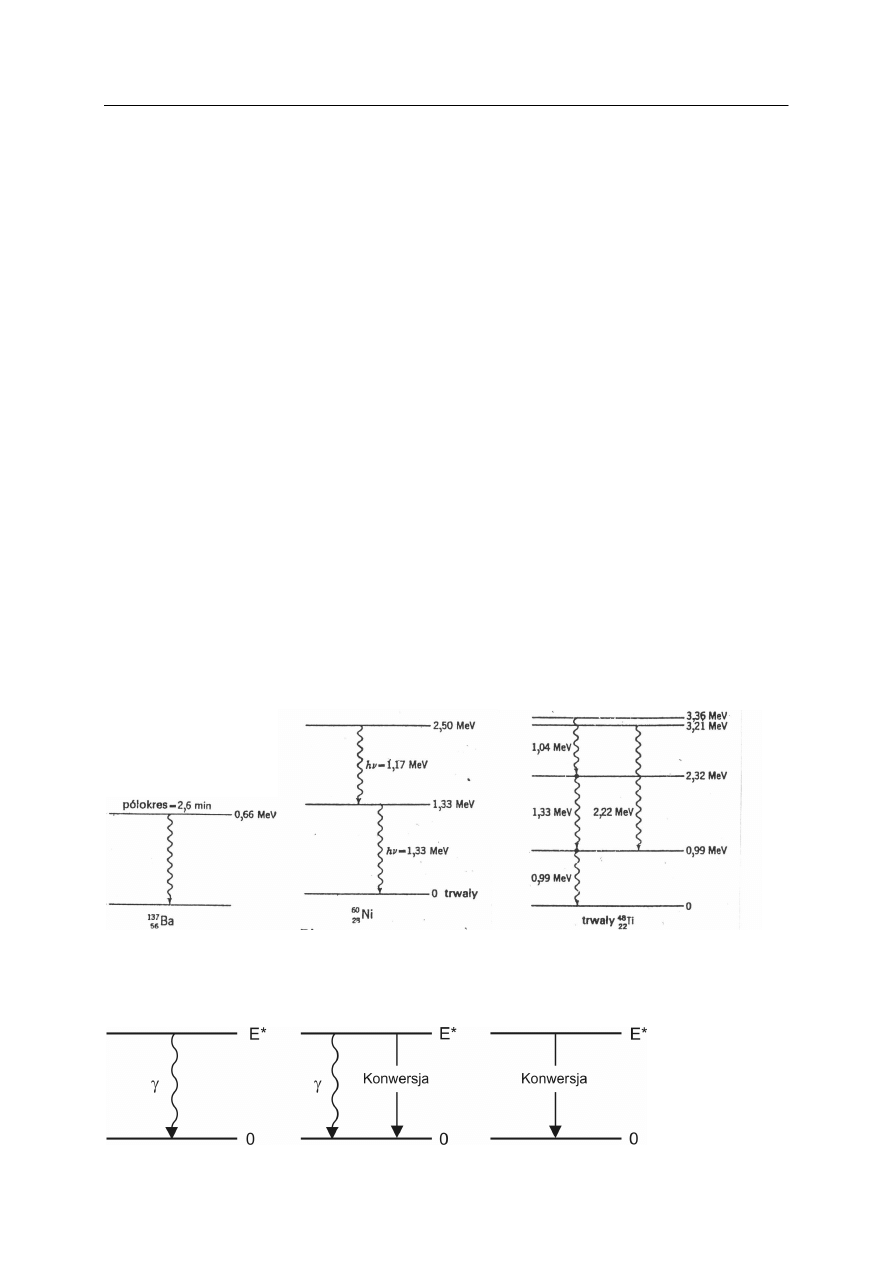
46
Rozdział 5. Sztuczna promieniotwórczość
Inne otrzymane dotąd pierwiastki to np.: 104Rf (rutheford), 105Db (dubnium), 106Sg
(seaborgium), 107Bh (bohrium), 108Hs (hassium), 109Mt (meitnerium) i inne.
5.3. Promieniowanie γ
Promieniowaniem
γ
nazywamy samoistną emisję promieniowania elektromagnetycznego
przez jądro atomowe, wywołaną przejściem jądra ze stanu wzbudzonego do stanu o niższej
energii, którym może być zarówno stan podstawowy, jak i inny stan wzbudzony. Jest to tak
zwane przejście radiacyjne:
γ
+
→
∗
M
)
M
(
A
Z
A
Z
M
A
Z
oznacza stan podstawowy, a
∗
)
M
(
A
Z
stan wzbudzony jądra. Podczas rozpadu
γ
ani liczba
atomowa, ani masowa jądra nie ulega zmianie. Przejście radiacyjne może być jednokrotne lub
schodkowe (kaskadowe). Przejście do stanu podstawowego może zajść bezpośrednio ze stanu
wzbudzonego i wtedy mamy przejście jednokrotne (rys. 21a). Przejście schodkowe zachodzi
wtedy, gdy jądro przechodzi w stan podstawowy przez kolejne poziomy energetyczne
również wzbudzone (rys. 21b, c).
Jeżeli chodzi o istotę promieniowania
γ
, to jest ono krótkofalowym promieniowaniem
elektromagnetycznym pochodzenia jądrowego. Energia kwantów
γ
zawiera się w przedziale
od 10 keV do 5 MeV. Tym energiom odpowiadają długości fal
m
10
5
13
−
⋅
i
m
10
4
11
−
⋅
.
Jądro może się znaleźć w stanie wzbudzonym z różnych przyczyn, np. wskutek rozpadu
β
α
,
lub bombardowania cząstkami. Po emisji
α
lub
β
jądro ma zbyt małą energię
Rys.21. Przykłady przejść jąder ze stanu wzbudzonego do stanów niższych energetycznie; przejścia jednokrotne
i przejścia kaskadowe [8].
Rys. 23. Ilustracja możliwych rozpadów
γ
i konwersji wewnętrznej.

Rozdział 5. Sztuczna promieniotwórczość
47
wzbudzenia, niewystarczającą do emisji nukleonu. Ten wniosek można rozszerzyć na reakcje
jądrowe, w których jednym z produktów jest jądro końcowe w stanie wzbudzonym. W obu
przypadkach energia ta jest mniejsza od energii wiązania nukleonu lub grupy nukleonów
(
t
d
,
,
α
) i emisja
γ
jest wtedy jedynym sposobem prowadzącym do stanu podstawowego.
Najprostszym sposobem pozbycia się przez jądro nadmiaru energii byłaby emisja z jądra
nukleonu. Jednakże jądro musiałoby mieć wówczas nadwyżkę energii równą energii wiązania
nukleonu w jądrze, czyli około 8 MeV. Dodatkowo ta energia musiałaby się skupić na jednym
tylko nukleonie, a to jest mało prawdopodobne. Energia wzbudzenia jądra rozdziela się na
wiele nukleonów, co uniemożliwia emisję nukleonu z jądra, dlatego nie występuje
promieniotwórczość protonowa ani neutronowa. Drugim najprostszym sposobem pozbycia
się przez jądro nadmiaru energii jest przejście radiacyjne.
5.4. Konwersja wewnętrzna
Konwersja wewnętrzna polega na tym, że jądro wzbudzone przechodzi do stanu
podstawowego bez wyświecania promieniowania
γ
, a całą energię wzbudzenia przekazuje
bezpośrednio elektronowi powłokowemu, który zostaje wyrzucony poza atom z energią:
e
w
e
E
E
T
,
)
(
−
=
∗
gdzie
∗
)
(E – jest energią wzbudzenia jądra ,
e
w
E
,
– energią wiązania elektronu na powłoce,
z której został on wyrzucony.
Ważne jest to, by energia przejścia
∗
)
(E była większa od energii wiązania elektronu na
powłoce. Gdy energia wzbudzenia jądra jest zbyt mała, żeby wyrzucić elektron z powłoki K,
może nastąpić emisja elektronu z powłoki L lub M. Jeżeli konwersja wewnętrzna występuje
po uprzedniej emisji
β
(tworzy się jądro końcowe w stanie wzbudzonym), to na tle ciągłego
widma
β
pojawiają się linie elektronów konwersji. Są to elektrony monoenergetyczne (rys.
22).
Po wyrzuceniu elektronu konwersji wewnętrznej na puste po nim miejsce spadają
elektrony z wyższych powłok. Może zostać wyrzucony kwant X lub może dojść do powstania
elektronów Augera.
Rys. 22. Widmo energetyczne cząstek
β
. Ostre maksima wywołane są emisją elektronów konwersji z powłok K,
L, M
[6].

48
Rozdział 5. Sztuczna promieniotwórczość
W trakcie konwersji wewnętrznej jądro przekazuje energię wzbudzenia bezpośrednio
elektronowi powłokowemu, bez wyświecenia kwantu
γ
. Obecnie nie wiadomo jeszcze,
w jaki sposób przekazywana jest energia elektronowi i czy w tym procesie uczestniczy jakiś
„pośrednik” czy też nie.
Konwersja wewnętrzna i promieniowanie
γ
mogą występować razem lub osobno. Jeżeli
występują razem, konwersja konkuruje z rozpadem
γ
. Część jąder jakiegoś izotopu wraca ze
stanu wzbudzonego do stanu podstawowego za pośrednictwem emisji kwantów
γ
, część zaś
ulega konwersji wewnętrznej. Jeżeli zjawiska te nie występują razem, jądro wraca do stanu
podstawowego tylko poprzez rozpad
γ
lub tylko wskutek konwersji. Możliwe są trzy rodzaje
powrotu jądra ze stanu wzbudzonego do stanu podstawowego (rys. 23):
1)
Wyłącznie przez emisję
γ
,
2)
Przez emisję kwantów
γ
i konwersję wewnętrzną,
3)
Wyłącznie przez konwersję wewnętrzną.
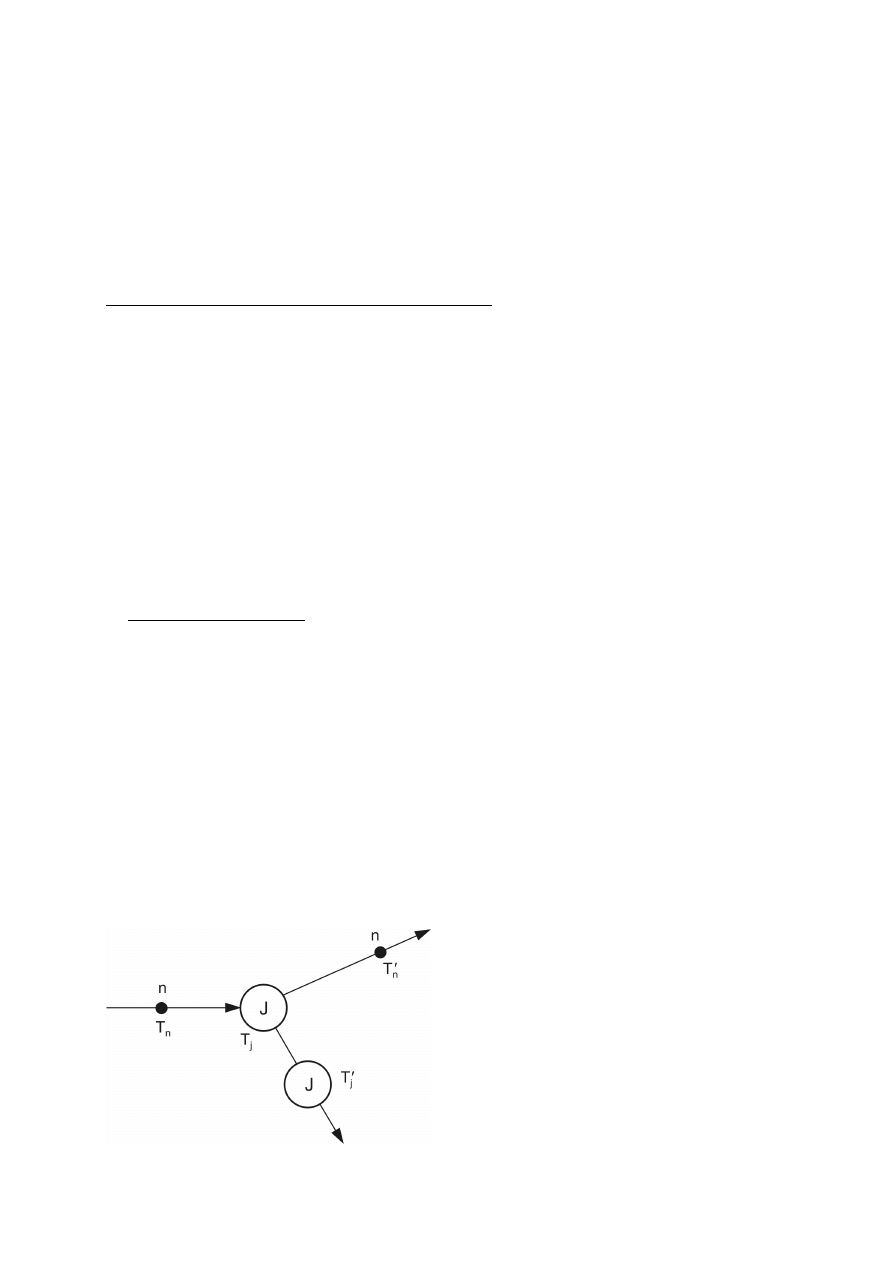
Rozdział 6.
Reakcje rozszczepienia jądra atomowego
Oddziaływanie neutronów z jądrami atomowymi. Oddziaływanie neutronów z jądrami
atomowymi ma (wobec braku ładunku elektrycznego neutronu) charakter oddziaływania sił
jądrowych – nie kulombowskich. Siły jądrowe są siłami o bardzo dużym potencjale i małych
zasięgach. Podział neutronów na grupy ze względu na ich energię:
1)
Neutrony powolne,
–
Neutrony zimne
eV,
001
,
0
<
n
T
–
Neutrony termiczne
eV
025
,
0
=
=
kT
T
n
w temp. T = 300 K. Neutrony termiczne są
w równowadze temperaturowej z ośrodkiem, w którym się znajdują. Mają one
energię zbliżoną do średniej energii kinetycznej ruchu cząstek tego ośrodka, czyli kT.
W temperaturze pokojowej (T = 300 K) energia neutronu termicznego wynosi
eV.
025
,
0
=
n
T
2)
Neutrony pośrednie
MeV,
5
,
0
keV
1
≤
≤
n
T
3)
Neutrony szybkie
MeV,
10
MeV
5
,
0
≤
≤
n
T
4)
Neutrony ponadszybkie
MeV,
50
MeV
10
≤
≤
n
T
5)
Neutrony wysokoenergetyczne
MeV.
50
>
n
T
Rozpraszanie sprężyste. Jest to takie oddziaływanie, w wyniku którego spełnione jest
prawo zachowania energii kinetycznej, oprócz prawa zachowania energii całkowitej.
W zderzeniach sprężystych prawo zachowania energii jest spełnione równocześnie z prawem
zachowania pędu (rys. 24):
j
n
j
n
T
T
T
T
′
+
′
=
+
0
0
0
n
T – energia kinetyczną neutronu-pocisku,
0
j
T
– energia kinetyczna jądra-tarczy,
n
T
′
– energia
kinetyczna neutronu po zderzeniu,
j
T
′
– energia kinetyczna jądra odrzutu.
Zakładamy, że
0
=
j
T
, wtedy:
j
n
n
T
T
T
′
−
=
′
0
0
n
n
T
T
<
′
Rys. 24. Schemat rozproszenia sprężystego neutronu na ciężkim jądrze.

50
Rozdział 6. Reakcje rozszczepienia jądra atomowego
W zderzeniach sprężystych neutron przekazuje część energii kinetycznej innemu jądru.
Zjawisko to wykorzystywane jest w reaktorach jądrowych do spowalniania neutronów.
Zderzenia niesprężyste. W tym oddziaływaniu nie zostaje spełnione prawo zachowania
energii kinetycznej, spełnione jest natomiast prawo zachowania energii całkowitej. W każdym
zderzeniu z jądrem neutron traci część energii kinetycznej. Tę energię jądro przejmuje
w postaci energii kinetycznej jądra odrzutu i dodatkowo wzbudza się.
Prawo zachowania energii całkowitej:
∗
+
′
+
′
=
+
)
(
j
j
n
j
n
E
T
T
T
T
gdzie
∗
)
(
j
E
– energia wzbudzenia trafionego jądra. Przyjmujemy, jak poprzednio, że
0
=
′
j
T
i otrzymujemy:
∗
−
′
−
=
′
)
(
j
j
n
n
E
T
T
T
Widzimy więc, że energia kinetyczna rozproszonego neutronu maleje, a zatem prawo
zachowania energii kinetycznej nie jest spełnione
j
n
n
T
T
T
′
+
′
>
W wyniku przejścia jądra ze stanu wzbudzonego do podstawowego powstaje zwykle
kwant
γ
:
γ
+
+
→
+
∗
n
n
A
Z
A
Z
1
0
1
0
)
X
(
X
Ten rodzaj oddziaływania także jest wykonywany do spowalniania neutronów. Neutron
uczestniczy w wielu zderzeniach, dopóki jego energia nie zmaleje do wartości rzędu kT.
Neutrony spowalniamy, gdyż przekroje czynne jąder na wychwyt neutronu zależą odwrotnie
proporcjonalnie do jego prędkości:
v
A
n
1
~
)
,
(
σ
(A – oznacza absorpcję neutronu)
Reakcje typu (n,
α
), (n, p) itp., są typowymi reakcjami jądrowymi.
Reakcje jądrowe typu wychwytu radiacyjnego. Istnieje prawdopodobieństwo, że neutron
będzie oddziaływał z jądrem i zostanie zaabsorbowany w procesie radiacyjnego wychwytu
neutronu. Jak mówi sama nazwa, wychwytowi neutronu przez jądro towarzyszy emisja
promieniowania
γ
:
γ
+
→
+
+
X
X
1
1
0
A
Z
A
Z
n
(20)
Powstaje jądro końcowe, które jest izotopem jądra macierzystego. Jest ono zazwyczaj
−
β
promieniotwórcze. Reakcja ta jest niepożądana w procesie rozruchu reaktora, gdyż jej
wynikiem jest ubytek neutronów. W późniejszej fazie pracy reaktora dzięki tej reakcji
powstaje „czyste” paliwo jądrowe
Pu
239
94
:
Pu
Np
U
U
239
94
239
93
239
92
238
92
1
0
→
→
→
+
−
−
β
β
n
W fizyce jądrowej używa się pojęcia przekroju czynnego. Przekrój czynny, np. na jakąś
reakcję, jest miarą prawdopodobieństwa wystąpienia tej reakcji. Jeżeli prawdopodobieństwo
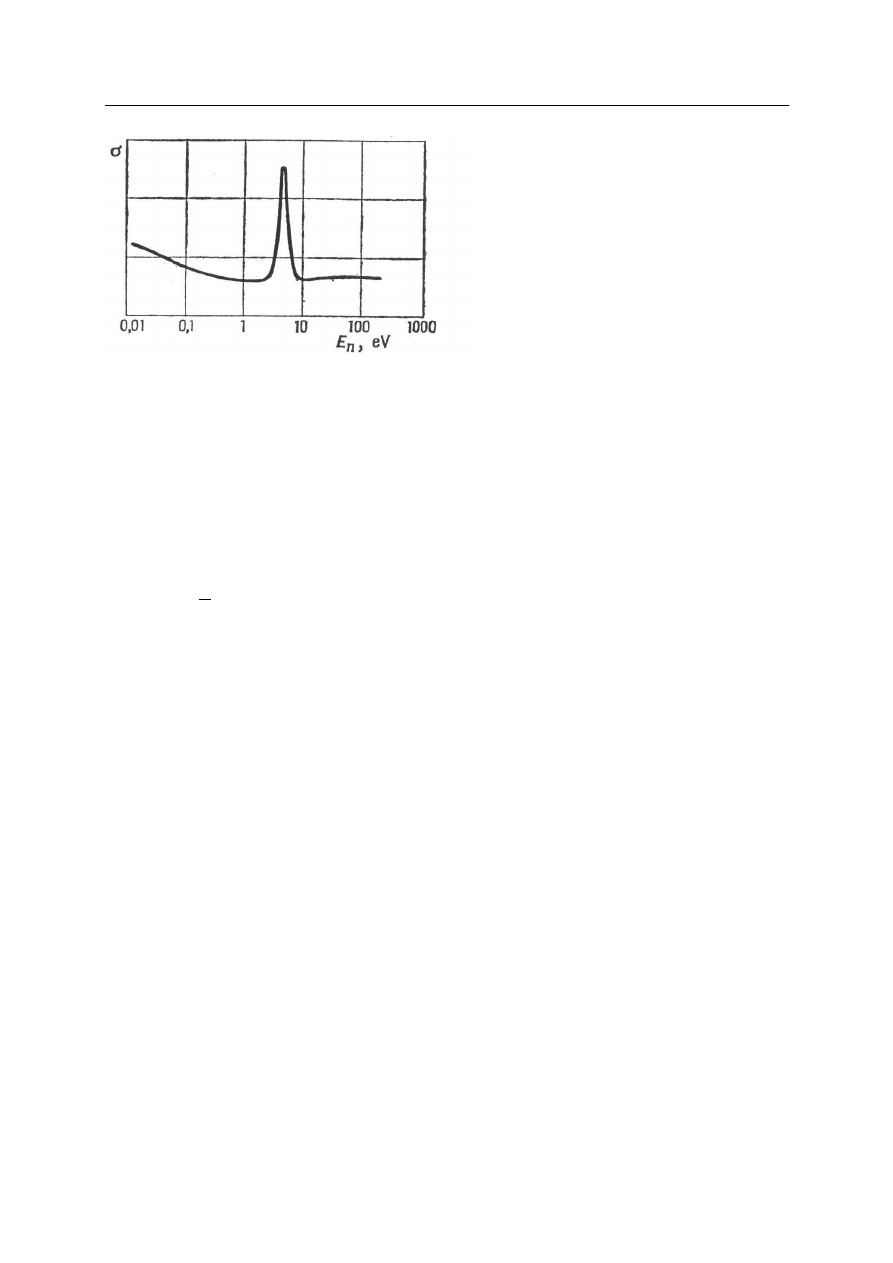
Rozdział 6. Reakcje rozszczepienia jądra atomowego
51
jest duże, przekrój czynny też jest duży; a jeśli małe, to przekrój czynny również jest mały.
Przekrój czynny oznaczamy symbolem
σ
, a jednostką jest 1barn =
24
10
−
cm
2
.
Przekrój czynny na radiacyjny wychwyt neutronu
)
,
(
γ
σ
n
rośnie monotonicznie wraz ze
zmniejszaniem się prędkości neutronów, aż do wystąpienia tzw. absorpcji rezonansowej.
Przekrój czynny na wychwyt neutronu można przedstawić w postaci
v
a
n
~
)
,
(
γ
σ
gdzie a jest stałą i v prędkością neutronu. Łatwo zrozumieć „prawo 1/
ν
”, ponieważ
prawdopodobieństwo oddziaływania z jądrem jest wprost proporcjonalne do czasu, jaki
neutron spędza w pobliżu jądra, a czas ten jest odwrotnie proporcjonalny do prędkości
neutronu. „Prawo 1/
ν
” jest spełnione dla małych energii neutronów. Dla energii większych od
1 eV pojawiają się obszary tzw. energii rezonansowych odpowiadające różnym stanom
wzbudzenia jąder. W zakresie energii rezonansowych „prawo 1/
ν
” nie obowiązuje; przekrój
czynny na wychwyt radiacyjny neutronu jest wyjątkowo duży (rys. 25).
Praktycznie każdy neutron z energią z tego przedziału jest wychwytywany przez jądro,
grzęźnie w nim i jest bezpowrotnie stracony. Powstaje wtedy izotop tego jądra i kwant
γ
(np.
według schematu 20). Ten przedział energii rezonansowych należy omijać, ponieważ może
zabraknąć neutronów niezbędnych do podtrzymywania pracy reaktora. Trzeba pamiętać
również o tym, że w reaktorze znajdują się różnego rodzaju elementy konstrukcyjne, czynnik
chłodzący, moderator (spowalniacz), materiały ochronne, itp., które również pochłaniają
neutrony. Reaktor należy tak konstruować, aby przekrój czynny tych materiałów na tę reakcję
był jak najmniejszy. Różne pierwiastki wykazują różne przedziały energii rezonansowych.
Dla uranu 238 ten przedział energii rezonansowych zawiera się w zakresie energii
eV
1000
eV
5
≤
≤
n
T
(dokładniej kwestia ta zostanie omówiona później). „Prawo 1/
ν
” jest
spełnione z dala od poziomów rezonansowych. Wynika z tego, że przekrój czynny na
wychwyt neutronów jest tym większy, im mniejszą energię mają neutrony i jest największy
dla neutronów termicznych. Jądra niektórych izotopów ciężkich pierwiastków (np.
)
Pu
,
U
,
U
239
94
235
92
233
92
po absorpcji neutronu dzielą się na dwa fragmenty. Mamy wtedy do
czynienia z reakcjami rozszczepienia jądra (zwanymi też reakcjami podziału jądra). Każdy
neutron schwytany przez takie jądro nie ulega wychwytowi radiacyjnemu, lecz wywołuje
podział jądra. Przekrój czynny na ten proces,
)
,
(
f
n
σ
, rośnie zgodnie z „prawem 1/
ν
” i jest
największy dla neutronów termicznych. W takim przypadku
0
)
,
(
=
γ
σ
n
a
)
,
(
f
n
σ
osiąga
dużą wartość.
Rys. 25. Przekrój czynny na reakcje jądrowe w zależności od energii cząstki w obszarze energii
rezonansowych [5].
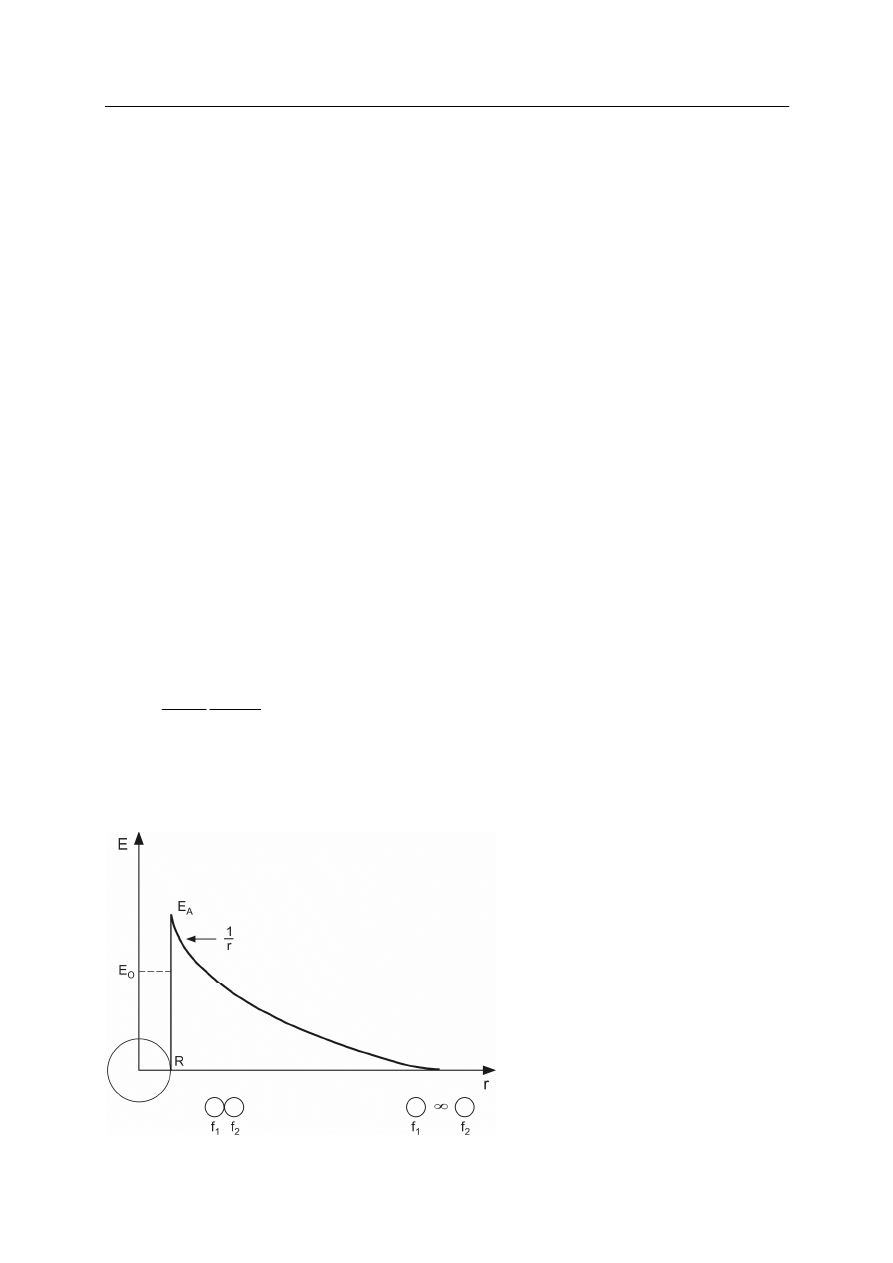
52
Rozdział 6. Reakcje rozszczepienia jądra atomowego
6.1. Reakcja rozszczepienia jądra
Reakcje rozszczepienia jądra polegają na tym, że ciężkie jądra można dzielić na dwa (bardzo
rzadko na trzy) inne jądra w wyniku bombardowania tych jąder cząstkami. Najdogodniejszą
cząstką jest neutron, bo nie ulega oddziaływaniu kulombowskiemu z bombardowanym
jądrem. W reakcji podziału jądro X
A
Z
dzieli się na dwa fragmenty:
n
n
A
Z
A
Z
A
Z
2
Y
Y
X
2
1
1
0
2
2
1
1
+
+
→
+
Przy czym:
2
1
Z
Z
Z
+
=
2
1
2
1
+
+
=
+
A
A
A
1
2
1
+
+
=
A
A
A
Reakcja podziału jest możliwa, gdy zostaną spełnione pewne warunki energetyczne. Aby
je określić, zbadajmy energię potencjalną dwóch fragmentów podziału w zależności od
odległości między nimi. Rozważmy proces odwrotny do rozszczepienia. Będziemy zbliżać do
siebie dwa fragmenty, które w wyniku podziału znalazły się daleko od siebie. Przechodzimy
więc od stanu końcowego reakcji podziału do początkowego, tzn. z obu fragmentów chcemy
utworzyć jądro niepodzielone. Gdy fragmenty są daleko od siebie, energia ich oddziaływania
jest równa zeru. Oba fragmenty są silnie naładowane
e
Z
1
+
i
e
Z
2
+
między nimi działa siła
odpychania
2
2
2
1
0
4
1
r
e
Z
Z
F
πεε
=
Oddziaływanie obu fragmentów jest przedstawione na rysunku 26.
Pierwszej fazie oddziaływania i zbliżaniu się jednego fragmentu do drugiego odpowiada
zmniejszanie się odległości r między nimi oraz wzrost energii układu obu fragmentów,
Rys. 26. Zmiana energii potencjalnej dwóch fragmentów podziału ciężkiego nuklidu w zależności od odległości
między nimi. Fragmenty zbliżamy do siebie, by powstało jądro wyjściowe, niepodzielone.

Rozdział 6. Reakcje rozszczepienia jądra atomowego
53
według prawa Coulomba od zera do wartości
A
E
. Zależność energii potencjalnej od
odległości między fragmentami opisana jest zależnością:
r
e
Z
Z
U
0
2
2
1
π
4
εε
=
Energia wzajemnego oddziaływania obu fragmentów rośnie hiperbolicznie. Zależność ta
jest prawdziwa, gdy odległości między fragmentami są rzędu rozmiarów liniowych atomu,
przy których istotną rolę grają siły kulombowskie. Dla odległości mniejszych,
porównywalnych z rozmiarami fragmentów, rolę sił kulombowskich przejmują siły jądrowe,
które są siłami przyciągającymi, krótkozasięgowymi. Dla odległości mniejszych od promienia
jądra, które się utworzy (jądra niepodzielonego)
R
r
≤
, potencjał musi być funkcją bardzo
silnie malejącą. Dla
R
r
=
krzywa energii potencjalnej ma maksimum, które nosi nazwę
bariery potencjału
A
E
. Po połączeniu obu fragmentów powstaje jądro wyjściowe. Energia
tego jądra
0
E jest równa sumie energii spoczynkowej obu fragmentów. Aby jądro wyjściowe
podzielić, należy mu dostarczyć energii równej wysokości bariery potencjału
A
E
. Tę energię
nazywamy energią aktywacji (na podział). Może dostarczyć jej bombardująca cząstka,
najlepiej neutron. Możliwy jest także efekt tunelowy – wówczas cząstka bombardująca nie
jest potrzebna. Nastąpi spontaniczny podział jadra.
6.2. Podział jądra pod wpływem bombardowania
neutronami
Pochłonięty przez jądro neutron przekazuje mu energię w postaci energii wzbudzenia (jądra).
Na energię wzbudzenia składają się trzy czynniki: energia kinetyczna neutronu
n
T , energia
wiązania neutronu w jądrze bombardowanym
n
W i energia odrzutu jądra
j
T .
j
n
n
Wzb
T
W
T
E
−
+
=
Ponieważ jądro bombardowane jest jądrem ciężkiego pierwiastka, można przyjąć, że
0
=
j
T
. Więc:
n
n
Wzb
W
T
E
+
=
(21)
Gdy energia wzbudzenia jest większa od energii aktywacji
A
Wzb
E
E
≥
, wówczas może
nastąpić podział jądra. W tabeli 5 porównane są energie wiązania neutronu i energie
wzbudzenia dla różnych jąder.
Z tabeli 5 wynika, że na przykład dla
U
235
A
n
E
W
>
. Z równania (21) wnioskujemy, że
aby podzielić jądro
U
235
, energia kinetyczna cząstki jest niepotrzebna. Do rozszczepienia
wystarcza sama energia wiązania neutronu. Podobnie jest dla
Np
,
Pa
,
U
237
231
233
i
Pu
239
. To
oznacza, że jądra te ulegną podziałowi, gdy pochwycą neutron z zerową energią kinetyczną.
Oczywiście jest to możliwe w temperaturze zera bezwzględnego. Ponieważ wartość graniczna
do jakiej można spowolnić neutron jest rzędu kT, jądro może pochwycić neutron termiczny,
a więc nastąpi jego podział. Jądra, które dzielą się pod wpływem wszystkich neutronów,
w tym termicznych, nazywamy paliwami jądrowymi (czystymi paliwami jądrowymi). Inaczej
jest w przypadku
U
238
i
Th
232
. Aby podzielić jądro
U
238
, neutron musi mieć energię równą
co najmniej 0,6 MeV.

54
Rozdział 6. Reakcje rozszczepienia jądra atomowego
Uran 235 występuje w przyrodzie. W naturalnym uranie (występującym w przyrodzie)
procentowy skład izotopów przedstawia się następująco:
U
238
– 99,280%,
U
235
– 0,714%,
U
234
– 0,006%.
Uranu 235, jako paliwa, jest bardzo mało. Uran 233 i Pluton 239 można otrzymać
w reakcjach jądrowych z neutronami:
γ
+
→
+
*
233
90
1
0
232
90
)
Th
(
Th
n
U
Pa
)
Th
(
233
92
233
91
*
233
90
→
→
−
−
β
β
γ
+
→
+
*
239
92
1
0
238
92
)
U
(
U
n
Pu
Np
)
U
(
239
94
239
93
*
239
92
→
→
−
−
β
β
W energetyce jądrowej istotnym jest posiadanie jak największej ilości czystego paliwa
jądrowego, takiego jak
U
235
czy
Pu
239
. Wniosek jest następujący. Aby reakcja, która daje
w wyniku czyste paliwo jądrowe, była wydajna, musi być dużo neutronów. Dużo neutronów
powstaje w reaktorze. Reaktor spala paliwo i jednocześnie je produkuje, z tym że w efekcie
otrzymujemy czyste paliwo jądrowe, tzn. takie izotopy, których jądra dzielą się pod wpływem
wszystkich neutronów, w tym termicznych. Reakcja z
U
238
jest szkodliwa w fazie rozruchu
reaktora, bo w jej wyniku giną neutrony. Należy zapewnić taką ilość neutronów, żeby
w reaktorze podtrzymać reakcję podziału i zapewnić w ten sposób ciągłą pracę reaktora,
a nadmiar neutronów kierować do wytwarzania
Pu
239
.
6.3. Przebieg reakcji podziału
Gdy neutron rozszczepia jądro, powstają dwa (bardzo rzadko trzy) fragmenty. Jednocześnie
w elementarnym akcie podziału z jądra wyrzucane są 2–3 neutrony (rys. 27). Są to neutrony
natychmiastowe. Wyrzucane są jednocześnie z aktem podziału. Stanowią one 92,27%
wszystkich neutronów pojawiających się w reakcjach podziału. W tabeli 6 przedstawiono
liczbę neutronów natychmiastowych emitowanych podczas reakcji podziału różnych jąder.
Ś
rednia energia neutronów natychmiastowych wynosi
MeV
2
≈
n
T
. W uranie naturalnym
znajduje się dużo
U
238
, o energii aktywacji na podział 0,6 MeV. Inne izotopy uranu
Tabela 5. Przykłady wartości energii aktywacji E
A
oraz energii wiązania neutronu W
n
.
Jądro
E
A
[MeV]
W
n
[MeV]
W
n
– E
A
[MeV]
233
U
4,6
6,6
+2,0
235
U
5,3
6,4
+1,1
238
U
5,5
4,9
–0,6
232
Th
6,5
5,1
–1,4
231
Pa
5,0
5,4
+0,4
237
Np
4,2
5,0
+0,8
239
Pu
4,0
6,4
+2,4
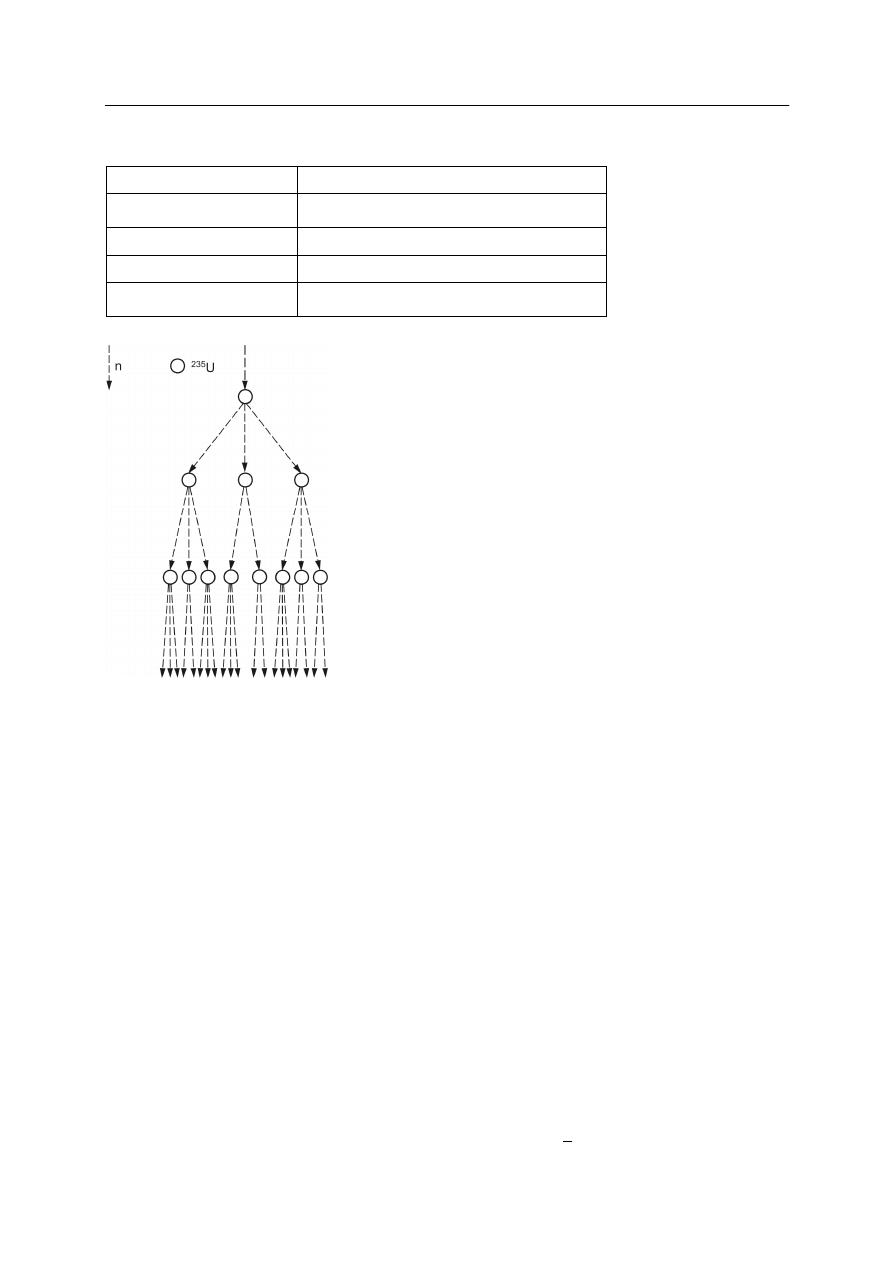
Rozdział 6. Reakcje rozszczepienia jądra atomowego
55
naturalnego ulegają rozpadowi zarówno pod wpływem neutronów szybkich jak i termicznych.
(Neutron szybki to taki, którego energia mieści się w granicach
MeV
10
MeV
5
,
0
≤
≤
n
T
).
Widzimy, że istnieją potencjalne możliwości rozwinięcia w uranie naturalnym reakcji
łańcuchowej, a nawet lawinowej, ponieważ powstają 2–3 neutrony o energii
MeV
2
=
n
T
wystarczającej do podziału
U
238
, którego próg energetyczny na podział wynosi 0,6 MeV i
którego jest najwięcej w uranie naturalnym. Każdy z tych neutronów może dzielić następne
jądra uranu, dając nowe 2–3 neutrony natychmiastowe zdolne do dzielenia kolejnych jąder.
Może rozwinąć się reakcja lawinowa, której liczba neutronów natychmiastowych narasta
lawinowo (rys. 28).
W reakcji łańcuchowej wystarczy, by podczas podziału jądra wywołanego przez jeden
neutron powstawał średnio więcej niż jeden neutron, a mimo to w uranie naturalnym jest
bardzo trudno rozwinąć reakcję łańcuchową.
6.4. Energia wydzielana w akcie podziału jądra
Reakcja podziału jest procesem egzotermicznym. Wydzieloną podczas podziału jądra energię
można łatwo oszacować, korzystając z wykresu przedstawiającego zależność średniej energii
wiązania na nukleon od liczby masowej A (rys.2).
Dla uranu 238 średnia energia wiązania nukleonu wynosi
MeV
6
,
7
=
ε
. Dla fragmentów
podziału (są to jądra z okolic środka układu okresowego) wynosi 8,4 MeV (rys. 29). Podczas
Tabela 6. Przykładowe liczby neutronów natychmiastowych emitowanych podczas reakcji podziału jąder.
Jądro
Liczba natychmiastowych neutronów
233
U
2,47
±
0,06
235
U
2,46
±
0,05
239
Pu
3,01
±
0,06
Uran naturalny
2,56
±
0,01
Rys. 28. Schematyczne przedstawienie rozwoju reakcji
rozszczepienia
235
U. Liczba neutronów narasta lawinowo
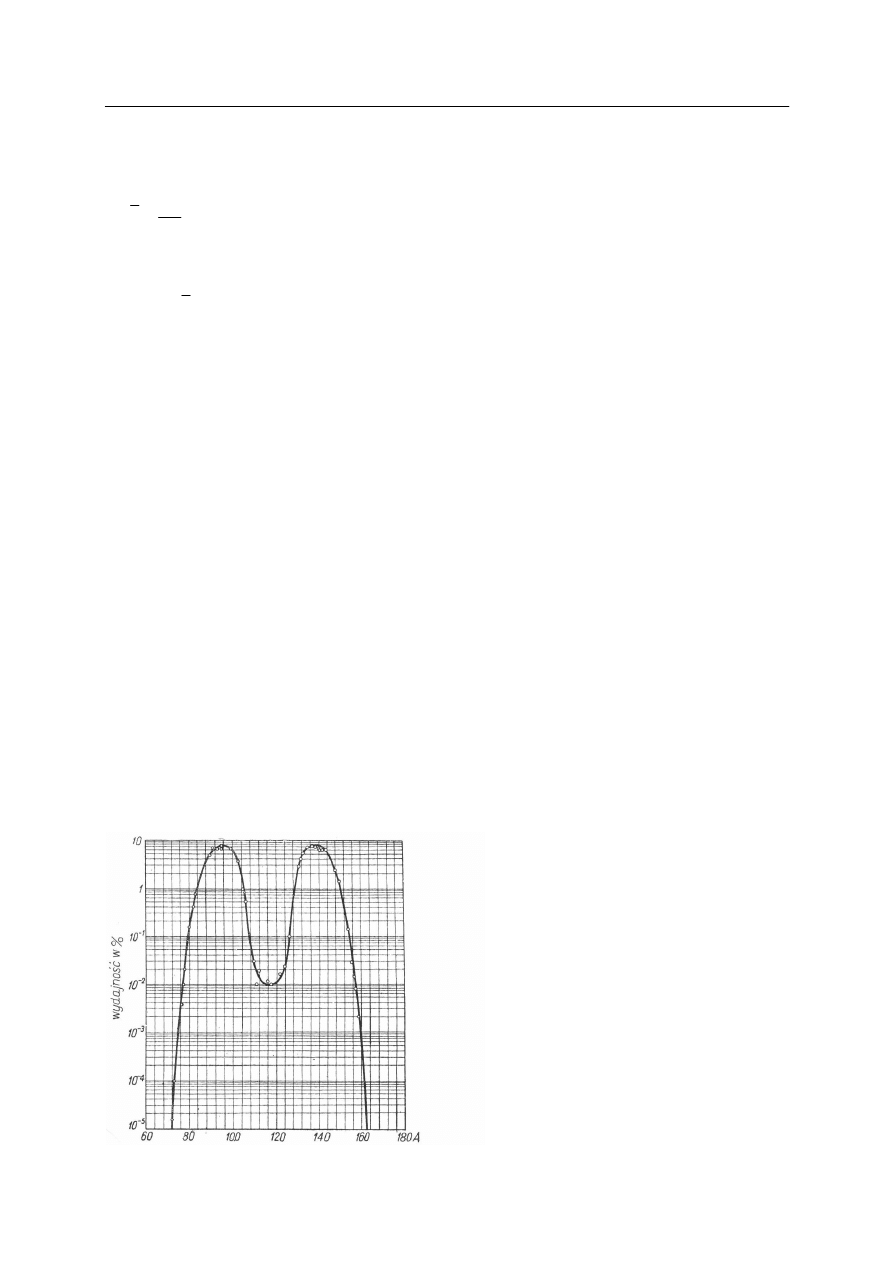
56
Rozdział 6. Reakcje rozszczepienia jądra atomowego
podziału jądra uranu wyzwalana jest energia 8,4 – 7,6 MeV = 0,8 MeV na jeden nukleon.
Ponieważ jest to średnia energia wiązania na nukleon:
A
E
w
=
ε
a dla uranu A = 238, więc energia wydzielana w trakcie podziału jednego jądra wynosi:
MeV
200
MeV
8
,
0
238
≈
⋅
=
=
ε
A
E
w
Biorąc pod uwagę rozmiary obiektów (jąder), z jakimi mamy tu do czynienia, jest to
energia olbrzymia. Energia ta w przeważającej części jest unoszona przez fragmenty podziału
w postaci energii kinetycznej.
6.5. Fragmenty podziału
Fragmenty podziału są izotopami pierwiastków leżących w środkowej części układu
okresowego. Z niezrozumiałych powodów jeden z fragmentów jest zwykle większy od
drugiego. Rysunek 30 przedstawia wykres zależności liczby rozszczepień od liczby
masowej A fragmentu. Jądra
U
235
może się dzielić na ponad 40 różnych sposobów. Powstaje
40 par, czyli ponad 80 różnych fragmentów. Różne fragmenty powstają z różnym
prawdopodobieństwem. To znaczy, że fragmenty nie powstają w takich samych ilościach.
Liczby masowe fragmentów zawierają się od 70 do 140. Najczęściej powstają fragmenty,
których liczby masowe wynoszą od 90 do 100 i od 135 do 145. Widzimy to na wykresie
przedstawionym na rysunku 29.
Najmniej prawdopodobny jest podział na dwa równe fragmenty. (Na rysunku 32
zakładano, że dzieli się 100 jąder uranu dając 200 fragmentów. Całka po krzywej wynosi
200).
Oba fragmenty są silnie
β
promieniotwórcze, ponieważ występuje w nich bardzo duży
nadmiar neutronów. Jak już była o tym mowa, fragmenty podziału są izotopami pierwiastków
Rys. 29. Krzywa rozkładu liczb masowych fragmentów podziału powstających przy rozszczepieniu
235
U [6].

Rozdział 6. Reakcje rozszczepienia jądra atomowego
57
ze środkowej części układu okresowego. Każde jadro trwałe ma określony skład protonowo-
neutronowy. Dla różnych jąder trwałych izotopów stosunek liczby neutronów do protonów
wynosi:
Jądro
O
16
8
K
40
20
Ag
108
47
Ba
137
56
U
238
92
p
n
N
N
1
1
1,3
1,45
1,6
Dla jąder trwałych izotopów (fragmentów podziału ze środka układu okresowego)
stosunek N
n
/N
p
wynosi około 1,3. Dzielą się jądra
235
U albo
239
Pu dla których ten stosunek
wynosi 1,6. Przy podziale na dwa fragmenty stosunek 1,6 jest w obu fragmentach zachowany.
Ich trwałe izotopy mają N
n
/N
p
= 1,3. Oba fragmenty mają więc olbrzymi nadmiar neutronów.
Nadwyżkę neutronów znoszona jest przez rozpad
−
β
(
ν
β
+
+
→
−
p
n
1
1
0
1
1
0
) lub emisję tzw.
neutronów opóźnionych. Nadmiar neutronów jest tak duży, że następuje po sobie kilka
kolejnych rozpadów stanowiacych łańcuch promieniotwórczy. Oto przykłady:
fragment:
Ce
La
Ba
Cs
Xe
140
58
)
lat
5
,
4
(
140
57
)
dni
128
(
140
56
)
s
56
(
140
55
)
s
16
(
140
54
→
→
→
→
−
−
−
−
β
β
β
β
(trwały)
fragment:
Mo
Nb
Zr
Y
Sr
Rb
Kr
97
42
97
41
97
40
97
39
97
38
97
37
97
36
→
→
→
→
→
→
−
−
−
−
−
−
β
β
β
β
β
β
(trwały)
Do roku 1942 w układzie okresowym nie znano prometu (miejsce 61) i technetu (miejsce
43). Odkryto je w łańcuchach promieniotwórczych:
fragment:
Eu
Sm
Pm
Nd
147
63
)
lat
10
(
147
62
)
lata
4
(
147
61
)
dni
11
(
147
60
11
→
→
→
−
−
−
β
β
β
fragment:
Ru
Tc
Mo
99
44
)
lat
10
2
,
2
(
99
43
)
s
66
(
99
42
6
→
→
⋅
−
−
β
β
(trwały)
Zwraca uwagę to, że każdy następny produkt rozpadu ma okres półrozpadu dłuższy od
swojego poprzednika.
6.6. Promieniowanie neutronowe. Neutrony opóźnione
Innym sposobem usuwania nadmiaru neutronów we fragmentach podziału jest
promieniowanie neutronowe (
∗
– stan metastabilny):
Kr
)
Kr
(
88
36
1
0
89
36
+
→
∗
n
Kr
)
Kr
(
86
36
1
0
87
36
+
→
∗
n
Xe
)
Xe
(
136
56
1
0
137
56
+
→
∗
n
Są to tzw. neutrony opóźnione, emitowane podczas przemiany promieniotwórczej
fragmentów podziału ciężkiego nuklidu (jądra
U
235
).
Okresy półtrwania wynoszą T
1/2
=
.
s
6
,
55
;
s
0
,
22
;
s
51
,
4
;
s
525
,
1
;
s
43
,
0
Zaobserwowano
tylko tyle okresów. Przykład emisji neutronu opóźnionego przez jeden z członów łańcucha
rozpadu fragmentu widzimy na rysunku 30.
Należy podkreślić, że nie można tych przypadków emisji neutronów opóźnionych
traktować jak spontaniczną promieniotwórczość neutronową, bo zjawisko to występuje
jedynie wśród fragmentów podziału. W przyrodzie nie ma takich izotopów. Zjawisko takie
może wystąpić w przypadku fragmentów, ponieważ są one bardzo silnie wzbudzone, mają

58
Rozdział 6. Reakcje rozszczepienia jądra atomowego
ogromną nadwyżkę energii i nadmiar neutronów (co zostało omówione już wcześniej).
Neutrony te określa się mianem neutronów opóźnionych. Neutrony opóźnione stanowią
0,73%, a neutrony natychmiastowe 99,27% wszystkich neutronów powstających w reakcjach
podziału. Neutronów opóźnionych jest niewiele, ale są one bardzo pożyteczne, bo
umożliwiają sterowanie reaktorem i zapewniają jego bezpieczną pracę.
6.7. Możliwość wykorzystania energii rozszczepienia
W każdym akcie podziału jądra uranu wydziela się duża energia i powstają neutrony
natychmiastowe. Emisja neutronów podczas rozszczepienia jądra daje możliwość
wykorzystania ich do rozszczepienia sąsiednich jąder. Temu procesowi będzie towarzyszyć
wydzielanie się nowej porcji energii i emisja nowych neutronów, które z kolei spowodują
podział nowych jąder uranu, itd. Jeżeli w jednym akcie rozszczepienia powstanie więcej niż
jeden neutron natychmiastowy, pojawią się warunki do zaistnienia narastającego procesu
łańcuchowego reakcji rozszczepienia (reakcja lawinowa), rysunek 28. Na przykład, jeśli
podczas każdego aktu podziału wyłonią się dwa neutrony, to w najlepszym wypadku mogą
one dokonać podziału dwóch innych jąder uranu i doprowadzić do powstania czterech
neutronów, które następnie rozszczepią cztery jądra uranu i doprowadzą do emisji ośmiu
neutronów, itd. Jest to rozmnażanie neutronów. Wskutek dużej szybkości tego procesu liczba
dzielących się jąder może bardzo silnie wzrosnąć w krótkim czasie, w rezultacie czego
wydzieli się ogromna ilość energii, zwanej energią jądrową. W trakcie jednego aktu podziału
jednego jądra wydziela się, jak pamiętamy, 200 MeV energii.
Przypomnienie: W jednym akcie podziału powstaje 2–3 neutronów natychmiastowych.
W uranie naturalnym
56
,
2
=
ν
neutronów. Energia kinetyczna tych neutronów wynosi
MeV
2
≈
n
T
. W uranie naturalnym ponad 99% stanowi uran 238, a do podziału jądra tego
uranu potrzebna jest energia 0,6 MeV. Wszystko wskazuje na to, że występują tu
sprzyjające warunki do rozwinięcia i podtrzymania reakcji łańcuchowej, a nawet lawinowej.
W rzeczywistości reakcji łańcuchowej nie można rozwinąć w samym tylko uranie
Rys. 30. Emisja neutronów opóźnionych. Nuklid
Br
87
35
jest fragmentem podziału jądra
U
235
92
i rozpoczyna
łańcuch przemian
β
. Jednym z członów tego łańcucha jest
Kr
87
36
, który emituje neutrony opóźnione [9].

Rozdział 6. Reakcje rozszczepienia jądra atomowego
59
naturalnym. Aby doszło do rozwinięcia się reakcji łańcuchowej, muszą zostać spełnione trzy
warunki:
1)
Reakcja musi być egzotermiczna,
2)
Czynnik wywołujący reakcję musi być produktem reakcji, tzn. musi się stale odnawiać
(tutaj rolę tę spełniają neutrony),
3)
Liczba neutronów nie może maleć w czasie.
Dwa pierwsze warunki są spełnione, gdyż w reakcji podziału wydziela się ciepło,
a czynnikiem wywołującym reakcję jest neutron, który po podziale jądra daje nowe
neutrony.
Warunkowi trzeciemu należy poświęcić więcej uwagi. Należy wprowadzić pojęcie
pokolenia neutronowego. Neutrony pierwszego pokolenia dają w efekcie neutrony drugiego
pokolenia, te z kolei trzeciego, itd. Wprowadzimy też współczynnik powielania (lub
rozmnażania) neutronów. Definiujemy go jako stosunek liczby neutronów wywołujących
rozszczepienie w danym pokoleniu (i + 1) do liczby takich neutronów w pokoleniu
poprzedzającym
i
n :
i
i
n
n
k
1
+
=
W pokoleniu poprzedzającym liczba neutronów wynosi
i
n , a w danym pokoleniu
1
+
i
n
.
Liczbę neutronów wywołujących rozszczepienie w danym pokoleniu (i + 1) możemy
przedstawić jako:
i
i
k n
n
=
+
1
Pomijając dla przejrzystości indeksy, możemy napisać, że jeżeli w pewnym pokoleniu było
n neutronów, to w następnym będzie ich kn. Przyrost neutronów w ramach jednego pokolenia
przedstawiamy następująco:
n
kn
n
−
=
d
n
k
n
)
1
(
d
−
=
Przyrost liczby neutronów w czasie wynosi:
τ
)
1
(
d
d
−
=
k
n
t
n
(22)
τ
jest średnim czasem życia jednego pokolenia neutronów. Jest to czas, jaki upływa między
dwoma kolejnymi aktami rozszczepienia jądra. Czas ten dla neutronów powolnych wynosi
s
10
3
−
=
τ
, a dla szybkich ~
s
10
9
−
. Po przekształceniu wzoru (22) mamy:
t
k
n
n
d
)
1
(
d
τ
−
=
(23)
Całkujemy (23):
∫
∫
−
=
t
k
n
n
d
1
d
τ
C
t
k
n
+
−
=
⋅
τ
1
ln
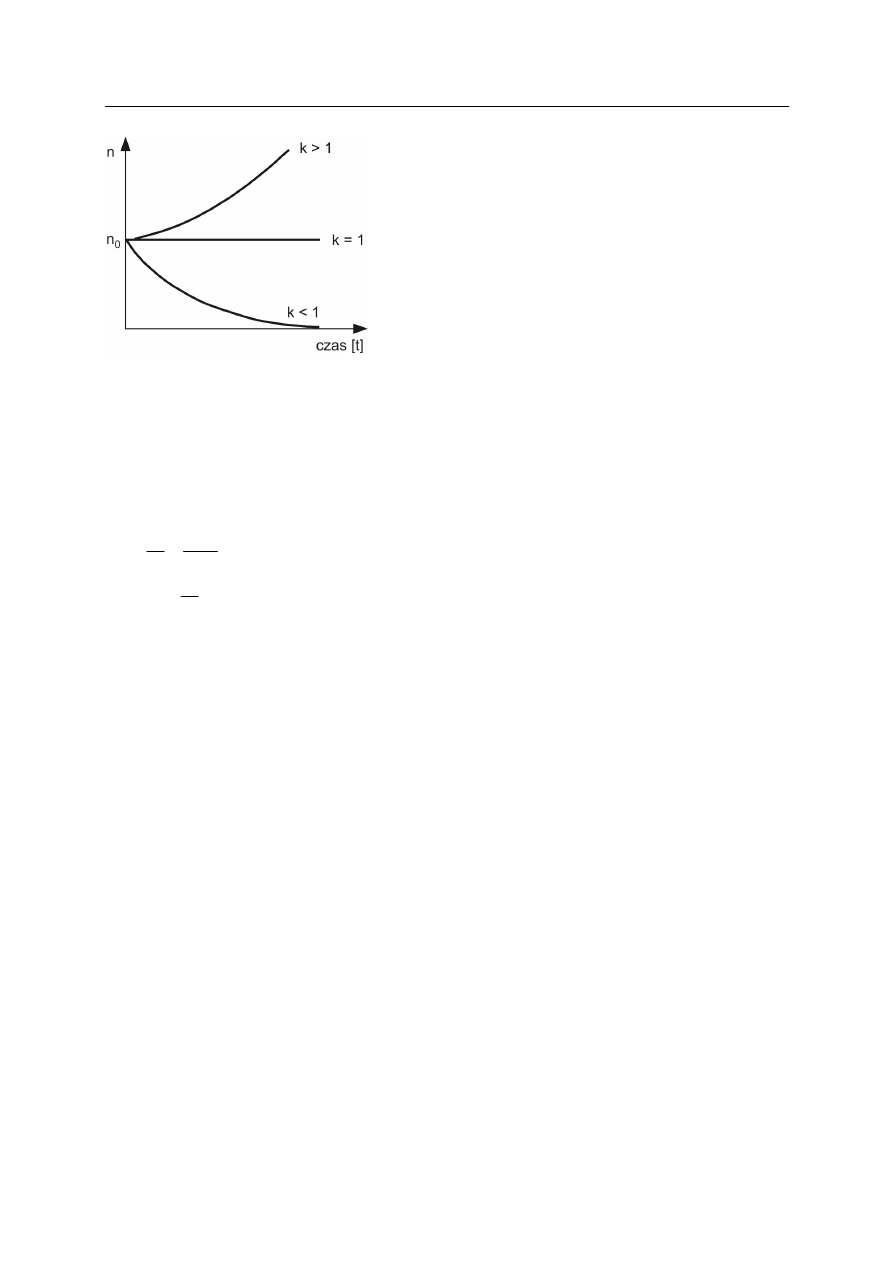
60
Rozdział 6. Reakcje rozszczepienia jądra atomowego
Stałą całkowania określamy z warunków początkowych. Przyjmując, że w chwili
początkowej t = 0 było
0
n neutronów, otrzymujemy:
0
ln n
c
⋅
=
stąd :
t
k
e
n
n
t
k
n
n
τ
τ
1
0
0
1
ln
−
=
−
=
(24)
Jest to prawo opisujące przyrost liczby neutronów (rys. 31):
– dla k = 1 mamy stan krytyczny, reakcja się rozwinie,
– dla k < 1 mamy stan podkrytyczny, reakcja zanika,
– dla k > 1 mamy stan nadkrytyczny, reakcja się rozwinie (liczba neutronów rośnie
w czasie wykładniczo).
Warunkiem rozwinięcia się reakcji łańcuchowej jest, aby k ≥ 1. Może budzić zdziwienie
to, że szukamy warunku k ≥ 1, skoro w każdym akcie podziału jądra powstaje 2–3 neutronów.
Szkopuł w tym, że z tych 2–3 neutronów tylko część powoduje podział, nawet jeśli dotrą do
jądra uranu. Definicja współczynnika rozmnożenia obejmuje tylko neutrony powodujące
rozszczepienie. Część neutronów ulegnie wychwytowi radiacyjnemu w
U
238
92
, dając
Pu
239
94
,
część zostanie pochłonięta przez elementy konstrukcyjne w reaktorze, przez moderator,
chłodziwo, materiały ochronne, pręty sterujące; reszta zaś po prostu ucieka z reaktora. Są to
neutrony stracone (rys. 32). W pierwszym reaktorze, w którym moderatorem był grafit
uzyskano K = 1.08.
Najłatwiej jest przeprowadzić reakcję łańcuchową w bombie atomowej, czyli w czystym
paliwie jądrowym, takim jak
U
235
czy
Pu
239
, bo w nich reakcje podziału przebiegają na
neutronach szybkich, w reaktorze natomiast, na neutronach powolnych. Jeżeli już reakcja
łańcuchowa została zapoczątkowana, np. w
U
235
, to jedynym czynnikiem uszczuplającym
liczbę neutronów (a tym samym jedyną przeszkodą w rozwinięciu reakcji łańcuchowej)
będzie ich ucieczka na zewnątrz. Strumień neutronów uciekających
n
φ
jest proporcjonalny do
powierzchni paliwa, a strumień neutronów powstających do masy paliwa, czyli do jego
objętości. Stosunek powierzchni do objętości jest najkorzystniejszy (najmniejszy) dla kuli.
Gdybyśmy uformowali uran w kulę, strumień neutronów uciekających byłby proporcjonalny
do kwadratu promienia:
n
φ
~
2
r , a strumień neutronów powstających do objętości:
3
~ r
p
φ
.
Zwiększając promień kuli, można dojść do takiego promienia r, dla którego strumień
neutronów uciekających można zaniedbać. Neutrony będą uciekać, ale ich ucieczka nie
Rys. 31. Zależność liczby neutronów wywołujących
rozszczepienie
od
czasu
dla
różnych
wartości
współczynnika powielania neutronów k.
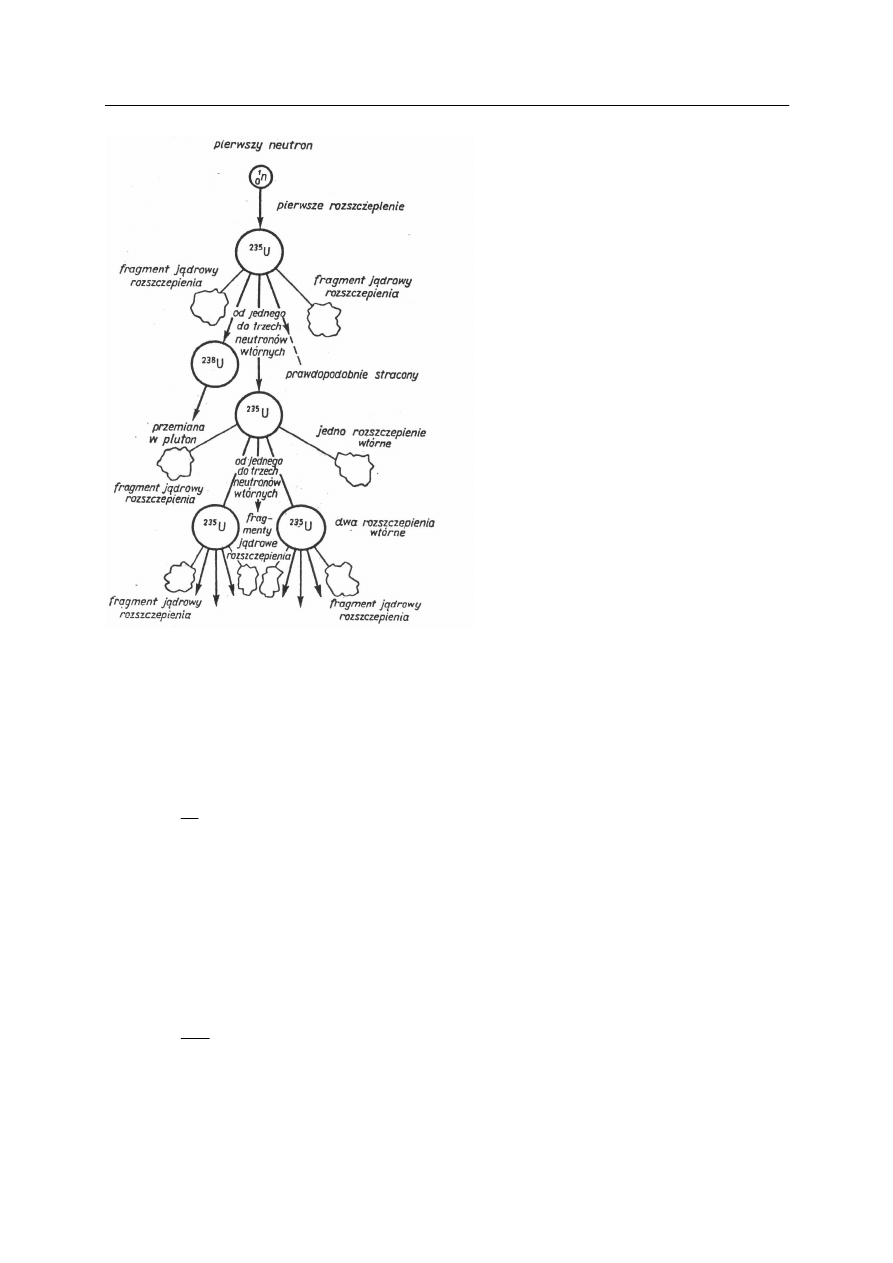
Rozdział 6. Reakcje rozszczepienia jądra atomowego
61
będzie powodować zahamowania reakcji łańcuchowej, bo będzie powstawać więcej nowych
neutronów. Promień kuli, przy którym rozpoczyna się reakcja łańcuchowa, nazywamy
promieniem krytycznym, objętość kuli wyznaczoną przez ten promień – objętością krytyczną,
a masę paliwa zawartego w tej kuli – masą krytyczną. W każdej masie paliwa większej od
krytycznej zachodzi reakcja łańcuchowa i wtedy liczba neutronów wzrasta w czasie według
prawa
t
k
e
n
n
τ
1
0
−
=
n
0
oznacza liczbę neutronów dla
t = 0.
Przyjmijmy, że
k = 1.05 (dla czystego paliwa jądrowego jest on znacznie większy;
w pierwszym reaktorze otrzymano k = 1.08).
W masie krytycznej
U
235
czy
Pu
239
reakcja podziału przebiega na neutronach szybkich.
Przyjmujemy, że średni czas życia pokolenia neutronów wynosi
s
10
3
−
=
τ
(w istocie dla
neutronów szybkich jest on krótszy i wynosi
s
10
9
−
). Podstawiając te wartości
k i
τ
do wzoru
(24) obliczymy liczbę neutronów pojawiających się w czasie
t = 1 s.
22
0
50
0
1
10
1
05
,
1
0
10
3
⋅
=
=
=
⋅
−
−
n
e
n
e
n
n
Każdy z tych neutronów rozszczepia jądro. W akcie podziału jądra zostaje wydzielona
energia 200 MeV. Każdy z n neutronów rozbija n jąder, a całkowita energia, jaka się wyzwala
wynosi:
eV
10
10
MeV
200
30
0
0
22
⋅
=
⋅
=
n
n
E
Rys. 32. Procesy zachodzące w uranie naturalnym
podczas bombardowania go neutronami [7].
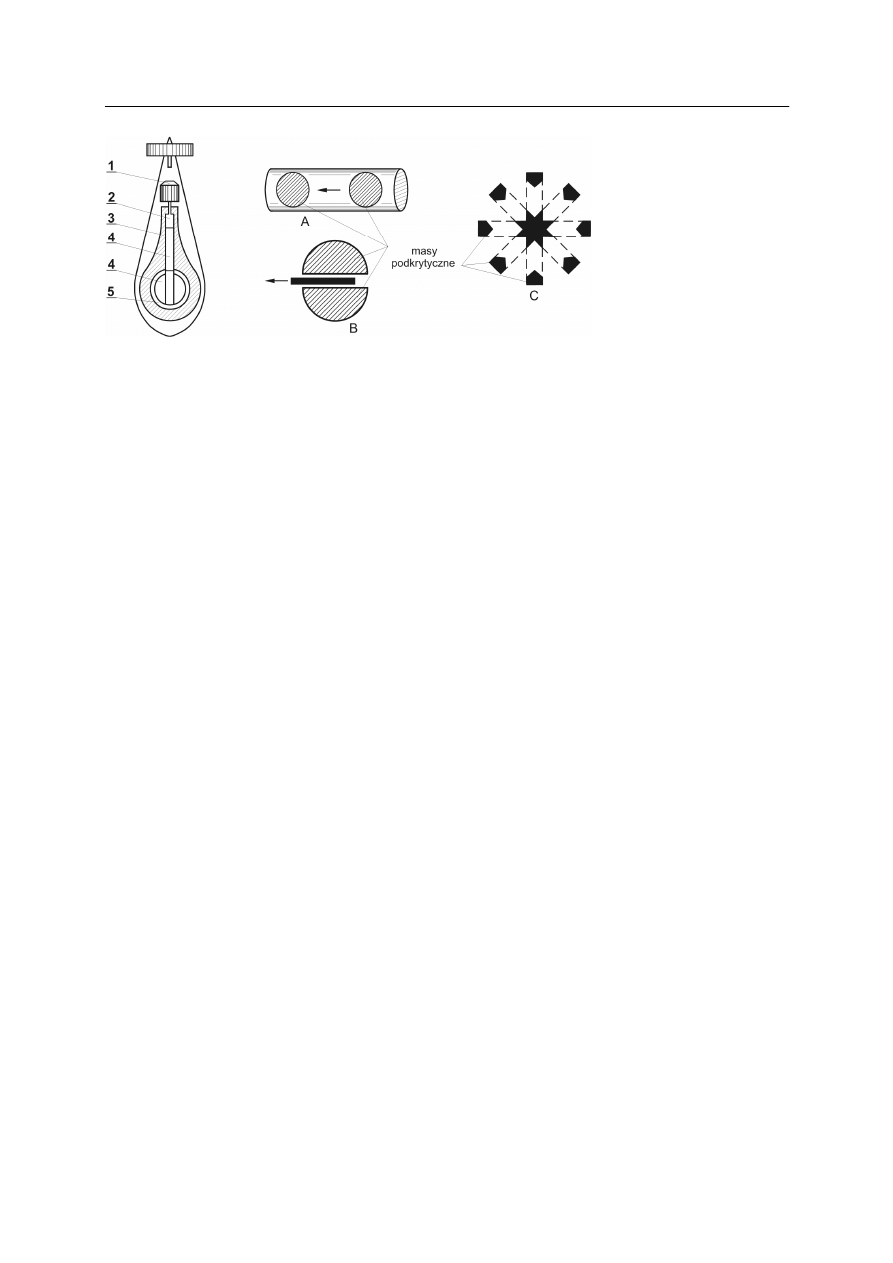
62
Rozdział 6. Reakcje rozszczepienia jądra atomowego
Widzimy, że w ciągu jednej sekundy, wyzwala się olbrzymia energia i reakcja zachodzi
w sposób niekontrolowany – dochodzi więc do eksplozji.
Na rysunku 33 pokazane są niektóre z możliwych konstrukcji bomby atomowej. Każda
z tych konstrukcji zawiera przynajmniej dwie części ładunku jądrowego, z których każdy ma
masę mniejszą od krytycznej, ale po ich połączeniu powstaje masa co najmniej krytyczna.
Należy gwałtownie zbliżyć masy ładunku jądrowego. Doprowadzamy do tego za pomocą
konwencjonalnego materiału wybuchowego i zapalnika.
Reakcja łańcuchowa kontrolowana przebiega w reaktorze atomowym. Kontrola nad
reakcją polega na wpływaniu na wartość współczynnika k. Nie może on osiągać zbyt dużych
wartości. Wartość k obniżamy, zmniejszając liczbę neutronów, które dzielą jądra. Efekt ten
uzyskujemy poprzez zanieczyszczenie paliwa. To spowoduje, że część neutronów będzie
pochłaniana przez domieszki i wskutek tego wyeliminowana z reakcji podziału. A więc
przejście od bomby atomowej do reaktora, najogólniej mówiąc, polega na wykorzystaniu
zanieczyszczonego paliwa jądrowego oraz zastosowaniu prętów regulacyjnych.. Takim
zanieczyszczonym paliwem może być uran naturalny, który zawiera czyste paliwo w postaci
U
235
.
Jednak w samym tylko uranie naturalnym nie da się rozwinąć reakcji łańcuchowej, mimo
ż
e powstaje średnio 2,56 neutronów natychmiastowych o energii 2 MeV, wystarczającej do
pokonania progu energetycznego jądra
U
238
. Ponadto w uranie naturalnym znajduje się
ponad 99% tego izotopu.
Kłopot sprawia sam uran 238, który ma duży przekrój czynny na rozpraszanie niesprężyste
i praktycznie już w pierwszym zderzeniu z jądrem
U
238
neutron traci energię poniżej
0,6 MeV – progu potrzebnego do podziału tego jądra. Dochodzi do tego jeszcze fakt, że uran
238 ma znaczny przekrój czynny na wychwyt rezonansowy (nawet poza przedziałem energii
rezonansowych). Z tych dwóch powodów (rozproszenie niesprężyste i wychwyt
rezonansowy) 4/5 neutronów „wypada z gry”, jeżeli idzie o wykorzystanie ich do podziału
jądra uranu 238. Z tego wynika, że reakcja łańcuchowa na szybkich neutronach w
U
238
mogłaby się rozwinąć tylko wtedy, gdy podczas rozszczepienia powstawałoby co najmniej
5 neutronów (
5
=
ν
) o energii
MeV
1
≥
T
. Ponieważ tworzy się ich 2–3 (
56
,
2
=
ν
), to
realizacja takiej reakcji jest niemożliwa. (Podobnie ma się rzecz z innymi rozszczepialnymi
pierwiastkami –
Th
232
90
i
Pa
231
91
). Jednak uran naturalny wykorzystuje się do przeprowadzenia
reakcji łańcuchowej. Wykorzystanie uranu naturalnego jako źródła energii stało się możliwe,
gdy wykryto rozszczepienie uranu 235 przez neutrony termiczne. Uran 235 nie ma progowej
energii dla reakcji rozszczepienia, a sam proces niesprężystego rozproszenia jest nie tylko
nieszkodliwy, ale pomaga w spowalnianiu neutronów do energii termicznych i umożliwia
przeprowadzenie reakcji łańcuchowej. Izotop
U
235
stanowi tylko 1/140 część naturalnej
Rys. 33. Przykłady możliwych konstrukcji bomby atomowej [6, 7]. 1 – zapalnik, 2 – materiał wybuchowy,
3 – powłoka, 4 – ładunek jądrowy, 5 – reflektor.

Rozdział 6. Reakcje rozszczepienia jądra atomowego
63
mieszaniny izotopów uranu. Przekrój czynny na rozszczepienie
U
235
przez neutrony
termiczne wynosi 590 barnów. W tabeli 7 przedstawione są różne przekroje czynne różnych
jąder dla neutronów termicznych.
Tak duża wartość przekroju czynnego na rozszczepienie
U
235
powoduje, że
prawdopodobieństwo rozszczepienia uranu przez neutrony termiczne jest porównywalne
z prawdopodobieństwem rezonansowego wychwytu neutronu przez jądra uranu podczas ich
spowalniania, mimo że w procesie rezonansowego wychwytu biorą udział wszystkie jądra
uranu, a w procesie rozszczepienia tylko ich 1/140 część. Dlatego spowalniamy neutrony do
energii termicznych. Spowalnianie neutronów przynosi same korzyści, bo izotop
U
238
i tak
jest nieprzydatny do rozszczepienia;
U
235
ma zaś wyjątkowo duży przekrój czynny na
podział dla neutronów termicznych, 85% neutronów termicznych schwytanych przez jądra
U
235
daje ich podział. Do spowalniania neutronów można by wykorzystać
U
238
, którego jest
dużo w uranie naturalnym i który ma duży przekrój czynny na rozpraszanie. Jednakże uran
238 jest kiepskim spowalniaczem. Złe własności uranu 238 jako spowalniacza polegają na
tym, że od 2 MeV do osiągnięcia energii termicznych (kT) neutron musi się zderzyć ponad
2000 razy. Tabela 8 przedstawia zdolności spowalniające różnych jąder.
W zderzeniach z uranem 238 neutron traci energię małymi porcjami. Uzyskanie energii
termicznej neutronów jest możliwe poprzez stany rezonansowe. Przedział energii tych stanów
dla
U
238
zawarty wynosi od 5 do 1000 eV (rys. 34 i 35). Jest zatem bardzo prawdopodobne,
ż
e neutron, tracąc energię małymi porcjami, po którymś kolejnym zderzeniu ma energię
z tego przedziału. Może się zdarzyć, że neutron zostanie schwytany przez jądro
U
238
(nie
podzieli go) i powstanie izotop
U
239
. Neutron ten jest bezpowrotnie stracony dla reakcji
rozszczepienia. W taki sposób może zginąć zbyt wiele neutronów i nie uda się rozwinąć
reakcji łańcuchowej. Istnieją dwa sposoby rozwinięcia reakcji łańcuchowej w naturalnym
Tabela 7. Przekroje czynne dla neutronów termicznych (przekrój czynny w barnach).
Jądro
Absorpcja
σ
A
Rozproszenie
σ
s
Rozszczepienie
σ
t
Uran naturalny
7,42
8,2
3,92
233
U
593
–
524
235
U
*
698
8,2
590
238
U
2,8
8,2
0
239
Pu
1032
8,0
729
*– 85% neutronów schwytanych przez
235
U powoduje podział jąder.
Tabela 8. Zdolności spowalniające wybranych jąder.
Spowalniacz
(moderator)
Liczba zderzeń potrzebnych do osiągnięcia energii termicznej
przez neutron natychmiastowy o energii 2 MeV
H
1
1
18
D
2
1
28
Li
7
3
67
C
12
6
114
U
238
92
2172
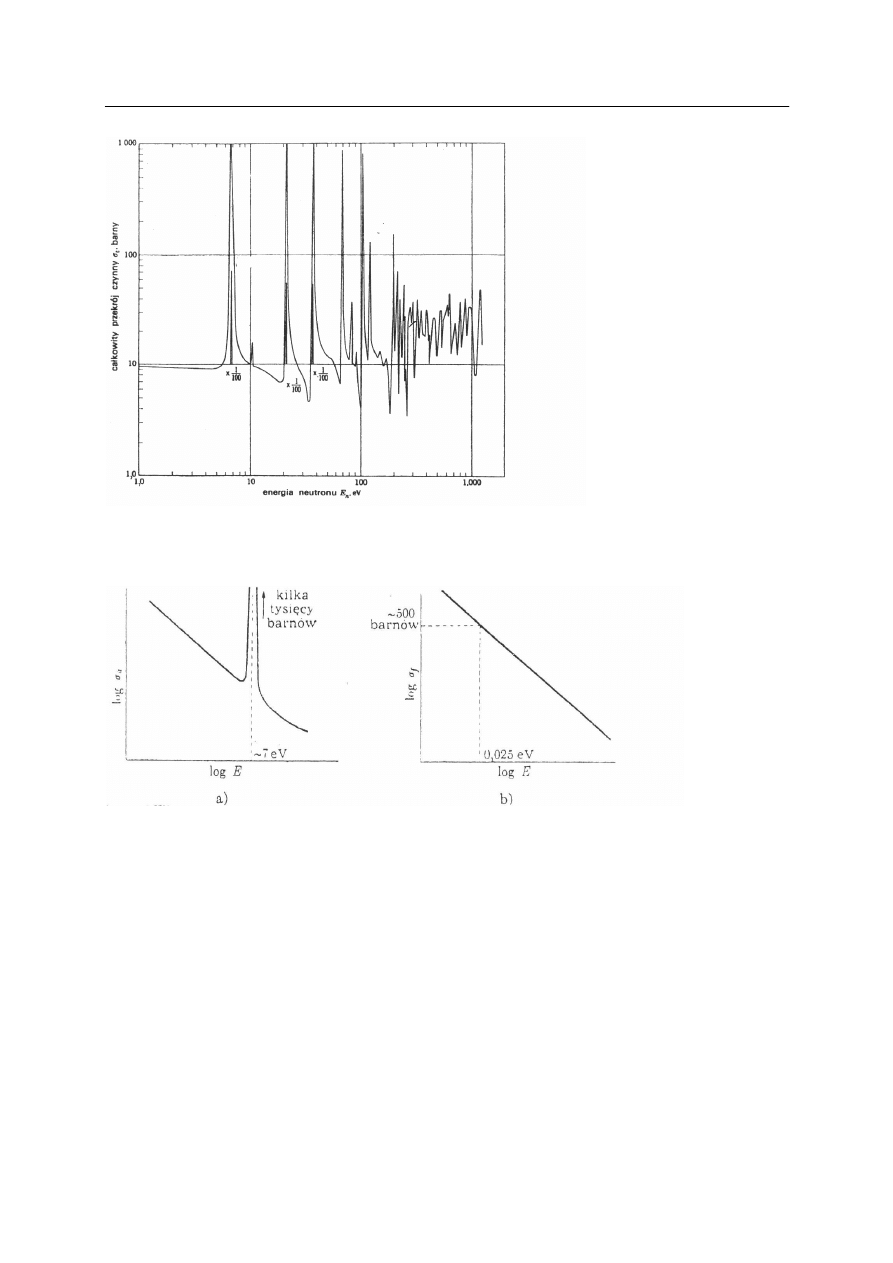
64
Rozdział 6. Reakcje rozszczepienia jądra atomowego
uranie. Pierwszy, to użyć innego moderatora, takiego by neutron schodząc do energii
termicznej tracił energię dużymi porcjami poprzez uczestnictwo w niewielkiej liczbie
zderzeń. Wtedy bowiem jest bardzo duża szansa na to, że ominie przedział energii
rezonansowych. Dobrym spowalniaczem jest woda, lecz próby wykorzystania jej jako
moderatora kończyły się niepowodzeniem, woda bowiem ulega radiolizie; neutrony łączą się
z wodorem (protonami) dając ciężką wodę. W tym procesie ubywało zbyt dużo neutronów,
nie udawało się więc rozwinąć reakcji łańcuchowej. Bardzo dobrym moderatorem jest ciężka
woda. Tu jednak wyłaniają się problemy technologiczne, ponieważ jej otrzymywanie jest
procesem kosztownym i czasochłonnym. Dobrym moderatorem jest grafit, czyli węgiel,
a węgla w przyrodzie jest dużo. Grafit wykorzystywano do spowalniania neutronów
w pierwszym reaktorze.
Drugi sposób rozwinięcia reakcji łańcuchowej w uranie naturalnym polega na
wzbogaceniu tego uranu w izotop
U
235
. Zmieniamy dzięki temu skład procentowy uranu
naturalnego na niekorzyść
U
238
. Zyskujemy to, że przy większej zawartości
U
235
neutrony
Rys. 35. Przekrój czynny
238
U na wychwyt neutronów powolnych (a). Przekrój czynny na rozszczepienie
235
U
przez neutrony powolne przy założeniu zależności
σ
f
~ 1/
ν
(b), (oba wykresy w skali logarytmicznej).
Rys.
34.
Przekrój
czynny
238
U
w
funkcji
energii
neutronów.
W
zakresie
energii
5–1000 eV występuje bardzo duży przekrój czynny na wychwyt rezonansowy.
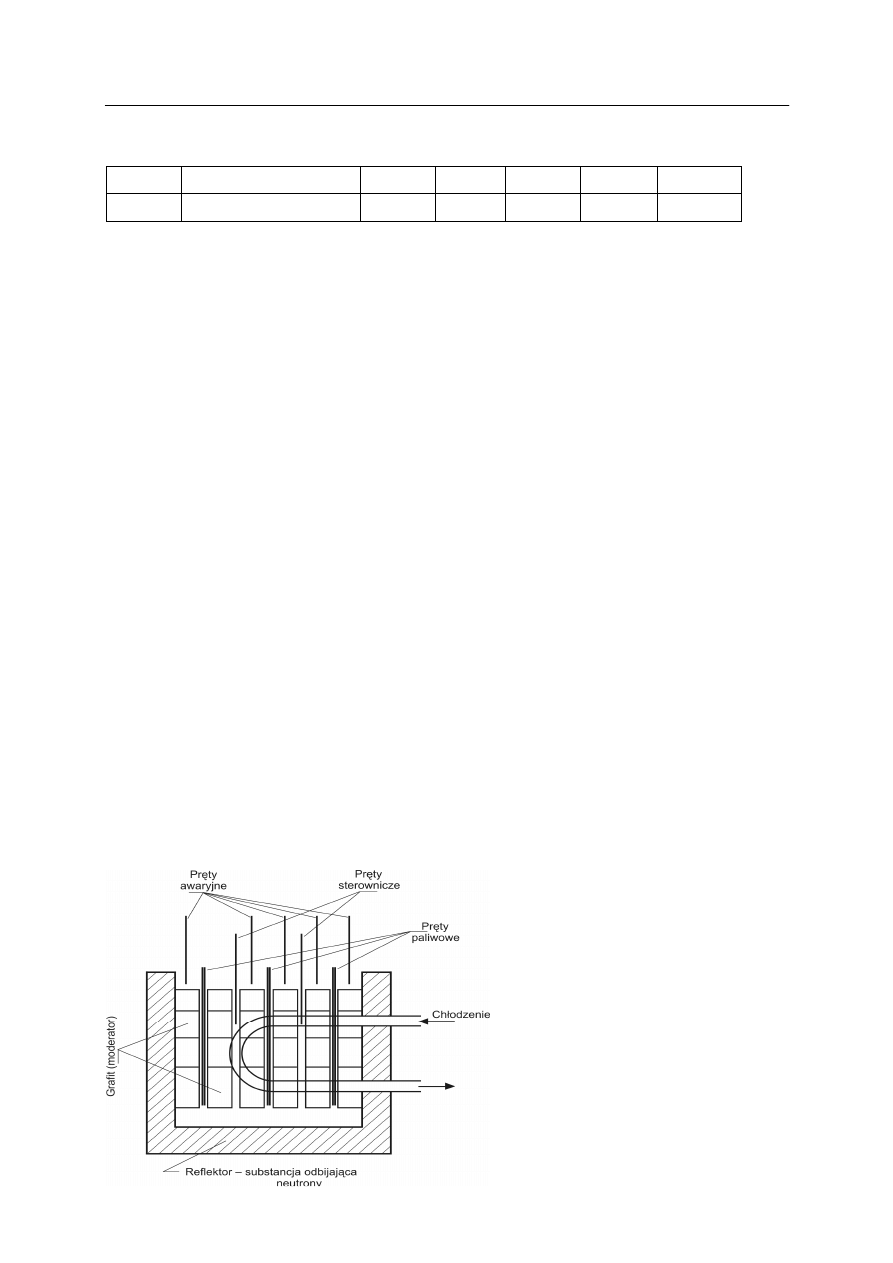
Rozdział 6. Reakcje rozszczepienia jądra atomowego
65
będą częściej napotykać jądra uranu 235, wskutek czego zostanie ograniczony wychwyt
rezonansowy neutronów przez
U
238
na tyle, by można było podtrzymać reakcję łańcuchową.
W praktyce obie metody stosuje się jednocześnie; używamy moderatora i uranu naturalnego
wzbogaconego w izotop
U
235
. Gdy spowalniaczem jest grafit, uran naturalny wzbogacamy
w izotop
U
235
w granicach od 5% do 15%. W tabeli 9 podane są wartości współczynnika
rozmnażania neutronów
∞
k
dla różnych zawartości
U
235
. Należy pamiętać, że od stopnia
wzbogacenia zależą wymiary reaktora.
Widzimy, że nie opłaca się dawać zbyt dużych ilości
U
235
, bo już od 10% współczynnik
∞
k
niewiele wzrasta. Dla rzeczywistego reaktora współczynnik
∞
k
należy pomnożyć przez
czynnik geometryczny zależny od kształtu reaktora (kula, sześcian, prostopadłościan, cylinder
itp.).
W reaktorach jądrowych w reakcja łańcuchowa biorą udział neutrony powolne, a więc
reakcja może być kontrolowana. Kontrola nad reakcją łańcuchową polega na tym, żeby nie
dopuścić do zbyt dużego wzrostu współczynnika k , czyli do zbyt dużego strumienia
neutronów. W tym celu do rdzenia reaktora (paliwo zmieszane z moderatorem)
wprowadzamy substancje łatwo wychwytujące neutrony. Są to zwykle pręty kadmowe, stale
zanurzone w rdzeniu na pewną głębokość. Funkcjonują one jako pręty sterownicze (rys. 36).
Osłabienie strumienia neutronów zależy od tego, jak głęboko są one zanurzone w rdzeniu.
Im wyłapywanie będzie mniejsze, tym większa będzie wartość k. Tak się stanie, gdy pręty
zostaną zanurzone płytko. Głębokość zanurzenia pręta jest miarą reaktywności reaktora. Obok
prętów sterowniczych, są także pręty awaryjne, również wykonane z kadmu. Wiszą one
zawsze nad reaktorem i w razie niebezpieczeństwa, sygnalizowanego przez różne typy
czujników (jonizacyjne, temperaturowe, chemiczne itp.), gwałtownie zanurzają się w rdzeniu
na całą głębokość.
Tabela 8. Warość współczynnika rozmnażania neutronów dla różnych zawartości
235
U w paliwie jądrowym.
235
U
0.07% uran naturalny
1%
2%
5%
10%
100%
k
∞
1,08
1,24
1,5
1,69
1,78
1,98
k
∞
–współczynnik rozmnażania dla reaktora o nieskończonych wymiarach, czyli bez uwzględnienia kształtu
reaktora i tym samym ucieczki neutronów.
Rys. 36. Schemat reaktora z moderatorem
grafitowym.
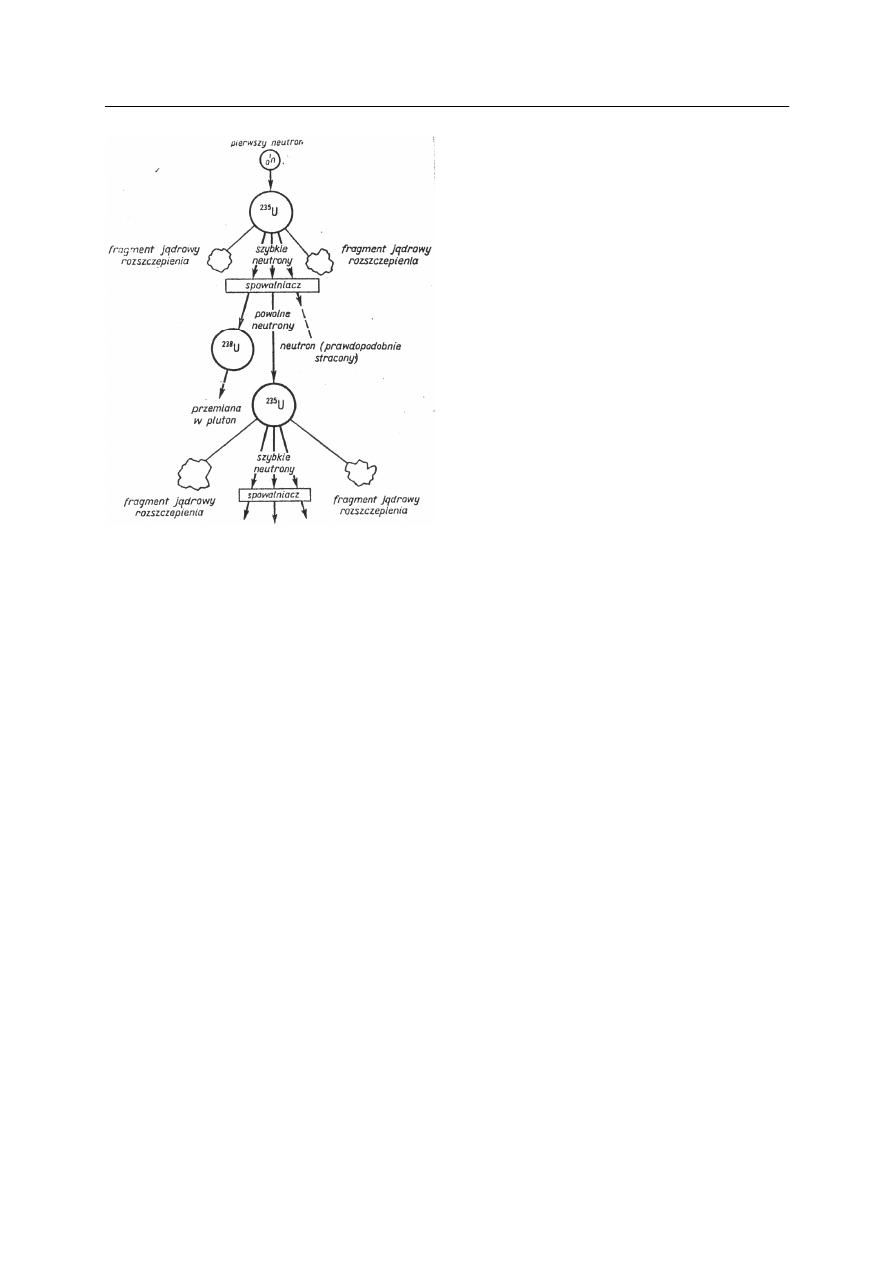
66
Rozdział 6. Reakcje rozszczepienia jądra atomowego
Bezpieczny przedział pracy reaktora wynosi
075
,
1
1
≤
≤
k
. Najmniejsze nawet
przekroczenie wartości
0075
,
1
=
k
musi być szybko redukowane, bo reaktor może się stopić
lub wyparować. Przedział bezpiecznej pracy reaktora jest więc bardzo wąski. W realizacji
bezpiecznej pracy reaktora pomagają neutrony opóźnione. Każdy układ sterujący strumieniem
neutronów ma pewną bezwładność, czyli pewien czas trwania. Jest on rzędu 1 sekundy.
W ciągu tego czasu strumień neutronów i moc reaktora mogłyby niekontrolowanie wzrastać.
W reaktorze znajduje się 99,25% neutronów natychmiastowych i 0,75% neutronów
opóźnionych. Neutrony natychmiastowe powstają w chwili pękania jąder. Inaczej jest
z neutronami opóźnionymi. Wśród jąder wysyłających neutrony opóźnione są takie, których
czas życia wynosi kilkadziesiąt sekund i takie, których czas życia wynosi ułamek sekundy. Są
takie, które żyją 55 sekund i takie, które żyją 0,4 sekundy. To znaczy, że w jednym przypadku
neutrony pojawiają się po 55 sekundach, a w drugim po 0,4 sekundy od chwili rozpadu.
Neutrony natychmiastowe pojawiają się od razu. Wobec tego średni czas neutronów
τ
jest
różny dla różnych jąder i różni się o trzy rzędy wielkości. W związku z tym, że niektóre
neutrony są neutronami opóźnionymi sterowanie reakcją łańcuchową okazało się zadaniem
stosunkowo prostym. Przyjmijmy, że
005
,
1
=
k
, a więc z przedziału bezpiecznej pracy
reaktora. Uwzględniając, że około 0,75% to neutrony opóźnione, można się przekonać, że
reakcja łańcuchowa nie przebiega wyłącznie przy udziale neutronów natychmiastowych, lecz
ż
e powinny w tym procesie uczestniczyć także neutrony opóźnione. Łatwo obliczyć, że
1
9975
,
0
towych
natychmias
<
=
k
1
0075
,
0
h
opóźpóźnio
<
=
k
oraz
005
,
1
nych
opóźpóźnio
towych
natychmias
=
+
=
k
k
k
Z tego powodu, określając czas życia jednego pokolenia neutronów, należy uwzględnić
czas emisji neutronów opóźnionych. Gdy weźmiemy pod uwagę ich udział, otrzymamy
Rys. 37. Schemat przebiegu kontrolowanej reakcji
rozszczepienia.

Rozdział 6. Reakcje rozszczepienia jądra atomowego
67
wartość
s
1
,
0
=
τ
, zamiast
s
10
3
−
=
τ
dla samych neutronów natychmiastowych. Rozwiązując
dla k =
1,005 i
τ
= 0,1 s równanie (24) otrzymamy:
t
t
s
e
n
e
n
n
05
,
0
0
1
,
0
1
005
,
1
0
=
=
−
Co oznacza, że w ciągu jednej sekundy (t = 1 s) liczba neutronów wzrasta jedynie 1,5 razy:
0
1
05
,
0
0
5
,
1 n
e
n
n
=
=
⋅
a przy
s
10
3
−
=
τ
liczba neutronów w ciągu jednej sekundy wzrasta 150 razy. Reakcja
łańcuchowa narasta więc powoli, co pozwala łatwo kontrolować jej przebieg (rys. 37).


Rozdział 7.
Reaktory jądrowe
7.1. Typy reaktorów
Reaktor grafitowy (rys. 36)
–
rdzeń: moderator grafitowy i pręty paliwowe (uran naturalny – wzbogacony),
–
pręty sterownicze,
–
pręty awaryjne,
–
chłodzenie.
Grafit sproszkowany i sprasowany, ułożony jest blokami (z wydrążonymi otworami na
pręty paliwowe, sterownicze i awaryjne). Pręty paliwowe ułożone są obok siebie,
w odległości około 30 cm jeden od drugiego. Taka odległość wystarcza w zupełności do
spowolnienia neutronów w graficie. Pręty paliwowe otoczone są koszulkami ochronnymi
chroniącymi uran przed zetknięciem z moderatorem i chłodziwem (najczęściej wodą).
Uran jest bardzo aktywny chemicznie. Koszulki wykonuje się z materiału elastycznego
i wytrzymałego (cyrkon, aluminium), gdyż są one narażone na bombardowanie silnym
strumieniem neutronów oraz fragmentami podziału. Powoduje to trwałe zmiany i deformacje
sieciowe, a co za tym idzie, osłabienie materiału. Reaktory grafitowe są wewnętrznie bardzo
niestabilne; obserwujemy duże fluktuacje strumienia neutronów w małych odstępach czasu.
Wymaga to dużej koncentracji uwagi podczas pracy reaktora.
Nowe typy reaktorów to reaktory wodno–wodne. Woda pełni tu rolę moderatora
i chłodziwa. Używanie wody jako moderatora stało się możliwe od chwili opanowania
metody wzbogacania uranu naturalnego w izotop
U
235
. Przedtem wszelkie próby kończyły
się niepowodzeniem, gdyż woda ulegała radiolizie. Neutrony łączyły się z protonami
i tworzyła się ciężka woda. Podczas tego procesu ginęło zbyt dużo neutronów, w wyniku
czego nie udawało się rozwinąć reakcji łańcuchowej.
7.2. Reaktor PWR
Jest to jeden z typów reaktora wodno–wodnego to reaktor PWR (Pressurized Water Reactor)
– reaktor ciśnieniowo-wodny (rys. 38).
Do „bańki” wkłada się rdzeń cyrkonowy albo glinowy w postaci cylindra. Rdzeń zalany
jest wodą, która chłodzi reaktor w obiegu zamkniętym. Woda pełni rolę moderatora,
chłodziwa i reflektora. Wymiennik ciepła odbiera ciepło z wężownicy. Woda nie może wrzeć,
gdyż powstaje para, która chłodzi gorzej. Ponieważ temperatura wrzenia wody jest niska,
zysk energetyczny jest niewielki. Dlatego w zależności od temperatury wody stosujemy
odpowiednie ciśnienie, by nie dopuścić do wrzenia. Stąd nazwa reaktora. Przy temperaturze
wejścia
C
264
1
°
=
T
i temperaturze wyjścia
C
283
2
°
=
T
ciśnienie wody wynosi p = 140 atm.
„Bańka” musi wytrzymać takie ciśnienie.
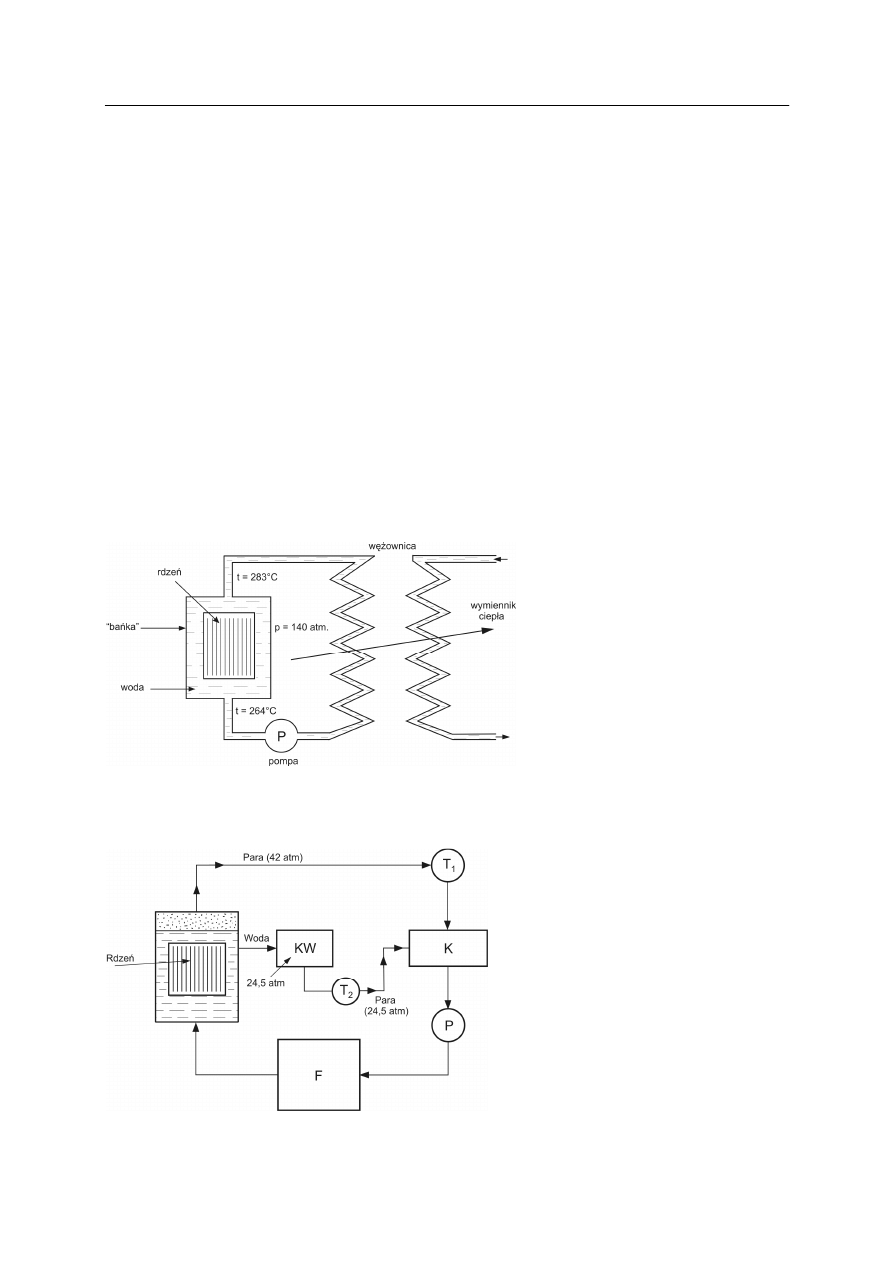
70
Rozdział 7. Reaktory jądrowe
7.3. Reaktor BWR
Drugi typ reaktora wodnego to reaktor BWR (Boiling Water Reactor) (rys. 39). Ten typ
reaktora jeszcze bardziej wskazuje na postęp techniki w fizyce reaktorów. Woda, oprócz roli
opisanej w PWR, jest ciałem roboczym (uruchamia turbiny), a także automatycznie reguluje
moc.
Obniżamy ciśnienie tak, by woda zawrzała. Poziom wody obniżamy w celu wytworzenia
pary. Reaktor pracuje przy ciśnieniu 42 atm. Połowę energii cieplnej unosi para, a połowę
woda. Para porusza łopatki turbiny wysokociśnieniowej. Woda odprowadzana jest w punkcie
leżącym poniżej poziomu lustra wody. Woda ta przechodzi do „komory wrzenia”. Tu panuje
ciśnienie 24 atm. Pod wpływem obniżonego ciśnienia duża ilość wody przekształca się w parę
poruszającą turbinę niskociśnieniową. Potrzebnego ciepła parowania dostarcza ta część wody,
która nie przekształciła się w parę. Ochłodzona w ten sposób woda miesza się z wodą
powstałą w wyniku skroplenia się pary zasilającej turbinę, w kondensorze K. Następnie
woda przepompowywana jest z powrotem do reaktora, przechodząc po drodze proces
oczyszczania w komorze zespołu filtrów. Woda może pełnić rolę regulatora mocy. Wiemy, że
Rys. 38. Schemat reaktora wodno–wodnego typu PWR.
Rys. 39. Schemat reaktora wodno-wodnego typu BWR; KW – komora wrzenia, T
1
– turbina
wysokociśnieniowa, P – pompa, T
2
– turbina niskociśnieniowa, K – kondensor (komora skraplania), F – zespół
filtrów.

Rozdział 7. Reaktory jądrowe
71
woda wrze w pewnej objętości. Wzrost mocy reaktora powoduje nagrzanie wody. Woda,
wrząc w pewnej objętości, gwałtownie zamienia się w parę. Tworzy się coraz więcej pary,
zostaje zaś coraz mniej wody. Ponieważ gęstość pary jest mniejsza od gęstości wody,
neutrony nie mają się na czym spowalniać. Będzie coraz więcej neutronów szybkich, a te nie
wywołują rozszczepienia uranu naturalnego. W ten sposób zanika reakcja łańcuchowa
i reaktor wygasza się automatycznie sam. Reaktory te są bardzo stabilne wewnętrznie.
Niezmiernie trudno zmienić ich raz ustaloną moc; to znaczy, że strumień neutronów nie
wykazuje żadnych fluktuacji. Reaktory te są bardzo kosztowne z uwagi na proces
oczyszczania wody. W reaktorach woda pełniąca rolę moderatora musi być idealnie czysta,
dejonizowana i demineralizowana. Reaktory wodne mogą pracować tylko ze wzbogaconym
uranem naturalnym jako paliwem.


Rozdział 8.
Reakcje syntezy termoądrowej
Proces rozszczepiania ciężkich jąder stanowi źródło wielkiej energii, ale obok tego procesu
istnieje jeszcze drugi sposób wydzielania się energii jądrowej. Tym sposobem jest reakcja
syntezy jąder cięższych (np. helu) z jąder najlżejszych (izotopów wodoru). Taki wniosek
można wyciągnąć po analizie krzywej zależności średniej energii wiązania przypadającej na
jeden nukleon od liczby masowej A (rys. 2). Z analizy tej krzywej wynika, że kombinacja
dwóch lekkich jąder z początkowej, stromej części krzywej tworzy cięższe jądro, które ma
energię wiązania na jeden nukleon większą niż każde z jąder lżejszych. Ponieważ energia
wiązania jest większa, maleje masa jądrowa (wyjściowa), co daje dodatnią wartość Q
i wyzwolenie energii (
)
(
)
(
Y
y
x
x
M
m
M
m
Q
+
−
+
=
jest różnicą mas wejściowych
i wyjściowych). Gdy Q > 0 , pewna część masy zostaje zamieniona na energię. Wytworzona
energia jest różnicą między wyjściową a wejściową energią kinetyczną. Następuje zamiana
masy na energię, zgodnie ze wzorem:
2
mc
E
∆
=
∆
Proces połączenia (syntezy) lekkich jąder w cięższe jądro daje znaczny zysk energii.
Wynika stąd, że w reakcjach łączenia się lekkich jąder w cięższe jądro powinna wydzielać się
duża ilość energii.
Rozważmy reakcję:
p
+
→
+
T
D
D
3
1
2
1
2
1
(25)
)
T
(
D
2
)
T
(
)
D
D
(
1
1
3
1
2
1
3
1
2
1
2
1
p
p
m
+
−
⋅
=
+
−
+
=
∆
jma
028204
,
4
jma
014102
,
2
2
D
2
2
1
=
⋅
=
⋅
jma
02387
,
4
jma
)
007825
,
1
016049
,
3
(
T
1
1
3
1
=
+
=
+
p
jma
00433
,
0
jma
)
023874
,
4
028204
,
4
(
=
−
=
∆
m
MeV
48
,
931
jma
1
=
MeV
03
,
4
MeV
48
,
931
0043
,
0
=
⋅
=
∆
m
MeV
008
,
1
MeV
4
03
,
4
=
=
ε
Taka energia wyzwala się podczas reakcji (25).
W reakcji
n
1
0
3
2
2
1
2
1
He
D
D
+
→
+
masa
)
He
(
D
2
1
0
3
2
2
1
n
m
+
−
⋅
=
∆
zamieniona zostaje na
energię:
jma
028204
,
4
jma
014102
,
2
2
D
2
2
1
=
⋅
=
⋅
jma
024695
,
4
jma
)
008665
,
1
016030
,
3
(
He
1
0
3
2
=
+
=
+
n

74
Rozdział 8. Reakcje syntezy termoądrowej
Defekt masy wynosi:
jma
10
509
,
3
jma
)
024695
,
4
028204
,
4
(
3
−
⋅
=
−
=
∆
m
MeV
25
,
3
MeV
48
,
931
10
509
,
3
3
=
⋅
⋅
=
∆
−
m
MeV
812
,
0
MeV
4
25
,
3
=
=
ε
Jeszcze większa energia wydziela się w reakcji łączenia deuteru z trytem, w wyniku której
powstaje hel i neutron:
n
1
0
4
2
3
1
2
1
He
T
D
+
→
+
. Defekt masy wynosi:
)
He
(
)
T
D
(
1
0
4
2
3
1
2
1
n
m
+
−
+
=
∆
jma
018883
0
jma
011268
5
jma
03015
5
jma
)
008665
1
002603
4
(
jma
)
016049
3
014102
2
(
,
,
,
,
,
,
,
m
=
−
=
=
+
−
+
=
∆
MeV
6
,
17
MeV
48
,
931
018883
,
0
=
⋅
=
∆
m
MeV
56
,
3
MeV
5
6
,
17
=
=
ε
Jeszcze bardziej efektywna energetycznie jest reakcja syntezy jądra helu He
4
2
z czterech
protonów:
β
0
1
4
2
1
1
2
He
4
+
⋅
+
→
⋅
p
Defekt masy wynosi:
jma
02815
0
jma
)
003153
4
0313
4
(
jma
)
00055
0
002603
4
(
jma
007825
1
4
)
2
He
(
4
0
1
4
2
1
1
,
,
,
,
,
,
p
m
=
−
=
=
+
−
⋅
=
⋅
+
−
⋅
=
+
β
∆
MeV
8
,
26
MeV
48
,
931
02815
,
0
=
⋅
=
∆
m
MeV
7
,
6
MeV
4
8
,
26
=
=
ε
Wydzielana w dwóch ostatnich reakcjach energia przypadająca na jeden nukleon jest kilka
razy większa od średniej energii wiązania wydzielanej w reakcjach rozszczepienia.
Pamiętamy, że podczas rozszczepienia jądra uranu 238 wydziela się energia około 200 MeV,
a więc na jeden nukleon przypada
(
)
MeV.
9
,
0
MeV
238
200
≈
Rozważmy warunki, w jakich mogą przebiegać reakcje syntezy lekkich jąder. Reakcje te
wywołane są przez cząstki naładowane. W tym przypadku istotną rolę odgrywa bariera
potencjału elektrostatycznego, która przeciwdziała zbliżaniu się jąder. Jeżeli energia
kinetyczna cząstki naładowanej bombardującej jądro jest niewielka, to taka cząstka nie może
wywołać reakcji jądrowej. W przypadku lekkich jąder bariera potencjału jest niewielka
(z uwagi na mały ładunek), mimo to reakcja połączenia się dwóch zderzających się
deuteronów jest możliwa dopiero dla energii rzędu 0,1 MeV. Aby dwa jądra deuteru

Rozdział 8. Reakcje syntezy termoądrowej
75
połączyły się, trzeba je zbliżyć na odległość
m
10
4
,
1
m
10
4
,
1
15
3
15
3
0
−
−
⋅
≈
⋅
=
=
A
A
r
r
i pokonać przy tym potencjalną energię odpychania elektrostatycznego:
MeV
1
,
0
m
10
3
m
F
10
85
,
9
π
4
)
10
6
,
1
(
π
4
15
12
2
19
0
2
≈
⋅
⋅
⋅
⋅
⋅
⋅
=
=
−
−
−
c
r
e
U
p
ε
Deuterony mogą uzyskać taką energię w odpowiednio wysokiej temperaturze.
Temperaturę, która odpowiada średniej energii kinetycznej deuteronu równej 0,1 MeV,
potrzebnej do pokonania bariery, możemy obliczyć z zależności:
kT
E
k
2
3
=
stąd
k
E
T
k
3
2
=
K
eV
10
89
,
0
K
J
10
38
,
1
4
23
−
−
⋅
=
⋅
=
k
K
10
K
eV
10
89
,
0
MeV
1
,
0
3
2
9
4
≈
⋅
=
−
T
W takiej temperaturze muszą znajdować się deuterony, by dzięki uzyskanej energii
kinetycznej mogły pokonać kulombowską barierę i by mogła zajść reakcja syntezy. Wynika
stąd, że reakcja łączenia się dwóch deuteronów wymaga temperatury znacznie większej od
temperatury, jaka panuje w centralnych rejonach Słońca. Takie reakcje noszą nazwę reakcji
termonuklearnych (termojądrowych). Bardziej szczegółowe rozważania doprowadziły do
wniosku, że dolną granicę temperatury reakcji syntezy można obniżyć do
K
10
7
. Wynika to
z tego, że w bardzo wysokich temperaturach, rzędu kilkudziesięciu milionów stopni, atomy
pierwiastków tworzą plazmę, tzn. elektronowo-jądrowy gaz złożony z całkowicie
zjonizowanych atomów, czyli ze swobodnych elektronów i pozbawionych elektronów jąder.
W wysokich temperaturach łączenie się lekkich jąder zachodzi dzięki zjawisku tunelowania.
Na takich reakcjach termojądrowych oparta jest budowa bomby termojądrowej, zwanej
potocznie bombą wodorową. Wybuch bomby atomowej (uranowej, plutonowej) powoduje
wytworzenie się temperatury rzędu
K
10
7
, dzięki czemu rozpoczyna się reakcja
termojądrowa wyzwalająca dodatkowa energię – to powoduje utrzymanie wysokiej
temperatury i podtrzymanie reakcji. Prawdopodobnie zachodzą reakcje:
MeV
6
,
17
He
T
D
1
0
4
2
3
1
2
1
+
+
=
+
n
MeV
0
,
15
He
He
D
Li
1
0
4
2
4
2
2
1
7
3
+
+
+
=
+
n
Energia wyzwolona podczas wybuchu zwykłej bomby atomowej ograniczona jest przez to,
ż
e nie można dowolnie zwiększać w niej ilości
U
235
czy
Pu
239
, gdyż przed wybuchem nie
możemy przekroczyć krytycznych rozmiarów bryły uranu (plutonu). W bombie

76
Rozdział 8. Reakcje syntezy termoądrowej
termojądrowej ilość materiału wybuchowego praktycznie nie jest niczym ograniczona.
Możliwości techniczne transportu bomby termojądrowej stanowią jedyne ograniczenie energii
wybuchu, dlatego energia takiej bomby może być o kilka rzędów większa od energii wybuchu
bomby atomowej.

Literatura
1.
V.Acosta, C.L.Cowan, B.J.Graham: Podstawy fizyki współczesnej, PWN 1981.
2.
G.E.Pustowałow: Fizyka atomowa i jądrowa, PWN 1975.
3.
L.Kaplan: Fizyka jądrowa, PWN 1957.
4.
Sz.Szczeniowski: Fizyka doświadczalna, cz.6 Fizyka jądra i cząstek elementarnych,
PWN 1974.
5.
A.Strzałkowski: Wstęp do fizyki jądra atomowego, PWN 1979.
6.
K.N.Muchin: Fizyka jądrowa, cz.1 Fizyka jądra atomowego, WNT 1978.
7.
M.Korsunski: Jądro atomowe, PWN 1958.
8.
O.Oldenberg, N.C.Rasmussen: Fizyka wspołczesna, PWN 1970.
9.
M.R.Wehr, J.A.Richards: Fizyka atomu, PWN 1963.
10.
E.M.Rogers: Fizyka dla dociekliwych, cz.5 Fizyka atomowa i jądrowa, PWN 1972.
11.
J.Orear: Fizyka, t.2, WNT 1995.
12.
H.A.Enge, M.R.Wehr, J.A. Richards: Wstęp do fizyki atomowej, PWN 1983.
13.
D.Holliday, R.Resnick, J.Walker: Podstawy fizyki, t.5, PWN 2003.
14.
B.Jaworski, A.Dietłaf: Procesy falowe, optyka, fizyka atomowa i jądrowa. Kurs fizyki t.3,
PWN 1976.
15.
I.W.Sawieliew: Wykłady z fizyki, t.3, PWN 1994.
16.
B.M.Jaworski, A.A.Piński: Elementy fizyki, t.2, PWN 1976.
Wyszukiwarka
Podobne podstrony:
3 Podstawy fizyki polprzewodnik Nieznany (2)
Podstawy fizyki z elementami biofizyki mat 02d
fiele25, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
,Laboratorium podstaw fizyki, WYZNACZANIE WSPÓŁCZYNNIKA ROZSZERZALNOŚCI LINIOWEJ METODĄ
Laboratorium podstaw fizyki ćw ?
Laboratorium Podstaw Fizykipa
Laboratorium Podstaw Fizykiw
Podstawy Fizyki ćw 7 i 8
Laboratorium Podstaw Fizyki id Nieznany
fiele15, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
,laboratorium podstaw fizyki, pytania do laborek
Zagadnienia egzaminacyjne PF3-09, SKRYPTY, NOTATKI, WYKŁADY, Podstawy Fizyki 3, wykład
,Laboratorium podstaw fizyki,?danie drgań wymuszonych
,laboratorium podstaw fizyki,WYZNACZENIE GĘSTOŚCI CIAŁ STAŁYCH
,Laboratorium podstaw fizyki, Sprawdzanie prawa Stefana Boltzmanna
Laboratorium podstaw fizyki ćw 3 d, e
Laboratorium podstaw fizyki ćw 8
,Laboratorium podstaw fizyki,?danie zależności rezystancji od temperatury dla metali i półprzewodnik
,laboratorium podstaw fizyki,pomiar i mieszanie?rw
więcej podobnych podstron