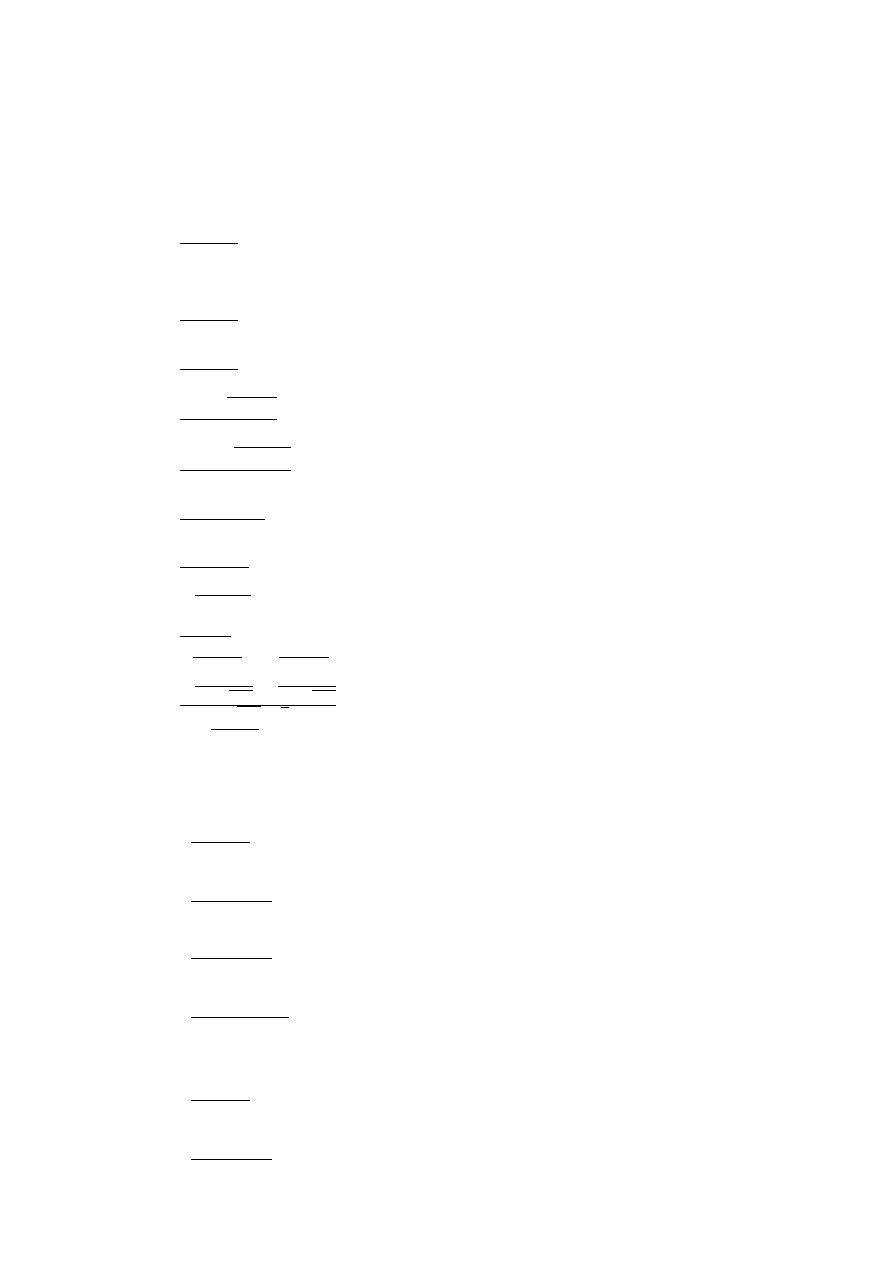
Analiza 1 - ćwiczenia SIMR 2010/2011 ćw 1 - 2 godz.
Temat: Ciąg, granica ciągu

1. Obliczyć granicę ciągu lim

n→∞

a

n

(a) a

n

=

n

2

+ 3n

2n

2

+ 4

(b) a

n

= n

4

− 40n

2

+ n

(c) a

n

=

n

2

− 4n

n

4

+ 6

(d) a

n

=

n

4

− 4n

2n − n

3

(e) a

n

=

n −

√

4n + 1

n + 3

(f) a

n

=

n

2

−

√

n

4

+ n

3

n + 7

(g) a

n

=

n

2

+ (−1)

n

n

2

+ (−n)

n

(h) a

n

=

n + cos n

n + sin n

(i) a

n

=

n

√

2

n

+ 7

n

(j) a

n

=

n+(−1)

n

n

(k) a

n

=

√

n

2

+ n −

√

n

2

− n

(l) a

n

=

√

n

2

+

√

n+1−

√

n

2

−

√

n−1

√

n+1−

√

n

(m) a

n

= n(

3

√

n

3

+ 1 − n)

2. Obliczyć granicę ciągu lim

n→∞

a

n

(a) a

n

=

n

2

+ 3n

n

2

+ 4

!

n−1

(b) a

n

=

n

3

+ n − 1

n

3

+ 4

!

2n

2

−4

(c) a

n

=

n + 2n

2

n + n

2

− 1

!

n−3

(d) a

n

=

n

3

+ 2n − 1

n

3

+ 3n

2

− n

!

n

2

−3

(e) a

n

= n(ln(n + 3) − ln n)

(f) a

n

=

n

2

+ 3n

n

2

+ 4

!

n−1

(g) a

n

=

n

3

+ n − 1

n

3

+ 4

!

2n

2

−4

(h) a

n

=

n

2

+

√

n

n

2

+

3

√

n

!

2n+1

(i) a

n

=

n + 2n

2

n + n

2

− 1

!

n−3

(j) a

n

=

n

3

+ 2n − 1

n

3

+ 3n

2

− n

!

n

2

−3