Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

I6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. W zbiorze liczb zespolonych rozwiązać równanie

.

1 − i

i z − 1

=

3 + i

z − 3i + 1

2. Przedstawić w postaci algebraicznej liczbę zespoloną

( sin

π

12

− i cos

π

12

)

63

.

3. Wielomian

x

6

− 5x

4

+ 2x

2

+ 8

rozłożyć na nierozkładalne czynniki rzeczywiste.

4. Funkcję wymierną

1

x

3

+ 3x + 4

rozłożyć na rzeczywiste ułamki proste.

Odpowiedzi do zestawu

I6

1. .

;

z =

−7 + i

10

2.

;

2

2

−

2

2

i

3.

;

( x + 2 ) ( x − 2 ) ( x + 2 ) ( x − 2 ) ( x

2

+ 1 )

4.

.

1

6 ( x + 1 )

+

2 − x

6 ( x

2

+ x + 4 )

Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

J6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. Wyznaczyć wszystkie liczby zespolone spełniające warunek

z

z

2

+ z

2

= 18 + 12 i .

2. Obliczyć

wykorzystując wzór de Moivre'a.

(

1 + i ctg

π

24

1 − i ctg

π

24

)

4

3. Znaleźć wszystkie pierwiastki wielomianu

z

4

− 2z

3

+ 8z

2

− 6z + 15

wiedząc, że liczba

jest jednym z nich.

i

3

4. Rozłożyć na ułamki proste funkcję wymierną

.

( x + 1 ) ( x − 2 ) ( x + 3 )

( x + 4 ) ( x − 5 ) ( x + 6 ) ( x − 7 )

Odpowiedzi do zestawu

J6

1.

;

z

1

= 3 − 2i, z

2

= −3 + 2i

2.

;

1
2

−

3

2

i

3.

;

1 − 2i, 1 + 2i, −i 3

4.

.

−

1

11 ( x + 4 )

−

8

11 ( x − 5 )

+

60

143 ( x + 6 )

+

200

143 ( x − 7 )

Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

K6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. Na płaszczyźnie zespolonej przedstawić zbiór

.

{ z ∈ C : 6 Im z < z

2

,

z − 1 ≥ z + 1 }

2. Stosując wzór de Moivre'a wyrazić liczbę

w zależności od

cos 10

i

.

sin 2

cos 2

3. Wielomian

3x

4

− 8x

3

+ 6x

2

− 1

rozłożyć na czynniki stopnia 1.

4. Rozłożyć na ułamki proste funkcję wymierną

.

( x − 1 )

3

( x + 3 )

4

Odpowiedzi do zestawu

K6

1. Część półpłaszczyzny

leżąca na zewnątrz koła o środku

Re z ≤ 0

3i

i promieniu ;

3

2.

;

cos

5

2 − 10 cos

3

2 sin

2

2+ 5 cos 2 sin

4

2

3.

;

( x − 1 )

3

( 3x + 1 )

4.

.

1

x + 3

−

12

( x + 3 )

2

+

48

( x + 3 )

3

−

64

( x + 3 )

4

Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

L6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. Przedstawić na płaszczyźnie zespolonej zbiór

.

{ z ∈ C : Im

1 + z
1 − z

= 1 }

2. Wyrazić

w zależności od

wykorzystując wzór de

cos 5ϕ

cos ϕ

Moivre'a.

3. Liczba

jest pierwiastkiem wielomianu

z

0

= 1 + i

,

W ( z ) = az

3

+ bz + 1

gdzie

. Znaleźć liczby

.

a

, b ∈ R

a

, b

4. Znaleźć rozkład na rzeczywiste ułamki proste funkcji wymiernej

.

x

2

− 2x + 2

x

3

− 2x

2

+ 2x − 1

Odpowiedzi do zestawu

L6

1. Okrąg o środku

i promieniu

bez punktu

;

z

0

= 1 + i

r = 1

z

1

= 1

2.

;

16 cos

5

ϕ − 20 cos

3

ϕ + 5 cos ϕ

3.

,

;

a =

1
4

b = −

1
2

4.

.

1

x − 1

−

1

x

2

− x + 1

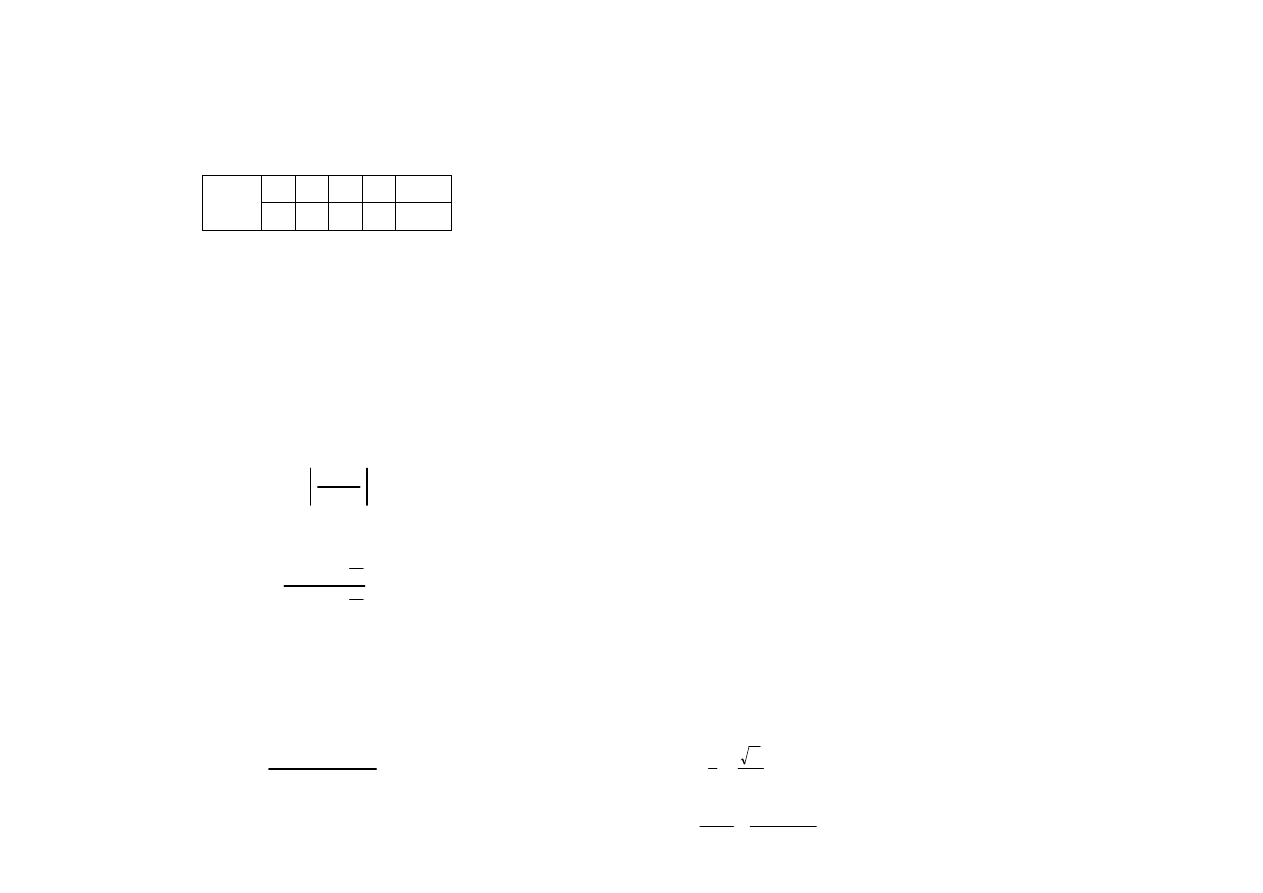
Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

M6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. Na płaszczyźnie zespolonej naszkicować zbiór

.

{ z ∈ C :

4i − 3

3i − z

≥ 5 }

2. Stosując wzór de Moivre'a obliczyć

.

(

1 − i ctg

π

24

1 + i ctg

π

24

)

8

3. Zbadać krotność pierwiastka

wielomianu

z

0

= −i

.

z

4

+ 2iz

3

+ 2iz − 1

4. Znaleźć rozkład na rzeczywiste ułamki proste funkcji wymiernej

.

x

2

+ 3

x

3

− x

2

− x − 2

Odpowiedzi do zestawu

M6

1. Koło o środku

i promieniu

bez punktu

;

z

0

= 3i

r = 1

z

0

2.

;

−

1
2

+

3

2

i

3. krotność wynosi ;

3

4.

.

1

x − 2

−

1

x

2

+ x + 1

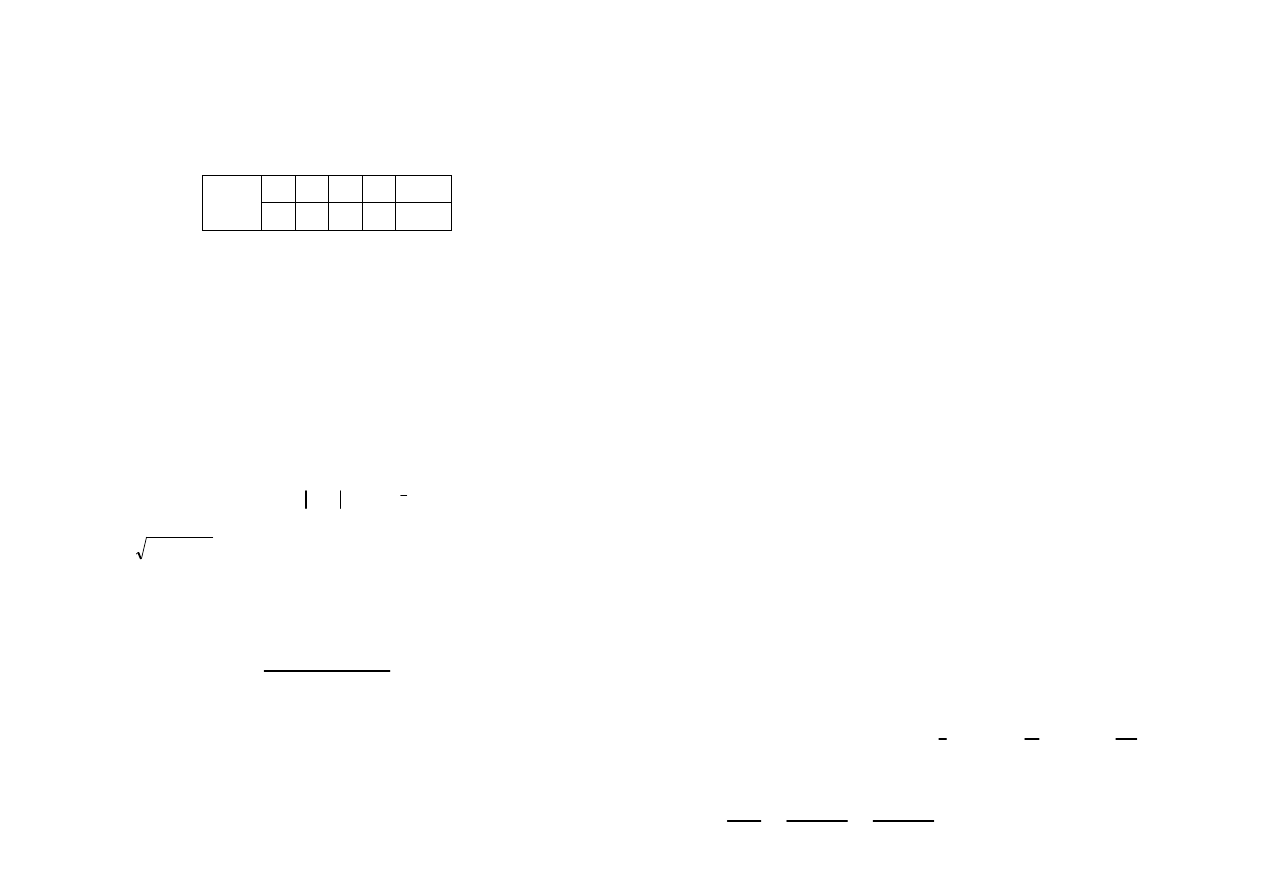
Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

N6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. Stosując postać trygonometryczną lub wykładniczą liczb zespolonych

przedstawić graficznie zbiór

.

{ z ∈ C : z

5

= i z

4

z }

2. Obliczyć

.

8i − 15

3. Wielomian

rozłożyć na nierozkładalne czynniki rzeczywiste.

x

6

+ 27

4. Funkcję wymierną

x

4

+ 3x

3

− x − 4

x

3

+ 3x

2

+ 3x + 1

zapisać w postaci sumy wielomianu i ułamków prostych.

Odpowiedzi do zestawu

N6

1. Suma trzech półprostych

,

;

arg z =

π
2

arg z =

7π

6

, arg z =

11π

6

2.

;

{1 + 4i, −1 − 4i }

3.

;

( x

2

+ 3 ) ( x

2

− 3x + 3 ) ( x

2

+ 3x + 3 )

4.

.

x −

3

x + 1

+

4

( x + 1 )

2

−

5

( x + 1 )

3

.

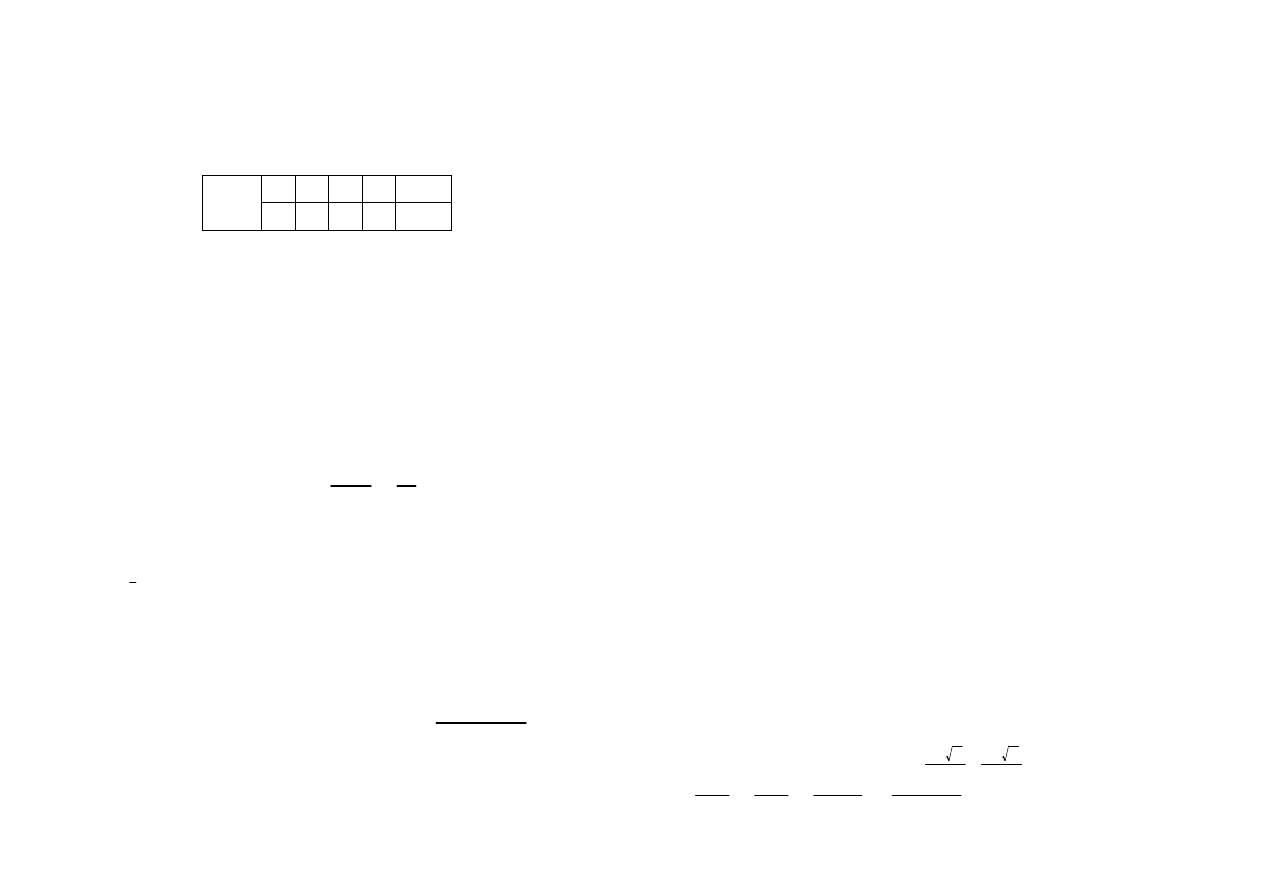
Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

O6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. Przedstawić na płaszczyźnie zespolonej zbiór

.

{ z ∈ C : arg

i − 1

z + 2i

=

3π

2

}

2. Przedstawić graficznie wszystkie pierwiastki stopnia z liczby

8

zespolonej

i wybrać spośród nich te, dla których zachodzi

16

związek

z

2

= −z

2

.

3. Po obliczeniu

znaleźć wszystkie pierwiastki wielomianu

V ( −i )

.

V ( z ) = z

4

− z

3

+ 2z

2

− z + 1

4. Napisać ogólną postać rozkładu funkcji wymiernej

na

x

2

+ 3x − 4

x

6

+ 3x

4

− 4

rzeczywiste ułamki proste.

Odpowiedzi do zestawu

O6

1. Półprosta bez punktu określona wzorem

dla

Im z = Re z − 2

Re z < 0

2.

;

1 + i, 1 − i, −1 + i, −1 − i

3.

, pierwiastki:

;

V( i ) = 0

i

, −i,

1−i 3

2

,

1+i 3

2

4.

(tutaj

.

A

x − 1

+

B

x + 1

+

Cx + D

x

2

+ 2

+

Ex + F

( x

2

+ 2 )

2

A = 0)

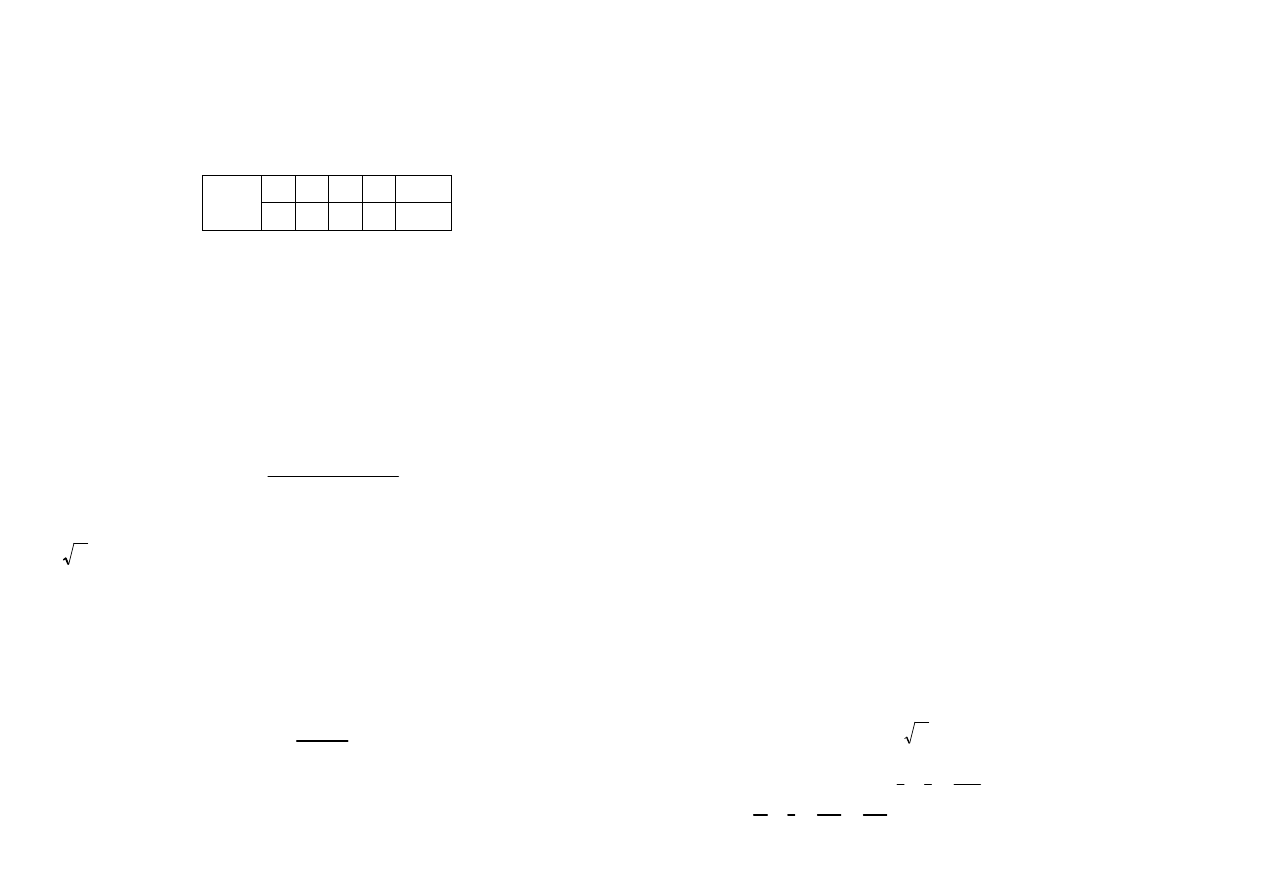
Algebra liniowa 1

I kolokwium, semestr zimowy 2008/2009

Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.

P6

1

2

3

4

Suma

Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!

Teresa Jurlewicz

ZADANIA

1. Obliczyć

dla

z

19

.

z =

( 1 + 3i ) ( 2 − 3i )

4 + 7i

2. Jednym z pierwiastków stopnia z liczby zespolonej jest liczba

3

z

. Znaleźć pozostałe pierwiastki i wyznaczyć . Sporządzić

3 − i

z

rysunek.

3. Wyznaczyć resztę z dzielenia wielomianu

przez wielo-

z

71

− 1

mian

.

z

3

− iz

4. Znaleźć rozkład na i) rzeczywiste; ii) zespolone ułamki proste

funkcji wymiernej

.

1

z

3

+ 9z

Odpowiedzi do zestawu

P6

1.

;

−2

9

( 1 + i )

2. pozostałe pierwiastki

;

2i, − 3 − i, z = −8i

3.

;

−iz − 1

4. rzeczywiste ułamki proste:

, zespolone ułamki

1
9

(

1

z

−

z

z

2

+9

)

proste:

.

1

18

(

2

z

−

1

z+3i

−

1

z−3i

)