UNIWERSYTET TECHNOLOGICZNO-PRZYRODNICZY

w Bydgoszczy

Wydział Telekomunikacji i Elektrotechniki

Instytut Elektrotechniki

Zakład Elektroenergetyki

TECHNOLOGIA INFORMACYJNA

LABORATORIUM

ROK I SEM. I

INSTRUKCJA DO ĆWICZENIA IV

Arkusz kalkulacyjny Microsoft Excel – solver,

wykorzystanie wbudowanych funkcji

Opracował: dr inż. Marcin Drechny

Wrzesień 2008 r.

2

1. Cel ćwiczenia

Celem tego ćwiczenia jest poznanie i utrwalenie wiadomości związanych z arkuszem

kalkulacyjnym Excel 97/2000, a w szczególności wykorzystaniu wbudowanych

podstawowych funkcji oraz narzędzia optymalizującego o nazwie „solver”.

2. Wprowadzenie

2.1. Funkcje Excela

Funkcja jest predefiniowaną formułą posiadającą nazwę, która pobiera wartość lub

wartości (zwane argumentami funkcji) i zwraca wynik lub wyniki.

Używając funkcji możemy znacznie uprościć i skrócić formułę, a nawet uzyskać informacje,

których nie można zdobyć bez użycia funkcji.

Jeżeli chcemy w formule zastosować funkcję musimy użyć odpowiedniej składni.

FUNKCJA(Argument1; Argument2; ... ;ArgumentN)

A oto kilka zasad używania funkcji:

•

Nazwa funkcji może być pisana dużymi lub małymi literami. Jeżeli napiszemy nazwę

funkcji małymi literami, zostaną one zamienione na duże jeżeli nazwa funkcji jest

prawidłowa.

•

Przed i za nawiasami nie powinno być spacji.

•

Jeżeli funkcja jest bezargumentowa po nazwie funkcji należy wpisać parę nawiasów.

•

Argumenty funkcji oddzielamy separatorami argumentów listy (średnikami).

•

Funkcja może nie posiadać argumentów, posiadać ich kilka, mieć ich zmienną ilość lub

może zawierać argumenty opcjonalne.

•

Argumentami funkcji mogą być liczby, adresy, tekst, wartości logiczne, tablice, wartości

błędu lub inne funkcje.

•

Gdy argumentem funkcji jest inna funkcja, formułę nazywamy zagnieżdżona.

•

Gdy funkcja znajduje się na początku formuły wstawiamy przed nią znak równości =.

•

Funkcje Microsoft Excel podzielone są na kategorie: finansowe, daty i czasu,

matematyczne i trygonometryczne, statystyczne, wyszukiwania i adresu, bazy danych,

tekstowe, logiczne, informacyjne i inżynierskie.

3

2.1.1. Podział funkcji ze względu na ilość argumentów

Rodzaj funkcji Przykład

Notacja symboliczna

Uwagi

Bez -

argumentowa

data

systemowa

czas

systemowy

DZIŚ()

TERAZ()

Nie wymaga żadnych

argumentów, bo data
systemowa (i czas) jest jedna.
Pusta para nawiasów oznacza
brak argumentów i wskazuje
na funkcję arkusza (a nie np.
na nazwę obszaru)

Ze stałą liczbą

argumentów

wyliczenie

sinusa kąta

dzielenie z

resztą

SIN(arg)
lub
SIN(liczba|adres)
MOD(arg1;arg2)
lub
MOD(liczba1|adres1;liczba2|a
dres2)

Sinus wyliczany jest tylko

dla jednego kąta. Poprzez arg
rozumie się argument będący
liczbą lub adresem komórki.
W drugim zapisie znak [|]
należy czytać "albo". Funkcja
dzielenia z resztą zawsze
wymaga dwóch argumentów:
dzielnej i dzielnika

Ze zmienną

listą

argumentów

suma

wyliczenie

liczby

największej

SUMA(arg1;arg2;...)
lub
SUMA(liczba1|adres1|zakres1
;...)
MAX(arg1;arg2;...)
lub
MAX(liczba1|adres1|zakres1;.
..)

Sumę można wyliczyć

z bliżej nieokreślonej ilości
komórek, obszarów czy liczb.
Argumentem może tu być
liczba, adres komórki lub
zakres. Znak wielokropka
oznacza powtarzanie się
wcześniej przedstawionej
sekwencji. Podobnie funkcja
wyliczająca wartość
maksymalną.

Z argumentami

opcjonalnymi

wyliczenie

ś

redniej

kwoty raty

PMT(stopa;liczba_rat;wa;wp;t
yp

)

znaczenie argumentów

- stopa - odsetki za okres;
- liczba_rat - ilość okresów,
- wa - wysokość pożyczki
- wp - wartość w przyszłości,
czyli kwota, której się nie
spłaci
- typ - sposób wyliczenia
odsetek
0 - na końcu okresu
1 - na początku okresu

Pierwsze trzy argumenty

muszą wystąpić, ostatnie dwa
mogą - a więc są opcjonalne.
Takie dane, decydują o sposobie
działania funkcji i jeśli nie
zostaną podane funkcja
przyjmie wartości domyślne
(zerowe).

Tab. nr 1 Podział funkcji ze względu na ilość argumentów, zapis i przykłady

4

2.1.2. Wklejanie funkcji za pomocą palety formuł

Wszystkich funkcji jakimi dysponuje Excel jest kilkaset. Każda z nich wymaga innej

ilości i typów argumentów. Nie sposób zapamiętać wszystkich nazw i składni funkcji.

Dlatego zamiast wpisywać funkcję z klawiatury możemy posłużyć się “Paletą formuł”. W ten

sposób zautomatyzujemy (po części) wprowadzanie funkcji, gwarantując sobie tym samym

poprawność wpisania nazwy funkcji, ich argumentów oraz odpowiednią ich kolejność.

Wklejenie funkcji można rozpocząć od wciśnięcia przycisku

“Wklej funkcję”,

(rysunek 1) wybierając polecenie Wstaw|funkcja... lub wykorzystując przycisk “Edytuj

formułę” . Wklejenie to przebiega w dwóch etapach:

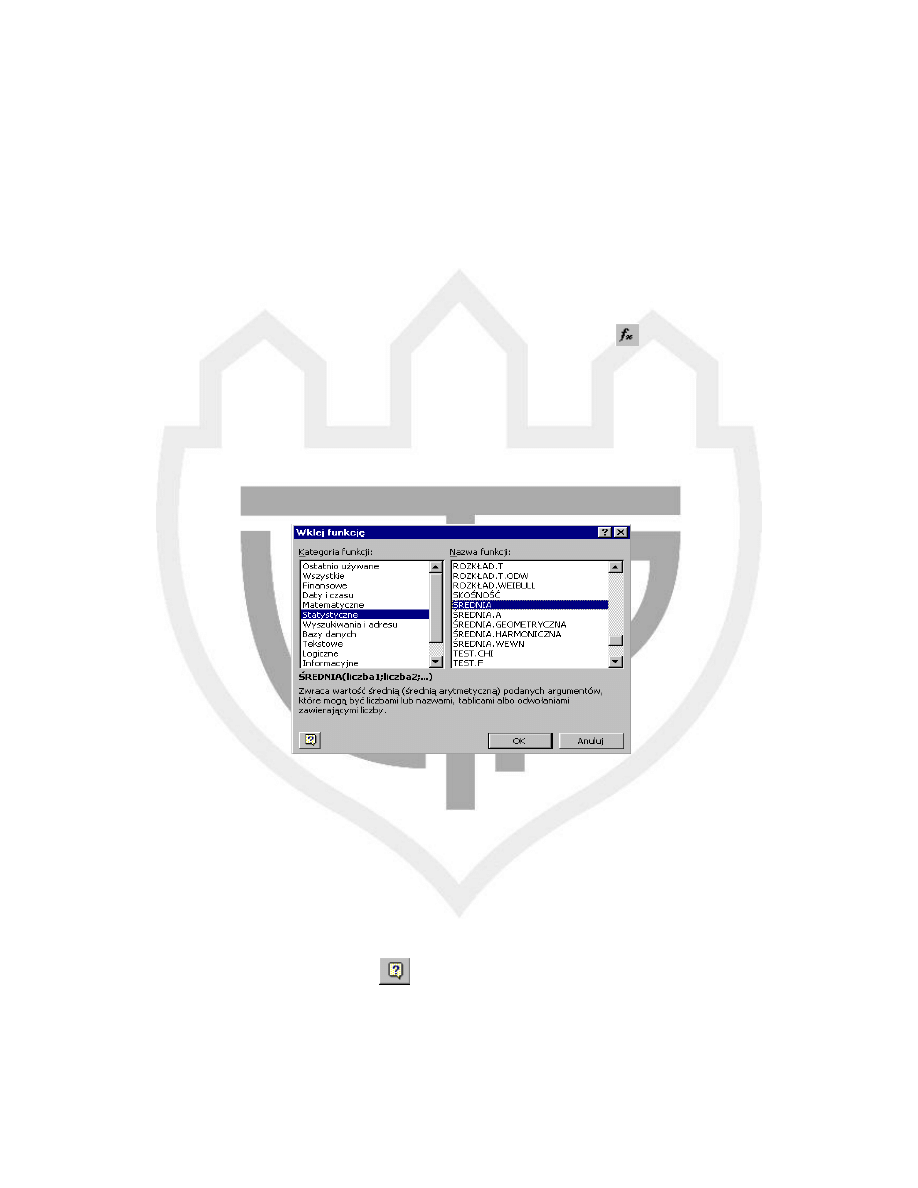
W pierwszym etapie pojawia się okienko dialogowe “Wklej funkcję”, w którym

wybieramy kategorię i funkcję, która nas interesuje. Można tam znaleźć oprócz nazwy

funkcji, jej krótki opis oraz listę argumentów.

Rys. 1. Formularz wyboru funkcji

W drugim etapie wyświetla się “Paleta formuł” (rysunek 2), na której definiujemy

parametry wejściowe do wybranej funkcji ( komórki zmiennych oraz ich zakresy).

W wyświetlanym okienku znajduje się również wszystko to może nam pomóc

w prawidłowym skonstruowaniu funkcji: opis działania funkcji, opis i miejsce, w które można

wstawić argumenty oraz wynik funkcji. Dostępna jest szczegółowa pomoc na temat tej

funkcji po wciśnięciu przycisku

, znajdującego się w lewym dolnym rogu “Palety

formuł”.

5

.

Rys. 2. Okienko „ Palety formuł”

2.1.2.

Funkcje matematyczne, trygonometryczne, statystyczne

Poniżej przedstawiono najczęściej używane funkcje matematyczne trygonometryczne

i statystyczne wraz z krótkim opisem:

KOMBINACJE(n; k) - oblicza ilość kombinacji k - elementowych ze zbioru n -

elementowego.

LICZ.JEŻELI(zakres; kryteria) - Podaje liczbę komórek wewnątrz zakresu, które

odpowiadają podanym kryteriom.

LICZBA.CAŁK(liczba; liczba_cyfr) - Obcina część ułamkową liczby, pozostawiając

liczę_cyfr

po przecinku.

LN(liczba) - Oblicza wartość logarytmu naturalnego dla zadanej liczby.

LOG(liczba, podstawa) - Podaje wartość logarytmu liczby przy zadanej podstawie.

LOG10(liczba) - Oblicza wartość logarytmu przy podstawie 10 dla danej liczby.

LOS() - Generuje liczbę losową z przedziału (0;1). Wynik funkcji zmienia się przy

każdorazowym przeliczaniu arkusza.

MOD(liczba; dzielnik) - Zwraca resztę z dzielenia argumentu liczba przez argument dzielnik.

MODUŁ.LICZBY(liczba) - Podaje wartość bezwzględną z liczby.

PI() - Daje w wyniku liczbę p

PIERWIASTEK(liczba) - Zwraca wartość pierwiastka kwadratowego z liczby.

SILNIA(liczba) - Zwraca wartość silni argumentu liczba.

SUMA(liczba1;liczba2...) - Dodaje do siebie wszystkie wartości wymienione w liście

argumentów.

SUMA.ILOCZYNÓW(tablica1;tablica2; tablica3...) - Mnoży odpowiadające sobie

elementy dwóch lub więcej tablic, a następnie zwraca wartość sumy iloczynów.

6

SUMA.JEŻELI(zakres; kryteria; zakres_suma) - Sumuje komórki z zakresu_suma, jeśli

odpowiadające im koórki z zakresu spełniają podane kryteria.

ZAOKR(liczba; liczba_cyfr) - Zwraca liczbę zaokrągloną z dokładnością do podanej

liczby_cyfr

.

ZAOKR.DO.CAŁK(liczba) - Zwraca liczbę zaokrągloną w dół do najbliższej liczby

całkowitej.

MAX(liczba1;liczba2 ...) - Zwraca największą spośród wartości na liście argumentów.

MAX.K(tablica; k) - Zwraca k-tą największą spośród wartości tablicy.

MEDIANA(liczba1; liczba2 ...) - Wyznacza medianę podanej grupy argumentów.

MIN(liczba1; liczba2 ...) - Zwraca najmniejszą spośród wartości na liście argumentów.

MIN.K(tablica; k) - Zwraca k-tą najmniejszą spośród wartości tablicy.

ŚREDNIA(liczba1; liczba2 ...) - Wyznacza średnią arytmetyczną argumentów.

ŚREDNIA.GEOMETRYCZNA(liczba1; liczba2 ...) - Wyznacza średnią geometryczną

argumentów.

COS(kąt) - Podaje wartość cosinus kąta.

SIN(kąt) - Podaje wartość sinus kąta.

TAN(kąt) - Podaje wartość tangens kąta.

RADIANY(kąt) - Zmienia liczbę stopni podaną w argumencie kąt na radiany.

STOPNIE(kąt) - Zmienia miarę kąta podanego w radianach na stopni.

2.2. Solver

Dodatek „Solver” pozwala zoptymalizować wartość formuły w jednej z komórek

arkusza – nazywanej komórką celu. Zakresem działania jest grupa komórek związanych

bezpośrednio lub pośrednio z formułą w komórce celu. Wartości w komórkach określonych

przez użytkownika – nazywanych komórkami zmienianymi – są zmieniane tak, aby

osiągnąć żądany wynik w komórce celu. Zakres zmian wartości występujących w modelu

można ograniczyć, wprowadzając ograniczenia. Mogą one także dotyczyć innych komórek,

które mają wpływ na formułę w komórce celu.

2.2.1. Przykład obliczeń z użyciem „Solvera”

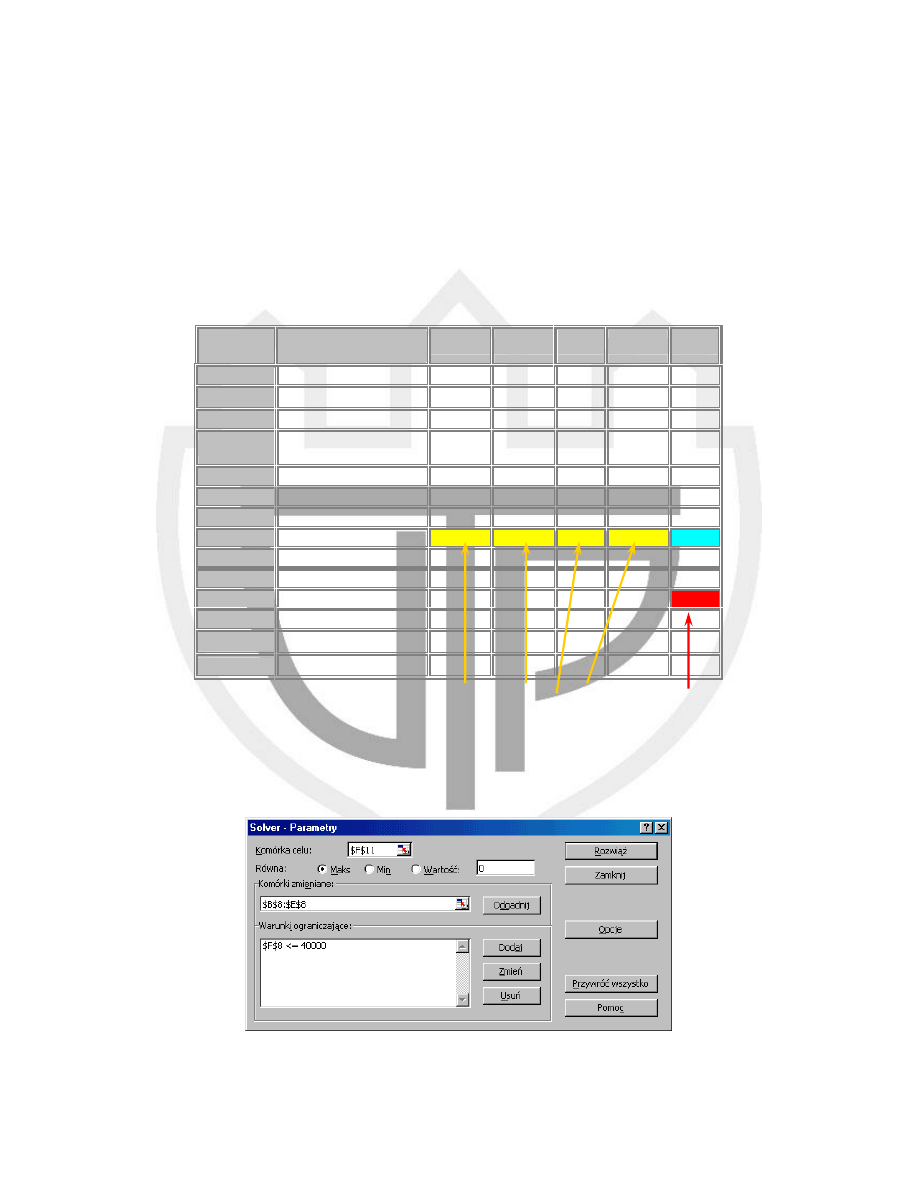
W podanym dalej przykładzie, (rysunek 3) wydatki na "Reklamę" w poszczególnych

kwartałach mają wpływ na liczbę "Sprzedanych jednostek", określając pośrednio "Przychód

7

ze

sprzedaży"

[według

równania

=35*B2*(B8+3000)^0,5]

czyli:

35*wskaźnik

sezonowości*(reklama+3000)^0,5] ( rysunek 4).

Optymalizacja polega na zmienianiu kwartalnego budżetu na "Reklamę" (komórki

B8:E8) do jego wartości maksymalnej, którą ogranicza całkowity budżet 40 000 (komórka

G8), aż do osiągnięcia największego możliwego "Zysku". Wartości w komórkach

zmienianych są używane do obliczenia "Zysku" w poszczególnych kwartałach i są związane

z formułą w komórce celu G11, =SUMA(B11:E11).

A

B

C

D

E

F

1

Miesiąc

Kw. I

Kw. II

Kw. III

Kw. IV

Razem

2

Sezonowość

0,9

1,1

0,8

1,2

3

Sprzedane jednostki

3592

4390

3192

4789

15962

4

Przychód ze sprzedaży w
zł

143662

175587 127700

191549 638498

5

Koszt zakupu

89789

109742

79812

119718 399061

6

Marża brutto

53873

65845

47887

71831 239437

7

Wydatki służbowe

8000

8000

9000

9000

34000

8

Reklama

10000

10000

10000

10000

40000

9

Koszt ogólnozakładowy

21549

26338

19155

28732

95775

10

Koszt całkowity

39549

44338

38155

47732 169775

11

Zysk z produktów w zł

14324

21507

9732

24099

69662

12

Rentowność sprzedaży

10%

12%

8%

13%

11%

13

Cena produktu

40

14

Koszt produktu

25

Rys.3. Rozróżnienie w przykładzie komórek celu i komórek zmienianych

Po otworzeniu okienka Solvera (menu Narzedzia-> Solver) (rysunek 5) definiujemy komórki
zmienne oraz komórkę celu a następnie określamy warunki ograniczające.

Rys. 5. Okienko parametrów Solvera wraz z ograniczeniami.

Komórka celu

Komórki zmieniane

8

Reklama

7273

12346

5117

15263

40000

Koszt ogólnozakładowy

19156

28616

15136

34056

96965

Koszt całkowity

34430

48963

29253

58319

170965

Zysk z produktów w zł

13461

22578

8587

26820

71447

Tab. 2. Wynik optymalizacji

Dodawanie ograniczeń w dodatku Solver.

W menu Narzędzia klikamy polecenie Solver, a następnie Dodaj ( rysunek 5).

W polu Odwołanie do komórki podaj nazwę lub adres zakresu komórek, których wartości

chcemy ograniczyć.

Definiujemy symbol relacji ( <=, =, >=, int lub bin ), która ma zachodzić pomiędzy wskazaną

komórką, a wartością ograniczającą. Dla symbolu int, w polu Warunki ograniczające pojawi

się informacja "Liczba całkowita". Dla symbolu bin, w polu Warunki ograniczające pojawi

się informacja "binary"- liczba binarna – 1lub 0.

W polu Warunki ograniczające wpisujemy liczbę, nazwę lub adres komórki, albo formułę.

Aby potwierdzić warunek ograniczający i dodać następny, kliknij przycisk Dodaj.

Aby zaakceptować warunek ograniczający i powrócić do okna dialogowego Solver -

Parametry, klikamy przycisk OK.

Uwagi

•

Relacje int i bin mogą występować tylko w więzach nałożonych na komórki

zmieniane.

•

Jeśli w oknie dialogowym Opcje dodatku Solver jest zaznaczone pole wyboru Model

liniowy, nie obowiązuje żaden limit liczby ograniczeń. W przypadku problemów

nieliniowych każda komórka może zawierać, oprócz ograniczeń dla zmiennych,

do 100 innych ograniczeń. Informacje o opcjach w oknie dialogowym Dodawanie

warunku ograniczającego

9

3.

Przebieg ćwiczenia – zadania do wykonania

3.1. Nadać komórce B2 wartość obrotów ( np. 2000) oraz wpisać do komórki C2 koszty

stanowiące 20% obrotów plus koszty stałe (np. 300) następnie:

- obliczyć w komórce C3 zyski stanowiące różnicę pomiędzy obrotami a kosztami,

- za pomocą Solvera rozwiać następujące zadanie: Jakie powinny być obroty aby

zysk osiągnął określoną wartość ( np. 3000).

3.2. Za pomocą Solvera należy rozwiązać następujące zadanie:

Mając do dyspozycji drut o długości 100 cm budujemy prostopadłościan

o długościach boków a, b, c. Należy wyznaczyć wszystkie długości boków przy

założeniu , że prostopadłościan będzie posiadał największą objętość.

Długość wszystkich boków opisana jest zgodnie z wzorem :

DD = 4(a+b+c);

Objętość prostopadłościanu

V=abc;

3.3. Utworzyć arkusz obliczający równanie kwadratowe typu: y(x) = ax

2

+bx+c dla

parametrów wejściowych a, b, c. Arkusz powinien:

- obliczać pierwiastki rzeczywiste równania,

- obliczać współrzędne wierzchołka paraboli :

X

w

=-b/2a Y

w

= -∆/4a,

- obliczać wzory Viette’a na sumę i iloczyn:

x

1

+x

x

=-b/a x

1

•x

2

=c/a,

- wykreślić w granicach od x

min

do x

max

powyższą funkcję (parametry x

min

do x

max

poda prowadzący)

3.4. Wygenerować funkcję sinus o złożonych parametrach (częstotliwość, amplituda, faza,

ilość obliczeń itp.). Funkcja sinus musi zostać opisana wartościami w tabeli oraz

przedstawiona na wykresie.

3.5. Wygenerować przebiegi sin(x), sin(3x), sin(5x), sin(7x), gdzie (x=2πft) a następnie

dodać je do siebie i wykreślić wykres sumaryczny. Funkcje napisać w taki sposób aby

10

móc zmieniać częstotliwość, amplitudę, fazę składowych częstotliwościowych oraz

ilość obliczeń. Spróbować wykreślić przebieg jak najbardziej zbliżony do

prostokątnego.

3.6. Wygenerować 30 losowych wartości rzeczywistych w granicach od –5 do 3

i następnie obliczyć:

- wartość maksymalną i minimalną,

- rozstęp,

- wartość średnią (wzór i wbudowana funkcja),

- odchylenie standardowe (wzór i wbudowana funkcja)

(

)

1

1

0

2

−

−

=

∑

−

=

N

x

x

s

N

n

i

.

3.7. Utworzyć arkusz, który przelicza liczby podane w formacie dziesiętnym na format

binarny oraz heksadecymalny.

3.8. Utworzyć arkusz, który przelicza liczby podane w formacie binarnym na format

dziesiętny oraz heksadecymalny.

3.8. Utworzyć arkusz, który przelicza liczby podane w formacie heksadecymalnym na

format dziesiętny oraz binarny (za pomocą wbudowanych funkcji konwertujących

formaty oraz za pomocą formuł.

3.9. Zakładamy, że wpłacamy na lokatę w banku 10000zł. Kwotę tą wpłacamy na 5 lat.

Utwórz arkusz obliczający kwotę, którą otrzymamy z banku po 5 latach.

Oprocentowanie lokaty jest stałe i wynosi 12% w skali roku. A kapitalizacja odsetek

jest wykonywana kwartalnie.

11

4.

Proponowana literatura:

[1] Michalski W., Arkusze kalkulacyjne w zastosowaniach praktycznych : Excel 5, Quattro

Pro 6

, Zakład Nauczania Informatyki Mikom, Warszawa, 1996,

[2] Szymacha I., Ćwiczenia z arkusza kalkulacyjnego Excel, Zakład Nauczania Informatyki

Mikom, Warszawa, 1995,

[3] Łuszczyk E., Kopertowska M., Ćwiczenia z Excel 2003 : wersja polska, Wydawnictwo

Mikom, Warszawa, 2004,

[4] Kandzia T., Klik S., Excel : wersja 7.0 dla WIN '95, Wydawnictwo PLJ, Warszawa, 1996,

[5] Korol J., Excel 5 : krok po kroku, Zakład Nauczania Informatyki Mikom, Warszawa,

1994,

[6] Korol J., Chmielewska A., Excel 97 : krok po kroku, Zakład Nauczania Informatyki

Mikom, Warszawa, 1998,

[7] Chester T., Excel 7 dla Windows 95 : od podstaw do mistrzostwa, Komputerowa Oficyna

Wydawnicza Help, Warszawa, 1996,

[8] Harvey G., Excel 7 dla Windows 95 dla opornych : wersja polska, Oficyna Wydawnicza

Read Me, Warszawa, 1996,

[9] Hoffman F., Tatarkiewicz Ł., Excel 7.0 dla Windows 95, Exit, Warszawa, 1996,

[10] Bucki A. L., Kinlan J., Tucker S., EXCEL 97 : narzędzia praktyczne, Wydawnictwo

Mikom, Warszawa, 1998,

[11] Tor A., Excel 97 : nauka przez ćwiczenia, Tortech, Warszawa, 1998,

[12] Hardy P., Thomsen K., Excel 97 : samouczek dla każdego, Egmont Polska, Warszawa,

1999,

[13] Warner N., Excel 2000, Dom Wydawniczy Rebis, Poznań, 2000,

[14] Uss S., Excel 2000 PL, Komputerowa Oficyna Wydawnicza Help, Warszawa, 1999,

[15] Ivens K., Carlberg C., Excel 2002 PL : księga eksperta, Helion, Gliwice, 2002,

[16] Masłowski K., Excel w praktyce : przykłady i ćwiczenia, Edition 2000, Kraków, 2000,

[17] Stinson C., Dodge M., Microsoft Excel 2002 dla ekspertów, Wydawnictwo RM,

Warszawa, 2003,

[18] Dodge M., Stinson C., Podręcznik Microsoft Excel 2000, Wydawnictwo RM, Warszawa,

1999.