
str. 1
Politechnika Śląska
Wydział: Mechaniczny Technologiczny
Automatyka i Robotyka
Kinematyka i Dynamika Robotów i
Manipulatorów
Projekt:
Budowa Robota: częśd obliczeniowa
Grupa I
Sekcja:
Mateusz Borkowski
Łukasz Chejduk
Jakub Cieloch
Dawid Gach
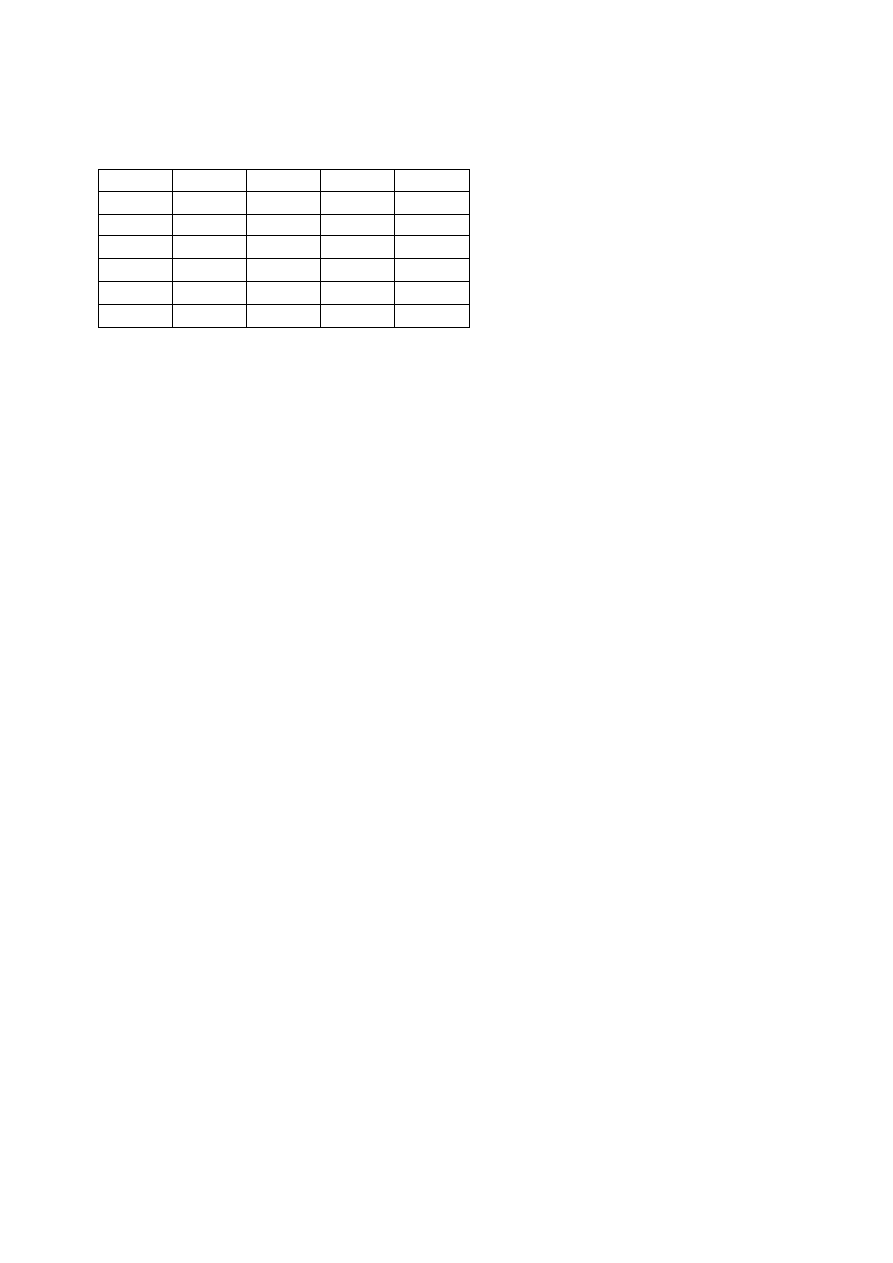
str. 2
Proste zadanie kinematyki
Lp.
Α
i
l
i
Θ
i
d
i
T
1
-
-
0
50
T
2
90
0
-
30
0
-
T
3
-90
0
-
-
180
T
4
90
0
-
-45
0
+90
0
-
T
5
-
100
-
-
1.Transformacja T(0-
1) Rot(z; θ1)*Trans(Z;l1)
2.Transformacja T(1-
2) Rot(x; 90)*Rot(Z;θ2)
3.Transformacja T(2-3) Rot(X;-90)Trans(Z:d3)
4.Transformacja T(3-
4) Rot(X:90)*Rot(Z;θ3+90)
5.Transformacja T(4-5) Trans(X;l5)
T
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
50
1
T
1
T
2
0.866
0
0.5
0
0.5
0
0.866
0
0
1
0
0
0
0
50
1
T
1
T
2
T
3
0.866
0
0.5
0
0
1
0
0
0.5
0
0.866
0
90
1.477
10
15
205.885
1
T
1
T
2
T
3
T
4
0.966
0
0.259
0
0.259
0
0.966
0
0
1
0
0
90
1.477
10
15
205.885
1
T
1
T
2
T
3
T
4
T
5
0.966
0
0.259
0
0.259
0
0.966
0
0
1
0
0
186.593
0
231.766
1

str. 3
1.Transformacja T(0-
1) Rot(z; θ1)*Trans(Z;l1)
l
1
50
1
0
l
2
80
2
6
d
3
180
3
4
l
5
100
RZ
1
cos
1
sin
1
0
0
sin
1
cos
1
0
0
0
0
1
0
0
0
0
1
TZ
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
l
1
1
T
1
RZ
1
TZ
1
T
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
50
1
2.Transformacja T(1-
2) Rot(x; 90)*Rot(Z;θ2)
2
2
RX
2
1
0
0
0
0
cos
2
sin
2
0
0
sin
2
cos
2
0
0
0
0
1
RZ
2
cos
2
sin
2
0
0
sin
2
cos
2
0
0
0
0
1
0
0
0
0
1
T
2
RX
2
RZ
2
T
2
3
2
0
1
2
0
1
2
0
3
2
0
0
1
0
0
0
0
0
1
T
1
T
2
0.866
0
0.5
0
0.5
0
0.866
0
0
1
0
0
0
0
50
1

str. 4
3.Transformacja T(2-3) Rot(X;-90)Trans(Z:d3)
RX
3
1
0
0
0
0
cos
3
sin
3
0
0
sin
3
cos
3
0
0
0
0
1
TZ
3
1
0
0
0
0
1
0
0
0
0
1
0
0
0
d
3
1
T
3
RX
3
TZ
3
T
3
1
0
0
0
0
0
1
0
0
1
0
0
0
180
0
1
3
2
T
1
T
2
T
3
0.866
0
0.5
0
0
1
0
0
0.5
0
0.866
0
90
1.477
10
15
205.885
1
4
2
4.Transformacja T(3-
4) Rot(X:90)*Rot(Z;θ3+90)
RZ
4
cos
3
2
sin
3
2
0
0
sin
3
2
cos
3
2
0
0
0
0
1
0
0
0
0
1
RX
4
1
0
0
0
0
cos
4
sin
4
0
0
sin
4
cos
4
0
0
0
0
1
T
4
RX
4
RZ
4
T
4
2
2
0
2
2
0
2
2
0
2
2
0
0
1
0
0
0
0
0
1
T
1
T
2
T
3
T
4
0.966
0
0.259
0
0.259
0
0.966
0
0
1
0
0
90
1.477
10
15
205.885
1
5.Transformacja T(4-5) Trans(X;l5)
TX
5
1
0
0
0
0
1
0
0
0
0
1
0
l
5
0
0
1
T
5
1
0
0
0
0
1
0
0
0
0
1
0
100
0
0
1
T
1
T
2
T
3
T
4
T
5
0.966
0
0.259
0
0.259
0
0.966
0
0
1
0
0
186.593
0
231.766
1

str. 5
Odwrotne Zadanie Kinematyki
T
2
T
3
T
4
T
5
cos
2
3
cos
2
sin
2
3
sin
2
0
cos
2
3
sin
2
sin
2
3
cos
2
0
cos
2
3
sin
2
sin
2
3
cos
2
0
cos
2
3
cos
2
sin
2
3
sin
2
0
0
1
0
0
100 cos
2
3
cos
2
180 sin
2
100 sin
2
3
sin
2
0
180 cos
2
100 cos
2
3
sin
2
100 sin
2
3
cos
2
1
Aby wyznaczyd pierwszy kąt niewiadomy, decydujemy się na porównanie komórki (1,3)
Po wprowadzeniu kąta do macierzy otrzymujemy :
To
0.966
0
0.259
0
0.259
0
0.966
0
0
1
0
0
186.593
0
231.766
1
Macierz końcowa To=T01*T12*T23*T34
tutaj oznaczona jako To
Oblicz
anie pierwszego kąta t1, czyli teta 1
T
1
1
To
0.966cos
1
cos
1
2
sin
1
2
0.966sin
1
cos
1
2
sin
1
2
0.259
0
0.259cos
1
cos
1
2
sin
1
2
0.259sin
1
cos
1
2
sin
1
2
0.966
0
sin
1
cos
1
2
sin
1
2
cos
1
cos
1
2
sin
1
2
0
0
186.593cos
1
cos
1
2
sin
1
2
186.593sin
1
cos
1
2
sin
1
2
181.766
1
sin
1
cos
1
2
sin
1
2
0
2
sin(θ1)=0 czyli θ1=0
.. To1=T01^(-1) *To
To1
0.966
0
0.259
0
0.259
0
0.966
0
0
1
0
0
186.593
0
181.766
1
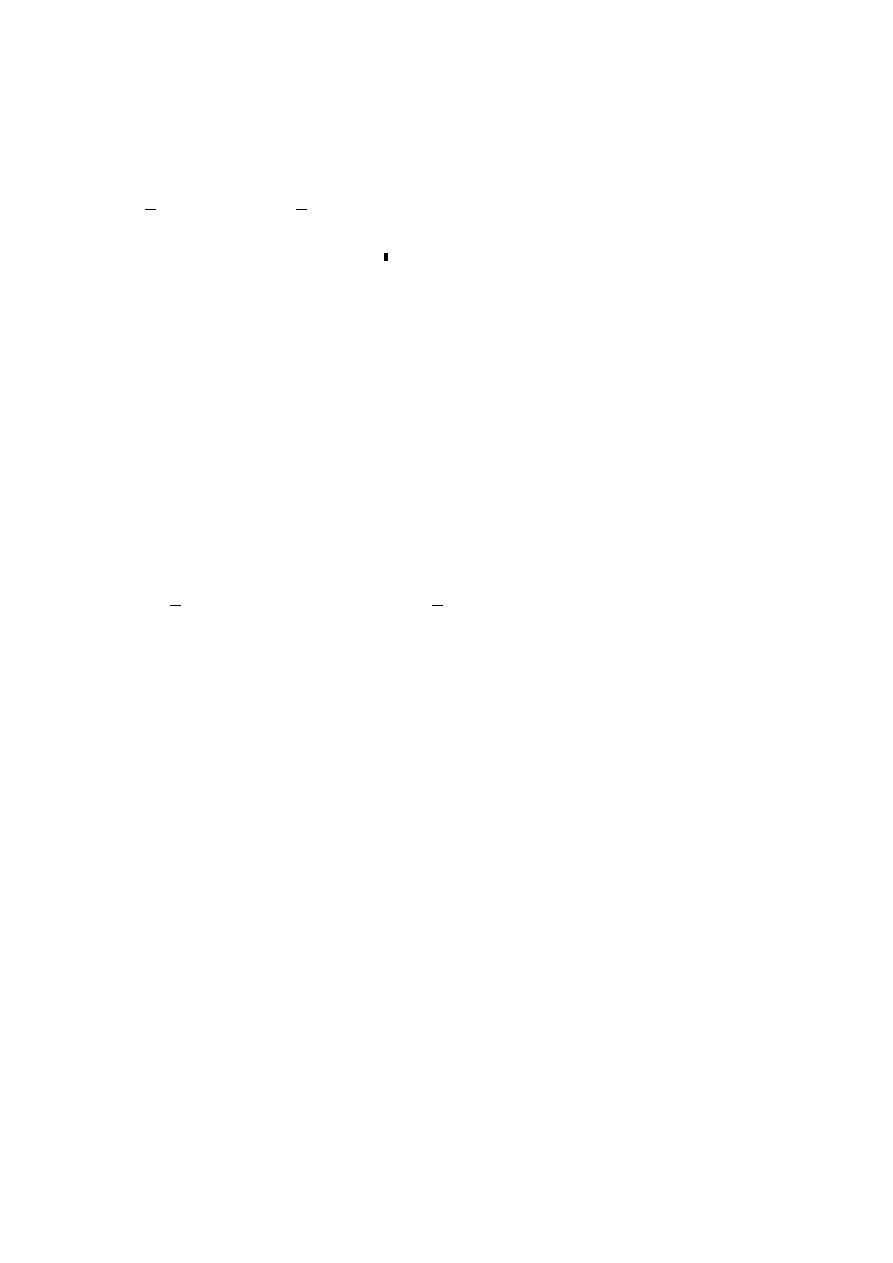
str. 6
Z powyższych macierzy wyznaczamy również zależności między kolejnymi dwoma kątami.
Dla θ
1
=0
.
cos
2
3
cos
2
sin
2
3
sin
2
0.966
2
sin
3
cos
2
cos
3
sin
2
0.966
- sin
3
cos
2
cos
3
sin
2
)=0.966
-sin(
3
+
2
)=0.966
sin(
3
+
2
)=-0.966
3
+
2
=arcsin(-0.966)
3
+
2
=-750
2
=-75o-
3
100 cos
2
3
cos
2
180 sin
2
100 sin
2
3
sin
2
=186.593
100(-sin(
3
))cos(
2
)-100cos(
3
)sin(
2
)-180sin(
2
)=186.593
-100(sin(
3
)cos(
2
)+cos(
3
)sin(
2
))--180sin(
2
)=186.593
-100sin(
3
+
2
)-180sin(
2
)=186.593
2
=-75o-
3
-100sin(-75o-
3
+
3
)-180sin(-75o-
3
)=186.593
-100sin(-75o)-180sin(-75o-
3
)=186.593
-180sin(-75o-
3
)=186.593-96.593//-180
180sin(-75o-
3
)= -0.5
-75o-
3
=arcsin(-0.5)
-75o-
3
=-30o
3
=-45o
3
=-45o
2
=-75o-
3
2
=-75o-(-450)
2
=-300

str. 7
Dla θ
1
=180
o
Manipulator może byd ustawiony w 2 różnych pozycjach aby ostatni człon był w tym samym miejscu,
jednakże dla θ
1
=180
o
wartośd innego kąta θ
2
=120
o
co nie zawiera się w założeniach konstrukcyjnych, i
nie może byd zrealizowane.
100 cos
2
3
cos
2
180 sin
2
100 sin
2
3
sin
2
=-186.593
100(-sin(
3
))cos(
2
)-100cos(
3
)sin(
2
)-180sin(
2
)=-186.593
-100(sin(
3
)cos(
2
)+cos(
3
)sin(
2
))--180sin(
2
)=-186.593
-100sin(
3
+
2
)-180sin(
2
)=-186.593
2
=-75o-
3
-100sin(-75o-
3
+
3
)-180sin(-75o-
3
)=-186.593
-100sin(-75o)-180sin(-75o-
3
)=-186.593
-180sin(-75o-
3
)=-186.593-96.593//-180
180sin(-75o-
3
)= 0.5
-75o-
3
=arcsin(0.5)
-75o-
3
=30o
3
=45o
3
=45o
2
=-75o-
3
2
=-75o-(450)
2
=1200
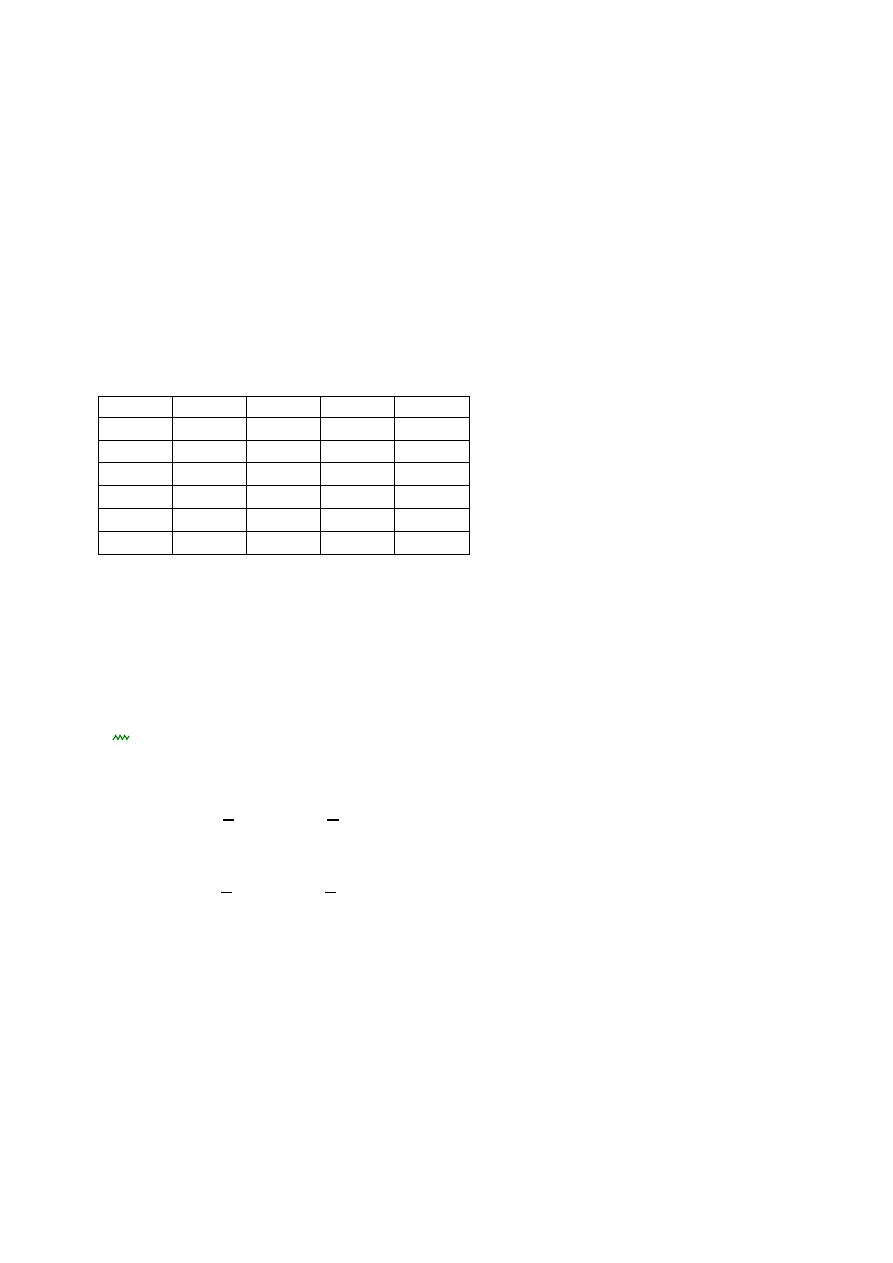
str. 8
Kinematyka Manipulatora metodą macierzową
Kinematykę manipulatora przedstawimy dla dokładnie takiego samego układu manipulatora jak w
prostym i odwrotnym zadaniu kinematyki.
Dla przypomnienia:
Lp.
Α
i
l
i
Θ
i
d
i
T
1
-
-
0
50
T
2
90
0
-
30
0
-
T
3
-90
0
-
-
180
T
4
90
0
-
-45
0
+90
0
-
T
5
-
100
-
-
Postad macierzy kierunkowych:
Macierz R
1
jest nie używana w obliczeniach, ze względu na brak ruchu w parze obrotowej
Postad wektorów przesuwu:
Pozostałe wektory są równe zero.
R
2
cos
2
0
sin
2
sin
2
0
cos
2
0
1
0
R
3
1
0
0
0
0
1
0
1
0
R
4
cos
3
2
0
sin
3
2
sin
3
2
0
cos
3
2
0
1
0
R
5
1
0
0
0
1
0
0
0
1
P
3
0
d
3
0
P
5
l
5
0
0

str. 9
Dobrane wartości prędkości kątowych: w
i
=ω*Z
Z- wersor kierunkowy
=
Prędkości kątowe wynikające z odpowiednich transformacji układu:
Obliczanie prędkości liniowych:
Prędkośd V
3
odpowiada prędkości liniowej punktu B
w
2
0
0
0.5
w
3
0
0
0.5
1
0
0
0
2
R
2
T
1
w
2
0
0
0.5
3
R
3
T
2
0
0.5
0
4
R
4
T
3
w
4
0
0
1
5
R
5
T
4
0
0
1
V
1
0
0
0
V
2
R
2
T
V
1
1
0
0
0
0
0
0
V
3
R
3
T
V
2
2
P
3
V3
0.09
0
0.5
0.09
2
0.5
2
0.508
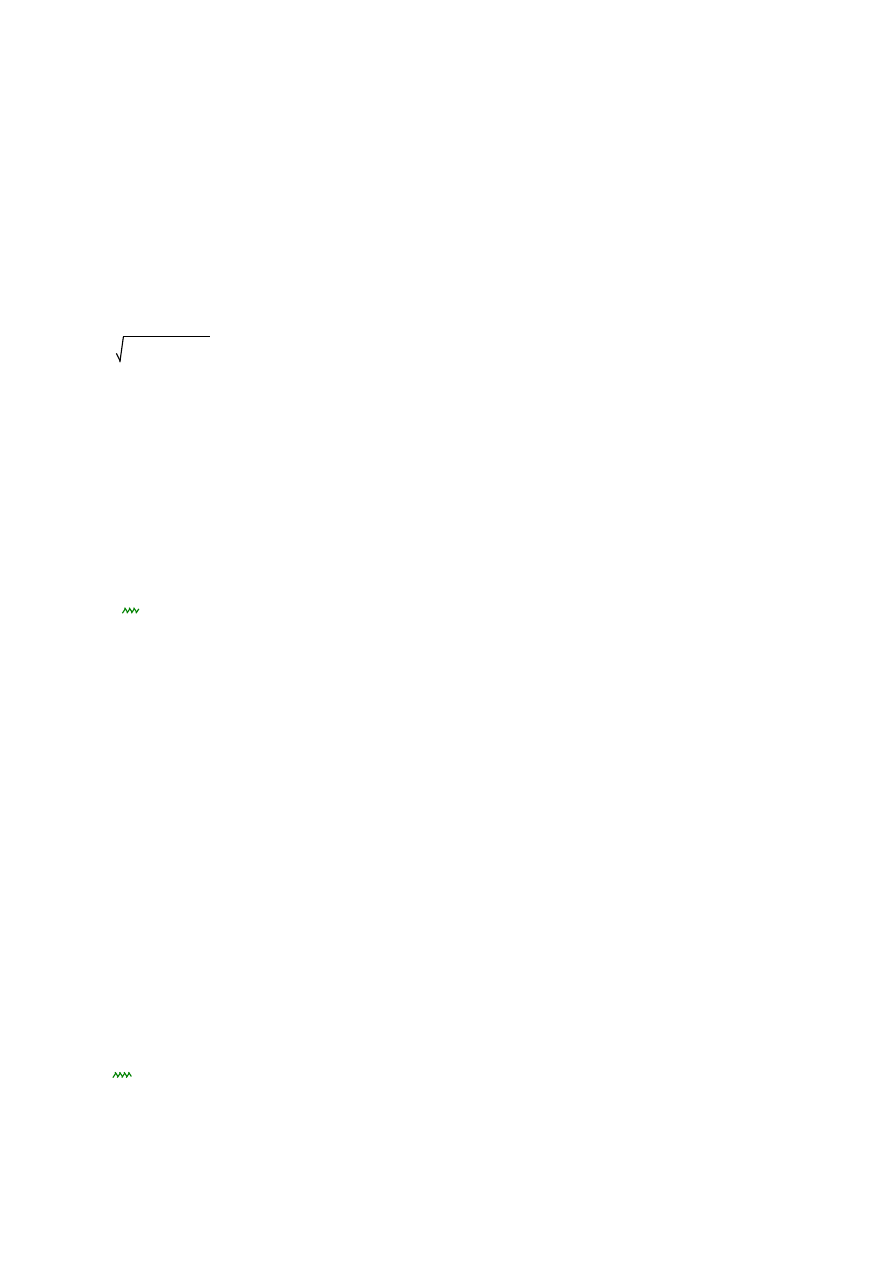
str. 10
Prędkośd V
5
odpowiada prędkości liniowej punktu C
Obliczanie przyspieszeo kątowych.
Przyspieszenie kątowe wynikające z charakterystyki silników:
Obliczanie przyspieszeo liniowych:
Przyspieszenie kątowe wynikające z charakterystyki silników:
V
5
R
5
T
V
( )
4
4
P
5
0
0.417
0.19
0
V
4
R
4
T
V
3
3
0
0
0
0.417
0.29
0
0.417
2
0.19
2
0.458
E
2
0
0
0.1
E
4
0
0
0.1
1
0
0
0
2
R
2
T
1
R
2
T
1
w
2
E
2
0
0
0.1
3
R
3
T
2
0
0.1
0
4
R
4
T
3
R
4
T
3
w
4
E
4
0
0
0.2
5
R
5
T
4
0
0
0.2
A
2
0
0
0.05
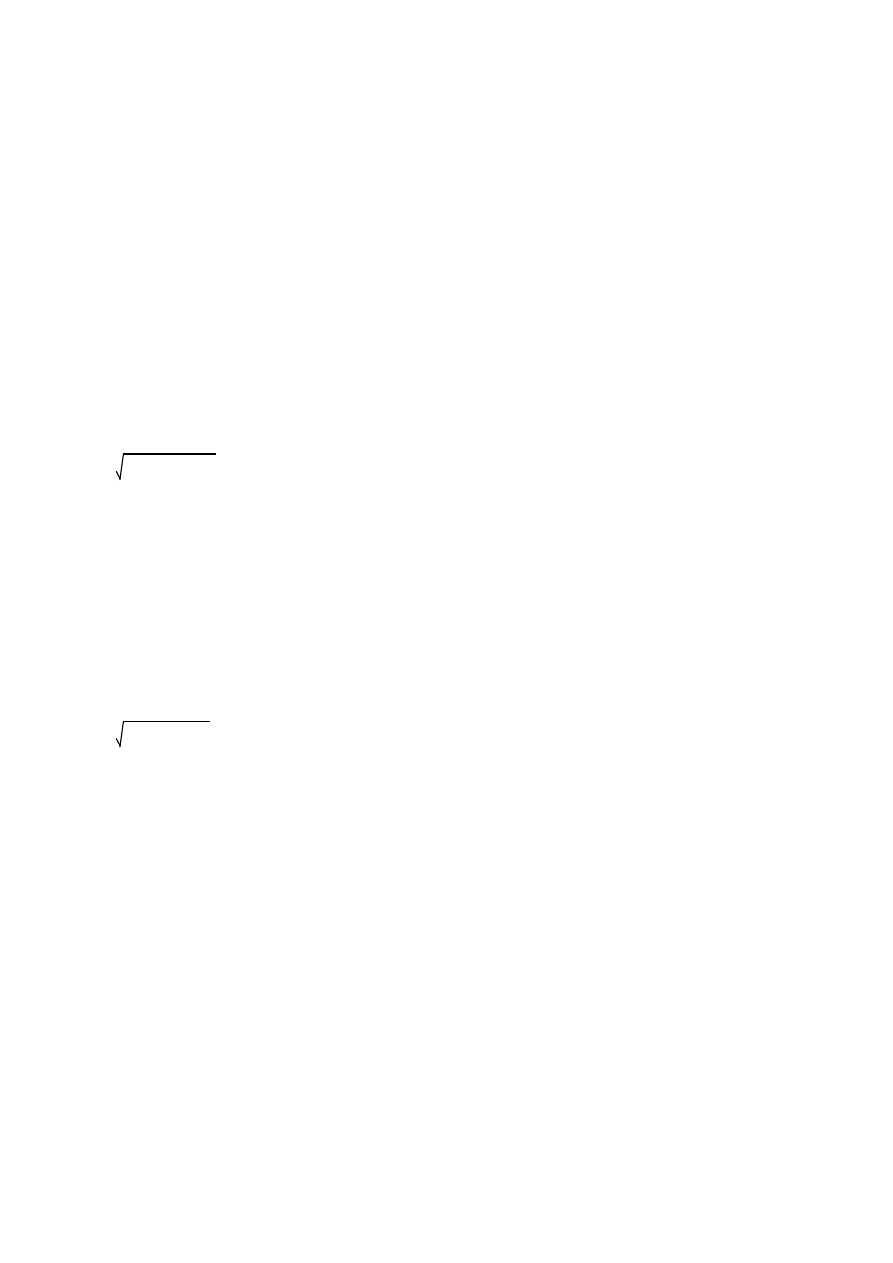
str. 11
Przyspieszenie a
3
odpowiada przyspieszeniu liniowemu punktu B :
Przyspieszenie a
5
odpowiada przyspieszeniu liniowemu punktu C:
a
1
0
0
0
a
2
R
2
T
1
P
2
1
1
P
2
a
1
0
0
0
a
3
R
3
T
2
P
3
2
2
P
3
a
2
2
3
V3
A
2
0.518
0
5
10
3
0.518
2
0.005
2
0.518
a
4
R
4
T
3
P
4
3
3
P
4
a
3
0.37
0.363
0
a
5
R
5
T
4
P
5
4
4
P
5
a
4
2
5
V5
A
5
0.27
0.383
0
0.27
2
0.383
2
0.469

str. 12
Dynamika
Aby wyznaczyd działające siły i momenty w manipulatorze, które będą przybliżone do warunków
panujących w rzeczywistości, należy przyspieszenia liniowe powiększyd o działanie grawitacji
ziemskiej. Aby tego dokonad wystarczy do wektora odpowiadającemu za przyspieszenie liniowe 1
członu dodad g=9.87m/s^2. W takim wypadku przyspieszenia przyjmują postad :
ag
1
0
0
g
0
0
9.87
ag
2
R
2
T
1
P
2
1
1
P
2
ag
1
4.935
8.548
0
ag
3
R
3
T
2
P
3
2
2
P
3
ag
2
2
3
V3
A
2
4.417
0
8.553
ag
4
R
4
T
3
P
4
3
3
P
4
ag
3
2.924
9.171
0
ag
5
R
5
T
4
P
5
4
4
P
5
ag
4
2
5
V5
A
5
2.824
9.151
0
Kolejnym krokiem który należy wykonać jest określenie masy danego ramienia. Ze względu na
wtyczne projektu m
asa musi zostać określona jako masa punktowa znajdująca się na końcu danego
ramienia. Aby, wykonać taki zabieg korzystamy z zależności energi kinetycznej. Wiadomo, że energia
kinetyczna w każdym punkcie danego ciała przyjmuje takie same wartości, dlatego:
m
s
V
sr
2
m
k
V
k
2
2
2
m
k
m
s
V
sr
V
k
V
Gdzie:
M
s
-
Masa środka ciężkości
M
k
- Masa zredukowana na koniec ramienia

str. 13
V
sr
-
prędkość liniowa środka ciężkości ramienia
V
k
-
prędkość liniowa końcówki ramienia: w projekcie : V
B
i V
C
Aby wyznaczyć prędkość liniową środka ciężkości ramienia, należy określić położenie środka
ciężkości. W naszym przypadku, środek ciężkości znajduje się w połowie ramienia, czyli :
Położenie środka ciężkości dla ramienia pierwszego:
Ps
3
1
2
P
3
0
0.09
0
Do wyznaczenia prędkości liniowej tegoż ramienia użyjemy gotowych wzorów:
Vs
3
R
3
T
V
2
2
Ps
3
V3
0.045
0
0.5
Położenie środka ciężkości dla ramienia drugiego:
Ps
5
1
2
P
5
0.05
0
0
Wyznaczenie prędkości liniowej środka ciężkości ramienia drugiego, wykonujemy adekwatnie jak w
poprzednim kroku:
Vs
5
R
5
T
V
( )
4
4
Ps
5
0
0.417
0.24
0
Zakładamy, że masy poszczególnych ramion przyjmują wartości:
M
3
=0.3 kg, m
5
=0.25kg
Po skorzystaniu z zale
żności na równowagę energii kinetycznej, otrzymujemy wartości mas:
mk
3
m
3
V
3
Vs
3
0.304
mk
5
m
5
V
5
Vs
5
0.238

str. 14
Wyznaczanie sił działających w manipulatorze.
Do wyznaczenia sił skorzystamy ze wzoru :
1
1
1
1
1
i
i
i
i
i
a
m
F
Gdzie :
F- siła
M
i+1
-masa aktualnego członu, zredukowana do kooca członu
A
i+1
–przyspieszenie liniowe aktualnego członu, powiększone o wartośd przyspieszenia ziemskiego.
F
1
m
1
ag
1
0
0
0
F
2
m
2
ag
2
0
0
0
F
3
mk
3
ag
3
1.343
0
2.6
F
4
m
4
ag
4
0
0
0
F
5
mk
5
ag
5
0.672
2.178
0
Siły napędowe
Aby obliczyd siły napędowe, skorzystamy z wzoru:
i
i
i
i
i
i
i
i
F
f
R
f
1
1
1
Gdzie,
f
i
- siła napędowa
R
i
- macierz przekształcenia dla danego członu
F
i
- siła działająca na dany człon.

str. 15
f
5
F
5
0.935
3.029
0
f
4
R
5
f
5
F
4
1.903
6.065
0
f
3
R
4
f
4
F
3
4.255
0
8.174
f
2
R
3
f
3
F
2
6.722
12.448
0
f
1
R
2
f
2
F
1
0.402
0
19.076
Momenty napędowe:
n
5
N
5
P
5
F
5
0
0
0.303
n
4
N
4
R
5
n
5
P
4
F
4
P
5
R
5
f
5
0
0
0.606
n
3
N
3
R
4
n
4
P
4
F
3
P
4
R
4
f
4
0
0.606
0
n
2
N
2
R
3
n
3
P
2
F
2
P
3
R
3
f
3
0
0
1.372
n
1
N
1
R
2
n
2
P
2
F
1
P
2
R
2
f
2
0
1.372
0
N
5
0
0
0
N
4
0
0
0
N
3
0
0
0
N
2
0
0
0
N
1
0
0
0
Wyszukiwarka
Podobne podstrony:
kosta wersja gotowa do druku
projekt wersja niemiecka
Cz M Struktury Zespolow Projektowych wersja 2011 egz
projekt wersja elektroniczna
REGULAMIN ZALICZENIA ĆWICZEŃ PROJEKTOWYCH wersja nowa, Studia, Technologia i Organizacja Robót Budow
Filozofia (projekt) wersja dla studentów
Podstawy Mechaniki i Konstrukcji Maszyn (Projekt 1 wersja 1)
Podstawy Mechaniki i Konstrukcji Maszyn (Projekt 1 wersja 2)
seminarium4 wersja gotowa
Nasz projekcik WERSJA?ta
PROJEKT I 2 wersja, Nasypy
projekt wersja 2
projekt wersja polska
projekt wersja okrojona
Projekt wersja ostateczna
nasz projekt13 2 wersja
więcej podobnych podstron