Atomowa teoria dyfuzji
Efekt izotopowy
Zależność współczynnika dyfuzji od ciśnienia
Objętość aktywacji
Korelacje pomiędzy dyfuzją a innymi własnościami
Efekt izotopowy (efekt masy)
W przypadku badania dyfuzji własnej, gdy znacznikiem jest rzadki izotop pierwiastka występującego
w sieci krystalicznej (po to, żeby go odróżnić od innych atomów tego pierwiastka), to jest on identyczny
chemicznie z atomami sieci, ale różni się od nich masą, co ma wpływ na wartość współczynnika dyfuzji.
Współczynnik dyfuzji znacznika izotopowego oznacza się jako
D*
.
Niech dyfundują dwa izotopy tego samego pierwiastka o masach
m
α
i
m
β
, Ich współczynniki dyfuzji
oznacza się
i . Różnica mas dyfundujących izotopów tego samego pierwiastka ma przede
wszystkim znaczenie dla częstotliwości drgań tych atomów w sieci i . Inne parametry, takie jak
energia aktywacji czy współczynnik korelacji w bardzo niewielkim stopniu zależą od masy.
Można wykazać (używając modelu oscylatora harmonicznego), że:
Ta zależność prowadzi do następującego wyrażenia:
- parametr efektu izotopowego
ΔK
–
współczynnik energii kinetycznej
– jest to ułamek całkowitej energii kinetycznej przeskakującego
atomu w punkcie siodłowym w odniesieniu do całkowitej energii kinetycznej związanej z ruchem wszystkich
atomów w kierunku przeskoku (tzn. przeskakujący atom oddziałuje z innymi atomami i w związku z tym
część jego energii kinetycznej jest zużywana na pobudzenie sąsiadujących atomów do ruchu).
W przypadku mechanizmu międzywęzłowego
ΔK=1
, a w przypadku mechanizmu wakancyjnego:
gdzie
Z
– liczba najbliższych sąsiadów
– objętość związana z powstaniem jednej wakancji
*
Dα
*
D
β
0
α
ν
0
β
ν
α
ν
α
ν
β
β
m
m
0
0
≈
E
K
f
m
/
m
1
*
D
/
*
D
m
/
m
1
*
D
/
*
D
≡
⋅
≈
−
≈
−
Δ
β
α
α
β
α
β
α
β
1
1
3
2
1
−
⎥⎦
⎤
⎢⎣
⎡
−
⋅
+
≈
)
V
(
/
Z
K
F
V
Δ
Δ
F
V
V
Δ
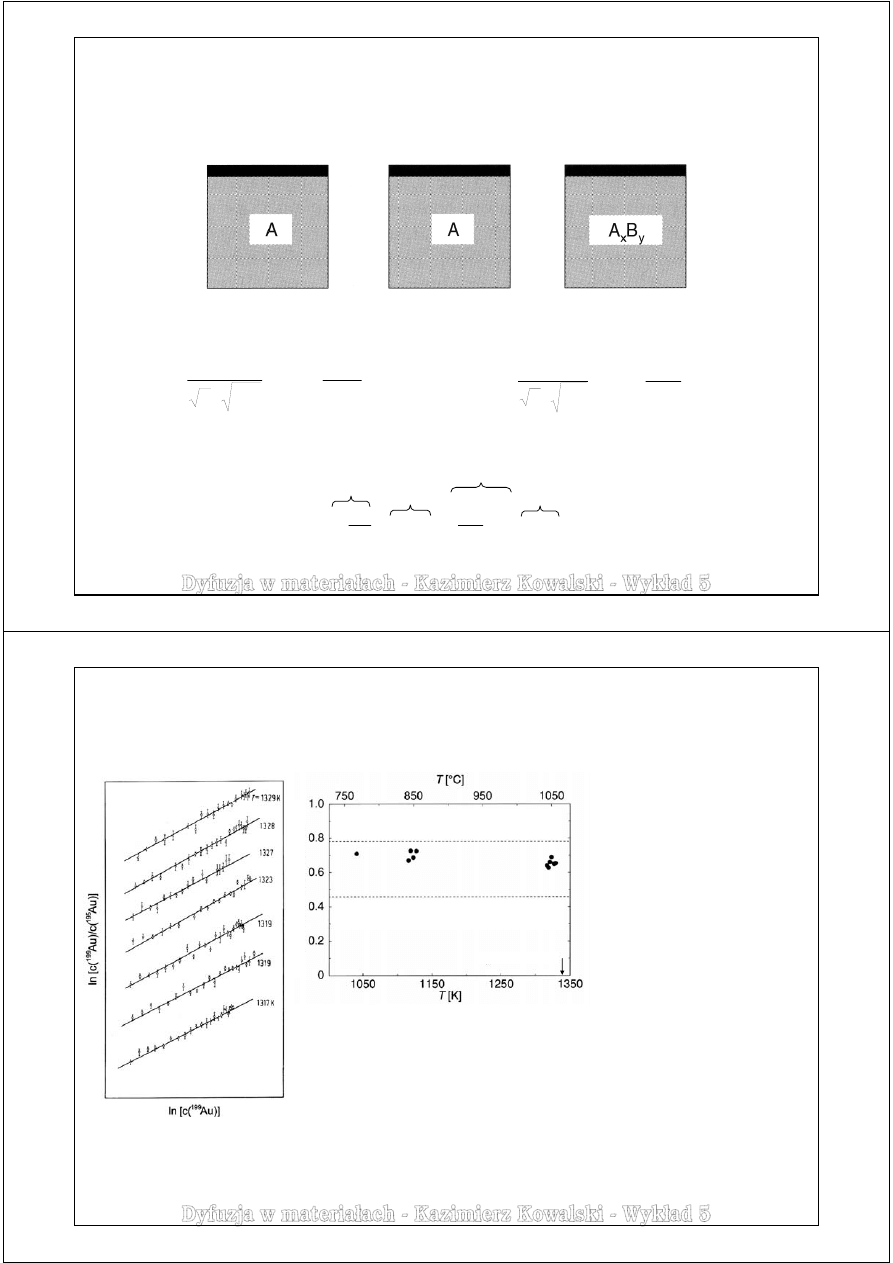
Efekt izotopowy (efekt masy) - eksperyment
Po wygrzewaniu dyfuzyjnym rozkład dyfundujących izotopów
α
i
β
wewnątrz próbki opisuje funkcja Gaussa:
Po podzieleniu obu rozwiązań stronami, zlogarytmowaniu wyniku dzielenia i wyeliminowaniu zmiennej
x
2
(np z pierwszego równania) otrzymuje się taką zależność:
Jest to zależność liniowa typu
y(z) = a + bz
, w której współczynnik nachylenia prostej
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⋅
⋅
=
t
*
D
4
x
exp
t
*
D
M
c
2
α
α
α
α
π
oraz
*
Aα
*
A
β
oraz
*
Bα
*
B
β
oraz
*
Bα
*
B
β
oraz
*
Cα
*
C
β
oraz
*
Aα
*
A
β
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⋅
⋅
=
t
*
D
4
x
exp
t
*
D
M
c
2
β
β
β
β
π
Dyfuzja własna (samodyfuzja)
(self-diffusion)
Heterodyfuzja
(heterodiffusion)
Dyfuzja własna (A i B)
Heterodyfuzja (C)
α
α
α
β
β
c
ln
1
*
D
*
D
const
c
c
ln
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
1
*
D
/
*
D
b
−
=
β
α
y
a
b
z
Przed wygrzewaniem na powierzchnię próbki nanosi się
cienką warstwę dwóch izotopów tego samego pierwiastka
Efekt izotopowy (efekt masy) - eksperyment
Stężenie izotopów było wyznaczane
metodami radioizotopowymi.
Przykład badań przeprowadzonych dla dyfuzji własnej złota w monokrysztale złota.
Do badania użyto promieniotwórczych izotopów
195
Au oraz
199
Au.
Złoto występujące w stanie naturalnym składa się prawie w 100% z izotopu
197
Au.
Badania Harta i współpracowników, 1978
Wyznaczony współczynnik
korelacji wskazuje na
przeważającą rolę mechanizmu
wakancyjnego oraz pewien udział
mechanizmu diwakancyjnego,
który wzrasta wraz z temperaturą.
W przypadku dyfuzji atomów złota
poprzez mechanizm
międzywęzłowy:
Parametr efektu izotopowego
Współczynnik korelacji f = 0,4579
Mechanizm diwakancyjny
Mechanizm wakancyjny
Współczynnik korelacji f = 0,7815
Badanie efektu izotopowego pozwala wyznaczyć
eksperymentalnie współczynnik korelacji, którego
znajomość z kolei pozwala określić jaki mechanizm
atomowy odpowiada za dyfuzją danego pierwiastka
w danym materiale.
9
,
0
K
≈
Δ
T
t
(Au) = 1337,5 K
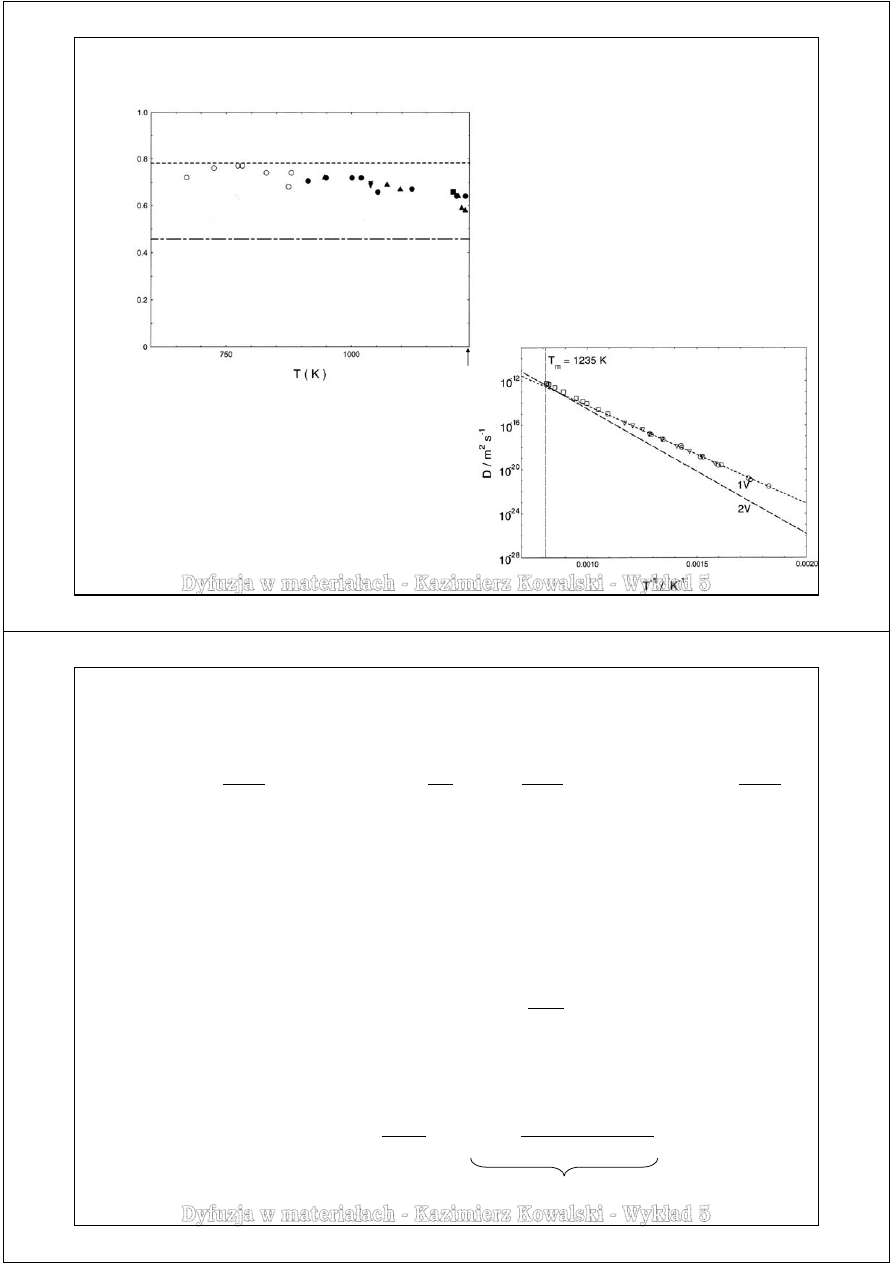
Efekt izotopowy (efekt masy) - eksperyment
Przykład badań przeprowadzonych dla dyfuzji własnej srebra.
Wyznaczony współczynnik korelacji wskazuje
na przeważającą rolę mechanizmu
wakancyjnego oraz pewien udział
mechanizmu diwakancyjnego, który wzrasta
wraz z temperaturą i jest już znaczny tuż
przed temperaturą topnienia.
W przypadku dyfuzji atomów srebra poprzez
mechanizm międzywęzłowy:
Parametr efektu izotopowego E = f·K
Δ
Współczynnik korelacji f = 0,4579
Mechanizm diwakancyjny
Mechanizm wakancyjny
Współczynnik korelacji f = 0,7815
9
,
0
K
≈
Δ
Kompilacja H. Mehrera (2007) wyników podanych
przez różnych autorów, co pokazują różne symbole.
T
t
(Ag) = 1234,9 K
Temperaturowa zależność współczynnika dyfuzji
własnej srebra – interpretacja danych w oparciu
o model wakancyjny i diwakancyjny.
Wpływ diwakancji jest widoczny dopiero w
najwyższych temperaturach
Backus i inni, 1978
Zależność współczynnika dyfuzji od ciśnienia
Zależność współczynnika dyfuzji od ciśnienia wynika bezpośrednio z zależności temperaturowej
(Arrheniusa) współczynnika dyfuzji:
Ale:
ΔG = ΔH - TΔS = ΔU + pΔV - TΔS ΔH = ΔU + pΔV
W dotychczasowych rozważaniach dotyczących dyfuzji milcząco zakładano, że proces dyfuzji zachodzi
przy stosunkowo niewielkich ciśnieniach będących rzędu atmosfery fizycznej. W takich warunkach
rzeczywiście czynnik
pΔV
może być pominięty (mała ściśliwość ciał stałych) i wówczas
ΔH ≈ ΔU
.
Przy zastosowaniu bardzo wysokich ciśnień nie można już zaniedbać ściśliwości ciała stałego.
Z równania na
ΔG
wynika, że przy stałej temperaturze:
ΔV
– objętość aktywacji dyfuzji.
Zatem z zależności temperaturowej współczynnika dyfuzji wynika, że przy
T = const
:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
−
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
−
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
−
⋅
=
⋅
⋅
⋅
⋅
⋅
⋅
=
T
k
G
exp
T
k
H
exp
k
S
exp
T
k
Q
exp
D
B
0
2
B
B
0
2
B
0
a
g
f
a
g
f
D
Δ
Δ
Δ
ν
ν
T
p
G
V
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
Δ
Δ
p
)
a
g
f
ln(
T
k
p
D
ln
T
k
V
0
2
B
T
B
∂
⋅
⋅
⋅
∂
⋅
⋅
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⋅
⋅
−
=
ν
Δ
składowa korygująca
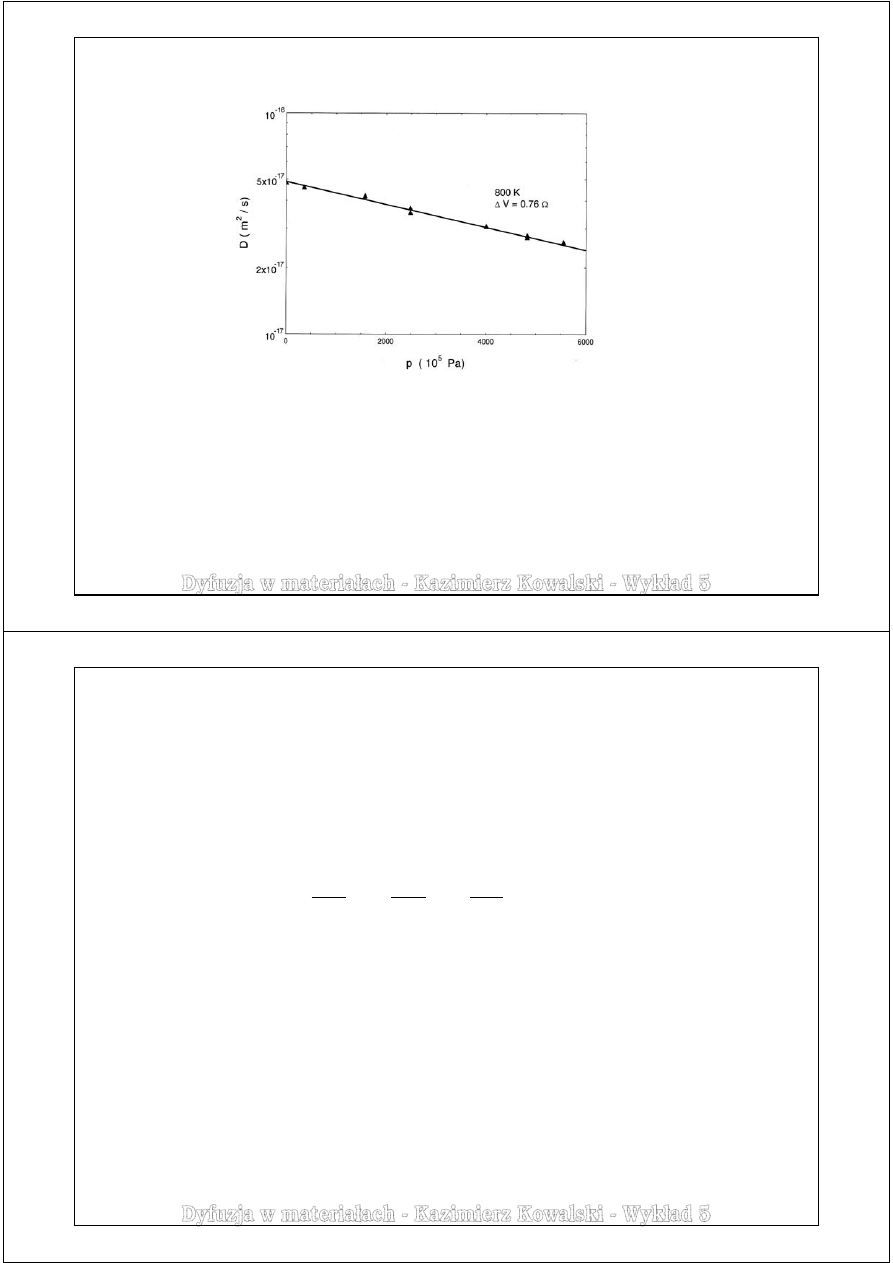
Zależność współczynnika dyfuzji od ciśnienia
Przykład danych eksperymentalnych:
Dyfuzja własna złota
198
Au w monokrysztale Au
Badania Wernera i Mehrera (1983)
Nachylenie prostej
ln(D)
w funkcji
p
pozwala wyznaczyć pierwszą składową we wzorze na
ΔV
.
Druga składowa – korygująca, może być wyznaczona z następującego przybliżenia:
gdzie:
κ
T
– współczynnik ściśliwości izotermicznej
γ
G
– parametr Grüneisena – określa zmianę
częstotliwości drgań atomów w sieci
krystalicznej przy zmianie objętości
Czynnik korygujący przyjmuje wartości rzędu ~ 0,01÷0,03
Ω
. Jest to wartość znacznie mniejsza od wartości
otrzymywanej z nachylenia prostej
ln(D)
w funkcji
p
. Zatem, biorąc pod uwagę dokładność z jaką można
eksperymentalnie wyznaczać tę wartość, czynnik korygujący może być pomijany.
G
T
B
T
k
γ
κ
⋅
⋅
⋅
≈
korygująca
składowa
Ω
- objętość atomowa
Zależność współczynnika dyfuzji od ciśnienia
Objętość aktywacji – dyfuzja własna
W przypadku dyfuzji zachodzącej według mechanizmu międzywęzłowego:
ΔG = G
M
W przypadku mechanizmu wakancyjnego:
ΔG = G
M
+ G
F
Gdzie indeksy
M
i
F
oznaczają energię swobodną Gibbsa ruchu (M - migracji) atomu
i tworzenia (F - formowania) się wakancji.
Zatem objętość aktywacji można podzielić na dwie składowe (mechanizm wakancyjny):
gdzie:
V
M
– objętość aktywacji związana z ruchem atomu
V
F
– objętość aktywacji związana z utworzeniem się wakancji
F
M
T
F
T
M
T
V
V
p
G
p
G
p
G
V
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
Δ
Δ
Objętość aktywacji dyfuzji związana z formowaniem się defektów
V
F
.
Mechanizm wakancyjny:
Mechanizm międzywęzłowy:
„Sztywna” sieć
Rzeczywista sieć „Sztywna” sieć
Rzeczywista sieć
Zależność współczynnika dyfuzji od ciśnienia
Objętość aktywacji – dyfuzja własna
relaksacja sieci
relaksacja
sieci
Ω
=
F
V
V
relaks
V
F
V
V
V
−
=
Ω
Ω
−
=
F
i
V
relaks
F
i
i
V
V
+
−
=
Ω
F
V
V
- objętość potrzebna do utworzenia jednej wakancji
F
i
V
- objętość potrzebna do umiejscowienia jednego atomu w pozycji międzywęzłowej
relaks
V
V
- objętość relaksacji sieci związanej z utworzeniem jednej wakancji
relaks
i
V
- objętość relaksacji sieci związanej z umiejscowieniem jednego atomu
w pozycji międzywęzłowej
Objętość aktywacji dyfuzji związana z przemieszczaniem się atomów
V
M
.
Mechanizm wakancyjny:
Mechanizm międzywęzłowy:
Atom w pozycji
Atom w pozycji
Atom w pozycji
Atom w pozycji
równowagi
siodłowej
równowagi
siodłowej
Zależność współczynnika dyfuzji od ciśnienia
Objętość aktywacji – dyfuzja własna
przeskok atomu
~ 10
-12
s
M
V
V
- objętość aktywacji przeskoku atomu w przypadku mechanizmu wakancyjnego
M
V
i
przeskok atomu
~ 10
-12
s
- objętość aktywacji przeskoku atomu w przypadku mechanizmu międzywęzłowego
Objętość aktywacji związana z ruchem (przeskokiem) atomu
V
M
jest to różnica między objętością
otoczenia atomu w punkcie siodłowym a położeniem równowagi.
Zależność współczynnika dyfuzji od ciśnienia
Objętość aktywacji – dyfuzja własna – przykład eksperymentu
Badania eksperymentalne przeprowadzone dla niektórych metali np. złota i platyny wykazały , że
wartości objętości aktywacji ruchu atomów mają wartości rzędu
V
M
≈ 0,15
Ω
.
Całkowita wartość objętości aktywacji dyfuzji w przypadku metali o gęstym upakowaniu atomów jest
najczęściej zawarta w przedziale
ΔV ≈ 0,6 ÷ 0,9
Ω
.
Zatem, o wielkości objętości aktywacji dyfuzji w przypadku mechanizmu wakancyjnego decyduje
przede wszystkim objętość związana z formowaniem się wakancji
V
F
:
V
F
>> V
M
Eksperymentalnie wyznaczona wartość objętości aktywacji
ΔV
dyfuzji własnej złota w zależności od temperatury.
Kompilacja H. Mehrera (2007) wyników badań kilku autorów.
Stała wartość objętości aktywacji dyfuzji w funkcji temperatury
świadczy o tym, że tylko jeden mechanizm dyfuzji jest
odpowiedzialny za dyfuzję własną złota.
T
t
(Au) = 1337,5 K
W przypadku dyfuzji obcych atomów jakiejś domieszki pojawia się dodatkowy czynnik związany
z oddziaływaniem przyciągającym lub odpychającym pomiędzy atomami domieszki a wakancjami.
Wówczas entalpia swobodna Gibbsa potrzebna do powstania jednej wakancji jest powiększana lub
pomniejszana w zależności od typu oddziaływania przez mniejszą od zera lub większą od zera entalpię
swobodną Gibbsa
wynikającą z oddziaływania pomiędzy wakancją a atomem domieszki.
Współczynnik dyfuzji ma znaną już postać:
Pamiętając, że:
Otrzymuje się wzór na całkowitą objętość aktywacji dyfuzji domieszki:
Zależność współczynnika dyfuzji od ciśnienia
Objętość aktywacji – dyfuzja domieszek przy ich niedużym stężeniu (heterodyfuzja)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
T
k
G
exp
T
k
G
G
exp
ga
f
D
B
M
B
B
F
V
2
0
2
2
2
ν
- objętość związana z utworzeniem pary atom domieszki - wakancja
B
F
V
V
V
−
W przypadku dyfuzji międzywęzłowej małych atomów jak: C, N, O objętość aktywacji dyfuzji wynosi:
Dyfuzja międzywęzłowa małych atomów domieszek charakteryzuje się bardzo małymi wartościami
objętości aktywacji, np. w przypadku dyfuzji C i N w
α
-Fe wynoszą -0,08
Ω
i +0,05
Ω
.
Dyfuzja międzywęzłowa domieszek jest zatem praktycznie niezależna od ciśnienia.
F
V
G
B
G
T
p
G
V
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
=
Δ
Δ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⋅
⋅
−
+
−
=
p
f
ln
ln
T
k
V
V
V
V
2
B
M
2
B
F
V
2
Δ
C
2
- zależność ciśnieniowa współczynnika korelacji
M
2
2
V
V
=
Δ
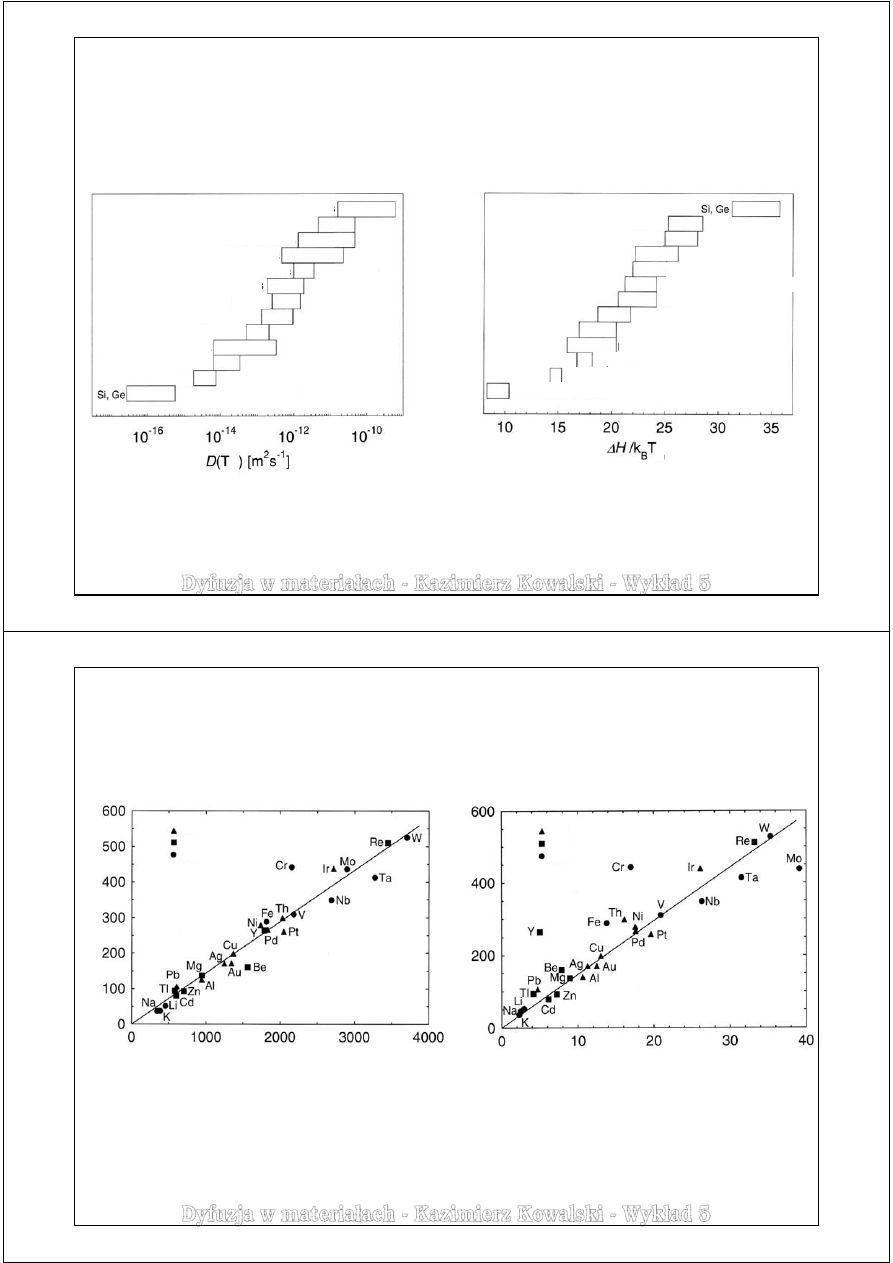
Korelacje między dyfuzją a innymi własnościami materiałów
Związek własności dyfuzyjnych materiałów z ich temperaturą i entalpią topnienia
Takie termodynamiczne własności materiałów jak temperatura i ciepło topnienia albo moduł sprężystości
wynikają ze stabilności danej fazy krystalicznej. Zatem, parametry dyfuzji własnej w tych materiałach, jako
zależne od własności sieci krystalicznej mogą być powiązane z tymi własnościami.
Wielkość entalpii dyfuzji odniesionej do energii w temperaturze
topnienia dla kilku grup materiałów o różnej strukturze krystalicznej
Wielkość współczynnika dyfuzji w temperaturze topnienia
dla kilku grup materiałów o różnej strukturze krystalicznej
RPC metale ziem rzadkich
RPC metale alakliczne
węgliki metali
RPC metale przejściowe
metale o strukturze heksagonalnej
RSC metale
grafit
halogenki metali alkalicznych
ind
tlenki
struktura tetragonalna
lód
t
RPC metale ziem rzadkich
RPC metale alkaliczne
węgliki
RPC metale przejściowe
RSC metale
grafit
halogenki metali alkalicznych
struktura trójskośna
tlenki
struktura tetragonalna
lód
metale o strukturze heksagonalnej
t
Brown i Ashby, 1980
Brown i Ashby, 1980
Niewielkie różnice wartości współczynnika
dyfuzji w temperaturze topnienia materiałów o tej
samej strukturze krystalicznej i takim samym
wiązaniu chemicznym wynikają z tego, że
wartości
D
0
i
ΔH/k
B
T
t
są do siebie bardzo
zbliżone.
Zasada van Liempta:
ΔH ≈ K
1
·T
t
,
która
poprzez zasadę Troutona
(
S
t
= H
t
/T
t
≈ 9,6 J/mol
) prowadzi do zależności:
ΔH ≈ (K
1
/S
t
)·H
t
≡ K
2
·H
t
gdzie
K
1
i
K
2
są stałymi w danej grupie
materiałów.
Korelacje między dyfuzją a innymi własnościami materiałów
Związek własności dyfuzyjnych materiałów z ich temperaturą i entalpią topnienia
Temperatura topnienia T
t
/ K
Entalpia topnienia H
t
/ kJmol
-1
Entalpia akty
w
acji
Δ
H / kjmol
-1
Entalpia akty
w
acji
Δ
H / kjmol
-1
Wartość entalpii (ciepła) dyfuzji własnej
w metalach o gęstym upakowaniu atomów
w funkcji temperatury topnienia
Wartość entalpii (ciepła) dyfuzji własnej
w metalach o gęstym upakowaniu atomów
w funkcji entalpii (ciepła) topnienia
Tiwari i inni, 2005
Tiwari i inni, 2005
Z nachylenia prostych wyznaczonych metodą regresji
liniowej wyznaczono wartości stałych
K
1
i
K
2
dla
metali o gęstym upakowaniu atomów:
K
1
≈ 146 Jmol
-1
K
-1
K
2
≈ 14,8
RSC
RPC
HZ
RSC
RPC
HZ
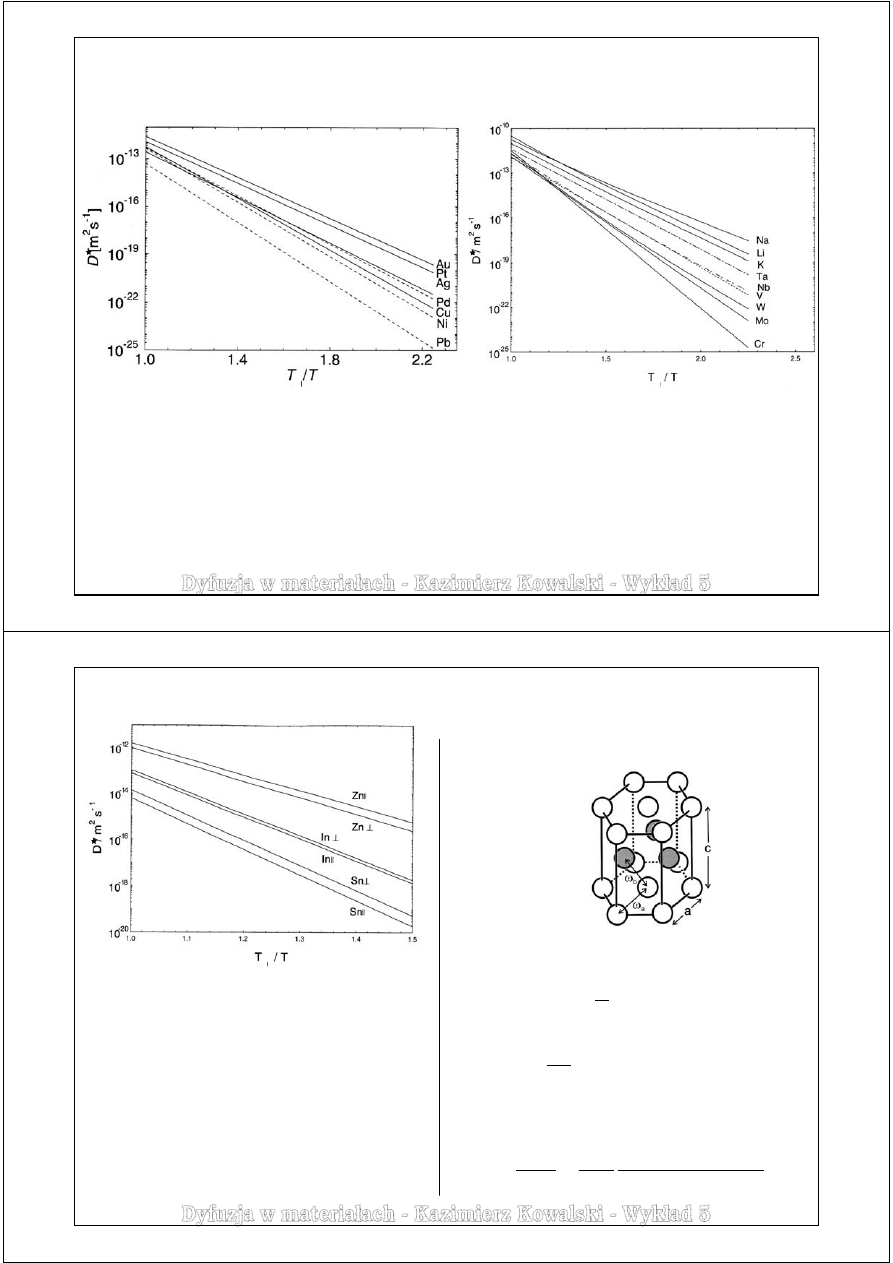
Przykłady danych dyfuzyjnych
Metale o strukturze regularnej – dyfuzja własna
Metale o strukturze RSC
D(T
t
) = 10
-12
÷10
-13
m
2
s
-1
Q = ΔH = (15÷19)·k
B
·T
t
kilka10
-6
m
2
s
-1
< D
0
< kilka10
-4
m
2
s
-1
Metale o strukturze RPC
t
t
D(T
t
) = 10
-11
÷10
-12
m
2
s
-1
Znacznie większy rozrzut wartości
współczynników dyfuzji w danej temperaturze
zredukowanej niż w przypadku metali RSC
Ogólna zasada dotycząca dyfuzji własnej obowiązująca w metalach mających strukturę RSC lub RPC:
W danej temperaturze zredukowanej T
t
/T w każdej grupie układu okresowego pierwiastków
dyfuzja własna pierwiastków lżejszych jest wolniejsza od dyfuzji własnej pierwiastków cięższych
W przypadku sieci HZ współczynniki dyfuzji dane
są następującymi wzorami:
Współczynnik anizotropii:
b
b
V
2
f
c
c
4
3
*
D
ω
=
||
Przykłady danych dyfuzyjnych
Metale – dyfuzja własna – anizotropia
W kryształach tetragonalnych (np. In, Sn)
i heksagonalnych (np. Zn) osie główne dyfuzji
charakteryzują się zależnością:
D
1
= D
2
≠ D
3
czyli wykazują jednoosiową symetrię dyfuzji
wzdłuż głównego kierunku dyfuzji
a
3
.
Wyróżnia się zatem dwa współczynniki dyfuzji:
D*
||
- współczynnik dyfuzji w kierunku równoległym
do tej osi
D*
⊥
- w kierunku prostopadłym
W strukturze tetragonalnej:
D*
|| < D*⊥
W strukturze heksagonalnej:
D*
|| > D*⊥
Anizotropia w materiałach
o strukturze HZ (heksagonalnej zwartej)
t
||
(
)
b
b
a
a
V
2
f
f
3
c
2
a
*
D
ω
ω
+
=
⊥
⊥
⊥
(
)
b
b
b
b
a
a
2
2
f
f
f
3
c
3
a
2
*
D
*
D
A
ω
ω
ω
+
=
≡
⊥
⊥
⊥
||
||
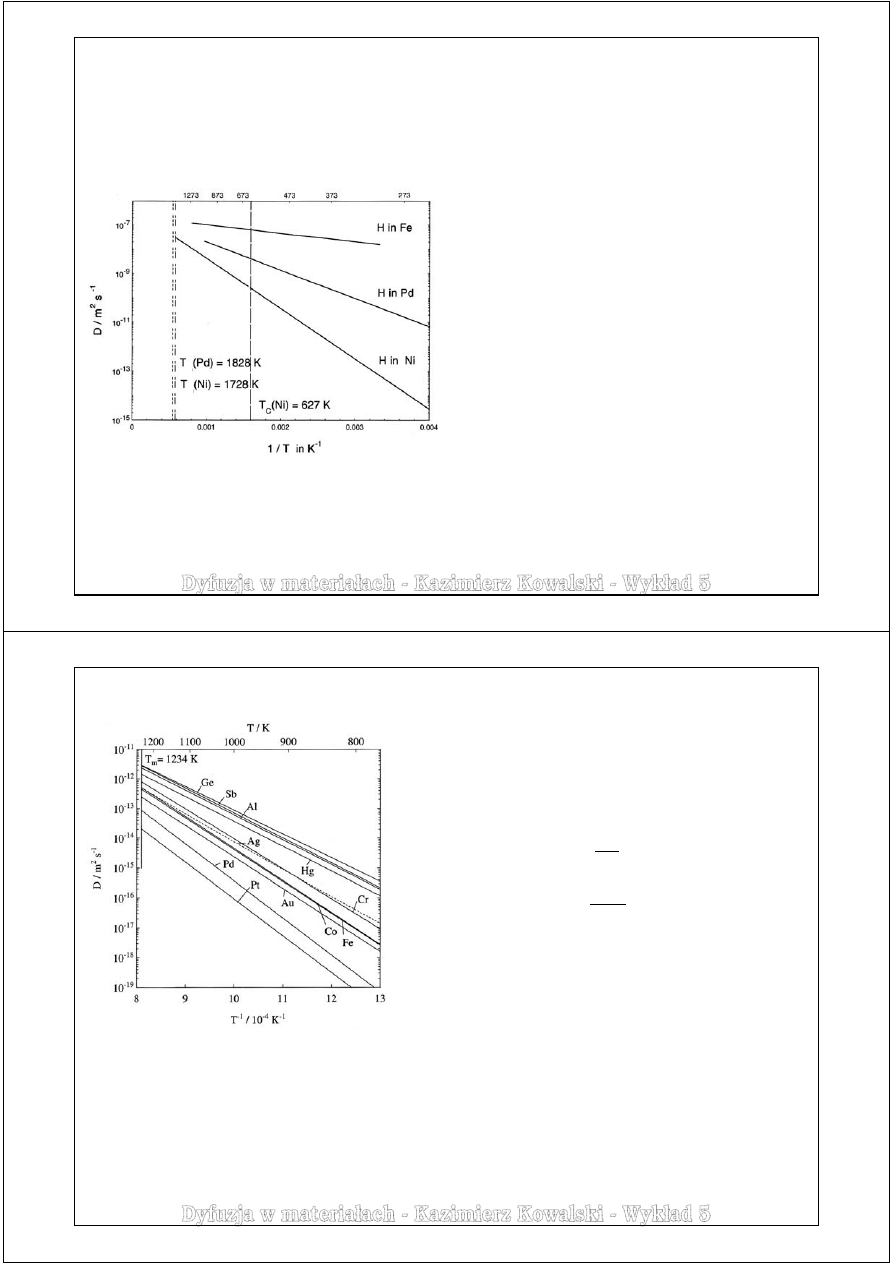
Przykłady danych dyfuzyjnych
Metale – dyfuzja domieszek (heterodyfuzja) – mechanizm międzywęzłowy
Porównanie współczynników dyfuzji wodoru
w żelazie, palladzie i niklu.
T
C
– temperatura Curie niklu (przejście
ferromagnetyk-paramagnetyk) nie ma
znacznego wpływu na mechanizm
dyfuzji
Dyfuzja małych atomów (H, C, N, O) w metalach jest znacznie szybsza od dyfuzji własnej
oraz heterodyfuzji mechanizmem wakancyjnym. Wynika to przede wszystkim ze znacznie
mniejszych wartości energii aktywacji, w której skład wchodzi jedynie entalpia ruchu atomów.
Znaczna dyfuzja wodoru w żelazie ma duże
znaczenie praktyczne ze względu na szkodliwe
zjawisko kruchości wodorowej w żelazie i stali.
Prezentowane dane dyfuzyjne dotyczą bardzo
małych stężeń wodoru.
W metalach typu Ti, Zr, Hf, Nb, Ta, Pd i inne
rozpuszczalność wodoru jest znaczna co wynika
z ujemnej entalpii mieszania. Przy większych
stężeniach tworzy on wodorki metali.
Rozpuszczalność wodoru w metalach
z VI i VII grupy układu okresowego, w Fe, Co, Ni
oraz w metalach szlachetnych, ze względu na
dodatnią entalpię mieszania, jest niewielka.
t
t
Dyfuzja domieszek, gdy ich stężenie jest małe (nie oddziałują na siebie wzajemnie, gdyż można je
uznać za izolowane od siebie) zależy od:
•
wielkości atomu domieszki
, co ma wpływ na energię swobodną Gibbsa związaną z przeskokiem
•
jego wartościowości względem wartościowości atomów własnych danego metalu
, co ma wpływ
zarówno na energię swobodną Gibbsa związaną z przeskokiem atomu, jak i na oddziaływanie
przyciągające bądź odpychające wakancje, w wielu przypadkach stwierdzono, że domieszki
o większej wartościowości niż atomy własne metalu przyciągają do siebie wakancje i wobec tego
ich dyfuzja jest szybsza
• współczynnik korelacji dyfuzji domieszek
w odróżnieniu od współczynnika korelacji atomów
własnych jest parametrem zmiennym,
zależy od rodzaju domieszki i jej stężenia
.
Dyfuzja domieszek w srebrze
– tzw. „normalna” dyfuzja
domieszek, tzn. parametry dyfuzji domieszek mieszczą się
w stosunkowo wąskim, dobrze określonym przedziale wokół
tych parametrów dotyczących dyfuzji własnej:
0,01 < D
2
/D < 100
(blisko
T
t
)
Podobny charakter ma dyfuzja domieszek w metalach
o strukturze RSC: Au, Cu, Ni i strukturze HZ: Zn, Cd.
Przykłady danych dyfuzyjnych
Metale – dyfuzja domieszek substytucyjnych – mechanizm wakancyjny
10
D
D
1
,
0
0
0
2
<
<
25
,
1
H
H
75
,
0
2
<
<
Δ
Δ
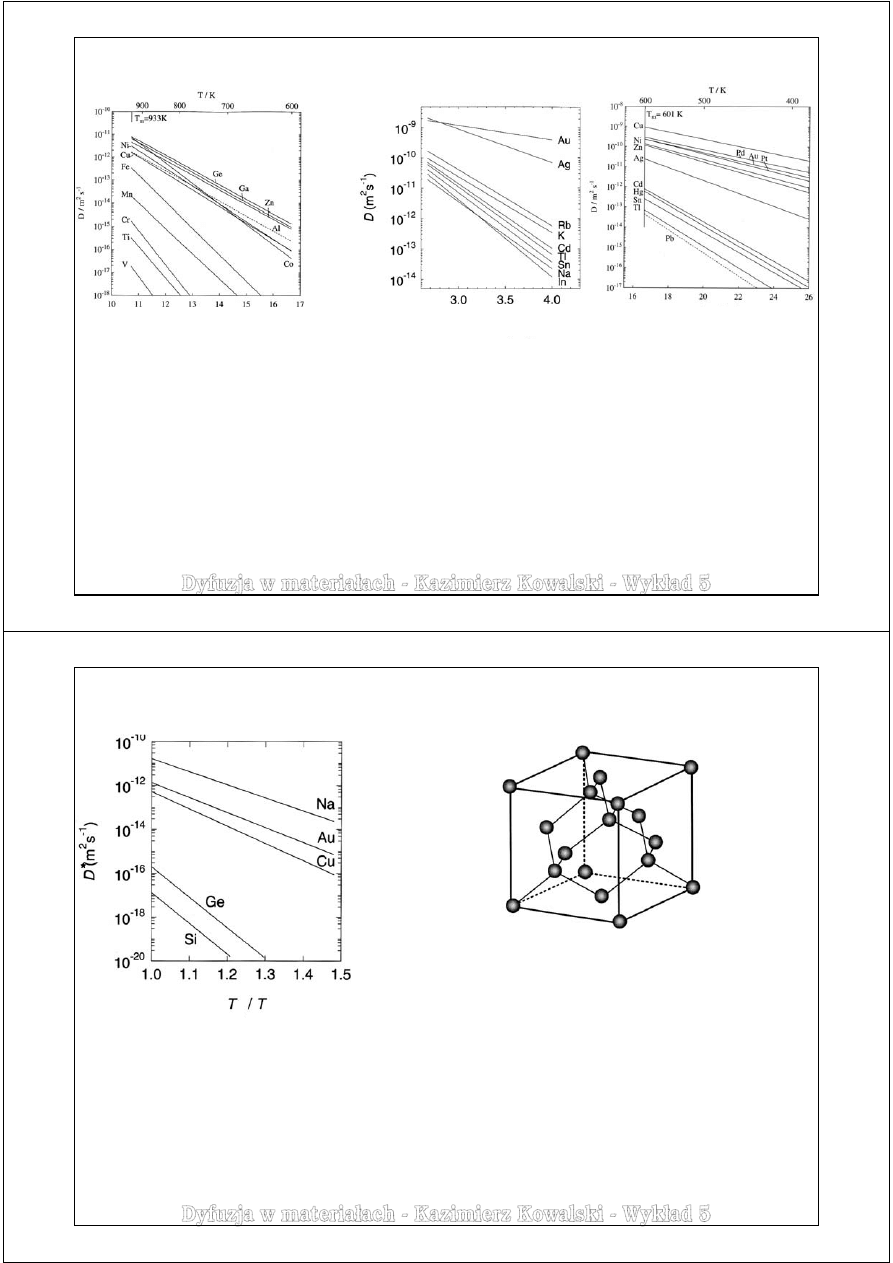
Przykłady danych dyfuzyjnych
Metale – dyfuzja domieszek substytucyjnych
10
4
/T
/
K
-1
10
3
/T
/
K
-1
10
4
/T
/
K
-1
Dyfuzja domieszek w Al (struktura RSC)
.
Domieszki metali przejściowych
dyfundują niezwykle wolno (wartości Q i
D
0
są znacznie większe niż dla innych
domieszek).
Jest to spowodowane silnym
oddziaływaniem odpychającym między
tymi atomami a wakancjami.
Skutkuje to zwiększeniem zarówno
energii aktywacji ruchu
jak i zmniejszeniu częstotliwości
przeskoków (gdyż entalpia związana
z oddziaływaniem jest ujemna).
Domieszki metali szlachetnych w Na lub metali szlachetnych
i metali z grupy Ni w Pb dyfundują niezwykle szybko.
Inne metale dyfundują w sposób bardziej „normalny”.
Bardzo szybka dyfuzja niektórych domieszek wynika z faktu, że
atomy tych domieszek są małe w porównaniu z atomami
macierzystymi (np.
R
Au
/R
Pb
≈ 0,83
).
W związku z tym pewna, niewielka część atomów tych domieszek
może przebywać w pozycjach międzywęzłowych i porusza się
jakiś czas szybko dzięki mechanizmowi międzywęzłowemu, po
czym zajmuje pozycję substytucyjną, gdzie przebywa dłuższy
czas i porusza się z „normalną” prędkością, charakterystyczną dla
mechanizmu wakancyjnego (domieszki hybrydowe, mechanizm
dysocjacyjny).
Przykłady danych dyfuzyjnych
Półprzewodniki Ge i Si
Porównanie współczynników dyfuzji własnej
Ge i Si z dyfuzją własną w kilku metalach.
„Luźna” struktura diamentu, w której krystalizują
german i krzem.
W germanie dyfuzja własna zachodzi praktycznie
wyłącznie dzięki mechanizmowi wakancyjnemu.
W krzemie dyfuzja własna zachodzi dzięki dwóm
mechanizmom: wakancyjnemu
i międzywęzłowemu z wypieraniem.
t
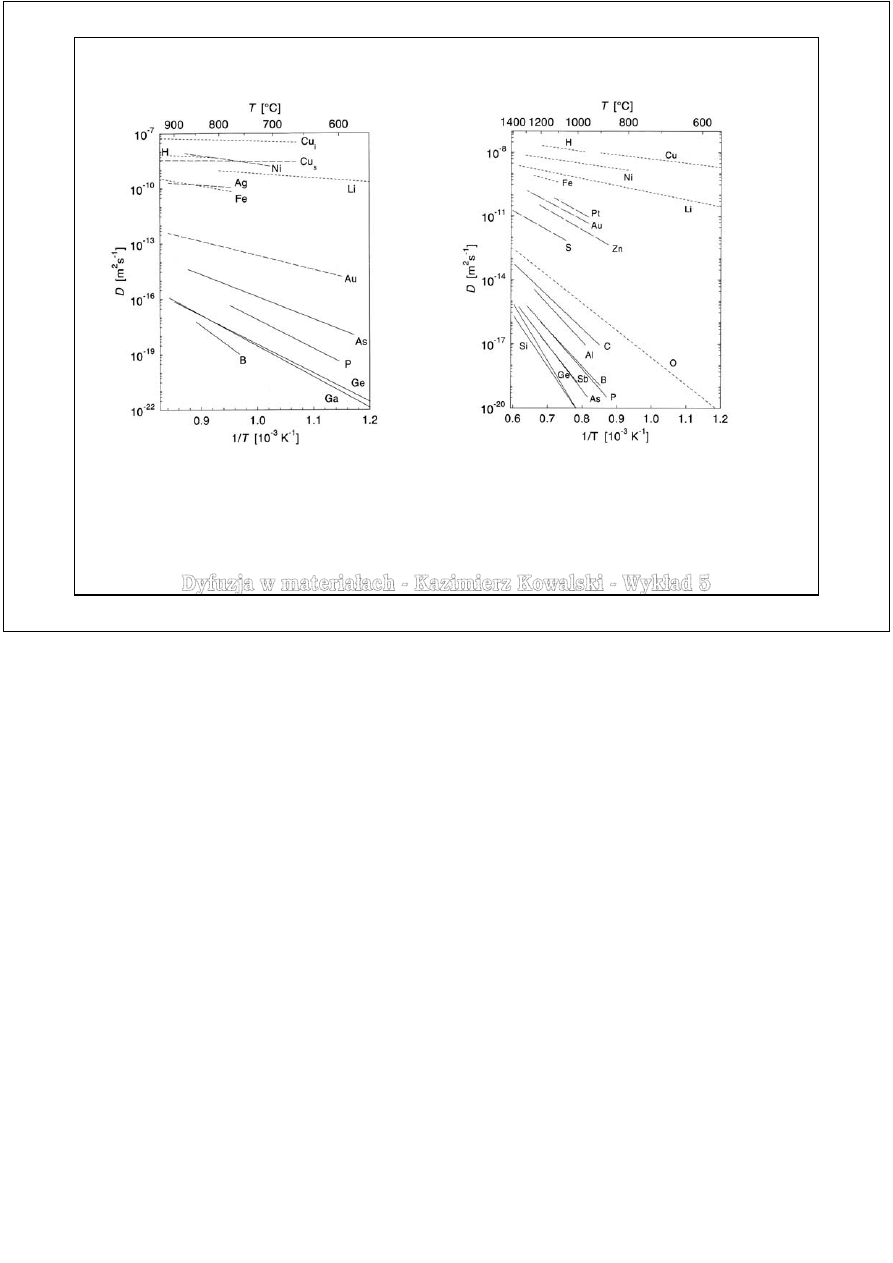
Przykłady danych dyfuzyjnych
Półprzewodniki Ge i Si – dyfuzja domieszek
Dyfuzja domieszek w germanie:
Linie ciągłe – mechanizm wakancyjny
Linie przerywane długie – pierwiastki
hybrydowe – mechanizm dysocjacyjny
Linie przerywane krótkie – mechanizm
międzywęzłowy
Dyfuzja domieszek w krzemie:
Linie ciągłe – mechanizm wakancyjny lub
międzywęzłowy z wypieraniem
Linie przerywane długie – pierwiastki hybrydowe –
mechanizm dysocjacyjny
Linie przerywane krótkie – mechanizm
międzywęzłowy (tlen dyfunduje znacznie wolniej
ze względu na silne oddziaływanie krzem-tlen)
t