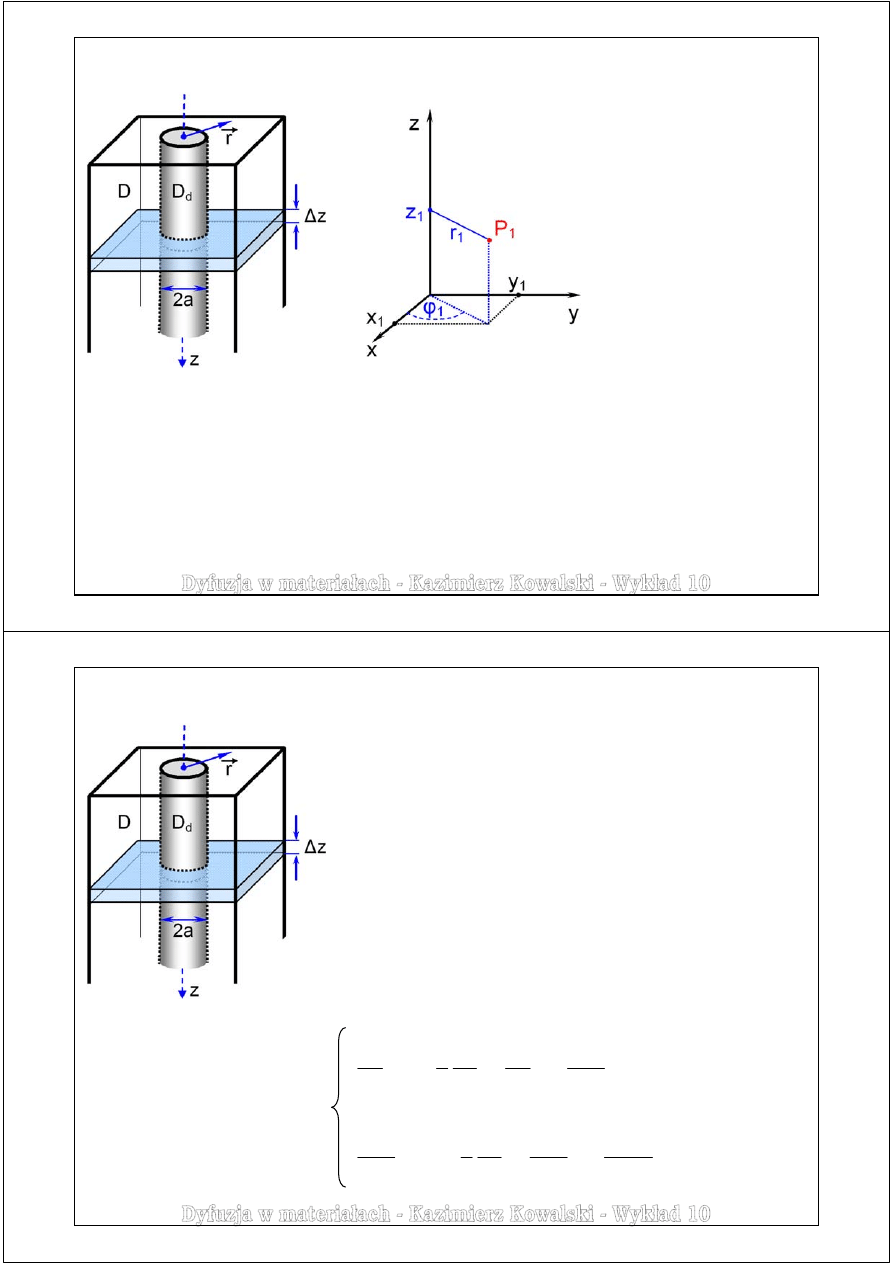
Dyfuzja wzdłuż pojedynczej dyslokacji – model Smoluchowskiego

Model dyslokacji jako rurki (ang. dislocation pipe model)

Ze względu na rodzaj symetrii, proces dyfuzji wzdłuż dyslokacji najwygodniej jest opisywać
w walcowym (cylindrycznym) układzie współrzędnych, którego oś

Z

pokrywa się z osią dyslokacji.

Współrzędne dowolnego punktu w przestrzeni opisują 3 parametry:
- położenie punktu

z

na osi

Z

określającego początek wektora prostopadłego do osi

Z

, którego

koniec znajduje się w tym punkcie

- długość

r

wektora

- kąt biegunowy

φ

określający o ile wektor jest obrócony względem osi

Z

.

Ze względu na izotropię materiału zmienna

φ

nie ma znaczenia i do opisu dyfuzji wzdłuż dyslokacji

wystarczają tylko dwie zmienne:

z

i

r

.

rr

rr

Układy współrzędnych

kartezjański (x, y, z)

walcowy (z, r,

φ

)

Położenie dowolnego punktu
w przestrzeni

P

1

może być

opisane w układzie:
kartezjańskim

(x

1

, y

1

, z

1

)

lub

walcowym

(z

1

, r

1

, φ

1

)

.

rr

x =

r

·cos

φ

y =

r

·sin

φ

z =

z

Związki między współrzędnymi:

Dyfuzja wzdłuż pojedynczej dyslokacji – model Smoluchowskiego

Model dyslokacji jako rurki (ang. dislocation pipe model)

Roman Smoluchowski, 1953

Założenia modelu dyfuzji wzdłuż dyslokacji:

1. Dyslokacja jest rurką o bardzo małym promieniu

a

(≈ 0.5 nm) prostopadłą do powierzchni materiału,

2. Wewnątrz dyslokacji współczynnik dyfuzji jest

znacznie większy niż poza nią: D

d

>> D,

3. Współczynniki dyfuzji D i D

d

są izotropowe i nie

zależą od stężenia,

4. Na „ściance” rurki spełniony jest warunek

ciągłości stężenia oraz strumienia dyfundującego
pierwiastka.

a

r

z

c

r

c

r

r

r

D

t

c

≥

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

∂

∂

=

∂

∂

2

2

1

a

r

z

c

r

c

r

r

r

D

t

c

d

d

d

d

<

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

∂

∂

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

∂

∂

=

∂

∂

2

2

1

Układ II równań Ficka na
zewnątrz dyslokacji
i wewnątrz dyslokacji
w cylindrycznym układzie
współrzędnych.

Warunki brzegowe:
1. Ciągłość strumienia dyfundującego pierwiastka

2. Ciągłość stężenia dyfundującego pierwiastka (gdy nie ma segregacji)

Dyfuzja wzdłuż pojedynczej dyslokacji – model Smoluchowskiego

Model dyslokacji jako rurki (ang. dislocation pipe model)

−

+

=

=

∂

∂

=

∂

∂

a

r

d

d

a

r

r

c

D

r

c

D

)

a

r

(

c

)

a

r

(

c

d

−

+

=

=

=

Istnieją analityczne rozwiązania modelu dyfuzji wzdłuż izolowanej dyslokacji jako rurki.
Podobnie jak w przypadku modelu Fishera dyfuzji wzdłuż izolowanej granicy ziaren

rozwiązanie w obszarze poza dyslokacją składa się z dwóch części:

gdzie: c

1

(z,t) – stężenie wynikające z dyfuzji pierwiastka od powierzchni prostopadle do

wnętrza kryształu; w zależności od warunków początkowych: źródło

chwilowe bądź stałe, rozwiązanie ma postać funkcji Gaussa lub

odwrotnej funkcji błędu

c

2

(r,z,t) – stężenie wynikające z dyfuzji pierwiastka prostopadle od dyslokacji do

wnętrza kryształu (te rozwiązania nie są tutaj pokazywane).

)

t

,

z

,

r

(

c

)

t

,

z

(

c

)

t

,

z

,

r

(

c

2

1

+

=

Dyfuzja wzdłuż sieci równoległych dyslokacji w krysztale

Gęstość dyslokacji w materiale

ρ

d

określa się jako liczbę dyslokacji przecinających

jednostkę powierzchni. Wielkość tę łatwo przeliczyć na całkowitą długość dyslokacji

w jednostce objętości.

Przykładowe gęstości dyslokacji:

1. Dobrze wyżarzony metal

2. Silnie odkształcony metal

Regularna sieć równoległych dyslokacji Heksagonalna sieć równoległych dyslokacji
prostopadłych do powierzchni materiału prostopadłych do powierzchni materiału

3

2

6

10

10

cm

/

km

cm

d

⇔

≈

−

ρ

3

6

5

2

12

11

10

10

cm

/

km

cm

d

÷

−

÷

⇔

≈

ρ

Średnia odległość między dyslokacjami

Λ

wyraża się następującą zależnością:

Gdzie

K

jest stałą rzędu 1 zależną od

sposobu ułożenia sieci dyslokacji.

d

d

K

ρ

ρ

Λ

1

≈

=

1

=

K

2

3 /

K =

Dyfuzja wzdłuż sieci równoległych dyslokacji w krysztale

Podział na zakresy kinetyczne

Proces dyfuzji wzdłuż sieci dyslokacji można podzielić na zakresy kinetyczne

analogicznie do podziału Harrisona w przypadku dyfuzji wzdłuż granic ziaren

w materiale polikrystalicznym.

Zakresy kinetyczne dyfuzji wzdłuż sieci dyslokacji:
Zakres A:

Nie można traktować dyslokacji jako izolowanych od siebie.

Eksperymentalnie wyznacza się jedynie efektywny

współczynnik dyfuzji:

gdzie

σ

– ułamek objętości materiału, którą zajmują dyslokacje.

Po przekształceniach:

Λ

>

Dt

d

eff

D

D

)

(

D

σ

σ

+

−

≈ 1

d

a

ρ

σ

π

2

=

⎟

⎠

⎞

⎜

⎝

⎛

−

+

≈

1

1

2

D

D

a

D

D

d

eff

d

ρ

π

Dyfuzja wzdłuż sieci równoległych dyslokacji w krysztale

Podział na zakresy kinetyczne

Zakres B:

Dyfuzja wzdłuż dyslokacji (izolowanych) zachodzi

niezależnie, gdyż atomy dyfundującego pierwiastka

nie są w stanie pokonać odległości między dyslokacjami.

Ten zakres kinetyczny może być wykorzystany do

jednoczesnego wyznaczenia współczynnika dyfuzji

objętościowej i dyfuzyjności wzdłuż dyslokacji.

Zakres C:

Dyfundujący pierwiastek znajduje się tylko wewnątrz

dyslokacji. Eksperymentalnie wyznaczona zależność

średniego stężenia dyfundującego pierwiastka od
głębokości pozwoliłaby bezpośrednio wyznaczyć

D

d

z zależności (źródło chwilowe):

Jest to jednak niezwykle trudne eksperymentalnie z takich

samych powodów, jak w przypadku dyfuzji wzdłuż granic

ziaren i praktycznie nie stosowane.

t

D

z

c

ln

d

4

1

2

−

=

∂

∂

Λ

<<

<< Dt

a

a

Dt <<

Dyfuzja wzdłuż sieci równoległych dyslokacji w krysztale

Zakres kinetyczny typu B

A. D. Le Claire i A. Rabinovitch (1981-82) wykorzystali ścisłe rozwiązania

matematyczne problemu dyfuzji dla pojedynczej dyslokacji do zakresu kinetycznego

typu B sieci licznych równoległych dyslokacji.

Zmienne zredukowane (bezwymiarowe):

t

D

a

t

D

z

⋅

≡

⋅

≡

α

η

głębokość wyrażona miarą

średniego zasięgu dyfuzji

objętościowej

stosunek promienia dyslokacji

do średniego zasięgu dyfuzji

objętościowej

t

D

)

(

D

D

d

⋅

−

≡

≡

2

1

α

Δ

β

Δ

Dyfuzja wzdłuż sieci równoległych dyslokacji w krysztale

Zakres kinetyczny typu B

Zależność średniego stężenia dyfundującego pierwiastka od głębokości:
1. Rozwiązanie dla źródła chwilowego (dyfuzja z cienkiej warstwy na powierzchni):

Gdzie

M

– początkowe stężenie powierzchniowe dyfundującego pierwiastka

2. Rozwiązanie dla źródła stałego (dyfuzja z fazy gazowej):

Gdzie

c

0

– stałe stężenie dyfundującego pierwiastka na powierzchni.

⎥

⎦

⎤

⎢

⎣

⎡

+

⎟

⎠

⎞

⎜

⎝

⎛

=

I

Q

a

erfc

c

)

(

c

d

ρ

π

η

η

2

0

2

⎥

⎥
⎦

⎤

⎢

⎢
⎣

⎡

+

−

=

II

Q

a

)

(

exp

Dt

M

)

(

c

d

ρ

π

η

π

η

2

4

2

Matematyczna postać funkcji

Q

I

i

Q

II

nie jest tutaj podawana.

Dyfuzja wzdłuż sieci równoległych dyslokacji w krysztale

Zakres kinetyczny typu B

1. Profil dyfuzyjny średniego stężenia dyfundującego pierwiastka w funkcji głębokości

składa się z dwóch części (podobnie jak w dyfuzji po granicach ziaren):
- pierwsza cześć jest stroma i ma kształt funkcji Gaussa w przypadku źródła

chwilowego i odwrotnej funkcji błędu w przypadku źródła stałego – z tej części

wyznacza się objętościowy współczynnik dyfuzji D (analogicznie jak w przypadku

dyfuzji z udziałem granic ziaren)

- druga część jest łagodniej nachylona – odpowiada ona za dyfuzję od dyslokacji do

wnętrza kryształu – z tej części wyznacza się współczynnik dyfuzji wzdłuż

dyslokacji D

d

.

2. Okazuje się, że dla

η

> 4

(czyli na takiej głębokości, gdzie dyfuzja z powierzchni do

wnętrza kryształu nie odgrywa już roli – łagodniejsza część profilu) oraz

α

<< 1

(co

występuje w zakresie kinetycznym typu B) zachodzi liniowa zależność:

3. Ponadto, dla określonych wartości

α

oraz

αβ

liniowa zależność nachylenia

nie zależy od tego, czy dyfuzja zachodzi ze źródła stałego czy chwilowego:

αβ

α

η

η

)

(

A

Q

ln

Q

ln

II

I

−

=

∂

∂

=

∂

∂

z

~

c

ln

z

~

c

ln

Dyfuzja wzdłuż sieci równoległych dyslokacji w krysztale

Zakres kinetyczny typu B

Zależność nachylenia logarytmu średniego stężenia dyfundującego pierwiastka od

głębokości wyznaczona dla drugiej, łagodniejszej części profilu dyfuzyjnego pozwala

wyznaczyć współczynnik dyfuzji wzdłuż dyslokacji z następującej zależności:

Wartość współczynnika dyfuzji objętościowej

D

wyznacza się z pierwszej, stromej części profilu.

1

−

⋅

−

=

∂

∂

D

/

D

d

)

(

A

z

c

ln

α

α

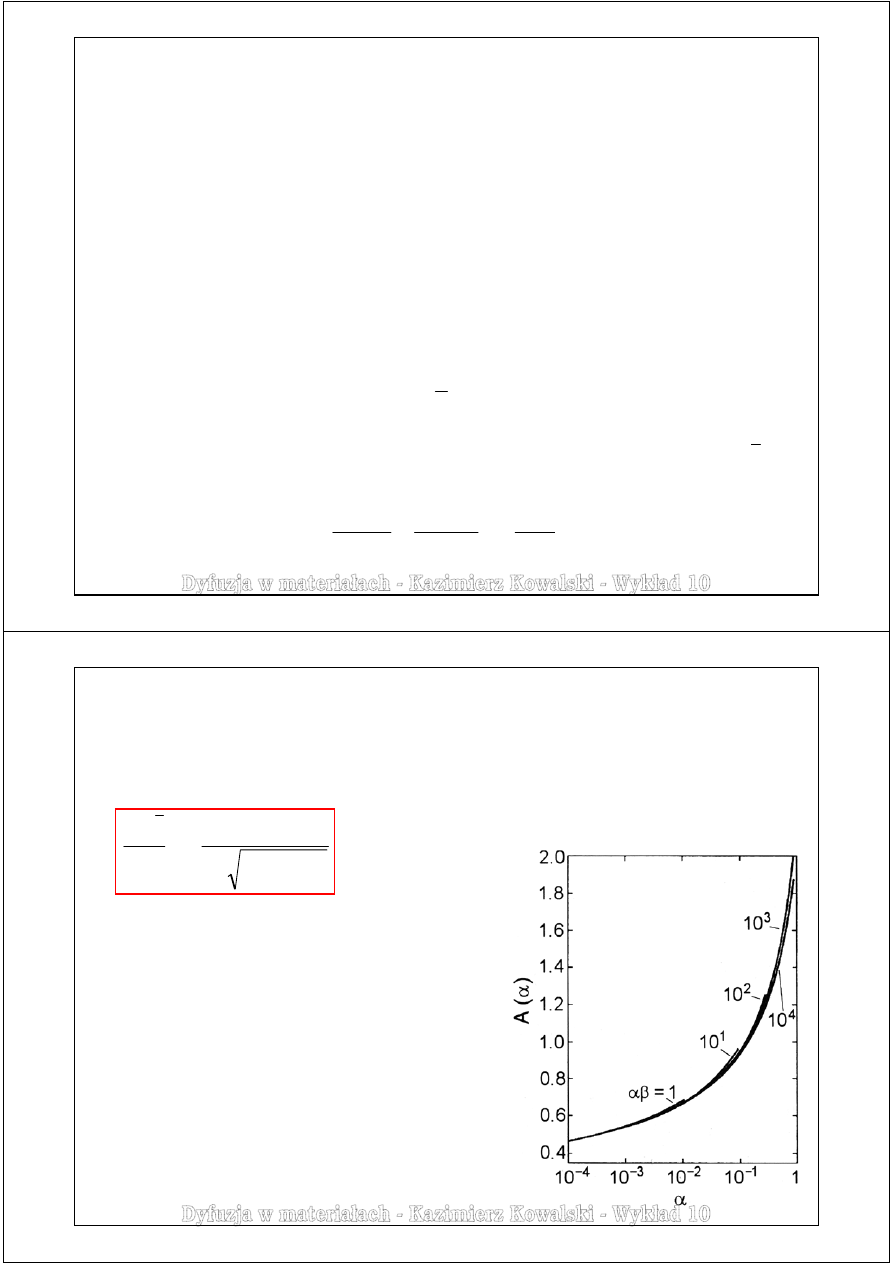
Wykres funkcji

A(

α

)

służący do odczytu wartości A.

Le Claire, Rabinowitch

Dyfuzja wzdłuż dyslokacji i wzdłuż granic ziaren - porównanie

profili dyfuzyjnych w zakresie kinetycznym typu B

Aby odróżnić od siebie profile dyfuzyjne należy posłużyć się cechami

charakterystycznymi płaskich (odpowiadających większym głębokościom) części profili

dyfuzyjnych (tzw. „ogon” profilu):

1. Różnica w zależności średniego stężenia od głębokości zmierzona dla jakiegoś

konkretnego czasu dyfuzji:

- dyfuzja wzdłuż dyslokacji

- dyfuzja wzdłuż granic ziaren

Biorąc pod uwagę rozrzut punktów eksperymentalnych spowodowany błędem

pomiarowym małych stężeń dyfundującego pierwiastka, które występują w „ogonie”

profilu, bardzo trudno jest stwierdzić, która z powyższych zależności jest prawdziwa.

2. Zależność nachylenia logarytmu średniego stężenia dyfundującego pierwiastka od

czasu trwania procesu dyfuzyjnego:

- nachylenie płaskiej części profilu nie zależy od czasu

- nachylenie płaskiej części profilu zależy od czasu dyfuzji

Wyznaczając profil dyfuzyjny w danej temperaturze dla kilku różnych czasów trwania

dyfuzji można zauważyć, czy nachylenie profilu się zmienia, czy nie – ta metoda jest

skuteczniejsza w określaniu czy dany profil dyfuzyjny wynika z dyfuzji wzdłuż

dyslokacji czy wzdłuż granic ziaren.

z

~

c

ln

6/5

z

~

c

ln

z

/

c

ln ∂

∂

-1/4

6/5

t

~

z

/

c

ln ∂

∂

Dyfuzja w materiale polikrystalicznym

zawierającym duże ilości dyslokacji

Kształt profilu dyfuzyjnego – tj. zależności
średniego stężenia dyfundującego
pierwiastka w funkcji głębokości –
w zakresie kinetycznym typu B
w materiale o dużej gęstości dyslokacji
oraz granic ziaren.

Wyróżnia się trzy części profilu, których
wzajemna relacja zależna jest od gęstości
dyslokacji i granic ziaren.

Gdy gęstość dyslokacji jest mała (np.
w materiale ceramicznym), to wówczas
część środkowa profilu jest niewidoczna.

W materiałach o dużej gęstości dyslokacji
(w metalach) i o bardzo dużych ziarnach
praktycznie nie ma trzeciej części profilu.

Dyfuzja powierzchniowa

Przykład:
Dyfuzja radioaktywnego polonu (Po) na powierzchni
srebra (cienkiej folii) w 480

o

C

Autoradiogram, J. A. Schwartz 1978

t = 0

t > 0

1 cm

Średnia droga swobodna atomów Po na powierzchni była rzędu 1 cm, natomiast praktycznie
w ogóle nie wniknął on w głąb materiału. Wynika to ze znacznej różnicy energii aktywacji:

1

1

2

193

3

43

−

−

⋅

=

<<

⋅

=

mol

kJ

,

Q

mol

kJ

,

Q

obj

pow

Współczynnik dyfuzji powierzchniowej materiału może być wyznaczany bezpośrednio
z zależności Einsteina-Smoluchowskiego (dla dwóch wymiarów), jeśli dyfuzja zachodzi
ze źródła punktowego:

t

R

D

pow

⋅

=

4

2

Gdzie

R

2

jest średnim kwadratowym przemieszczeniem atomów na powierzchni, a

t

jest

czasem trwania dyfuzji.

Dyfuzja powierzchniowa

Dyfuzja powierzchniowa bardzo silnie zależy od stanu powierzchni:

1. Zaadsorbowanych zanieczyszczeń.

2. Chropowatości.

3. Orientacji krystalicznej płaszczyzny, na której zachodzi.

4. Wielkości ziaren materiału polikrystalicznego (gęstość granic ziaren).

Wpływ stanu powierzchni badanego materiału na szybkość dyfuzji
powierzchniowej oraz parowanie i kondensacja dyfundujących
pierwiastków w wysokiej temperaturze są głównym powodami
uniemożliwiającymi otrzymywanie jednoznacznych i porównywalnych
wyników.

Dyfuzja wzdłuż dróg łatwej dyfuzji - mechanizmy

Duża szybkość dyfuzji wzdłuż dróg łatwej dyfuzji - wzdłuż dyslokacji

- po granicach ziaren
- po granicach faz
- po powierzchni zewnętrznej

wynika z następujących czynników:

1. Mniejszej energii aktywacji w porównaniu do dyfuzji objętościowej,

co zwiększa częstotliwość przeskoków atomów,

2. Mechanizmów dyfuzji: - możliwość kolektywnych przeskoków

(jednocześnie przeskakuje cała grupa atomów),

- możliwość przeskoków pojedynczych atomów

lub ich grup na odległości wielu stałych sieciowych.

Możliwość zachodzenia powyższych mechanizmów, które nie mogą zachodzić
w objętości materiałów ze względu na zbyt gęste ułożenie atomów,
potwierdzono przy użyciu symulacji komputerowych w oparciu o metody
dynamiki molekularnej.