Z. Zieliński – Diagnostyka i wiarygodność systemów

1

Metody diagnostyki

systemowej

Z. Zieliński –Diagnostyka systemowa sieci procesorów

2

Plan wykładu



Wprowadzenie do diagnostyki systemowej



Strategie i metody diagnostyczne



Interpretacja wyników testów – modele diagnostyczne



Diagnoza i jej rodzaje



Typy systemów samodiagnozowalnych i ich własności



Systemy jednoznacznie diagnozowalne - opiniowanie
diagnostyczne



Struktury samodiagnozowalne i ich rodzaje



Algorytmy diagnozowania sieci



Podsumowanie

Z. Zieliński –Diagnostyka systemów

3

Wprowadzenie - Systemy tolerujące uszkodzenia



System tolerujący uszkodzenia –

to system, który może wykonywać zadane

funkcje użytkowe pomimo występujących

w nim uszkodzeń (pewnej klasy).



Warunkiem koniecznym tolerowania

uszkodzeń jest poprawna ich diagnostyka.

Jej jakość ma decydujące znaczenie dla

przywrócenia zdatności systemu:

- wymiana uszkodzonych jednostek,

- odłączenie niezdatnych jednostek i

rekonfiguracja zadań (łagodna degradacja

systemu).

Z. Zieliński –Diagnostyka systemów

4

Cechy systemów tolerujących uszkodzenia



Jednostki systemu (tzn. (mikro)procesory, komputery) posiadają

oprócz zadanych możliwości użytkowych także określone

zdolności do oceny poprawności wykonania własnych funkcji

i/lub funkcji realizowanych przez inne jednostki;



Systemy takie nie są w pełni bezpieczne, tzn. zawsze

można wskazać pewne uszkodzenia, których pojawienie

się dezorganizuje pracę systemu. Innymi słowy, są to

systemy z niezawodnym jądrem, którego niezawodność

powinna znacznie przewyższać niezawodność

pozostałych elementów systemu.

Z. Zieliński –Diagnostyka systemów

5

Cechy systemów tolerujących uszkodzenia



System samodiagnozowalny

-

jest to system zdolny do diagnozy własnych uszkodzeń.

Istota metod diagnostyki systemowej (1)



Nie zakłada się w nich istnienia niezawodnego jądra

systemu (testera).



Diagnozowany system rozpatrywany jest jako zbiór

jednostek, każda z których zdolna jest do realizowania

funkcji testowania innych jednostek systemu.



Diagnostyka systemowa sieci komputerowej

(procesorowej) bazuje na tym, że wyróżnione węzły sieci

(jednostki przetwarzające) mają zdolność do testowania

innych węzłów (jednostek przetwarzających).



Zakłada się, że istnieje pewien zbiór testów, który

umożliwia funkcjonalne sprawdzenie jednostek

przetwarzających (JP) sieci komputerowej oraz systemu

(sieciowego) jako całości.

Z. Zieliński –Diagnostyka systemów

6

Istota metod diagnostyki systemowej (2)



Celem testowania przeprowadzanego przez określoną JP

(lub grupę jednostek), którego obiekt testowania stanowi

inna JP sieci, jest wydanie opinii, że testowana JP jest

(lub nie jest) w funkcjonalnym stanie zdatności.



Rozpoznanie funkcjonalnego stanu niezawodnościowego

testowanej JP realizowane jest na bazie prób

funkcjonalnych.



Przy takim podejściu podstawowym problemem jest to, że

opinie o stanie niezawodnościowym jednostek

testowanych mogą być wydawane przez jednostki

niezdatne,

a o jednostce wykonującej testowanie nie

wiadomo a priori czy jest w stanie zdatności, czy nie.

Z. Zieliński –Diagnostyka systemów

7

Z. Zieliński –Diagnostyka systemów

8

Diagnoza

Opinia globalna (syndrom) systemu jest zmienną losową,
zależną od zmiennej losowej n, którą jest nieznany stan
niezawodnościowy oraz od grafu G opiniowania
diagnostycznego tego systemu.

Diagnozą

nazywamy identyfikację stanu

niezawodnościowego systemu na podstawie syndromu.

Diagnoza

Z. Zieliński –Diagnostyka systemów

9

Niech

S

oznacza zbiór możliwych wartości wyników testów (syn-

dromów) dla określonego przydziału testów.

Diagnozą nazywamy identyfikację zbioru niezdatnych procesorów

sieci (stanu niezawodnościowego systemu) na podstawie zbioru

wyników testów (syndromu globalnego) i możemy przedstawić ją

przy pomocy funkcji:

:

2 .

E

Diag

S



Diagnoza - rodzaje

Z. Zieliński –Diagnostyka systemów

10

Diagnozę nazywamy kompletną, jeżeli na podstawie uzyskanego
syndromu

s

S



zidentyfikowany podzbiór niezdatnych procesorów

( )

Diag s

E





zawiera wszystkie niezdatne procesory, występujące w

rzeczywistym (rozpoznawanym) stanie niezawodnościowym

*

n

, to

jest

1

*

( )

E n

E





.

Diagnozę nazywamy poprawną, jeżeli

0

*

( )

E

E n



 

, to jest, w

procesie diagnozy procesory zdatne nie są identyfikowane jako nie-
zdatne.

Z. Zieliński –Diagnostyka systemów

11

Rodzaje diagnozy

Stan niezawodnościowy systemu n jest jednoznacznie
diagnozowalny, jeżeli jego syndrom d(n) jest unikalny dla
wszystkich możliwych (prawdopodobnych) stanów
niezawodnościowych

.

Diagnoza jest kompletna

, jeżeli wszystkie niezdatne jednostki

systemu mogą być zidentyfikowane na podstawie syndromu dla danego
stanu niezawodnościowego, w przeciwnym przypadku diagnoza jest
niekompletna.

Diagnoza jest poprawna

, jeżeli na bazie syndromu systemu

jednostki zdatne nie są identyfikowane jako niezdatne.

Z. Zieliński –Diagnostyka systemów

12

Jeżeli istnieją stany niezawodnościowe {n

1

, n

2

, . . . , n

p.

}, dla których

system generuje identyczne syndromy, najczęściej stosuje się jedną z
następujących

strategii diagnostycznych

:

1 -

identyfikacja częściowego zbioru niezdatnych jednostek

{E

1

(n

1

) ∩

E

1

(n

2

) ∩ …

∩ E

1

(n

p

) };

2 -

określenie rozszerzonego zbioru jednostek niezdatnych

{E

1

(n

1

) U E

1

(n

2

) U … U E

1

(n

p

) };

Z. Zieliński –Diagnostyka systemów

13

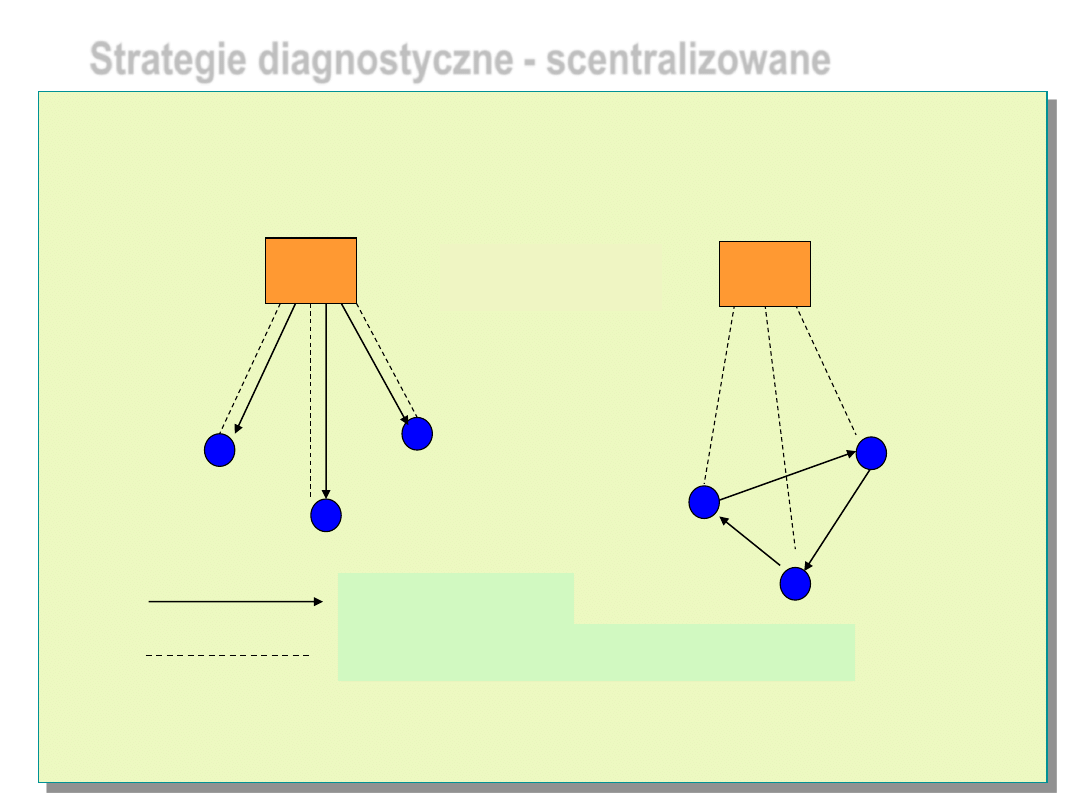
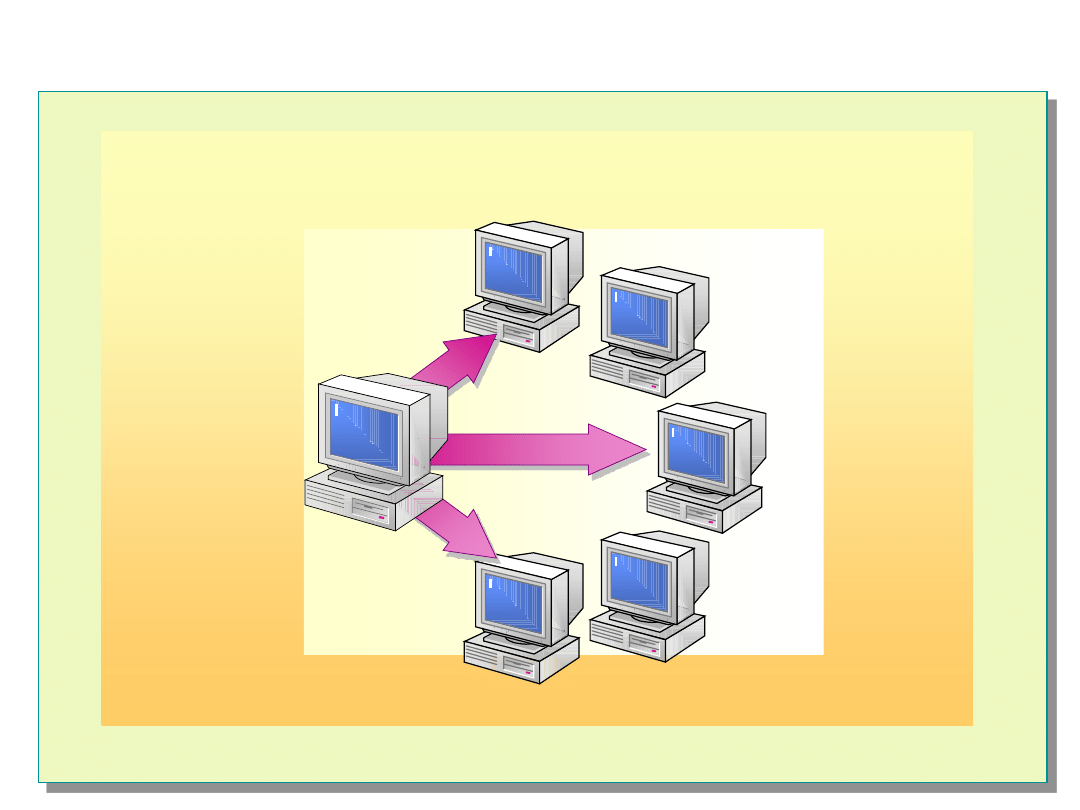
Strategie diagnostyczne - scentralizowane

Decyzje

testy

przepływ informacji diagnostycznych

Z. Zieliński –Diagnostyka systemów

14

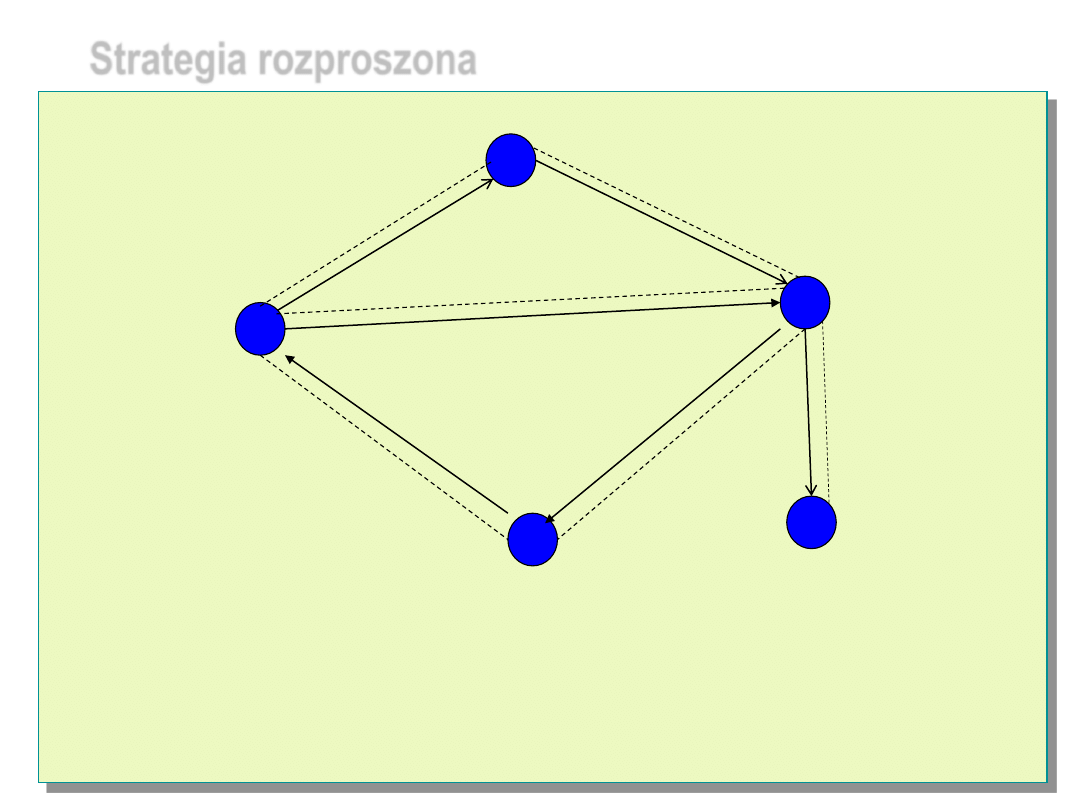
Strategia rozproszona

Z. Zieliński –Diagnostyka systemów

15

Strategie diagnostyczne



Strategia off-line

jest strategią, w której jednostki biorące udział

w diagnozowaniu nie uczestniczą w realizacji zadań użytkowych



Strategia on-line

jest strategią, w której stan systemu jest wyznaczany

na bieżąco bez zawieszania zadań użytkowych



Strategia jednokrokowa

polega na wykonaniu wszystkich

dopuszczalnych testów w systemie i wyznaczeniu wszystkich
uszkodzonych jednostek na podstawie otrzymanego syndromu



W przypadku

strategii wielokrokowej

proces diagnozy i naprawy

przeplatają się nawzajem. Przyjmuje się, że na podstawie syndromu
jesteśmy w stanie określić tylko pewien niepusty podzbiór uszkodzonych
jednostek. Następnie wymienia się je na zdatne i ponawia się testowanie.
Proces powtarzany jest dopóty, dopóki nie stwierdzi się poprawnego
funkcjonowania wszystkich jednostek systemu

Z. Zieliński –Diagnostyka systemów

16

Podstawowe metody diagnostyki systemowej



metody opiniowania diagnostycznego



metody dialogu diagnostycznego



metody porównawcze



metody adaptacyjne

Z. Zieliński –Diagnostyka systemów

17

Podstawowe metody diagnostyki systemowej – (1)



Metody opiniowania diagnostycznego - zalicza się do
grupy scentralizowanych metod diagnozowania sieci
komputerowych – możliwa jest też implementacja
rozproszona.



Cechą charakterystyczną tej metody jest to, że
identyfikacji stanu niezawodnościowego sieci
komputerowej dokonuje się po uzyskaniu wszystkich
wyników testowań (opinii globalnej), wykonanych przez
każdą jednostkę sieci.

Z. Zieliński –Diagnostyka systemów

18

Podstawowe metody diagnostyki systemowej – (2)



Metody dialogu diagnostycznego należą do grupy
rozproszonych metod diagnozowania sieci
komputerowych.



W przypadku tych metod proces testowania inicjowany
jest przez dowolny komputer sieci komputerowej
i obejmuje zazwyczaj pewien podzbiór komputerów
sieci przyległych do komputera inicjującego.



Proces testowania inicjowany jest w momencie, gdy
komputer inicjujący oraz komputer testowany nie
realizują zadań obliczeniowych na potrzeby systemu.

Z. Zieliński –Diagnostyka systemów

19

Podstawowe metody diagnostyki systemowej – (3)



Metody porównawcze polegają na wnioskowaniu z
wyników określonego zbioru testów porównawczych, w
każdym z których uczestniczą trzy procesory. Jeden z
nich zwany komparatorem, zleca przyległym
procesorom jednakowe zadanie funkcjonalne oraz
sprawdza, czy wyniki wykonania tego zadania są
identyczne.



Metody porównawcze znajdują szczególne
zastosowanie w jednorodnych sieciach
(mikro)procesorowych i dają możliwości testowania
sieci podczas wykonywania zadań funkcjonalnych.

Z. Zieliński –Diagnostyka systemów

20

Podstawowe metody diagnostyki systemowej – (4)



W metodach adaptacyjnych (w odróżnieniu od
pozostałych metod diagnostyki systemowej) nie zakłada
się istnienia stałego przydziału testów.



Przydział testów konstruowany jest w sposób
dynamiczny i jest on zależny od wyników testowania się
między określonymi procesorami sieci tj.
dostosowywany jest do stanu niezawodnościowego
sieci procesorów.



Proces testowania ma charakter rozproszony i zwykle
(DSD, HiDSD) zakłada się możliwość bezpośredniej
komunikacji między wszystkimi węzłami sieci.

Z. Zieliński –Diagnostyka systemów

21

Typy systemów samodiagnozowalnych



Systemy jednoznacznie diagnozowalne



Systemy częściowo diagnozowalne



Systemy nadmiarowo diagnozowalne



Systemy sekwencyjnie diagnozowalne



Systemy przyrostowo diagnozowalne



Systemy diagnozowalne adaptacyjnie

Z. Zieliński –Diagnostyka systemów

22

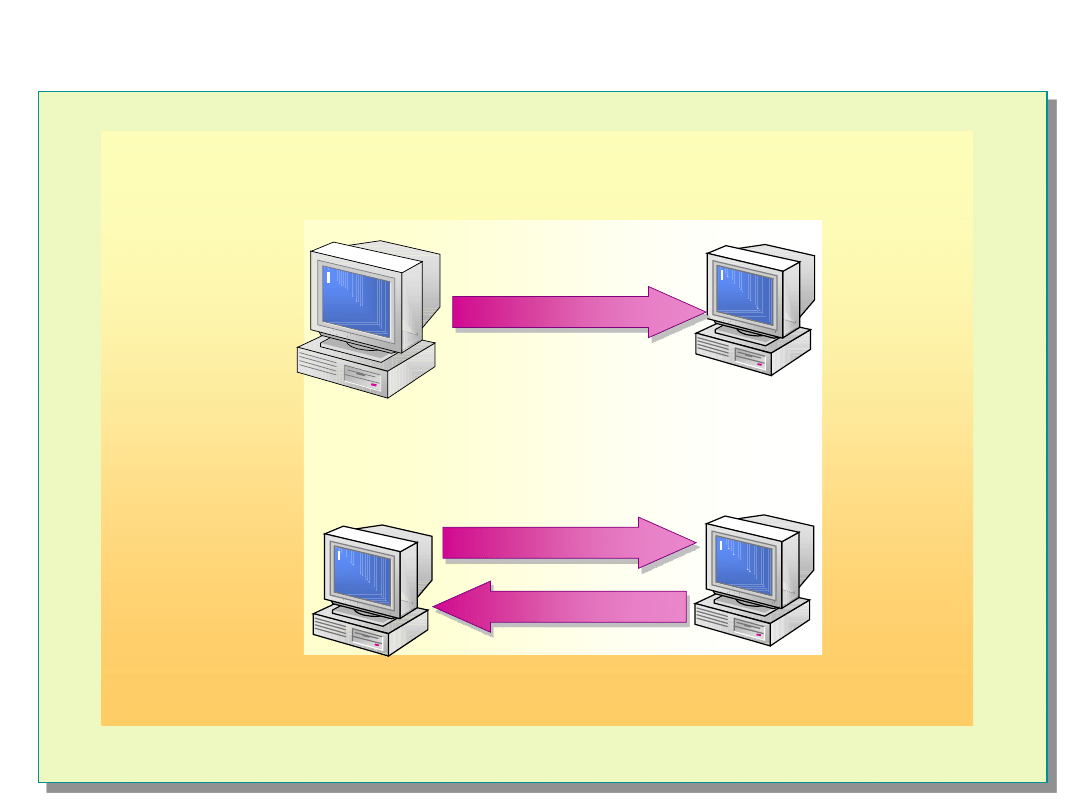
Sposoby testowania

Test asymetryczny

Test symetryczny

(wzajemne testowanie się jednostek)

Z. Zieliński –Diagnostyka systemów

23

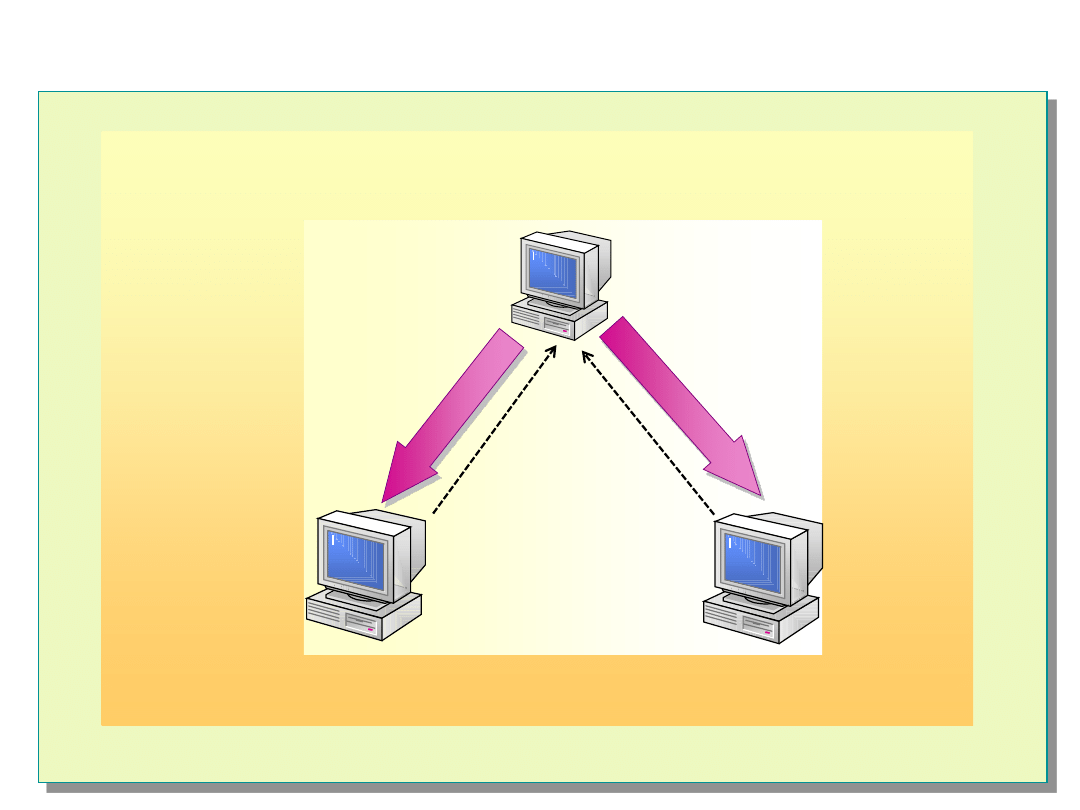
Sposoby testowania

Testowanie porównawcze (comparison method)

KOMPARATOR

Z. Zieliński –Diagnostyka systemów

24

Przydział testów

Z. Zieliński –Diagnostyka systemów

25

Wynik testu

}

1

,

0

{



ij

d

Niech

d

ij

oznacza

, wynik testu, za pomocą którego

e

i

opiniuje stan niezawodnościowy

e

j

.

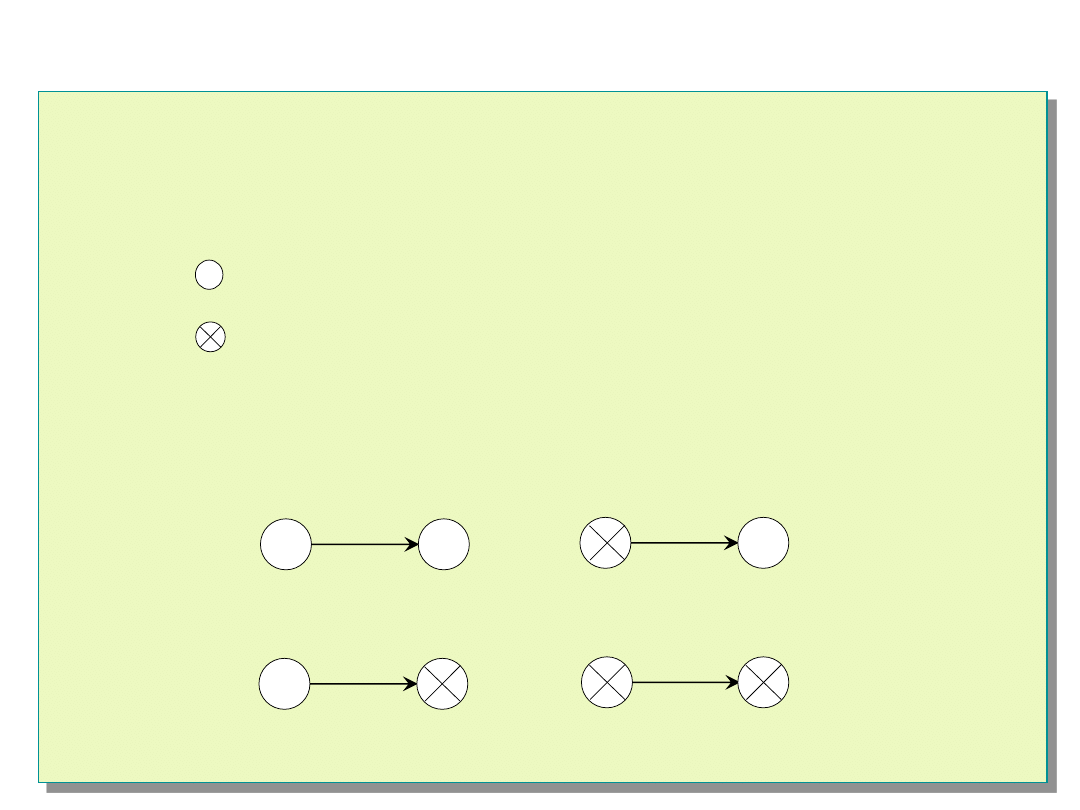
Wynik testu ma zawsze binarną klasyfikację, tj. jednostka
przeprowadzająca testowanie ocenia testowany moduł
zawsze jako „zdatny” lub „niezdatny”.

Wyniki testu są zawsze poprawne: zdatna (wolna od
błędów) jednostka jest zawsze opiniowana jako „zdatna”.

Z. Zieliński –Diagnostyka systemów

26

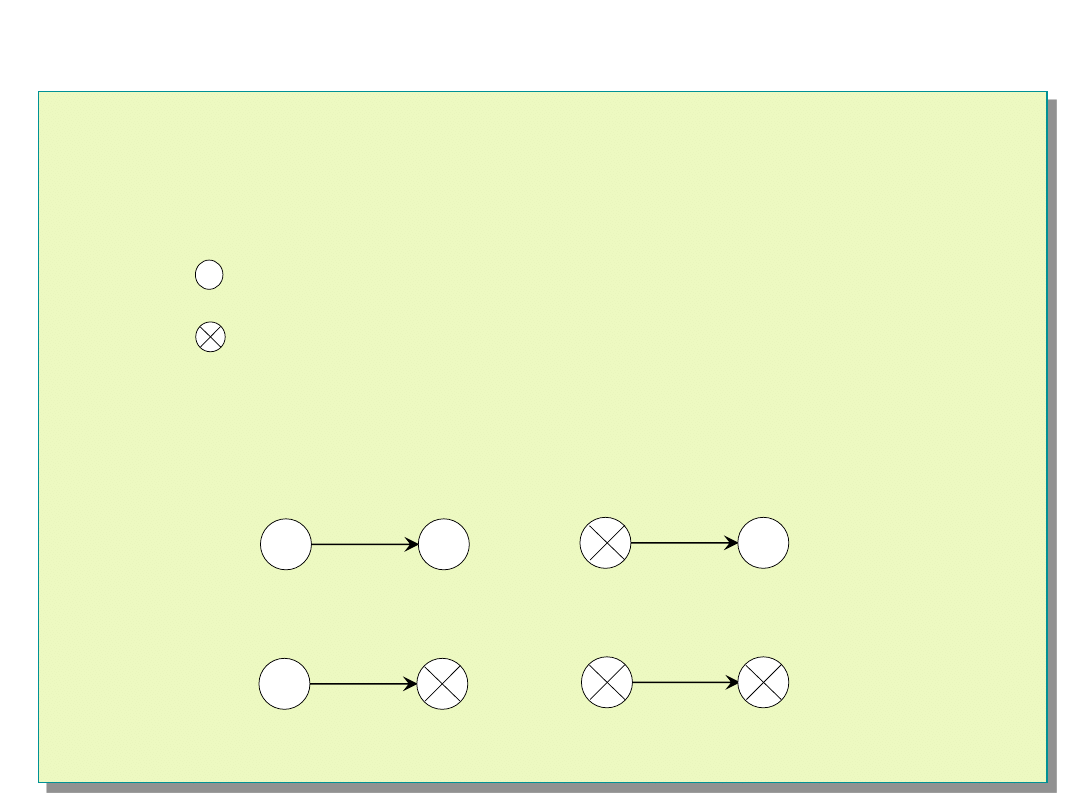
Model z symetrycznym unieważnianiem testu (PMC)

d

ij

= 0

Oznaczenia:

- jednostka zdatna

- jednostka niezdatna

x -

wartość przypadkowa (0 lub 1)

e

i

e

j

e

i

e

j

e

i

e

j

d

ij

= 1

d

ij

= x

d

ij

= x

e

i

e

j

Modele diagnostyczne

Z. Zieliński –Diagnostyka systemów

27

Modele diagnostyczne (1)

Model z asymetrycznym unieważnianiem testu (BGM)

d

ij

= 0

Oznaczenia:

- jednostka zdatna

- jednostka niezdatna

x -

wartość przypadkowa (0 lub 1)

e

i

e

j

e

i

e

j

e

i

e

j

d

ij

= 1

d

ij

= x

d

ij

= 1

e

i

e

j

Z. Zieliński –Diagnostyka systemów

28

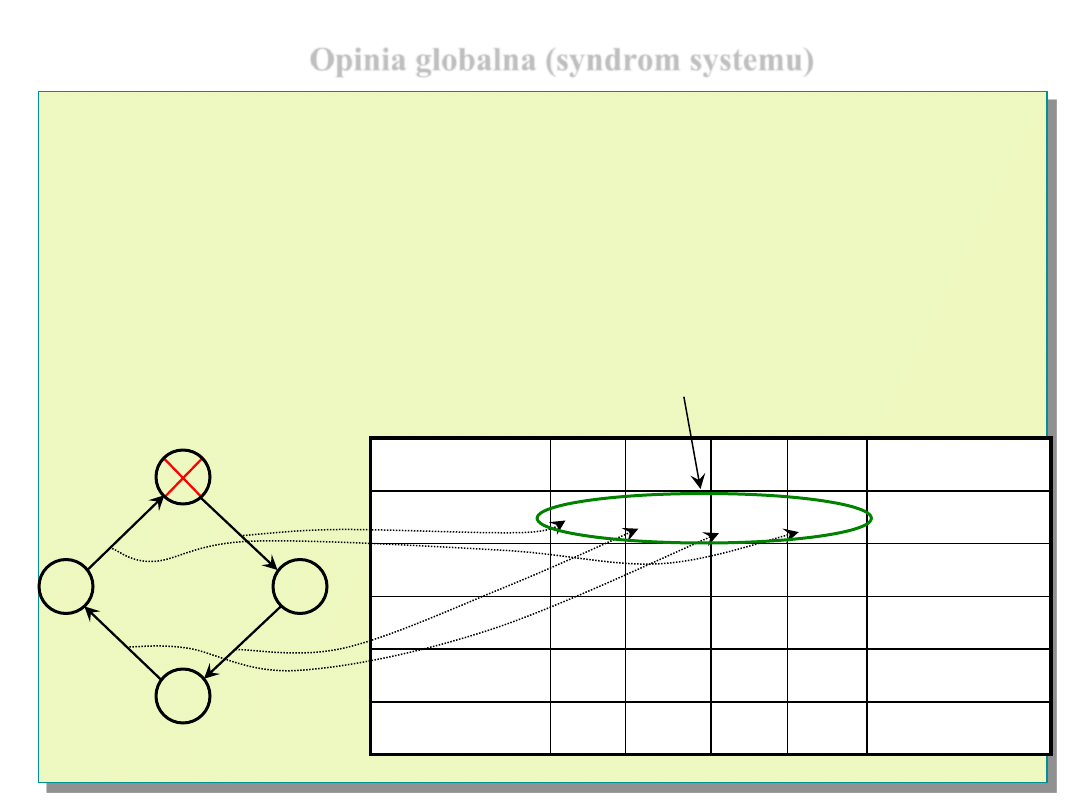
Opinia globalna (syndrom systemu)

Wynik testu

Dla ustalonego G (G=<E, U>) po

określonym uporządkowaniu opinii

(wydanych przez wszystkie komputery,

które testują inne komputery)

otrzymamy |U| - wymiarowy wektor binarny nazywany

opinią globalną

systemu (syndromem systemu).

Opinia globalna

d

12

d

23

d

34

d

41

Niezdatności

A

e

1

B

e

2

C

e

3

D

e

4

E

e

2

, e

3

e

1

e

2

e

3

e

4

x

0

0

1

Opinia globalna

Z. Zieliński –Diagnostyka systemów

29

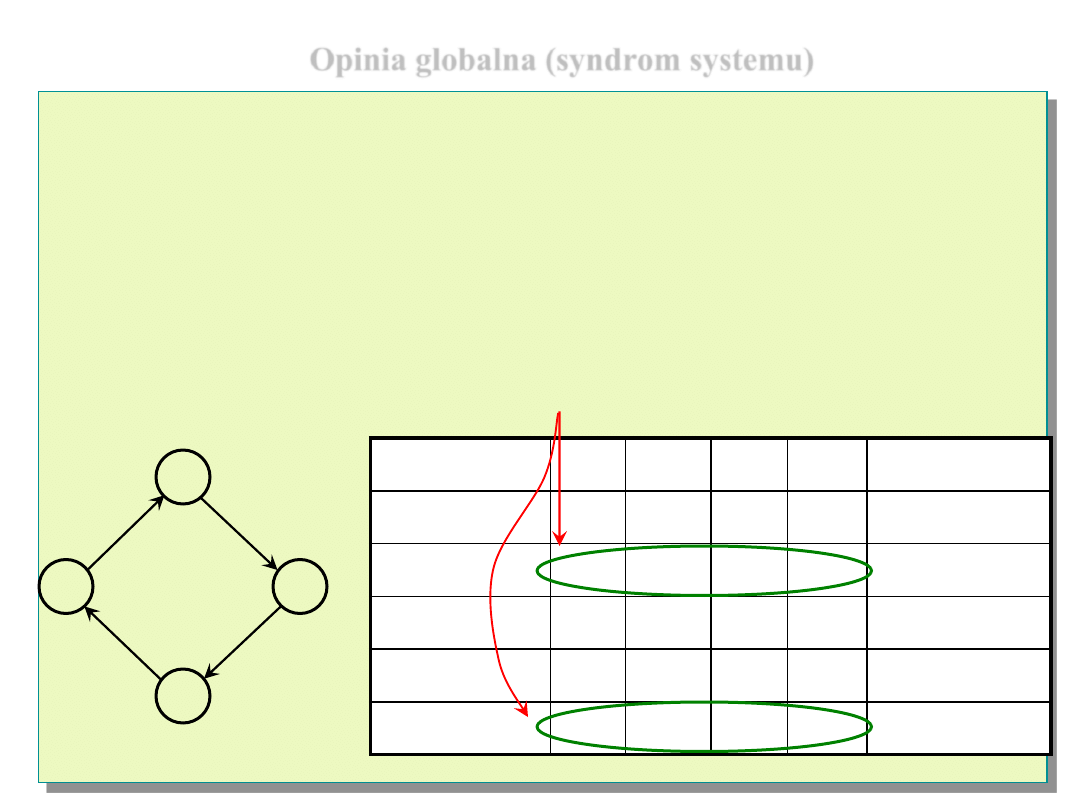
Opinia globalna (syndrom systemu)

Dla ustalonego G (G=<E, U>) po

określonym uporządkowaniu opinii

(wydanych przez wszystkie komputery,

które testują inne komputery)

otrzymamy |U| - wymiarowy wektor binarny nazywany

opinią globalną

systemu (syndromem systemu).

Opinia globalna

d

12

d

23

d

34

d

41

Niezdatności

A

e

1

B

e

2

C

e

3

D

e

4

E

e

2

, e

3

e

1

e

2

e

3

e

4

x

0

0

1

1

x

0

0

0

1

x

0

0

0

1

x

1

x

x

0

Opinia globalna

Z. Zieliński –Diagnostyka systemów

30

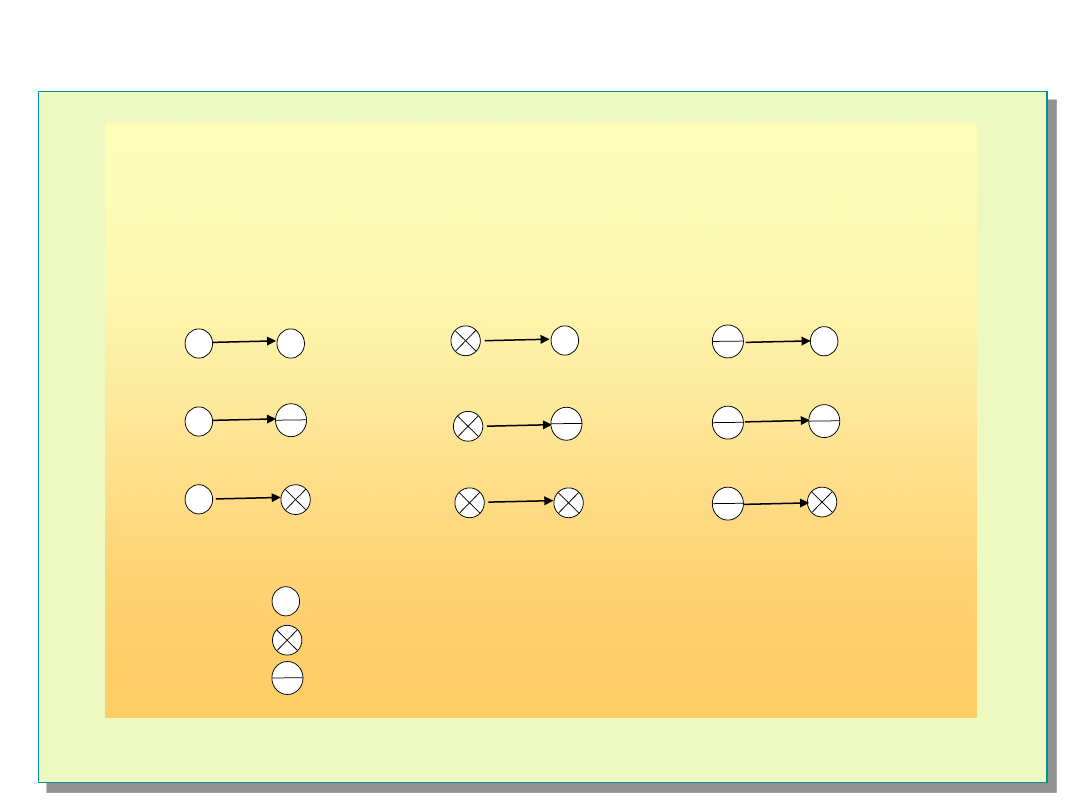
Interpretacja wyników testów – niezdatności przemijające

Model z symetrycznym unieważnianiem testu

0

1

x

x

x

x

x

x

x

- jednostka zdatna

- jednostka z niezdatnością trwałą

- jednostka z niezdatnością przemijającą

Z. Zieliński –Diagnostyka systemów

31

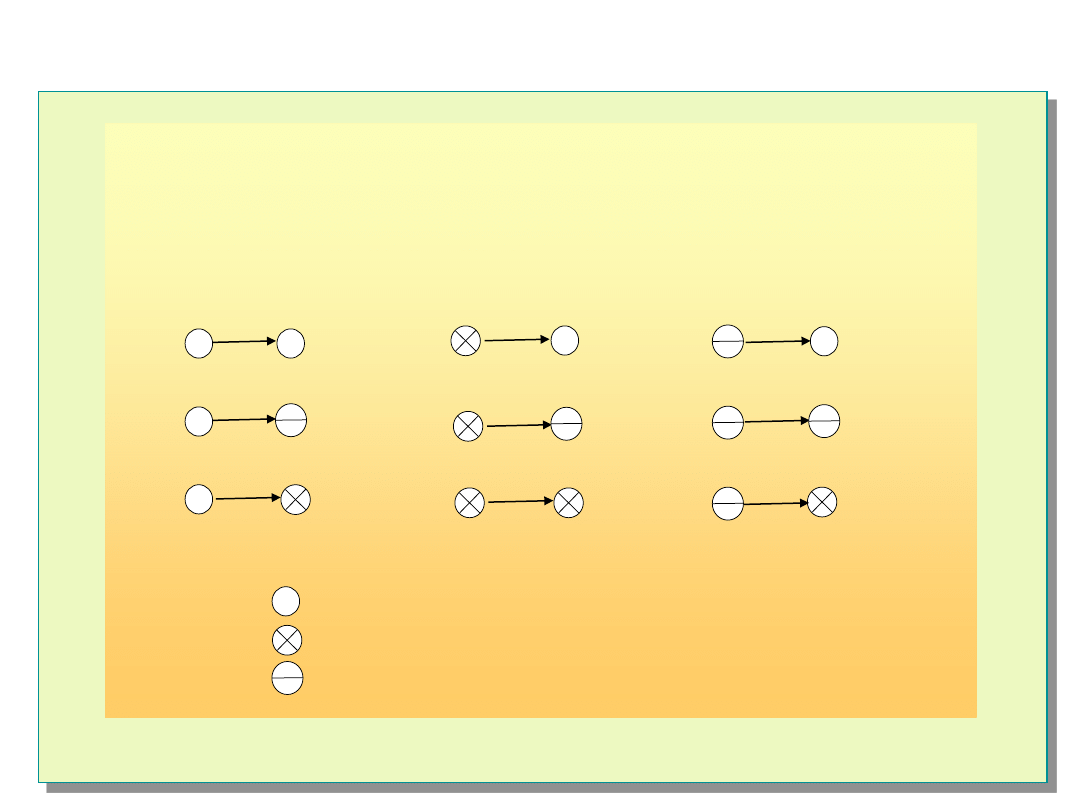
Interpretacja wyników testów – niezdatności przemijające

Model z asymetrycznym unieważnianiem testu

0

1

1

x

1

x

x

x

x

- jednostka zdatna

- jednostka z niezdatnością trwałą

- jednostka z niezdatnością przemijającą

Z. Zieliński –Diagnostyka systemów

32

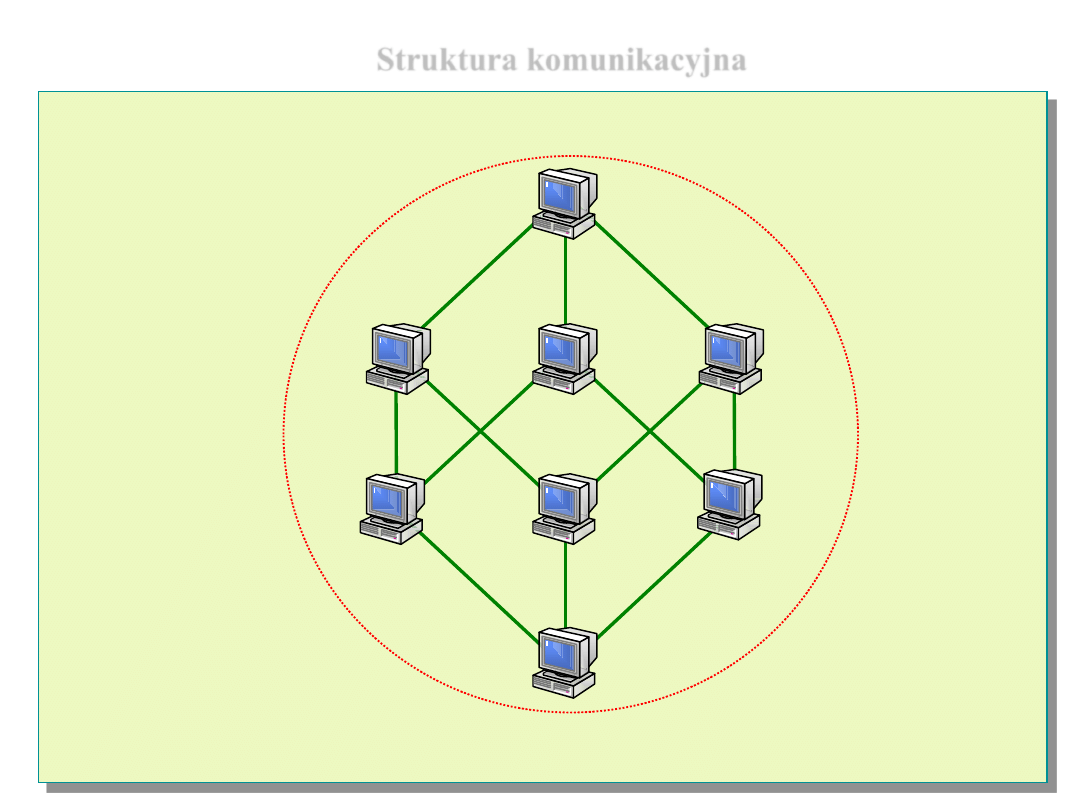
Struktura komunikacyjna

Struktura hipersześcianu

,

G

E U





(001)

(000)

(010)

(110)

(101)

(111)

(011)

(100)

|

| 2

n

E



1

|

|

2

n

U

n



 

H

3

Z. Zieliński –Diagnostyka systemów

34

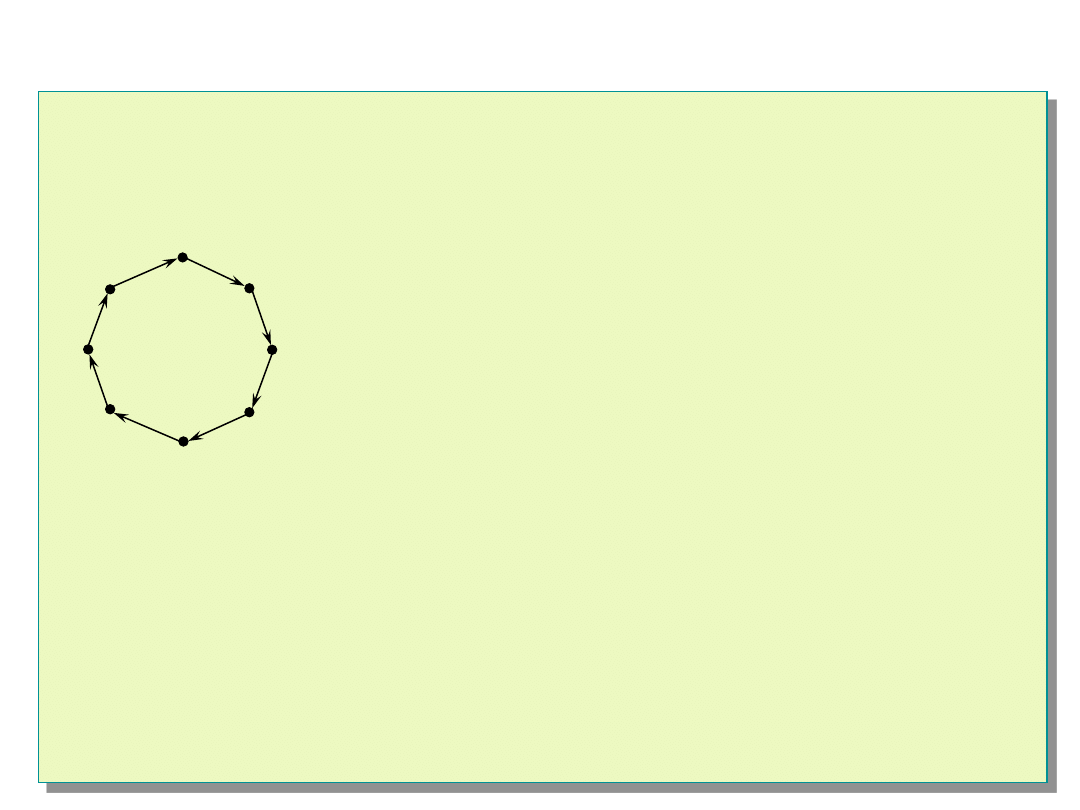
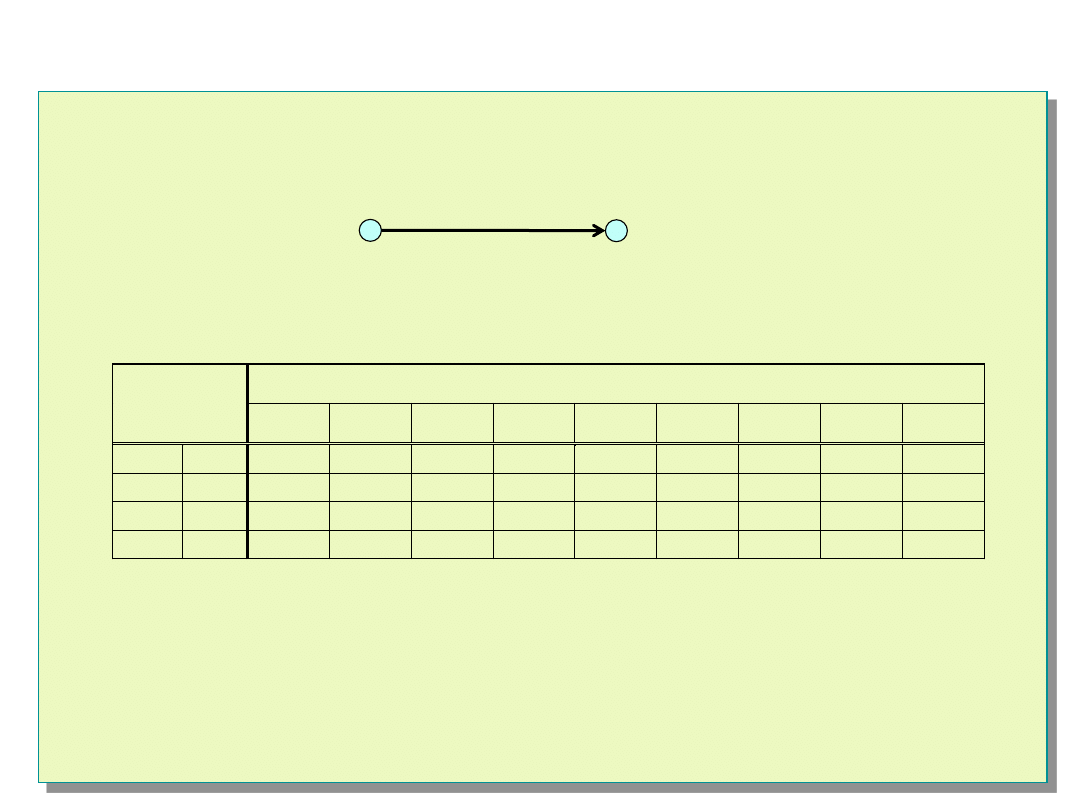
Graf opiniowania diagnostycznego - przykład

e

3

e

2

e

1

e

0

e

4

e

5

e

6

e

7

Przykład grafu opiniowania diagnostycznego o postaci

cyklu Hamiltona dla |E| = 8.

35

Oznaczenia

Niech oznacza stan niezawodnościowy sieci ,

- stan zdatności

- oznacza zbiór takich stanów niezawodnościowych systemu, że

.

Dla modelu PMC: jeżeli element jest w stanie zdatności, to jego

opinia o stanie niezawodnościowym elementu

jest poprawna (zgodna z rzeczywistym stanem niezawodnościowym

elementu ) natomiast w przeciwnym przypadku - przypadkowa, to

jest

oraz

1

( ,...,

)

E

n

n

n



0

( )

0

E

n



m

N

1

E

n

n

m

 



i

e

(

,

, ,

)

i

j

i

j

d

e e

n n





j

e

j

e

(

,

, 0,

)

i

j

j

j

d

e e

n

n







(

,

,1,

)

(

{0,1})

i

j

j

d

e e

n

x x









Inne modele diagnostyki systemowej

i

n

j

n

(

,

, ,

)

i

j

i

j

d e e

n n





D



W

D

BGM

D

Y

D

D



D



PMC

D

pT

D

0

D

0

0

0

0

0

0

0

0

0

0

x

0

1

1

1

1

1

1

1

1

x

x

1

0

0

1

x

0

0

1

x

x

x

1

1

1

1

1

0

x

x

x

x

x

i

e

j

e

Z. Zieliński –Diagnostyka systemów

37

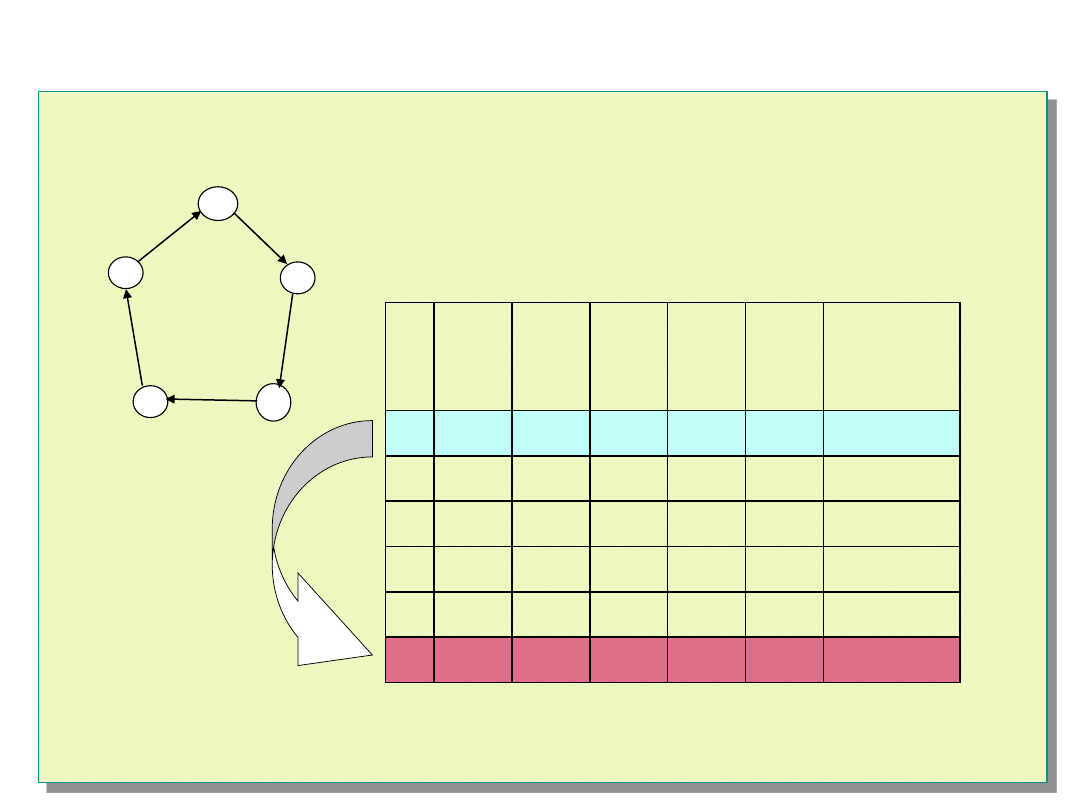
Miary diagnozowalności

System jest jednokrokowo m–diagnozowalny

, jeżeli

wszystkie uszkodzone jednostki mogą być zlokalizowane

na podstawie jednego syndromu wyników testowania, o

ile liczba aktualnie uszkodzonych jednostek nie

przekracza m.

System jest wielokrokowo m–diagnozowalny

, jeżeli co

najmniej jedna niezdatna jednostka może być

zlokalizowana na podstawie jednego syndromu wyników

testowania, o ile liczba aktualnie uszkodzonych jednostek

nie przekracza m

.

Z. Zieliński –Diagnostyka systemów

38

Przykład – system 1-diagnozowalny – model PMC

1

2

5

4

3

d

12

d

23

d

34

d

45

d

51

n

(węzły

niezdatne)

a

x

0

0

0

1

1

b

1

x

0

0

0

2

c

0

1

x

0

0

3

d

0

0

1

x

0

4

e

0

0

0

1

x

5

f

x

x

0

0

1

{1,2}

Opinie (syndromy)

nierozróżnialne

Z. Zieliński –Diagnostyka systemów

39

Problemy diagnostyki systemowej

1. Problem opisowy:

określenie warunków koniecznych i wystarczających,
które musi spełniać przydział testów (struktura
diagnostyczna), aby uzyskać określone właściwości
diagnostyczne.

2. Problem diagnozowalności:

ocena poziomu diagnozowalności systemu.

Struktura opiniowania diagnostycznego

Strukturę opiniowania diagnostycznego systemu (sieci

komputerowej), przedstawia się w postaci spójnego digrafu

(unigrafu zorientowanego)

bez pętli, w którym łuk oznacza, że element systemu

(komputer), wyraża opinię (na podstawie wyniku testowania) o

stanie niezawodnościowym elementu .

7

1

2

6

5

3

4

,

G

E U

 



,

e e

 





e



e



42

Wzorzec opinii diagnostycznych

Numerując łuki grafu G i znając stan niezawodnościowy

elementu, który jest początkowym węzłem łuku (o określonym

numerze), w stanie niezawodnościowym n

wyznaczamy parę

którą nazwiemy wzorcem opinii diagnostycznych struktury G ,

dla stanu niezawodnościowego n.

:

( ),

d n n





1

( ( )

( ( ),...,

( ) ),

( ) {0,1, },

i

U

d n

d n

d

n

d n

x





{1,...,

}),

i

U



43

Oznaczenia

Wektor

przedstawiający wszystkie możliwe opinie, wyrażone przez

elementy systemu nazywamy opinią globalną.

Opinia globalna jest syndromem stanu niezawodnościowego

systemu - stanowi podstawę do wnioskowania o rozpoznawanym

stanie niezawodnościowym systemu.

1

( ,...,

),

{0,1},

i

U

d

d

d

d





{1,...,

},

i

U



44

Oznaczenia

Znajomość zbioru

pozwala określić, dla zaobserwowanej opinii globalnej

zbiór alternatywnych stanów niezawodnościowych systemu -

(zbiór, którego elementem jest rozpoznawany

stan niezawodnościowy systemu),

{

( ),

:

}

m

d n n

n

N







( )

N d

( )

N d

{

:

( )

})

m

n

N

d

d n







 

[

( )

]

d

d n



  

[

{1,...,

}: ( ( )

)

(

( ))]

i

i

i

i

U

d n

x

d

d n

 

 



([(

( )

)]

[

( )

])

d

d n

d

d n

d



  





45

Status niezawodnościowy

Niech oznacza zbiór tych elementów

systemu, które w każdym z alternatywnych stanów niezdatności

(dla opinii globalnej d), mają jednakowy stan niezawodnościowy.

Opinia globalna d, określa status niezawodnościowy elementów

zbioru

Elementy zbioru

nie mają określonego statusu.

( ) (

{0,1})

E

d







1

( )

E d

0

( )

E d

( )

\

E d

E



1

{

( )

E d

0

( )}

E d

46

Wnikliwość rozpoznania stanu niezdatności

Wektor

taki, że

oraz

nazywamy bezpośrednią wnikliwością rozpoznania stanu

niezdatności systemu przez opinię globalną d.

:

1

( )

( ( ),...,

( )), ( ) {0,1, }

i

E

n d

n d

n

d

n d

x





(

( ))

( ( )

)

i

i

e

E

d

n d











(

i

e



( ))

E d

( ( )

)

i

n d

x





Klasy struktur opiniowania diagnostycznego

Dwie podstawowe klasy struktur:

- struktury jednoznacznie (jednokrokowo-)

m-diagnozowalne

- struktury (niejednoznacznie) sekwencyjnie

m-diagnozowalne



Dla struktury (jednokrokowo) m-diagnozowalnej, każda

(możliwa) opinia globalna identyfikuje stan

niezawodnościowy systemu;



Dla struktury sekwencyjnie m-diagnozowalnej - każda

(możliwa) opinia globalna nie identyfikuje każdego stanu

niezdatności systemu lecz określa status, co najmniej,

jednego niezdatnego elementu systemu.

:

0

( , ) \

:

( )

1

d

D m G

d

N d

 



1

0

( , ) \

:

( )

d

D m G

d

E d

 

 

Z. Zieliński –Diagnostyka systemów

48

Warunki konieczne – model PMC

Twierdzenie o warunkach koniecznych

W m-diagnozowalnym systemie S z grafem opiniowania diagnostycznego
G (G =<E, U>) spełnione są warunki:

a)

2

1,

| E |

m +

 

b)

( )

,

;

-

e m e

E







Z. Zieliński –Diagnostyka systemów

49

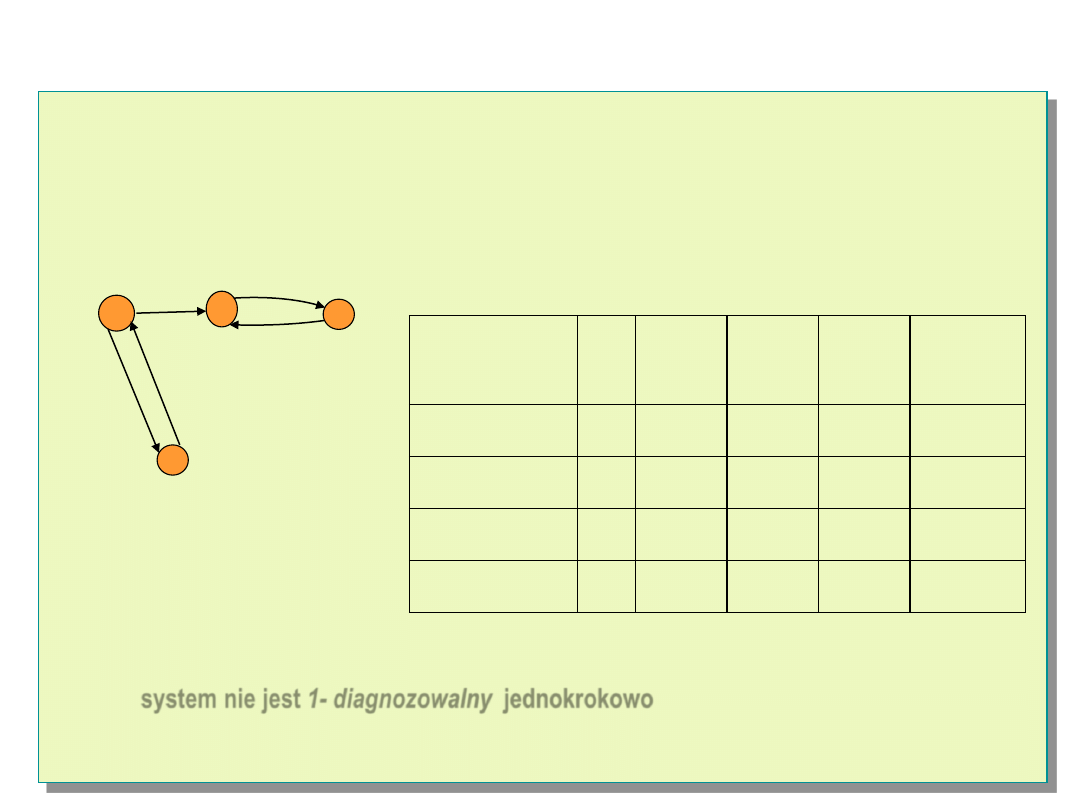
Warunki konieczne – model PMC - przykład

Warunki a) i b) twierdzenia są konieczne lecz nie są wystarczające :

1

2

4

3

węzły

niezdatne

d

12

d

13

d

21

d

34

d

43

(1)

x

x

1

0

0

(2)

1

0

x

0

0

(3)

0

1

0

x

1

(4)

0

0

0

1

x

Ponieważ syndromy testu przy niezdatnych węzłach (1) i (2) są nierozróżnialne –

system nie jest 1- diagnozowalny jednokrokowo

Z. Zieliński –Diagnostyka systemów

50

Warunki konieczne – model BGM

Jeżeli system S z grafem opiniowania diagnostycznego G (G =<E, U>) jest
systemem m-diagnozowalnym to:

a)

|

|

2,

E

m





b)

( )

,

e

m







Z. Zieliński –Diagnostyka systemów

51

Warunki konieczne i wystarczające (PMC)

m

Z

Z

Z

E

Z

















2

/

)

(

:

)

(

1

Dla modelu PMC warunki wystarczające m-diagnozowalności systemu zostały
sformułowane przez:

[Allan, Kameda, Toida] :

System S z grafem opiniowania diagnostycznego G (G =<E, U>) jest systemem m-
diagnozowalnym wtedy i tylko wtedy, gdy spełnione są warunki konieczne oraz

gdzie

)

(

1

Z





jest zbiorem testerów elementów należących do Z.

[ Hakimi, Amin ] :

( 0

1

:

2

) :

(

)

p m - E

E | E | = | E | - m + p |

E |> p







  









Z. Zieliński –Diagnostyka systemów

52

Warunki konieczne i wystarczające (PMC)

[Kohda] :

System S z grafem opiniowania diagnostycznego G (G =<E, U>) jest systemem
m-diagnozowalnym wtedy i tylko wtedy, gdy dla każdej pary

takiej że |E

1

| = |E

2

|= m istnieje co najmniej jeden test z ( E - E

1

– E

2

)

do ( E

1

– E

2

) U ( E

2

– E

1

).

E

E

E



2

1

,

Z. Zieliński –Diagnostyka systemów

53

Wyznaczanie optymalnych oraz najtańszych struktur OD

1.

Spójna, optymalna struktura OD ma dokładnie jedną składową

silnej spójności.

2.

Jeżeli podgraf < E \ {e’}>

G

spójnego grafu G, jest

m-diagnozowalnym grafem OD oraz ||Γ

-1

(e’)||≥ m,

to graf G również jest m-diagnozowalnym grafem OD.

Z. Zieliński –Diagnostyka systemów

54

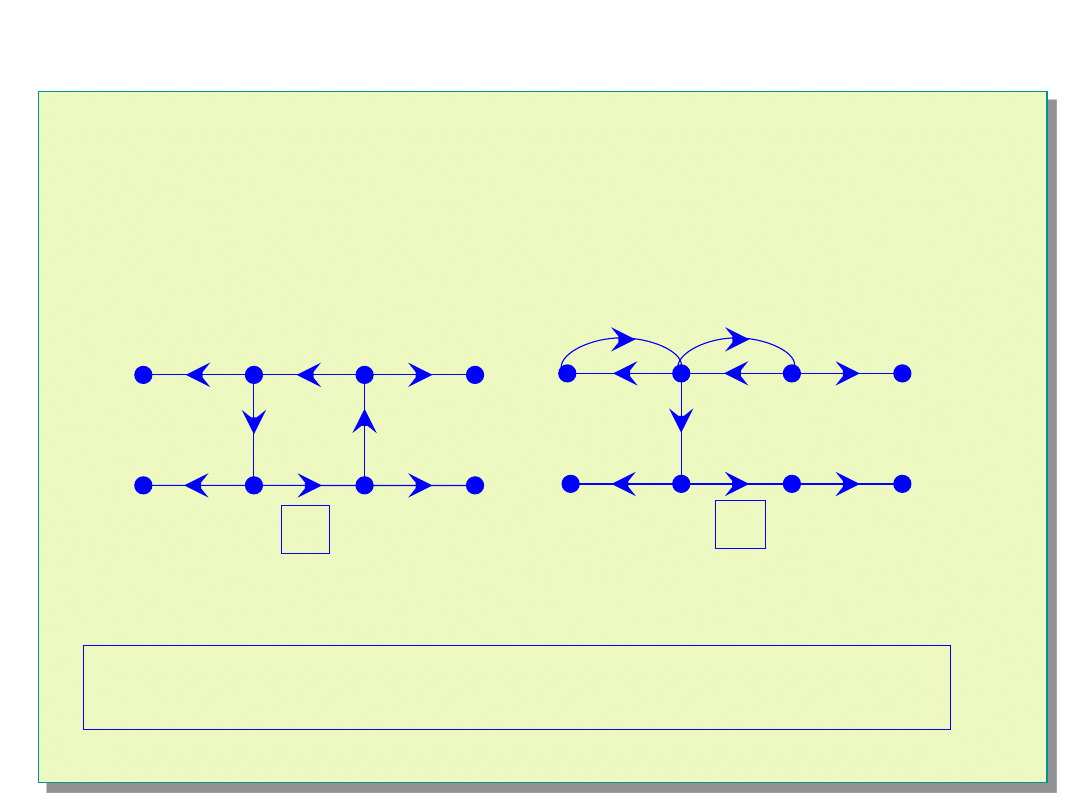
Wyznaczanie optymalnych oraz najtańszych struktur OD

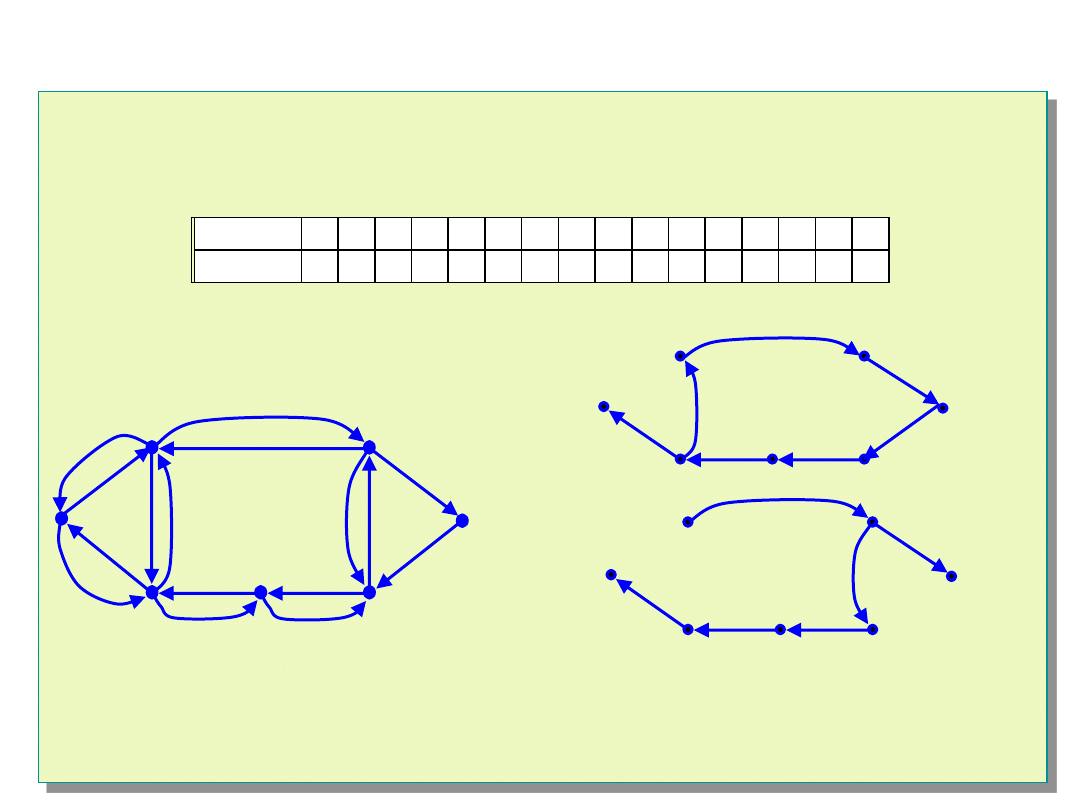
Składową silnej spójności spójnej 1-diagnozowalnej struktury
OD jest albo cykl zorientowany rzędu co najmniej trzeciego
albo para incydentnych cykli elementarnych.

a)

b)

Przykłady 1-diagnozowalnych struktur OD rzędu ósmego

(a-spójna struktura 1-optymalna; b)-spójna struktura 1-quasi-optymalna)

Z. Zieliński –Diagnostyka systemów

55

Tabela. Uogólnione koszty testowania

u

a b c d e f g h i

j k l

ł m n o

K(u)

5 4 1 2 3 2 3 2 2 5 3 3 5 4 4 4

1

2

4

3

5

6

7

a

b

c

d

e

f

g

h

i

j

l

k

m

n

o

ł

Przykład ekonomicznego grafu
opiniowania diagnostycznego

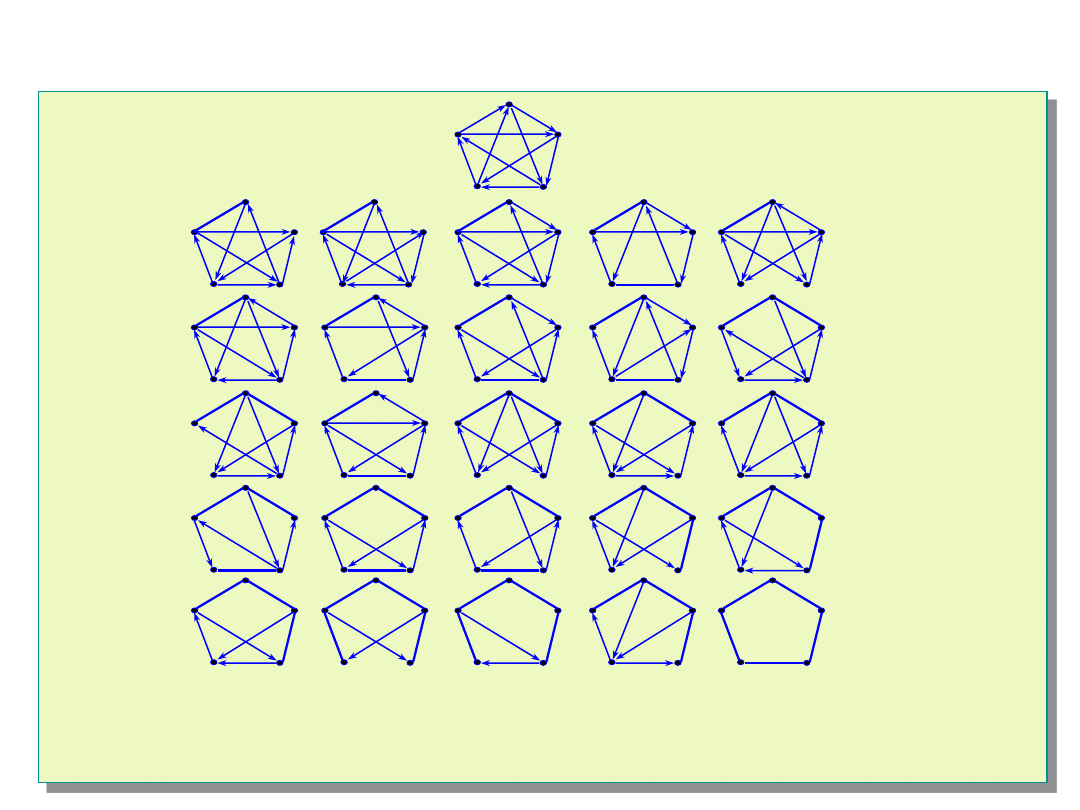
Najtańsze (względem struktury
przedstawionej obok) struktury 1-diagnozowalne

Przykład najtańszych struktur 1-diagnozowalnych

Z. Zieliński –Diagnostyka systemów

56

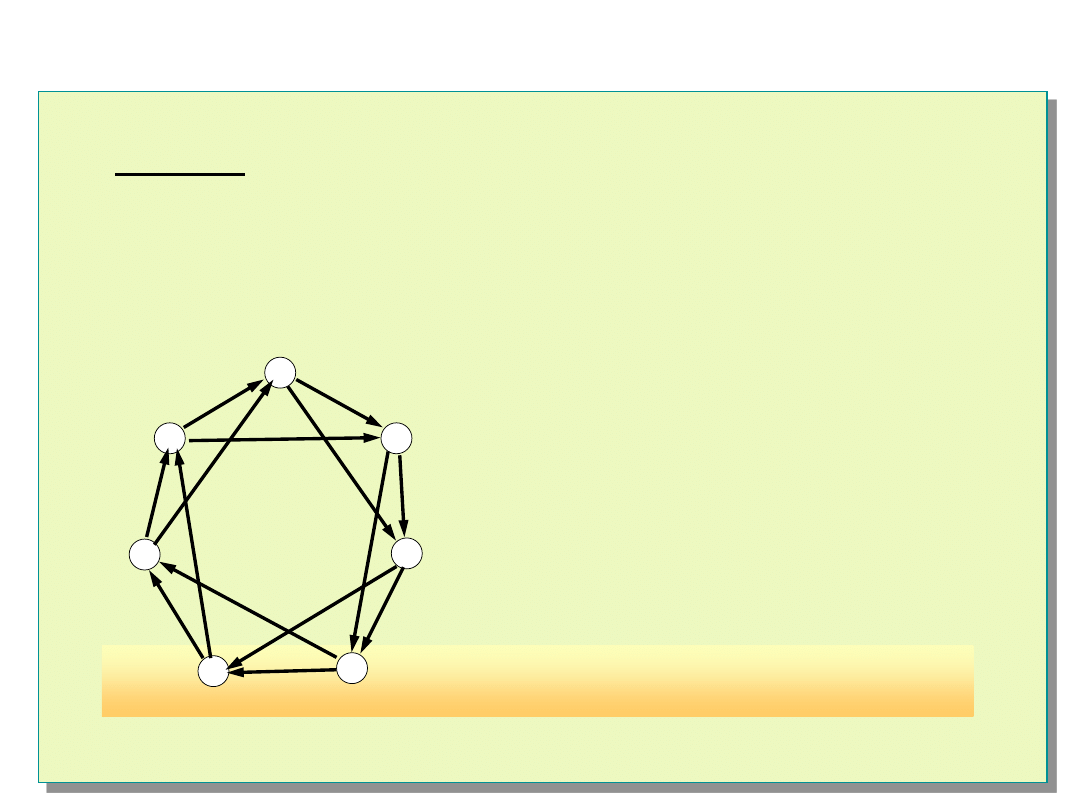
Struktury optymalne 2-diagnozowalne

(dla modelu PMC) rzędu piątego

Z. Zieliński –Diagnostyka systemów

57

Systemy częściowo diagnozowalne

Klasyczne podejście do systemów m-diagnozowalnych nie
zdaje egzaminu przy identyfikacji stanów
niezawodnościowych, dla których liczba niezdatnych
jednostek jest większa niż m.

W konkretnym systemie interesuje nas często określenie,
czy dany (krytyczny ze względu na aplikacje ) zbiór stanów
niezawodnościowych jest jednoznacznie diagnozowalny.

Z. Zieliński –Diagnostyka systemów

58

Systemy częściowo diagnozowalne

Przykład.

System typu D

δ,m

, składający się z k=7 jednostek, z których każda

(i=0, 1, …, k-1) testuje m innych jednostek wg zależności:
i + δ mod k,

i + 2 δ mod k, …, i + (m-1)δ mod k.

Dla δ=1 i m=2 :

7

1

2

6

5

3

4

System jest 2-diagnozowalny dla modelu z
symetrycznym unieważnianiem testu.

Rozpatrując ten system w odniesieniu do klasy
niezdatności o liczności ≤ 3 mamy

jednoznacznie diagnozowalne:

wszystkie stany niezawodnościowe o liczbie

niezdatności 1;

14 z 21 stanów o liczbie niezdatnych jednostek 2

;

21 z 35 stanów o liczbie niezdatności 3

.

Z. Zieliński –Diagnostyka systemów

59

Systemy nadmiarowo diagnozowalne

System jest

m/p

– diagnozowalny, jeżeli syndrom systemu dla stanu

niezawodnościowego

pozwala na izolację wszystkich jednostek ze zbioru , z których co
najwyżej p jednostek może być wolnych od niezdatności

gdzie jest zbiorem niezdatnych jednostek w stanie .

,

'

m

N

n



W systemach tego typu dopuszcza się pewną liczbę (p)
niepoprawnie diagnozowanych jednostek.

n



)

(n

F



,

)

(

p

n

F

F









F



Z. Zieliński –Diagnostyka systemów

60

Systemy sekwencyjnie diagnozowalne

System jest sekwencyjnie (wielokrokowo) m – diagnozowalny,
jeżeli co najmniej jedna niezdatna jednostka może być
zlokalizowana na podstawie jednego syndromu wyników
testowania, o ile liczba aktualnie uszkodzonych jednostek nie
przekracza m.

W tym przypadku proces diagnozy i naprawy przeplatają się nawzajem.
Przyjmuje się, że na podstawie syndromu jesteśmy w stanie określić
tylko pewien niepusty podzbiór uszkodzonych jednostek. Następnie
wymienia się je na zdatne i ponawia się testowanie. Proces powtarzany
jest dopóty, dopóki nie stwierdzi się poprawnego funkcjonowania
wszystkich jednostek systemu (wymagana liczba iteracji



m, gdzie m

jest liczbą niezdatności).

Z. Zieliński –Diagnostyka systemów

61

Systemy sekwencyjnie diagnozowalne

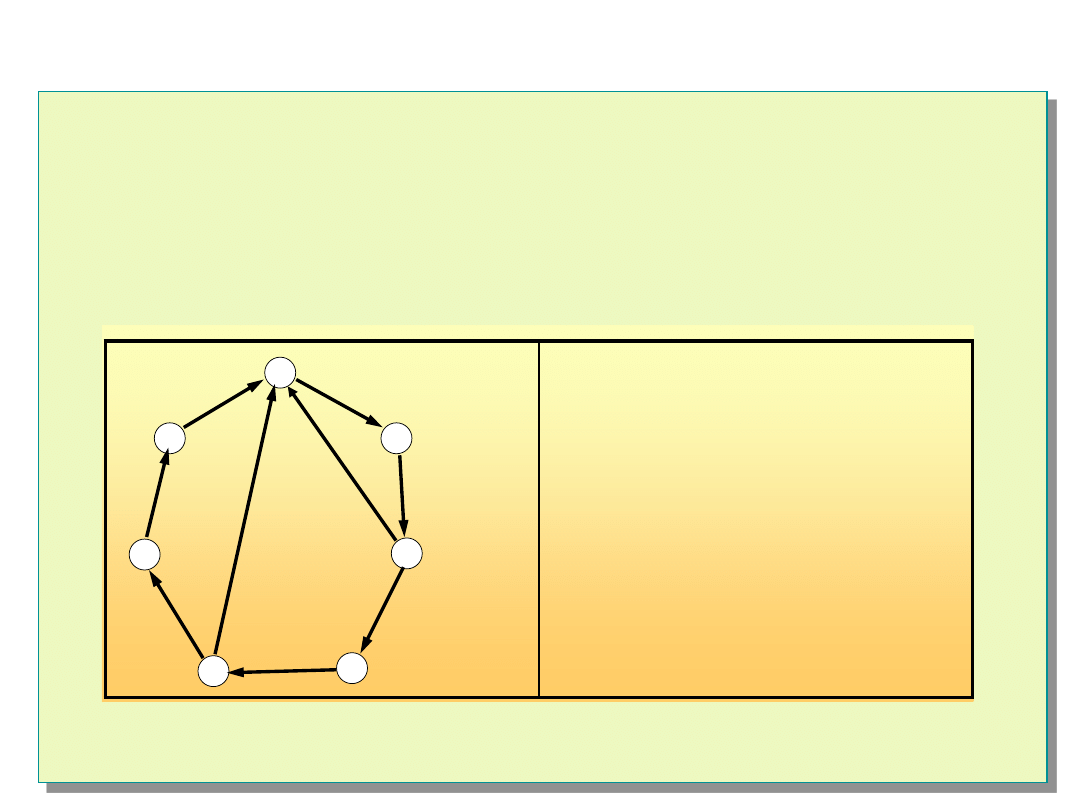
Można wykazać, że silnie spójny graf posiadający węzeł, który
jest testowany przez m innych węzłów, a każdy z nich z kolei jest
testowany przez co najmniej jeden (inny) węzeł jest grafem

sekwencyjnie

m-diagnozowalnym.

Przykład grafu 3-diagnozowalnego

sekwencyjnie

7

1

2

6

5

3

4

Z. Zieliński –Diagnostyka systemów

62

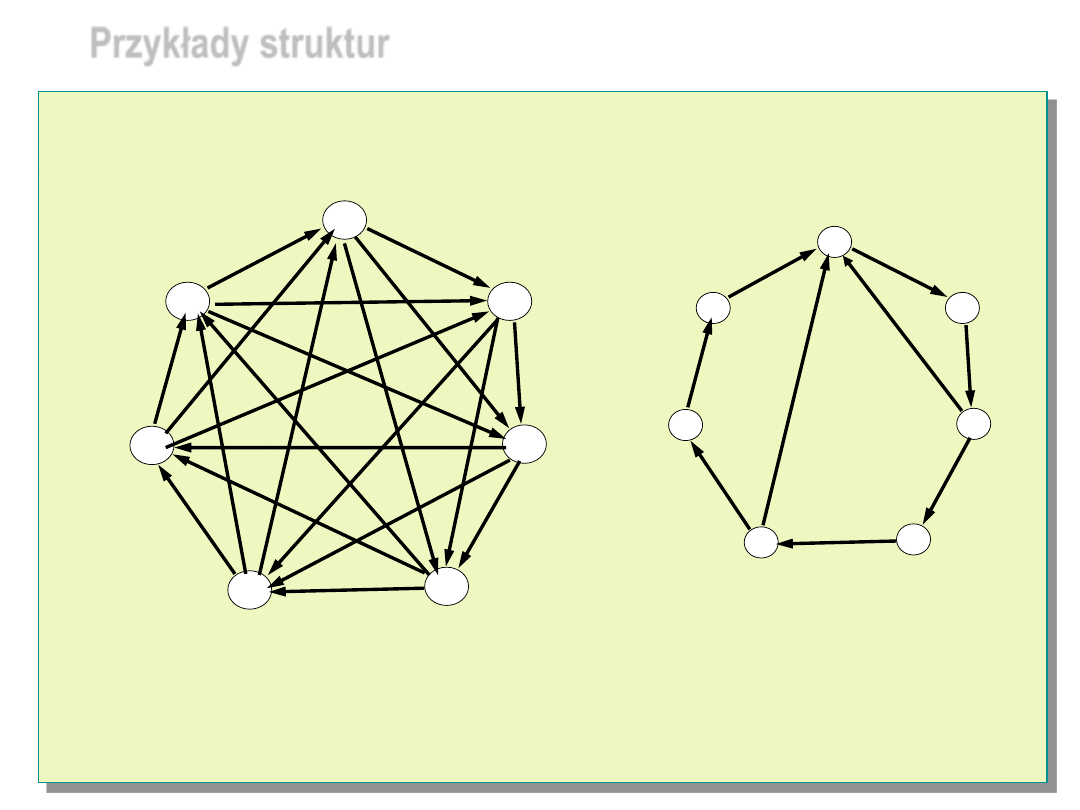
Przykłady struktur

7

1

2

6

5

3

4

Struktura jednokrokowo
3-diagnozowalna

7

1

2

6

5

3

4

Struktura sekwencyjnie
3-diagnozowalna

Z. Zieliński –Diagnostyka systemów

63

Ogólna charakterystyka struktur opiniowania diagnostycznego dla strategii

wielokrokowej

Struktura , jest strukturą sekwencyjnie m-diagnozowalną wtedy i

tylko wtedy, gdy

:

0

[

\

:

( )

]

m

n N

N

N

n

d n











 



  

(

( ) )]

n N

E

n













0

Z. Zieliński –Diagnostyka systemów

64

Ogólna charakterystyka struktur opiniowania diagnostycznego dla strategii

wielokrokowej



Charakterystyka grafu G, który jest grafem m-diagnozowalnym

sekwencyjnie (m.d.s) jest znacznie trudniejsza niż w przypadku

systemów jednoznacznie diagnozowalnych i jak do dzisiaj ogólne

warunki dla struktury m.d.s. nie zostały określone.



W projektowaniu struktur typu m.d.s należy kierować się

własnościami wielokrotnych zbiorów niezdatności (stanów

niezawodnościowych) lub poszukiwać struktur m.d.s określonej

klasy.

:

Z. Zieliński –Diagnostyka systemów

65

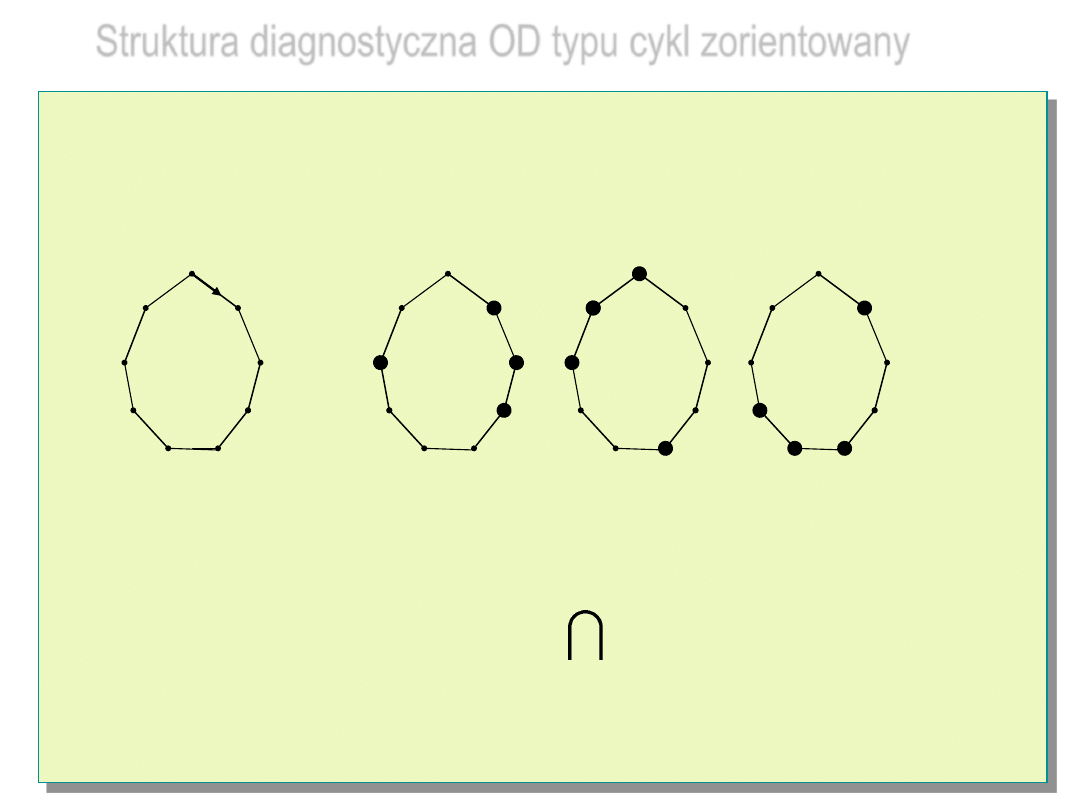
Struktura diagnostyczna OD typu cykl zorientowany

podzbiór alternatywnych stanów niezdatności systemu
dla opinii globalnej

(100100100)

d



1

0

0

Cykl zorientowany rzędu dziewiątego, nie jest strukturą sekwencyjnie
4-diagnozowalną typu PMC

*

*

1

( ) :

( )

P

n N

N

N

d

E n









 

1

0

0

0

1

0

1

n

2

n

3

n

*

1

2

3

{ ,

,

}

N

n n n



Z. Zieliński –Diagnostyka systemów

66

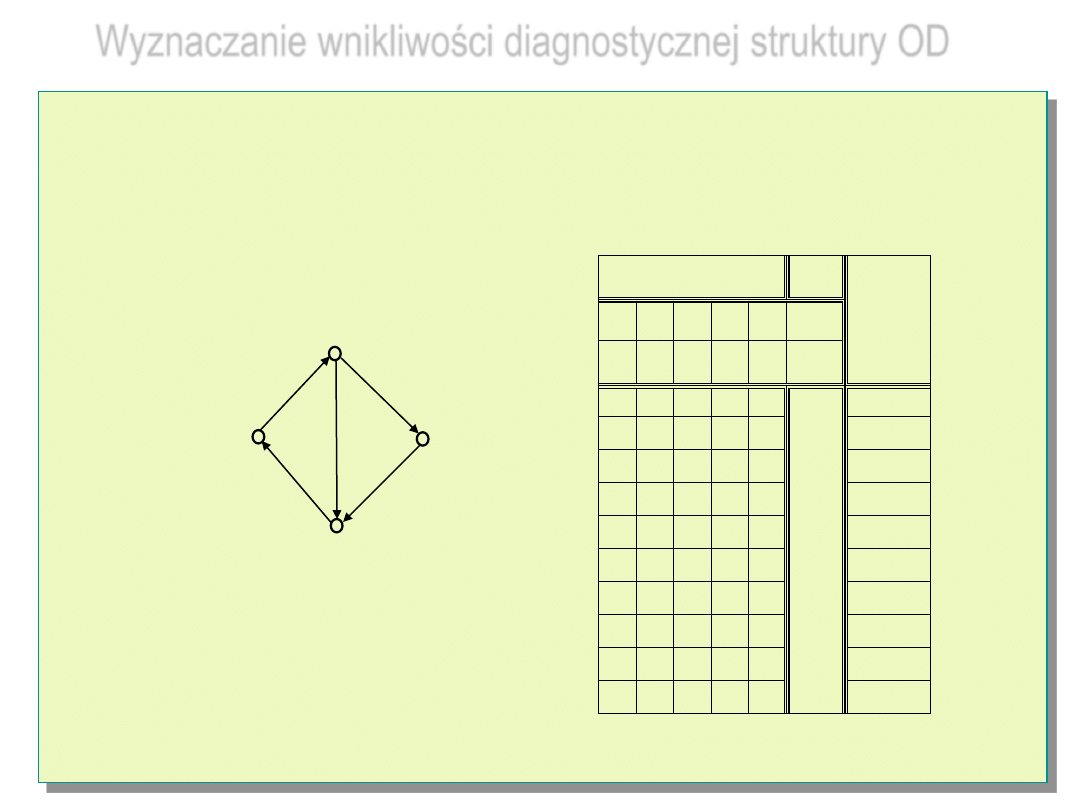
Wyznaczanie wnikliwości diagnostycznej struktury OD

(

,

, )

d e e

n

 





1

2

3

4

1

e



2

3

4

1

3

e



n

x

0

0

1

x

(1000)

1

x

0

0

0

(0100)

0

1

x

0

1

(0010)

0

0

1

x

0

(0001)

x

x

0

1

x

(1100)

x

1

x

1

x

(1010)

x

0

1

x

x

(1001)

1

x

x

0

1

(0110)

1

x

1

x

0

(0101)

0

1

x

x

1

(0011)

1

4

3

2

Wzorzec opinii diagnostycznych tej struktury

2

( )

W G

23.03.12; STAC
24.03.2012 NSTAC

Z. Zieliński –Diagnostyka systemów

67

Wyznaczanie wnikliwości diagnostycznej struktury OD

Wzorzec nie pozwala, z wyjątkiem struktur jednokrokowo m-

diagnozowalnych, określić (w sposób bezpośredni) wnikliwość diagnostyczną

struktury.

Należy go przedstawić w postaci rozłącznych podsześcianów sześcianu

:

( )

m

W

G

U

H

(

( )

{

,

( ) :

( , )})

m

G

N

m G









 





0

[

( )]

[ ( )

](

\

)

m

n N

d n

N

N

N

N

n



















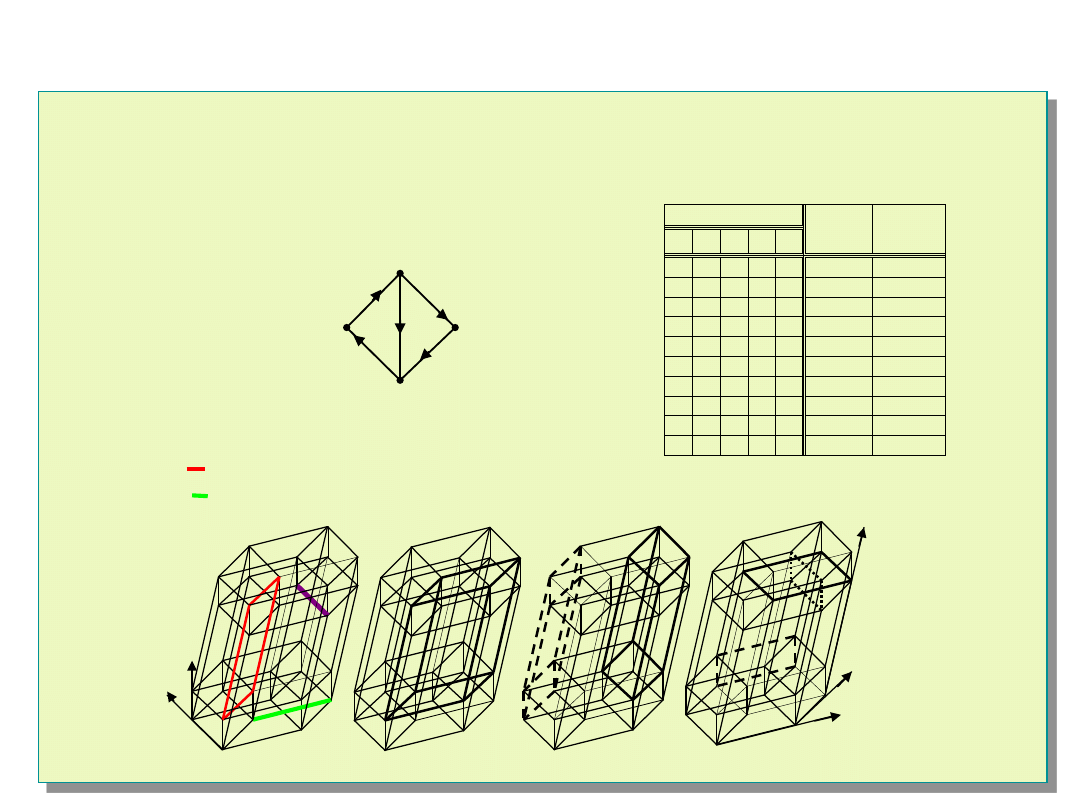
Wyznaczanie wnikliwości diagnostycznej



Zastosowanie działań na sześcianach binarnych

1

n

8

n

2

n

6

n

9

n

3

n

5

n

7

n

10

n e

4

n

d
a

c b

( , )

d u n

1
d a

4

e

2

c b

3

u

n

( )

j n

a

b

c

d

e

x

0

0

1

x

(1000)

1

1

x

0

0

0

(0100)

2

0

1

x

0

1

(0010)

3

0

0

1

x

0

(0001)

4

x

x

0

1

x

(1100)

5

x

1

x

1

x

(1010)

6

x

0

1

x

x

(1001)

7

1

x

x

0

1

(0110)

8

1

x

1

x

0

(0101)

9

0

1

x

x

1

(0011)

10

69

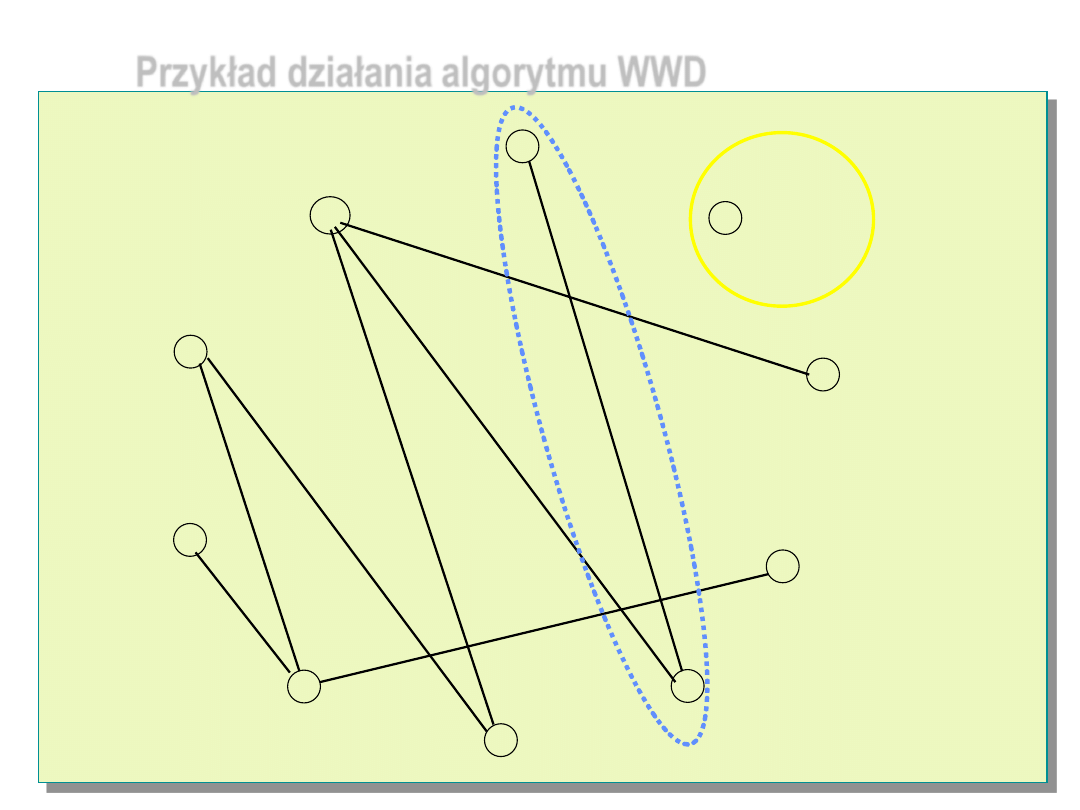
Przykład działania algorytmu WWD

1

2

3

4

10

9

8

7

6

5

(x001x)

(1x000)

(01x01)

(001x0)

(x01xx)

(x1x1x)

(xx01x)

(1x1x0)

(1xx01)

(01xx1)

1

1

0

2

0

1

1

0

70

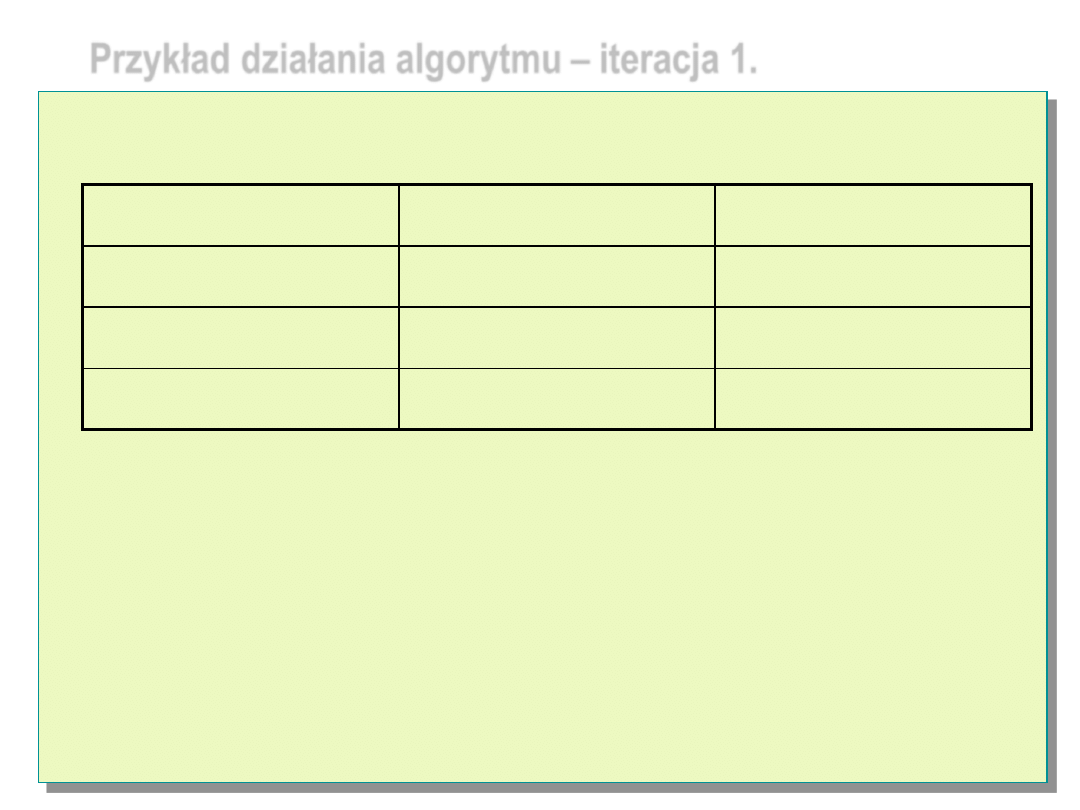
Przykład działania algorytmu – iteracja 1.

(1x000)

(0100)



( )

N



( )

n



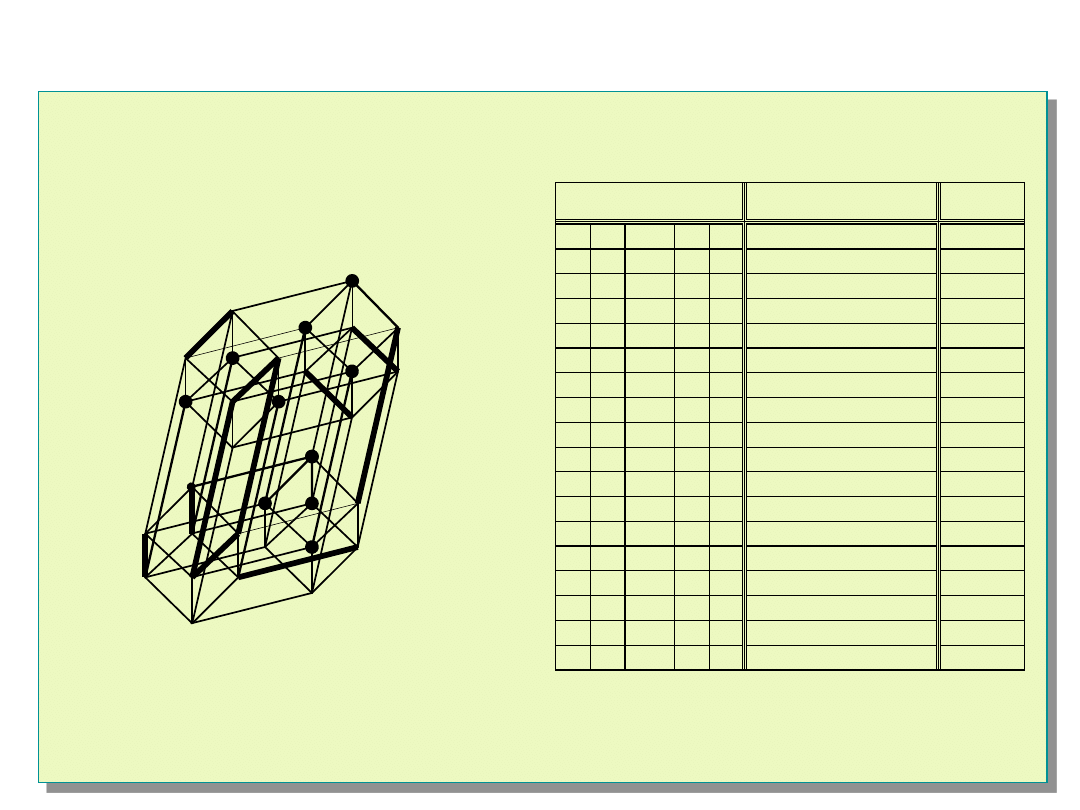
Rezultat działania algorytmu WWD



( )

N



( )

n



1

x

0

0

0

(0100)

x

0

0

1

x

(1000)(1100)

(1x00)

0

1

x

0

1

(0010)(0011)

(001x)

0

0

1

x

0

(0001)(1001)

(x001)

1

0

1

x

0

(1001)(0101)

(xx01)

1

1

1

1

0

(1010)(0101)

(xxxx)

0

1

1

1

0

(1010)

1

1

1

1

1

(1010)

1

1

1

0

0

(0101)

1

0

1

0

1

(0110)(1001)

(xxxx)

1

0

0

0

1

(0110)

1

1

x

0

1

(0110)

0

0

1

0

1

(1001)

x

0

1

1

1

(1001)

0

1

0

1

1

(1100)(1010)(0011)

(xxxx)

0

1

0

1

0

(1100)(1010)

(1xx0)

1

1

0

1

x

(1100)(1010)

(1xx0)

0

1

1

1

1

(0011)(1010)

(x01x)

Miary własności diagnostycznych struktury

Jedną z miar własności diagnostycznych struktury

G

, która nie jest strukturą

(jednokrokowo)

m

-diagnozowalną, może być wektor

( , )

(

m G





1

( , ),

m G



2

( , ),

m G



3

( , ))

m G



,

gdzie:

0

1

( )

1

: ( )

\

( , )

(

( , )

1)

2

m

r

n

N

n

m G

D m G





















;

2

( , )

m G





(

)

1

1

( )

: ( )

(

( , )

1)

2

E G

x

r

n

H

D m G

















;

3

( , )

m G



(

)

1

( )

: ( ) ( )

(

( , )

1)

2

E G

r

n

x

D m G



















,

przy czym

1

E

x

H

oznacza zbiór takich

E

-wymiarowych podsześcianów, które

zawierają składową równą

x

i składową równą 1.

Dla podanego przykładu:

(2, )

(11/ 28,14 / 28,3/ 28)

G





.

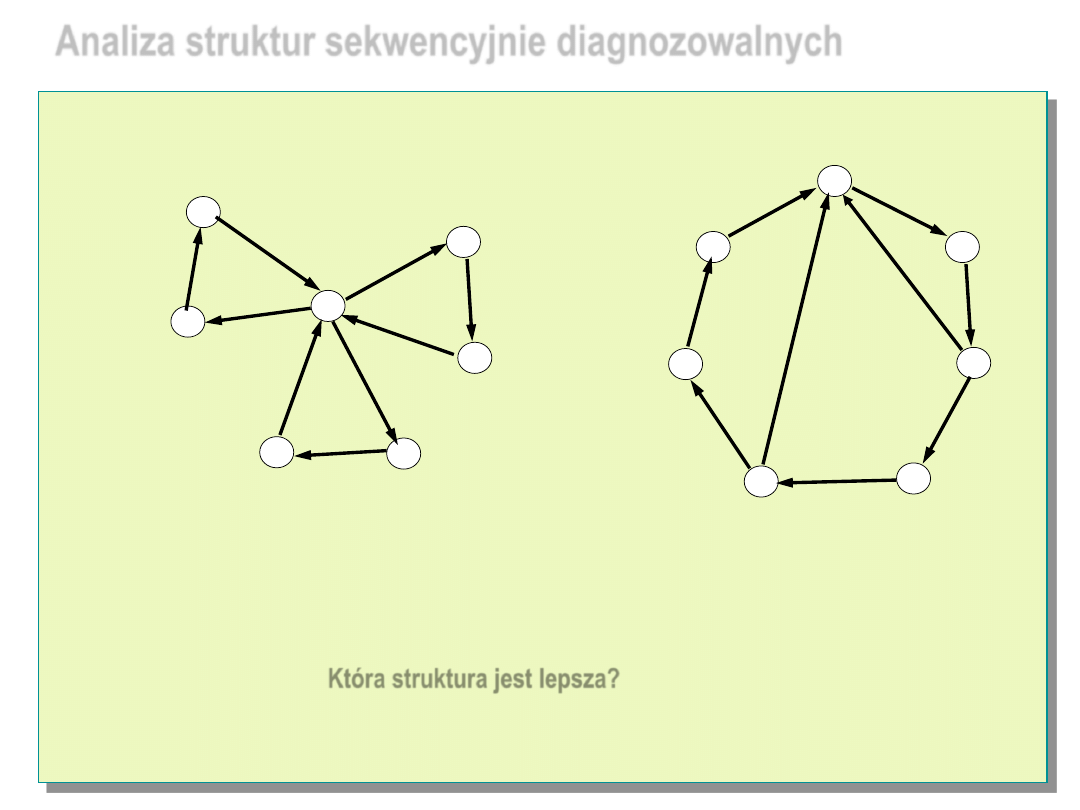
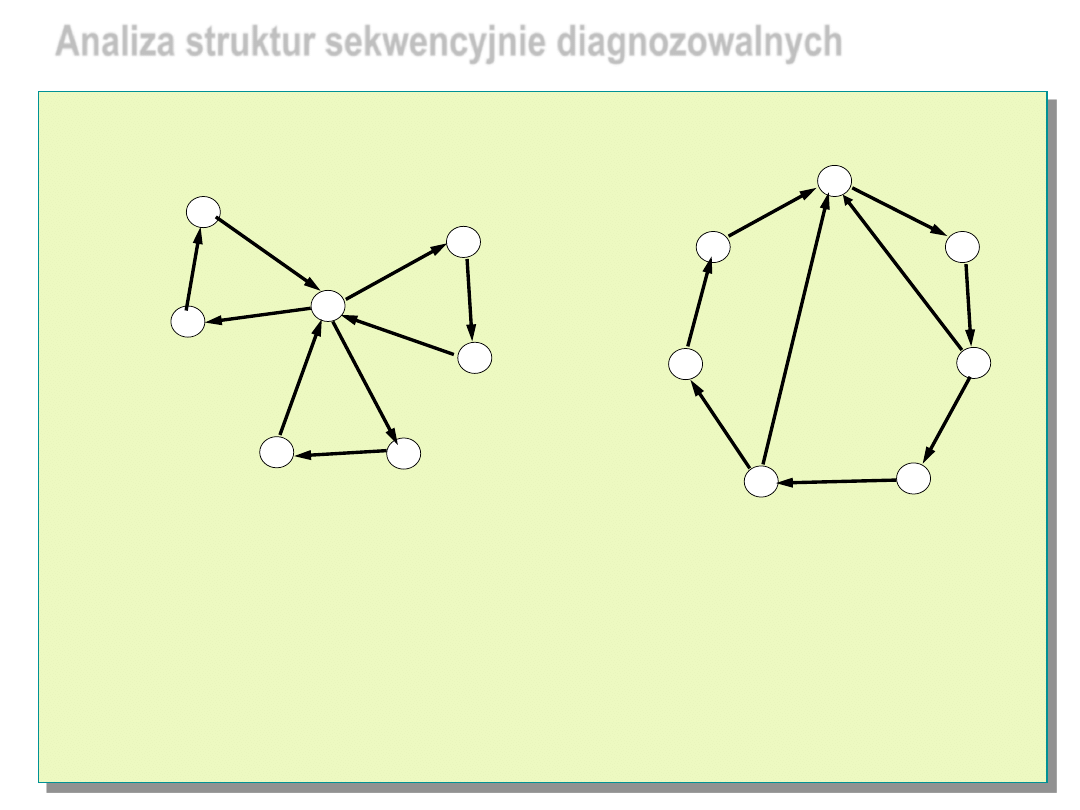
Analiza struktur sekwencyjnie diagnozowalnych

Struktura sekwencyjnie
3-diagnozowalna

7

1

2

6

5

3

4

Struktura sekwencyjnie
3-diagnozowalna

7

1

2

6

5

3

4

Która struktura jest lepsza?

Analiza struktur sekwencyjnie diagnozowalnych

Struktura sekwencyjnie
3-diagnozowalna

7

1

2

6

5

3

4

Struktura sekwencyjnie
3-diagnozowalna

7

1

2

6

5

3

4

1

166 / 376





2

210 / 376





3

0





1

174 / 354





2

180 / 354





3

0





Wzorzec alternatywnych stanów niezdatności struktury



Daje możliwość sprawdzenia różnych miar jakości

struktury opiniowania diagnostycznego opartych o

wnikliwość.



Może być również wykorzystany do realizowania

określonej strategii eksploatowania sieci komputerowej

tj. diagnozowania, regeneracji oraz rekonfiguracji sieci.



Można go także zastosować bezpośrednio w algorytmie

diagnozowania dla struktur sekwencyjnie

diagnozowalnych.

Uogólnienie diagnozowalności struktur OD



Wnikliwość diagnostyczna może stanowić podstawę

określania wielu miar diagnozowalności struktur OD



m-diagnozowalnych (jednoznacznie diagnozowalnych) –

strategia jednokrokowa



sekwencyjnie m-diagnozowalnych (strategia

wielokrokowa)



sekwencyjnie (m,k)-diagnozowalnych (strategia

wielokrokowa)



m/p –diagnozowalnych



i innych

Z. Zieliński –Diagnostyka systemów

77

ALGORYTMY DIAGNOZOWANIA SYSTEMU ROZPROSZONEGO

WG METODY PMC

Ruting IP

Algorytm NEW_SELF.
Algorytm EVENT_SELF.
Algorytmy adaptacyjne

Z. Zieliński –Diagnostyka systemów

78

Algorytm NEW_SELF

Założenia:

1. Maksymalna liczba niezdatnych węzłów jest ograniczona ≤ m;
2. Dla sieci określony jest stały (niezmienny) przydział testów;
3. Każdy węzeł jest testowany przez co najmniej m+1 innych węzłów;
4. Węzły zdatne przekazują raport z testowania do węzłów sąsiednich,

raporty docierają do wszystkich węzłów poprzez węzły pośrednie;

5. Nie przyjmuje się założeń, dotyczących zachowania węzłów

niezdatnych;

6. Każdy węzeł niezależnie od innych określa diagnozę stanu

niezawodnościowego sieci, wykorzystując wyniki testów własnych
oraz otrzymane raporty z węzłów sąsiednich.

Z. Zieliński –Diagnostyka systemów

79

Algorytm NEW_SELF

Sposób działania:



Każdy węzeł testuje swoich sąsiadów i generuje raport dla każdego
otrzymanego rezultatu testu. Raport ten jest przechowywany lokalnie i jest
stopniowo przesyłany do wszystkich węzłów testujących dany węzeł.



Algorytm zapewnia poprawność przesyłanych raportów poprzez
ograniczenie przesyłania raportów pomiędzy węzłami zdatnymi.



Węzeł akceptuje jedynie informacje z innych węzłów, które są przez niego
testowane i ich stan został określony jako zdatny. Potwierdzony raport
wyniku jest przesyłany pomiędzy węzłami zdatnymi w odwrotnym kierunku
niż testy.

i

k

n

j

l

m

o

Z. Zieliński –Diagnostyka systemów

80

Algorytm NEW_SELF

Schemat testowania i walidacji:

1)

węzeł i testuje węzeł j, wynik testu – zdatny;

2)

węzeł i otrzymuje raport od węzła j;

3)

węzeł i testuje węzeł j – wynik – zdatny;

4)

węzeł i zakłada, że informacje diagnostyczne otrzymane w
kroku 2 są potwierdzone (wiarygodne).

W celu zapewnienia poprawnej diagnozy algorytm NEW_SELF

zakłada, że każdy zdatny węzeł otrzymuje raporty
generowane przez inne zdatne węzły. Warunek ten może być
spełniony jeżeli każdy węzeł jest testowany przez m+1
węzłów.

Z. Zieliński –Diagnostyka systemów

81

Algorytm NEW_SELF

Ocena efektywności algorytmu NEW_SELF

Rozważmy system składający się z K węzłów, która ma być

m-diagnozowalny.

Liczba testów:

≥ K



(m + 1)

Liczba komunikatów, potrzebna do przesłania wyników testów:

K

2



(m + 1)

2

Dla 2-diagnozowalnego systemu o K=8 węzłach liczba przesyłanych

komunikatów: 576.

Z. Zieliński –Diagnostyka systemów

82

Algorytm EVENT_SELF

Modyfikacja NEW_SELF

Raport o wynikach testowania jest przekazywany przez dany

węzeł dalej (do innych węzłów), jeżeli jego dane różną się
od dotychczasowych wyników, przechowywanych w tym
węźle.

W algorytmie EVENT_SELF liczba przesyłanych komunikatów

jest znacznie zredukowana.

Istotnym parametrem jest opóźnienie diagnozy – jest to czas

jaki upływa od momentu wykrycia niezdatności do momentu
przekazania tej informacji do wszystkich węzłów.

Z. Zieliński –Diagnostyka systemów

83

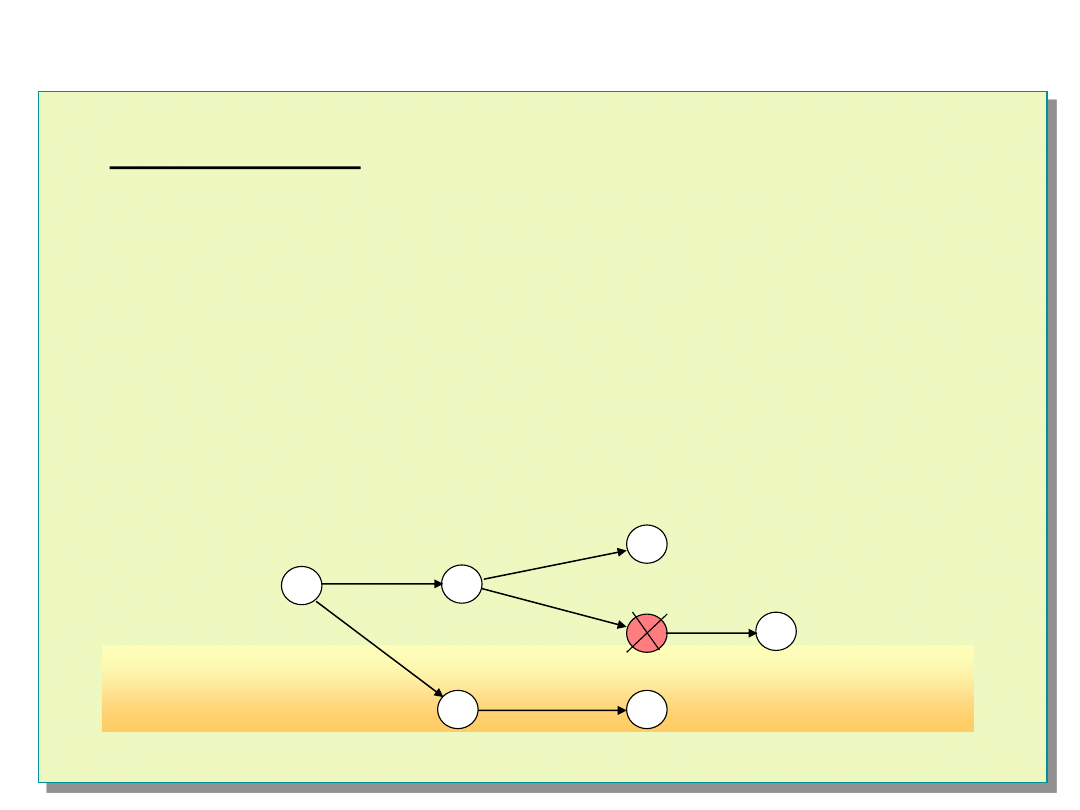
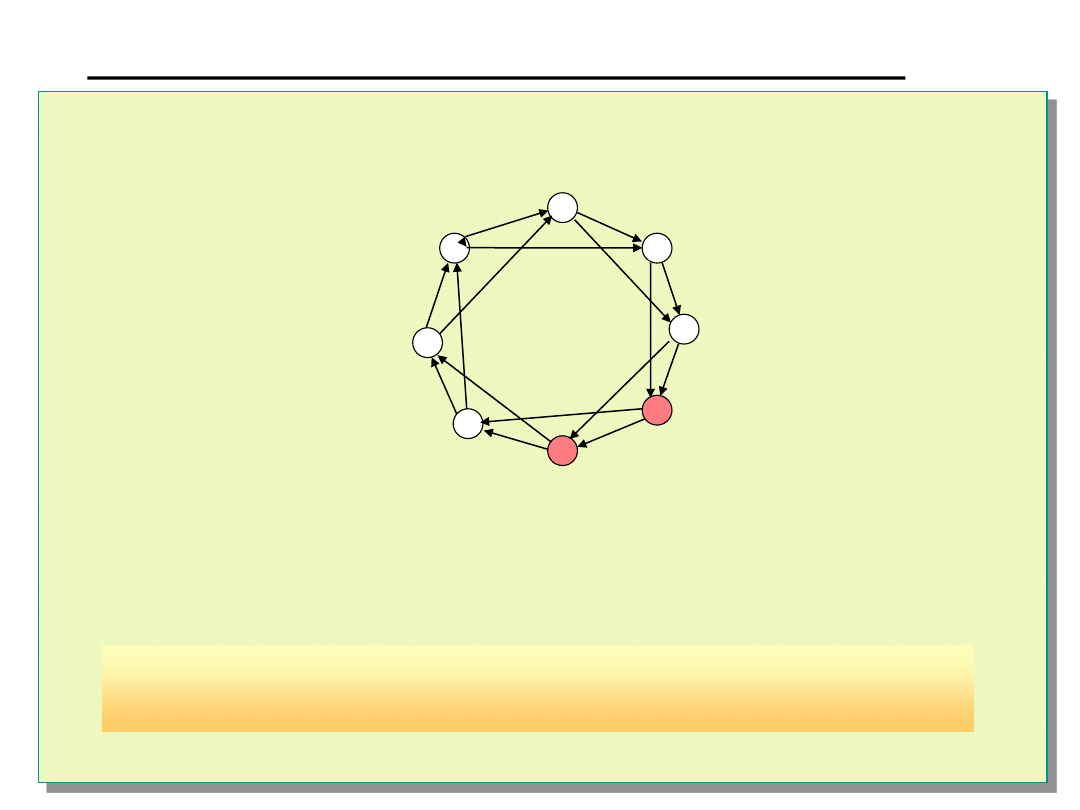
Wady algorytmów: NEW_SELF i EVENT_SELF

1.

Ograniczona diagnozowalność.

0

1

7

6

5

2

3

4

W przypadku niezdatnych węzłów 3 i 4 rezultaty testów nie będą

przekazywane do pozostałych zdatnych węzłów. Przykładowo, węzeł nr 2
nie otrzyma informacji o stanie węzła nr 5.

2. Występuje znaczna redundancja w testowaniu między poszczególnymi

węzłami, jak i przy przesyłaniu komunikatów.

Z. Zieliński –Diagnostyka systemów

84

Adaptacyjny algorytm DSD

(Distributed System

Diagnosing)

Struktury danych

Każdy węzeł n

X

przechowuje tablicę TESTED_UP

X

, zawierającą K

elementów.
TESTED_UP

X

[i] = j wskazuje, że węzeł n

X

otrzymał informację

diagnostyczną od zdatnego węzła: n

i

przetestował n

j

i określił jego stan jako

zdatny.
Adaptacyjny algorytm DSD wykonywany jest w każdym węźle i identyfikuje
pierwszy wolny od niezdatności węzeł, a następnie aktualizuje lokalne
informacje diagnostyczne na podstawie informacji otrzymanych z tego węzła.
Osiągane jest to w sposób następujący:
Ustalana jest lista węzłów w porządku sekwencyjnym (n

0

, n

1

, … , n

K-1

).

Węzeł n

X

identyfikuje stan kolejnych węzłów z listy tj.:

n

X+1

, n

X+2

, …. ,

dopóki nie określi węzła zdatnego.
Dodawanie wykonywane jest modulo K.

Z. Zieliński –Diagnostyka systemów

85

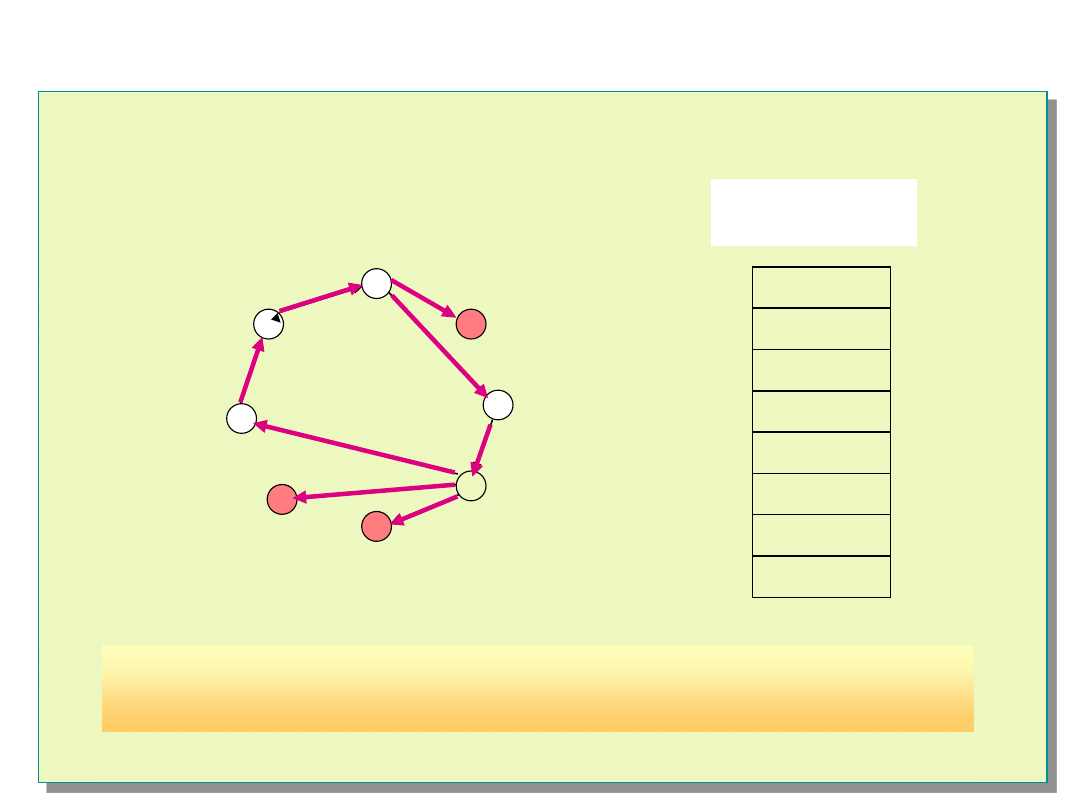
Adaptacyjny algorytm DSD

(Distributed System

Diagnosing)

/* Adaptacyjny algorytm DSD */
y=x;
REPEAT
{ y=(y+1) mod K
request n

y

to forward

TESTED_UP

y

to n

x;

} UNTIL (n

x

tests n

y

as “FAULT-FREE”);

TESTED_UP

X

[x] = y

for i=0 to K-1

if (i ≠ x) TESTED_UP

X

[i] = TESTED_UP

y

[i];

Z. Zieliński –Diagnostyka systemów

86

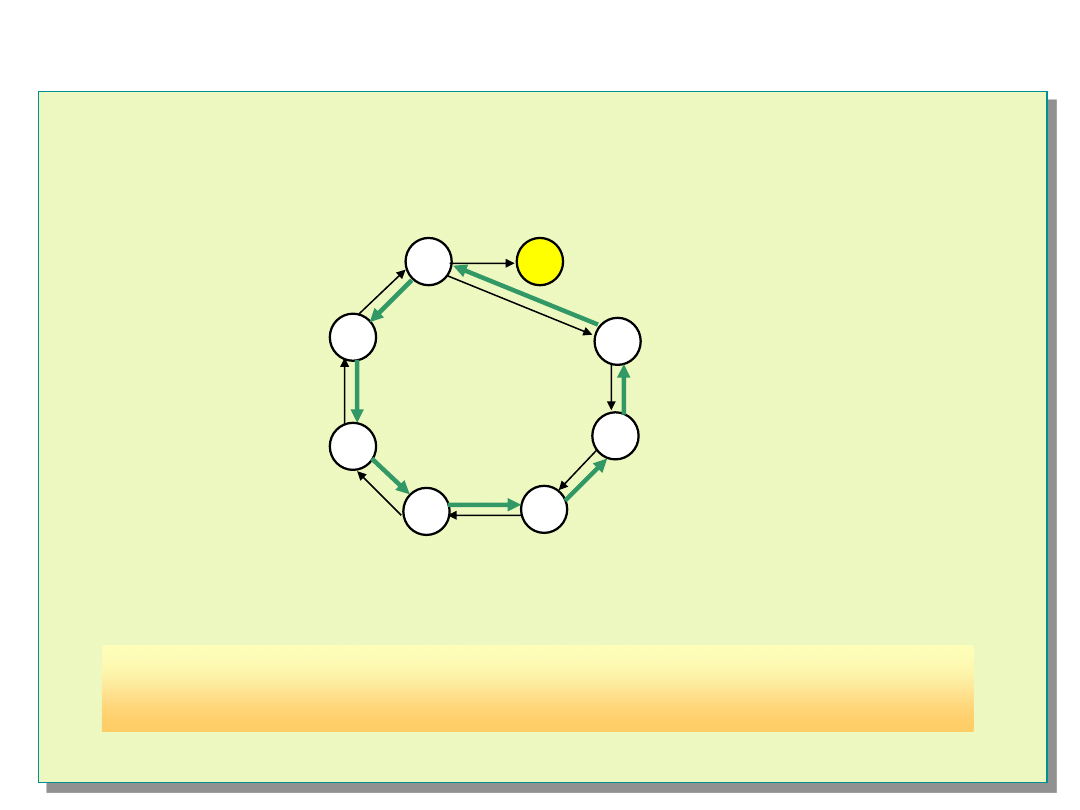
Adaptacyjny algorytm DSD

(Distributed System

Diagnosing)

Przykład

0

1

7

6

5

2

3

4

2

x

3

6

x

x

7

0

TESTED_UP

2

:

Z. Zieliński –Diagnostyka systemów

87

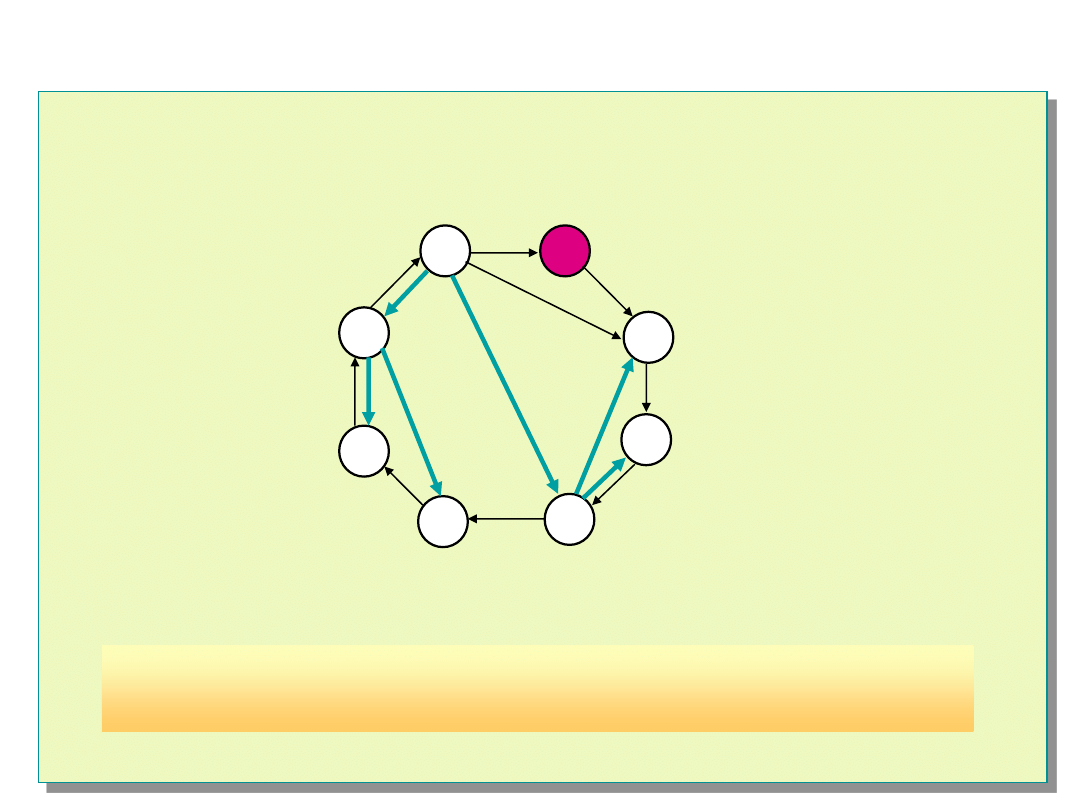
DSD

symetryczne przekazywanie raportów

5

2

3

4

6

7

0

1

Z. Zieliński –Diagnostyka systemów

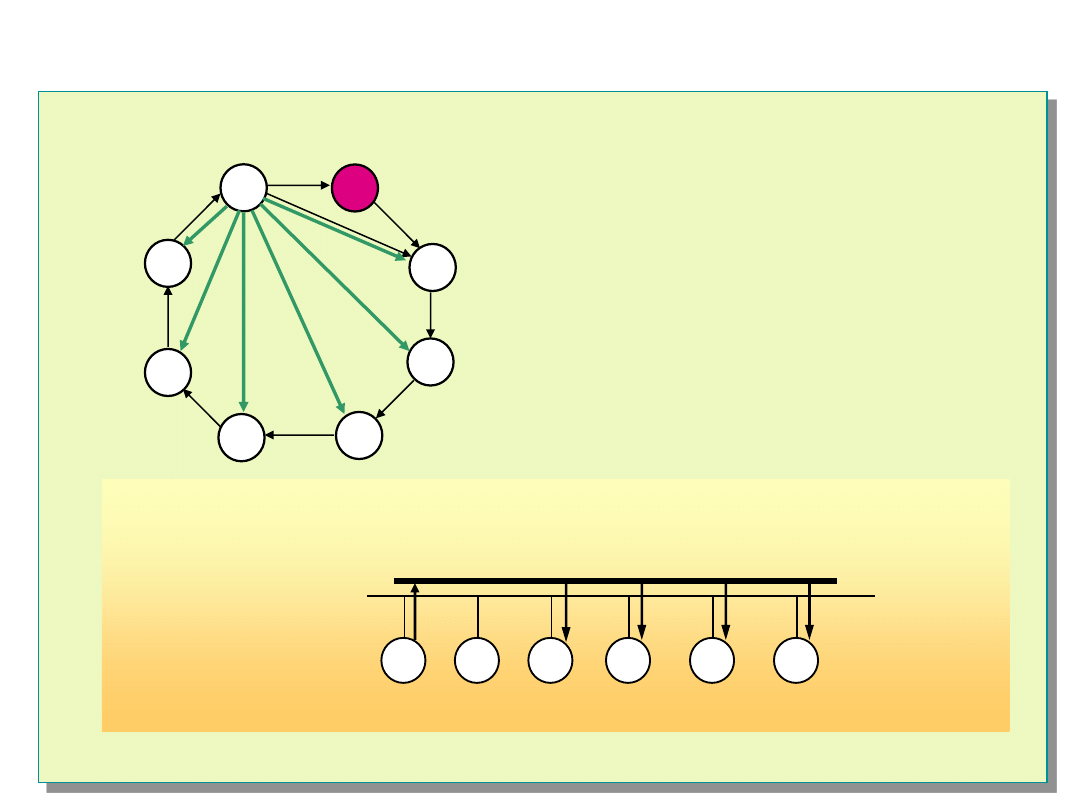
88

DSD

asymetryczne przekazywanie raportów

5

2

3

4

6

7

0

1

Z. Zieliński –Diagnostyka systemów

89

DSD -

sposoby przekazywania raportów

5

2

3

4

6

7

0

1

Wykorzystanie transmisji typu multicast

0

1

2

5

4

3

Z. Zieliński –Diagnostyka systemów

90

Adaptacyjny algorytm Adapt2

Adapt2 jest adaptacyjnym algorytmem służącym diagnozowaniu węzłów w
sieciach i systemach wieloprocesorowych (wielokomputerowych). Algorytm
dopuszcza dynamiczne uszkodzenia i naprawy węzłów i połączeń między
węzłami w czasie jego działania.
W wyniku jego działania konstruowany jest przydział testów, który
gwarantuje, że każde uszkodzenie węzła zostanie wykryte przez co najmniej
jeden sprawny węzeł sieci. Adapt2 wykonuje się w dwóch fazach: pasywnej i
aktywnej.
W fazie pasywnej węzeł okresowo testuje sąsiadów wg przydziału testów.
Faza aktywna jest inicjowana w momencie wykrycia zmiany stanu węzła
(uszkodzenie bądź restart po naprawie). Prawidłowo działające węzły
konstruują wtedy nowy przydział testów i odświeżają swoją diagnozę
wszystkich jednostek w sieci.

Z. Zieliński –Diagnostyka systemów

91

Adaptacyjny algorytm Adapt2

Pakiet nazywany jest kompletnym, kiedy przejdzie przez wszystkie zdatne
węzły i powróci do pierwotnego nadawcy (zwanego root). Ścieżka przebyta
przez pakiet determinuje przydział testów. Przydział testów ma strukturę
drzewa. Każdy węzeł testuje węzeł, od którego otrzymał dany pakiet (ojca) i
wszystkie węzły do których go wysłał (dzieci).

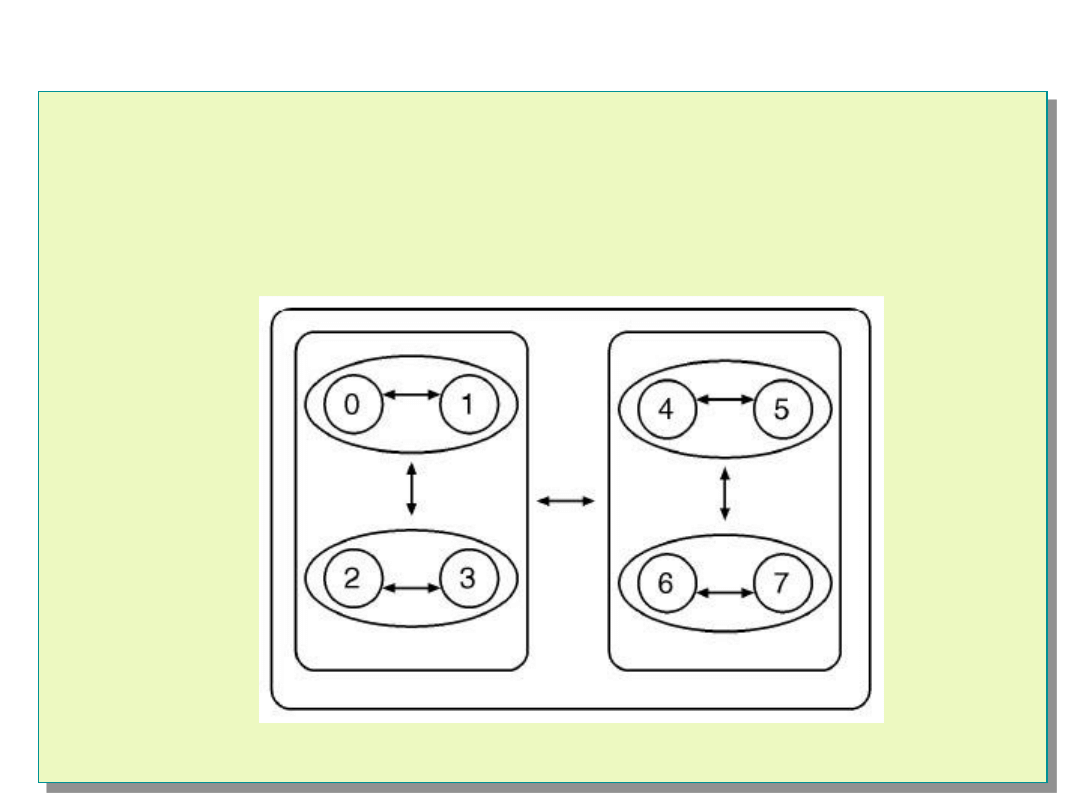
Algorytm Hi-A-DSD



Testowanie innych węzłów w sposób hierarchiczny

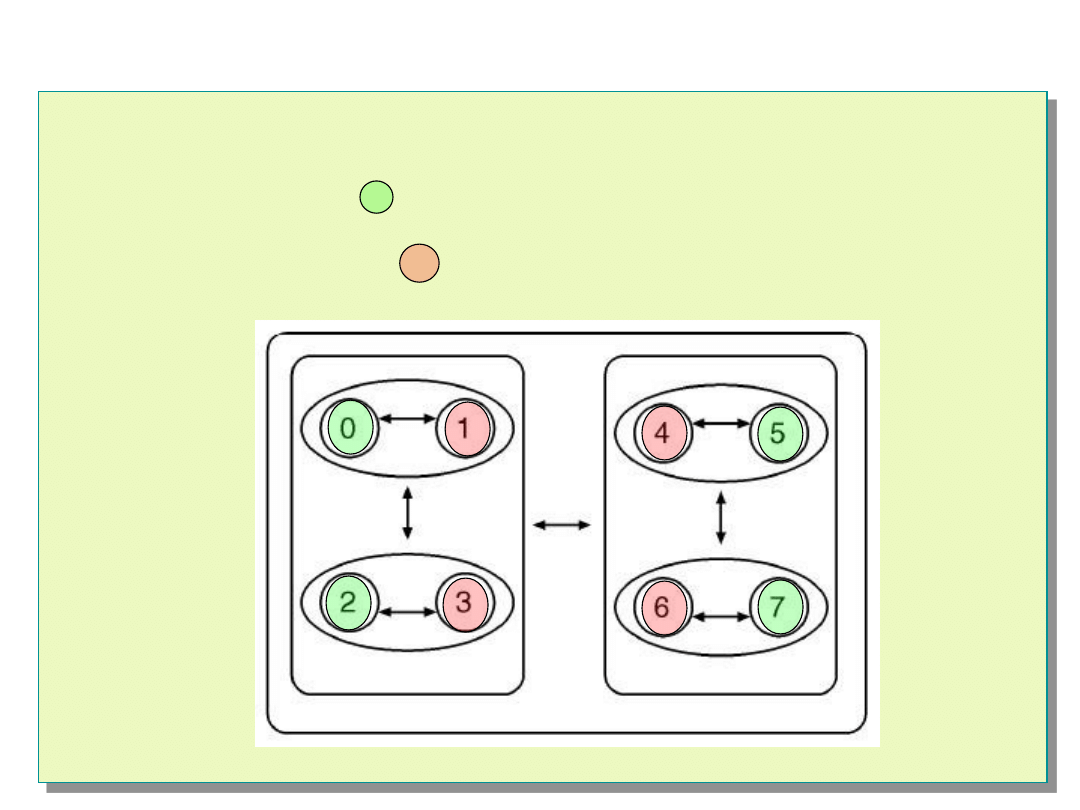
Algorytm Hi-A-DSD



Zdatne węzły



Niezdatne węzły

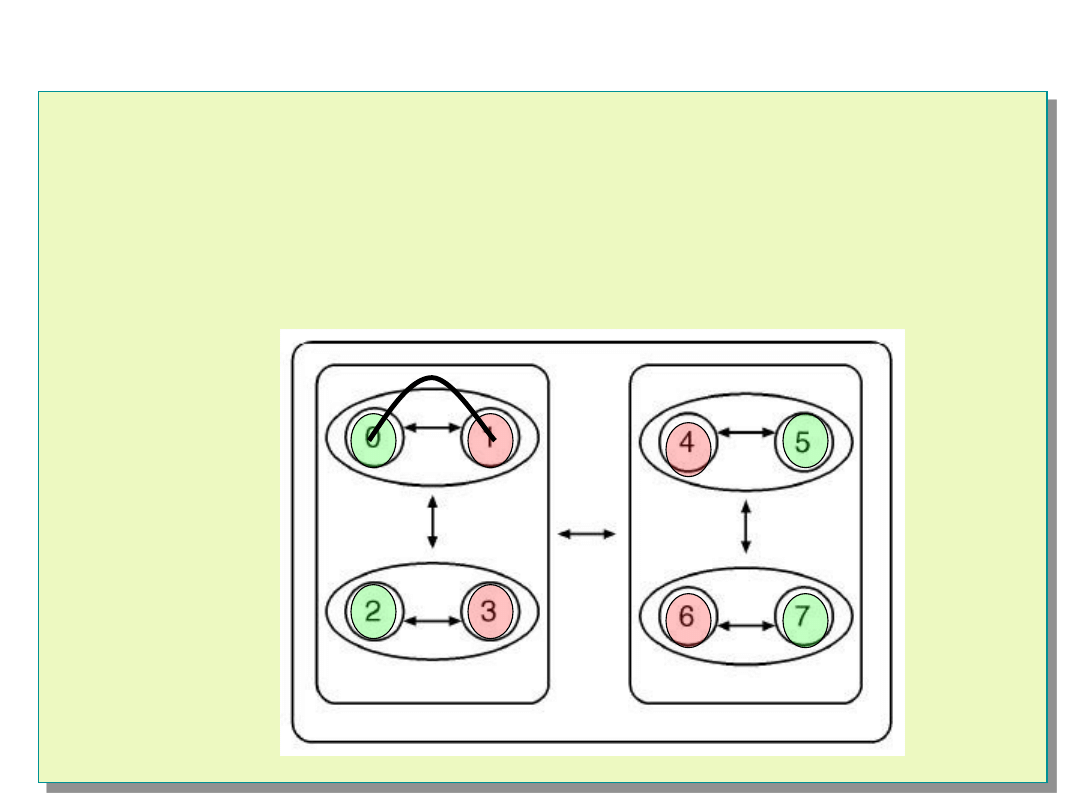
Algorytm Hi-A-DSD



Węzeł 0 rozpoczyna testowanie.

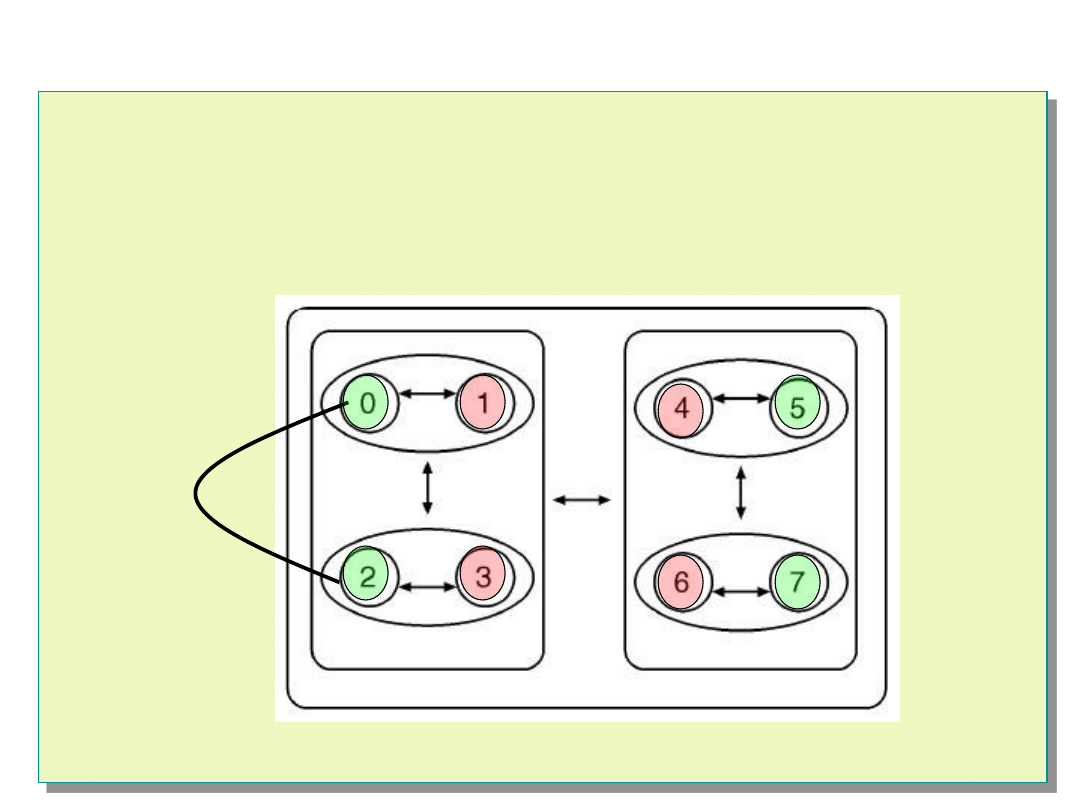
Algorytm Hi-A-DSD



Testowanie - n

astępny klaster

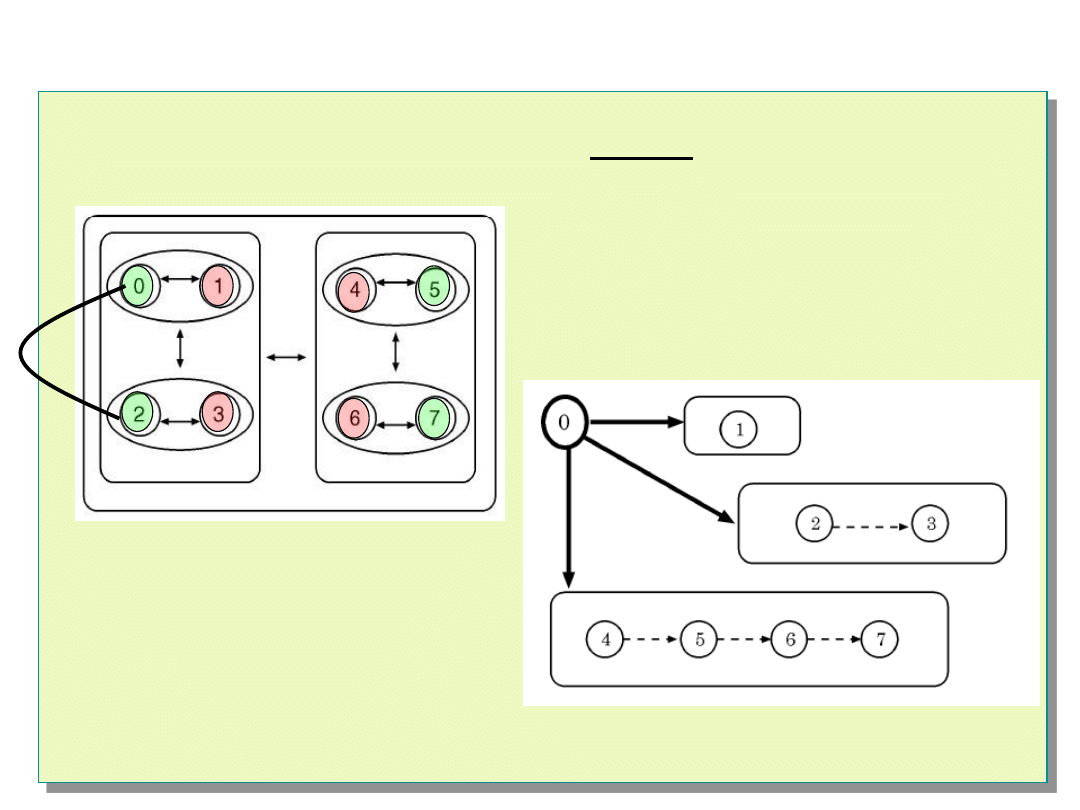
Algorytm Hi-A-DSD



Testowanie z perspektywy

węzła 0

następny klaster

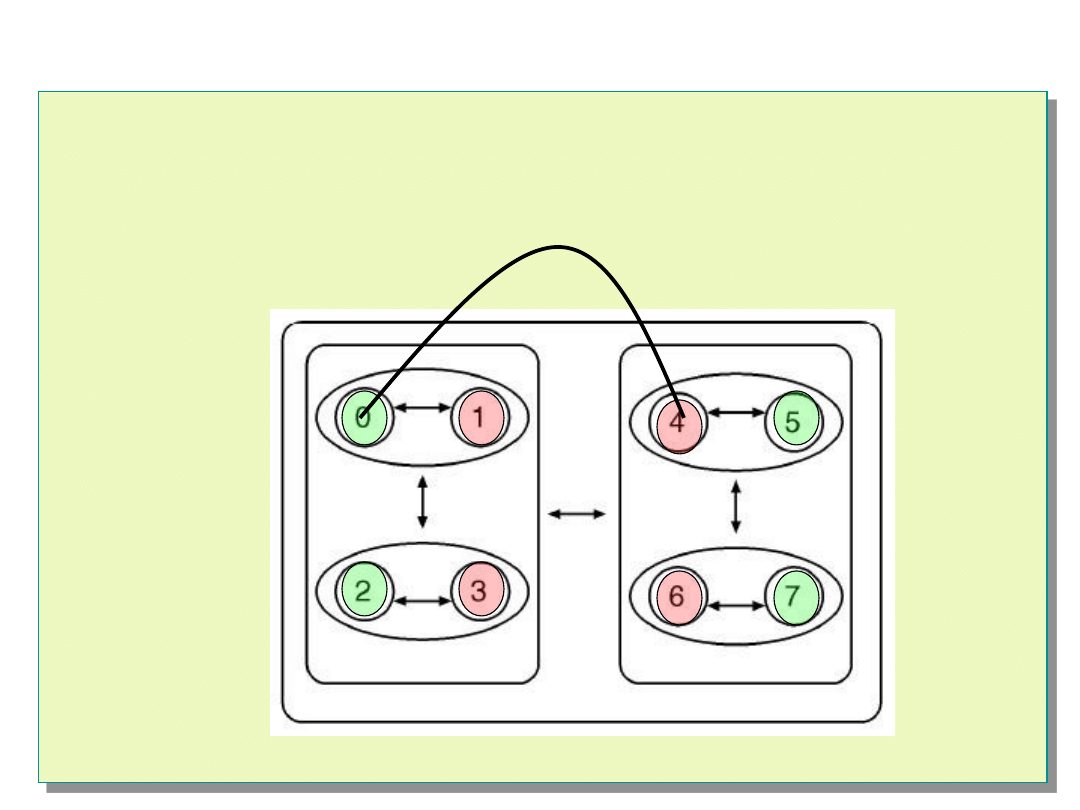
Algorytm Hi-A-DSD



Następny klaster

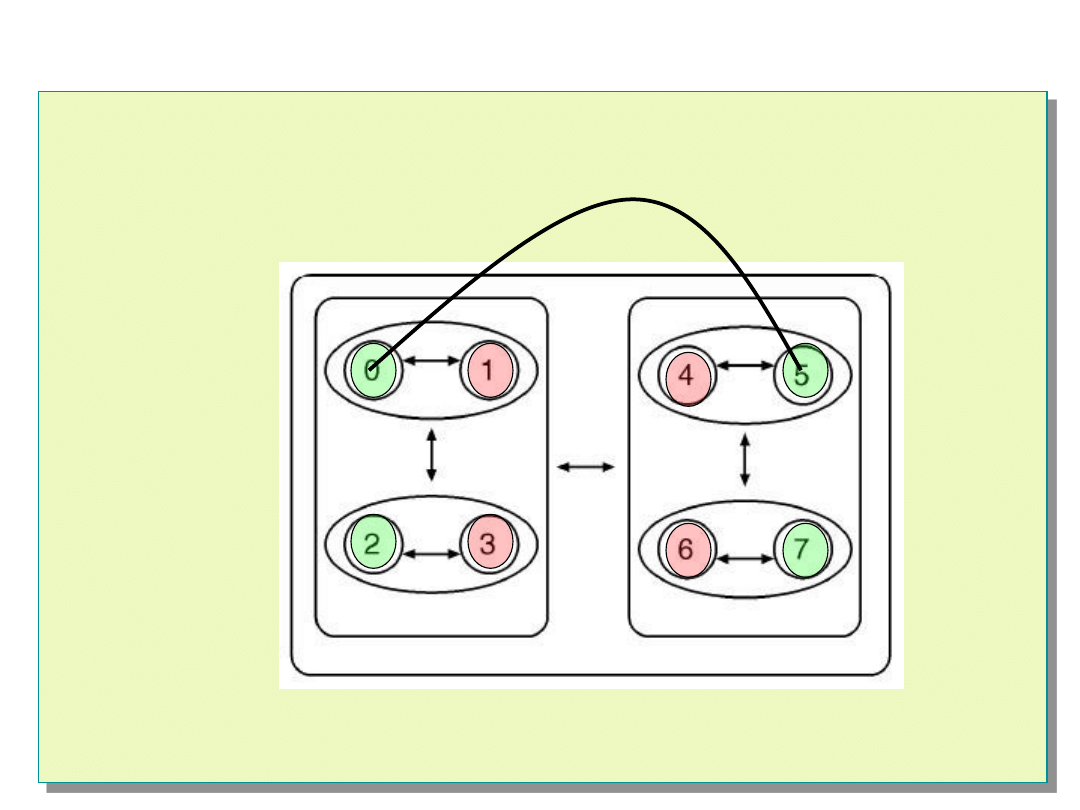
Algorytm Hi-A-DSD



Następny węzeł

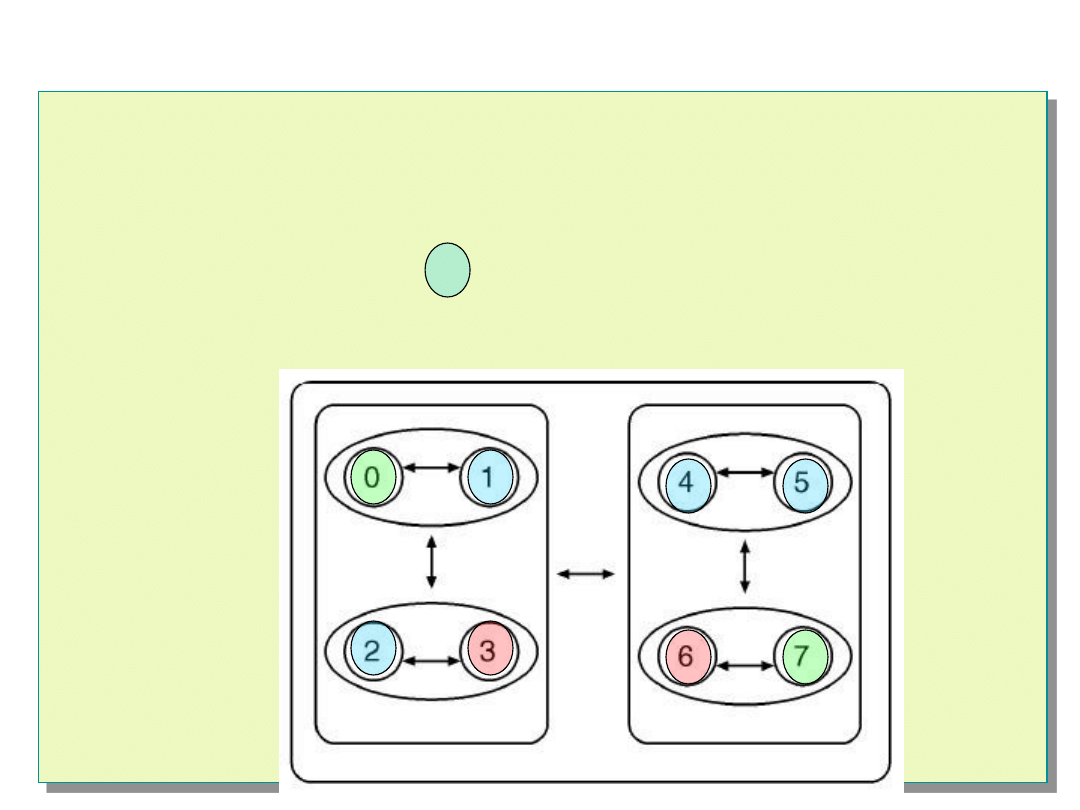
Algorytm Hi-A-DSD



Więcej klastrów już nie ma – runda testowania kończy się.



Przetestowane węzły

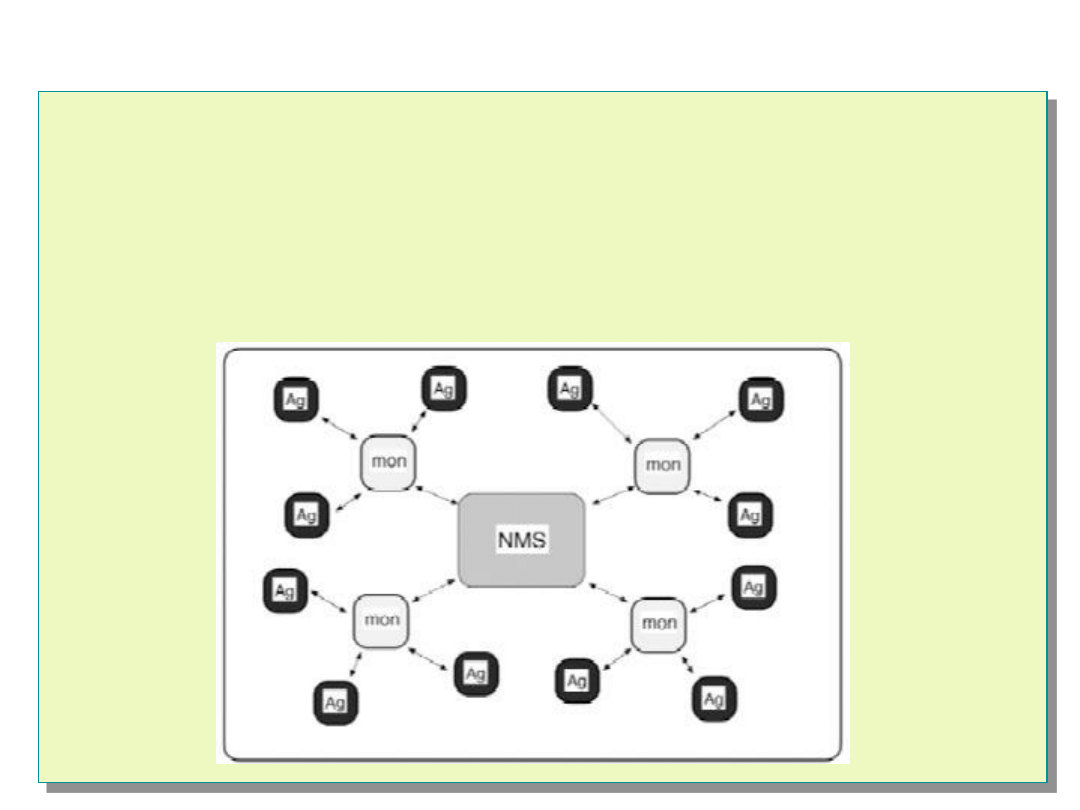
Sieć SNMP



Agent -> Zarządca -> Super Zarządca

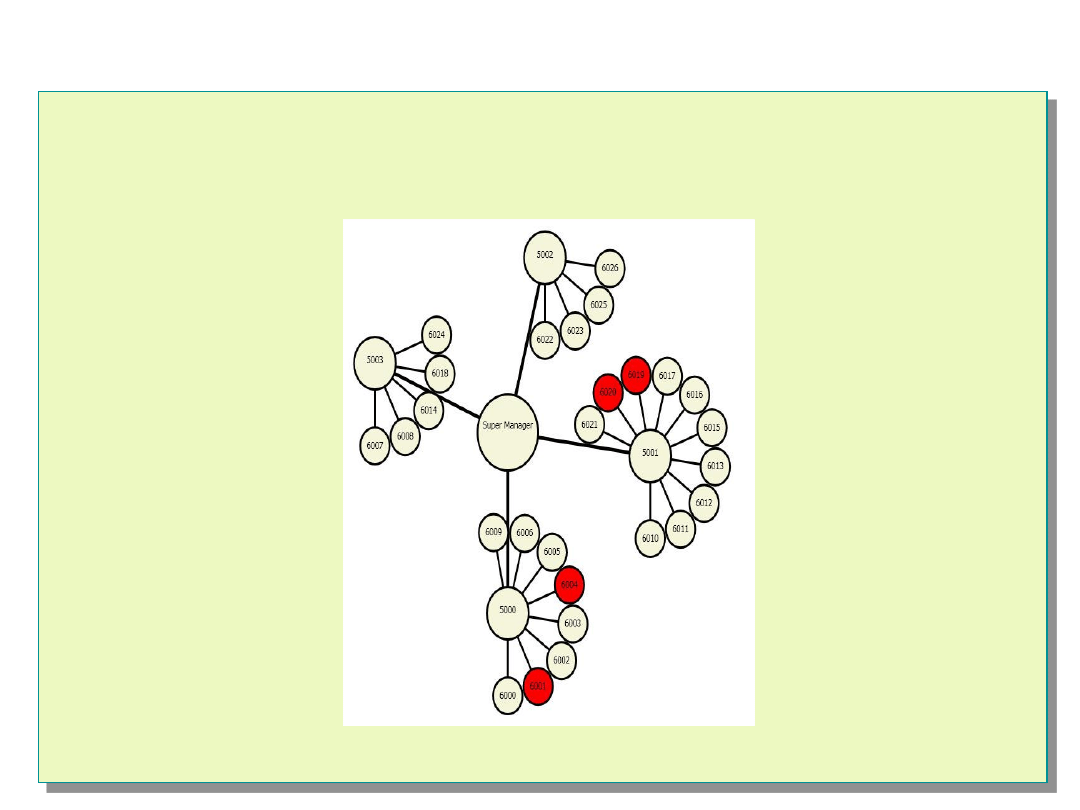
Interfejs użytkownika – wynik

Z. Zieliński –Diagnostyka systemów

102

Podsumowanie



Podstawowymi modelami opiniowania diagnostycznego są modele

PMC i BGM;



Niezdatności przemijające nie wnoszą nic istotnego z punktu

widzenia projektowanej struktury diagnostycznej



Niektóre typy systemów samodiagnozowalnych rozszerzają

możliwości diagnostyczne kosztem utraty pewnej liczby jednostek

zdatnych;



W ogólnym przypadku wyznaczanie struktur diagnostycznych

charakteryzuje się dużą złożonością obliczeniową – należy

poszukiwać metod niwelujących złożoność wynikającą z

izomorfizmu struktur



Algorytmy adaptacyjne można lepiej dostosować dla zapewnienia

min. czasu opóźnienia diagnozy.