RACHUNEK CAŁKOWY
FUNKCJI
JEDNEJ ZMIENNEJ
RACHUNEK CAŁKOWY
FUNKCJI
JEDNEJ ZMIENNEJ
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 2 / 33
CAŁKI NIEOZNACZONE
Definicja 1 (funkcji pierwotnej)
Funkcja F jest funkcją pierwotną funkcji f na przedziale I, jeŜeli
)
(
)
(
'
x
f
x
F
=
, dla kaŜdego
I
x
∈
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 3 / 33
Twierdzenie 1 (
podstawowe o funkcjach pierwotnych
)
Niech
F
będzie funkcją pierwotną funkcji
f
na przedziale
I
.
Wówczas
1.
C
x
F
x
G
+
=
)
(
)
(
(gdzie
R
C
∈
)
jest funkcją pierwotną funkcji
f
na
I
,
2. kaŜdą funkcję pierwotną funkcji f na
I
moŜna przedstawić
w postaci
D
x
F
+
)
(
, gdzie
R
D
∈
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 4 / 33
Definicja 2 (
całki nieoznaczonej
)
Niech
F
będzie funkcją pierwotną funkcji
f
na przedziale
I
. Całką
nieoznaczoną funkcji
f
na przedziale
I
nazywamy zbiór funkcji
}
:
)
(
{
R
C
C
x
F
∈
+
.
Całkę nieoznaczoną funkcji
f
oznaczamy przez
∫
dx
x
f
)
(
.
)
(x
f
nazywamy funkcj
ą
podcałkow
ą
.
C nazywamy stał
ą
całkowania,
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 5 / 33
Wniosek 1
Zachodzi wzór
C
x
F
dx
x
f
+
=
∫
)
(
)
(
gdzie F jest jak
ą
kolwiek funkcj
ą
pierwotn
ą
funkcji f na
rozwa
Ŝ
anym przedziale. C jest dowoln
ą
, stał
ą
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 6 / 33
Fakt 1
(pochodna całki nieoznaczonej)
Niech funkcja f ma funkcj
ę
pierwotn
ą
, na przedziale I.
Wtedy, dla ka
Ŝ
dego
I
x
∈
[
]
)
(
)
(
x
f
dx
x
f
=
′
∫
.
Fakt 2
(całka nieoznaczona pochodnej)
Niech funkcja f ma pochodn
ą
na przedziale I.
Wtedy, dla ka
Ŝ
dego
I
x
∈
C
x
f
dx
x
f
+
=
′
∫
)
(
)
(
, gdzie
R
C
∈
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 7 / 33
C
AŁKI NIEOZNACZONE WAśNIEJSZYCH FUNKCJI ELEMENTARNYCH
C
dx
=
∫
0
dla
R
x
∈
C
x
n
dx
x
n
n
+
+
=
+
∫
1
1
1
dla
}
0
{
∪
∈
N
n
oraz
R
x
∈
C
x
x
dx
+
=
∫
ln
dla
)
0
,
(
−∞
∈
x
lub
)
,
0
(
∞
∈
x
C
a
a
dx
a
x
x
+
=
∫
ln
dla
1
0
≠
<
a
oraz
R
x
∈
C
e
dx
e
x
x
+
=
∫
dla
R
x
∈
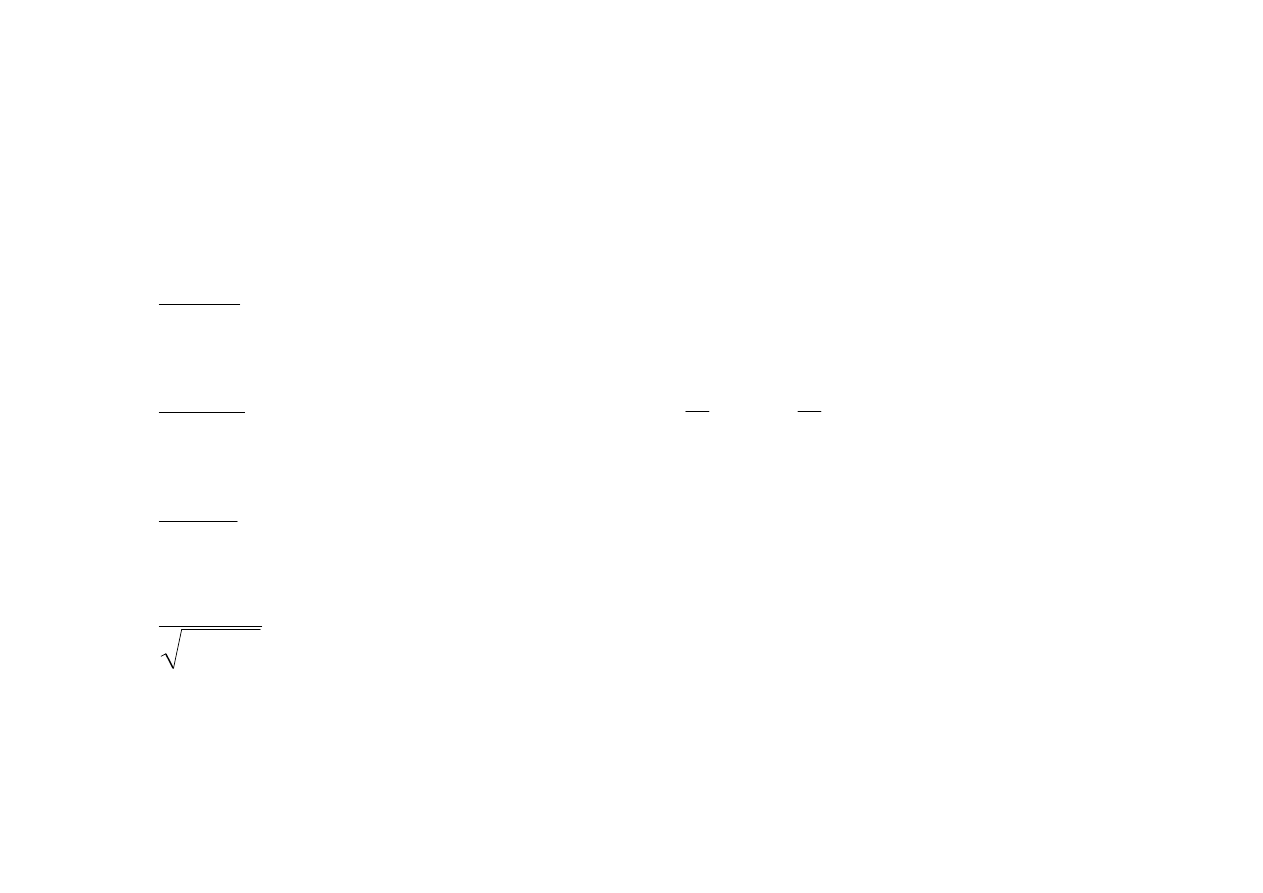
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 8 / 33
C
x
xdx
+
−
=
∫
cos
sin
dla
R
x
∈
C
x
xdx
+
=
∫
sin
cos
dla
R
x
∈
C
x
dx
x
+
−
=
∫
ctg
sin
1
2
dla
)
)
1
(
,
(
π
π
+
∈
k
k
x
, gdzie
Z
k
∈
C
x
dx
x
+
=
∫
tg
cos
1
2
dla
+
+
−
∈
π
π
π
π
k
k
x
2
,
2
, gdzie
Z
k
∈
C
x
dx
x
+
=
+
∫
arctg
1
1
2
dla
R
x
∈
C
x
dx
x
+
=
−
∫
arcsin
1
1
2
dla
)
1
,
1
(
−
∈
x
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 9 / 33
Twierdzenie 2
(o liniowości całki nieoznaczonej)
JeŜeli funkcje f i g mają funkcje pierwotne, to
(
)
∫
∫
∫
+
=
+
dx
x
f
dx
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
β
α
β
α
dla
R
∈
β
α
,
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 10 / 33
Twierdzenie 3
(o całkowaniu przez części)
JeŜeli funkcje f i g mają ciągle pochodne, to
∫
∫
−
=
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
)
(
)
(
'
)
(
)
(
)
(
'
)
(
.
MoŜna krócej:
∫
∫
−
=
v
u
uv
uv
'
'
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 11 / 33
Twierdzenie 4
(o całkowaniu przez podstawienie)
JeŜeli
1. funkcja
R
I
f
→
:
jest ciągła na przedziale I,
2. funkcja
I
J
→
:
ϕ
ma ciągłą, pochodną na przedziale J,
to
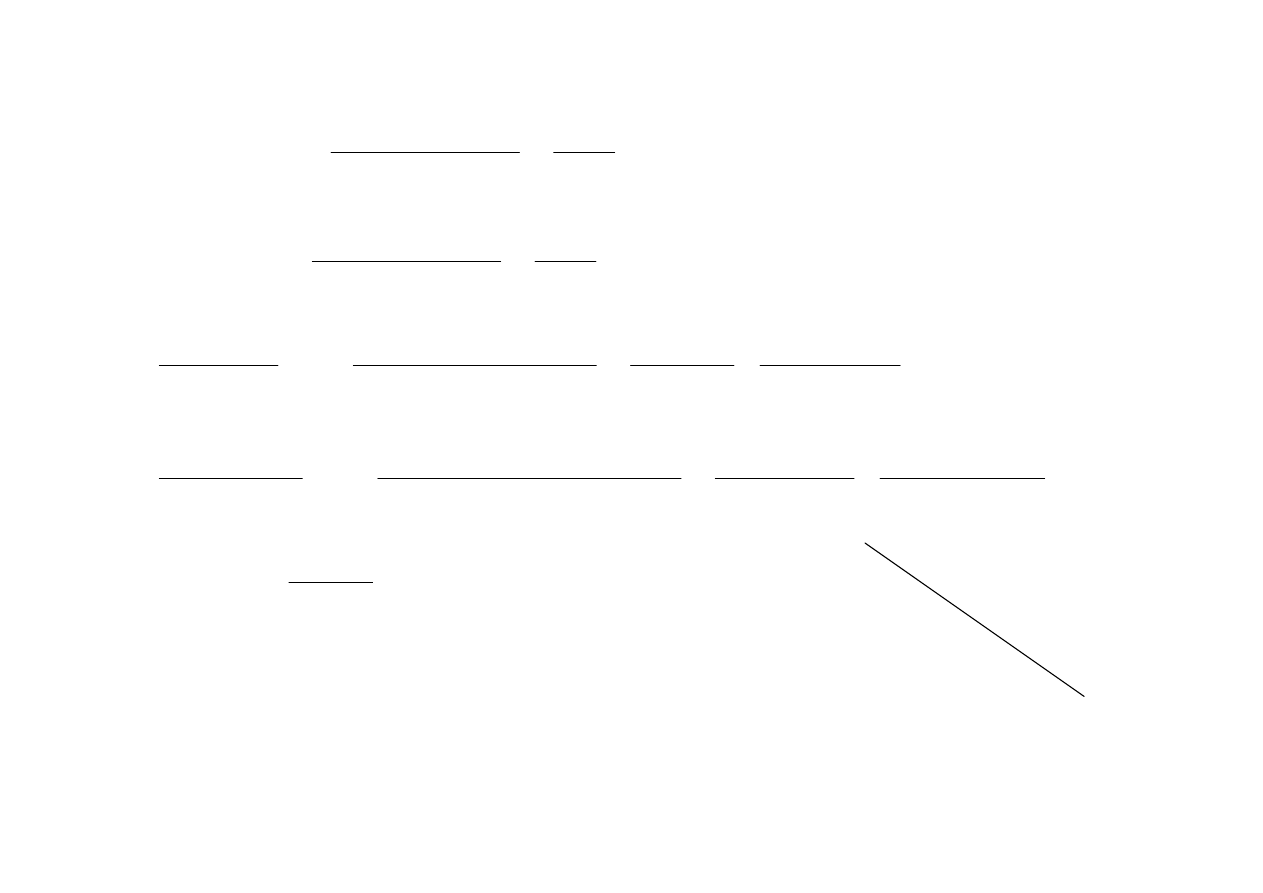
C
t
F
dt
t
t
f
dx
x
f
+
=
=
∫
∫
))
(
(
)
(
'
))
(
(
)
(
ϕ
ϕ
ϕ
,
gdzie F jest dowolną funkcją pierwotną funkcji f oraz
R
C
∈
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 12 / 33
W
ZORY REKURENCYJNE
∫
∫
−
−
−
+
⋅
−
=
xdx
n
n
n
x
x
xdx
n
n
n
2
1
sin
1
cos
sin
sin
,
2
≥
n
∫
∫
−
−
−
+
⋅
=
xdx
n
n
n
x
x
xdx
n
n
n
2
1
cos
1
sin
cos
cos
,
2
≥
n
∫
∫
−
−
+
−
−
+
+
−
=
+
dx
x
n
n
x
n
x
dx
x
n
n
n
1
2
1
2
2
)
1
(
1
)
1
(
2
3
2
)
1
)(
1
(
2
)
1
(
1
,
2
≥
n
∫
∫
−
−
−
−
+
−
=
dx
x
a
a
n
n
x
a
a
n
x
dx
x
a
n
n
n
1
2
2
2
1
2
2
2
2
2
)
(
1
)
1
(
2
3
2
)
(
)
1
(
2
)
(
1
m
m
m
,
∫
∫
−
−
−
−
=
xdx
n
x
xdx
n
n
n
2
1
tg
1
tg
tg
,
2
≥
n
0
>
a
,
2
≥
n
∫
∫
−
−
=
dx
x
n
x
x
dx
x
n
n
n
1
)
(ln
)
(ln
)
(ln
∫
∫
−
−
=
dx
e
x
n
e
x
dx
e
x
x
n
x
n
x
n
1
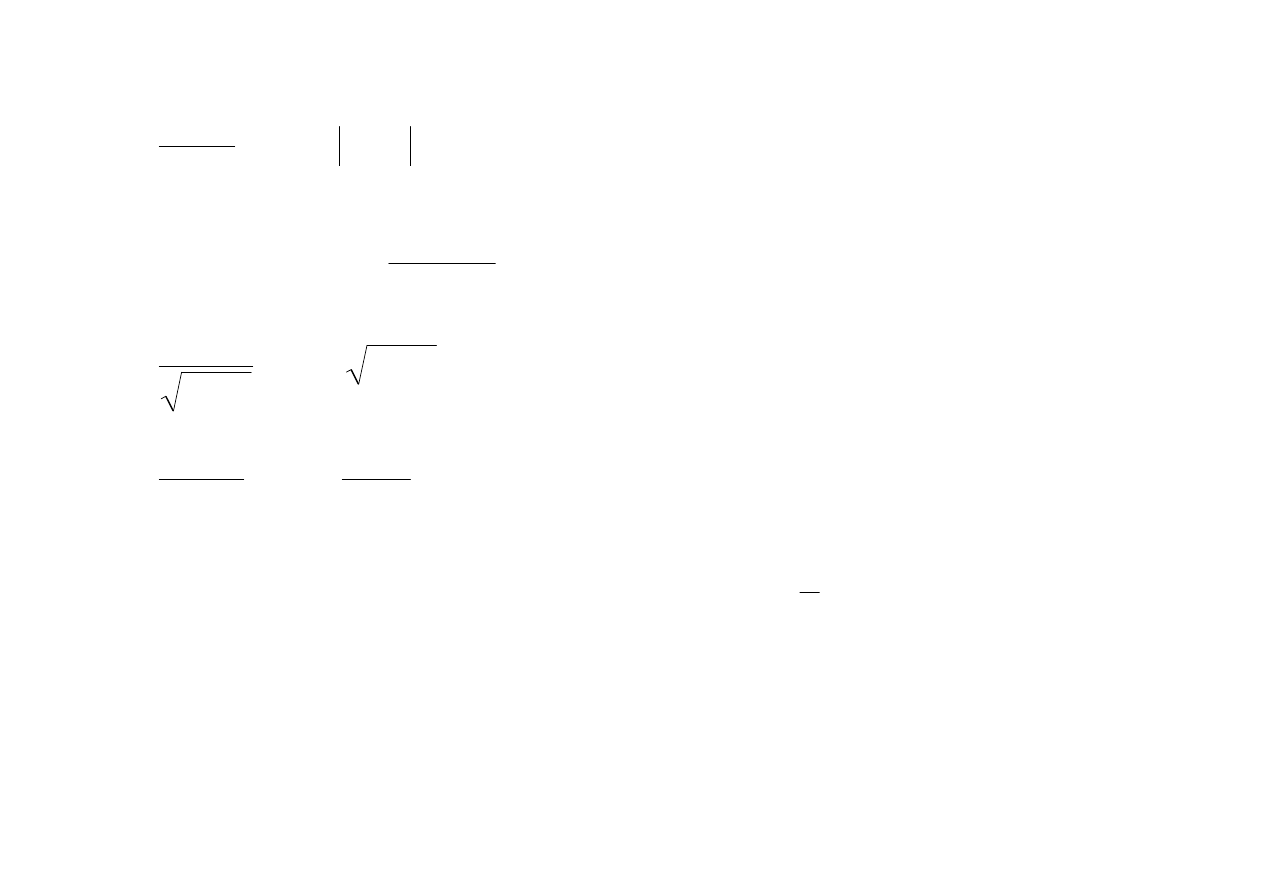
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 13 / 33
U
ś
YTECZNE WZORY
C
x
f
dx
x
f
x
f
+
=
′
∫
)
(
ln
)
(
)
(
,
0
)
(
≠
x
f
C
n
x
f
dx
x
f
x
f
n
n
+
+
=
′
+
∫
1
)
(
)
(
)
(
1
,
}
0
{
∪
∈
N
n
C
x
f
dx
x
f
x
f
+
=
′
∫
)
(
2
)
(
)
(
,
0
)
(
>
x
f
C
x
f
dx
x
f
x
f
+
−
=
′
∫
)
(
1
)
(
)
(
2
,
0
)
(
≠
x
f
Je
Ŝ
eli
C
x
F
dx
x
f
+
=
∫
)
(
)
(
, to
C
b
ax
F
a
dx
b
ax
f
+
+
=
+
∫
)
(
1
)
(
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 14 / 33
CAŁKOWANIE FUNKCJI WYMIERNYCH
Definicja 3
(funkcji wymiernej wła
ś
ciwej)
Funkcj
ą
wymiern
ą
)
(
)
(
)
(
x
M
x
L
x
W
n
m
=
nazywamy wła
ś
ciw
ą
, gdy stopie
ń
wielomianu w liczniku jest
mniejszy od stopnia wielomianu w mianowniku, tj. m < n.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 15 / 33
Uwaga 1
Ka
Ŝ
d
ą
funkcj
ę
wymiern
ą
niewła
ś
ciw
ą
(
n
m
>
) mo
Ŝ
na przedstawi
ć
w postaci sumy wielomianu i funkcji wymiernej wła
ś
ciwej.
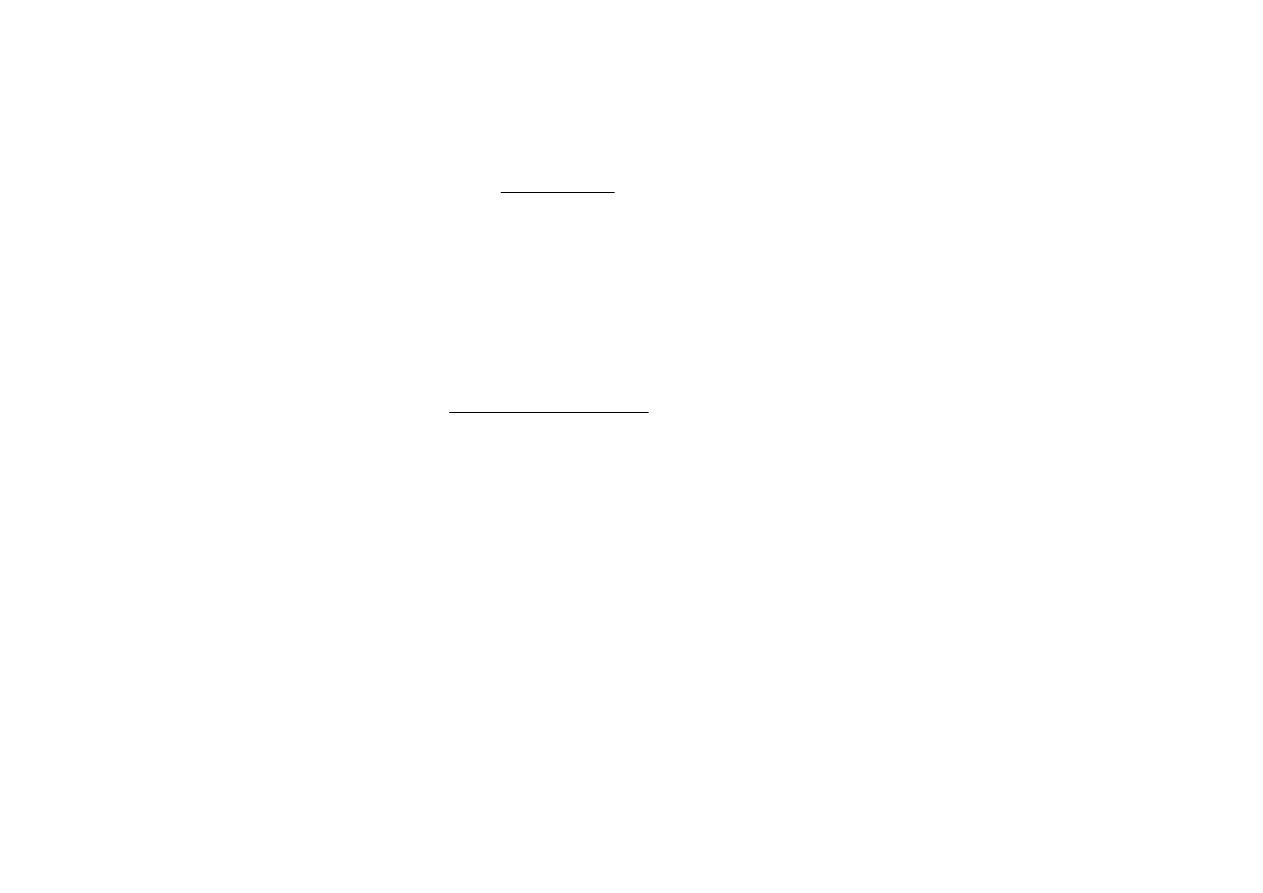
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 16 / 33
Definicja 4
(
ułamków prostych pierwszego i drugiego rodzaju
)
1. Funkcj
ę
wymiern
ą
wła
ś
ciw
ą
postaci
n
a
x
A
)
(
+
, gdzie
N
n
∈
i
R
A
∈
,
nazywamy ułamkiem prostym pierwszego rodzaju.
2. Funkcj
ę
wymiern
ą
wła
ś
ciw
ą
postaci
n
q
px
x
B
Ax
)
(
2
+
+
+
,
gdzie
N
n
∈
,
R
q
p
B
A
∈
,
,
,
oraz
0
4
2
<
−
=
∆
q
p
,
nazywamy ułamkiem prostym drugiego rodzaju.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 17 / 33
Twierdzenie 7
(o rozkładzie funkcji wymiernej na ułamki proste)
Ka
Ŝ
d
ą
funkcj
ę
wymiern
ą
wła
ś
ciw
ą
mo
Ŝ
na przedstawi
ć
w postaci
sumy ułamków prostych. Przedstawienie to jest jednoznaczne.
Funkcja wymierna wła
ś
ciwa
s
r
l
s
s
l
l
k
k
k
q
x
p
x
q
x
p
x
q
x
p
x
x
x
x
x
x
x
x
P
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
1
2
2
1
1
1
1
1
+
+
+
+
+
+
−
−
−
K
jest sum
ą
r
k
k
k
+
+
+
K
2
1
ułamków prostych pierwszego rodzaju oraz
s
l
l
l
+
+
+
K
2
1
ułamków prostych drugiego rodzaju,
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 18 / 33
przy czym
• czynnikowi
i
k
i
x
x
)
(
−
odpowiada suma
i
k ułamków prostych
pierwszego rodzaju postaci:
i
i
k
k
i
i
i
i
i
i
x
x
A
x
x
A
x
x
A
)
(
)
(
2
2
1
−
+
+
−
+
−
K
,
• czynnikowi
j
l
j
j
q
x
p
x
)
(
2
+
+
odpowiada suma
j
l ułamków prostych
drugiego rodzaju postaci:
j
j
l
j
l
l
j
j
j
j
j
j
j
j
j
j
j
j
q
x
p
x
C
x
B
q
x
p
x
C
x
B
q
x
p
x
C
x
B
)
(
)
(
2
2
2
2
2
2
1
1
+
+
+
+
+
+
+
+
+
+
+
+
K
.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 19 / 33
C
AŁKOWANIE UŁAMKÓW PROSTYCH PIERWSZEGO RODZAJU
n
a
x
A
)
(
+
Stosujemy podstawienie
a
x
t
+
=
i korzystamy ze wzoru:
∫
−
≠
+
−
=
+
=
+
1
1
1
|
|
ln
1
α
α
α
α
α
dla
t
dla
C
t
dt
t
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 20 / 33
C
AŁKOWANIE UŁAMKÓW PROSTYCH DRUGIEGO RODZAJU
n
q
px
x
B
Ax
)
(
2
+
+
+
a)
q
x
B
+
2
Stosujemy podstawienie
q
t
x
=
i korzystamy ze wzoru:
∫
+
=
+
C
t
t
dt
arctg
1
2
,
b)
q
px
x
B
+
+
2
Stosujemy podstawienie
2
p
t
x
−
=
i postępujemy jak w a),
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 21 / 33
c)
q
x
Ax
+
2
Stosujemy podstawienie
q
x
t
+
=
2
i korzystamy ze wzoru:
∫
+
=
C
t
t
dt
ln
,
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 22 / 33
d)
ułamek
q
px
x
B
Ax
+
+
+
2
przedstawiamy w postaci sumy ułamków
q
px
x
q
px
x
p
x
+
+
+
+
+
+
2
2
)
2
(
β
α
(
2
A
=
α
,
2
Ap
B
−
=
β
),
Całkę z pierwszego ułamka obliczamy stosując podstawienie
q
px
x
t
+
+
=
2
i wzór z punktu c).
Całkę z drugiego ułamka obliczamy jak w punkcie b).
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 23 / 33
e)
n
q
px
x
B
Ax
)
(
2
+
+
+
przedstawiamy w postaci sumy ułamków
n
n
q
px
x
q
px
x
p
x
)
(
)
(
)
2
(
2
2
+
+
+
+
+
+
β
α
.
Całkę z pierwszego ułamka obliczamy, stosując podstawienie
q
px
x
t
+
+
=
2
i wzór
∫
+
−
=
−
C
t
n
t
dt
n
n
1
)
1
(
1
.
Całkę z drugiego ułamka obliczamy, stosując podstawienie
2
p
t
x
−
=
. Następnie korzystamy ze wzoru rekurencyjnego
∫
∫
−
−
+
−
−
+
+
−
=
+
dx
x
a
a
n
n
x
a
a
n
x
dx
x
a
n
n
n
1
2
2
2
1
2
2
2
2
2
)
(
1
)
1
(
2
3
2
)
(
)
1
(
2
)
(
1
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 24 / 33
A
LGORYTM CAŁKOWANIA FUNKCJI WYMIERNYCH
1.
Funkcję wymierną zapisujemy w postaci sumy wielomianu (być
moŜe zerowego) i funkcji wymiernej właściwej.
2.
Mianownik funkcji wymiernej właściwej rozkładamy na czynniki
liniowe i kwadratowe nierozkładalne.
3.
Zapisujemy rozkład (teoretyczny) funkcji wymiernej właściwej
na ułamki proste pierwszego i drugiego rodzaju.
4.
Znajdujemy nieznane współczynniki tego rozkładu.
5.
Obliczamy całki poszczególnych składników rozkładu funkcji
wymiernej, tj. wielomianu i ułamków prostych.
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 25 / 33
CAŁKOWANIE FUNKCJI TRYGONOMETRYCZNYCH
Dla
∫
dx
x
x
m
n
cos
sin
(
N
m
n
∈
,
) stosujemy:
1.
1
2
+
=
l
n
(nieparzyste)
2.
1
2
+
=
k
m
(nieparzyste)
Wykorzystujemy
x
x
2
2
cos
1
sin
−
=
.
Stąd
x
x
x
l
l
sin
)
cos
1
(
sin
2
1
2
−
=
+
.
Podstawienie:
x
t
cos
=
Wykorzystujemy
x
x
2
2
sin
1
cos
−
=
.
Stąd
x
x
x
k
k
cos
)
sin
1
(
cos
2
1
2
−
=
+
.
Podstawienie:
x
t
sin
=
.
3. n, m – parzyste
Wykorzystujemy
)
2
cos
1
(
2
1
sin
2
x
x
−
=
,
)
2
cos
1
(
2
1
cos
2
x
x
+
=
.
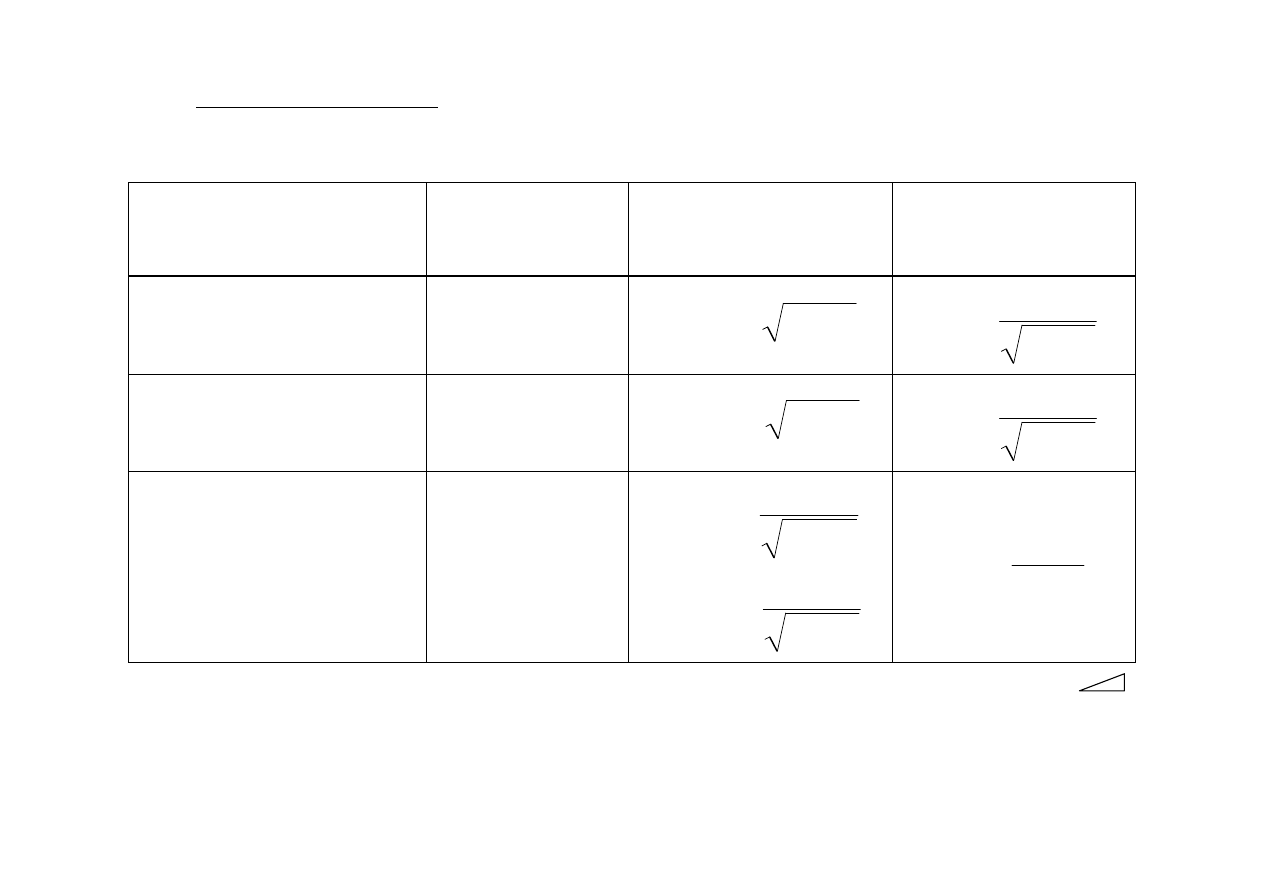
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 26 / 33
Dla
∫
dx
x
x
R
)
cos
,
(sin
.
)
cos
,
(sin
x
x
R
jest funkcją wymierną dwóch zmiennych:
x
sin i
x
cos .
Warunek
Podstawienie
Przedstawienie
funkcji
RóŜ
niczka
)
,
(
)
,
(
v
u
R
v
u
R
−
=
−
x
t
cos
=
2
1
sin
t
x
−
=
2
1 t
dt
dx
−
−
=
)
,
(
)
,
(
v
u
R
v
u
R
−
=
−
x
t
sin
=
2
1
cos
t
x
−
=
2
1 t
dt
dx
−
=
)
,
(
)
,
(
v
u
R
v
u
R
=
−
−
x
t
tg
=
2
1
sin
t
t
x
+
=
2
1
1
cos
t
x
+
=
2
1 t
dt
dx
+
=
)
cos
,
(sin
)
,
(
x
x
R
v
u
R
=
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 27 / 33
∫
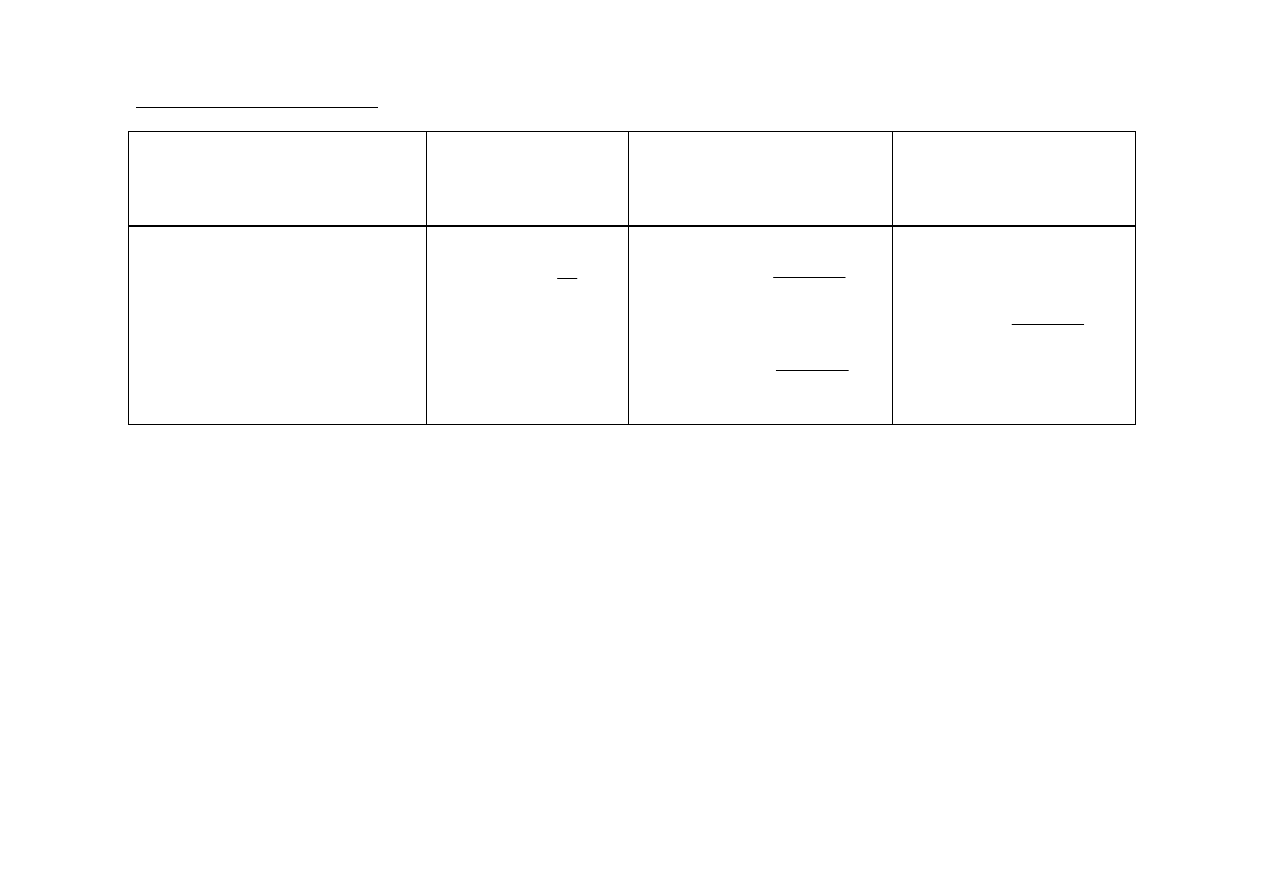
dx
x
x
R
)
cos
,
(sin
(cd.)
Warunek
Podstawienie
Przedstawienie
funkcji
RóŜniczka
R – dowolna
funkcja
2
tg
x
t
=
podstawienie
uniwersalne
2
1
2
sin
t
t
x
+
=
2
2
1
1
cos
t
t
x
+
−
=
2
1
2
t
dt
dx
+
=
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ 28 / 33
Dla
∫
⋅
dx
bx
ax
cos
sin
,
∫
⋅
dx
bx
ax
sin
sin
,
∫
⋅
dx
bx
ax
cos
cos
stosujemy toŜsamości trygonometryczne:
[
]
x
b
a
x
b
a
bx
ax
)
sin(
)
sin(
2
1
cos
sin
−
+
+
=
⋅
,
[
]
x
b
a
x
b
a
bx
ax
)
cos(
)
cos(
2
1
sin
sin
+
−
−
=
⋅
,
[
]
x
b
a
x
b
a
bx
ax
)
cos(
)
cos(
2
1
cos
cos
−
+
+
=
⋅
.