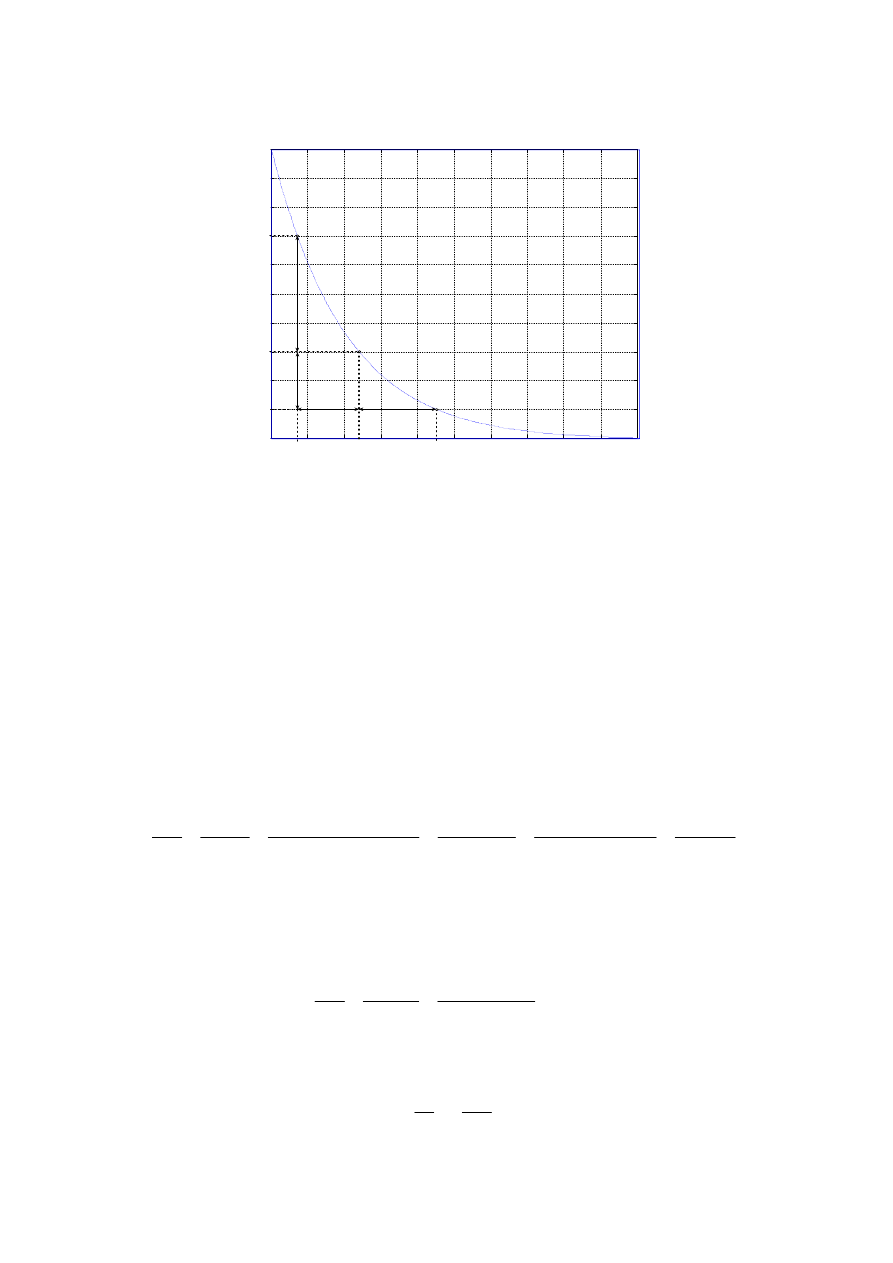
Wyznaczanie wykładnika funkcji eksponencjalnej
0
1
2
3
4
0
0.2
0.4
0.6
0.8
1
t
1
t
2
t
3
u
1
u
2
u
3
u(t)
t
∆u
1
∆u
2
∆t
1
∆t
2
Dana jest krzywa opisana zależnością ( )
at
u t
Ke
−
=
. Podczas pomiarów za pomocą
oscyloskopu występują błędy związane z przesunięciem punktu (0, 0). Obserwowaną krzywą
można zapisać ogólnie
0
(
)
0
( )
a t t
u t
u
Ke
−
+
=
+
,
gdzie u
0
, t
0
– stałe określające przesunięcie w pionie i poziomie.
Trzy dowolne punkty na krzywej eksponencjalnej określone są zależnościami:
1
0
(
)
1
1
0
( )
a t t
u
u t
u
Ke
−
+
=
=
+
,
2
0
(
)
2
2
0
( )
a t
t
u
u t
u
Ke
−
+
=
=
+
,
3
0
(
)
3
3
0
( )
a t t
u
u t
u
Ke
−
+
=
=
+
.
Oznaczając
1
1
2
2
2
,
u
u
u
u
u
u
∆ = −
∆ =
−
3
2
oraz
1
2
1
2
3
,
t
t
t
t
t
t
∆ = −
∆ = −
uzyskuje się
(
)
(
)
(
)
(
)
2
1
2
1
0
2
0
1
2
1
2
0
3
0
3
2
2
3
2
2
(
)
(
)
1
1
2
(
)
(
)
2
2
3
1
1
1
1
a t
t
at
a t t
a t
t
at
at
a t
a t
t
a t t
at
at
a t
a t t
at
e
e
u
u
u
Ke
Ke
e
e
e
u
u
u
Ke
Ke
e
e
e
e
e
−
−
−
+
−
+
−
−
∆
−
+
−
+
−
−
−
−
−
−
−
∆
−
−
−
=
=
=
=
=
∆
−
−
−
−
−
∆
−
t
.
Równanie to można łatwo rozwiązać tylko przy założeniu, że
1
2
t
t
∆ = ∆ = ∆ .
Wówczas
(
)
1
2
1
1
1
1
a t
a t
a t
a t
a t
a t
e
e
u
e
e
u
e
e
∆
− ∆
∆
∆
− ∆
− ∆
−
∆
−
=
=
=
∆
−
−
i wykładnik a wyznacza się z zależności
1
2
1
ln
u
a
t
u
∆
=
∆
∆
.