Temat ćwiczenia: Analiza drgań harmonicznych struny

Wstęp teoretyczny

Fala stojąca to fala, której pozycja w przestrzeni nie zmienia się, są to właściwie drgania ośrodka, a
idealna fala stojąca tak naprawdę nie jest falą - drgania się nie propagują. W przypadku struny
zamocowanej na dwóch końcach fala stojąca jest wynikiem interferencji fali biegnącej w kierunku
zamocowania z falą odbitą.

Dyspersja fal jest to zjawisko rozchodzenia się fali w ośrodku z prędkością fazową zależną od ich
częstotliwości. Prawdziwe dla ośrodków, których właściwości zależą od częstotliwości. W takich
ośrodkach fale o różnych częstotliwościach rozchodzą się z różną prędkością.

Opis stanowiska

Stanowisko pomiarowe przystosowane do badań drgań harmonicznych struny złożone z:
1. naprężonej struny o regulowanej długości;
2. linijki do określenia długości struny;
3. komputera ze wzmacniaczem sterującym elektromagnesem, podłączonym w miejscu głośnika,
przetwarzającym sygnał elektryczny na siłę mechaniczną działającą na strunę;
4. oscyloskopu z podłączonym do struny przetwornikiem piezoelektrycznym.

Przebieg doświadczenia

1. Odpowiednio dobrać skale na obu osiach oscyloskopu: poziomej (czas) i pionowej (napięcie).
2. Ustawić elektromagnes na środku struny.
3. Znaleźć częstotliwość podstawową drgań zwiększając powoli częstotliwość i jednocześnie
obserwować strunę oraz ekran oscyloskopu.
4. Odszukać kolejne harmoniczne drgań struny.

Opracowanie wyników pomiarów

Tabela 1

N

1

68

2

136

3

205

4

273

5

342

6

410

7

478

8

547

9

619

10

687

11

759

12

828

13

890

14

966

15

1042

ν

N

, Hz

W Tabeli 1 zebrano zaobserwowane częstotliwości harmonicznych i ich numery.
Długość struny ustawiono na L=0,85m.
Przy braku dyspersji zachodziłaby zależność:

ν

N '=

N ν

1

, a wartości kolejnych harmonicznych

przedstawiałyby się jak w Tabeli 2.

Tabela 2

Na Wykresie 1 przedstawiono zależność rejestrowanych częstotliwości harmonicznych

ν

N

od ich

kolejnego numeru N. Na tym samym wykresie zaznaczono przebieg funkcji

ν

N '=

N ν

1

, która zakłada

liniową zależność między częstotliwością

ν

N '

wyższych harmonicznych a częstotliwością podstawową

ν

1

.

N

1

68

2

136

3

204

4

272

5

340

6

408

7

476

8

544

9

612

10

680

11

748

12

816

13

884

14

952

15

1020

ν

N

'=Nν

1

, Hz

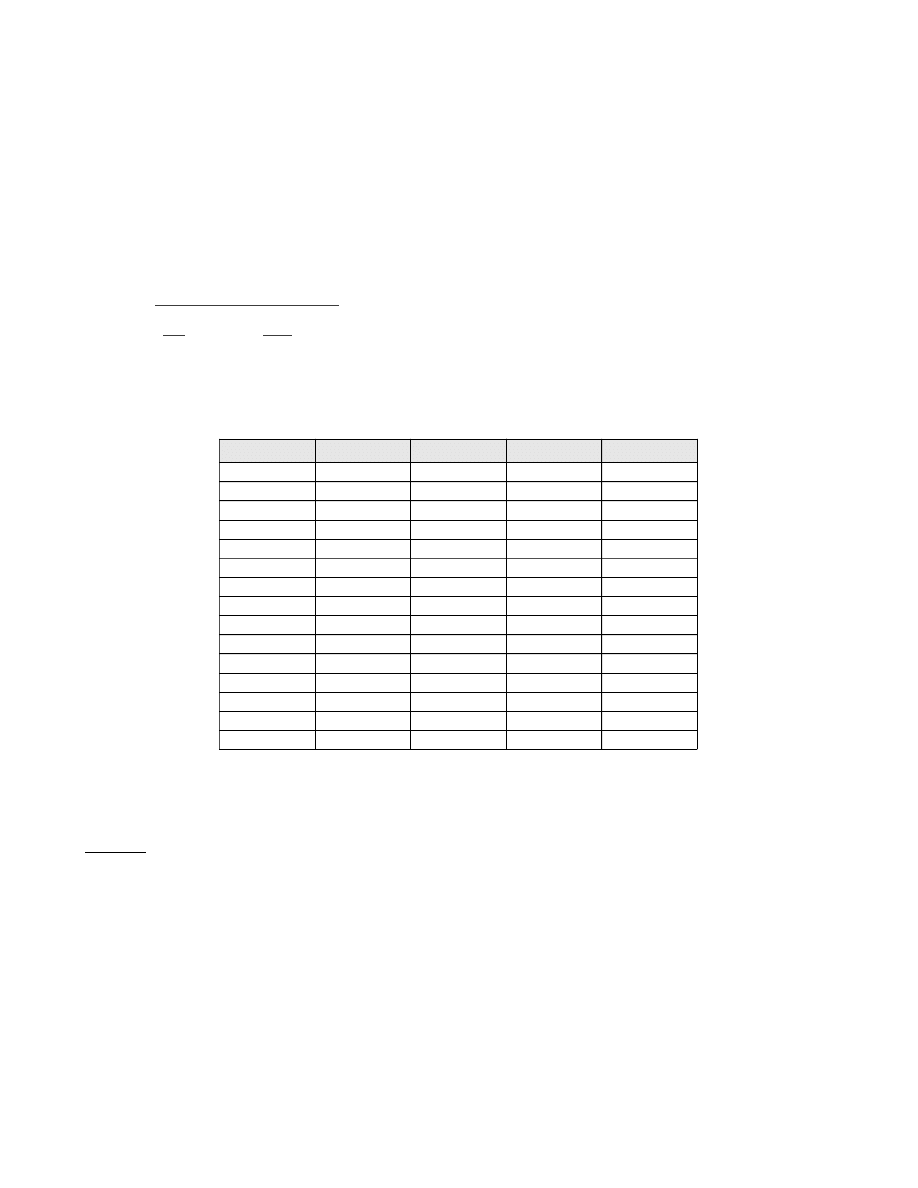
Niepewność pomiaru długości dla struny:
u(L)=1mm=0,001m
Czyli:
L=0,850(1)m
Założona niepewność:
u(

ν

N

)=2Hz

Prędkość rozchodzenia się fali wyznaczona jest ze wzoru:

v

=2L

ν

N

/N

Niepewność prędkości wyznaczona jest na podstawie prawa propagacji niepewności:

u v=



[

2L

N

u ν

N

]

2

[

2ν

N

N

u  L]

2

Tabela 3 przedstawia uzyskane wyniki obliczeń.

Tabela 3

Wykres 2 przedstawia zależność prędkości fali od częstotliwości wraz z niepewnościami.

Wnioski

Wykres zmierzonych kolejnych częstotliwości harmonicznych nie pokrywa się z wykresem
teoretycznym. Im większa harmoniczna tym bardziej częstotliwość zmierzona odbiega od teoretycznej.
Wykres prędkości rozchodzenia się fali od częstotliwości pokazuje, że im wyższa częstotliwość tym
większa jest prędkość fali, a ewentualne odstępstwa od tego mogły być wynikiem niedokładności
pomiaru długości struny, ustawienia elektromagnesu lub odczytu z oscyloskopu. Dowodzi to istnienia
zjawiska dyspersji fali czyli istnienia zależności prędkości fali od częstotliwości.

N

v, m/s

u(v)

1

68

68

115.6 3.4027189129

2

136

136

115.6 1.7054313237

3

205

204 116.16666667 1.141543789

4

273

272

116.025 0.8608903821

5

342

340

116.28 0.6936239904

6

410

408 116.16666667 0.5829141351

7

478

476 116.08571429 0.5045494252

8

547

544

116.2375 0.4464589147

9

619

612 116.92222222 0.4020417643

10

687

680

116.79 0.3667134576

11

759

748

117.3 0.3384984344

12

828

816

117.3 0.3151535781

13

890

884 116.38461538 0.2952122895

14

966

952

117.3 0.2793270338

15

1042

1020 118.09333333 0.2658575726

ν

N

, Hz

ν

N

'=Nν

1

, Hz