$

,

H

=

Ψ

Ψ Ψ Ψ

=

E

(x,y,z)

-

2m

E

2

h

∇

−

= ⋅

2

2

4

Ψ

Ψ

Ψ

e

r

o

πε

(

)

∂

∂

∂

∂

∂

∂

πε

2

2

2

2

2

2

x

2

2m

E

+

+

+

+ ⋅ =

y

z

o

e

r

h

Ψ

Ψ

Ψ

1

4

2

0

r

x

y

z

=

+

+

2

2

2

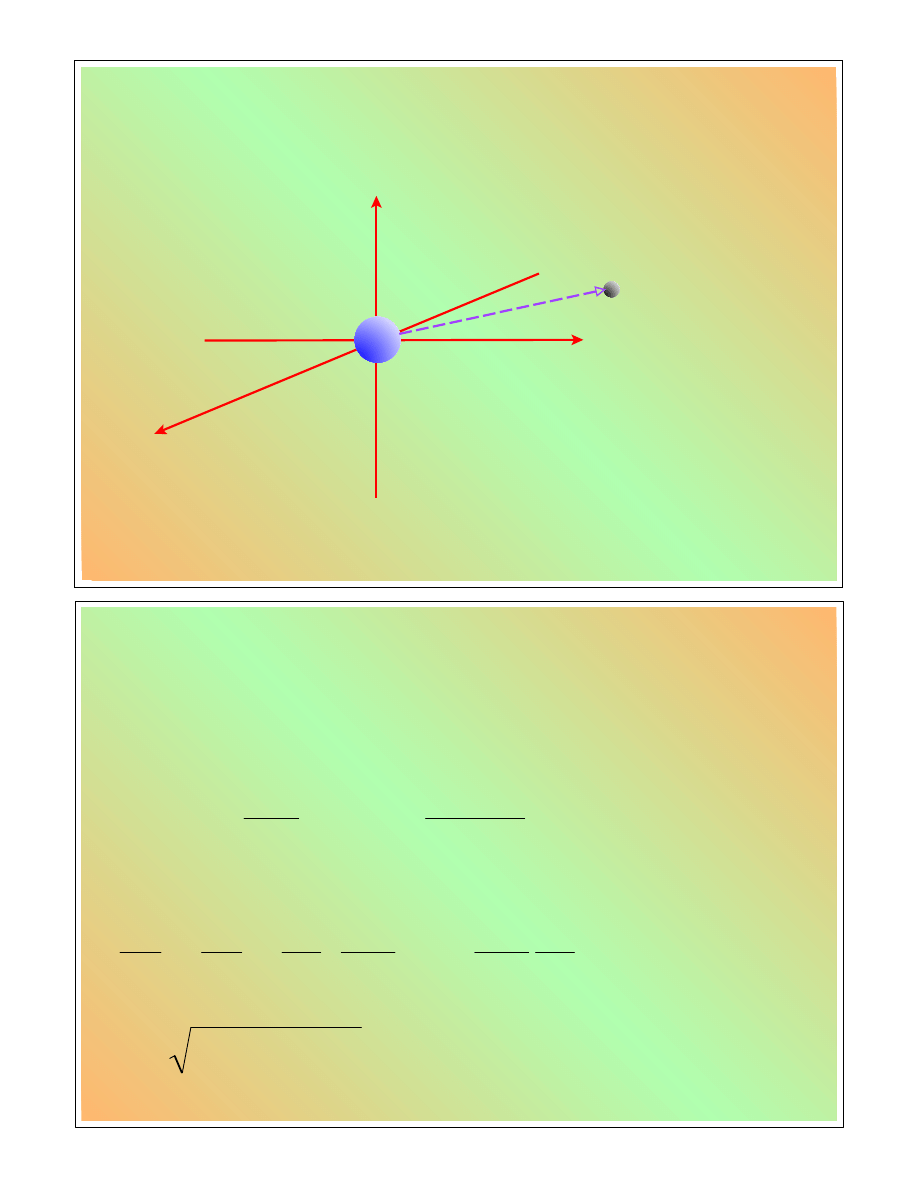
Atom wodoru

x

y

z

r

Równanie Schrödingera dla atomu wodoru

∂

∂

∂

∂

∂

∂

πε

2

2

2

2

2

2

x

y

z

Ψ

Ψ

Ψ

Ψ

+

+

+

⋅

+

+

+

















=

2

0

1

4

2

2

2

2

m

E

e

x

y

z

o

h

2

Równanie Schrödingera dla atomu wodoru (c.d.)

NIE DA SI

Ę

ROZWI

Ą

ZA

Ć

ANALITYCZNIE !!

!!!

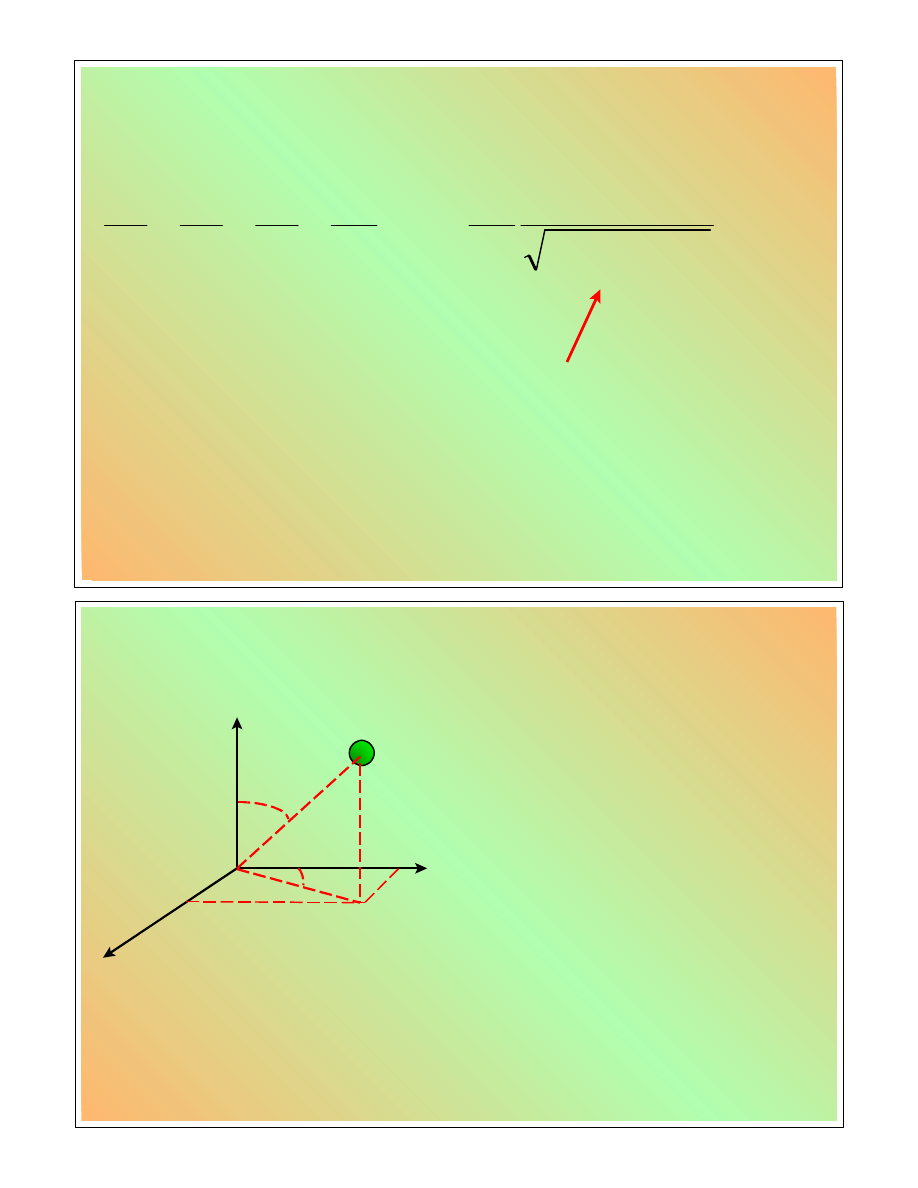
Układ współrzędnych

M

x

y

z

W układzie

współrz

ę

dnych

kartezja

ń

skich:

x

M

, y

M

, z

M

r

h

n

W układzie współrz

ę

dnych

biegunowych sferycznych:

r,

h

,

n

r

x

y

z

=

+

+

2

2

2

ϑ

=











arccos

z

r

ϕ

=

+













arccos

x

x

y

2

2

1

1

2

4

0

2

2

2

2

2

2

r

r

r

r

m

E

e

r

o

⋅











+











+













+

+

+

⋅











=

sin

sin

sin

sin

ϑ

ϑ ∂

∂

∂

∂

∂

∂ϑ

ϑ ∂

∂ϑ

ϑ

∂

∂ϕ

πε

Ψ

Ψ

Ψ

Ψ

h

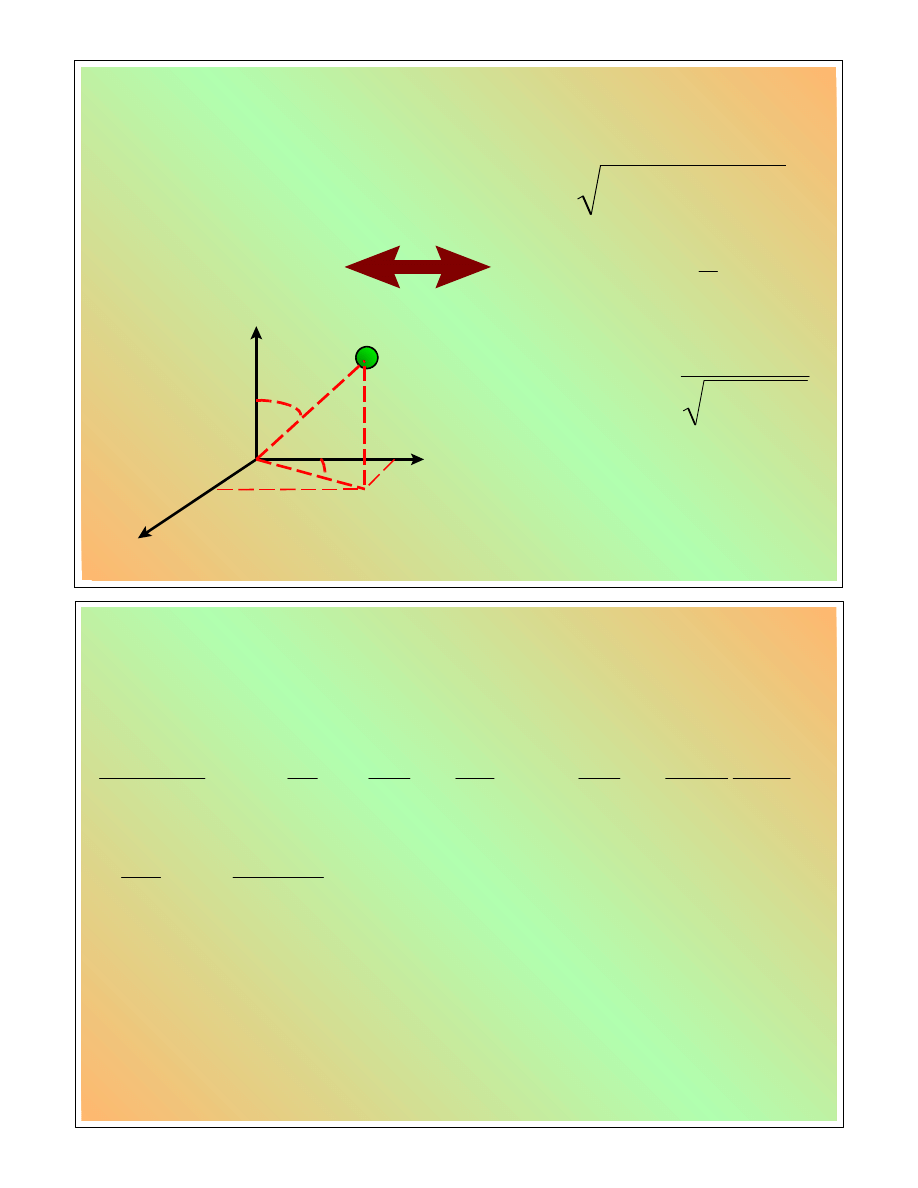
Układ współrzędnych (2)

M

x

y

z

r

h

n

x

M

=

r

@

cos

n@

sin

h

y

M

=

r

@

sin

n@

sin

h

z

M

=

r

@

cos

h

Równanie Schrödingera dla atomu wodoru (3)

Po zamianie układu współrzędnych na biegunowe sferyczne:

NIE UCZY

Ć

SI

Ę

NA PAMI

ĘĆ

!!!

Obejrze

ć

i zapomnie

ć

...

Rozwiązanie r. Schrödingera dla atomu

wodoru

*

R(r)

*

2

dr

prawdopodobie

ń

stwo radialne,

elektron pomi

ę

dzy r a r + dr

*

Y(

h

,

n

)

*

2

MhMn

prawdopodobie

ń

stwo k

ą

towe,

elektron w kierunku pomi

ę

dzy

h

a

h

+

Mh

oraz

n

a

n

+

Mn

Równanie Schrödingera dla atomu wodoru (2)

Q

Q

Q

Q

(x,y,z) =

Q

Q

Q

Q

(r,

h

h

h

h

,

n

n

n

n

)

Q

Q

Q

Q

(r,

h

h

h

h

,

n

n

n

n

) = R(r)

@@@@

Y(

h

h

h

h

,

n

n

n

n

)

Rozdzielenie zmiennych w równaniu

ró

ż

niczkowym =

rozdział na kilka równa

ń

WARUNEK KONIECZNY:

Q

Q

Q

Q

(r,

h

h

h

h

,

n

n

n

n

)

JEST

FUNKCJ

Ą

PORZ

Ą

DN

Ą

R(r)
Y(

h

h

h

h

,

n

n

n

n

) S

Ą

TAK

ś

E KLASY Q

E

m e

const

e

o

= −

=

π

ε

4

2

2 h n

n

2

2

r

r

r

M

m v

r

= × ×

M

l(l

)

=

+

1 h

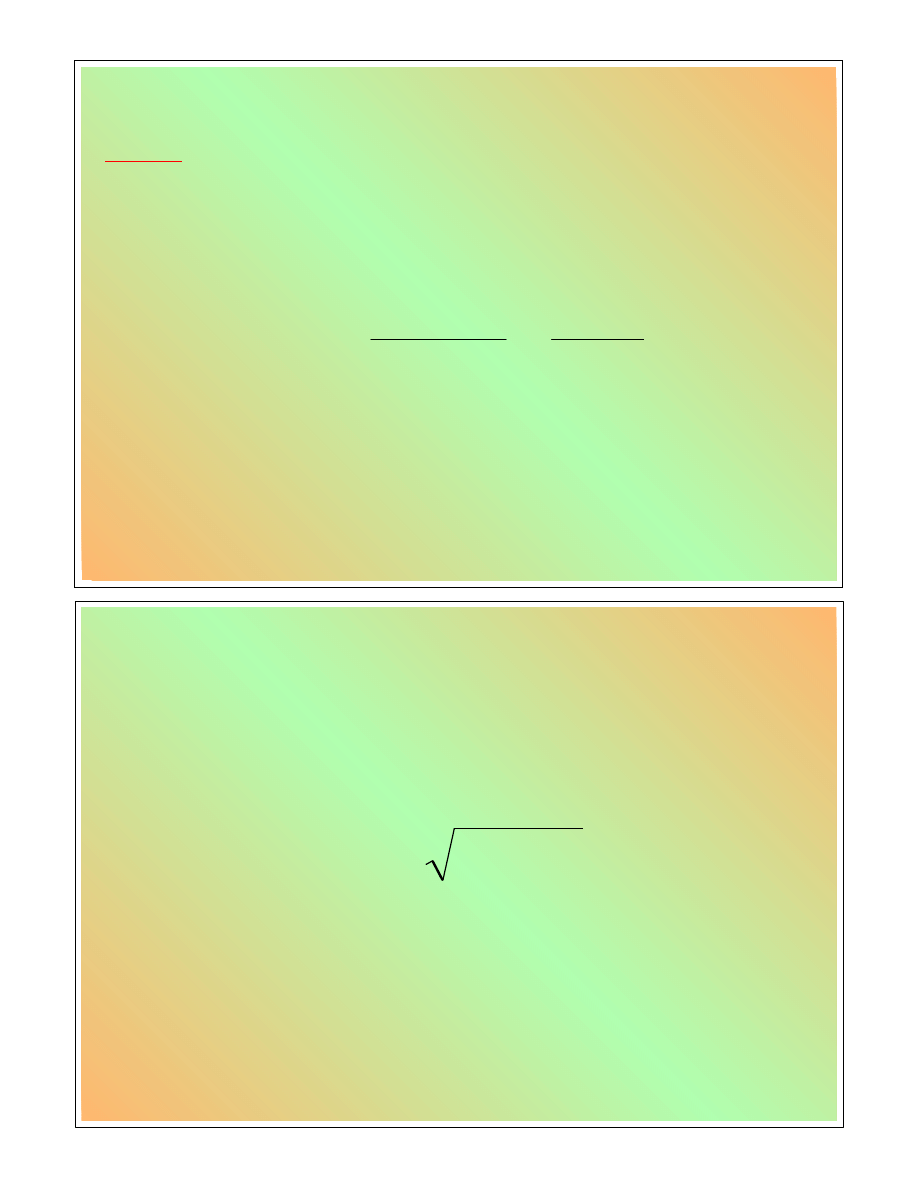
Warunki dla funkcji klasy Q (1)

Energia całkowita mo

ż

e przybiera

ć

tylko

pewne warto

ś

ci:

gdzie n = 1,2,3, .......

GŁÓWNA LICZBA KWANTOWA

muszą być spełnione, żeby rozwiązanie dla atomu wodoru

składało się z funkcji porządnych

Warunki dla funkcji klasy Q (2)

Moment pędu:

Moment p

ę

du elektronu mo

ż

e przybiera

ć

tylko

pewne warto

ś

ci:

gdzie l = 0,1,2, ..... (n-1)

POBOCZNA LICZBA KWANTOWA
ORBITALNA LICZBA KWANTOWA

M

m

z

= ⋅

h

Warunki dla funkcji klasy Q (3)

Moment p

ę

du mo

ż

e mie

ć

tylko pewne orientacje

w przestrzeni, tj. jego składowa w wybranym

kierunku osi z mo

ż

e przybiera

ć

pewne warto

ś

ci:

gdzie m = -l, -l + 1,....,0, .....l - 1, l

MAGNETYCZNA LICZBA KWANTOWA

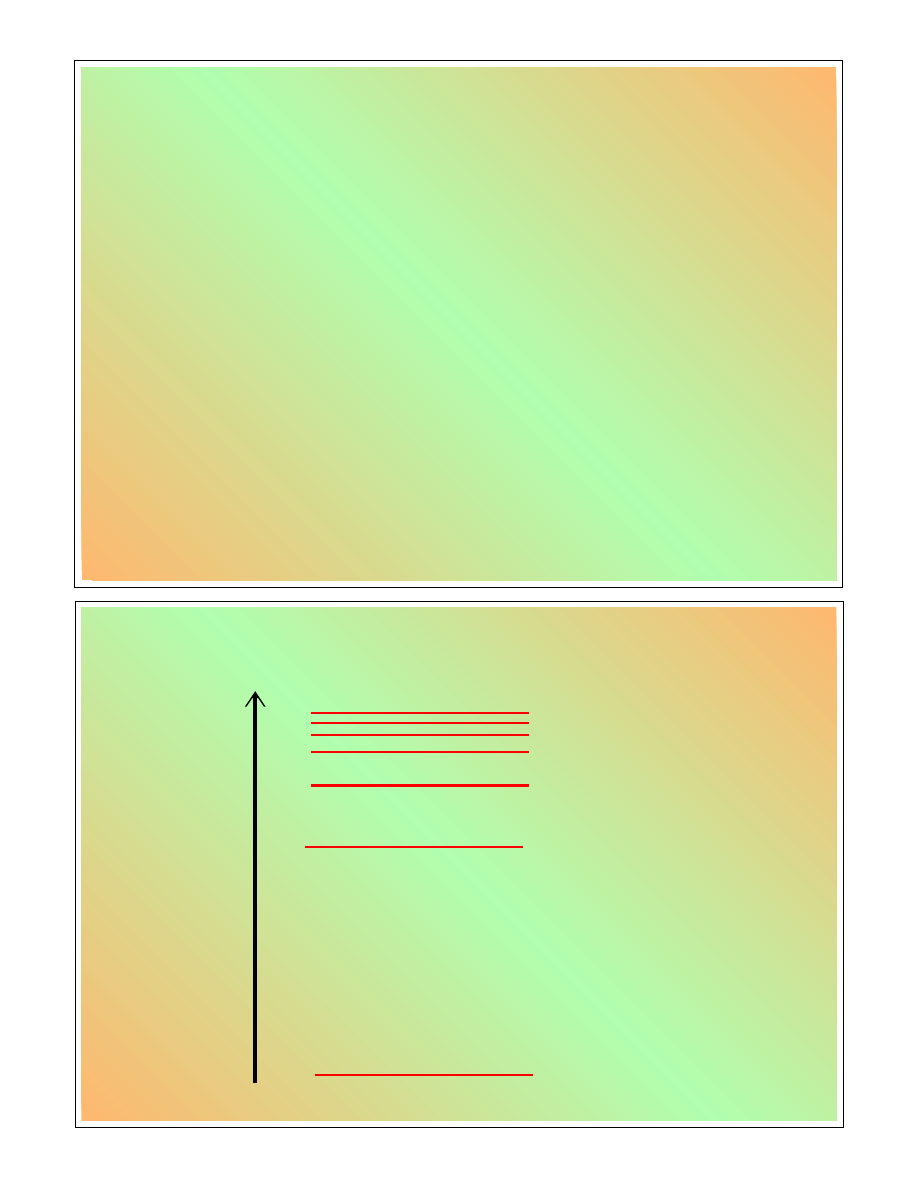
Wartości energii całkowitej

Energia

elektronu

n = 1

n = 2

n = 3

n = 4

n = 7

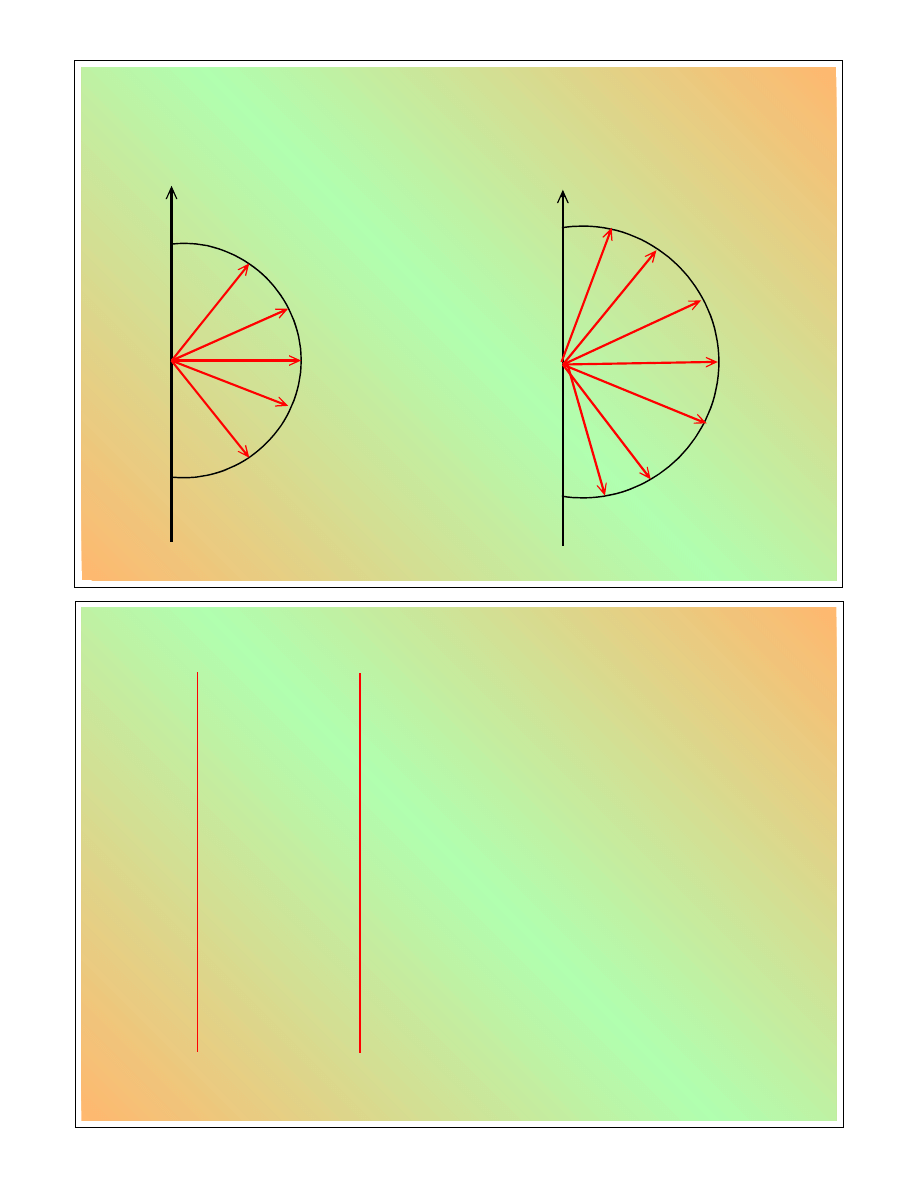
Moment pędu i jego składowa M

z

z

l

=2

m = 0,±1,±2

0

l

=3

£

-

£

2

£

-2

£

z

m = 0,±1,±2,±3

0

£

-

£

2

£

-2

£

3

£

-3

£

Liczby kwantowe

n

l

m

1

0

0

2

0

0

1

-1,0,+1

3

0

0

1

-1,0,+1

2

-2,-1,0,+1,+2

4

0

0

1

-1,0,+1

2

-2,-1,0,+1,+2

3

- 3,-2,-1,0,+1,+2+3

Każda kombinacja liczb odpowiada jednej funkcji falowej