G. Wieczorkowska & J. Wierzbiński (2005)
1
Rozdział 2
Co to znaczy, że wyniki badań są istotne statystycznie?
W poprzednim rozdziale powiedzieliśmy, że aby dowieść wpływu zielonej herbaty,
powinniśmy porównać średni poziom energii w dwóch grupach. W tym celu musimy przedstawić
poziom energii w postaci liczb, a następnie stwierdzić, jaką różnice uznamy za wystarczającą
– istotną statystycznie. W tym rozdziale spróbujemy wytłumaczyć, jak to robimy.
Liczby wykorzystywane w naukach społecznych maja różne znaczenie. Pierwsze pytanie,
jakie musimy zadać, dotyczy skali pomiarowej.
2.1. Skale pomiarowe
Wyobraźmy sobie, że chcemy sprawdzić, jakie są preferencje naszych studentów dotyczące
form egzaminowania - należymy do bardzo liberalnych wykładowców, więc chcemy dowiedzieć się,
jaka forma zaliczenia najbardziej odpowiadałaby studentom. Dopuszczamy następujące formy:
1. egzamin testowy,
2. esej pisany w domu,
3. egzamin ustny.
W jaki sposób sprawdzimy preferencje studentów? Możemy na zajęciach omawiać poszczególne
opcje, obserwując równocześnie reakcje studentów i klasyfikując je - np. w następujące kategorie
(załóżmy, że są one rozłączne):
1. zmarszczenie brwi,
2. rozmowa z sąsiadem,
3. patrzenie w okno,
4. reakcja werbalna (zadawanie pytań, komentarze).
Przy kodowaniu takich wyników do komputera (tabela 2.1) możemy używać dowolnych liczb, np.:
1, 2, 3, 4 lub: 32, 14, -9, 7, ponieważ przekazują one informację, że opisywane reakcje zostały
zakwalifikowane jako różne. Tego rodzaju „pomiar” (przypisanie reakcjom studentów liczb) określany
jest jako nominalny (jakościowy).
Tab. 2.1. Sposób kodowania zmiennej ze skali nominalnej. Użyte cyfry: 1, 2, 3, 4 oznaczają
WYŁĄCZNIE numery kategorii
Pomiar preferencji możemy skomplikować, prosząc o porangowanie tych trzech form - od
najbardziej do najmniej preferowanej (tabela 2.2).
Tab. 2.2 Sposób kodowania zmiennej ze skali porządkowej. Cyfra 1 oznacza opcję najbardziej
preferowaną, 3 – najmniej
Ustny
Testowy
Esej
Ustny
Testowy
Esej
Osoba A
1
3
4
Osoba B
4
2
3
Osoba C
4
3
3
G. Wieczorkowska & J. Wierzbiński (2005)
2
Osoba A
1
2
3
Osoba B
3
1
2
Osoba C
2
3
1
W ten sposób dowiadujemy się więcej o preferencjach pojedynczej osoby (np. osoba A
najbardziej preferuje egzamin ustny, a najmniej pisanie eseju), ale nadal nie wiemy, jak silnie odrzuca
pracę pisaną w domu. Może różnice w preferencjach między tymi formami egzaminu są nieznaczne,
ale mogą też być bardzo duże. Ten typ pomiaru nazywany jest skalą porządkową.
Możemy także poprosić studentów o wypełnienie krótkiej ankiety, w której te trzy formy
egzaminu byłyby oceniane na następującej skali:
1
Zdecydowanie nie
odpowiada mi.
2
Nie odpowiada
mi.
3
Nie
mam
zdania.
4
Odpowiada mi.
5
Zdecydowanie
odpowiada mi.
Choć puryści metodologiczni nie chcą tego zaakceptować, w naukach społecznych
powszechnie tego typu pomiar uznaje się za skalę przedziałową, czyli uznaje się, że różnica między
„nie odpowiada mi” a „zdecydowanie odpowiada mi” jest taka sama, jak różnica między „nie
odpowiada mi” i „nie mam zdania”. Problem opisu tego typu skal, sposobu traktowania odpowiedzi
„nie mam zdania”, jest omówiony w literaturze – dlatego pominiemy go w naszym maksymalnie
uproszczonym przykładzie dydaktycznym. Dla skali ilościowej, która pozwala na wykonywanie
operacji matematycznych, konieczne jest zdefiniowanie jednostki skali.
Tab. 2.3. Sposób kodowania zmiennej ze skali przedziałowej. Użyte cyfry (1,2,3,4,5) oznaczają
wartości na skali odpowiedzi
Ustny
Testowy
Esej
Osoba A
5
4
3
Osoba B
1
5
4
Osoba C
3
2
3
W tym przypadku możemy zobaczyć, że najmniej preferowana opcja odpowiada poglądowi
„nie mam zdania” dla osoby A i „zdecydowanie nie odpowiada mi” dla osoby B. Informacje zawarte w
tabeli 2.3 przedstawiliśmy na rysunku 2.1.
Rys. 2.1. Ilustracja graficzna preferencji opisanych w tabeli 2.3
Testowy
Ustny
Ustny
Esej
NIE
Nie mam zdania
TAK
1
2
3
4
5
Osoba A
Osoba B
Osoba C
Esej
Esej
Ustny
Testowy
Testowy
Zdecydowanie NIE
Zdecydowanie TAK

G. Wieczorkowska & J. Wierzbiński (2005)
3
Jeżeli chcemy pomiar wysublimować , możemy prosić o udzielenie odpowiedzi przy
komputerze, gdzie zadaniem studenta jest wybór odpowiedzi TAK lub NIE przy każdej formie
egzaminu - wskaźnikiem siły preferencji będzie dla nas czas podejmowania decyzji. Można założyć,
że szybkie TAK świadczy o silnie pozytywnym przekonaniu, a szybkie NIE o silnym odrzuceniu opcji.
Jeżeli od czasu odpowiedzi NIE odejmiemy stałą zależną od czasów występujących w badaniu, np.
100, zaś od czasu odpowiedzi TAK odejmiemy także 100, otrzymamy „ładną” skalę pomiarową, gdzie
wysokie wyniki będą oznaczały pozytywne preferencje.
Podsumowując: oglądając liczby (np. w komputerze) należy zawsze pamiętać, z jakiej skali
pomiarowej pochodzą. Komputer z łatwością policzy średnią z kategorii, ale wiemy, że mimo
podobieństwa liczb sugerowane przez nie uporządkowanie kategorii nie istnieje. Ponieważ jedyna
informacja polega na odróżnianiu reakcji na różne opcje, równie dobrze moglibyśmy zakodować
kategorie za pomocą liczb: -7, 12, 3, 79.
O możliwych przekształceniach ze skal nominalnych i porządkowych warto przeczytać w
literaturze
[20]
.
Dalsze rozważania ograniczymy jedynie do zmiennych ilościowych, gdy zdefiniowana
jest jednostka pomiaru.
2.2. Podstawowe statystyki opisowe dla skal ilościowych
Chcąc porównać wyniki kobiet i mężczyzn w teście wyobraźni przestrzennej, możemy
oceniać różnice „na oko”, ale zdecydowanie lepszym pomysłem jest posługiwanie się pewnymi
liczbami, które służą do opisu rozkładu wyników. Liczby wyliczane na podstawie próby wyników
nazywane są statystykami.
Podstawowe statystyki opisowe można pogrupować na miary tendencji centralnej, opisujące
położenie wyników, oraz miary dyspersji, które opisują rozproszenie wyników. Najczęściej
wykorzystywaną miarą tendencji centralnej jest średnia arytmetyczna wyrażona wzorem:
n
X
X
X
n
X
M
n
...
2
1
gdzie
n
X
X
X
,...
,
2
1
to wyniki poszczególnych osób, a N to liczba osób w próbie.
Przykład: jeśli w teście pięć osób uzyskało odpowiednio: 2, 2, 6, 7 i 8 punktów, średnia wynosi
5 punktów.
Średnią wyników w próbie oznaczamy literą M od angielskiego słowa mean. W wielu podręcznikach
średnia dla próby oznaczana jest także jako
.
M
X
2.2.1 Miary rozproszenia wokół średniej
Choć może to wyglądać niezbyt poważnie , podstawowe pojęcia statystyczne tłumaczyć
będziemy, porównując wysokości kwiatków w doniczkach. Doświadczenie dydaktyczne nauczyło mnie
(gw), że ilustrowanie liczb w ten sposób bardzo ułatwia zrozumienie.
Porównajmy zatem dwa zbiory wyników (wysokości kwiatków w doniczkach):
G. Wieczorkowska & J. Wierzbiński (2005)
4
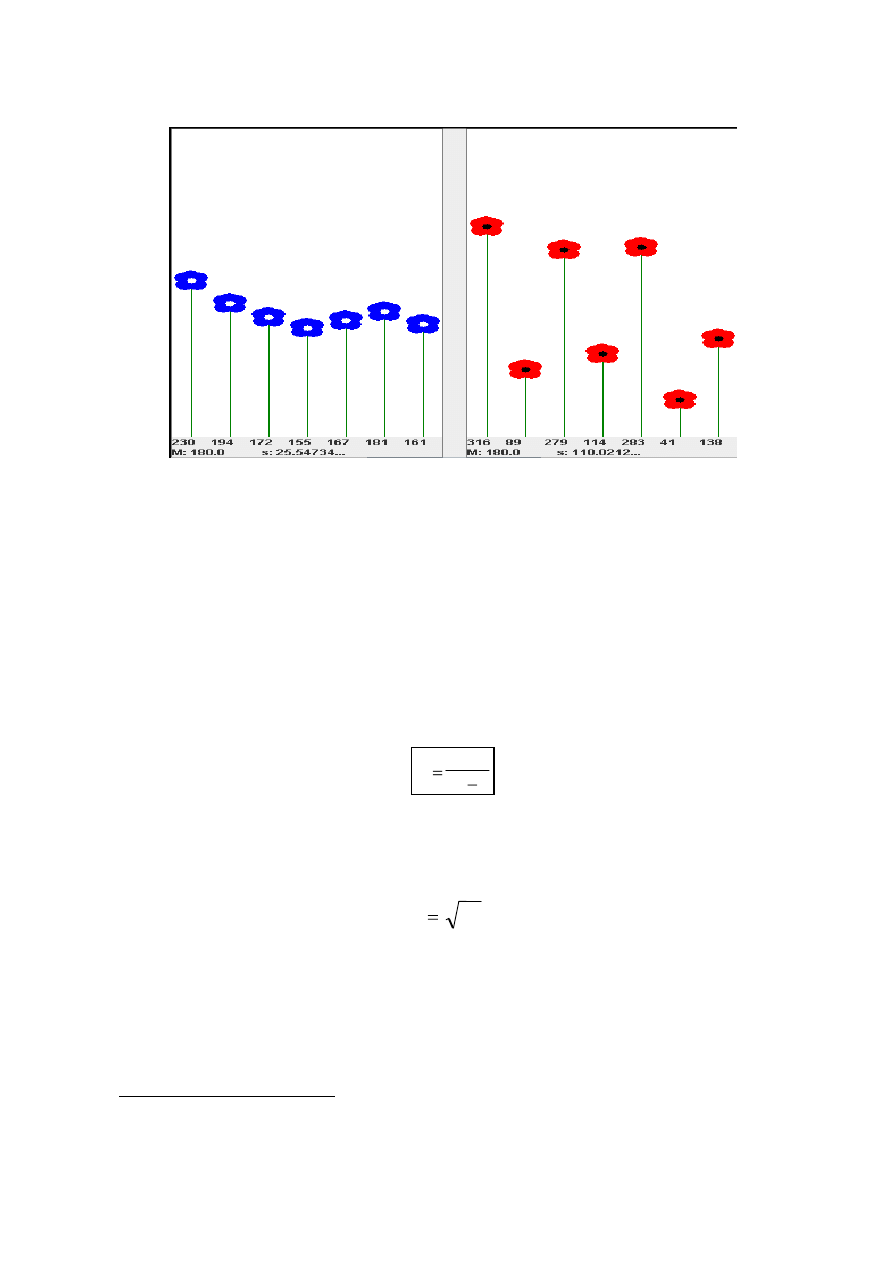
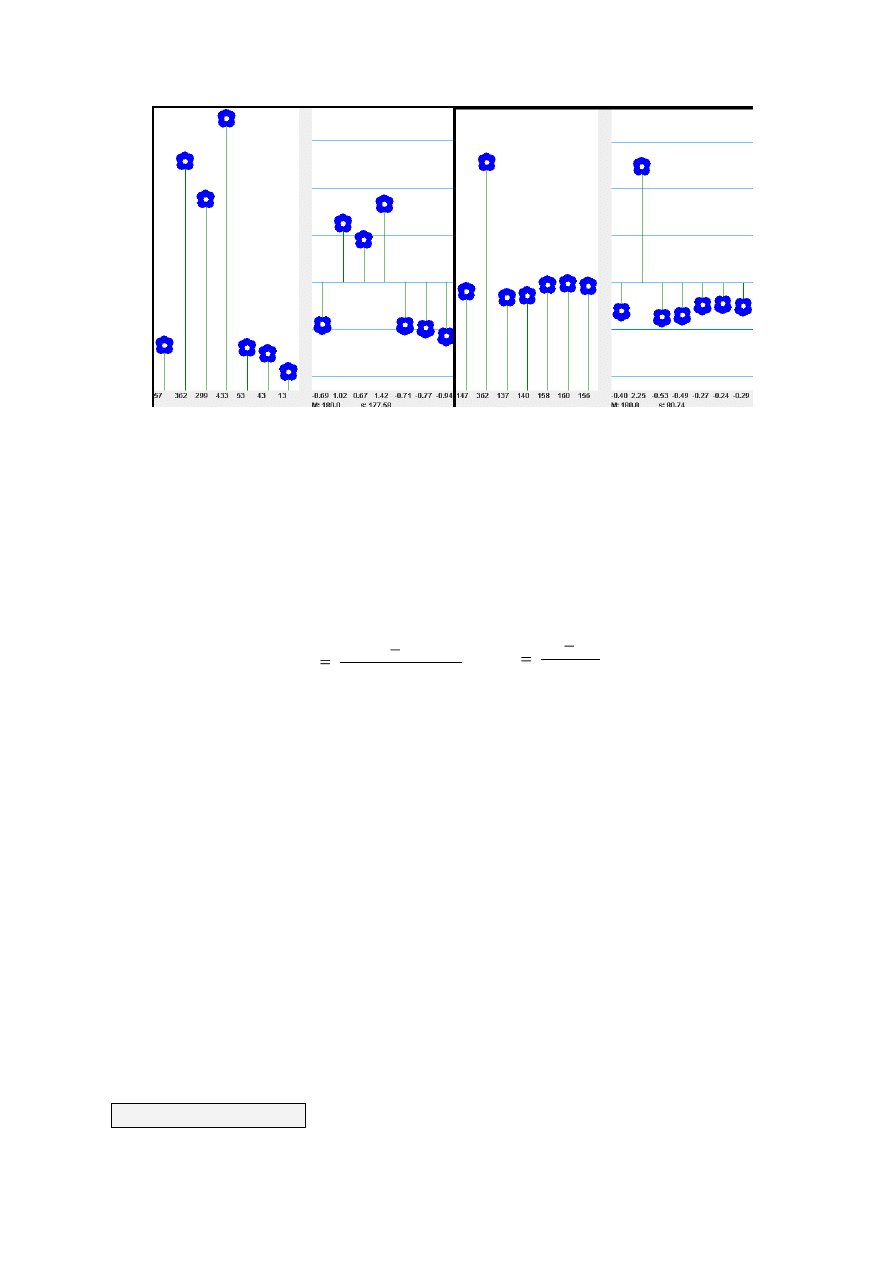
Rys. 2.2. Porównanie dwóch rozkładów o tej samej średniej, a różnej wariancji
W obu doniczkach średnia wysokość kwiatków wynosi 180. To, co je różni, to stopień
skupienia wyników wokół średniej. Dla każdego kwiatka możemy obliczyć jego „odległość” od
średniej, odejmując od X (wysokość kwiatka) M (średnią arytmetyczną wysokości wszystkich
kwiatków w danej doniczce). Zsumowanie podniesionych do kwadratu różnic X -M da nam miarę
rozproszenia wyników wokół średniej, oznaczaną jako SS (sum of squares). Suma kwadratów
odchyleń od średniej zazwyczaj
1
rośnie wraz ze wzrostem liczby osób w próbie.
Aby nasza miara nie zależała od wielkości próby, musimy uśrednić SS, dzieląc ją przez liczbę
stopni swobody określoną na podstawie liczebności próby (n-1). W naszej doniczce jest 7 kwiatków,
zatem n=7, czyli n-1=6. Wynikiem tych obliczeń jest podstawowa miara rozproszenia dla próby,
nazywana wariancją.
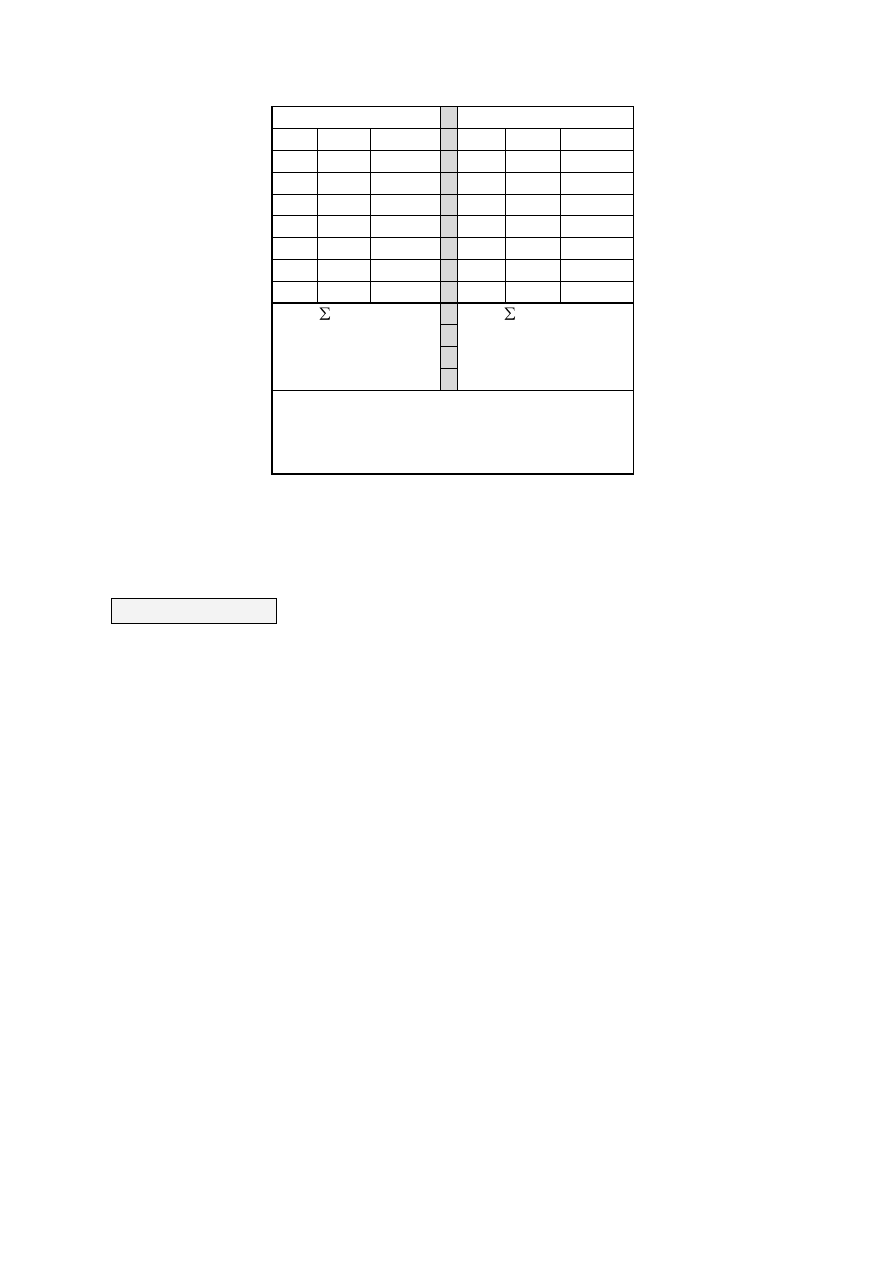
W statystyce często wykorzystujemy pierwiastek z wariancji, określany jako odchylenie
standardowe.
W tabeli poniżej policzona została wariancja i odchylenie standardowe dla obu
przedstawionych na rysunku doniczek.
Tab. 2.4. Ilustracja sposobu wyliczania wariancji i odchylenia standardowego dla danych z rysunku
2.2
1
Wyjątkiem jest sytuacja, gdy dodatkowe wyniki mają wynik równy średniej, ponieważ wtedy ich odchylenia od średniej
równe są zeru.
2
s
s
)
1
(
2
n
SS
s
G. Wieczorkowska & J. Wierzbiński (2005)
5
Pojęcia odchylenia standardowego i wariancji są najważniejsze ze statystyk opisowych jednej
zmiennej i zawierają tę samą informację. Znając wariancję, znamy odchylenie standardowe
- i odwrotnie. Odgrywają one również kluczową rolę w badaniu współzależności pomiędzy dwiema
(i więcej) zmiennymi.
2.3. Standaryzacja
Formułując dowolny sąd, nie tylko o liczbach, należy zawsze określić standard porównań.
Jeśli chcę powiedzieć, że Antek jest wysoki, muszę określić w porównaniu do kogo. Antek jest wysoki,
jeśli porównuję go do innych szóstoklasistów - lub niski, jeśli porównuję go z jego starszym bratem.
Jeżeli chcę określić, jak wysoki jest kwiatek, rozsądnym wydaje się być pytanie o relację do średniej w
doniczce.
Najprostszą metodą porównania wartości zmiennej jest CENTROWANIE, czyli zamiana
wartości X w odległość od średniej. Gdy różnica X - M jest większa od zera, kwiatek jest wyższy niż
przeciętna w doniczce, gdy ujemna - kwiatek jest niższy. Odległość od średniej może być mylącą
informacją, ponieważ - jak widzimy na rysunku (rysunek 2.3) - w obu doniczkach mamy identyczną
średnia M = 180 i kwiatek o wysokości 362, dla którego w wyniku centrowania X - M wyniesie 182. W
prawej doniczce zróżnicowanie kwiatków jest większe, zatem „unikalność” kwiatka o wysokości 362
jest mniejsza. Metodą uwzględniania zróżnicowania jest dzielenie X - M przez odchylenie
standardowe.
Doniczka lewa
Doniczka prawa
X
X -M (X -M)
2
X
X -M (X -M)
2
230 50
2500
316 136
18496
194 14
196
89
-91
8281
172 -8
64
279 99
9801
155 -25
625
114 -66
4356
167 -13
169
283 103
10609
181 1
1
41
-139
19321
161 -19
361
138 -42
1764
SS = (X – M)²=3916
s
2
=652,667
s=25,547
SS = (X – M)²=72628
s
2
=12104,67
s=110,021
Różnica wariancji obu rozkładów i ich odchyleń
standardowych wskazuje, że drugi rozkład
charakteryzuje się większym rozproszeniem
wyników wokół średniej niż rozkład pierwszy.
G. Wieczorkowska & J. Wierzbiński (2005)
6
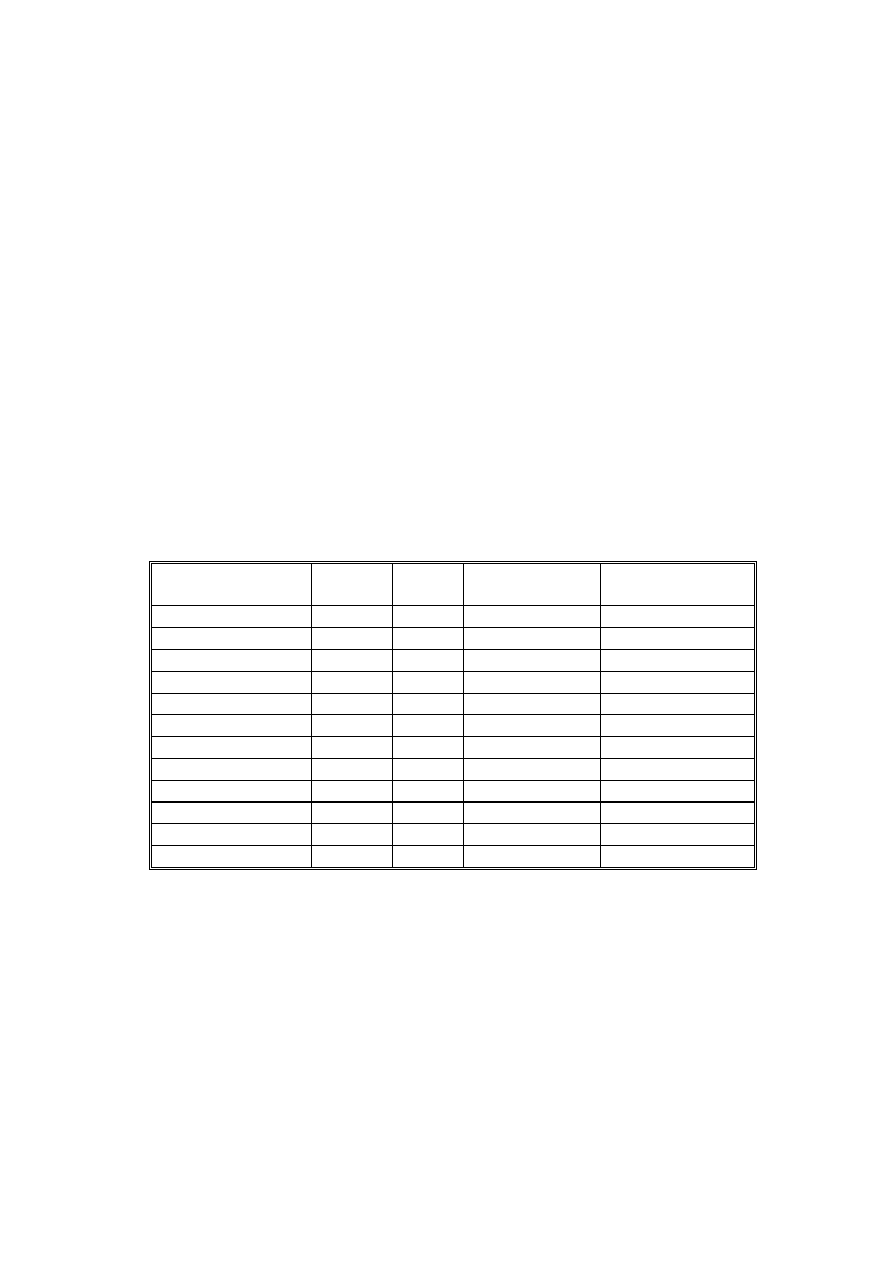
Rys. 2.3. Ilustracja standaryzacji wyników. Kwiatki z ujemnymi wynikami standaryzowanymi zostały
narysowane „do góry nogami”
Standaryzacja polega na zamianie wyników surowych (X ) w wyniki standaryzowane (z).
Standaryzować możemy wyłącznie zmienne ilościowe - bo tylko wtedy możemy policzyć średnią
i odchylenie standardowe.
Standaryzacja przekształca rozkład każdej zmiennej ilościowej (pod warunkiem, że jego
odchylenie standardowe nie wynosi zero) w rozkład o średniej równej zero i odchyleniu
standardowym wynoszącym jeden.
.
stand
odchylenie
średnia
wynik
z
czyli
s
M
X
z
Wynik standaryzowany z pokazuje, o ile odchyleń standardowych uzyskany przez nas wynik
jest położony poniżej (gdy z < 0) lub powyżej (gdy z > 0) średniej. Innymi słowy - jak daleko
(w jednostkach odchylenia standardowego) leży nasz wynik od średniej. Dla X = M wynik
standaryzowany wynosi zero.
Na rysunku 2.3 kwiatki z ujemnymi „zetami” zostały narysowane „do góry nogami”.
W lewej doniczce wynik standaryzowany dla kwiatka o wysokości 362 wynosi 1,02. Oznacza
to, że znajduje się on w swojej doniczce ponad jedno odchylenie standardowe powyżej średniej.
W prawej doniczce wynik standaryzowany dla kwiatka o wysokości 362 wynosi 2,25. Oznacza
to, że znajduje się on w swojej doniczce więcej niż dwa odchylenia standardowe powyżej średniej.
Standaryzacja pozwala porównać dwie liczby wyrażone oryginalnie w różnych jednostkach,
np. wyniki dwóch studentów piszących egzamin ze statystyki na różnych uczelniach. Jeżeli Darek
otrzymał w teście 17 punktów, a Andrzej 12, nic nie możemy powiedzieć, dopóki nie wiemy, jaka była
średnia i odchylenie standardowe na obu uczelniach. Jeżeli w uczelni Darka M = 15, s = 2, a w
uczelni Andrzeja M = 11, s = 1, obaj uzyskali wynik z = 1, a więc ich wyniki są równoważne.
2.4. Rozkład zmiennej

G. Wieczorkowska & J. Wierzbiński (2005)
7
Nie musimy już chyba Czytelnika przekonywać, że zanim powiemy cokolwiek o jakiejś liczbie,
musimy zapytać, z jakiego rozkładu (doniczki ) pochodzi.
Pierwszym krokiem w analizie jest sprawdzenie rozkładów naszych zmiennych. Mówiąc
najprościej, rozkład zmiennej w próbie pokazuje, jak często w naszej próbie występowała dana
wartość. Jeżeli wśród 30 badanych było 14 mężczyzn, co stanowi 0,47 próby, to zmienna PŁEĆ,
przyjmująca wartości 1 – mężczyzna, 2 – kobieta, ma następujący rozkład (1; 0,47) (2; 0,53)
- ponieważ kobiet było 16, co stanowi 0,53 próby. W rozkładzie zamiast procentów podajemy
proporcje, ponieważ są one odpowiednikiem prawdopodobieństwa definiowanego w podejściu
empirycznym (a posteriori).
2.4.1 Definicja prawdopodobieństwa
W szkole poznaliśmy klasyczną definicję prawdopodobieństwa (a priori). Pomaga nam
ona odpowiedzieć na pytania, które dotyczą prawdopodobieństwa zajścia różnych zdarzeń, bez
konieczności przeprowadzania doświadczeń weryfikujących wynik. Gdy staramy się dowiedzieć, jakie
jest prawdopodobieństwo wyrzucenia orła przy rzucie symetryczną monetą albo wyrzucenia cyfry
większej od 4 przy rzucie kostką, nie musimy koniecznie rzucać monetą lub kostką. Stosując
klasyczną definicję prawdopodobieństwa, definiujemy prawdopodobieństwa zajścia tych zdarzeń jako
stosunek liczby zdarzeń sprzyjających do liczby zdarzeń możliwych. Oczywiście milcząco zakładamy,
że orły będą wypadać tak samo często jak reszki (moneta jest „uczciwa” – nie wyróżnia ani reszki, ani
orła). Podobnie kostka musi być uczciwa – żadna liczba oczek nie może być wyróżniona. Gdybyśmy
mieli do czynienia z „oszukaną” kostką lub monetą, klasyczna definicja prawdopodobieństwa nic nam
nie da – chyba że wiemy, w jaki sposób moneta czy kostka jest oszukana (np. wiemy, że orzeł
wypada dwa razy częściej niż reszka).
W naukach społecznych nie możemy stosować klasycznej definicji prawdopodobieństwa,
gdyż w zasadzie nigdy nie znamy prawdopodobieństw a priori - dlatego stosujemy definicję
empiryczną (albo a posteriori) prawdopodobieństwa. Oznacza to, że aby odpowiedzieć na pytanie,
jakie jest prawdopodobieństwo spotkania na ulicy w Warszawie osoby rozwiedzionej, musimy
przeprowadzić badania. Jeżeli zapytamy o stan cywilny sto osób spotkanych na ulicy i cztery
powiedzą, że są rozwiedzione, to będziemy mogli stwierdzić, że prawdopodobieństwo spotkania
osoby rozwiedzionej wynosi 0,04.
2
To zupełnie inny sposób rozumienia prawdopodobieństwa niż ten
często spotykany na ulicy – uczestnicy IDOLA na pytanie, jakie jest prawdopodobieństwo, że wygrają,
odpowiadają czasami: „1/2”, co w potocznym języku oznacza 50% szans na sukces. Widząc
zdziwienie na twarzy pytającego, dana osoba wyjaśniła, że albo wygra, albo przegra, a w związku
z tym są dwie możliwości i stąd prawdopodobieństwo wygrania to 1/2. Wiemy oczywiście, że definicja
częstościowa prawdopodobieństwa nakazywałaby rozważać to zdarzenie nie z punku widzenia
indywidualnego interesu, ale z punktu widzenia wszystkich możliwych uczestników IDOLA. A to
oznacza, że szansa wygrania, jeżeli nie wiemy nic więcej na temat osoby, która startuje, jest
równoważna prawdopodobieństwu obliczonemu jako iloraz „1” i liczby wszystkich uczestników tego
konkursu – jeśli startuje 10 000 osób, szansa pojedynczej osoby na wygranie wynosi 1/10 000. Jeżeli
wiemy, że ta osoba jest zdecydowanie lepsza od sporej części kandydatów oraz że wśród tych 10 000
jest tylko trzystu, którzy mają odpowiednie uzdolnienia wokalne, moglibyśmy zaryzykować tezę, że
prawdopodobieństwo, że dana osoba zwycięży, to 1/300.
Podsumowując: rozkład zmiennej można przedstawić jako zbiór par (wartość, częstość),
gdzie częstość oznacza to, ile razy dana wartość wystąpiła w naszej próbie - wtedy rozkład płci
wygląda następująco: (1, 14) (2, 16), ale poprawniej jest przedstawić rozkład jako zbiór par (wartość,
2
O tym, jakie warunki muszą być spełnione, abyśmy mogli formułować sądy ogólne na podstawie zbadanej próby, należy
przeczytać w literaturze
[15]
.
G. Wieczorkowska & J. Wierzbiński (2005)
8
prawdopodobieństwo), gdzie prawdopodobieństwo należy rozumieć jako proporcję osób, którym
przypisano daną wartość, w stosunku do całej liczebności próby.
Podstawowym sposobem prezentacji zmiennej jest rozkład częstości (frekwencje, frakcje).
Rozkład częstości (tabela 2.5) przedstawia wartość danej zmiennej oraz jej częstość pojawiania się.
W rozkładzie częstości mamy pięć kolumn. W pierwszej wypisane są wartości zmiennej,
uporządkowane od najmniejszej do największej. W drugiej - liczba osób (częstość), które udzieliły
takiej odpowiedzi. W trzeciej kolumnie liczba została zamieniona na procent osób, które udzieliły
takiej odpowiedzi - jest to wynik dzielenia liczby osób udzielających takiej odpowiedzi przez liczbę
osób, którym zadano to pytanie. W kolumnie czwartej znajduje się procent ważnych odpowiedzi.
Jest to wynik dzielenia przez liczbę osób, które odpowiedziały na zadane pytanie. Osoby, które
pominęły to pytanie celowo lub przez nieuwagę, nie są uwzględniane przy wyliczaniu procentów. To,
czy odpowiedź „trudno powiedzieć” zostanie zakwalifikowana jako brak danych, zależy od interpretacji
badacza. W analizowanym przykładzie tylko dwie osoby nie mają zapisanej odpowiedzi, więc
„procent” różni się od „procentu ważnych” nieznacznie. W pytaniu o satysfakcję z pracy, którego nie
zadaje się bezrobotnym i emerytom, różnice między tymi procentami są duże.
Piąta kolumna zawiera procent skumulowany, który mówi nam o tym, jaki procent próby
uzyskał wynik mniejszy lub równy danej wartości. Procent skumulowany jest wynikiem dodawania
„procentów ważnych”. Procent skumulowany dla X = 2 (respondent ma co najwyżej dwoje dzieci) jest
sumą procentów ważnych odpowiedzi dla X = 0, X = 1, X = 2.
Tab. 2.5. Rozkład zmiennej LICZBA DZIECI na podstawie próby reprezentatywnej dorosłych Polaków
Wartości zmiennej
Częstość Procent Procent ważnych Procent
skumulowany
0 nie ma dzieci
317
25,878
25,920
25,920
1 jedno
223
18,204
18,234
44,154
2 dwoje
364
29,714
29,763
73,917
3 troje
184
15,020
15,045
88,962
4 czworo
79
6,449
6,460
95,421
5 pięcioro
24
1,959
1,962
97,383
6 sześcioro
16
1,306
1,308
98,692
7 siedmioro
8
0,653
0,654
99,346
8 ośmioro lub więcej 8
0,653
0,654
100,000
Ogółem
1223
99,837
100,000
9 brak danych
2
0,163
ogółem
1225
100
Źródło: PGSS 2005
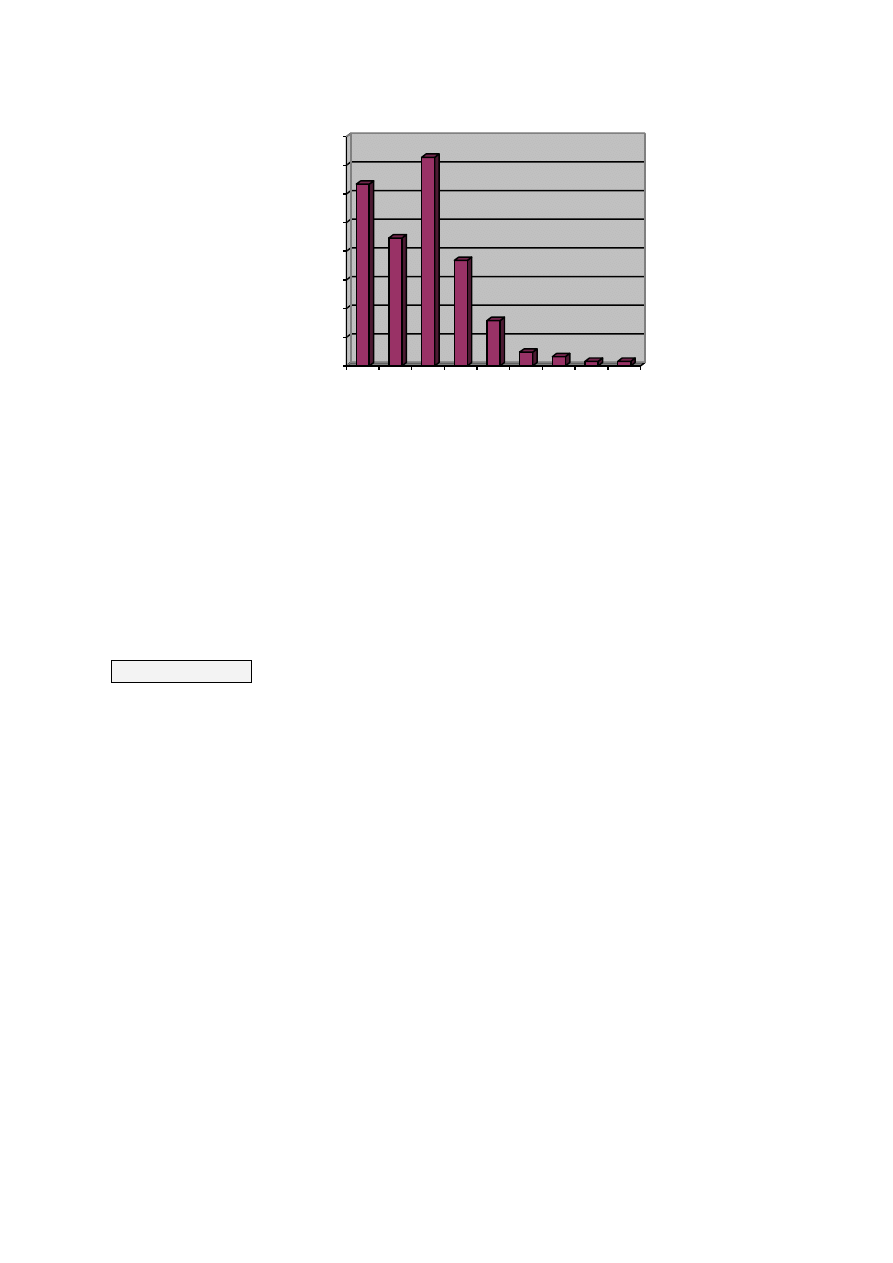
Rozkład zmiennej możemy przedstawić też graficznie: na osi poziomej przedstawione są
wartości zmiennej (pogrupowane, jeśli zachodzi taka konieczność) a na osi pionowej częstość
występowania tej wartości w zbiorze danych.
G. Wieczorkowska & J. Wierzbiński (2005)
9
0
50
100
150
200
250
300
350
400
0
1
2
3
4
5
6
7
8
Rys. 2.4. Graficzna prezentacja rozkładu zmiennej LICZBA DZIECI
Znając rozkład zmiennej, możemy odpowiedzieć na pytanie, jakie jest prawdopodobieństwo,
że zmienna przyjmie określoną wartość. Zanim to jednak zrobimy, wprowadzimy rozróżnienie na
zmienne ciągłe i skokowe. Zmienna skokowa przyjmuje jedynie wyróżnione wartości na osi liczbowej.
Przykładem takiej zmiennej jest liczba dzieci. Można mieć 0, 1, 2, 3 czy 1000 dzieci, ale nie można
mieć 1,5 ani 1,25 dziecka. Wartości zmiennej są wyraźnie od siebie oddzielone. Zmienna ciągła może
przyjąć dowolną wartość na osi liczbowej. Przykładem zmiennej ciągłej jest czas wykonywania
zadania, który możemy podawać w godzinach, minutach, sekundach, milisekundach itd. W praktyce
nasz sposób pomiaru zmiennych ciągłych czyni te zmienne skokowymi – zaokrąglamy np. wiek
do całych lat, ale mimo to - w rzeczywistości - jest to zmienna ciągła.
Przykład 2.4.1.
Na podstawie rozkładu zmiennej WZROST dla próby dorosłych mężczyzn określ
prawdopodobieństwo, że wylosowana osoba ma więcej niż 181 cm wzrostu.
G. Wieczorkowska & J. Wierzbiński (2005)
10
Tab. 2.6. Rozkład zmiennej WZROST w próbie dorosłych Polaków
Wzrost
Liczba osób Procent Procent
skumulowany
Proporcja
3
Proporcja
skumulowana
160
6
1,005
1,005
0,010
0,010
161
1
0,168
1,173
0,002
0,012
162
8
1,340
2,513
0,013
0,025
163
3
0,503
3,015
0,005
0,030
164
10
1,675
4,690
0,017
0,047
165
11
1,843
6,533
0,018
0,065
166
5
0,838
7,370
0,008
0,074
167
13
2,178
9,548
0,022
0,095
168
19
3,183
12,730
0,032
0,127
169
9
1,508
14,238
0,015
0,142
170
76
12,730
26,968
0,127
0,270
171
7
1,173
28,141
0,012
0,281
172
34
5,695
33,836
0,057
0,338
173
19
3,183
37,018
0,032
0,370
174
17
2,848
39,866
0,028
0,399
175
44
7,370
47,236
0,074
0,472
176
89
14,908
62,144
0,149
0,621
177
8
1,340
63,484
0,013
0,635
178
52
8,710
72,194
0,087
0,722
179
10
1,675
73,869
0,017
0,739
180
51
8,543
82,412
0,085
0,824
181
7
1,173
83,585
0,012
0,836
182
22
3,685
87,270
0,037
0,873
183
15
2,513
89,782
0,025
0,898
184
6
1,005
90,787
0,010
0,908
185
12
2,010
92,797
0,020
0,928
186
14
2,345
95,142
0,023
0,951
187
6
1,005
96,147
0,010
0,961
188
8
1,340
97,487
0,013
0,975
189
2
0,335
97,822
0,003
0,978
190
4
0,670
98,492
0,007
0,985
191
1
0,168
98,660
0,002
0,987
192
2
0,335
98,995
0,003
0,990
193
1
0,168
99,162
0,002
0,992
194
1
0,168
99,330
0,002
0,993
195
1
0,168
99,497
0,002
0,995
198
2
0,335
99,832
0,003
0,998
200
1
0,168
100,000
0,002
1,000
Ogółem 597
100
Źródło: PGSS 2005
Z tabeli 2.6 możemy odczytać, że procent mężczyzn niższych niż 165 cm wynosi
w zaokrągleniu 4,69. Oznacza to, że prawdopodobieństwo, że wylosowany Polak będzie niższy od
165 cm, wynosi w zaokrągleniu 0,0469.
3
Proporcja nazywana jest także frakcją lub częstością względną.
G. Wieczorkowska & J. Wierzbiński (2005)
11
Analogicznie - procent mężczyzn, którzy mają więcej niż 181 cm wzrostu, wynosi w
zaokrągleniu 100 - 83,585 = 16,415. Oznacza to, że prawdopodobieństwo, że wylosowany Polak
będzie miał co najmniej 181 cm, wynosi 0,16415.
Analogicznie - procent mężczyzn, którzy mają nie więcej niż 180 cm wzrostu, wynosi w zaokrągleniu
82,412. Oznacza to, że prawdopodobieństwo, że wylosowany Polak nie będzie wyższy niż 180 cm,
wynosi 0,824.
Podsumowując - znając rozkład zmiennej, możemy wyliczyć prawdopodobieństwa
przyjęcia przez zmienną wartości znajdujących się w określonym przedziale.
Czasami zamiast korzystania z rozkładu empirycznego możemy posłużyć się rozkładem
teoretycznym, opisanym odpowiednim równaniem matematycznym.
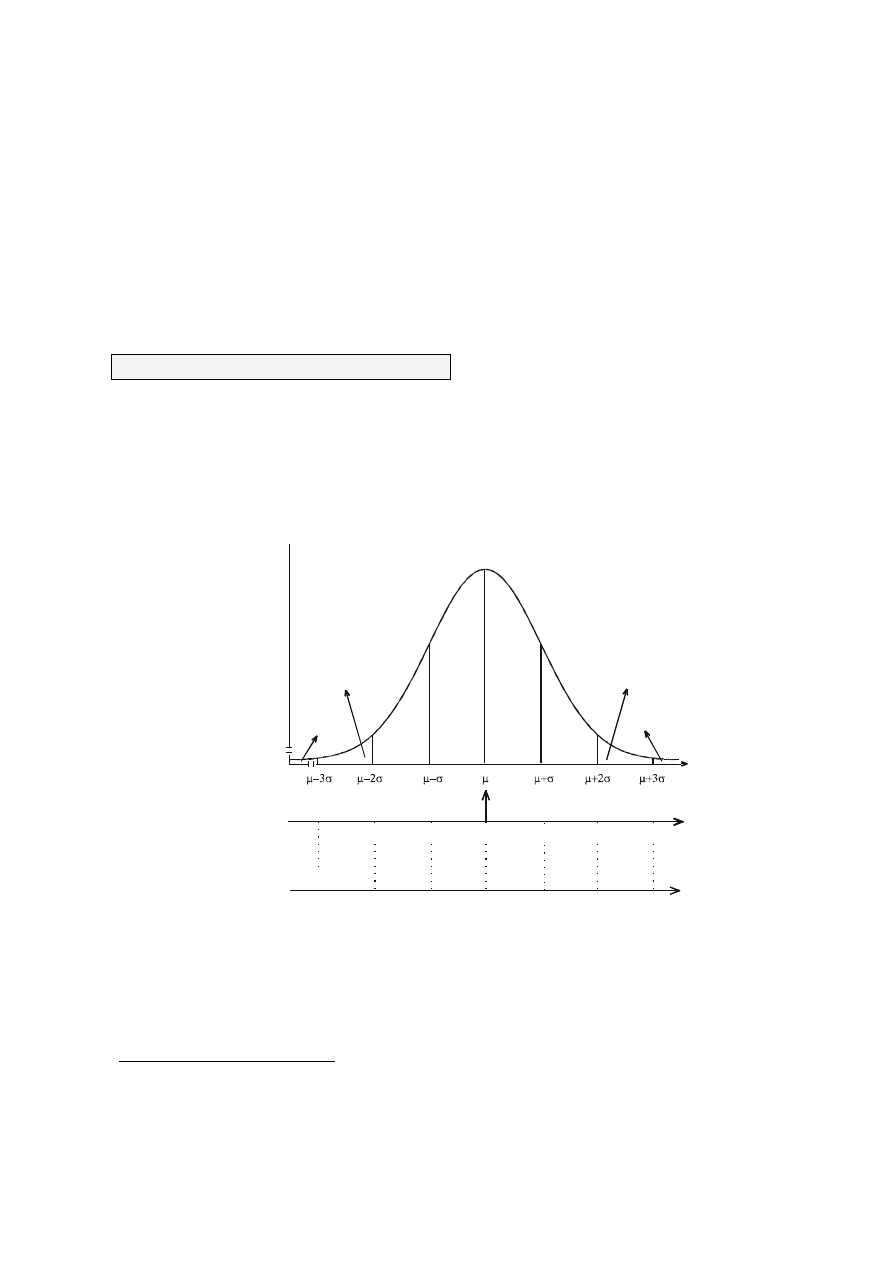
2.5. Rozkład normalny (krzywa Gaussa)
Wiele zmiennych w populacji ma rozkład normalny, który można opisać za pomocą krzywej
normalnej (Gaussa). Ma ona kształt dzwonu, który jest symetryczny względem średniej równej
modalnej (modzie) i medianie
4
rozkładu. Lewa i prawa gałąź rozkładu zbliża się asymptotycznie do
osi poziomej (nigdy jej nie przecina).
34,13%
34,13%
13,59%
13,59%
2,15%
0,13%
0,13%
2,15%
Rozkład X N(100, 10)
Jednostki Z
120
110
100
90
80
130
0
2
1
3
-2
-1
N(0,1)
Rys. 2.5. Rozkład normalny
Około 68,27% powierzchni pod krzywą mieści się w granicach jednego odchylenia
standardowego na prawo i lewo od średniej. Pole obszaru w granicach od z = –1,96 do z = +1,96
obejmuje 95% powierzchni pod krzywą, a od z = –2,58 do z = +2,58 obejmuje 99% całkowitej
powierzchni pod krzywą, przy czym odpowiednio 5% i 1% mieści się poza tymi granicami.
4
Mediana i wartość modalna (dominanta) to miary tendencji centralnej używane także dla skal nieilościowych
(nominalnych i porządkowych). Modalna (moda) określa wartość najczęściej występującą w rozkładzie. Mediana zaś
powinna dzielić rozkład wyników na połowy. W rozkładzie liczby dzieci [tabela 2.5] najczęściej występującą liczbą jest 2.
Wyznaczenie mediany nie jest proste, ponieważ nie jest to zmienna ciągła. Zachęcamy do lektury
[20,21]
dotyczącej miar
tendencji centralnej.
G. Wieczorkowska & J. Wierzbiński (2005)
12
Równanie krzywej normalnej zależy tylko od dwóch parametrów: średniej i odchylenia
standardowego. Ma to podstawowe znaczenie praktyczne - pozwala wyznaczyć rozkład zmiennej,
jeżeli znamy średnią oraz odchylenie standardowe i wiemy, że jest to rozkład normalny. Powierzchnia
pod krzywą normalną odpowiada 100% przypadków.
Bardzo ważną własnością krzywej normalnej jest to, że powierzchnia pod krzywą (czyli
proporcja przypadków) w przedziale od średniej do jakiegokolwiek punktu zależy tylko od
odległości tego punktu od średniej wyrażonej w jednostkach odchylenia standardowego.
Między średnią i punktem, który oddalony jest od niej o jedno odchylenie standardowe, mieści
się zawsze 0,3413 powierzchni pod krzywą - bez względu na to, czy analizujemy rozkład wzrostu,
wagi, inteligencji, czy jakiejkolwiek innej zmiennej. Wielkość obszaru pod krzywą, czyli proporcja
przypadków, ma bardzo duże znaczenie - ponieważ wyznacza prawdopodobieństwo, że
zmienna przyjmie wartość z tego przedziału. Na rysunku 2.5 widzimy, że w odległości ±2 odchyleń
standardowych od średniej znajduje się ponad 90% przypadków. W tabeli poniżej znajdują się
używane określenia słowne
[21]
dla wyników w różnym stopniu odległych od średniej rozkładu.
z<-3
-3<z<-2 -2<z<-1 -1<z<1 1<z<2 2<z<3 z>3
wyjątkowo
małe
bardzo
małe
małe
typowe duże
bardzo
duże
wyjątkowo
duże
Warto zapamiętać, że zapis N(μ, σ)
5
oznacza, że zmienna ilościowa ma rozkład normalny o
średniej μ i odchyleniu standardowym σ.
Pamiętajmy, że rozkład normalny jest zdefiniowany dla zmiennych ciągłych. W rezultacie
musimy pamiętać, że prawdopodobieństwo, że badana zmienna przyjmuje konkretną wartość, jest
równe zeru: p(X =35)=0. Przykładem zmiennej ciągłej może być wzrost. Jeżeli zmierzymy czyjś
wzrost, otrzymując np. 173 cm, musimy pamiętać, że jest to tylko wartość przybliżona, zależna od
dokładności naszej miarki. Osoby w grupie ludzi o wzroście 173 cm mogą się od siebie pod względem
tej zmiennej różnić, ale nasze urządzenie pomiarowe może nie być wystarczająco dokładne, aby to
wykryć. Jeżeli nawet weźmiemy dokładniejszą miarkę, która pozwala na pomiar z dokładnością do
milimetrów, mikrometrów czy nanometrów, to i tak pozostaje pewien margines błędu. Nigdy nie
możemy mieć pewności, że dana osoba ma dokładnie 173 cm wzrostu, a odzwierciedleniem tego
faktu jest właśnie określenie prawdopodobieństwa, że X =173 (dokładnie), jako równego zeru. Dlatego
dla zmiennych ciągłych zawsze obliczamy prawdopodobieństwa, że zmienna przyjmie wartość
należącą do jakiegoś przedziału, a nie równą jakiejś liczbie.
W przypadku zmiennej ciągłej prawdopodobieństwa wypisane w ramce poniżej są sobie
równe.
p(z
1
<z<z
2
) = p(z
1
≤z≤z
2
) = p(z
1
≤z<z
2
) = p(z
1
<z≤z
2
)
Rozkład normalny jest symetryczny, więc tyle samo przypadków mieści się między średnią
a wynikiem: z = 1 (0 < z < 1), jak i między średnią a wynikiem: z = –1 (–1 < z < 0).
W sumie 0,6826 (2 x 0,3413) przypadków mieści się w odległości jednego odchylenia standardowego
(–1 < z < 1) od średniej.
W odległości dwóch odchyleń standardowych (–2 < z < 2) mieści się ponad 95% (2 x 0,4773)
przypadków.
W odległości trzech odchyleń standardowych (–3 < z < 3) mieszczą się praktycznie wszystkie
przypadki, chociaż teoretycznie krzywa normalna biegnie nieskończenie daleko i nigdy nie osiąga
5
Parametry populacji oznaczamy greckimi: μ [mi] i σ [sigma].

G. Wieczorkowska & J. Wierzbiński (2005)
13
wartości zerowej (nie przecina osi OX). Otrzymanie dla rozkładu normalnego z > 5 lub z < –5 jest więc
możliwe, ale niesłychanie mało prawdopodobne.
Korzystając z tablic rozkładu normalnego (tablica 2.1), możemy wyznaczyć pole pod krzywą
normalną, odcięte przez dowolne dwa punkty. Aby to uczynić, musimy zamienić wartości naszej
zmiennej na wyniki standaryzowane. W tablicy odnajdujemy interesującą nas wartość z
k
i odczytujemy wartość p
26
:
p
2
= p(z>z
k
)
Przykład: dla z
k
=1,96 p
2
=p(z>1,96)=p(z<-1,96)= 0,025
Omówiona wcześniej standaryzacja zachowuje kształt rozkładu wyjściowego. Rozkład
standaryzowanych wyników zmiennej LICZBA DZIECI będzie miał kształt rozkładu przedstawionego
na rysunku 2.4 - z tą różnicą, że średnia rozkładu standaryzowanego zawsze wynosi 0,
a odchylenie standardowe równe jest 1.
Standaryzacja rozkładu normalnego N(μ, σ) powoduje przekształcenie go w rozkład normalny
standaryzowany N(0, 1). W ten sposób niezależnie od tego, czy interesuje nas wzrost dorosłych
mężczyzn N(175, 6) czy inteligencja N(100, 15), korzystać będziemy z tych samych tablic dla wartości
z. Tablice są przygotowane dla wartości standaryzowanych, a więc są uniwersalne.
6
Wartość z
k
dzieli połowę obszaru pod krzywą normalną na dwie części : p
1
(od średniej do z
k
) i p
2
(od z
k
do końca
rozkładu).
G. Wieczorkowska & J. Wierzbiński (2005)
14
Tablica 2.1.
Rozkład normalny N(0,1)
z
P
2
z
p
2
z
p
2
Z
P
2
z
p
2
z
p
2
z
p
2
0
0,5000 0,5
0,3085 1
0,1587 1,5
0,0668 2
0,0228 2,5
0,0062
3
0,0013
0,01 0,4960 0,51 0,3050 1,01 0,1562 1,51 0,0655 2,01 0,0222 2,51 0,0060
3,01 0,0013
0,02 0,4920 0,52 0,3015 1,02 0,1539 1,52 0,0643 2,02 0,0217 2,52 0,0059
3,02 0,0013
0,03 0,4880 0,53 0,2981 1,03 0,1515 1,53 0,0630 2,03 0,0212 2,53 0,0057
3,03 0,0012
0,04 0,4840 0,54 0,2946 1,04 0,1492 1,54 0,0618 2,04 0,0207 2,54 0,0055
3,04 0,0012
0,05 0,4801 0,55 0,2912 1,05 0,1469 1,55 0,0606 2,05 0,0202 2,55 0,0054
3,05 0,0011
0,06 0,4761 0,56 0,2877 1,06 0,1446 1,56 0,0594 2,06 0,0197 2,56 0,0052
3,06 0,0011
0,07 0,4721 0,57 0,2843 1,07 0,1423 1,57 0,0582 2,07 0,0192 2,57 0,0051
3,07 0,0011
0,08 0,4681 0,58 0,2810 1,08 0,1401 1,58 0,0571 2,08 0,0188 2,58 0,0049
3,08 0,0010
0,09 0,4641 0,59 0,2776 1,09 0,1379 1,59 0,0559 2,09 0,0183 2,59 0,0048
3,09 0,0010
0,1
0,4602 0,6
0,2743 1,1
0,1357 1,6
0,0548 2,1
0,0179 2,6
0,0047
3,1
0,0010
0,11 0,4562 0,61 0,2709 1,11 0,1335 1,61 0,0537 2,11 0,0174 2,61 0,0045
3,11 0,0009
0,12 0,4522 0,62 0,2676 1,12 0,1314 1,62 0,0526 2,12 0,0170 2,62 0,0044
3,12 0,0009
0,13 0,4483 0,63 0,2643 1,13 0,1292 1,63 0,0516 2,13 0,0166 2,63 0,0043
3,13 0,0009
0,14 0,4443 0,64 0,2611 1,14 0,1271 1,64 0,0505 2,14 0,0162 2,64 0,0041
3,14 0,0008
0,15 0,4404 0,65 0,2578 1,15 0,1251 1,65 0,0495 2,15 0,0158 2,65 0,0040
3,15 0,0008
0,16 0,4364 0,66 0,2546 1,16 0,1230 1,66 0,0485 2,16 0,0154 2,66 0,0039
3,16 0,0008
0,17 0,4325 0,67 0,2514 1,17 0,1210 1,67 0,0475 2,17 0,0150 2,67 0,0038
3,17 0,0008
0,18 0,4286 0,68 0,2483 1,18 0,1190 1,68 0,0465 2,18 0,0146 2,68 0,0037
3,18 0,0007
0,19 0,4247 0,69 0,2451 1,19 0,1170 1,69 0,0455 2,19 0,0143 2,69 0,0036
3,19 0,0007
0,2
0,4207 0,7
0,2420 1,2
0,1151 1,7
0,0446 2,2
0,0139 2,7
0,0035
3,2
0,0007
0,21 0,4168 0,71 0,2389 1,21 0,1131 1,71 0,0436 2,21 0,0136 2,71 0,0034
3,21 0,0007
0,22 0,4129 0,72 0,2358 1,22 0,1112 1,72 0,0427 2,22 0,0132 2,72 0,0033
3,22 0,0006
0,23 0,4090 0,73 0,2327 1,23 0,1093 1,73 0,0418 2,23 0,0129 2,73 0,0032
3,23 0,0006
0,24 0,4052 0,74 0,2296 1,24 0,1075 1,74 0,0409 2,24 0,0125 2,74 0,0031
3,24 0,0006
0,25 0,4013 0,75 0,2266 1,25 0,1056 1,75 0,0401 2,25 0,0122 2,75 0,0030
3,3
0,0005
0,26 0,3974 0,76 0,2236 1,26 0,1038 1,76 0,0392 2,26 0,0119 2,76 0,0029
3,4
0,0003
0,27 0,3936 0,77 0,2206 1,27 0,1020 1,77 0,0384 2,27 0,0116 2,77 0,0028
3,5
0,0002
0,28 0,3897 0,78 0,2177 1,28 0,1003 1,78 0,0375 2,28 0,0113 2,78 0,0027
3,6
0,0002
0,29 0,3859 0,79 0,2148 1,29 0,0985 1,79 0,0367 2,29 0,0110 2,79 0,0026
3,7
0,0001
0,3
0,3821 0,8
0,2119 1,3
0,0968 1,8
0,0359 2,3
0,0107 2,8
0,0026
0,31 0,3783 0,81 0,2090 1,31 0,0951 1,81 0,0351 2,31 0,0104 2,81 0,0025
0,32 0,3745 0,82 0,2061 1,32 0,0934 1,82 0,0344 2,32 0,0102 2,82 0,0024
0,33 0,3707 0,83 0,2033 1,33 0,0918 1,83 0,0336 2,33 0,0099 2,83 0,0023
0,34 0,3669 0,84 0,2005 1,34 0,0901 1,84 0,0329 2,34 0,0096 2,84 0,0023
0,35 0,3632 0,85 0,1977 1,35 0,0885 1,85 0,0322 2,35 0,0094 2,85 0,0022
0,36 0,3594 0,86 0,1949 1,36 0,0869 1,86 0,0314 2,36 0,0091 2,86 0,0021
0,37 0,3557 0,87 0,1922 1,37 0,0853 1,87 0,0307 2,37 0,0089 2,87 0,0021
0,38 0,3520 0,88 0,1894 1,38 0,0838 1,88 0,0301 2,38 0,0087 2,88 0,0020
0,39 0,3483 0,89 0,1867 1,39 0,0823 1,89 0,0294 2,39 0,0084 2,89 0,0019
0,4
0,3446 0,9
0,1841 1,4
0,0808 1,9
0,0287 2,4
0,0082 2,9
0,0019
0,41 0,3409 0,91 0,1814 1,41 0,0793 1,91 0,0281 2,41 0,0080 2,91 0,0018
0,42 0,3372 0,92 0,1788 1,42 0,0778 1,92 0,0274 2,42 0,0078 2,92 0,0018
0,43 0,3336 0,93 0,1762 1,43 0,0764 1,93 0,0268 2,43 0,0075 2,93 0,0017
0,44 0,3300 0,94 0,1736 1,44 0,0749 1,94 0,0262 2,44 0,0073 2,94 0,0016
0,45 0,3264 0,95 0,1711 1,45 0,0735 1,95 0,0256 2,45 0,0071 2,95 0,0016
0,46 0,3228 0,96 0,1685 1,46 0,0721 1,96 0,0250 2,46 0,0069 2,96 0,0015
0,47 0,3192 0,97 0,1660 1,47 0,0708 1,97 0,0244 2,47 0,0068 2,97 0,0015
0,48 0,3156 0,98 0,1635 1,48 0,0694 1,98 0,0239 2,48 0,0066 2,98 0,0014
0,49 0,3121 0,99 0,1611 1,49 0,0681 1,99 0,0233 2,49 0,0064 2,99 0,0014

G. Wieczorkowska & J. Wierzbiński (2005)
15
Przykład 2.5.1.
Jeżeli dowiedzielibyśmy się, że wzrost polskich mężczyzn ma rozkład normalny o średniej
175 i odchyleniu standardowym 6, możemy wyliczać prawdopodobieństwa, posługując się tablicami
rozkładu normalnego. Możemy np. wyliczyć, jakie jest prawdopodobieństwo, że wylosowany
mężczyzna będzie miał co najmniej 181 cm wzrostu.
Pierwszym krokiem jest zamiana wartości zmiennej na wartości standaryzowane. Przy
założeniu, że wzrost dorosłych mężczyzn ma rozkład normalny N(175,6), 181 cm oznacza z=1.
Z tablic odczytamy, że dla z
k
=1 p
2
=p(z>1)=p(z<-1)= 0,1587. Rozbieżność między wynikiem
odczytanym z rozkładu empirycznego (prawdopodobieństwo, że X ≥181, wyniosło 0,164154)
a wynikiem odczytanym z tablic jest efektem następujących różnic:
1. Korzystając z tablic rozkładu normalnego, zakładamy ciągłość zmiennej WZROST, która w
rozkładzie empirycznym była zmienną skokową, i dlatego p(X ≥181) ≠ p(X >181).
2. Rozkład w populacji może mieć inną średnią lub odchylenie standardowe. W naszych
obliczeniach wykorzystaliśmy zaokrąglone wartości średniej i odchylenia standardowego,
pochodzące z próby reprezentatywnej dorosłych mężczyzn.
3. Tak, jak to omawiamy w ostatnim rozdziale, badania sondażowe obarczone są błędami
związanymi zarówno z doborem osób do próby, jak i zniekształceniami odpowiedzi (nie
można wykluczyć, że mężczyźni zawyżali swój wzrost).
Podsumowując:
1. Zanim zaczniemy formułować sądy o liczbach, musimy określić skalę pomiarową.
2. Operacje matematyczne (takie jak dodawanie, mnożenie) są dozwolone tylko dla zmiennych
ilościowych (gdzie określona jest jednostka pomiaru).
3. Podstawowe charakterystyki rozkładu zmiennej ilościowej to średnia arytmetyczna i wariancja
/odchylenie standardowe.
4. Aby porównać dwie liczby pochodzące z różnych rozkładów, należy je najpierw
wystandaryzować.
5. Znajomość rozkładu zmiennej może wynikać z przeprowadzonych badań lub naszej wiedzy
na temat danej zmiennej. W obu przypadkach znajomość rozkładu pozwala wyliczać
prawdopodobieństwa tego, że w badaniach empirycznych otrzymamy wartość zmiennej
z danego przedziału.
Wyszukiwarka
Podobne podstrony:
Cwiczenie 3A id 99454 Nieznany
ekonomia 3a id 155736 Nieznany
Projekt 3A id 398296 Nieznany
mech 3a id 290417 Nieznany
matematyka2 3a id 284102 Nieznany
3a WBS id 36567 Nieznany (2)
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
więcej podobnych podstron