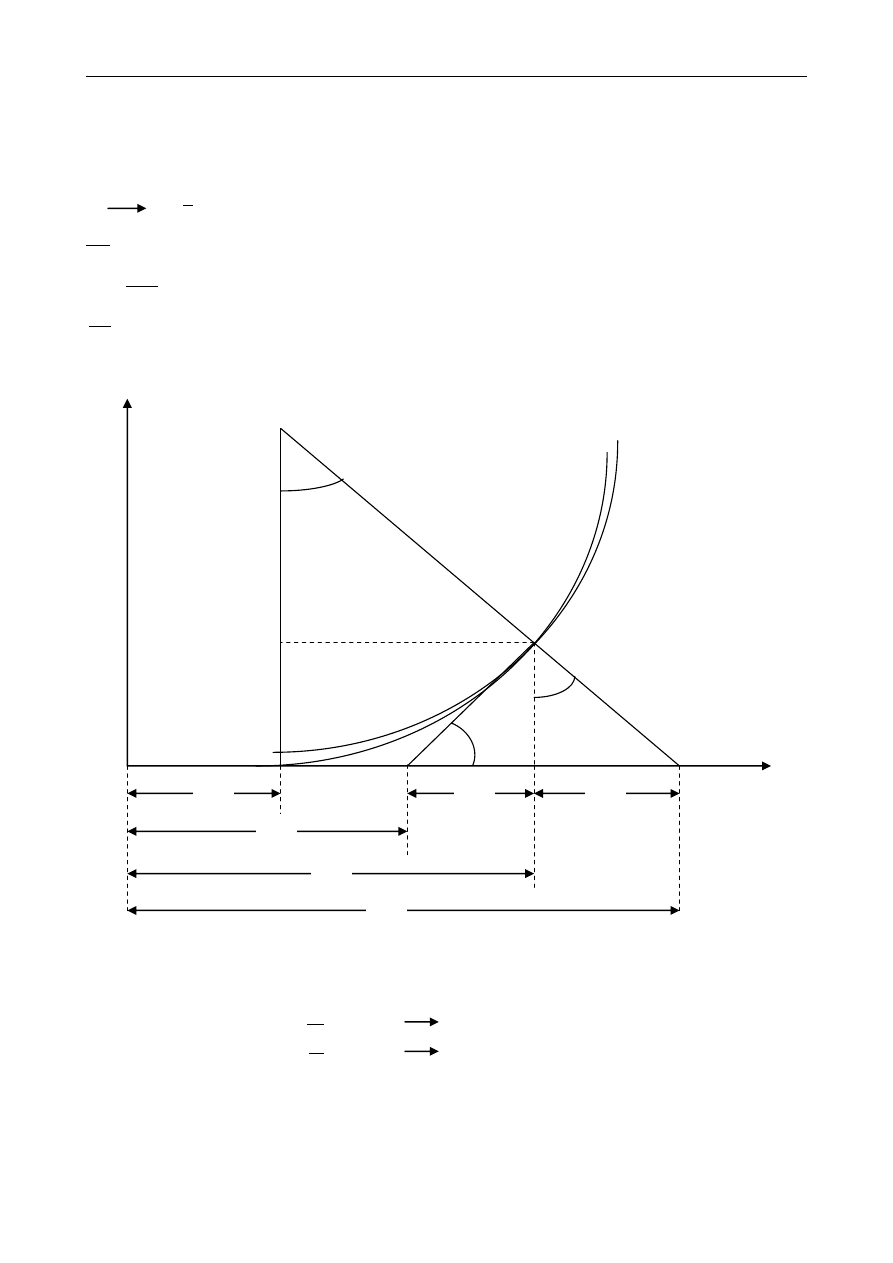
20. KLOTOIDA JAKO KRZYWA PRZEJŚCIOWA MIĘDZY PROSTĄ A ŁUKIEM KOŁOWYM

Dane: X

P

, Y

P

, R, τ

Szukane: X

S

, Y

S

, H, u, v, T, T

D

, T

K

, N

R, γ, a – dane pozyskiwane z projektu

X

P

, Y

P

, τ – obliczamy

Z równania różniczkowego klotoidy:

R L=a

2

L

=

Wykorzystując podstawowe funkcje trygonometryczne otrzymujemy:

n

OP= R sin (1)

co OS= R co (2)

X

S

= X

P

– OP, podstawiamy (1)

X

S

= X

P

- R n

Y

S

= Y

P

+ OS, podstawiamy (2)

Y

S

= Y

P

+ R co (3)

H= Y

S

– R, podstawiamy (3) H= Y

P

+ R co – R= Y

P

+R(co -1), to ujemy funkcję połowy kąta

Y

X

R

S

P

N

Y

P

O

H

τ

τ

τ

T

K

X

S

T

D

u

v

X

P

T

H= Y

P

- 2Rsin

2

(4)

v= Y

P

tg (5)

T= X

P

+ v, podstawiamy (4) T= X

P

+ Y

P

tg (6)

T

D

= T – u – v, podstawiamy (4,5,6) T

D

= X

P

+ Y

P

tg - Y

P

ctg - Y

P

tg T

D

= X

P

– Y

P

ctg

n

co

Opracowała: Marta Kalbarczyk, gr. 1