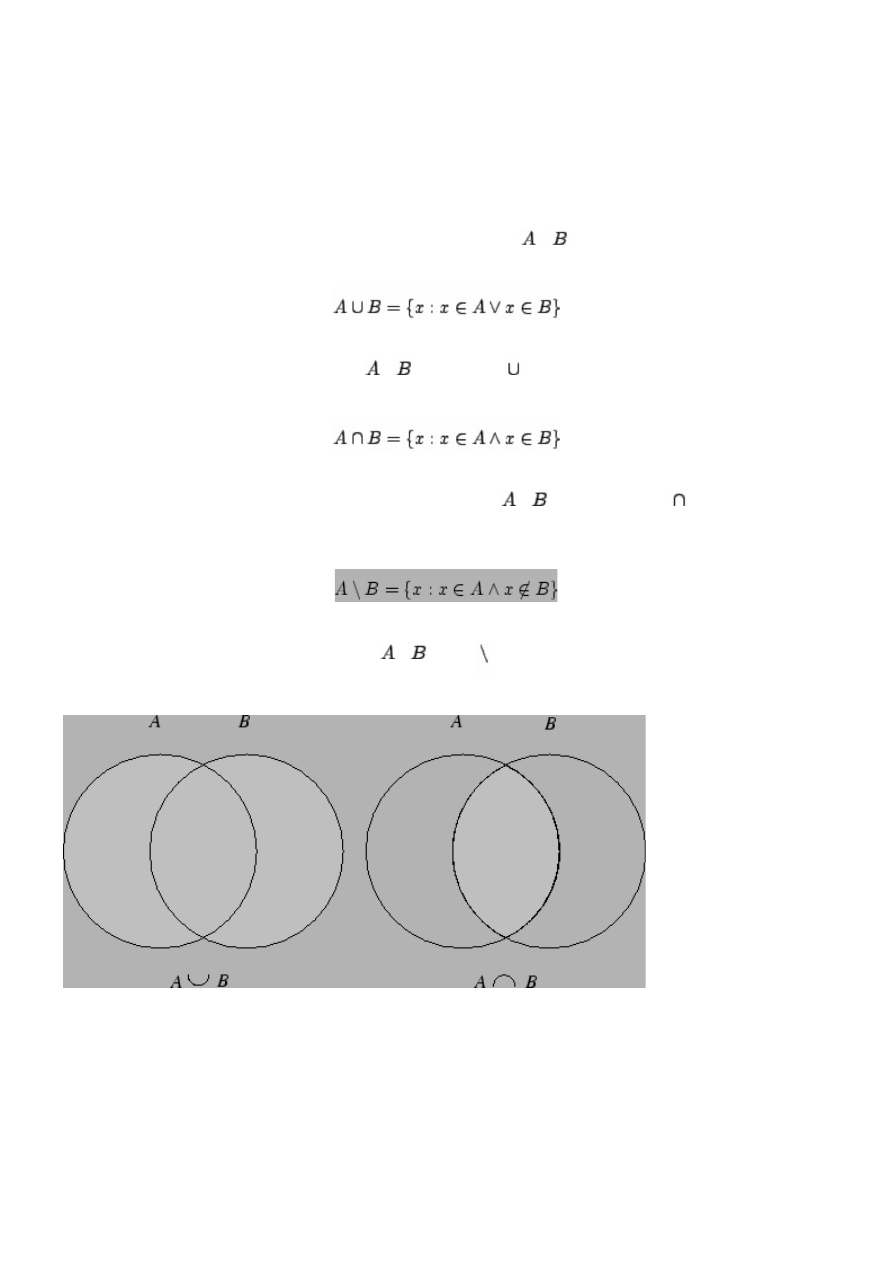
Rachunek zbiorów

Na zbiorach możemy wykonywać różne działania. Załóżmy, że

i

są zbiorami.

1. Zbiór

nazywamy sumą (mnogościową) zbiorów

i

. Znak sumy czytamy jako ``plus''.

2. Zbiór

nazywamy przekrojem (iloczynem mnogościowym) zbiorów

i

. Znak przekroju odczytujemy jako

``razy''.
3. Zbiór

nazywamy różnicą (mnogościową) zbiorów

i

. Znak odczytujemy jako ``minus''.

Zbiory opisane wyżej wygodnie jest przedstawiać na diagramach Venna.

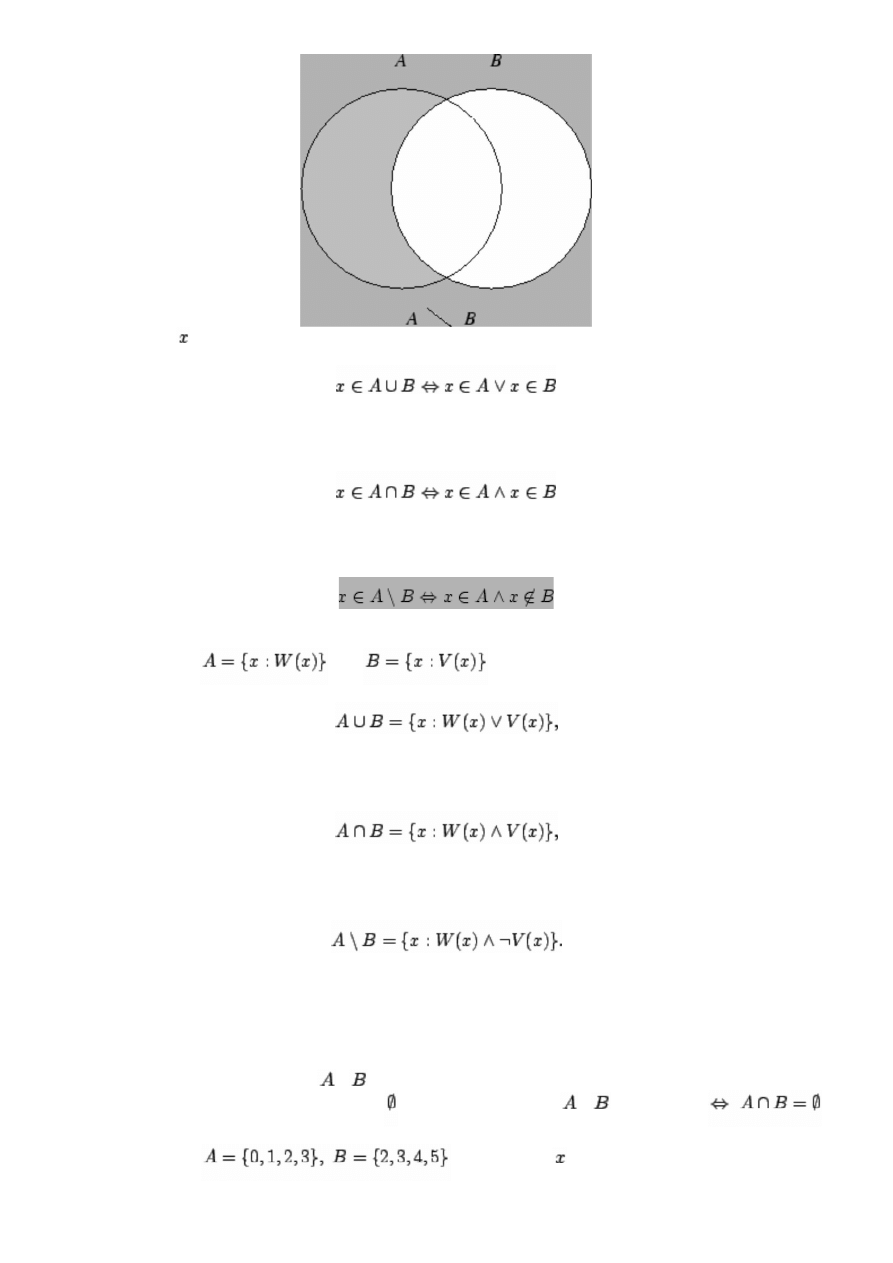
Dla wszystkich zachodzą następujące równoważności.

W przypadku, gdy

, zaś

, dostajemy

Działania na zbiorach odpowiadają w ten sposób operacjom logicznym na funkcjach zdaniowych.

Przyjmujemy następującą definicję.

Definicja 4..1 Mówimy, że zbiory

i

są rozłączne, gdy nie mają wspólnych elementów. W tym

przypadku ich przekrój jest zbiorem pustym . Innymi słowy, zbiory

i

są rozłączne

.

Przykład 1. Niech

. Dla każdego mamy:

Dlatego

czyli

. Podobnie

i

czyli

Przykład 2.

. Zakładamy, że

to różne przedmioty. Wtedy

.

Okazuje się, że własności działań i na zbiorach odpowiadają własnościom spójników logicznych i

wyrażonym w tautologiach na początku rozdziału 2 (tak więc zewnętrzne podobieństwo tych symboli

jest nieprzypadkowe).

Własności i .

(przemienność

).

1.

(łączność

).

2.

(rozdzielność względem ).

3.

(rozdzielność względem ).

4.

.

5.

.

6.

Przed przystąpieniem do dowodu tych równości (zwanych tożsamościami lub prawami rachunku zbiorów)
warto unaocznić je sobie zaznaczając odpowiednie zbiory na diagramach Venna. Dla przykładu robimy to
poniżej dla zbioru

. Ponadto, podobnie jak w przypadku i , na

mocy łączności i możemy pomijać nawiasy w wielokrotnych przekrojach i sumach.

Dowód. (1) Dla dowodu równości

wystarczy udowodnić, że dla wszystkich mamy:

Weźmy więc dowolne . Wtedy

W pierwszej i trzeciej równoważności korzystamy z definicji , w drugiej równoważności korzystamy z
tautologii

(przemienność ).

Dlatego

, czyli

.

W dowodzie

stosujemy definicję i tautologię

(przemienność ).

(2) W dowodzie stosujemy definicje

i tautologie

(łączność ) i

(łączność ). Przykładowo udowodnimy łączność . W tym celu wystarczy

pokazać, że dla dowolnego mamy

Rozważmy więc dowolne . Mamy następujący ciąg zdań równoważnych.

Dlatego

, czego chcieliśmy dowieść.

W dowodach dalszych punktów stosujemy odpowiednio tautologie

(rozdzielność względem ),

(rozdzielność względem ),

.

Inkluzja zbiorów. Mówimy, że zbiór

jest podzbiorem zbioru

wtedy i tylko wtedy, gdy każdy

element zbioru

jest elementem zbioru

. Fakt ten zapisujemy symbolicznie w postaci

. W tej

sytuacji mówimy też, że zbiór

zawiera się w zbiorze

oraz że zbiór

jest nadzbiorem zbioru

.

Mamy więc

Powyższa równoważność może być również przyjęta za definicję pojęcia zawierania zbiorów. Zawieranie
zbiorów nazywamy też inkluzją zbiorów.

Mówimy, że zbiór

jest podzbiorem właściwym zbioru

wtedy i tylko wtedy, gdy

jest podzbiorem

i

jest różny od

. Symbolicznie fakt ten zapisujemy w postaci

. Mówimy wówczas, że

jest nadzbiorem właściwym zbioru

. Mamy więc

Tu

jest skrótem zdania

.

Na przykład mamy

, jak również

.

Wprost z definicji dostajemy, że i zbiór

są podzbiorami zbioru

. nazywamy podzbiorem

trywialnym zbioru

, zaś

podzbiorem niewłaściwym zbioru

.

Należy tu położyć nacisk na poprawną terminologię: element zbioru

należy do zbioru

, zaś

podzbiór

zbioru

zawiera się w zbiorze

. Może się zdarzyć, że zbiór

równocześnie zawiera się w

zbiorze

(tzn. jest jego podzbiorem), jak i należy do zbioru

(tzn. jest jego elementem).

Przykład 1. Niech

zaś

. Oba zbiory

i

są jednoelementowe. Jedynym

elementem zbioru

jest

, czyli zbiór

. Dlatego

należy do

(czyli

). Nie jest jednak

prawdą, że zbiór

zawiera się w zbiorze

, nie jest on bowiem podzbiorem zbioru

. Mianowicie

jedynym elementem zbioru

jest zbiór pusty . I niestety ten właśnie element nie należy do zbioru

(bo jedynym elementem zbioru

jest właśnie zbiór

oraz

).

Przykład 2. Niech

, zaś

. Tu

należy do

oraz zawiera się w

.

Poniżej podajemy własności inkluzji zbiorów i dalsze prawa rachunku zbiorów.

Jeśli

i

, to

.

1.

(przechodniość inkluzji) Jeśli

i

, to

.

2.

.

3.

Jeśli

i

, to

i

.

4.

.

5.

.

6.

.

7.

.

8.

.

9.

Dowód. (1) Załóżmy, że

i

. Znaczy to, że dla każdego mamy

czyli

Zatem

.

(2) Załóżmy, że

i

. Pokażemy, że

. Na mocy definicji inkluzji,

oznacza, że

dla wszystkich

, jeśli

, to

. Aby tego dowieść, rozważmy dowolne

. Skoro

,

to na mocy definicji

,

. Skoro

, to na mocy definicji

,

, czego należało dowieść.

W punkcie (3) udowodnimy, że

. W tym celu rozważmy dowolny element zbioru

.

Na mocy definicji , należy zarówno do

, jak i do

. W szczególności

. W ten sposób

pokazaliśmy, że dla dowolnego mamy

czyli

.

Dowody pozostałych punktów pozostawiamy jako ćwiczenie.

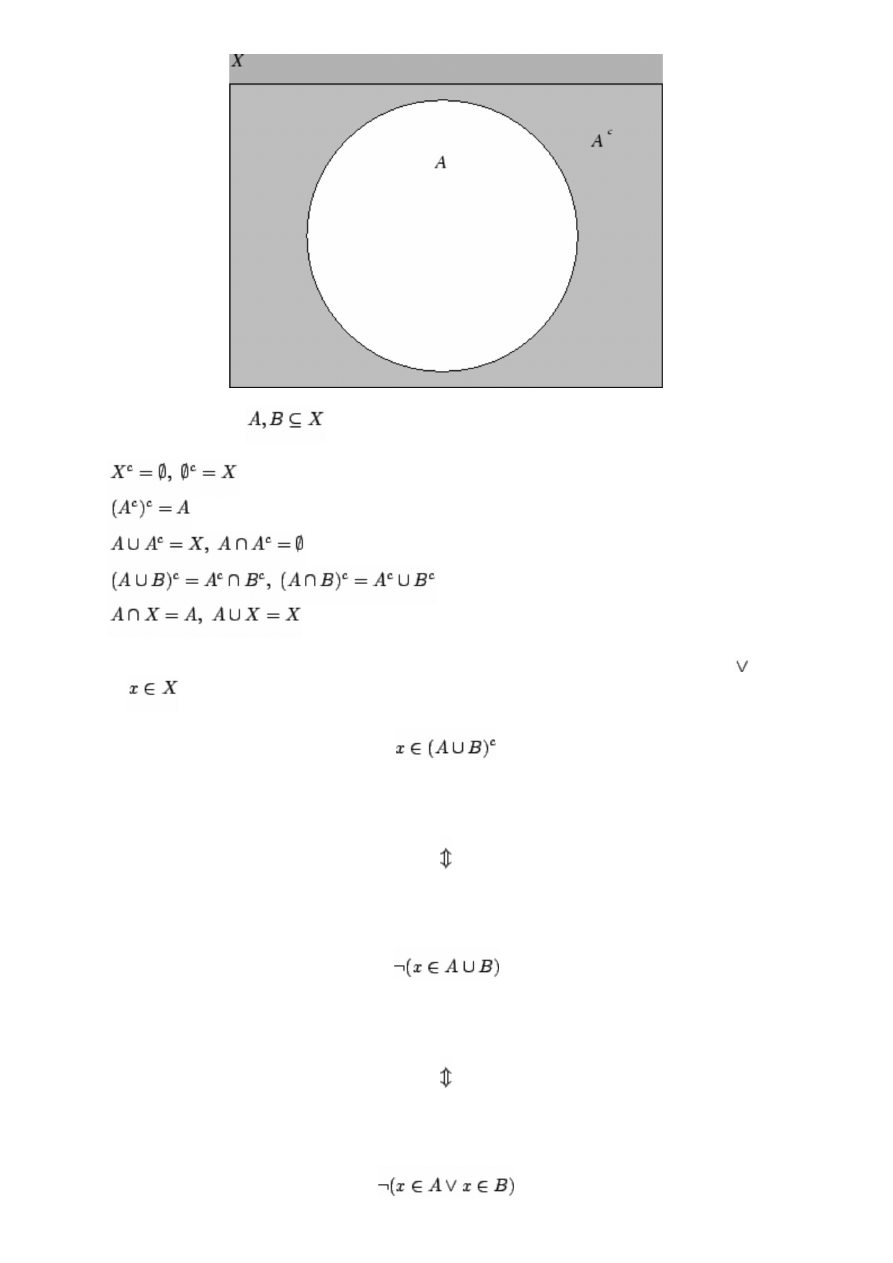
Przestrzeń, dopełnienie zbioru. Spójnikom logicznym i odpowiadają działania i na zbiorach.
Dotychczas nie wprowadziliśmy działania na zbiorach odpowiadającego spójnikowi negacji. Często zdarza
się, że rozważamy podzbiory ustalonego zbioru

. W takiej sytuacji zbiór

nazywamy przestrzenią. W

tym kontekście negacji odpowiada tak zwane dopełnienie zbioru.

Dla zbioru

zbiór

nazywamy dopełnieniem zbioru

(w przestrzeni

). Zatem dla

wszystkich

mamy

W przypadku, gdy

, mamy

. Dopełnienie zbioru

zaznaczamy na diagramie Venna w następujący sposób.

Używając operacji dopełnienia zbioru możemy wyrazić kolejne prawa (tożsamości) rachunku zbiorów.
Mianowicie, dla zbiorów

mamy:

.

1.

.

2.

.

3.

(prawa de Morgana rachunku zbiorów).

4.

.

5.

Przykładowo uzasadnimy część punktu 4. Korzystając z definicji oraz prawa de Morgana dla , dla
każdego

mamy ciąg zdań równoważnych:

Zatem dla wszystkich

mamy

. Oba zbiory

i

są

podzbiorami przestrzeni

. Wynika więc stąd, że mają te same elementy i

.

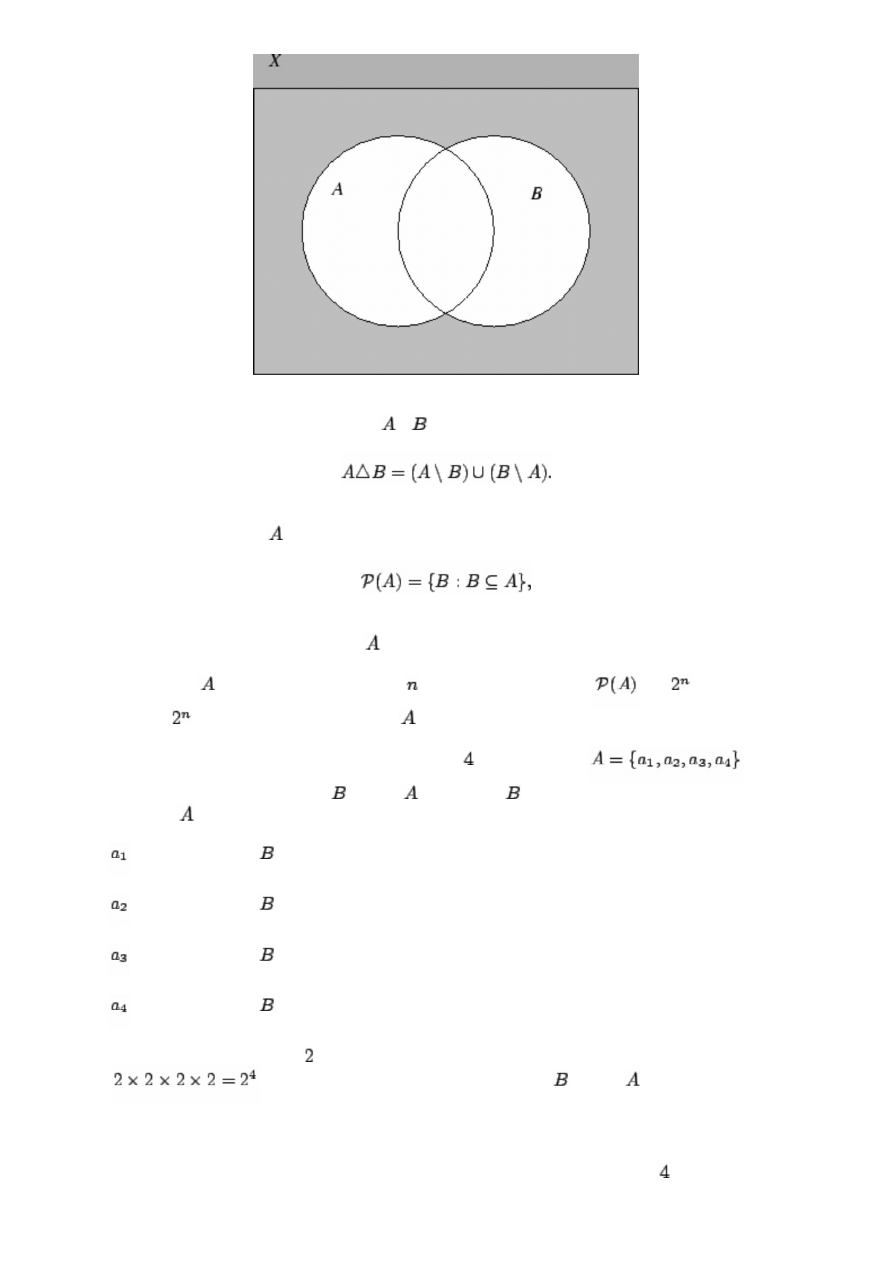
Warto unaocznić sobie powyższe prawa rachunku zbiorów na diagramach Venna dla podzbiorów
przestrzeni

. Przykładowo zaznaczymy na diagramie Venna zbiór

.

Na koniec rozważań o rachunku zbiorów poznamy jeszcze operację różnicy symetrycznej i zbioru
potęgowego. Różnicą symetryczną zbiorów

i

nazywamy zbiór

Zbiorem potęgowym zbioru

nazywamy zbiór

czyli zbiór wszystkich podzbiorów zbioru

. Nazwę zbioru potęgowego uzasadnia następująca uwaga.

Uwaga 4..2 Jeśli

jest skończonym zbiorem -elementowym, to zbiór

ma

elementów (tzn.

jest dokładnie

różnych podzbiorów zbioru

).

Dowód. Dowód przeprowadzimy na przykładzie zbioru -elementowego

. Na ile

sposobów możemy wybrać podzbiór

zbioru

? Podzbiór

jest wyznaczony przez swoje elementy,

które należą do

. Zatem mamy następujące możliwości:

może należeć do

lub nie.

1.

może należeć do

lub nie.

2.

może należeć do

lub nie.

3.

może należeć do

lub nie.

4.

W każdym z punktów 1-4 mamy możliwości, punkty 1.-4. są wzajemnie niezależne. Dlatego łącznie
mamy

możliwości, i tyleż różnych podzbiorów

zbioru

.

Jako ćwiczenie sugerujemy czytelnikowi wypisanie wszystkich podzbiorów zbioru -elementowego

. Najlepsza metoda, to wypisywać kolejno podzbiory -elementowe (jest tylko jeden:

zbór pusty ), 1-elementowe, 2-elementowe, 3-elementowe i wreszcie 4-elementowe (jest tylko jeden:

cały zbiór

). Wiadomo, że jest dokładnie

-elementowych podzbiorów zbioru -elementowego.

W szczególności zbiór potęgowy zbioru pustego

ma

element ( jest -elementowy).

Jedynym elementem zbioru

jest zbiór pusty , który jest tu zarówno podzbiorem trywialnym, jak i

niewłaściwym.