- 1 -
7. WIDMOWY OPIS SYGNAŁÓW
ELEKTRYCZNYCH
PRZYPOMNIENIE
A) Funkcja wykładnicza pełni wyjątkową rolę, ponieważ:
•
każdy sygnał występujący w praktyce może być zawsze wyra-
ż
ony w postaci sumy funkcji wykładniczych;
•
w przypadku obwodów liniowych odpowiedź obwodu na wy-
muszenie wykładnicze jest także wykładnicza.
B) Metoda symboliczna zapisu przebiegów sinusoidalnych po-
zwala traktować je jako przebiegi wykładnicze
7.1. OPIS SYGNAŁU ODKSZTAŁCONEGO
TRYGONOMETRYCZNY SZEREG FOURIERA
Dowolną funkcję okresową niesinusoidalną x(t) o okresie T, spełniają-
cą warunki Dirichleta - można przedstawić w postaci szeregu harmonicz-
nego nieskończonego, zwanego
szeregiem trygonometrycznym Fouriera:
( )
(
)
∑
∞
=
+
+
=
1
1
0
sin
k
k
k
m
t
k
F
F
t
x
Ψ
ω
(7.1)
k-ta harmoniczna rozwinięcia Fouriera
gdzie:
ω
ωω
ω
1
=2
ππππ
/T – pulsacja podstawowa
k – rząd harmonicznej
F
mk
– amplituda k-tej harmonicznej
Ψ
k
– faza początkowa k-tej harmonicznej
składowa stała
- 2 -
Wiadomo jednak, że
(
)
(
)
k
k
k
m
k
k
m
t
k
t
k
F
t
k
F
Ψ
+
Ψ
=
Ψ
+
sin
cos
cos
sin
sin
1
1
1
ω
ω
ω
(7.2)
Jeśli oznaczymy
k
k
k
m
k
k
k
m
B
F
A
F
=
Ψ
=
Ψ
cos
sin
(7.3)
to
(
)
t
k
B
t
k
A
t
k
F
k
k
k
k
m
1
1
1
sin
cos
sin
ω
ω
ω
+
=
Ψ
+
(7.4)
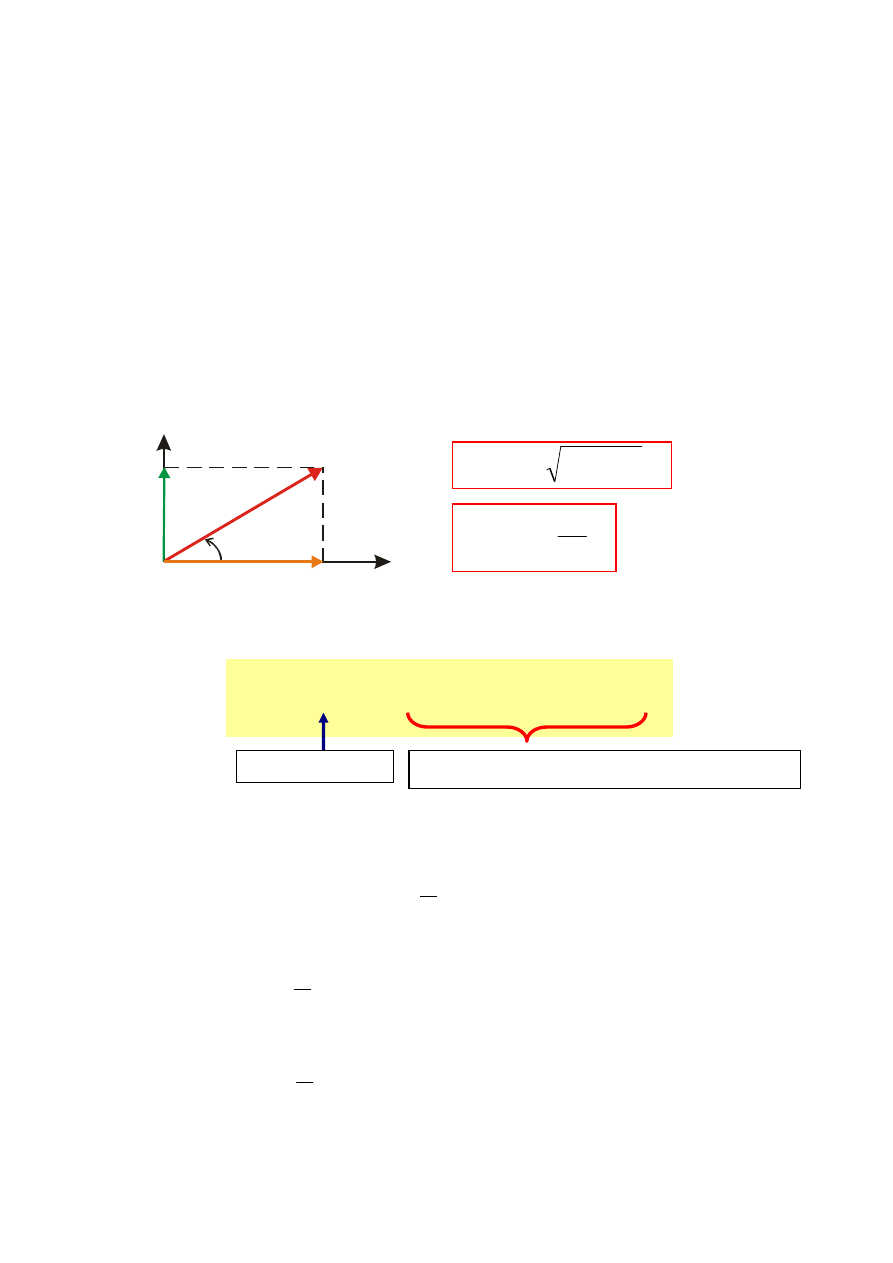
Gdy amplitudę k-tej harmonicznej przedstawimy jako wektor wirują-
cy, to z zależności trygonometrycznych (rys) wynikają wzory (7.3) oraz
Re
Im
F
mk
Ψ
k
A
k
B
k
2
2
k
k
k
m
B
A
F
+
=
(7.5)
k
k
k
B
A
tg
=
Ψ
(7.6)
Uwzględniając powyższe zależności możemy szereg (7.1) przedstawić
( )
(
)
∑
∞
=
+
+
=
1
1
1
0
sin
cos
k
k
k
t
k
B
t
k
A
A
t
x
ω
ω
(7.7)
Współczynniki A
0
, A
k
, B
k
wyznacza się ze wzorów:
( )
dt
t
x
T
A
T
t
t
∫
+
=
0
0
1
0
(7.8)
( )
K
,
2
,
1
cos
2
1
0
0
=
=
∫
+
k
dla
dt
t
k
t
x
T
A
T
t
t
k
ω
(7.9)
( )
K
,
2
,
1
sin
2
1
0
0
=
=
∫
+
k
dla
dt
t
k
t
x
T
B
T
t
t
k
ω
(7.10)
k-ta harmoniczna rozwinięcia Fouriera
składowa stała
- 3 -
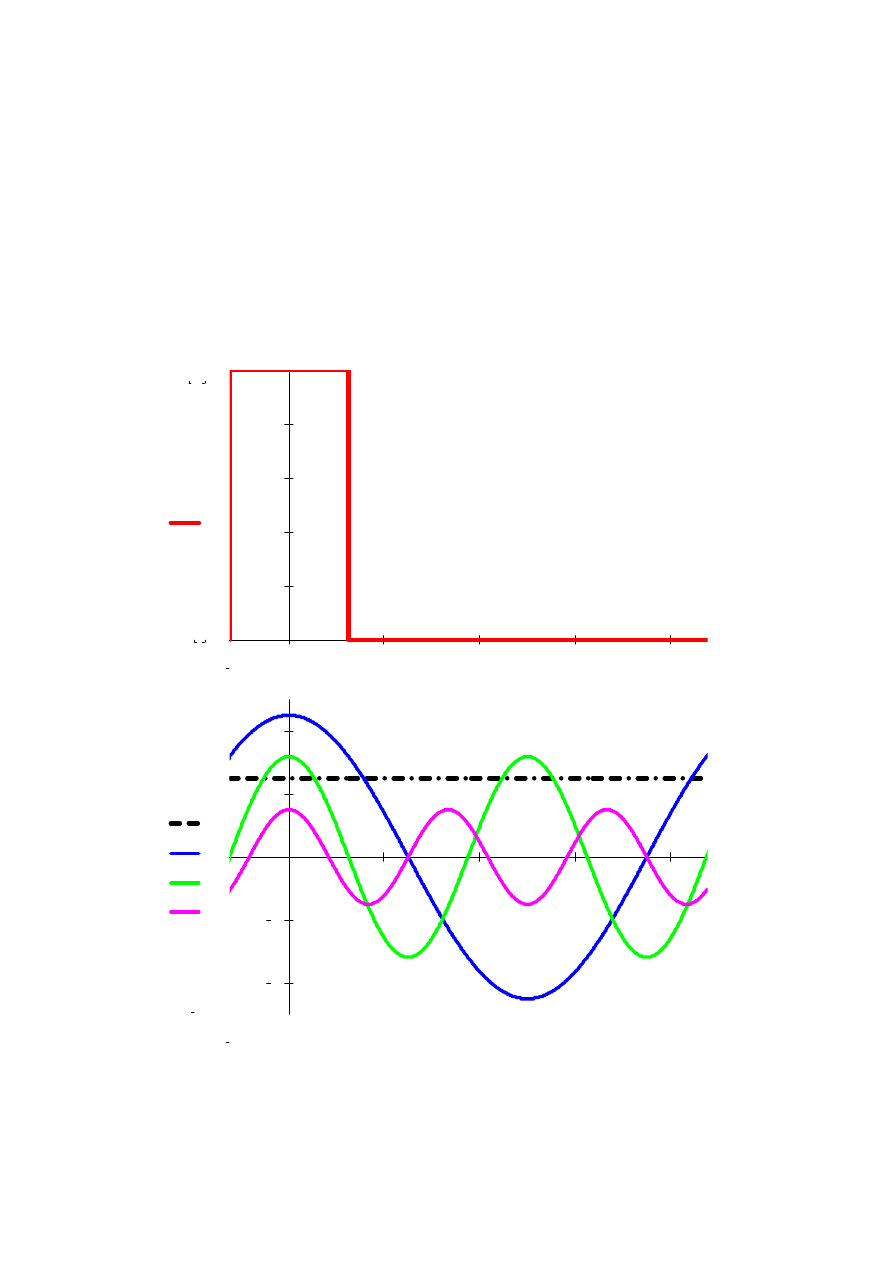
Interpretacja:
Dowolny przebieg elektryczny można przedstawić w postaci sumy
wielkości stałej
oraz
nieskończenie wielu wielkości sinusoidalnych zwanych
harmonicznymi.
Wielkość sinusoidalną o k=1 nazywamy harmoniczną podstawową (pierwszą
harmoniczną). Wielkości o k>1 nazywamy wyższymi harmonicznymi.
10
0
u t
( )
0.875
0.125
t
0
0.2
0.4
0.6
0.8
2
4
6
8
10
5
5
Uo
u1 t
( )
u2 t
( )
u3 t
( )
0.875
0.125
t
0
0.2
0.4
0.6
0.8
4
2
2
4
- 4 -
ANALIZA OBWODÓW SLS PR
Ą
DU ODKSZTAŁCONEGO
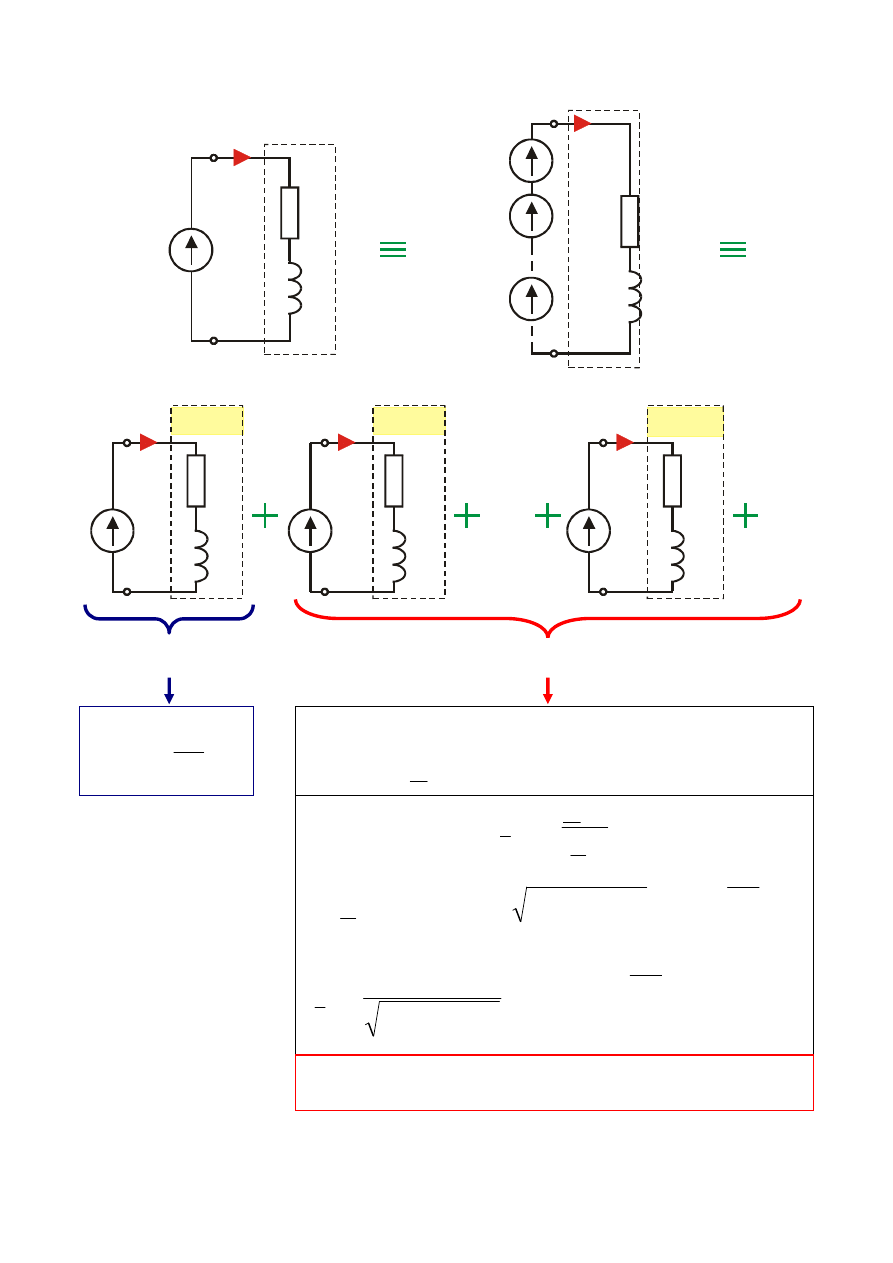
Załóżmy, że do dwójnika zawierającego elementy R, L w połączeniu
szeregowym przyłożono napięcie odkształcone u(t). Wielkością poszuki-
waną jest prąd płynący przez elementy dwójnika. Rozwinięcie rozpatry-
wanego wymuszenia w szereg Fouriera ma postać
( )
(
)
( )
( )
( )
( )
∑
∑
∞
=
∞
=
+
=
+
+
+
+
=
+
+
=
1
0
3
2
1
0
1
1
0
sin
k
k
k
uk
k
m
t
u
U
t
u
t
u
t
u
U
t
k
U
U
t
u
K
Ψ
ω
(7.11)
Ponieważ obwód jest liniowy, więc możemy zastosować zasadę su-
perpozycji w sposób następujący:
1.
Przyjmujemy, że jedynym wymuszeniem jakie działa na obwód jest
ź
ródło napięcia stałego U
0
i rozpatrywany obwód obliczamy za pomocą
metod dotyczących obwodów prądu stałego, wyznaczając prąd I
0
;
2.
Przyjmujemy, że jedynym wymuszeniem jakie działa na obwód jest k-te
ź
ródło napięcia harmonicznego o napięciu
( )
(
)
uk
k
m
k
t
k
U
t
u
Ψ
ω
+
=
1
sin
i za pomocą metod obliczania obwodów prądu harmonicznego wyzna-
czamy prąd obwodu
( )
(
)
ik
k
m
k
t
k
I
t
i
Ψ
ω
+
=
1
sin
,
obliczenie to powtarzamy wielokrotnie, przyjmując kolejno k=1,2,3,...
Zgodnie z zasadą superpozycji przez elementy obwodu płynie prąd
( )
( )
(
)
∑
∑
∞
=
∞
=
+
+
=
+
=
1
1
0
1
0
sin
k
ik
k
m
k
k
t
k
I
I
t
i
I
t
i
Ψ
ω
(7.12)
- 5 -
R
L
u(t)
i(t)
u (t)
1
i(t)
R
L
U
0
u (t)
k
R
L
I
0
ω=0
U
0
R
L
ω=ω
1
u (t)
1
i (t)
1
...
R
L
ω= ω
k
1
i (t)
k
...
u (t)
k
R
U
I
0
0
=
( )
(
)
uk
k
m
k
t
k
U
t
u
Ψ
ω
+
=
1
sin
uk
j
mk
mk
e
U
U
Ψ
=
k
mk
mk
Z
U
I
=
(
)
+
=
+
=
R
L
k
arctg
j
k
e
L
k
R
L
k
j
R
Z
ω
ω
ω
2
2
(
)
ik
uk
j
mk
R
L
k
arctg
j
mk
k
e
I
e
L
k
R
U
I
Ψ
ω
Ψ
ω
=
+
=
−
2
2
( )
(
)
ik
k
m
k
t
k
I
t
i
Ψ
ω
+
=
1
sin
Obwody prądu harmonicznego
Obwód prądu stałego
- 6 -
ZESPOLONY (WYKŁADNICZY) SZEREG FOURIERA
Jeśli w rozwinięciu w szereg Fouriera danym wyrażeniem (7.7) zasto-
sujemy podstawienie wynikające z wzorów Eulera
2
cos
1
1
1
t
jk
t
jk
e
e
t
k
ω
ω
ω
−
+
=
,
j
e
e
t
k
t
jk
t
jk
2
sin
1
1
1
ω
ω
ω
−
−
=
(7.13)
to otrzymamy
( )
∑
∞
=
−
−
−
+
+
+
=
1
0
2
2
1
1
1
1
k
t
jk
t
jk
k
t
jk
t
jk
k
j
e
e
B
e
e
A
A
t
x
ω
ω
ω
ω
(7.14)
Wprowadzając oznaczenia
2
,
2
,
0
0
k
k
k
k
k
k
jB
A
C
jB
A
C
A
C
+
=
−
=
=
−
(7.15)
szereg Fouriera przyjmuje postać
( )
[
]
∑
∞
=
−
−
+
+
=
1
0
1
1
k
t
jk
k
t
jk
k
e
C
e
C
C
t
x
ω
ω
(7.16)
i ostatecznie
( )
∑
∞
−∞
=
=
k
t
jk
k
e
C
t
x
1
ω
(7.17)
którą to postać nazywamy postacią ze-
spoloną szeregu Fouriera lub krótko
zespolonym szeregiem Fouriera.
( )
∫
+
−
±
±
=
=
=
T
t
t
j
k
t
k
j
k
k
e
C
dt
e
t
x
T
C
k
0
0
1
,
2
,
1
,
0
1
K
η
ω
(7.18)
Uwaga:
*
k
k
C
C
−
=
k
k
k
k
i
C
C
−
−
−
=
=
η
η
k-ty współczynnik wykładniczego
szeregu Fouriera
C
k
– moduł k-tego współczynnika wy-
kładniczego szeregu Fouriera
η
k
– argument k-tego współczynnika
wykładniczego szeregu Fouriera
- 7 -
WIDMO AMPLITUDOWE I FAZOWE SYGNAŁU
Wykres, w układzie współrzędnych prostokątnych, stanowiący
zbiór
modułów C
k
współczynników wykładniczego szeregu Fouriera
lub amplitud F
mk
poszczególnych harmonicznych,
określony dla odpo-
wiednich pulsacji
ω
ωω
ω
=k
ω
ωω
ω
1
(bądź częstotliwości f=kf
1
) nazywamy
dys-
kretnym widmem amplitudowym
sygnału x(t).
Wykres, w układzie współrzędnych prostokątnych, stanowiący
zbiór
argumentów
ηηηη
k
współczynników wykładniczego szeregu Fourie-
ra lub faz początkowych
ψ
k
poszczególnych harmonicznych,
określony
dla odpowiednich pulsacji
ω
ωω
ω
=k
ω
ωω
ω
1
(bądź częstotliwości f=kf
1
) nazywa-
my
dyskretnym widmem fazowym
sygnału x(t).
Znajomo
ść
obydwu widm, amplitudowego i fazowego jedno-
znacznie okre
ś
la sum
ę
cz
ęś
ciow
ą
szeregu Fouriera czyli z za-
ło
ż
on
ą
dokładno
ś
ci
ą
opisuje analizowany sygnał x(t). Widma
(cz
ę
stotliwo
ś
ciowe) s
ą
równowa
ż
nym opisem do analitycznego
zapisu w dziedzinie czasu tego sygnału - jest to jego reprezen-
tacja widmowa.
Ponieważ pomiędzy współczynnikami rozwinięcia w trygonometrycz-
ny i w zespolony szereg Fouriera zachodzą następujące związki:
K
,
2
,
1
2
2
2
2
=
+
=
=
=
−
k
dla
B
A
F
C
C
k
k
k
m
k
k
(7.19)
K
,
2
,
1
2
=
−
=
k
dla
k
k
π
Ψ
η
(7.20)
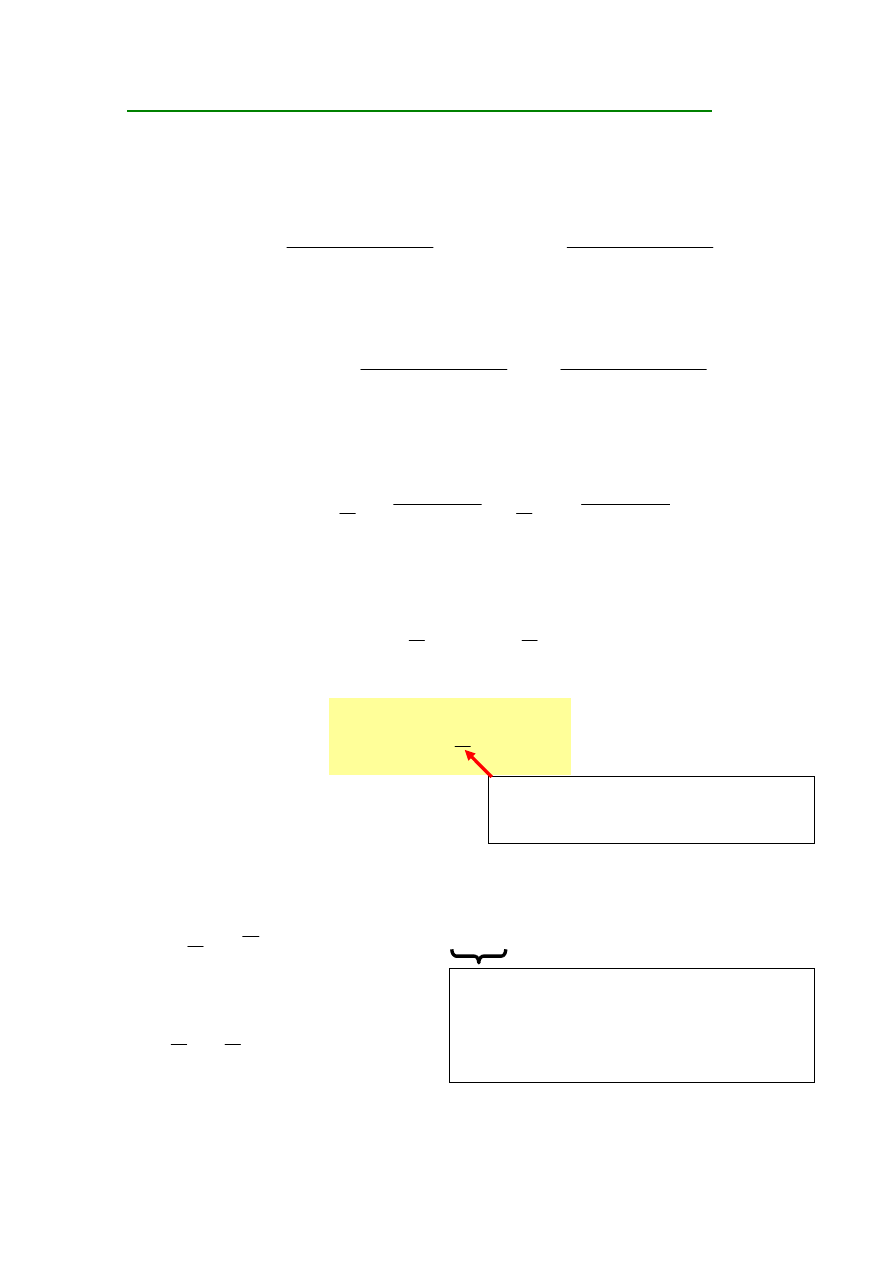
dla przykładowego sygnału x(t) można przedstawić następujące widma:
- 8 -
WIDMO AMPLITUDOWE
SPORZ
Ą
DZONE W OPARCIU O POSTA
Ć
:
TRYGONOMETRYCZN
Ą
ZESPOLON
Ą
F
mk
k
ω
1
0
1
2
3
4
C
k
k
ω
1
0
1
2
3
4
-1
-2
-3
-4
WIDMO FAZOWE
SPORZ
Ą
DZONE W OPARCIU O POSTA
Ć
:
TRYGONOMETRYCZN
Ą
ZESPOLON
Ą
Ψ
k
k
ω
1
1
2
3
4
k
ω
1
1
2
3
4
-1
-2
-3
-4
η
k
Widmo amplitudowe sygnału okresowego jest funkcją parzystą a widmo
fazowe funkcją nieparzystą. Prawostronne widma amplitudowe i fazowe
stanowią reprezentację sygnału okresowego w dziedzinie częstotliwości.
- 9 -
RODZAJE SYMETRII SYGNAŁÓW
Znaczna liczba funkcji okresowych przedstawiających wielkości elek-
tryczne spełnia pewne warunki symetrii, co w wyraźny sposób ułatwia
rozwinięcie tych funkcji w szereg Fouriera przez uproszczenie wyrażeń
(7.1), (7.7) i (7.17). Wyróżniamy trzy zasadnicze rodzaje symetrii sygna-
łów okresowych.
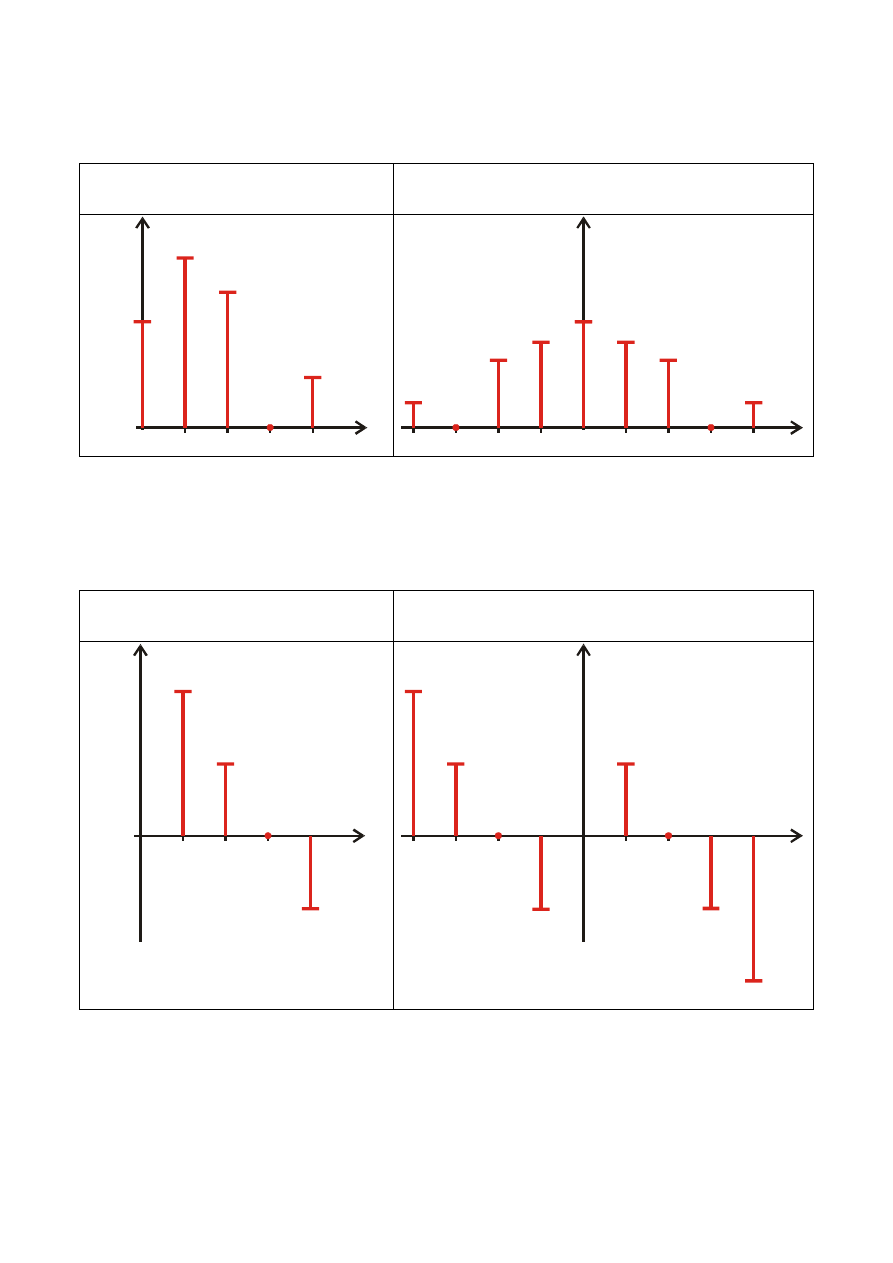
1)
SYMETRIA WZGL
Ę
DEM POCZ
Ą
TKU UKŁADU WSPÓŁRZ
Ę
DNYCH
Funkcję nazywamy symetryczną względem początku układu współ-
rzędnych lub
funkcj
ą
nieparzyst
ą
jeśli spełnia ona zależność
( )
( )
t
x
t
x
−
−
=
(7.21)
x(t)
t
0
,
0
0
=
=
k
A
A
0
lub
=
=
k
k
Ψ
π
Ψ
( )
∑
∞
=
=
1
1
sin
k
k
t
k
B
t
x
ω
(7.22)
2)
SYMETRIA WZGL
Ę
DEM OSI RZ
Ę
DNYCH
Funkcję nazywamy symetryczną względem osi rzędnych, lub
funkcj
ą
parzyst
ą
jeśli spełnia ona zależność
( ) ( )
t
x
t
x
−
=
(7.23)
x(t)
t
0
=
k
B
2
lub
2
π
Ψ
π
Ψ
−
=
=
k
k
( )
∑
∞
=
+
=
1
1
0
cos
k
k
t
k
A
A
t
x
ω
(7.24)
- 10 -
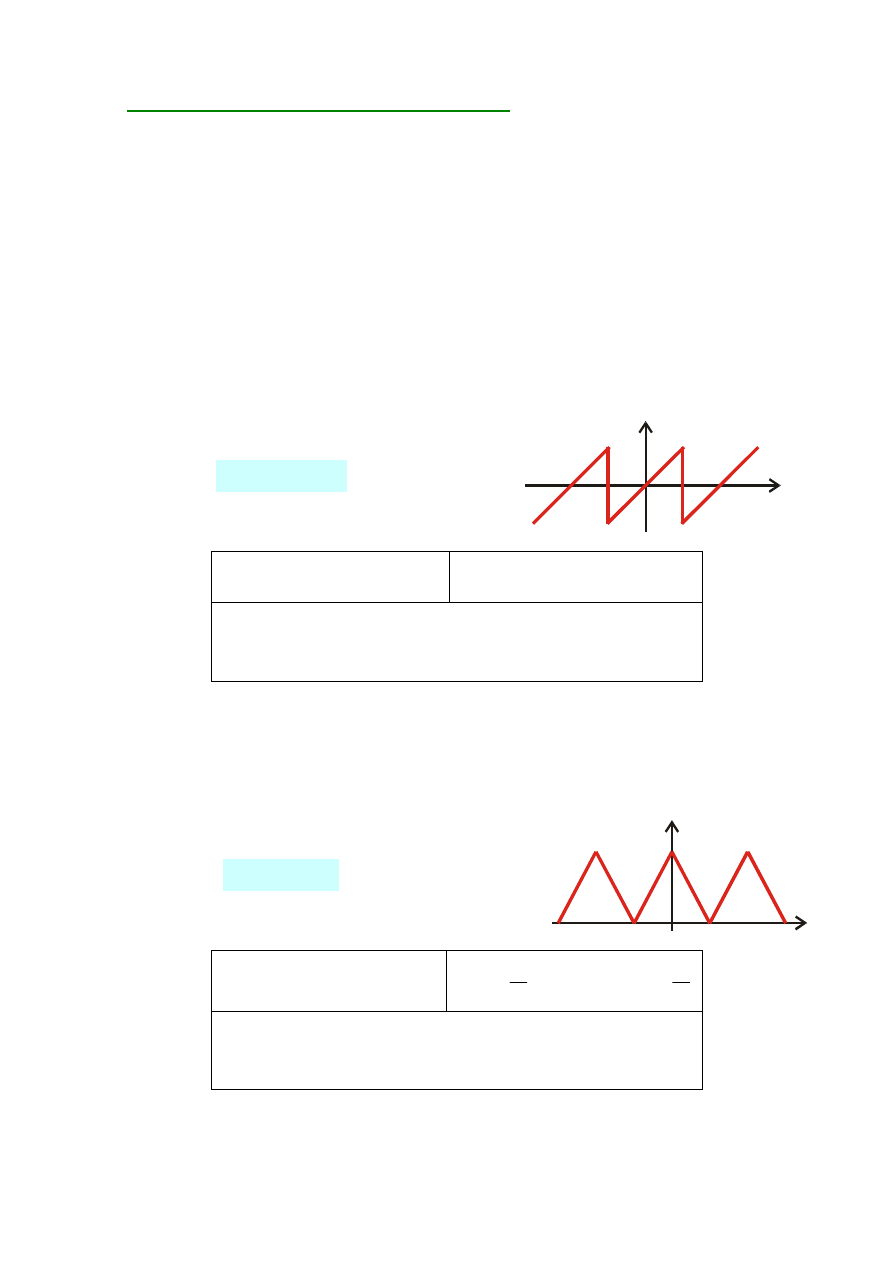
3)
SYMETRIA WZGL
Ę
DEM OSI ODCI
Ę
TYCH
Funkcję nazywamy
antysymetryczn
ą
(symetryczną względem osi
odciętych), jeśli rzędne funkcji okresowej powtarzają się co pół okresu ze
zmienionym znakiem, tzn.
( )
+
−
=
2
T
t
x
t
x
(7.25)
x(t)
t
0
0
=
A
i
K
,
2
,
1
0
2
2
=
=
=
n
dla
B
A
n
n
występują tylko nieparzyste harmoniczne
WIDMO MOCY SYGNAŁU
Ważnym parametrem charakteryzującym sygnał jest jego moc średnia
P, która w przypadku sygnału okresowego x(t) zdefiniowana jest za pomo-
cą wzoru:
( )
dt
t
x
T
P
T
∫
=
0
2
1
Moc sygnału okresowego x(t), można również wyznaczyć w dziedzi-
nie częstotliwości obliczając wartości mocy zawartej w każdej składowej
harmonicznej. W ten sposób tworzy się
widmo mocy sygnału
.
Przykładowo dla n-tej składowej harmonicznej, wartość mocy tej
składowej jest równa
(
)
2
sin
1
2
0
1
2
2
n
m
T
n
n
m
n
F
dt
t
n
F
T
P
=
+
=
∫
Ψ
ω
(7.26)
- 11 -
Wyrażając funkcję okresową x(t) za pomocą jej rozwinięcia w szereg
trygonometryczny Fouriera otrzymujemy:
(
)
∑
∑
∞
=
∞
=
+
=
+
+
=
1
2
2
0
1
2
2
2
0
2
2
k
mk
k
k
k
F
F
B
A
A
P
(7.27)
Podobnie jak w przypadku widma amplitudowego jest to widmo jed-
nostronne (istnieje tylko dla
ω≥
0)
Wyznaczając widmo mocy przebiegu okresowego x(t) za pomocą
wykładniczego
szeregu Fouriera, korzysta się z twierdzenia Parsevala:
( ) ( )
∑
∞
−∞
=
=
k
k
k
C
C
t
x
t
x
*
2
1
1
2
1
1
ω
ω
(7.28)
mówiącego: wartość średnia za okres iloczynu dwóch funkcji okresowych
o tym samym okresie jest równa sumie od -
∞
do +
∞
szeregu
nieskończonego, którego wyrazami są iloczyny współczynni-
ków rozwinięcia wykładniczego jednej z tych funkcji przez
współczynniki sprzężone rozwinięcia wykładniczego drugiej
Czyli wartość średnia kwadratu funkcji okresowej zakładając
( )
( ) ( )
t
x
t
x
t
x
=
=
1
2
1
1
ω
ω
wynosi
( )
∑
∑
∞
−∞
=
∞
−∞
=
=
=
k
k
k
k
k
C
C
C
t
x
2
*
2
(7.29)
Zatem:
∑
∞
−∞
=
=
k
k
C
P
2
(7.30)
Wówczas
widmem mocy sygnału nazywamy wykres zmienności kwadra-
tów modułów współczynników wykładniczego szeregu Fouriera. Podobnie
jak w przypadku widma amplitudowego jest to widmo dwustronne-
symetryczne.
UWAGA:
2
0
2
0
C
F
=
,
4
2
2
mk
k
F
C
=
- 12 -
APROKSYMACJA SYGNAŁU
W zagadnieniach praktycznych często zachodzi konieczność ograni-
czenia się do reprezentacji sygnału okresowego skończoną liczbą wyrazów
szeregu Fouriera (do aproksymacji sygnału sumą częściową szeregu).
Ograniczamy się do uwzględnienia w rozwinięciu N-harmonicznych.
Dla zespolonego szeregu Fouriera taką aproksymację zapiszemy jako
( )
∑
+
=
−
=
≅
N
k
N
k
t
jk
k
e
C
t
x
1
ω
(7.31)
Jako kryterium dokładności aproksymacji sygnału x(t) sumą częścio-
wą jego rozwinięcia przyjmuje się błąd względny
%
100
⋅
=
X
N
N
sk
ε
δ
ε
(7.32)
gdzie:
X – wartość skuteczna sygnału x(t) :
( )
( )
P
t
x
dt
t
x
T
X
T
=
=
=
∫
2
0
2
1
N
sk
ε
- wartość skuteczna błędu :
∑
∑
∞
+
=
+
=
−
=
=
−
=
1
2
2
2
2
N
k
k
N
k
N
k
k
sk
C
C
X
N
ε
Jeśli a priori założymy pewną wartość błędu aproksymacji, to przy
znajomości , możemy ustalić ten rząd harmonicznej N, której uwzględnie-
nie w sumie częściowej zapewnia wymaganą dokładność. Mówimy wów-
czas, że sygnał x(t) zajmuje pasmo N
ω
1
(N
⋅
f
1
).
Sens fizyczny tak określonego pasma wiąże się z mocą średnią sygna-
łu a mianowicie, jeśli przyjęliśmy kryterium dokładności
δε
N
to oznacza,
ż
e N uwzględnionych w rozwinięciu harmonicznych niesie (100 -
δε
N
)%
mocy jaką reprezentuje sobą sygnał x(t).
- 13 -
PRZYKŁAD:
Dany jest sygnał u(t) będący ciągiem impulsów prosto-
kątnych o okresie T=1ms, czasie trwania t
i
=0,25ms oraz
amplitudzie U
m
=10V. Wyznaczyć widmo amplitudowe i
fazowe sygnału.
1) Opisujemy sygnał u(t) analitycznie w przedziale czasu odpowiada-
j
ą
cym okresowi:
( )
−
<
<
<
<
−
=
2
2
0
2
2
i
i
i
i
m
t
T
t
t
dla
t
t
t
dla
U
t
u
2) Wybieramy posta
ć
szeregu Fouriera, dla której b
ę
dziemy rozwijali
sygnał
( )
(
)
∑
∞
=
+
+
=
1
1
1
0
sin
cos
k
k
k
t
k
B
t
k
A
A
t
u
ω
ω
3) Sprawdzamy rodzaj symetrii sygnał u(t)
Występuje symetria względem osi rzędnych (
( )
( )
t
f
t
f
−
=
). Ponieważ
jest to funkcja parzysta znikają wyrazy z sinusami (
0
=
k
B
).
Zatem:
( )
∑
∞
=
+
=
1
1
0
cos
k
k
t
k
A
A
t
u
ω
4) Obliczamy składow
ą
stał
ą
( )
dt
t
u
T
A
U
T
t
t
∫
+
=
=
0
0
1
0
0
[ ]
V
T
t
U
t
t
T
U
t
U
T
dt
U
T
U
i
m
i
i
m
t
t
m
t
t
m
i
i
i
i
5
,
2
4
1
10
2
2
1
1
1
2
2
2
2
0
=
⋅
=
=
+
=
=
=
−
−
∫
- 14 -
5) Obliczamy współczynniki
( )
K
,
2
,
1
cos
2
1
0
0
=
=
∫
+
k
dt
t
k
t
u
T
A
T
t
t
k
ω
(
)
2
2
1
1
1
2
2
sin
1
2
cos
2
i
i
i
i
t
t
m
t
t
m
k
t
k
k
T
U
dt
t
k
U
T
A
−
−
=
=
∫
ω
ω
ω
T
t
k
t
k
k
T
U
A
i
i
m
k
π
ω
ω
ω
ω
2
2
sin
2
sin
1
2
1
1
1
1
=
−
−
=
−
=
−
−
−
=
4
sin
4
sin
4
sin
4
sin
π
π
π
π
π
k
k
k
k
k
U
m
=
=
+
=
4
sin
37
,
6
4
sin
2
4
sin
4
sin
π
π
π
π
π
π
k
k
k
k
U
k
k
k
U
m
m
6) Obliczamy warto
ś
ci amplitud i faz pocz
ą
tkowych N-harmonicznych
k
k
A
2
k
k
m
A
F
=
k
m
k
k
F
A
arcsin
=
Ψ
1.
4,502
4,502
90
o
2.
3,183
3,183
90
o
3.
1,501
1,501
90
o
4.
0
0
-
5.
-0,9
0,9
-90
o
6.
-1,061
1,061
-90
o
7.
-0,643
0,643
-90
o
8.
0
0
-
9.
0,5
0,5
90
o
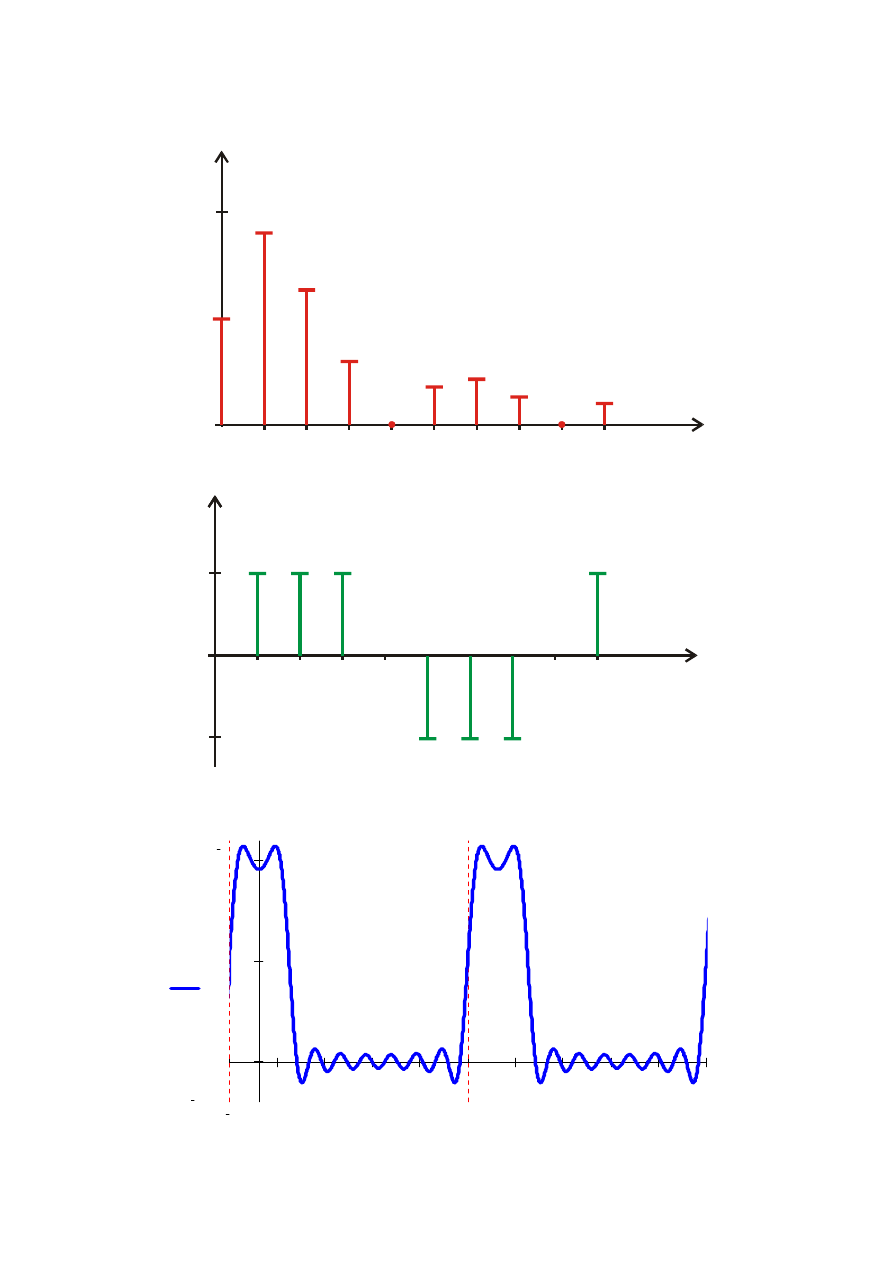
- 15 -
7) Przedstawiamy widmo amplitudowe i fazowe sygnału
F
mk
0
1
2
3
4
5
6
7
8
9
5
2,5
f [kHz]
Ψ
k
1
2
3
4
5
6
7
8
9
90
o
-90
o
f [kHz]
11
2
u t
( )
1.875
0.125
0.125
0.875
t
5
10