Systemy MES

Wykonał: Wojciech Ćwikliński
ETI, sem. VI

Ćwiczenie nr 10

Prowadzący: dr inż. P. Wasilewicz

Data wykonania ćwiczenia:
30.05.2014

Podpis:

1. Na laboratorium przeprowadziliśmy badania wytrzymałościowe oraz optymalizację stempla

i dwuteownika.

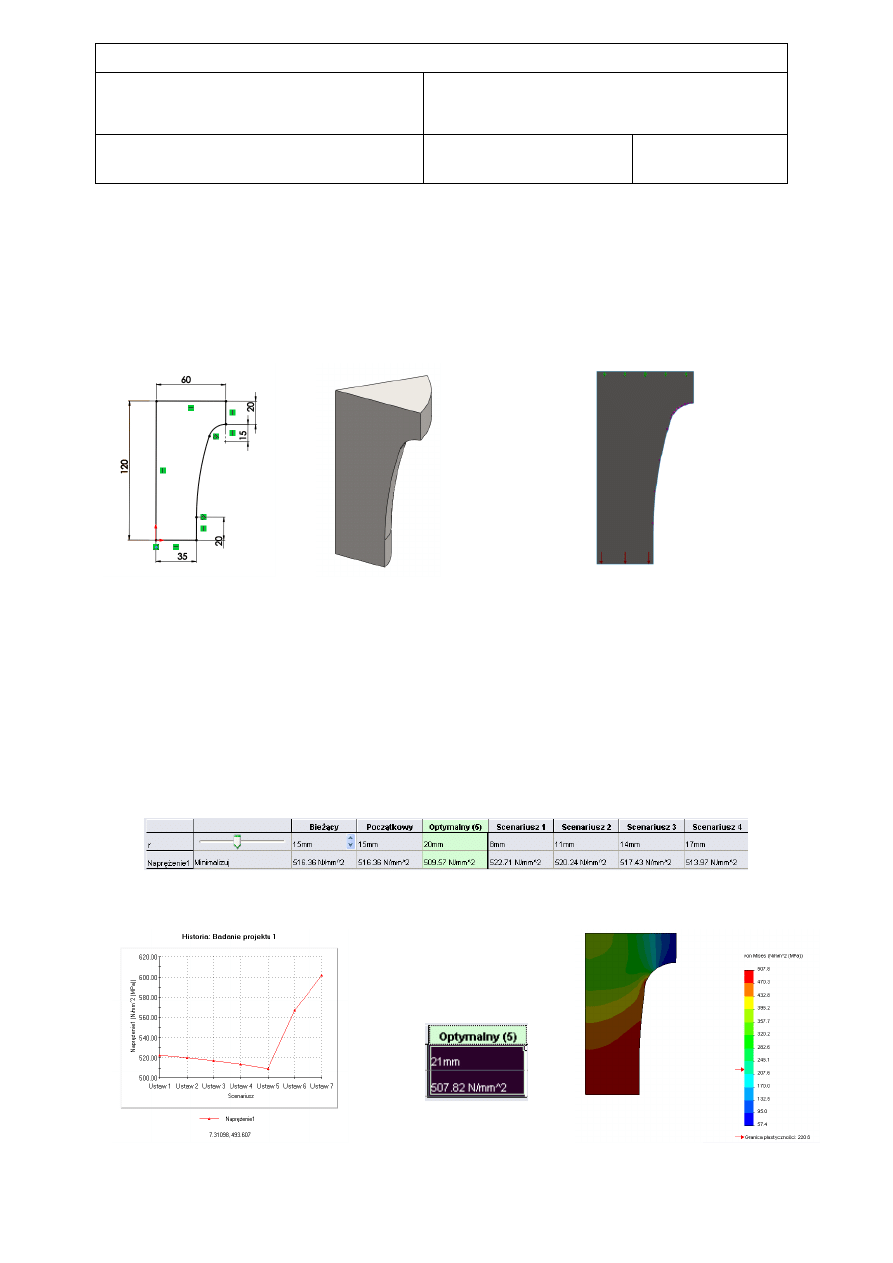
Końcówka stempla musi wytrzymać wysokie naprężenia, dlatego stosuje się łagodne przejście, aby nie było

dużych spiętrzeń naprężeń. Najczęściej stosuje się przejście jednopromieniowe, jednak my wykonaliśmy przejście
dwupromieniowe, które jeszcze lepiej niweluje spiętrzenia. Materiał jaki użyliśmy to stal węglowa, natomiast
ciśnienie działające na tłok wynosi 500 MPa.

Rys.1 Wymiary stempla Rys.2 Model 3D Rys.3 Zaznaczone umocowanie przesuwne
(zielony) oraz miejsce działania siły (czerwony)

Jeżeli chcemy zoptymalizować przedmiot należy najpierw wykonać nową symulację, np. badanie

statyczne. Następnie utworzyć nowe badanie projektu, dodać zmienne oraz cel. W naszej symulacji zmienną był
promień r, natomiast celem była minimalizacja naprężeń.

Pierwsze wyniki optymalizacji pozwoliły stwierdzić, że zmiana promienia z 15mm na 20mm spowoduje

zmniejszenie naprężeń. Na rys.5 widać, że zwiększenie promienia powyżej 20mm spowoduje nagły wzrost
naprężeń. Jednak w badaniu zastosowaliśmy krok 3mm, może się okazać że powyżej 20mm znajdziemy następną
najmniejszą wartość naprężeń.

Po zmianie kroku na 1mm uzyskaliśmy wartość najbardziej optymalną dla zaokrąglenia

o promieniu 21mm (rys.6).

Rys.4 Widok wyników optymalizacji

Rys.5 Wykres naprężeń od Rys.6 Wartość optymalna Rys.7 Rozmieszczenie naprężeń
promienia zaokrąglenia w stemplu

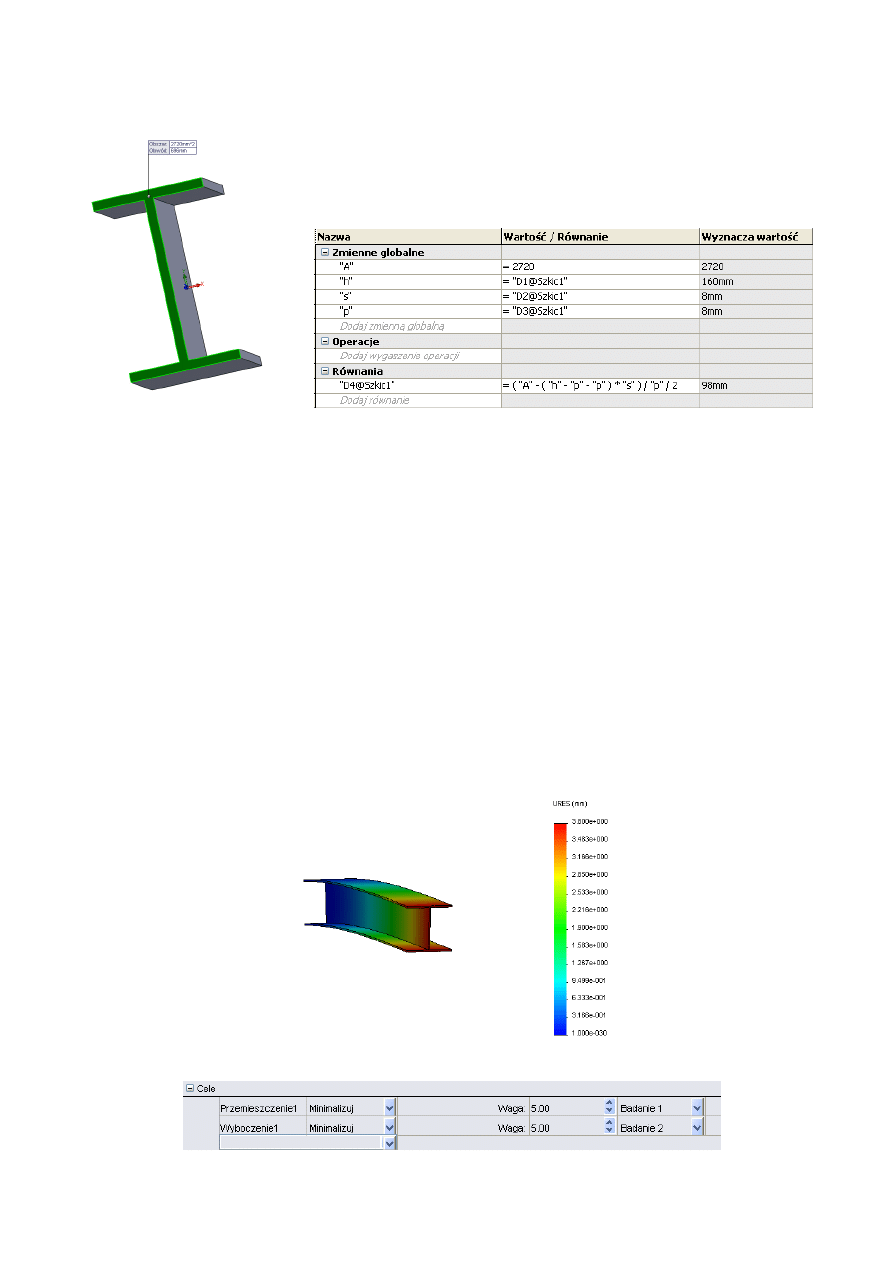
2. Kolejnym obiektem badań optymalizacyjnych był dwuteownik.

Ważne było utrzymanie stałego pola przekroju poprzecznego o wartości

2

2720mm

Rys.8 Rys.9 Tabela równań oraz zmiennych globalnych

Przy badaniu projektu należało zawęzić zmienne grubości środnika oraz pasów do takich, jakie możliwe są do

kupienia. My użylismy następujących grubości: dla pasów (zmienna p) 6,8,10,12,16 [mm], natomiast dla środnika
(zmienna s) 5,6,8,10,12 [mm].

Naszym celem było uzyskanie jak najmniejszych przemieszczeń, natomiast masę poddaliśmy tylko

monitrowaniu.

Pierwsze badanie optymalizacyjne dwuteownika bazowało tylko na analizie statycznej, spowodowało to, że

uzyskaliśmy niepoprawnie zaprojektowany kształt. Początkowe wartości p=16mm, s=12mm zostały zmienione
przez program na p=6mm oraz s=5mm, gdyż dla tych wartości zostały wyznaczone najmniejsze przemieszczenia.

Chcąc uzyskać poprwanie zoptymalizowany dwuteownik musieliśmy utworzyć nowe badanie z analizą

wyboczenia. Po odpowiednim umocowaniu z zastosowaniem geometrii nieprzesuwnej oraz przyłożeniu pionowej
siły skierowanej pionowo w dół o wartości 10000N mogliśmy przejść do dalszych badań projektu.

W widoku zmiennej pojawiła się waga badań: analizy statycznej oraz wyboczenia. Zmieniając wagę wybieramy

co jest dla nas ważniejsze przy optymalnym projektowaniu przedmiotu.

Rys.10 Dwuteownik z celem: minimalizacja przemieszczeń

Rys.11 Cele z podziałem na wagę poszczególnych badań