305

Portfele obciążone gaussowskim szumem multiplikatywnym

Krzywa Markowitz’a

zbiór obarczonych ryzykiem finansowych instrumentów podstawowych

















n

i

C

t

i

i

,

,

2

,

1

:

~

~

,

,

1

,

0





























,

i

C

~

prognoza wartości przyszłej instrumentu podstawowego

i





.

i

f

~

czynnik akumulacji kapitału zainwestowanego w instrument podstawowe

i





i

i

C

f

~

~



.

306





i

i

i

i

i

i

i

f

s

f

C



















1

~

,

 

1

;

0

~

~

N

i



 

i

i

f







F

oczekiwany czynnik aprecjacji kapitału zainwestowanego w instrument

i





;

-

 

0







i

i

s



V

współczynnik zmienności czynnika aprecjacji kapitału zainwestowanego w

i





;

-

 

i

i

i

i

s

f











M



odchylenie standardowe czynnika aprecjacji kapitału zainwestowanego w

i





;

307

Macierz kowariancji wektora





T

n

f

f

f

~

,

,

~

,

~

2

1



jest dana w postaci

 

j

i,











j

i

j

i

j

i

j

i

j

i

j

i

j

i

j

i

j

i

f

f

s

s

f

f

s

s















,

cov

,

,

,



























.





jest scharakteryzowana przez





T

n

f

f

f

f

,

,

,

2

1





i macierz kowariancji



Wariancja

i

i,



jest względną miarą ryzyka obciążającego instrument finansowy

i





.

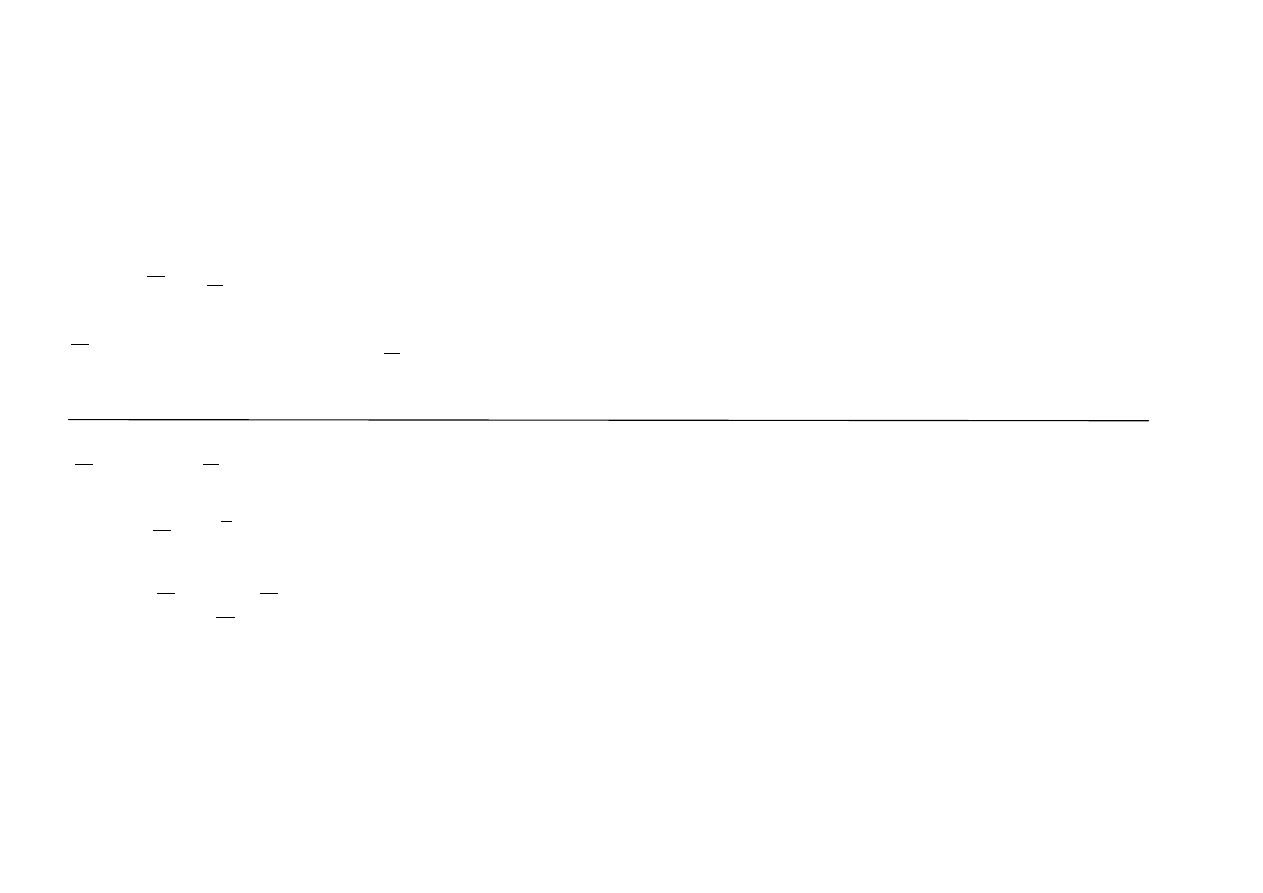
308



 







n

n

c

c

c

































2

2

1

1

bieżąca cenę portfela





0

1

0







c

C

T

,





n

T

R





1

;

;

1

;

1

1







T

n

c

c

c

c

,

,

,

2

1





.

c

C

p







1

0

,

f

p

f

T







,

p

p

T











2



.

Zbiór





wszystkich par











,

f

nazywamy zbiorem portfeli dopuszczalnych.

309

Krzywa Markowitz’a

 

0

:









R

R

 























,

:

min

f

f

.

min









p

p

T

1

1





T

p

,

f

f

p

T





.

 















 

 



2

2

2

2

1

1

1

1

2

1

1

f

f

f

f

f

f

f

f

f

T

T

T

T

T

T







































































,

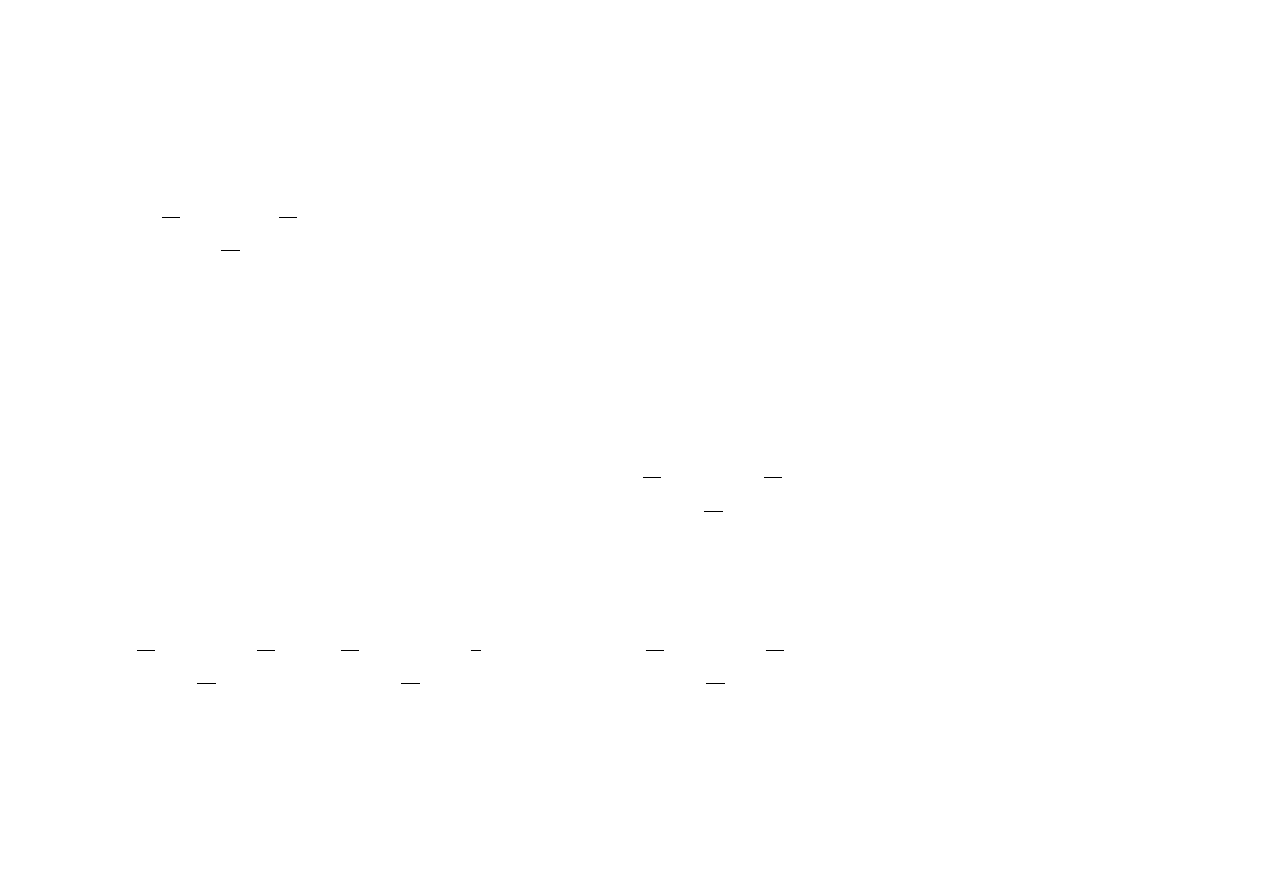
310

dolne oszacowanie wariancji dopuszczalnego portfela









1

2

1

1















T



.

Dowolna para różnych portfeli z minimalną wariancją replikuje dowolny portfel z minimalną

wariancją .

zbiór portfeli efektywnych





 













1

1

1

,

:

max

:

,





















T

ef

f

f

f







.

krzywa portfeli efektywnych jest dana jako funkcja



 

























































,

1

1

,

1

1

1

:

1

1

T

T

T

f

Dowolna para różnych portfeli efektywnych replikuje dowolny portfel efektywny.

311

zmodyfikowana krzywa Markowitz’a

 





















s

f

f

s

f

,

:

min

.

 

 















 

 







2

2

2

2

2

2

2

1

1

1

1

2

1

1

f

f

f

f

f

f

f

f

f

f

f

f

s

T

T

T

T

T

T











































































.

oszacowanie minimalnej wartości współczynnika zmienności



s

portfela dopuszczalnego





1

2















f

f

s

T

.

312

zmodyfikowany zbiór portfeli efektywnych





 













1

,

:

max

:

,





















f

f

s

s

f

f

s

f

T

ef

.



 

























































,

,

1

:

1

1

f

f

f

f

f

T

T

T

Krzywa portfeli efektywnych jest wypukła do góry i rośnie wraz ze wzrostem współczynnika

zmienności.

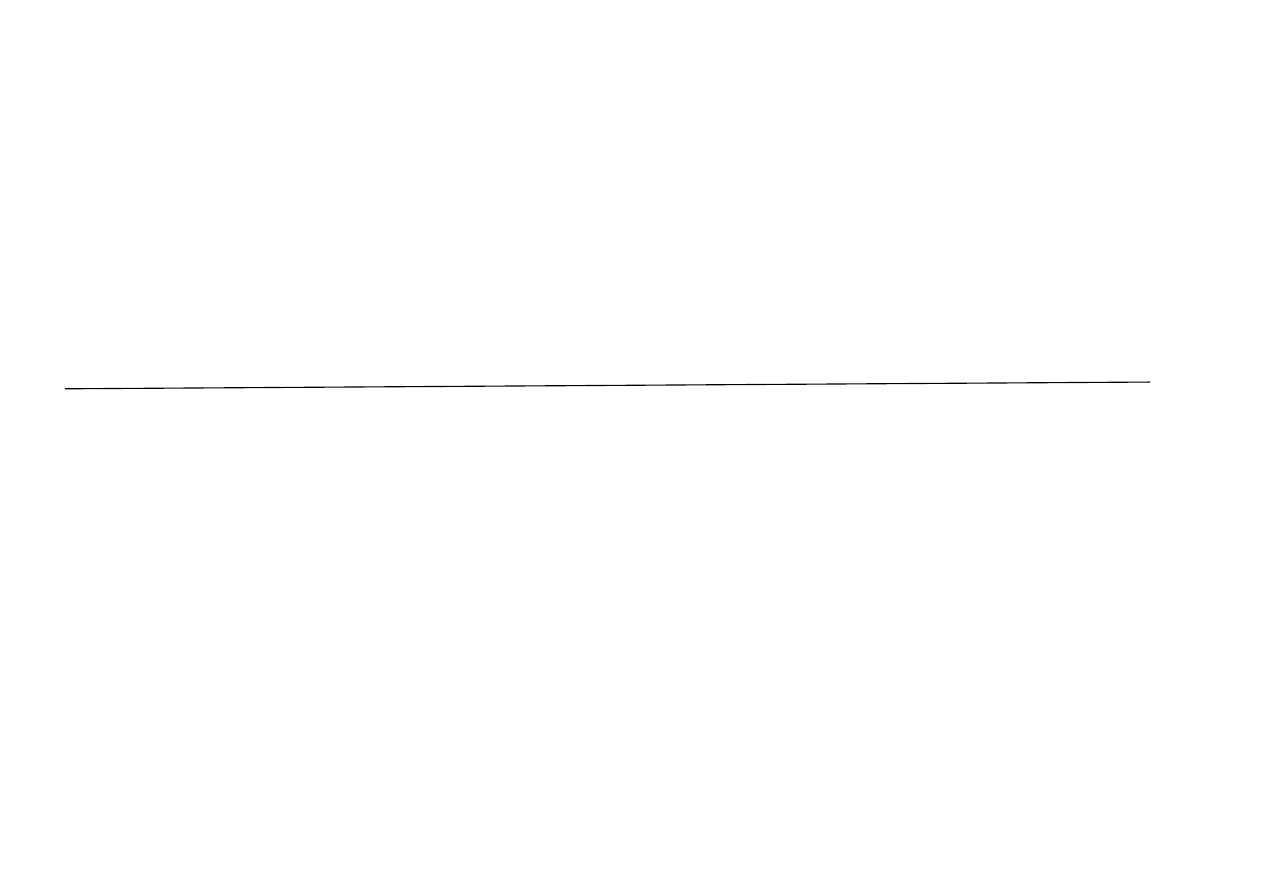
313

Hiperbola rynku kapitałowego

jednostkowy instrument dłużny























C

t ;

,

1

;

0

0



.

0

f

C





,

instrument dłużny

0





jest reprezentowany przez





0

;

0

f

.





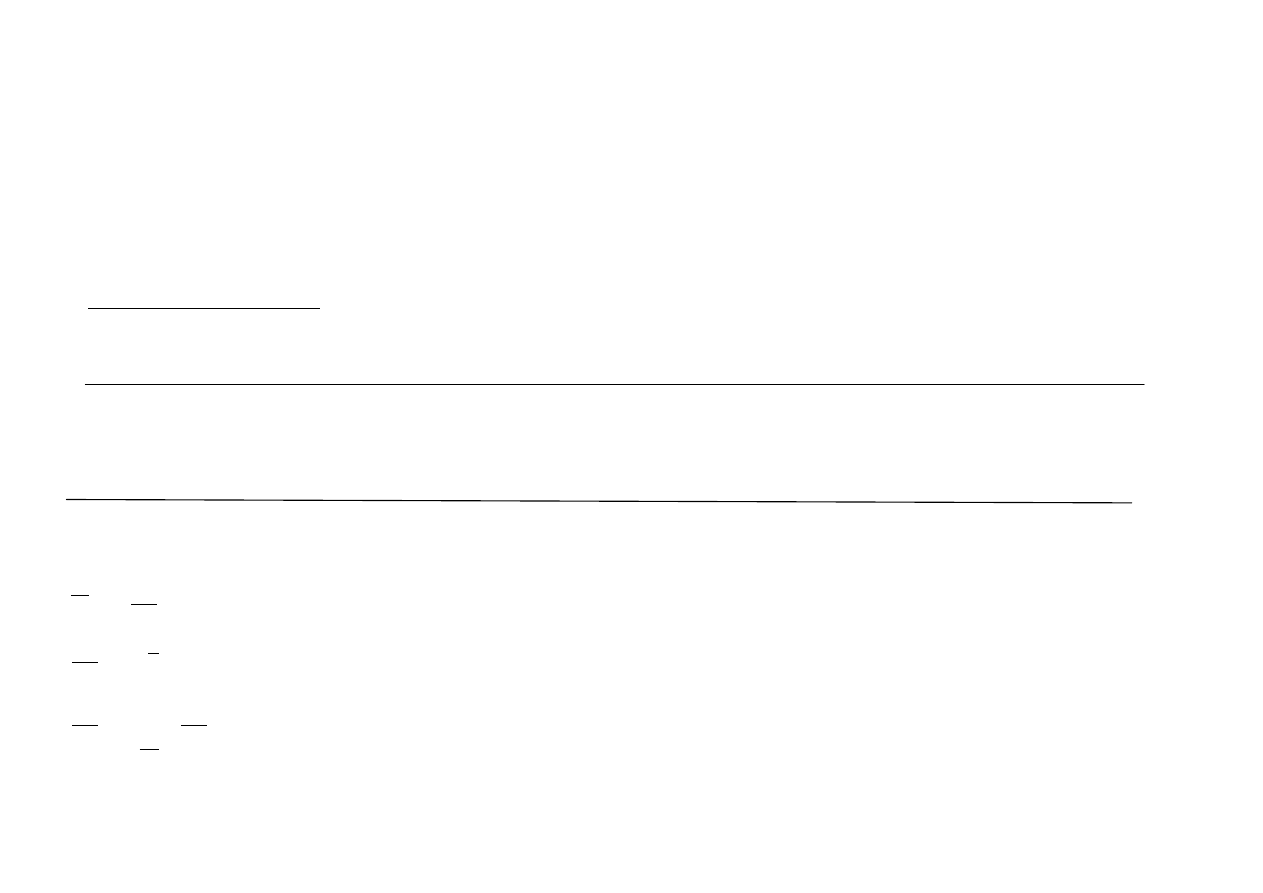
f

f

f

ef









0

:

,



.

Portfel złożony jedynie z instrumentu

0





jest portfelem efektywnym.

314







 





























0

1









 

s

f

f

f

f

f

s

f

f

























0

0

.

portfel rynkowy





jest scharakteryzowany przez parę









s

f ,

.



 







n

n

m

m

m

































2

2

1

1

1

1





m

T

,







f

f

m

T

,

2

2















s

f

m

m

T

,

315

hiperbola rynku kapitałowego









 

s

f

f

f

f

f

s

f

f

























0

0

.

[Tobin58]: Jeśli istnieje instrument dłużny, to dowolny portfel efektywny jest replikowany przez

kombinację tego instrumentu i portfela rynkowego.

316

Jeśli istnieje wolny od ryzyka instrument finansowy z czynnikiem aprecjacji

0

f

, to:

-chcąc uzyskać najefektywniejszy portfel o założonym oczekiwanym czynniku aprecjacji

kapitału

f

nieprzekraczającym rynkowy czynnika aprecjacji



f

należy inwestować w portfel

replikowany przez parę złożoną z istniejącego instrumentu dłużnego i z portfela rynkowego;

-chcąc uzyskać najefektywniejszy portfel o założonym oczekiwanym czynniku aprecjacji

kapitału

f

przekraczającym czynnik rynkowy aprecjacji



f

należy inwestować we właściwy

portfel efektywny złożony jedynie z instrumentów obciążonych ryzykiem.

317

jednostkowy kredyt komercyjny























C

t ;

,

1

;

0

0



.







f

C

,

kredyt komercyjny

0





jest reprezentowany przez parę





0

;



f

.





f

f

0

.







































1

0









 

s

f

f

f

f

f

s

f

f





























. (2.13)

318

portfel aktywów netto





jest scharakteryzowany przez parę



 

















s

f

f

f

,

,



.







f

f

.



 







n

n

a

a

a

































2

2

1

1

1

1





a

T

,







f

f

a

T

,

2

2















s

f

a

a

T

,

hiperbola rynku kredytowego

.









s

f

f

f

f

s

f

f























319

Jeśli jest dostępny kredyt konsumpcyjny z oczekiwanym czynnikiem aprecjacji



f

, to:

-chcąc uzyskać najefektywniejszy portfel o założonej wartości oczekiwanego czynnika

aprecjacji kapitału

f

przekraczającej wartość czynnika aprecjacji



f

w portfelu aktywów

netto należy inwestować w portfel replikowany przez parę złożoną z kredytu konsumpcyjnego i

z portfela aktywów netto;

-chcąc uzyskać najefektywniejszy portfel o założonej wartości oczekiwanego czynnika

aprecjacji kapitału nie przekraczającej wartości czynnika akumulacji



f

w portfelu aktywów

netto należy inwestować we właściwy portfel efektywny złożony jedynie z instrumentów

obarczonych ryzykiem.

320

Model CAPM II rodzaju

instrument dłużny

0





,

portfel rynkowy





reprezentowany przez parę



 

















s

f

f

f

,

,



.

portfel efektywny





reprezentowany przez parę



 

















s

f

f

f

,

,



.

współzależność portfela





i portfela r





określona przy pomocy współczynnika korelacji





,



.

model CAPM II rodzaju

























































f

f

s

s

f

f

f

f

0

,

0

0

1

1

1





321

zbiór obarczonych ryzykiem podstawowych instrumentów finansowych

















n

i

C

t

i

i

,

,

2

,

1

:

~

~

,

,

1

,

0





























,



 







n

n

m

m

m

































2

2

1

1





T

n

m

m

m

m

,

,

,

2

1





1

1





m

T

.







f

f

m

T

.

dla każdego efektywnego

i





tutaj mamy



























f

f

f

f

R

i

i

i

0

0

1

1

:





.

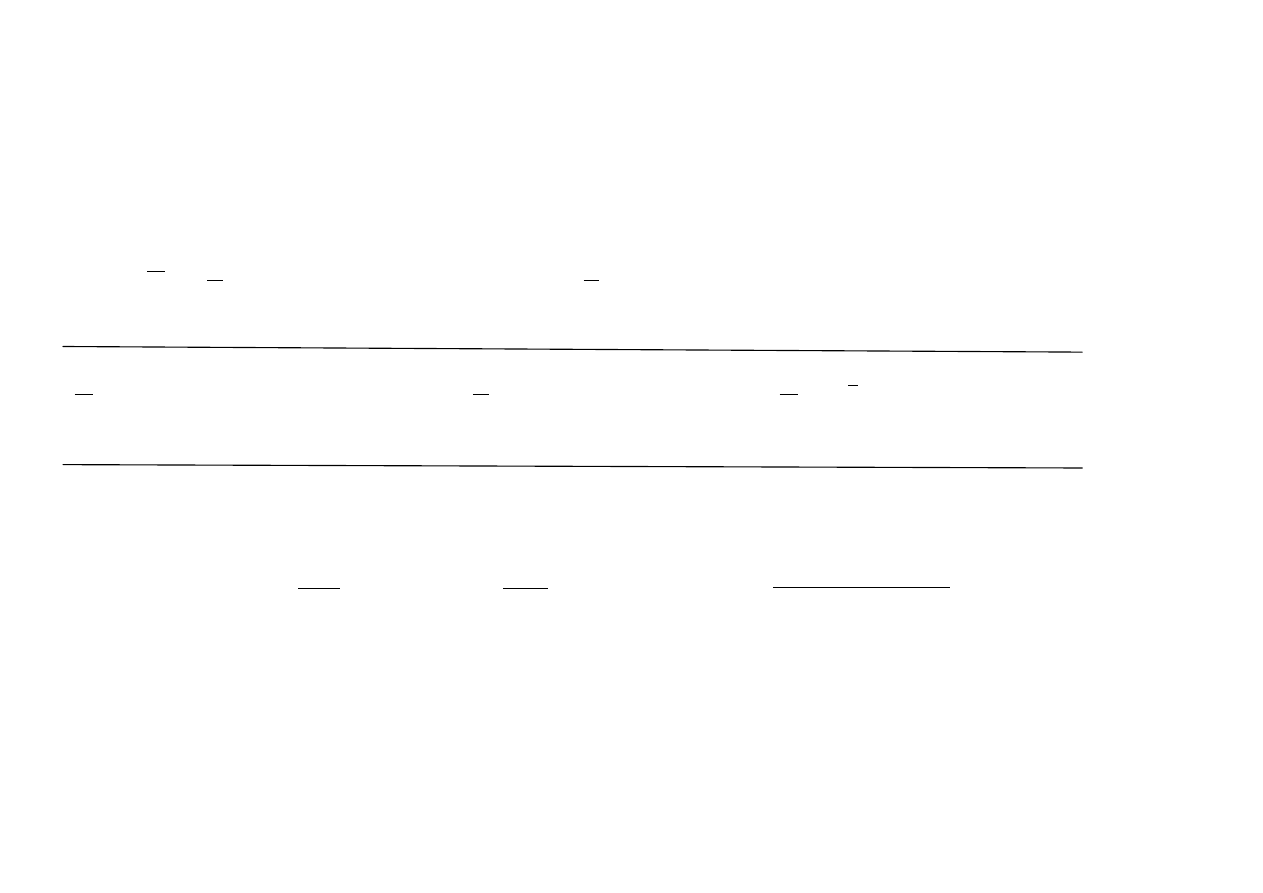
322



 







n

n

c

c

c

































2

2

1

1

0

1

0







c

C

T

,





T

n

c

c

c

c

,

,

,

2

1









c

C

p

p

p

p

T

n









1

0

2

1

,

,

,



,

f

p

f

T







.

































f

f

f

f

R

0

0

1

1

:





.



















n

i

i

i

n

i

i

i

i

f

p

f

p

1

1





.

323

i



może posłużyć do określenia właściwości podstawowych instrumentów finansowych:

- jeśli mamy

1



i



to

i





reaguje na zmiany sytuacji na rynku kapitałowym silniej, niż portfel

rynkowy i dlatego jest to instrument o podniesionym ryzyku;

-

- jeśli mamy

1

0





i



to

i





reaguje na zmiany sytuacji na rynku kapitałowym słabiej, niż

portfel rynkowy i dlatego jest to instrument o obniżonym ryzyku;

-

- jeśli mamy

0



i



to

i





broni przed skutkami bessy;

-

- jeśli mamy

0



i



to

i





wykorzystuje pozytywne skutki hossy.

324





można także wykorzystać do użytecznej zaklasyfikowania portfela





;

- jeśli mamy

1







, to portfel





jest portfelem agresywnym;

-

- jeśli mamy

1







, to portfel





jest portfelem zrównoważonym i może być uważany za

indeks rynkowy typu benchmark.;

-

- jeśli mamy

1

0









, to portfel





`

jest portfelem umiarkowanego wzrostu;

-

- jeśli mamy

0







, to portfel





jest portfelem wolnym od ryzyka rynkowego.

325

Model CAPM II rodzaju pozwala cenę równowagi rynkowej każdego efektywnego portfela























C

t

C

~

;

,

;

0

0



.



0

C

obowiązująca w chwili bieżącej cenę inwestycji





.

R

C







:

~

prognoza wartości przyszłej inwestycji





. Dzięki tej prognozie otrzymujemy

daną w postaci

CAPM



 















f

C

C

C

0

~

E

uzasadniona wartość przyszłą inwestycji





f

spodziewany przez inwestorów czynnik aprecjacji kapitału zainwestowanego w portfel















f

C

C

0

. spodziewana wartość przyszła

326

cena równowagi rynkowej









1

1

0

1

0

0

0

0



















































f

f

f

f

C

f

f

C

f

C

C











f

f

,



KUPUJ.









f

f

.



TRZYMAJ



STAN RÓWNOWAGI









f

f

,



SPRZEDAJ.

wyceny portfela





w oparciu o cenę bieżąca i układ czynników aprecjacji





0

,

,

f

f

f







.

327

i

i

f

f





,



KUPUJ

i





.

i

i

f

f





,



TRZYMAJ

i





.

i

i

r

r





,



SPRZEDAJ

i





.

328

Kryteria zarządzania portfelem



 



















C

t

C

~

,

,

,

0

0



efektywna inwestycja,













,

f





f

obserwowany na rynku finansowym przypuszczalny czynnik aprecjacji



0

C

opisuje obserwowaną na rynku bieżącą cenę





,

R

C







:

~

prognozę wartości przyszłej





.



f

oczekiwany czynnik aprecjacji wyznaczony przy pomocy jednego z racjonalnie uzasadnionych

modeli analizy rynku finansowego.

cena równowagi

















f

f

C

C

0

0

.

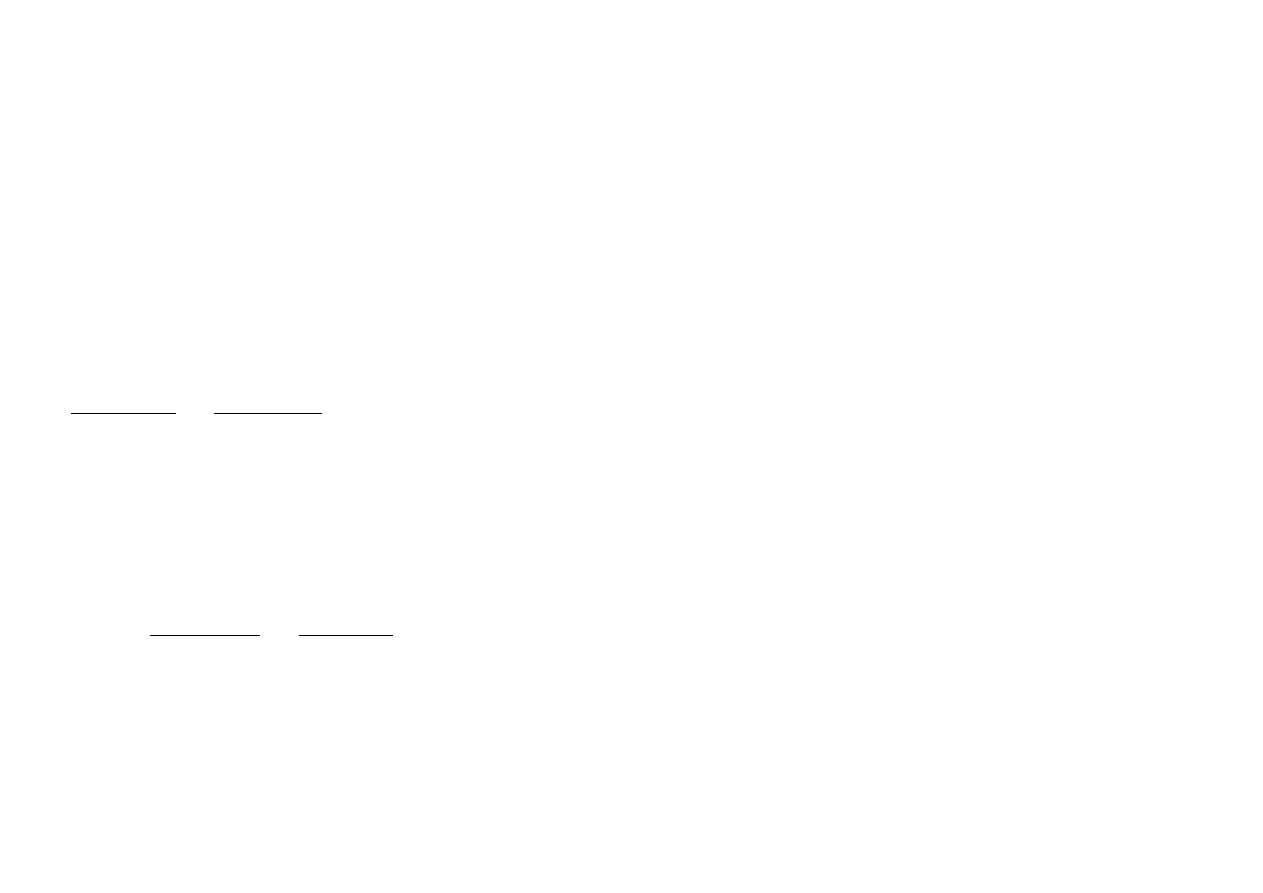
329

Kryterium Sharpe’a

0





instrument dłużny





0

,

0

f





portfel rynkowy











,

f

.

Twierdzenie Tobina



każdy dopuszczalny portfel efektywny











,

f

spełnia warunek

wyznaczony przez linię rynku kapitałowego zapisaną tutaj w postaci



















0

0

f

f

f

f

.





inwestycja reprezentowana przez portfel dopuszczalny













,

f

.

miernik typu Sharpe’a























S

r

r

f

f

S





0

0

ˆ

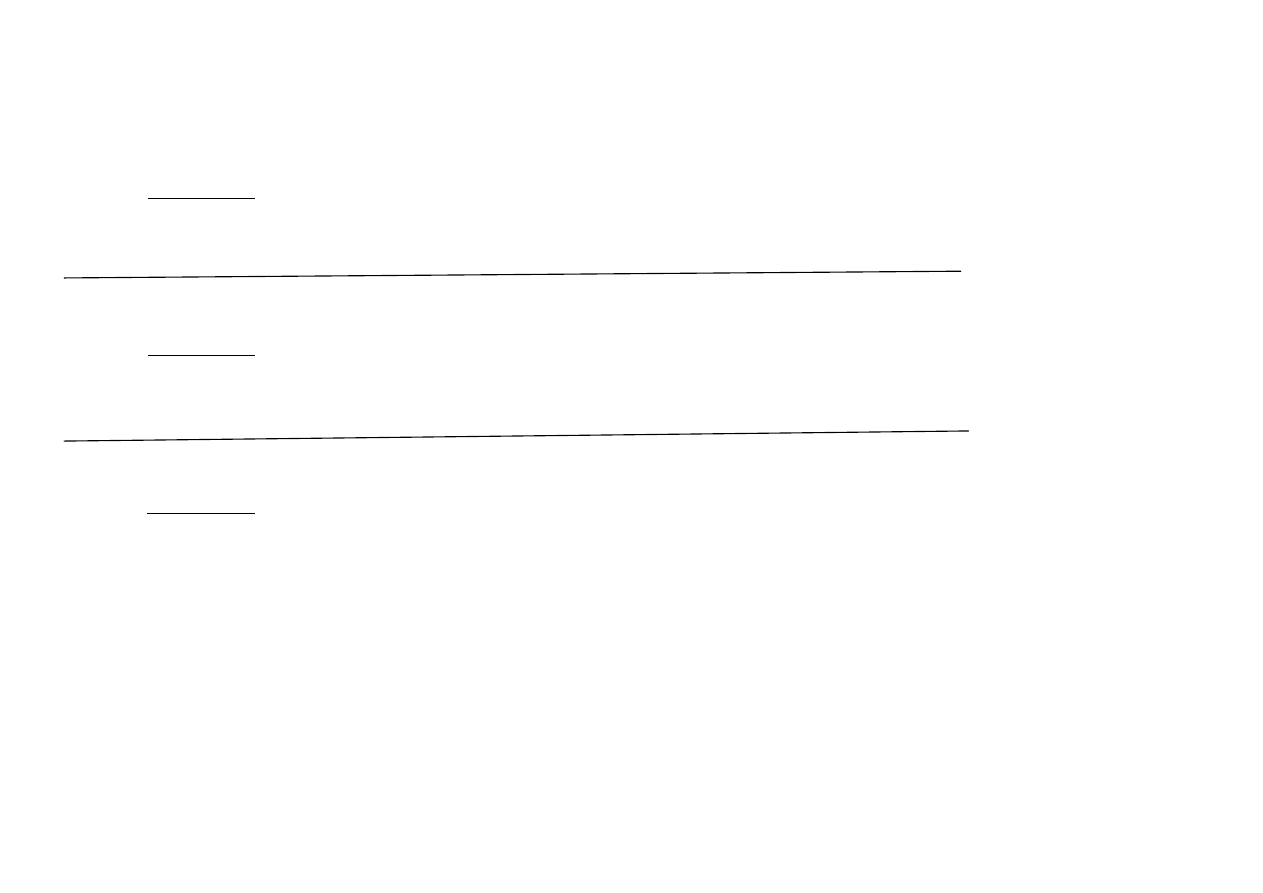
330













0

f

f

S

,











f

f



KUPUJ

















0

f

f

S

,











f

f



TRZYMAJ

















0

f

f

S

,











f

f



SPRZEDAJ





.

331

Kryterium typu Jensena

0

f

wolny od ryzyka czynnik aprecjacji



f

rynkowy czynnik aprecjacji.











,

f

efektywna inwestycja

model CAPM II













































f

f

f

f

0

0

1

1



.





inwestycja reprezentowaną przez parę













,

f

.

miernik typu Jensena











































f

f

f

J

0

1

1

ˆ



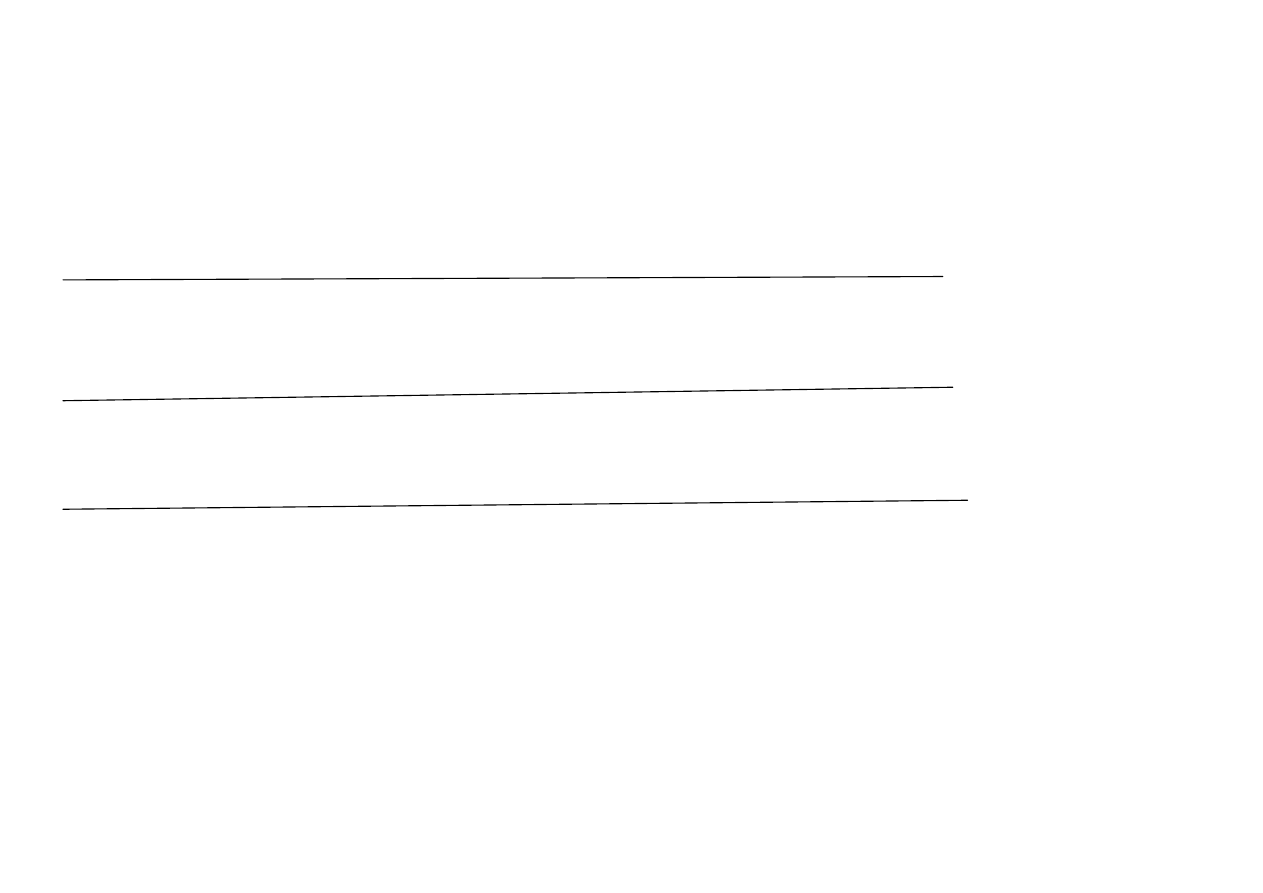
332

0

ˆ

f

J





,











f

f



KUPUJ





0

ˆ

f

J





,











f

f



TRZYMAJ





0

ˆ

r

J





,











f

f



SPRZEDAJ





.

333

Kryterium typu Treynora

0

f

wolny od ryzyka czynnik aprecjacji



f

rynkowy czynnik aprecjacji.











,

f

efektywna inwestycja

model CAPM II



 

1

1

0

1

1

0





















f

f

f

f



.





inwestycja reprezentowaną przez parę













,

f

, gdzie

0







.

miernik typu Treynora

 



















1

1

0

ˆ

f

f

T

334

1

1

0

ˆ













f

f

T

,











f

f



KUPUJ





1

1

0

ˆ













f

f

T

,











f

f



TRZYMAJ





1

1

0

ˆ













f

f

T

,











f

f



SPRZEDAJ





.

Miernik Sharpe’a



ranking wysokości premii jednostkowej za ryzyko ogólne.

Miernik typu Jensena



ranking wartości premii za ryzyko stopy rynkowej.

Miernik typu Treynora



ranking wysokości premii jednostkowej za ryzyko stopy rynkowej.