1

Skrypt z logiki na podstawie podręcznika

prof. Widły

Rozdział II – Znak, kategorie syntaktyczne

1. Znak – nadany przez kogoś dostrzegalny zmysłowo układ rzeczy lub zjawisko o określonej treści

umożliwiający pewnej grupie odbiorców odczytanie tej treści. Najczęściej jest to element jakiegoś języka,
przedmiot, który w procesie porozumiewania się ludzi służy do przekazywania określonych treści (informacji
czy znaczeń)

2. Elementy znaku:

a. nadawca -> twórca zn. lub osoba, która go przekazuje
b. treść znaku -> reguły znaczeniowe nadane przez człowieka w celu komunikacyjnym, które są

zrozumiałe dla okr. grupy odbiorców

c. odbiorca -> osoba, do której znak jest skierowany

3. Znak oznaka – powstaje samoistnie, współtowarzyszy danemu stanowi rzeczy i niekiedy kieruje w jego

stronę myśli: spadający liść = oznaka jesieni

4. Język – zbiór znaków przyjętych na gruncie danego systemu, które służą do porozumiewania się

a. homonimy – wyrazy identycznie brzmiące, niemające wspólnych elementów znaczeniowych
b. idiomy – wyrażenia, w których poszczególnym wyrazom lub całemu wyrażeniu nadano odmienne

znaczenie

c. synonimy – różnią się brzmieniem, znaczenie jest jednakowe

5. Stopnie języka:

a. I stopnia – język zwany językiem przedmiotowym, odnosi się do bezpośrednio nazywanych obiektów
b. II stopnia – gdy mówimy o języku I stopnia; zwany jest metajęzykiem
c. III stopnia – metajęzyk II stopnia -> język prawniczy = glosa (komentarz orzeczenia sądowego <II

stopień>, które interpretuje przepisy prawa <I stopień>)

6. Role semiotyczne wypowiedzi – służą do posługiwania się językiem w sposób najodpowiedniejszy w danej

sytuacji komunikatywnej

a. funkcja opisowa (deskryptywna) – jeżeli chcemy przekazać komuś informację, przedstawić mu

urywek otaczającej rzeczywistości bez zabarwienia emocjonalnego

i. np. Jan czyta gazetę.

b. funkcja ekspresywna – gdy celem wypowiedzi jest uzewnętrznienie stanu psychicznego i

emocjonalnego osoby wypowiadającej się

i. np. Dłużej już tego nie wytrzymam! Mam w dupie logikę!

c. funkcja sugestywna – jest bodźcem do określonego zachowania; korzystamy z niej, gdy chcemy

zmusić odbiorcę wypowiedzi do określonego działania -> wpływamy na zachowanie innej osoby

i. np. Chodźmy na wykład. Pomóż mi.

d. funkcja performatywna – jeśli poprzez wypowiedź następuje jakiś stan o charakterze czysto

umownym. Każda wypowiedź pełniąca funkcję performatywną musi być sformułowana w warunkach
ściśle określonych wywołujących jej performatywne znaczenie. W przeciwnym przypadku wypowiedź
performatywna jest nieważna.

7. Kategorie syntaktyczne

a. Syntaktyka – nauka zajmująca się badaniem związków jakie zachodzą między znakami wewnątrz

danego języka. 2 wyrazy należą do tej samej kategorii syntaktycznej, jeżeli wyraz „a” zastąpimy
wyrazem „b”, a całość składniowa nie ulegnie zmianie.

b. Wśród kategorii syntaktycznych wyróżniamy:

2

i. nazwy – wyrazy bądź wyrażenia nadające się na podmiot bądź orzecznik orzeczenia

imiennego => n

ii. zdania – każda wypowiedź oznajmująca i jednoznaczna, że tak a tak jest, albo tak a tak nie

jest => z

iii. funktory – jest łącznikiem. Jego rola polega na wiązaniu w wyrażenia bardziej złożone.

1. nazwotwórczy – jeżeli w połączeniu z innym wyrazem lub wyrażeniem daje nazwę
2. zdaniotwórczy – jeżeli wyraz w połączeniu z innym wyrazem lub wyrażeniem daje

zdanie

3. funktorotwórczy – jeżeli wyraz w połączeniu z innym wyrazem lub wyrażeniem daje

sensowną całość niebędącą ani nazwą, ani zdaniem, to ta sensowna całość zwie się
funktorem funktorotwórczym

4. zapisujemy je w postaci ułamka -> nad kreską wpisujemy co tworzy, pod kreską to,

co jest potrzebne, by dana sensowna całość powstała

5. przy f. funktorotwórczym-> nad i pod kreską zawsze to samo

iv. operatory – wyrażenia wiążące zmienne jak np. kwantyfikatory

Rozdział III – Nazwy

1. Nazwy – uzewnętrznianie pojęć; tj. procesów intelektualnych jakie powstają w efekcie kontaktu z obiektami

świata rzeczywistego, lub wyobrażonego

2. Budowa nazwy

a. prosta – zbudowana z jednego wyrazu
b. złożona – zbudowana z dwóch lub więcej wyrazów -> jądro tej nazwy to wyraz, który w innych

okolicznościach może funkcjonować samoistnie jako nazwa -> argument nazwy; druga część nazwy
złożonej to funktor nazwotwórczy

c. nazwa kategorematyczna – nazwa która w zależności od okoliczności może być nazwą albo

funktorem

d. wyraz syntakategorematyczny – wyraz, który może być tylko funktorem/operatorem, a nigdy nie

mogą posłużyć za podmiot lub orzecznik zdania

e. oksymoron – jeżeli znaczenie funktora kłóci się ze znaczeniem argumentu
f. pleonazm – jeżeli znaczenie wyrażenia stanowiącego funktor stanowi ponowienie całości lub części

znaczenia argumentu (plusy dodatnie i plusy ujemne)

g. pojęcia proste – takie, które obejmują tylko jedną cechę
h. pojęcia złożone – wyróżnić można wiele cech (człowiek – zwierzęcość + rozumność)
i. akronimy – wygłaszane jako jedna nazwa pierwszych liter wyrazów składowych (PCK, IPN)
j. abrewiacja – kiedy nazwa zostaje skrócona (matma)
k. nazwa hybrydalna – zbitka wyrazów powstała z wyrazów pochodzących z różnych języków
l. słowa-wytrychy – doraźnie tworzone, utrwalane przez używane nowotwory językowe stosowane do

nazywania obiektów o nieznanych nazwach (dinks)

3. Denotacja nazwy – zbiór obiektów niejako wywołanych, wskazanych przez jej użycie

a. desygnaty – obiekty
b. zakres nazwy – zbiór obiektów

i. nazwa ostra – jeżeli zakres nazwy w sposób obiektywnie jednoznaczny można określić

(człowiek, taboret)

ii. nazwy nieostre – nie ma obiektywnej i jednoznacznej granicy umożliwiającej oddzielenie

zakresu desygnatów (wysoki chłopiec)

c. z uwagi na zakres dzieli się nazwy na:

3

i. oznaczające – nazwy, które mają desygnaty. W zależności od ilości desygnatów:

1. jednostkowe – jeden desygnat
2. ogólne – więcej niż jeden desygnat
3. nazwa wyrażająca pojęcie szczegółowe – jeżeli zakres nazwy ogólnej zawęzić do

bliżej nieokreślonej liczby desygnatów (np. przez użycie wyrażenia „niektóre”

ii. puste – nie mają desygnatów -> „prosty egzamin z HUPu”; „kosmodrom w Chorzowie”

iii. zbiorowe – nazwy, które mają desygnaty w postaci zespołów -> zbiory w ujęciu kolektywnym

= desygnatami są podmioty zbiorowe, a nie poszczególne elementy tych zbiorów: bibliotek,
wojsko, las

4. Konotacja nazwy – to jej treść, zbiór cech znamionujących desygnaty, pozwalających na odróżnienie

desygnatów tej nazwy od desygnatów innej nazwy. Owe cechy to właściwości konstytutywne lub
konsekutywne.

a. cechy konstytutywne – są cechami dodatkowymi, które nie są niezbędne dla określenia danego

desygnatu; cechy najistotniejsze

b. cechy konsekutywne – są cechami dodatkowymi, które nie są niezbędne dla określenia danego

desygnatu

c. z uwagi na konotację dzieli się nazwy na:

i. konkretne – nazwy, których desygnaty zdolne są do bytu samoistnego (realnego lub

wyimaginowanego)

ii. abstrakcyjne – nie mają takiej możliwości; istnieją jedynie jako własności bytów samoistnych

1. błąd hipostazowania – pojmowanie konkretnie nazwy abstrakcyjnej

d. W efekcie innego podziału wyróżnia się nazwy

i. zależne – relatywne; wyrażają pojęcia w jakiś sposób ustosunkowane wobec innych

ii. niezależne – wyrażają pojęcia nierodzące skojarzeń z innymi

e. Inne zróżnicowania prowadzą do wyróżnienia nazw:

i. pozytywnych

ii. negatywnych (w aspekcie ich prywatności bądź pejoratywności)

5. Supozycje – nazwy mogą pełnić różne role znaczeniowe, występować w różnych supozycjach

a. supozycja materialna – używając nazwy w tej supozycji wypowiadamy się o nazwie jako takiej np.

Prestidigitator to nazwa trudna do wymówienia

b. supozycja formalna – odnosimy się do zakresu danej nazwy, mówimy o zbiorze np. Student powinien

złożyć potrzebne egzaminy w terminach wskazanych w harmonogramie sesji.

c. supozycja prosta – gdy wypowiedź odnosi się do jednostkowo oznaczonego desygnatu np. To ten

student, któremu podczas egzaminu odebrano ściągawkę

Rozdział IV – Definiowanie

1. Definicje – wypowiedzi informujące o znaczeniu nazwy, sposobie jej rozumienia w danym języku lub

subjęzyku. Ustalić znaczenie jakiejś nazwy to tyle samo co ustalić jej pojęcie.

2. Podział definicji

a. w zależności od tego, jakie informacje zawarte są w wypowiedzi definicyjnej, definicje dzieli się na

i. nominalne – są wypowiedziami o nazwach jako takich

1. odmiana słownikowa – zastąpienie nazwy o nieznanym lub niesprecyzowanym

znaczeni nazwą o znaczeniu znanym-> np. Forteca znaczy tyle samo co twierdza.

2. odmiana semantyczna – dochodzi w niej do wskazania przedmiotu definiowanej

nazwy, ale bez jego charakterystyki -> np. Sprawa spadła z wokandy

4

ii. realne –dostarczają informacji o desygnatach definiowanej nazwy, zawierają ich

charakterystykę

b. z uwagi na budowę (postać konstrukcyjną) definicje dzieli się na

i. równościowe (normalne) – w def. równościowej czytelne są 3 elementy składowe

a. DEFINIENDUM – nazwa, której znaczenie chcemy zakomunikować
b. DEFINIENS – wyrażenie zawierające komunika o znaczeniu definiowanej

nazwy

c. ZWROT ŁĄCZĄCY – np. jest to

2. definicja klasyczna – postać definicji równościowej; powstaje według wskazania

zawartego w paremii: „definiuje się przez podanie rodzaju i różnicy gatunkowej”.
Przybiera postać wypowiedzi „A jest B o cechach C”

a. gdy posłużymy się cechami konstytutywnymi – definicja esencjalna np.

Człowiek to zwierzę rozumne

b. definicja luźna – odwołuje się do cech konsekutywnych np. Człowiek to

zwierzę posiadające zdolność oceny cudzych postępków.

3. definicje opisowe

a. alternatywna (przez wyliczenie) – tworzy się wymieniając w definiensie

desygnaty definiowanej nazwy

b. przyczynowa – podajemy w definiensie rację zaistnienia desygnatów

definiowanej nazwy

c. genetyczna – z definiensu można dowiedzieć się o sposobie powstania

desygnatów

ii. nierównościowe (anormalne)

1. definicja kontekstowa (w uwikłaniu) – zbudowana jest na podobieństwie

sąsiadujących z nią przepisów

2. definicja aksjomatyczna (przez postulaty) – wypowiedź w której wyrażono wymogi,

jakie musi spełnić obiekt, by zostać uznany za desygnat danej nazwy np. Komunizm
to władza plus elektryfikacja kraju

c. definicje są zdaniami, więc wyrażają sądy

i. definicja sprawozdawcza – informuje jak definiowana nazwa jest rozumiana w danym języku

ii. definicja projektująca – informuj jak (od momentu zdefiniowania) nazwa ta będzie

rozumiana

1. tzw. definicje operacyjne przygotowywane np. przez naukowców

iii. definicja konstrukcyjna – w najmniejszym stopniu nie liczy się z dotychczasowym

rozumieniem definiowanej nazwy – o ile takowe dotąd istniało. Tworzy się je głównie dla
nowych nazw, tworzonych w związku z powstawaniem nowych obiektów

iv. definicja regulacyjna – mniej lub bardziej liczą się z dotychczasowym rozumieniem danej

nazwy. Znaczenie jednak zostaje zmodyfikowane, zazwyczaj przez zawężenie
dotychczasowego rozumienia, choć niekiedy spotyka się i definicje rozszerzające to
rozumienie.

5

v. definicja zakresowa – taka, która wylicza elementy składowe zakresu definiowanego pojęcia

3. Budowa definicji -> budować definicje można budować na różne sposoby. Cztery główne:

a. metoda indukcyjna – najbardziej cenione, klasyczne definicje. Po znalezieniu nazwy, wobec której

definiowana jest podrzędną, znaleźć należy cechy wspólne, konstytutywne. Posłużą one za
wskazanie różnicy gatunkowej, wydzielającej desygnaty definiowanej nazwy z grupy desygnatów
nazwy, wobec której definiowana jest podrzędną

b. metoda syntetyczna – wychodzi się w niej od znalezienia zakresu nadrzędnego, przy czym nie musi

to być zakres najbliższy. Następnie należy porównać desygnaty definiowanej nazwy z pozostałymi
desygnatami. W ten sposób uchwycona zostanie różnica gatunkowa

c. metoda filologiczna – badając znaczenie danej nazwy w różnych zdaniach, różnych kontekstach

(może prowadzić do nieporozumień)

d. metoda etymologiczna – odwołująca się do źródłosłowu. Sprawdza się, jeśli rzeczywiście intencją

twórcy nazwy było jednoznacznie określić jej zakres i odpowiednio do tego dobierać źródłosłów.

4. Bez względu którą metodą i jaką definicję budujemy, powinna ona spełniać 5 postulatów głoszących, że

a. Nazwa definiowana nie powinna pojawić się w części informującej o znaczeniu tej nazwy ->

zalecane jest wystrzegać się błędu idem per idem (to samo przez to samo) = odwoływanie się w
definiensie do definiendum. Błąd błędnego koła (bezpośredniego i pośredniego)

b. Definiens powinien być zrozumiały dla adresata -> zalecane jest wystrzegać się błędu ignotum per

ignotum (nieznane przez nieznane) = gdy definicja adresowana jest do tzw. przeciętnego ogółu
definiens należy budować posługując się wyłącznie językiem naturalnym, ale gdy adresowana jest do
specjalisty wolno posłużyć się subjęzykiem danej specjalności.

c. Zakres definiowanej nazwy powinien być równoważny z zakresem zawierającym komunikat o

znaczeniu -> zalecane jest wystrzegać się błędu inadekwacji. Błąd w tym zakresie polega na tym, że
powstają definicje za szerokie lub za wąskie.

d. Zachowana powinna być jednorodność ontologiczna -> zalecane jest wystrzegać się błędu

przesunięcia kategorialnego. Nie wolno mylić sposobów, w jaki poszczególne byty mogą zaistnieć –

definicje

sprawozdawcze

informują jak

definiowana nazwa

jest rozumiana w

danym języku

projektujące - ustalają

znaczenie wyrazu na

przyszłość

Regulujące - uściślają

znaczenie wyrazu

licząc się z

dotychczasowym

znaczeniem

Konstrukcyjne - nie

liczą się z dot.

znaczeniem danego

wyrazu

6

metafizycznie lub logicznie. Przejawem takiego błędu będzie hipostazowanie w definicjach, mylenie
zjawisk ze znamionami.

e. Definicja powinna być zwięzła. Nie należy mylić definiowania, które jest czynnością terminologiczną,

z encyklopedyzacją. W definicji powinny znaleźć się jedynie dane umożliwiające odróżnienie
desygnatów definiowanej nazwy od desygnatów innej.

5. Indefilibilia – nazwy, które nie poddają się definiowaniu. Są to np. terminy podstawowe – istnienie,

możność, abstrakty (prawda, sprawiedliwość), nazwy powszechne, poszczególne jednostki, niemierzalne
doznania (np. ból)

a. w takich przypadkach można posłużyć się pseudodefinicjami:

i. definicja ostensywna – wskazanie przykładu np. rysunku

ii. definicja negatywna – generalnie nie można definiować przez przeczenie, są jednak syt.

kiedy zakaz jest łamany np. „dziedziną prawa administracyjnego jest to wszystko co nie jest
dziedziną prawa cywilnego i karnego”

iii. definicja porównawcza – desygnaty danej nazwy odnosimy do desygnatów nazwy o znanym

znaczeniu np. zdrajca to człowiek, który postępuje jak Judasz

iv. definicja deskryptywna – dokonuje się prezentacji cech desygnatów danej nazwy, ale nie

będącymi cechami charakterystycznymi (nawet konsekutywnymi)

v. charakterystyka – autor ujmuje w niej najważniejsze znamiona obiektu

Rozdział VII – Podział logiczny

1. Podział logiczny – proces myślowy polegający na wyłączaniu z zakresu danej nazwy (dzielonego) zakresów do

niego podrzędnych. Dotyczy zakresów nazw, a nie ich znaczenia

a. nie należy go mylić z podziałem rzeczowym
b. partycja – proces myślowy, którego jednak nie należy mylić z podziałem logicznym
c. podział metafizyczny – obiekty pojmuje się jako agregaty cech: np. krzesło -> uroda kształtu, kolor

obicia tapicerskiego, wygoda siedziska

2. Podział logiczny nazwy zegar:

a. zegar ścienny
b. zegar kominkowy
c. zegarek kieszonkowy

3. Partycja nazwy zegar:

a. wskazówka
b. tarcza zegarowa
c. wahadło

4. Produkty podziału –musiały być podrzędne wobec zakresu dzielonego. Produkty partycji z zakresem

dzielonym się wykluczają.

5. Podział sztuczny – charakteryzuje się małą ilością cech wspólnych występujących wśród desygnatów z

danego zakresu dzielonego. Charakterystyczną cechą przedmiotów wchodzących w zakres danego członu
podziału zazwyczaj bywa jedynie cecha charakterystyczna dla kryterium podziału

6. Podział naturalny – charakteryzuje się dużą ilością cech wspólnych występujących wśród desygnatów z

danego zakresu dzielonego. Przedmioty wchodzące w zakres danego członu podziału mają wiele cech
charakterystycznych, które odróżniają je od przedmiotów należących do innych członów podziału.

a. np. podział mebli pod względem ich przeznaczenia

7. Co zrobić, żeby podział logiczny był poprawny?

a. Podziału należy dokonać według jednego, jednoznacznie sprecyzowanego kryterium

i. powinien być użyteczny pod względem celu dokonanego podziału

7

ii. jeżeli podział jest wielopoziomowy (klasyfikacja), wówczas dla każdego poziomu trzeba

sformułować takie kryterium (inaczej uzyskamy podział krzyżowy)

iii. podział skrzyżowany – polega na tym, że dany zakres dzieli się najpierw z użyciem jednego

kryterium dla danego poziomu, potem (dla tego samego poziomu) według innego kryterium,
a po zakończeniu: łączy się produkty podziałów dokonanych na poszczególnych poziomach

b. Produkty podziału (wydzielone zakresy podrzędne) powinny być zakresami najbliższymi. Nie można

dowolnie przeskakiwać osiągalnych poziomów, a podział powinien być stopniowy i w miarę ciągły.

c. Podział powinien być rozłączny – wszystkie produkty podziału na każdym poziomie powinny wobec

siebie pozostawać w stosunku wykluczania.

i. Jeżeli stosunkiem znamionującym produkty podziału będzie stosunek sprzeczności –

powstanie podział dychotomiczny (dwuczłonowy)

ii. Częściej mamy do czynienia ze stosunkiem przeciwieństwa, a na nim bazujący podział

nazywany jest politomicznym (wieloczłonowy)

d. Podział powinien być zupełny - wymóg ten zostanie spełniony jeśli podział zostanie

przeprowadzony tak, że razem wzięte desygnaty wszystkich wydzielonych zakresów otworzą zakres
dzielony. Taki podział nosi miano adekwatnego. Jeżeli nie – powstanie podział za szeroki lub za
wąski

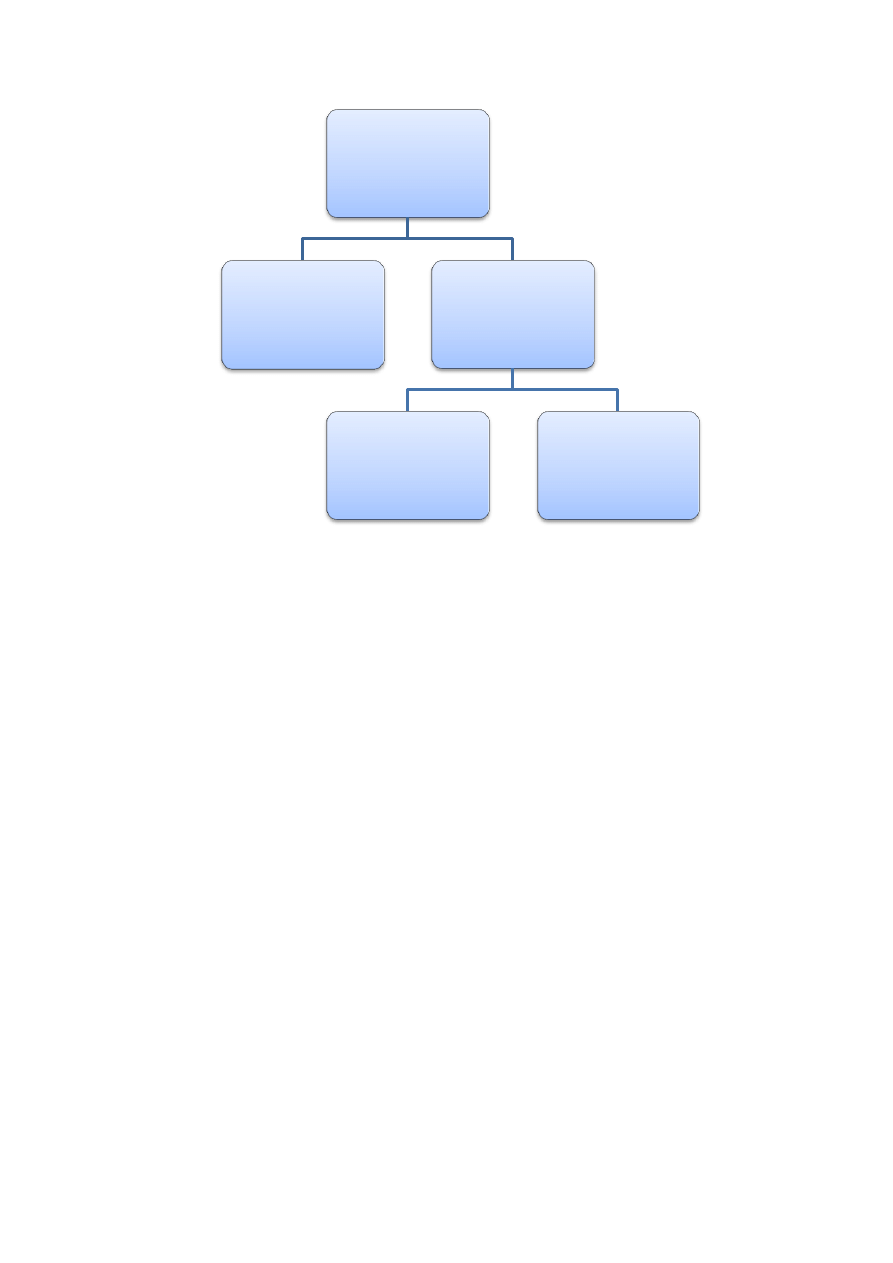
8. Przykład prawidłowego podziału logicznego:

a. podział ludzi na

i. A – osoby posiadające zdolność do czynności prawnych

ii. B – osoby posiadające ograniczoną zdolność do czynności prawnych

iii. C – osoby posiadające pełną zdolność do czynności prawnych

9. Przykład nieprawidłowego podziału logicznego:

a. podział ludzi na:

i. A – osoby, które nie ukończyły 17 lat

ii. B – osoby pełnoletnie

iii. -> nie jest zupełny – brak adekwatności(osoby które ukończyły 17 a nie mają 18??)

b. podział ludzi na:

i. A – osoba, która ukończyła 17 lat

ii. B – osoba niepełnoletnia

iii. -> brak rozłączności

c. podział ludzi na:

i. A – osoba nieletnia (do 21 rż)

ii. B – osoba pełnoletnia (powyżej 18)

iii. C – osoba posiadająca ograniczoną zdolność do czynności prawnych
iv. -> brak rozłączności i adekwatności

8

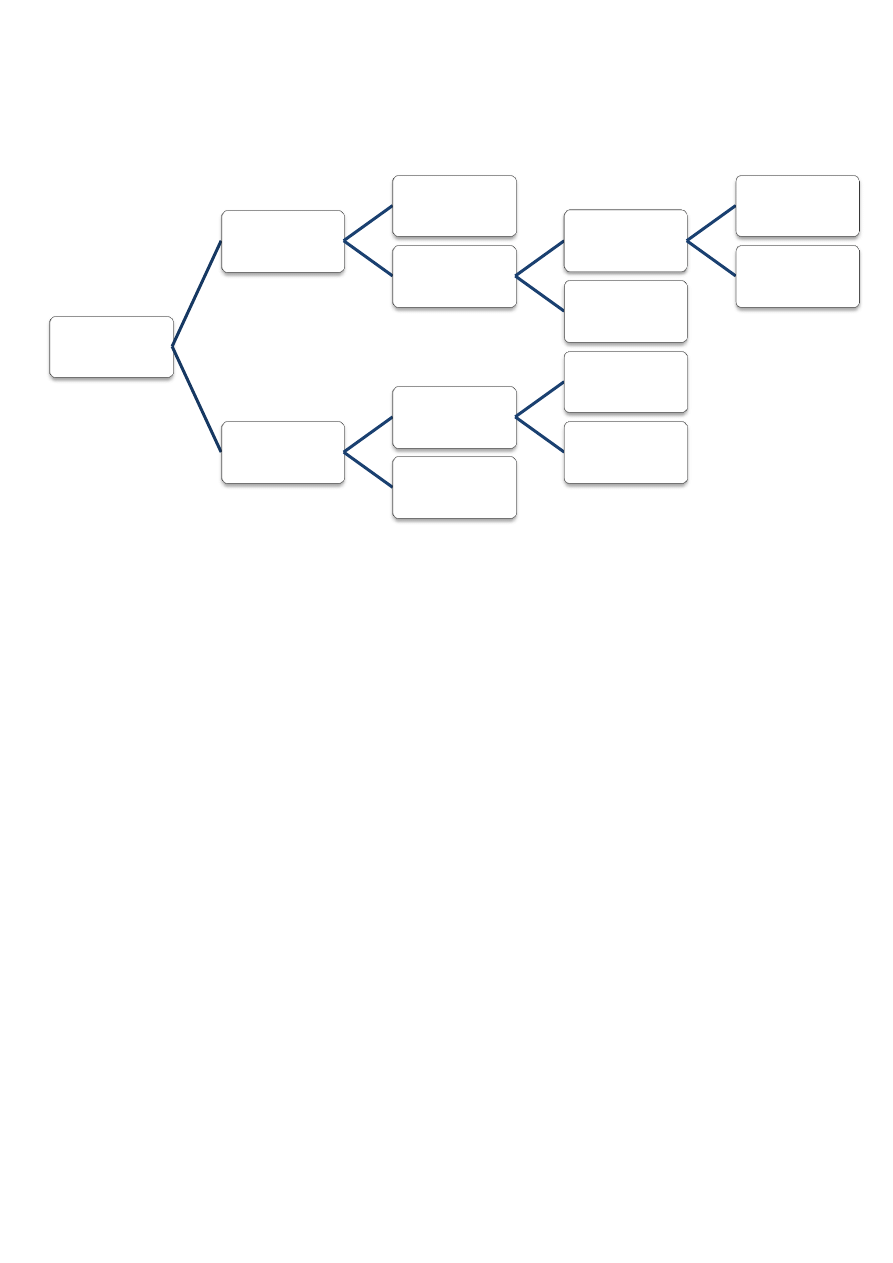
10. Przykład wielostopniowego podziału przestępstw:

1. Wypowiedź niezupełna – skróty myślowe, używana w mowie potocznej, pominięcie elementów zbędnych z

punktu widzenia zrozumiałości

2. ZDANIE I JEGO WARTOŚĆ LOGICZNA

a. zdanie jest logiczne, gdy zachowana jest kategoria syntaktyczna (zdanie prawdziwe), zdanie fałszywe,

gdy zmieniony wyraz nie należy do tej samej kategorii. Stwierdza, że taka a tak jest lub nie jest

b. Do zdań nie możemy zaliczyć wypowiedzi:

i. sugestywnych,

ii. per formatywnych,

iii. zawierającej cz. przyszły,
iv. oceniającej,

v. wyrażającej pragnienia,

vi. normy prawne,

vii. zdania pytające, wykrzyknikowe oraz wieloznaczne, (wyjątek pytania retoryczne),

3. PRAWDZIWOŚĆ ZDAŃ:

a. Kryterium moralne:

i. Zdanie prawdziwe: jeżeli wypowiedź jest zgodna z sądem wypowiadającego się,

ii. Zdanie fałszywe: jeśli wypowiedź jest niezgodna z sądem wypowiadającego się,

b. Kryterium logiczne:

i. Prawda logiczna : gdy zdanie jest zgodne ze stanem rzeczy, o którym traktuje,

c. Prawda psychologiczna:

i. Głębokie przekonanie, że podawany opis jest zgodny ze stanem rzeczy, a w rzeczywistości

opis ten nie będzie korespondował z faktycznym stanem rzeczy

d. Prawda materialna

i. Zdanie wyrażające sąd zgodny ze stanem rzeczy

przestępstwa

zbrodnie

niewykryte

wykryte

popełnione przez

osoby

niepełnoletnie

popełnione przez

osoby płci męskiej

popełnione przez

osoby płci żeńskiej

popełnione przez

osoby pełnoletnie

występki

wykryte

popełnione z winy

umyślnej

popełnione z winy

nieumyślnej

niewykryte

9

4. ZDANIA O NIEJEDNOZNACZNEJ WARTOŚCI LOGICZNEJ:

a. Wartości logiczne:

i. Prawda

ii. Fałsz,

iii. Półprawda

1. Zdania, które nie są prawdziwe ani fałszywe, może wydarzyć się to o czym mówią,

ale nie musi. Wypowiedź tego typu i ich negacja mają taką samą wartość logiczną.

5. RODZAJE ZDAŃ:

a. Zdanie proste:

i. Wypowiedź jednozdaniowa,

ii. Wyraz, z podmiotem domyślnym

iii. Zdania kategoryczne (zdanie proste, nie zawierające funktorów zdaniotwórczych od

argumentów zdaniowych)

b. Zdania złożone:

i. Składa się z co najmniej dwóch zdań,

ii. W zdaniu złożonym występują co najmniej trzy funktory zdaniotwórcze

iii. Podział zdań złożonych ze względu na struktury:

1. Zdanie atoniczne- orzekające, że jakieś indywiduum X, określona jednostka

oznaczona nazwą indywidualną, przynależy albo nie przynależy do określonej klasy

a. Podmiot- nazwa indywidualna,
b. Orzecznik- generalna

2. Zdanie subsumcyjne- orzekające, że jakaś klasa A w całości czy w części zawiera się

(lub nie) w jakiejś klasie B

3. Zdanie prawdziwe- zgodne z rzeczywistym stanem rzeczy
4. Zdanie fałszywe- przedstawiają rzeczywistość w sposób zakłamany. W syt., gdy

stwierdzamy coś, co nie ma miejsca w rzeczywistości lub zaprzeczamy czemuś, co
jest zgodne z rzeczywistością.

5. Zdanie analityczne- zdanie, którego prawdziwość jest przesądzona ze względy na

samo znaczenie użytych w nim słów; obalić nie można, chyba że zmienimy reguły
znaczeniowe danego języka.

6. Zdanie wew. kontradyktoryczne- zdanie, którego fałszywość jest przesądzona ze

względy na samo znaczenie użytych w nim słów,

7. Zdanie syntetyczne- zdania, których sposób ustalenia wartości logicznej nie wynika

ze znaczenia wyrażeń występujących w zdaniu,

iv. proces uznawania dochodzenie do prawdziwości zdania, zdania prawdziwe muszą być

racjonalne

6. Podział zdań z uwagi na kategoryczność:

a. Zdania ogólnotwierdzące: posiada strukturę odpowiadającą funkcji każde S jest P, zapisujemy jako

SaP

b. Zdania ogólnoprzeczące : o strukturze żadne S nie jest P, zapisujemy jako SeP
c. Zdania szczegółowotwierdzące: o strukturze niektóre S jest P, zapisujemy jako SiP
d. Zdanie szczegółowoprzeczące: o strukturze niektóre S nie jest P, zapisujemy jako SoP

7. Związki logiczne między zdaniami

a. Równoważność- gdy dwa zdania mają zawsze tę samą wartość logiczną
b. Wykluczanie- gdy, jedno ze zdań jest prawdziwe lub fałszywe, a drugie posiada wartość przeciwną
c. Sprzeczność- gdy, zdania są jednocześnie prawdziwe lub jednocześnie fałszywe

8. Funkcja zdaniowa

a. Funkcja nazwowa- wyraz lub wyrażenie zawierające zmienne, które po zastąpieniu zmiennych

elementami stałymi przeobrażą się w nazwę

b. Funkcja zdaniowa- nie jest zdaniem, jest wyrażeniem zawierającym zmienne, które po zastąpieniu

zmiennych elementami stałymi zamienia przeobraża się w zdanie.

9. Błędy w przekazywaniu myśli

a. Błąd ekwiwokacji- osoba w jednym rozumowaniu używa słowa wieloznacznego w różnych

znaczeniach, sądząc, że używa tego słowa jednoznacznie

10

b. Logomachia- spór słowny- dwóch ludzi spiera się o coś nie dostrzegając, że każdy z nich używa

pewnego wieloznacznego słowa w innym jego znaczeniu

c. Błąd myślenia figuralnego- branie pewnych zwrotów obrazowych w znaczeniu dosłownym
d. Błąd amfibologii- osoba wygłasza wypowiedź wieloznaczną ze względu na składnię, nie zdając sobie z

tej wieloznaczności sprawy

e. Błąd hipostazowania- pojmowanie abstraktów w sposób konkretny

Rozdział IX – Modalność wypowiedzi

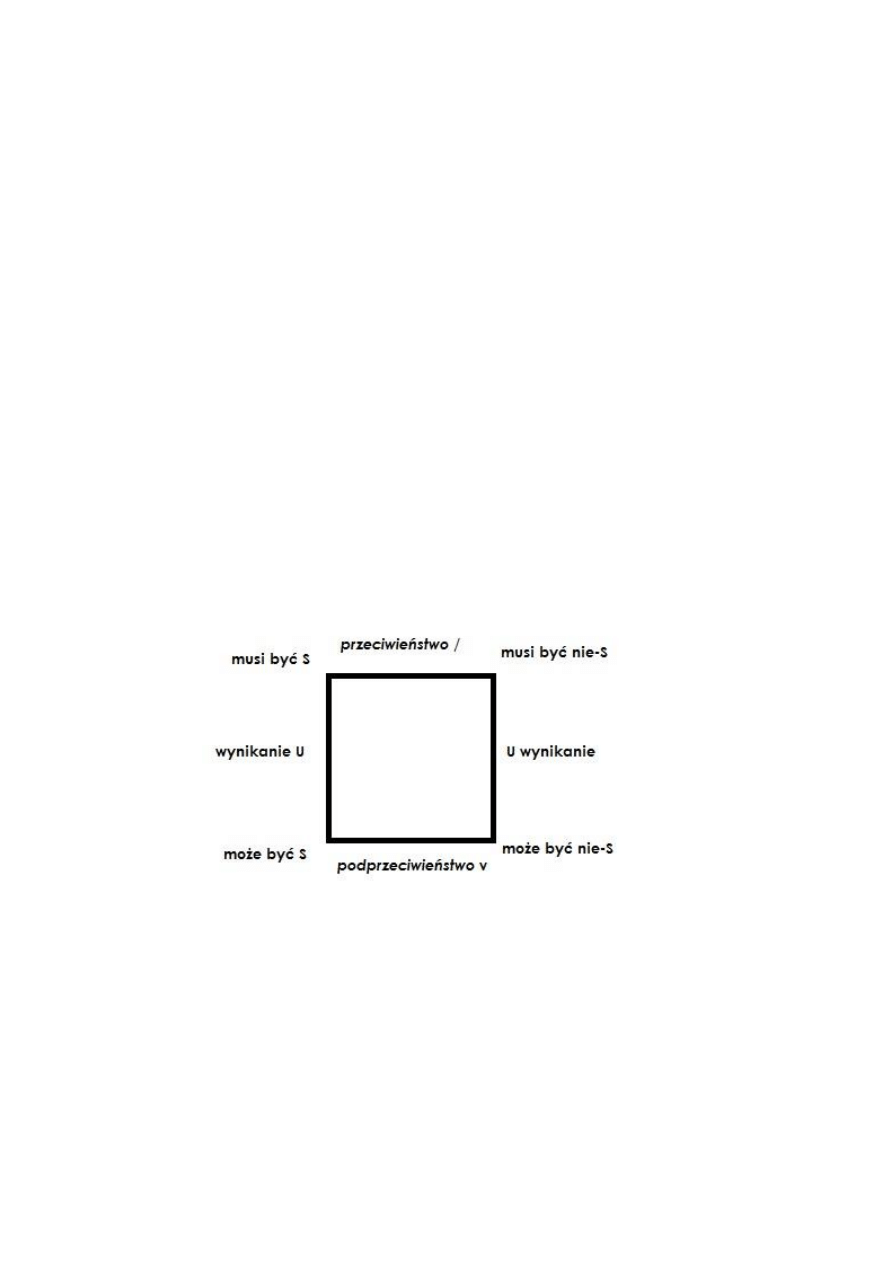
1. Podstawowe zwroty modalne:

a. musi być „s”
b. musi być „nie-s”
c. może być „s”
d. może być „nie-s”

2. Modalność zdań – odnosi się do stopnia pewności sądu, zgodności sądu z rzeczywistością. Zdania modalne

wyrażają możliwość zaistnienia czegoś w większym lub mniejszym stopniu

3. Podział zdań modalnych:

a. zdanie asertoryczne – stwierdza dany stan rzeczy nie akcentując stopnia pewności takiego stanu

i. stwierdza, że tak, a tak jest” albo „tak a tak nie jest”

b. zdanie apodyktyczne – stwierdza konieczność zaistnienia danego stanu rzeczy. Przy zdaniu

apodyktycznym akcentujemy stopień pewności danego stanu rzeczy. Stwierdzamy, że „musi być S”,
„albo musi być nie-S”. Wyrażamy sąd stanowczy, konieczny i pewny. Funktor modalny: musi

i. stwierdza, że „tak a tak być musi”

ii. np. Po zimie musi nastąpić wiosna

c. zdanie problematyczne – stwierdza możliwość zaistnienia określonego stanu rzeczy. Za pomocą tego

zdania wyrażamy stan wątpliwy i niepewny. Funktor modalny: może.

i. Gdy przewidujemy możliwość zaistnienia jakiegoś stanu rzeczy używamy zwrotu: „tak a tak

być może”. Stwierdzamy, że „może być S” albo „może być nie-S”.

ii. np. Może jutro pójdę do kina

d. * To, że tak a tak jest nie oznacza, że tak a tak być musi. => prawdziwość zdania asertorycznego nie

przesadza o wartości logicznej zdania apodyktycznego.

i. ze zdania apodyktycznego wynika zdanie asertoryczne (prawda->prawda)

4. Interpretacja wypowiedzi modalnych – biorąc pod uwagę różne znaczenia zwrotów modalnych wyróżniamy

różne interpretacje wypowiedzi modalnych:

a. interpretacja tetyczna – modalność wypowiedzi ujęta w interpretacji tetycznej zwana jest

modalnością normatywną lub deontyczną. Odwołuje się do obowiązujących norm prawnych. Z
interpretacją tą mamy do czynienia wówczas, jeżeli przy wypowiadaniu wypowiedzi modalnych
przekazywane informacje znajdują swoje odzwierciedlenie w zbiorze norm prawnych.

i. normy ze zwrotem „musi” są normami nakazującymi, narzucającymi adresatowi określony

sposób zachowania

ii. np. Treść przepisu + wypowiedź odwołująca się do informacji zawartych w przepisie

iii. modalność deontyczna – wyraża uprawnienie, obowiązek lub zakaz. Uprawnienie wyrażane

jest zazwyczaj przy użyciu funktora „może”. Normy ze zwrotem „może” wyrażają
kompetencje, dają uprawnienie do określonego zachowania.

b. interpretacja aksjologiczna – odwołuje się do określonego systemy wartości. przy interpretacji

aksjologicznej najczęściej odwołujemy się do własnych lub cudzych ocen. Uważamy, iż musimy
postąpić w określony sposób, gdyż takie zachowanie oceniamy pozytywnie.

11

i. np. Z aksjologicznego punktu widzenia musimy ustąpić w autobusie miejsca osobie

schorowanej, gdyż źle by było, gdybyśmy tego nie uczynili.

c. interpretacja logiczna – odwołuje się do schematów sprawdzonych i niezawodnych. W interpretacji

logicznej odwołujemy się do stanu naszej wiedzy.

i. np. Wiemy, że każdy sędzia musi być prawnikiem.

d. interpretacja psychologiczna – wyraża nasze przeświadczenie. W interpretacji tej uzewnętrzniamy

swoje przekonania w oparciu o to, co czujemy.

i. np. Jan sądzi, że musi się rozstać z dziewczyną.

e. interpretacja dynamiczna – kładzie nacisk na przyczynę, która wpływa na określony stan rzeczy.

Informuje ona, iż zaistnienie, albo niezaistnienie określonego stanu, spowodowane jest określoną
przyczyną.

i. użycie zwrotu musi oznacza, że istnieje jakiś czynnik, który bezapelacyjnie powoduje taki, a

nie inny stan rzeczy.

ii. z kolei zwrot może oznacza iż brak jest czynnika, który spowodowałby, że dana sytuacja jest

niemożliwa

iii. np. Drzewa liściaste muszą jesienią tracić liście

5. Wieloznaczność wypowiedzi modalnych

a. Interpretacja jednostronna – jednostronne znaczenie wypowiedzi modalnych odnosi się tylko do

wypowiedzi w jednym kierunku.

i. np. Jeżeli w telefonie komórkowym rozładowaną baterię, to telefon nie może zalogować się

do sieci. -> zwrot może użyty jest tutaj użyty w interpretacji jednostronnej

ii. przy interpretacji jednostronnej zależności pomiędzy zdaniami modalnymi układają się na

wzór kwadratu logicznego

b. Interpretacja dwustronna – przy interpretacji dwustronnej, jeżeli stwierdzimy że zdanie „może być

S” jest prawdziwe, to i zdanie „może być nie-S” musi być prawdziwe.

i. zależności między zdaniami modalnymi przy interpretacji dwustronnej przedstawia trójkąt

modalny:

12

ii. między przedstawionymi w trójkącie zdaniami modalnymi zachodzi relacja przeciwieństwa.

Prawdziwość jednego ze zdań modalnych przesądza o fałszywości pozostałych zdań
modalnych. Fałszywość natomiast zdania modalnego nie przesądza o wartości logicznej
pozostałych zdań.

iii. np. Pozwany może wnieść odpowiedź na pozew -> w interpretacji dwustronnej jest zdaniem

prawdziwym. Skoro zdanie „Pozwany może wnieść odpowiedź na pozew” jest zdaniem
prawdziwym, to pozostałe zdania muszą być fałszywe.

iv. z trzech wymienionych zdań zawsze tylko jedno zdanie jest prawdziwe

Rozdział X – Pytania i odpowiedzi

1. Pytania – są wyrażeniami zmierzającymi do uzyskania pewnych informacji. Pytania nie są zdaniami w sensie

logicznym, gdyż nie opisują rzeczywistości.

a. zredagowanie pytania -> istotne znaczenie = od niego zależy możliwość uzyskania odpowiedzi

2. Założenie pytania – twierdzenie postawione w pytaniu np. „W jakich przypadkach osoba pełnoletnia może

być ubezwłasnowolniona” = zakładamy, że istnieje możliwość ubezwłasnowolnienia

a. pozytywne – gdy wśród odpowiedzi właściwych istnieje przynajmniej jedno zdanie prawdziwe
b. negatywne – gdy wśród odpowiedzi właściwych istnieje przynajmniej jedno zdanie fałszywe

3. Pytanie właściwie postawione – pytanie, na które istnieje co najmniej 1 odpowiedź prawdziwa -> Stawiając

pytanie za punkt wyjścia, przyjmujemy wcześniej przez nas uznane stwierdzenia, które stanowią pozytywne
lub negatywne założenie pytania.

13

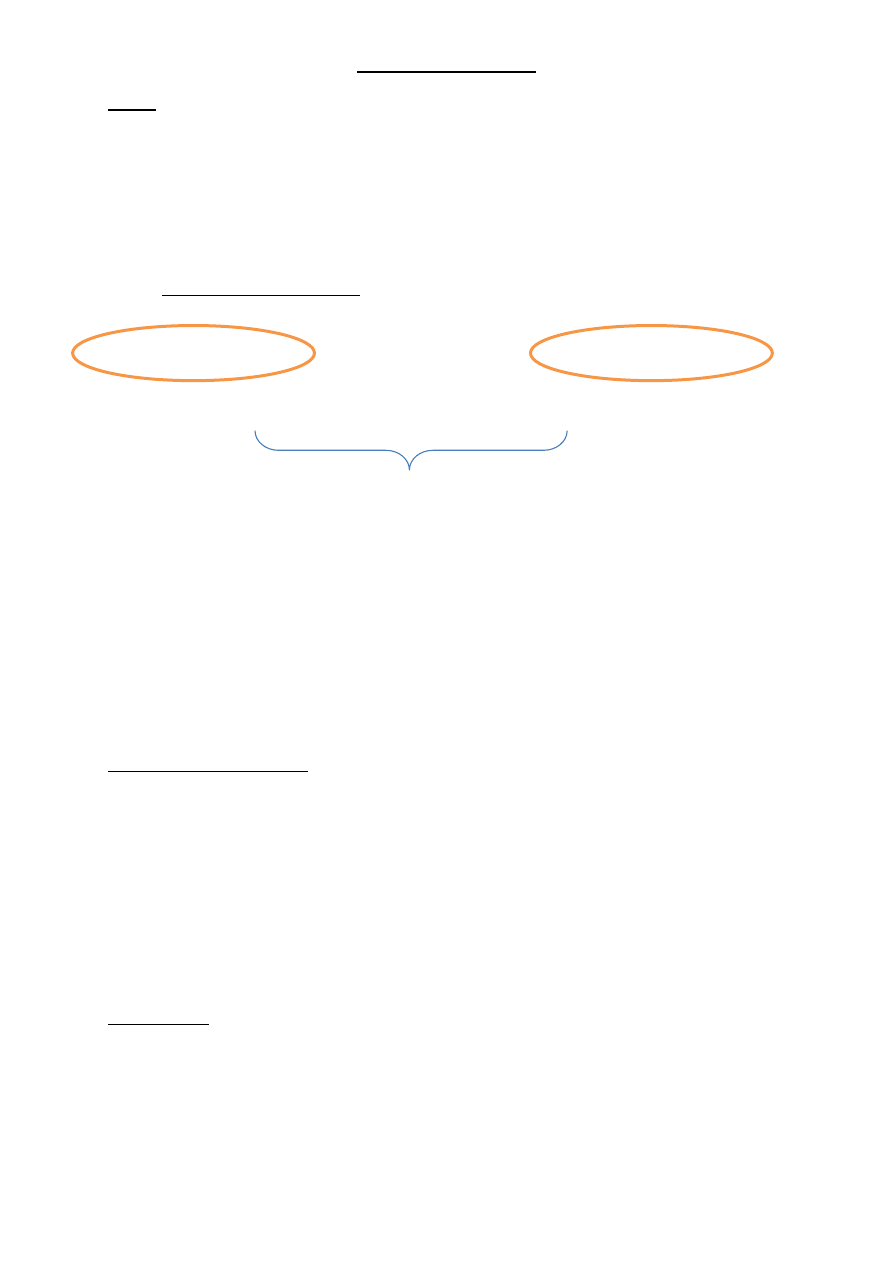
4. Podział pytań:

ze względu na

pytania

charakterystyka

przykład

liczba zapytań

pojedyncze

zawiera jedno pytanie

Kiedy wyjeżdżasz?

złożone

zawarte jest w nim kilka pytań; z uwagi na
złożoność nie zawsze są trafne

Kiedy i gdzie wyjeżdżasz?

rodzaj
oczekiwanej
odpowiedzi

otwarte

nie narzucają schematu przy udzielaniu
odpowiedzi, dają swobodę wypowiedzi
pytającemu

Dlaczego wybrałeś studia
prawnicze?

zamknięte

narzucają pewien schemat odpowiedzi i żądają,
by pytany odpowiedział na nie: „tak”, „nie”;
odmianą są pytania alternatywne – przewidują
dwie możliwości odpowiedzi – negatywną lub
pozytywną

Czy zacząłeś
przygotowywać się do
egzaminu z logiki?

możliwości
odpowiedzi

dysjunktywne

wymagają wyboru jednej z wielu wskazanych
odpowiedzi; można udzielić odpowiedzi przez
wybór tylko jednej z wielu wskazanych
odpowiedzi

Czy jesteś panną, wdową,
czy mężatką?

koniunktywne

zezwalają na dokonanie wyboru kilku z
podanych odpowiedzi; dają możliwość
udzielenia odpowiedzi pozytywnej przy
wszystkich wariantach

Czy znasz biegle język
francuski, niemiecki lub
angielski?

konstrukcja

do
rozstrzygnięcia

zaliczane są do pytań zamkniętych; wymagają
rozstrzygnięcia poprzez udzielenie odpowiedzi
potwierdzającej, albo zaprzeczającej; narzuca
określony schemat udzielenia odpowiedzi przez
usunięcie z pytania partykuły pytajnej i
potwierdzenie, albo zanegowanie, pozostałej
wypowiedzi zawartej w pytaniu: czy istnieje A

Czy na postanowienie
sądu rejonowego
oddalającego skargę na
czynności komornika
przysługuje zażalenie?

do uzupełnienia

mogą być pytaniami otwartymi lub zamkniętymi,
wymagają uzupełnienia; wybór formy zależy od
celu do jakiego dążymy; pytający ma szersze
możliwości, gdyż może, ale nie musi narzucać
określonego schematu udzielenia odpowiedzi

Jaki środek odwoławczy
przysługuje na
postanowienie sądu
rejonowego oddalającego
skargę na czynności
komornika?

5. Wybór rodzaju pytania:

a. zależy od celu do jakiego dąży pytający
b. pyt. do uzupełnienia => na początku dialogu, by zachęcić rozmówcę do rozwijania wypowiedzi i

rozmowy

c. pyt. do rozstrzygnięcia => gdy chcemy potwierdzić tezę postawioną w założeniu danego pytania lub

gdy chcemy uzyskać konkretną informację.

d. do pytań zamkniętych uciekamy się gdy dokładnie wiemy jakich informacji nam brakuje, lub chcemy

potwierdzić nasze przypuszczenia

e. odpowiedzi na pytania otwarte dostarczają najwięcej informacji i umożliwiają pytanemu swobodę

wypowiedzi

6. Pytania prawne – jeżeli przy rozpatrywaniu apelacji powstanie zagadnienie prawne budzące poważne

wątpliwości sąd może przedstawić to zagadnienie do rozstrzygnięcia Sądowi Najwyższemu, odraczając
rozpoznanie sprawy

a. pytający => chce wiedzieć jak problem prawny rozwiązać oraz dlaczego takie rozwiązanie jest

właściwe

14

b. odpowiedź => uzasadnienie każdej uchwały
c. przedmiot pytania => zagadnienie, które budzi poważne wątpliwości musi być niezbędne dla

rozstrzygnięcia konkretnej sprawy

d. przedstawione pytanie prawne będzie zgodne z nauką logiki o ile zawierać będzie właściwą tezę i

postawione zostanie w sposób jednoznaczny i zrozumiały zarówno dla osoby pytającej, jak i pytanej

e. ustawodawca szczegółowo określa treść niektórych pytań ->np. przesłuchanie świadka zaczyna się

od zapytania o imię, nazwisko etc.

f. pytania winny być właściwie postawione
g. muszą być użyteczne i istotne

7. Odpowiedzi – pytanie musi być tak postawione, by istniała na nie przynajmniej jedna właściwa odpowiedź

prawdziwa

a. odpowiedź właściwa – odpowiedź, która jest zgodna z żądaniem zawartym w pytaniu, w której

zawarte jest wyrażenie należące do zakresu niewiadomej pytania, może być albo prawdziwa albo
fałszywa. Wśród odpowiedzi właściwych na dane pytanie przynajmniej jedna odpowiedź winna być
zdaniem prawdziwym

b. odpowiedź prawdziwa – odpowiednik zdania prawdziwego
c. odpowiedź fałszywa – odpowiada zdaniu fałszywemu
d. odpowiedź niewłaściwa – nie zawiera elementu należącego do zakresu niewiadomej pytania

ze względu na

odpowiedź charakterystyka

przykład

potwierdzenie
tezy zawartej w
pytaniu

twierdząca

aprobuje tezę zawartą w
pytaniu

Czy przepis np.40 ust. 4. ustawy o drogach
publicznych może być stosowany wyłącznie w
wypadku zawinionego zajęcia pasa drogowego. =>
NSA udzielił odpowiedzi twierdzącej

przecząca

neguje tezę zawartą w
pytaniu

Czy wykładnia pojęcia dobrej wiary posiadacza
zawarta w uchwale z 1955 jest nadal aktualna => SN
udzielił odpowiedzi przeczącej

zakres
udzielonej
odpowiedzi

całkowita*

taka, z której bezpośrednio
lub pośrednio wynika
odpowiedź właściwa

częściowa

niepełna, cząstkowa,
fragmentaryczna

*całkowita (do
zakresu
odpowiedzi)

wprost

jest odpowiedzią właściwą

-Jakie Jan posiada wykształcenie?
-Jan posiada wykształcenie wyższe.

nie wprost

nie jest odpowiedzią
właściwą

- Jakie Jan posiada wykształcenie?
-Jan ukończył uniwersyteckie studia i wykonuje
zawód adwokata.

15

Rozdział XI logika – Relacje

1. Relacje – wyrażenia odzwierciedlające zależności występujące między przedmiotami, osobami, zdarzeniami,

faktami lub innymi elementami uniwersum

a. może określać zależności między jednym elementem, dwoma lub większą ilością elementów
b. najprostsza: stosunki dwuschematowe
c. przy relacji badamy jak się ma x do y oraz y do x
d. relacja pozwala określić związek zachodzący między elementami danego zbioru
e. dla prawnika: stosunki zobowiązaniowe wynikające z zawartych umów, stosunki wynikające ze

stosunku pokrewieństwa, stosunki wynikające ze stosunku pokrewieństwa etc.

f. sformalizowana postać relacji: x R y

g. dowiadujemy się, że x pozostaje w relacji do y
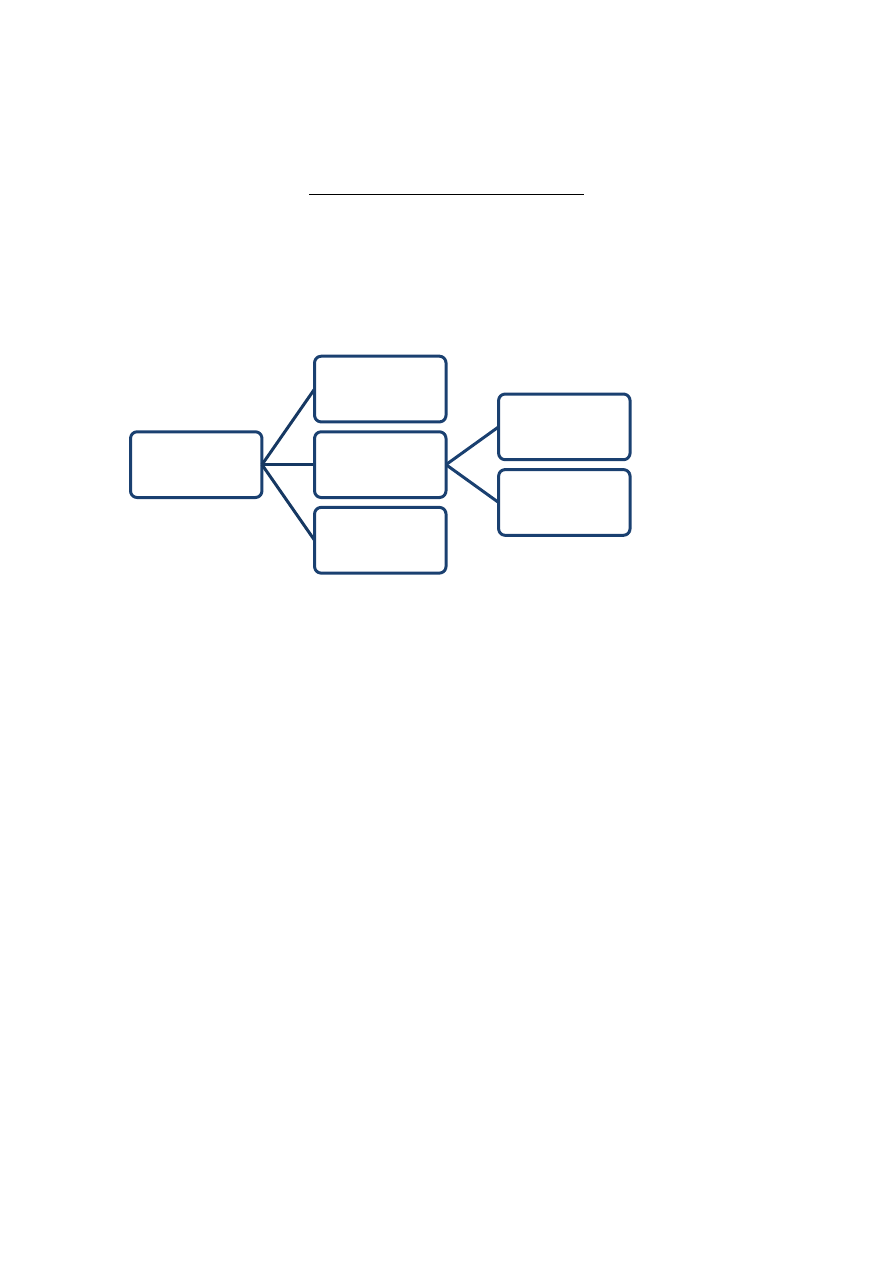
h. element x nazywamy poprzednikiem stosunku

i. w skład zbioru x wchodzą wszystkie elementy x o których jest mowa na pierwszym miejscu

w opisie relacji; zbiór wszystkich x – dziedzina

i. relację oznaczamy literą R od łacińskiego słowa relatio
j. elementy zbioru y zwane są następnikiem stosunku, gdyż w relacji mowa jest o nich na 2 miejscu

i. zbiór elementów y określamy mianem przeciwdziedziny

k. suma elementów x i y tworzy pole relacji

i. w skład pola relacji wchodzą wszystkie elementy dziedziny relacji oraz jej przeciwdziedziny

2. Konwers relacji (odwrotność)

a. relacja symetryczna – xRy zachodzi w obydwu kierunkach i jej konwers polega jedynie na zamianie

poprzednika z następnikiem yRx. Relację między dwoma elementami można analizować zatem
dwojako -> jako relacja x do y i jako relacja y do x

b. relacja odwrotna – mamy z nią do czynienia zawsze, gdy x pozostaje w relacji do

do y, to y

pozostaje w relacji

do x. I właśnie relacja

jest konwersem danej relacji

. Jeżeli zamienimy

poprzednik z następnikiem to powstaje relacja przedstawiająca zazwyczaj stosunek o innej nazwie:

i. Jeżeli x jest starszy od y, to y jest młodszy od x. => x pozostaje w relacji do y w stosunku

,

natomiast y pozostaje w relacji do x w stosunku

.

ii. ∏

3. Rodzaje relacji:

a. relacja symetryczna – zachodzi w jednym i drugim kierunku. Jeżeli x pozostaje w relacji do y, to

zawsze y pozostaje w relacji do x.

i. przykład: rówieśnictwo => Jeżeli x jest rówieśnikiem y, to y musi być rówieśnikiem

ii.

∏

iii. do relacji symetrycznej zaliczamy również stosunek zamienności, wykluczania i krzyżowania

się zakresów dwóch nazw.

Dziedzina

Przeciwdziedzina

Pole relacji

x - poprzednik

R - relacja

y - następnik

16

b. relacja asymetryczna (przeciwsymetryczna) – jeżeli zachodzi w jednym kierunku xRy, to nie może

zachodzić w drugim kierunku yRx. Jeżeli x pozostaje w jakiejś relacji do y, to nieprawdą jest, że y
pozostaje w tej samej relacji do z. Zaliczamy do niej również stosunek podrzędności lub nadrzędności
między dwoma zakresami.

i. przykład: wyższość => Jeżeli x jest wyższy od y, to nieprawdą jest, że y jest wyższy od

ii.

∏

c. relacja nonsymetryczna (niesymetryczna) – jeżeli stwierdzimy, że zachodzi w jednym kierunku xRy,

to na tej podstawie nie możemy stwierdzić, że zachodzi w drugim kierunku yRx. Jeżeli x pozostaje w
relacji do y, to nie wiadomo, czy y pozostaje w relacji do x. Relacja jest nonsymetryczna jeżeli
istnieją takie elementy pola relacji między którymi relacja ta zachodzi w obu kierunkach, jak
również istnieją i takie elementy, dla których relacja zachodzi tylko w jednym kierunku. => relacje
miłości, szacunku, znajomości to relacje nonsymetryczne

d. relacja tranzytywna (przechodnia) – taka relacja, która jeżeli zachodzi między elementami x, y, oraz

elementami y, z, to zachodzi również między elementami x, z. => jeżeli x pozostaje w relacji do y, a y
pozostaje w relacji do z, to musi również pozostawać w relacji do z. Przy relacji tranzytywnej
elementem relacji mogą być również zdania. Takim przykładem jest wynikanie, albo równoważność.

i. przykład: Jeżeli Jan zna angielski lepiej od Adama, a Adam zna angielski lepiej od Małgosi, to

znaczy, że Jan zna angielski lepiej od Małgosi.

ii.

∏

e. relacja atranzytywna (przeciwprzechodnia) – jeżeli x pozostaje w relacji do y i y pozostaje w relacji

do z, to nieprawdą jest, że x pozostaje w relacji do z.

i. przykład: Jeżeli Ala jest matką Asi, a Asia jest matką Gabrysi, to nieprawda, że Ala jest matką

Gabrysi

ii.

∏

f. relacja nontranzytywna (nieprzechodnia) – jeżeli nie zawsze między 3 elementami istnieje

przechodniość mówimy, że relacja jest nontranzytywna. Przy tej relacji na podstawie tego że x
pozostaje w relacji do y, a y pozostaje w relacji do z, nie można stwierdzić, czy x pozostaje w relacji
do z. Może być tak, że x pozostaje w relacji d→→w relacji do z.

i. przykład: zależności uczuciowe => Jeżeli x obdarza uczuciem y, a y obdarza uczuciem z, to w

oparciu o te informacje nie jesteśmy w stanie stwierdzić, czy x obdarza uczuciem z – Jeżeli
Edgar ma zaufanie do Oliwiera, a Oliwier ma zaufanie do Ernesta, to nie znaczy, że Edgar ma
zaufanie do Ernesta.

ii. ∑ [ ] ∑ [ ]

g. relacja spójna (w danym zbiorze elementów) – gdy w danym zbiorze między dwoma dowolnymi

elementami zbioru zachodzi relacja R w jednym lub w drugim kierunku. Jeżeli z danego zbioru
wybierzemy dwa dowolne elementy (x,y), to x pozostawać będzie w relacji R do y lub y pozostawać
będzie w relacji R do x. W relacji spójnej poprzednik nie może pokrywać się z następnikiem

i. przykład: W rodzinie wielodzietnej dzieci spaja stosunek starszeństwa, bo zawsze, nawet przy

bliźniakach jedno dziecko będzie starsze od drugiego, albo drugie dziecko będzie starsze od
drugiego.

ii. ∏

h. relacja przeciwspójna (akoherentna) – gdy w danym zbiorze między dwoma dowolnymi elementami

zbioru nie zachodzi relacja R w jednym, albo w drugim kierunku. Jeżeli z danego zbioru wybierzemy

17

dwa dowolne elementy (x,y), to nieprawdą jest, że albo x pozostawać będzie w relacji R do y, albo y
pozostawać będzie w relacji R do x.

i. przykład: W grupie ludzi stosunkiem aspójnym będzie tożsamość śladów linii papilarnych.

Nieprawdą jest, że x pozostawiać będzie tożsame ślady linii papilarnych co y albo y
pozostawiać będzie tożsame ślady linii papilarnych co x.

ii. ∏

i. relacja niespójna (inkoherentna) – zachodzi, gdy w danym zbiorze między dwoma dowolnymi

elementami nie zawsze istnieje relacja R w jednym, albo w drugim kierunku. Jeżeli z danego zbioru
wybierzemy dwa dowolne elementy (x,y) to może się tak zdarzyć, że x pozostawać będzie w relacji R
do y albo y pozostawać będzie w relacji R do x, a może i to być nieprawdą. W relacji nonspójnej
istnieją takie dwa elementy, które są spójne, ale również istnieją i takie, które nie są spójne.

i. przykład: Jeżeli weźmiemy relację starszeństwa wśród ludzi, to okaże się, że istnieje taki

człowiek, który jest starszy od innego człowieka, ale istnieje również taka para osób, o której
nie możemy powiedzieć, że jeden człowiek jest starszy od drugiego.

ii. ∑ ∑ ∑ [ ]

j. relacja zwrotna – relacja w danym zbiorze jest zwrotna, jeżeli zachodzi między każdym elementem

tego zbioru, a nim samym. W relacji zwrotnej każdy element pola relacji pozostaje sam do siebie w
relacji R

i. przykład: Każdy człowiek jest własnym imiennikiem. Każda prosta jest równa samej sobie.

ii. ∏

k. relacja przeciwzwrotna (azwrotna) – relacja, która nie zachodzi między żadnym elementem a nim

samym. W danym zbiorze żaden element nie pozostaje w relacji z samym sobą.

i. przykład: W zbiorze ludzi – relacja wyższości. Żaden człowiek nie może być wyższy od siebie

samego.

ii. ∏

l. relacja nonzwrotna (niezwrotna) – w tej relacji istnieje element pola relacji, który pozostaje w relacji

R do siebie samego i istnieje taki element, który nie pozostaje w relacji R do siebie samego.

i. przykład: W grupie ludzi istnieje taka osoba, która jest wymagająca wobec siebie samego i

istnieje taka osoba, która nie jest wymagająca wobec siebie samego.

ii. ∑ ∑

4. Mnożenie relacji

a. relacja porządkująca – wprowadza w określonym zbiorze porządek wśród elementów przypisując

każdemu elementowi w zbiorze ściśle określone miejsce. Dzięki temu możemy ustawić elementy
danego zbioru w jeden szereg. By każdy element zbioru posiadał ściśle określone miejsce, relacja ta
winna się charakteryzować:

i. spójnością – musi zachodzić między dowolnie wybranymi elementami zbioru w jednym, albo

w drugim kierunku

ii. asymetrycznością – nie może ona zachodzić w jednym i w drugim kierunku

iii. przechodniością – jeżeli weźmiemy trzy elementy, to o ile x pozostaje w relacji do y, a y

pozostaje w relacji do z, to x musi również pozostawać w relacji do z

b. relacja równościowa – kieruje się równym, jednakowym doborem elementów. Pozwala np.

zgrupować w danym zbiorze ludzi równych wiekiem, czy zatrudnionych na równorzędnych
stanowiskach. Relacja równościowa musi być zarazem:

18

i. zwrotna

ii. symetryczna

iii. przechodnia

Rozdział XII – Funktory prawdziwościowe

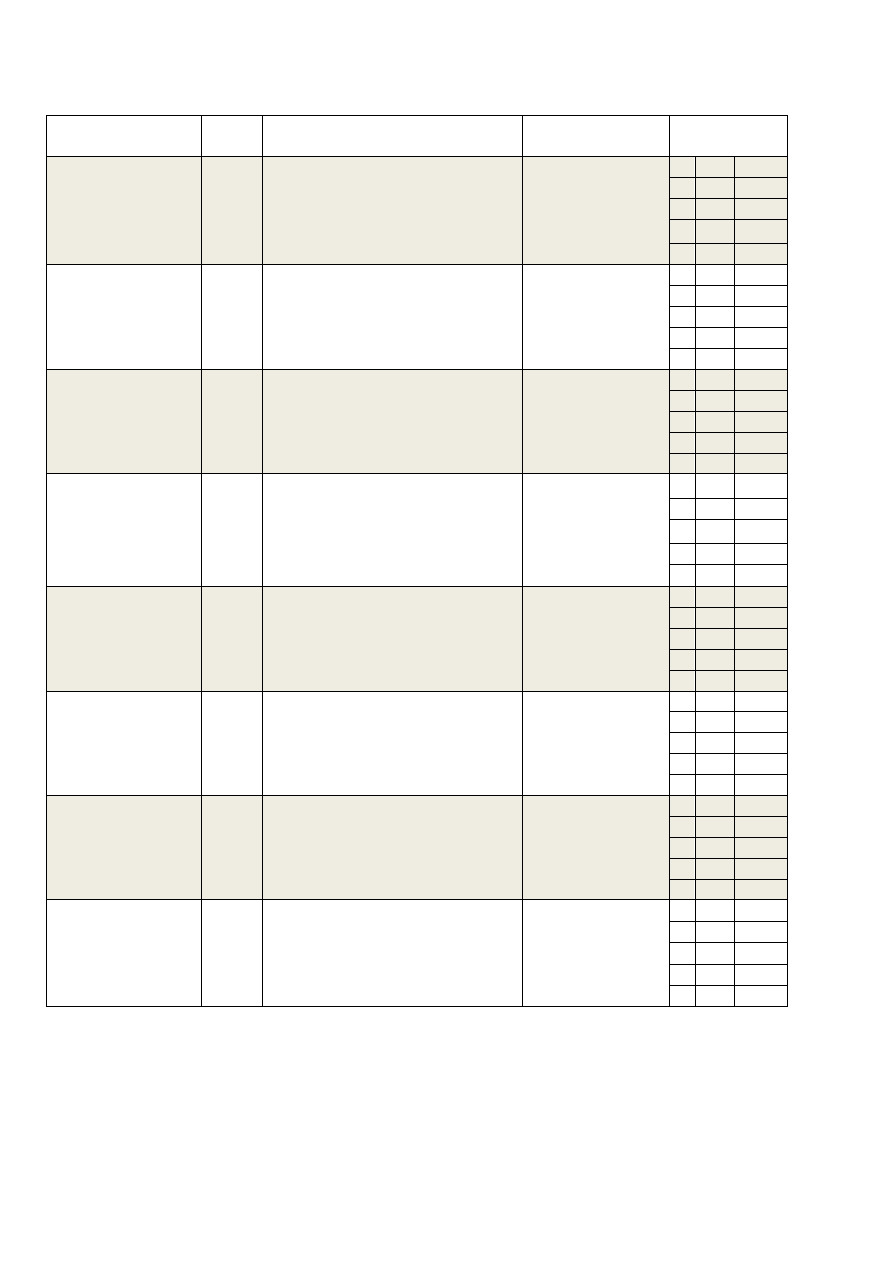
1. Funktor prawdziwościowy – jest funktorem zdaniotwórczym od argumentów zdaniowych. Funktor

zdaniotwórczy = łącznik, za pomocą którego z danych zdań tworzy się nowe zdanie. Funktor
prawdziwościowy pozwala określić wartość logiczną z uwagi na swoją konstrukcję.

2. Wartość logiczna zdania złożonego – uzależniona jest od rodzaju spójnika prawdziwościowego i od wartości

logicznej poszczególnych zdań składowych.

3. Funktor prawdziwościowy – może być jedno albo wieloargumentowy.

a. afirmacja (potwierdza prawdę) – przykład funktora ednoargumentowego; jest potwierdzeniem

istniejącej wartości logicznej zdania p. Funktorem jest: „prawdą jest, że”

i. Każdy adwokat jest prawnikiem = Prawdą, że każdy adwokat jest prawnikiem

b. negacja czyli przeczenie -> negacja zdania p = zaprzeczenie zdania p. Funktorem jest „nieprawda, że

p”. Zawsze ma wartość logiczną sprzeczną do tej jaką miało zdanie wyjściowe.

i. sprzeczne: Każde S są P i Niektóre S są P

ii. negacja zdania: Każde S są P = Niektóre S nie są P, co zapisujemy:

1.
2.

iii. zdanie: „Każdy radca prawny jest prawnikiem” ma taką samą wartość logiczną jak

„Nieprawda, że niektórzy radcowie prawni nie są prawnikami”

funktory

nazwotwórcze od

argumentów

nazwowych

zdaniotwórcze

od argumentów

nazwowych

od argumentów

zdaniowych

funktorotwórcze

od argumentów

funktorowych

19

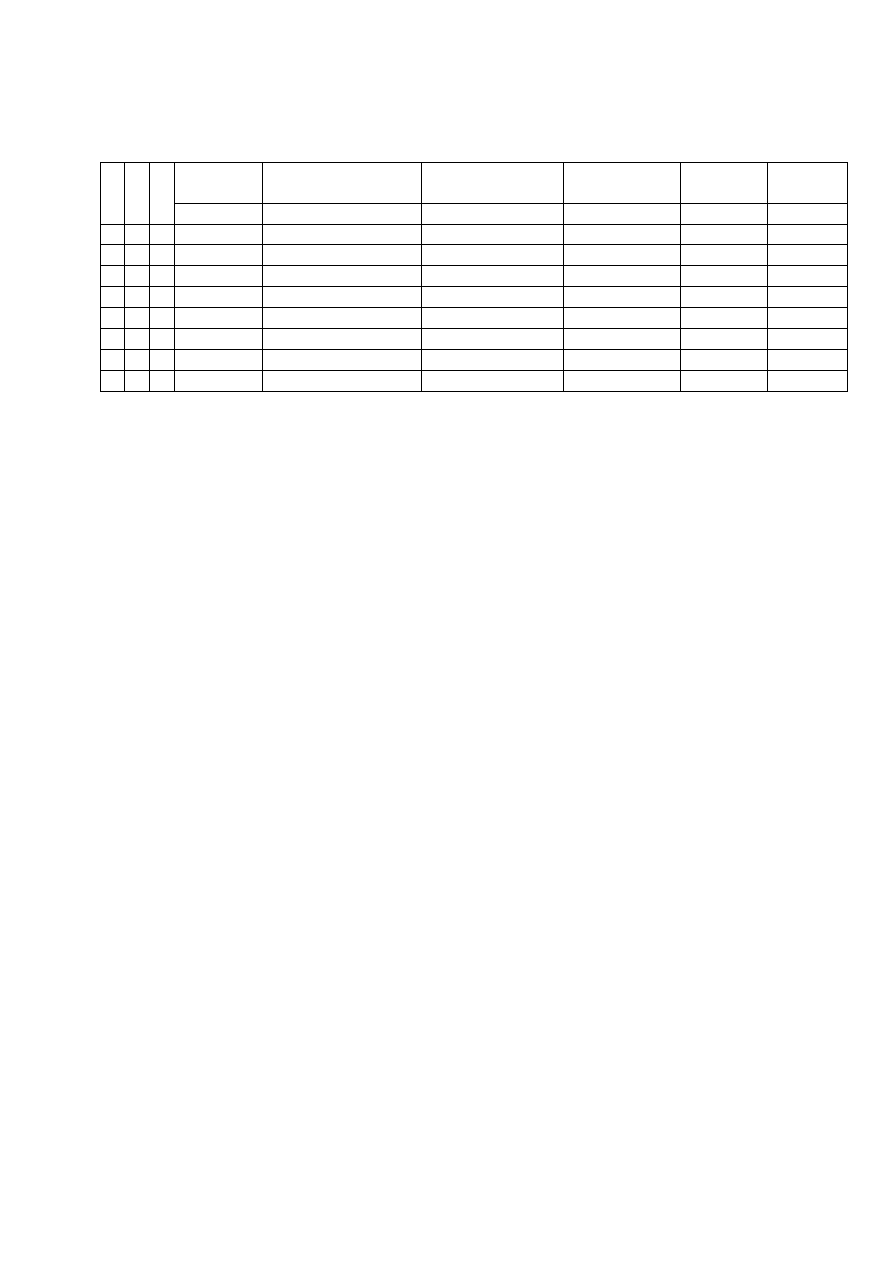
4. Funktory prawdziwościowe:

funktor

zapis

wykładniki
leksykalne

matryca

koniunkcja

p ˄ q

jest prawdziwa wtedy i tylko wtedy,
gdy wszystkie zdania składowe (p,q)
są prawdziwe

i, oraz, lecz, a, a
także, jak również,
pomimo że,
chociaż

p q

p ˄ q

1 1

1

1 0

0

0 1

0

0 0

0

alternatywa

p V q

jest prawdziwa wtedy i tylko wtedy,
gdy przynajmniej jedno ze zdań
składowych jest prawdziwe

lub, bądź, albo

p q

p V q

1 1

1

1 0

1

0 1

1

0 0

0

alternatywa
rozłączna

p q

jest prawdziwa wtedy i tylko wtedy,
gdy jedno i tylko jedno ze zdań
składowych jest prawdziwe

p bądź q

p q

p q

1 1

0

1 0

1

0 1

1

0 0

0

implikacja zwykła
(ekstensywna)

p→q

implikacja jest tylko w jednym
przypadku fałszywa – gdy jej
poprzednik p jest prawdziwy, a
następnik q fałszywy

jeżeli … to …

p q

p→q

1 1

1

1 0

0

0 1

1

0 0

1

implikacja odwrotna
(intensywna)

p←q

implikacja odwrotna jest tylko w
jednym przypadku fałszywa, gdy jej
poprzednik p jest fałszywy, a
następnik q prawdziwy

tylko wtedy … gdy
…

p q

p←q

1 1

1

1 0

1

0 1

0

0 0

1

implikacja wzajemna
(równoważność)

p↔q

równoważność jest prawdziwa
wtedy i tylko wtedy, gdy wszystkie
zdania składowe

zawsze wtedy i
tylko wtedy

p q

p↔q

1 1

1

1 0

0

0 1

0

0 0

1

dysjunkcja (negacja
koniunkcji

p/q

dysjunkcja jest tylko w jednym
przypadku fałszywa, gdy wszystkie
zdania składowe są prawdziwe

co najwyżej p lub q

p q

p/q

1 1

0

1 0

1

0 1

1

0 0

1

binegacja (negacja
alternatywy)

p↓q

binegacja jest prawdziwa wtedy i
tylko wtedy, gdy wszystkie zdania
składowe są fałszywe

ani p ani q

p q

p↓q

1 1

0

1 0

0

0 1

0

0 0

1

5. Inne funktory prawdziwościowe:

a. Co najwyżej p a nie q -> jest prawdziwe wtedy gdy wszystkie zdania składowe są fałszywe, oraz gdy p

jest prawdziwe, a q fałszywe.

i. np. Co najwyżej pójdę do lekarza a nie pójdę do szpitala

20

b. P bez względu na to czy q -> prawdziwość tej wypowiedzi uzależniona jest od prawdziwości zdania p.

Wartość logiczna zdania q nie wpływa na wartość logiczną całej wypowiedzi

i. np. Pójdę do kina bez względu na to czy będzie ładna pogoda.

6. Funktory trójargumentowe:

p q r

koniunkcja

alternatywa

nierozłączna

alternatywa

rozłączna

równoważność dysjunkcja binegacja

p q r

p q r

p q r

p q ↔ r

p / q / r

p ↓ q ↓ r

1 1 1

1

1

0

1

0

0

1 0 0

0

1

1

0

1

0

0 1 0

0

1

1

0

1

0

0 0 1

1

1

1

0

1

0

1 1 0

0

1

0

0

1

0

0 1 1

1

1

0

0

1

0

1 0 1

1

1

0

0

1

0

0 0 0

0

0

0

1

1

1

7. Funktory nieprawdziwościowe – nieprawdziwościowe nie pozwalają określić wartości logicznej danego

zdania. Funktorem nieprawdziwościowym jest każdy łącznik za pomocą którego z danych zdań tworzy się
nowe zdanie, a który to łącznik nie pozwala określić wartości logicznej zdania uzyskanego.

a. np. zwroty: „musi być tak, że”, „prawdopodobnie jest tak, że”, „możliwe jest, że”

8. Wynikanie:

a. zachodzi wówczas, gdy mamy do czynienia z prawdziwą implikacją i między tym co głosi poprzednik,

a tym co głosi następnik, zachodzi jakiś związek

b. np. ze zdania: „Każdy adwokat jest prawnikiem” wynika „Niektórzy prawnicy są adwokatami”
c. jeżeli ze zdania „p” wynika zdanie „q” to zdanie „p” jest racją, a zdanie „q” następstwem
d. przy wynikaniu prawdziwość zdania p przesądza o prawdziwości zdania q
e. fałszywość racji nie przesądza o wartości logicznej następstwa
f. fałszywość następstwa przesądza o fałszywości racji

9. Przy wynikaniu zdania muszą być powiązane ze sobą treściowo lub strukturalnie – musi istnieć między nimi

związek. Wyróżniamy kilka rodzajów takich związków:

a. tetyczny – wynika z ustanowienia norm prawnych -> mogą to być normy powszechnie ustanowione

przez normodawcę drogą aktów prawnych lub inne normy obowiązujące z czyjegoś ustanowienia,
które nie mają swojego odzwierciedlenia w żadnym powszechnie obowiązującym akcie prawnym.

b. analityczny – wynika z treści użytych słów. Przykładem zdania łączącego inne zdania związkiem

analitycznym może być wypowiedź: Jeżeli coś jest kwadratem, to musi być czworokątem o kątach i
bokach równych. Powiązanie treściowe wypowiedzi z uwagi na znaczenie użytych w zdaniu słów jest
tak oczywiste, jak prawda w zdaniu analitycznym.

c. logiczny – jeżeli daną implikację materialną przeobrazimy w implikację formalną a uzyskany wzór

będzie niezawodny dla wszystkich zmiennych to zdania takiej implikacji materialnej niewątpliwie
łączy związek logiczny

i. np. Jeżeli Jan jest starszy od Piotra, a Piotr starszy od Adama, to Jan jest starszy od Adama.

d. strukturalny – stanowi powiązanie między racją a następstwem. Ze związkiem tym mamy do

czynienia wówczas, gdy zależność, o której mowa w wypowiedzi, wynika z rozmieszczenia zdarzeń
lub przedmiotów w czasie lub w przestrzeni w sposób właściwy dla danego systemu.

i. np. Skoro za plecami mam południe, to przed sobą muszę mieć północ.

e. przyczynowy – zachodzi między dwoma zdaniami, jeżeli w jednym zdaniu mowa jest o przyczynie, a

w drugim o skutku. Z tego też względu zwany jest on również związkiem przyczynowo – skutkowym.

21

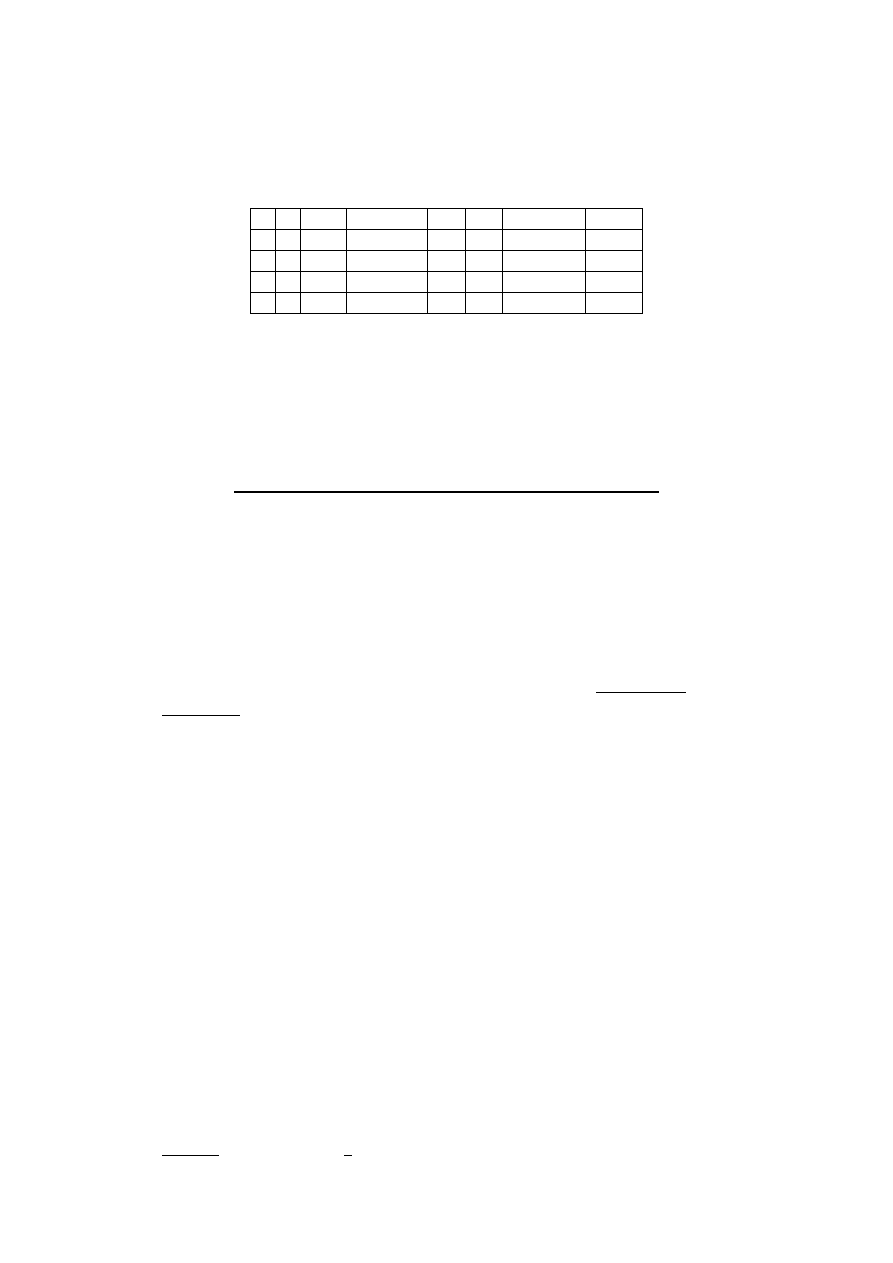
Rozdział XIII – Prawa rachunku zdań

1. Tautologia – rozumowanie niezawodne – jeżeli w schemacie zdania złożonego niezależnie od wartości

logicznych zdań składowych otrzymujemy zawsze zdanie prawdziwe. Tautologia rachunku zdań stanowi
pewien schemat. Klasyczny rachunek zdań opiera się na logice dwuwartościowej stąd nazywany jest
dwuwartościowym rachunkiem zdań

2. W logice dwuwartościowej przyjmuje się tylko dwie wartości logiczne – każde zdanie jest albo fałszywe, albo

prawdziwe:

a. zasada tożsamości – głosi, że ze zdania p zawsze wynika zdanie p. Jeżeli wykazano prawdziwość

zdania p, to zdanie to może posłużyć jako racja innego wnioskowania.

b. zasada wyłączonego środka - dotyczy zdań względem siebie sprzecznych. Głosi, że prawdziwe jest

zdanie, albo jego zaprzeczenie. Dwa zdania względem siebie sprzeczne nie mogą być jednocześnie
fałszywe

c. zasada sprzeczności –głosi, że dwa zdania względem siebie sprzeczne nie mogą być jednocześnie

prawdziwe

d. zasada podwójnego przeczenia – negacja negacji dowolnego zdania nie zmienia wartości logicznej

zdania wyjściowego. Jeżeli zanegujemy podwójnie jakieś zdanie, to jego wartość logiczna nie ulegnie
zmianie.

PIERWSZE PRAWO DE MORGANA



(p ˄ q)



(



p v



q)

nie jest tak, że zarazem p i q więc:

nie jest tak że p lub nie jest tak że q

DRUGIE PRAWO DE MORGANA



(p v q)



(



p ˄



q)

nie jest tak że p lub q więc: nie jest

tak że p i nie jest tak że q

PRAWO NEGACJI IMPLIKACJI



(p



q)



(p





q)

nie jest tak, że jeżeli p to q więc:

jeżeli p to nie jest tak że q

PRAWO TRANSPOZYCJI

(p



q) ↔ (



q





p)

jeżeli p to q więc: jeżeli nie jest tak

że q to nie jest tak że p

PRAWO SYLOGIZMU
HIPOTETYCZNEGO

[(p



q) ˄ (q



r)]



(p



r)

jeżeli p to q i jeżeli q to r więc jeżeli p

to r

MODUS PONENDO PONENS

[(p



q) ˄ p]



q

jeżeli p to q i p więc: q

MODUS TOLLENDO TOLLENS

[(p



q) ˄



q]





p

jeżeli p to q i nie jest tak że q więc:

nie jest tak że p

MODUS TOLLENDO PONENS

[(p v q) ˄



p]



q

p lub q i nie jest tak że p więc q

MODUS PONENDO TOLLENS

[(p/q) ˄ p]





q

bądź p bądź q i p więc: nie jest tak że

q

PRAWO EKSPORTACJI

[(p ˄ q)



r] ↔ [p



(q



r)]

jeżeli zarazem p i q to r więc: jeżeli p

to jeśli q to r (eksportacja)

PRAWO IMPORTACJI

[p



(q



r)]



[(p˄q)



r]

jeżeli p to jeśli q to r więc: jeżeli

zarazem p i q to r

PRAWO DYLEMATU
KONSTRUKCYJNEGO PROSTEGO

[(p



r) ˄ (r



q) ˄ (p v r)]



q

zarazem jeżeli p to r i jeżeli r to q i p

lub r więc q

PRAWO DYLEMATU
KONSTRUKCYJNEGO ZŁOŻONEGO

[(p



q) ˄ (r



s) ˄ (p v r)]



(q v s)

zarazem jeżeli p to q i jeżeli r to s i p

lub r więc q lub s

22

3. Metody badania funkcji logicznych

a. znajomość matryc funktorów prawdziwościowych pozwala nam sprawdzić, czy faktycznie funkcja

logiczna przybiera wartość prawdy bez względu na wartość logiczną zdań składowych. Najprostszy
sposób – metoda matrycowa (podstawianie pod zmienne zdaniowe wartości logicznych jakie mogą
przybierać poszczególne zdania składowe.

b. matryca funkcji zdaniowej o postaci:

⋁ ⋁

p q

⋁ całość

1 1

1

0

0

0

0

1

1 0

1

0

0

1

1

0

0 1

1

0

1

0

1

0

0 0

0

1

1

1

1

1

c. z powyższej matrycy wynika, że we wszystkich podstawieniach nie uzyskujemy zdania prawdziwego -

> taka funkcja zdaniowa nie sięga do rangi prawa logicznego, gdyż rozumowanie oparte na takim
schemacie nie jest rozumowaniem niezawodnym.

Logika rozdział XIV – Rozumowania na zdaniach kategorycznych

1. Zdania kategoryczne – zdanie proste w odpowiedni sposób uformowane. Uformowanie to polega na

nadaniu zdaniu postaci

a. podmiotowo-orzecznikowej – zdanie takie musi być zbudowane z 2 nazw: prostych lub złożonych,

oraz funktora zdaniotwórczego od 2 argumentów nazwowych. Argumenty = nazwa spełniająca rolę
podmiotu, oraz nazwa tworząca orzecznik.

i. nazwy powinny wystąpić w postaci terminów (konotacja i denotacja powinny być

sprecyzowane)

b. jakościowej – zdanie kategoryczne może być tylko albo zdaniem twierdzącym, albo zdaniem

przeczącym.

c. ilościowej – na skutek takich operacji logicznych przyjmuje się, że zdanie kategoryczne może być

tylko albo zdaniem ogólnym, albo zdaniem szczegółowym.

i. za zdanie ogólne uważa się zdanie, w którym treść orzecznika odnosi się do wszystkich

desygnatów nazwy pełniącej rolę podmiotu

ii. za zdanie szczegółowe należy uznać każde zdanie, w którym treść orzecznika odnosi się

przynajmniej do części desygnatów podmiotu, ale nie jest gwarantowane, że do wszystkich.

d. *sformalizowany zapis zdań kategorycznych polega na oznaczeniu odpowiednimi symbolami nazw:

i. nazwa pełniąca rolę podmiotu to S (subiectum)

ii. nazwa tworząca orzecznik to P (praedictum)

iii. samogłoski a i e -> zdania ogólne
iv. samogłoski i i o -> zdania szczegółowe

2. Zdania kategoryczne mają postać zdań

a. ogólnotwierdzącego SaP

->

Każde S jest P

b. szczegółowotwierdzącego SiP

->

Niektóre S jest P

c. ogólnoprzeczącego SeP

->

Żadne S nie jest P

d. szczegółowoprzeczącego SoP

->

Niektóre S nie jest P

3. Termin rozłożony – termin, do którego wszystkich desygnatów odnosi się treść drugiego terminu

a. w zdaniu ogólnotwierdzącym za rozłożony należy uważać termin pełniący rolę podmiotu -> Każdy

człowiek jest śmiertelny => SaP

23

b. w zdaniu ogólnoprzeczącym za rozłożone uważa się obydwa terminy -> Żaden pijak nie jest dobrym

pracownikiem => SoP

c. w zdaniu szczegółowoprzeczącym za rozłożony należy uważać termin tworzący orzecznik => SoP
d. w zdaniu szczegółowotwierdzącym żaden termin nie jest wzięty w całym swym zakresie, a zatem

żaden termin nie jest rozłożony => SiP

4. Rozumowania bezpośrednie przez dodanie funktorów:

a. rozumowanie przez dodawanie cech determinujących – polega na dodawaniu funktorów do nazw, z

których zbudowane zostało zdanie

b. tworzenie pojęć złożonych – polega na wykorzystaniu podmiotu i orzecznika, jako funktorów, przy

użyciu których powstają nazwy złożone, lub jeszcze bardziej złożone

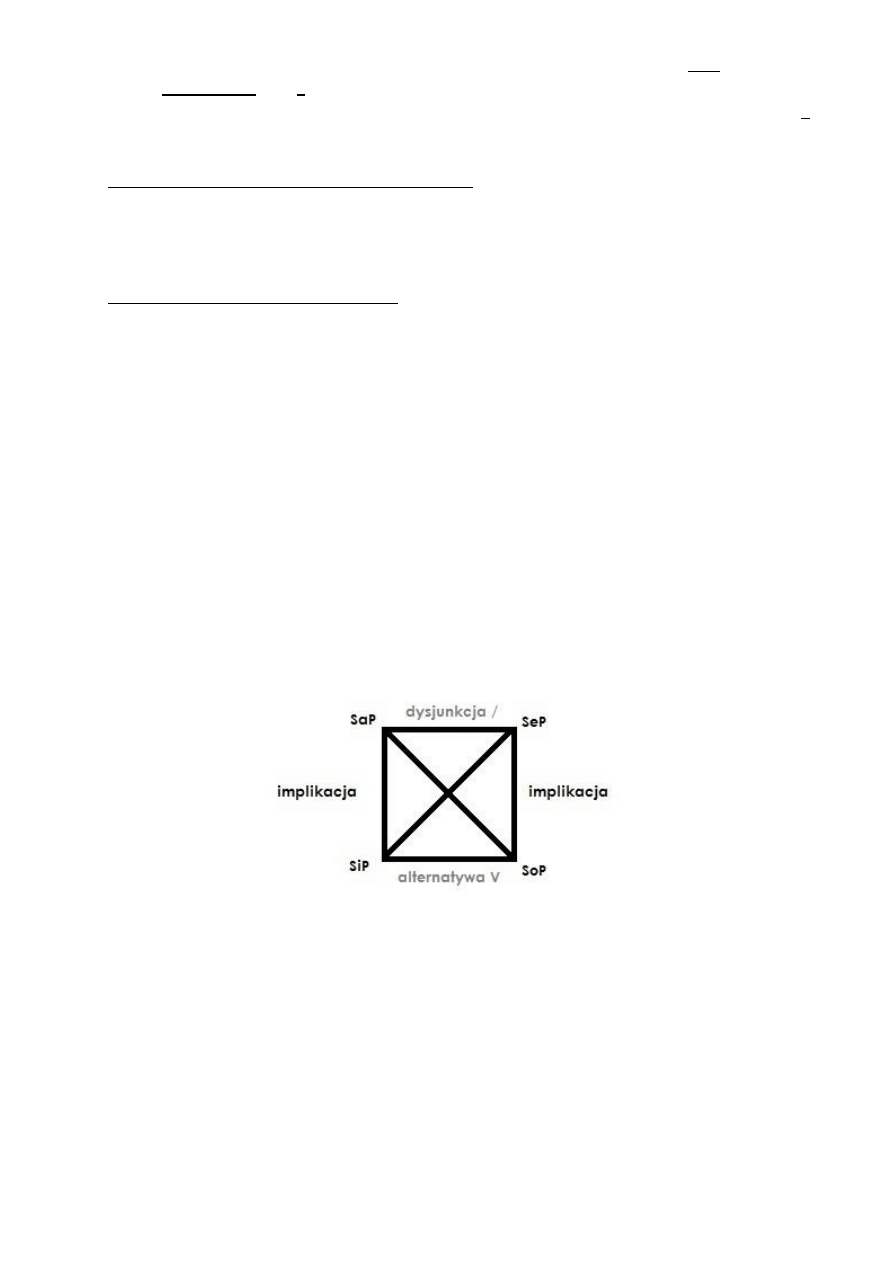
5. Rozumowania z opozycji (kwadrat logiczny) – ważniejsze, niezawodne; odwołujące się do zależności

mogących zachodzić między poszczególnymi typami zdań kategorycznych i do własności funktorów od
argumentów zdaniowych (prawdziwościowych). Stosunki te, to:

a. stosunek przeciwieństwa, zachodzący między różniącymi się jakością zdaniami ogólnymi (SaP – SeP).

Stosunek ten można wyrazić połączywszy te zdania funktorem dysjunkcji

b. stosunek podprzeciwieństwa zachodzący między różniącymi się jakością zdaniami szczegółowymi SiP

– SoP. Można wyrazić połączywszy te zdania funktorem alternatywy zwykłej bo zdania te dopełniają
się, a nie wykluczają

c. stosunek nadrzędności zachodzący miedzy zdaniami tej samej jakości, ale o odmiennej postaci

ilościowej (SaP – SiP), (SeP – SoP). Stosunek ten zazwyczaj wyraża się przez połączenie tych zdań
funktorem implikacji zwykłej, w której za poprzednik służy wtedy odpowiednie zdanie ogólne

d. stosunek sprzeczności, zachodzący między zdaniami różniącymi się zarazem jakością i ilością (SaP –

SoP), (SeP – SiP). Stosunek ten można wyrazić posłużywszy się funktorem alternatywy rozłącznej, bo
zdania te wykluczają się i dopełniają.

6. Zależności można wyrazić budując KWADRAT LOGICZNY

7. Rozumowanie z opozycji – znając wartość logiczną któregoś ze zdań kategorycznych i będąc świadomym

zależności między poszczególnymi typami zdań, można podjąć próbę ustalenia wartości logicznej pozostałych
zdań przeprowadzając rozumowanie z opozycji:

a. Jeżeli prawdziwym jest zdanie SaP, wówczas:

i. fałszywe – SeP

-> dysjunkcja

ii. fałszywe – SoP

-> alternatywa

iii. prawdziwe – SiP

-> implikacja

b. Jeżeli prawdziwym jest zdanie SeP -> SaP, SiP – fałszywe, SoP – prawdziwe

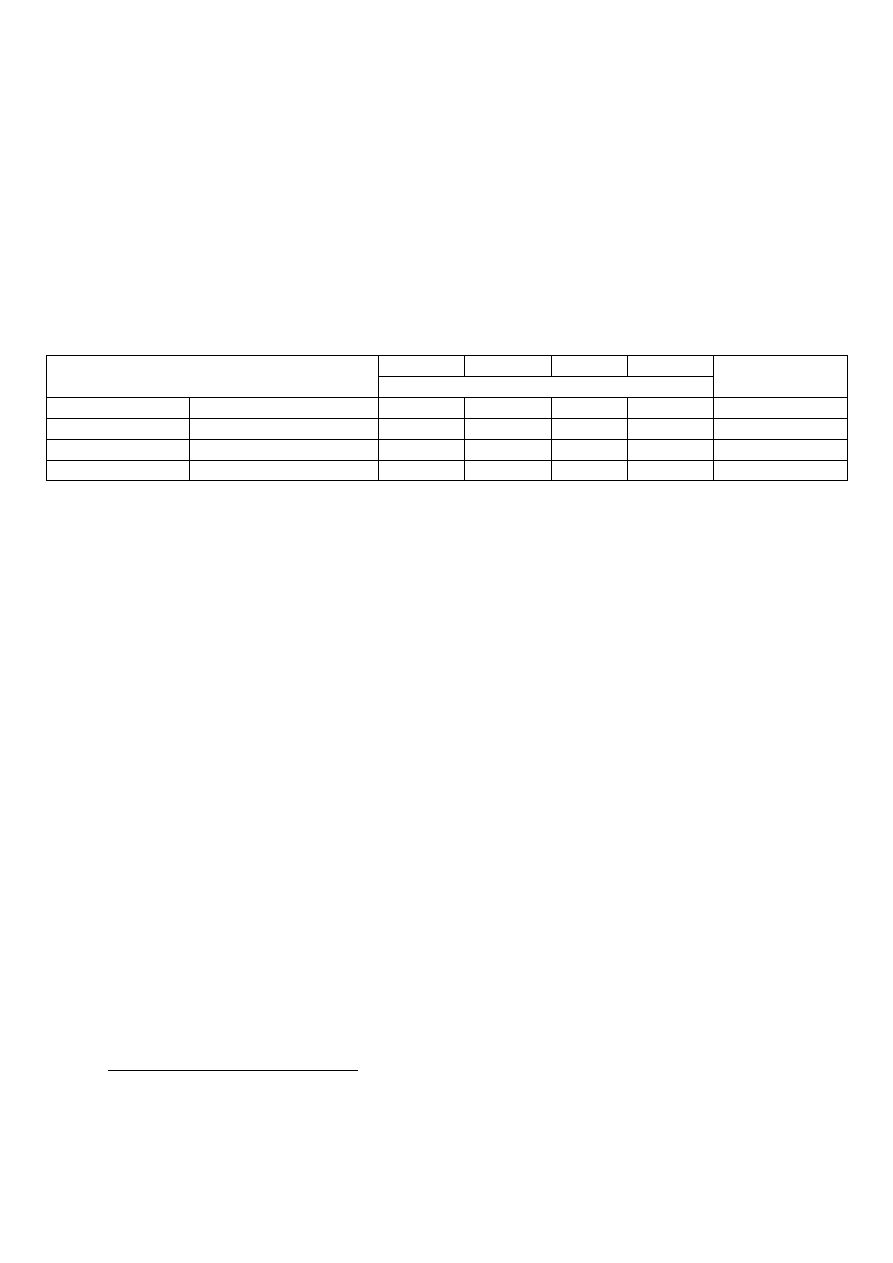
24

c. Jeżeli za punkt wyjścia przyjmiemy założenie o fałszywości któregoś ze zdań ogólnych, wówczas

możemy ustalić tylko wartość (fakt prawdziwości) zdania szczegółowego, które jest sprzeczne wobec
zdania wyjściowego

d. non sequitur – błąd następnika -> jeżeli podejmiemy próbę wskazania wartości logicznej innego ze

zdań, wówczas popadniemy w ten błąd

e. Przyjmując za punkt wyjścia założenie o fałszywości zdania SoP

i. SiP – prawdziwe

ii. SaP – prawdziwe

iii. SeP – fałszywe

f. SiP – fałszywa

i. SeP, SoP – prawdziwe

ii. SaP – fałszywe

Prawdziwe

SaP

SeP

SiP

SoP

Fałszywe

przybiera wartość logiczną

SaP

każde

1

0

1

0

SoP

SeP

żadne

0

1

1

0

SiP

SiP

niektóre są

?

0

1

?

SeP

SoP

niektóre nie są

0

?

?

1

SaP

g. Zwrot „tylko” w zdaniach kategorycznych

i. dodany do zdania kategorycznego zmienia znaczenie wypowiedzi

h. Zdanie o budowie „Tylko S jest P”:

i. prawdziwe będzie jedynie dla takich S oraz P, dla których między zakresem nazwy S, a

zakresem nazwy P zachodzić będzie stosunek zamienności, albo stosunek nadrzędności S do
P

ii. „tylko S jest P” nie jest równoważne „każde S jest P”

iii. tylko S jest P = każde P jest S

i. zdanie o budowie „Tylko S i każde S jest P”

i. będzie prawdziwe jeżeli między podmiotem a orzecznikiem zachodzić będzie stosunek

zamienności

ii. Tylko S i każde S jest P = koniunkcja SaP i PaS

j. podsumowanie:

i. „Tylko S jest P” „Każde S jest P”

ii. tylko jest partykułą ograniczającą

iii. zwrot tylko wyodrębnia pod względem zakresu to, do czego się odnosi
iv. Wzory:

1. Tylko S jest P

= PaS

2. Tylko S nie są P

= nie-SaP

3. Tylko P nie są S

= nie-PaS

4. Tylko i każde S jest P = (SaP ˄ PaS)
5. Tylko SiP

= (SiP ˄ SeP)

6. Tylko SiP

= Tylko SoP

8. Przekształcenia zdań kategorycznych:

a. obwersja – przekształcenie zmierzające do uzyskania to samo znaczącego zdania o odmiennej

jakości, a więc uczynienia ze zdania twierdzącego zdania przeczącego lub vice versa

i. negujemy termin, który w przekształconym zdaniu tworzył orzecznik:

1. SaP=SeP’ -> Jeżeli każdy człowiek jest rozumny, to żaden nie jest nierozumny

25

2. SeP=SaP’ -> Jeżeli żaden student nie jest analfabetą, to każdy jest nie-analfabetą
3. SiP=SoP’
4. SoP=SiP’

b. konwersja – odwrócenie zdania, przestawienie jego terminów. Po przestawieniu termin, który dotąd

tworzył orzecznik odtąd pełni rolę podmiotu, a przy pomocy terminu, który był podmiotem,
tworzony jest orzecznik czyli: orzecznik=> podmiot; podmiot => orzecznik

i. konwersja wprost:

1. SeP=PeS -> Jeżeli żaden człowiek nie jest nieśmiertelny, to żaden nieśmiertelny nie

jest człowiekiem.

2. SiP=PiS -> Jeżeli niektórzy ludzie są niepełnosprawni, to niektórzy niepełnosprawni są

ludźmi.

ii. konwersja z ograniczeniem:

1. SaP = PiS

iii. szczegółowoprzeczących zdań – nie konwertuje się -> konwersja przez kontrapozycję

1. przeprowadza się ją jak każdą konwersję prostą
2. każdy z terminów odwróconego zdania opatrzyć należy zaprzeczeniem

a. Jeżeli niektórzy ludzie nie są lekarzami -> to niektórzy nie-lekarze nie są nie-

ludźmi = niektórzy nie-lekarze są ludźmi

c. inne przekształcenia:

i. zdanie ogólnotwierdzące:SaP = S e P’ – P’e S = P’a S’ – S’i P’ = S’o P => można uzyskać:

1. kontrapozycję niezupełną: P’e S
2. kontrapozycję zupełną: P’a S’
3. inwersja zupełna: S’i P’
4. inwersja niezupełna: S’o P

ii. zdanie ogólnoprzeczące: SeP = SaP’ – P’i S = P’o S’

1. kontrapozycja niezupełna: P’i S
2. kontrapozycja zupełna: P’o S’
3. dalej: zakaz konwertowania zdania szczegółowoprzeczącego

iii. zdanie szczegółowoprzeczące: SoP = SiP’ – P’i S = P’o S’

1. kontrapozycja niezupełna: P’i S
2. kontrapozycja zupełna: P’ o S’
3. koniec przekształcania

d. przekształcenia rozwinięte:

i. zupełne – za zupełną postać przekształcenia rozwiniętego uważa się zdanie o tej samej

jakości co zdanie wyjściowe

ii. niezupełne – jeżeli jakość jest odmienna, wówczas tę postać nazywamy niezupełną

e. obwersja – polega na zamianie jakości i zaprzeczeniu orzecznika

i. każde zdanie kategoryczne można zamienić w zdanie równoważne jeżeli zmienimy jego

jakość i zaprzeczymy orzecznik

ii. zmiana jakości = ze zdania twierdzącego przejdziemy na przeczące, a ze zdania przeczącego

na zdanie twierdzące

iii. prawo obwersji w poszczególnych zdaniach kategorycznych:

1. SaP=SeP’ ->Każdy sędzia(S) jest prawnikiem(P) = Żaden sędzia (S) nie jest nie-

prawnikiem (P’)

2. SeP=SaP’ ->Żaden adwokat nie jest sędzią = Każdy adwokat jest nie-sędzią
3. SiP=SoP’ -> Niektóre wnioskowania są zawodne = Niektóre wnioskowania nie są nie-

zawodne

26

4. SoP=SiP’ -> Niektórzy mężczyźni nie są przystojni = Niektórzy mężczyźni są nie-

przystojni

f. konwersja – polega na zamianie podmiotu z orzecznikiem

i. w zdaniu ogólnotwierdzącym -> między zakresami nazwy S a P zachodzi stosunek

zamienności albo stosunek podrzędności S do P -> z uwagi na podrzędność S do P zdania
ogólnotwierdzącego nie można konwertować wprost (podlega konwersji z ograniczeniem).

1. zamieniamy podmiot z orzecznikiem (S z P)
2. zmieniamy ilość – ze zdania ogólnego zdanie szczegółowe

a. Każdy sędzia jest prawnikiem -> Niektórzy prawnicy są sędziami
b. sformalizowane: SaP → PiS

ii. zdania szczegółowotwierdzące i ogólnoprzeczące podlegają konwersji wprost

1. dla uzyskania konwersji wystarczy w tych zdaniach zamienić miejscami podmiot z

orzecznikiem

2. Niektórzy mężczyźni są ubezwłasnowolnieni -> Niektórzy ubezwłasnowolnieni są

mężczyznami => sformalizowane: SiP=PiS

3. Żadna zbrodnia nie jest występkiem = żaden występek nie jest zbrodnią => SeP=PeS

g. kontrapozycja – polega na zamianie podmiotu z orzecznikiem i zaprzeczeniu obydwu terminów

i. kolejność kontrapozycja zupełna

1. obwersja
2. konwersja
3. obwersja

ii. kolejność kontrapozycja niezupełna

1. obwersja
2. konwersja

iii. szczegółowotwierdzące – nie posiada kontrapozycji ponieważ otrzymujemy po obwersji

zdanie szczegółowoprzeczące, które się nie konwertuje

h. inwersja – polega na przekształceniu zdania po uzyskaniu kontrapozycji

i. konwersja kontrapozycji -> inwersja zupełna

ii. obwersja inwersji zupełnej -> inwersja niezupełna

iii. zdanie szczegółowotwierdzące i szczegółowoprzeczące -> nie podlega inwersji
iv. wyprowadzenie inwersji zdania ogólnotwierdzącego:

1. SaP = SeP’ = P’e S = P’a S’ – S’i P (inwersja zupełna) = S’o P(inwersja niezupełna)
2. SeP = SaP’ → P’I S = P’o S’ – S’o P’ = S’I P

Rozdział XV – Rozumowania pośrednie, sylogizm kategoryczny

1. Sylogizm kategoryczny – 4 zasady

a. metafizyczne:

i. zasada zgodności – dwa terminy, jeżeli zgodne są z tym samym terminem trzecim, zgodne są

i ze sobą

ii. zasada różnicy – zgodnie z nią nie są zgodne ze sobą dwa terminy, z których jeden jest, a

drugi nie jest zgodny z tym samym trzecim terminem

b. logiczne:

i. zasada twierdzenia o wszystkim – to, co twierdzi się o wszystkich obiektach danego rodzaju

twierdzić można i o poszczególnych obiektach tego rodzaju

ii. zasada twierdzenia o niczym –cokolwiek zaprzeczyć można odnośnie całego zakresu nazwy,

to samo zaprzeczy się odnośnie każdego z desygnatów tej nazwy

27

2. Sylogizm – jest rozumowaniem, w którym z dwóch zdań kategorycznych, pełniących rolę przesłanek,

wyprowadza się wniosek (w postaci zdania kategorycznego), a wszystkie te trzy zdania zbudowane są z
trzech nazw

a. nazwy:

i. termin mniejszy – nazwa, która we wniosku pełniła rolę podmiotu => S

ii. termin większy – nazwa, którą we wniosku budowano orzecznik => P

iii. termin średni – występuje w obu zdaniach pełniących rolę przesłanek i tylko tam => M

b. zdania sylogizmu

i. wniosek -> zbudowany z terminu mniejszego i z terminu większego (S + P)

ii. przesłanka mniejsza -> zbudowana z terminu mniejszego i średniego (S + M)

iii. przesłanka większa -> zbudowana z terminu większego i średniego (P + M)

3. Zapis sylogizmu:

a. przesłanka większa
b. przesłanka mniejsza
c. wniosek

4. Dyrektywy poprawności sylogizmu

a. Przynajmniej jedna z przesłanek musi być zdaniem twierdzącym, a jeżeli obie przesłanki są

twierdzące, to i wniosek musi być twierdzący

i. nie do przyjęcia – tryb o dwóch przeczących przesłankach

ii. gdy tylko jedna jest twierdząca, to wniosek musi być przeczący

b. Przynajmniej jedna z przesłanek musi być zdaniem ogólnym, a wniosek może być ogólny, jeżeli obie

przesłanki są ogólne

i. niepoprawny jest sylogizm o dwóch przesłankach szczegółowych

c. Przynajmniej w jednej z przesłanek powinien zostać rozłożony termin średni, a jeżeli jakiś termin

(skrajnik) został rozłożony we wniosku, to i on musi być rozłożony w odpowiedniej przesłance.

i. za rozłożony uważa się termin, który w zdaniu ogólnym pełni rolę podmiotu, lub który w

zdaniu przeczącym tworzy orzecznik.

5. Sylogizmy – postaci nieklasyczne

a. dylemat – za punkt wyjścia przyjmuje alternatywę głoszącą, że A jest B lub C

i. jeżeli zatem z B i z C wynika X, to jeżeli A jest B to jest X lub jeżeli A jest C to jest X

ii. tak czy zatem A jest X

iii. dylemat Omara: „jeżeli te zbiory zawierają to co Koran, to są zbędne, a zatem należy je

spalić. Jeżeli zaś zawierają co innego, to są szkodliwe, więc należy je spalić. Tak czy tak więc
należy je spalić”

b. epichremat – jest sylogizmem rozbudowanym w inny sposób – jego przesłankom towarzyszą zdania,

na których bazujemy uznając przesłanki za prawdziwe.

i. przykładem epicherematu – fragment mowy Cycerona w sprawie Klodiusza: „Morderca

powinien zostać skazany na śmierć, bo tak stanowi prawo naturalne i prawo stanowione, a
Klodiusz jest mordercą, bo tego dowodzą zeznania świadków i okoliczności zbrodni, zatem
Klodiuszowi należy wymierzyć karę śmierci”

c. sorites – sylogizm rozbudowany, w którym orzecznik pierwszego zdania w następnym staje się

podmiotem, którego to zdania orzecznik staje się podmiotem następnego zdania np.

i. przykład: „My rządzimy światem, a nami kobiety”

d. polisylogizm – w istocie ciąg sylogizmów, w którym wniosek jesdnego (prosylogizmu) staje się

przesłanką następnego (episylogizmu), a wniosek tego przesłanką kolejnego

e. sylogizm entymematyczny – jedna z przesłanek pozostaje domyślna, a to dlatego, że sylogizmy te

występują często, podobnie jak sylogizmy klasyczne. Sprawdzenie poprawności polega na
odtworzeniu brakującej przesłanki z materiału nazwowego jaki tworzy część ujawniona. -> jeżeli,

28

wykorzystując dyrektywy poprawności, to się powiedzie, a całość okaże się poprawna, spójna i
sensowna, wówczas rozumowanie należy uznać za prawidłowe

i. Przeżuwacze nie są krwiożercze, a zatem lwy nie są przeżuwaczami -> wnioskiem tego

rozumowania jest zdanie: Żaden lew nie jest przeżuwaczem:

1. termin mniejszy (S) – lew
2. termin większy (P) – przeżuwacz
3. ujawniona przesłanka: żaden przeżuwacz nie jest krwiożerczy = przesłanka większa

(zawiera termin większy)

4. termin średni (M) – krwiożerczy
5. poszukujemy przesłanki mniejszej
6. zdanie będzie zbudowane z nazw lew i krwiożerczy
7. wniosek jest zdaniem ogólnoprzeczącym – poszukiwana przesłanka będzie musiała

być zdaniem ogólnym (tylko z dwóch zdań ogólnych może wynikać ogólny wniosek)

8. poszukiwana przesłanka musi być zdaniem twierdzącym -> prawidłowy sylogizm nie

może mieć dwóch przesłanek przeczących

9. czyli: zdanie ogólnotwierdzące
10. przesłanka ujawniona jest zdaniem ogólnoprzeczącym -> obydwa terminy są

rozłożone => spełniona jest dyrektywa o rozłożeniu terminów, która wymaga, aby w
przynajmniej jednej z przesłanek rozłożony został termin średni

11. musimy rozłożyć jeszcze termin mniejszy
12. przesłanka mniejsza = zdanie ogólnotwierdzące -> żeby to uczynić trzeba terminowi

mniejszemu przeznaczyć w niej rolę podmiotu, bo tylko taka rola w zdaniu
ogólnotwierdzącym gwarantuje rozłożenie

13. poszukiwana przesłanka: SaM – każdy lew jest krwiożerczy

ii. dyrektywa dodatkowa dla entymematów: jeżeli zadowala nas mniej to nie szukamy więcej

– jeżeli jesteśmy w stanie odbudować sylogizm ustalając, że poszukiwana przesłanka będzie
zdaniem szczegółowym, to nie poszukujemy rozwiązania w postaci zdania ogólnego. od
dyrektywy tej należy jednak odstąpić, gdyby okazało się, że przez odtworzenie poszukiwanej
przesłanki jako szczegółowej naruszymy inną dyrektywę (np. termin średni nie miałby
zagwarantowanego rozłożenia przynajmniej w jednej z przesłanek)

6. Błędy we wnioskowaniach – wnioskowanie jest błędne, jeśli opiera się na mylnych i nieuzasadnionych

podstawach; wnioskowanie błędne nie może przesądzać o prawdziwości wniosku. Rozumowanie oparte na
błędnym wnioskowaniu nie przesądza również o fałszywości wniosku (może być prawdziwy). Wnioskowanie
przesądza o zawodności rozumowania.

a. błąd materialny – zwany błędem merytorycznym, dotyczy treści przesłanek; polega na uznaniu za

prawdziwą przesłanki, która prawdziwą nie jest => Wyprowadzenie wniosku na podstawie fałszywej
przesłanki nie jest dopuszczalne

i. tylko prawdziwa racja => prawdziwe następstwo

b. błąd formalny – dotyczy wad w konstrukcji danego rozumowania. Polega na zastosowaniu we

wnioskowaniu niepoprawnego wzoru rozumowania czyli zastosowaniu we wnioskowaniu schematu,
który nie jest prawem logicznym.

i. wzór powinien być prawidłowy, rozumowanie wedle takiego schematu powinno być

niezawodne

29

Rozdział XVI logika – Rozumowania

1. Rozumowania – procesy myślowe polegające na wyprowadzaniu sądów z sądów wcześniej uznanych za

prawdziwe

a. w zależności od tego, czy ów wcześniej uznany sąd jest racją, czy też następstwem rozumowania

dzieli się na

i. dedukcyjne – uważane za niezawodne

1. zdaniem wyjściowym, uznawanym za prawdziwe, jest racja, a w redukcyjnym za

punkt wyjścia służy następstwo uznawane jako prawdziwe

2. w dowodzeniu, chcąc uznać następstwo za prawdziwe, należy dobrać właściwą mu

rację, niewątpliwie prawdziwą

3. przeprowadzając wnioskowanie z prawdziwej racji wywodzimy o prawdziwości

następstwa

4. przykład wnioskowania: rozumowania według zasad sylogistyki arystotelejskiej

ii. redukcyjne – rozumowania zawodne

1. z prawdziwości następstwa wywodzimy o prawdziwości racji
2. rozumowaniami redukcyjnymi są różne odmiany wyjaśniania i sprawdzania

a. wyjaśnianie – polega na dobieraniu racji do następstwa uznawanego za

prawdziwe; dowodzenie sądowe jest wyjaśnianiem; szczególną postacią
wyjaśniania są rozumowania indukcyjne (wyjaśnienia ogólne) => na
podstawie informacji o posiadaniu jakiejś własności przez poszczególne
desygnaty wnosimy o posiadaniu tej własności przez całą klasę, czy tylko u
niektórych; wyróżnia się indukcję zupełną i niezupełną

b. istnieją inne wnioskowania, które nie zawsze są niezawodne = bez których podjęcie decyzji

niejednokrotnie byłoby utrudnione

i. wnioskowania zawodne są akceptowane, jeżeli są wnioskowaniami należycie

uprawdopodobniającymi, tj. gdy prawdziwość wyprowadzonego wniosku opiera się na
wysokim prawdopodobieństwie prawdy

1. wnioskowanie redukcyjne
2. wnioskowanie indukcyjne przez indukcję zupełną
3. sprawdzanie ze skutkiem pozytywnym
4. wnioskowanie przez analogie

ii. wnioskowania niezawodne, które nie były omówione:

1. wnioskowanie indukcyjne przez indukcję zupełną
2. sprawdzanie ze skutkiem negatywnym

2. Wyjaśnianie

a. wyjaśnianie to rodzaj rozumowania zmierzającego do wskazania racji dla uznanego następstwa.

Zmierza do udzielenia odpowiedzi na pytanie dlaczego jest tak, jak głosi następstwo.

b. Indukcja zupełna – rozumowanie przez indukcję zupełną jest niezawodne, ponieważ zbadanie

wszystkich jednostkowych elementów zbioru upoważnia nas w stu procentach do wyprowadzenia
wniosku o całym zbiorze

i. od analizy zdań szczegółowych do wniosku ogólnego

ii. kwadrat logiczny => od zdań szczegółowych do zdania ogólnego

iii. ze zdania ogólnego wynika zdanie szczegółowe, ale ze zdania szczegółowego nie wynika

zdanie ogólne = zdanie ogólne jest racją, a zdanie szczegółowe następstwem

iv. jeżeli jednak zbadamy wszystkie zdania szczegółowe, to na tej podstawie możemy

skonstruować zdanie ogólne

30

v. np. stwierdzenie szczegółowe: Niektóre jabłka na mojej jabłoni są robaczywe /zrywając

poszczególne jabłka będziemy stwierdzenie do podtrzymywać aż do ostatniego, to na
podstawie tych wszystkich możemy wywnioskować, że skoro poszczególne jabłka okazały się
robaczywe, tzn. że każde jabłko jest

c. Indukcja niezupełna – nie mamy pewności, że zbadaliśmy wszystkie przesłanki. Biorąc pod uwagę

ilość zbadanych przesłanek czujemy się uprawnieni do wyprowadzenia wniosku ogólnego, że każde S
należy do P. Na podstawie obserwacji jednostkowych dochodzimy do uogólnień. Uogólnienia
obejmują również przypadki niezaobserwowane. Istnieje prawdopodobieństwo, że taki wniosek jest
prawdziwy, ale nie mamy całkowitej pewności, że tak jest.

i. prawdopodobieństwo prawdy wzrasta z liczbą zbadanych elementów

ii. nie możemy natrafić na element, który nie posiada badanej cechy

iii. nie oznacza to, ze przy indukcji niezupełnej, jakiś element nieprzebadany cechy takiej może

być pozbawiony, stąd wnioskowanie zaliczamy do wnioskowań zawodnych

iv. jeśli przynajmniej jeden element nie spełnia badanych warunków obowiązani jesteśmy taki

wniosek odrzucić

v. musimy być przekonani, że nie istnieją jednostkowe elementy, które byłyby niezgodne z

wnioskiem ogólnym

d. Indukcja eliminacyjna

i. John Stuart Mill ->schematy wnioskowania = kanony Milla

ii. w schematach określał związki przyczynowe zachodzące między występującymi zjawiskami

iii. badając zjawiska i zachodzące między nimi zależności Mill drogą eliminacji wyprowadzał

wniosek, stąd rodzaj wnioskowania indukcyjnego nazwano indukcją eliminacyjną

iv. wyróżniamy 5 kanonów mila

1. Kanon jedynej zgodności – polega na wskazaniu spośród wielu zjawisk tego

zjawiska, które jest przyczyną powstania zjawiska Z, lub skutkiem zjawiska Z.

a. musimy przeanalizować wszelkie zjawiska wpływające na zjawisko Z
b. należy zbadać wszystkie zjawiska współwystępujące ze zjawiskiem Z
c. następnie drogą eliminacji wyłaniamy to zjawisko, które w istotny sposób

oddziaływuje na badane zjawisko

d. na badane zjawisko będzie oddziaływać takie zjawisko, które stale

towarzyszy zjawisku badanemu

e. wnioskowanie to jest zawodne, gdyż najczęściej trudno jest poddać

eliminacji wszystkie czynniki wpływające na występowanie zjawiska

2. Kanon jedynej różnicy – polega na wskazaniu spośród wielu zjawisk tego zjawiska,

które jest przyczyną powstawania zjawiska Z lub skutkiem zjawiska Z. Przy kanonie
jedynej różnicy będziemy szukać z sumy zjawisk takiego zjawiska, którego
wyeliminowanie sprawi, że zniknie również zjawisko Z, lub co jest jego skutkiem

a. winniśmy z sumy zjawisk współtowarzyszących zjawisku Z odejmować

kolejno poszczególne zjawiska

b. musimy obserwować, czy wyeliminowanie któregoś ze zjawisk ma wpływ na

zjawisko Z.

c. jeżeli usunięcie jakiegoś zjawiska X spowoduje niewystępowanie zjawiska Z,

to możemy pokusić się o wniosek, że zjawisko X w istotny sposób
oddziaływało na zjawisko Z

d. wnioskowanie jest zawodne, gdyż najczęściej trudno jest poddać eliminacji

wszystkie czynniki wpływające na niewystępowanie zjawiska Z

e. prawdopodobieństwo uzyskanego wniosku wzrasta wraz z liczbą zbadanych

zjawisk

31

3. Kanon zgodności i różnicy – wnioskowanie oparte na połączeniu kanonu jedynej

zgodności z kanonem jedynej różnicy

a. na podstawie kanonu jedynej zgodności ustalamy drogą eliminacji, które

zjawisko jest przyczyną powstania zjawiska Z

b. następnie na podstawie kanonu jedynej różnicy pozbywamy się zjawiska,

które naszym zdaniem jest przyczyną powstania zjawiska Z i obserwujemy,
czy zjawisko Z również zanika

c. wnioskowanie oparte na kanonach zgodności i różnicy jest wnioskowaniem

zawodnym w mniejszym stopniu niż wnioskowanie oparte wyłącznie na
którymś z nich

4. Kanon zmian towarzyszących – polega na wskazaniu spośród wielu zjawisk tego

zjawiska, którego nasilenie jest przyczyną nasilenia zjawiska Z

a. badamy stopień oddziaływania jednego zjawiska na drugie
b. nasilenie zjawiska Z – pogrubienie Z

i. przy zjawiskach ABCD występuje Z

ii. przy zjawiskach ABCD nasilenie A nie wpływa na Z

iii. przy zjawiskach ABCD nasilenie B nie wpływa na Z
iv. przy zjawiskach ABCD nasilenie C nie wpływa na Z

v. przy zjawiskach ABCD stwierdzamy, że nasilenie D wpływa na

nasilenie zjawiska Z

c. rozumowanie to może okazać się zawodne
d. nie zawsze poddamy eliminacji wszystkie czynniki, które oddziaływają na

badane zjawisko

5. Kanon reszt – polega na przypisaniu dla danego zjawiska spośród wielu przyczyn tej

przyczyny, której nie udało się wyeliminować

a. załóżmy, że ze zjawiskiem Z współwystępują zjawiska ABCD, które są

przyczyną zjawiska Z

i. wyeliminowanie zjawiska A nie wpływa na zjawisko Z

ii. wyeliminowanie zjawiska B nie wpływa na zjawisko Z

iii. wyeliminowanie zjawiska C nie wpływa na zjawisko Z
iv. na tej podstawie sądzimy, że w takim razie zjawisko D musi mieć

wpływ na zjawisko Z

e. Indukcja statystyczna – w schemacie tego wyjaśniania, tak jak w trybie sylogizmu, występują

przesłanki i wniosek:

i. za przesłankę większą służą zdania ogólne uznawane za prawa, tj. opisujące prawidłowości.

ii. za przesłankę mniejszą – zdania jednostkowe – wyrażające sądy głoszące, że w danym

przypadku prawa zadziałały

iii. warunki uznawania rezultatów rozumowań:

1. należyty opis populacji
2. opis losowej próby
3. prawidłowo sformułowane hipotezy statystyczne
4. należycie wyprowadzony wniosek

iv. powstała też probabilistyczna odmiana modelu indukcyjno – predyktywnego, umożliwiająca

czynić uzasadnione przewidywania: diagnozy, prognozy i postgnozy

v. do predykcji uciekamy się, gdy wyjaśnione zjawisko w swej istocie jest nieobserwowalne,

trudne do zaobserwowania, albo rozważyć należy sam fakt jego zaistnienia

vi. gdy przewidywane jest zaistnienie zjawiska przyszłego, formułowana jest prognoza

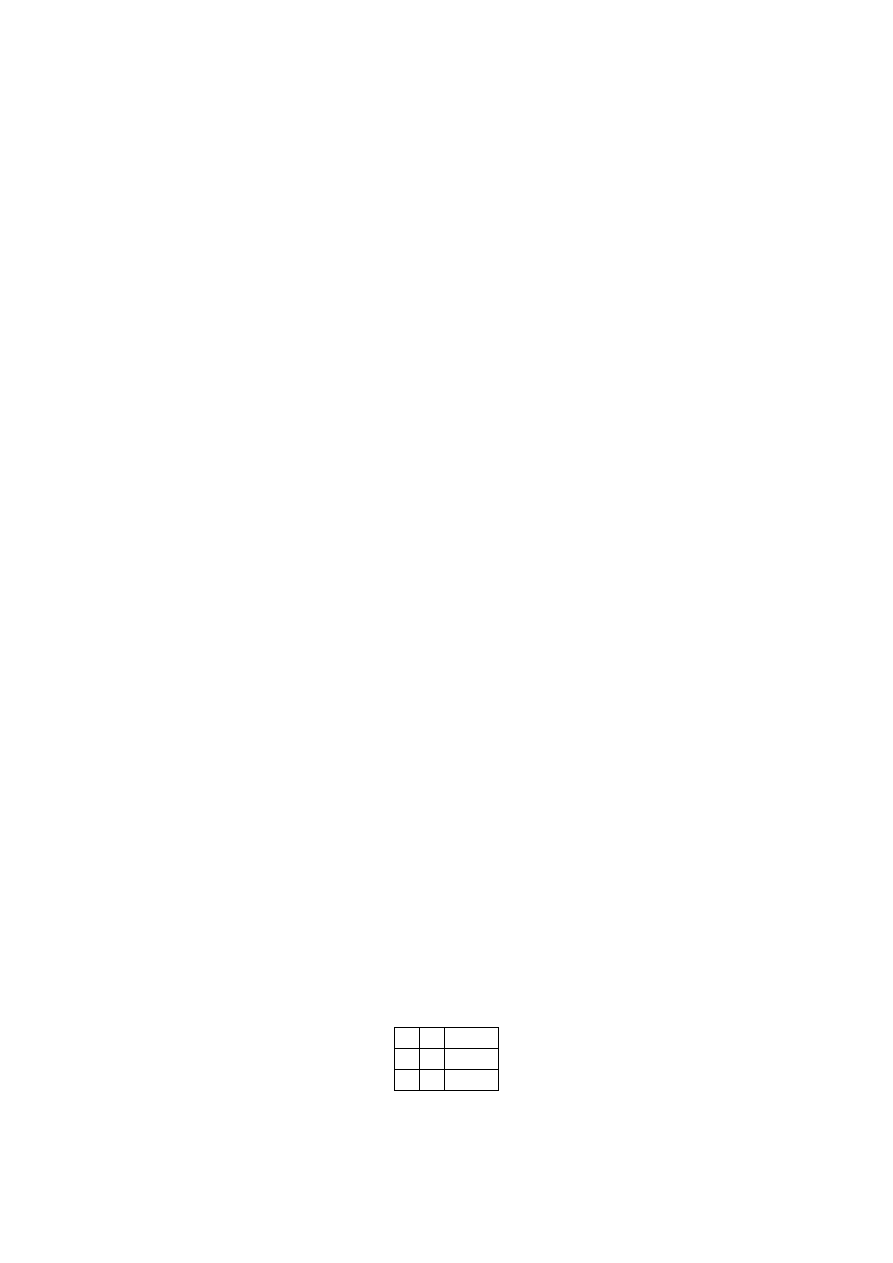
32

vii. ta postać rozumowania znajduje zastosowanie np. w opiniach psychiatrycznych zasięganych

przed zastosowaniem środka zabezpieczającego

viii. nomologiczno-predyktywne rozumowania dotyczące faktów teraźniejszych to diagnozy

ix. postgnoza – to np. opinia psychiatryczna o stanie zdrowia psychicznego oskarżonego,

właściwego mu w momencie czynu

3. Rozumowania redukcyjne, a rozumowania dedukcyjne

a. we wnioskowaniu redukcyjnym z następstwa wnioskujemy o redukcji
b. tego typu wnioskowanie jest zawodnie, ponieważ prawdziwe następstwo nie zawsze przesądza o

prawdziwej racji

c. przy wnioskowaniu redukcyjnym dobieramy do zdania prawdziwego takie zdanie, z którego to

pierwsze logicznie wynika; prawdziwość przesłanki nie gwarantuje prawdziwego wniosku

d. wnioskowanie dedukcyjne -> racja (przesłanka) => następstwo (wniosek)
e. wnioskowanie redukcyjne -> następstwo (przesłanka) <= racja (wniosek)
f. kierunek wnioskowania redukcyjnego z następstwa do racji jest niezgodny z kierunkiem

rozumowania dedukcyjnego

g. we wnioskowaniu tym z wniosku (racji) wynika przesłanka (następstwo), ale z przesłanki

(następstwa) nie wynika wniosek (racja) -> np. Zawsze jeżeli Jan chrapie to Jan śpi (prawda).

h. Jeżeli na podstawie tego, że Jan śpi, będziemy wnioskowali, że Jan chrapie, to nasze rozumowanie

będzie zawodne. Może być tak: Jan śpi, ale nie chrapie. (skubany)

i. Schemat tego rozumowania opiera się na prawie modus ponendo ponens

i. Jeżeli sprawcę skazano na karę pozbawienia wolności (p) to uznano go winnym popełnienia

przestępstwa (q) i prawdą jest, że sprawcę uznano winnym popełnienia przestępstwa (q, a
zatem skazano go na karę pozbawienia wolności (p).

1. [(p → q) ˄ q] → p

ii. przy implikacji zwykłej prawdziwość następnika nie przesądza o prawdziwym poprzedniku

iii. wnioskowanie to jest wnioskowaniem zawodnym, gdyż sprawca uznany winnym popełnienia

przestępstwa niekoniecznie jest skazany na karę pozbawienia wolności

iv. na wnioskowaniu redukcyjnym opiera się sprawdzanie ze skutkiem pozytywnym

4. Sprawdzanie – polega na skontrolowaniu wartości logicznej pewnego stwierdzenia.

a. przy sprawdzaniu na podstawie prawdziwości albo fałszywości następstwa dochodzimy do wartości

logicznej zdania sprawdzanego

b. w zależności od uzyskanego rezultatu wyróżniamy sprawdzanie:

i. ze skutkiem negatywnym

ii. ze skutkiem pozytywnym

c. sprawdzanie ze skutkiem pozytywnym:

i. jest postacią wnioskowania redukcyjnego

ii. polega na tym, że na podstawie prawdziwego następstwa stanowimy, iż zdanie sprawdzane

jest również prawdziwe

iii. przy sprawdzaniu tym mamy ustalić wartość logiczną poprzednika przy założeniu, że

następstwo jest prawdziwe

iv. z poniższej tabeli wynika, że takie wnioskowanie jest zawodne:

p q q→p
1 1

1

0 1

0

33

v. wnioskowanie to jest zawodne, gdyż prawdziwe następstwo nie przesądza o prawdziwej

racji

vi. sprawdzanie ze skutkiem pozytywnym opiera się na wzorze:

1. [(p→q) ˄ q] → p

d. Sprawdzanie ze skutkiem negatywnym – polega na tym, że na podstawie fałszywego następstwa

wnosimy, iż zdanie sprawdzane musi być również fałszywe

i. mamy ustalić wartość logiczną racji przy założeniu, że następstwo jest fałszywe

ii. z poniższej tabeli wynika, że takie wnioskowanie jest niezawodne:

p q q→p
1 1

1

0 1

1

0 0

1

iii. ten rodzaj wnioskowania odpowiada schematowi:

1. [(p→q) ˄~ q] → ~p

iv. opiera się na prawie modus tollendo tollens

5. Eksperyment – doświadczenie przeprowadzone w sztucznych warunkach, polegające na celowym wywołaniu

określonego zjawiska dla zbadania jego przebiegu poprzez ustalenie związku zachodzącego między badanymi
czynnikami.

a. Podział eksperymentów:

i. eksperyment klasyczny – eksperyment, w którym badacz manipuluje tzw. niezależnymi

zmiennymi wg. założonego planu badawczego i obserwuje zmienne zależne

ii. eksperyment naturalny – po wytypowaniu zmiennych i dokonaniu ich charakterystyki w

obserwowanym obszarze poszukuje się sposobów przejawiania się zmiennych uznawanych
za niezależne i zależne

iii. eksperyment myślowy – kiedy to badacz myślowo tworzy proces oddziaływania zmiennych

b. osoba, która przeprowadza eksperyment zwana jest eksperymentatorem. W zależności od wyniku

eksperymentu wyróżniamy

i. eksperyment pozytywny – jeżeli przeprowadzone doświadczenie potwierdza, że między

badanymi czynnikami zachodzi jakaś zależność

ii. eksperyment negatywny – między badanymi czynnikami określona zależność nie zachodzi.

c. z uwagi na cel eksperymentu wyróżniamy

i. eksperyment naukowy – należy do podstawowych metod badawczych, celem jego jest

przede wszystkim korzyść poznawcza; ustawodawca eksperyment ten traktuje priorytetowo

1. eksperyment medyczny – szczegółowo uregulowany przez ustawę o zawodzie

lekarza

ii. eksperyment dydaktyczny

iii. eksperyment procesowy – najważniejszy dla prawnika; jest czynnością procesową, którą

można przeprowadzić w postępowaniu sądowym, bądź przygotowawczym, o ile jest to
celowe dla sprawdzenia okoliczności mających istotne znaczenie dla sprawy

by zielut