Rozdział I. PŁASKI UKŁAD SIŁ
1. Siły działające wzdłuż jednej prostej
M_3. Na jednej lince wiszą dwa odważniki, 100 N i 50 N, umocowane na niej
w różnych punktach, przy czym większy z nich wisi niżej od mniejszego. Jaka
jest siła w lince powyżej lżejszego odważnik, a jaka poniżej niego?
Rozw:
Prowadzimy myślowy przekrój I, wyodrębniamy ciężar P
1
= 100 N.
Oznaczamy przez S
1
siłę w lince działającą między punktem A i B.
Równanie równowagi na oś y:
N
100
0
1
1
1
=
⇒
=
−
=
∑
S
P
S
P
iy
Po wyznaczeniu siły S
1
prowadzimy przekrój myślowy II, obejmujący ciężar P
2
i przecinający linkę w dwóch miejscach: między punktem A i B oraz ponad
punktem B.
Równanie równowagi na oś y:
N
150
0
1
1
2
2
=
⇒
=
−
−
=
∑
S
S
P
S
P
iy
Odp.: 100 N i 150 N.
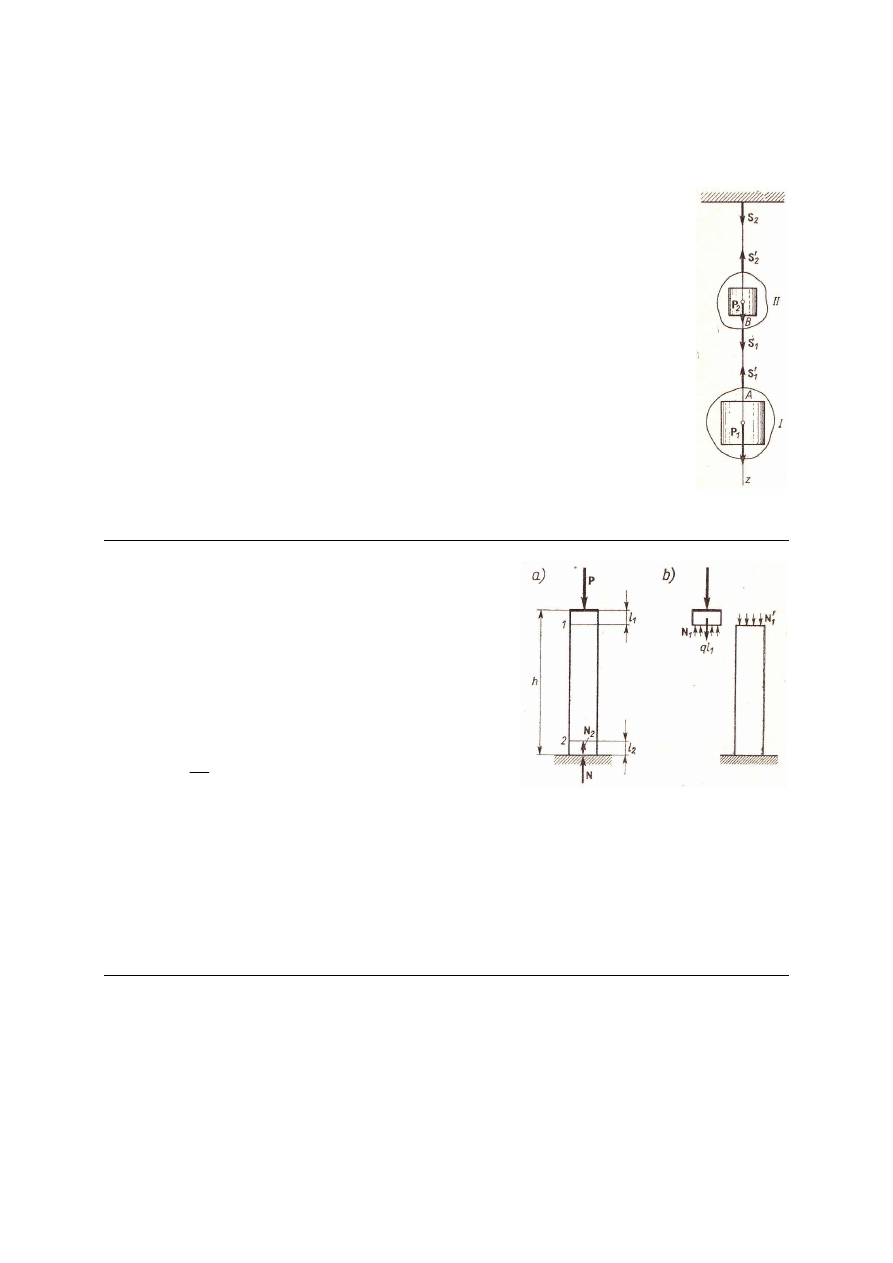
M_4. Jednorodna pionowa kolumna walcowa o
wysokości h = 5 m i ciężarze Q = 30 kN stoi na
fundamencie i podtrzymuje ciężar P = 40 kN. Obliczyć
oddziaływanie kolumny na fundament i osiową siłę
ściskającą w jej przekrojach oddalonych o l
1
= l
2
= 0.5
m od górnego i dolnego końca kolumny.
Rozw.
Ciężar jednostkowy kolumny:
kN/m
6
5
30
=
=
q
Nacisk w przekroju 1:
kN
43
5
.
0
6
40
1
1
=
⋅
+
=
+
=
ql
P
N
Nacisk w przekroju 2:
(
)
(
)
kN
67
5
.
0
5
6
40
2
2
=
−
⋅
+
=
−
+
=
l
h
q
P
N
Nacisk na fundament:
kN
70
30
40
=
+
=
+
=
Q
P
N
Odp. T = 70 kN, N
1
= 43 kN, N
2
= 67 kN.
M_5. Holownik parowy ciągnie trzy barki o różnych wymiarach, połączone linami, jedna za
drugą. Ciąg śruby holownika wynosi w danej chwili 18 kN. Opór stawiany parowcowi przez
wodę wynosi 6 kN, opór wody działający na pierwszą barkę 6 kN, na drugą 4 kN, na trzecią
2 kN. Użyta przy tym lina może być bezpiecznie obciążona siłą 2 kN. Iloma linami należy
połączyć parowiec z pierwszą barką, pierwszą barkę z drugą oraz drugą barkę z trzecią, jeśli
ruch jest prostoliniowy i jednostajny?
Rozw.
Siła w linach łączących ostatnią barkę z drugą wynosi 2 kN – wystarczy jedna lina.
Między drugą a pierwszą:
2 + 4 = 6 kN, 6/2 = 3 liny.
Między holownikiem i pierwszą barką:
2 + 4 + 6 = 12 kN, 12/2 = 6 lin.
Odp. 6, 3, 1.
2. Zbieżny układ sił
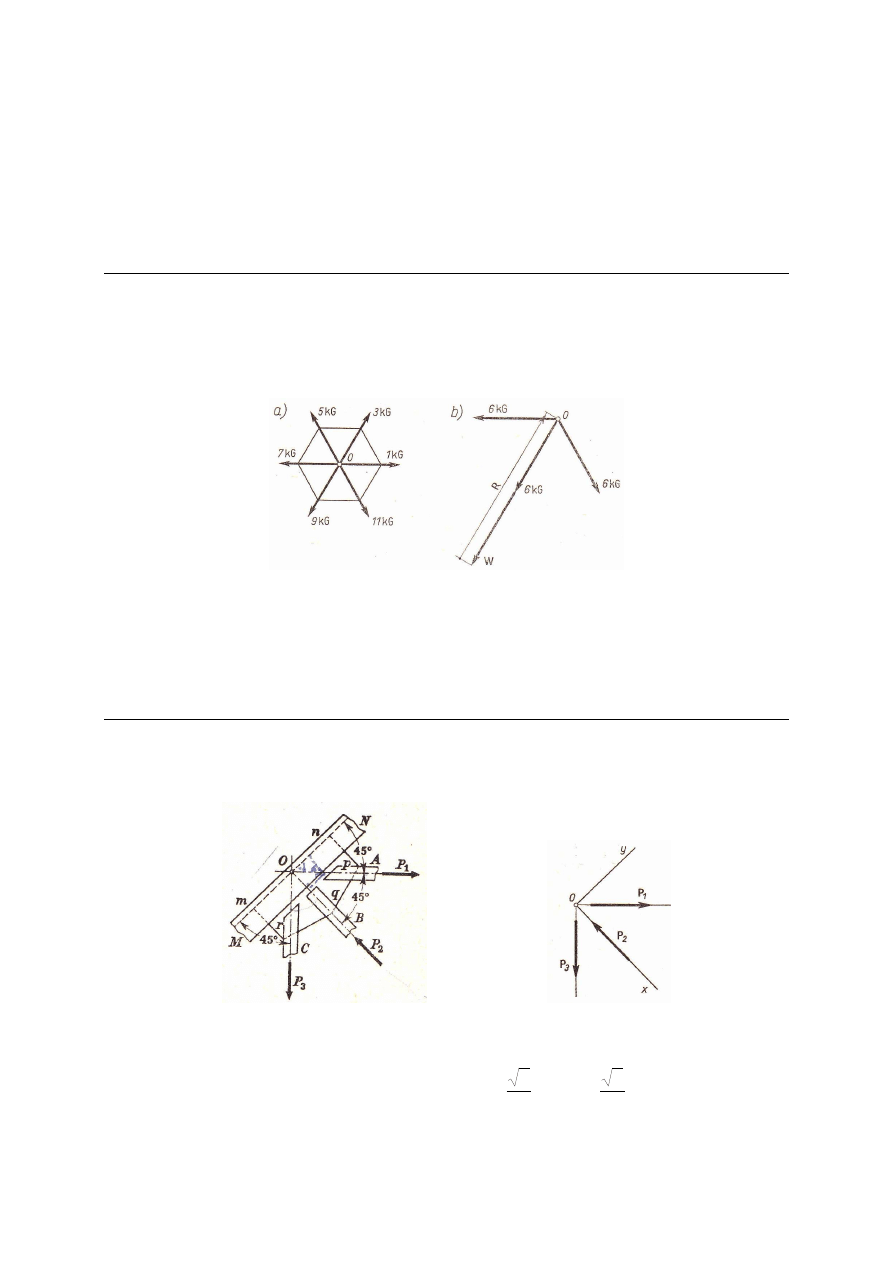
M_11. W środku sześciokąta foremnego zaczepione są siły o wartościach 10, 30, 50, 70, 90
i 110 N, skierowane ku jego wierzchołkom. Wyznaczyć wartość i kierunek siły wypadkowej
i równoważącej.
Rozw.
Sumując algebraicznie siły mające wspólną linię działania otrzymamy trzy siły po 60 N.
Wypadkowa:
N
120
60
cos
60
2
60
=
°
⋅
⋅
+
=
W
ma kierunek i zwrot siły 90 N
Odp. 120 N; kierunek wypadkowej pokrywa się z kierunkiem danej siły o wielkości 90 N.
M_12. Wyznaczyć siłę, jaką węzeł mnpqr wywiera na belkę MN, jeżeli siły działające wzdłuż
prętów OA, OB i OC wynoszą P
1
= P
3
= 1.41 kN i P
2
= 1 kN. Kierunki sił pokazano na
rysunku.
Obliczając sumy rzutów sił na kierunek siły P
2
(oś x) i prostopadły do niej (oś y)
znajdziemy:
kN
1
2
2
41
.
1
1
2
2
41
.
1
45
cos
45
cos
3
2
1
=
+
−
=
°
+
−
°
=
∑
P
P
P
P
ix
∑
=
°
−
°
=
0
45
sin
45
sin
2
1
P
P
P
iy

Odp. 1 kN; kierunek działania wzdłuż OB, zwrot przeciwny zwrotowi siły P
2
.
M_15. Dwa ciągniki jadące ze stałą prędkością wzdłuż brzegów prostego kanału ciągną barkę
za pomocą dwu lin. Siły napinające liny wynoszą 800 N i 960 N, a liny tworzą między sobą
kąt 60º. Znaleźć opór wody wywierany na barkę przy jej ruchu oraz kąty α i β, jakie liny
tworzą z brzegami, jeżeli barka porusza się równolegle do brzegów.
Rozw.
Składowe poprzeczne sił w linach muszą się równoważyć:
β
S
α
S
sin
sin
2
1
=
Stąd:
2
1
sin
sin
S
S
α
β
=
(
)
α
α
α
α
α
sin
sin
60
cos
cos
60
sin
sin
60
sin
⋅
°
−
⋅
°
=
−
960
800
2
1
cot
2
3
=
−
α
54
.
1
cot
=
α
°
=
33
α
,
°
=
27
β
Odp.
P = 1530 N, α = 33º, β = 27º.
M_17. Pręty AC i BC połączone są między sobą i z pionową ścianą za pomocą przegubów.
Na sworzeń przegubu
C działa pionowa siła P = 10 kN. Wyznaczyć reakcję tych prętów na
sworzeń przegubu
C, jeżeli kąty między prętami a ścianą są α = 30º i β = 60º.
A
C
α
β
P
Rozw.
0
sin
sin
Σ
=
+
−
=
β
S
α
S
P
B
A
ix
0
cos
cos
Σ
=
−
+
=
P
β
S
α
S
P
B
A
iy
albo przy odwróconym układzie współrzędnych:
0
cos
Σ
=
−
=
β
P
S
P
B
ix
kN
5
60
cos
10
cos
=
°
⋅
=
=
β
P
S
B
0
sin
Σ
=
−
=
β
P
S
P
A
iy
kN
66
.
8
60
sin
10
sin
=
°
⋅
=
=
β
P
S
A
Odp. S
A
= 8.66 kN, S
B
= 5 kN.
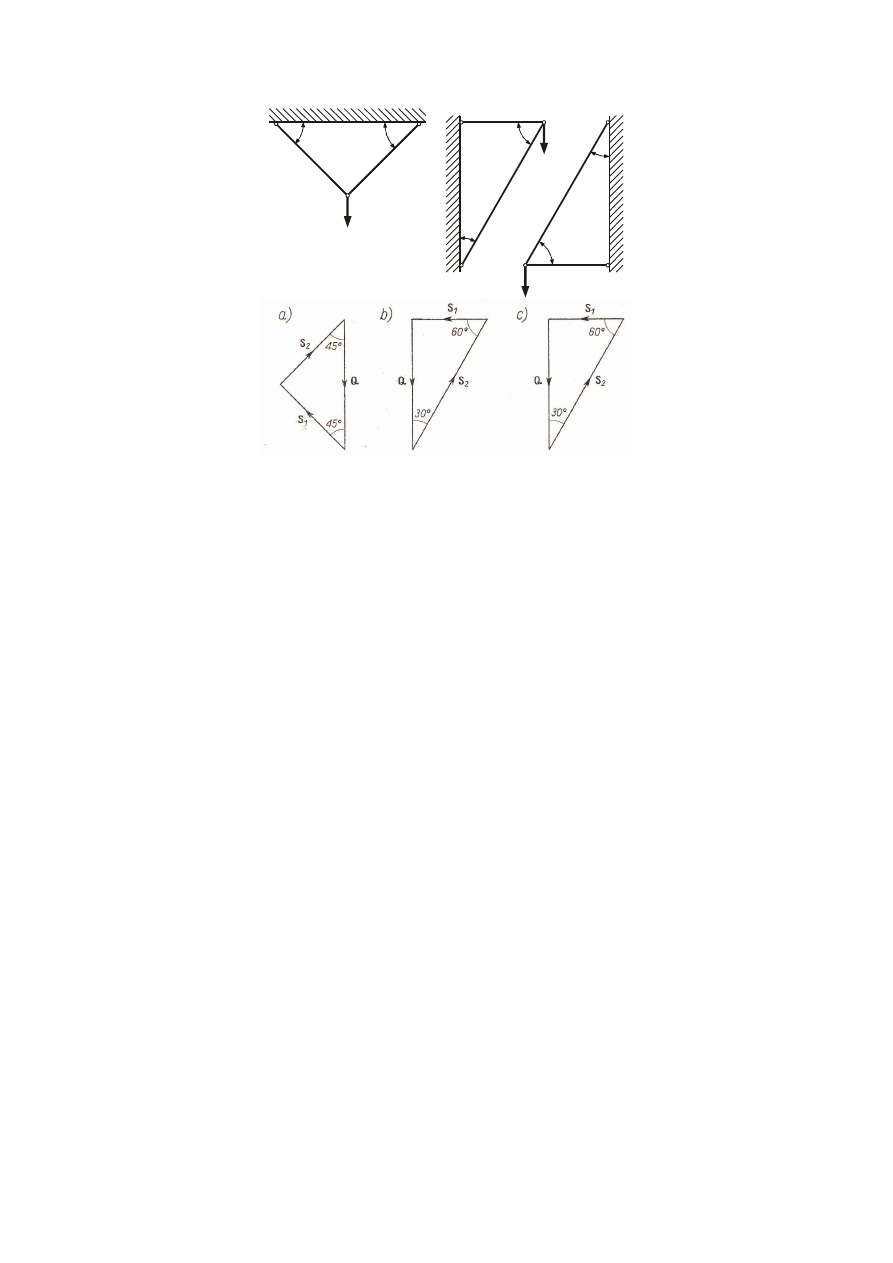
M_18. Na rysunkach (a), (b), (c), podobnie jak w zadaniu poprzednim, pokazano
schematycznie układy prętów połączonych przegubowo ze sobą, z sufitem i ze ścianą. Na
sworzniach przegubów B, F, K zawieszono ciężary Q = 10 kN. Obliczyć siły w prętach w
przypadkach, gdy:
(a) α = β = 45º;
(b) α = 30º, β = 60º;
(c) α = 60º, β = 30º.
A
D
M
C
F
K
B
E
N
α
α
α
β
β
β
Q
Q
Q
1
2
1
2
1
2
Odp. (a) S
1
= S
2
= 7.07 kN;
(b) S
1
= 5.77 kN, S
2
= -11.54 kN;
(c) S
1
= -5.77 kN, S
2
= 11.54 kN.
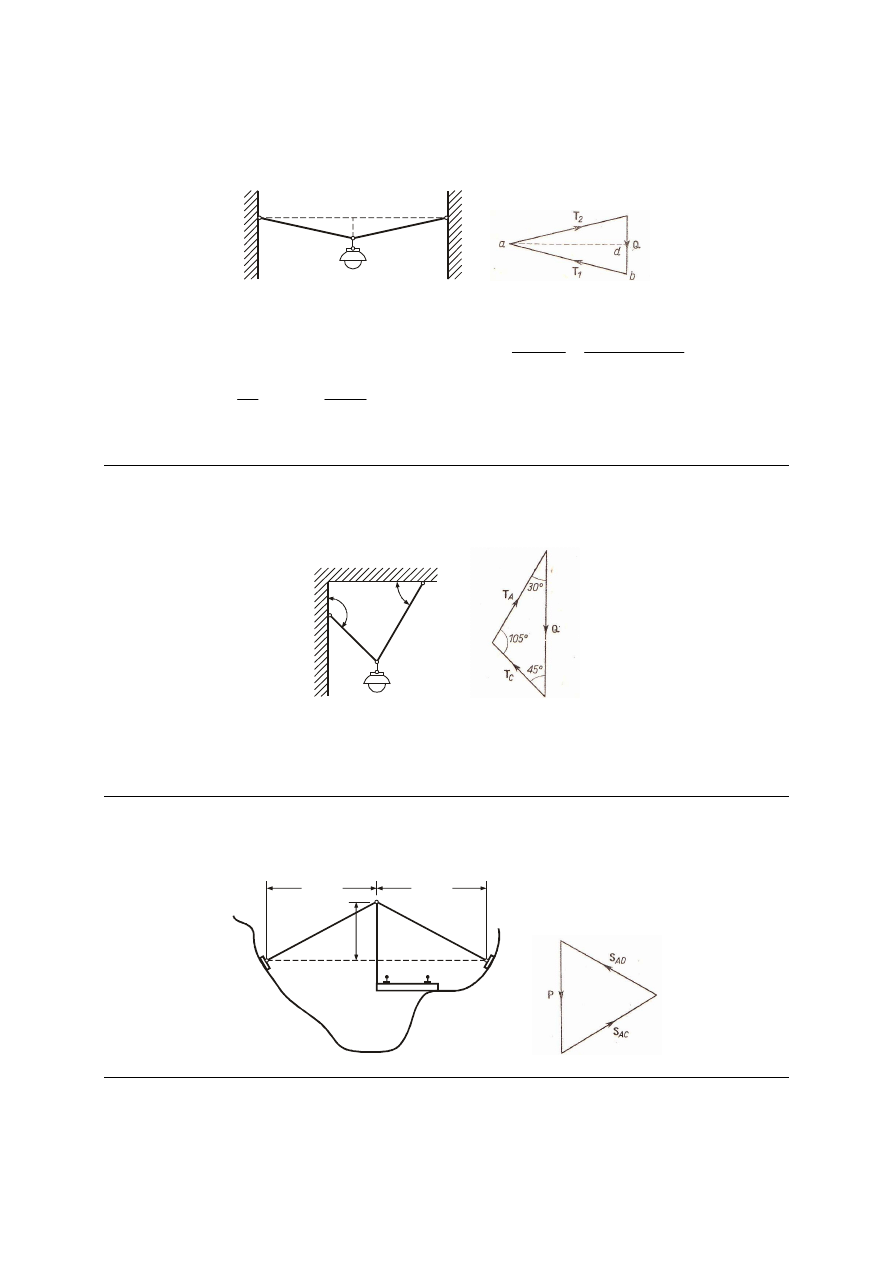
M_19. Latarnia uliczna zawieszona jest w punkcie B w środku linki ABC przyczepionej do
haków A i C znajdujących się na jednym poziomie. Znaleźć siły T
1
i T
2
rozciągające części
linki AB i BC, jeżeli ciężar latarni wynosi 150 N, długość całej linki 20 m, odległość zaś BD
punktu zawieszenia B od poziomej AC wynosi 0.1 m. Ciężar linki pominąć.
A
D
B
C
Rozw.
0
cos
cos
Σ
2
1
=
+
−
=
α
T
α
T
P
ix
2
1
T
T
=
0
sin
sin
Σ
2
1
=
+
+
−
=
α
T
α
T
Q
P
iy
N
7500
5729
.
0
sin
2
150
sin
2
1
=
°
⋅
=
⋅
=
α
Q
T
°
=
⋅
=
=
5729
.
0
20
1
.
0
2
arctan
2
arctan
l
h
α
Odp. T
1
= T
2
= 7500 N.
M_21. Lampa elektryczna o ciężarze 20 N zawieszona jest u sufitu na sznurze AB i
przyciągnięta do ściany linką BC. Wyznaczyć siły: T
A
w sznurze AB i T
C
w lince BC, jeżeli
wiadomo, że kąt α = 60º, a kąt β = 135º. Ciężar sznura i linki pominąć.
C
A
α
β
B
Rozw.
0
cos
sin
Σ
=
+
−
=
α
T
β
T
P
A
C
ix
0
sin
cos
Σ
=
−
+
−
=
Q
α
T
β
T
P
A
C
iy
Odp. T
A
= 14.6 N, T
C
= 10.4 N
M_23. Pewien odcinek kolei żelaznej, przebiegającej w górach, przeprowadzony jest w
wąwozie i zawieszony jak na rysunku. Wymiary zaznaczono na rysunku. Zakładając, że
podciąg AB obciąża siła P = 500 kN, znaleźć siły w prętach AC i AD.
C
A
D
B
11,65m
11,65m
6
,1
0
m
Odp. Pręty AC i AD są ściskane siłami 539 kN.
M_26. Do linki AB, której jeden koniec umocowany jest w punkcie A, przywiązano w
punkcie B ciężar P i linkę BCD przerzucono przez krążek. Do końca D linki przywiązano
ciężar Q = 100 N. Obliczyć siłę T w lince AB i ciężar P, jeżeli w położeniu równowagi kąty
utworzone przez linki z pionem BE wynoszą α = 45º i β = 60º. Tarcie na krążku pominąć.
A
C
D
α β
B
E
Q
P
Rozw.
0
sin
sin
Σ
=
−
=
α
T
β
Q
P
ix
N
5
.
122
45
sin
60
sin
100
sin
sin
=
°
°
⋅
=
⋅
=
α
β
Q
T
0
sin
cos
Σ
=
−
+
=
P
α
T
β
Q
P
iy
N
6
.
136
45
sin
5
.
122
60
cos
100
sin
cos
=
°
⋅
+
°
⋅
=
+
=
α
T
β
Q
P
Odp. T = 122.5 N, P = 136.6 N.
M_28. Na dwóch wzajemnie prostopadłych gładkich pochyłych płaszczyznach AB i BC
spoczywa jednorodna kula o ciężarze 60 N. Znaleźć oddziaływania kuli na każdą
z płaszczyzn wiedząc, że płaszczyzna BC tworzy z poziomem kąt 60º.
60°
A
D
E
O
C
B
Rozw.
0
60
sin
Σ
=
°
−
=
Q
N
P
D
ix
N
96
.
51
60
sin
60
60
sin
=
°
⋅
=
°
=
Q
N
D
0
60
cos
Σ
=
°
−
=
Q
N
P
E
iy
N
Q
N
E
30
60
cos
60
60
cos
=
°
⋅
=
°
=
Odp. N
D
= 51.96 N, N
E
= 30 N.
M_29. Przy pionowej gładkiej ścianie AB zawieszono jednorodną kulę O na lince AC. Linka
tworzy ze ścianą kąt α, ciężar kuli wynosi P. Obliczyć siłę T w lince i oddziaływanie Q kuli
na ścianę.
A
α
O
C
B
Rozw.
0
sin
Σ
=
+
−
=
α
T
Q
P
ix
α
P
Q
tan
=
0
cos
Σ
=
+
−
=
α
T
P
P
iy
α
P
T
cos
/
=
Odp. T = P/cosα, Q = Ptanα.
M_29_v2. Przy pionowej gładkiej ścianie AB zawieszono jednorodną kulę O na lince AC.
Linka tworzy ze ścianą kąt α = 30°, ciężar kuli wynosi P = 500 N. Obliczyć siłę T w lince i
oddziaływanie Q kuli na ścianę.
A
α
O
C
B
Rozw.
0
sin
Σ
=
+
−
=
α
T
Q
P
ix
N
7
.
288
30
tan
500
tan
=
°
⋅
=
=
α
P
Q
0
cos
Σ
=
+
−
=
α
T
P
P
iy
N
4
.
577
30
cos
/
500
cos
/
=
°
=
=
α
P
T
Odp. T = 577.4 N, Q = 288.7 N.
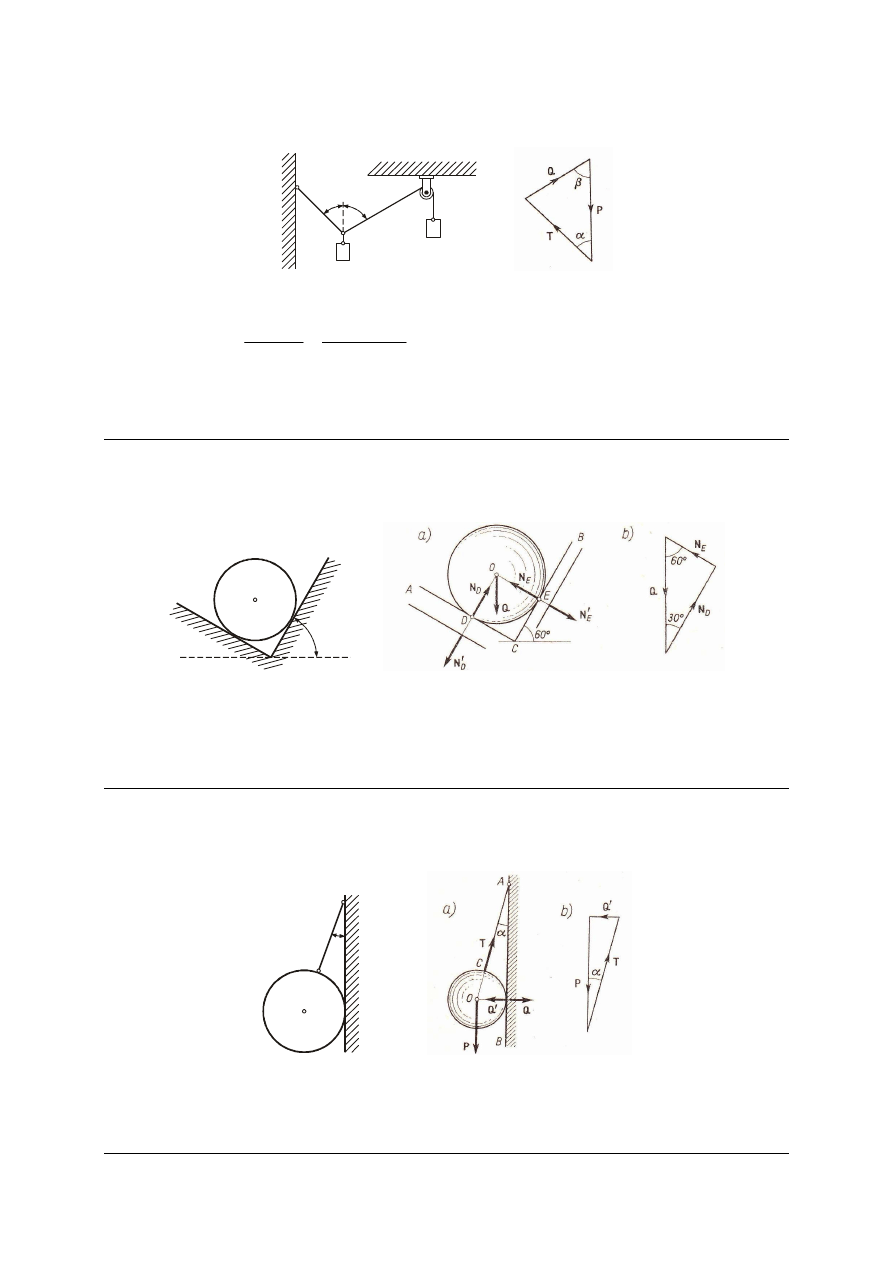
M_31. Kulka B o ciężarze P, wisząca na nici AB umocowanej nieruchomo w punkcie A,
opiera się o powierzchnię gładkiej kuli o promieniu r; odległość punktu A od powierzchni kuli
AC
= d, długość nici AB = l, prosta CA jest pionowa. Wyznaczyć siłę T w nici i reakcję Q
powierzchni kulistej. Promień kulki pominąć.
O
C
B
A
d
l
r
Odp.
r
d
l
P
T
+
=
,
r
d
r
P
Q
+
=
.
M_32. Jednorodna kula o ciężarze 100 N utrzymywana jest w położeniu równowagi przez
dwie linki AB i CD rozpięte w jednej płaszczyźnie pionowej i tworzące kąt 150º. Linka AB
tworzy z poziomem kąt 45º. Obliczyć siły w linkach.
A
O
B
C
D
45°
150°
Odp. T
B
= 193 N, T
C
= 141 N.
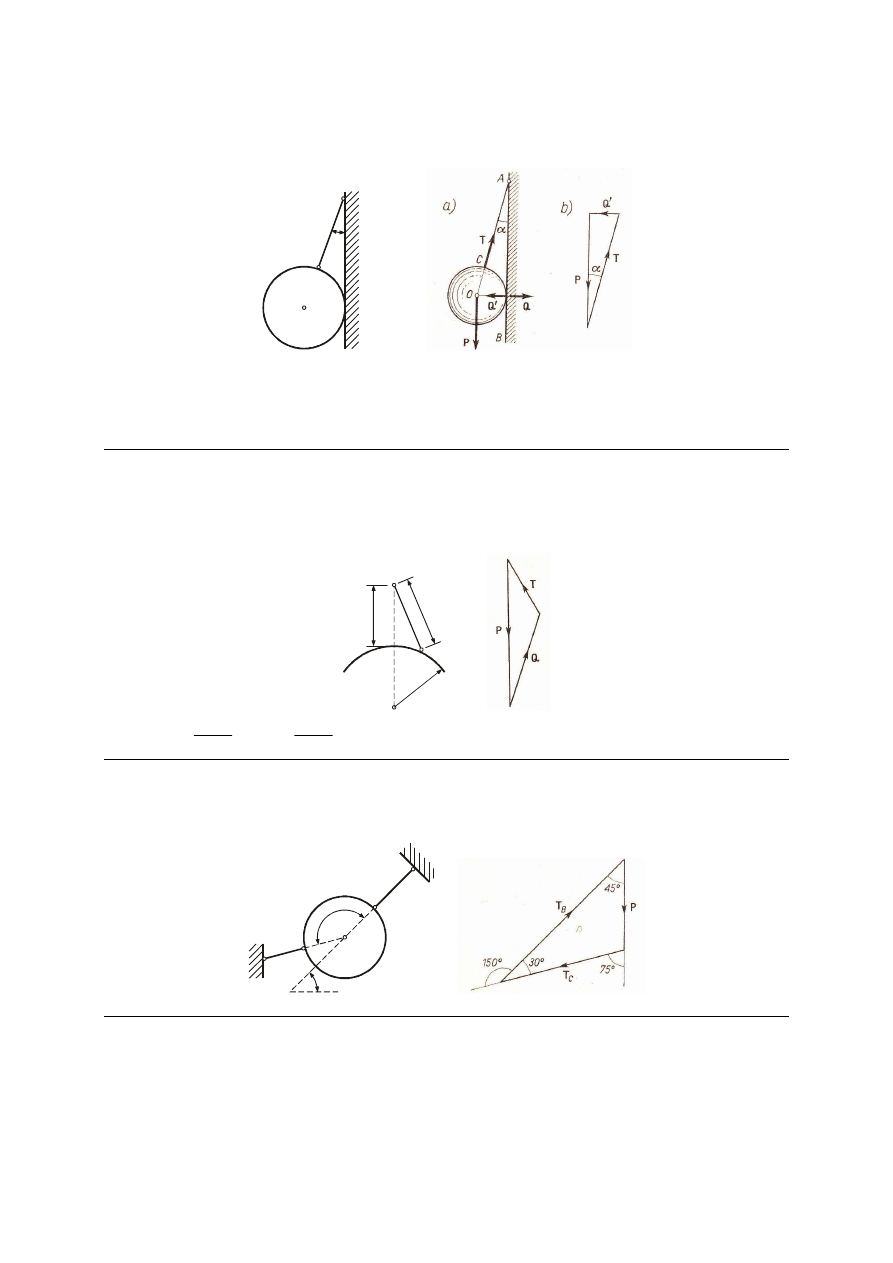
M_34. Ciężar jednorodnego walca drogowego wynosi 20 kN, a jego promień 60 cm.
Obliczyć poziomą siłę P niezbędną do przetoczenia walca przez kamienną płytę o wysokości
8 cm, położoną jak pokazano na rysunku.
8
cm
6
0
c
m
A
C
B
Rozw.
0
cos
Σ
=
+
−
=
α
N
P
P
ix
kN
55
.
11
60
cos
09
.
23
cos
=
°
⋅
=
=
α
N
P
0
sin
Σ
=
+
−
=
α
N
Q
P
iy
kN
09
.
23
60
sin
20
sin
=
°
=
=
α
Q
N
°
=
−
=
−
=
60
60
8
60
arcsin
arcsin
r
h
r
α
Odp. P = 11.55 kN.
M_36. Jednorodny pręt AB jest przymocowany do pionowej ściany przegubem A i
utrzymywany pod kątem 60º względem pionu przez linkę BC tworzącą z nim kąt 30º. Znaleźć
wielkość i kierunek reakcji R przegubu, jeżeli wiadomo, że ciężar pręta wynosi 20 N.
A
C
B
60°
30°
Rozw. Trójkąt BAC jest trójkątem równoramiennym, reakcja R musi być opuszczona wzdłuż
jego wysokości, aby wszystkie siły przecinały się w jednym punkcie. Stąd
°
=
60
α
.
0
sin
30
sin
Σ
=
+
°
−
=
α
R
S
P
ix
°
=
30
sin
sin α
R
S
0
cos
30
cos
Σ
=
−
+
°
=
P
α
R
S
P
iy
P
α
R
α
R
=
+
°
°
⋅
cos
30
sin
30
cos
sin
N
10
60
cos
30
cot
60
sin
20
cos
30
cot
sin
=
°
+
°
⋅
°
=
+
°
⋅
=
α
α
P
R
Odp. R = 10 N, kąt(R, AC) = 60º.
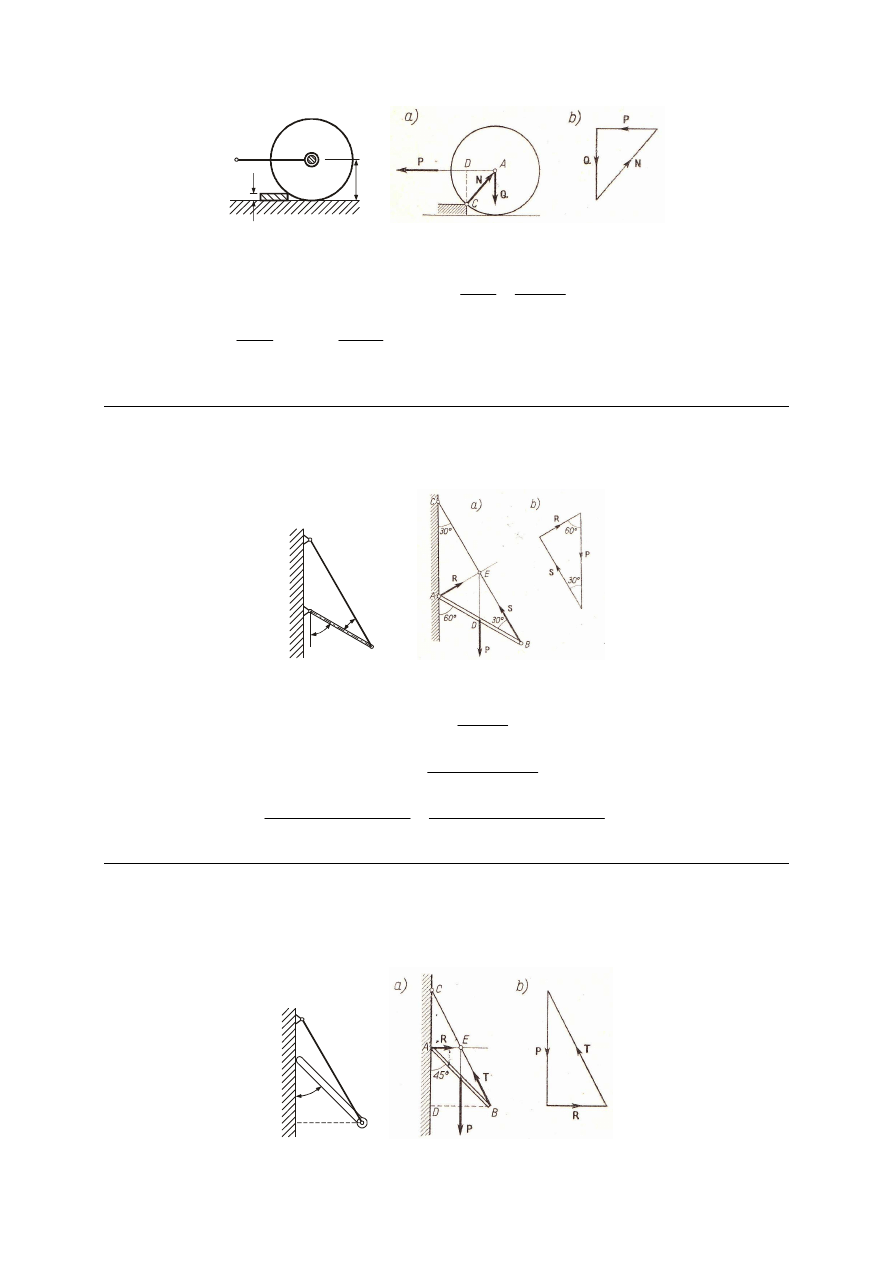
M_37. Górny koniec A jednorodnej belki AB o długości 2 m i ciężarze 50 N opiera się na
gładkiej pionowej ścianie. Do dolnego końca B przymocowana jest linka BC. Obliczyć, w
jakiej odległości AC należy przymocować linkę do ściany, aby belka, znajdująca się w
równowadze, tworzyła ze ścianą kąt BAD = 45º. Znaleźć siłę T w lince i reakcję R ściany.
A
C
B
45°
D

Odp. AC = AD = 1.41 m, T = 56 N, R = 25 N.
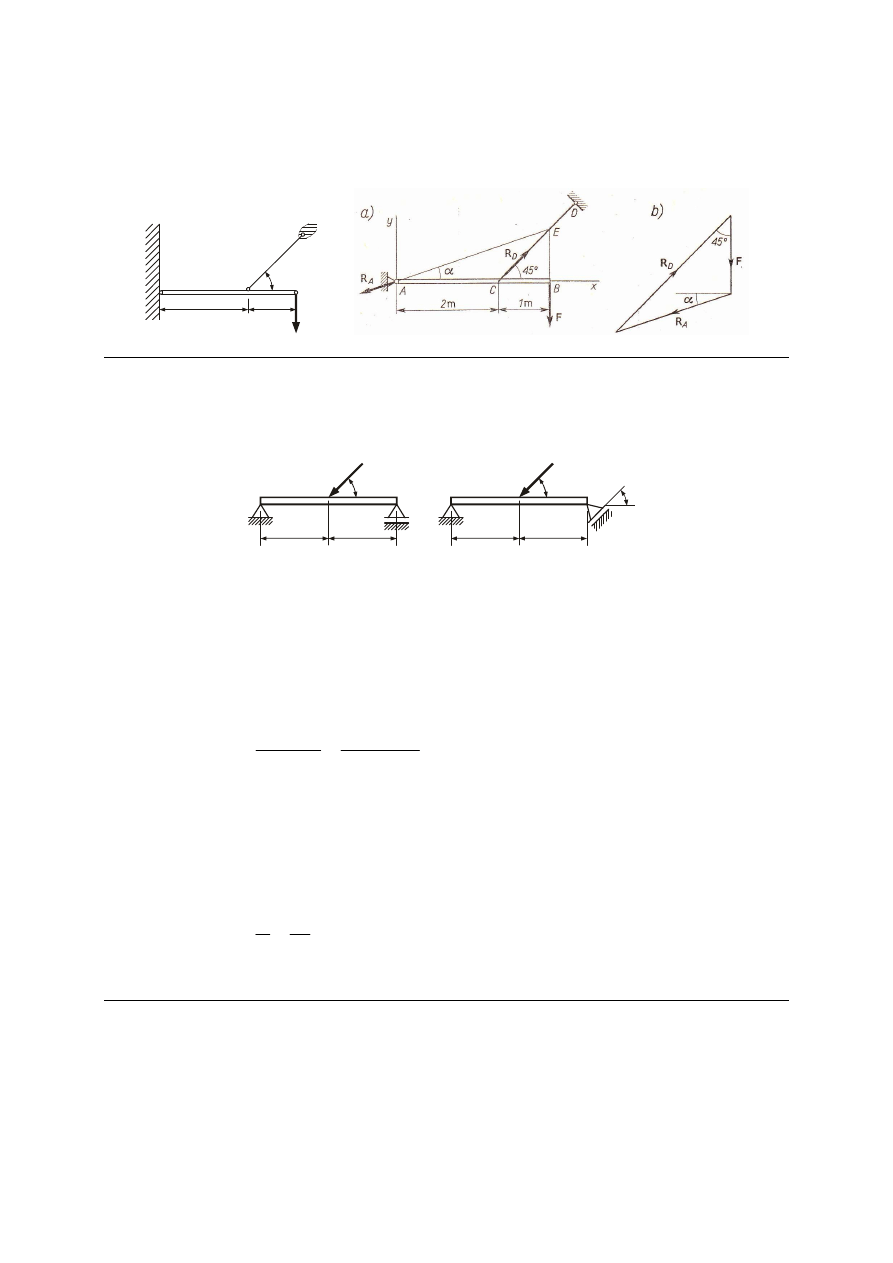
M_39. Belka AB utrzymywana jest w położeniu poziomym przez pręt CD; połączenia
w punktach A, C, D są przegubowe. Wyznaczyć reakcję podpór A i D, jeżeli na koniec belki
działa pionowa siła F = 50 kN. Wymiary pokazane są na rysunku. Ciężar własny belki
pominąć.
A
45°
B
D
C
2m
1m
F
Odp. R
A
= 79 kN, R
D
= 106 kN.
M_40. Koniec A belki umocowany jest przegubowo, koniec B zaś wsparty na wałkach. W
środku belki zaczepiona jest siła P = 20 kN, działająca pod kątem 45º do jej osi. Biorąc
wymiary z rysunku, wyznaczyć w przypadkach (a) i (b) reakcje podpór A i B. Ciężar własny
belki pominąć.
45°
45°
A
A
P
P
B
B
2m
2m
2m
2m
45°
Rozw.
(a)
0
45
cos
Σ
=
°
−
=
P
R
P
Ax
ix
kN
14
.
14
45
cos
20
45
cos
=
°
⋅
=
°
=
P
R
Ax
0
45
sin
Σ
=
+
°
−
=
B
Ay
iy
R
P
R
P
kN
071
.
7
071
.
7
45
sin
20
45
sin
=
−
°
⋅
=
−
°
=
B
Ay
R
P
R
0
4
2
45
sin
Σ
=
⋅
+
⋅
°
−
=
B
iA
R
P
M
kN
071
.
7
2
45
sin
20
2
45
sin
=
°
⋅
=
°
=
P
R
B
(b)
0
45
cos
45
cos
Σ
=
°
⋅
−
°
−
=
B
Ax
ix
R
P
R
P
kN
21
.
21
45
cos
10
45
cos
20
45
cos
45
cos
=
°
⋅
+
°
⋅
=
°
+
°
=
B
Ax
R
P
R
0
45
sin
45
sin
Σ
=
°
+
°
−
=
B
Ay
iy
R
P
R
P
kN
071
.
7
45
sin
10
45
sin
20
45
sin
45
sin
=
°
⋅
−
°
⋅
=
°
−
°
=
B
Ay
R
P
R
0
4
45
sin
2
45
sin
Σ
=
⋅
°
⋅
+
⋅
°
−
=
B
iA
R
P
M
kN
10
2
20
2
=
=
=
P
R
B
Odp. (a) R
Ax
= 14.14 kN, R
Ay
= 7.071 kN, R
B
= 7.071 kN;
(b) R
Ax
= 21.21 kN, R
Ay
= 7.071 kN, R
B
= 10 kN;
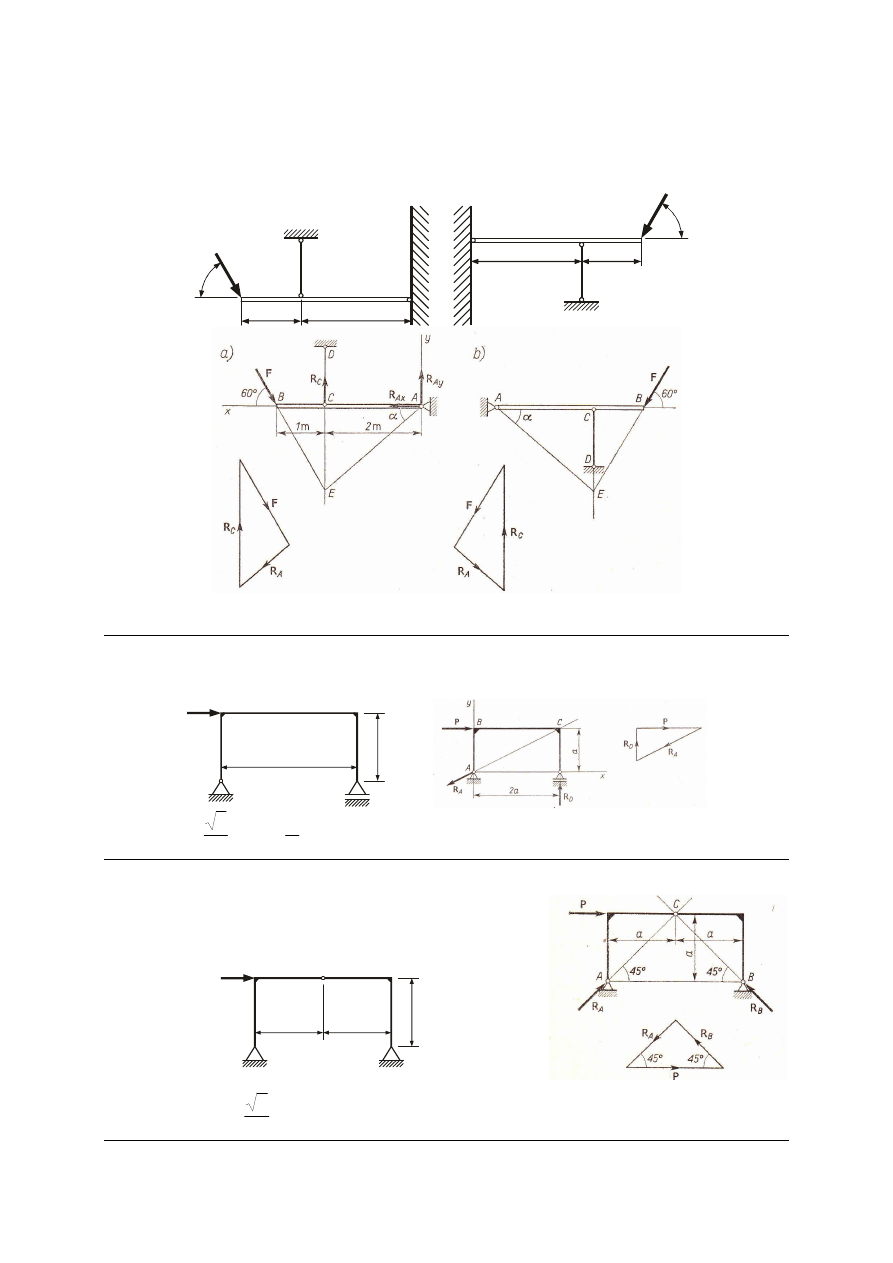
M_41. Pokazane na rysunkach belki AB utrzymywane są w położeniu poziomym przez pręt
CD
. Na końcach belek działają siły F = 30 kN pod kątem 60º do poziomu. Biorąc wymiary
z rysunków wyznaczyć siły S w prętach CD oraz oddziaływania Q belek na ściany
przyjmując, że połączenia A, C, D są przegubowe. Ciężar prętów i belek pominąć.
A
A
B
B
C
C
2m
2m
1m
1m
F
F
60°
60°
D
D
Odp. (a) S = 39 kN, Q = 19.8 kN;
(b) S = 39 kN, Q = -19.8 kN.
M_43. Dla ramy pokazanej na rysunku wyznaczyć reakcje podporowe R
A
i R
D
powstające
pod działaniem siły P przyłożonej w punkcie B. Ciężar ramy pominąć.
A
P
B
C
D
2a
a
Odp.
2
5
P
R
A
=
,
2
P
R
D
=
.
M_50. Dla trójprzegubowego łuku ACB pokazanego na
rysunku wyznaczyć reakcje podpór A i B powstające pod
działaniem poziomej siły P.
A
P
B
C
a
a
a
Odp.
2
2
P
R
R
B
A
=
=
.
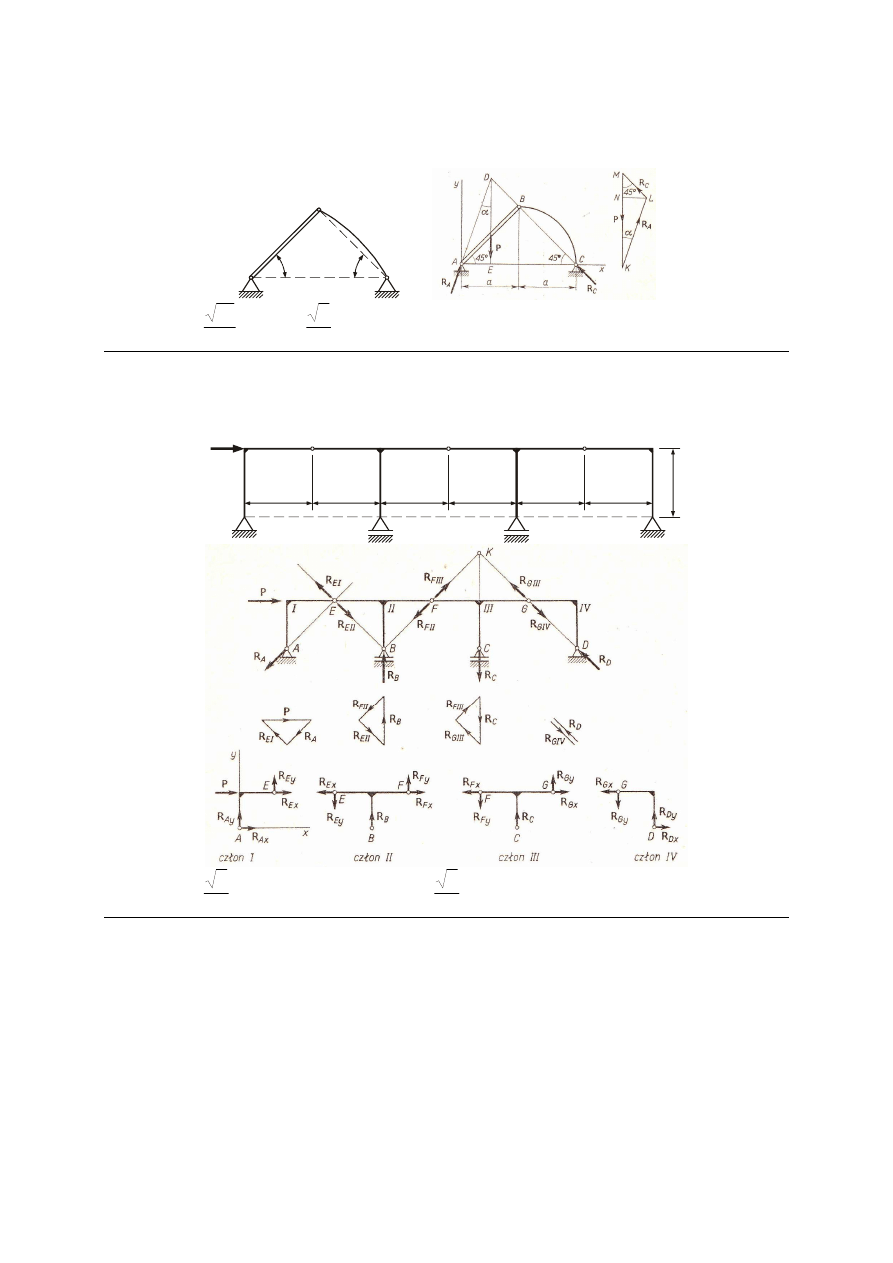
M_51. Jednorodna prosta belka AB o ciężarze P i nieważki zakrzywiony pręt BC są połączone
przegubowo w punkcie B oraz z odpowiednimi podporami A i C leżącymi na jednej poziomej
AC
. Proste AB i BC tworzą z prostą AC kąty α = 45º. Wyznaczyć reakcje podpór A i C.
A
C
B
α
α
Odp.
4
10
P
R
A
=
,
4
2
P
R
C
=
.
M_52. Dany jest układ złożony z trzech trójprzegubowych łuków których wymiary pokazane
są na rysunku. Wyznaczyć reakcje podpór A, B, C i D powstające pod działaniem poziomej
siły P.
A
P
a
a
a
a
a
a
a
B
C
D
Odp.
2
2
P
R
A
=
,
P
R
B
=
,
P
R
C
=
,
2
2
P
R
D
=
.
M_63. Nasyp ziemny podparty jest pionowym murem. Znaleźć konieczną grubość muru a
zakładając, że parcie ziemi skierowane jest poziomo, przyłożone na ⅓ wysokości ściany
i równe 60 kN/mb. Grubość ściany należy obliczyć zakładając możliwość obrotu ściany
dookoła krawędzi A. Ciężar właściwy muru wynosi 20 kN/m
3
.
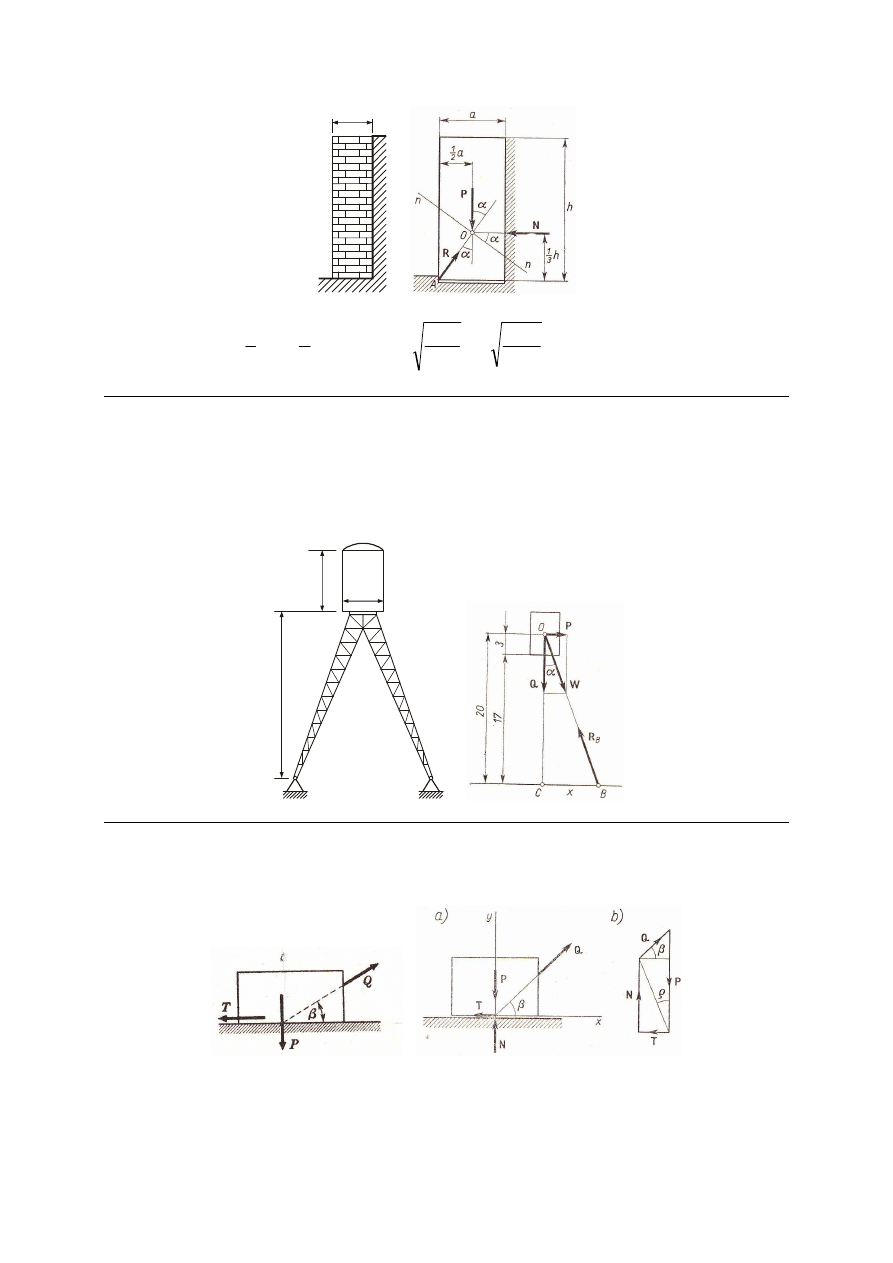
A
B
a
Rozw. Ciężar muru wynosi:
a
h
p
P
⋅
⋅
=
0
2
1
3
1
Σ
=
−
⋅
=
a
P
h
N
M
iA
m
414
.
1
20
3
60
2
3
2
=
⋅
⋅
±
=
⋅
⋅
±
=
p
N
a
Odp. a ≥ 1.414 m.
M_64. Wieża ciśnień składa się z walcowego zbiornika o wysokości 6 m i średnicy 4 m,
ustawionego na czterech symetrycznie rozstawionych, pochyłych słupach. Dno zbiornika
znajduje się na wysokości 17 m nad fundamentem. Ciężar wieży 80 kN; przy obliczaniu siły
wiatru bierzemy pod uwagę powierzchnię rzutu zbiornika na płaszczyznę prostopadłą do
kierunku wiatru i przyjmujemy, że parcie wiatru wynosi 1.25 kN/m
2
. Obliczyć niezbędną
odległość AB między podstawami słupów.
A
B
1
7
m
6
m
4m
Odp. AB ≥ 15 m.
M_74. Skrzynka o ciężarze P leży na chropowatej poziomej płaszczyźnie; współczynnik
tarcia wynosi µ. Wyznaczyć wielkość Q najmniejszej siły potrzebnej do przesunięcia skrzynki
oraz kąt β, jaki tworzy ta siła z poziomem.
Rozw. Sumy rzutów sił na kierunki x i y:
0
cos
Σ
=
−
=
T
β
Q
P
ix
0
sin
Σ
=
−
+
=
P
β
Q
N
P
iy
N
µ
T
=
β
Q
µ
P
µ
N
µ
T
β
Q
sin
cos
−
=
=
=
β
µ
β
P
µ
Q
sin
cos
−
=
Wartość Q osiągnie ekstremum, gdy mianownik ułamka osiągnie ekstremum. Odpowiednią
wartość kąta β wyznaczymy przyrównując do zera pochodną mianownika względem β:
(
)
0
cos
sin
sin
cos
d
d
=
+
−
=
+
β
µ
β
β
µ
β
β
stąd:
µ
β
=
tan
,
czyli:
µ
β
arctan
=
podstawiając do wyrażenia:
β
P
β
β
β
P
β
β
β
β
P
Q
sin
sin
cos
sin
cos
sin
cos
tan
2
2
2
=
+
=
+
=
Odp. β = arctgµ,
2
1
sin
µ
P
µ
β
P
Q
+
=
=
.
3. Siły równoległe i pary sił
M_77. Jednorodny pręt AB, o długości 1 m i ciężarze 20 N, zawieszony jest poziomo na
dwóch równoległych linkach AC i BD. Na pręcie w punkcie E, odległym o AE = ¼ m od
punktu A, zawieszono ciężar P = 120 N. Obliczyć siły w linkach, T
C
i T
D
.
A
C
B
D
P
E
Odp. T
C
= 100 N, T
D
= 40 N.
M_78. Na poziomej belce leżącej na dwóch podporach odległych o 4 m położono dwa
ciężary: jeden C = 2 kN, drugi D = 1 kN, tak że reakcja podpory A jest dwa razy większa od
reakcji podpory B. Ciężar własny belki pomijamy, odległość CD między ciężarami wynosi 1
m. Jaka jest odległość x ciężaru C od podpory A?
A
x
1m
4m
B
C
D
Odp. x = 1 m.
M_80. Znaleźć siłę wywieraną przez dźwig mostowy na szyny w zależności od położenia
wózka C, na którym umocowany jest kołowrót podnoszący. Położenie wózka określić przez
stosunek odległości jego środka od lewej szyny do całkowitej długości mostu AB. Ciężar
mostu P = 60 kN, ciężar wózka z podnoszonym ciężarem P
1
= 40 kN.
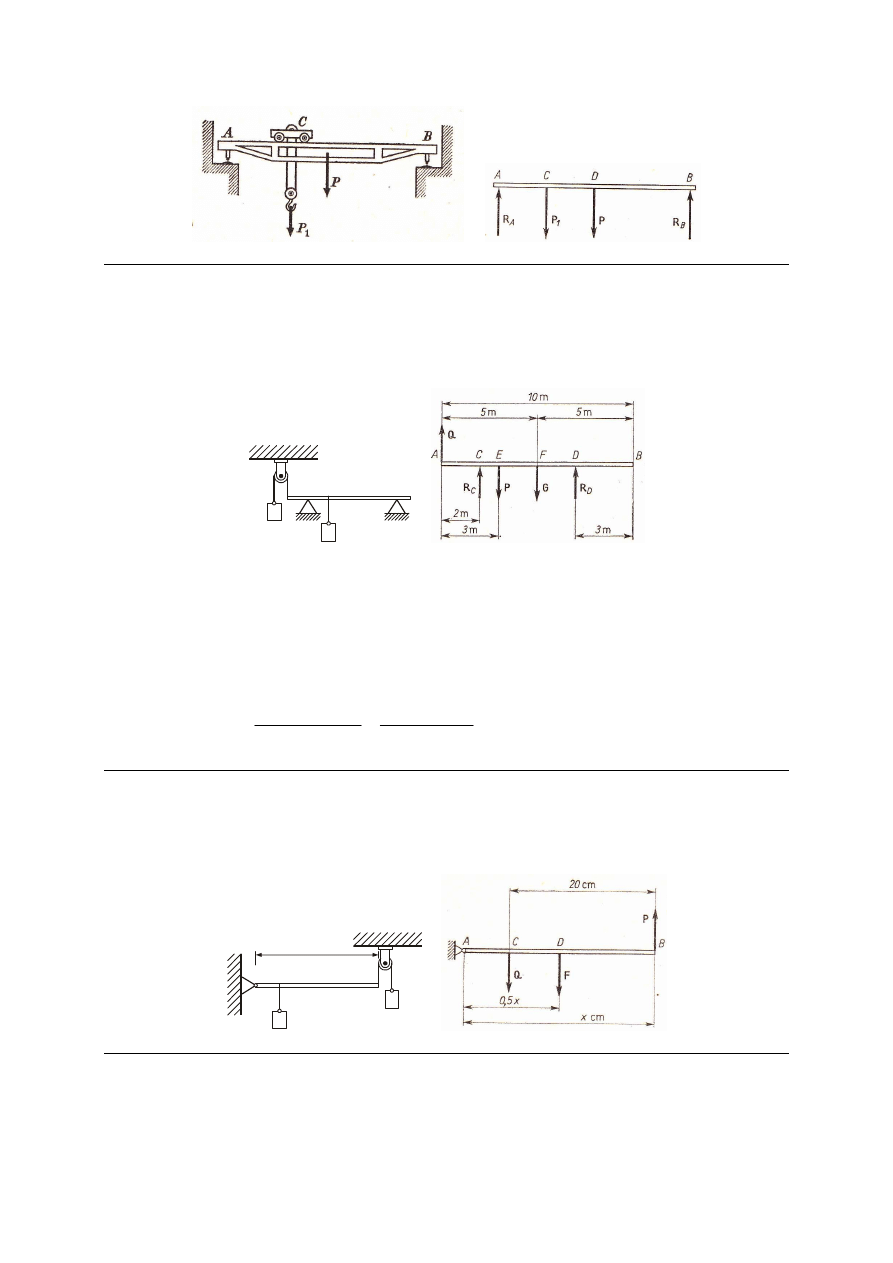
Odp. R
A
= (7 – 4n)T, R
B
= (3 + 4n)T, gdzie n = AC/AB.
M_81. Jednorodna belka AB o długości 10 m i ciężarze 2 kN leży na dwóch podporach C i D.
Podpora C odległa jest od końca A o 2 m, podpora D od końca B o 3 m. Koniec belki A
podciągany jest pionowo ku górze przez ciężar Q = 3 kN, przywiązany do liny przerzuconej
przez krążek. W odległości 3 m od końca A zawieszony jest na belce ciężar P = 8 kN.
Wyznaczyć reakcje podpór pomijając tarcie na krążku.
C
D
Q
P
A
D
B
Rozw.
0
Σ
=
=
Cx
ix
R
P
0
=
Cx
R
0
Σ
=
+
−
−
+
=
D
Cy
iy
R
G
P
R
Q
P
kN
3
4
3
2
8
=
−
−
+
=
−
−
+
=
D
Cy
R
Q
G
P
R
0
5
3
1
2
Σ
=
⋅
+
⋅
−
⋅
−
⋅
−
=
D
iC
R
G
P
Q
M
kN
4
5
3
2
8
2
3
5
3
2
=
⋅
+
+
⋅
=
⋅
+
+
⋅
=
G
P
Q
R
D
Odp. R
Cx
= 0, R
Cy
= 3 kN, R
D
= 4 kN.
M_82. Poziomy pręt AB o ciężarze 1 N może obracać się dookoła nieruchomego punktu A.
Koniec B pręta jest podciągany ku górze przerzuconą przez krążek linką z uwiązanym na
końcu ciężarem P = 1.5 N. W punkcie znajdującym się 20 cm od końca B zawieszony jest
ciężar Q = 5 N. Jaka jest długość x pręta AB, jeżeli znajduje się on w równowadze?
C
Q
P
A
B
x
Odp. x = 25 cm.
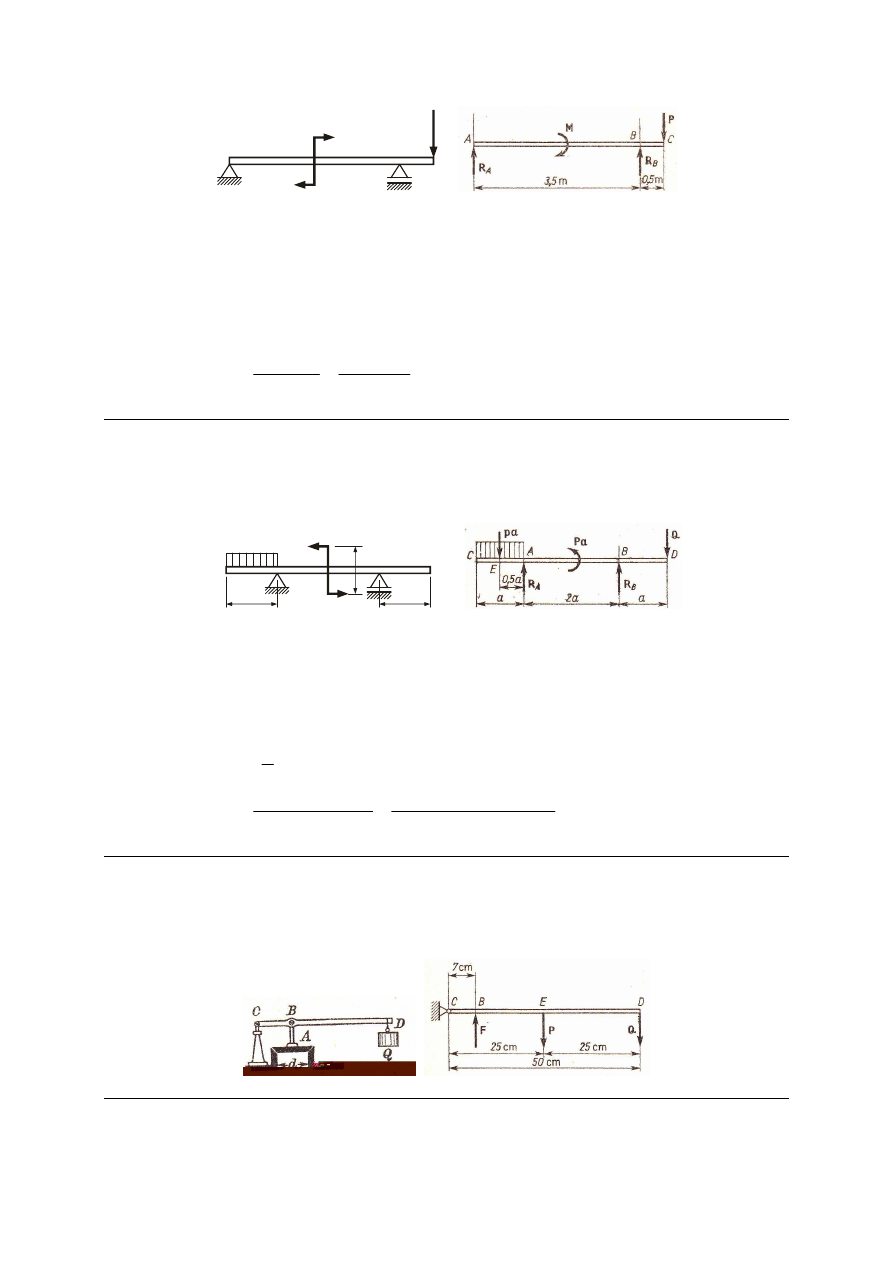
M_89. Na poziomą belkę wspornikową działa para sił o momencie M = 60 kNm, a w punkcie
C pionowa siła P = 20 kN. Rozpiętość belki AB = 3.5 m, długość wspornika BC = 0.5 m.
Wyznaczyć reakcje podpór.
A
B
P
M
Rozw.
0
Σ
=
=
Ax
ix
R
P
0
=
Ax
R
0
Σ
=
−
+
=
P
R
R
P
B
Ay
iy
kN
20
40
20
−
=
−
=
−
=
B
Ay
R
P
R
0
4
5
.
3
Σ
=
⋅
−
⋅
+
−
=
P
R
M
M
B
iA
kN
40
5
.
3
4
20
60
5
.
3
4
=
⋅
+
=
⋅
+
=
P
M
R
B
Odp. R
Ax
= 0, R
Ay
= -20 kN, R
B
= 40 kN.
M_90. Na dwuwspornikową poziomą belkę działa para sił (P, P), na jej lewy wspornik –
jednostajnie rozłożone obciążenie bieżące p, a w punkcie D prawego wspornika – pionowe
obciążenie Q. Wyznaczyć reakcje podpór, jeśli P = 10 kN, Q = 20 kN, p = 20 kN/m,
a = 0.8 m, AB = 2a.
A
B
Q
P
P
p
C
D
a
a
a
Rozw.
0
Σ
=
=
Ax
ix
R
P
0
=
Ax
R
0
Σ
=
⋅
−
−
+
=
a
p
Q
R
R
P
B
Ay
iy
kN
15
21
8
.
0
20
20
=
−
⋅
+
=
−
⋅
+
=
B
Ay
R
a
p
Q
R
0
3
2
2
Σ
=
⋅
−
⋅
+
⋅
+
⋅
⋅
=
a
Q
a
R
a
P
a
a
p
M
B
iA
kN
21
2
10
8
.
0
20
5
.
0
20
3
2
5
.
0
3
=
−
⋅
⋅
−
⋅
=
−
⋅
−
=
P
a
p
Q
R
B
Odp. R
Ax
= 0, R
Ay
= 15 kN, R
B
= 21 kN.
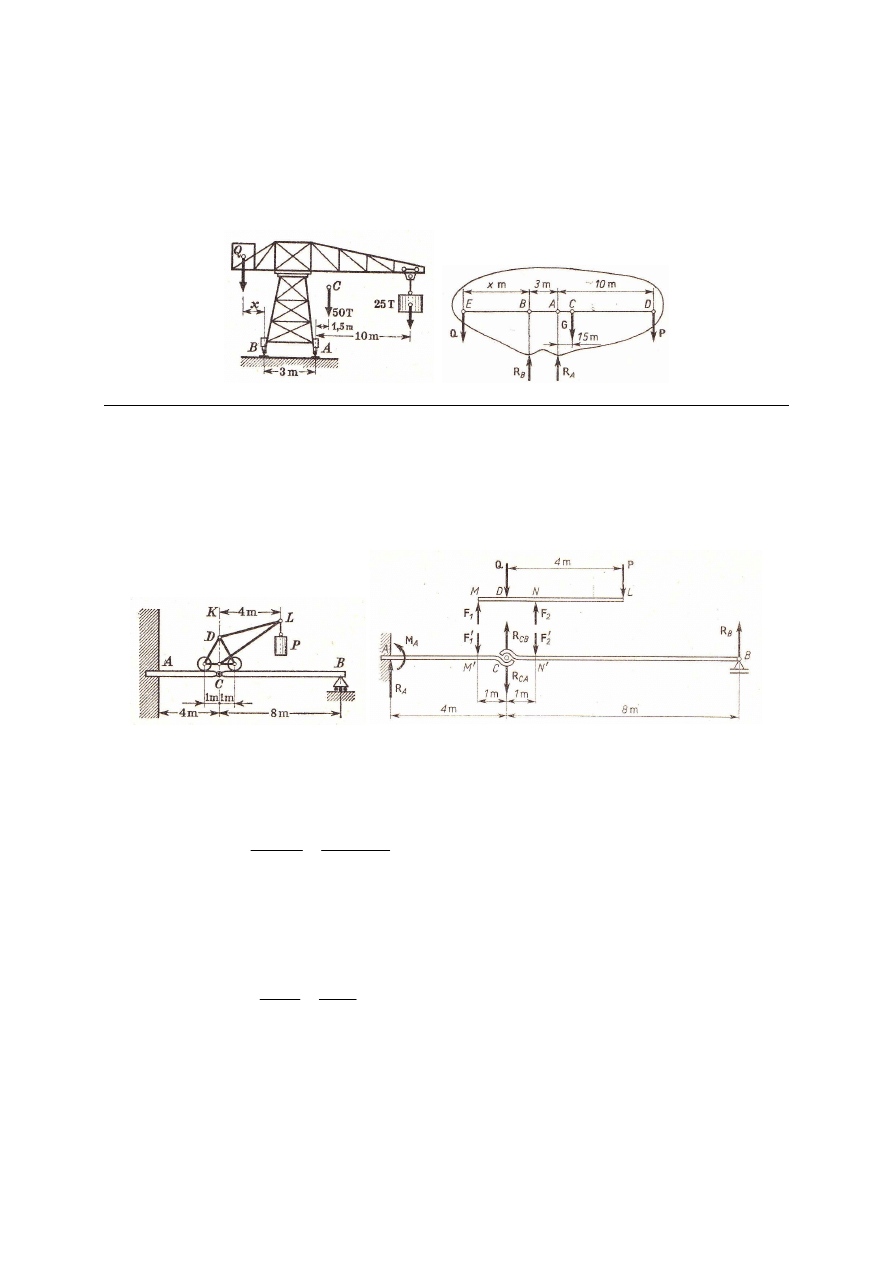
M_92. Zawór bezpieczeństwa kotła parowego połączony jest prętem AB z jednorodną
dźwignią CD o długości 50 cm i ciężarze 10 N, która może obracać się dookoła
nieruchomego punktu C; średnica zaworu d = 6 cm, ramię BC = 7 cm. Jaki ciężar Q należy
zawiesić na końcu D dźwigni, aby zawór otwierał się przy 1.1 MPa nadciśnienia?
Odp. Q = 430 N.
M_95. Ciężar dźwigu bez przeciwwagi wynosi 500 kN i działa wzdłuż prostej odległej od
pionu prawej szyny A o 1.5 m. Udźwig wózka wynosi 250 kN, a wysięg 10 m od pionu
prawej szyny. Wyznaczyć najmniejszy ciężar Q oraz największą odległość x środka ciężkości
przeciwwagi od pionu lewej szyny, tak aby dźwig nie wywrócił się przy wszelkich
położeniach wózka zarówno obciążonego, jak i nie obciążonego. Ciężar własny wózka
pominąć.
Odp. Q = 333 kN, x = 6.75 m.
M_112. Pozioma belka przegubowa ACB ma koniec A zamurowany w ścianie, koniec B zaś
oparty na przesuwnej podporze; w punkcie C znajduje się przegub. Belka obciążona jest
dźwigiem unoszącym ciężar P = 10 kN. Przy wysunięciu ramienia dźwigu na odległość
KL = 4 m środek ciężkości dźwigu leży na pionowej CD. Ciężar dźwigu wynosi Q = 50 kN.
Wymiary pokazane są na rysunku. Pomijając ciężar belki, obliczyć reakcje podpór w
punktach A i B. Ramię z ciężarem leży w jednej płaszczyźnie z belką AB.
Rozw. Z warunków równowagi dźwigu:
0
Σ
2
1
=
−
−
+
=
Q
P
F
F
P
iy
kN
10
50
10
50
2
1
=
−
+
=
−
+
=
F
P
Q
F
0
5
1
2
Σ
2
=
⋅
−
⋅
−
⋅
=
P
Q
F
M
iM
kN
50
2
50
10
5
2
5
2
=
+
⋅
=
+
=
Q
P
F
Z warunków równowagi belki BC
0
'
Σ
2
=
−
+
=
F
R
R
P
B
CB
iy
kN
25
.
6
75
.
43
50
'
2
=
−
=
−
=
CB
B
R
F
R
0
7
'
8
Σ
2
=
⋅
+
⋅
−
=
F
R
M
CB
iB
kN
75
.
43
8
50
7
8
'
7
2
=
⋅
=
⋅
=
F
R
CB
Z warunków równowagi belki AC
0
Σ
=
=
Ax
ix
R
P
0
=
Ax
R
0
'
Σ
1
=
−
−
=
CA
Ay
iy
R
F
R
P
kN
75
.
53
75
.
43
10
'
1
=
+
=
+
=
CA
Ay
R
F
R

0
4
3
'
Σ
1
=
⋅
−
⋅
−
=
CA
A
iA
R
F
M
M
kNm
205
75
.
43
4
10
3
4
'
3
1
=
⋅
+
⋅
=
⋅
+
⋅
=
CA
A
R
F
M
Odp.
0
=
Ax
R
,
kN
75
.
53
=
Ay
R
,
kNm
205
=
A
M
,
kN
25
.
6
=
B
R
.
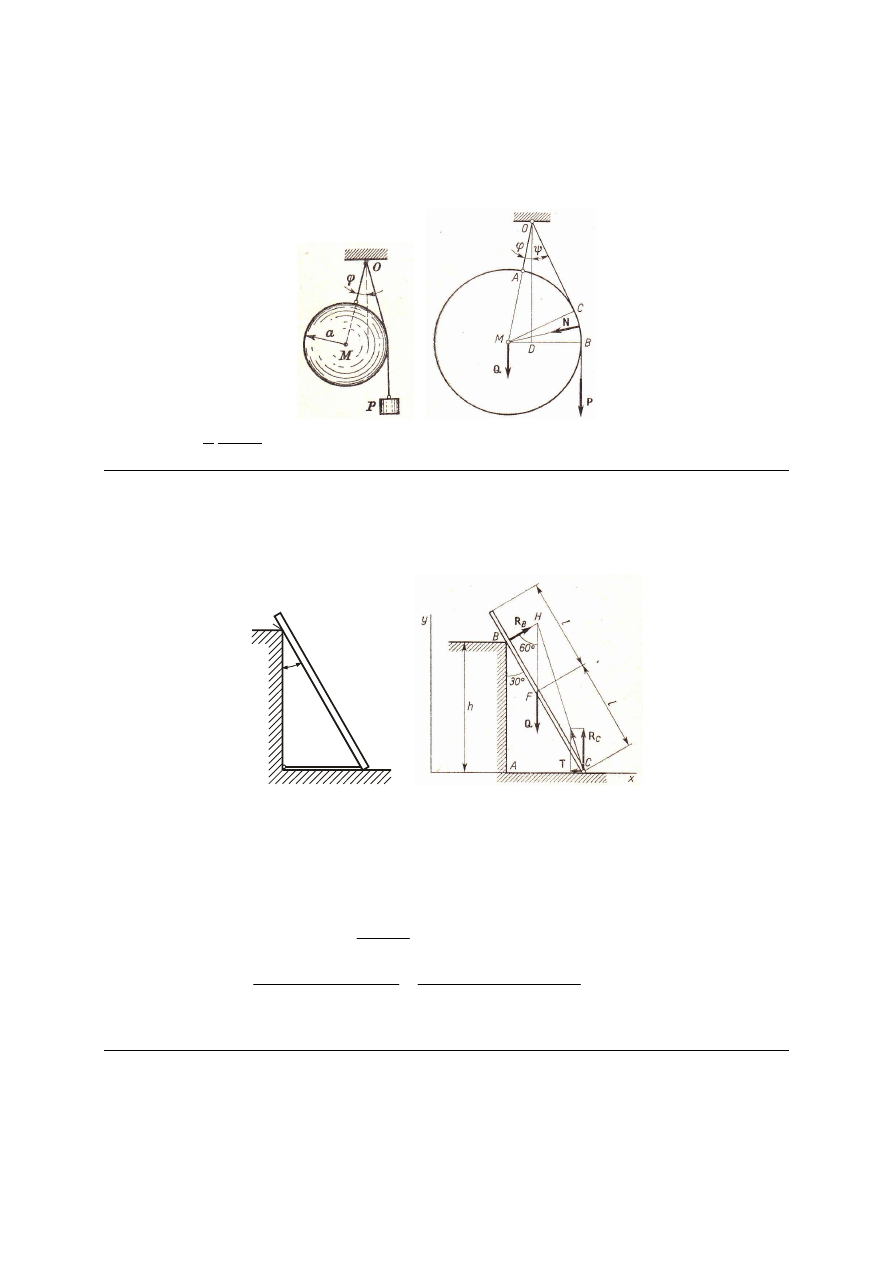
4. Dowolny płaski układ sił
M_115. Jednorodna kula o ciężarze Q i promieniu a oraz ciężarek P wiszą na linkach
zaczepionych w punkcie O, jak pokazano na rysunku. Odległość OM = b. Wyznaczyć kąt φ,
jaki tworzy w położeniu równowagi prosta OM z pionem.
Odp.
Q
P
P
b
a
+
=
ϕ
sin
.
M_119. Jednorodna belka o ciężarze 600 N i długości 4 m, opierająca się jednym końcem na
gładkiej podłodze, a w pośrednim punkcie B – na słupie o wysokości 3 m, tworzy z pionem
kąt 30º. Belka utrzymywana jest w takim położeniu przez linkę AC, przeciągniętą wzdłuż
podłogi. Wyznaczyć siłę w lince T, reakcje R
B
i R
C
. Tarcie pominąć.
A
C
B
30°
Rozw.
0
60
sin
Σ
=
−
°
=
T
R
P
B
ix
N
150
60
sin
2
.
173
60
sin
=
°
⋅
=
°
=
B
R
T
0
60
cos
Σ
=
−
°
+
=
Q
R
R
P
B
C
iy
N
4
.
513
60
cos
2
.
173
600
60
cos
=
°
⋅
−
=
°
−
=
B
C
R
Q
R
0
30
cos
30
sin
Σ
=
°
⋅
−
°
⋅
⋅
=
h
R
l
Q
M
B
iC
N
2
.
173
3
30
cos
30
sin
2
600
30
cos
30
sin
=
°
⋅
°
⋅
⋅
=
°
⋅
°
⋅
⋅
=
h
l
Q
R
B
Odp. T = 150 N, R
B
= 173.2 N, R
C
= 513.4 N.
M_122. Jednorodny pręt AB o ciężarze 1 kN opiera się jednym końcem na gładkiej poziomej
podłodze, drugim zaś na gładkiej płaszczyźnie nachylonej pod kątem 30º do poziomu. Koniec
B pręta podtrzymywany jest przez linkę przerzuconą przez krążek C i obciążoną ciężarem P.
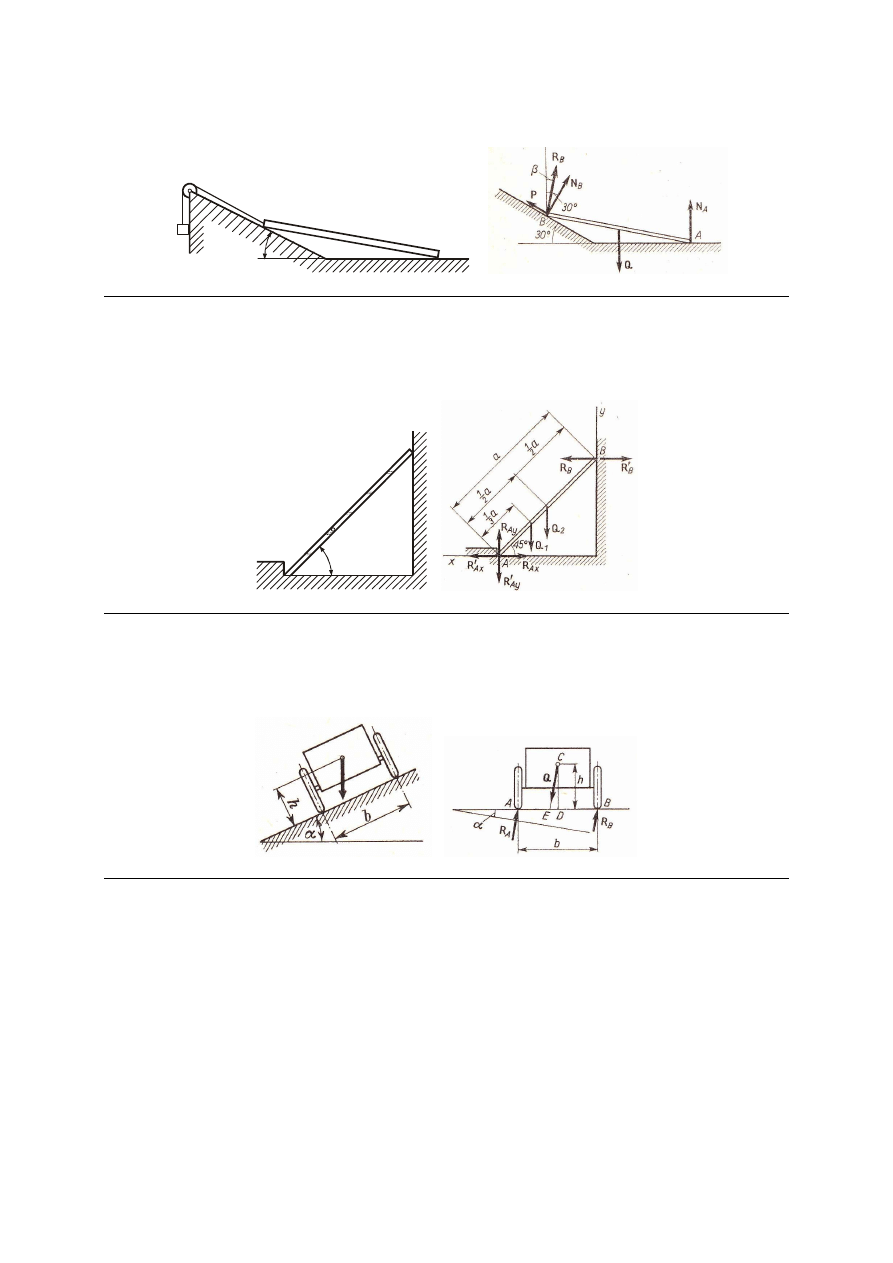
Część linki BC jest równoległa do pochyłej płaszczyzny. Pomijając tarcie na krążku
wyznaczyć ciężar P i oddziaływania N
A
i N
B
na podłogę i pochyłą płaszczyznę.
A
C
P
B
30°
Odp. P = 250 N, N
A
= 500 N, N
B
= 433 N.
M_125. Do gładkiej ściany jest przystawiona jednorodna drabina AB, nachylona pod kątem
45º do poziomu. Ciężar drabiny wynosi 200 N. W punkcie D odległym od dolnego końca o ⅓
długości drabiny stoi człowiek o ciężarze 600 N. Znaleźć oddziaływanie drabiny na podporę
A i na ścianę.
A
D
B
O
45°
Odp. X
A
= 300 N, Y
A
= 800 N, X
B
= –300 N.
M_137. Normalne oddziaływanie każdego z tylnych kół samochodu na nawierzchnię na
drodze poziomej wynosi 5 kN. Jakie będzie normalne oddziaływanie tych kół na drogę
nachyloną do poziomu pod kątem α = 5º, jeżeli wzniesienie środka ciężkości wynosi h = 0.8
m, a rozstaw kół b = 1.4 m?
Odp. Oddziaływanie niższego koła wynosi 5.48 kN, wyższego 4.48 kN.
M_143. Most składa się z dwóch części złączonych przegubem A i przymocowanych do
przyczółków przegubami B i C. Ciężar każdej części mostu wynosi 40 kN, ich środki
ciężkości leżą w punktach D i E. Na moście znajduje się ciężar P = 20 kN. Wymiary
pokazane są na rysunku. Obliczyć reakcję działającą na przegub A i reakcje w punktach B i C.
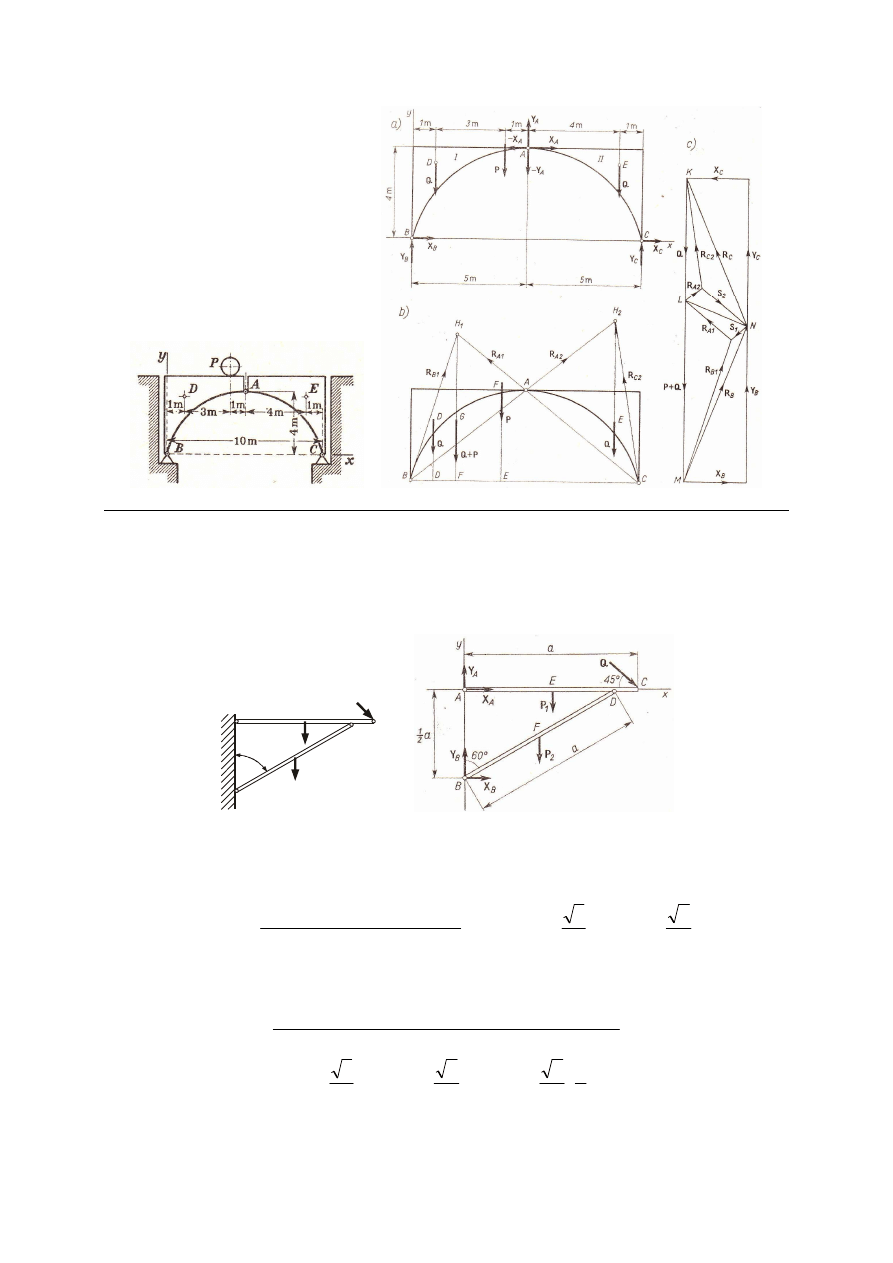
Odp. X
A
= ±20 kN, X
B
= –X
C
= 20 kN, Y
A
= ±8 kN, Y
C
= 48 kN, Y
B
= 52 kN.
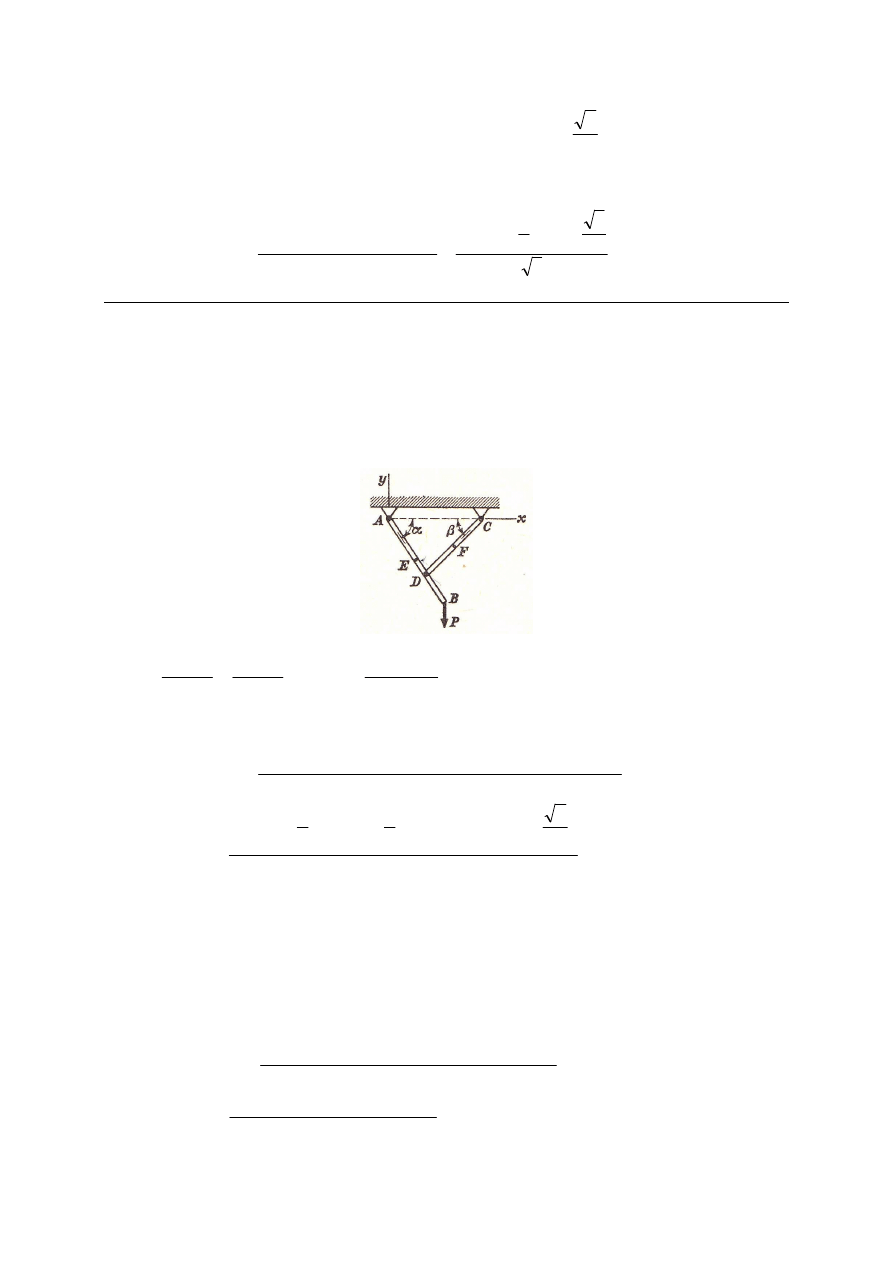
M_153. Dwa pręty AC i BD mające równe długości są połączone przegubowo w punkcie D
oraz przymocowane do pionowej ściany w punktach A i B. Pręt AC jest obciążony w punkcie
E pionową siłą P
1
= 400 N, a w punkcie C siłą Q = 1 kN nachyloną do poziomu pod kątem
45º. Pręt BD w punkcie F obciąża pionowa siła P
2
= 400 N. Wiedząc, że AE = EC, BF = FD,
wyznaczyć reakcje przegubów A i B.
A
P
1
P
2
60°
B
C
D
E
F
Q
Rozw. Przedstawić najpierw rozwiązanie dla dwóch belek oddzielnie, a następnie szybsze w
następujący sposób:
Równania równowagi dla całego układu:
0
60
cos
2
60
sin
2
45
sin
Σ
2
1
=
°
⋅
⋅
+
°
⋅
⋅
−
⋅
°
−
⋅
−
=
a
R
a
P
a
Q
a
P
M
Bx
iA
N
2161
2
2
1000
2
2
3
400
400
60
cos
45
sin
2
60
sin
2
1
=
⋅
⋅
+
⋅
+
=
°
°
+
°
⋅
+
=
Q
P
P
R
Bx
0
60
cos
2
60
sin
60
cos
2
45
cos
2
45
sin
Σ
2
1
=
°
⋅
⋅
−
+
°
⋅
⋅
−
°
⋅
⋅
°
−
⋅
°
−
⋅
−
=
a
R
a
P
a
Q
a
Q
a
P
M
Ax
iB
N
2868
2
1
2
2
1000
2
2
2
1000
2
2
3
400
400
60
cos
60
cos
45
cos
2
45
sin
2
60
sin
2
1
−
=
⋅
⋅
⋅
+
⋅
⋅
+
⋅
+
−
=
=
°
°
°
+
°
+
°
⋅
+
−
=
Q
Q
P
P
R
Ax
0
45
sin
Σ
2
1
=
+
+
°
−
−
−
=
By
Ay
iy
R
R
Q
P
P
P
N
59
1448
2
2
1000
400
400
45
sin
2
1
=
−
⋅
+
+
=
−
°
+
+
=
By
Ay
R
Q
P
P
R
Dla belki BD:
0
60
sin
60
sin
2
60
cos
2
Σ
2
=
°
⋅
⋅
+
°
⋅
⋅
−
°
⋅
⋅
=
a
P
a
R
a
R
M
By
Bx
iD
N
1448
3
2
3
400
2
1
2161
2
60
sin
2
60
sin
60
cos
2
2
=
⋅
+
⋅
⋅
=
°
⋅
°
+
°
⋅
=
P
R
R
Bx
By
Odp. R
Ax
= –2868 N, R
Ay
= 59 N, R
Bx
= 2161 N, R
By
= 1448 N.
M_154. Wieszak składa się z dwóch belek AB i CD połączonych przegubowo w punkcie D i
przymocowanych do sufitu przegubami A i C. Ciężar belki AB wynosi Q
1
= 600 N i
przyłożony jest w punkcie E. Ciężar belki CD wynosi Q
2
= 500 N i przyłożony jest w punkcie
F. W punkcie B do belki AB przyłożona jest pionowa siła P = 2000 N. Wyznaczyć reakcje
przegubów A i C, jeżeli dane są następujące wymiary: AB = 1 m, CD = 0.8 m, AE = 0.4 m,
CF = 0.4 m oraz kąty nachylenia belek do poziomu wynoszące odpowiednio: α = 60° i β =
45°.
Rozw:
°
=
°
60
sin
75
sin
CD
AC
,
m
892
.
0
866
.
0
966
.
0
8
.
0
=
⋅
=
AC
Równania równowagi dla całego układu:
(
)
0
cos
cos
cos
Σ
2
1
=
⋅
+
−
⋅
−
⋅
⋅
−
⋅
⋅
−
=
AC
R
β
CF
AC
Q
α
AB
P
α
AE
Q
M
Cy
iA
(
)
N
1597
892
.
0
2
2
4
.
0
892
.
0
500
2
1
1
2000
2
1
4
.
0
600
cos
cos
cos
2
1
=
⋅
−
⋅
+
⋅
⋅
+
⋅
⋅
=
=
−
⋅
+
⋅
⋅
+
⋅
⋅
=
AC
β
CF
AC
Q
α
AB
P
α
AE
Q
R
Cy
0
Σ
2
1
=
−
−
−
+
=
P
Q
Q
R
R
P
Cy
Ay
iy
N
1503
1597
2000
500
600
2
1
=
−
+
+
=
−
+
+
=
Cy
Ay
R
P
Q
Q
R
0
Σ
=
+
=
Cx
Ax
ix
R
R
P
N
1347
−
=
−
=
Cx
Ax
R
R
Dla belki DC:
(
)
0
sin
cos
cos
Σ
2
=
⋅
⋅
−
⋅
⋅
+
⋅
−
⋅
−
=
β
CD
R
β
CD
R
β
CF
CD
Q
M
Cx
Cy
iD
(
)
(
)
N
1347
8
.
0
8
.
0
1597
4
.
0
8
.
0
500
sin
cos
cos
2
=
⋅
+
−
⋅
−
=
=
⋅
⋅
⋅
+
⋅
−
⋅
−
=
β
CD
β
CD
R
β
CF
CD
Q
R
Cy
Cx
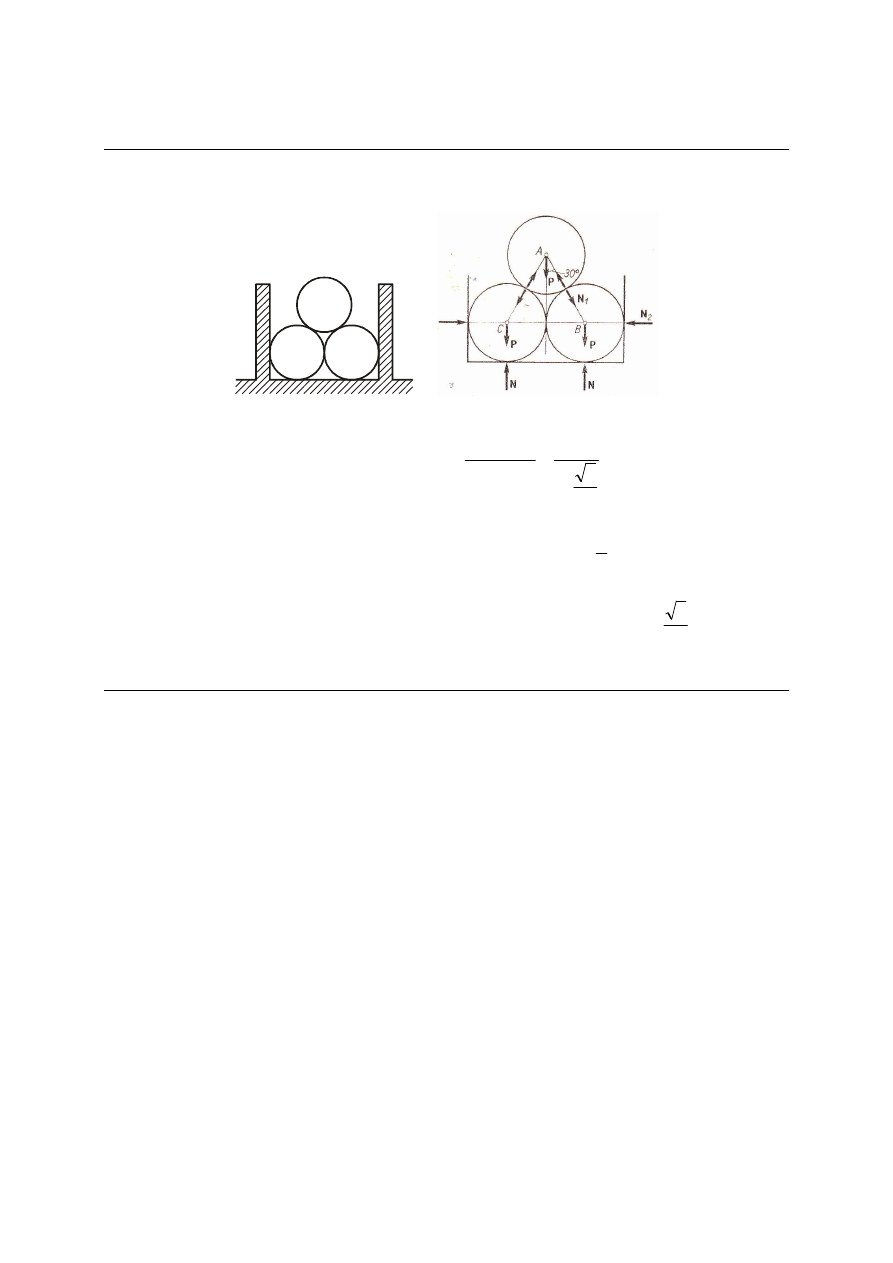
Odp. R
Ax
= –1347 N, R
Cx
= 1347 N, R
Ay
= 1503 N, R
Cy
= 1597 N.
M_170. Trzy jednakowe rury o ciężarze P = 1200 N każda leżą, jak pokazano na rysunku.
Obliczyć oddziaływanie dolnych rur na podłoże i na boczne gładkie ściany. Tarcie pominąć.
Rozw:
Równanie równowagi dla górnej rury:
0
30
cos
2
Σ
1
=
−
°
⋅
=
P
N
P
iy
N
693
2
3
2
2000
30
cos
2
1
=
⋅
=
°
⋅
=
P
N
Nacisk na ścianę boczną:
0
30
sin
Σ
2
1
=
−
°
⋅
=
N
N
P
ix
N
346
2
1
693
30
sin
1
2
=
⋅
=
°
⋅
=
N
N
Nacisk rur dolnych na podłoże:
0
30
cos
Σ
1
=
+
−
°
⋅
−
=
N
P
N
P
iy
N
1800
2
3
693
1200
30
cos
1
=
⋅
+
=
°
+
=
N
P
N
Odp. Oddziaływanie każdej dolnej rury na podłoże równa się 1800 N, a oddziaływanie na
ścianę 346 N.
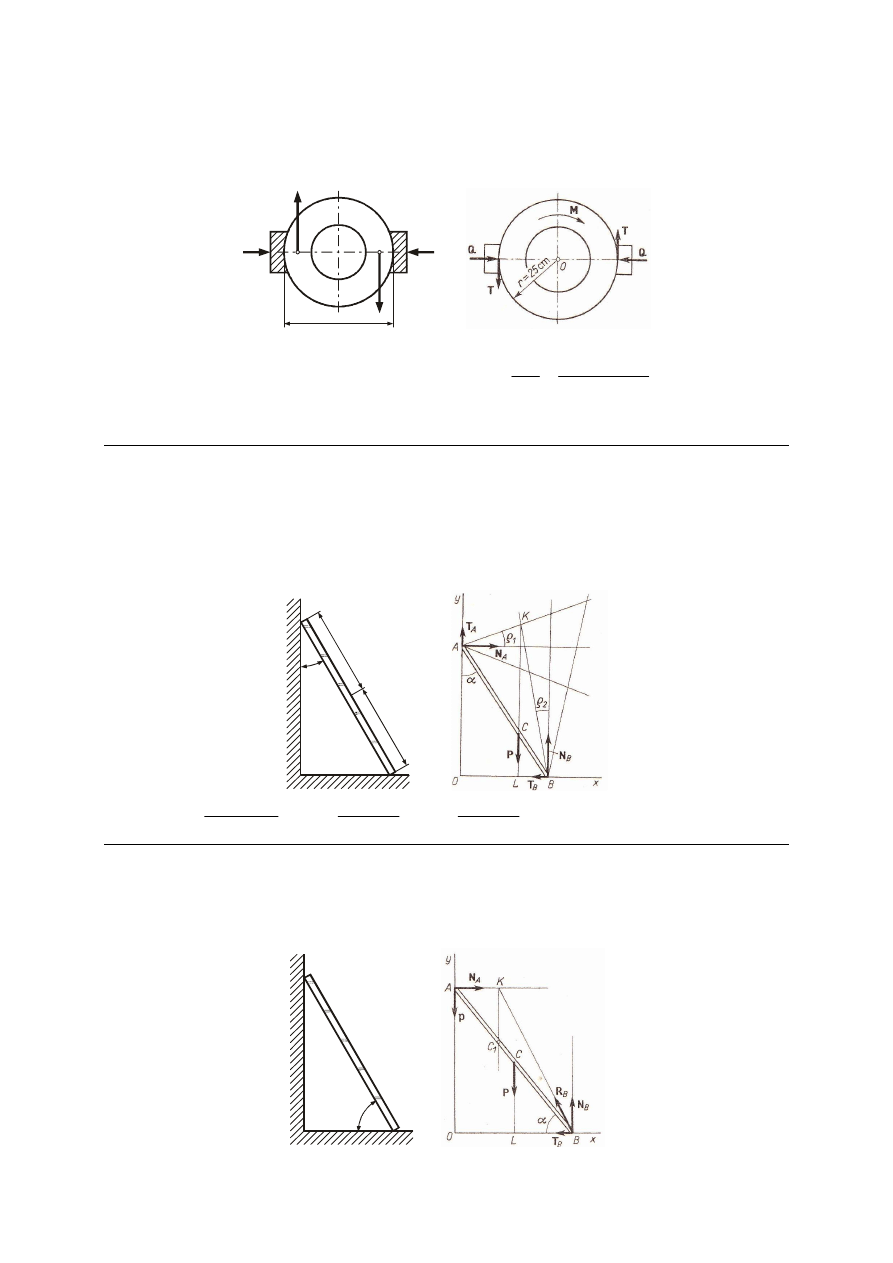
M_171. Do wału przyłożono parę sił o momencie M = 1 kNm. Na wale zaklinowany jest
bęben hamulcowy, którego promień r = 25 cm. Obliczyć jaką siłą Q należy dociskać do bębna
klocki hamulcowe, aby unieruchomić wał, jeżeli współczynnik tarcia statycznego klocków po
bębnie µ = 0.25.
Q
Q
2r
Rozw. Siły tarcia wynoszą
Q
µ
T
=
. Zatrzymanie nastąpi, gdy
0
2
=
−
rT
M
,
0
2
=
−
Q
µ
r
M
,
kN
8
25
.
0
25
.
0
2
1
2
=
⋅
⋅
=
=
µ
r
M
Q
Odp. Q = 8 kN.
M_177. Do pionowej ściany przystawiona jest drabina AB oparta dolnym końcem o poziomą
podłogę. Współczynnik tarcia drabiny o ścianę wynosi µ
1
, a o podłogę µ
2
. Ciężar drabiny
wraz ze znajdującym się na niej człowiekiem wynosi P i przyłożony jest w punkcie C, który
dzieli długość drabiny w stosunku m:n. Wyznaczyć największy kąt α zawarty między ścianą
a drabiną w położeniu równowagi oraz normalne składowe reakcji ściany N
A
i podłogi N
B
dla
tej wartości kąta α.
A
B
C
α
na
m
a
Odp.
(
)
2
1
2
tan
µ
µ
µ
α
n
m
n
m
−
+
=
,
2
1
2
1
µ
µ
µ
+
=
P
N
A
,
2
1
1
µ
µ
+
=
P
N
B
.
M_178. Drabina AB o ciężarze P opiera się o gładką ścianę i o poziomą chropowatą podłogę.
Siła tarcia w punkcie B nie przekracza µ
0
N, gdzie µ
0
oznacza współczynnik tarcia statycznego,
N – normalną reakcję podłogi. Pod jakim kątem α należy przystawić drabinę do ściany, aby
mógł po niej wejść do samej góry człowiek ważący p?
A
B
α
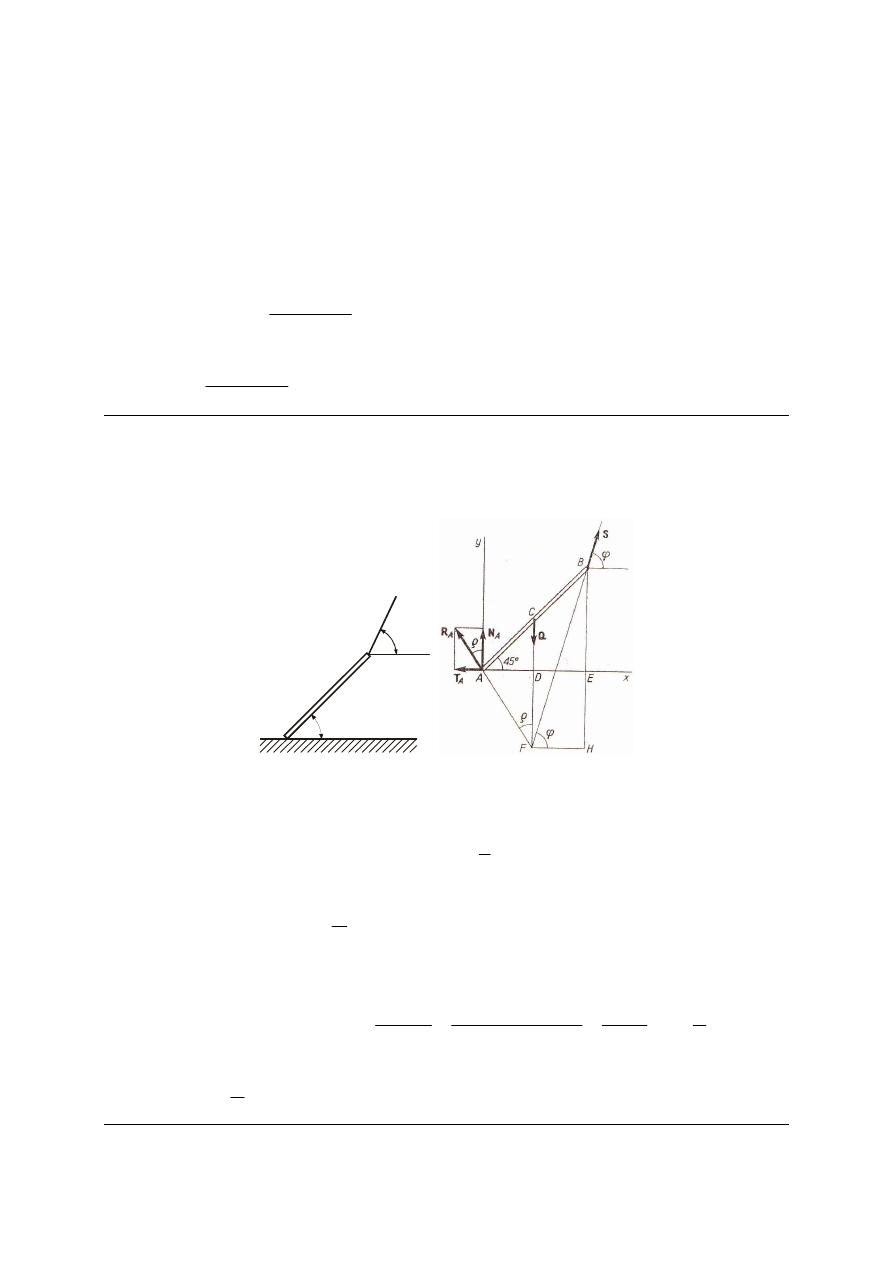
Rozw.
0
Σ
=
−
=
B
A
ix
T
N
P
0
Σ
=
−
−
=
p
P
N
P
B
iy
0
sin
2
cos
cos
2
Σ
=
⋅
⋅
−
⋅
⋅
+
⋅
⋅
=
α
a
N
α
a
P
α
a
p
M
A
iB
B
B
N
µ
T
⋅
=
0
(
)
p
P
µ
N
µ
T
N
B
B
A
+
=
⋅
=
=
0
0
(
)
0
sin
2
cos
cos
2
0
=
⋅
+
−
⋅
+
⋅
α
p
P
µ
α
P
α
p
(
)
p
P
µ
p
P
α
+
+
=
0
2
2
tan
Odp.
(
)
p
P
p
P
+
+
=
0
2
2
tan
µ
α
.
M_181. Jednorodna belka AB opiera się w punkcie A na chropowatej poziomej podłodze,
koniec B zaś jest podtrzymywany przez linkę. Współczynnik tarcia belki o podłogę wynosi µ,
a kąt α utworzony przez belkę i podłogę wynosi 45º. Przy jakim kącie nachylenia linki do
poziomu belka zacznie się poruszać?
A
B
α
φ
Rozw. Równania równowagi pręta
0
cos
Σ
=
−
=
A
ix
T
φ
S
P
0
sin
Σ
=
−
+
=
Q
φ
S
N
P
A
iy
0
45
cos
2
45
sin
45
cos
Σ
=
°
⋅
⋅
+
°
⋅
⋅
−
°
⋅
⋅
−
=
l
Q
l
T
l
N
M
A
A
B
A
A
N
µ
T
=
0
2
=
+
⋅
−
−
Q
N
µ
N
A
A
(
)
A
N
µ
Q
⋅
+
=
1
2
(1)
A
N
Q
φ
S
−
=
sin
(2)
A
T
φ
S
=
cos
Dzieląc stronami (1) i (2):
(
)
µ
µ
µ
N
µ
N
N
µ
N
µ
N
Q
φ
A
A
A
A
A
1
2
2
1
1
2
tan
+
=
+
=
−
⋅
+
=
−
=
Odp.
µ
ϕ
1
2
tan
+
=
M_191. Wyznaczyć siłę P potrzebną do jednostajnego toczenia walca o średnicy d = 60 cm
i o ciężarze Q = 3 kN po poziomej płaszczyźnie, jeżeli współczynnik tarcia przy toczeniu
wynosi δ = 0.5 cm, a kąt jaki siła tworzy z poziomem, α = 30º.
P
α
Rozw. Warunek równowagi
0
2
cos
sin
Σ
=
⋅
+
⋅
−
⋅
=
d
α
P
δ
α
P
δ
Q
M
iA
N
18
.
57
2
6
.
0
30
cos
005
.
0
30
sin
005
.
0
3000
2
cos
sin
=
⋅
°
+
⋅
°
⋅
=
⋅
+
⋅
⋅
=
d
α
δ
α
δ
Q
P
Odp. P = 57.18 N.
5. Statyka wykreślna
M_198. Wyznaczyć reakcje podpór i siły w prętach wiązania dachowego przedstawionego na
rysunku.
M_203. Wyznaczyć wykreślnie i sprawdzić analitycznie reakcje podpór i siły w prętach
kratownicy przedstawionej na rysunku:
4T
2T
1
8
7
6
9
4
5
2
3
A
B
5m
5m
1.5m
1.5m
204. Wyznaczyć reakcje podpór i siły w prętach kratownicy przedstawionej na rysunku.
4T
1T
a
a
a
a
a
a
1
2
3
6
7
8
5
9
4
A
B
Odp. X
A
= –10 kN, Y
A
= 30 kN, Y
B
= 10 kN.
Rozdział II. PRZESTRZENNY UKŁAD SIŁ
6. Przestrzenny układ sił zbieżnych
7. Sprowadzenie układu sił do najprostszej postaci
8. Równowaga dowolnego układu sił
M_255. Na poziomy wał AB nasadzono koło zębate C o promieniu koła podziałowego 1 m i
koło D o promieniu koła podziałowego 10 cm. Inne wymiary podano na rysunku Na koło C
wzdłuż stycznej do koła podziałowego działa w kierunku poziomym siła P = 100 N, a na koło
D, też wzdłuż stycznej, siła pionowa Q. Wyznaczyć siłę Q i reakcje w łożyskach A i B
w przypadku równowagi.
Rozw.
0
Σ
=
⋅
−
⋅
=
r
Q
R
P
M
iy
N
1000
1
.
0
1
100
=
⋅
=
⋅
=
r
R
P
Q
0
Σ
=
⋅
+
⋅
=
AD
Q
AB
R
M
Bz
ix
N
100
1
1
.
0
1000
−
=
⋅
−
=
⋅
−
=
AB
AD
Q
R
Bz
0
Σ
=
⋅
−
⋅
−
=
AC
P
AB
R
M
Bx
iz
N
90
1
9
.
0
100
−
=
⋅
−
=
⋅
−
=
AB
AC
P
R
Bx
0
Σ
=
+
+
=
P
R
R
P
Bx
Ax
ix
N
10
90
100
−
=
+
−
=
−
−
=
Bx
Ax
R
P
R
0
Σ
=
+
+
=
Bz
Az
iz
R
R
Q
P
N
900
100
1000
−
=
+
−
=
−
−
=
Bz
Az
R
Q
R
Odp. Q = 1000 N, R
Ax
= –10 N, R
Az
= –900 N, R
Bx
= –90 N, R
Bz
= –100 N.
M_256. Robotnik podnosi ciężar Q = 800 N za pomocą kołowrotu przedstawionego
schematycznie na rysunku. Promień bębna R = 5 cm, długość ramienia korby AK = 40 cm,
AC = BC = 50 cm. Wyznaczyć siłę P działającą na korbę i oddziaływanie osi kołowrotu na
podpory A i B przy poziomym położeniu ramienia korby. Siłę P przyjąć jako pionową.
Odp. P = 100 N, N
Ax
= 400 N, N
Az
= –100 N, N
Bx
= 400 N, N
Bz
= 0.
M_257. Za pomocą kołowrotu, przedstawionego schematycznie na rysunku, podnoszony jest
ciężar Q = 1000 N. Promień bębna wynosi R = 5 cm, długość ramienia korby KD = 40 cm,
DA = 30 cm, AC = 40 cm, CB = 60 cm. Lina schodzi z bębna po stycznej nachylonej do
poziomu pod kątem 60º. Wyznaczyć siłę P działającą na korbę i reakcje podpór A i B, jeśli
ramię korby jest w położeniu poziomym.
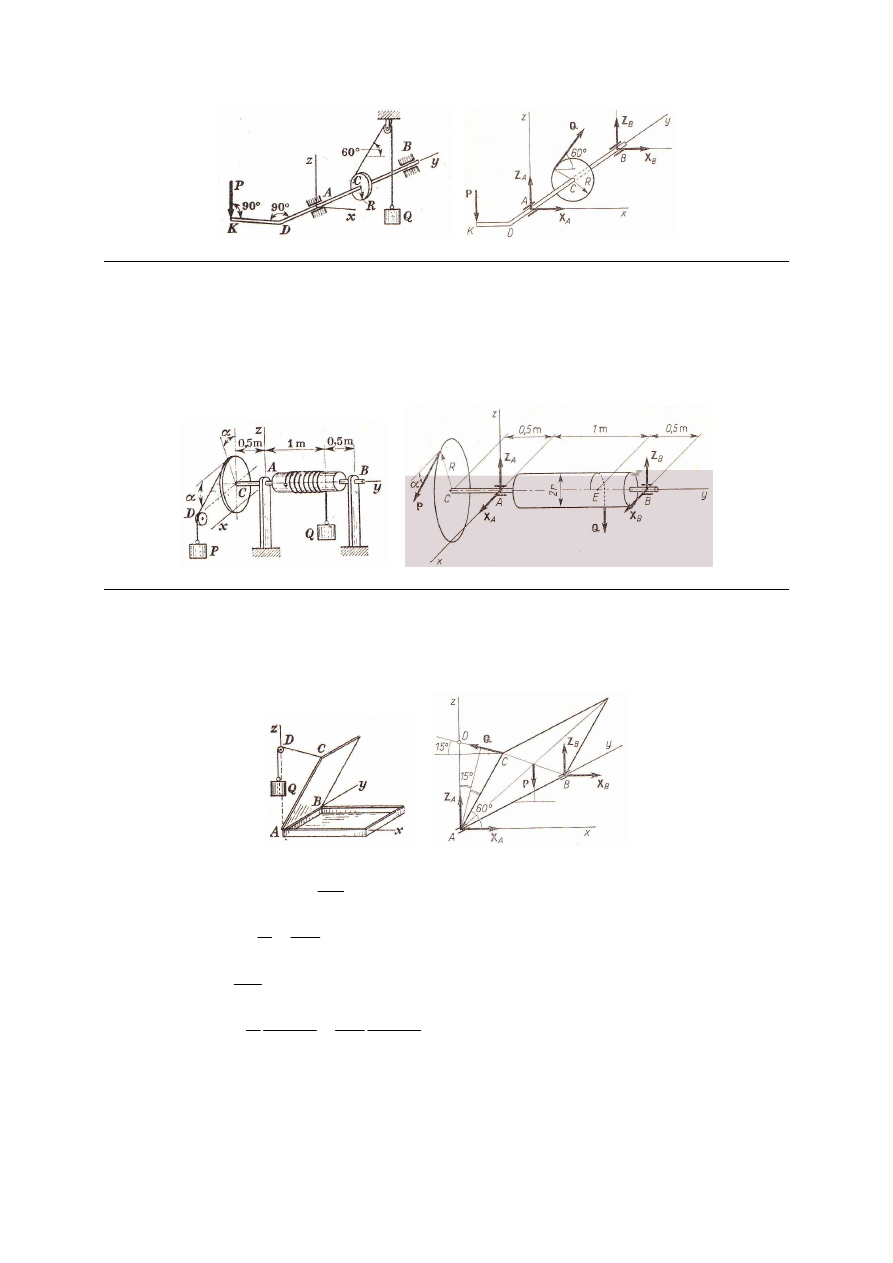
Odp. P = 125 N, X
A
= –300 N, Z
A
= –357 N, X
B
= –200 N, Z
B
= –384 N.
M_258. Na wał AB kołowrotku nawiniętą jest lina z zawieszonym na niej ciężarem Q.
Promień koła C nasadzonego na wał jest sześć razy większy od promienia wału; inne
wymiary podano na rysunku. Lina nawinięta na koło C i ciągnięta ciężarkiem P = 60 N
schodzi z koła po stycznej nachylonej do poziomu pod kątem α = 30º. Wyznaczyć wielkość
ciężaru Q, dla którego kołowrót będzie w równowadze, a także reakcje w łożyskach A i B,
pomijając ciężar własny wału i tarcie.
Odp. Q = 360 N, X
A
= –69.3 N, Z
A
= 160 N, X
B
= 17.3 kN, Z
B
= 230 N.
M_260. Jednorodna pokrywa prostokątna o ciężarze P = 400 N jest podtrzymywana przez
ciężar Q, tak że tworzy z poziomem kąt 60º. Wyznaczyć (pomijając tarcie w bloku D) ciężar
Q i reakcje w zawiasach A i B, jeśli blok D jest zamocowany na prostej pionowej
przechodzącej przez A oraz jeśli AD = AC.
Rozw.
0
2
Σ
=
⋅
−
⋅
=
AB
P
AB
R
M
Bz
ix
N
200
2
400
2
=
=
=
P
R
Bz
0
15
cos
60
cos
2
Σ
=
°
⋅
⋅
−
°
=
AC
Q
AC
P
M
iy
N
5
.
103
15
cos
60
cos
2
400
15
cos
60
cos
2
=
°
°
=
°
°
=
P
Q
0
Σ
=
⋅
−
=
AB
R
M
Bx
iz
N
0
=
Bx
R
0
15
cos
Σ
=
°
⋅
−
+
=
Q
R
R
P
Bx
Ax
ix
N
97
.
99
15
cos
5
.
103
15
cos
=
°
⋅
=
−
°
⋅
=
Bx
Ax
R
Q
R
0
15
sin
Σ
=
−
°
⋅
+
+
=
P
Q
R
R
P
Bz
Az
iz
N
2
.
173
15
sin
5
.
103
200
400
15
sin
=
°
⋅
−
−
=
°
⋅
−
−
=
Q
R
P
R
Bz
Az
Odp. Q = 103.5 N, R
Ax
= 99.97 N, R
Az
= 173.2 N, R
Bx
= 0 N, R
Bz
= 200 N.
M_265. Jednorodna rama prostokątna o ciężarze 200 N przymocowana do ściany za pomocą
kulistego przegubu A i zawiasu B jest utrzymywana w położeniu poziomym linką CE
zaczepioną do ramy w punkcie C i do gwoździa w punkcie E. Gwóźdź jest wbity do ściany na
prostej pionowej przechodzącej przez A, przy czym kąt ECA = kąt BAC = 30º. Wyznaczyć
siłę w lince i reakcje podpór.
Odp. T = 200 N, X
A
= 86.6 N, Y
A
= 150N, Z
A
= 100 N, X
B
= Z
B
= 0.
M_266. Półka wagonowa ABCD, która może obracać się dookoła osi AB, jest utrzymywana
w położeniu poziomym za pomocą pręta ED przymocowanego przegubowo w punkcie E do
pionowej ściany BAE. Ciężar półki wynosi 800 N, przy czym siła ta przechodzi przez punkt
przecięcia przekątnych prostokąta ABCD. Dane są wymiary: AB = 150 cm, AD = 60 cm,
AK = BH = 25 cm, a długość pręta ED = 75 cm. Wyznaczyć reakcje w zawiasach K i H i siłę
S w pręcie ED pomijając jego ciężar własny.
Odp. S = –667 N, X
H
= 133 N, Z
H
= 500 N, X
K
= –667 N, Z
K
= -100 N.
M_270. Drzwi prostokątne o pionowej osi obrotu AB są uchylone o kąt CAD = 60º
i utrzymywane w tym położeniu dwiema linkami, z których jedna, CD, przerzucona jest przez
blok i obciążona ciężarem P = 320 N, druga, EF, jest przywiązana do punktu F podłogi.
Ciężar drzwi wynosi Q = 640 N, szerokość AD = AC = 180 cm, a wysokość AB = 240 cm.
Pomijając tarcie bloku wyznaczyć siłę T w lince EF oraz reakcje zawiasu walcowego
w punkcie A i stopowego w punkcie B.
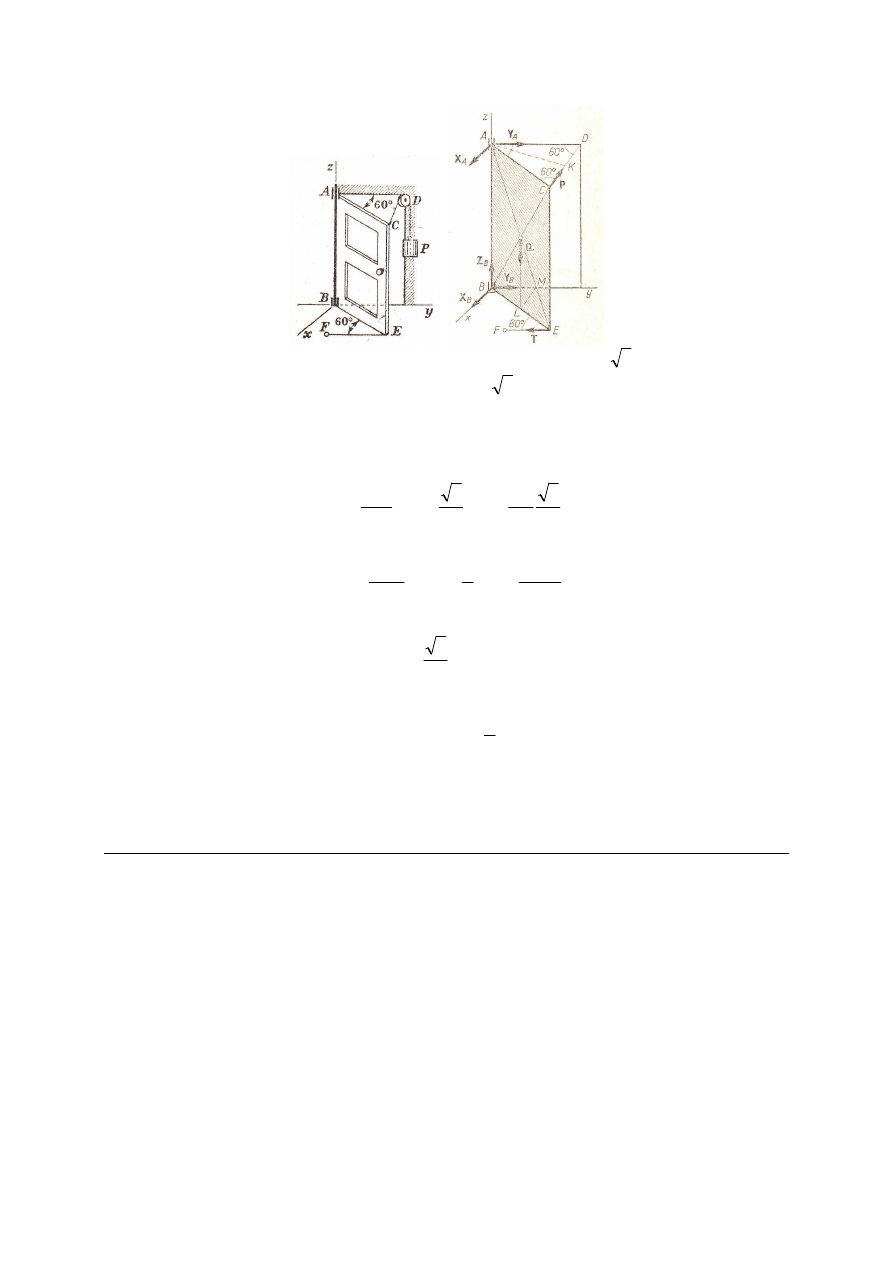
Rozw.
Z
rysunku
CD
AK
⊥
,
2
/
3
60
sin
AC
AC
AK
=
°
⋅
=
,
2
/
AC
BL
=
,
4
/
60
cos
AC
BL
BM
=
°
⋅
=
,
4
/
3
60
sin
AC
BL
LM
=
°
⋅
=
.
0
60
sin
Σ
=
°
⋅
⋅
−
⋅
=
AC
T
AK
P
M
iz
N
320
=
=
P
T
0
30
cos
Σ
=
⋅
+
⋅
°
⋅
−
⋅
=
LM
Q
AB
P
AB
R
M
Ax
iy
N
28
.
69
4
3
4
.
2
8
.
1
640
2
3
320
30
cos
=
−
=
−
°
⋅
=
AB
LM
Q
P
R
Ax
0
30
sin
Σ
=
⋅
−
⋅
°
⋅
−
⋅
−
=
BM
Q
AB
P
AB
R
M
Ay
ix
N
280
4
.
2
4
8
.
1
640
2
1
320
4
30
sin
−
=
⋅
−
−
=
−
°
⋅
−
=
AB
AC
Q
P
R
Ay
0
30
cos
Σ
=
°
⋅
−
+
=
P
R
R
P
Bx
Ax
ix
N
85
.
207
28
.
69
2
3
320
30
cos
=
−
⋅
=
−
°
⋅
=
Ax
Bx
R
P
R
0
30
sin
Σ
=
°
⋅
+
−
+
=
P
T
R
R
P
By
Ay
iy
N
440
280
2
1
320
320
30
sin
=
+
−
=
−
°
⋅
−
=
Ay
By
R
P
T
R
0
Σ
=
−
=
Q
R
P
Bz
iz
N
640
=
=
Q
R
Bz
Odp. T = 320 N, R
Ax
= 69.28 N, R
Ay
= –280 N, R
Bx
= 207.85 N, R
By
= 440 N, R
Bz
= 640 N.
M_271. Wyznaczyć reakcje łożyska szyjnego B i stopowego A żurawia oraz siłę S
przenoszoną przez linę, jeśli wysięgnik żurawia ciągnięty jest linką poziomą przerzuconą
przez blok i obciążoną ciężarem Q = 1000 N. Kąt nachylenia liny S do poziomu wynosi 60º,
ciężar żurawia G = 20 kN, ciężar podnoszony P = 40 kN. Wymiary podano na rysunku.
Tarcie na bloku pominąć.
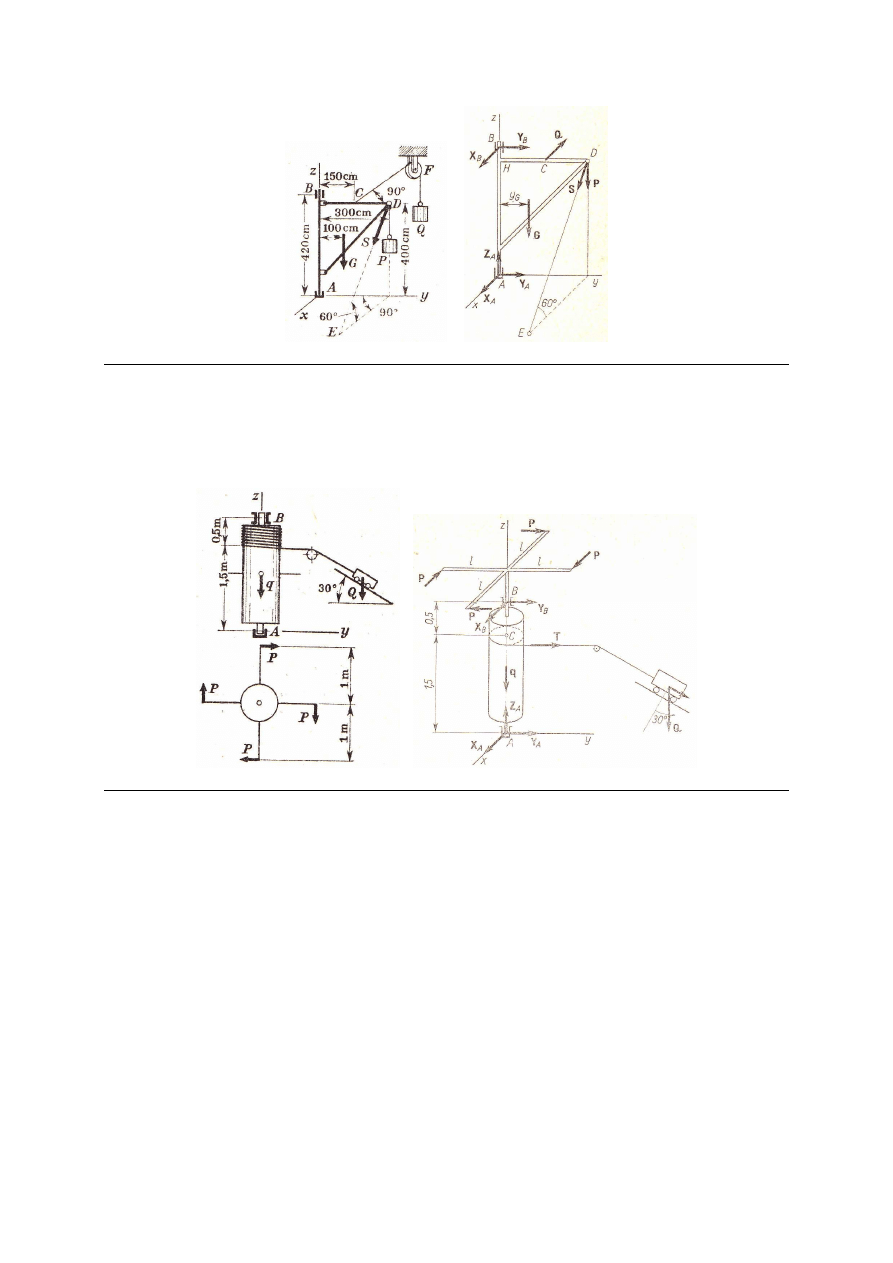
Odp. S = 1000 N, X
A
= 24 N, Y
A
= 33.95 kN, Z
A
= 60.87 kN, X
B
= 476 N, Y
B
= –33.95 kN.
M_278. Wagonik o ciężarze Q wyciągany jest ruchem jednostajnym za pomocą urządzenia
pokazanego na rysunku. Wyznaczyć siły P przyłożone do czterech dźwigni prostopadłych do
osi bębna z oraz reakcje podpór A i B, jeżeli ciężar bębna q = 0.1T, jego średnica d = 24 cm,
Q = 10 kN, długość ramienia l = 1 m. Oś bębna zamocowana jest pionowo w łożysku
stopowym A i zwykłym B.
Odp. Y
A
= –1250 N, Z
A
= 1000 N, Y
B
= –3750 N, X
A
= X
B
= 0, P = 150 N.
M_279. Ręczny kołowrót służący do wyciągania urobku z pochyłego wykopu składa się
z drewnianego wału o średnicy 0.25 m i długości 1.5 m obracanego w łożyskach A i B za
pomocą korby AC. Wyznaczyć siłę F przyłożoną do punktu C prostopadle do ramienia korby
oraz reakcje łożysk przy pionowym położeniu korby pokazanym na rysunku, jeżeli ciężar
wału wynosi 300 N, ciężar sań z urobkiem 1000 N, współczynnik tarcia sań o drewniany tor
0.5, kąt nachylenia wykopu do poziomu 30º, długość ramienia korby 0.5 m, a miejsce zejścia
liny z bębna jest odległe o 50 cm od łożyska B. Odległości punktu C od prostej pionowej
przechodzącej przez A nie uwzględniać, a obrót przyjąć jako jednostajny.
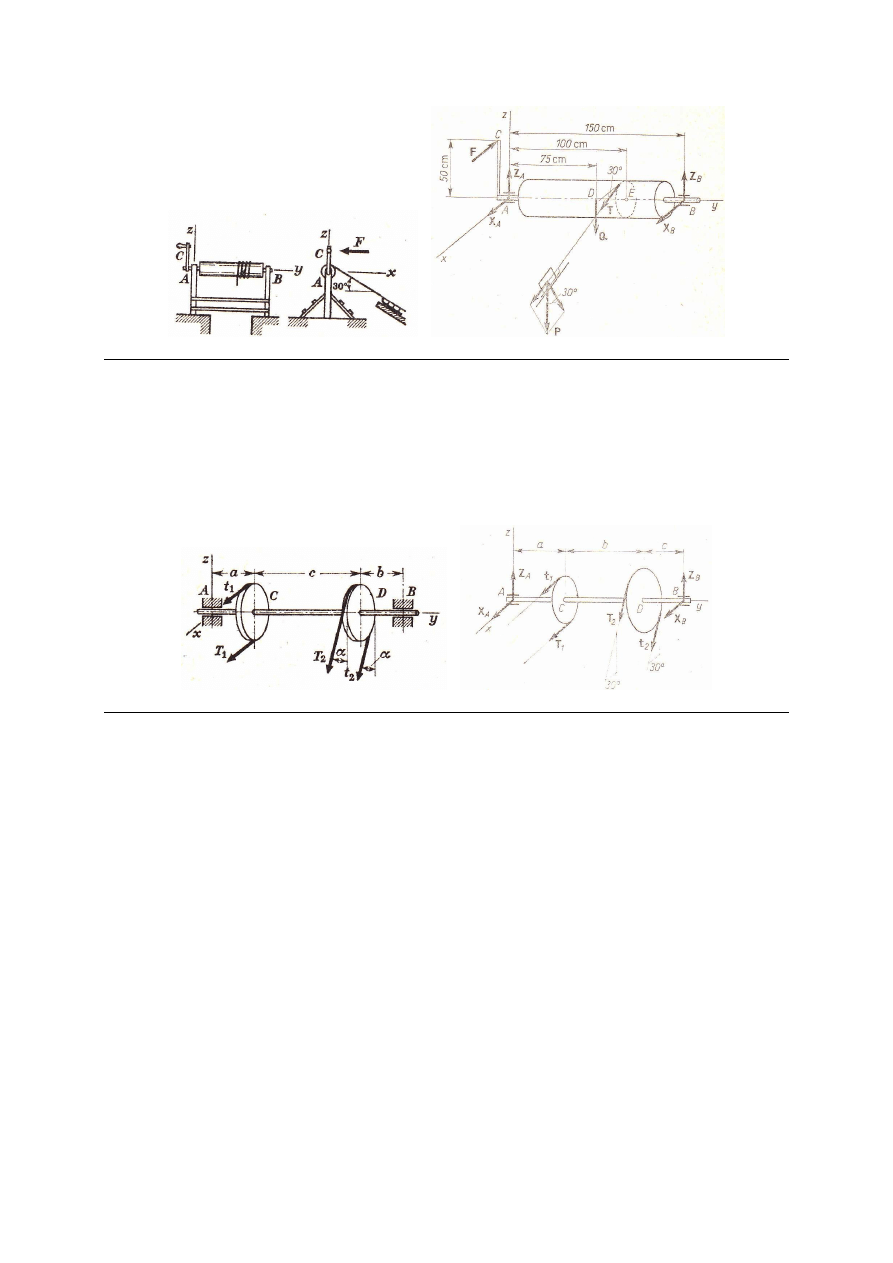
Odp. X
A
= –36.1 N, Z
A
= 306 N, X
B
= –539 N, Z
B
= 461 N, F = 233 N.
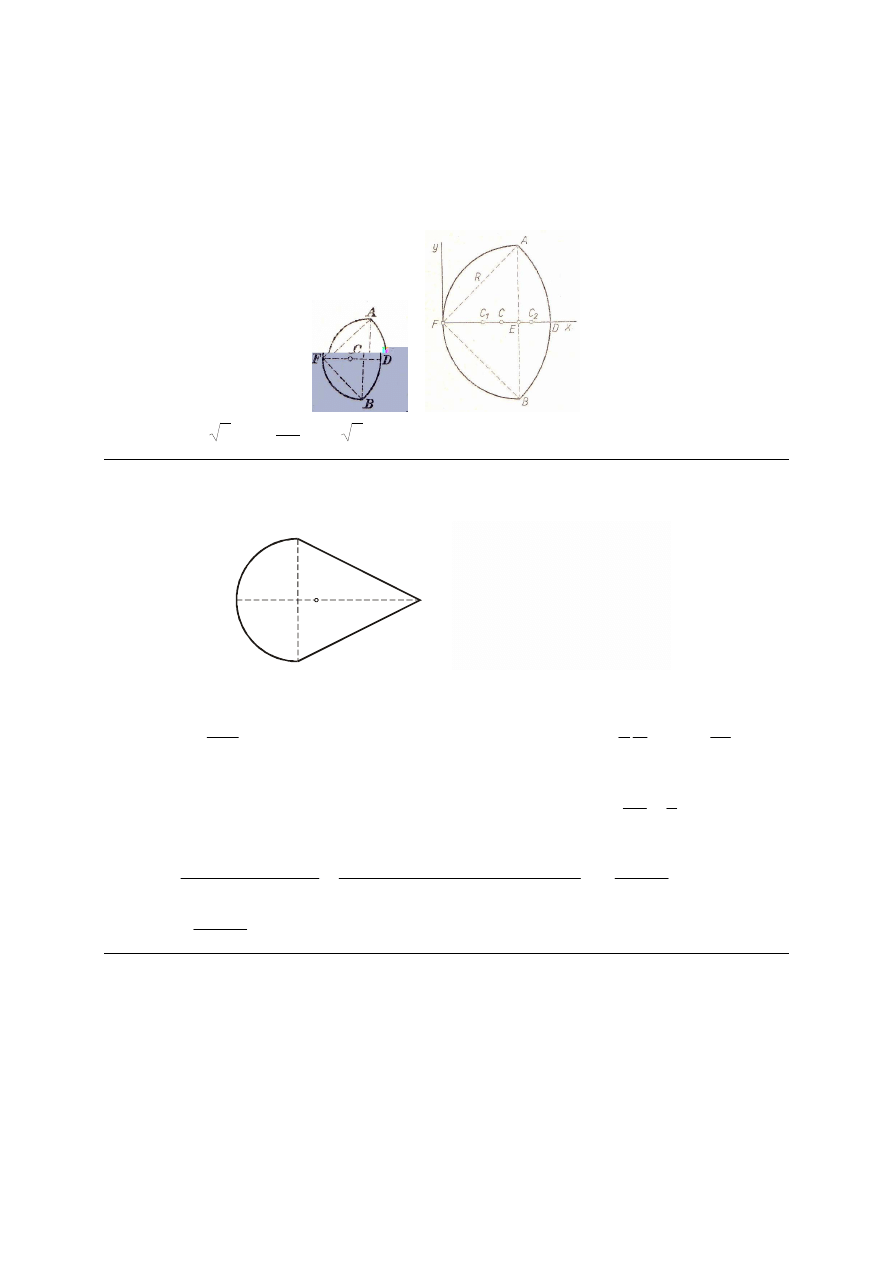
M_280. Poziomy wał pędniany, na którym są osadzone dwa koła pasowe C i D, może się
obracać w łożyskach A i B. Promienie kół są r
1
= 20 cm, r
2
= 25 cm, odstęp kół od łożysk
a = b = 50 cm, a odległość między kołami c = 100 cm. Siły w gałęziach pasa nałożonego na
koło C są skierowane poziomo i mają wartości T
1
i t
1
, przy czym T
1
= 2t
1
= 5000 N, a siły
w gałęziach pasa nałożonego na koło D tworzą z pionem kąt α = 30º i mają wartości T
2
i t
2
,
przy czym T
2
= 2t
2
. Wyznaczyć siły T
2
i t
2
dla położenia równowagi oraz reakcje łożysk
spowodowane siłami w pasach.
Odp. T
2
= 4000 N, t
2
= 2000 N, X
A
= –6375 N, Z
A
= 1300 N, X
B
= –4125 N, Z
B
= 3900 N.
9. Środek ciężkości
M_286. Wyznaczyć położenie środka ciężkości C ramki AFBD składającej się z łuku ADB
będącego ćwiartką okręgu koła o promieniu FD = R i półokręgu AFB zbudowanego na
cięciwie AB jako na średnicy. Ciężar jednostki długości obu prętów tworzących ramkę jest
jednakowy.
Odp.
(
)
(
)
R
R
R
CF
524
.
0
2
2
3
2
1
2
=
−
+
−
=
π
.
M_287. Wyznaczyć położenie środka ciężkości C powierzchni ograniczonej półokręgiem
AOB o promieniu R i dwoma odcinkami równej długości AD i DB, jeśli OD = 3R.
O
A
B
C
D
Rozw.
Półkole ABO:
pole
2
2
1
R
π
S
=
, odcięta środka ciężkości
−
=
−
=
−
=
π
R
π
R
R
EC
OE
OC
3
4
1
3
4
1
1
Trójkąt ABD:
pole
2
2
2R
S
=
, odcięta środka ciężkości
R
R
R
EC
OE
OC
3
5
3
2
2
2
=
+
=
+
=
Dla całości:
(
)
(
)
R
π
π
R
R
R
π
R
R
R
π
π
R
S
S
S
OC
S
OC
OC
185
.
1
12
3
16
3
2
2
/
2
3
/
5
2
/
3
/
4
1
2
2
2
2
2
1
2
2
1
1
≈
+
+
=
+
⋅
+
−
=
+
⋅
+
⋅
=
Odp.
R
R
π
π
OC
185
.
1
12
3
16
3
≈
+
+
=
.
M_289. Wyznaczyć położenie środka ciężkości C jednorodnego krążka z okrągłym otworem
zakładając, że promień krążka wynosi r
1
, promień otworu r
2
, a środek otworu znajduje się w
odległości r
1
/2 od środka krążka.
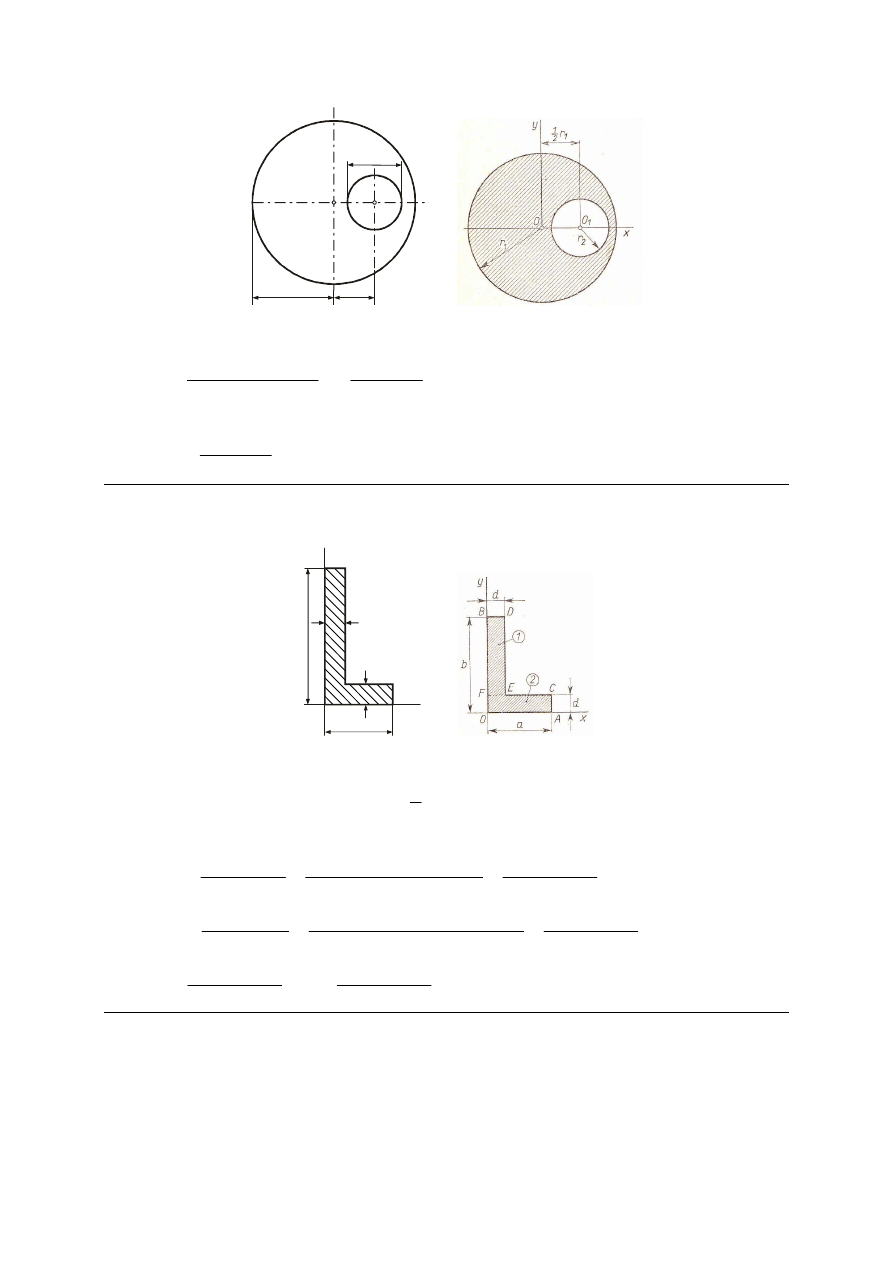
r
1
r
1
/2
O
O
1
x
2r
2
Rozw.
Pole figury:
(
)
2
2
2
1
r
r
π
S
−
=
(
)
(
)
2
2
2
1
2
2
1
2
2
2
1
1
2
2
2
1
2
2
/
0
r
r
r
r
r
r
π
r
r
π
r
π
x
C
−
−
=
−
⋅
+
⋅
−
=
Odp.
(
)
2
2
2
1
2
2
1
2
r
r
r
r
x
C
−
−
=
.
M_290. Znaleźć współrzędne środka ciężkości przekroju poprzecznego kątownika
nierównoramiennego, którego półki mają szerokość OA = a, OB = b, a grubość AC = BD = d.
d
d
y
x
B
D
C
A
O
a
b
Rozw. Przekrój kątownika dzielimy na dwa prostokąty, których pola i współrzędne środków
ciężkości oznaczamy przez S
1
i (x
1
, y
1
) oraz S
2
i (x
2
, y
2
).
(
)
d
d
b
S
−
=
1
,
2
/
1
d
x
=
,
(
)
d
b
y
+
=
2
1
1
,
ad
S
=
2
,
2
/
2
a
x
=
,
2
/
2
d
y
=
,
(
)
(
)
(
)
d
b
a
d
bd
a
ad
d
d
b
a
ad
d
d
d
b
S
S
x
S
x
S
x
C
−
+
−
+
=
+
−
⋅
+
⋅
−
=
+
+
=
2
2
/
2
/
2
2
2
1
2
2
1
1
,
(
) (
)
(
)
(
)
d
b
a
d
ad
b
ad
d
d
b
d
ad
d
b
d
d
b
S
S
y
S
y
S
y
C
−
+
−
+
=
+
−
⋅
+
+
⋅
−
=
+
+
=
2
2
/
2
/
2
2
2
1
2
2
1
1
Odp.
(
)
d
b
a
d
bd
a
x
C
−
+
−
+
=
2
2
2
,
(
)
d
a
b
d
ad
b
y
C
−
+
−
+
=
2
2
2
.
M_291. Znaleźć odległość środka ciężkości przekroju teownika ABCD od jego boku AC,
jeżeli wysokość środnika DB = h, szerokość półki AC = c, grubość półki wynosi d, a grubość
środnika b.
A
B
C
D
d
d
a
h
Rozw. Teownik dzielimy na dwa prostokąty pokazane na rysunku
(
)
b
d
h
S
−
=
1
,
(
)
2
/
1
d
h
y
+
=
,
ad
S
=
2
,
2
/
2
d
y
=
(
) (
)
(
)
(
)
bd
bh
ad
bd
bh
ad
ad
b
d
h
d
ad
d
h
b
d
h
S
S
y
S
y
S
y
C
−
+
−
+
=
+
−
⋅
+
+
−
=
+
+
=
2
2
/
2
/
2
2
2
2
1
2
2
1
1
Odp.
(
)
bd
bh
ad
bd
bh
ad
y
C
−
+
−
+
=
2
2
2
2
.
M_295. Przeprowadzić przez wierzchołek D jednorodnego prostokąta ABCD prostą DE tak,
aby po odcięciu części wzdłuż tej prostej i zawieszeniu pozostałego trapezu za wierzchołek E,
bok AD o długości a znalazł się w położeniu poziomym.
D
C
E
B
A
Rozw. Aby bok AD pozostawał w położeniu poziomym przy zawieszeniu płytki w punkcie E,
środek ciężkości F obciętej płytki musi leżeć na prostopadłej opuszczonej z punku E na bok
AD, a więc x
F
= EB.
Pole prostokąta AXEB:
xh
S
=
1
,
2
1
x
x
=
,
Pole trójkąta DXE:
h
x
a
S
2
2
−
=
,
3
2
x
a
x
x
−
+
=
0
2
2
2
2
2
1
2
2
1
1
=
−
+
⇒
+
+
=
a
ax
x
S
S
x
S
x
S
x
a
a
a
a
x
366
.
0
2
1
3
4
3
2
2
≈
−
=
+
−
=
Odp.
a
EB
x
366
.
0
≈
=
M_296. Dany jest kwadrat ABCD, którego boki mają długość a. Znaleźć takie położenie
punktu E, aby był on środkiem ciężkości powierzchni powstałej po wycięciu z kwadratu
równoramiennego trójkąta AEB.
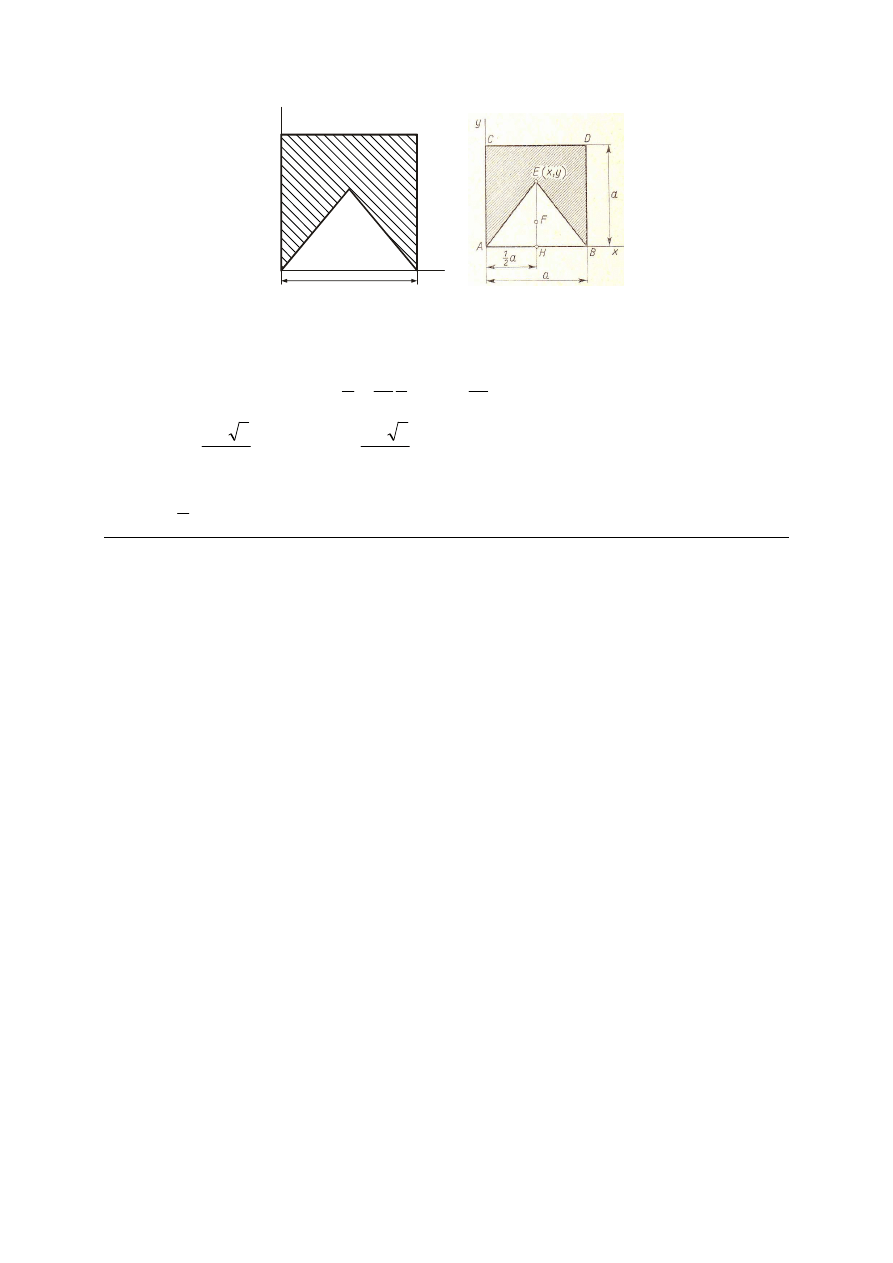
z
x
a
A
E
B
D
C
Pole trójkąta ABE:
2
/
1
az
S
=
,
3
/
1
z
HF
z
=
=
,
2
/
1
a
x
=
Pole figury AEBDC:
2
/
2
2
az
a
S
−
=
Pole kwadratu:
2
3
a
S
=
,
2
/
3
a
z
=
z
S
z
S
z
S
2
1
1
3
3
+
=
,
z
az
a
z
az
a
a
−
+
=
2
3
2
2
2
2
,
0
3
6
2
2
2
=
+
−
a
az
z
,
2
3
3
±
=
a
z
,
a
a
z
634
.
0
2
3
3
=
−
=
Odp.
2
a
x
=
,
a
z
634
.
0
=
.
Wyszukiwarka
Podobne podstrony:
30 Struktury zaleznosci miedzy wskaznikami zrow rozw K Chmura
Mieszcza
Ekon Rozw W 5 9
Ekon Rozw W 13
Ekon Rozw W 9
4 Statyka Kinetyka
Ekon Rozw W 17
logika rozw zadan v2
kolos2 rozw id 242277 Nieznany
al lin zad3 rozw
2010kolo1 rozw
ICh S schemat rozw zad konwekcja
ust. o szczeg. sposobach rozw. stos. pr., bhp
Podstawy Statyki Budowli
więcej podobnych podstron