
M
ię
d
zy
n
ar
o
d
o
w
e
S
to
su
n
k
i
G
o
sp
o
d
ar
cz
e
C
E
U
W
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
d
r
L
es
ze
k
W
in
ce
n
ci
ak
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
2
/
3
3
P
la
n
w
yk
ła
d
u
:
B
ila
n
s
p
ła
tn
ic
zy
P
o
d
st
aw
ow
e
p
oj
ęc
ia
Z
as
ad
y
ks
ię
go
w
an
ia
tr
an
sa
kc
ji
S
tr
u
kt
u
ra
b
ila
n
su
p
ła
tn
ic
ze
go
P
o
d
st
aw
ow
a
to
żs
am
oś
ć
b
ila
n
su
p
ła
tn
ic
ze
go
R
ów
n
ow
ag
a
b
ila
n
su
p
ła
tn
ic
ze
go
T
oż
sa
m
oś
ć
in
w
es
ty
cj
i
i
os
zc
zę
d
n
oś
ci
w
go
sp
o
d
ar
ce
ot
w
ar
te
j
P
rz
ep
ły
w
y
d
ób
r
i
ka
p
it
ał
u
w
go
sp
o
d
ar
ce
ot
w
ar
te
j
H
ip
ot
ez
a
b
liź
n
ia
cz
yc
h
d
efi
cy
tó
w
P
ar
ad
ok
s
F
el
d
st
ei
n
a-
H
or
io
ki
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
3
/
3
3
P
o
d
st
aw
o
w
e
p
o
ję
ci
a
B
ila
n
s
p
ła
tn
ic
zy
–
p
o
d
st
aw
ow
e
p
o
ję
ci
a
D
E
F
IN
IC
JA
:
B
ila
n
s
p
ła
tn
ic
zy
je
st
st
at
ys
ty
cz
n
ym
ze
st
aw
ie
n
ie
m
tr
an
sa
kc
ji
d
ok
on
yw
an
yc
h
w
p
ew
n
ym
pr
ze
d
zi
al
e
cz
as
u
p
om
ię
d
zy
re
zy
d
en
ta
m
i
d
an
ej
go
sp
o
d
ar
ki
a
re
sz
tą
św
ia
ta
.
T
ra
n
sa
kc
je
m
ię
d
zy
d
an
ą
go
sp
o
d
ar
ką
a
re
sz
tą
św
ia
ta
d
ot
yc
zą
:
◮
pr
ze
p
ły
w
u
d
ób
r,
u
sł
u
g
i
d
o
ch
o
d
u
◮
pr
ze
p
ły
w
u
ak
ty
w
ów
fi
n
an
so
w
yc
h
(n
al
eż
n
oś
ci
i
zo
b
ow
ią
za
ń
)
◮
tr
an
sf
er
ów
je
d
n
os
tr
on
n
yc
h
(p
rz
ek
az
ów
,
d
ar
ów
,
p
om
o
cy
m
ię
d
zy
n
ar
o
d
ow
ej
)
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
4
/
3
3
P
o
d
st
aw
o
w
e
p
o
ję
ci
a
B
ila
n
s
p
ła
tn
ic
zy
–
p
o
d
st
aw
ow
e
p
o
ję
ci
a
D
E
F
IN
IC
JA
:
P
oj
ęc
ie
re
zy
d
en
ta
d
an
ej
go
sp
o
d
ar
ki
–
re
zy
d
en
te
m
d
an
ej
go
sp
o
d
ar
ki
je
st
p
o
d
m
io
t,
kt
ór
eg
o
ce
n
tr
u
m
za
in
te
re
so
w
an
ia
go
sp
o
d
ar
cz
eg
o
zn
aj
d
u
je
si
ę
n
a
te
re
n
ie
d
an
ej
go
sp
o
d
ar
ki
.
P
oj
ęc
ie
gr
an
ic
w
se
n
si
e
p
ol
it
yc
zn
ym
n
ie
za
w
sz
e
o
d
p
ow
ia
d
a
gr
an
ic
om
w
se
n
si
e
ek
on
om
ic
zn
ym
.
T
er
yt
or
iu
m
d
an
eg
o
kr
aj
u
w
se
n
si
e
ek
on
om
ic
zn
ym
n
al
eż
y
w
ię
c
u
to
żs
am
ia
ć
z
ob
sz
ar
em
,
d
o
kt
ór
eg
o
m
a
za
st
os
ow
an
ie
p
oj
ęc
ie
re
zy
d
en
tu
ry
d
an
eg
o
kr
aj
u
.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
5
/
3
3
P
o
d
st
aw
o
w
e
p
o
ję
ci
a
B
ila
n
s
p
ła
tn
ic
zy
–
p
o
d
st
aw
ow
e
p
o
ję
ci
a
D
E
F
IN
IC
JA
:
N
a
ob
sz
ar
ek
on
om
ic
zn
y
d
an
eg
o
kr
aj
u
sk
ła
d
a
si
ę
te
ry
to
ri
u
m
ge
og
ra
fi
cz
n
e
ad
m
in
is
tr
ow
an
e
pr
ze
z
rz
ąd
,
n
a
ob
sz
ar
ze
kt
ór
eg
o
n
as
tę
p
u
je
sw
ob
o
d
n
y
pr
ze
p
ły
w
os
ób
,
d
ób
r
i
ka
p
it
ał
u
.
T
er
yt
or
iu
m
ek
on
om
ic
zn
e
d
an
eg
o
kr
aj
u
ob
ej
m
u
je
pr
ze
st
rz
eń
p
ow
ie
tr
zn
ą,
w
o
d
y
te
ry
to
ri
al
n
e,
sz
el
f
ko
n
ty
n
en
ta
ln
y
p
oł
oż
on
y
n
a
w
o
d
ac
h
m
ię
d
zy
n
ar
o
d
ow
yc
h
,
d
o
kt
ór
eg
o
kr
aj
m
a
w
ył
ąc
zn
e
pr
aw
a
or
az
ob
sz
ar
p
oł
ow
ów
,
zł
óż
p
al
iw
i
b
og
ac
tw
n
at
u
ra
ln
yc
h
zl
ok
al
iz
ow
an
yc
h
p
o
d
p
ow
ie
rz
ch
n
ią
m
ór
z.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
6
/
3
3
P
o
d
st
aw
o
w
e
p
o
ję
ci
a
B
ila
n
s
p
ła
tn
ic
zy
–
p
o
d
st
aw
ow
e
p
o
ję
ci
a
D
E
F
IN
IC
JA
:
M
ów
im
y,
że
d
an
y
p
o
d
m
io
t
p
os
ia
d
a
ce
n
tr
u
m
za
in
te
re
so
w
an
ia
go
sp
o
d
ar
cz
eg
o
w
d
an
ym
kr
aj
u
,
je
śl
i
w
ra
m
ac
h
je
go
gr
an
ic
is
tn
ie
je
lo
ka
liz
ac
ja
,
m
ie
js
ce
pr
o
d
u
kc
ji
lu
b
in
n
e
pr
ze
d
st
aw
ic
ie
ls
tw
o,
w
ra
m
ac
h
kt
ór
eg
o
p
o
d
m
io
t
pr
ow
ad
zi
i
za
m
ie
rz
a
pr
ow
ad
zi
ć
w
pr
zy
sz
ło
śc
i
(p
rz
ez
cz
as
n
ie
ok
re
śl
on
y
lu
b
ok
re
śl
on
y,
al
e
b
ar
d
zo
d
łu
gi
)
d
zi
ał
al
n
oś
ć
go
sp
o
d
ar
cz
ą
i
d
ok
on
u
je
tr
an
sa
kc
ji
n
a
is
to
tn
ą
sk
al
ę.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
7
/
3
3
Z
a
sa
d
y
k
si
ęg
o
w
a
n
ia
tr
a
n
sa
k
cj
i
B
ila
n
s
p
ła
tn
ic
zy
–
za
sa
d
a
p
o
d
w
ó
jn
eg
o
ks
ię
g
ow
an
ia
P
o
d
st
aw
ow
a
ko
n
w
en
cj
a
sp
or
zą
d
za
n
ia
b
ila
n
su
p
ła
tn
ic
ze
go
op
ie
ra
si
ę
n
a
za
sa
d
zi
e
p
o
d
w
ój
n
eg
o
ks
ię
go
w
an
ia
tr
an
sa
kc
ji
.
O
zn
ac
za
to
,
że
ka
żd
a
tr
an
sa
kc
ja
zn
aj
d
u
je
sw
ój
za
p
is
w
b
ila
n
si
e
p
ła
tn
ic
zy
m
p
o
d
w
ó
ch
st
ro
n
ac
h
b
ila
n
su
,
o
je
d
n
ak
ow
ej
w
ar
to
śc
i:
◮
p
o
st
ro
n
ie
kr
ed
yt
ow
ej
ze
zn
ak
ie
m
d
o
d
at
n
im
◮
p
o
st
ro
n
ie
d
eb
et
ow
ej
ze
zn
ak
ie
m
u
je
m
n
ym
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
8
/
3
3
Z
a
sa
d
y
k
si
ęg
o
w
a
n
ia
tr
a
n
sa
k
cj
i
B
ila
n
s
p
ła
tn
ic
zy
–
za
sa
d
y
ks
ię
g
ow
an
ia
tr
an
sa
kc
ji
S
to
so
w
an
e
za
sa
d
y
ks
ię
go
w
oś
ci
p
ow
o
d
u
ją
,
że
:
◮
za
p
is
p
o
st
ro
n
ie
d
eb
et
ow
ej
oz
n
ac
za
w
zr
os
t
ak
ty
w
ów
za
gr
an
ic
zn
yc
h
p
os
ia
d
an
yc
h
pr
ze
z
re
zy
d
en
tó
w
lu
b
zm
n
ie
js
ze
n
ie
si
ę
ic
h
zo
b
ow
ią
za
ń
w
ob
ec
za
gr
an
ic
y
◮
za
p
is
p
o
st
ro
n
ie
kr
ed
yt
ow
ej
oz
n
ac
za
w
zr
os
t
zo
b
ow
ią
za
ń
w
ob
ec
za
gr
an
ic
y
(n
p
.
w
zr
os
t
ak
ty
w
ów
kr
aj
ow
yc
h
p
os
ia
d
an
yc
h
pr
ze
z
za
gr
an
ic
ę)
lu
b
sp
ad
ek
n
al
eż
n
oś
ci
re
zy
d
en
tó
w
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
9
/
3
3
Z
a
sa
d
y
k
si
ęg
o
w
a
n
ia
tr
a
n
sa
k
cj
i
B
ila
n
s
p
ła
tn
ic
zy
–
za
sa
d
y
ks
ię
g
ow
an
ia
tr
an
sa
kc
ji
P
oz
yc
je
p
o
st
ro
n
ie
kr
ed
yt
ow
ej
b
ila
n
su
p
ła
tn
ic
ze
go
ob
ej
m
u
ją
n
as
tę
p
u
ją
ce
tr
an
sa
kc
je
:
◮
ek
sp
or
t
d
ób
r
i
u
sł
u
g
◮
d
o
ch
ó
d
n
al
eż
n
y
re
zy
d
en
to
m
◮
za
p
is
y
w
yr
ów
n
aw
cz
e
d
la
tr
an
sf
er
ów
ot
rz
ym
an
yc
h
z
za
gr
an
ic
y
◮
zw
ię
ks
ze
n
ie
kr
aj
ow
yc
h
zo
b
ow
ią
za
ń
w
ob
ec
za
gr
an
ic
y
◮
zm
n
ie
js
ze
n
ie
ak
ty
w
ów
za
gr
an
ic
zn
yc
h
p
os
ia
d
an
yc
h
pr
ze
z
re
zy
d
en
tó
w
P
oz
yc
je
p
o
st
ro
n
ie
kr
ed
yt
ow
ej
p
ow
o
d
u
ją
zw
ię
ks
za
n
ie
si
ę
p
o
d
aż
y
w
al
u
t
ob
cy
ch
z
p
u
n
kt
u
w
id
ze
n
ia
ry
n
ku
w
al
u
to
w
eg
o.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
0
/
3
3
Z
a
sa
d
y
k
si
ęg
o
w
a
n
ia
tr
a
n
sa
k
cj
i
B
ila
n
s
p
ła
tn
ic
zy
–
za
sa
d
y
ks
ię
g
ow
an
ia
tr
an
sa
kc
ji
P
oz
yc
je
p
o
st
ro
n
ie
d
eb
et
ow
ej
b
ila
n
su
p
ła
tn
ic
ze
go
ob
ej
m
u
ją
n
as
tę
p
u
ją
ce
tr
an
sa
kc
je
:
◮
im
p
or
t
d
ób
r
i
u
sł
u
g
◮
d
o
ch
ó
d
n
al
eż
n
y
n
ie
re
zy
d
en
to
m
◮
za
p
is
y
w
yr
ów
n
aw
cz
e
d
la
tr
an
sf
er
ów
pr
ze
ka
zy
w
an
yc
h
n
a
rz
ec
z
za
gr
an
ic
y
◮
zm
n
ie
js
ze
n
ie
kr
aj
ow
yc
h
zo
b
ow
ią
za
ń
w
ob
ec
za
gr
an
ic
y
◮
zw
ię
ks
ze
n
ie
ak
ty
w
ów
za
gr
an
ic
zn
yc
h
p
os
ia
d
an
yc
h
pr
ze
z
re
zy
d
en
tó
w
P
oz
yc
je
p
o
st
ro
n
ie
d
eb
et
ow
ej
p
ow
o
d
u
ją
zw
ię
ks
za
n
ie
si
ę
p
op
yt
u
n
a
w
al
u
ty
ob
ce
z
p
u
n
kt
u
w
id
ze
n
ia
ry
n
ku
w
al
u
to
w
eg
o.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
1
/
3
3
S
tr
u
k
tu
ra
b
il
a
n
su
p
ła
tn
ic
ze
g
o
S
tr
u
kt
u
ra
b
ila
n
su
p
ła
tn
ic
ze
g
o
S
ta
n
d
ar
d
ow
o,
b
ila
n
s
p
ła
tn
ic
zy
sk
ła
d
a
si
ę
z
p
os
zc
ze
gó
ln
yc
h
ra
ch
u
n
kó
w
,
gr
u
p
u
ją
cy
ch
p
os
zc
ze
gó
ln
e
ty
py
tr
an
sa
kc
ji
d
ok
on
yw
an
yc
h
m
ię
d
zy
re
zy
d
en
ta
m
i
a
n
ie
re
zy
d
en
ta
m
i.
1.
B
ila
n
s
ob
ro
tó
w
b
ie
żą
cy
ch
1
.1
D
o
br
a
1
.2
U
sł
u
g
i
(t
ra
n
sp
or
to
w
e,
tu
ry
st
yc
zn
e,
ko
m
u
n
ik
ac
yj
n
e,
u
b
ez
p
ie
cz
en
io
w
e,
fi
n
an
so
w
e
it
d
.)
1
.3
D
o
ch
o
d
y
1
.3
.1
W
yn
ag
ro
d
ze
n
ia
si
ły
ro
b
o
cz
ej
1
.3
.2
D
o
ch
o
d
y
in
w
es
ty
cy
jn
e
z
ka
p
it
ał
u
(F
D
I,
in
w
es
ty
cj
e
p
o
tr
fe
lo
w
e)
1
.4
T
ra
n
sf
er
y
b
ie
żą
ce
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
2
/
3
3
S
tr
u
k
tu
ra
b
il
a
n
su
p
ła
tn
ic
ze
g
o
S
tr
u
kt
u
ra
b
ila
n
su
p
ła
tn
ic
ze
g
o
2.
B
ila
n
s
ob
ro
tó
w
ka
p
it
ał
ow
yc
h
–
ob
ej
m
u
je
tr
an
sf
er
y
ka
p
it
ał
ow
e,
d
o
kt
ór
yc
h
za
lic
za
si
ę
d
ar
y
i
śr
o
d
ki
z
ty
tu
ł
p
om
o
cy
b
ez
zw
ro
tn
ej
,
d
ok
on
an
e
z
w
yr
aź
n
ym
pr
ze
zn
ac
ze
n
ie
m
n
a
fi
n
an
so
w
an
ie
śr
o
d
kó
w
tr
w
ał
yc
h
,
ja
k
ró
w
n
ie
ż
u
m
or
ze
n
ie
d
łu
gó
w
or
az
n
ab
yw
an
ie
/z
by
w
an
ie
ak
ty
w
ów
ka
p
it
ał
ow
yc
h
o
ch
ar
ak
te
rz
e
n
ie
fi
n
an
so
w
ym
(p
at
en
ty
,
lic
en
cj
e,
pr
aw
a
w
ła
sn
oś
ci
,
zn
ak
i
h
an
d
lo
w
e,
gr
u
n
ty
p
o
d
b
u
d
ow
ę
am
b
as
ad
)
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
3
/
3
3
S
tr
u
k
tu
ra
b
il
a
n
su
p
ła
tn
ic
ze
g
o
S
tr
u
kt
u
ra
b
ila
n
su
p
ła
tn
ic
ze
g
o
3.
B
ila
n
s
ob
ro
tó
w
fi
n
an
so
w
yc
h
3
.1
In
w
es
ty
cj
e
b
ez
p
o
śr
ed
n
ie
–
n
ak
ła
d
y
p
o
n
ie
si
o
n
e
w
ce
lu
u
st
an
ow
ie
n
ia
tr
w
ał
yc
h
i
b
ez
p
o
śr
ed
n
ic
h
w
ię
zi
ek
o
n
o
m
ic
zn
yc
h
,
p
o
pr
ze
z
n
ab
yc
ie
co
n
aj
m
n
ie
j
1
0
%
u
d
zi
ał
ów
w
ka
p
it
al
e
p
o
d
st
aw
ow
ym
pr
ze
d
si
ęb
io
rs
tw
a
3
.2
In
w
es
ty
cj
e
p
or
tf
el
ow
e
–
p
ła
tn
o
śc
i
z
ty
tu
łu
za
ku
p
u
i
sp
rz
ed
aż
y
u
d
zi
ał
ow
yc
h
(n
ie
b
ęd
ąc
yc
h
in
w
es
ty
cj
am
i
b
ez
p
o
śr
ed
n
im
i)
or
az
d
łu
żn
yc
h
p
ap
ie
ró
w
w
ar
to
śc
io
w
yc
h
3
.3
P
o
zo
st
ał
e
in
w
es
ty
cj
e
–
tr
an
sa
kc
je
fi
n
an
so
w
e,
kt
ór
e
n
ie
są
u
jm
ow
an
e
z
in
w
es
ty
cj
ac
h
b
ez
p
o
śr
ed
n
ic
h
,
in
w
es
ty
cj
ac
h
p
or
tf
el
ow
yc
h
an
i
o
fi
cj
al
n
yc
h
ak
ty
w
ac
h
re
ze
rw
ow
yc
h
,
al
e
kt
ór
yc
h
o
br
o
ty
m
aj
ą
w
p
ły
w
n
a
w
ie
lk
o
ść
kr
aj
ow
yc
h
n
al
eż
n
o
śc
i
(a
kt
yw
a)
or
az
kr
aj
ow
yc
h
zo
b
ow
ią
za
ń
w
o
b
ec
za
g
ra
n
ic
y
(p
as
yw
a)
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
4
/
3
3
S
tr
u
k
tu
ra
b
il
a
n
su
p
ła
tn
ic
ze
g
o
S
tr
u
kt
u
ra
b
ila
n
su
p
ła
tn
ic
ze
g
o
4.
S
al
d
o
b
łę
d
ów
i
op
u
sz
cz
eń
–
w
yn
ik
a
z
tr
an
sa
kc
ji
n
ie
za
re
je
st
ro
w
an
yc
h
lu
b
n
ie
pr
aw
id
ło
w
o
u
ję
ty
ch
w
sp
ra
w
oz
d
an
ia
ch
b
an
kó
w
5.
O
fi
cj
al
n
e
ak
ty
w
a
re
ze
rw
ow
e
–
tr
an
sa
kc
je
d
ok
on
yw
an
e
pr
ze
z
b
an
k
ce
n
tr
al
n
y
w
za
kr
es
ie
ob
ro
tó
w
n
a
ra
ch
u
n
ka
ch
b
ie
żą
cy
ch
i
lo
ka
t
w
b
an
ka
ch
za
gr
an
ic
zn
yc
h
,
ob
ro
tó
w
za
gr
an
ic
zn
ym
i
p
ap
ie
ra
m
i
w
ar
to
śc
io
w
ym
i,
tr
an
sz
y
re
ze
rw
ow
ej
M
F
W
or
az
za
ku
p
ów
i
sp
rz
ed
aż
y
zł
ot
a
m
on
et
ar
n
eg
o.
W
ra
m
ac
h
p
oz
yc
ji
fi
n
an
su
ją
cy
ch
w
yr
óż
n
ia
si
ę
ta
kż
e
tz
w
.
tr
an
sa
kc
je
fi
n
an
so
w
an
ia
w
yj
ąt
ko
w
eg
o
(e
xc
ep
ti
on
al
fi
n
an
ci
n
g)
.
O
b
ej
m
u
ją
on
e
tr
an
sa
kc
je
se
kt
or
a
rz
ąd
ow
eg
o,
d
ot
yc
zą
ce
fi
n
an
so
w
an
ia
ob
ro
tó
w
b
ila
n
su
p
ła
tn
ic
ze
go
w
fo
rm
ie
re
st
ru
kt
u
ry
za
cj
i
zo
b
ow
ią
za
ń
(k
w
ot
a
o
d
ro
cz
on
yc
h
sp
ła
t
zo
b
ow
ią
za
ń
,
w
yn
ik
aj
ąc
yc
h
z
u
m
ów
za
w
ar
ty
ch
z
w
ie
rz
yc
ie
la
m
i
za
gr
an
ic
zn
ym
i)
or
az
zm
ia
n
y
za
le
gł
oś
ci
z
ty
tu
łu
n
al
eż
n
oś
ci
i
zo
b
ow
ią
za
ń
kr
ed
yt
ow
yc
h
(k
ap
it
ał
i
o
d
se
tk
i)
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
5
/
3
3
S
tr
u
k
tu
ra
b
il
a
n
su
p
ła
tn
ic
ze
g
o
P
rz
yk
ła
d
ks
ię
g
ow
an
ia
tr
an
sa
kc
ji
Z
ał
ó
żm
y,
że
p
o
ls
ka
fi
rm
a
sp
rz
ed
aj
e
d
o
N
ie
m
ie
c
m
eb
le
o
w
ar
to
śc
i
1
m
ln
zł
.
D
o
br
a
d
o
st
ar
cz
an
e
są
d
o
N
ie
m
ie
c
pr
ze
z
p
o
ls
ką
fi
rm
ę
sp
ed
yc
yj
n
ą
za
1
0
0
ty
s.
zł
.
N
ie
m
ie
ck
i
n
ab
yw
ca
p
ła
ci
za
m
eb
le
i
tr
an
sp
or
t
p
o
pr
ze
z
sw
ó
j
b
an
k,
kt
ór
y
p
o
si
ad
a
ra
ch
u
n
ek
n
a
żą
d
an
ie
w
p
o
ls
ki
m
b
an
ku
.
B
an
k
n
ie
m
ie
ck
i
d
o
ko
n
u
je
tr
an
sf
er
u
śr
o
d
kó
w
z
d
ep
o
zy
tu
n
a
żą
d
an
ie
n
a
ra
ch
u
n
ek
p
o
ls
ki
ej
fi
rm
y.
S
p
o
só
b
za
ks
ię
g
ow
an
ia
tr
an
sa
kc
ji
:
◮
S
pr
ze
d
aż
m
eb
li
–
1
m
ln
zł
p
o
kr
ed
yc
ie
n
a
ra
ch
u
n
ku
o
br
o
tó
w
b
ie
żą
cy
ch
(e
ks
p
or
t
d
ó
br
)
◮
T
ra
n
sp
or
t
m
eb
li
–
1
0
0
ty
s.
zł
p
o
kr
ed
yc
ie
n
a
ra
ch
u
n
ku
o
br
o
tó
w
b
ie
żą
cy
ch
(e
ks
p
or
t
u
sł
u
g
)
◮
Z
m
n
ie
js
ze
n
ie
d
ep
o
zy
tu
n
a
żą
d
an
ie
n
ie
m
ie
ck
ie
g
o
b
an
ku
w
p
o
ls
ki
m
b
an
ku
o
zn
ac
za
sp
ad
ek
p
o
ls
ki
ch
zo
b
ow
ią
za
ń
,
co
zo
st
an
ie
za
ks
ię
g
ow
an
e
p
o
st
ro
n
ie
d
eb
et
ow
ej
w
b
ila
n
si
e
o
br
o
tó
w
ka
p
it
ał
ow
yc
h
w
p
o
zy
cj
i
„
P
o
zo
st
ał
e
in
w
es
ty
cj
e”
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
6
/
3
3
P
o
d
st
aw
o
w
a
to
żs
a
m
o
ść
b
il
a
n
su
p
ła
tn
ic
ze
g
o
P
o
d
st
aw
ow
a
to
żs
am
oś
ć
b
ila
n
su
p
ła
tn
ic
ze
go
:
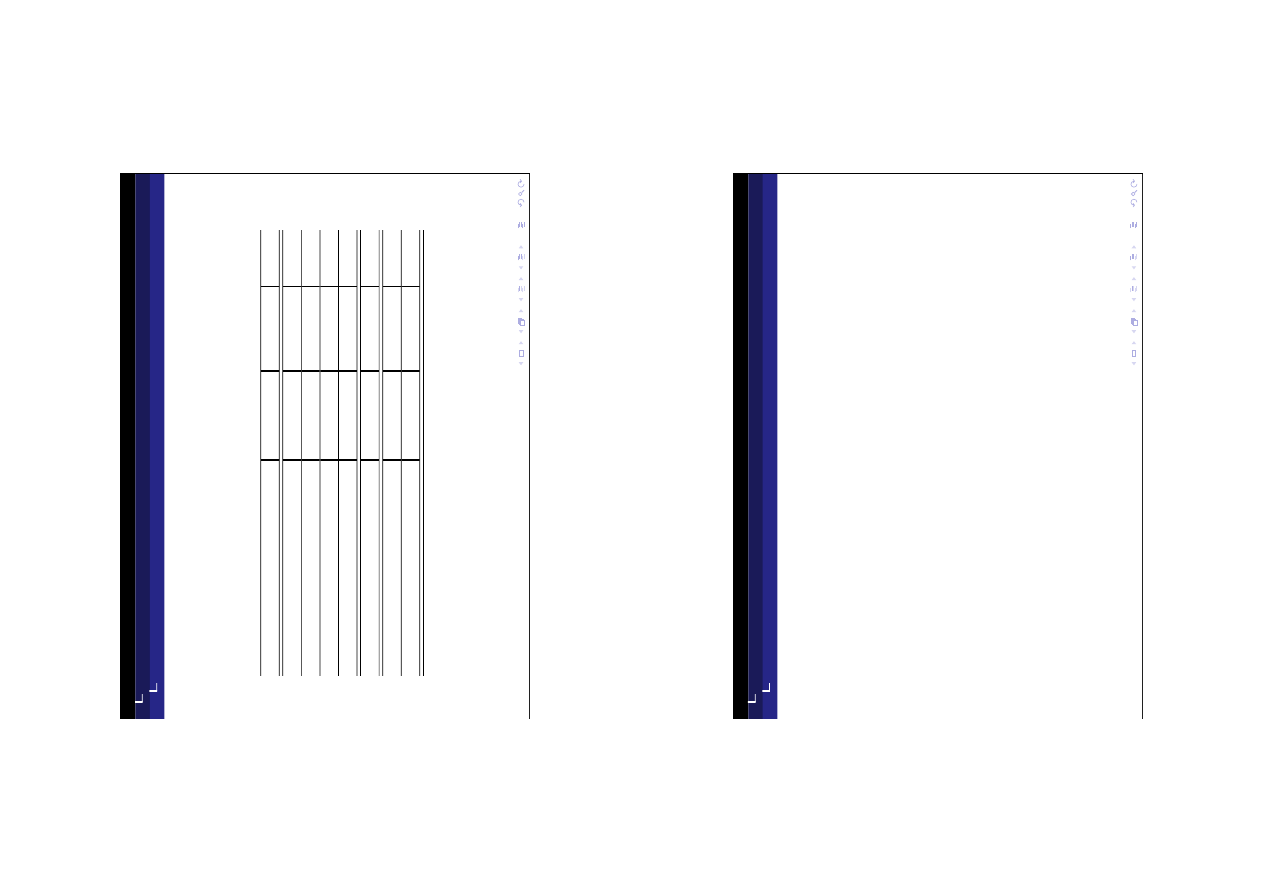
C
A
+
K
A
+
F
A
+
E
R
+
R
E
S
≡
0
B
ila
n
s
p
ła
tn
ic
zy
za
w
sz
e
su
m
u
je
si
ę
d
o
0!
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
7
/
3
3
P
o
d
st
aw
o
w
a
to
żs
a
m
o
ść
b
il
a
n
su
p
ła
tn
ic
ze
g
o
B
ila
n
s
p
ła
tn
ic
zy
P
o
ls
ki
,
2
0
0
7
(m
ld
zł
)
P
o
zy
cj
a
K
re
d
yt
(+
)
D
eb
et
(−
)
S
al
d
o
A
.
B
ila
n
s
o
br
o
tó
w
b
ie
żą
cy
ch
5
4
8
,8
6
0
3
,8
−
5
5
,0
B
.
B
ila
n
s
o
br
o
tó
w
ka
p
it
ał
ow
yc
h
1
4
,5
1
,7
1
2
,8
C
.
B
ila
n
s
o
br
o
tó
w
fi
n
an
so
w
yc
h
1
4
7
,2
3
8
,9
1
0
8
,3
D
.
S
al
d
o
b
łę
d
ów
i
o
p
u
sz
cz
eń
3
1
,0
−
3
1
,0
R
az
em
A
d
o
D
7
1
0
,6
6
7
5
,4
3
5
,2
E
.
O
fi
cj
al
n
e
ak
ty
w
a
re
ze
rw
ow
e
3
5
,2
−
3
5
,2
R
az
em
A
d
o
E
0
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
8
/
3
3
R
ó
w
n
o
w
a
g
a
b
il
a
n
su
p
ła
tn
ic
ze
g
o
R
ów
n
ow
ag
a
b
ila
n
su
p
ła
tn
ic
ze
g
o
B
ila
n
s
p
ła
tn
ic
zy
w
se
n
si
e
ks
ię
go
w
ym
za
w
sz
e
su
m
u
je
si
ę
d
o
0.
D
la
cz
eg
o
za
te
m
m
ów
i
si
ę
o
n
ad
w
yż
ce
,
d
efi
cy
ci
e
lu
b
ró
w
n
ow
ad
ze
b
ila
n
su
p
ła
tn
ic
ze
go
?
K
on
ie
cz
n
e
je
st
tu
p
ew
n
e
ro
zr
óż
n
ie
n
ie
ka
te
go
ri
i.
O
ró
w
n
ow
ad
ze
b
ila
n
su
p
ła
tn
ic
ze
go
(l
u
b
n
ie
ró
w
n
ow
ad
ze
w
p
os
ta
ci
n
ad
w
yż
ki
b
ąd
ź
d
efi
cy
tu
)
m
ów
im
y
je
d
yn
ie
w
o
d
n
ie
si
en
iu
d
o
ra
ch
u
n
kó
w
b
ila
n
su
z
w
ył
ąc
ze
n
ie
m
p
oz
yc
ji
fi
n
an
su
ją
cy
ch
(c
zy
li
ofi
cj
al
n
yc
h
ak
ty
w
ów
re
ze
rw
ow
yc
h
).
P
oz
yc
je
b
ila
n
su
p
ła
tn
ic
ze
go
z
w
ył
ąc
ze
n
ie
m
re
ze
rw
n
az
yw
a
si
ę
b
ila
n
se
m
p
ła
tn
ic
zy
m
w
w
ąs
ki
m
ro
zu
m
ie
n
iu
.
B
ila
n
s
p
ła
tn
ic
zy
je
st
w
ró
w
n
ow
ad
ze
,
je
śl
i:
B
P
=
C
A
+
K
A
+
F
A
+
E
R
=
0
Je
śl
i
p
ow
yż
sz
a
su
m
a
sa
ld
je
st
d
o
d
at
n
ia
(u
je
m
n
a)
,
m
ów
im
y
o
n
ad
w
yż
ce
(d
efi
cy
ci
e)
b
ila
n
su
p
ła
tn
ic
ze
go
w
w
ąs
ki
m
ro
zu
m
ie
n
iu
.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
B
il
a
n
s
p
ła
tn
ic
zy
1
9
/
3
3
R
ó
w
n
o
w
a
g
a
b
il
a
n
su
p
ła
tn
ic
ze
g
o
R
ów
n
ow
ag
a
b
ila
n
su
p
ła
tn
ic
ze
g
o
Ł
at
w
o
za
uw
aż
yć
,
że
z
d
efi
n
ic
ji
m
am
y:
B
P
=
−
R
E
S
O
zn
ac
za
to
,
że
b
ila
n
s
p
ła
tn
ic
zy
je
st
w
ró
w
n
ow
ad
ze
w
te
d
y
i
ty
lk
o
w
te
d
y,
gd
y
sa
ld
o
re
ze
rw
n
ie
zm
ie
n
ia
si
ę.
D
efi
cy
t
b
ila
n
su
p
ła
tn
ic
ze
go
oz
n
ac
za
sy
tu
ac
ję
,
w
kt
ór
ej
ob
se
rw
u
je
m
y
zm
n
ie
js
ze
n
ie
si
ę
re
ze
rw
(U
W
A
G
A
:
zm
n
ie
js
ze
n
ie
re
ze
rw
ks
ię
go
w
an
e
je
st
p
o
st
ro
n
ie
kr
ed
yt
ow
ej
ze
zn
ak
ie
m
d
o
d
at
n
im
,
gd
yż
je
st
to
zm
n
ie
js
ze
n
ie
si
ę
ak
ty
w
ów
za
gr
an
ic
zn
yc
h
p
os
ia
d
an
yc
h
pr
ze
z
re
zy
d
en
tó
w
).
N
ad
w
yż
ka
b
ila
n
su
p
ła
tn
ic
ze
go
z
ko
le
i
oz
n
ac
za
sy
tu
ac
ję
,
w
kt
ór
ej
m
am
y
d
o
cz
yn
ie
n
ia
ze
w
zr
os
te
m
za
so
b
u
re
ze
rw
.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
0
/
3
3
P
rz
ep
ły
w
y
d
ó
b
r
i
k
a
p
it
a
łu
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
P
rz
ep
ły
w
y
d
ó
br
i
ka
p
it
ał
u
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
W
go
sp
o
d
ar
ce
ot
w
ar
te
j
u
ch
yl
am
y
je
d
n
o
z
n
aj
w
aż
n
ie
js
zy
ch
za
ło
że
ń
m
ak
ro
ek
on
om
ii
go
sp
o
d
ar
ki
za
m
kn
ię
te
j:
w
yd
at
ki
n
ie
m
u
sz
ą
by
ć
ró
w
n
e
w
ie
lk
oś
ci
pr
o
d
u
kc
ji
te
j
go
sp
o
d
ar
ki
.
G
os
p
o
d
ar
ka
m
oż
e
w
yd
ać
w
ię
ce
j
n
iż
pr
o
d
u
ku
je
,
je
śl
i
za
p
oż
yc
zy
si
ę
u
n
ie
re
zy
d
en
tó
w
lu
b
m
oż
e
w
yd
ać
m
n
ie
j
n
iż
w
yp
ro
d
u
ku
je
,
p
oż
yc
za
ją
c
z
ko
le
i
za
gr
an
ic
y
n
ad
w
yż
kę
.
W
go
sp
o
d
ar
ce
ot
w
ar
te
j
w
yd
at
ki
n
a
d
ob
ra
i
u
sł
u
gi
fi
n
al
n
e
w
yp
ro
d
u
ko
w
an
e
w
kr
aj
u
m
oż
n
a
p
o
d
zi
el
ić
n
a
cz
te
ry
sk
ła
d
n
ik
i:
Y
=
C
d
+
I
d
+
G
d
+
E
X
gd
zi
e:
C
d
–
w
yd
at
ki
ko
n
su
m
p
cy
jn
e
n
a
kr
aj
ow
e
d
ob
ra
i
u
sł
u
gi
I
d
–
w
yd
at
ki
in
w
es
ty
cy
jn
e
n
a
kr
aj
ow
e
d
ob
ra
i
u
sł
u
gi
G
d
–
w
yd
at
ki
rz
ąd
ow
e
za
ku
py
kr
aj
ow
yc
h
d
ób
r
i
u
sł
u
g
E
X
–
ek
sp
or
t
kr
aj
ow
yc
h
d
ób
r
i
u
sł
u
g
(z
ag
ra
n
ic
zn
e
w
yd
at
ki
ko
n
su
m
p
cy
jn
e,
in
w
es
ty
cy
jn
e
i
rz
ąd
ow
e
n
a
kr
aj
ow
e
d
ob
ra
i
u
sł
u
gi
or
az
tr
an
sf
er
y)
.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
1
/
3
3
P
rz
ep
ły
w
y
d
ó
b
r
i
k
a
p
it
a
łu
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
P
rz
ep
ły
w
y
d
ó
br
i
ka
p
it
ał
u
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
Z
au
w
aż
m
y
je
d
n
ak
,
że
ca
łk
ow
it
e
w
yd
at
ki
ko
n
su
m
p
cy
jn
e
C
ró
w
n
e
są
su
m
ie
w
yd
at
kó
w
n
a
d
ob
ra
i
u
su
gi
pr
o
d
u
kc
ji
kr
aj
ow
ej
or
az
n
a
d
ob
ra
i
u
sł
u
gi
pr
o
d
u
ko
w
an
e
za
gr
an
ic
ą:
C
=
C
d
+
C
f
.
P
o
d
ob
n
ie
m
oż
em
y
zd
ek
om
p
on
ow
ać
in
w
es
ty
cj
e
i
w
yd
at
ki
rz
ąd
ow
e:
I
=
I
d
+
I
f
or
az
G
=
G
d
+
G
f
.
W
st
aw
ia
ją
c
za
le
żn
oś
ci
te
d
o
to
żs
am
oś
ci
za
p
is
an
ej
p
ow
yż
ej
ot
rz
ym
am
y:
Y
=
(C
−
C
f
)
+
(I
−
I
f
)
+
(G
−
G
f
)
+
E
X
Y
=
C
+
I
+
G
+
E
X
−
(C
f
+
I
f
+
G
f
)
P
on
ie
w
aż
(C
f
+
I
f
+
G
f
)
to
su
m
a
kr
aj
ow
yc
h
w
yd
at
kó
w
n
a
za
gr
an
ic
zn
e
d
ob
ra
i
u
sł
u
gi
,
cz
yl
i
w
ar
to
ść
im
p
or
tu
I
M
,
m
oż
em
y
za
p
is
ać
,
że
Y
=
C
+
I
+
G
+
E
X
−
I
M
lu
b
Y
=
C
+
I
+
G
+
C
A
,
je
śl
i
zd
efi
n
iu
je
m
y
b
ila
n
s
ob
ro
tó
w
b
ie
żą
cy
ch
ja
ko
C
A
=
E
X
−
I
M
.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
2
/
3
3
P
rz
ep
ły
w
y
d
ó
b
r
i
k
a
p
it
a
łu
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
P
rz
ep
ły
w
y
d
ó
br
i
ka
p
it
ał
u
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
P
ro
d
u
kt
w
go
sp
o
d
ar
ce
o
d
st
ro
n
y
w
yd
at
kó
w
m
oż
n
a
w
yz
n
ac
zy
ć
w
n
as
tę
p
u
ją
cy
sp
os
ób
:
Y
=
C
+
I
+
G
+
C
A
A
lt
er
n
at
yw
n
ie
,
m
oż
em
y
p
ow
ie
d
zi
eć
,
że
je
śl
i
w
ró
w
n
ow
ad
ze
w
yd
at
ki
ró
w
n
aj
ą
si
ę
d
o
ch
o
d
om
,
to
:
Y
−
T
=
C
+
S
,
co
oz
n
ac
za
,
że
d
o
ch
ó
d
ro
zp
or
zą
d
za
ln
y
je
st
w
cz
ęś
ci
za
os
zc
zę
d
zo
n
y,
w
cz
ęś
ci
za
ś
w
yd
an
y
n
a
ko
n
su
m
p
cj
ę.

W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
3
/
3
3
P
rz
ep
ły
w
y
d
ó
b
r
i
k
a
p
it
a
łu
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
P
rz
ep
ły
w
y
d
ó
br
i
ka
p
it
ał
u
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
W
ta
ki
m
ra
zi
e
m
am
y:
Y
=
C
+
I
+
G
+
C
A
=
C
+
S
+
T
Z
cz
eg
o
w
yn
ik
a,
że
:
S
+
(T
−
G
)
−
I
=
C
A
W
yr
aż
en
ie
S
+
(T
−
G
)
oz
n
ac
za
su
m
ę
os
zc
zę
d
n
oś
ci
kr
aj
ow
yc
h
,
oz
n
ac
zm
y
je
st
pr
ze
z
N
S
.
M
am
y
za
te
m
:
N
S
−
I
=
C
A
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
4
/
3
3
P
rz
ep
ły
w
y
d
ó
b
r
i
k
a
p
it
a
łu
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
T
o
żs
am
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
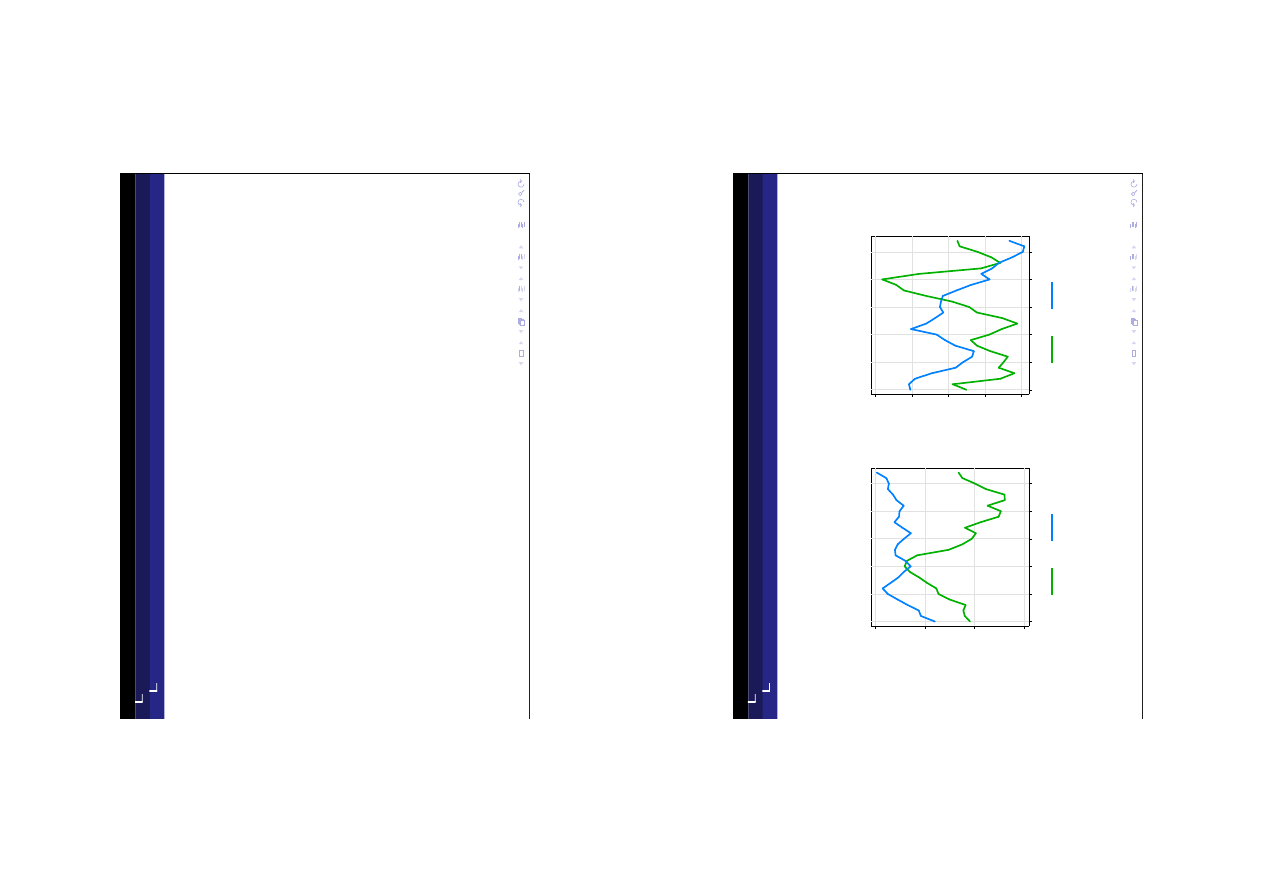
−2
0
2
4
6
CA (% PKB)
20
25
30
35
S, I (% PKB)
1980
1985
1990
1995
2000
2005
I
S
CA
Japonia
−6
−4
−2
0
CA (% PKB)
14
16
18
20
22
S, I (% PKB)
1980
1985
1990
1995
2000
2005
I
S
CA
USA
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
5
/
3
3
P
rz
ep
ły
w
y
d
ó
b
r
i
k
a
p
it
a
łu
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
P
rz
ep
ły
w
y
ka
p
it
ał
u
a
sa
ld
o
h
an
d
lu
N
S
−
I
=
C
A
L
ew
a
st
ro
n
a
te
go
ró
w
n
an
ia
,
ró
żn
ic
a
m
ię
d
zy
kr
aj
ow
ym
i
os
zc
zę
d
n
oś
ci
am
i
a
in
w
es
ty
cj
am
i
m
oż
e
by
ć
in
te
rp
re
to
w
an
a
ja
ko
o
d
p
ły
w
ka
p
it
ał
u
n
et
to
(k
ra
jo
w
e
in
w
es
ty
cj
e
za
gr
an
ic
ą
w
u
ję
ci
u
n
et
to
).
D
o
d
at
n
i
o
d
p
ły
w
ka
p
it
ał
u
n
et
to
oz
n
ac
za
,
że
kr
aj
p
oż
yc
za
n
ie
re
zy
d
en
to
m
n
ad
w
yż
kę
kr
aj
ow
yc
h
os
zc
zę
d
n
oś
ci
n
ad
in
w
es
ty
cj
am
i.
O
d
p
ły
w
ka
p
it
ał
u
n
et
to
je
st
ró
w
n
y
w
ró
w
n
ow
ad
ze
sa
ld
u
b
ila
n
su
ob
ro
tó
w
b
ie
żą
cy
ch
.
Je
śl
i
C
A
<
0
w
ys
tę
p
u
je
d
efi
cy
t
ob
ro
tó
w
b
ie
żą
cy
ch
i
kr
aj
je
st
p
oż
yc
zk
ob
io
rc
ą
n
et
to
n
a
św
ia
to
w
yc
h
ry
n
ka
ch
fi
n
an
so
w
yc
h
.
P
rz
ep
ły
w
y
fi
n
an
so
w
e
zw
ią
za
n
e
z
ak
u
m
u
al
ac
ją
ka
p
it
ał
u
i
pr
ze
p
ły
w
y
d
ób
r
i
u
sł
u
g
są
ze
so
b
ą
za
te
m
b
ar
d
zo
b
lis
ko
p
ow
ią
za
n
e.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
6
/
3
3
P
rz
ep
ły
w
y
d
ó
b
r
i
k
a
p
it
a
łu
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
T
o
żs
am
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
W
yz
n
ac
zo
n
ą
za
le
żn
oś
ć
m
oż
n
a
pr
ze
d
st
aw
ić
ró
w
n
ie
ż
w
ta
ki
ej
p
os
ta
ci
:
I
=
S
+
(T
−
G
)
−
C
A
T
oż
sa
m
oś
ć
ta
p
ok
az
u
je
,
że
in
w
es
ty
cj
e
kr
aj
ow
e
w
go
sp
o
d
ar
ce
ot
w
ar
te
j
m
og
ą
by
ć
fi
n
an
so
w
an
e
p
op
rz
ez
ak
u
m
u
la
cj
ę
os
zc
zę
d
n
oś
ci
kr
aj
ow
yc
h
(N
S
=
S
+
(T
−
G
))
i/
lu
b
pr
ze
z
n
ap
ły
w
ka
p
it
ał
u
za
gr
an
ic
zn
eg
o
(−
C
A
).
Je
śl
i
C
A
<
0,
w
ów
cz
as
I
>
N
S
.
M
oż
liw
e
je
st
zw
ię
ks
ze
n
ie
in
w
es
ty
cj
i
b
ez
zw
ię
ks
ze
n
ia
os
zc
zę
d
n
oś
ci
kr
aj
ow
yc
h
.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
7
/
3
3
H
ip
o
te
za
b
li
źn
ia
cz
yc
h
d
efi
cy
tó
w
H
ip
o
te
za
b
liź
n
ia
cz
yc
h
d
efi
cy
tó
w
Z
ap
is
zm
y
to
żs
am
oś
ć
in
w
es
ty
cj
i
i
os
zc
zę
d
n
oś
ci
je
sz
cz
e
in
ac
ze
j:
C
A
=
(S
−
I
)
+
(T
−
G
)
N
a
p
o
d
st
aw
ie
p
ow
yż
sz
ej
ró
w
n
oś
ci
sf
or
m
u
ło
w
an
o
h
ip
ot
ez
ę
d
efi
cy
tó
w
b
liź
n
ia
cz
yc
h
.
D
efi
cy
t
b
u
d
że
to
w
y
(T
−
G
)
<
0
w
ed
łu
g
te
j
h
ip
ot
ez
y
m
ia
łb
y
by
ć
pr
zy
cz
yn
ą
d
efi
cy
tu
n
a
ra
ch
u
n
ku
h
an
d
lo
w
ym
C
A
<
0.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
8
/
3
3
H
ip
o
te
za
b
li
źn
ia
cz
yc
h
d
efi
cy
tó
w
D
efi
cy
ty
b
liź
n
ia
cz
e?
−10
−5
0
5
% PKB
1980
1985
1990
1995
2000
2005
T−G
CA
Japonia
−6
−4
−2
0
2
% PKB
1980
1985
1990
1995
2000
2005
T−G
CA
USA
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
2
9
/
3
3
P
ar
a
d
o
k
s
F
el
d
st
ei
n
a
-H
o
ri
o
k
i
H
ip
o
te
za
F
el
d
st
ei
n
M
.,
H
or
io
ka
C
.
(1
98
0)
D
om
es
ti
c
S
av
in
g
an
d
In
te
rn
at
io
n
al
C
ap
it
al
F
lo
w
s,
E
co
n
om
ic
Jo
u
rn
al
,
V
ol
.
90
,
st
r.
31
4-
32
9.
◮
W
go
sp
o
d
ar
ce
ot
w
ar
te
j,
pr
zy
d
os
ko
n
ał
ej
m
ob
iln
oś
ci
ka
p
it
ał
u
n
a
ry
n
ku
m
ię
d
zy
n
ar
o
d
ow
ym
,
zw
ią
ze
k
m
ię
d
zy
kr
aj
ow
ym
i
os
zc
zę
d
n
oś
ci
am
i
i
in
w
es
ty
cj
am
i
p
ow
in
ie
n
by
ć
st
os
u
n
ko
w
o
n
ie
w
ie
lk
i
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
3
0
/
3
3
P
ar
a
d
o
k
s
F
el
d
st
ei
n
a
-H
o
ri
o
k
i
P
rz
es
ła
n
ki
te
or
et
yc
zn
e
◮
W
g
o
sp
o
d
ar
ce
za
m
kn
ię
te
j,
is
tn
ie
je
śc
is
ły
zw
ią
ze
k
m
ię
d
zy
o
sz
cz
ęd
n
o
śc
ia
m
i
kr
aj
ow
ym
i
i
in
w
es
ty
cj
am
i,
p
o
n
ie
w
aż
in
w
es
ty
cj
e
są
w
ca
ło
śc
i
fi
n
an
so
w
an
e
z
kr
aj
ow
yc
h
o
sz
cz
ęd
n
o
śc
i.
Z
at
em
m
ar
g
in
al
n
y
w
zr
o
st
o
sz
cz
ęd
n
o
śc
i
p
ow
in
ie
n
zo
st
ać
o
d
zw
ie
rc
ie
d
lo
n
y
w
kr
aj
ow
yc
h
in
w
es
ty
cj
ac
h
(w
yz
n
ac
zo
n
yc
h
pr
ze
z
kr
ań
co
w
ą
pr
o
d
u
kt
yw
n
o
ść
kr
aj
ow
eg
o
ka
p
it
ał
u
)
◮
W
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
je
d
n
ak
,
ja
k
p
o
ka
zu
je
an
al
iz
a
m
ię
d
zy
o
kr
es
ow
a,
w
yg
ła
d
za
n
ie
śc
ie
żk
i
ko
n
su
m
p
cj
i
pr
ow
ad
zi
d
o
p
ow
st
aw
an
ia
ro
zd
źw
ię
ku
m
ię
d
zy
kr
aj
ow
ym
i
o
sz
cz
ęd
n
o
śc
ia
m
i
i
in
w
es
ty
cj
am
i,
g
d
yż
kr
aj
e
o
n
ad
w
yż
ko
w
yc
h
o
sz
cz
ęd
n
o
śc
ia
ch
m
o
g
ą
je
lo
ko
w
ać
w
n
aj
b
ar
d
zi
ej
zy
sk
ow
n
yc
h
za
st
o
so
w
an
ia
ch
w
in
n
yc
h
kr
aj
ac
h
,
za
ś
kr
aj
e
z
n
ie
d
o
st
at
ki
em
kr
aj
ow
yc
h
o
sz
cz
ęd
n
o
śc
i
m
o
g
ą
p
o
ży
cz
ać
o
sz
cz
ęd
n
o
śc
i
in
n
yc
h
kr
aj
ów
,
st
aj
ąc
si
ę
im
p
or
te
ra
m
i
ka
p
it
ał
u
◮
W
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
pr
zy
d
o
sk
o
n
ał
ej
m
o
b
iln
o
śc
i
ka
p
it
ał
u
,
zw
ię
ks
ze
n
ie
kr
aj
ow
yc
h
o
sz
cz
ęd
n
o
śc
i
n
ie
p
ow
in
n
o
pr
ow
ad
zi
ć
d
o
is
to
tn
eg
o
w
zr
o
st
u
in
w
es
ty
cj
i
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
3
1
/
3
3
P
ar
a
d
o
k
s
F
el
d
st
ei
n
a
-H
o
ri
o
k
i
D
an
e
i
m
et
o
d
y
an
al
iz
y
◮
16
kr
aj
ów
O
E
C
D
,
ok
re
s
19
60
–1
97
4
◮
E
st
ym
ac
ja
I
t
Y
t
=
α
+
β
S
t
Y
t
+
u
t
◮
S
p
o
d
zi
ew
an
y
w
yn
ik
:
p
ar
am
et
r
β
b
lis
ki
ze
ru
◮
O
sz
ac
ow
an
y
p
ar
am
et
r
β
=
0
.8
9
n
ie
je
st
b
lis
ki
ze
ru
!
◮
D
al
sz
e
pr
ób
y
es
ty
m
ac
ji
n
ie
sp
ow
o
d
ow
ał
y
is
to
tn
ej
zm
ia
n
y
os
za
co
w
an
ia
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
3
2
/
3
3
P
ar
a
d
o
k
s
F
el
d
st
ei
n
a
-H
o
ri
o
k
i
W
n
io
sk
i
au
to
ró
w
F
H
in
te
rp
re
tu
ją
u
zy
sk
an
e
w
yn
ik
i
ja
ko
św
ia
d
ec
tw
o
n
is
ki
ej
m
ob
iln
oś
ci
ka
p
it
ał
u
.
Je
st
to
w
n
io
se
k
d
oś
ć
ko
n
tr
ow
er
sy
jn
y
(s
tą
d
p
ow
st
ał
o
p
oj
ęc
ie
„F
el
d
st
ei
n
-H
or
io
ka
p
u
zz
le
”)
,
gd
yż
d
ow
o
d
y
em
p
ir
yc
zn
e
w
sk
az
u
ją
n
a
co
ś
zu
p
eł
n
ie
o
d
w
ro
tn
eg
o.
W
ci
ąg
u
os
ta
tn
ic
h
30
la
t
ry
n
ek
ka
p
it
ał
ow
y
u
le
gł
zn
ac
zą
ce
j
lib
er
al
iz
ac
ji
,
pr
ze
p
ły
w
y
ka
p
it
ał
ow
e
zn
ac
zn
ie
si
ę
zw
ię
ks
zy
ły
,
a
w
yn
ik
i
in
n
yc
h
pr
ac
em
p
ir
yc
zn
yc
h
ci
ąg
le
p
ot
w
ie
rd
za
ją
is
tn
ie
n
ie
„e
fe
kt
u
F
-H
”.
W
yk
ła
d
8
–
B
il
a
n
s
p
ła
tn
ic
zy
T
o
żs
a
m
o
ść
in
w
es
ty
cj
i
i
o
sz
cz
ęd
n
o
śc
i
w
g
o
sp
o
d
ar
ce
o
tw
ar
te
j
3
3
/
3
3
P
ar
a
d
o
k
s
F
el
d
st
ei
n
a
-H
o
ri
o
k
i
R
o
zw
ią
za
n
ie
za
g
ad
ki
?
B
ra
k
je
d
n
oz
n
ac
zn
yc
h
w
n
io
sk
ów
,
d
la
cz
eg
o
ob
se
rw
u
je
m
y
ta
k
si
ln
y
ef
ek
t
F
-H
.
W
ię
ks
zo
ść
au
to
ró
w
su
ge
ru
je
,
że
is
tn
ie
n
ie
si
ln
eg
o
ef
ek
tu
F
-H
n
ie
oz
n
ac
za
za
kw
es
ti
on
ow
an
ia
m
ob
iln
oś
ci
ka
p
it
ał
u
.
Is
tn
ie
je
d
zi
ś
p
ow
sz
ec
h
n
e
pr
ze
ko
n
an
ie
,
że
ef
ek
t
te
n
je
st
w
yw
oł
yw
an
y
pr
ze
z
cz
yn
n
ik
i
(s
zo
ki
m
ię
d
zy
n
ar
o
d
ow
e)
w
p
ły
w
aj
ąc
e
je
d
n
o
cz
eś
n
ie
n
a
os
zc
zę
d
n
oś
ci
i
in
w
es
ty
cj
e.
T
ak
im
i
sz
ok
am
i
m
og
ą
by
ć
zm
ia
n
y
pr
o
d
u
kt
yw
n
oś
ci
,
zm
ia
n
y
st
ru
kt
u
ry
d
em
og
ra
fi
cz
n
ej
it
p
.
N
ie
kt
ór
zy
ar
gu
m
en
tu
ją
,
że
w
p
ły
w
n
a
w
yn
ik
i
m
oż
e
m
ie
ć
p
ol
it
yk
a
rz
ąd
ów
,
n
ak
ie
ro
w
an
a
n
a
st
ab
ili
zo
w
an
ie
sa
ld
ra
ch
u
n
kó
w
ob
ro
tó
w
b
ie
żą
cy
ch
.
Wyszukiwarka
Podobne podstrony:
msg ce wyklad 04
msg ce wyklad 09
msg ce wyklad 05
msg ce wyklad 10
msg ce wyklad 06 id 309646 Nieznany
msg ce wyklad 12
msg ce wyklad 03
msg ce wyklad 02
msg ce wyklad 07
msg ce wyklad 01 id 309645 Nieznany
msg ce wyklad 13 14
msg ce wyklad 11
msg ce wyklad 04
więcej podobnych podstron