PROGRAM WYKŁADU

• Obwody liniowe i nieliniowe prądu stałego

• Podstawy analizy obwodów prądu

sinusoidalnie zmiennego

.

Literatura

• Tadeusiewicz M.: Teoria obwodów. Część I.

Wydawnictwo Politechniki Łódzkiej, Łódź 2000.

• Tadeusiewicz M. i inni: Teoria obwodów.

Zadania. Wydawnictwo Politechniki Łódzkiej,

Zadania. Wydawnictwo Politechniki Łódzkiej,
Łódź 1999.

• Osiowski J., Szabatin J.: Podstawy teorii

obwodów. T.I, II WNT, Warszawa 1995.

• M. Krakowski Elektrotechnika teoretyczna

Oznaczenia i jednostki

U, u – napięcie V (wolt)
I, i – prąd

A (amper)

E, e – napięcie źródłowe

V (wolt)

J, j – prąd źródłowy

A (amper)

R – rezystancja

Ω

Ω

Ω

Ω (om)

G – konduktancja

S (simens)

G – konduktancja

S (simens)

p – moc chwilowa

W (wat)

P – moc czynna

W (wat)

w – energia

J (dżul)

L – indukcyjność

H (henr)

C – pojemność

F (farad)

Ψ- strumień skojarzony

Wb (weber)

q – ładunek

C (kulomb)

Jednostki pochodne

3

6

9

12

10

-

k

-

kilo

10

-

M

-

mega

10

-

G

-

giga

10

-

T

-

tera

12

-

9

-

6

-

3

-

10

-

p

-

piko

10

-

n

-

nano

10

-

-

mikro

10

-

m

-

mili

1

10

-

k

-

kilo

µ

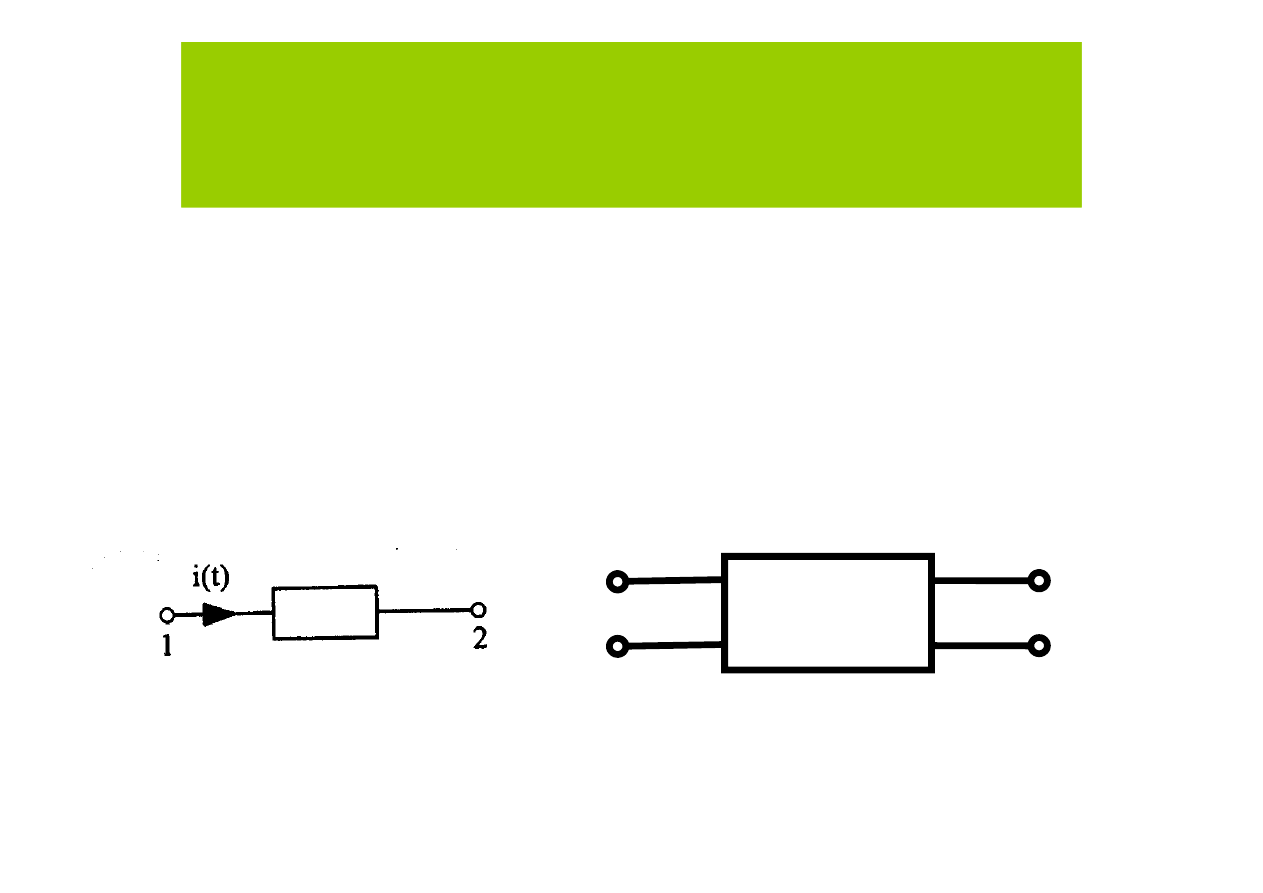
Elementy

–

modele zjawiska lub pewnej cechy fizycznej

związanej z obwodem elektrycznym

PODSTAWOWE WIADOMOŚCI o

OBWODACH ELEKTRYCZNYCH

zaciski

-

czyli punkty wyróżnione w elementach, w

których można je łączyć z innymi elementami

w zależności od ilości zacisków możemy mówić o

w zależności od ilości zacisków możemy mówić o
elementach

dwu – lub wielo

zaciskowych

Przykłady elementów z zaznaczonymi zaciskami 1 i 2
oraz zaznaczonym zwrotem prądu i (t)

1

1’

2

2’

Czwórnik

dwójnik

Przykładowe elementy

tworzące te struktury to –

opornik, cewka, kondensator, źródło napięcia,

ź

ródło prądu , tranzystor…

Z każdym z nich związana jest określona właściwość

czy cecha fizyczna

Obwody , sieci , układy

– bardziej złożone struktury ,

w których elementy połączone są ze sobą za pomocą
przewodów – przy czym zakładamy, że są to łączenia

idealne.

Połączenia elementów z zastosowaniem
odpowiednich symboli przedstawiane są w postaci

graficznej

jako

schematy obwodów

Na schemacie elementy dwu-zaciskowe wyznaczają
tzw

gałęzie

, a miejsce łączenia kilku gałęzi

zaznaczamy kropkami i nazywamy

węzłami

Sygnały

– oznaczają funkcje opisujące zmienność

w czasie wielkości fizycznej nazywane inaczej

przebiegami czasowymi

( np. prąd, napięcie )

Wyróżnimy sygnały – sinusoidalnie zmienne ,
stałe, okresowo zmienne

zaznaczamy kropkami i nazywamy

węzłami

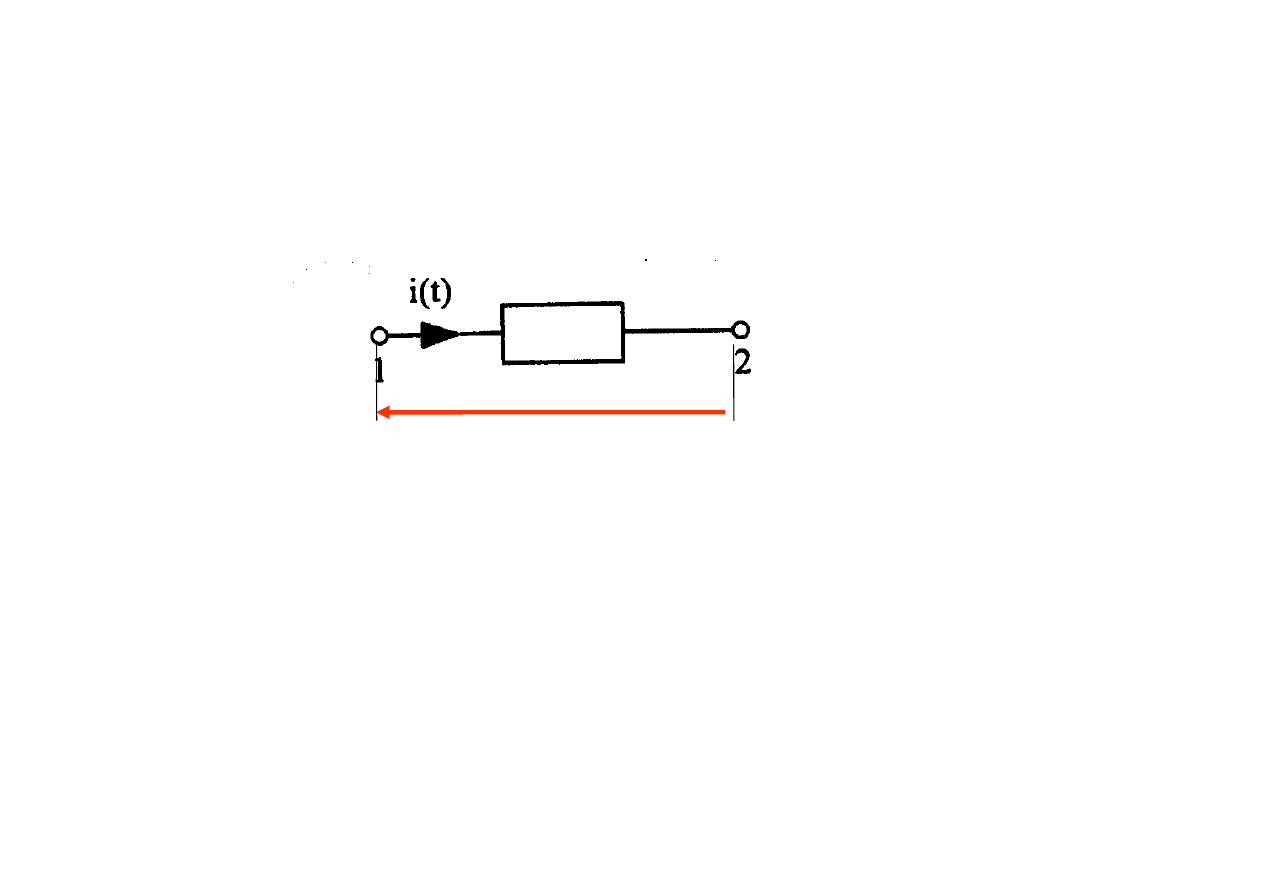
Z elementem obwodu związane są dwie wielkości:

prąd

elementu i

napięcie

na elemencie

u(t)

Zazwyczaj napięcie i prąd zmieniają się w czasie ,
więc ogólnie nie jest możliwe określenie
prawdziwego kierunku przepływu prądu .
Przyjmuje się więc pewne kierunki odniesienia,
które zaznacza się za pomocą strzałki

u(t)

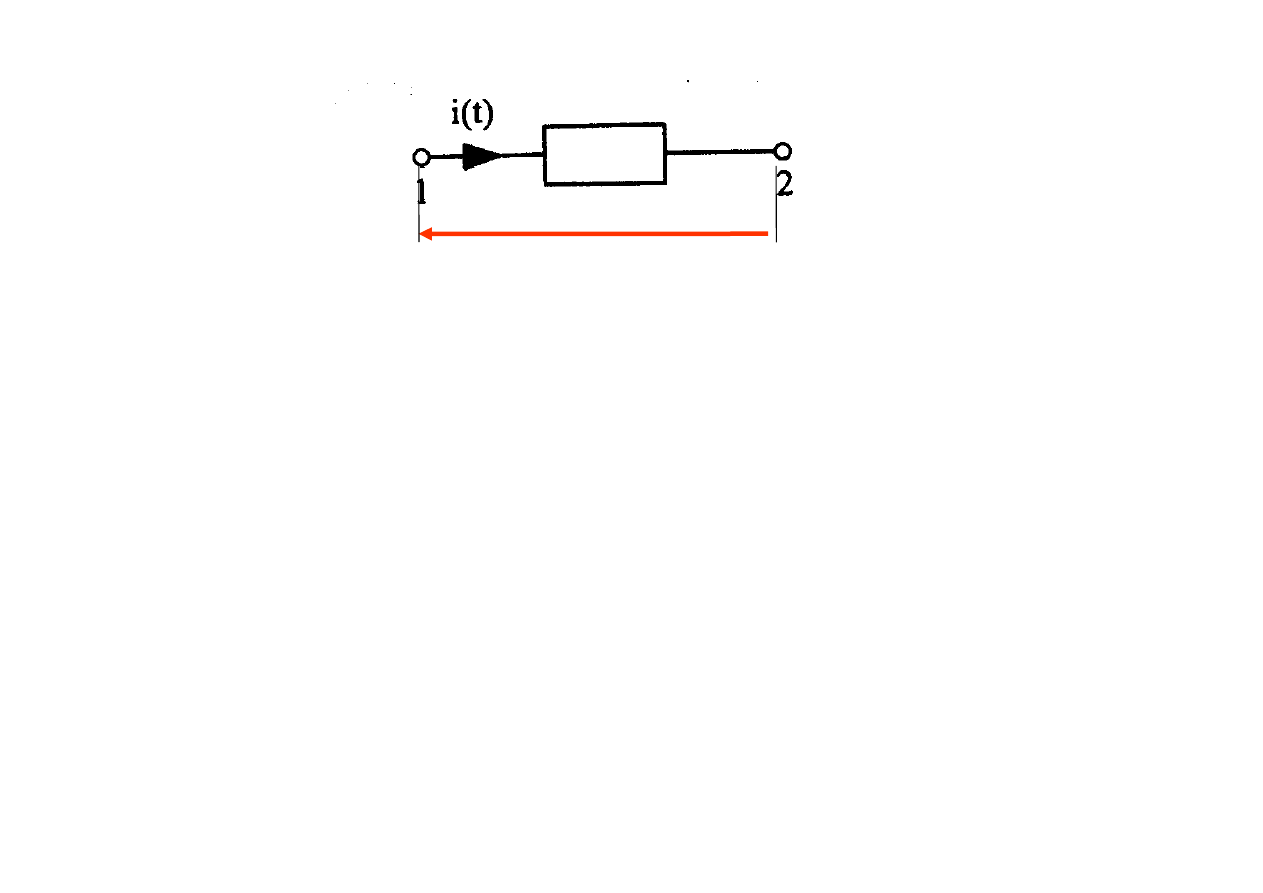
u(t)

Element obwodu z zaznaczonymi kierunkami napięcia i prądu

Znajomość znaku i wartości prądu w danej chwili oraz kierunku
odniesienia umożliwia jednoznaczne określenie rzeczywistego
prądu w tej chwili.

Często zastępujemy zwrot

kierunek odniesienia prądu lub

napięcia

zwrotem uproszczonym:

kierunek prądu lub

napięcia

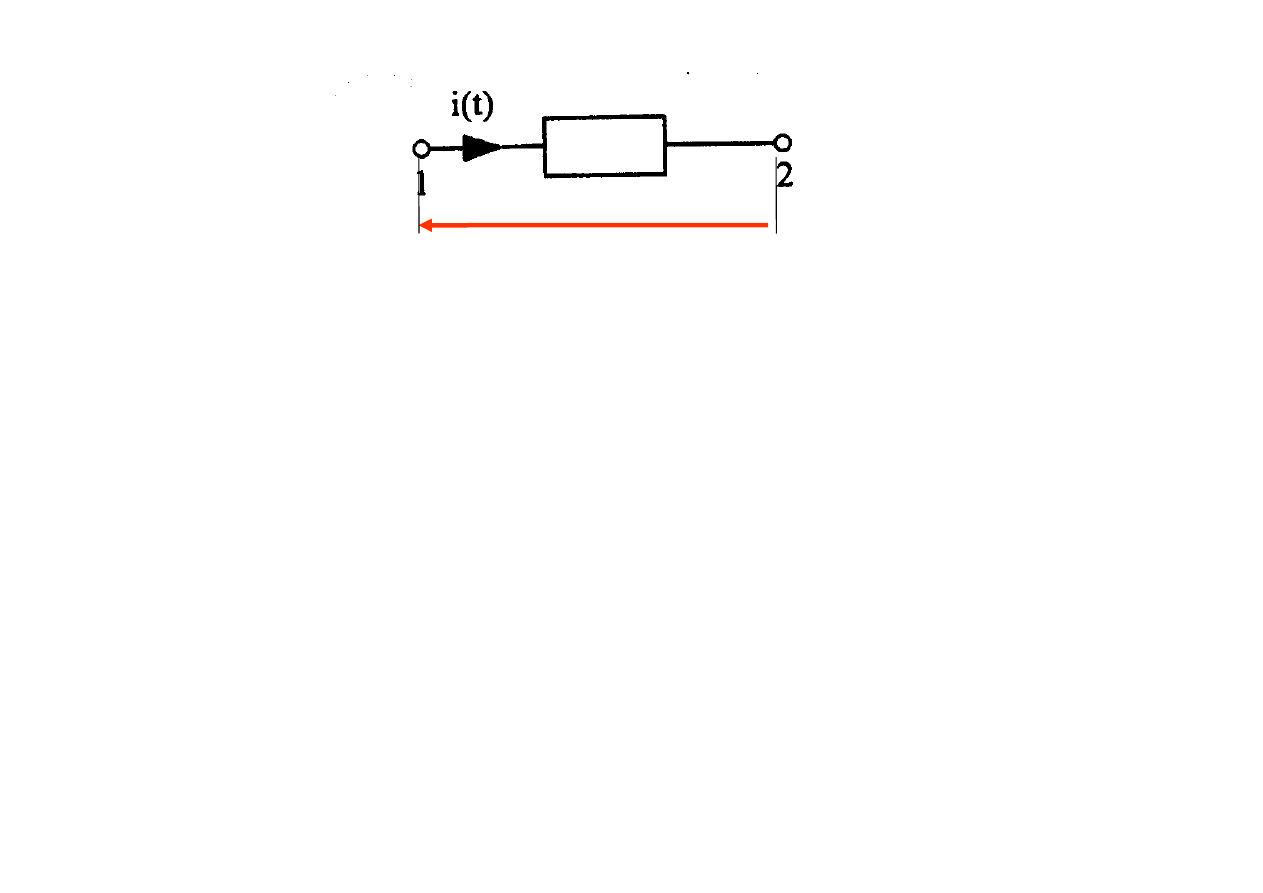
u(t)

oznacza, że w chwili t

1

płynie

prąd 1A w kierunku zgodnym

ze strzałką

A

t

i

1

)

(

1

=

oznacza, że w chwili t

2

płynie prąd

w kierunku przeciwnym do strzałki

A

t

i

5

)

(

2

−

=

V

u

6

=

w danej chwili

potencjał zacisku 1 jest

o 6Vwyższy od 2

V

u

15

−

=

tym razem potencjał zacisku

1 jest o 15V mniejszy od

potencjału zacisku2

u

1

u

2

u

4

u

2

i

1

i

i

6

i

4

1

4

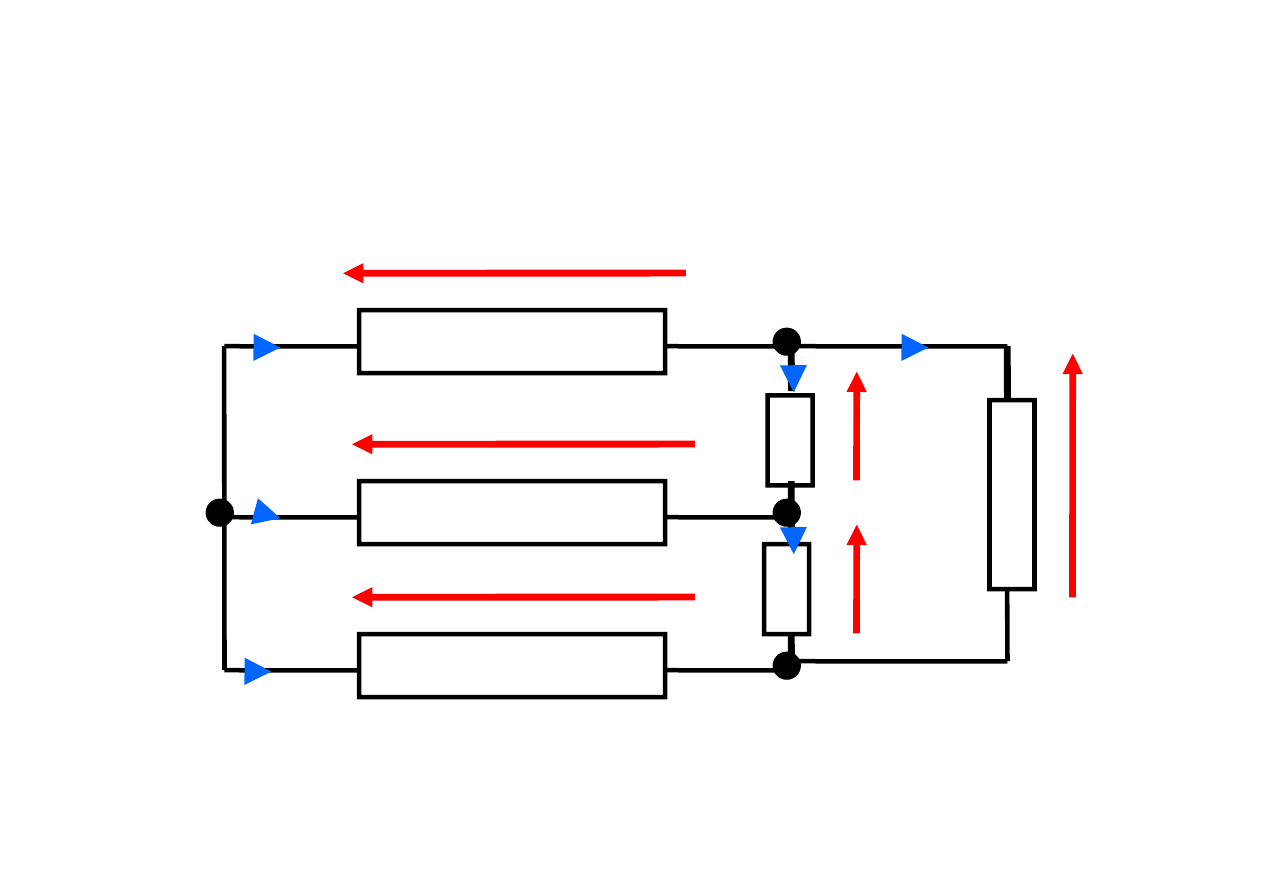
Przykład obwodu

u

3

u

5

u

6

1

4

i

2

i

3

i

5

3

2

3

5

6

Pętla

– jest pojęciem topologicznym

i jest to zbiór elementów zaczynających się
w jednym węźle, obejmujący kolejne

w jednym węźle, obejmujący kolejne
połączone ze sobą gałęzie i kończący się
w tym samym węźle.

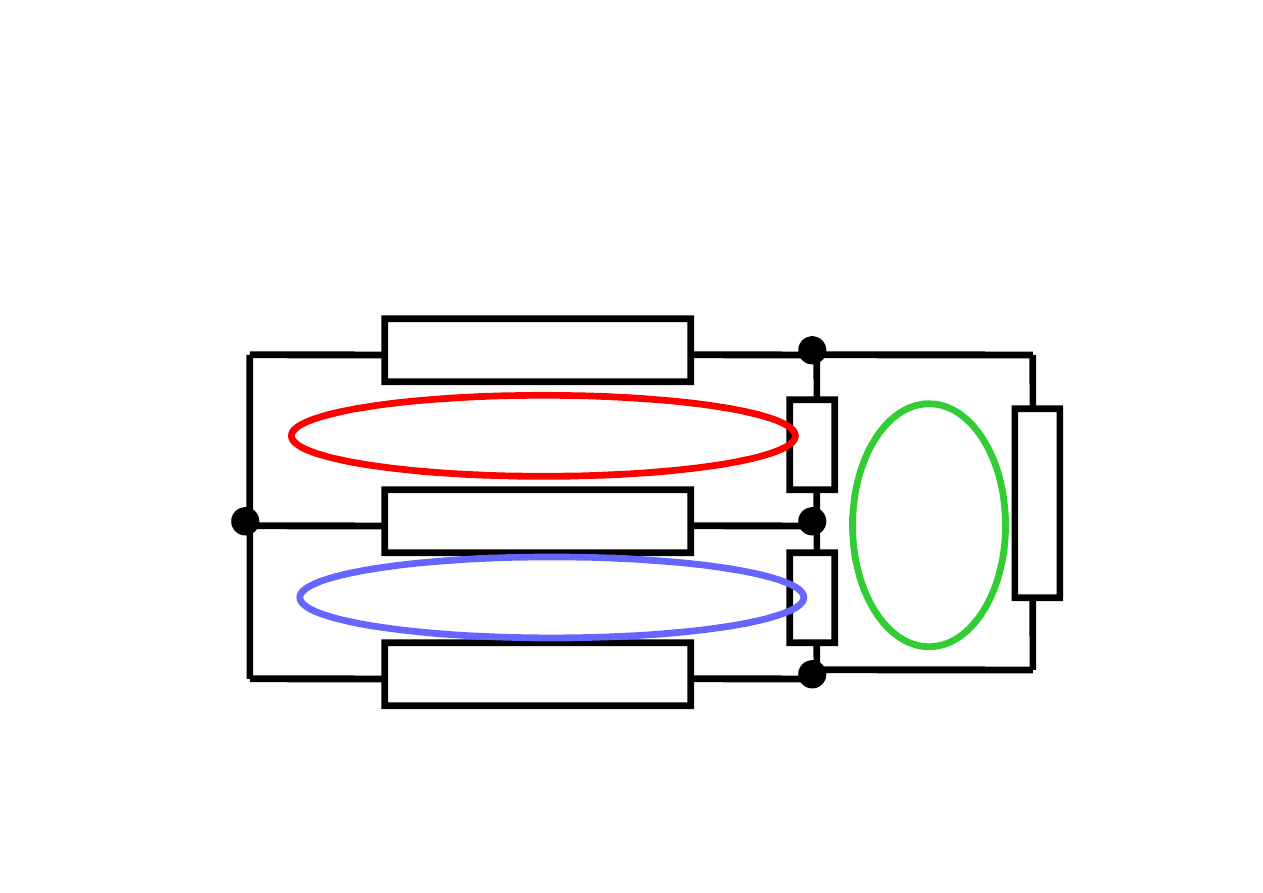
I

1

Przykład pętli

Pętla

– jest pojęciem topologicznym i jest to zbiór elementów

zaczynających się w jednym węźle, obejmujący kolejne połączone ze

sobą gałęzie i kończący się w tym samym węźle

I

II

III

2

3

4

5

6

pętle tworzą gałęzie 124 ,

235 ,

456

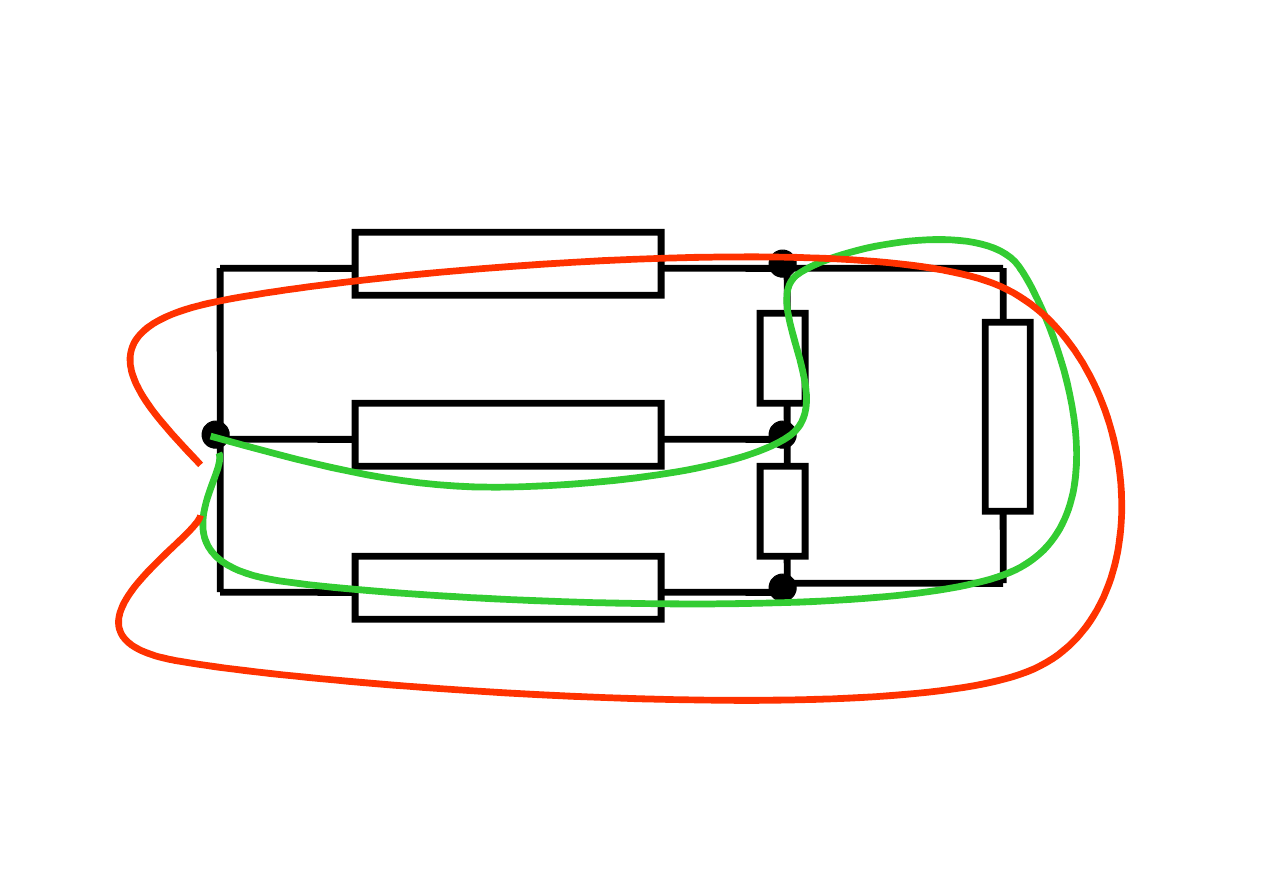
V

IV

1

2

4

6

Przykład pętli

V

3

5

Pętle tworzą gałęzie 1,3,6 oraz 2,3,4,6

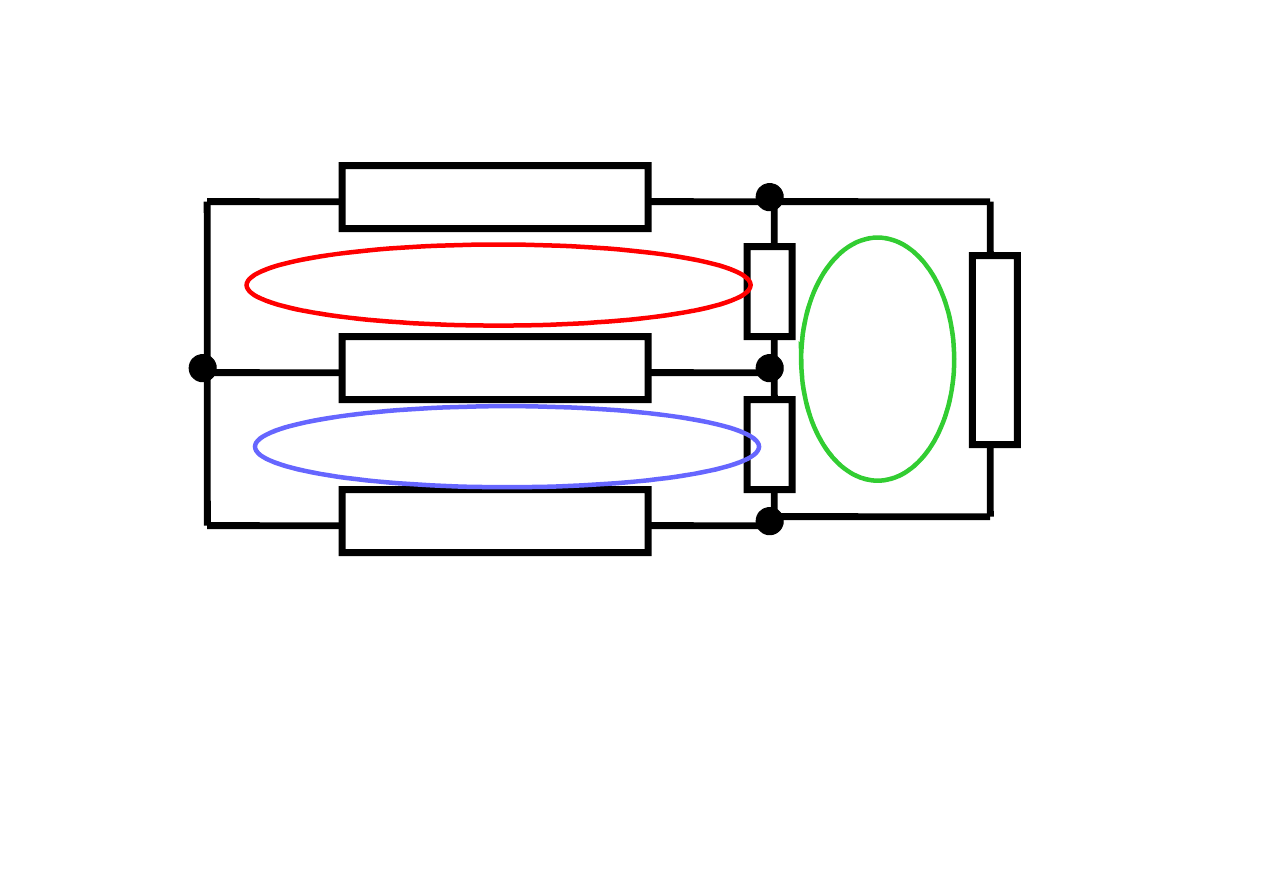
I

II

III

1

2

4

5

6

II

3

5

Pętle I, II, III nazywamy

oczkami

PRAWA KIRCHHOFFA

Są to podstawowe i najbardziej ogólne prawa
obowiązujące w obwodach elektrycznych

Mamy dwa prawa

Kirchhoffa :

PPK – pradowe prawo Kirchhoffa

NPK – napięciowe prawo Kirchhoffa

Prądowe prawo Kirchhoffa

Dla dowolnego węzła każdego obwodu , w
każdej chwili t , algebraiczna suma prądów w
gałęziach zbiegających się w tym węźle jest
równa zeru.

W wyznaczonej wyżej sumie algebraicznej
przypisujemy prądowi znak

plus, jeżeli jego

kierunek jest od węzła

i znak minus w

przypadku, gdy strzałka prądu jest skierowana
do węzła.

∑

=

=

n

k

k

i

1

0

PPK

=

k

1

Sumowanie odbywa się po wszystkich gałęziach
w węźle. Jest ich n

Można napisać tyle równań ile jest węzłów

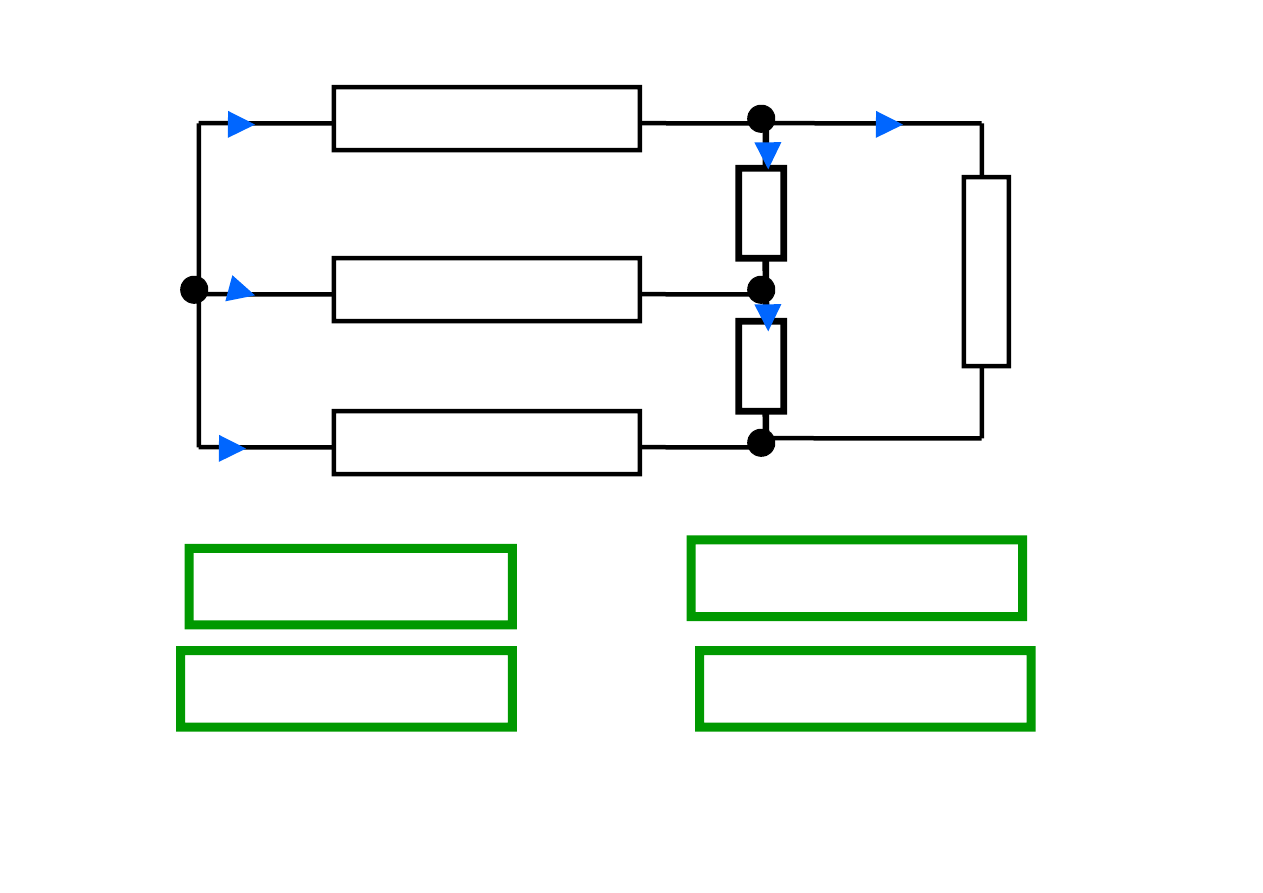
1

2

i

1

i

2

i

3

i

6

i

4

i

5

3

1

2

3

4

5

6

4

3

1: i

1

+ i

2

+ i

3

= 0

2: i

6

+ i

4

– i

1

= 0

3 : i

5

- i

2

– i

4

= 0

4 : - i

3

– i

5

– i

6

= 0

Napisaliśmy 4 równania, tzn. tyle, ile jest węzłów.
Tworzą one układ równań zależnych, gdy dodamy
je stronami otrzymamy

0=0

gdyż każdy prąd

gdyż każdy prąd

wypływa z jednego węzła („+”)

i wpływa do innego („-”).

1

−

α

Piszemy zawsze równań prądowych

α

-

liczba węzłów

Dla każdego obwodu, dla każdej jego pętli w każdej
chwili t suma algebraiczna napięć gałęziowych w
rozpatrywanej pętli jest równa zero.

NPK

W tej sumie znak + przypisujemy napięciom
zgodnym z przyjętym kierunkiem obiegu pętli

∑

=

=

n

k

k

u

1

0

NPK

=

k

1

Sumowanie odbywa się po wszystkich gałęziach
tworzących pętlę. Jest ich n.

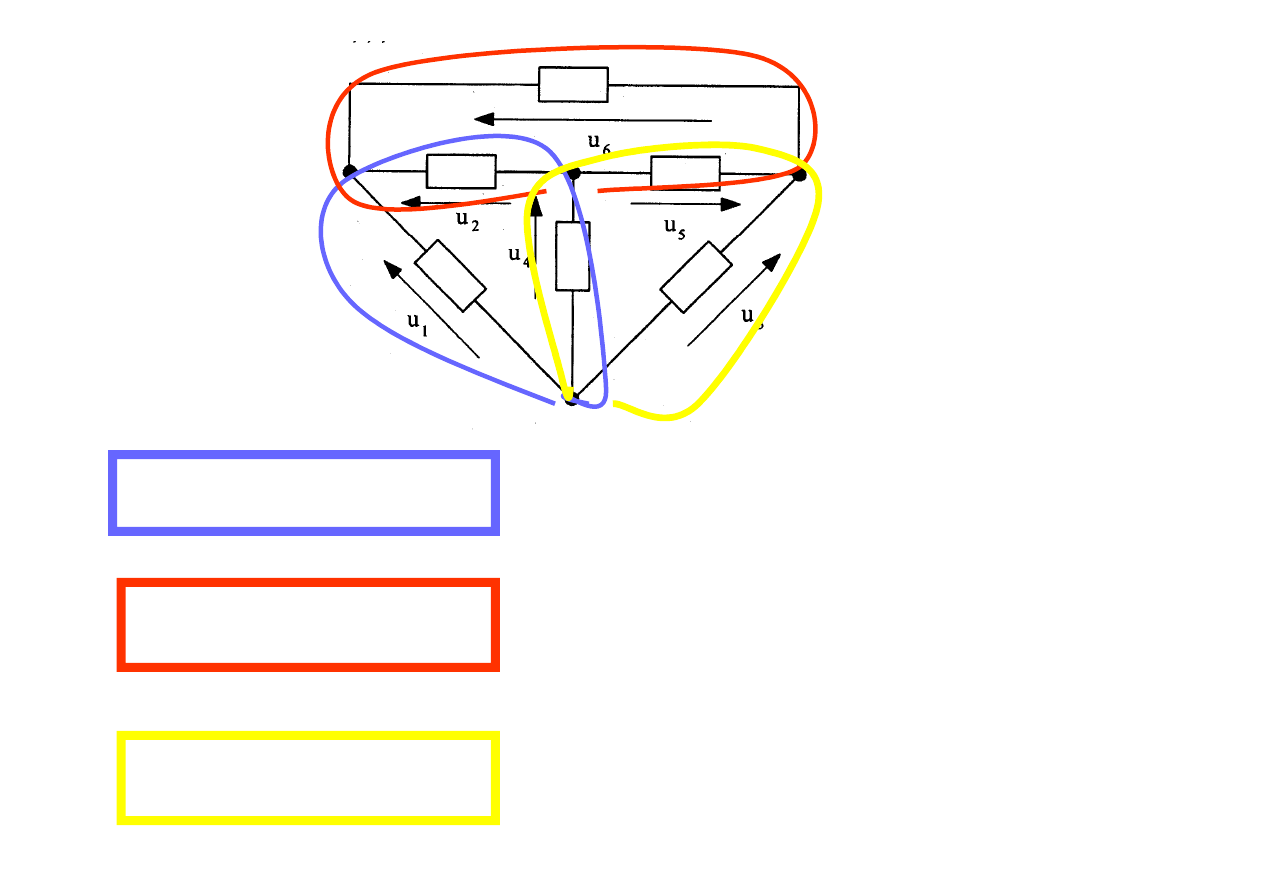
U

1

- U

2

– U

4

= 0

Kierunek obiegu zgodny z kierunkiem
ruchu wskazówek zegara

U

5

+ U

6

– U

2

= 0

Kierunek obiegu przeciwny do
kierunku ruchu wskazówek zegara

U

4

+ U

5

– U

3

= 0

Kierunek obiegu zgodny z kierunkiem
ruchu wskazówek zegara

Ile równań napisaliśmy na podstawie
praw Kirchhoffa?

Przyjmijmy, że gałęzi jest

b,

potrzebne jest zatem

b

równań – tyle , ile jest niewiadomych

1

−

α

Z PPK

równań

b

równań – tyle , ile jest niewiadomych

prądów w gałęziach.

Z NPK

1

+

−

α

b

równań

Właśnie jest oczek w obwodzie

1

+

−

α

b

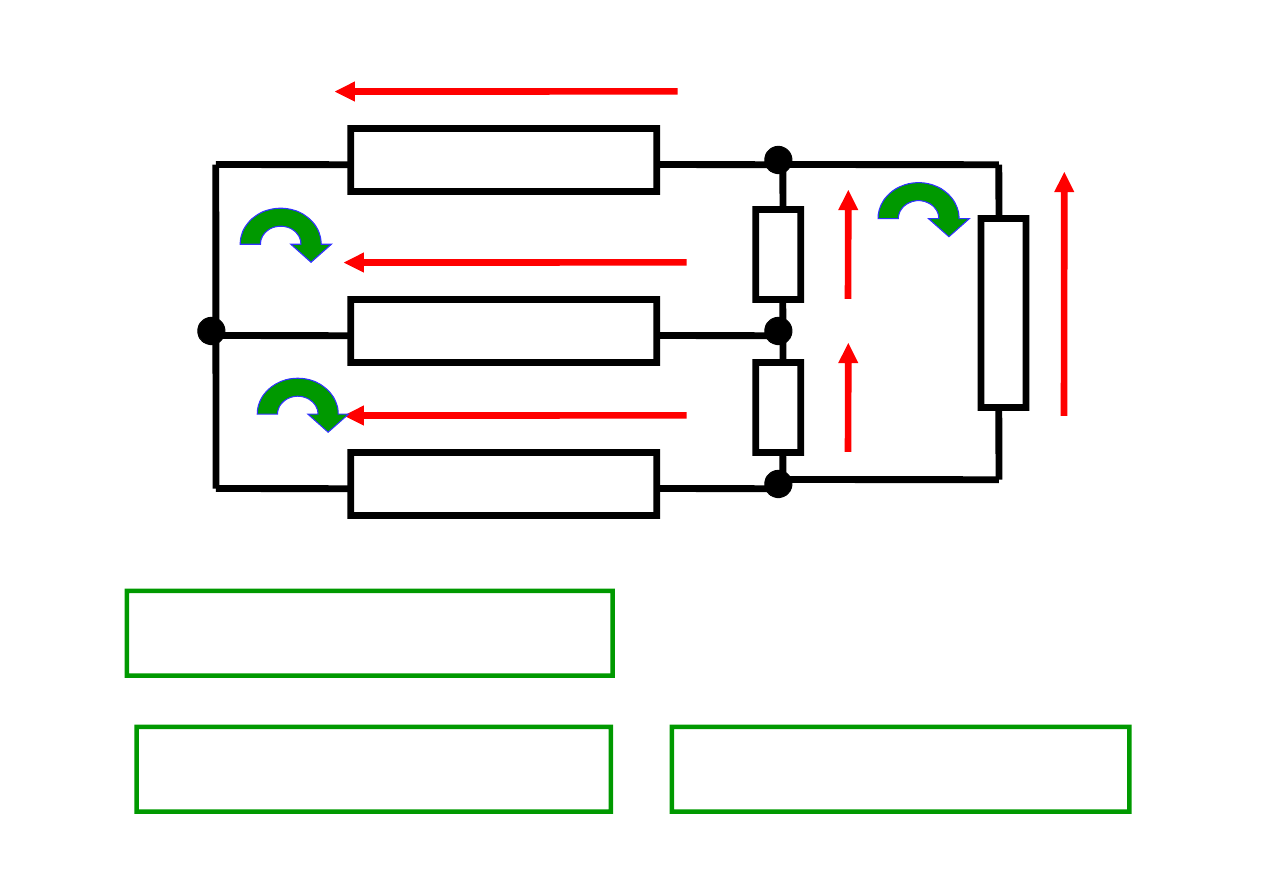
u

1

u

2

u

3

u

4

u

5

u

6

I

II

III

II

I:

- u

1

- u

4

+ u

2

= 0

II: - u

2

- u

5

+ u

3

= 0

III: u

4

- u

6

+ u

5

= 0

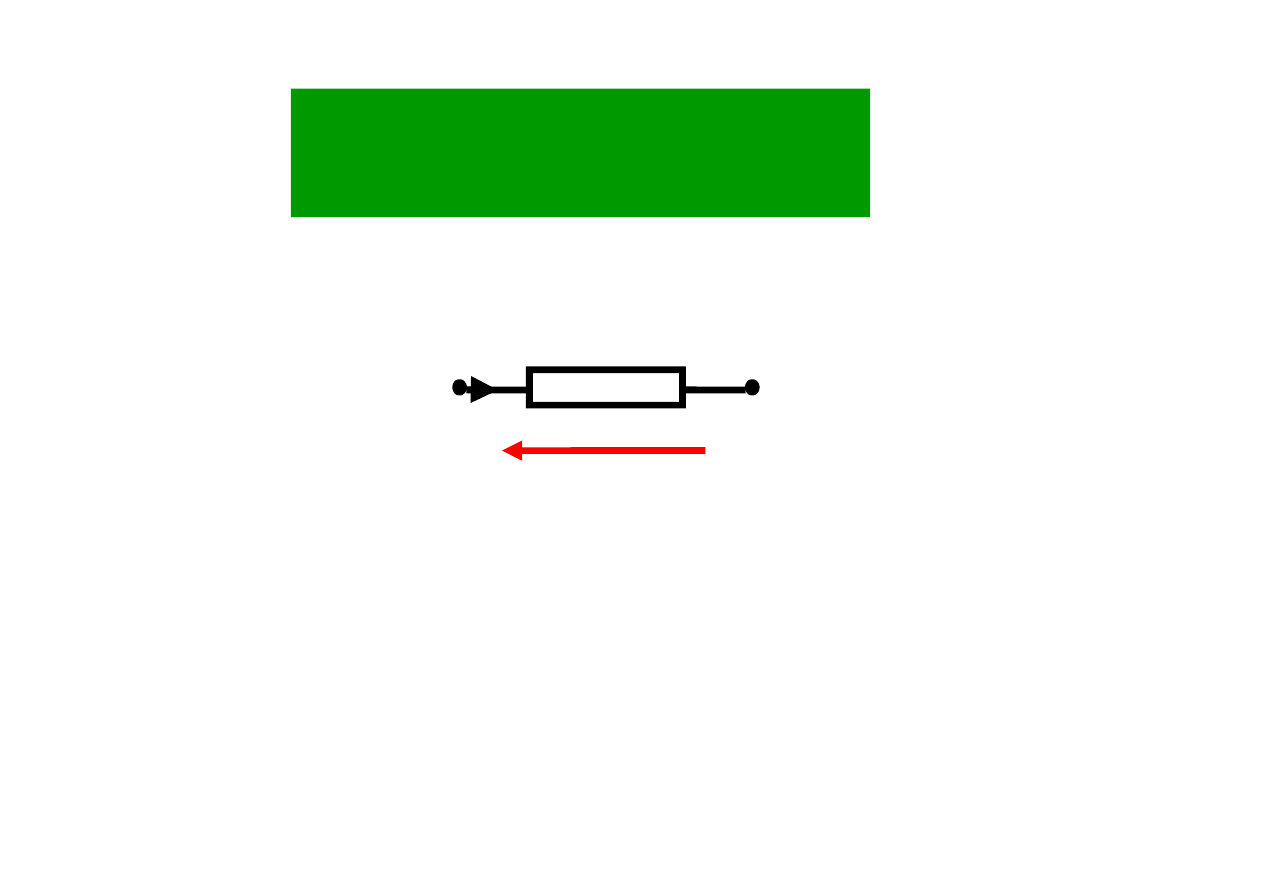
Moc i energia

i

Rozpatrujemy dwójnik jak na rysunku

u

moc chwilowa dwójnika jest iloczynem napięcia u(t) oraz
prądu i(t)

)

(

)

(

)

(

t

i

t

u

t

p

=

moc chwilowa dwójnika jest iloczynem
napięcia u(t) oraz prądu i(t)

)

(

)

(

)

(

t

i

t

u

t

p

=

VA

1

W

1

=

Przy standardowym ostrzałkowaniu prądu i napięcia

Przy standardowym ostrzałkowaniu prądu i napięcia
moc ta jest mocą pobieraną przez element z
otoczenia

Jeżeli w chwili t

1

p

(t

1

)>0 – moc w tej chwili jest

pobierana przez element.
Jeżeli w chwili t

1

p

(t

1

)<0 – moc w tej chwili jest

oddawana przez element do otoczenia.

Energia dostarczona do dwójnika ze źródła w
określonym przedziale czasu od - ∞ do t

∫

∞

−

=

t

d

i

u

t

w

τ

τ

τ

)

(

)

(

)

(

Zależność między mocą chwilową a energią

Zależność między mocą chwilową a energią

∫

∞

−

=

t

d

p

t

w

τ

τ

)

(

)

(

dt

t

dw

t

p

)

(

)

( =

Moc chwilowa jest pochodną względem czasu energii

OBWODY ELEKTRYCZNE

Rozpatrujemy obwody

SLS

S

kupione

L

iniowe

S

tacjonarne

Będziemy rozpatrywać obwody elektryczne, których

maksymalny wymiar jest znacznie mniejszy od

długości fali elektromagnetycznej.

Takie obwody można przedstawić za pomocą

schematów utworzonych ze skupionych w

określonych punktach geometrycznych elementów

połączonych ze sobą przewodami nie

połączonych ze sobą przewodami nie

posiadającymi oporu, indukcyjności ani pojemności

-

obwody o parametrach skupionych.

Jeżeli w równaniu danego elementu nie występuje

w sposób jawny czas, to element nazywamy

stacjonarnym.

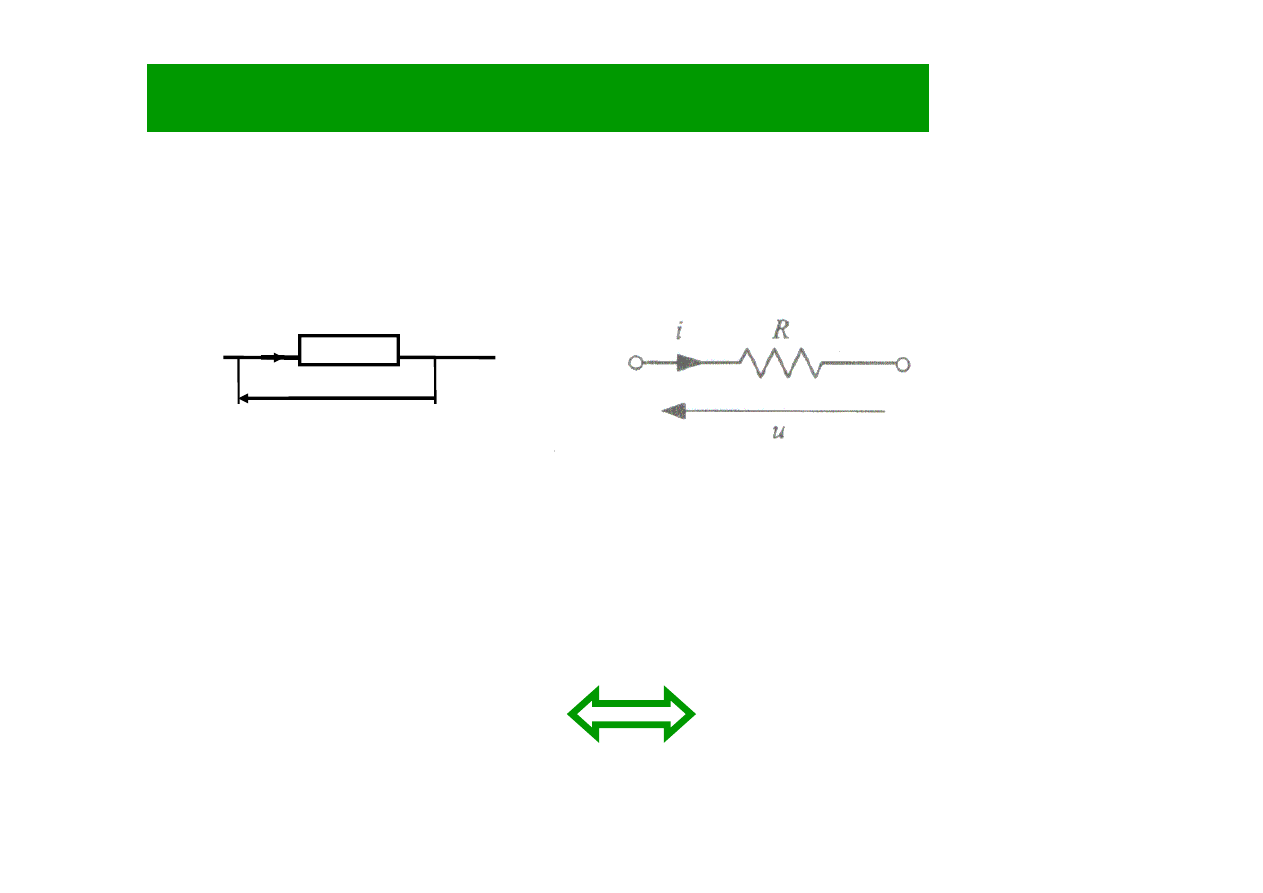
Opornik ( rezystor) liniowy

używane symbole graficzne :

R

u

i

Prawo Ohma

Ri

u

=

Gu

i

=

u

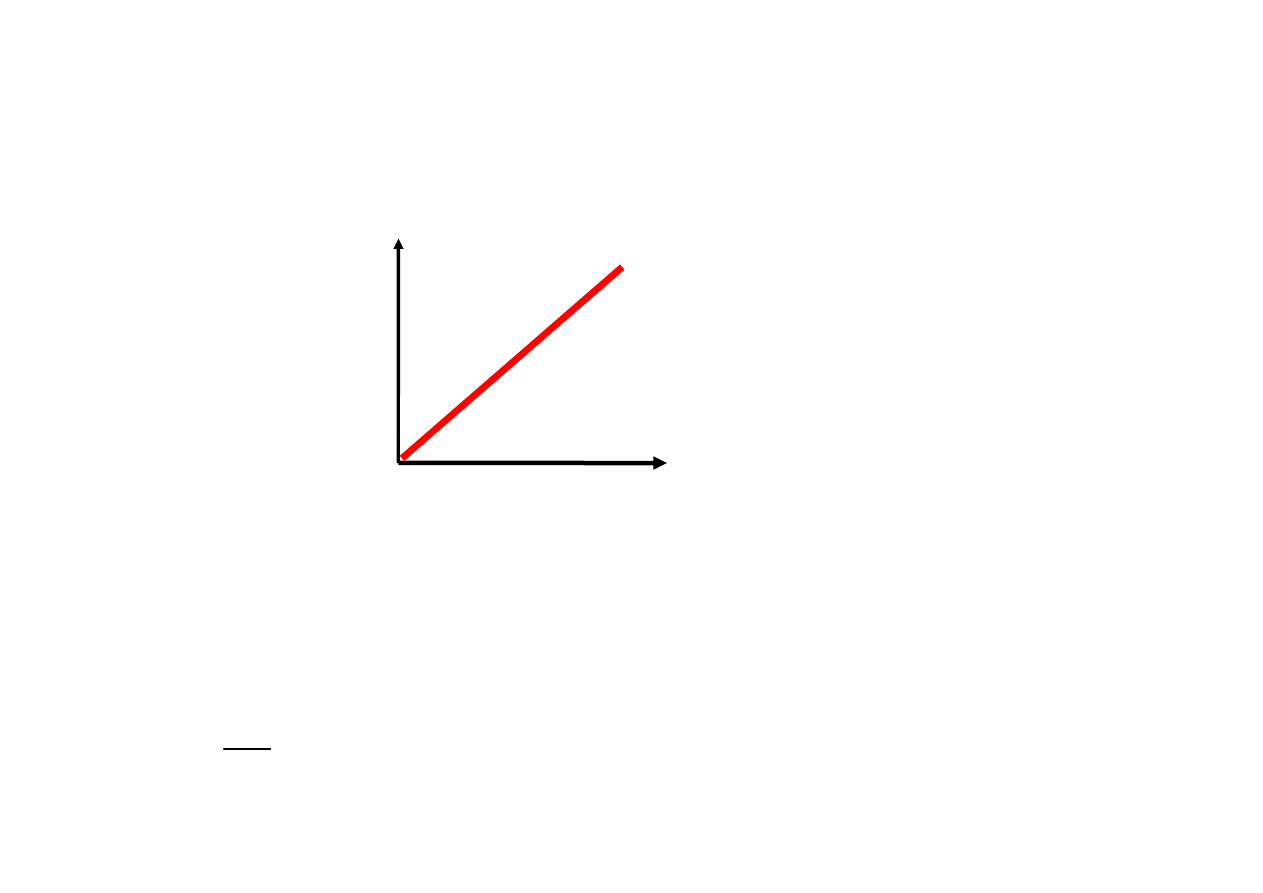
Jeżeli R = const ( jest stałe) to charakterystyka prądowo-

napięciowa ma postać

u(t)

i(t)

i(t)

Ri

u

=

R

– opór w omach

1Ω = 1V/1A

– przewodność w simensach

1S=1A/1V

G

R

1

=

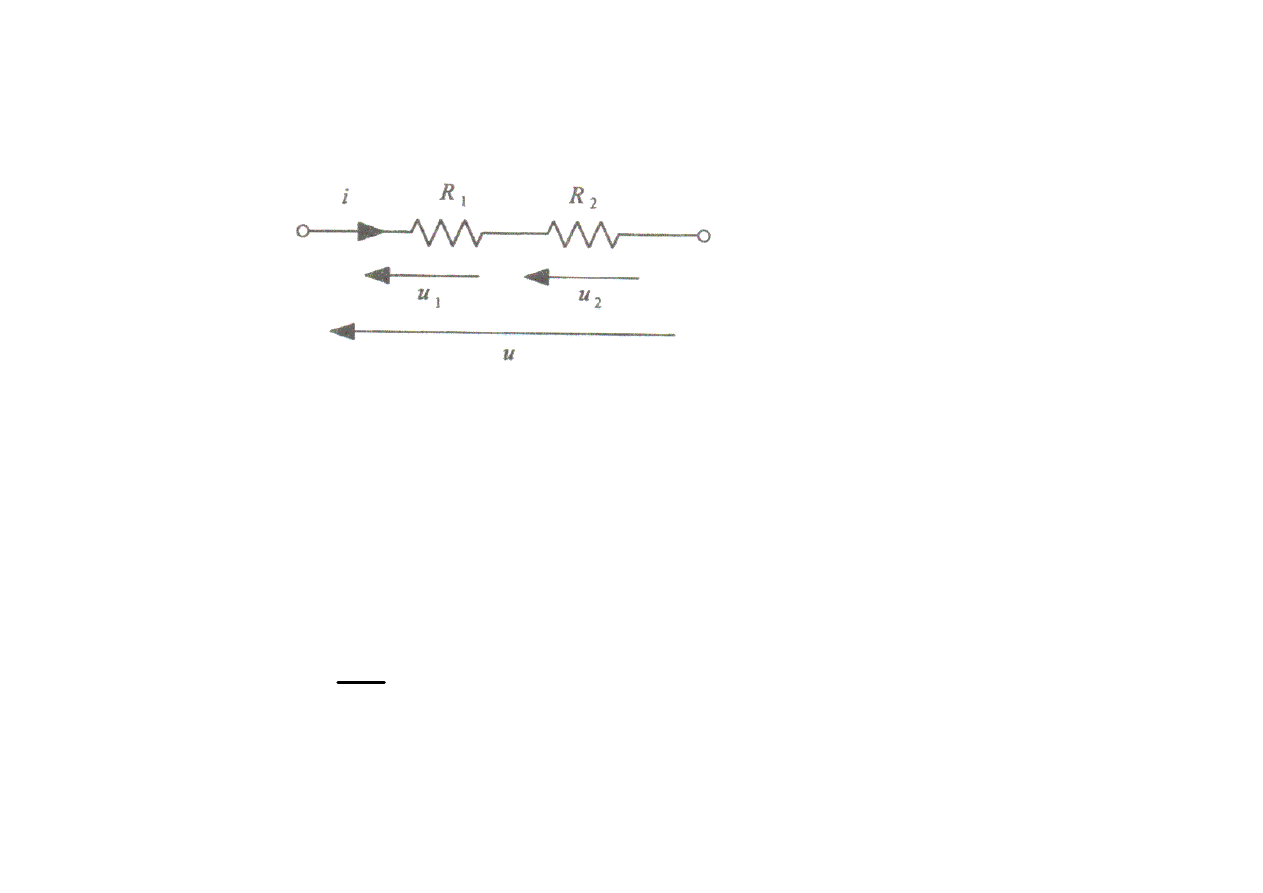
Szeregowe połączenie oporników

(

)

R

R

i

iR

iR

u

u

u

+

=

+

=

+

=

(

)

2

1

2

1

2

1

R

R

i

iR

iR

u

u

u

+

=

+

=

+

=

R

R

R

i

u

=

+

=

2

1

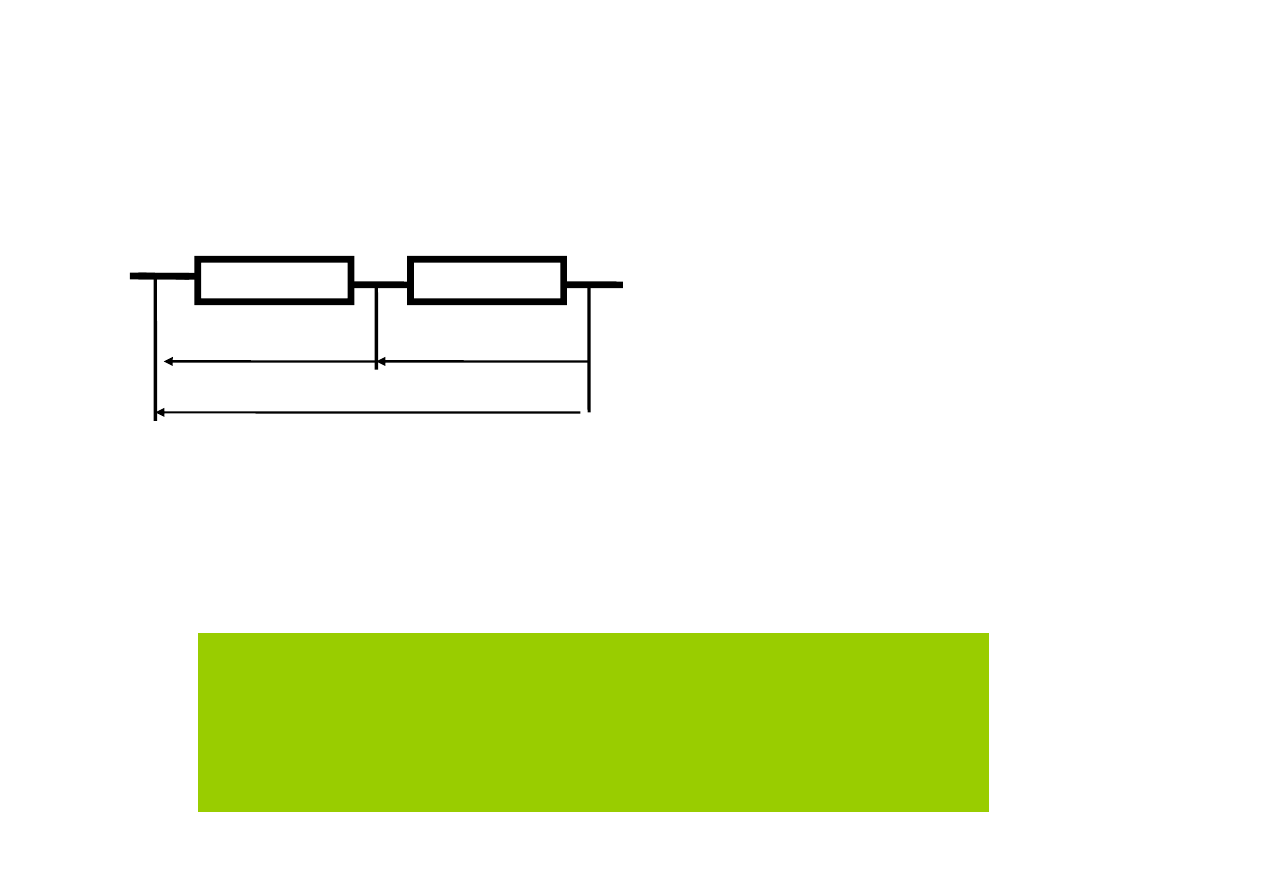
opór połączenia szeregowego

2

1

R

R

R

+

=

u

1

u

2

u

R

1

R

2

Zależność ta dotyczy n- oporników połączonych szeregowo

n

R

R

R

R

R

+

+

+

+

=

....

3

2

1

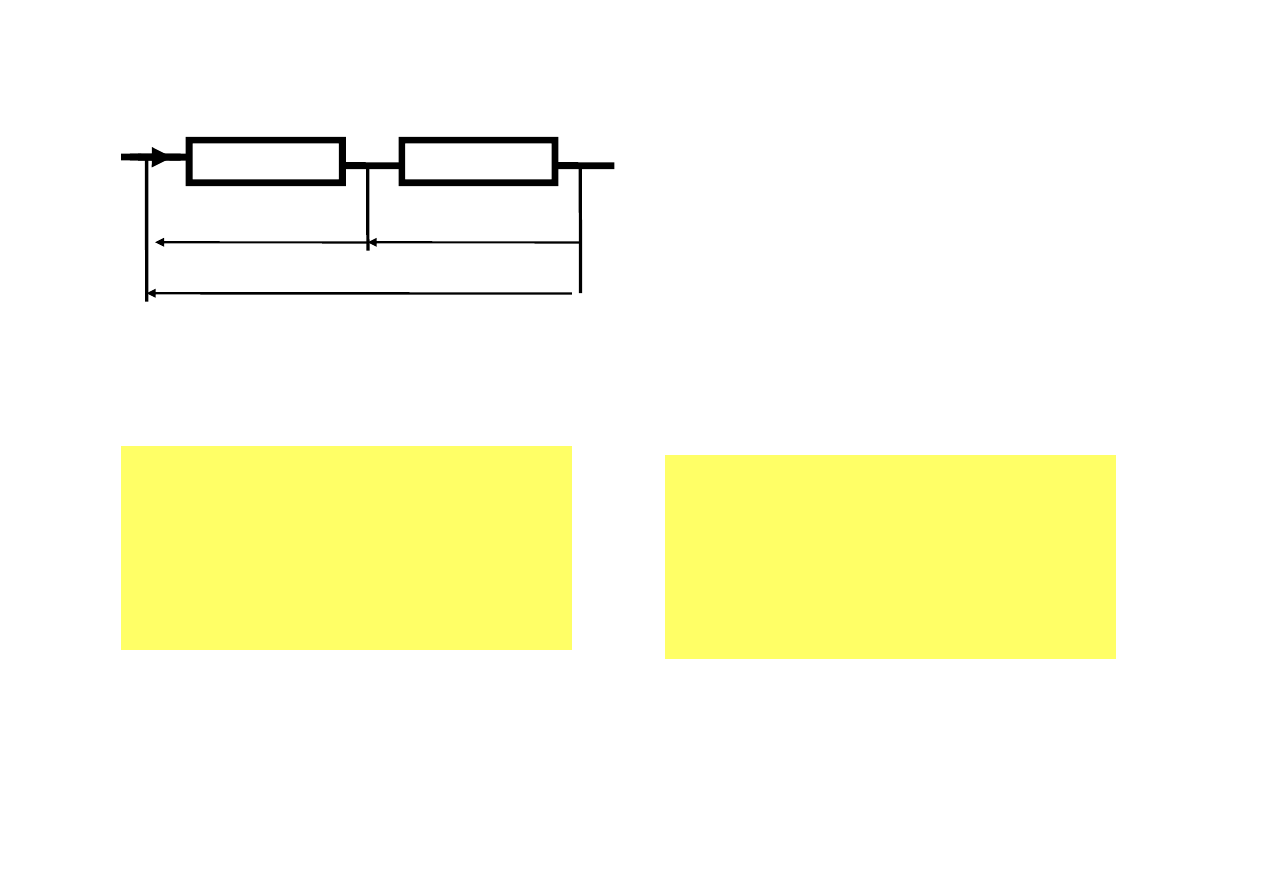
u

1

u

2

u

R

1

R

2

i

Szeregowe połączenie

jako dzielnik napięcia

Napięcie na połączeniu ulega podziałowi

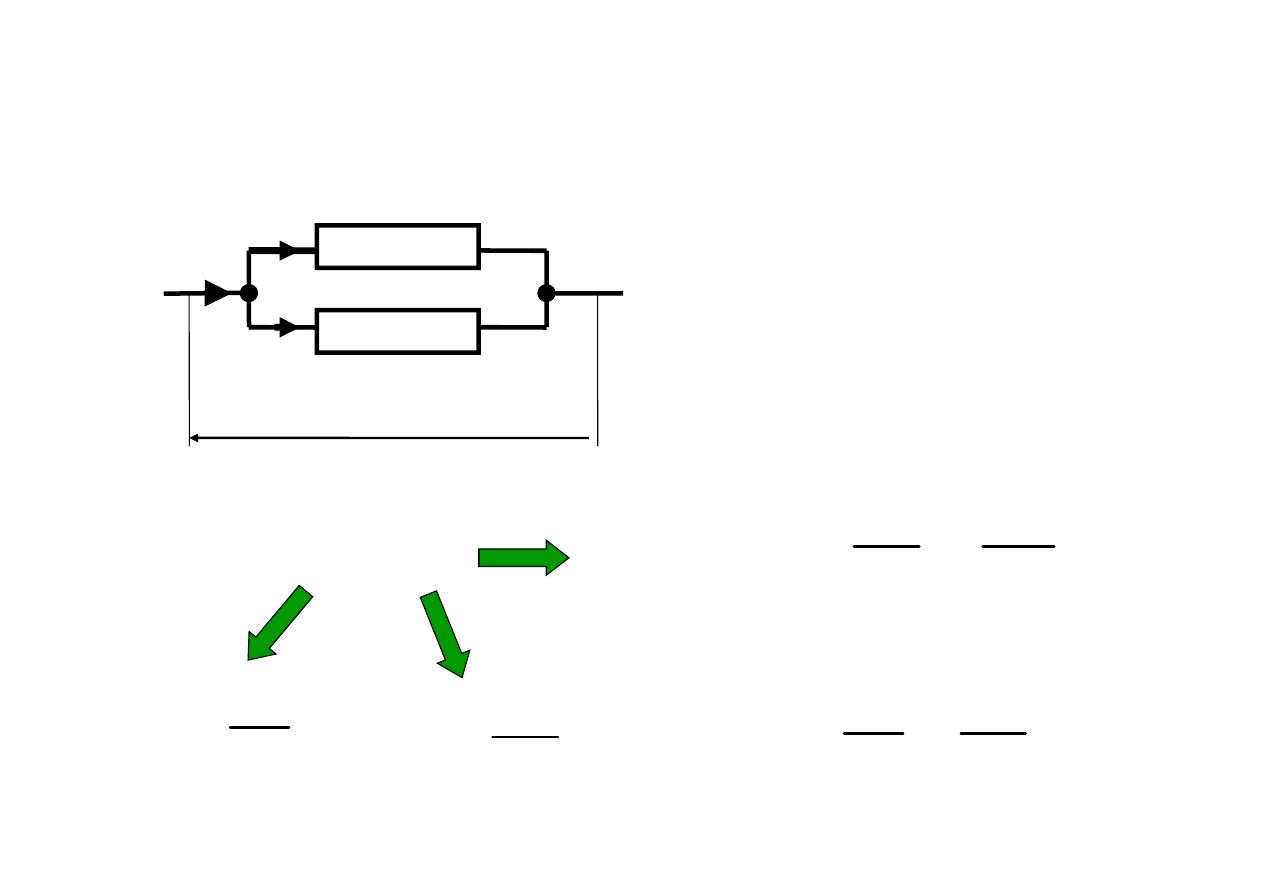
Równoległe połączenie oporników

Napięcie na obu

opornikach jest jednakowe

i

i

1

i

2

u

R

2

R

1

2

1

i

i

i

+

=

1

1

R

u

i

=

2

2

R

u

i

=

więc

2

1

R

u

R

u

i

+

=













+

=

2

1

1

1

R

R

u

i

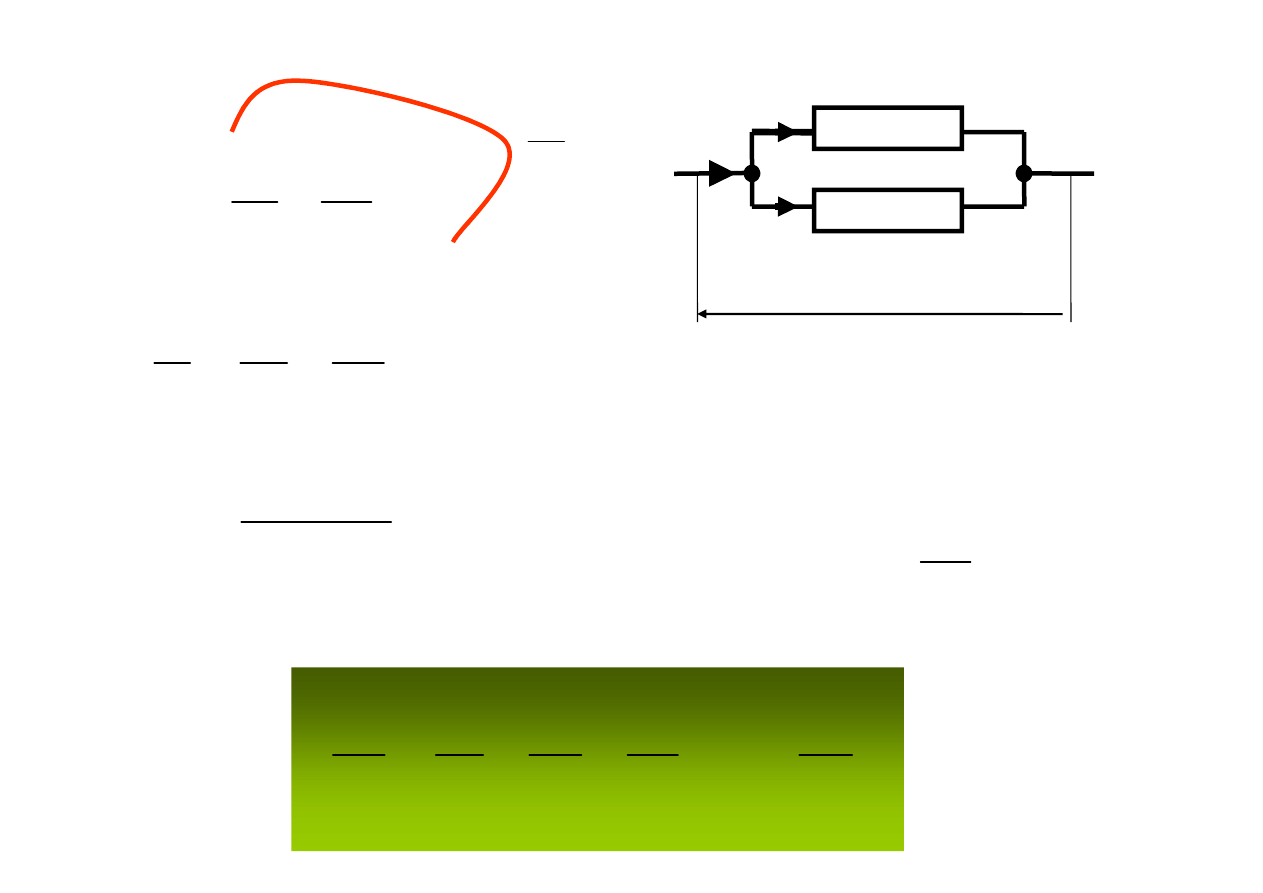
i

i

1

i

2

u

R

2

R

1













+

=

2

1

1

1

R

R

u

i

2

1

1

1

1

R

R

R

+

=

Jeżeli

a

R

R

R

=

=

2

1

R

1

2

1

2

1

R

R

R

R

R

+

=

Jeżeli

a

R

R

R

=

=

2

1

to

2

a

R

R

=

n

z

R

R

R

R

R

1

...

1

1

1

1

3

2

1

+

+

+

+

=

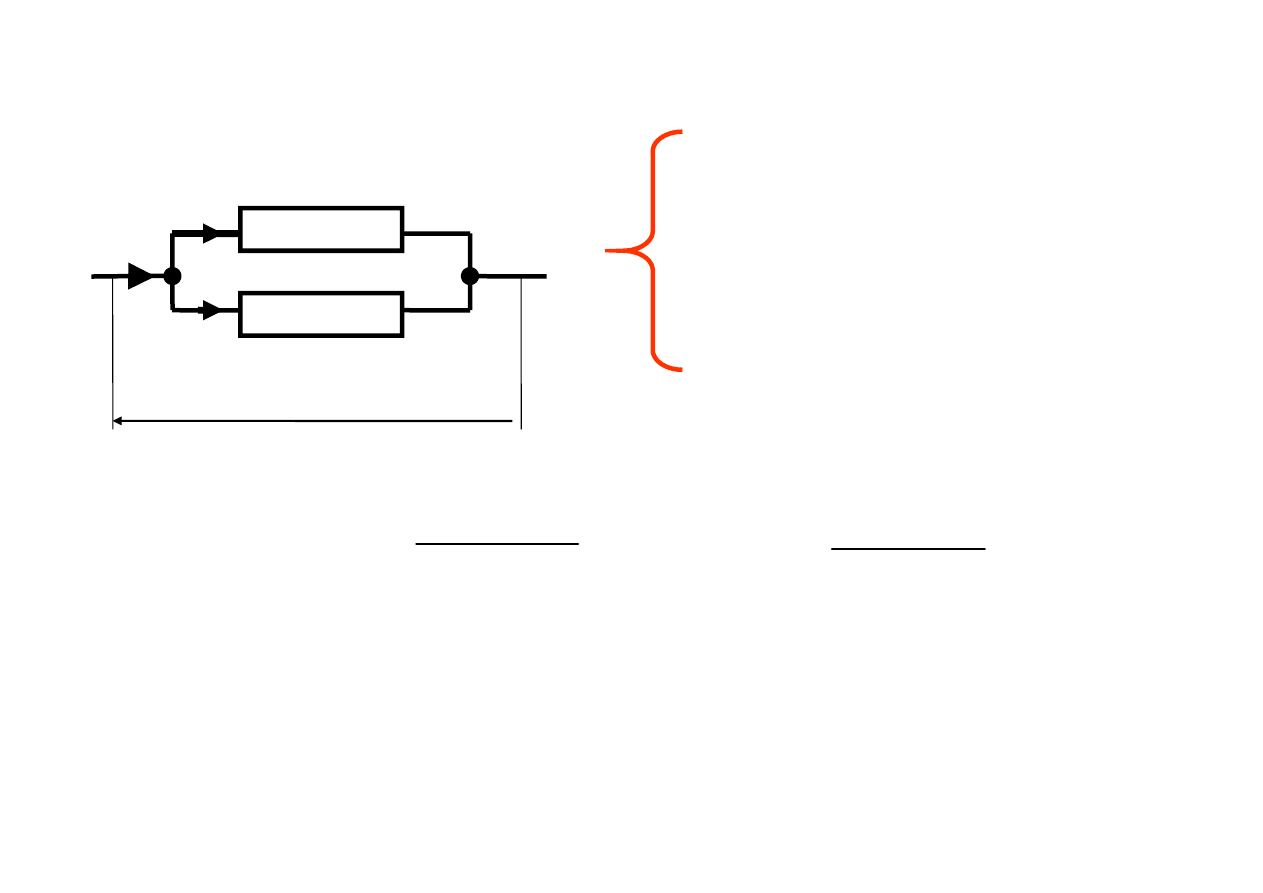
i

i

1

i

2

u

R

2

R

1

Dzielnik prądowy

2

1

i

i

i

+

=

2

2

1

1

R

i

R

i

=

2

1

2

1

R

R

R

i

i

+

=

2

1

1

2

R

R

R

i

i

+

=

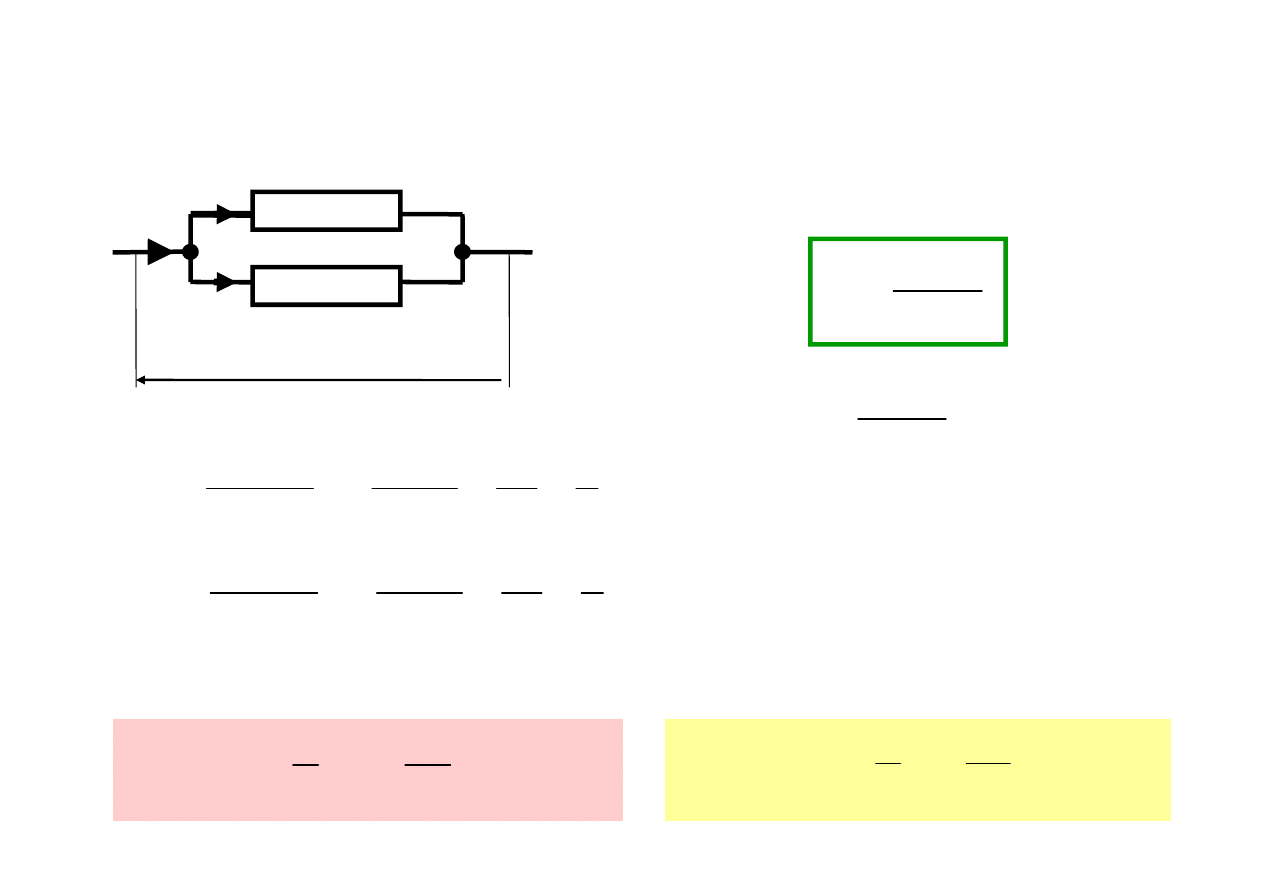
PRZYKŁAD

i

i

1

i

2

u

R

2

R

1

A

i

R

R

3

5

15

2

1

=

Ω

=

Ω

=

2

1

2

1

R

R

R

R

R

z

+

=

Ω

=

+

⋅

=

75

,

3

5

15

5

15

z

R

A

R

R

R

i

i

4

3

20

15

15

5

5

3

2

1

2

1

=

=

+

=

+

=

A

R

R

R

i

i

4

9

20

45

15

5

15

3

2

1

1

2

=

=

+

=

+

=

+ 5

15

V

R

i

u

25

,

11

4

45

15

4

3

1

1

=

=

=

=

V

R

i

u

25

,

11

4

45

5

4

9

2

2

=

=

=

=

moc opornika o oporze R

moc opornika liniowego jest w każdej chwili t
nieujemna

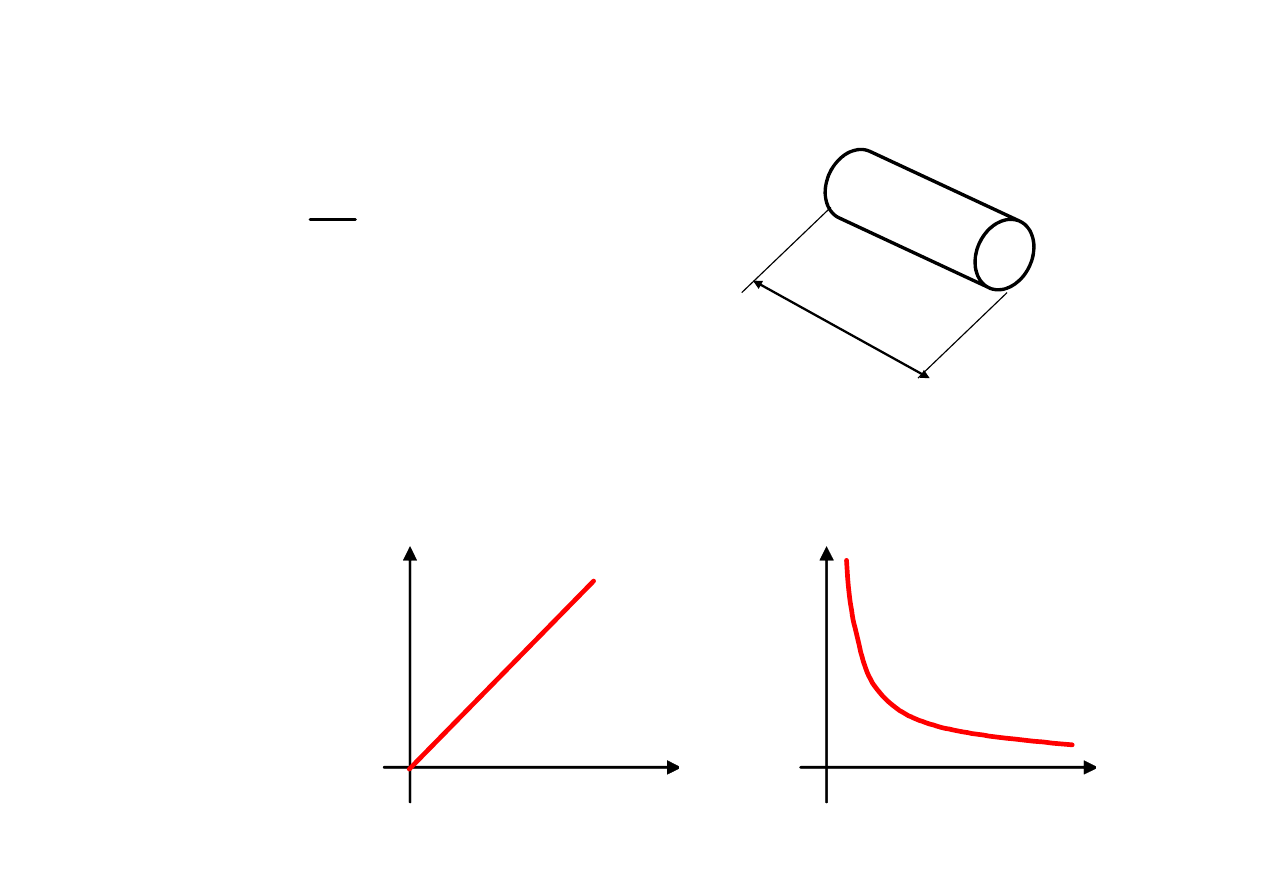
przypomnienie…

S

l

R

ρ

=

ρ

- opór właściwy [Ωm]

l

- długość

l

s

l

- długość

S - przekrój

l

R

S= const

S

R

l= const

[

]

)

(

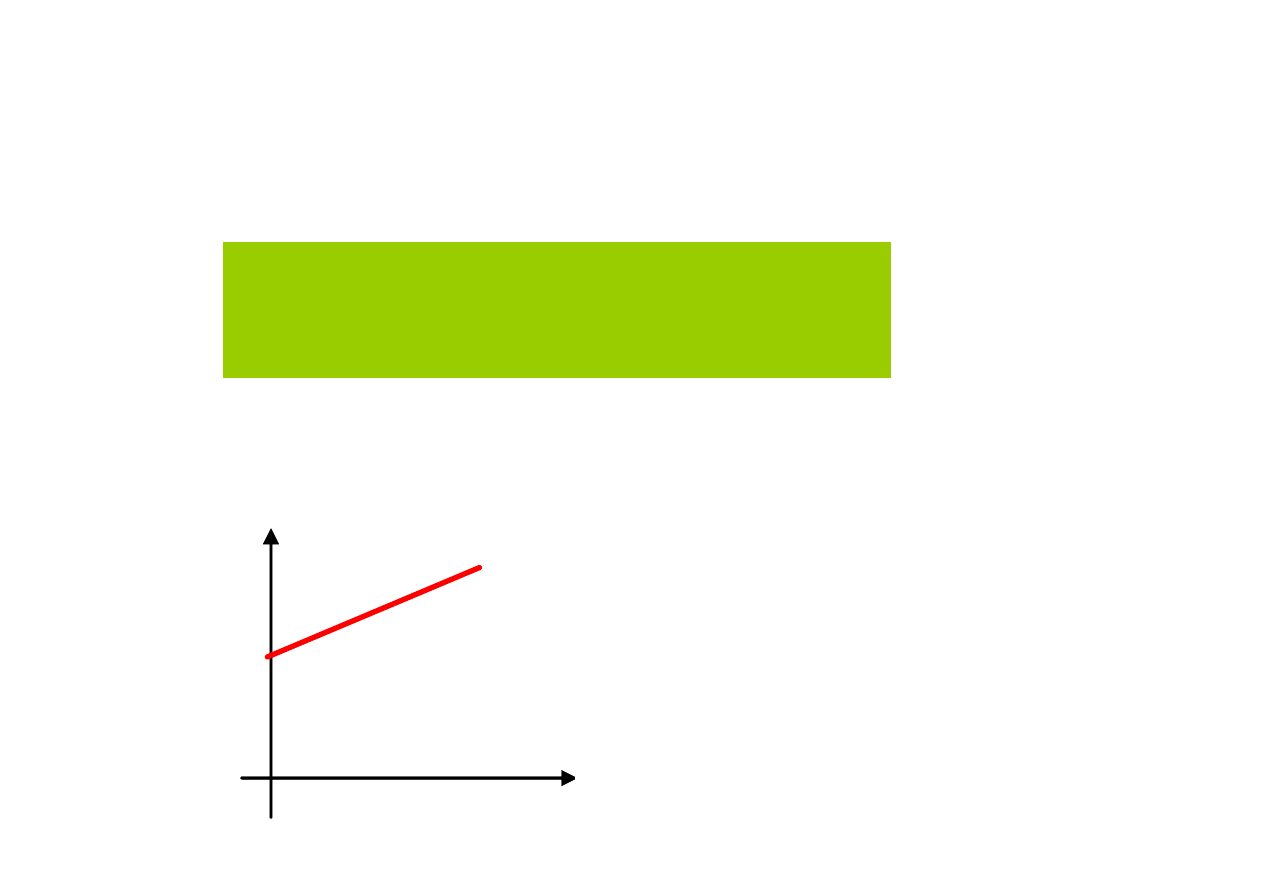
1

20

0

T

T

R

R

t

t

−

+

=

α

−

α

współczynnik temperaturowy oporu

Zależność rezystancji od temperatury

przypomnienie…

T

t

R

t

R

0

T

0

−

α

współczynnik temperaturowy oporu

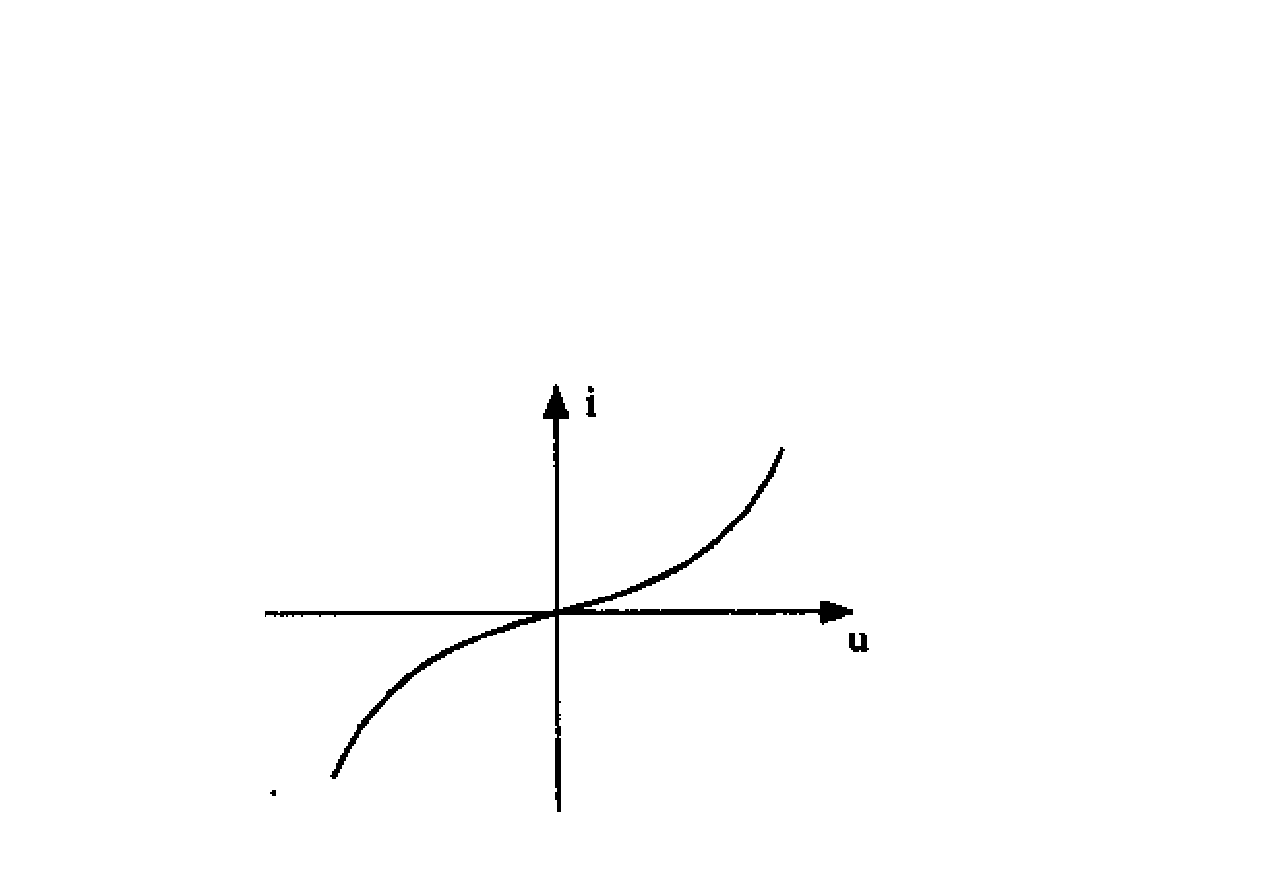
Opornik nieliniowy, dla którego u jest jednoznaczną
funkcją i dla i ∈

∈

∈

∈ (-∞

∞

∞

∞, ∞

∞

∞

∞) oraz i jest jednoznaczną

funkcją u dla u ∈

∈

∈

∈ (-∞

∞

∞

∞, ∞

∞

∞

∞) nazywamy

nieuzależnionym

.

warystor

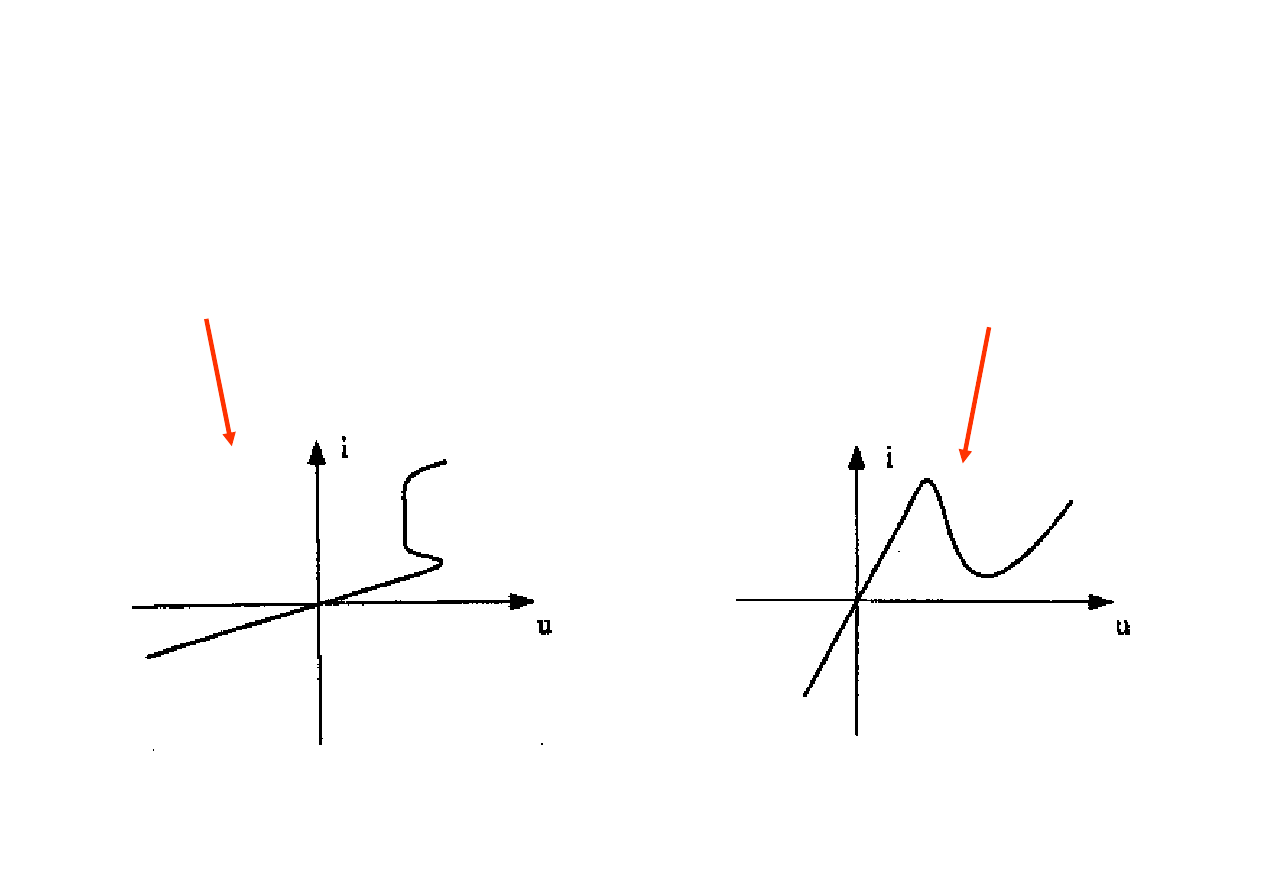
Opornik nieliniowy nazywamy

uzależnionym prądowo

,

jeżeli napięcie u jest jednoznaczną

funkcją prądu i dla i ∈

∈

∈

∈ (-∞

∞

∞

∞, ∞

∞

∞

∞)

Opornik nieliniowy nazywamy

uzależnionym napięciowo

,

jeżeli prąd i jest jednoznaczną

funkcją napięcia u dla u ∈

∈

∈

∈ (-∞

∞

∞

∞, ∞

∞

∞

∞)

lampa jarzeniowa

dioda tunelowa

Elementy niestacjonarne

Element jest

niestacjonarny

, jeżeli w jego opisie

matematycznym występuje w sposób jawny czas t.

opornik liniowy (niestacjonarny)

( )

i

t

R

u

=

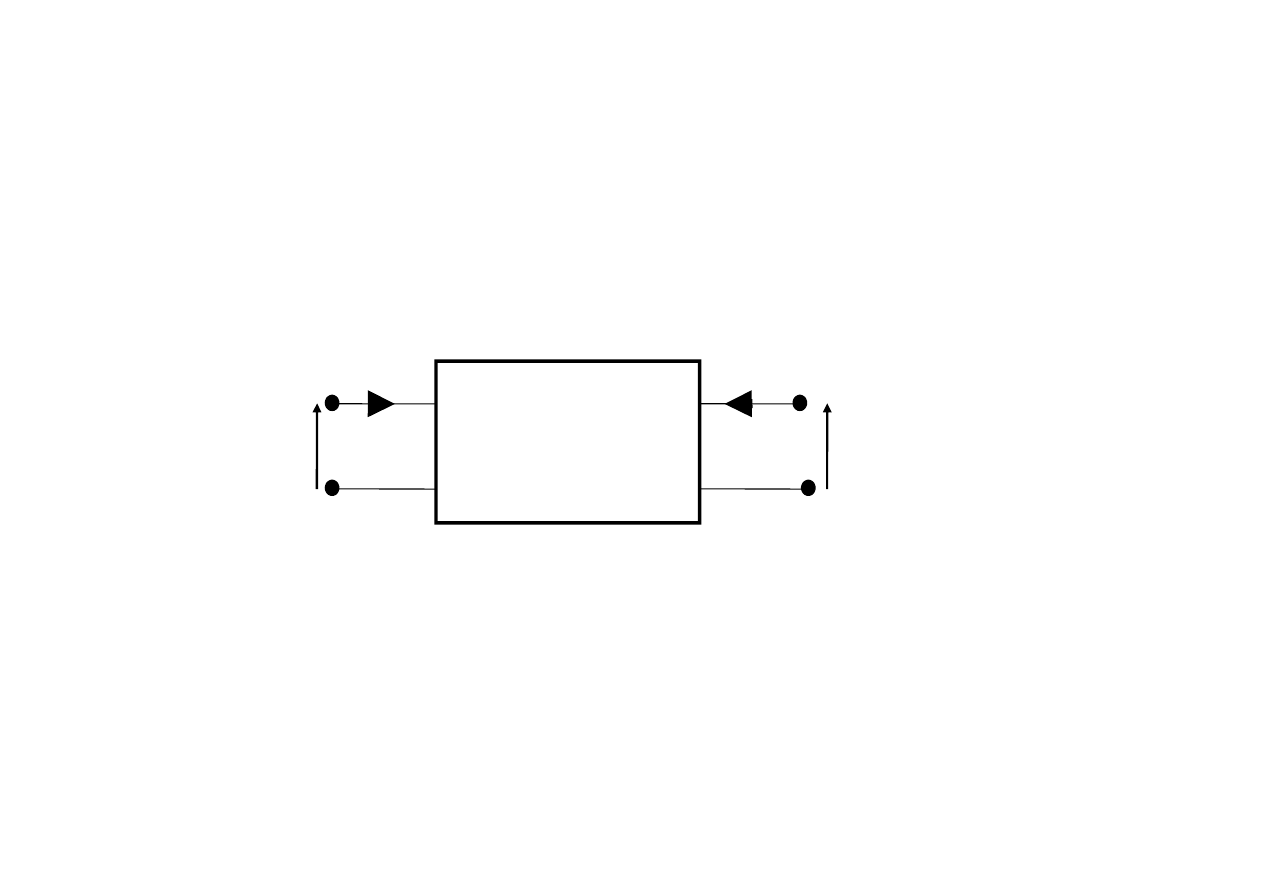
CZWÓRNIKI

i

1

i

2

u

1

u

2

1

2

u

1

u

2

1`

2`

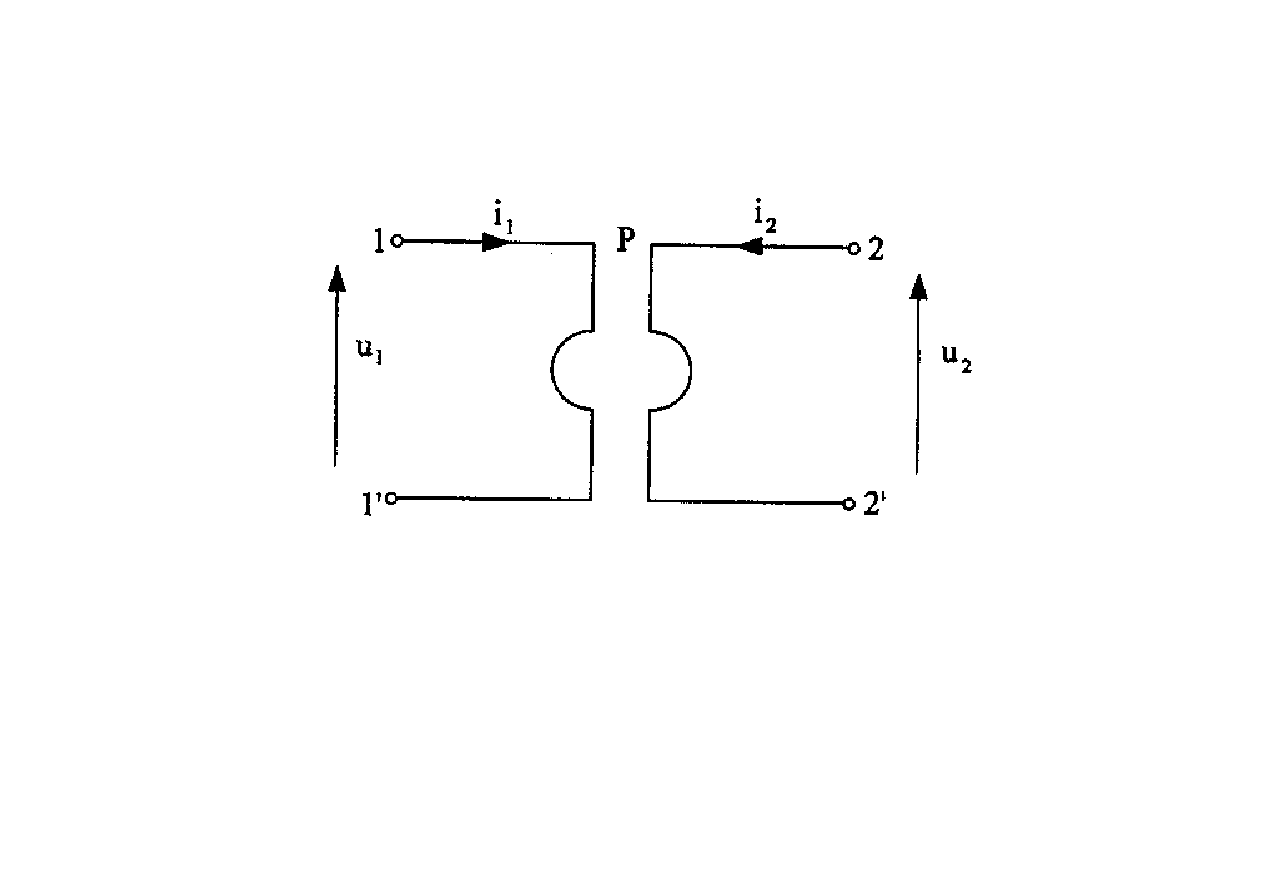
Transformator idealny

(wykorzystywany w syntezie

układów pasywnych )

2

1

u

p

u

=

2

1

1

i

p

i

−

−

=

p – liczba rzeczywista

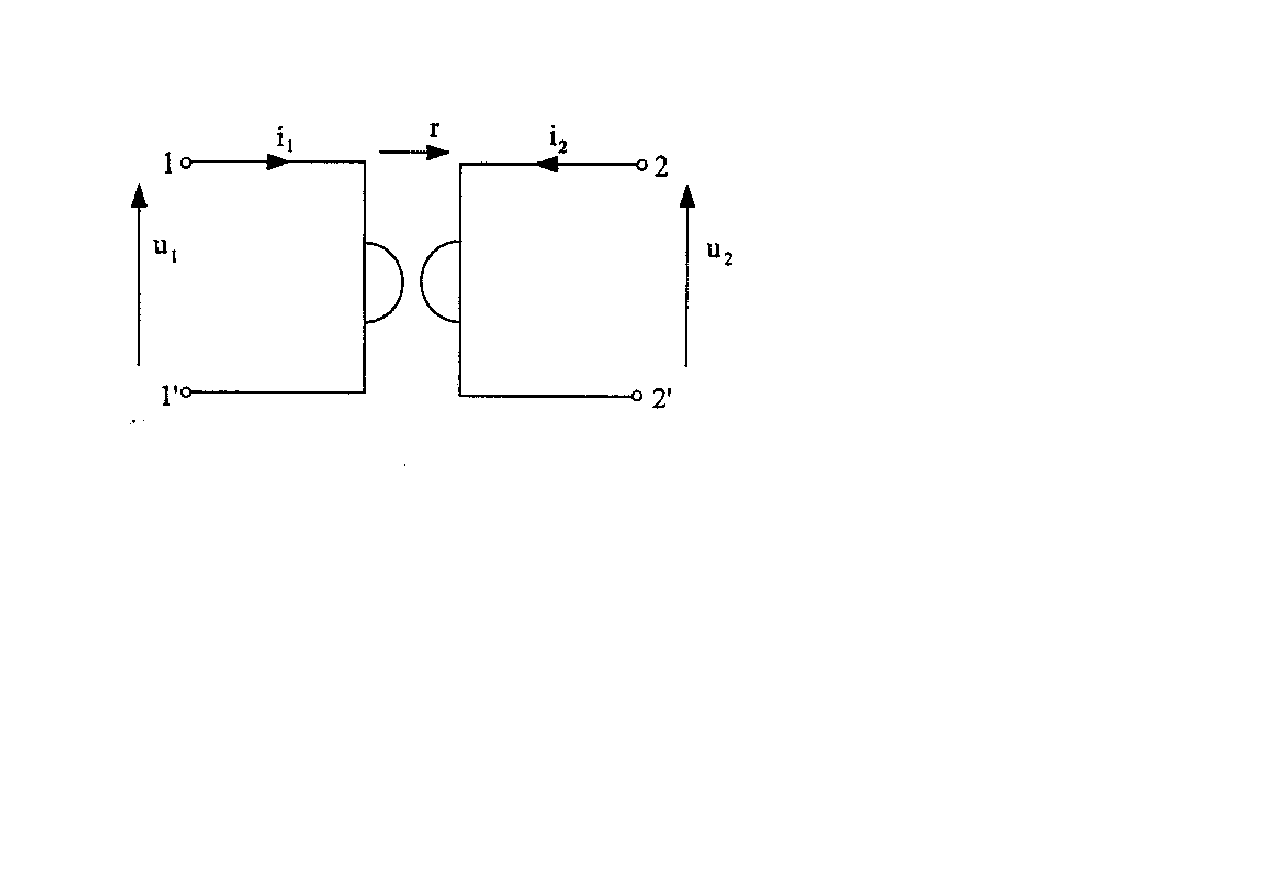
Żyrator idealny

2

1

i

r

u

−

=

1

2

i

r

u

=

r

- stała dodatnia zwaną oporem żyracji

Żyrator idealny jest stosowany w syntezie układów aktywnych.

ż

yrator idealny obciążony kondensatorem symuluje

cewkę o indukcyjności

C

r

L

2

=

.

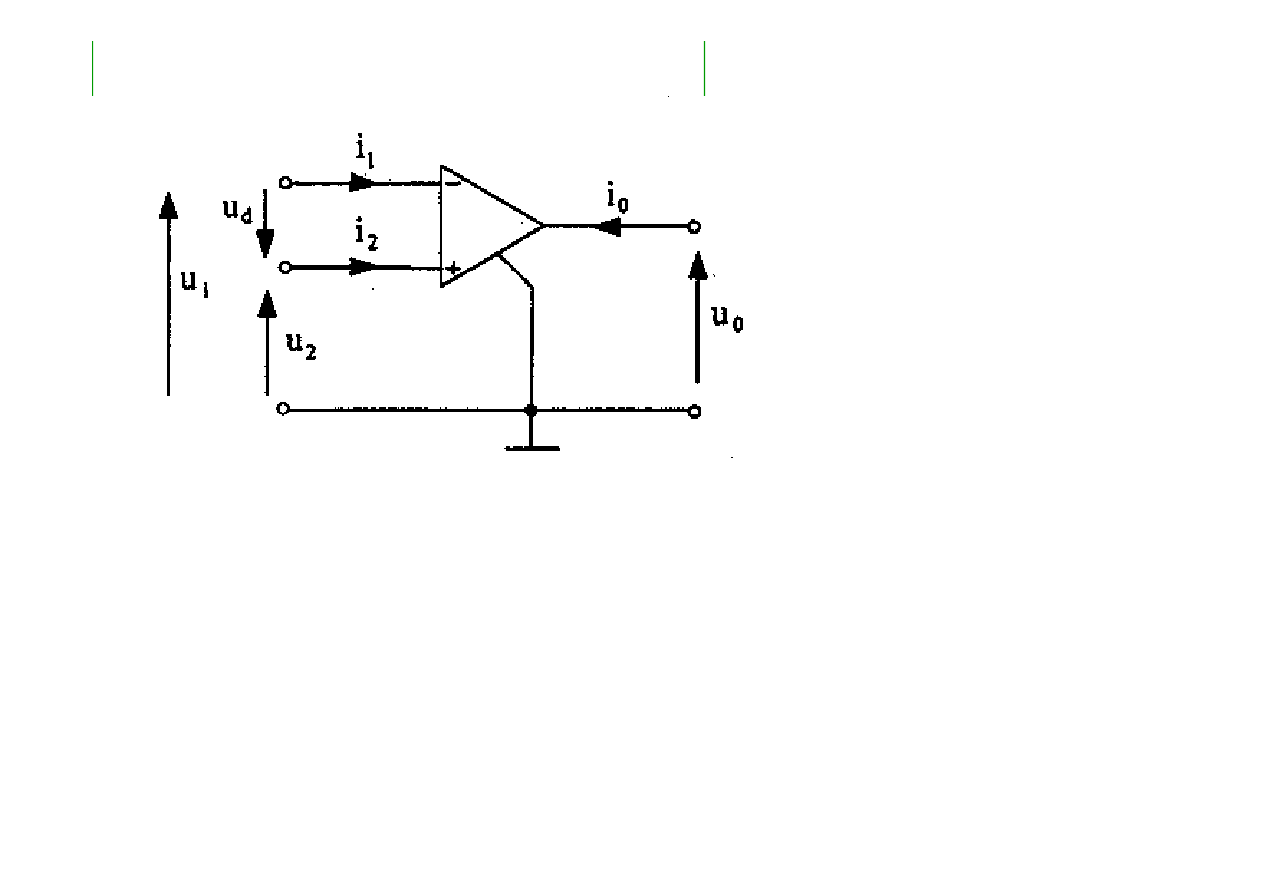
Wzmacniacz operacyjny idealny

0

1

=

i

0

2

=

i

,

u

,

E

u

E

d

s

s

0

gdy

0

=

≤

≤

−

,

u

,

E

u

d

s

0

gdy

0

<

−

=

,

u

,

E

u

d

s

0

gdy

0

>

=

E

s

- dodatnie napięcie, zwanym napięciem nasycenia,

o wartości zależnej od technologii wykonania w. o.

Inne elementy obwodów

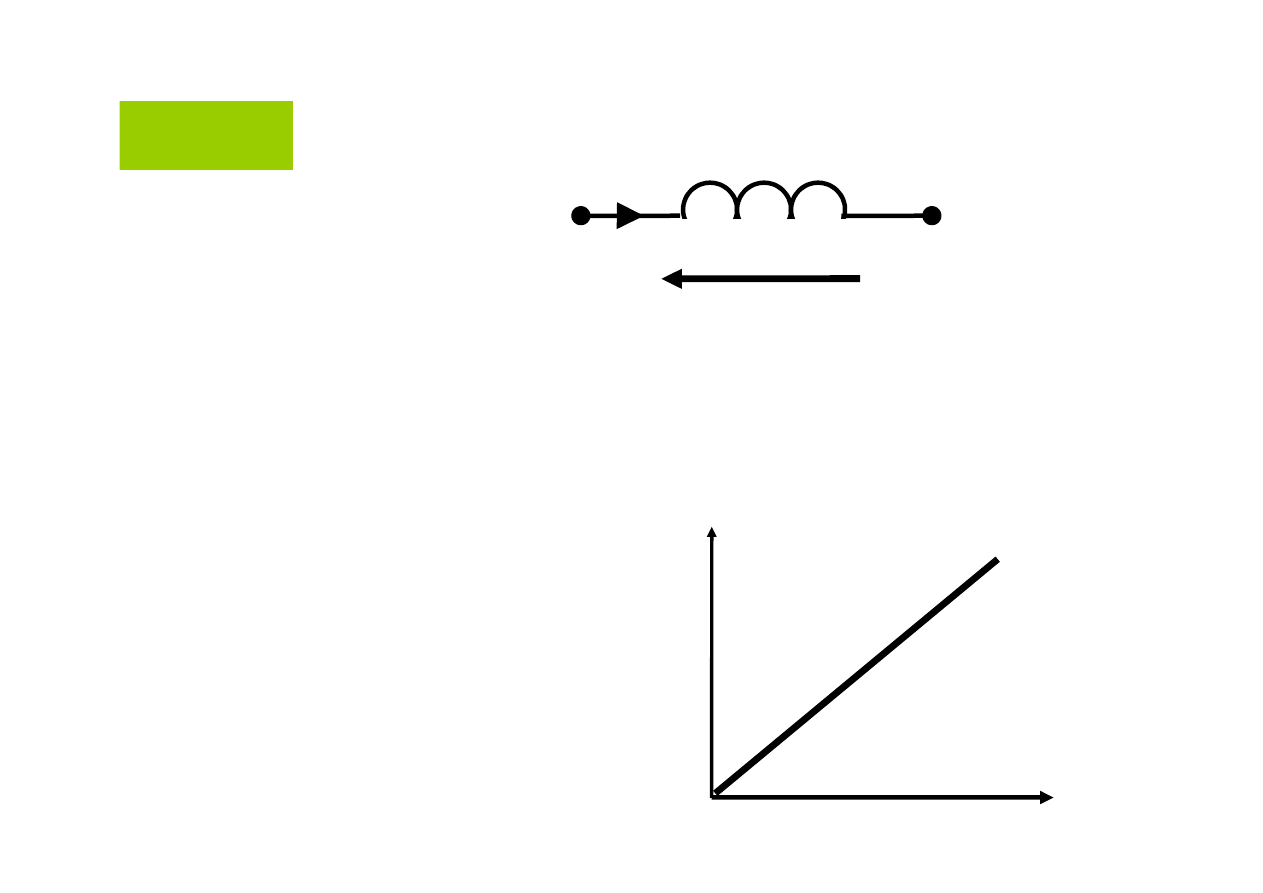
Cewka

i

u

L

( )

( )

t

i

L

t

=

φ

gdy

Strumień magnetyczny
przenikający przez uzwojenie
jest proporcjonalny do prądu

.

const

L

=

indukcyjność

gdy

jest proporcjonalny do prądu

Φ

i

.

const

L

=

charakterystyka
strumieniowo-prądowa
cewki liniowej
jest linią prostą
przechodzącą przez
początek układu współrzędnych

Li

=

φ

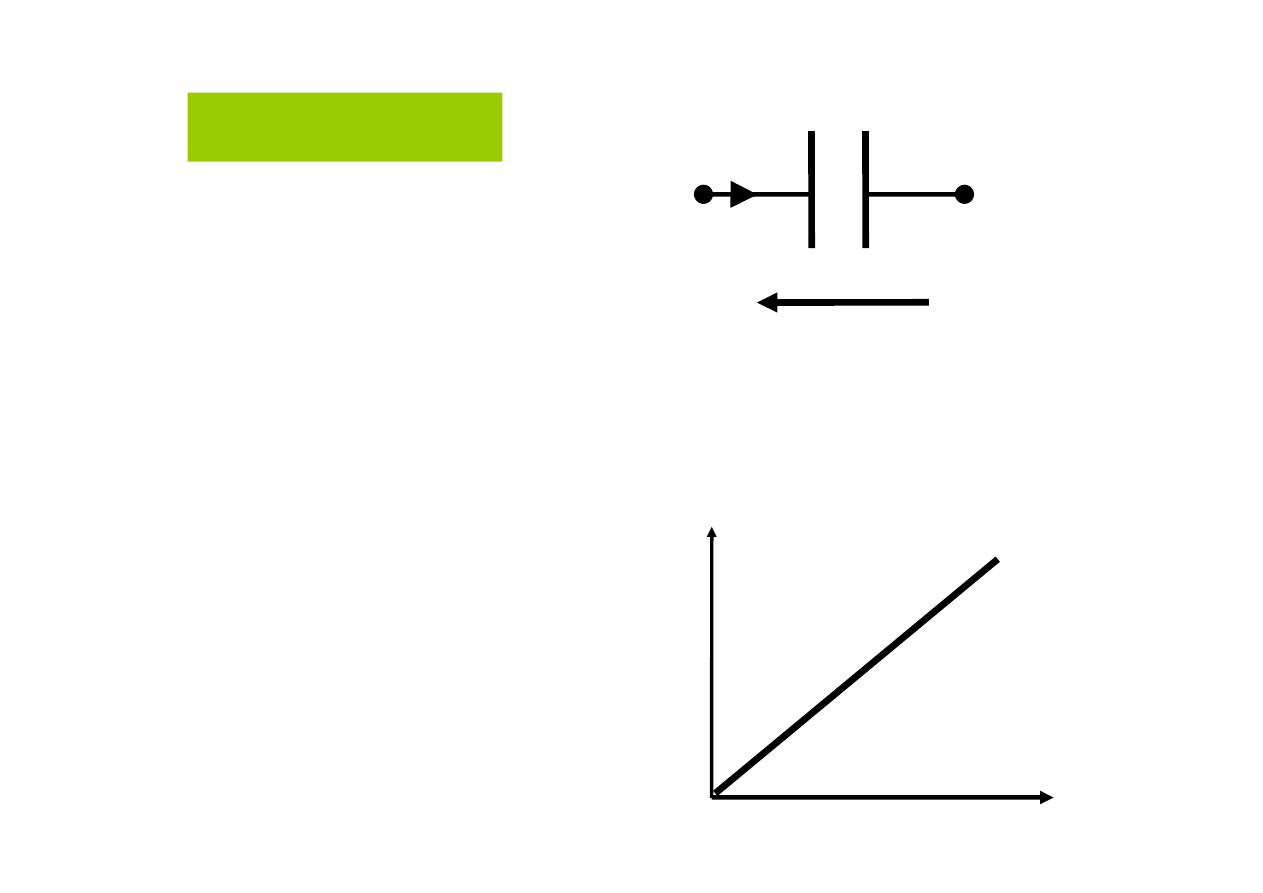
Kondensator

C

i

u

( )

( )

t

u

C

t

q

=

Ładunek elektryczny
na okładkach kondensatora
jest proporcjonalny do napięcia

gdy

pojemność

jest proporcjonalny do napięcia

gdy

.

const

C

=

charakterystyka
napięciowo-ładunkowa
kondensatora liniowego
jest linią prostą
przechodzącą przez
początek układu współrzędnych.

q

u

Cu

q

=

Źródła są modelami obwodowymi

Źródła niezależne

Źródła są modelami obwodowymi

przetworników energii,

które dokonują przemiany energii w postaci

np. mechanicznej, chemicznej na energię

elektryczną

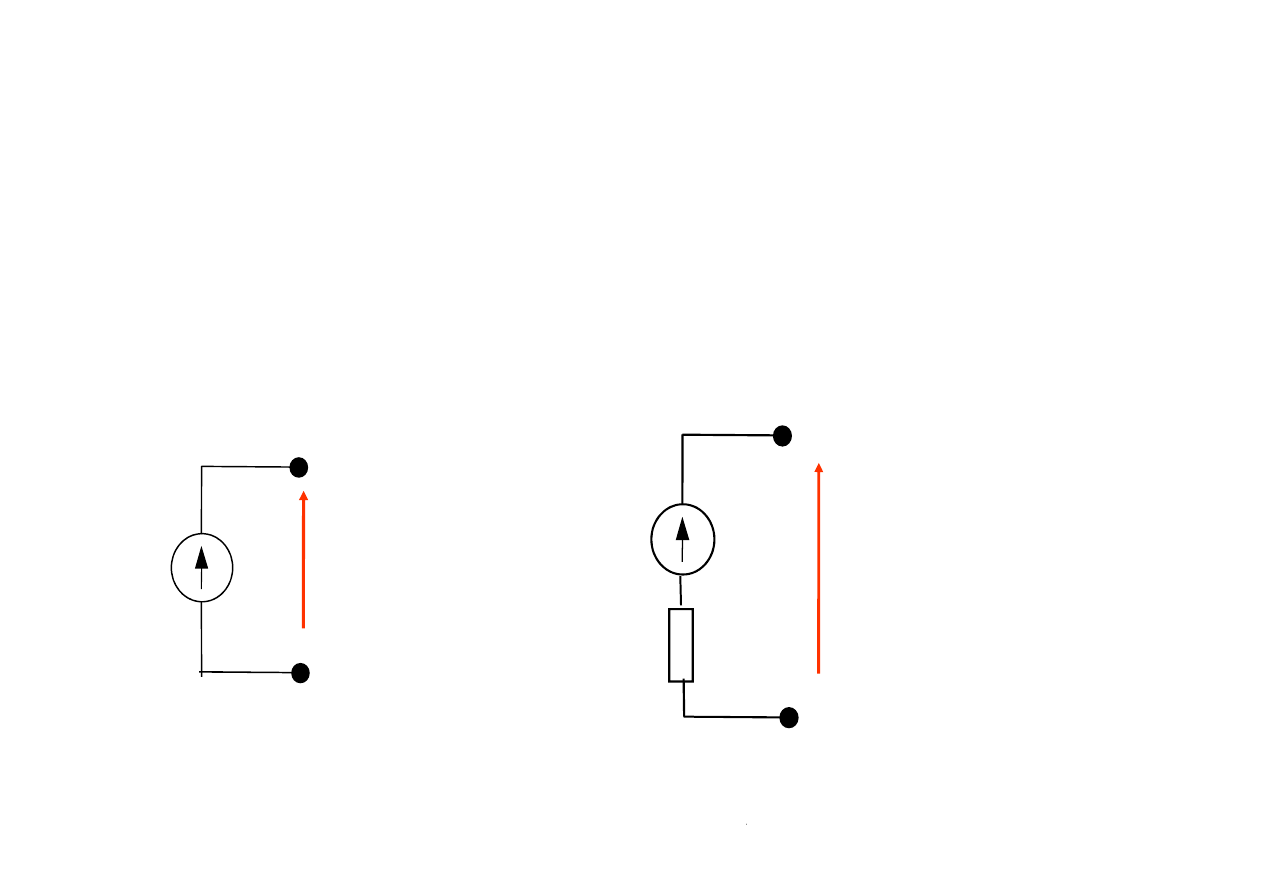
idealne

:

rzeczywiste

:

1. Źródło napięcia

A

A

E

u

AB

=E

B

B

E

R

w

u

AB

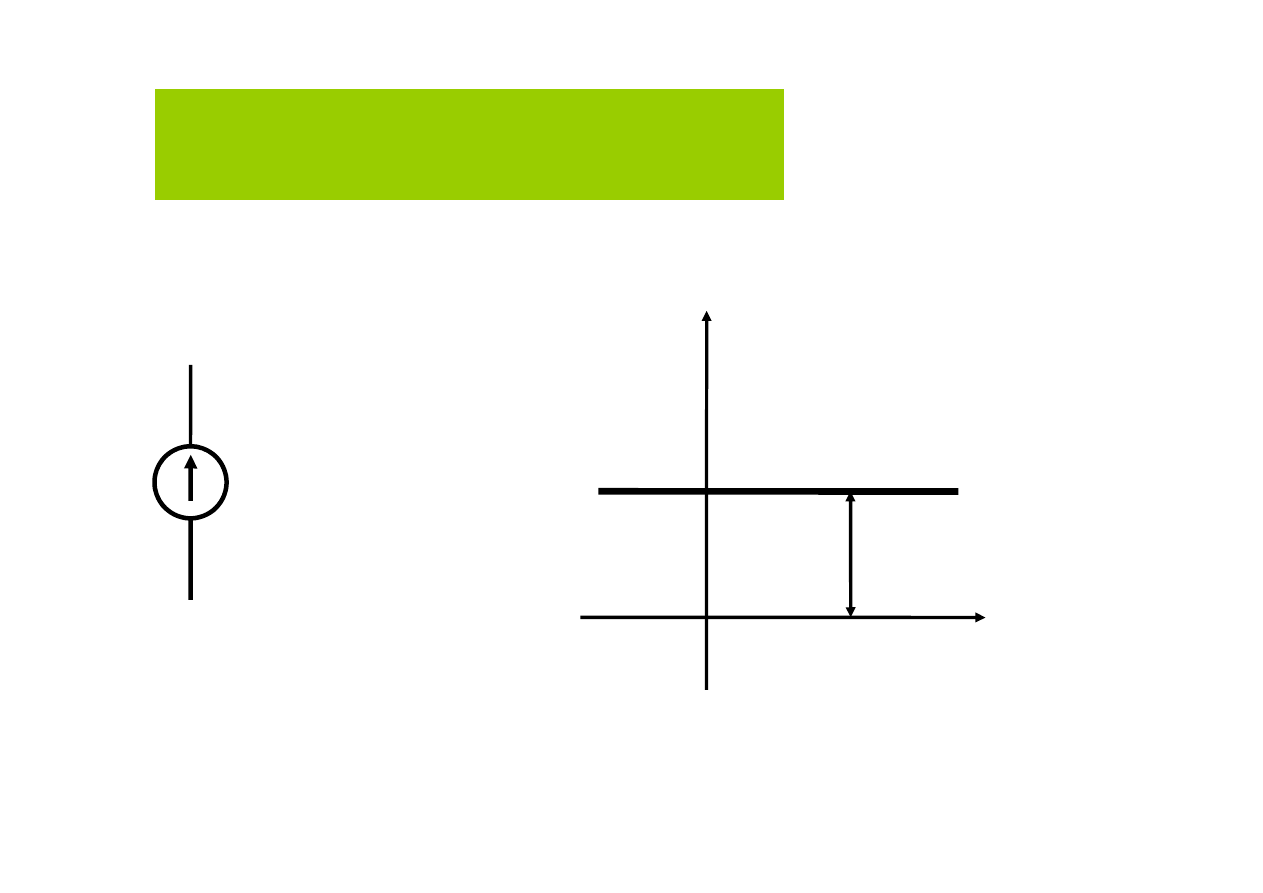
u

Idealne źródło napięcia stałego

i

E

E

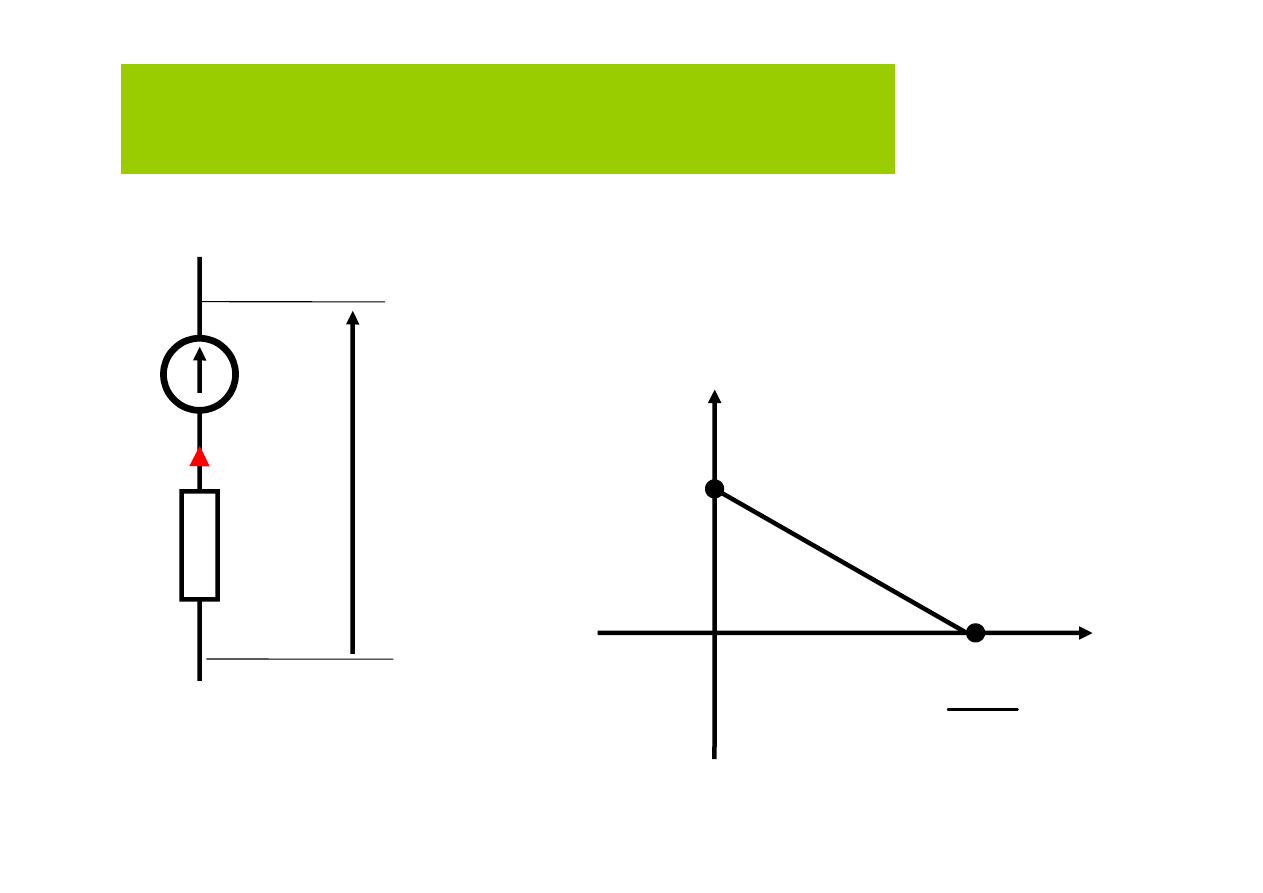
E

u

E

i

i

R

E

u

w

−

=

Źródło rzeczywiste napięcia stałego

E

i

w

R

E

R

w

u

i

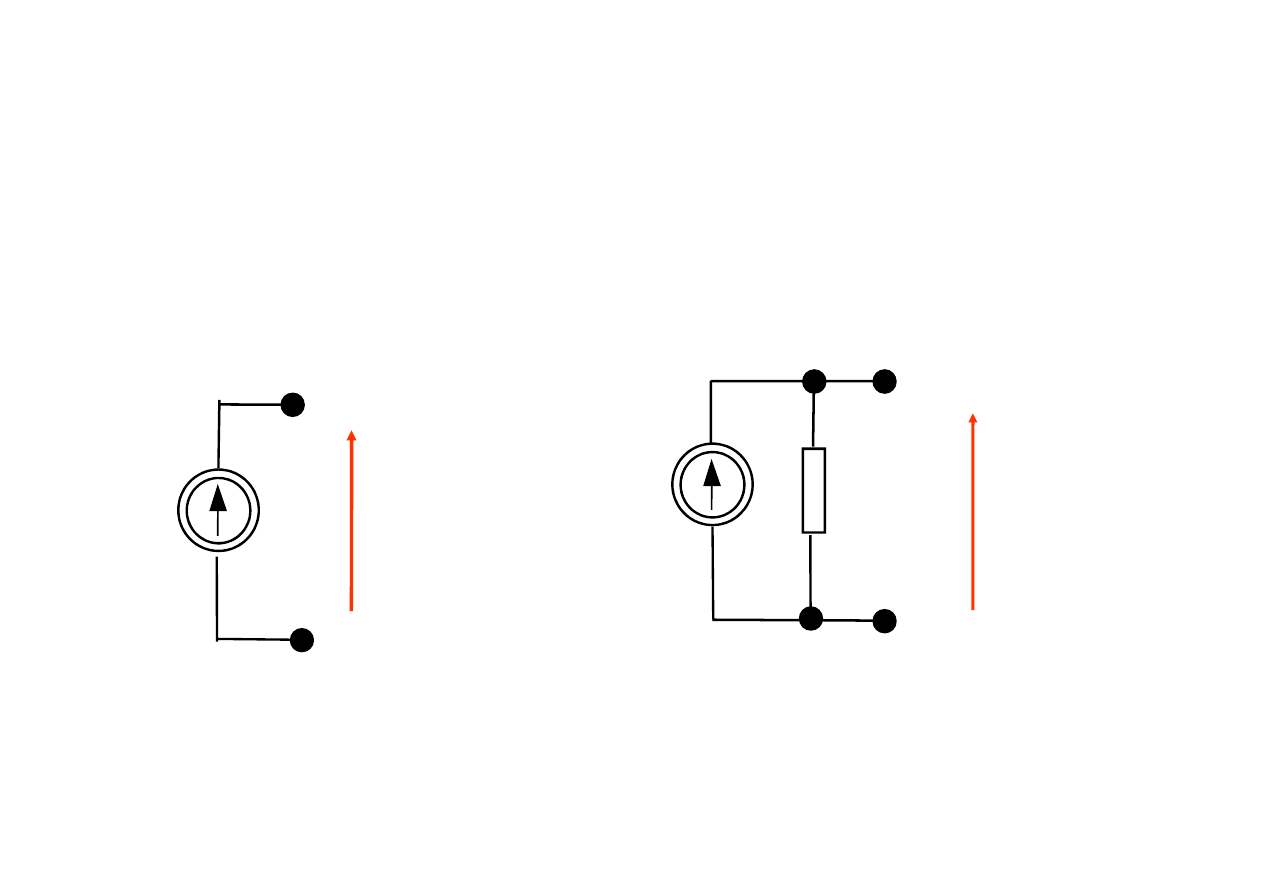
2. źródła prądu

Idealne

rzeczywiste

A

A

J

u

AB

B

J

G

w

u

AB

B

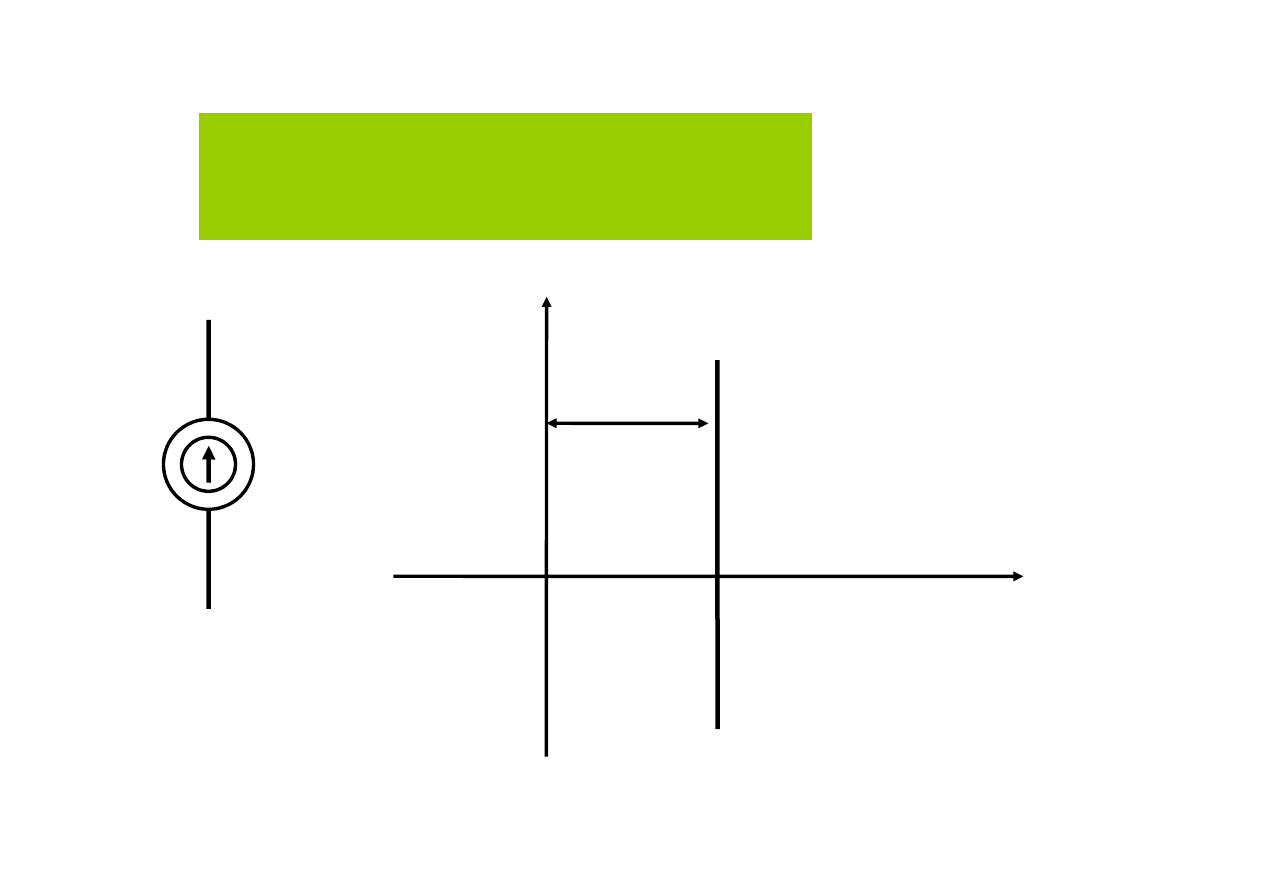
Źródło idealne prądu stałego

J

u

J

J

i

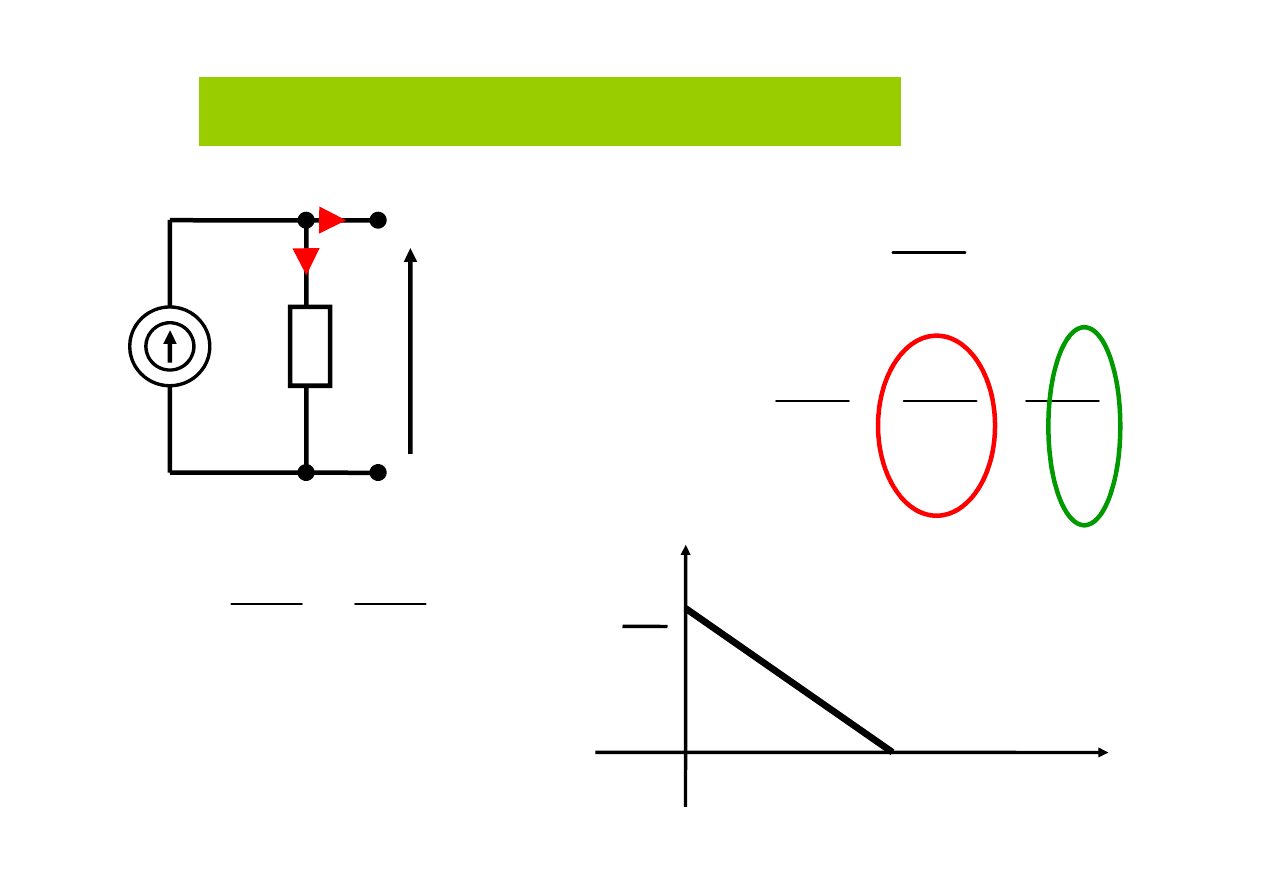
Źródło rzeczywiste prądu stałego

J

G

w

i

w

i

u

(

)

i

G

G

J

G

i

J

G

i

R

i

u

w

w

w

w

w

w

w

1

1

1

−

=

−

=

=

=

=

G

G

G

w

w

w

i

u

J

J

G

w

i

R

E

u

w

−

=

w

w

G

i

G

J

u

−

=

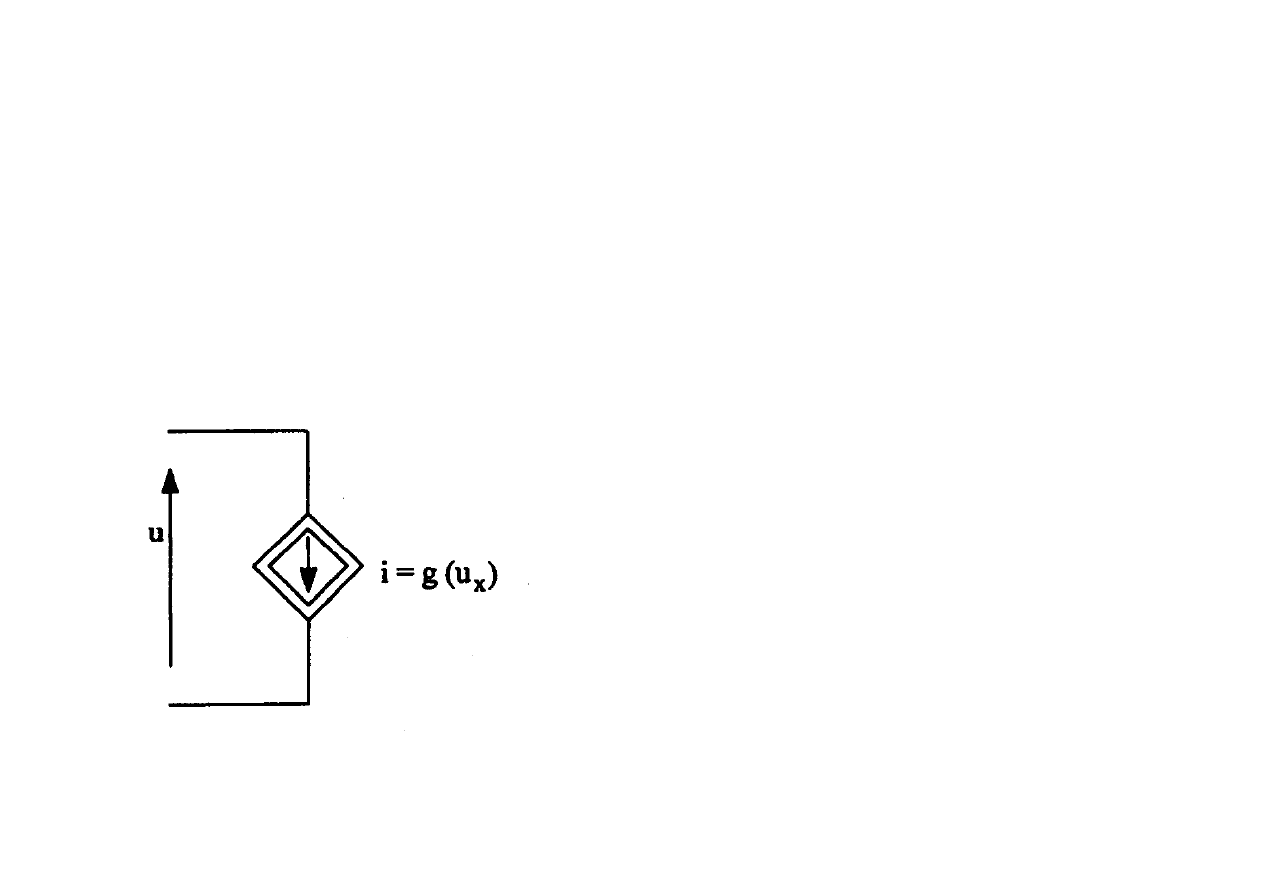
Źródła sterowane

Źródło sterowane jest dwójnikiem,
którego napięcie lub prąd zależy od napięcia lub prądu sterującego,
występującego w innej części obwodu.

Źródło prądowe sterowane napięciowo

( )

x

u

g

i

=

( )

x

u

g

i

=

x

g

u

k

i

=

liniowe

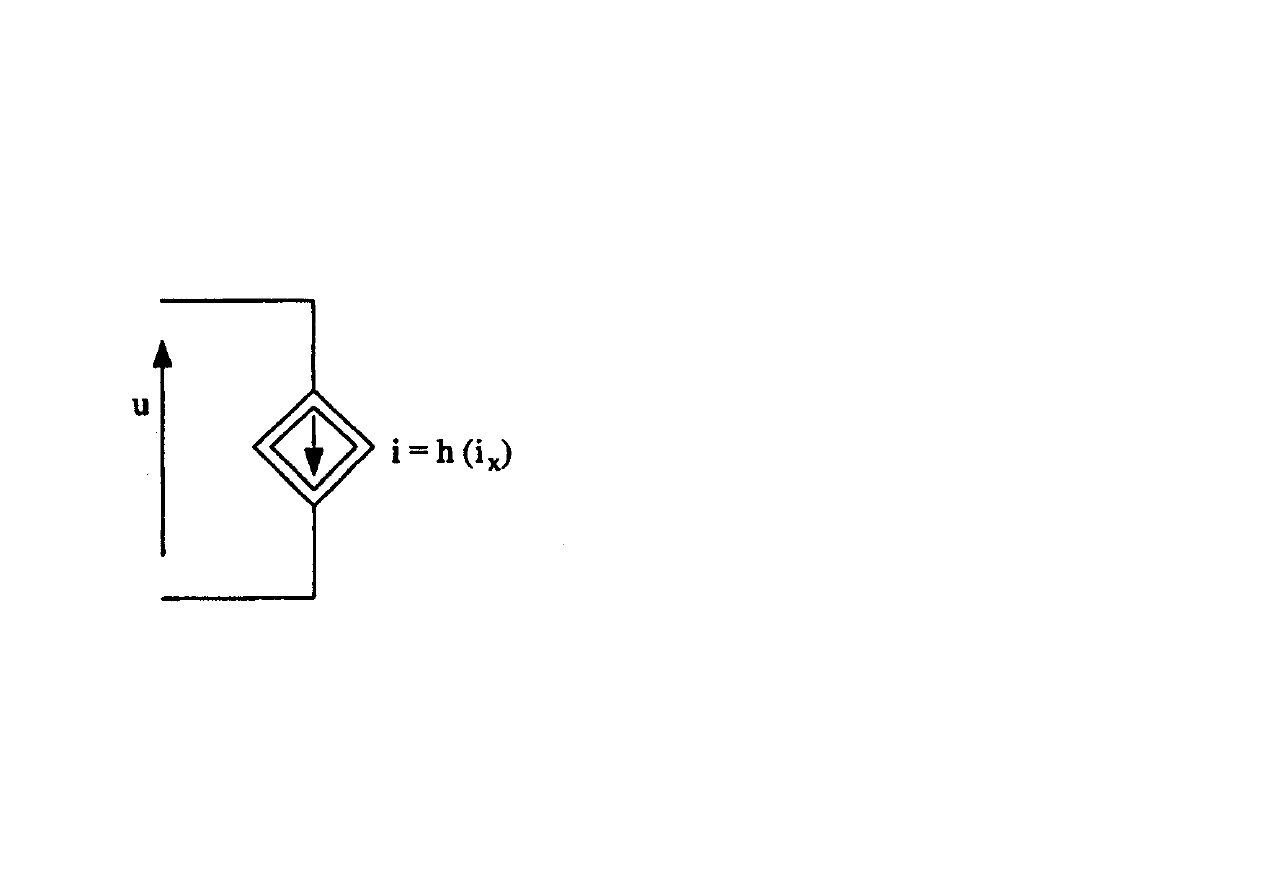
Źródło prądowe sterowane prądowo

( )

x

i

h

i

=

x

h

i

k

i

=

liniowe

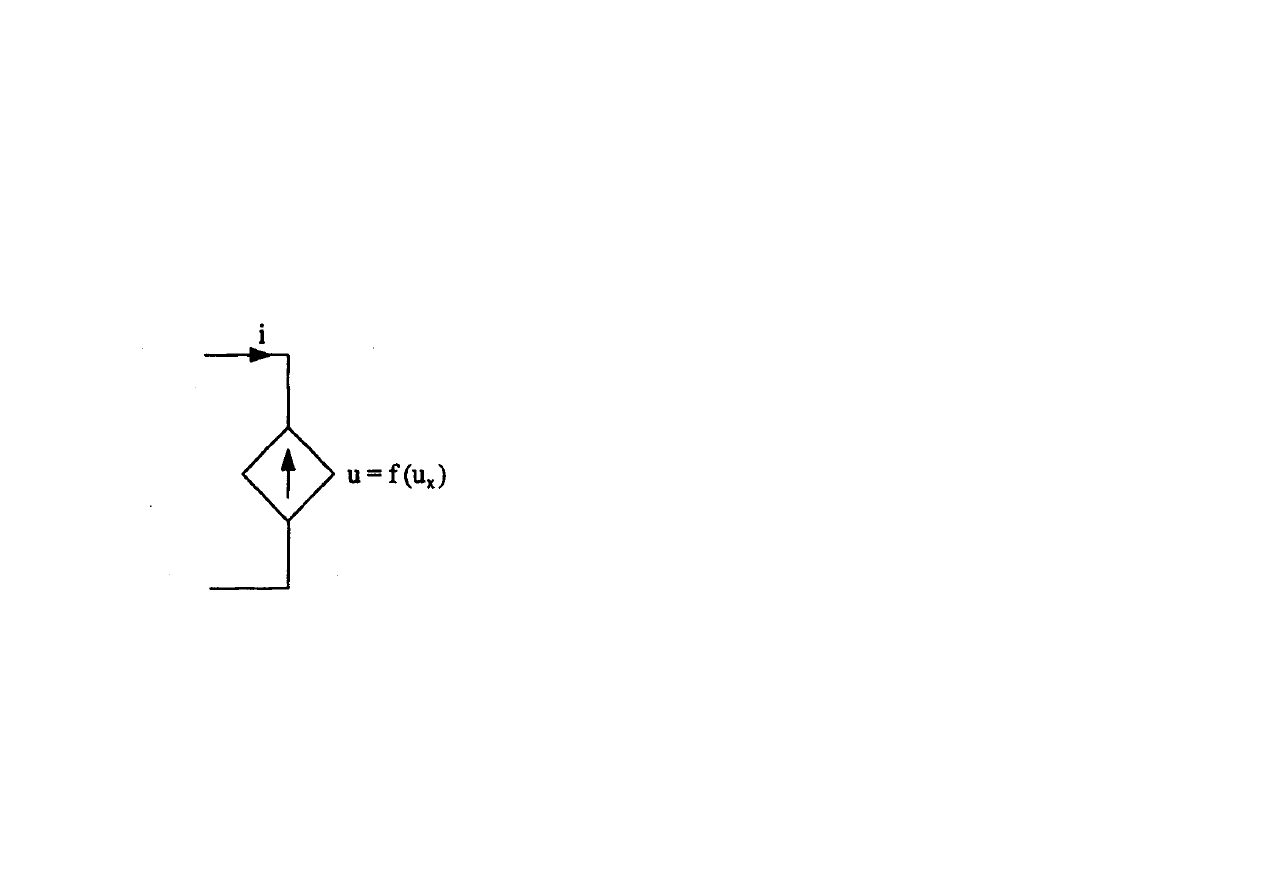
Źródło napięciowe sterowane napięciowo

( )

x

u

f

u

=

liniowe

x

x

f

u

k

u

=

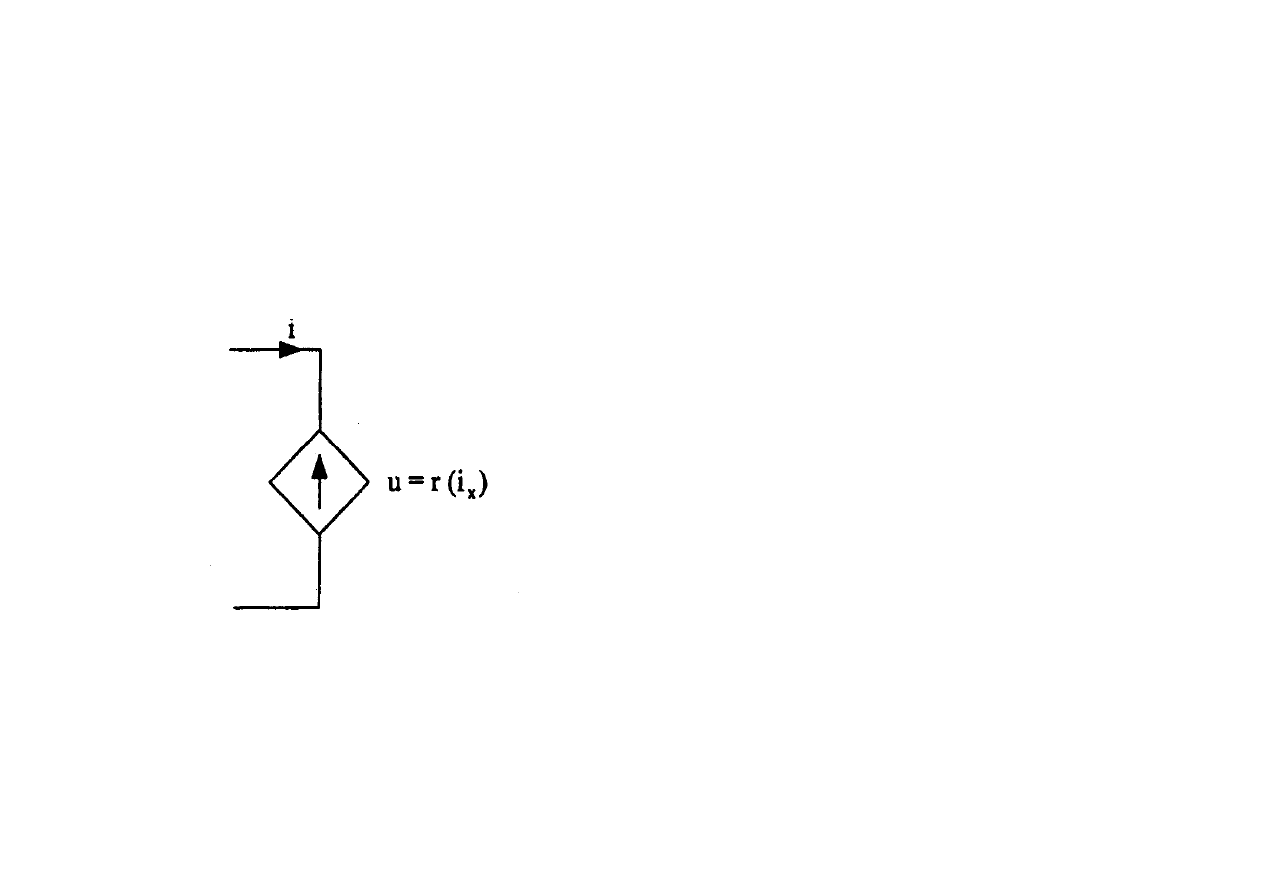
Źródło napięciowe sterowane prądowo

( )

x

i

r

u

=

x

x

r

i

k

u

=

liniowe

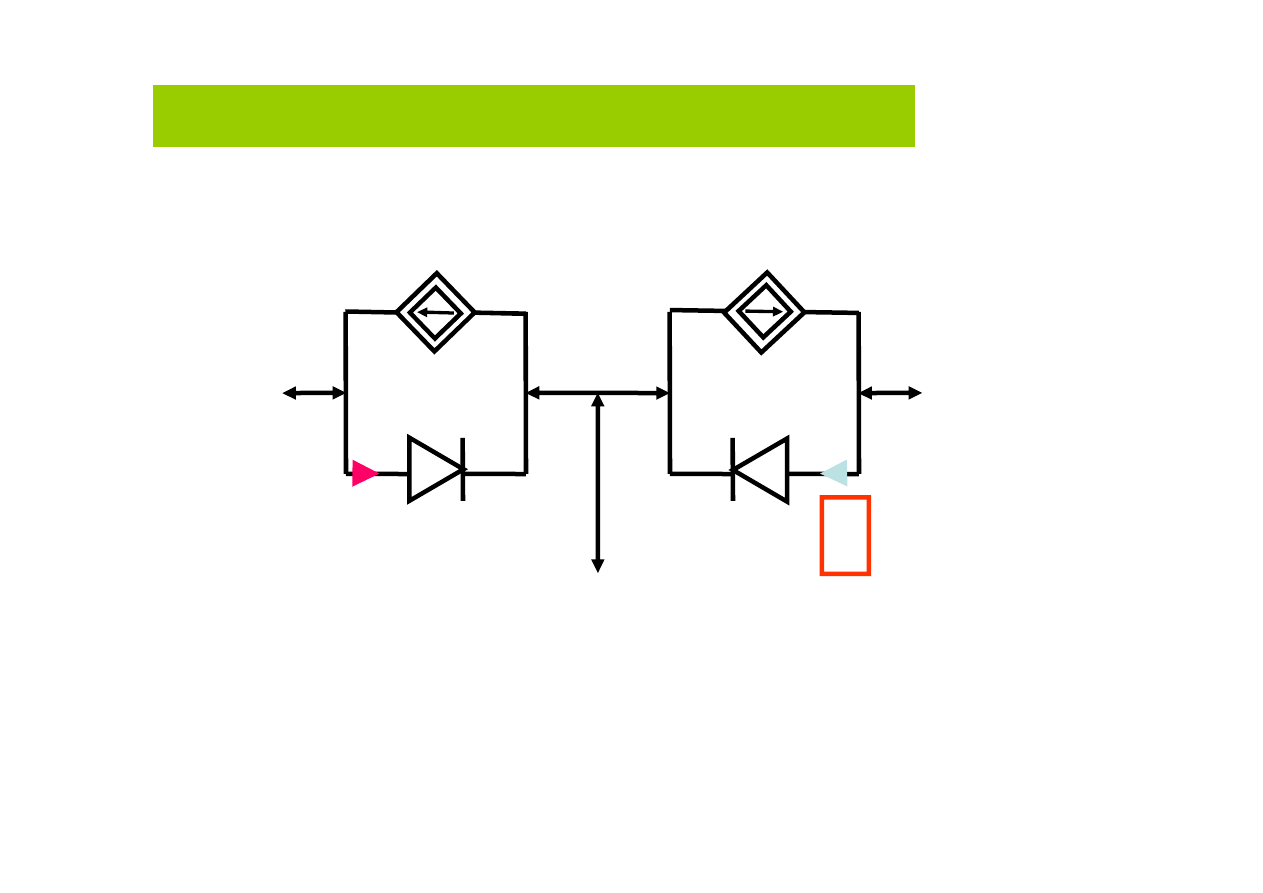
Przykład obwodu ze źródłami sterowanymi:

E

C

f

f

i

α

r

r

i

α

Jest to stałoprądowy model tranzystora
znany jako

model Ebersa-Molla

B

i

f

i

r

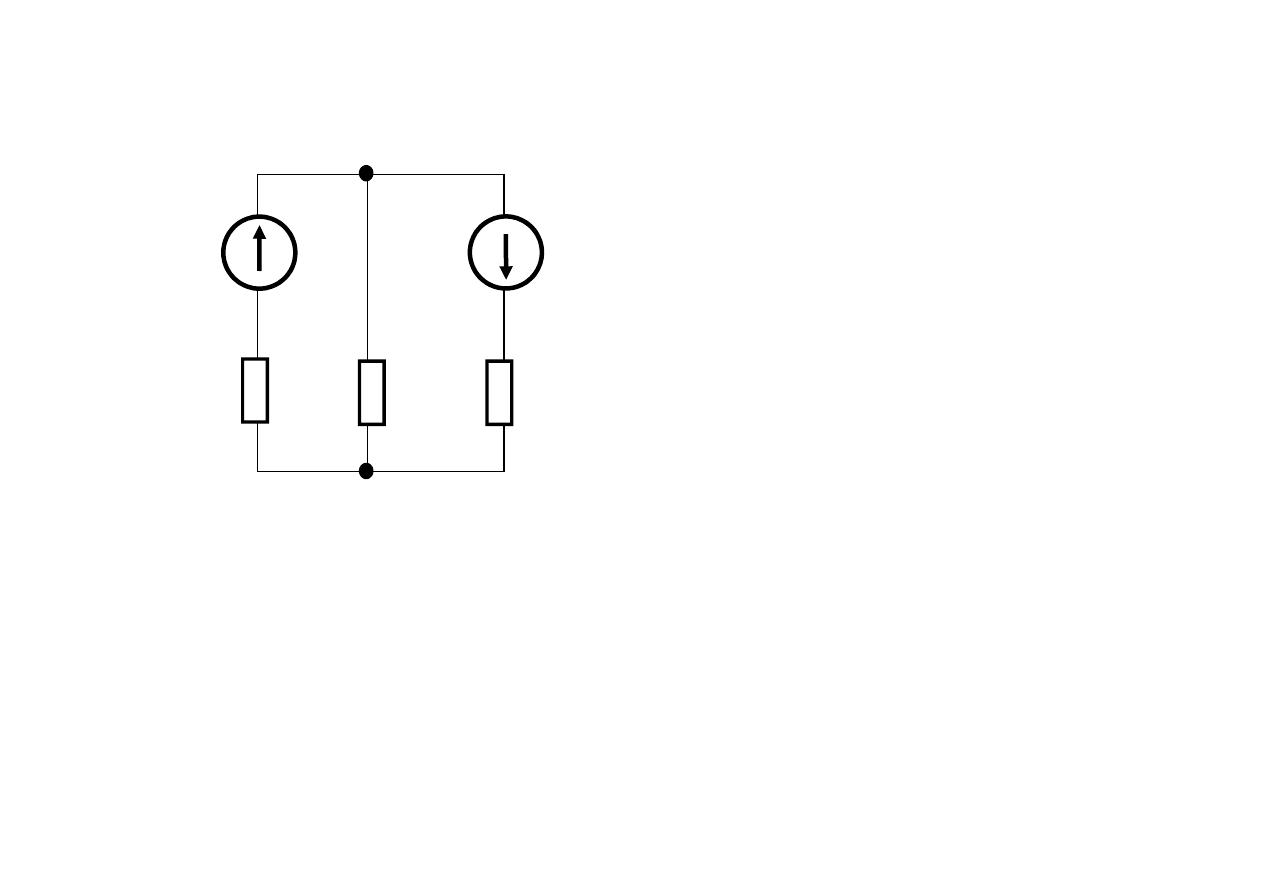
zadanie

W obwodzie jak na rys

obliczyć: prądy w

gałęziach, napięcie na

rezystancji R2 oraz

przeprowadzić bilans mocy

e2

e1

R1

R2

R3

ZASADA SUPERPOZYCJI

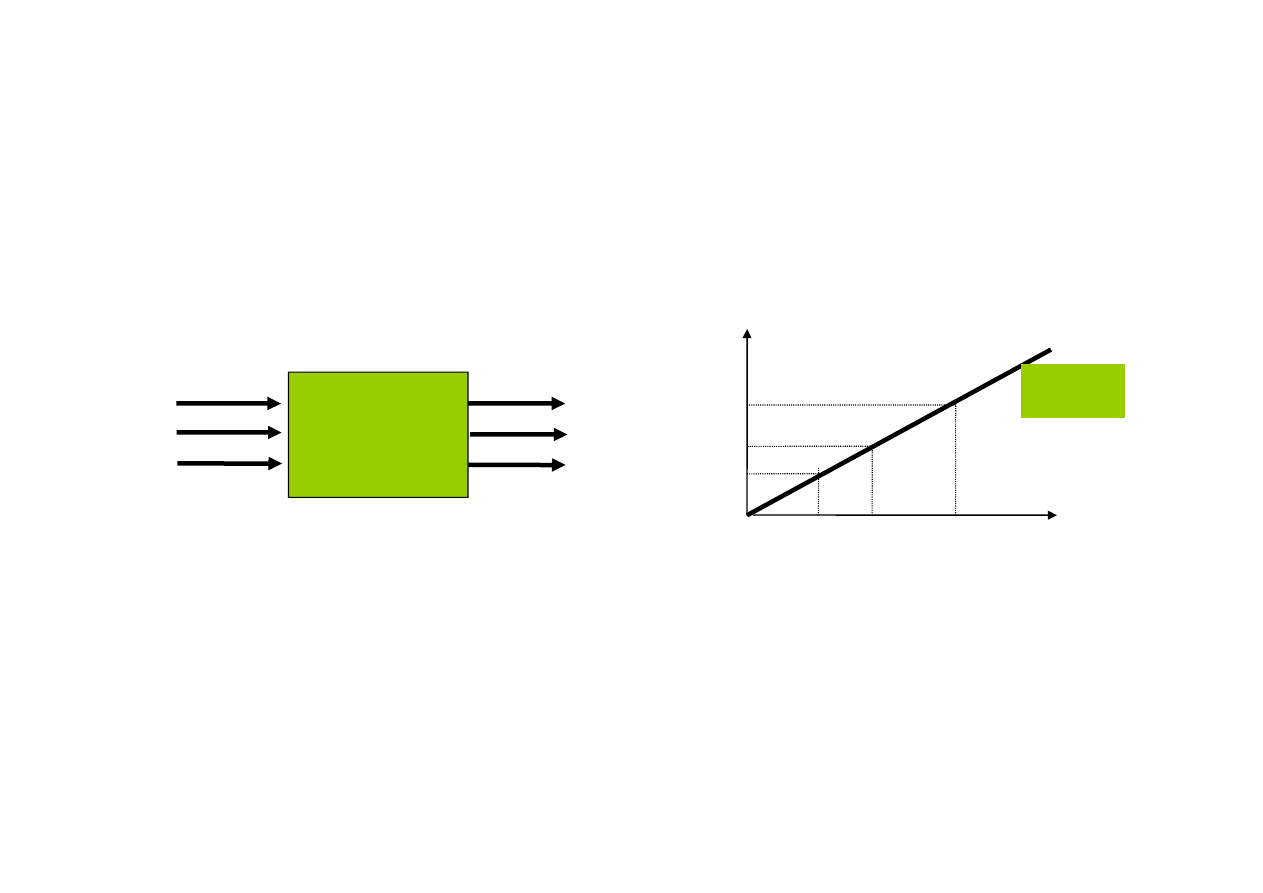
Zasada superpozycji

Odpowiedź układu liniowego na sumę wymuszeń

równa się sumie odpowiedzi na poszczególne

wymuszenia działające z osobna

y

y

1

+y

2

y

y=Ax

x

1

x

2

x

y

1

y

2

y

Uklad

liniowy

x

x

1

x

2

x

1

+x

2

y

2

y

1

x

2

x

3

y

2

y

3

liniowy

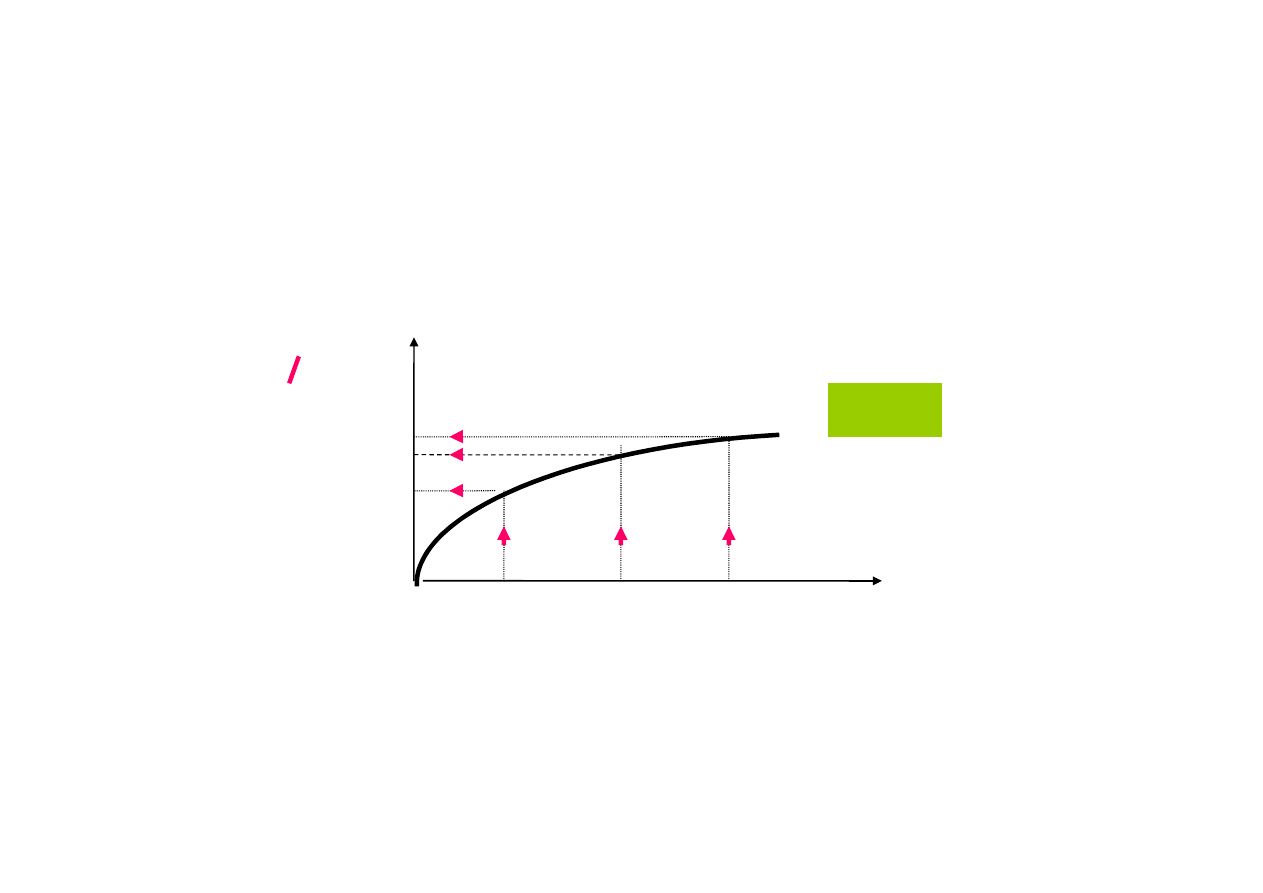
y

y

y=f(x)

y=y

1

+y

2

Dlaczego superpozycji nie można stosować
do układów nieliniowych:

x

x

1

x

2

x

1

+x

2

y

2

y

1

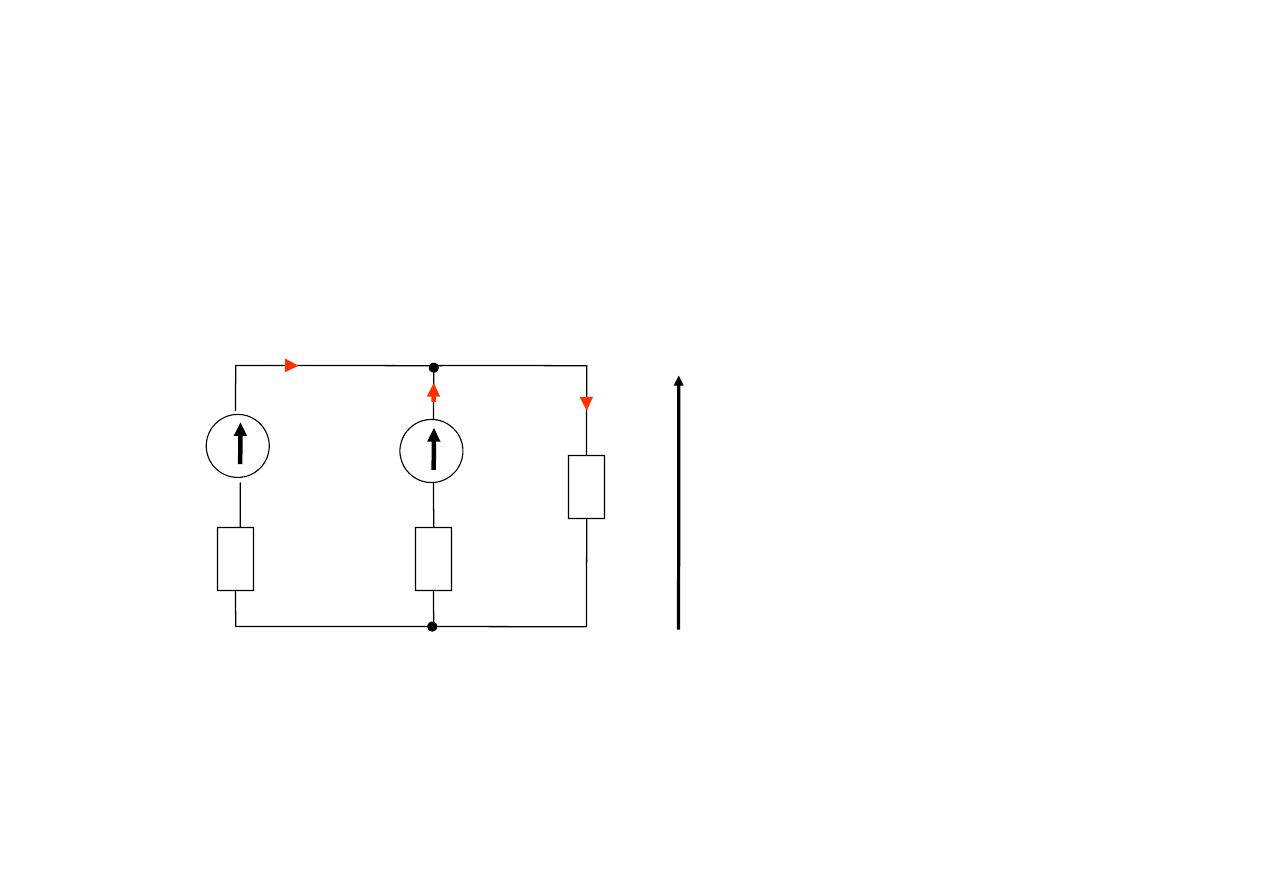
Przykład:

W obwodzie działają dwa źródła napięcia e

1

i e

2

. Celem

jest obliczenie napięcia u

AB

metodą superpozycji.

i

1

i

2

e

e

A

i

3

e

1

e

2

R

1

R

2

R

3

u

AB

B

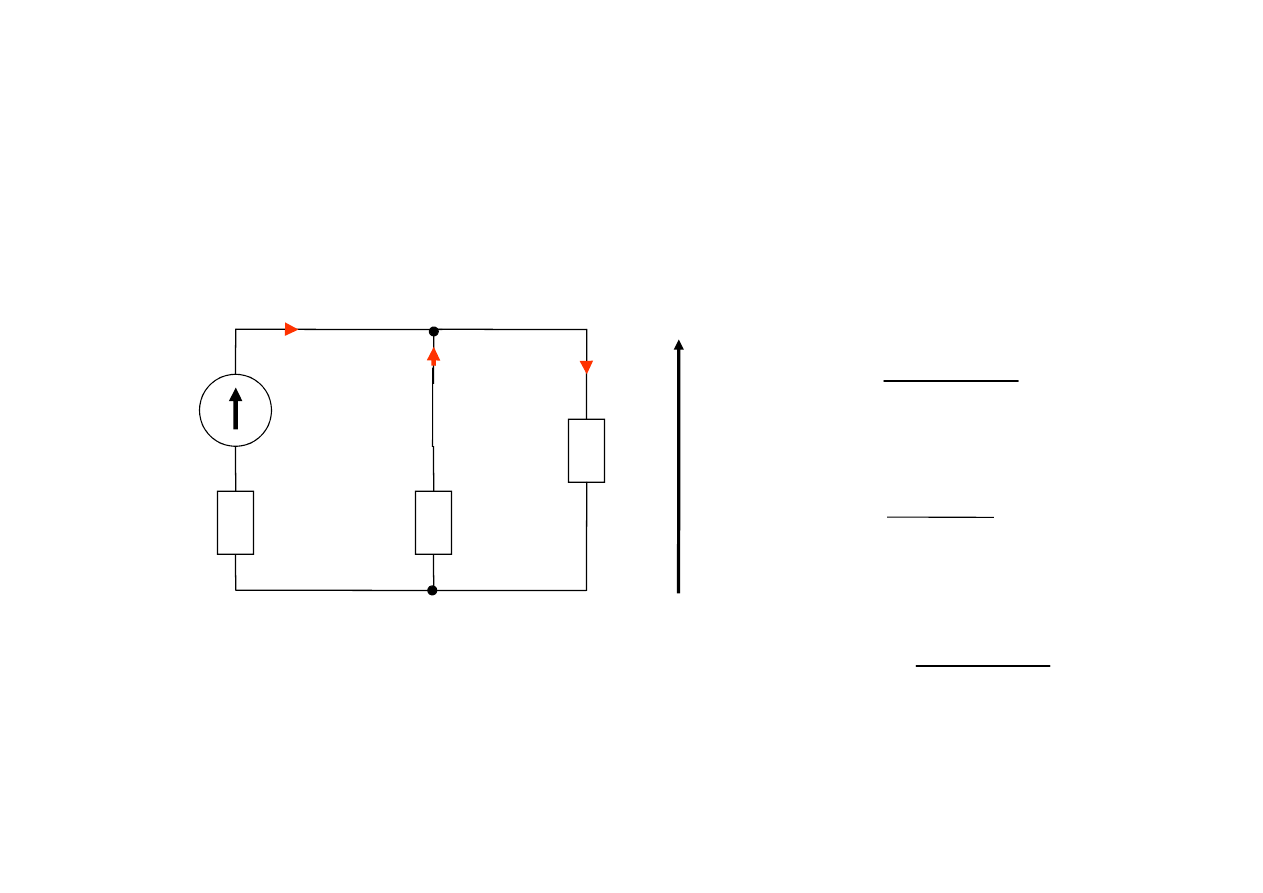
Pierwszy etap superpozycji

- pozostawiamy w

obwodzie tylko źródło e

1

, a źródło e

2

zwieramy:

i

2

’

e

1

u

AB

’

A

i

1

’

i

3

’

1

3

2

3

2

R

R

R

R

R

R

z

+

+

=

R

1

R

2

R

3

u

AB

’

B

i

1

’=

e

1

R

z

3

2

3

2

'

1

'

R

R

R

R

i

u

AB

+

=

Drugi etap superpozycji

- pozostawiamy w obwodzie

tylko źródło e

2

, a e

1

zwieramy:

i

1

’’

i

2

’’

e

2

R

3

u

AB

A

i

3

’’

2

3

1

3

1

''

R

R

R

R

R

R

z

+

+

=

R

1

R

2

R

3

u

AB

B

3

2

3

2

''

2

'

'

R

R

R

R

i

u

AB

+

=

''

2

''

2

z

R

e

i

=

i

1

’’

i

2

’’

e

2

R

1

R

2

R

3

u

AB

A

B

i

3

’’

i

2

’

e

1

R

1

R

2

R

3

u

AB

’

A

B

i

1

’

i

3

’

3

2

'

'

R

R

i

u

=

R

R

3

2

3

2

'

1

'

R

R

R

R

i

u

AB

+

=

AB

AB

AB

u

u

u

''

'

+

=

3

1

3

1

``

R

R

R

R

u

AB

+

=

3

2

3

2

'

1

'

R

R

R

R

i

u

AB

+

=

''

'

3

1

3

1

``

R

R

R

R

u

AB

+

=

AB

AB

AB

u

u

u

''

'

+

=

Równoważność źródeł

i

E

u

AB

−

=

AB

E

R

w

u

A

i

R

w

AB

iR

E

u

−

=

i

R

u

R

E

w

AB

w

+

=

i

R

R

w

w

−

=

B

R

i

R

E

A

B

AB

w

R

w

u

i

i

J

w

+

=

Układy równoważne

Układy równoważne

Q

j

1

j

n-1

1

v

P

i

1

i

n-1

1

u

j

n-1

v

n-1

n

i

n-1

u

n-1

n

[

]

T

1

n

2

1

i

i

i

−

=

K

i

[

]

T

1

n

2

1

u

u

u

−

=

K

u

[

]

T

1

n

2

1

j

j

j

−

=

K

j

[

]

T

1

n

2

1

v

v

v

−

=

K

v

•

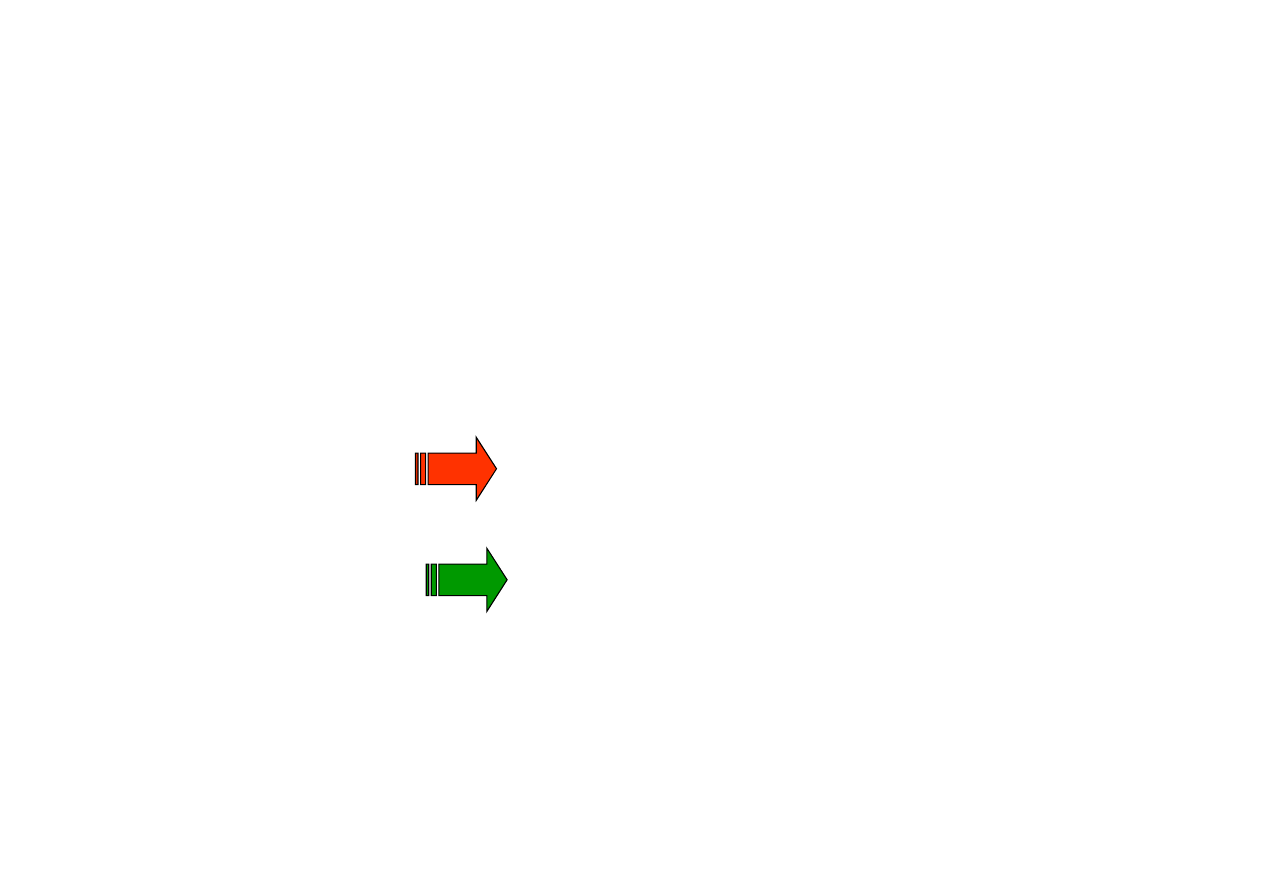
Układy P i Q nazywamy
równoważnymi, jeżeli ich
opis matematyczny jest taki
sam.

0

i

u

f

=

)

,

(

Opis obwodu P

Q

P

f

f ≡

0

i

u

f

=

)

,

(

P

Opis obwodu P

0

j

v

f

=

)

,

(

Q

Opis obwodu Q

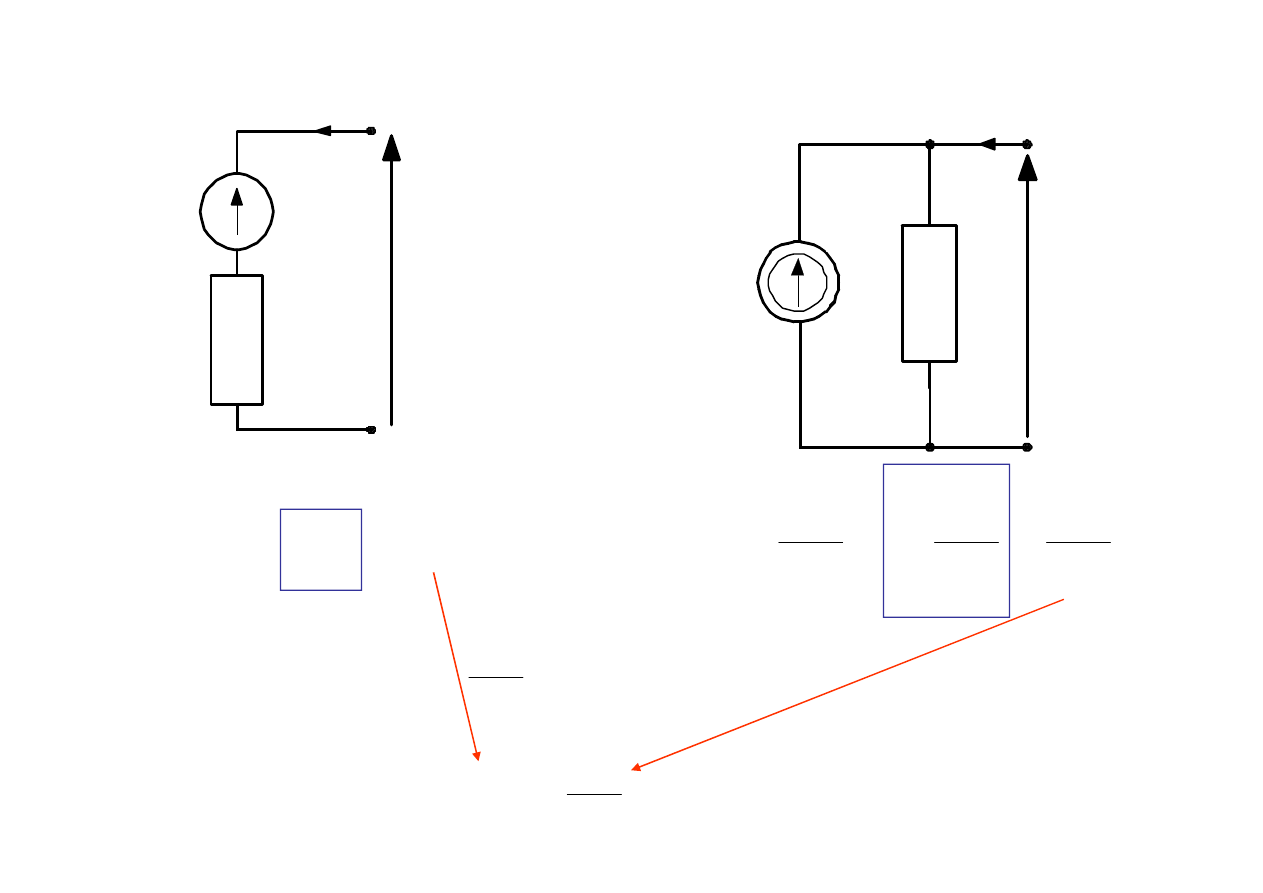
Przykład

i

u

R

w

u

z

j

v

G

w

j

z

i

R

u

u

w

z

+

=

(

)

j

G

1

G

1

j

G

1

j

j

v

w

w

z

w

z

+

=

+

=

w

z

z

G

1

j

u =

w

z

z

G

u

j =

w

w

G

1

R =

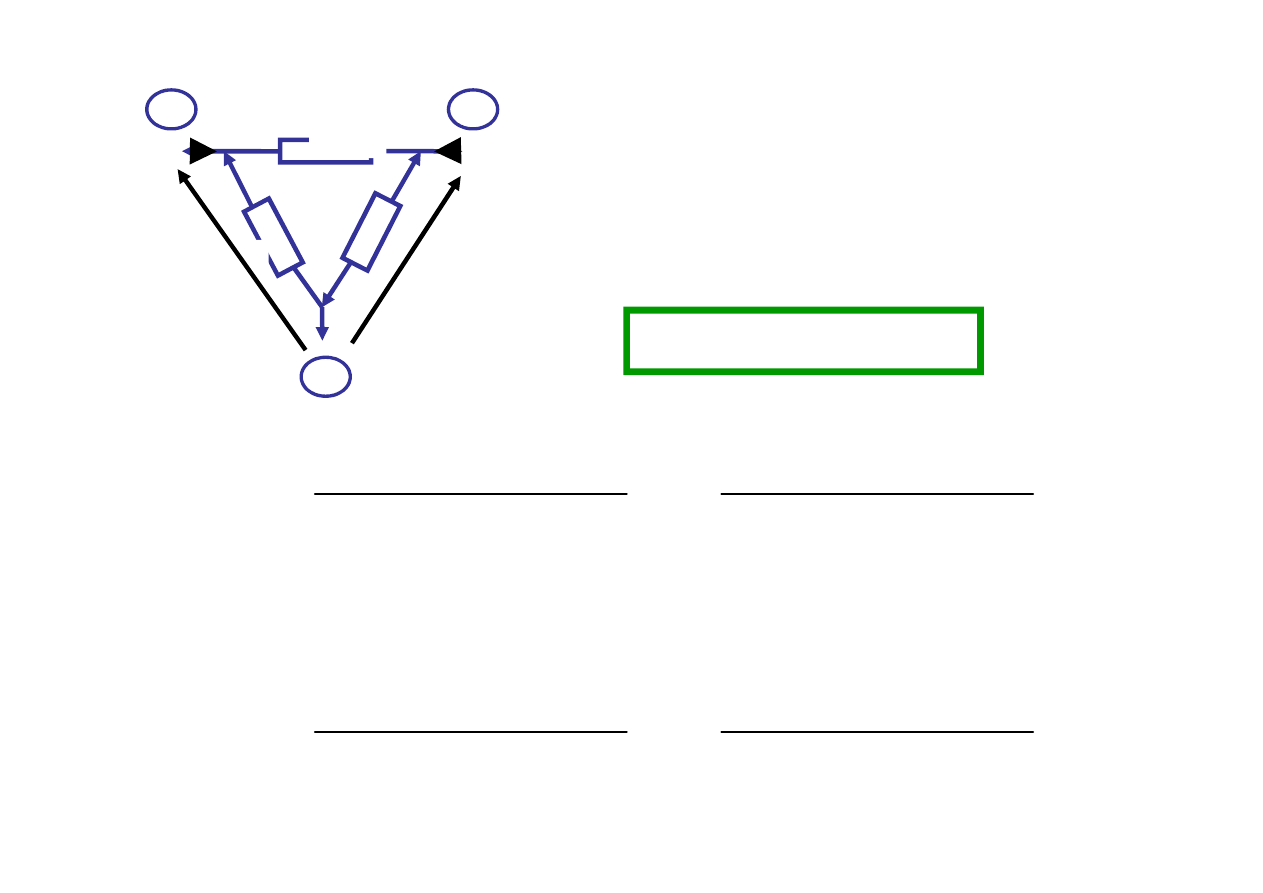
Równoważność połączenia

gwiazda - trójkąt

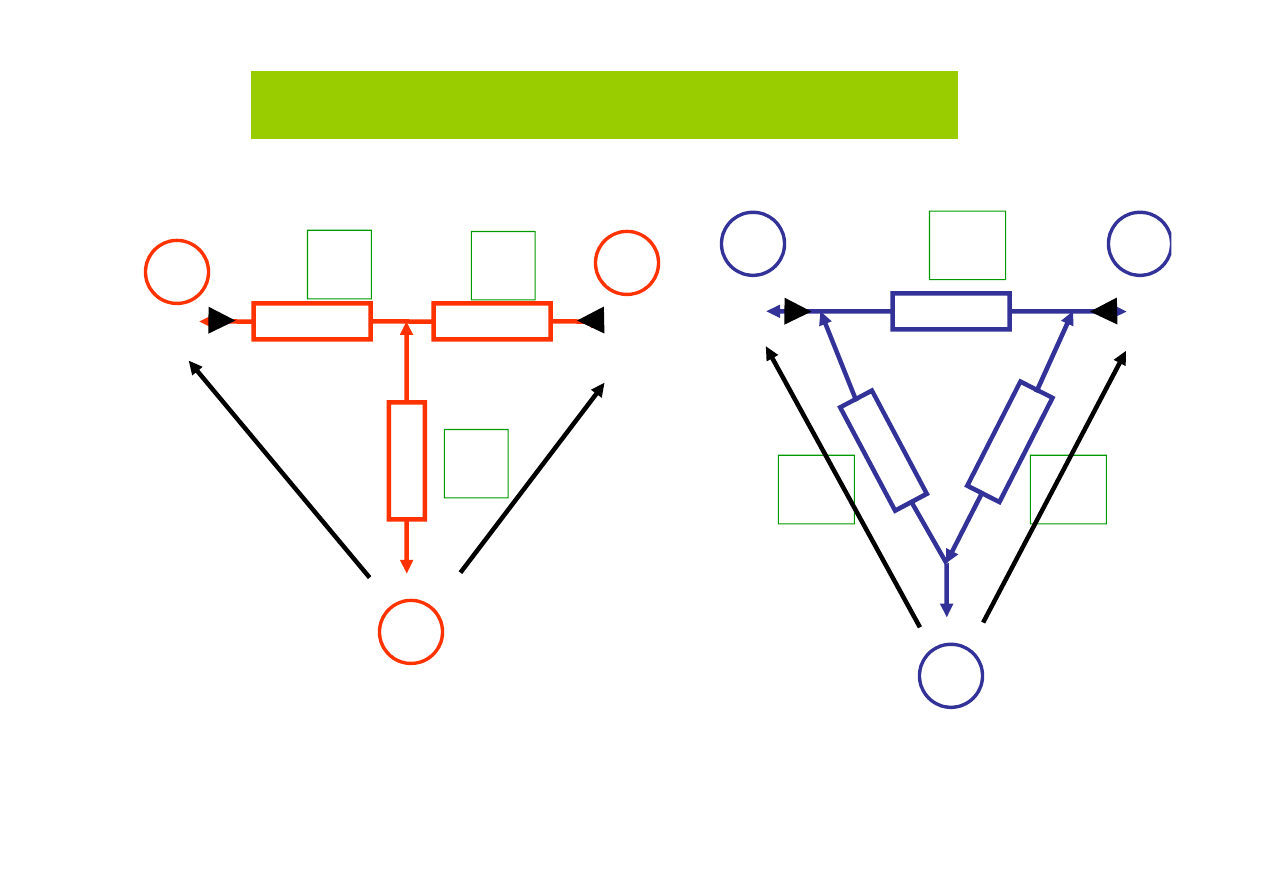
Zamiana GWIAZDA-TRÓJKĄT

R

1

R

2

R

1

2

i

1

i

2

2

1

R

12

j

1

j

2

R

3

3

u

1

u

2

3

R

31

R

23

V

1

V

2

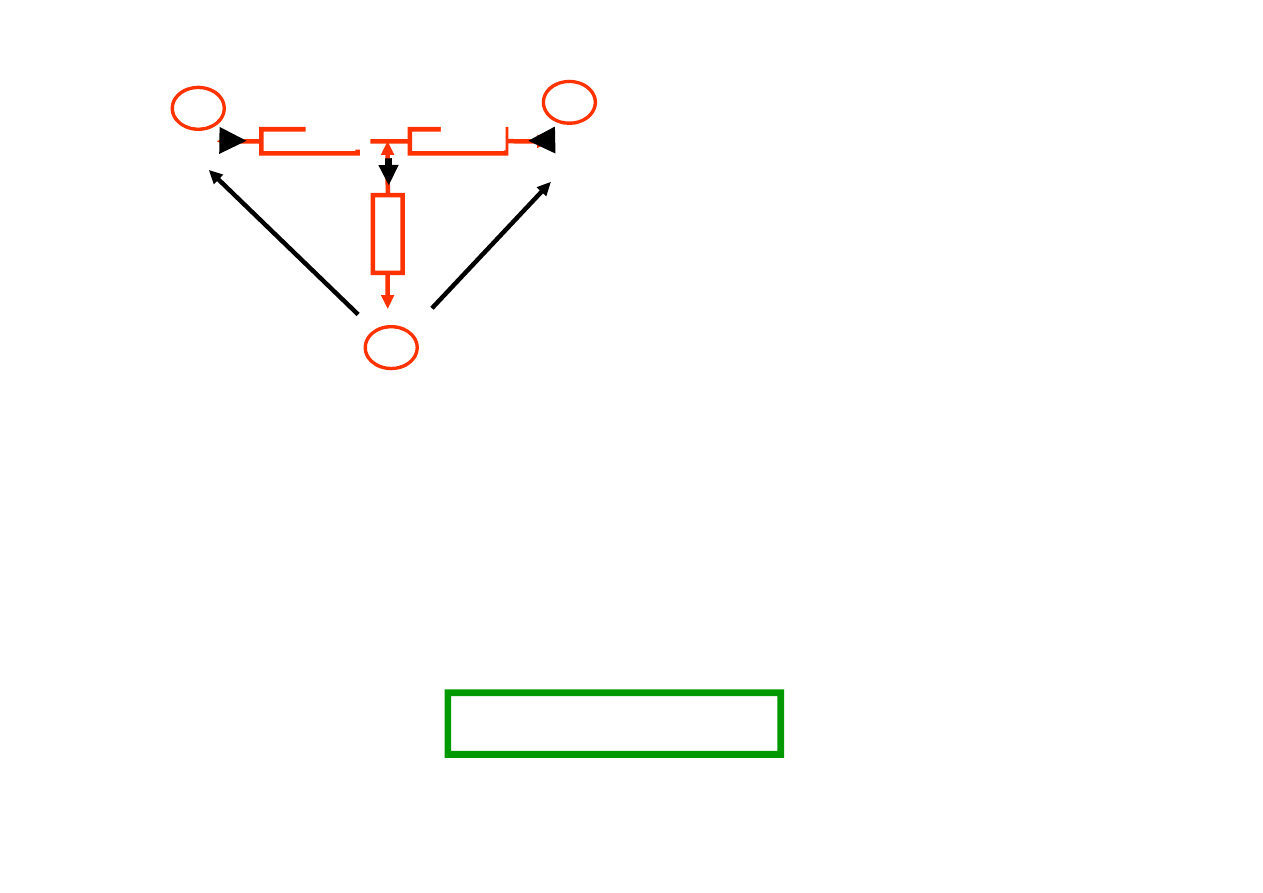
R

1

R

2

R

3

1

2

3

u

1

u

2

i

1

i

2

(

) (

)

2

3

1

3

1

2

1

3

1

1

1

i

R

i

R

R

i

i

R

i

R

u

+

+

=

+

+

=

i

1

+i

2

Przy wyprowadzaniu wzorów

korzystamy z zasady superpozycji

(

) (

)

(

)

(

)

2

3

2

1

3

2

1

3

2

2

2

2

3

1

3

1

2

1

3

1

1

1

i

R

R

i

R

i

i

R

i

R

u

i

R

i

R

R

i

i

R

i

R

u

+

+

=

+

+

=

+

+

=

+

+

=

Są to równania (*)

2

1

3

R

12

R

31

R

23

V

1

V

2

j

1

j

2

(

)

R

R

R

R

R

+

Są to równania (**)

(

)

(

)

2

31

23

12

31

12

23

1

31

23

12

23

31

1

2

31

23

12

31

23

1

31

23

12

23

12

31

1

j

R

R

R

R

R

R

j

R

R

R

R

R

v

j

R

R

R

R

R

j

R

R

R

R

R

R

v

+

+

+

+

+

+

=

+

+

+

+

+

+

=

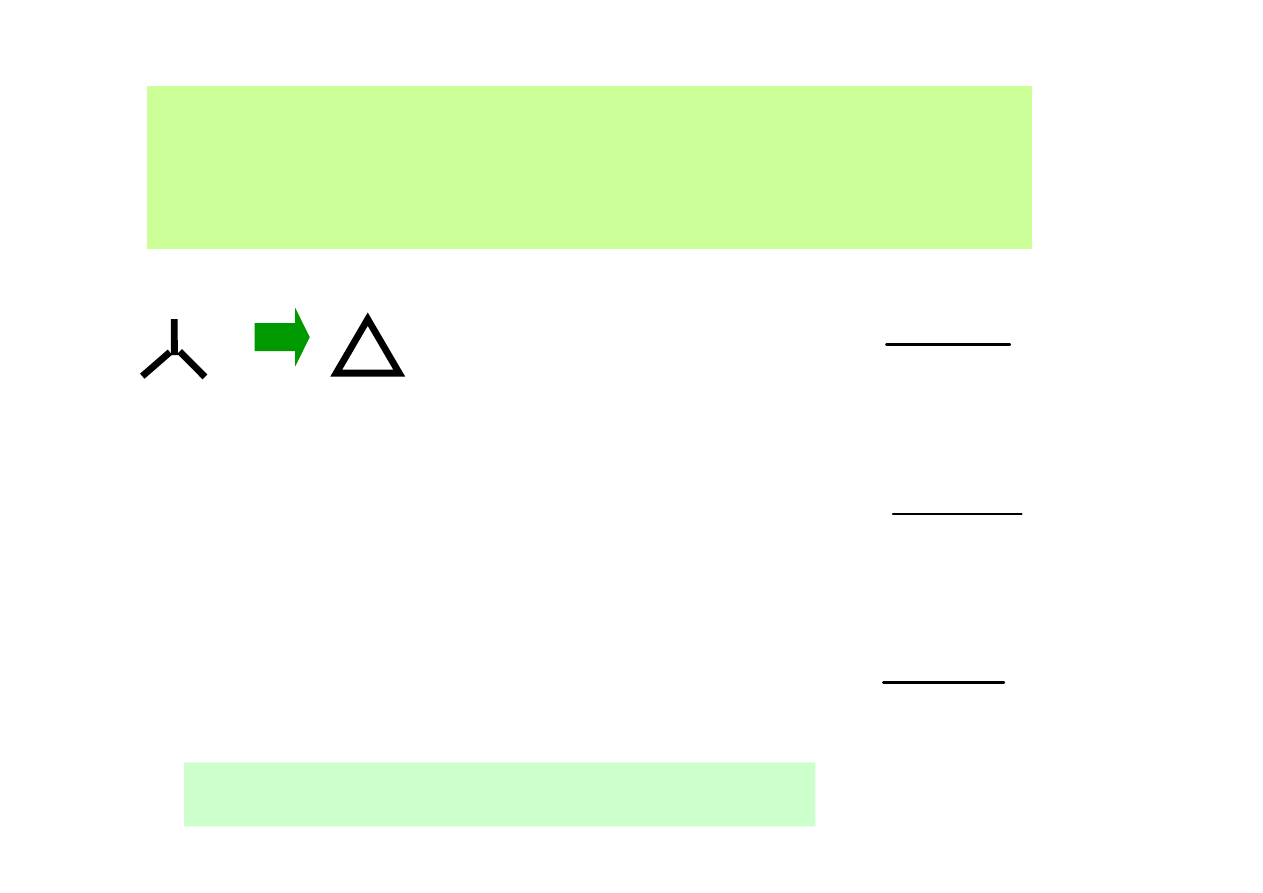
Z definicji równoważności układów
wynika równość odpowiednich współczynników
w równaniach (*) i (**). Wynikają stąd wzory:

3

2

1

2

1

12

R

R

R

R

R

R

R

R

+

+

=

2

1

3

1

3

31

1

3

2

3

2

23

R

R

R

R

R

R

R

R

R

R

R

R

+

+

=

+

+

=

Gdy R

1

=R

2

=R

3

=R

Y

R

∆

=3R

Y

31

23

12

23

12

2

31

23

12

31

12

1

R

R

R

R

R

R

R

R

R

R

R

R

+

+

=

+

+

=

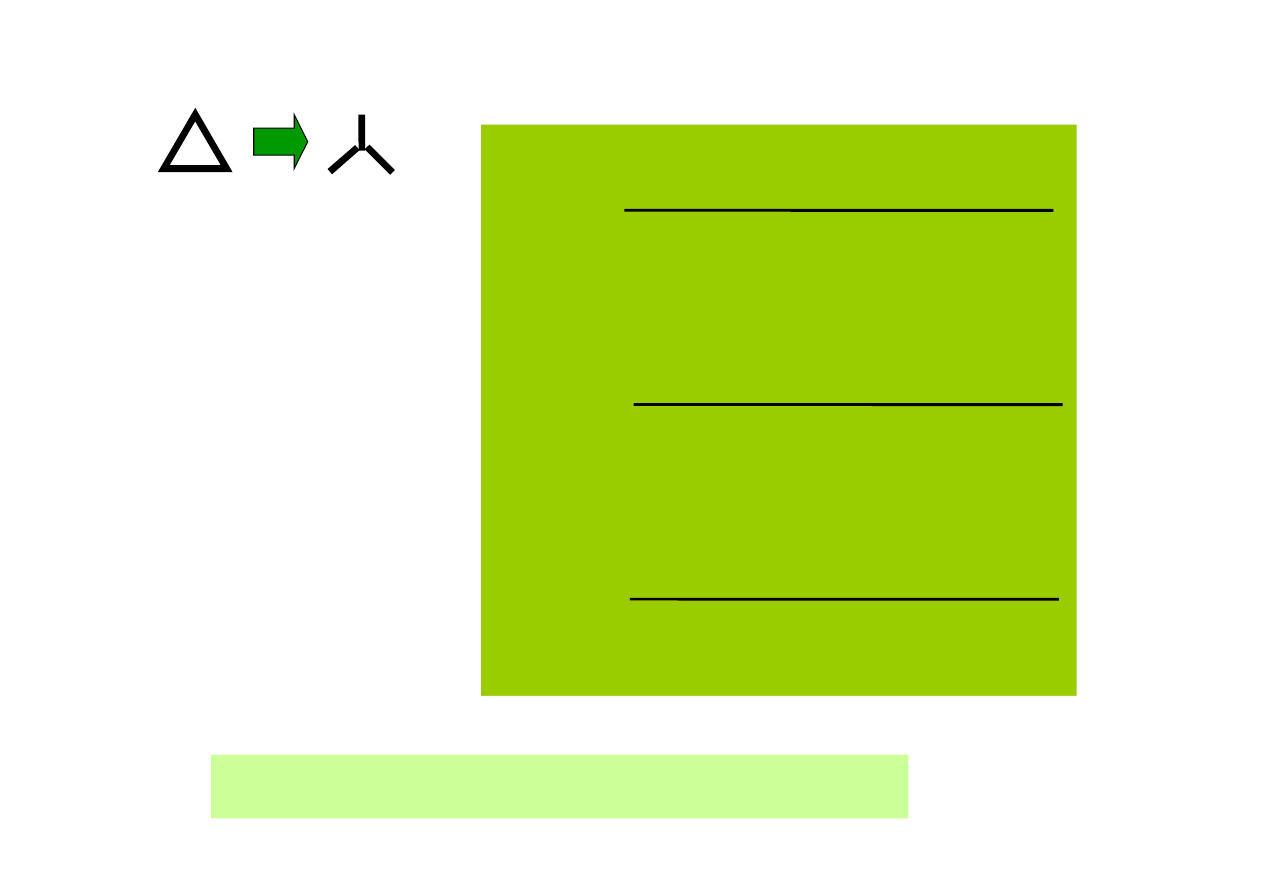
Gdy R

12

=R

23

=R

34

=R

∆

R

Y

=1/3R

∆

31

23

12

31

23

3

31

23

12

2

R

R

R

R

R

R

R

R

R

+

+

=

+

+

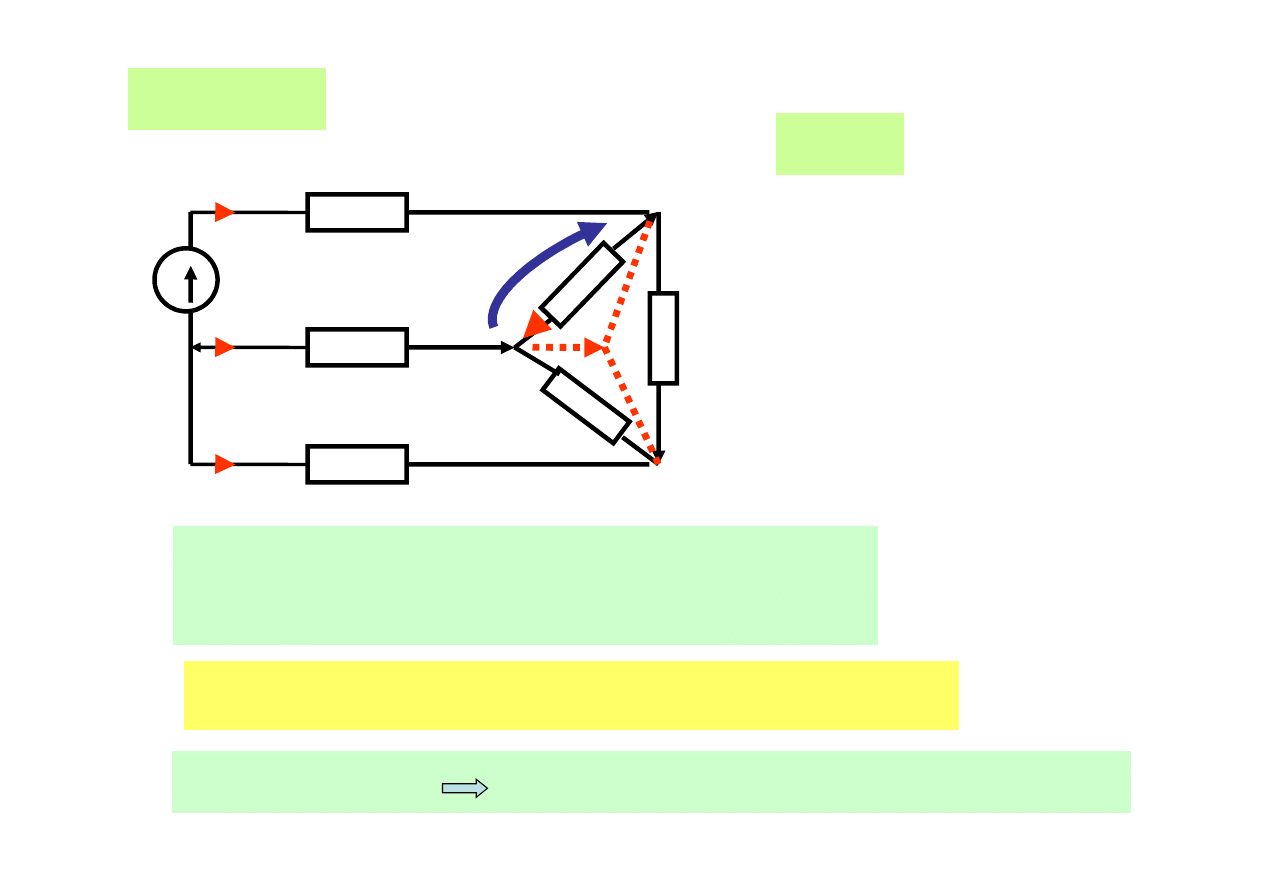
Przykład:

R

1

R

2

R

3

i

1

i

2

i

3

A

C

R

4

R

5

R

6

u

Dane:

R

R

R

R

R

R

2

3

5

4

,

1

5

,

0

1

5

4

3

2

1

Ω

=

Ω

=

Ω

=

Ω

=

Ω

=

Ω

=

i

4

u

AC

B

V

u

R

6

2

6

=

Ω

=

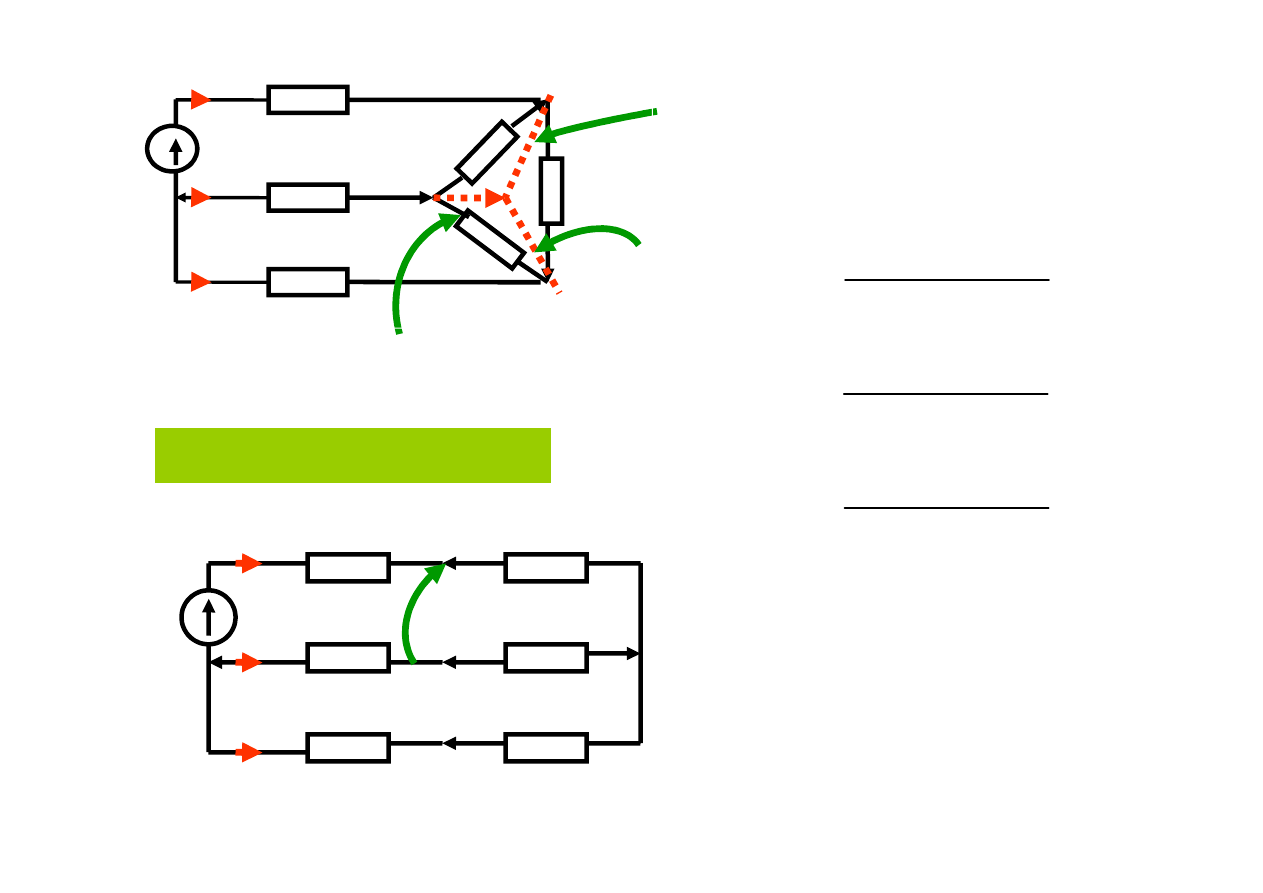
Celem jest obliczenie prądu
w jednej z gałęzi trójkąta, np. prądu i

4

Aby obliczyć ten prąd musimy znaleźć u

AC

Po zamianie ∆ Y nie możemy zgubić punktów AC

R

1

R

2

R

3

i

1

i

2

i

3

A

B

C

R

4

R

5

R

6

u

R

46

R

65

R

54

Ω

=

+

+

=

Ω

=

+

+

=

6

,

0

1

6

5

4

5

6

65

6

5

4

6

4

46

R

R

R

R

R

R

R

R

R

R

R

R

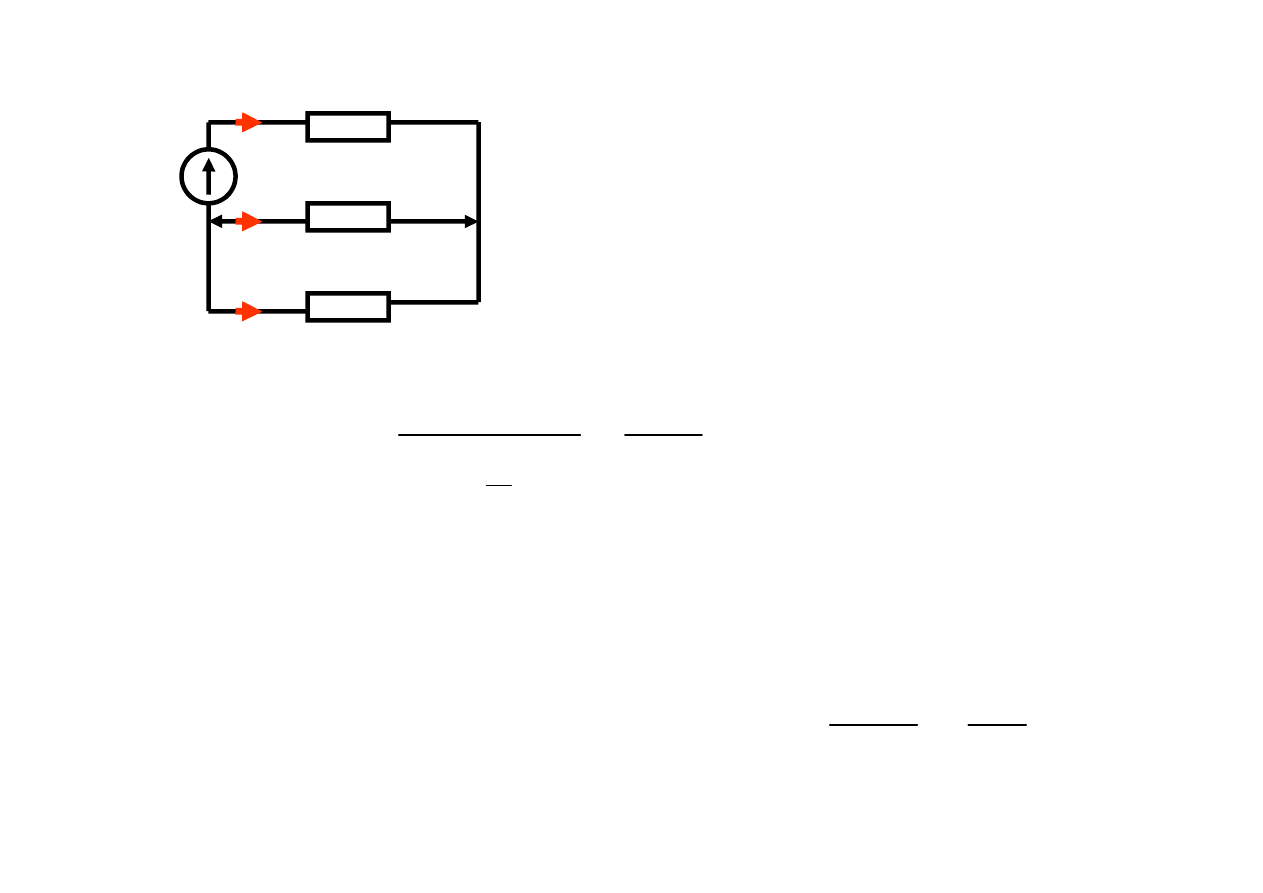
Obwód ma teraz postać:

Ω

=

+

+

=

5

,

1

6

5

4

4

5

54

6

5

4

R

R

R

R

R

R

Obwód ma teraz postać:

R

1

R

2

R

3

A

B

C

O

R

46

R

54

R

65

i

1

i

2

i

3

u

AC

1

46

2

54

i

R

i

R

u

AC

+

−

=

u

*

R

*

*

R

*

*

*

R

i

1

i

2

i

3

0

Ω

=

+

=

+

=

Ω

=

+

=

+

=

Ω

=

+

=

+

=

2

6

,

0

4

,

1

2

5

,

1

5

,

0

2

1

1

65

3

*

*

*

54

2

*

*

46

1

*

R

R

R

R

R

R

R

R

R

A

u

i

2

1

2

6

1

1

=

+

=

=

A

R

R

i

2

1

2

2

1

*

*

*

1

=

+

=

+

=

A

i

i

1

3

2

−

=

=

1

46

2

54

i

R

i

R

u

AC

+

−

=

A

R

u

i

AC

7

,

0

5

5

,

3

4

4

=

=

=

( )

V

u

AC

5

,

3

2

1

1

5

,

1

=

⋅

+

−

−

=

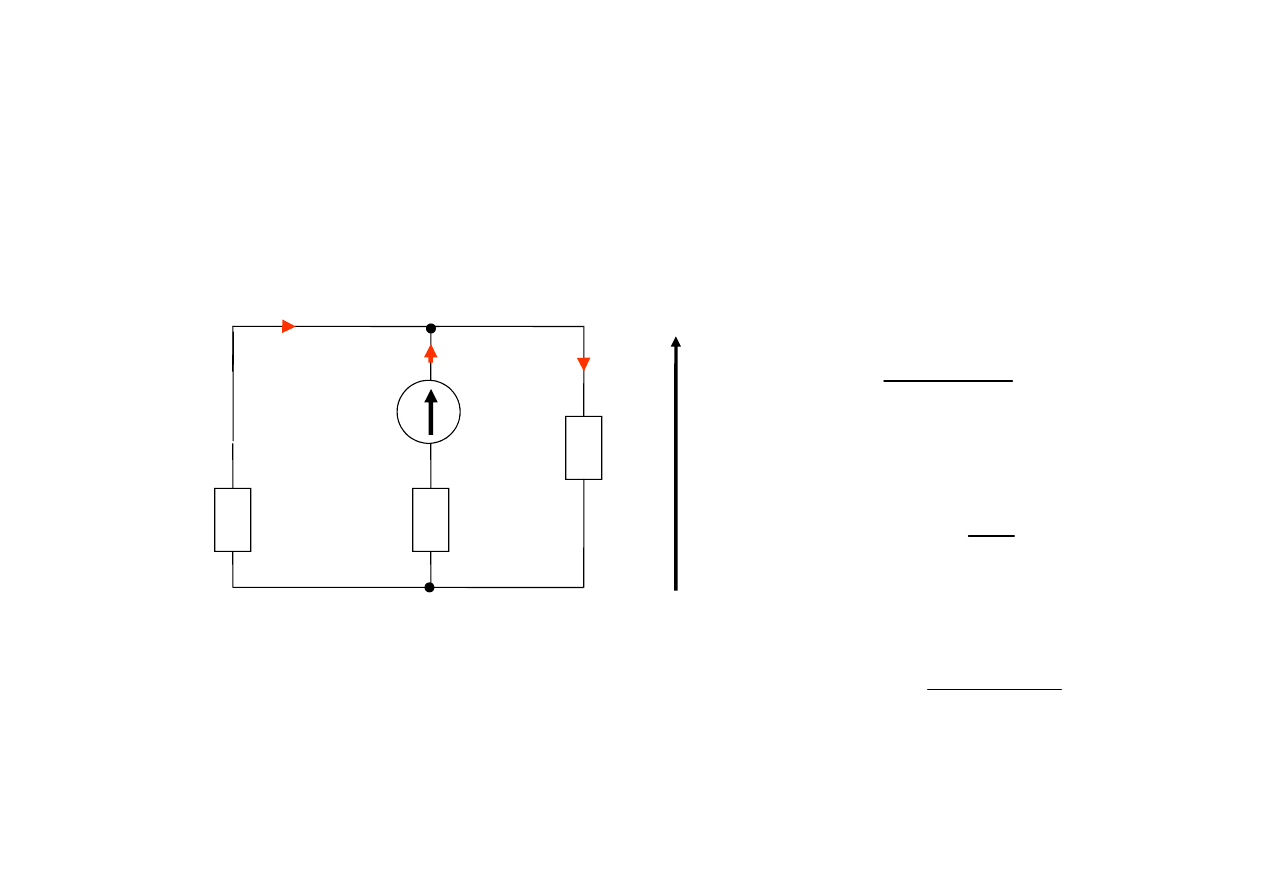
Twierdzenie o włączaniu dodatkowych źródeł

Rozpływ prądów w obwodzie nie zmieni się,
jeżeli we wszystkich gałęziach zbiegających się w węźle
(dowolnym) włączymy źródła napięcia
o tych samych wartościach napięć źródłowych
i tak samo skierowane względem węzła.

Dowód wynika z NPK

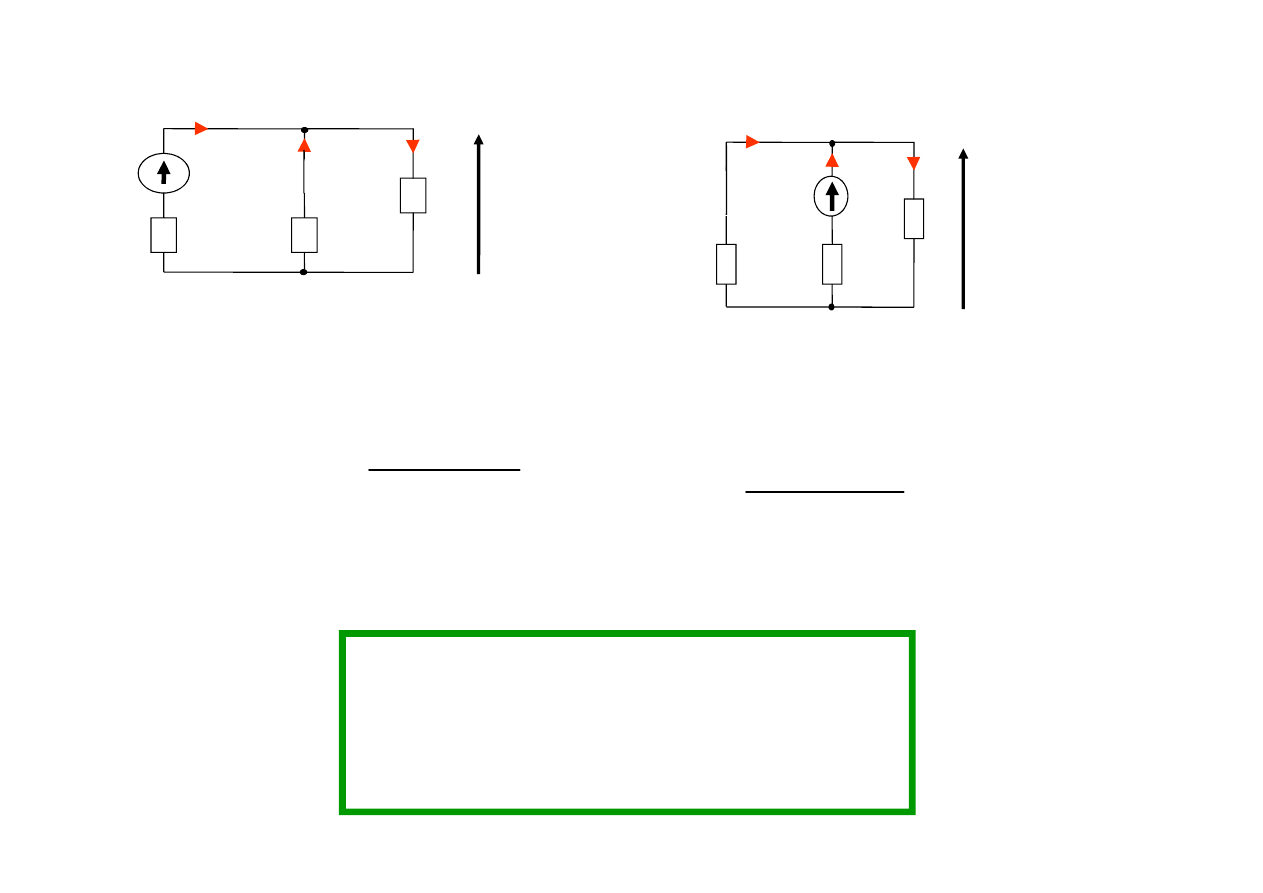
Rozkład napięć w obwodzie nie zmieni się,
jeżeli w pętli (dowolnej) pomiędzy kolejne węzły
włączymy źródła prądu
o tych samych prądach źródłowych
i tak samo skierowane względem kierunku obiegu pętli.

Dowód wynika z PPK

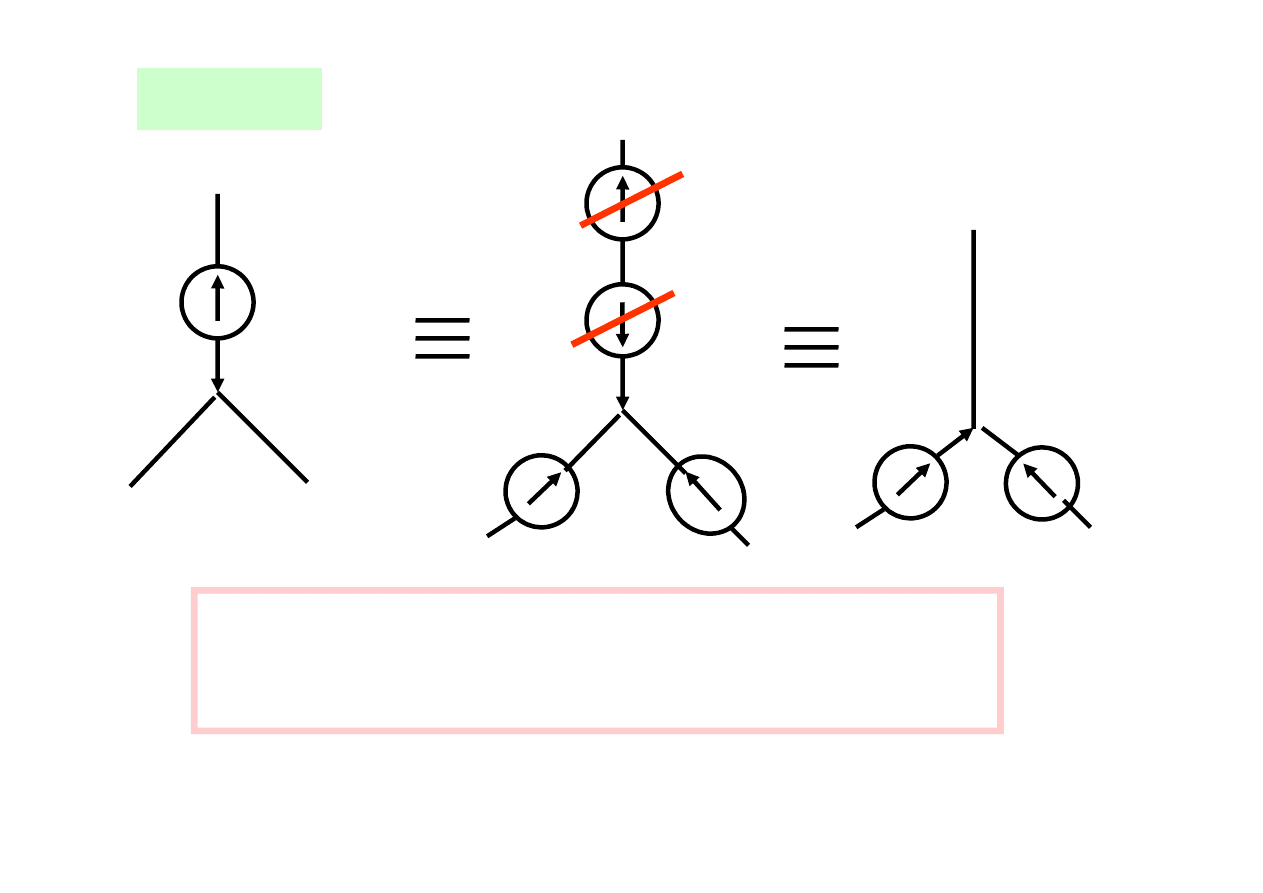
Wnioski:

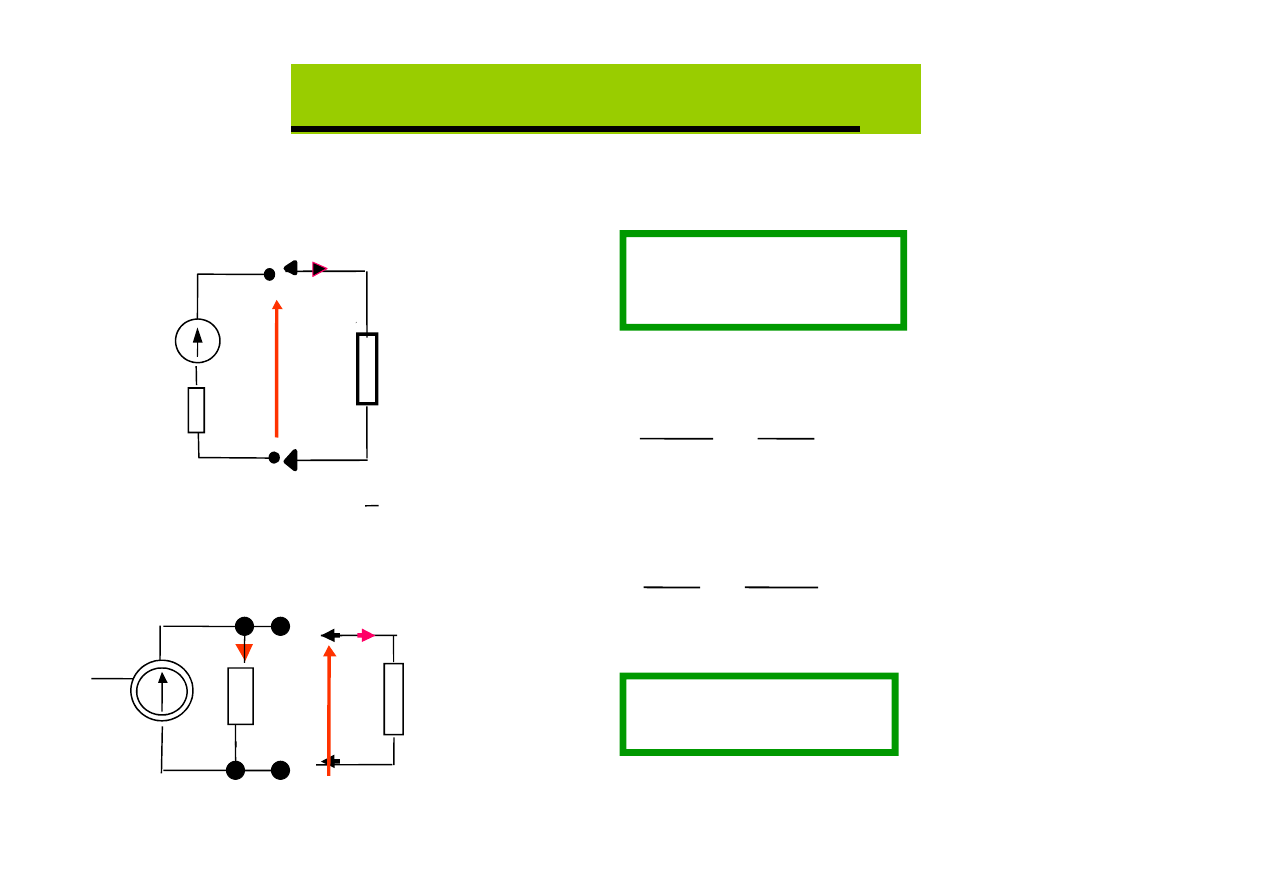
u

u

e=u

e

e

e

Źródło napięcia e=u zostało przeniesione
z jednej gałęzi obwodu
do pozostałych gałęzi zbiegających się w tym węźle.

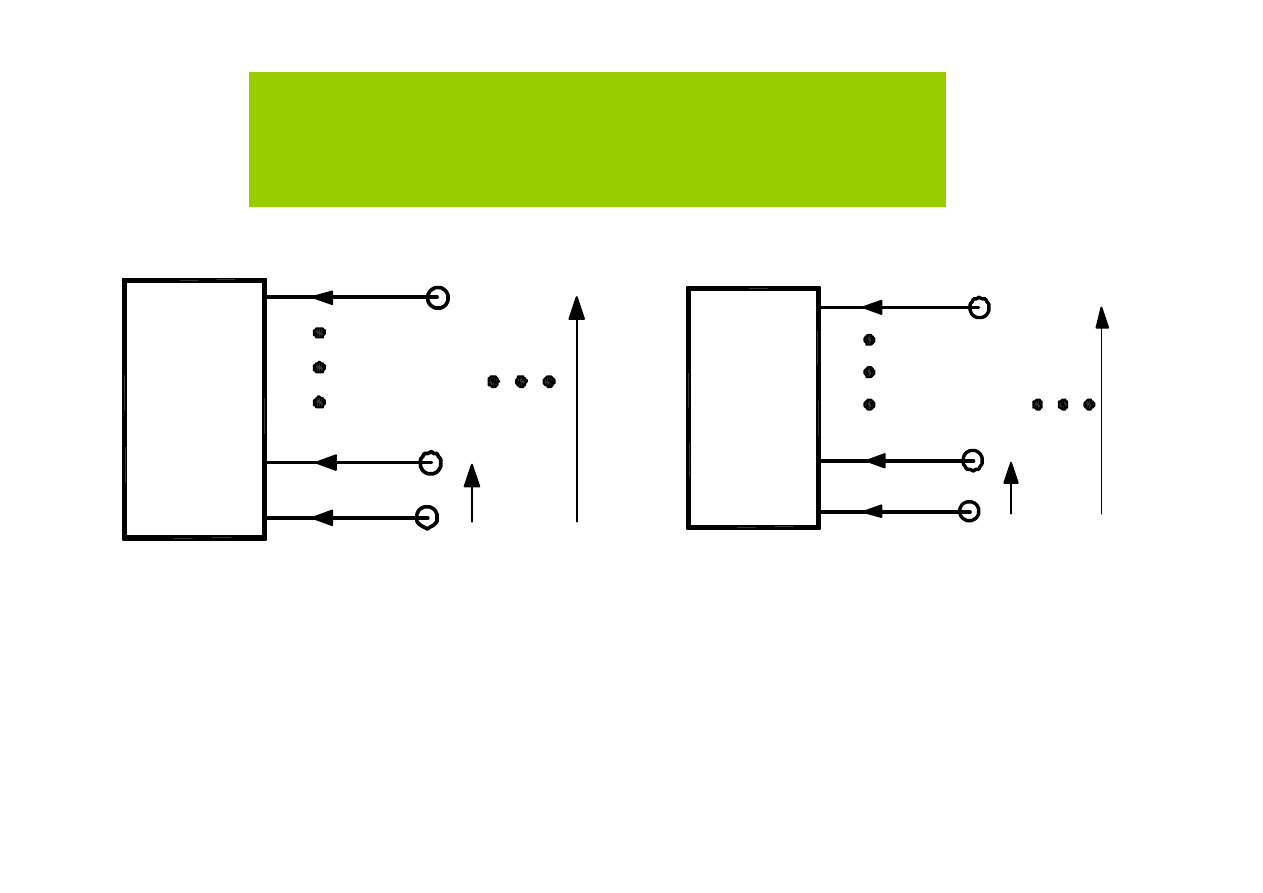
e

e

e

e

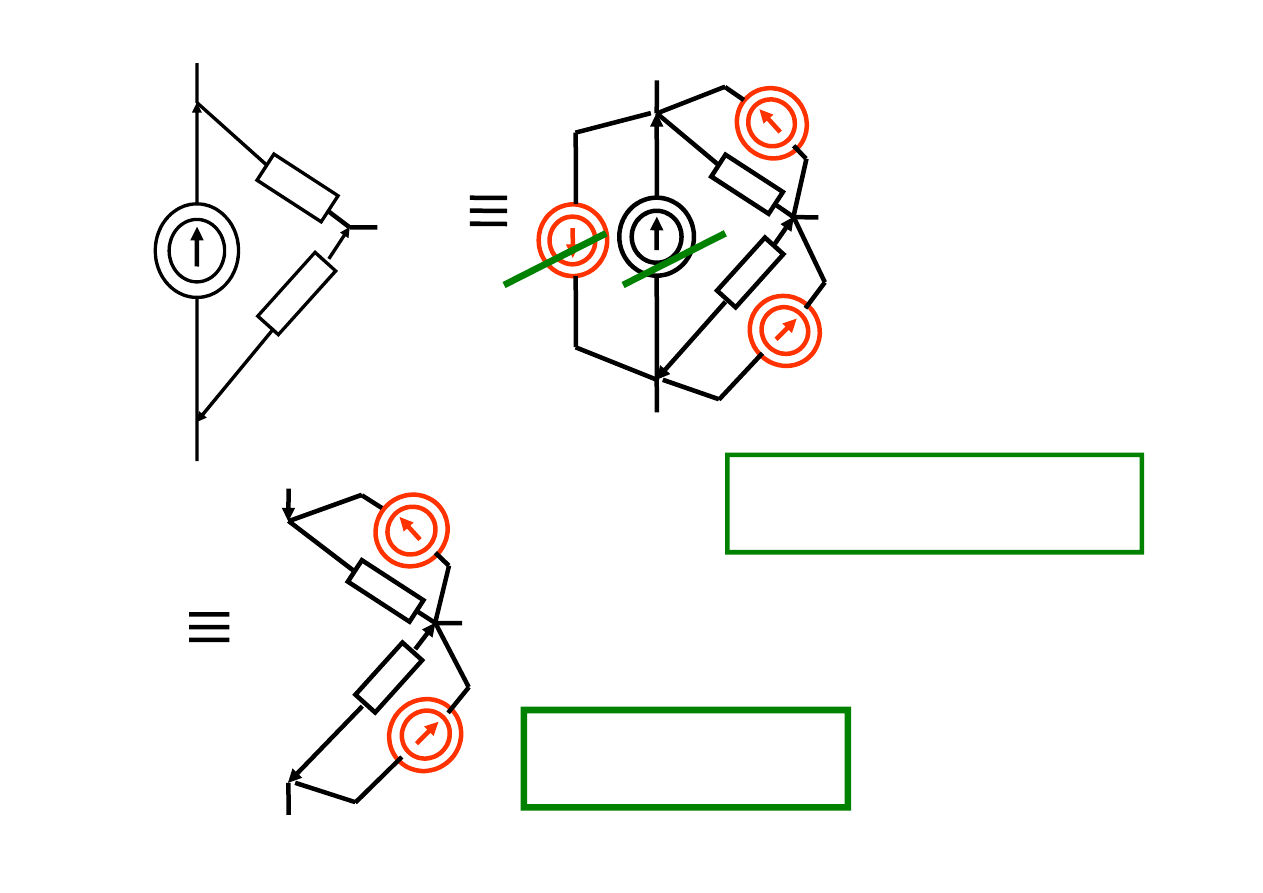
j

Ź

ródło prądu

zostało przeniesione.

Wszystkie prądy źródłowe
mają wartość j