TWIERDZENIE

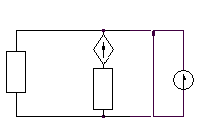
THEVENINA -NORTONA

TWIERDZENIE THEVENINA- NORTONA

• Rozpatrujemy obwód

liniowy.

i A

• Wykorzystując

u

zasadę s

uperpozycji

mamy :

B

k = l

m

∑ a e + ∑ b j + G u = i k k

k

k

z

k =1

k =1

Wprowadzamy

k l

=

m

∑ a e + ∑ b j + G u oznaczenie:

k k

k

k

z

k =1

k =1

 l

m



=

i



−

+

a e

b j

z

∑ k k ∑





k

k

=

=

k 1

k 1



i A

Otrzymujemy :

i =

i

i

−

+

i

G u

i

Gz

u

z

z

z

B

Dwójniki

i

Są opisane tym samym

równaniem więc są

równoważne.

i = i

−

+ G u

z

z

i

i

A

A

i

Gz

u

z

B

B

Wyznaczenie parametrów i , G dwójnika zast Z

Z

ępczego

Rozpatrujemy stan obwodu , gdy u = 0

i =

i

i

−

+

i

G u

z

z

i

A

wówczas :

iz

i = i

−

B

z

Zaciski AB są ZWARTE

Jeżeli w obwodzie

=

e

0

dla k = 1...l

=

j

0 dla j = 1...m

k

k

i

k l

=

m

A

a

∑ e + b

∑ j + Gu= i

k k

k k

z

k=1

k=1

i

u

G =

Gz

u

to

i

=

z

0 i mamy :

i = G u

z

B

i

G =

z

u

i = i

−

+ G u

z

z

Konduktancja obwodu

„widziana”z zacisków AB

i

G =

z

u

konduktancja „widziana” z zacisków A, B obwodu otrzymanego w wyniku przyrównania do zera wszystkich wymuszeń

Twierdzenie Nortona Obwód liniowy , rozpatrywany od strony wybranej pary zacisków AB można zastąpić równoległym połączeniem utworzonym ze źródła prądowego oraz opornika o konduktancji Gz .

Prąd źródłowy jest równy prądowi płynącemu w zwartej gałęzi AB, a Gz jest konduktancją „widzianą” z zacisków AB, po przyrównaniu do zera wszystkich napięć i prądów źródeł niezależnych.

Wiadomo, że rzeczywiste źródło prądowe i

, G

ż ,

z

można

zastąpić równoważnym źródłem napięciowym e , G

z

z .

1

e

gdzie

z

R =

z

u

Gz

Rz

e = R i

z

z z

Z równoważności dwójników źródłowych wynika ,że jest ez

napięciem na zaciskach AB .

i=0

Można je wyznaczyć w układzie

u

zaś rezystancję zastępczą

wyznaczamy tak jak GZ

UWAGA 1

Pomiarowe wyznaczenie prądu i wymaga z

zwarcia zacisków A, B co nie zawsze jest dopuszczalne.

Mo

M żn

ż a zm

z i

m er

e zy

z ć nap

a ięc

ę i

c e e i oblicz

c y

z ć i ze

z wz

w o

z ru

z

z

ez

i =

z

Rz

UWAGA

Pomiarowe wyznaczenie G (lub R ) wymaga przyrównania z

z

do zera wszystkich napięć i prądów źródeł niezależnych.

Jeżeli taka ingerencja w obwodzie nie jest możliwa dokonujemy pomiaru napięcia u w obwodzie z dołączonym do zacisków R

A, B opornikiem o znanej rezystancji R.

i = − i + G u z

z

i A

u

i = i

R

−

= −

R

R

R

uR

−

= −

u

i +

AB

G u

z

z

R

R

R i

− u

z

R

B

G =

z

R u

R

ez

i =

z

Re − R u

R

z

z

R

G =

z

z

R Ru

z

R

Przykłady

Przykład 1

W układzie jak na rys. obliczyć prąd i i

e

e

1

2

R

R

R

1

2

iZ

e

e

1

2

e

e

1

2

i =

+

R

R

z

1

2

R

R

1

2

A

R R

1

2

R =

z

R + R

1

2

R

R

R

1

2

Z

B

Zastępujemy układ wyjściowy rzeczywistym źródłem prądu i konduktancją zastępczą i

Rz

i =

i

iz

+

R

R

Rz

i

1

Z

G =

z

Rz

Przykład 2

Rozpatrzmy obwód zawierający źródło sterowane i

A

3

i

α i

i

3

s

R 1

R 2

B

Aby policzyć parametry zastępczego źródła i 3

A

Stosujemy NPK

'

i

α

R i + α i = 0

i

3

2 2

s

s

R 1

α i

`

R

`

'

i

i

i

s

2

1

i

= −

2

z

2

R 2

B

Stosujem

e y

m P

P

P K

P

`

`

i = i

=

i

0

3

s

'

'

1

−

+

+

=

i

i

i

0

3

2

z



α 

=

i

i

z

s 

 +

1





R 2 

2. Znajdujemy konduktancję układu Gz

``

i

i

3

A

u

'`

"

"

"

i

α

i

i =

=

i

−

1

3

u

3

1

R

R

1

1

R 2

'`

i 2

u

"

"

"

B

u =

− α i

+ R i

=

−

α

+ R i

1

2 2

2 2

i

R1

G =

Gz

u

``

``

"



α 

1

i − i

i =

+

1

u

2

3

2





G =

R

z

2 

R 1 

u

1 

α 

1

G =

1 +

+

z





R 

R 

R

2

1

1

Parametry zastępczego dwójnika wynoszą:



α 

=

i

i

z

s 

 +

1





R 2 

1 

α 

1

G =

1+

+

z





R 

R  R

2

1

1