Strop płytowo - żebrowy

Projekt stropu płytowo – żebrowego

Dane:

Długość budynku w świetle ścian: L=12,4 m

Szerokość budynku w świetle ścian B= 5,2 m

Przyjęto ściany grubości t =36 cm .

Klasa ekspozycji: XC1

Klasa konstrukcji: C3

Kategoria użytkowania stropu E1 ψ

0

=1,0 , ψ

1

=0,9 ,ψ

2

=0,8

Klasa odporności ogniowej REI=60
Obciążenie użytkowe charakterystyczne :

Materiały:

Beton C 25/30

Wytrzymałość charakterystyczna na ściskanie

f

ck

=25 MPa

Średnia wytrzymałość betonu na ściskanie

f

cm

=33 MPa

5% kwantyl wytrzymałości na rozciąganie

f

ctk ,0 ,05

=1,8 MPa

Średnia wytrzymałość na rozciąganie

f

ctm

=2,6 MPa

95% kwantyl wytrzymałości na rozciąganie

f

ctk , 0,95

=3,3 MPa

Moduł sprężystości betonu

E

cm

=31000 MPa

Stal zbrojenia głównego płyty - EPSTAL B500SP (klasa C)

Charakterystyczna granica plastyczności

f

yk

=500 MPa

Stal zbrojenia głównego żeber i podciągu – EPSTAL B500SP (klasa C)

Charakterystyczna granica plastyczności

f

yk

=500 MPa

Stal zbrojenia montażowego i strzemion EPSTAL B500SP (klasa C)

Charakterystyczna granica plastyczności

f

yk

=500 MPa

Konstrukcje betonowe PN-EN 1992

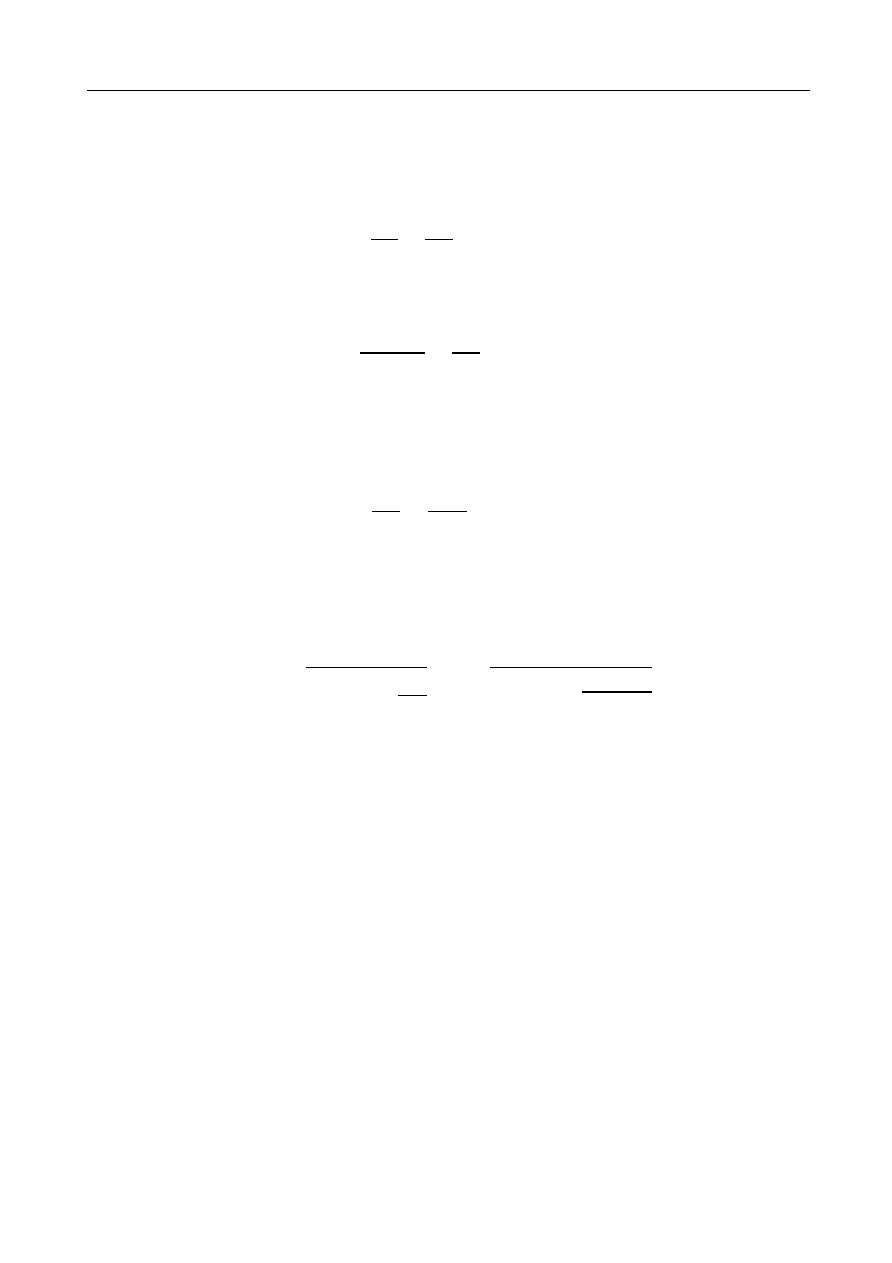
Strop płytowo - żebrowy

Częściowy współczynnik bezpieczeństwa dla betonu

Obliczeniowa wytrzymałość betonu na ściskanie

Obliczeniowa wytrzymałość betonu na rozciąganie

Częściowy współczynnik bezpieczeństwa dla stali

Obliczeniowa granica plastyczności

Graniczna wartość względnej wysokości strefy ściskanej dla stali B500SP

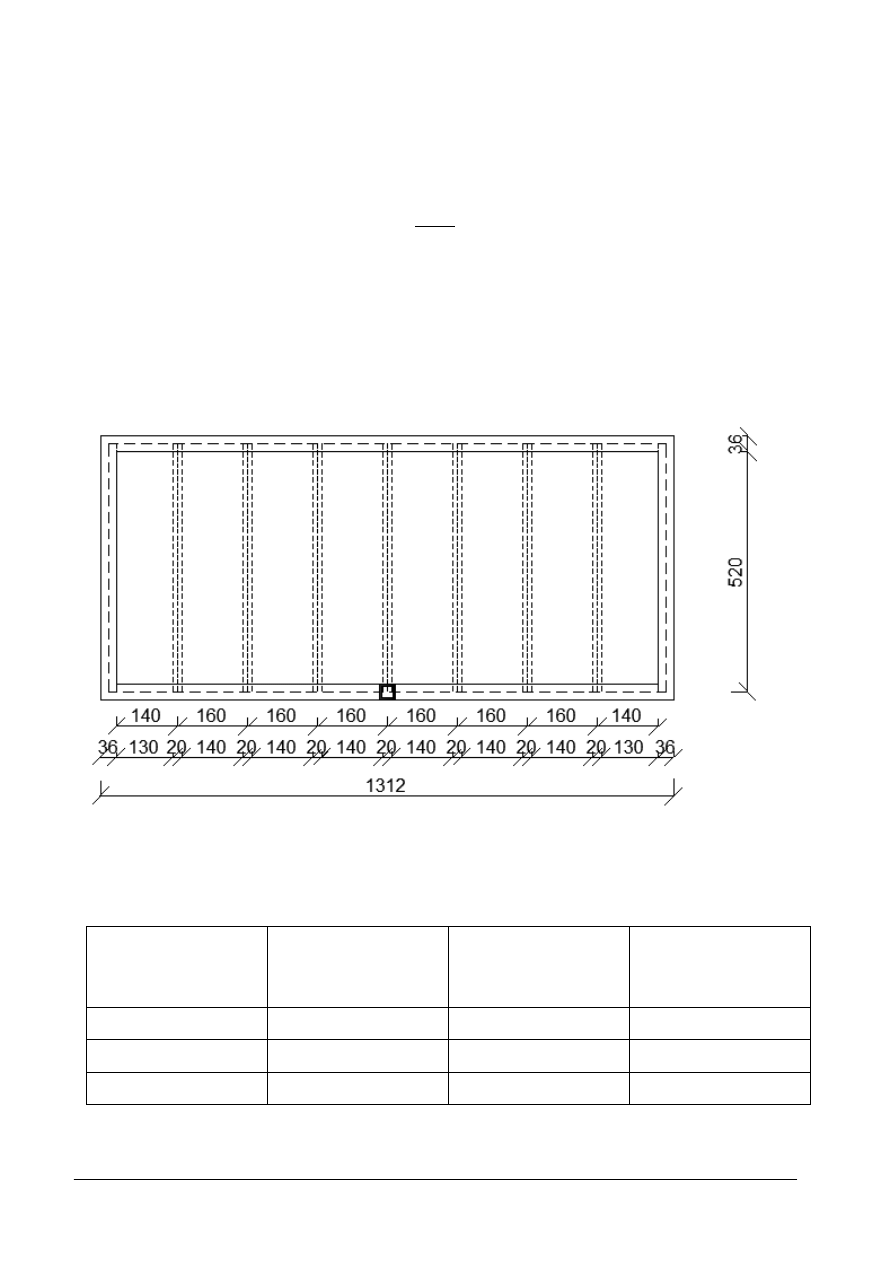
Rozmieszczenie żeber na stropie

Wstępnie założono osiowe rozstawy żeber

a

z

=160 cm

Przyjęto: n=6
Odległości żeber skrajnych od krawędzi ścian poprzecznych

Przyjęto rozmieszczenie żeber jak na rysunku 1.

1.

Wstępne wymiarowanie konstrukcji

Założone średnice prętów zbrojenia poszczególnych elementów

Element

Pręty główne [mm]

Pręty montażowe

lub rozdzielcze

[mm]

Strzemiona

[mm]

Płyta

8

8

–

Żebro

16

12

8

Podciąg

20

12

8

Konstrukcje betonowe PN-EN 1992

Strop płytowo - żebrowy

Grubość otuliny prętów zbrojenia

Z uwagi na klasę ekspozycji XC1 i klasę konstrukcji C3 określono:

Założono odchyłkę wymiarową Δ c

dev

=5÷10 mm .

Poz. 1 Płyta jednokierunkowo zginana

Rozpiętości efektywne przęseł płyty:

Skrajne: l

eff

=l +0,5 t =140 +0,5⋅36 =158 cm

Środkowe: l

eff

=160 cm

Wstępnie ustalona wysokość użytkowa płyty:

Przyjęto: d = 6,0 cm

Grubość otulenia prętów zbrojenia płyty

Założono odchyłkę wymiarową: Δ c

dev

=6 mm

Nominalna grubość otulenia: c

nom

=c

min

+Δ c

dev

=15+6=21 mm .

h=d + a

1

=6,0 +2,5=8,5 cm

Przyjęto grubość płyty: h=10,0 cm .

Wysokość użyteczna płyty: d = h – a

1

=10,0 – 2,5=7,5 cm

Przyjęta grubość spełnia wymagania dotyczące minimalnej grubości płyty dla klasy

odporności ogniowej REI60.

Konstrukcje betonowe PN-EN 1992

Strop płytowo - żebrowy

Grubość otuliny gwarantuje zachowanie osiowej odległości zbrojenia od krawędzi

przekroju a

min

=20 mm .

Korekta rozpiętości efektywnej przęsła skrajnego z uwagi na przyjętą grubość płyty

a

n

=min (0,5 t ; 0,5 h ) = min (0,5 ∙ 36= 18,0 cm ; 0,5 ∙10,0 cm) =5,0 cm

l

eff ,1

=l + a

n

=140 + 5=145,0 cm

Poz. 2 – Żebro

Rozpiętość przęsła w świetle – L=520 cm

Rozpiętość efektywna przęsła: L

eff

= L +0,5 t =520 +0,5⋅36=538,0 cm

Wstępna wysokość użyteczna

Przyjęto:

d =35,0 cm

Przyjęto odchyłkę wymiarową

Grubość otulenia:

Δ c

dev

=10 mm

c

nom

=c

min

+Δ c

dev

=16 +10=26 mm

Wysokość przekroju żebra: h=d +a

1

=35,0 + 4,2=39,2 cm

Przyjęto: h=40,0 cm

Wysokość użyteczna przekroju żebra: d =h – a

1

=40,0 – 4,2=35,8 cm

Szerokość żebra: b=

Przyjęto żebro szerokości b=25,0 cm

Uwaga:

Ostateczna wartość rozpiętości efektywnej żebra zostanie ustalona po wstępnym

wymiarowaniu podciągu.

Konstrukcje betonowe PN-EN 1992

Strop płytowo - żebrowy

Poz. 3 – Podciąg

Rozpiętość przęsła w świetle – L= 620 cm

Rozpiętość efektywna przęsła: L

eff

= L +0,5 t =620 +0,5⋅36=638,0 cm

Wstępnie wysokość użyteczna

Ze względów wykonawczych (ułożenie zbrojenia) dobrze jest aby różnica wysokości

żebra i podciągu wynosiła 10 ÷15 cm .

Przyjęto: d =45,0 cm

Przyjęto odchyłkę wymiarową Δ c

dev

=13 mm

Grubość otulenia:

c

nom

=c

min

+Δ c

dev

=20 +13=33 mm

Wysokość przekroju podciągu: h=d +a

1

=45,0 +4,9=49,9 cm

Przyjęto: h=50,0 cm

Wysokość użyteczna przekroju żebra: d =h – a

1

=50,0 – 4,9=45,1 cm

Szerokość żebra: b=

Przyjęto podciąg o szerokości b=30,0 cm


Korekta rozpiętości obliczeniowej żebra

a

1

=min (0,5 t; 0,5h )=min (0,5 ∙36=18,0 cm ; 0,5 ∙40)=20,0 cm

L

eff

= L +a

1

+0,5 b=520+0,5⋅36,0 +0,5⋅30,0 =553 cm .

Przyjęto : l

eff

= 553 cm.

Konstrukcje betonowe PN-EN 1992

Strop płytowo - żebrowy

Ustalenie obciążeń działających na stropie

Obciążenia stałe powierzchniowe:

Rodzaj

Obciążenie

charakterystyczne

[kN/m

2

]

Częściowy

współczynnik

bezpieczeństwa

γ

G , max /

γ

G , min

Obciążenie

obliczeniowe

[kN/m

2

]

posadzka betonowa

0,03⋅21,0

0,63

1,35/1,0

izolacja

0,05

1,35/1,0

Styropian – 4cm

0,04⋅0,45

0,02

1,35/1,0

izolacja

0,05

1,35/1,0

płyta żelbetowa

0,1⋅25,0

2,50

1,35/1,0

Sufit podwieszony

0,18

1,35/1,0

RAZEM:

3,43

Obciążenie zmienne powierzchniowe:

Rodzaj

Obciążenie

charakterystyczne

[kN/m

2

]

Częściowy

współczynnik

bezpieczeństwa

γ

Q

Obciążenie

obliczeniowe

[kN/m

2

]

Obciążenie zmienne

technologiczne

5,0

1,5

Konstrukcje betonowe PN-EN 1992

Strop płytowo – żebrowy

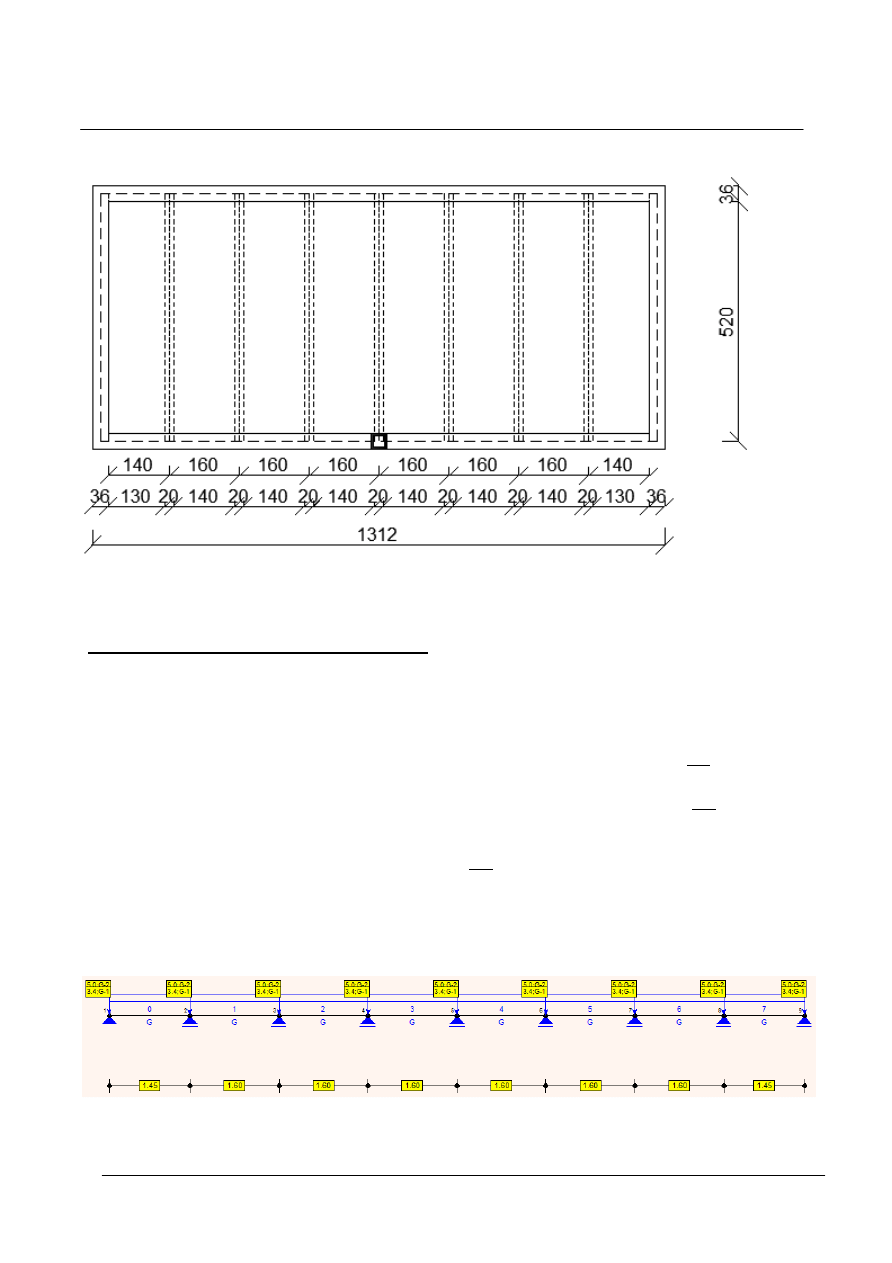
Schemat konstrukcyjny stropu

2.Obliczenia statyczne

Poz. 1 – Płyta jednokierunkowo zginana

Kombinacja obciążeń wg PN-EN 1990

Obliczenia statyczne programem SOLDIS Projektant v 6.0

Schemat statyczny:

Konstrukcje betonowe PN-EN 1992

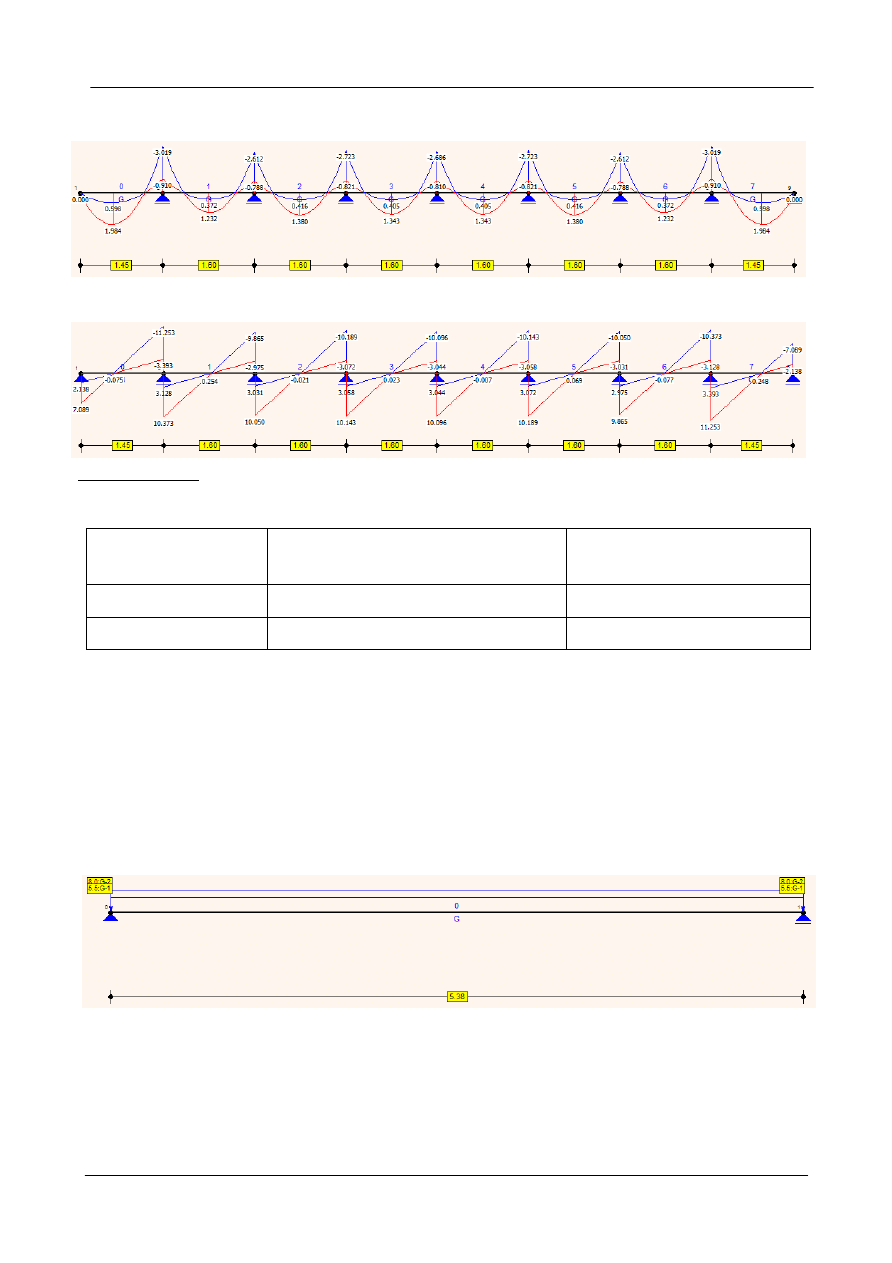
Strop płytowo - żebrowy

Obwiednia momentów zginających

Obwiednia sił poprzecznych

Poz. 2 – Żebro

Obciążenia z płyty stropowej

Obciążenie

Wartość charakterystyczna

[kN/m]

Współczynnik obciążenia

Stałe

3,43⋅1,6=5,5

1,35 /1,0

Użytkowe

5,0⋅1,6=8

1,5

Ciężar własny żebra – uwzględniony w programie.

Obliczenia statyczne programem SOLDIS Projektant v

6.0

Schemat statyczny:

Konstrukcje betonowe PN-EN 1992

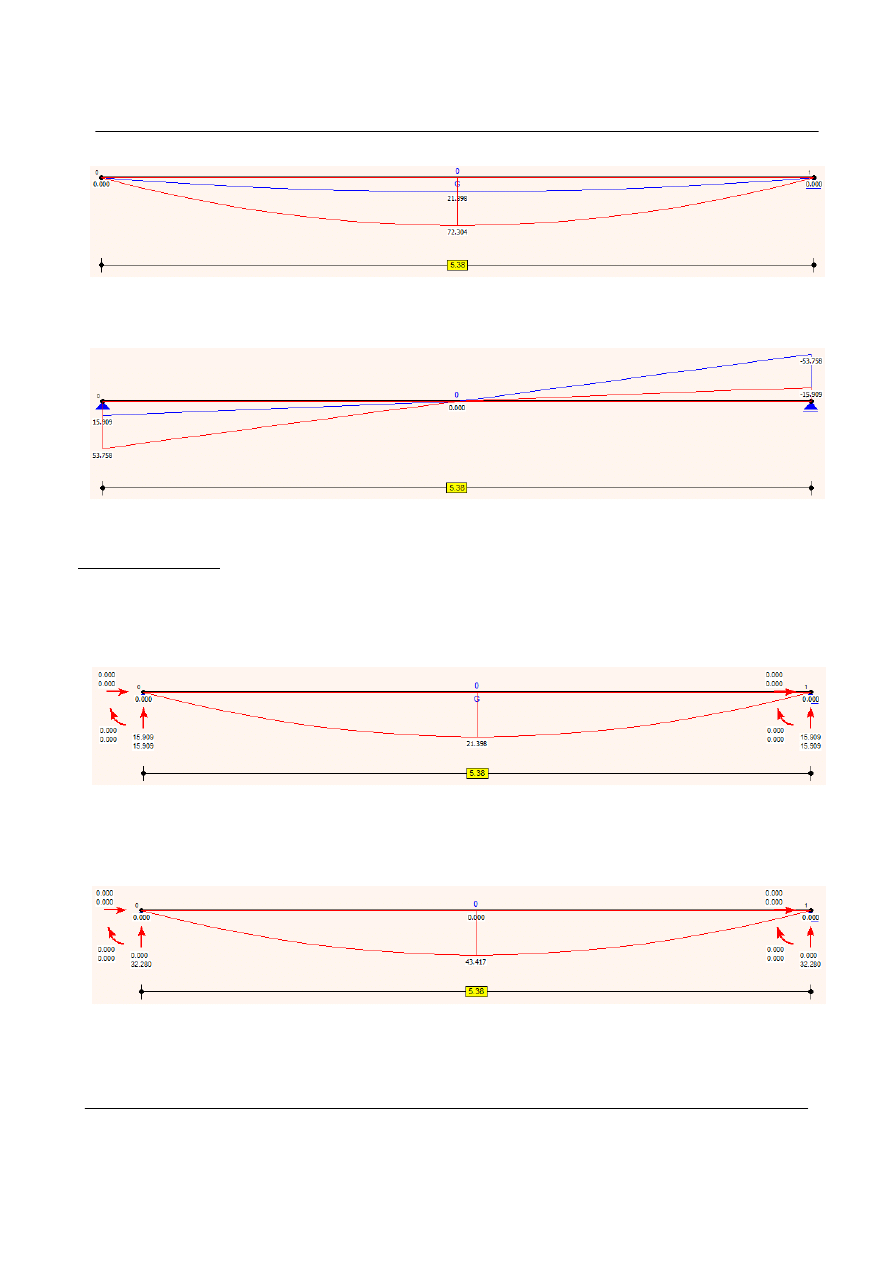
Strop płytowo - żebrowy

Obwiednia momentów zginających

Obwiednia sił poprzecznych

Poz. 3 – Podciąg
Obliczenia statyczne programem SOLDIS Projektant v 6.0
Reakcje żebra od obciążeń charakterystycznych:
stałych (łącznie z ciężarem własnym żebra):

R

G

=16,0 kN

użytkowych:

R

Q

=32,3 kN

Konstrukcje betonowe PN-EN 1992

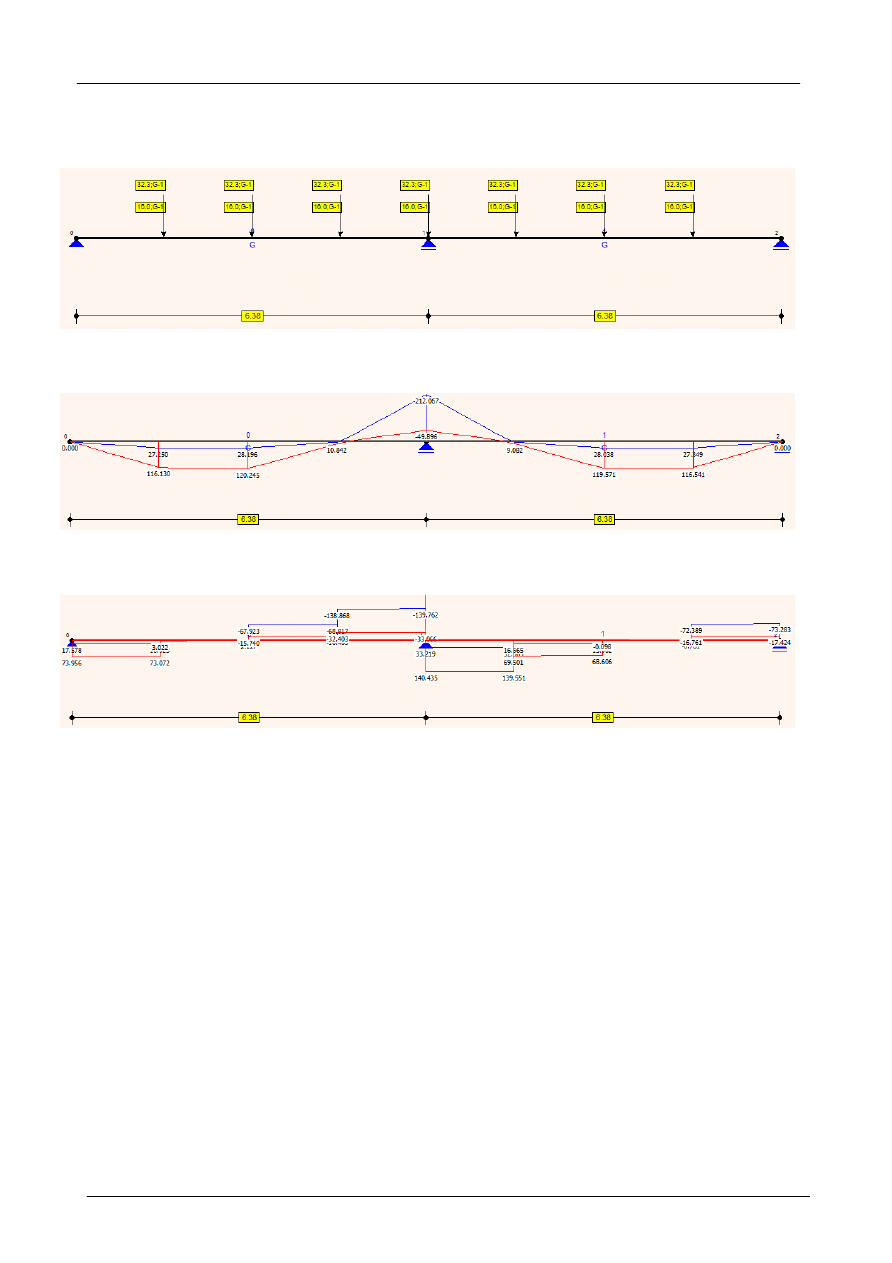
Strop płytowo - żebrowy

Schemat obliczeniowy:

Obwiednia momentów zginających:

Obwiednia sił poprzecznych:

Konstrukcje betonowe PN-EN 1992

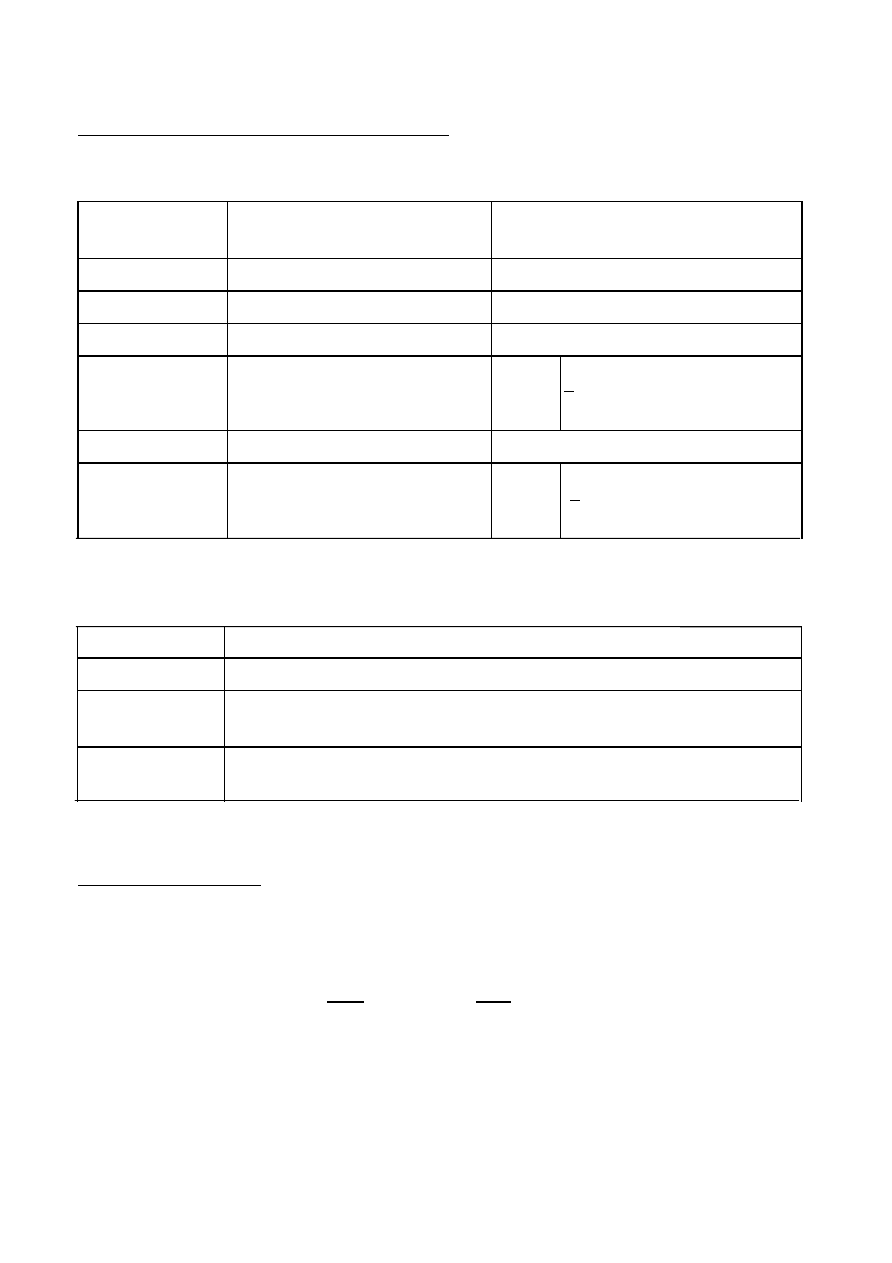
Poz. 1 – Płyta jednokierunkowo zginana

Zestawienie momentów zginających do wymiarowania:

Miejsce

Maksymalny moment

Minimalny moment zginający

zginający [kNm]

[kNm]

Podpora 0

0,00

0,00

Przęsło 02

2,0

0,372

Podpora 1

-3,02

-0,91

Przęsło 04

1,38

0,416

Podpora 2

-2,72

-0,82

Przęsło 06 1,34

0,40

Zestawienie sił poprzecznych do wymiarowania:

Miejsce

Siła poprzeczna [kN]

Podpora 0

7,10

Podpora 1

11,2– z lewej strony

10,4 – z prawej strony

Podpora 2

10,2 – z lewej strony

10,1 – z prawej strony

Minimalne pola przekroju zbrojenia

z uwagi na zginanie

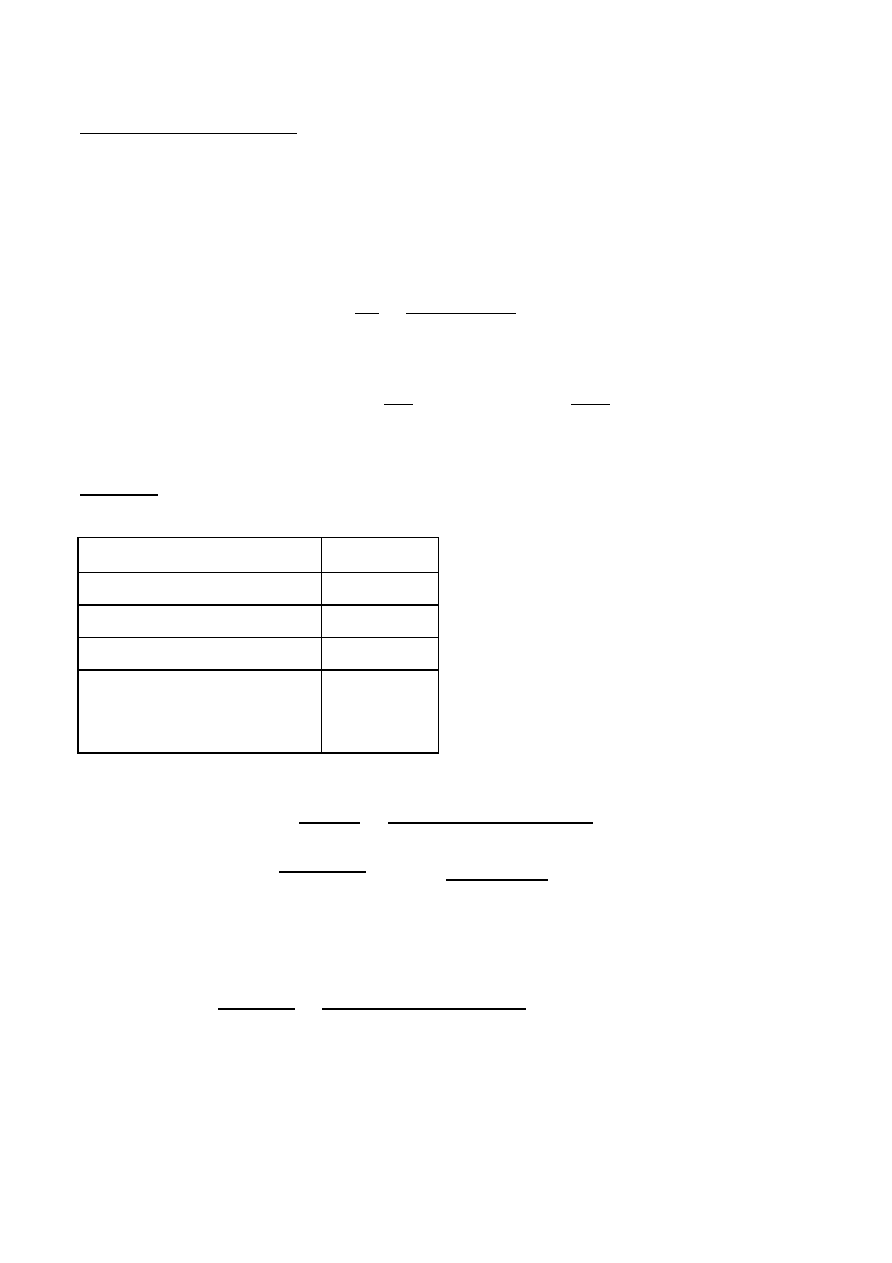
z uwagi na zarysowanie

Przyjęto:

w

max

= 0,4 mm ,

k

c

=0,4 – zginanie bez udziału siły podłużnej,

k =1,0 – odkształcenia wymuszone czynnikami zewnętrznymi,

σ

s

=400 MPa – średnica prętów zbrojenia podłużnego ϕ =8 mm

Przęsło 1

Dane:

Moment zginający

M

Ed

2,0 kNm

Szerokość przekroju: b

100,0 cm

Wysokość przekroju: h

10,0 cm

Wysokość użyteczna d

7,5 cm

Odległość zbrojenia

rozciąganego od krawędzi

2,5 cm

a

1

Uwzględniając minimalne pola zbrojenia z uwagi na zginanie i zarysowanie
oraz minimalne pole wynikające z warunku nośności

Rozstaw prętów zbrojenia wynikający z najmniejszego wymaganego pola zbrojenia

Maksymalny rozstaw prętów zbrojenia

Przyjęto rozstaw prętów wynoszący

s

slabs

=20,0 cm

Pole przekroju prętów

ϕ

8

w rozstawie

s

slabs

Wymagana liczba prętów

Przyjęto zbrojenie dołem w przęśle 02:

ϕ 8 co 20 cm

o polu

A

s , prov

=

2,513cm

2

– stal B500SP

Przęsło 04

Dane:

Moment zginający

M

Ed

1,38 kNm

Szerokość przekroju: b

100,0 cm

Wysokość przekroju: h

10,0 cm

Wysokość użyteczna d

7,5 cm

Odległość zbrojenia

rozciąganego od krawędzi

2,5 cm

a

1

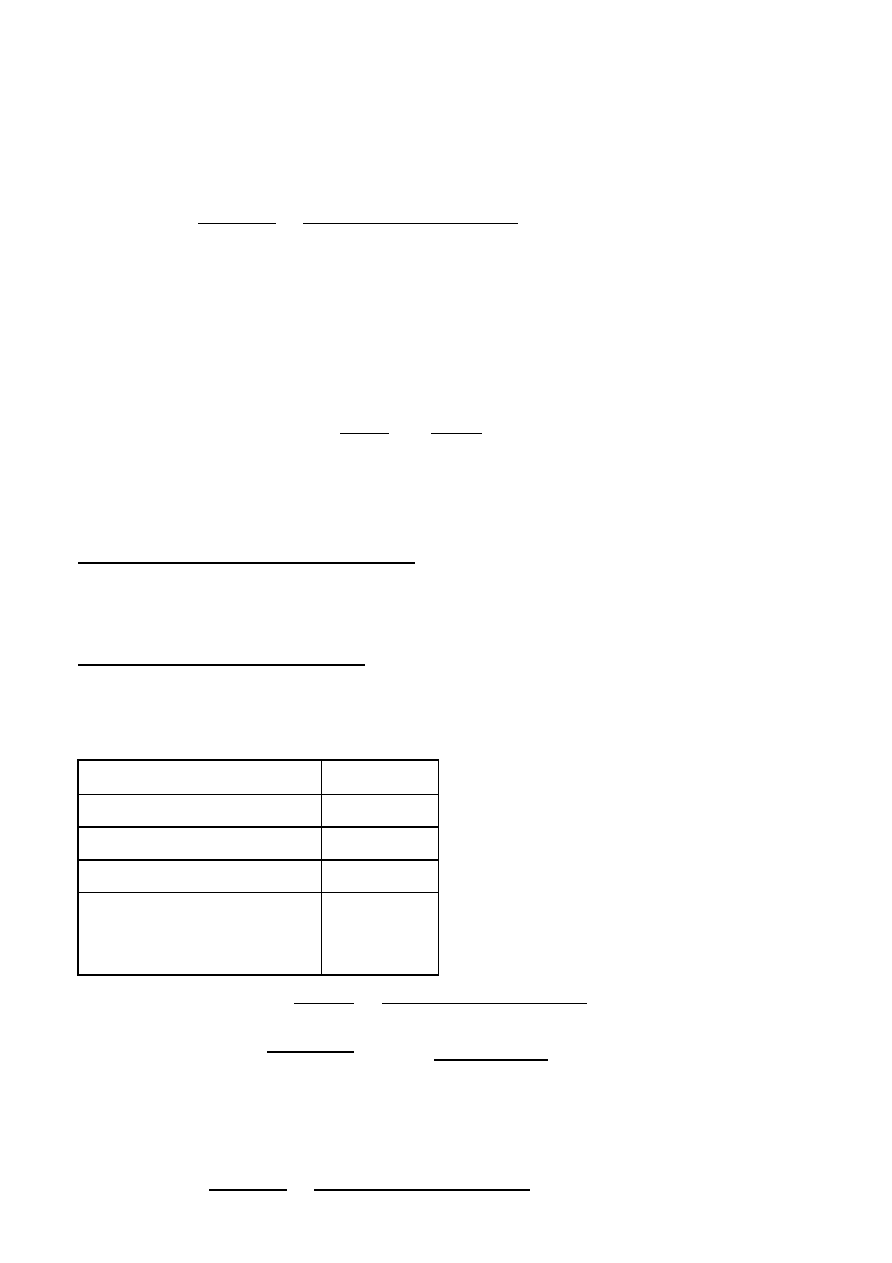
Przyjęto zbrojenie dołem w przęśle 2:

ϕ 8 co 20 cm

o polu

A

s , prov

=

2,513cm

2

– stal B500SP

Pole przekroju prętów

ϕ

8

w rozstawie

s

slabs

Przyjęto zbrojenie górą w przęśle 2:

ϕ 8 co 30 cm

o polu A

s , prov

=

1,68 cm

2

– stal B500SP

Zbrojenie w przęsłach pozostałych

Biorąc pod uwagę momenty zginające przyjęte zostanie zbrojenie jak w przęśle 2.

Podpora 1 (krawędź podpory):

Moment zginający w odległości x= 0,10 m (połowa szerokości żebra)
odczytany z programu SOLDIS:

M

kr ,1

=−5,05 kNm

Moment zginający

M

Ed

3,5 kNm

Szerokość przekroju: b

100,0 cm

Wysokość przekroju: h

10,0 cm

Wysokość użyteczna d

7,5 cm

Odległość zbrojenia

rozciąganego od krawędzi

2,5 cm

a

1

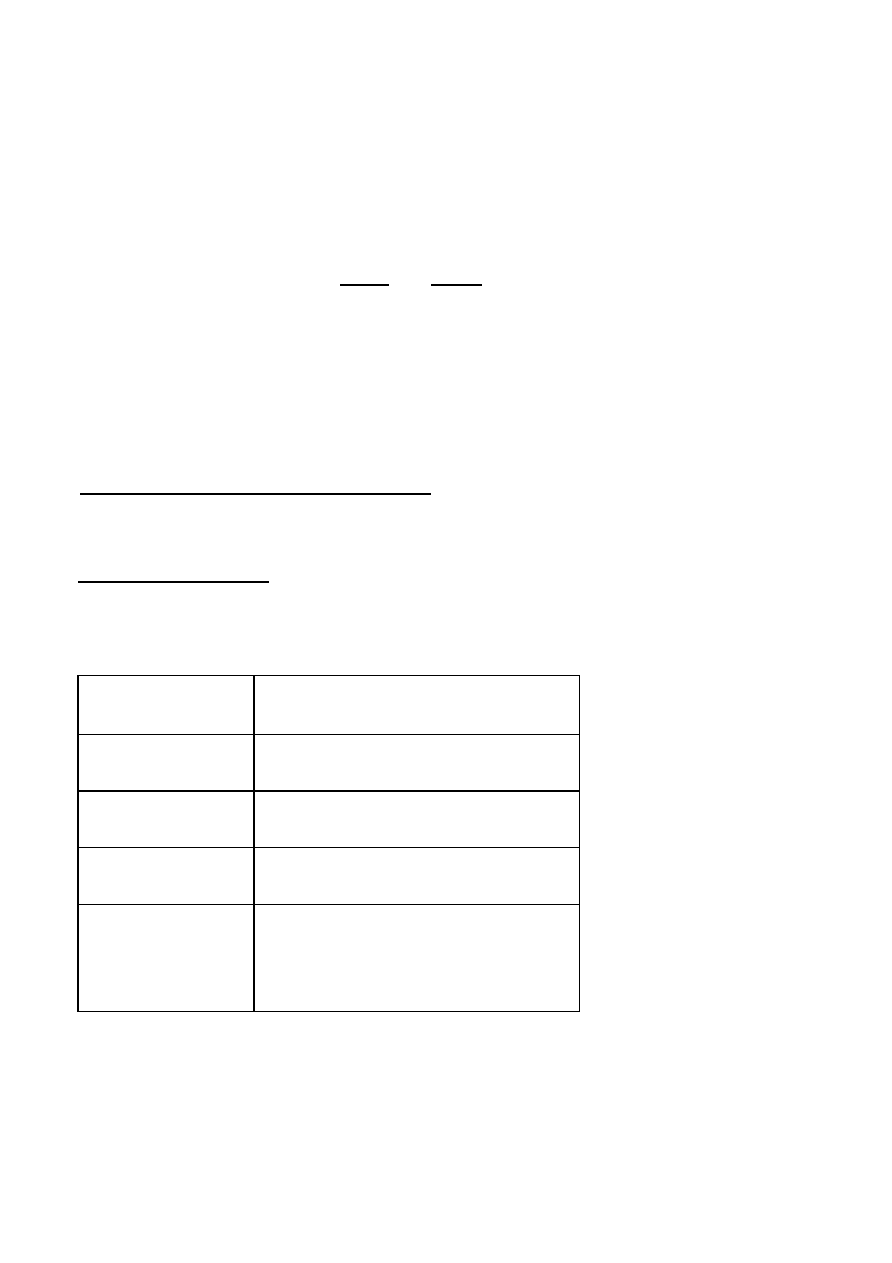
Przyjęto rozstaw:

s

slabs

=15,0 cm

Pole przekroju prętów

ϕ 8

w rozstawie

s

slabs

Przyjęto zbrojenie górą na podporze 1:

ϕ 8 co 15cm

o polu

A

s , prov

=

3,35cm

2

– stal B500SP

Zbrojenie na pozostałych podporach

Z uwagi na momenty zginające przyjęto zbrojenie, jak na podporze 1.

Podpora 0 (skrajna)

Zbrojenie górne przy wieńcu.

Dane:

Moment zginający

0,15 M

Ed ,1

=0,15

⋅2,0=0,3 kNm

M

Ed

Szerokość

100,0 cm

przekroju: b

Wysokość

10,0 cm

przekroju: h

Wysokość

7,5 cm

użyteczna d

Odległość

zbrojenia

2,5 cm

rozciąganego od

krawędzi

a

1

Biorąc pod uwagę wartość momentu zginającego przyjęto

zbrojenie górą

ϕ 8 co 30 cm

o polu

A

s , prov

=1,68 cm

2

– stal B500SP

Zbrojenie to powinno sięgać licząc od lica podpory (ściany) na długość nie
mniejszą niż

0,2 l

eff.1

=

0,2 ∙1,65=0,33 m

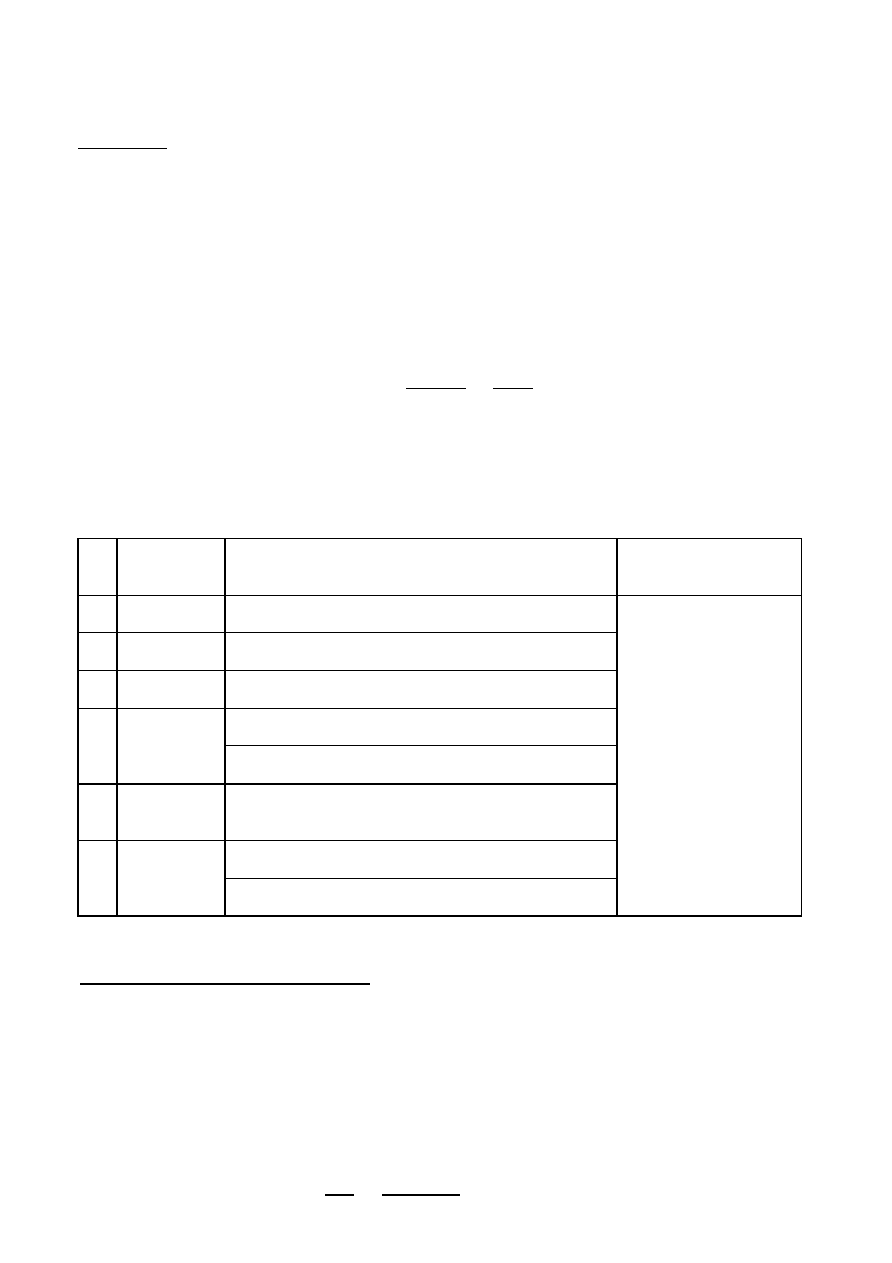
UWAGA:

Podobne zbrojenie należy zastosować w połączeniu płyty z podciągiem.

Zbrojenie rozdzielcze

jako

zbrojenie

rozdzielcze

przyjęto

ϕ 8 co 30 cm

o

polu

A

s

=

1,68 cm

2

>

0,2

⋅

2,513

=

0,503 cm

2

, co stanowi

Pręty rozdzielcze średnicy

=4,5 mm

, co 250 mm o polu

A

sr

=0,65 cm

2

Zestawienie wymaganego zbrojenia płyty

L.p

Miejsce

Przyjęte zbrojenie główne

Przyjęte zbrojenie

rozdzielcze

1

Podpora 0

Górą:

ϕ 8 co 30 cm

A

s , prov

=

1,68 cm

2

2

Przęsło 02

Dołem:

ϕ 8 co 20 cm

,

A

s , prov

=

2,513cm

2

3

Podpora 1

Górą:

ϕ 8 co15 cm

,

A

s , prov

=

3,35cm

2

4

Przęsło 04

Górą:

ϕ 8 co 30 cm

,

A

s , prov

=

1,68 cm

2

ϕ 8 co 30 cm

2

Dołem:

ϕ 8 co 20 cm

,

A

s , prov

=

2,513cm

A

s , prov

=

1,68 cm

2

5

Podpory

Górą:

ϕ 8 co15 cm

,

A

s , prov

=3,35cm

2

inne

6

Przęsła

Górą:

ϕ 8 co 30 cm

,

A

s , prov

=

1,68 cm

2

pozostałe

2

Dołem:

ϕ 8 co 20 cm

,

A

s , prov

=

2,513cm

Sprawdzenie płyty na ścinanie

Przyjęto doprowadzenie do podpory skrajnej całego zbrojenia wymaganego w

przęśle 01. Pole tego zbrojenia wynosi A

s

=

2,513 cm

2

. Zbrojenie to zostanie

odpowiednio

zakotwione na podporze, czyli na odległość

l

bd

+

d

.

Stopień zbrojenia w strefie podporowej

k=2,0

k

1

=0,15

Nie jest konieczne wymiarowanie zbrojenia na ścinanie.

Sprawdzenie warunków II stanu granicznego

Sprawdzenie szerokości rys prostopadłych

Stan graniczny użytkowalności zostanie sprawdzony z uwzględnieniem

obciążeń długotrwałych. Obowiązująca będzie zatem w obliczeniach quasi –

stała kombinacja obciążeń.

Quasi – stała kombinacja obciążeń w stanie granicznym
użytkowalności

G

k



2

Q

k

.

Obwiednia momentów zginających w quasi – stałej kombinacji
obciążeń

2

Maksymalny moment zginający w płycie wynosi

M

Ek



1,86 kNm .

Określenie końcowego współczynnika pełzania.

Założenia:

Element obciążony po 28 dniach – t

0



28 .

Wilgotność RH



50 %

.

Na podstawie normowego wykresu 3.1 przyjęto końcowy współczynnik pełzania

o wartości





, t

0



3,0 .

Relacja modułów sprężystości stali i betonu

Określenie cech geometrycznych przekroju sprowadzonego.

Cechy określa się dla przekroju przęsłowego ze zbrojeniem rozciąganym

A

s1



2,513 cm .

Położenie osi obojętnej w przekroju pracującym w fazie I

Moment bezwładności przekroju sprowadzonego

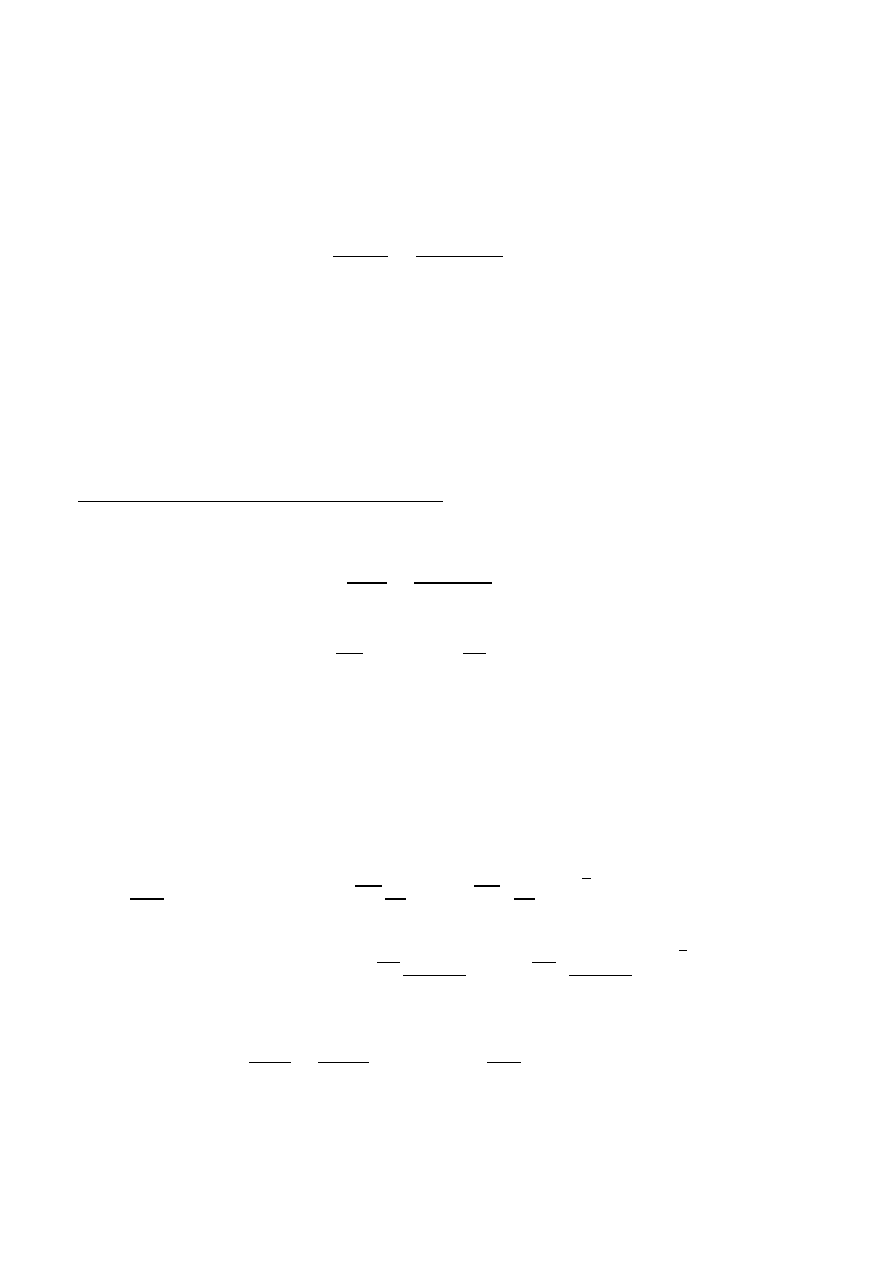
Wskaźnik wytrzymałości przekroju sprowadzonego

Moment rysujący

Przekrój nie ulega zarysowaniu. Sprawdzenie zarysowania jest zbędne.

Sprawdzenie ugięcia – metoda uproszczona

Przęsło skrajne o rozpiętości efektywnej l

eff



1,45 m .

Stopień zbrojenia podłużnego w przęśle

Porównawczy stopień zbrojenia

Współczynnik zależny od schematu pracy elementu

K



1,3

.

Maksymalny wskaźnik ugięcia

Ugięcie w przęśle skrajnym nie zostanie przekroczone.

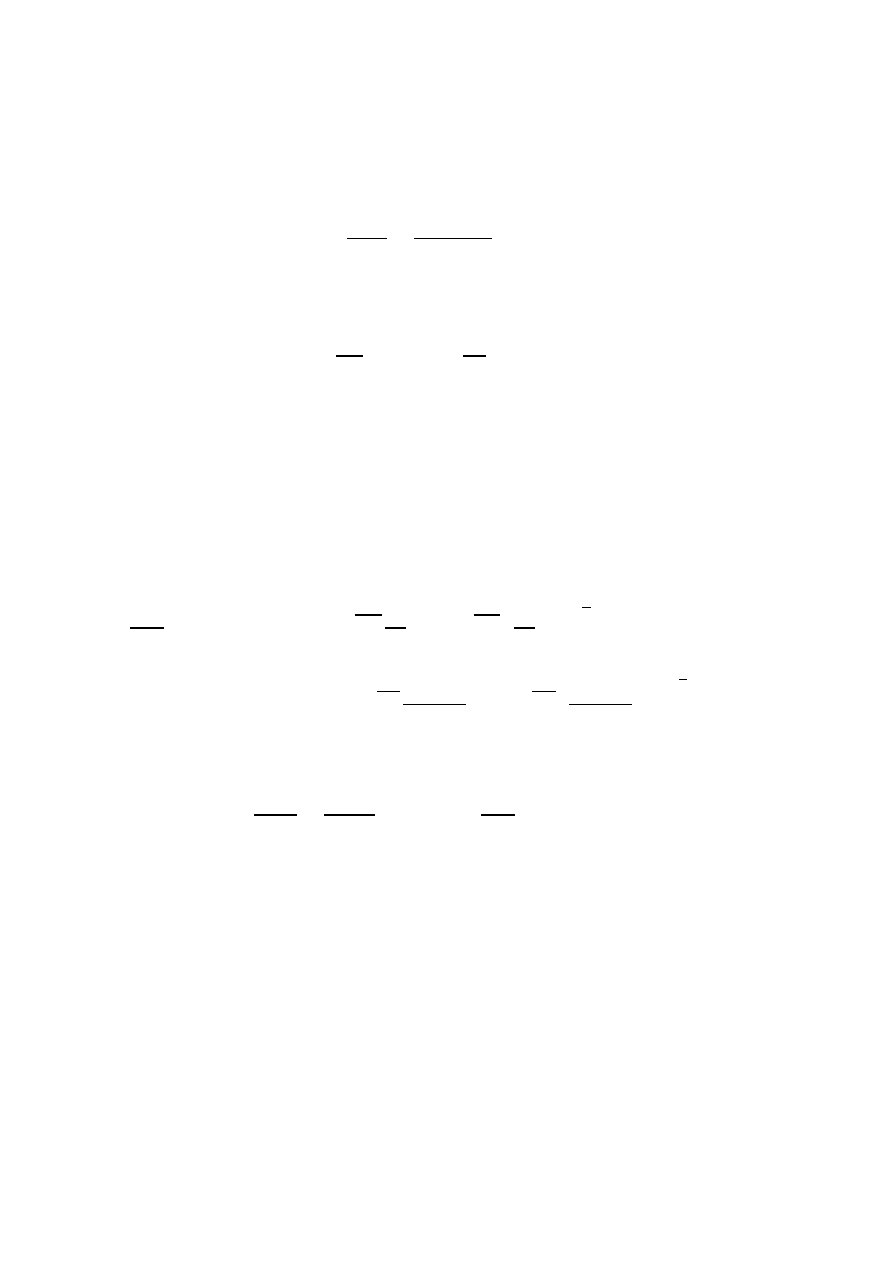
Przęsło środkowe o rozpiętości efektywnej

l

eff2



1,60 m .

Stopień zbrojenia podłużnego w przęśle

Porównawczy stopień zbrojenia

Współczynnik zależny od schematu pracy elementu

K



1,5 .

Maksymalny wskaźnik ugięcia

Ugięcie w przęśle środkowym nie zostanie przekroczone.

Określenie wymaganych długości zakotwienia.

Podpora skrajna

Podstawowa długość zakotwienia prętów



8 .

Zgodnie z rysunkiem 8.2 PN-EN 1992-1-1 przyjęto dobre warunki przyczepności.

Graniczne naprężenie przyczepności



1



1,0

– dobre warunki przyczepności,



2



1,0 z uwagi na





32 mm .

f

bd



2,25



1



2

f

ctd



2,25



1,0



1,0



1,28



2,89 MPa

Obliczeniowa długość zakotwienia

Współczynniki:



1



1,0 ,



3



1,0 ,



4



0,7 ,



5



1,0 ,

Przyjęto :

Długość zakładu prętów zbrojenia

Założono, że w jednym przekroju będzie łączonych co najmniej 50% prętów, co daje



6



1,5 .

Obliczeniowa długość zakładu

Przyjęto :

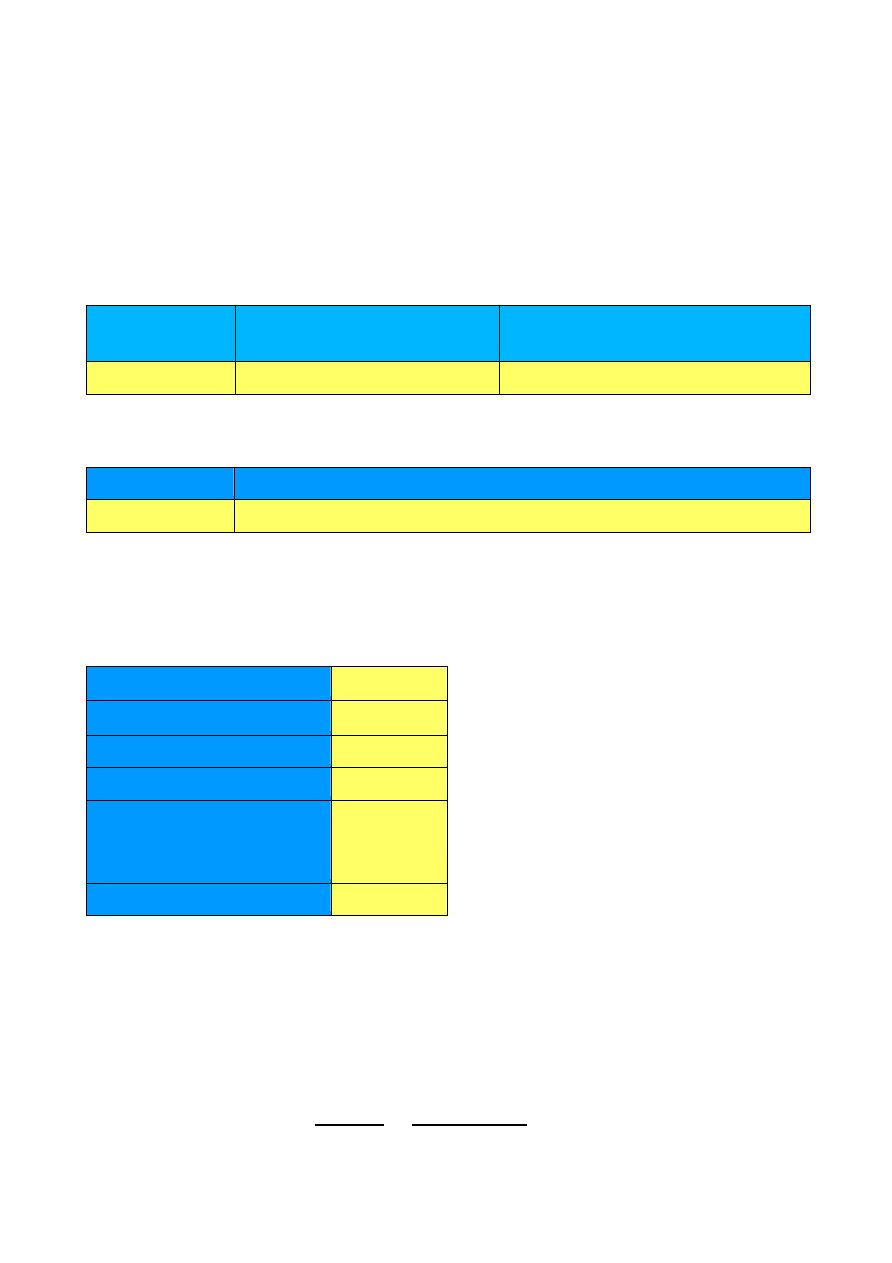
Poz. 2 Żebro

Zestawienie momentów zginających do wymiarowania:

Miejsce

Maksymalny moment

zginający [kNm]

Minimalny moment zginający

[kNm]

Przęsło AB

72,3

1,38

Zestawienie sił poprzecznych do wymiarowania:

Miejsce

Siła poprzeczna [kN]

Podpora A

62

Wymiarowanie przekroju przęsła AB

Przyjęto przekrój teowy z uwagi na to, że płyta znajduje się w strefie ściskanej.

Dane:

Moment zginający M

Ed

72,3 kNm

Szerokość przekroju: b

w

25,0 cm

Wysokość przekroju: h

40,0 cm

Wysokość użyteczna d

35,8 cm

Odległość zbrojenia

rozciąganego od krawędzi

a

1

4,2 cm

Grubość płyty

h

f

10,0 cm

Ustalenie szerokości współpracującej płyty

Odległość między miejscami zerowymi momentów zginających

L

0



L

eff



5,68 m .

Rozstaw żeber b

0



160,0 cm

b

eff ,1



0,2 b

1



0,1 l

0



0,2





0,1



538,0



67,3 cm



0,2 l

0



0,2



538



107,6 cm

b

eff



b

w



2 b

eff ,1



25,0



2



7,3



159,6 cm



b

0



160,0 cm

Przyjęto; b

eff



160,0 cm

Położenie osi obojętnej

Względna wysokość płyty

Maksymalny moment jaki przenosi płyta:

Przekrój jest pozornie teowy. Wymiaruje się zbrojenie w przekroju prostokątnym

Przekrój pojedynczo zbrojony.

Minimalne pola przekroju zbrojenia

z uwagi na zginanie

z uwagi na zarysowanie

Przyjęto:

w

lim



0,4 mm

k

c



0,4

– zginanie,

k



1,0

– odkształcenia wymuszone czynnikami zewnętrznymi,



s , lim



280 MPa

– ograniczenie naprężeń przy w

lim



0,4 i prętach



16 .

Maksymalne pole przekoju zbrojenia

Przyjęto zbrojenie:

dołem: 4



16 o polu A

s1 , prov



8,04 cm

2

górą zbrojenie montażowe: 2



12 o polu A

s



2,26 cm

2

Rozmieszczenie prętów w przekroju poprzecznym

s

1



max



; 20 mm ; d

g



5mm



max



16 mm ; 20 mm; 16



5



21 mm



21 mm

Minimalna szerokość środnika belki pozwalająca rozmieścić zbrojenie w

jednej warstwie

b

w , min



2 c

nom



2



s



4





3 s

1



2



26



2



8



4



16



3



21



195 mm



b

w



200 mm

Przyjęte zbrojenie można rozmieścić w jednej warstwie.

2

Sprawdzenie nośności przekroju w przęśle

Wysokość strefy ściskanej

Oś obojętna w półce – przekrój pozornie teowy.

Warunek nośności

Warunek nośności został spełniony.

Sprawdzenie ścinania – podpora A
Siła poprzeczna na podporze: V

Ed



62,0 kN .

Zbrojenie podłużne w strefie podporowej powinno być nie mniejsze niż

0,25 A

s1



0,25



8,04



2,01 cm .

Przyjęto doprowadzenie do podpory wszystkich prętów niezbędnych do przejęcia

momentu przęsłowego.

Warunek dotyczący zbrojenia podłużnego w strefie podporowej jest zatem spełniony.
Pole zbrojenia w strefie podporowej wyniesie:

A

s



8,04 cm

2

.

Stopień zbrojenia podłużnego w okolicy podpory.



cp



0 MPa

– brak siły podłużnej

W analizowanym przypadku: V

Ed



62,0 kN



V

Rd , c



45,8 kN .Wymagane jest

zaprojektowanie zbrojenia na ścinanie.

Przyjęto zbrojenie strzemionami pionowymi dwuciętymi



8 ze stali B500SP.

Pole przekroju strzemiona dwuciętego:

Z uwagi na oparcie żebra na podciągu (oparcie pośrednie) zbrojenie poprzeczne

oblicza się na maksymalna siłę poprzeczną (w osi podpory).

Długość odcinka II-go rodzaju (mierzona od krawędzi podparcia na podciągu lub

ścianie)

Z obliczeń statycznych (SOLDIS) odczytano, że w odległości l

c



0,80 m od osi

podparcia siła poprzeczna wynosi V

c , ED



45,8 kN .

l

t



l

c

– 0,5 b

p



0,80 – 0,5



36



0,62 m

Sprawdzenie nośności przekroju betonowego na ścinanie

Współczynnik redukcji wytrzymałości beton zarysowanego przy ścinaniu

Warunek nośności

Warunek nośności jest zachowany.

Wysokość strefy ścinanej

z



0,9 d



0,9



0,358



0,322 m

Cotangens kąta pochylenia krzyżulców betonowych

Podział odcinka drugiego rodzaju na pododcinki.

Maksymalna siła poprzeczna na drugim pododcinku (z obliczeń statycznych)

V

Ed



34,0 kN .

Maksymalny rozstaw strzemion na drugim pododcinku.

Przyjęto:

na pierwszym pododcniku: strzemiona dwucięte



8

co

s



15 cm ,

na drugim pododcinku: strzemiona dwucięte



8co

s



20cm .

Na pozostałej części belki: strzemiona



8 co s



20 cm .

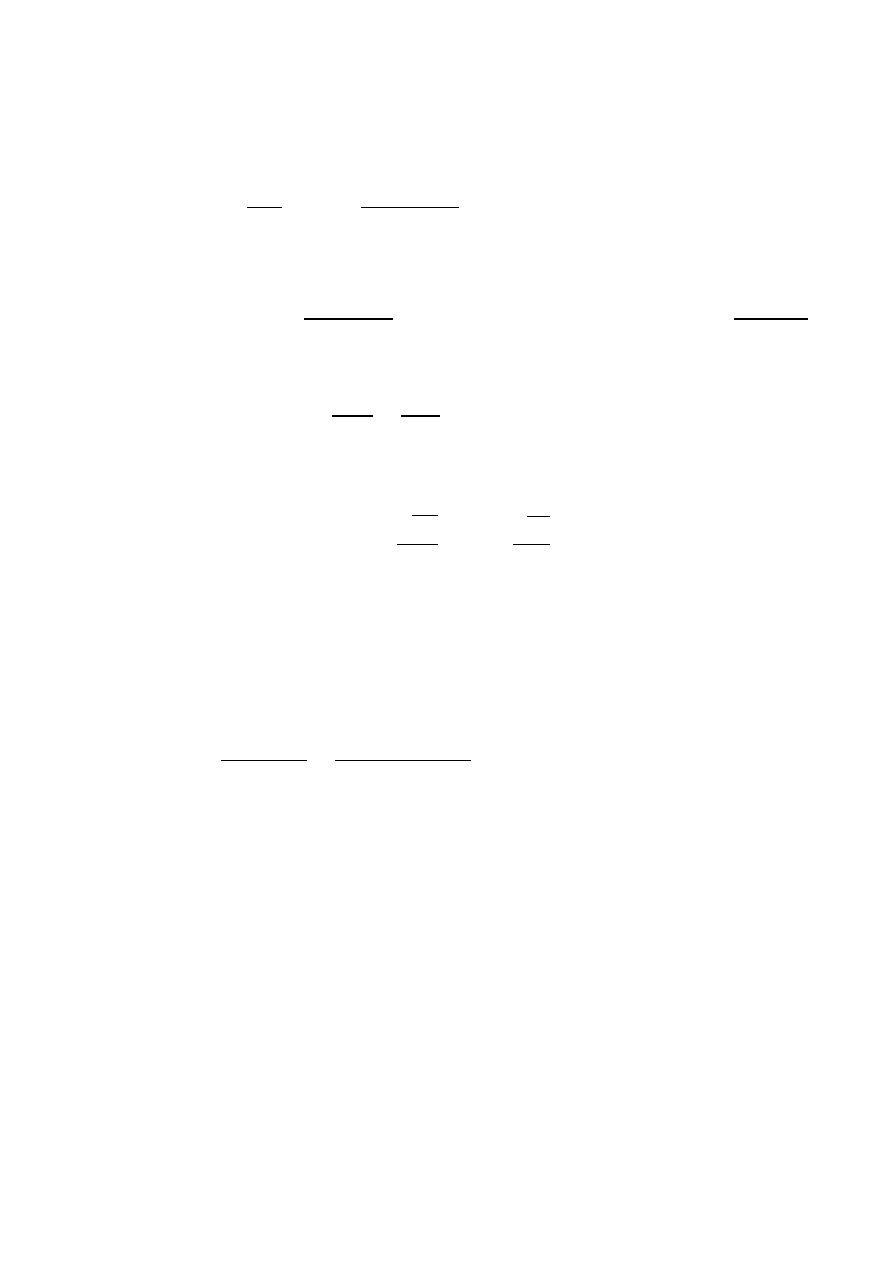
Nośność na ścinanie na pierwszym pododcinku

Minimalny stopień zbrojenia poprzecznego

Stopień zbrojenia poprzecznego

na pierwszym pododcinku

Maksymalne rozstawy z uwagi na bezpieczne przeniesienie sił

wewnętrznych bez nadmiernych odkształceń

s

l , max



0,75 d



0,75



0,306



0,23 m

Przyjęte rozstawy nie przekraczają wartości maksymalnej.

Sprawdzenie nośności zbrojenia podłużnego w strefie podporowej (odcinek

drugiego rodzaju)

Pole przekroju zbrojenia podłużnego w strefie podporowej

A

s1



8,04 cm

2

.

Moment zginający w odległości 0,86 m od osi podparcia (koniec długości odcinka

drugiego rodzaju) – odczytany z programu

M

Ed



36,1 kNm

Sila rozciągająca w zbrojeniu od momentu zginającego

Dodatkowa siła rozciągająca wywołana przez siły poprzeczne

Całkowita siła rozciągająca w zbrojeniu

Nośność zbrojenia na rozciąganie

Warunek nośności

Warunek nośności jest zachowany.

Sprawdzenie ścinania między półką a środnikiem belki

Określenie rozpatrywanej długości

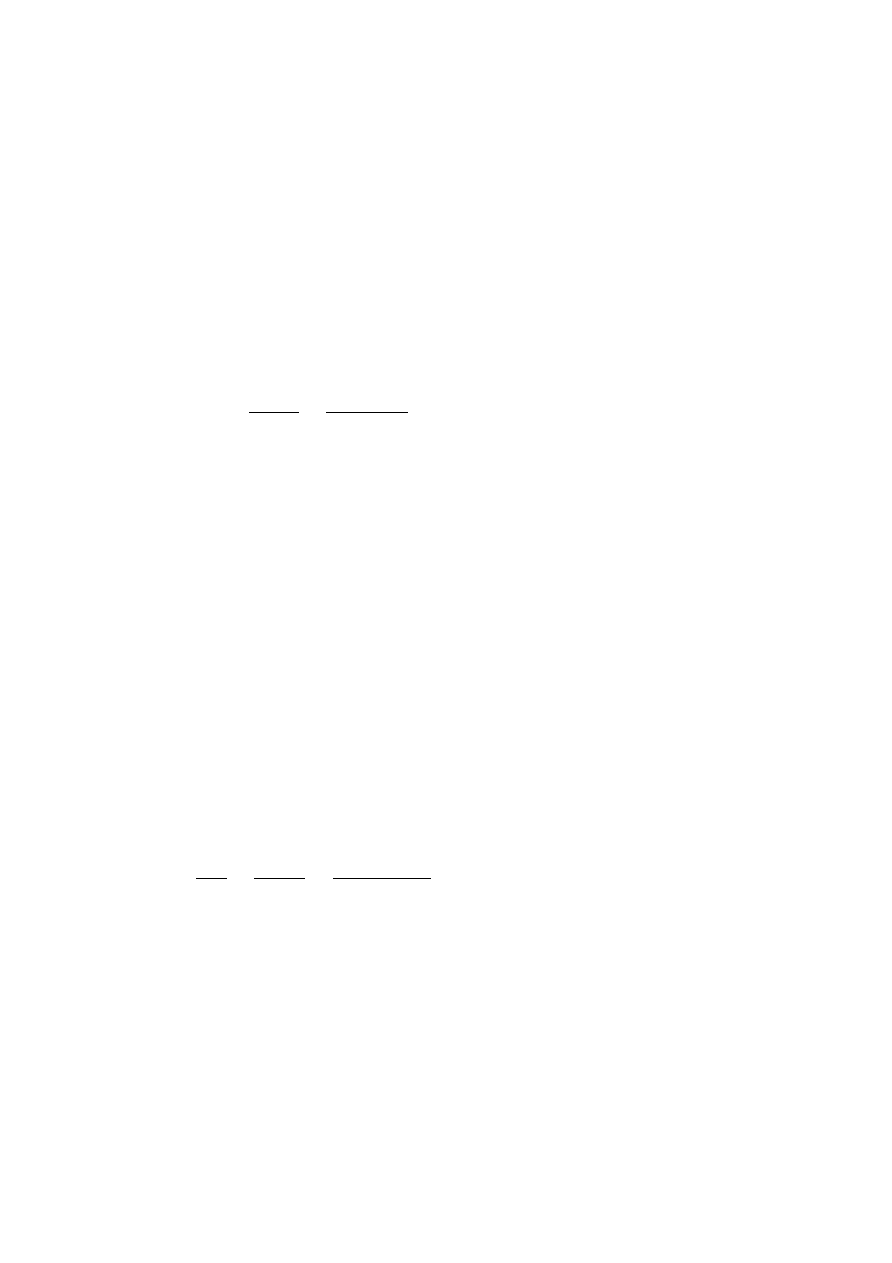
Zmiana siły normalnej w półce na rozpatrywanej długości

Podpora: M

Ed



0 kNm ,



eff



0 , F

Ed ,0



0 kN

Naprężenie styczne w płaszczyźnie styku między jedną stroną półki i środnikiem

Ścinaniu między półką a środnikiem przeciwdziała zbrojenie podporowe płyty

w postaci prętów



8 co

15 cm

.

Zgodnie z PN-EN 1992-1-1, w przypadku gdy

v

Ed



0,696 MPa



k f

ctd



0,4



1,28



0,512 MPa ,

zbrojenie A

sf

powinno być większe niż suma zbrojenia wymaganego zginaniem

płyty i połowy zbrojenia z uwagi na podłużne ścinanie między półką a środnikiem.

Wymagane zbrojenie z uwagi na zginanie płyty wynosi 0,95 cm

2

.

Zbrojenie z uwagi na ścinanie

Przyjęto kąt pochylenia betonowych krzyżulców



f



45

0

.

Sumaryczne zbrojenie: 0,95



1,55



2,40 cm

2



3,35 cm

2

Przyjęte w płycie zbrojenie jest wystarczające.
Sprawdzenie nośnosci betonowych krzyżulców

Warunek nośności jest zachowany.

Sprawdzenie stanu granicznego użytkowalności

Rozkład momentów zginających od prawie stałej kombinacji obciążeń

charakterystycznych

Maksymalny moment zginajacy M

k , Ed



50,3 kNm .

Końcowy współczynnik pełzania.

Przyjęto:





, t

0



3,0

Efektywny moduł sprężystości betonu

Relacja modułów sprężystości betonu i stali (dla obciążeń długotrwałych)

Charakterystyka geometryczna przekroju niezarysowanego (faza I)

Moment rysujący

Sprawdzenie czy belka ulega zarysowaniu.

M

k , Ed



50,3 kNm



M

cr



26,13 kNm

Belka ulega zarysowaniu.

Charakterystyka geometryczna przekroju zarysowanego (faza II)

Moment statyczny półki względem jej dolnej krawędzi

Moment statyczny zastępczego przekoju zbrojenia względem dolnej krawędzi półki

Z uwagi na to, że S

f



8000 cm

3



S



5354 cm

3

, oś obojętna znajduje się w półce

i przekrój jest pozornie teowy.

Równanie momentów statycznych

Z rozwiązania powyższego równania otrzymano

Sprawdzenie warunków ugięcia

Ugięcie elementu niezarysowanego

Ugięcie elementu zarysowanego

Ugięcie elementu zarysowanego uwzględniające współpracę betonu pomiędzy rysami

a

max



a

II





a

I



1







11,7



0,87



7,53



1 – 0,87



11,2 mm

Warunek ugięcia

Warunek ugięcia jest zachowany.

Sprawdzenie szerokości rozwarcia rys

Efektywne pole betonu rozciąganego

Efektywny stopień zbrojenia

Współczynniki:
k

1



0,8 ,

k

2



0,5 ,

k

3



3,4 ,

k

4



0,425

Maksymalny rozstaw rys

Naprężenie w zbrojeniu od momentu M

k , Ed

(dla fazy II)

k

t



0,4 dla obciążeń długotrwałych

Szerokość rysy

Warunek zarysowania.

Warunek jest spełniony.

Wymagane długości zakotwienia prętów

Podpora:

Podstawowa długość zakotwienia prętów



16 .

Zgodnie z rysunkiem 8.2 PN-EN 1992-1-1 przyjęto dobre warunki przyczepności.

Graniczne naprężenie przyczepności



1



1,0

– dobre warunki przyczepności,



2



1,0 z uwagi na





32 mm .

f

bd



2,25



1



2

f

ctd



2,25



1,0



1,0



1,28



2,88 MPa

Obliczeniowa długość zakotwienia
Współczynniki:



1



1,0 ,



3



1,0 ,



4



0,7 ,



5



1,0

Przyjęto :

Zestawienie zbrojenia podłużnego żebra (z uwagi na zginanie)

L.p

Miejsce

Przyjęte zbrojenie główne

Przyjęte zbrojenie

montażowe

1

Podpora A

Dołem:

4

16 ,

As prov



8,04 cm

2

Górą:

2

Φ 12

,

2

Przęsło AB

Dołem:

4

16 ,

As prov



8,04 cm

2

Górą:

2

Φ 12

Poz.3. Podciąg

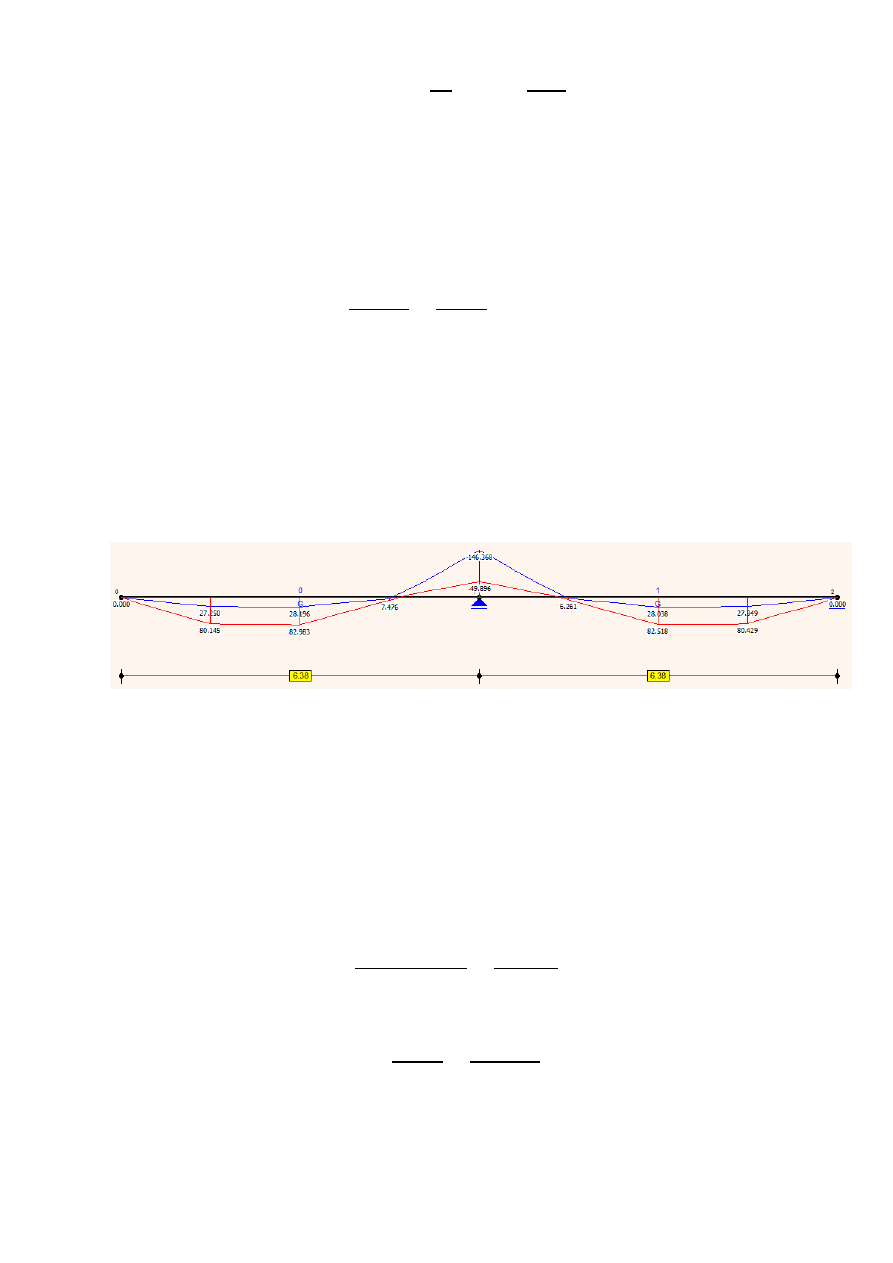
Zestawienie momentów zginających do wymiarowania:

Miejsce

Maksymalny moment

zginający [kNm]

Minimalny moment zginający

[kNm]

Podpora A

0,00

0,00

Przęsło AB

140,0

4,0

33

Podpora B

-187,0

-51,8

Zestawienie sił poprzecznych do wymiarowania:

Miejsce

Siła poprzeczna [kN]

Podpora A

59,0

Podpora B

139,2 – z lewej strony

139,2 – z prawej strony

Obliczenia zbrojenia przeprowadza się dla przekroju prostokątnego.

Wymiarowanie przekroju przęsła AB

Dane:

Moment zginający M

Ed

140,0 kNm

Szerokość przekroju: b

w

30,0 cm

Wysokość przekroju: h

50,0 cm

Wysokość użyteczna d

45,1 cm

Odległość zbrojenia

rozciąganego od krawędzi

a

1

4,9 cm

Grubość płyty

h

f

10,0 cm

ζ =1 – 0,5 ξ

eff

=1 – 0,5 ⋅ 0,122 =0,939

Minimalne pola przekroju zbrojenia

z uwagi na zginanie

z uwagi na zarysowanie

Przyjęto:

w

lim

=0,4 mm

k

c

=0,4 – zginanie,

k =1,0

– odkształcenia wymuszone czynnikami zewnętrznymi,

σ

s , lim

=240 MPa – ograniczenie naprężeń przy w

lim

=0,4 i prętach

ϕ

20.

Maksymalne pole przekoju zbrojenia

2

Przyjęto zbrojenie:

dołem:

3 ϕ 20 o polu A

s1 , prov

=9,43 cm

2

górą: zbrojenie montażowe: 2 ϕ 12 o polu A

s

=2,26 cm

Rozmieszczenie prętów w przekroju poprzecznym

s

1

=max (

ϕ

; 20 mm ; d

g

+5mm)=max ( 20 mm ; 20 mm; 16 +5=21 mm)=21 mm

Minimalna szerokość środnika belki pozwalająca rozmieścić zbrojenie w jednej

warstwie

b

w , min

=2 c

nom

+2

ϕ

s

+3

ϕ

+2 s

1

=2⋅29 +2⋅8 +3⋅20 + 2⋅21=176 mm<b

w

=300 mm

Przyjęte zbrojenie można rozmieścić w jednej warstwie.

Sprawdzenie nośności przekroju w przęśle

Wysokość strefy ściskanej

Warunek nośności

Warunek nośności został spełniony.

2

Wymiarowanie przekroju podporowego B – przekrój na krawędzi słupa 30x30 cm

Moment zginający M

Ed

187,0 kNm

Szerokość przekroju: b

w

30,0 cm

Wysokość przekroju: h

50,0 cm

Wysokość użyteczna d

43,2cm

Odległość zbrojenia

rozciąganego od krawędzi

a

1

6,8 cm

Przyjęto zbrojenie:

górą (rozciągane) 5

ϕ

20 o polu A

s1 , prov

=15,71 cm

2

dołem: montażowe 2

ϕ

12 A

s

=2,26 cm

Rozmieszczenie prętów w przekroju poprzecznym

s

1

=max (

ϕ

; 20 mm ; d

g

+5mm)=max ( 20 mm ; 20 mm 16 +5=21 mm)=21 mm

Minimalna szerokość środnika belki pozwalająca rozmieścić zbrojenie w jednej

warstwie

b

w , min

=2 c

nom

+2

ϕ

s

+5

ϕ

+4 s

1

=2⋅29 + 2⋅8 + 5⋅20 +4⋅21=258 mm<b

w

=300 mm

Przyjęte zbrojenie można rozmieścić w jednej warstwie.

2

Sprawdzenie nośności przekroju na podporze

Wysokość strefy ściskanej

Warunek nośności

Warunek nośności został spełniony.

Zbrojenie na ścinanie – podpora A

Maksymalna siła poprzeczna w osi podpory A

V

A , Ed

=59,0 kN

Zbrojenie podłużne w strefie podporowej powinno być nie mniejsze

0,25 A

s1

=0,25⋅9,43=2,36 cm

2

.

Przyjęto doprowadzenie do podpory wszystkich prętów niezbędnych do przejęcia
momentu przęsłowego.

Warunek dotyczący zbrojenia podłużnego w strefie podporowej jest zatem spełniony.

Pole zbrojenia w strefie podporowej wyniesie:

A

s

=9,43 cm

2

.

Stopień zbrojenia podłużnego w okolicy podpory.

σ

cp

=0 MPa – brak siły podłużnej

2

W analizowanym przypadku: V

Ed

=67,7 kN >V

Rd , c

=75,3 kN .

Nie jest wymagane projektowanie zbrojenia na ścinanie.

Zbrojenie na ścinanie – podpora B
Maksymalna siła poprzeczna w osi podpory B

V

A , Ed

=139,3 kN

Pole zbrojenia w strefie podporowej wynosi:

A

s

=15,71 cm .

Stopień zbrojenia podłużnego w okolicy podpory.



cp



0 MPa

– brak siły podłużnej

W analizowanym przypadku: V

Ed

=139,3 kN >V

Rd , c

=87,3 kN.Wymagane jest

zaprojektowanie zbrojenia na ścinanie.

Przyjęto zbrojenie strzemionami pionowymi dwuciętymi ϕ 8 ze stali B500SP.

Pole przekroju strzemiona dwuciętego:

Sprawdzenie nośności przekroju betonowego na ścinanie
Współczynnik redukcji wytrzymałości beton zarysowanego przy ścinaniu

Warunek nośności

Warunek nośności jest zachowany.

Wysokość strefy ścinanej

z



0,9 d



0,9



0,432



0,389 m

Długość odcinka, na którym wymagane jest zaprojektowanie zbrojenia na ścinanie.

Na podstawie rozkładu sił poprzecznych przyjęto długość odcinka

l

t

=1,60 m (odległość od osi podpory do pierwszej siły skupionej)

Cotangens kata pochylenia krzyżulców betonowych
Z uwagi na niewielkie zmiany siły poprzecznej i długość odcinka l

t

przyjęto

cot θ =2,0

.

Maksymalny rozstaw strzemion:

Przyjęto: strzemiona dwucięte ϕ 8 co s=20,0 cm .

Nośność na ścinanie:

Minimalny stopień zbrojenia poprzecznego

Stopień zbrojenia poprzecznego

Maksymalny rozstaw z uwagi na bezpieczne przeniesienie sił wewnętrznych bez

Nadmiernych odkształceń wynosi

s

l , max

=0,75 d =0,75 ⋅ 0,432 =0,32 m

Przyjęty rozstaw nie przekracza wartości maksymalnej.

2

Na pozostałej części przęsła podciągu siły poprzeczne nie przekraczają nośności

V

Rd , c

.

Na tych odcinkach przyjęto rozstaw strzemion ϕ 8 s=30,0 cm .

Sprawdzenie nośności zbrojenia podłużnego w strefie podporowej (odcinek

drugiego rodzaju) – podpora A

Pole przekroju zbrojenia podłużnego w strefie podporowej

A

s1

=9,43 cm .

Moment zginający w miejscu pierwszego żebra

M

Ed

=139,3 kNm

Sila rozciągająca w zbrojeniu od momentu zginającego

Dodatkowa siła rozciągająca wywołana przez siły poprzeczne

Całkowita siła rozciągająca w zbrojeniu

Nośność zbrojenia na rozciąganie

Warunek nośności

Warunek nośności jest zachowany.

2

Sprawdzenie nośności zbrojenia podłużnego w strefie podporowej (odcinek

drugiego rodzaju) – podpora B

Pole przekroju zbrojenia podłużnego w strefie podporowej

A

s1

=15,71 cm .

Moment zginający na krawędzi słupa (w odległosci 0,15 m od osi podpory)

M

Ed

=187,0 kNm

Sila rozciągająca w zbrojeniu od momentu zginającego

Dodatkowa siła rozciągająca wywołana przez siły poprzeczne

Całkowita siła rozciągająca w zbrojeniu

Nośność zbrojenia na rozciąganie

Warunek nośności

Warunek nośności jest zachowany.


Sprawdzenie ścinania w miejscu połączenia żebra z podciągiem

Przyjęto umieszczenie z obu stron żebra dwóch strzemion ϕ 8 w odległościach 20

mm pierwsze i 70 mm drugie, licząc od krawędzi żebra.

Sprawdzenie nośności strzemion

Obliczeniowa siła przekazana przez żebro

R

max

=1,35⋅16,0 +1,5⋅32,3 =70,0 kN

Nośność dodatkowych strzemion

Warunek nośności

Warunek nośności jest zachowany.

Sprawdzenie stanu granicznego użytkowalności

Rozkład momentów

zginających

od

prawie stałej

kombinacji obciążeń

charakterystycznych

Maksymalny moment zginajacy w przęśle

M

k , Ed

=83,0 kNm .

Maksymalny moment zginający na podporze M

kp , Ed

=146,4 kNm

Końcowy współczynnik pełzania.

Przyjęto:



(∞ , t

0

)=3,0

Efektywny moduł sprężystości betonu

Relacja modułów sprężystości betonu i stali (dla obciążeń długotrwałych)

Sprawdzenie zarysowania i ugięcia w przęśle

Charakterystyka geometryczna przekroju niezarysowanego (faza I)

Cechy określa się dla przekroju przęsłowego ze zbrojeniem rozciąganym

A

s1

=12,57 cm

2

.

Położenie osi obojętnej w przekroju pracującym w fazie I

Moment bezwładności przekroju sprowadzonego

Wskaźnik wytrzymałości przekroju sprowadzonego

Moment rysujący

Przekrój ulega zarysowaniu.

Cechy geometryczne przekroju zarysowanego (faza II)

Położenie osi obojętnej

Z rozwiązania równania kwadratowego postaci

otrzymano

x

II

=22,3 cm .

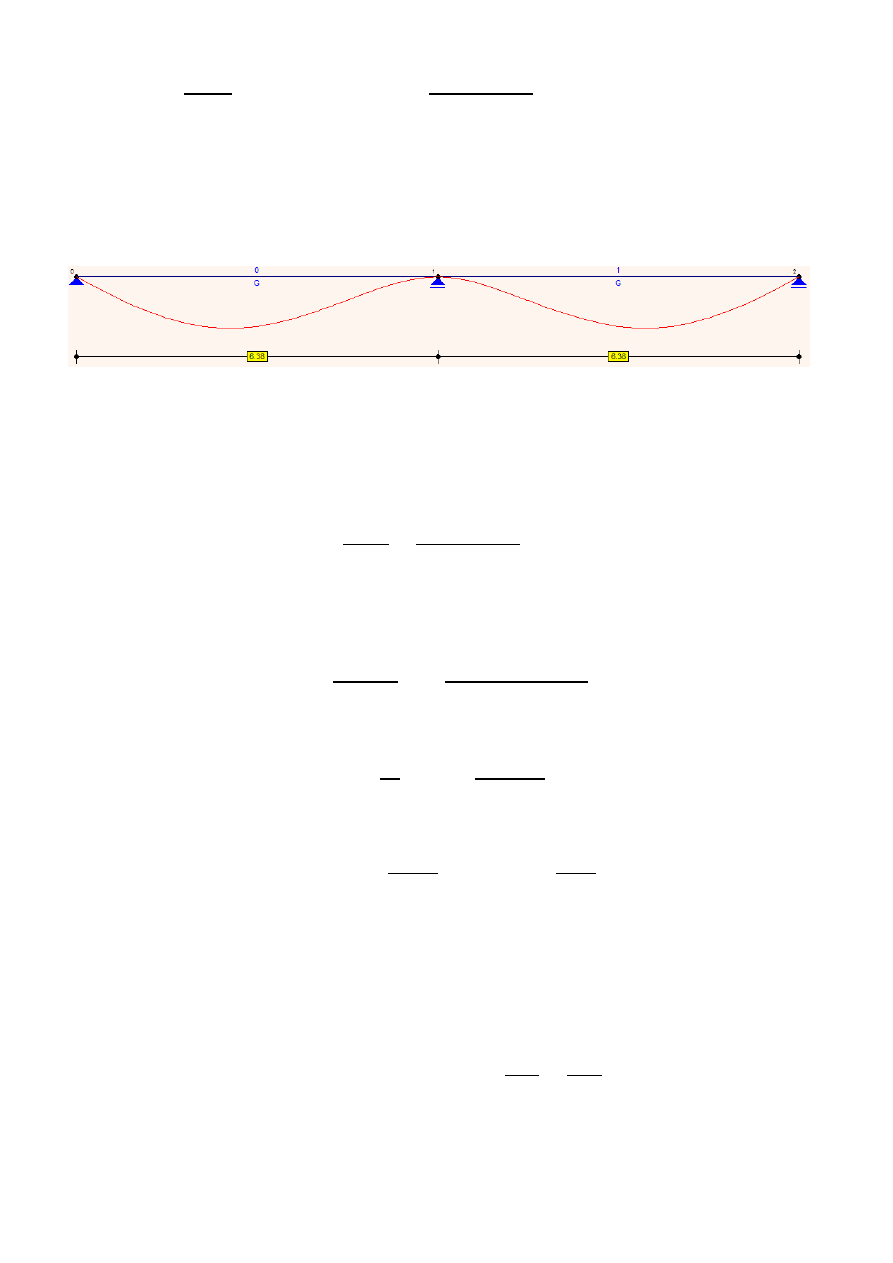
Sprawdzenie warunków ugięcia

Obwiednia ugięć uzyskana w programie obliczeniowym dla prawie stałej kombinacji

obciążeń charakterystycznych

Maksymalne ugięcie przęsła z programu a

0

=4 mm .

Moment bezwładności przekroju betonowego

Ugięcie elementu niezarysowanego

Ugięcie elementu zarysowanego

Ugięcie elementu zarysowanego uwzględniające współpracę betonu pomiędzy rysami

a

max



a

II





a

I



1







17,7



0,81



11,8



1 – 0,81



16,58 mm

Warunek ugięcia

Warunek ugięcia jest zachowany.

Efektywne pole betonu rozciąganego

Efektywny stopień zbrojenia

Współczynniki:

k

1



0,8 , k

2



0,5 ,

k

3



3,4 ,

k

4



0,425

Maksymalny rozstaw rys

Naprężenie w zbrojeniu od momentu M

k , Ed

(dla fazy II)

k

t



0,4 dla obciążeń długotrwałych

Szerokość rysy

Warunek jest spełniony.

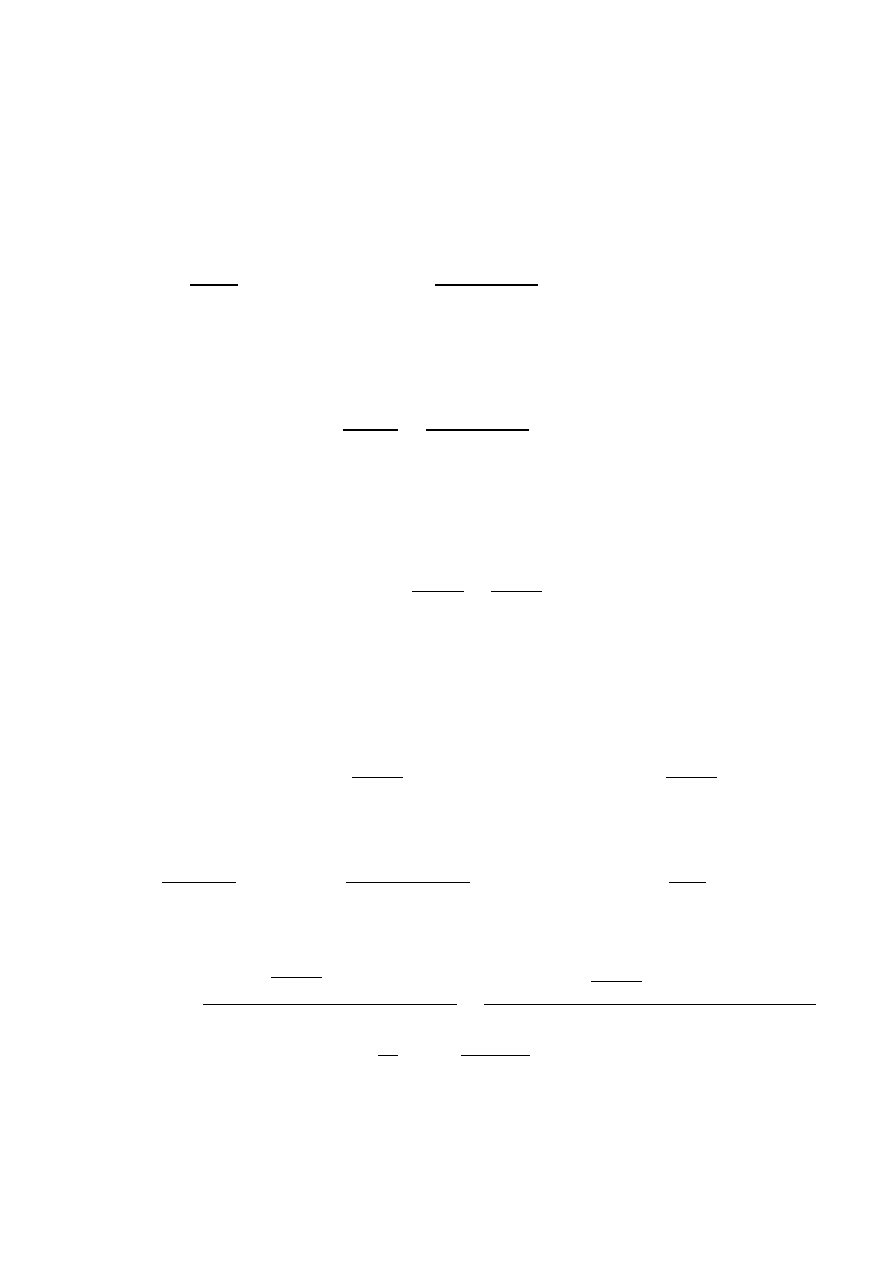
Sprawdzenie zarysowania nad podporą środkową

Cechy gemetryczne przekroju zarysowanego (faza II)

Położenie osi obojętnej

x

II

=22,3 cm

Efektywne pole betonu rozciąganego

Efektywny stopień zbrojenia

Współczynniki:

k

1

=0,8 , k

2

=0,5 , k

3

=3,4 , k

4

=0,425

Maksymalny rozstaw rys

Naprężenie w zbrojeniu od momentu M

k , Ed

(dla fazy II)

k

t



0,4 dla obciążeń długotrwałych

Szerokość rysy

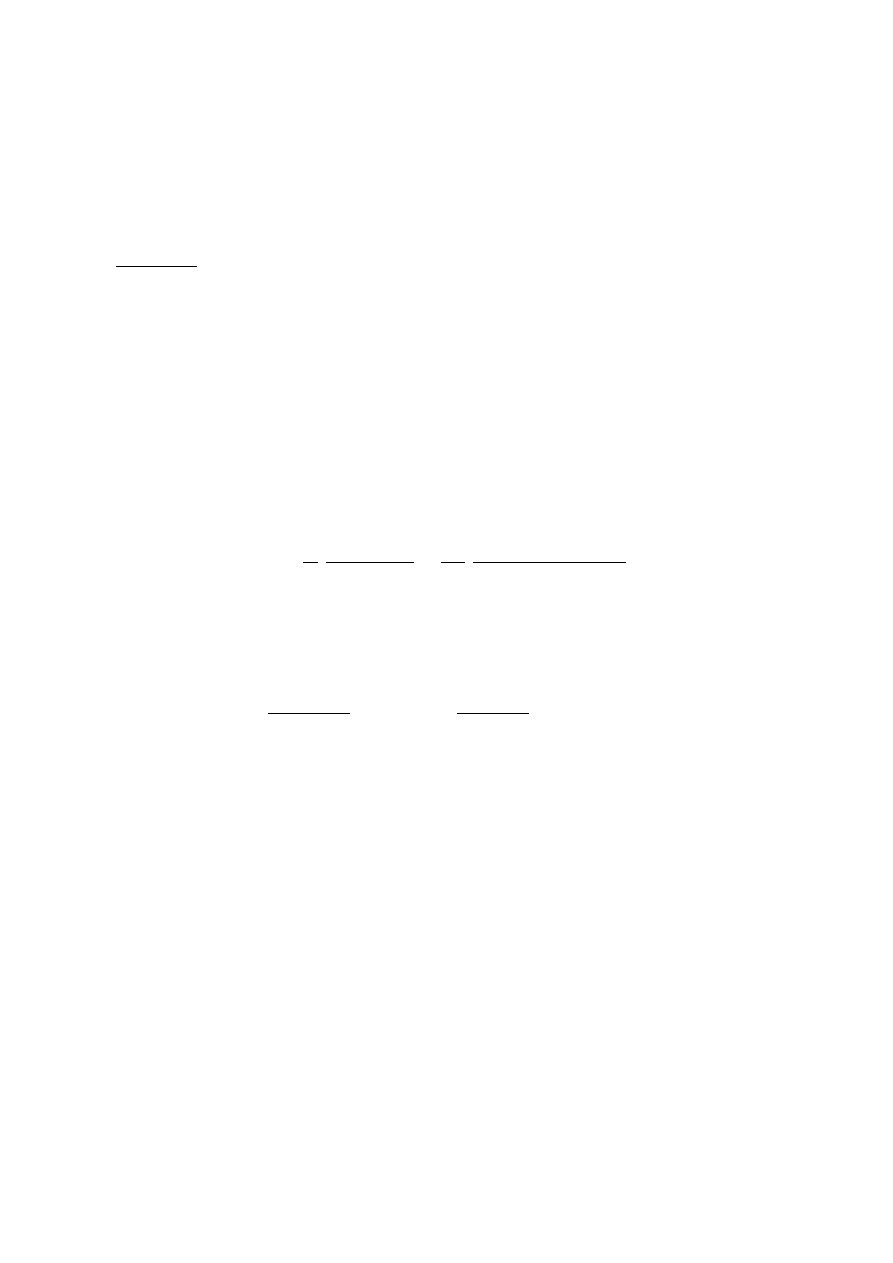
Warunek zarysowania

Warunek jest spełniony.

Wymagane długości zakotwienia prętów

Podpora:
Podstawowa długość zakotwienia prętów

ϕ

20 .

Zgodnie z rysunkiem 8.2 PN-EN 1992-1-1 przyjęto dobre warunki przyczepności.

Graniczne naprężenie przyczepności

η

1

=1,0 – dobre warunki przyczepności,

η

2

=1,0 z uwagi na ϕ <32 mm .

f

bd

=2,25 η

1

η

2

f

ctd

=2,25⋅1,0⋅1,0⋅1,28 =2,89 MPa

Obliczeniowa długość zakotwienia

Współczynniki:

α

1

=1,0 ,

α

3

=1,0 ,

α

4

=0,7 ,

α

5

=1,0

Przyjęto :