1

RJC

Alkiny

Alkiny

Alkiny

Hybrydyzacja

Hybrydyzacja

sp

sp

Uk

Uk

ł

ł

ady sprz

ady sprz

ęż

ęż

one

one

Alleny

Alleny

Nazewnictwo

Nazewnictwo

Slides 1 to 21

2

RJC

Alkiny

Alkiny

to

to

…

…

.

.

... klasa w

... klasa w

ę

ę

glowodor

glowodor

ó

ó

w, w kt

w, w kt

ó

ó

rej wyst

rej wyst

ę

ę

puje

puje

wi

wi

ą

ą

zanie potr

zanie potr

ó

ó

jne pomi

jne pomi

ę

ę

dzy atomami w

dzy atomami w

ę

ę

gla, a

gla, a

og

og

ó

ó

lny wz

lny wz

ó

ó

r sumaryczny daje si

r sumaryczny daje si

ę

ę

opisa

opisa

ć

ć

wzorem...

wzorem...

C

n

H

2n-2

3

RJC

Orbitale

Orbitale

zhybrydyzowane

zhybrydyzowane

sp

sp

Hybrydyzacja jednego

Hybrydyzacja jednego

orbitalu

orbitalu

s oraz jednego

s oraz jednego

orbitalu

orbitalu

p z pow

p z pow

ł

ł

oki walencyjnej atomu w

oki walencyjnej atomu w

ę

ę

gla,

gla,

prowadzi do utworzenia dw

prowadzi do utworzenia dw

ó

ó

ch orbitali

ch orbitali

sp

sp

; dwa

; dwa

orbitale p pozostaj

orbitale p pozostaj

ą

ą

niezhybrydyzowane

niezhybrydyzowane

.

.

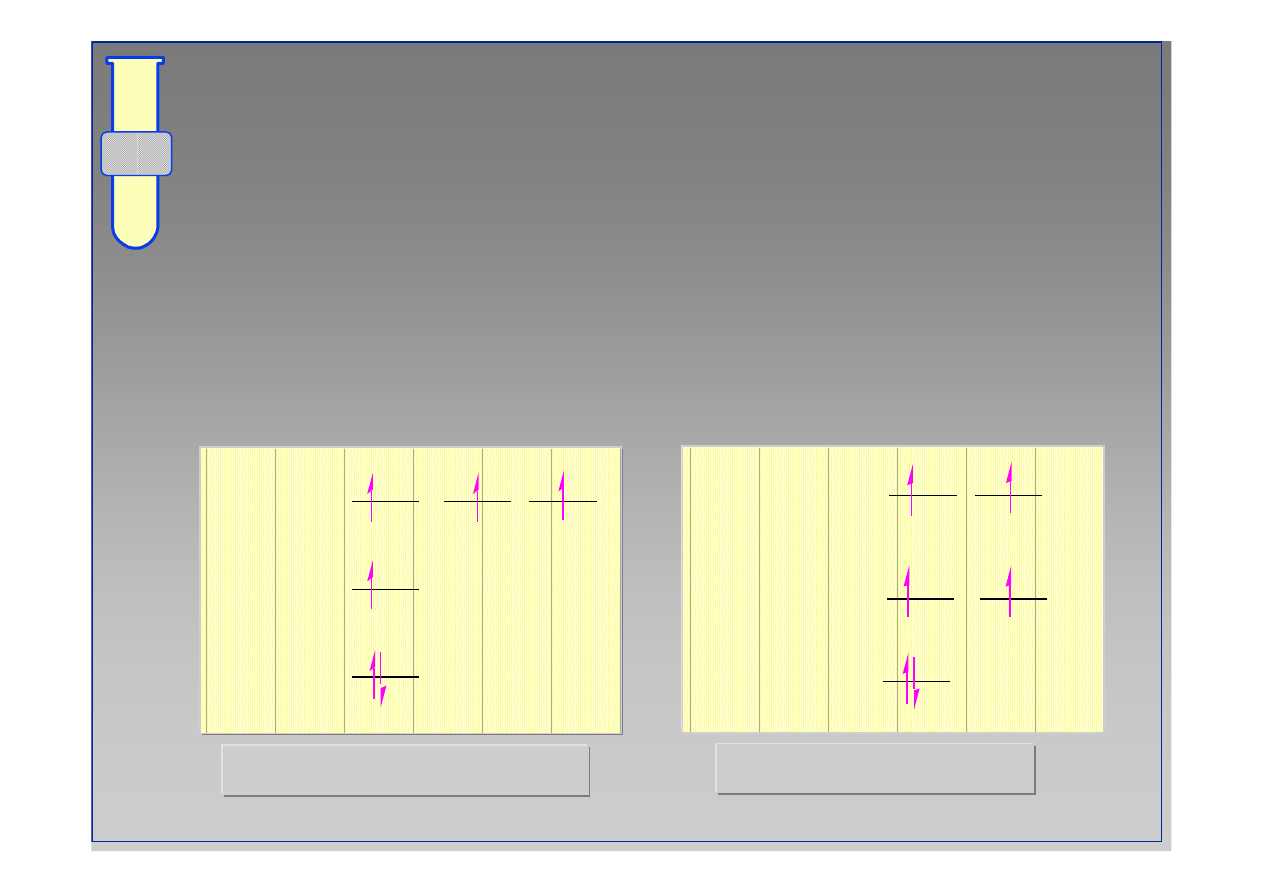
atom węgla

Stan wzbudzony

Stan wzbudzony

atom węgla

Stan po hybrydyzacji

Stan po hybrydyzacji

1s

2s

2p

1s

2sp

2p

4

RJC

Budowa Geometryczna

Budowa Geometryczna

Orbitalu

Orbitalu

sp

sp

Orbitale typu

Orbitale typu

sp

sp

posiadaj

posiadaj

ą

ą

geometri

geometri

ę

ę

liniow

liniow

ą

ą

(

(

dygonaln

dygonaln

ą

ą

).

).

sp

sp

sp

sp

p

p

p

p

5

RJC

Wi

Wi

ą

ą

zania

zania

Przenikanie dw

Przenikanie dw

ó

ó

ch orbitali

ch orbitali

sp

sp

prowadzi do

prowadzi do

utworzenia wi

utworzenia wi

ą

ą

zania

zania

σ

σ

...

...

...przenikanie dw

...przenikanie dw

ó

ó

ch pozosta

ch pozosta

ł

ł

ych,

ych,

niezhybrydyzowanych

niezhybrydyzowanych

orbitali p

orbitali p

stwarza

stwarza

mo

mo

ż

ż

liwo

liwo

ść

ść

utworzenia wi

utworzenia wi

ą

ą

za

za

ń

ń

π

π

.

.

6

RJC

Acetylen (C

Acetylen (C

2

2

H

H

2

2

)

)

Najprostszy

Najprostszy

alkin

alkin

, czyli acetylen, ulega spalaniu

, czyli acetylen, ulega spalaniu

wyzwalaj

wyzwalaj

ą

ą

c znaczn

c znaczn

ą

ą

nadwy

nadwy

ż

ż

k

k

ę

ę

energii. To

energii. To

powoduje,

powoduje,

ż

ż

e znajduje on wiele zastosowa

e znajduje on wiele zastosowa

ń

ń

praktycznych.

praktycznych.

H

H

7

RJC

Si

Si

ł

ł

a Wi

a Wi

ą

ą

zania... D

zania... D

ł

ł

ugo

ugo

ść

ść

Wi

Wi

ą

ą

zania

zania

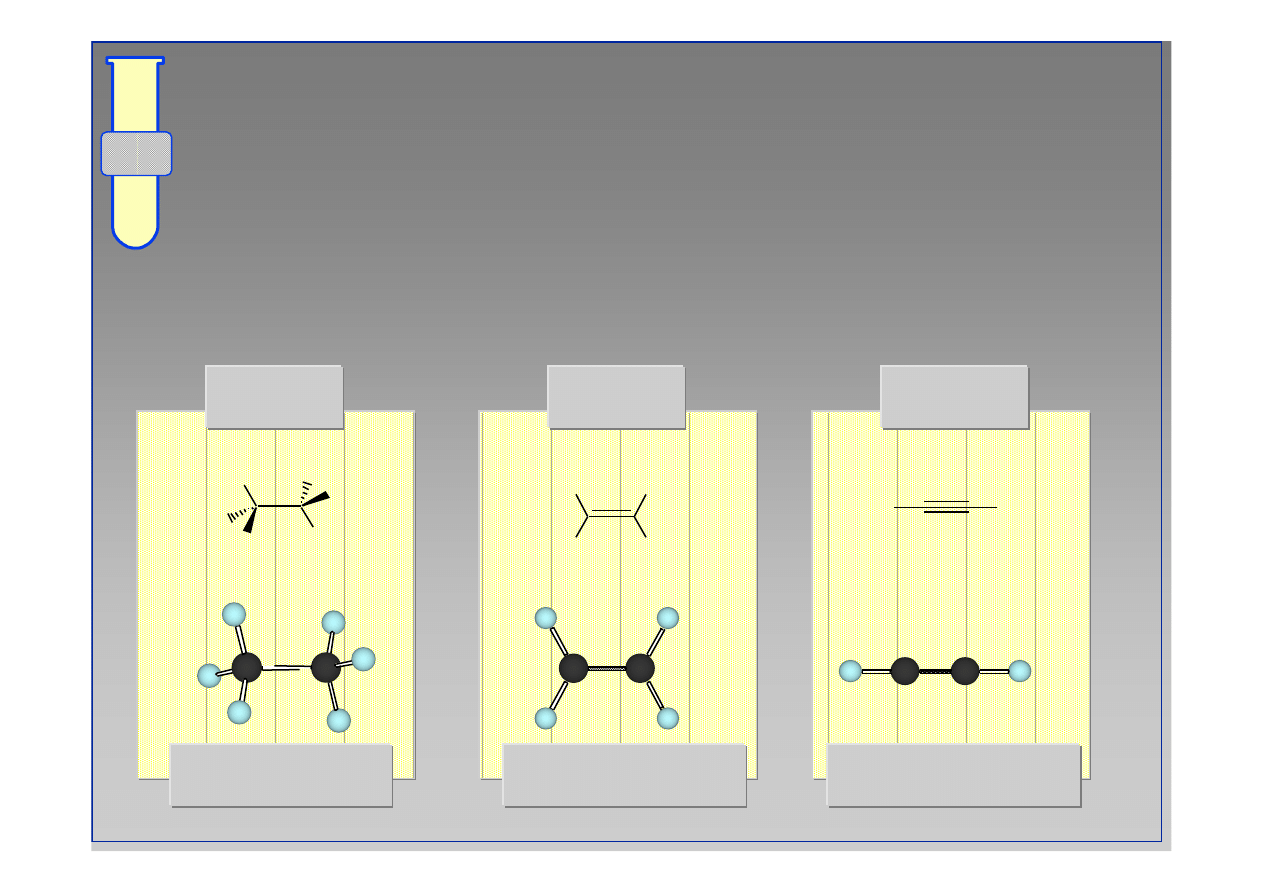
Im lepsze przenikanie orbitali, tym kr

Im lepsze przenikanie orbitali, tym kr

ó

ó

tsze, a tym

tsze, a tym

samym mocniejsze jest wi

samym mocniejsze jest wi

ą

ą

zanie kowalencyjne .

zanie kowalencyjne .

88 kcal/mol

1.54 Å

152 kcal/mol

1.33 Å

200 kcal/mol

1.20 Å

H

H

H

H

H

H

H

H

H

H

H

H

8

RJC

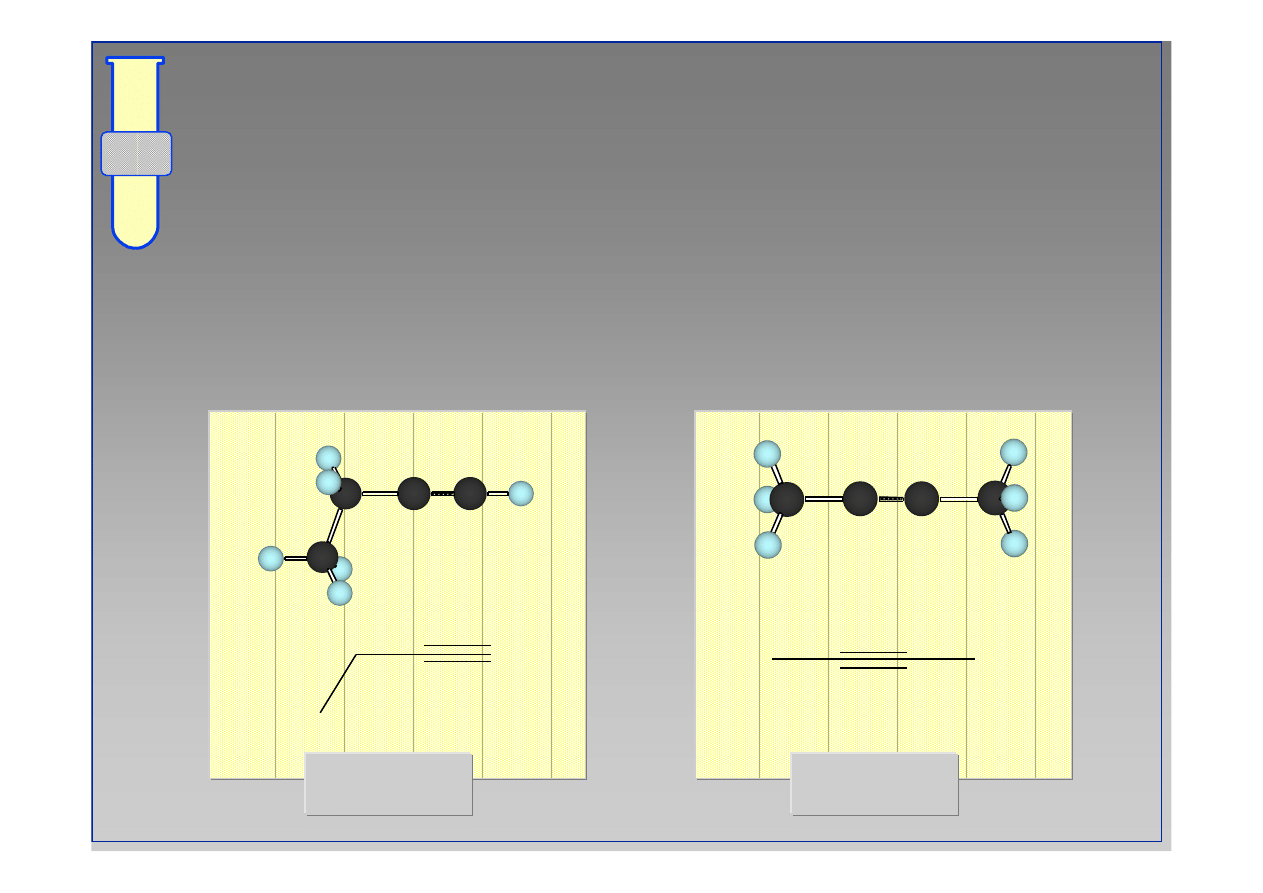
Izomery Strukturalne (Konstytucyjne)

Izomery Strukturalne (Konstytucyjne)

Podobnie do alkan

Podobnie do alkan

ó

ó

w oraz alken

w oraz alken

ó

ó

w,

w,

alkiny

alkiny

tworz

tworz

ą

ą

izomery strukturalne. W

izomery strukturalne. W

alkinach

alkinach

nie wyst

nie wyst

ę

ę

puje

puje

problem izomerii geometrycznej.

problem izomerii geometrycznej.

but-1-yn

but-2-yn

9

RJC

Nomenklatura IUPAC

Nomenklatura IUPAC

Zidentyfikuj macierzysty węglowodór.

Ponumeruj atomy węgla i przypisz wiązaniu
potrójnemu jak najniższy lokant.

Wskaż położenie wiązania potrójnego przez
podanie lokantu pierwszego węgla alkinowego.

10

RJC

Przyk

Przyk

ł

ł

ady ...

ady ...

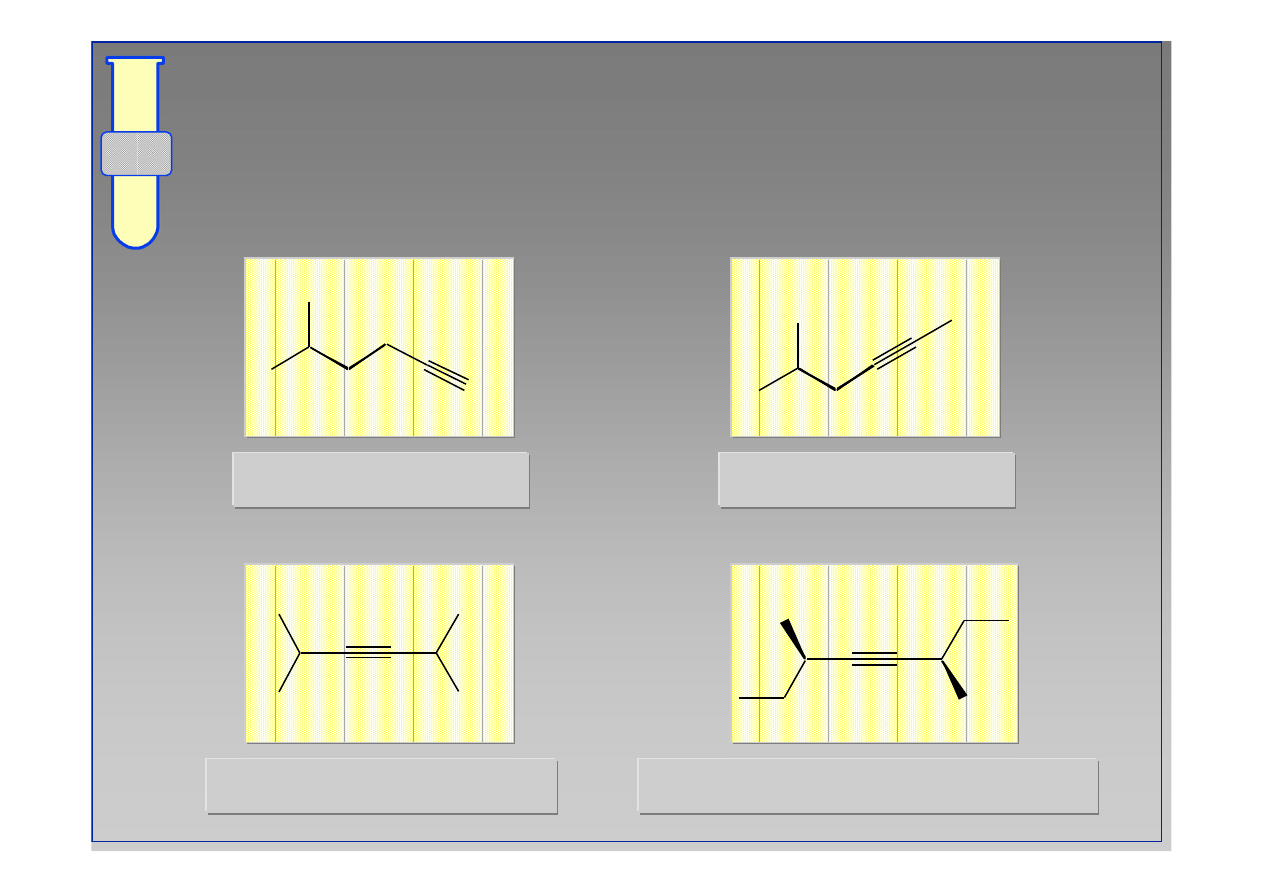
5-metyloheks-1-yn

5-metyloheks-2-yn

2,5-dimetyloheks-3-yn

(3R,6R)-3,6-dimetylookt-4-yn

11

RJC

Nomenklatura IUPAC

Nomenklatura IUPAC

Zwi

Zwi

ą

ą

zki z Wieloma Wi

zki z Wieloma Wi

ą

ą

zaniami

zaniami

Potr

Potr

ó

ó

jnymi

jnymi

-yn

dla jednego wiązania ≡

-diyn

dla dwóch wiązań

≡

-triyn

dla trzech wiązań

≡

12

RJC

Przyk

Przyk

ł

ł

ady ...

ady ...

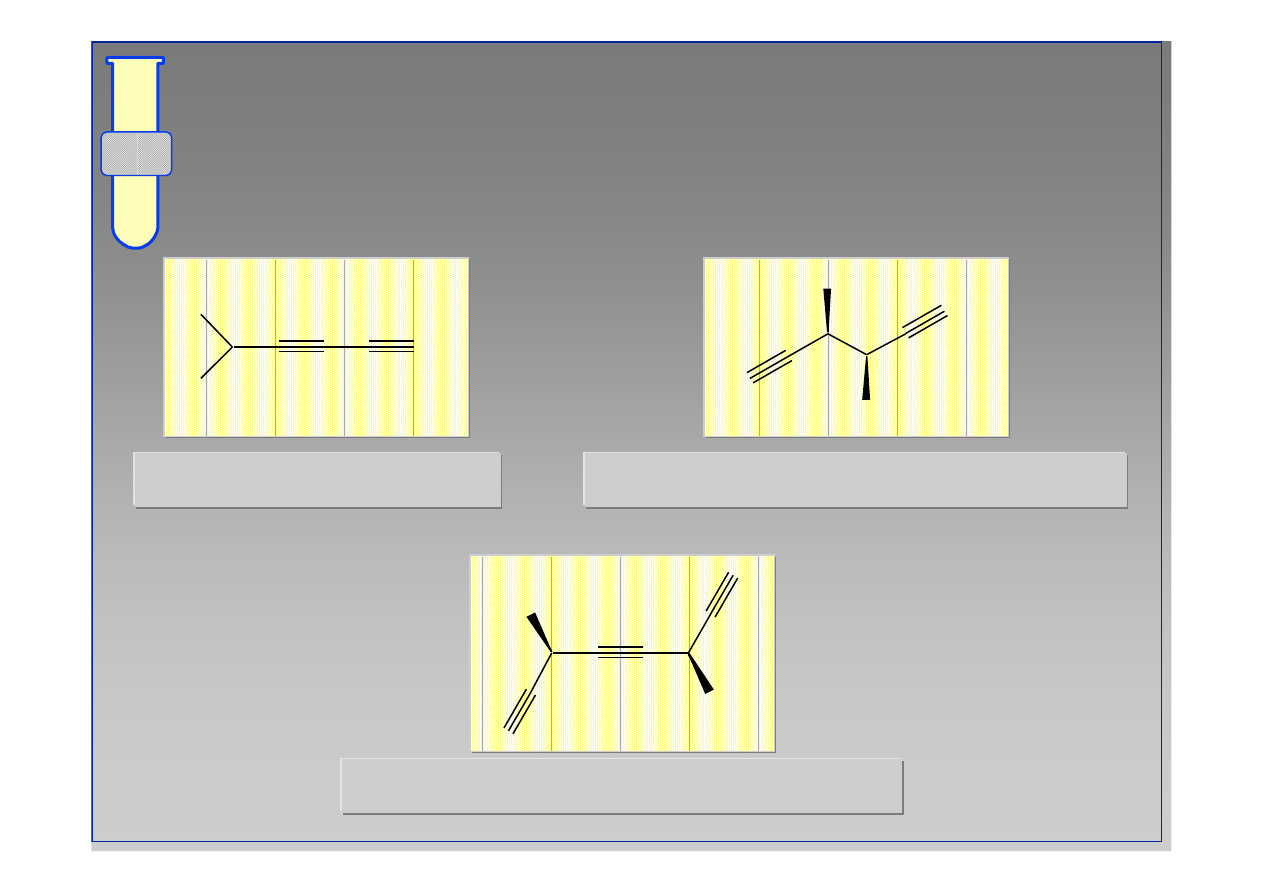
5-metyloheksa-1,3-

diyn

(3S,4S)-3,4-dimetyloheksa-1,5-

diyn

(3R,6R)-3,6-dimetylookta-1,4,7-

triyn

13

RJC

Nomenklatura IUPAC

Nomenklatura IUPAC

Wi

Wi

ą

ą

zania Podw

zania Podw

ó

ó

jne i Potr

jne i Potr

ó

ó

jne

jne

Związki, które zawierają jednocześnie wiązania
podwójne i potrójne otrzymują końcówkę .. -

enyn

.

Numeracja odbywa się od końca łańcucha, bliżej
wiązania wielokrotnego; jeżeli istnieje możliwość
wyboru, to wiązanie podwójne posiada pierwszeństwo
w przypisaniu lokantów.

14

RJC

Przyk

Przyk

ł

ł

ady...

ady...

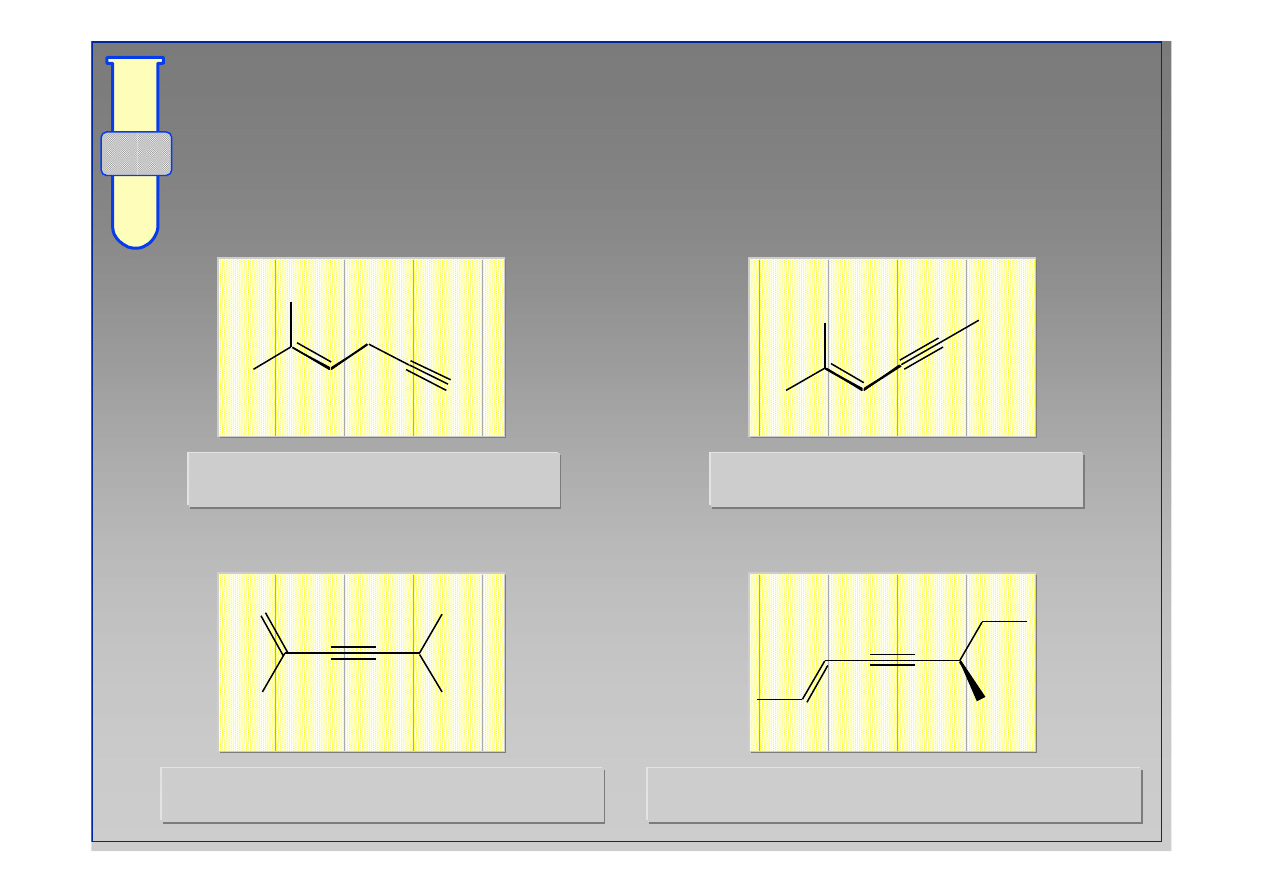
5-metyloheks-4-

en-1-yn

2-metylohex-2-

en-4-yne

2,5-dimetyloheks-1-

en-3-yne

(2E,6R)-6-metylookt-2-

en-4-yne

15

RJC

Nazewnictwo IUPAC; wi

Nazewnictwo IUPAC; wi

ą

ą

zania podw

zania podw

ó

ó

jne

jne

oraz potr

oraz potr

ó

ó

jne

jne

-dienyn

2 x podwójne + 1 x potrójne

-endiyn

1 x podwójne + 2 x potrójne

-dientriyn

2 x podwójne + 3 x potrójne

16

RJC

Na przyk

Na przyk

ł

ł

ad ...

ad ...

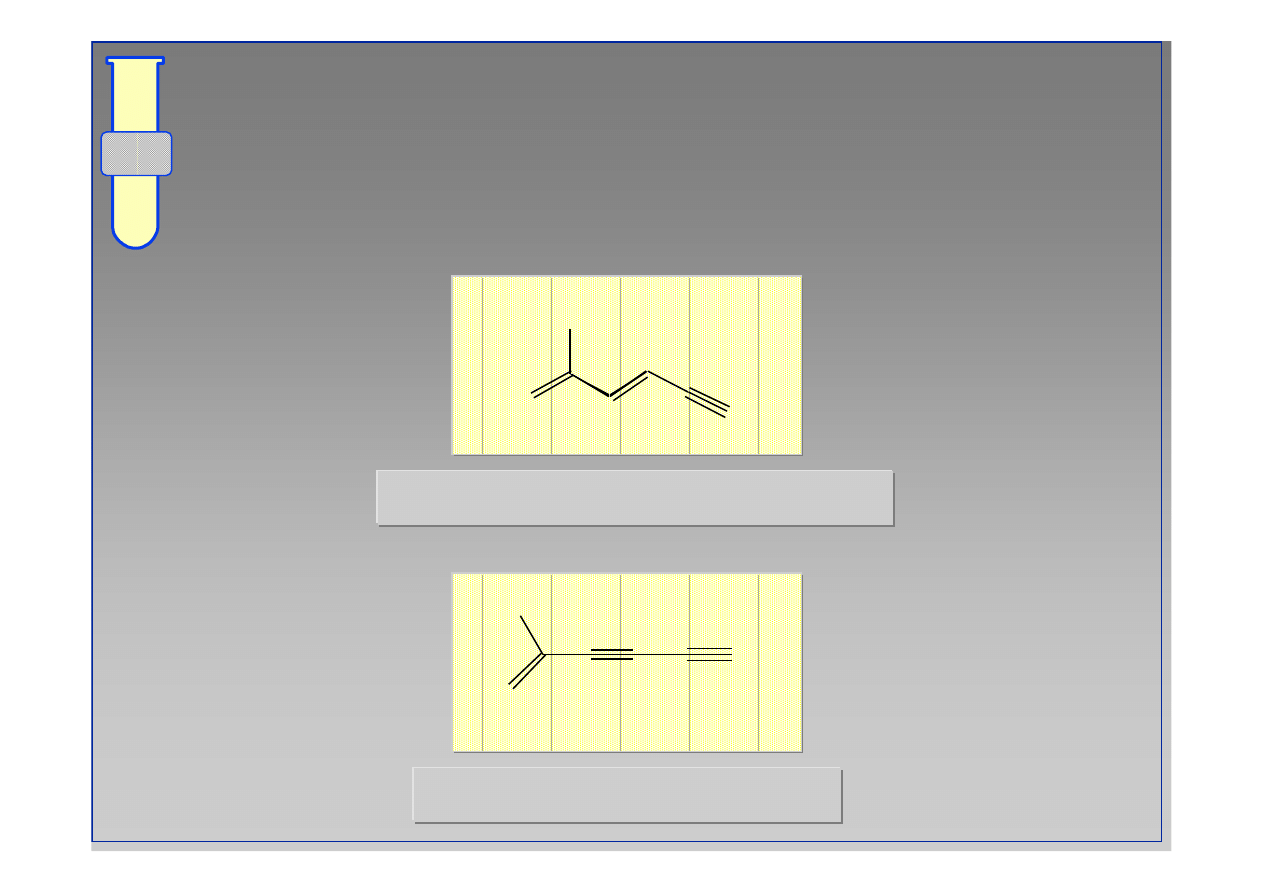
(E)-2-metyloheksa-1,3-

dien-5-yne

2-metylohex-1-

en-3,5-diyne

17

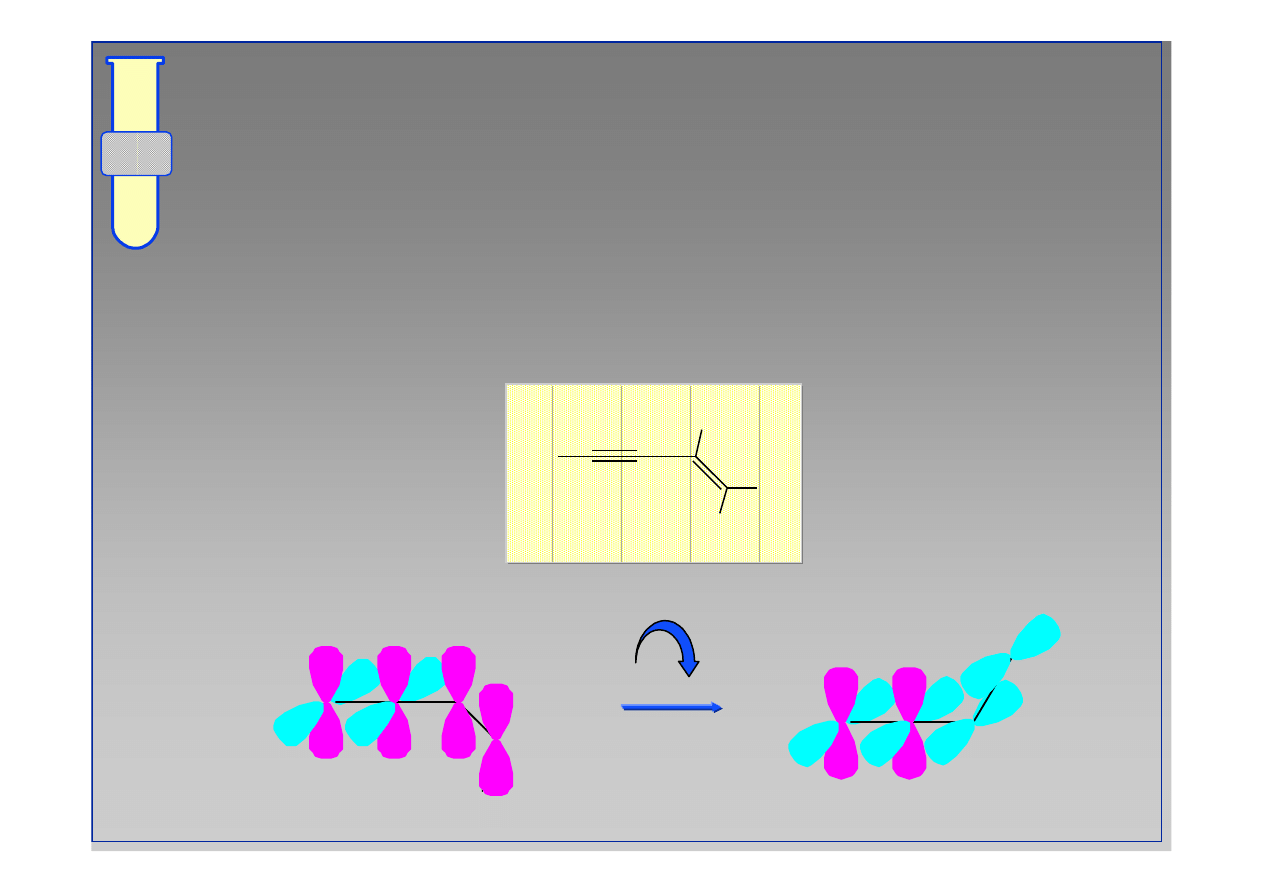
RJC

Sprz

Sprz

ęż

ęż

enie

enie

Podobnie jak w alkenach,

Podobnie jak w alkenach,

alkiny

alkiny

wykazuj

wykazuj

ą

ą

mo

mo

ż

ż

liwo

liwo

ść

ść

sprz

sprz

ęż

ęż

enia pomi

enia pomi

ę

ę

dzy wi

dzy wi

ą

ą

zaniami

zaniami

wielokrotnymi.

wielokrotnymi.

90°

H

H

H

H

18

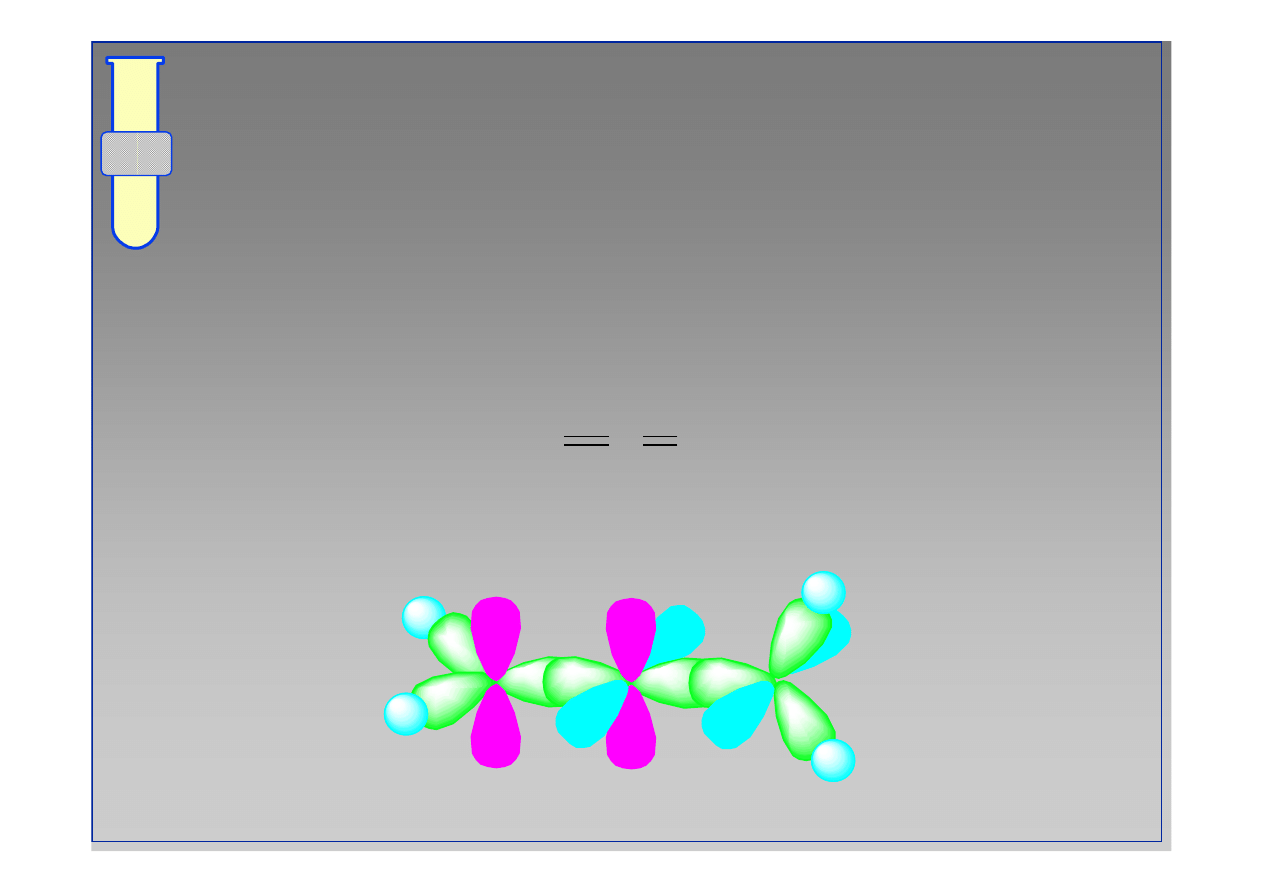
RJC

Skumulowane Wi

Skumulowane Wi

ą

ą

zania Podw

zania Podw

ó

ó

jne

jne

Tak samo jak w

Tak samo jak w

alkinach

alkinach

, atom C

, atom C

sp

sp

stanowi

stanowi

fragment struktury

fragment struktury

allen

allen

ó

ó

w

w

.

.

sp

sp

CH

2

C CH

2

19

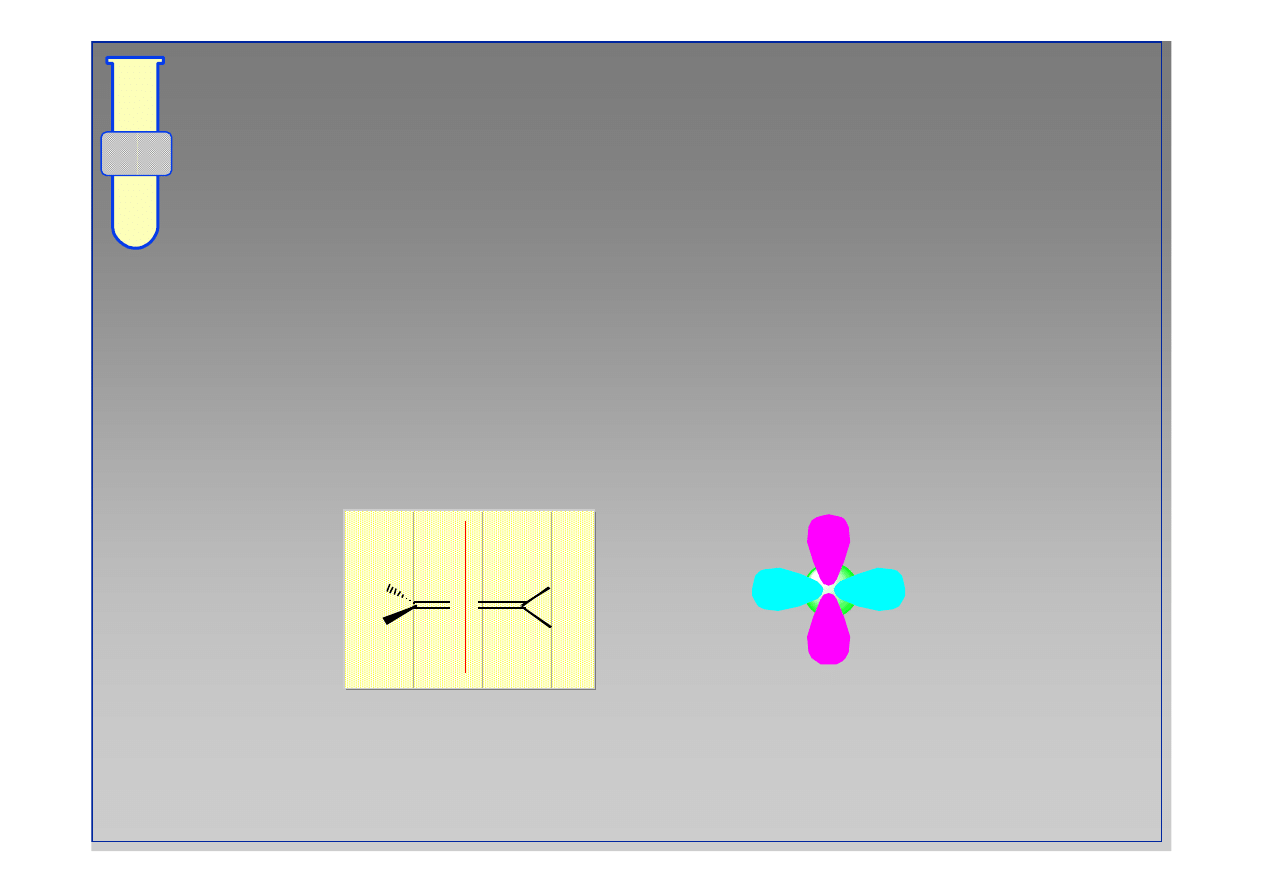
RJC

Skumulowane Wi

Skumulowane Wi

ą

ą

zania Podw

zania Podw

ó

ó

jne

jne

Wi

Wi

ą

ą

zania

zania

π

π

w cz

w cz

ą

ą

steczce

steczce

allenu

allenu

nie s

nie s

ą

ą

sprz

sprz

ęż

ęż

one

one

,

,

poniewa

poniewa

ż

ż

nie ma ani mo

nie ma ani mo

ż

ż

liwo

liwo

ś

ś

ci przenikania, ani

ci przenikania, ani

swobodnej rotacji.

swobodnej rotacji.

•

C

H

H

H

H

20

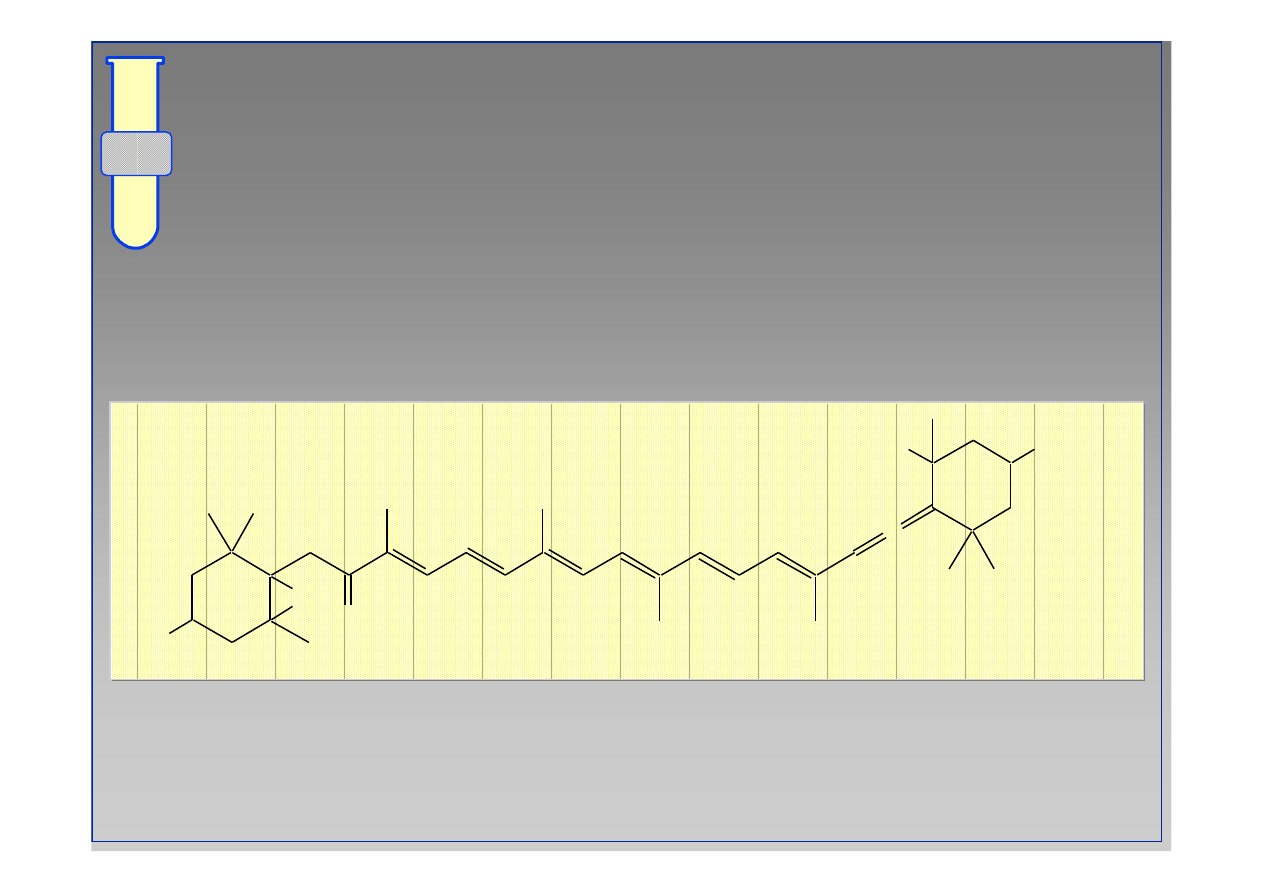
RJC

Fukoksantyna : Przyk

Fukoksantyna : Przyk

ł

ł

ad

ad

Allenu

Allenu

Wyst

Wyst

ę

ę

puj

puj

ą

ą

cego w Naturze

cego w Naturze

Popularny zwi

Popularny zwi

ą

ą

zek z grupy

zek z grupy

“

“

karotenoid

karotenoid

ó

ó

w

w

”

”

znaleziony w algach morskich.

znaleziony w algach morskich.

•

O

HO

HO

OCH

3

O

21

RJC

Podsumowanie

Podsumowanie

Alkiny

Orbitale sp

Acetylen

Geometria liniowa (dygonalna)

Reguły IUPAC

Układy sprzężone

Układy skumulowanych wiązań

podwójnych (alleny)

Alkiny

Orbitale sp

Acetylen

Geometria liniowa (dygonalna)

Reguły IUPAC

Układy sprzężone

Układy skumulowanych wiązań

podwójnych (alleny)