Politechnika Warszawska
Wydział Samochodów i Maszyn Roboczych
Instytut Maszyn Roboczych Ciężkich
Laboratorium Konstrukcji Nośnych
Analiza naprężeń w modelu wysięgnika teleskopowego
Wersja robocza
Tylko dla użytku wewnętrznego SiMR PW
Opracowanie:
Hieronim Jakubczak
Artur Jankowiak
Warszawa 2014
Wszelkie prawa zastrzeżone
2
Ćwiczenie 1
Analiza naprężeń w modelu wysięgnika teleskopowego
1.1 CEL ĆWICZENIA
Celem ćwiczenia jest zapoznanie studentów ze sposobem teoretycznego wyznaczania
naprężeń w niebezpiecznych obszarach wysięgnika teleskopowego oraz porównanie wyników
z wartościami określonymi doświadczalne. Szczególnie interesujące będzie porównanie
teoretycznych i doświadczalnych rozkładów naprężeń.
1.2 WPROWADZENIE
Wysięgnik teleskopowy składa się z kilku sekcji o budowie skrzynkowej, których
wymiary poprzeczne są tak dobrane, że istnieje możliwość umieszczania sekcji o wymiarach
mniejszych w sekcjach o wymiarach większych. Drugim warunkiem umożliwiającym takie
rozwiązanie jest brak poprzecznych żeber usztywniających. Jest to podstawowa różnica formy
konstrukcyjnej sekcji wysięgnika teleskopowego w stosunku do typowych elementów
skrzynkowych, np. mostów suwnic.
W głównej, pionowej płaszczyźnie, sekcja wysuwna podparta jest w dwóch punktach, co
zapewnia zarówno jej przesuwanie w sekcji zewnętrznej jak też przeniesienie momentu
wywołanego podnoszonym przez żuraw ładunkiem, rys. 1.1. Podpora dolna związana jest na
stałe z sekcją stałą, co umożliwia lokalne wzmocnienie tej sekcji. Natomiast podpora górna,
przymocowana do sekcji wysuwnej, styka się z sekcją stałą za pośrednictwem ślizgów,
wywołując w ten sposób bardzo niekorzystny, złożony układ obciążeń tej sekcji. Bowiem
poza głównym obciążeniem w postaci momentu gnącego w płaszczyźnie pionowej, w sekcji
stałej, w rejonie podpory górnej istnieje lokalny stan obciążeń, który powoduje odrywanie
górnego pasa sekcji od środników. Z tego względu obszar współpracy sekcji zewnętrznej z
podporą górną jest bardzo narażony na powstawanie uszkodzeń i wymaga dokładnej analizy
wytrzymałościowej.
1.3 OBLICZENIA TEORETYCZNE
Obciążenia główne
Konstrukcja rzeczywista jest obciążona w sposób bardzo złożony. Wprawdzie obciążenia
osiowe przenoszone są przez elementy mechanizmu teleskopowania, jednakże ich
3
mimośrodowe przyłożenie oraz ugięcie wysięgnika muszą być uwzględnione w obliczeniach.
Ponadto istnienie sił bocznych oraz skręcanie wysięgnika powoduje, że obliczenia prowadzi
się zwykle przy wykorzystaniu metod numerycznych. Poniżej przedstawiono uproszczony
sposób obliczeń wytrzymałościowych, jak również wynik numerycznej analizy naprężeń w
sekcji stałej modelu wysięgnika teleskopowego.
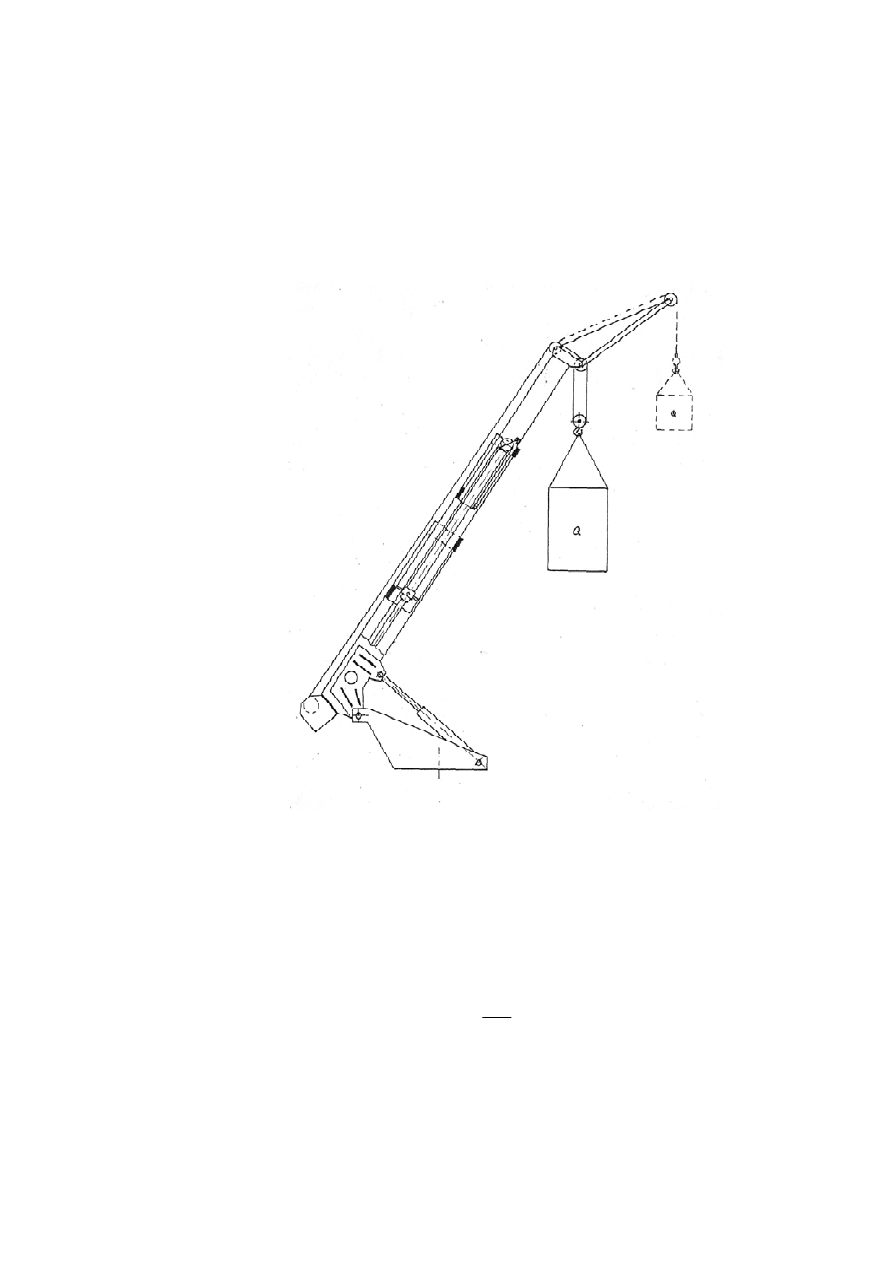
Rys. 1.1 Wysięgnik teleskopowy
Na rys. 1.2 przedstawiono uproszczony schemat obciążeń wysięgnika teleskopowego.
Naprężenia normalne, tzw. "ogólne", wywoływane tym obciążeniem są równoległe do osi x
i są obliczane ze wzoru (1.1):
z
I
M
y
y
x
o
⋅
=
σ
=
σ
(1.1)
gdzie:
M
y
- moment gnący dla przekroju wysięgnika względem osi y
I
y
- moment bezwładności zginanego przekroju względem osi y.
z - odległość punktu obliczeniowego od osi bezwładności przekroju,
4
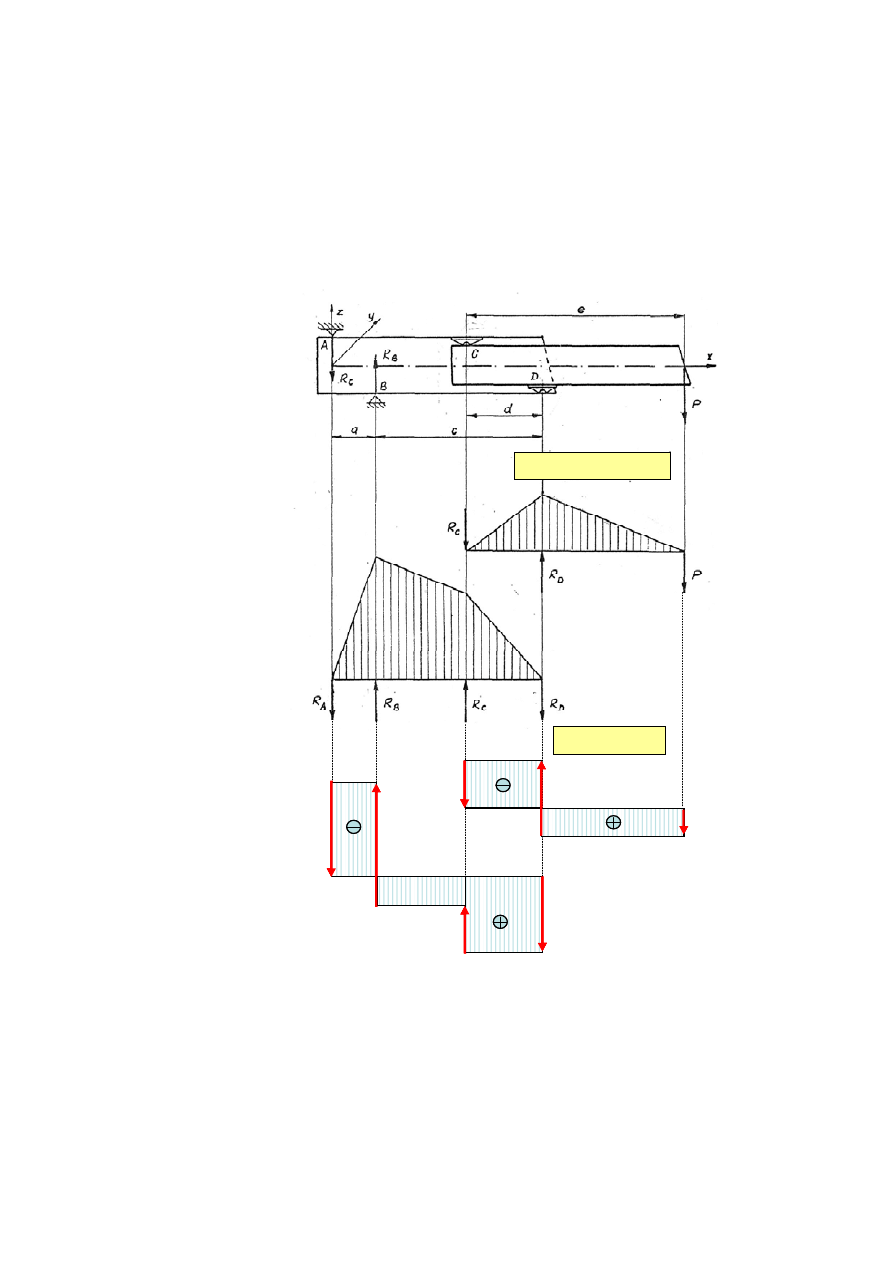
Obliczenie wartości momentu gnącego w przekrojach sekcji wysięgnika możliwe jest po
uprzednim wyznaczeniu reakcji w punktach podparcia całego wysięgnika (
R
A
,
R
B
) oraz w
punktach podparcia sekcji wysuwnej w sekcji stałej (
R
C
,
R
D
). Wykresy momentu gnącego
M
y
oraz sił tnących, obliczone z pominięciem mas własnych dla obu sekcji wysięgnika
przedstawiono na rys. 1.2.
R
D
R
C
R
B
R
A
R
D
R
C
R
B
R
A
R
D
P
R
C
R
D
P
R
C
Momenty gnące, My
Siły tnące, Tz
R
D
R
C
R
B
R
A
R
D
R
C
R
B
R
A
R
D
P
R
C
R
D
P
R
C
Momenty gnące, My
Siły tnące, Tz
Rys. 1.2 Schemat obciążeń modelu wysięgnika teleskopowego
Obciążenia lokalne
Jak wspomniano we wprowadzeniu, najbardziej niebezpiecznym miejscem wysięgnika
teleskopowego jest rejon sekcji stałej, współpracujący z podporą górną sekcji wysuwnej.
5
Dokładniejsze wyznaczenie naprężeń w tym obszarze wysięgnika możliwe jest przy
zastosowaniu metody elementów skończonych, natomiast przy zastosowaniu metod
analitycznych wytrzymałości materiałów można otrzymać rozwiązania przybliżone. Wymaga
to przy tym wprowadzenia pewnych założeń upraszczających.
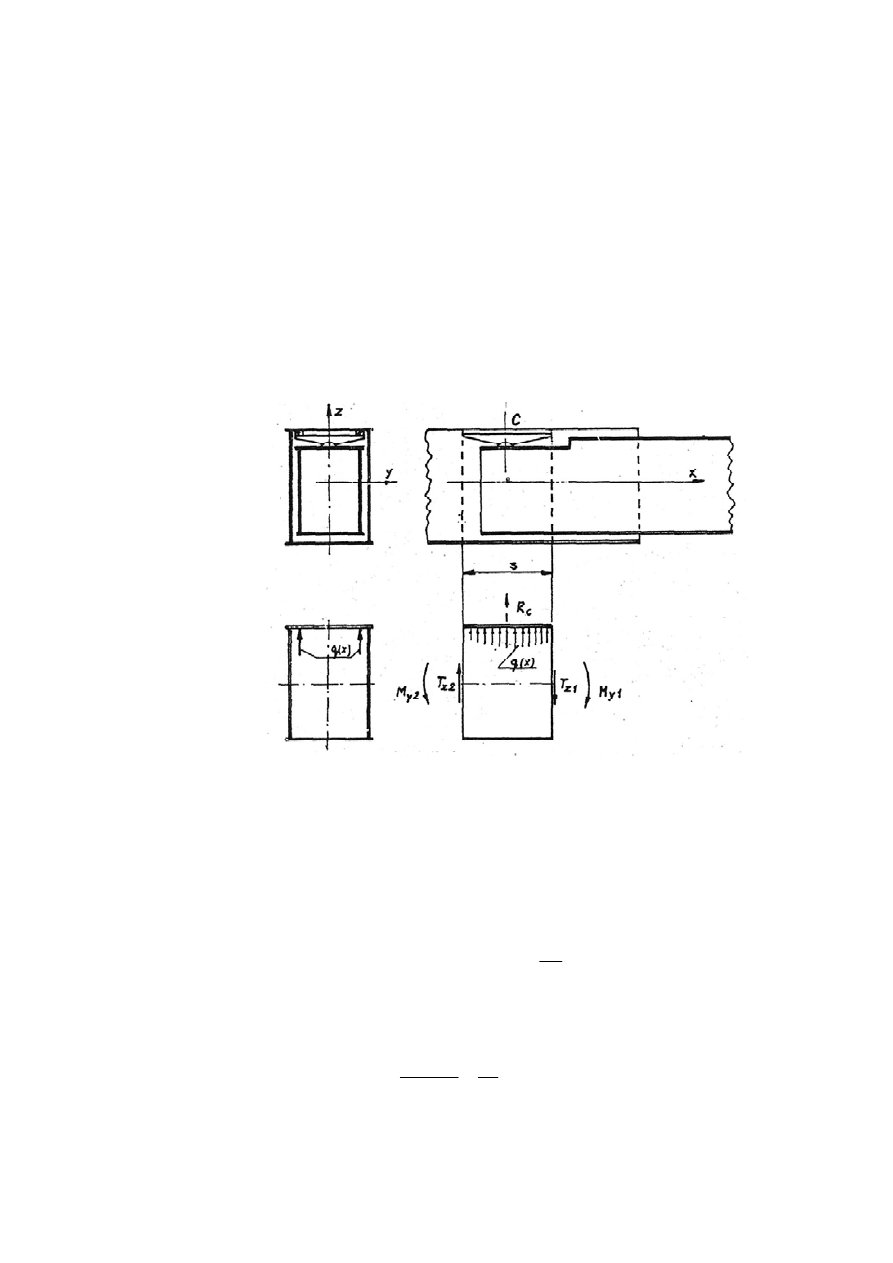
Wycięty myślowo odcinek sekcji stałej o długości
s (rys. 1.3) znajduje się w
równowadze, gdyż działanie sił zewnętrznych
q(x), będące efektem rozłożenia reakcji R
C
w
podporze na długości ślizgu
s, równoważne jest działaniom sił wewnętrznych: momentów
gnących
M
y
i sił tnących
T
z
Rys. 1.3 Obciążenia lokalne w sekcji zewnętrznej wysięgnika teleskopowego.
Dla wyznaczenia naprężeń "lokalnych" należy przyjąć następujące założenia
upraszczające:
1° Reakcja
R
C
rozkłada się równo na oba ślizgi, przy czym:
( )
s
R
q
const
x
q
C
2
=
=
=
(1.2)
2°
Siły tnące T
z
przenoszone są głównie przez środniki i można je rozłożyć na obciążenie
ciągłe:
q
const
s
R
s
T
T
c
z
z
=
=
=
−
2
2
2
1
(1.3)
3°
Momenty gnące M
y
nie mają wpływu na wartości naprężeń lokalnych.
6
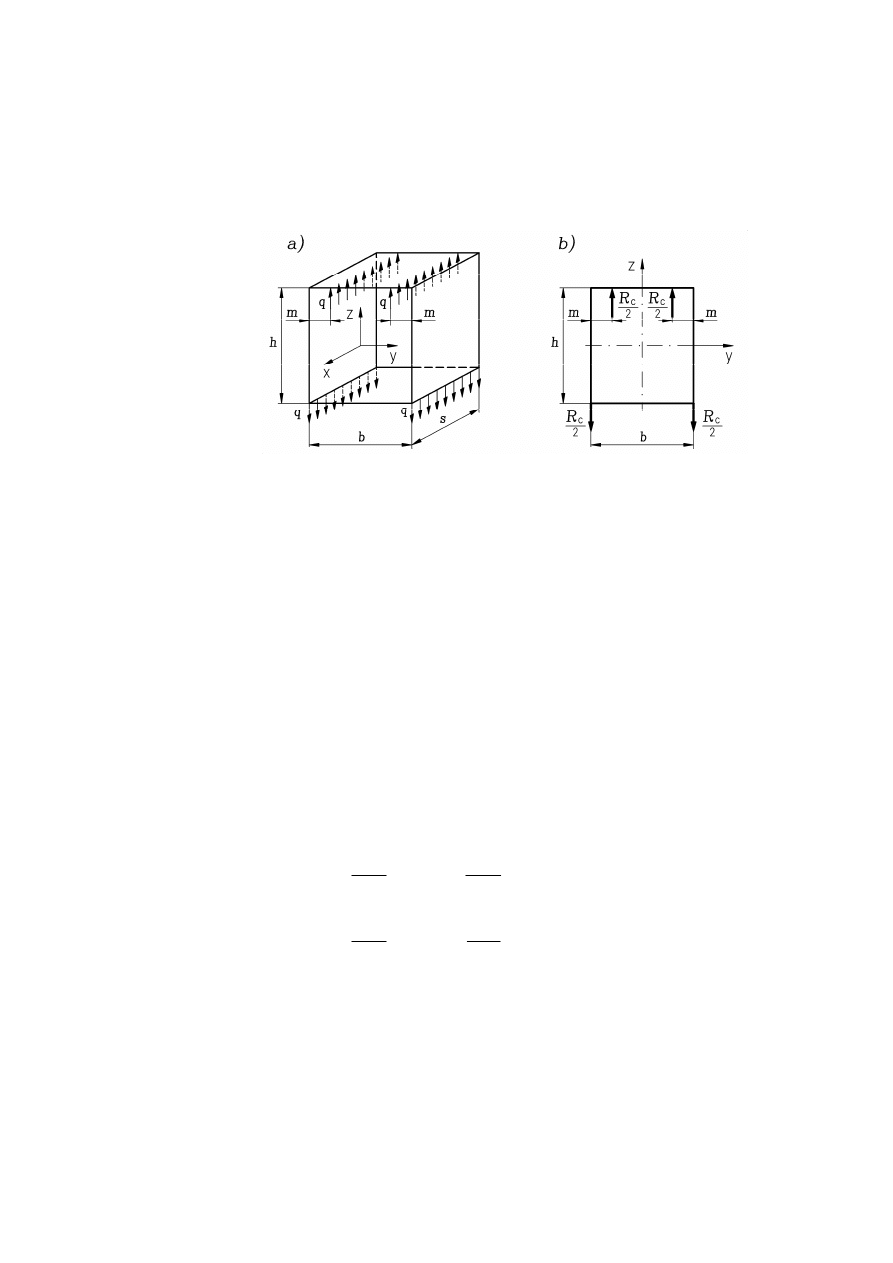
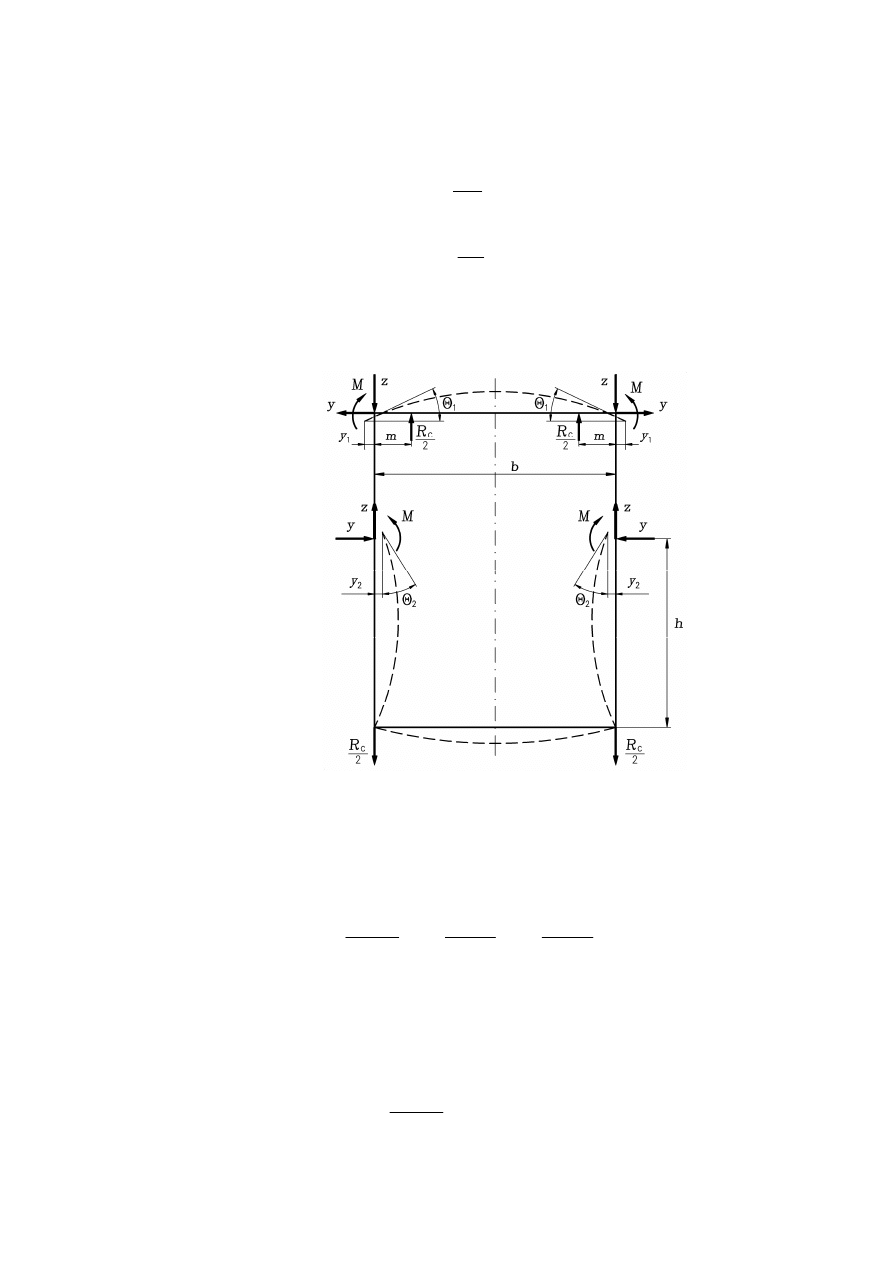
Przy tych założeniach wycinek sekcji stałej wygląda tak, jak na rys. 1.4a i znajduje się
nadal w równowadze. Ze względu na równomierne rozkłady obciążenia, w dalszych
rozważaniach można go rozwiązywać jako ramę płaską, przedstawioną na rys. 1.4b.
Rys. 1.4 Rozkład obciążeń lokalnych w sekcji stałej
Rozwiązanie ramy równoznaczne jest z możliwością wyznaczenia w dowolnym jej
przekroju sił wewnętrznych, a więc i naprężeń w dowolnym punkcie. Siły wewnętrzne N i M
x
w dowolnym przekroju ramy (rys. 1.5) mogą być wyznaczone po jej przecięciu. Równowagę
każdej z odciętych części zapewniają symetrycznie równe siły wewnętrzne M, Y i Z.
Równania statyki umożliwiają wyznaczenie tylko jednej niewiadomej - Z. Wielkości M i Y są
statycznie niewyznaczalne i wymagają dwóch dodatkowych równań, które mogą mieć różną
postać w zależności od przyjętego sposobu rozwiązania ramy.
W tym przypadku równania te będą wywodzić się z twierdzenia Castigliano. Po
oznaczeniu przez U
G
i U
D
energii odkształcenia sprężystego części górnej i dolnej przeciętej
ramy można napisać następujące równania:
1
θ
−
=
∂
∂
M
U
G
2
θ
−
=
∂
∂
M
U
D
(1.4)
1
y
Y
U
G
−
=
∂
∂
2
D
y
Y
U
−
=
∂
∂
(1.5)
Z warunku ciągłości przemieszczeń wynika jednak, że:
2
1
θ
θ
=
2
1
y
y
−
=
(1.6)
Uwzględniając powyższe zależności oraz oznaczając ponadto sumę energii części dolnej
i górnej przez U, tzn. U = U
G
+ U
D
7
równania (1.4) i (1.5) przyjmują postać:
0
=
∂
∂
M
U
(1.7)
0
=
∂
∂
Y
U
(1.8)
Powyższe równania noszą nazwę twierdzenia Menabrei dla sił wewnętrznych statycznie
niewyznaczalnych.
Rys. 1.5 Schemat rozwiązywania ramy
Energię odkształcenia sprężystego U można obliczyć jako pracę sił wewnętrznych
z równania (1.9):
dl
F
G
T
dl
F
E
N
dl
I
E
M
U
li
i
i
li
i
i
li
xi
xi
∫
∫
∫
⋅
+
⋅
+
⋅
=
2
2
2
2
2
2
(1.9)
Ze względu na przeważający wpływ momentów gnących na wartość energii U,
w obliczeniach pomija się zwykle siły normalne N
i
i tnące T
i
a wówczas zależność (1.9)
sprowadza się do postaci:
dl
I
E
M
U
li
xi
xi
∫
⋅
=
2
2
(1.10)
8
zaś równania (1.7) i (1.8) po podstawieniu zależności (1.9) i zróżniczkowaniu mają postać:
0
=
⋅
⋅
∂
∂
=
∂
∂
∫
dl
I
E
M
M
M
M
U
xi
xi
li
xi
(1.11)
0
=
⋅
⋅
∂
∂
=
∂
∂
∫
dl
I
E
M
Y
M
Y
U
xi
xi
li
xi
(1.12)
Po wyrażeniu wielkości M jedynie poprzez znane siły zewnętrzne oraz poszukiwane
niewiadome M i Y, otrzymuje się układ równań pierwszego stopnia z dwiema niewiadomymi
(M, Y). Z ich rozwiązania otrzymuje się wzory wyrażające poszukiwane wielkości
niewiadome:
(
)(
)
(
)(
)
b
h
h
b
b
h
m
b
m
R
M
c
3
2
3
2
+
+
+
−
⋅
=
(1.13)
(
)
(
)
b
h
h
m
b
mh
R
Y
c
3
2
3
2
+
−
=
(1.14)
Naprężenia normalne wywołane momentem siłą normalną oraz momentem gnącym w
rozpatrywanej ramie (wycinku sekcji stałej wysięgnika) mają kierunek zgodny z osią y w
półkach poziomych oraz kierunek z w środnikach sekcji. Dla półki górnej można je wyrazić
wzorem:
z
I
M
F
N
x
x
y
L
⋅
±
=
σ
=
σ
(1.15)
gdzie: N i M
x
- siła normalna i moment gnący w przekroju półki górnej
F i I
x
- pole powierzchni i moment bezwładności przekroju
Naprężenia zredukowane
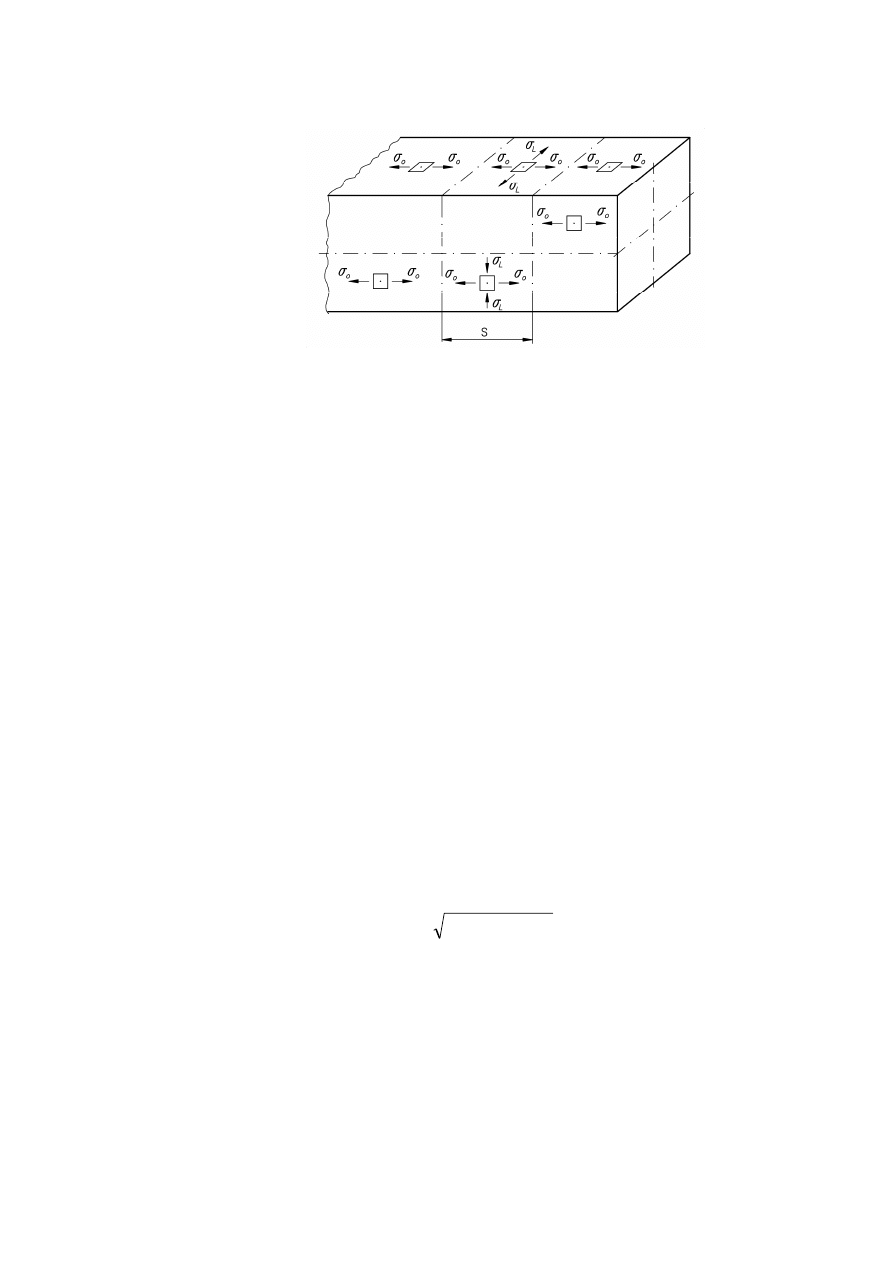
Z powyższej analizy teoretycznej wynika, że w rozpatrywanym rejonie stałej sekcji
wysięgnika teleskopowego, tzn. w pobliżu górnej podpory sekcji wysuwne występuje -
pomijając naprężenia styczne, wywołane siłami tnącymi - jednoosiowy bądź płaski stan
naprężeń (rys. 1.6). Płaski stan naprężeń wynika ze złożenia naprężeń lokalnych σ
L
z naprężeniami ogólnymi σ
o
.
9
Rys. 1.6 Naprężenia w sekcji wysięgnika.
Z przedstawionych obliczeń wynika, że naprężenia lokalne istnieją tylko na długości s
sekcji, przy czym na całej tej długości ich wartość jest jednakowa. Jest to jednak tylko wynik
założeń teoretycznych i przyjętej metody obliczeń, bowiem zgodnie z zasadą ciągłości
przemieszczeń naprężenia lokalne nie mogą pojawiać się w sposób skokowy. Oznacza to, że
obciążenie lokalne wywołuje naprężenia lokalne w znacznie większej części sekcji
wysięgnika niż długość ślizgów.
Przy wymiarowaniu konstrukcji niezbędna jest ocena jej wytężenia statycznego przez
porównanie naprężeń istniejących w konstrukcji z naprężeniami dopuszczalnymi,
określonymi na podstawie prób jednoosiowego rozciągania. Z tego względu wieloosiowy stan
naprężeń musi być zastąpiony umownym naprężeniem jednoosiowym, którego skutek
działania jest taki sami jak naprężeń wieloosiowych. Spośród wielu hipotez wytężeniowych,
dla stali najlepiej nadaje się hipoteza Hubera-Misesa-Hencky’ego (H-M-H), która za
kryterium zniszczenia materiału przyjmuje wartość energii odkształcenia postaciowego.
Dla płaskiego stanu naprężeń, naprężenia zastępcze według hipotezy H-M-H można
obliczyć ze wzoru:
1
0
2
1
2
0
σ
σ
σ
σ
σ
−
+
=
z
(1.16)
Analiza numeryczna naprężeń
W ramach pracy dyplomowej [4] została przeprowadzona analiza numeryczna dla sekcji
stałej modelu wysięgnika teleskopowego. Obciążenia główne w postaci reakcji w podporach,
sekcji zamodelowano zgodnie ze schematem przedstawionym na rys. 1.2. Obciążenie podpory
górnej zostało rozłożone na dwóch ślizgach o długości s (rys. 1.3), przy czym było ono
10
efektem odzwierciedlenia geometrii samej podpory, a nie założenia określonego rozkładu
obciążenia. Przeprowadzone analizy wykazały, że rozkład obciążenia q(x) nie jest w
rzeczywistości stały (rys. 1.7), jak to zakłada się w analizie teoretycznej (rys. 1.3).
Rys. 1.7 Rozkład obciążenia na podporze górnej (oś wzdłużna)
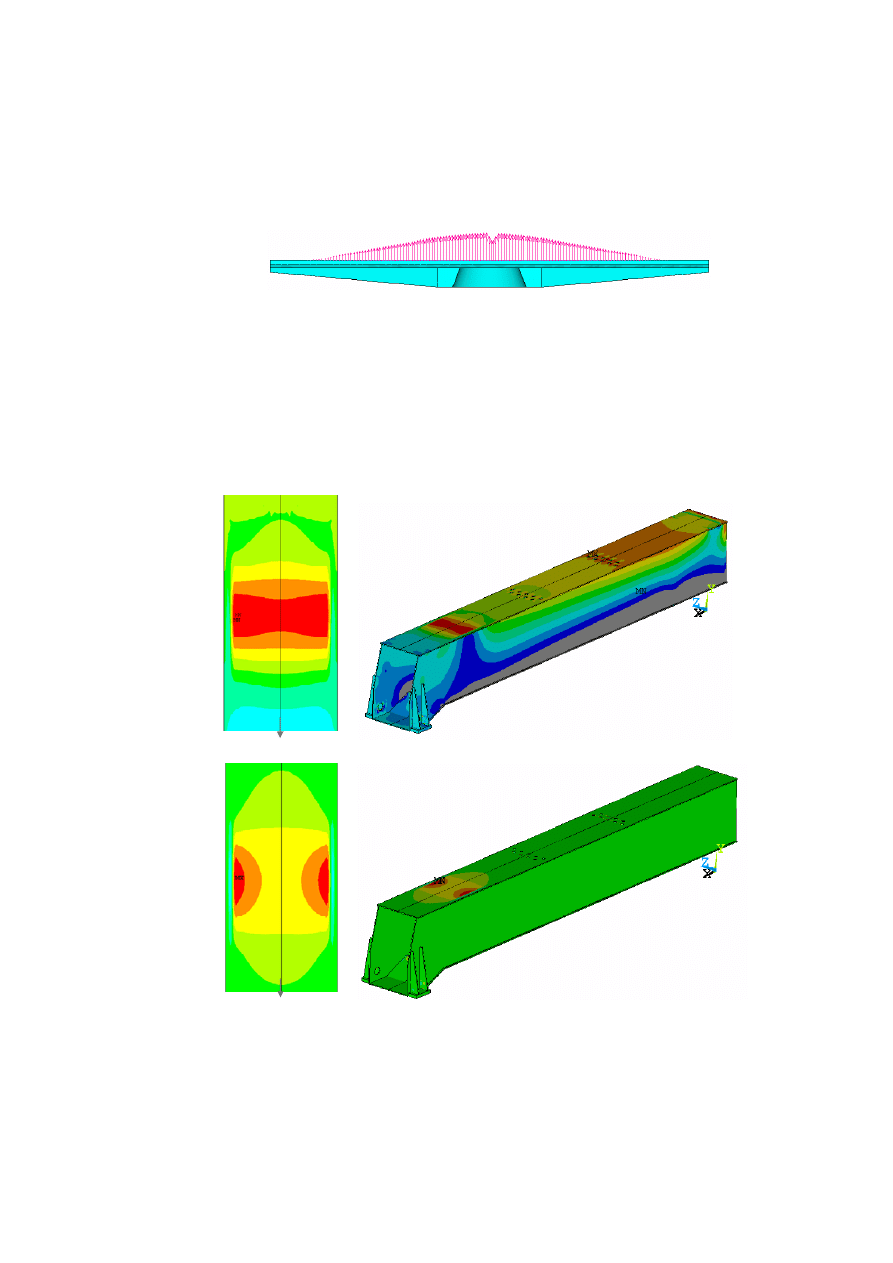
Na rys. 1.8 przedstawiono wyniki obliczeń numerycznych, wykonanych za pomocą
programu ANSYS. Rys. 1.8a przestawia rozkłady naprężeń ogólnych
σ
x
, natomiast rys. 1.8b –
rozkłady naprężeń lokalnych
σ
y
na zewnętrznej powierzchni półki górnej rozpatrywanego
wycinka sekcji (w modelu numerycznym os z pokrywa się z osią y na rys. 1.4).
a)
x
x
b)
x
x
Rys. 1.8 Rozkład naprężeń w badanej sekcji wysięgnika:
(a) naprężenia ogólne –
σ
x
, (b) naprężenia lokalne –
σ
y
Warto zwrócić uwagę, że rozkład naprężeń w sekcji zewnętrznej, w otoczeniu podpory
górnej, różni się znacznie od pozostałego obszaru sekcji.
11
1.5 OPIS STANOWISKA
Stanowisko
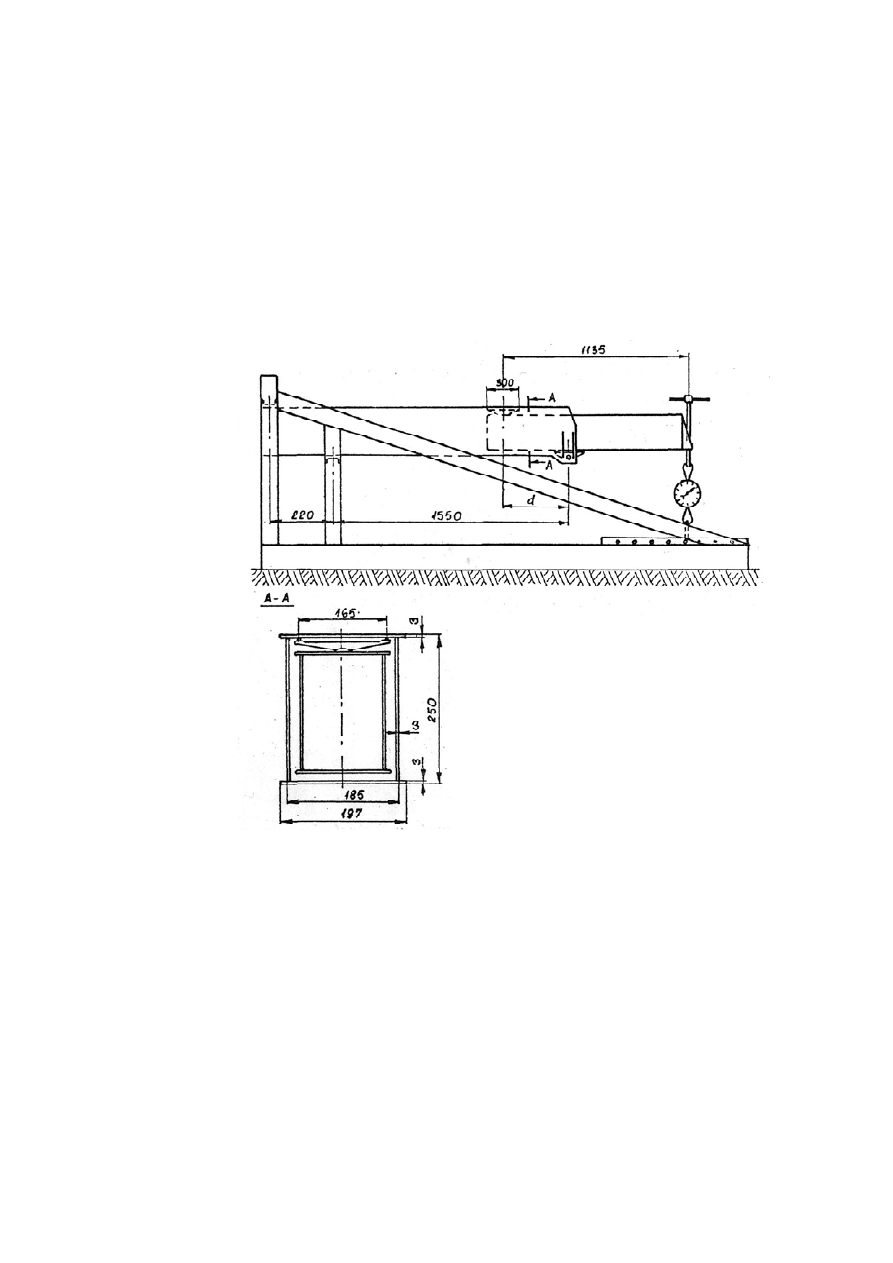
Na rys. 1.9 przedstawiono stanowisko do pomiarów naprężeń w modelu wysięgnika
teleskopowego. Jest to model uproszczony, bez mechanizmu teleskopowania sekcji. W celu
przybliżenia się do założeń teoretycznych, zamiast ślizgów w podporze górnej zastosowano
druty metalowe, dzięki czemu uzyskuje się liniowe styki z powierzchnią sekcji stałej.
Rys. 1.9 Stanowisko do pomiarów naprężeń w modelu wysięgnika teleskopowego.
Sekcja wysuwna wysięgnika może być ustawiona w dowolnym położeniu zależnie od
zadanego rozstawu d podpór sekcji. Obciążenie (pionowe) wysięgnika jest realizowane za
pomocą śruby, a wartość siły jest odczytywana z czujnika zegarowego.
Pomiary i analizy
W tej części ćwiczenia, zarówno wartości naprężeń, jak też ich rozkłady zostaną
określone eksperymentalnie. Porównanie wyników uzyskanych na drodze teoretycznej
(zarówno uproszczonej, jak też numerycznej) i doświadczalnej umożliwi wnioskowanie o
słuszności założeń przyjętych do uproszczonej analizy teoretycznej.
12
A
B
C
D
E
F
A
B
C
D
E
F
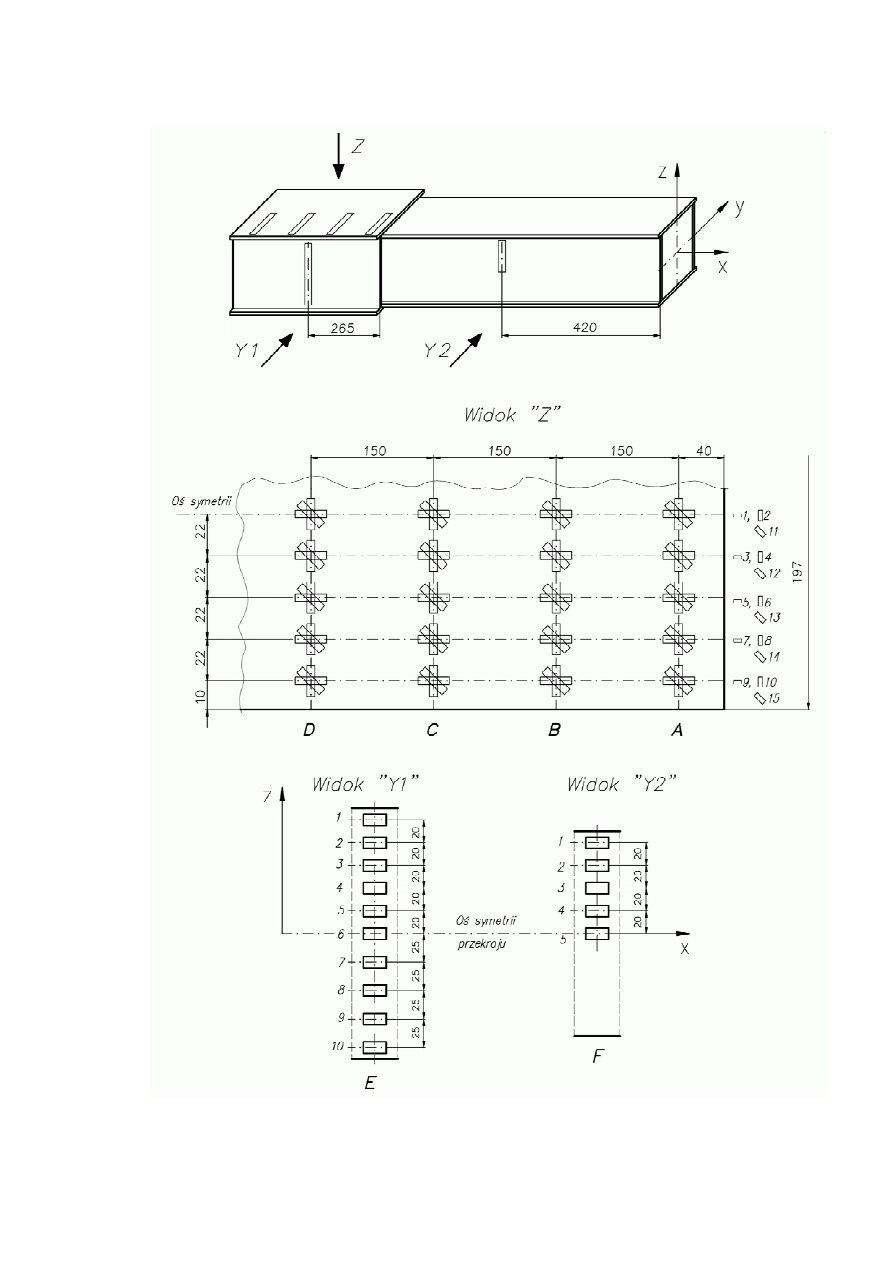
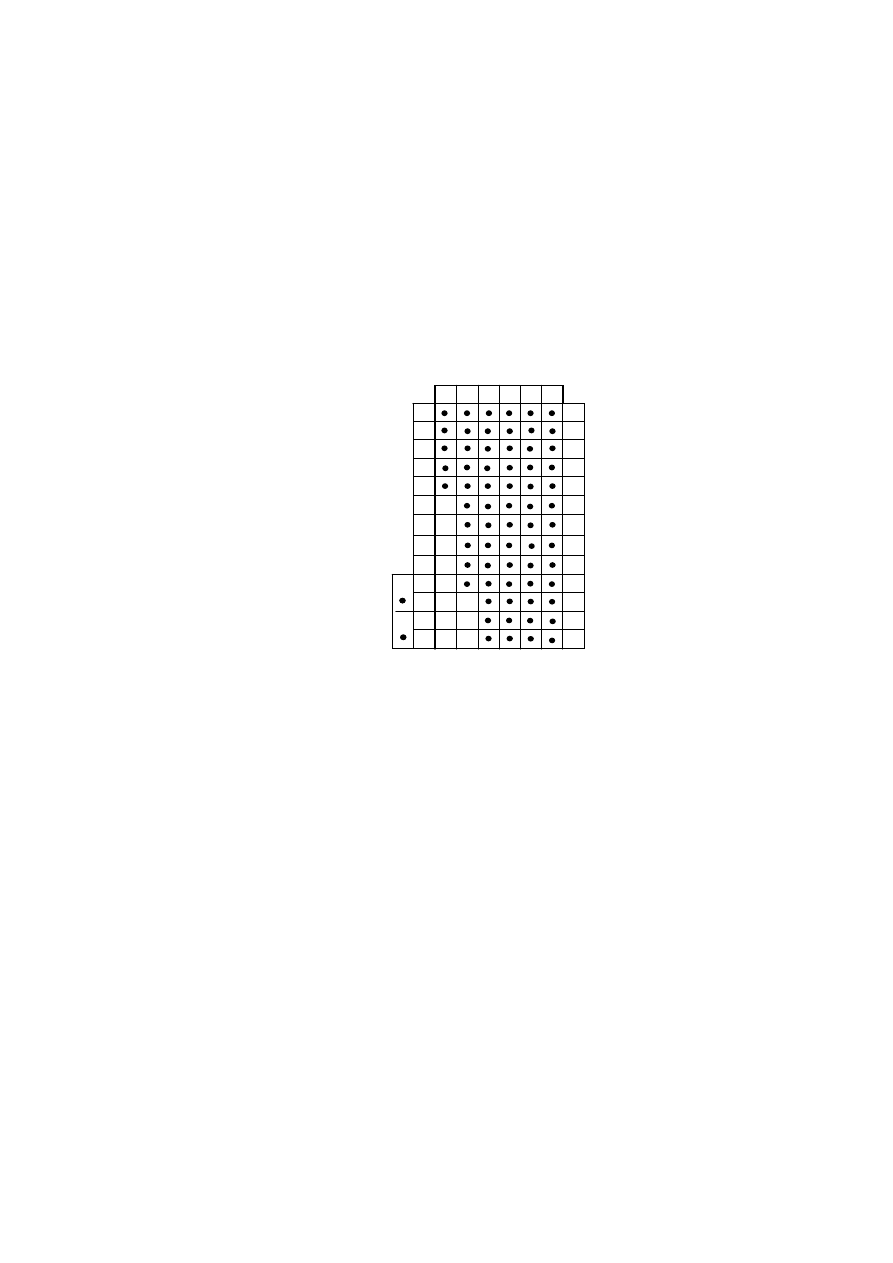
Rys. 1.10 Plan tensometrów
13
Na górnej półce sekcji stałej wysięgnika są naklejone rozety tensometryczne, a na
ściankach bocznych sekcji stałej oraz ruchomej naklejono tensometry jednoosiowe. Plan
tensometrów przedstawia rys. 1.10, natomiast w Załączniku A (rys. A.6) pokazano ogólny
sposób ich połączenia oraz wyprowadzenia przewodów na tablicę montażową (rys.1.11).
Układ oznaczeń w tablicy odpowiada oznaczeniom przyjętym na rys. 1.10. Tablica
montażowa pozwala na podłączenie do wyprowadzeń tensometrów mostków
tensometrycznych (zestaw zacisków) lub komputerowego zestawu pomiarowego (interfejsy
szeregowe).
2
1
4
3
5
6
7
8
9
10
11
13
15
2
1
4
3
5
6
7
8
9
10
11
13
15
0
K
A
B
C
D
E
F
2
1
4
3
5
6
7
8
9
10
11
13
15
2
1
4
3
5
6
7
8
9
10
11
13
15
0
K
A
B
C
D
E
F
Rys. 1.11 Schemat wyprowadzenia przewodów układu pomiarowego
Aparatura pomiarowa
W skład aparatury pomiarowej wchodzi:
1° Dynamometr (czujnik zegarowy), służący do pomiaru siły przykładanej na końcu sekcji
wysuwnej,
2° Komputerowy system pomiarowy (multiplekser ze wzmacniaczem pomiarowym,
przełącznik grup kanałów, karta pomiarowa, komputer PC) lub dowolny mostek
tensometryczny z przełączaniem kanałów (zasady pomiaru podano w Załączniku A).
Odpowiednie tensometry badanego przekroju należy połączyć z mostkiem
tensometrycznym poprzez zaciski tablicy montażowej. Wyjścia tensometrów z oznakowanej
tablicy zamocowanej na elemencie badanym łączymy kolejno z odpowiednimi zaciskami
mostka tensometrycznego, lub jego skrzynki rozdzielczej. Przy zastosowaniu komputerowego
systemu pomiarowego odpowiednie złącza szeregowe na tablicy montażowej należy
podłączyć ze złączami multipleksera.
14
1.6 WYKONANIE ĆWICZENIA
Na podstawie przedstawionych w rozdziale 1.3 wzorów teoretycznych można obliczyć
wartości naprężeń ogólnych i lokalnych w wybranych punktach konstrukcji. Można również
określić teoretyczne rozkłady naprężeń, tzn. ich zmianę w wybranych przekrojach i na
wybranych kierunkach.
Wykonanie ćwiczenia polega na:
1. Obliczeniu naprężeń we wskazanych punktach wysięgnika oraz wyznaczeniu
teoretycznych rozkładów naprężeń we wskazanych przekrojach.
2. Doświadczalnym określeniu rozkładów naprężeń we wskazanych przekrojach wysięgnika
3. Porównaniu rozkładów teoretycznych z rozkładami uzyskanymi z analizy numerycznej
oraz z badań doświadczalnych.
1.7 LITERATURA
1. Z. Dyląg, A. Jakubowicz, Z. Orłoś: Wytrzymałość materiałów, WNT Warszawa, 1996
2. J. Rutecki: Cienkościenne konstrukcje nośne, WNT 1966
3. W. Tyburski: Przetworniki tensometryczne, WNT 1971
4. Z. Orłoś: Doświadczalna analiza odkształceń i naprężeń, PWN, 1977
5. T. Jendrzejewski: Analiza naprężeń w modelu wysięgnika teleskopowego, Praca
dyplomowa, SiMR PW, 2013