
Politechnika Warszawska
Wydział Samochodów i Maszyn Roboczych
Instytut Maszyn Roboczych Ciężkich
Laboratorium Konstrukcji Nośnych
Analiza stanów naprężenia metodą elastooptyczną
Wersja robocza
Tylko dla użytku wewnętrznego SiMR PW
Opracowanie:
Paweł Gomoliński
Warszawa 2014
Wszelkie prawa zastrzeżone

2
Ćwiczenie 3
Analiza stanów naprężenia metodą elastooptyczną
3.1 CEL ĆWICZENIA
Celem ćwiczenia jest praktyczne zapoznanie studentów z podstawowymi zasadami
analizy naprężeń w elementach konstrukcji nośnej za pomocą metody elastooptycznej.
3.2 WPROWADZENIE
Ważnym elementem procesu projektowania nowej konstrukcji nośnej, jak również
analizy konstrukcji już istniejącej (np. w celu ustalenia przyczyn pojawiania się pęknięć lub
jej przedwczesnego zniszczenia) jest weryfikacja doświadczalna, pozwalająca na określenie
jej nośności granicznej, wyznaczenie stref wytężonych w zakresie sprężystym i stref
uplastycznionych, a w efekcie zdefiniowanie mechanizmu zniszczenia.
Z punktu widzenia dokładności i wiarygodności uzyskiwanych wyników, weryfikację
doświadczalną najlepiej jest przeprowadzać na obiektach rzeczywistych. Jednak ze względu
na wysoki koszt tego rodzaju badań, zjawiska takie jak koncentracja naprężeń, efekty lokalne,
czy propagacja stref uplastycznienia, z powodzeniem bada się na odpowiednio stworzonych
modelach, wykorzystując zasady tzw. podobieństwa modelowego.
Z metod badawczych mających zastosowanie w odniesieniu do konstrukcji nośnych
wymienić należy przede wszystkim tensometrię oporową oraz metody elastooptyczne. Do
rzadziej stosowanych należą metoda mory (do analizy znacznych odkształceń plastycznych)
i metoda kruchych pokryć (do badań podglądowych). Tensometria ma dość istotne
ograniczenie w postaci uśredniania wyników na obszarze zajmowanym przez tensometr oraz
praktycznie nie pozwala na kompleksową weryfikację całości konstrukcji nośnej. Wad tych
nie mają metody elastooptyczne. Należy przy tym pamiętać, że wszystkie wspomniane
metody badawcze pozwalają odzwierciedlać jedynie stan odkształcenia i dopiero na tej
podstawie wnioskujemy o stanie naprężenia. Zależnością, na której bazuje to wnioskowanie,
jest prawo Hooke’a.
3.3 CHARAKTERYSTYKA ELASTOOPTYCZNYCH METOD ANALIZY
ODKSZTAŁCEŃ I NAPRĘŻEŃ
Badania elastooptyczne są pewnego rodzaju techniką pomiarową, która wykorzystując

3
specyficzne cechy światła pozwala na podstawie uzyskiwanych obrazów optycznych
wnioskować o rozkładzie odkształceń (i naprężeń): określenie trajektorii naprężeń głównych,
identyfikację miejsc koncentracji naprężeń itp. Bardzo ważną zaletą tej metody badawczej
jest możliwość uzyskania kompleksowej dla całej badanej powierzchni, a nie tylko
punktowej, oceny stanu naprężenia. Właściwość ta jest bardzo istotna, ponieważ od razu daje
pogląd na cały badany obszar, pozwalając szybko ocenić stopień wytężenia konstrukcji i
określić rozkład występujących w niej naprężeń.
Spośród metod elastooptycznych największe zastosowanie mają metoda prześwietlania
oraz metoda warstwy powierzchniowej. W pierwszej z nich, weryfikacji doświadczalnej
poddaje się zbudowane ze specjalnych materiałów modele konstrukcji nośnych, zaś w drugiej
– rzeczywistą konstrukcję, na powierzchni której umieszcza się i trwale z nią łączy warstwę
specjalnego materiału. Podstawy fizyczne metody badawczej są w obu przypadkach
identyczne. Stosowany materiał jest ośrodkiem przepuszczającym światło i optycznie
czynnym, poprzez wykazywanie efektu tzw. dwójłomności wymuszonej. Własności takie mają
m.in. żywice (najczęściej stosowane): epoksydowe, fenolowo-formaldehydowe i poliestrowe,
a ponadto np. elastomery uretanowe, metakrylan, poliwęglany, szkło.
3.4 PODSTAWY FIZYCZNE METOD ELASTOOPTYCZNYCH
Światło można rozpatrywać jako falę elektromagnetyczną o określonej częstotliwości
i amplitudzie. W badaniach elastooptycznych z reguły stosuje się światło monochromatyczne.
Jest to światło jednobarwne, któremu odpowiada promieniowanie świetlne tylko jednej
długości (częstotliwości) drgań. Ponadto wykorzystywane są wspomniane wcześniej zjawiska
dwójłomności wymuszonej oraz polaryzacji, które również związane są z falową naturą
światła.
Światło wykorzystywane w badaniach elastooptycznych (niezbędne do uzyskania
efektów optycznych odzwierciedlających stan naprężenia), musi być spolaryzowane, tj.
drgania wektora świetlnego muszą być w szczególny sposób uporządkowane. Do tego celu
niezbędne jest zastosowanie odpowiednich układów optycznych z filtrami polaryzacyjnymi:
• polaryzatorem (przygotowującym wiązkę światła do prześwietlenia badanego
ośrodka) oraz
• analizatorem (pozwalającym obserwować uzyskiwane efekty optyczne).

4
3.5 ZJAWISKA OPTYCZNE WYKORZYSTYWANE W BADANIACH
ELASTOOPTYCZNYCH
W badaniach elastooptycznych wykorzystywane są zjawiska optyczne dwójłomności
wymuszonej oraz polaryzacji i interferencji, związane z falową naturą światła.
Dwójłomność wymuszona
Zjawisko dwójłomności wymuszonej polega na uzyskiwaniu przez pewnego rodzaju
ośrodki przepuszczające światło szczególnych własności optycznych pod wpływem
odkształcenia powodowanego przez obciążenia mechaniczne. Ciała takie stają się optycznie
anizotropowe. W przypadku płaskiego stanu naprężenia, liniowo spolaryzowany promień
światła monochromatycznego przechodząc przez ośrodek ulega rozszczepieniu na dwie
liniowo spolaryzowane składowe o płaszczyznach polaryzacji pokrywających się
z kierunkami naprężeń (odkształceń) głównych. Ponieważ promienie te rozchodzą się w ciele
z prędkością proporcjonalną do wielkości naprężeń (odkształceń) głównych, dochodzi do ich
przesunięcia fazowego, które jest proporcjonalne do różnicy naprężeń głównych.
Zależność opisująca przesunięcie liniowe rozszczepionych promieni jest następująca:
(
)
(
)
2
1
2
1
lub
ε
ε
λ
δ
σ
σ
λ
δ
ε
σ
−
⋅
=
−
⋅
=
K
g
K
g
(3.1)
gdzie: δ – względne przesunięcie fazowe; λ – długość fali świetlnej; g – grubość
prześwietlanego ośrodka; K
ε
i K
σ
– odpowiednio naprężeniowa i odkształceniowa stała
elastooptyczna, zależna od rodzaju ośrodka optycznie czułego.
Stałe K
σ
oraz K
ε
związane są zależnością:
ν
ε
σ
+
=
1
E
K
K
(3.2)
Jeżeli przesunięcie względne δ zostanie wyrażone w postaci wielokrotności m długości
fali λ zastosowanego światła:
λ
δ
⋅
= m
(3.3)
a w miejsce stałych elastooptycznych K
σ
i K
ε
zostaną wprowadzone elastooptyczne stałe
modelowe K
σm
i K
εm
:

5
g
K
K
oraz
g
K
K
m
m
ε
ε
σ
σ
=
=
(3.4)
otrzymamy zależności opisujące stan naprężenia (odkształcenia):
m
m
K
m
K
m
ε
σ
ε
ε
σ
σ
⋅
=
−
⋅
=
−
2
1
2
1
(3.5)
W praktyce badań elastooptycznych wykorzystywana jest tylko stała naprężeniowa K
σm
,
której wielkość wyznacza się doświadczalnie na prostym modelu, poddanym prostemu
stanowi obciążenia (np. czystemu rozciąganiu lub czystemu zginaniu), dla którego można
w łatwy sposób obliczyć wielkość odkształceń i naprężeń. Materiał elastooptyczny użyty do
wyznaczenia stałej modelowej musi być taki sam, z jakiego wykonany został model badanej
konstrukcji.
Polaryzacja
Obserwację i rejestrację zjawisk optycznych związanych z dwójłomnością wymuszoną
przeprowadza się z użyciem światła spolaryzowanego.
Zwykłe światło, niespolaryzowane, jest zbiorem chaotycznie rozchodzących się promieni
świetlnych. Drgania tych promieni wykonywane są w różnych płaszczyznach. Polaryzacja
światła polega na uporządkowaniu drgań promieni świetlnych w taki sposób, aby następowały
w określonych płaszczyznach. W badaniach elastooptycznych wykorzystuje się światło
spolaryzowane liniowo i kołowo, uzyskiwane w urządzeniu zwanym polaryskopem.
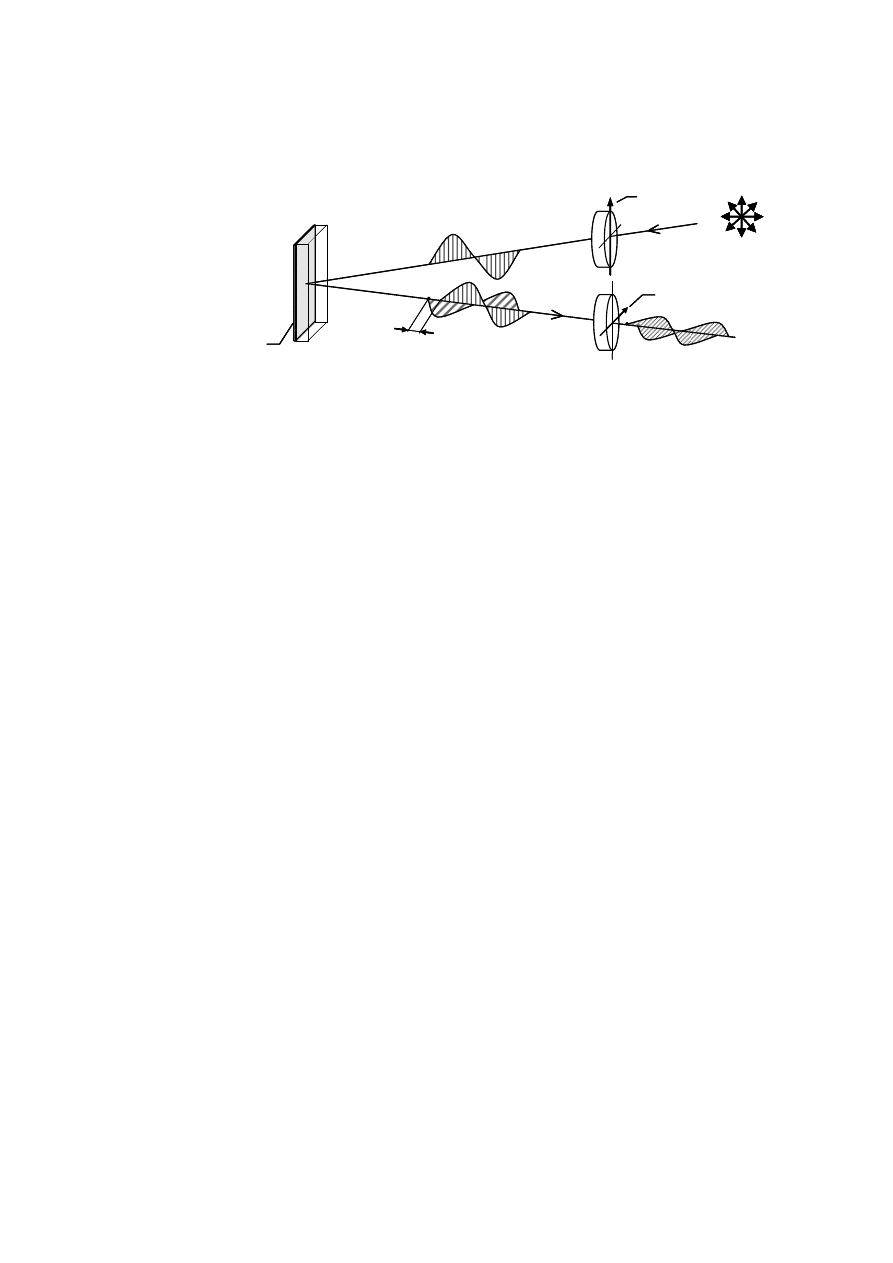
Na rys. 3.1 przedstawiony jest schemat układu optycznego do badań elastooptycznych
metodą światła odbitego z wykorzystaniem polaryzacji liniowej. W układzie tym wiązka
światła niespolaryzowanego przechodzi przez filtr polaryzacyjny – polaryzator, w którym
zostają wygaszone składowe drgań wektora świetlnego w płaszczyznach innych niż
płaszczyzna polaryzacji. Następnie, po przejściu przez ośrodek dwójłomny, wiązka zostaje
rozszczepiona na dwa przesunięte w fazie promienie o wzajemnie prostopadłych kierunkach
drgań wektora świetlnego, odpowiadających kierunkom głównym odkształcenia. (Kierunki te
nie muszą pokrywać się z pierwotną płaszczyzną polaryzacji). Na koniec, w kolejnym filtrze
polaryzacyjnym, zwanym analizatorem, przepuszczane są jedynie te składowe obu promieni,
które są równoległe do jego osi polaryzacji.
6
Polaryzator
Analizator
Prześwietlany
ośrodek dwójłomny
Powłoka
odblaskowa
Źródło światła
δ
Oś optyczna
Oś optyczna
Polaryzator
Analizator
Prześwietlany
ośrodek dwójłomny
Powłoka
odblaskowa
Źródło światła
δ
Oś optyczna
Oś optyczna
Rys. 3.1 Schemat układu optycznego do badań elastooptycznych metodą światła odbitego
z wykorzystaniem polaryzacji liniowej
Interferencja
Uzyskiwany obraz, składający się z występujących na przemian jasnych i ciemnych linii
powstaje dzięki interferencji dwóch wzajemnie przesuniętych w fazie składowych promienia
świetlnego, powstałych w wyniku zjawiska dwójłomności wymuszonej. W efekcie nakładania
się fal powstaje nowy rozkład amplitudy drgań z charakterystycznymi miejscami ich
wzmocnienia i wygaszenia, widocznymi w postaci prążków interferencyjnych, układających
się w formie izoklin lub izochrom.
3.6 OBRAZY ELASTOOPTYCZNE
Można wykazać, że natężenie I
a
światła opuszczającego analizator zależy od kąta α,
zawartego pomiędzy kierunkami głównymi naprężeń a osią analizatora, oraz od przesunięcia
względnego promieni opuszczających analizator, określonego zależnością (3.3):
m
I
I
p
a
π
α
2
2
sin
2
sin
=
(3.6)
gdzie: I
p
– natężenie wiązki światła po przejściu przez polaryzator.
Na podstawie własności funkcji trygonometrycznych można wysnuć wniosek, że
w określonych obszarach prześwietlanego obiektu natężenie I
a
będzie równe zeru, co można
obserwować w postaci ciemnych linii. Wygaszenie to nastąpi, gdy:
sin
2
2α = 0, tzn. gdy α = 0 lub 90°
(3.7)
lub
sin
2
πm = 0, tzn. gdy m = 0, 1, 2, 3, ...
(3.8)
7
Pierwszy z powyższych przypadków wygaszenia następuje w punktach pokrywania się
kierunków głównych naprężeń z osiami polaryzacji, natomiast drugi – w punktach, w których
przesunięcie fazowe rozszczepionych promieni świetlnych jest zerowe, bądź równe
całkowitej wielokrotności długości fali światła. W pierwszym przypadku wspomniane ciemne
linie określane są mianem izoklin, zaś w drugim – izochrom.
Izokliny
Izokliny są to linie łączące punkty o jednakowych kierunkach naprężeń głównych.
Izoklina jest określona kątem α, zwanym parametrem izokliny. Na podstawie obrazu izoklin
dla różnych wartości parametru, można zbudować rozkład kierunków głównych stanu
naprężenia dla całego badanego modelu. Aby rozkład taki był dokładny, wyznacza się
przebieg izoklin, których parametry różnią się o 5-10º w przedziale 0-90º.
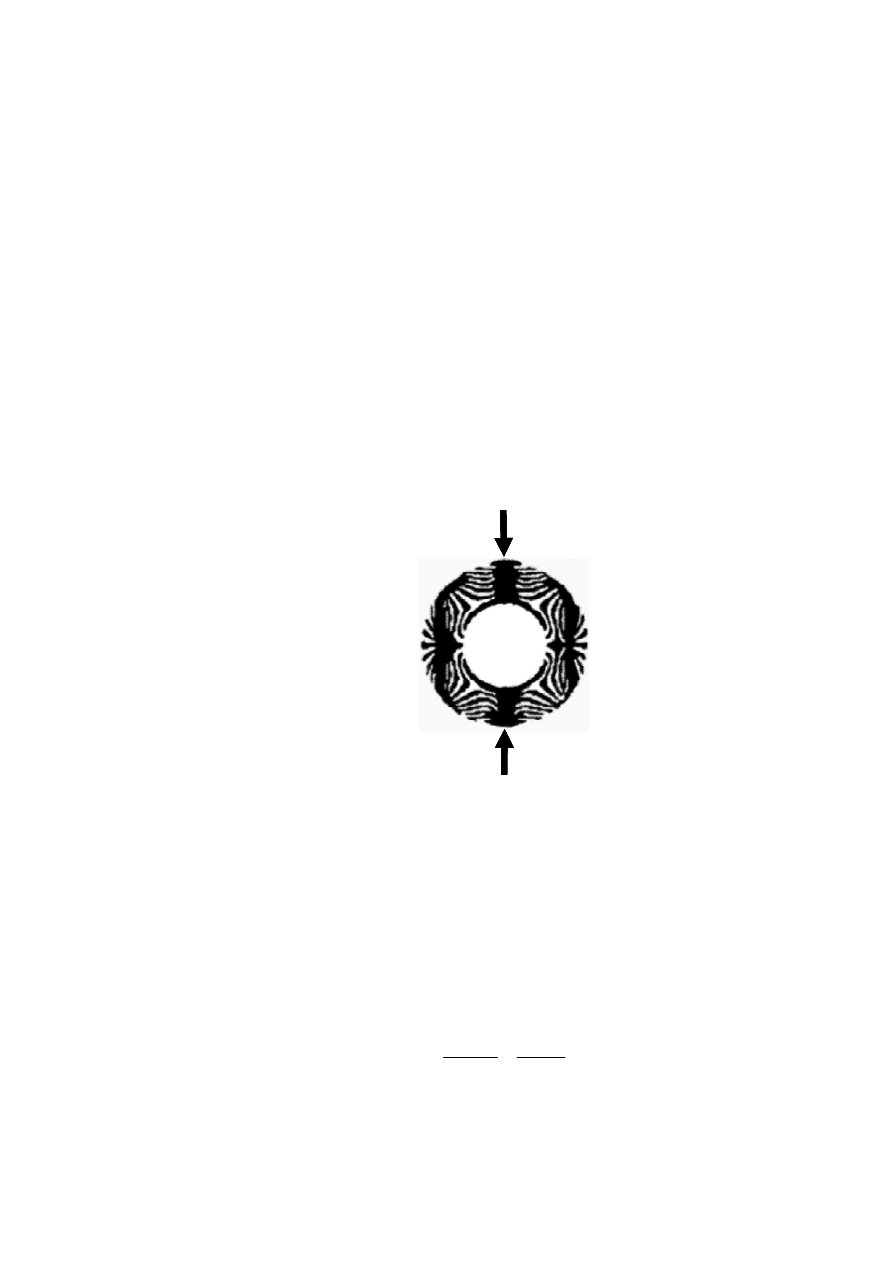
Rys. 3.2 Przykład zbiorczego układu izoklin
Na podstawie układów izoklin buduje się tzw. trajektorie naprężeń – układy linii
określających kierunki naprężeń w poszczególnych punktach badanego modelu.
Izochromy
Jak już zostało to wspomniane wcześniej, w miejscach, w których przebiegają
izochromy, spełniony jest warunek (3.8). A ponieważ z (3.5) wynika, że:
m
m
K
K
m
ε
σ
ε
ε
σ
σ
2
1
2
1
−
=
−
=
(3.9)
można zatem stwierdzić, że w tym przypadku wygaszenie promieni świetlnych następuje

8
w
tych miejscach, w których różnica naprężeń (odkształceń) głównych jest równa
wielokrotności stałej modelowej.
Czyli: Izochromy są to linie łączące punkty o jednakowej różnicy naprężeń głównych.
Określony wzorem (3.9) parametr m nazywany jest rzędem izochromy. Im wyższy rząd
izochromy, tym większa różnica naprężeń głównych i w ogólnym przypadku wyższy stopień
wytężenia materiału.
3.7 PODSTAWY INTERPRETACJI OBRAZÓW ELASTOOPTYCZNYCH
Przy interpretacji obrazów elastooptycznych wykorzystuje się szereg podstawowych
reguł, wynikających z charakteru rozpatrywanych zjawisk fizycznych. Poniżej zebrane są
najważniejsze z nich.
• Przy stopniowym obciążaniu jako pierwsza pojawia się izochroma rzędu zerowego,
odpowiadająca punktom izotropowym, czyli o zerowej różnicy naprężeń głównych.
• Kolejne rzędy izochrom pojawiają się w miejscach o najwyższych w danym momencie
wartościach różnicy naprężeń głównych (najczęściej na brzegach danego elementu
konstrukcji nośnej).
• Pojawiające się w miarę wzrostu obciążenia izochromy wyższych rzędów nie
powodują znikania izochrom niższych rzędów, lecz ich przesuwanie w kierunku
obszarów mniej wytężonych (stopniowe zagęszczanie linii izochrom).
• Izochromy różnych rzędów nie stykają się, nie przecinają, ani nie łączą ze sobą.
• Izochromy sąsiadujące ze sobą mogą być albo takiego samego rzędu, albo ich rząd
może się różnić o 1.
Przykładowy obraz izochrom obserwowany w modelu osprzętu roboczego
jednonaczyniowej koparki podsiębiernej przedstawiony jest na rys.3.3. Na obrazie tym można
wyróżnić kilka charakterystycznych obszarów:
1) Obszar jednoosiowego ściskania lub rozciągania (A)
W przypadku stanu jednoosiowego, tj. ściskania lub rozciągania, naprężenia są
jednorodne na całym obszarze danego elementu, tzn. w każdym punkcie mają jednakową
wartość. Czyli różnica naprężeń głównych jest również stała i na całej powierzchni
zaobserwujemy jednakowy obraz: ciemny (izochromę całkowitą), gdy różnica ta równa jest
stałej m, bądź jaśniejszy, gdy różnica naprężeń głównych odpowiada wartości pośredniej
pomiędzy kolejnymi rzędami izochromy.

9
Rys. 3.3 Obraz izochrom we fragmencie modelu osprzętu koparki
Stan taki wykazują widoczne na rysunku 3.3 elementy łączące siłownik z ramieniem
i łyżką. Są one połączone przegubowo, a zatem przenoszą wyłącznie naprężenia jednoosiowe
(rozciągające i ściskające), dlatego nie widać na nich prążków izochrom.
2) Obszar zginania (B)
Na podstawie mniej więcej równoległego przebiegu izochrom w środkowym odcinku
ramienia łyżki, przy założeniu płaskiego stanu naprężenia można stwierdzić, że panujący
w tym fragmencie stan naprężenia odpowiada w znacznym stopniu zginaniu. Na tej podstawie
można też zidentyfikować rzędy izochrom: dwie położone symetrycznie najbliżej osi
podłużnej ramienia – czyli osi obojętnej zginania – są rzędu pierwszego. Bezpośrednio
sąsiadujące z nimi i położone bliżej brzegów izochromy są rzędu drugiego, a przy dolnej
krawędzi ramienia łyżki widoczna jest również formująca się izochroma rzędu trzeciego.
Szczegółowe informacje o przebiegu izochrom w obszarze czystego zginania podane są
w następnym punkcie, opisującym wyznaczanie elastooptycznej stałej modelowej.
3) Obszar spiętrzenia naprężeń (C)
Obszary spiętrzeń naprężeń widoczne są w rejonach karbów geometrycznych. W tych
miejscach występuje zagęszczenie linii izochrom. Szczególnie wyraźnie można to
A
C
B
10
obserwować w okolicy załamania zarysu wysięgnika – pomiędzy sworzniem mocowania
siłownika a osią obrotu ramienia łyżki. W tym fragmencie na stosunkowo krótkim odcinku
szybko przyrasta rząd izochromy, a zatem gwałtownie rośnie różnica naprężeń głównych
i pojawia się ryzyko niebezpiecznego zbliżenia się do granicy plastyczności lub nawet jej
przekroczenia.
3.8 WYZNACZANIE ELASTOOPTYCZNEJ STAŁEJ MODELOWEJ
Ważnym uzupełnieniem poglądowych informacji uzyskanych z rozkładu prążków
izochrom jest ich „skalibrowanie”, tj. przyporządkowanie poszczególnym rzędom izochrom
konkretnych wartości różnicy naprężeń głównych, jakim odpowiadają. Kluczem do tego jest
zawarta we wzorze 3.9 elastooptyczna stała modelowa. Jest ona ściśle związana
z parametrami materiału optycznie czynnego użytego do badań elastooptycznych. Zazwyczaj
wyznacza się ją doświadczalnie, poddając próbkę takiego materiału stanowi obciążenia, dla
którego w łatwy sposób można wyznaczyć analitycznie wywołane nim naprężenia.
W praktyce stosuje się do tego celu próbę z czystym zginaniem belki lub ściskaniem tarczy
kołowej. W ramach niniejszego ćwiczenia wykorzystana będzie pierwsza z tych metod.
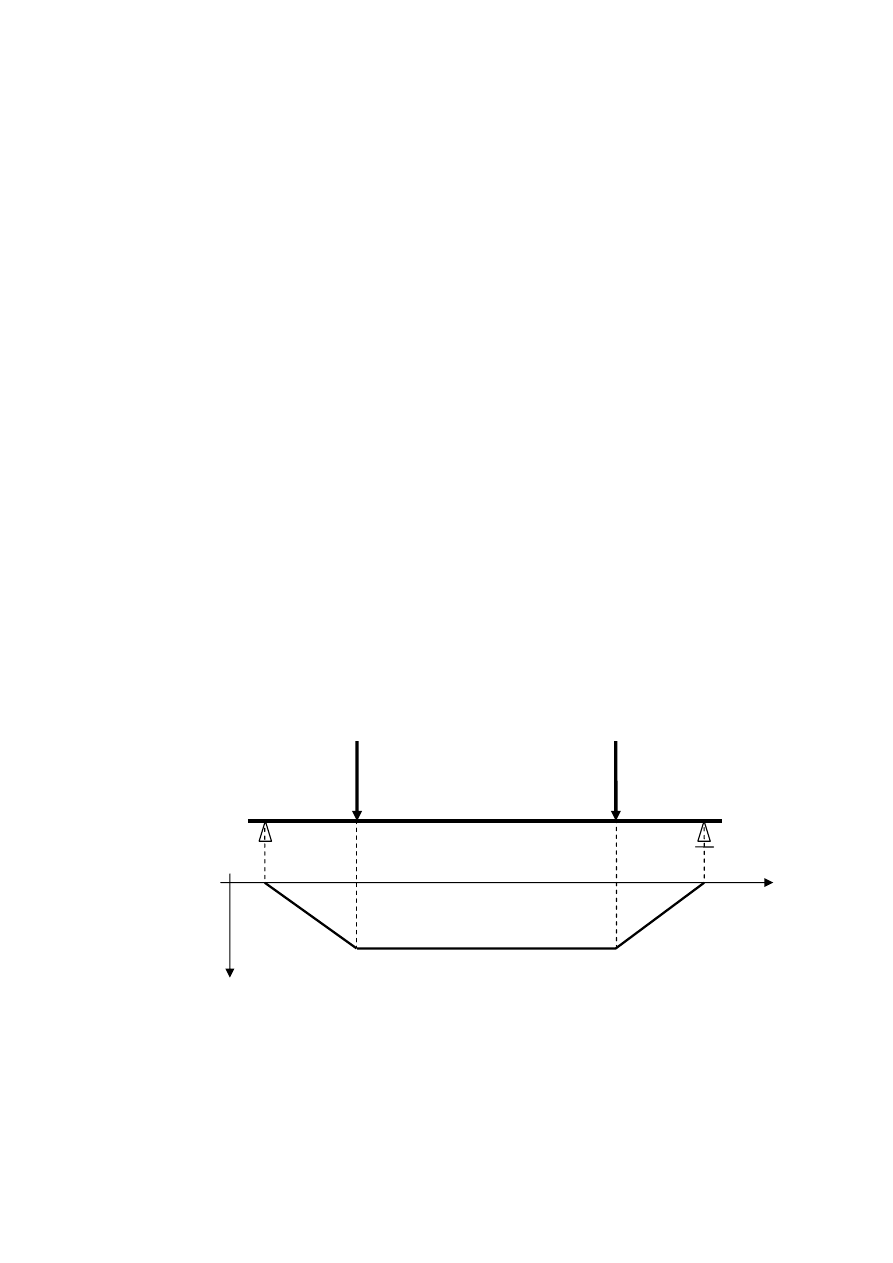
Dla przedstawionej na rys. 3.4 belki, podpartej przegubowo i obciążonej dwiema
równymi co do wartości siłami skupionymi, obszar czystego zginania wystąpi na odcinku
o stałej wartości momentu gnącego Mg.
Rys. 3.4 Czyste zginanie belki na odcinku pomiędzy siłami punktowymi
Stała wartość momentu gnącego oznacza, że rozkłady naprężeń w przekrojach
poprzecznych są identyczne, niezależnie od ich odległości od krańców belki (rys. 3.5).
Natomiast wzdłuż przekroju poprzecznego belki wartości naprężeń zmieniają się liniowo: na
P
P
M
g
x
11
osi obojętnej są zerowe i osiągają wartości maksymalne na brzegach. Czyli im dalej od osi
obojętnej, tym większa jest różnica naprężeń głównych. Stąd można wyciągnąć wniosek, że
czyste zginanie w płaskim stanie naprężenia objawiać się będzie równoległym przebiegiem
izochrom. Ponadto im dalej od osi obojętnej, tym rząd obserwowanej izochromy będzie
wyższy.
Rys. 3.5 Naprężenia w belce poddanej czystemu zginaniu
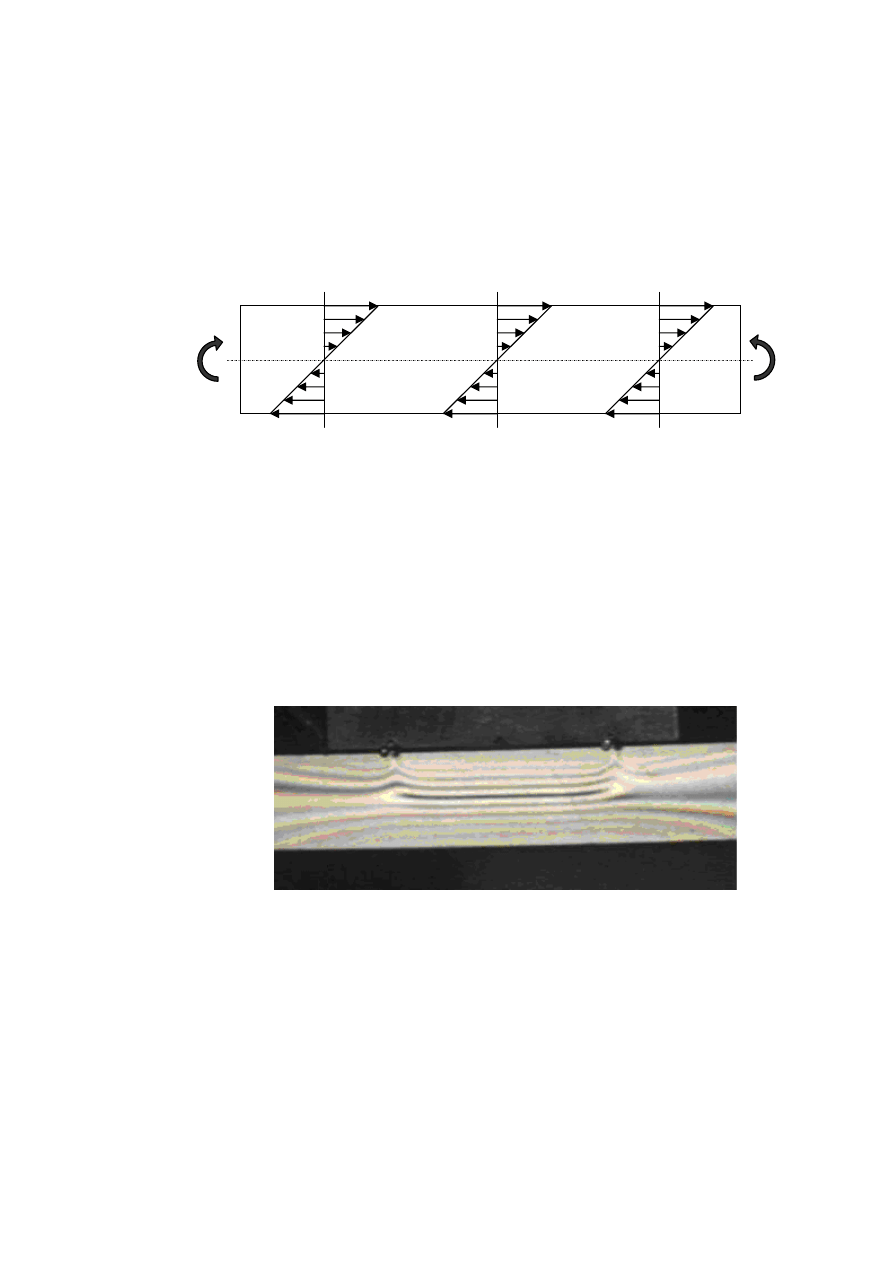
Obraz izochrom w zginanej belce przedstawiony jest na rys. 3.6. W osi obojętnej
widoczny jest fragment izochromy zerowej, odpowiadającej zerowej różnicy naprężeń
głównych. Sąsiadują z nią położone po obu stronach osi obojętnej izochromy rzędu
pierwszego (obraz jest symetryczny dla strony ściskanej i rozciąganej). Dalej – w miarę
zbliżania się do brzegów belki – widoczne są izochromy rzędu drugiego, trzeciego, czwartego
i piątego.
Rys. 3.6 Obraz izochrom w belce poddanej obciążeniom zginającym
Znając dla obciążonej belki wartości sił i parametrów geometrycznych układu, na
podstawie znanych zależności można wyznaczyć rozkład wartości naprężeń w przekroju
poprzecznym na odcinku czystego zginania, a następnie przyporządkować je poszczególnym
rzędom izochrom widocznym na obrazie elastooptycznym zginanej belki oraz ze wzoru (3.4)
wyznaczyć stałą naprężeniową K
σm
.
„+”
„–”
M
g
M
g
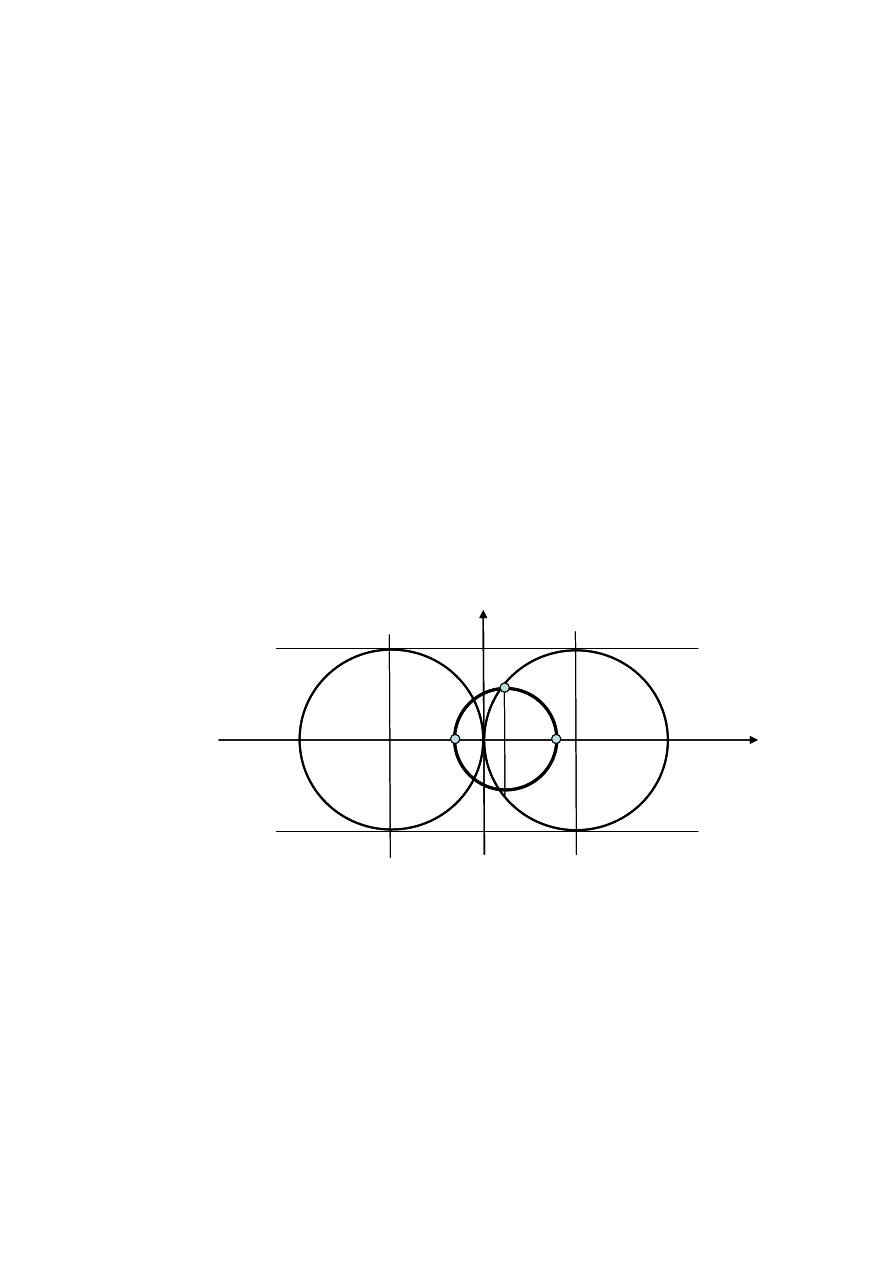
12
3.9 OKREŚLENIE STANU WYTĘŻENIA
Na podstawie uzyskanych z obrazów elastooptycznych wartości różnicy naprężeń
głównych w poszczególnych obszarach konstrukcji można określić jej stan wytężenia,
korzystając w tym celu z hipotez wytężeniowych. Najprościej jest tego dokonać korzystając z
hipotezy wytężeniowej Treski (zwanej inaczej hipotezą maksymalnych naprężeń stycznych),
z wystarczającą dla większości sytuacji dokładnością oddającą własności metali. W myśl tej
hipotezy, miarą wytężenia materiału jest wartość występującego w nim maksymalnego
naprężenia stycznego (rys. 3.7).
W płaskim stanie naprężenia (PSN), dla hipotezy tej można wyprowadzić zależność:
σ
1
–
σ
2
= 2
τ
max
(3.10)
Łącząc to z zależnością (3.9) można stwierdzić, że w tym przypadku izochromy stają się
jednocześnie liniami łączącymi punkty o jednakowym stopniu wytężenia. Pozwala to w łatwy
sposób szacować, jak daleko jest do przekroczenia granicy plastyczności w poszczególnych
obszarach badanej konstrukcji.
σ
plr
= R
e
σ
pls
= -R
e
σ
1
σ
2
σ
τ
τ
max
τ
max(pl)
σ
plr
= R
e
σ
pls
= -R
e
σ
1
σ
2
σ
τ
τ
max
τ
max(pl)
Rys. 3.7 Obraz kół Mohra dla warunku plastyczności Treski
3.10 OPIS STANOWISKA BADAWCZEGO
Ćwiczenie przeprowadzane jest na stanowisku dydaktycznym do badań elastooptycznych
stanu naprężenia w modelu osprzętu koparki. Analizie poddawany będzie obraz izochrom
uzyskany metodą światła odbitego, co umożliwia użycie polaryzatora zintegrowanego
z analizatorem w jednej obudowie, a także ustawienie po tej samej stronie źródła światła.
Model oraz wzorcowa belka, wykorzystywana w próbie czystego zginania, wykonane są

13
z tego samego materiału optycznie czułego – żywicy epoksydowej Epidian 5 (R
e
≈ 50 MPa),
a ich tylne powierzchnie pokryte są warstwą odblaskową. Obciążanie realizowane jest za
pomocą dostępnych na stanowisku obciążników. Uzyskany obraz izochrom przekazywany
jest za pośrednictwem kamery na ekran komputera; można go trwale zarejestrować
i wydrukować.
3.11 WYKONANIE ĆWICZENIA
W ramach ćwiczenia wykonywana jest rejestracja obrazów elastooptycznych dla
obciążonego modelu oraz belki kalibracyjnej podanej próbie czystego zginania, a następnie
dokonywana jest ich analiza i na tej podstawie przeprowadzane jest wnioskowanie o stanie
naprężenia i stopniu wytężenia poszczególnych fragmentów modelu konstrukcji.
Przebieg ćwiczenia
1. Omówienie podstawowych zagadnień związanych z wykonywanym ćwiczeniem.
2. Obciążenie badanego modelu i analiza uzyskanych stanów naprężenia.
• Zarejestrowanie obrazów elastooptycznych dla wybranych fragmentów modelu.
• Naniesienie wartości rzędów izochrom na każdym z zarejestrowanych obrazów.
• Krótki opis lokalnych stanów naprężenia na podstawie przebiegu izochrom.
3. Wyznaczenie elastooptycznej stałej modelowej K
σm
oraz skalibrowanie izochrom.
• Przeprowadzenie próby obciążenia zginającego belki kalibracyjnej.
• Zarejestrowanie obrazu izochrom dla obszaru czystego zginania.
• Obliczenie rozkładu naprężeń wzdłuż przekroju poprzecznego z obszaru czystego
zginania.
• Przyporządkowanie izochrom kolejnym rzędom wartości naprężeń na
zarejestrowanym obrazie.
• Wyznaczenie elastooptycznej stałej modelowej K
σm
.
4. Naniesienie odpowiednich wartości naprężeń na obrazy elastooptyczne badanego modelu.
5. Ocena stopnia wytężenia analizowanych fragmentów modelu.
3.12 LITERATURA
1. Z. Orłoś: Doświadczalna analiza odkształceń i naprężeń. PWN, Warszawa, 1977.
2. Z. Dyląg, A. Jakubowicz, Z. Orłoś: Wytrzymałość materiałów, WNT, Warszawa, 1996
3. H. Frąckiewicz i inni: Węzły i połączenia konstrukcyjne. WNT, Warszawa, 1985.
Wyszukiwarka
Podobne podstrony:
Lab KN cw 2
Lab KN cw 5 id 258468 Nieznany
Lab KN cw 4 id 258467 Nieznany
Lab KN cw 1
Lab KN cw 6
Lab KN cw 2
Lab KN cw 5 id 258468 Nieznany
Lab KN cw 5
Lab KN cw 6
Lab KN cw 4
Lab KN cw 3
Lab KN cw 2
Lab technologii ćw 2 ogarnijtemat com
Lab TP Ćw 7
Instr lab elektronika Cw 2
ćw 1 SRT4, SiMR, Pojazdy, Lab. Pojazdów, Ćw 1
teoria przezwojowana, Semestr 3 moje, FIZYKA LAB, fizyka cw 1
Lab technologii cw 4 id 258645 Nieznany
Lab technologii cw 6 id 258649 Nieznany
więcej podobnych podstron