WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

1

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

7.1. Wiadomości podstawowe

W niniejszym rozdziale przyjmiemy założenia przedstawione w punkcie 1.2. Założymy więc, że

mamy do czynienia z ośrodkiem ciągłym, izotropowym i jednorodnym.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

X

P

q(x)

N

M=M

Y

T=T

Z

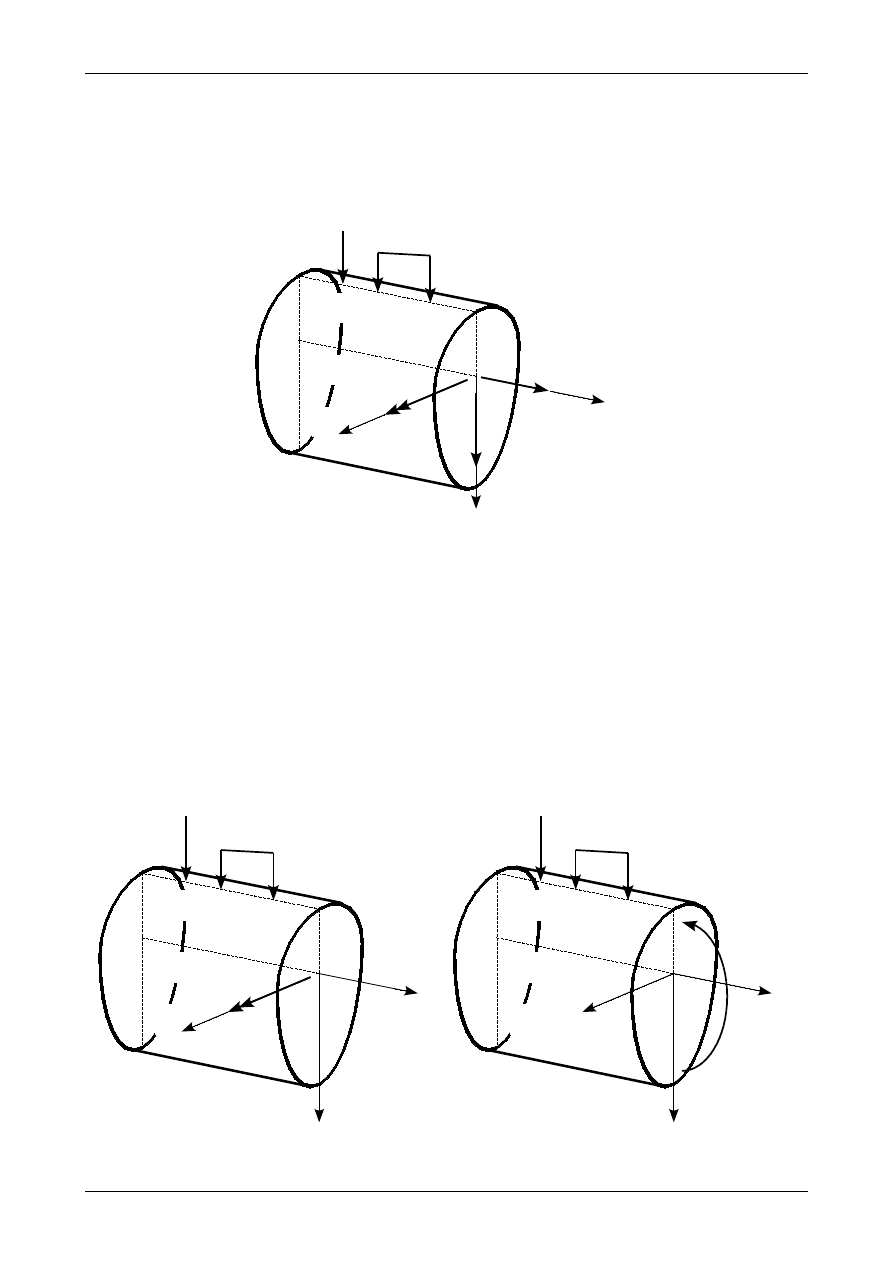
Rys. 7.1. Siły działające na pręt

Rysunek 7.1 przedstawia pręt wraz z działającymi na niego siłami. Zakładamy, że wszystkie siły

czynne i reakcje będą działały w płaszczyźnie ZX, która pokrywa się z główną osią bezwładności Z

gl

.

W takim przypadku w przekroju pręta działają trzy siły przekrojowe: siła normalna N, siła poprzeczna T=T

Z

oraz moment zginający M=M

Y

. Wartości i zwroty tych sił będziemy odczytywali z ich wykresów.

Siła normalna będzie dodatnia, jeżeli będzie rozciągała pręt. Moment zginający będzie dodatni,

jeżeli jego wektor będzie miał zwrot zgodny ze zwrotem osi Y. Jak wiadomo zwrot tego wektora jest
zgodny z kierunkiem kręcenia się śruby prawoskrętnej. Rysunek 7.2 przedstawia dodatni moment zginający.
Jak widać rozciąga on dolną część przekroju pręta. Obie zasady znakowania są więc zgodne z zasadami
znakowania tych sił przekrojowych na wykresach.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

X

P

q(x)

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

X

P

q(x)

M=M

Y

M

=M

Y

Rys. 7.2. Dodatni moment zginający

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

2

Nieco inaczej sprawa ma się z siłą poprzeczną T=T

Z

. Dodatnia siła poprzeczna kręcąca odciętą

częścią pręta zgodnie z ruchem wskazówek zegara nie zawsze będzie dodatnia w układzie związanym
z przekrojem pręta. W związku z tym w niniejszym opracowaniu będziemy operowali zwrotem oraz war-
tością bezwzględną siły poprzecznej odczytaną na podstawie wykresu. Rysunek 7.3 przedstawia siłę pop-
rzeczną, której wartość na wykresie jest dodatnia. Jak widać w układzie związanym z przekrojem pręta jej
zwrot jest zgodny ze zwrotem osi Z=Z

gl

. Na rysunku tym jest także przedstawiona dodatnia siła normalna

oraz dodatni moment zginający.

X

N

T

=

T

Z

M=M

Y

Z=Z

0

=Z

gl

Rys. 7.3. Siły przekrojowe

7.2. Wektor naprężenia

W dotychczasowych rozważaniach rozpatrywaliśmy działanie sił przekrojowych w całym przekroju

pręta. Teraz zajmiemy się tym, co dzieje się w dowolnym punkcie tego przekroju.

n

f

(n)

dA

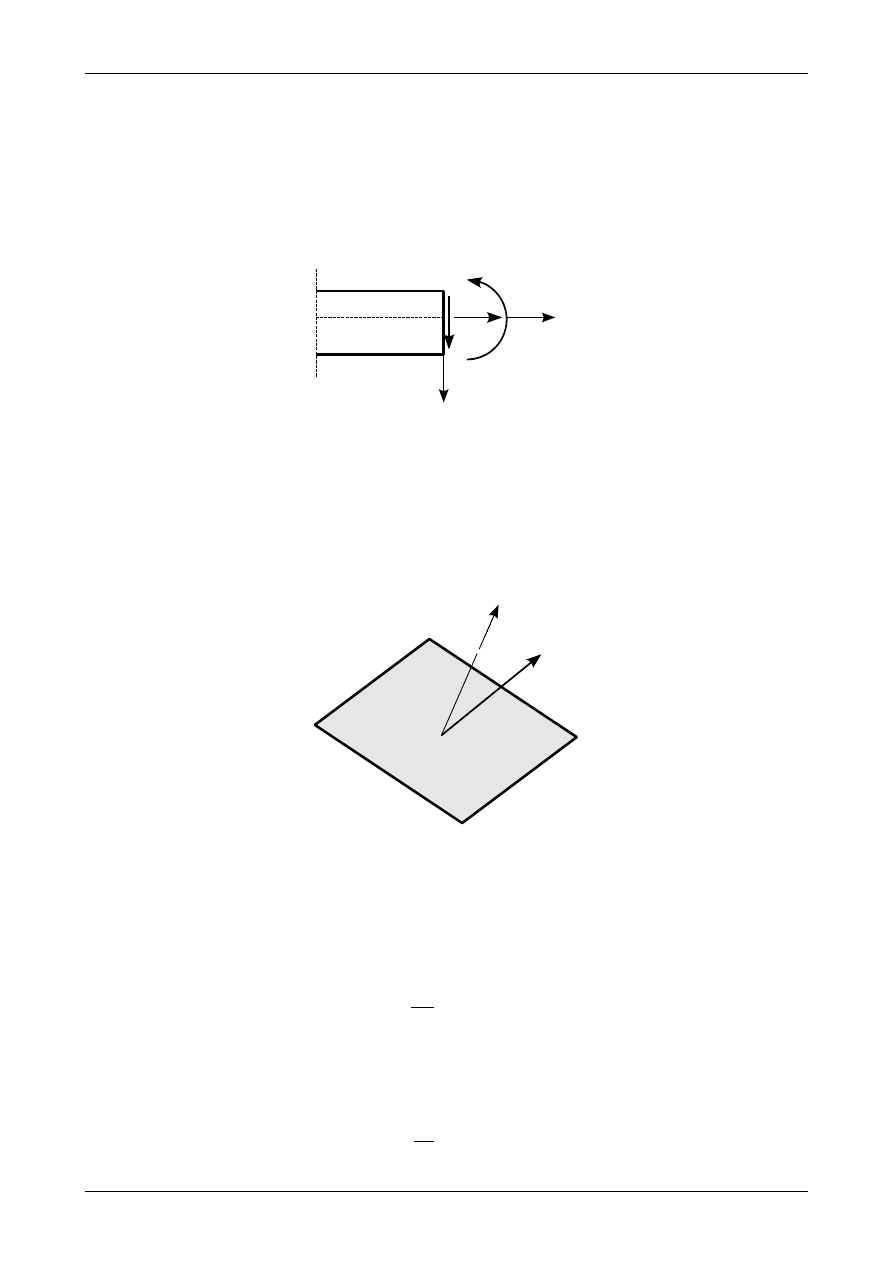
Rys. 7.4. Wektor naprężenia

Rysunek 7.4 przedstawia elementarne pole powierzchni dA, które jest określone przez jednostkowy

wektor normalny n. Wektor ten jest prostopadły do powierzchni dA. Na tą powierzchnię działa elemen-
tarna siła dF. Wprowadźmy pojęcie wektora naprężenia, który określimy jako

f



n



=

dF

dA

.

(7.1)

Jednostką wektora naprężenia jest Pascal czyli

[

Pa

]

=

[

N

m

2

]

.

(7.2)

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

3

W przypadku materiałów występujących w budownictwie będziemy korzystamy z wielokrotności MPa,
która wynosi

[

MPa

]

=

[

MN

m

2

]

.

(7.3)

Wartość wektora naprężenia możemy wyrażać także w

[

kN

cm

2

]

.

(7.4)

Jednostkę (7.4) stosujemy ze względu na to, że siły przekrojowe są wyrażone najczęściej w kN lub kNm
natomiast charakterystyki geometryczne wyraża się najczęściej w cm

2

, cm

3

lub cm

4

. Jednostkę tę w MPa

możemy wyrazić jako

1

kN

cm

2

=

1 kN

1 cm

2

=

10

−

3

10

−

4

MN

m

2

=

10MPa

.

(7.5)

Wektor naprężenia na powierzchni dA możemy rozłożyć na dwa wektory składowe. Pierwszym z nich

jest wektor normalny (prostopadły) do tej powierzchni nazywany naprężeniem normalnym

σ

(n)

. Drugim

jest wektor styczny (leżący na tej powierzchni) nazywany naprężeniem stycznym

τ

(n)

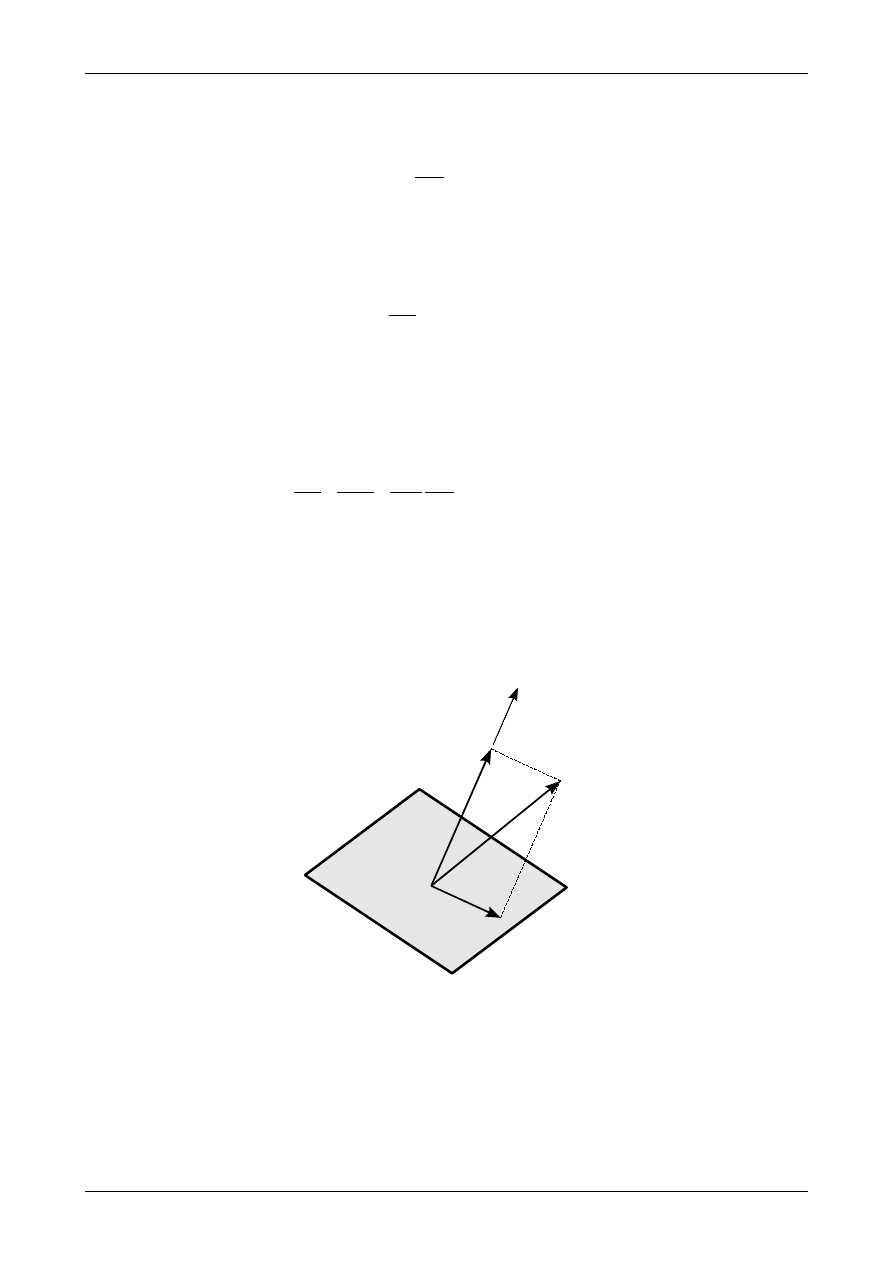
. Rysunek 7.5 przed-

stawia naprężenie normalne i styczne działające na elementarnej powierzchni dA. Jednostki naprężenia
normalnego i stycznego są takie same jak i dla wektora naprężenia.

dA

n

f

(n)

σ

(n)

τ

(n)

Rys. 7.5. Naprężenie normalne i styczne

Rysunek 7.6 przedstawia składowe wektora naprężenia w dowolnym punkcie przekroju pręta. Nap-

rężenie normalne oznaczamy jako

σ

X

. Indeks X oznacza, że naprężenie to ma kierunek osi X. Naprężenie

styczne będzie miało dwie składowe. Oznaczamy je jako

τ

XY

oraz

τ

XZ

. Pierwszy z indeksów, czyli X oznacza,

że naprężenia te działają na powierzchni prostopadłej do osi X. Drugi z nich określa kierunek naprężenia.
Naprężenie

τ

XY

ma kierunek osi Y natomiast naprężenie

τ

XZ

ma kierunek osi Z. Odpowiednie naprężenie

będzie dodatnie, jeżeli będzie miało zwrot zgodny ze zwrotem odpowiedniej osi. Naprężenia przed-
stawione na rysunku 7.6 są więc dodatnie.

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

4

X

dA

dA

σ

X

τ

XZ

τ

XY

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

Rys. 7.6. Składowe wektora naprężenia w punkcie przekroju pręta

7.3. Działanie siły normalnej

Jeżeli w przekroju pręta działa tylko siła normalna to w dowolnym punkcie działać będzie tylko

składowa normalna wektora naprężenia czyli naprężenie normalne

σ

X

. Przedstawia to rysunek 7.7.

X

dA

dA

σ

X

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

N

Rys. 7.7 Siła normalna w przekroju pręta

Naprężenie normalne w dowolnym punkcie przekroju pręta wyznacza się ze wzoru



X

=

N

A

,

(7.6)

w którym N oznacza wartość siły normalnej działającej w przekroju pręta natomiast A oznacza pole
powierzchni przekroju pręta. Jak widać naprężenie normalne od działania tylko siły normalnej jest stałe na
całej powierzchni przekroju pręta.

7.4. Działanie momentu zginającego

Jeżeli w przekroju pręta działa tylko moment zginający to w dowolnym punkcie działać będzie tylko

składowa normalna wektora naprężenia czyli naprężenie normalne

σ

X

. Naprężenie to przedstawia rysunek

7.8.

Dr inż. Janusz Dębiński

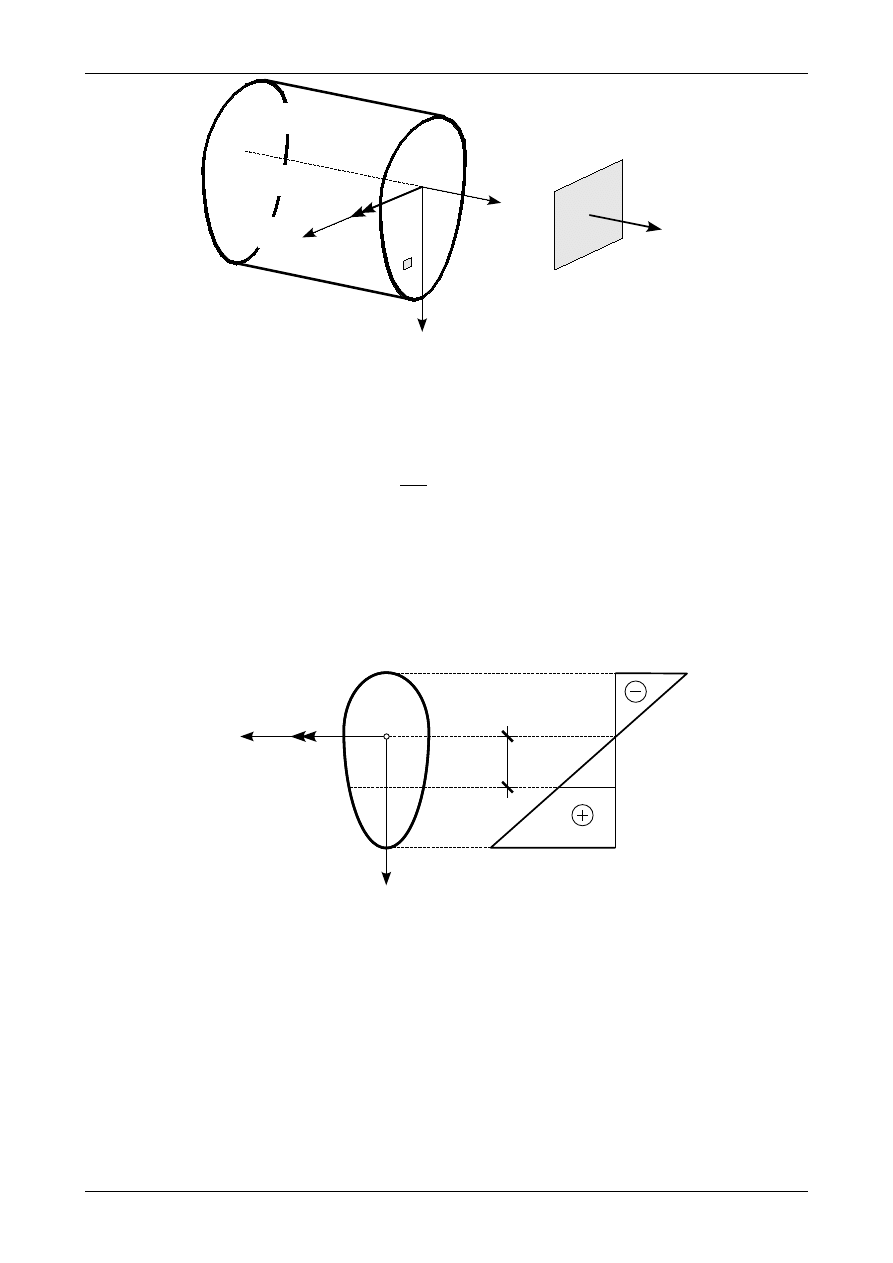
WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

5

X

dA

dA

σ

X

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

Rys. 7.8. Moment zginający w przekroju pręta

Naprężenie normalne w dowolnym punkcie przekroju pręta wyznacza się ze wzoru



X

=

M

Y

J

Y

⋅

z

,

(7.7)

w którym M

Y

oznacza moment zginający działający w przekroju pręta, J

Y

oznacza główny moment bezwład-

ności przekroju pręta względem osi Y=Y

gl

natomiast z oznacza współrzędną punktu, w którym wyznaczamy

wartość naprężenia normalnego. Jak więc widać wartość naprężenia normalnego od działania momentu
zginającego nie zależy od współrzędnej y. czyli dla punktów znajdujących się na jednej wysokości
naprężenie to jest jednakowe.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

0

sc

z

σ

X

σ

X

(z)

Rys. 7.9. Wykres naprężenia normalnego na wysokości przekroju od działania momentu zginającego

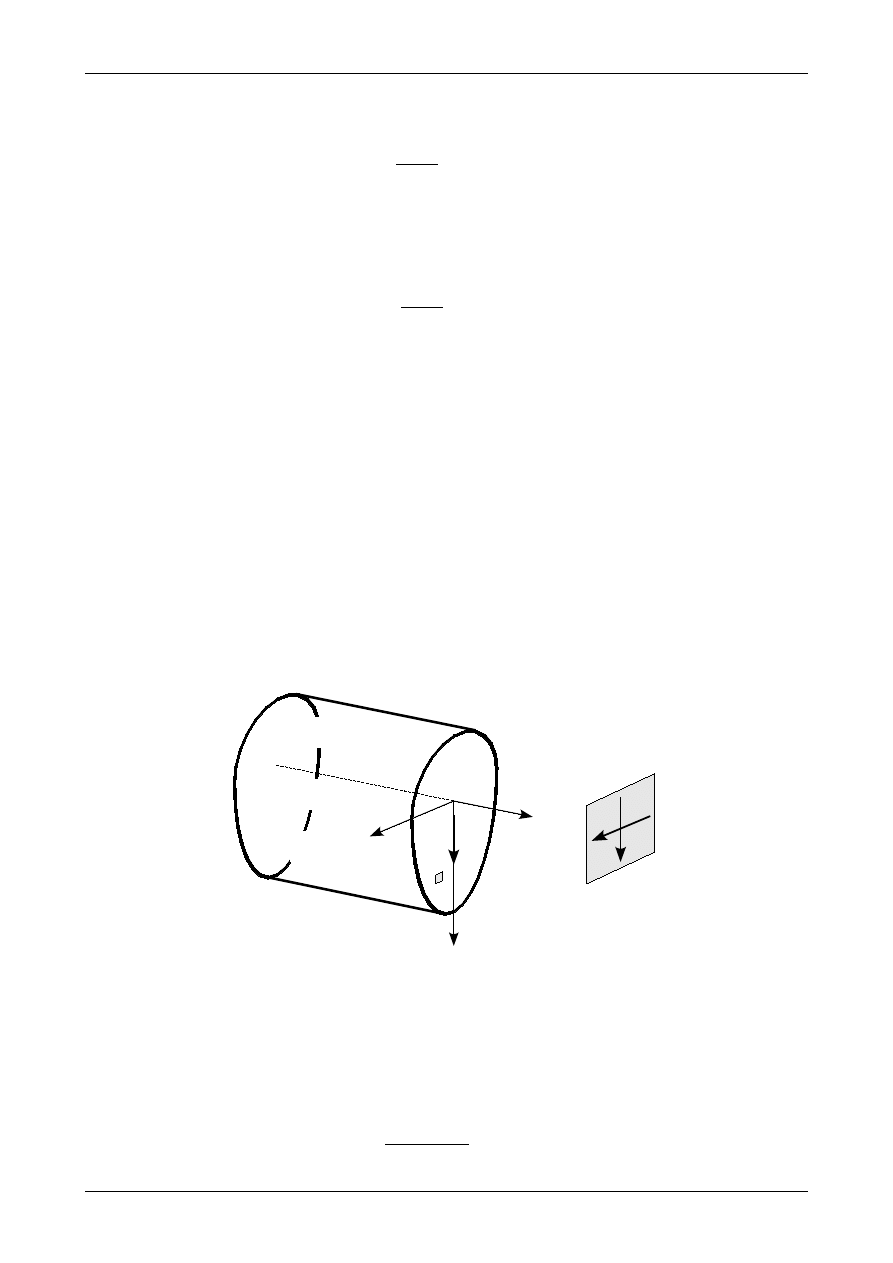
Rysunek 7.9 przedstawia wykres naprężenia normalnego od działania momentu zginającego na wyso-

kości przekroju. Jak widać największe naprężenia występują na krawędzi dolnej i górnej przekroju. Naprę-
żenie to wynosi zero w punktach leżących na wysokości środka ciężkości przekroju. Punkty te tworzą tak
zwaną oś obojętną.

7.5. Działanie siły normalnej i momentu zginającego

Jeżeli w przekroju pręta działa siła normalna oraz moment zginający to w dowolnym punkcie działać

będzie tylko składowa normalna wektora naprężenia czyli naprężenie normalne

σ

X

. Naprężenie to przedsta-

wia rysunek 7.10.

Dr inż. Janusz Dębiński

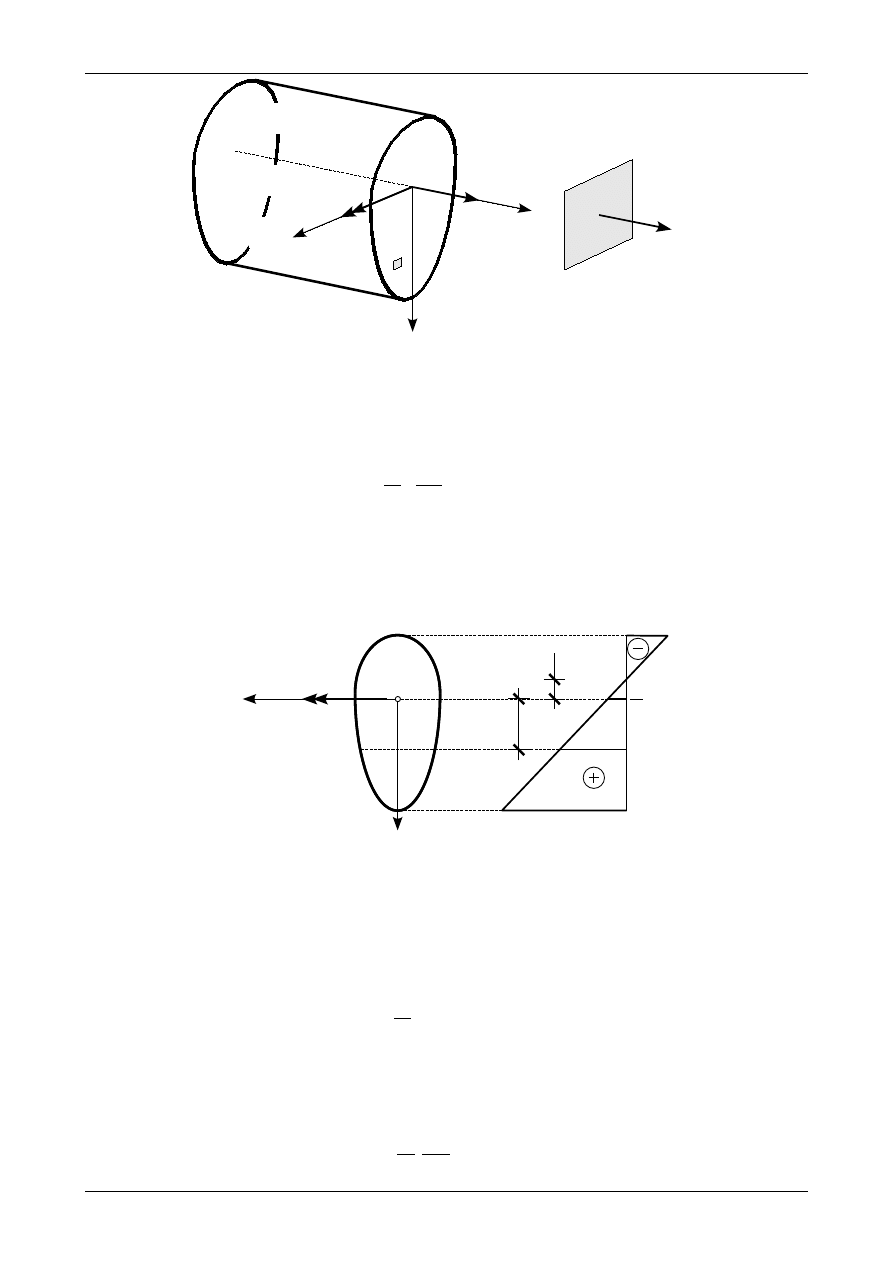
WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

6

X

dA

dA

σ

X

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

N

Rys. 7.10. Siła normalna i moment zginający w przekroju pręta

Naprężenie normalne w dowolnym punkcie przekroju pręta wyznacza się ze wzoru



X

=

N

A



M

Y

J

Y

⋅

z

.

(7.8)

Jak więc widać wartość naprężenia normalnego od działania siły normalnej oraz momentu zginającego nie
zależy od współrzędnej y. czyli dla punktów znajdujących się na jednej wysokości naprężenie to jest jedna-
kowe.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

z

N>0

z

0

σ

X

σ

X

(z)

sc

N

A

Rys. 7.11. Wykres naprężenia normalnego na wysokości przekroju od działania siły normalnej i momentu zginającego

Rysunek 7.11 przedstawia wykres naprężenia normalnego od działania siły normalnej i momentu

zginającego na wysokości przekroju. Największe naprężenia występują na krawędzi dolnej i górnej przek-
roju. W punktach znajdujących się na wysokości środka ciężkości naprężenie normalne jest równe

N

A

.

(7.9)

Oś obojętna będzie zbiorem punktów o współrzędnej z równej

z

0

=−

N

A

⋅

J

Y

M

Y

.

(7.10)

Dr inż. Janusz Dębiński

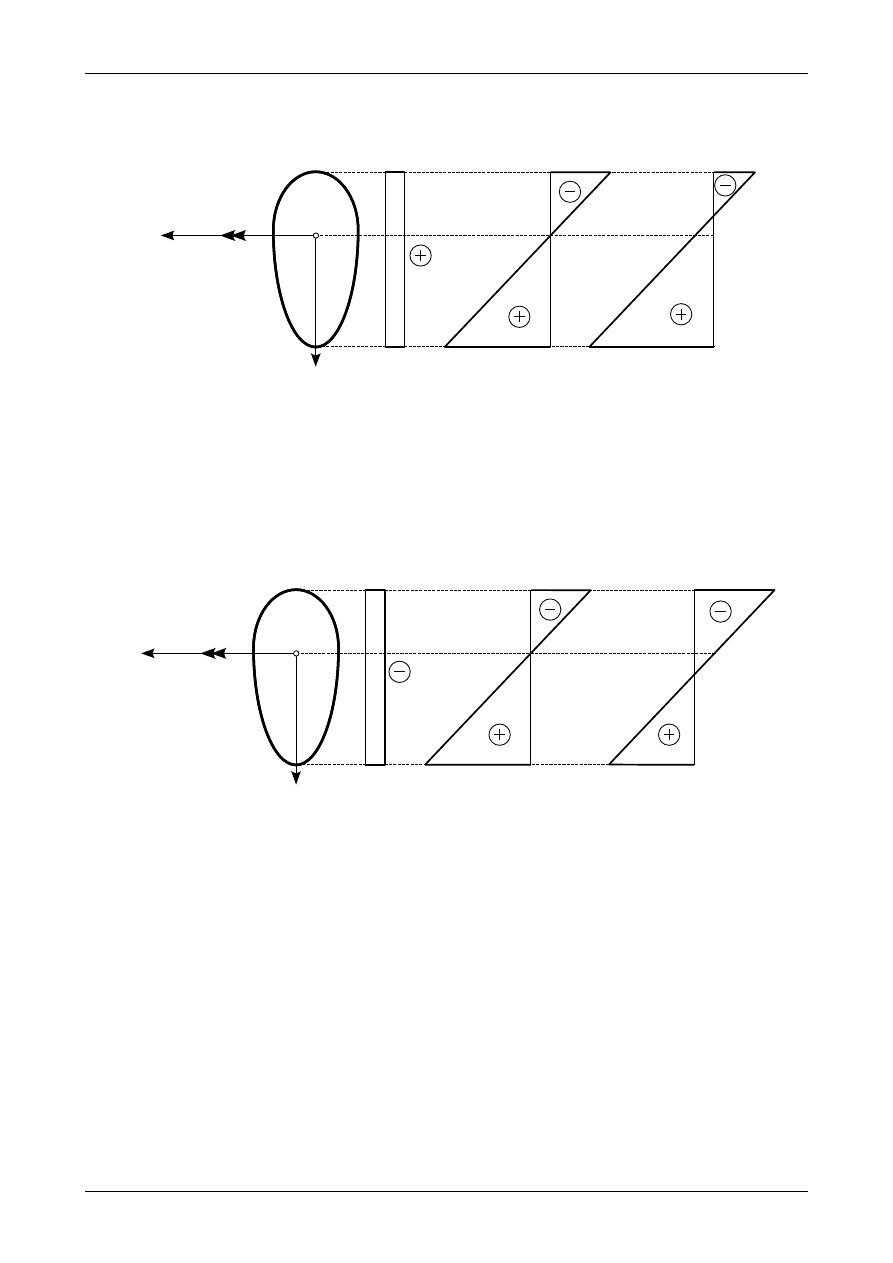
WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

7

Analizując wzór (7.8) widać, że naprężenie normalne jest sumą naprężenia od działania siły normal-

nej i od działania momentu zginającego. Także wykres naprężeń będzie sumą wykresu od siły normalnej i od
momentu zginającego.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

N>0

σ

X

sc

σ

X

(N)

σ

X

(M)

Rys. 7.12. Wykres naprężenia normalnego od dodatniej siły normalnej i dodatniego momentu zginającego

Rysunek 7.12 przedstawia wykres naprężeń normalnych od działania dodatniej siły normalnej i do-

datniego momentu zginającego. Na krawędzi dolnej dodatnie naprężenie normalne od siły normalnej i mo-
mentu zginającego sumuje się. W środku ciężkości mamy tylko naprężenie od dodatniej siły normalnej. Na
krawędzi górnej ujemne naprężenie od działania momentu zginającego zwiększa się o wartość naprężenia od
działania siły normalnej. Nachylenie wykresu od momentu zginającego i wykresu sumarycznego jest takie
samo.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

N<0

σ

X

sc

σ

X

(N)

σ

X

(M)

Rys. 7.13. Wykres naprężenia normalnego od ujemnej siły normalnej i dodatniego momentu zginającego

Rysunek 7.13 przedstawia wykres naprężeń normalnych od działania ujemnej siły normalnej i do-

datniego momentu zginającego. Na krawędzi górnej ujemne naprężenie normalne od siły normalnej i mo-
mentu zginającego sumuje się. W środku ciężkości mamy tylko naprężenie od ujemnej siły normalnej. Na
krawędzi dolnej dodatnie naprężenie od działania momentu zginającego zmniejsza się się o wartość naprę-
żenia od działania siły normalnej. Nachylenie wykresu od momentu zginającego i wykresu sumarycznego
jest takie samo.

Rysunek 7.14 przedstawia wykres naprężeń normalnych od działania dodatniej siły normalnej i ujem-

nego momentu zginającego. Na krawędzi górnej dodatnie naprężenie normalne od siły normalnej i momentu
zginającego sumuje się. W środku ciężkości mamy tylko naprężenie od dodatniej siły normalnej. Na
krawędzi dolnej ujemne naprężenie od działania momentu zginającego zwiększa się się o wartość naprę-
żenia od działania siły normalnej. Nachylenie wykresu od momentu zginającego i wykresu sumarycznego
jest takie samo.

Rysunek 7.15 przedstawia wykres naprężeń normalnych od działania ujemnej siły normalnej i ujem-

nego momentu zginającego. Na krawędzi dolnej ujemne naprężenie normalne od siły normalnej i momentu
zginającego sumuje się. W środku ciężkości mamy tylko naprężenie od ujemnej siły normalnej. Na krawędzi
górnej dodatnie naprężenie od działania momentu zginającego zmniejsza się o wartość naprężenia od

Dr inż. Janusz Dębiński

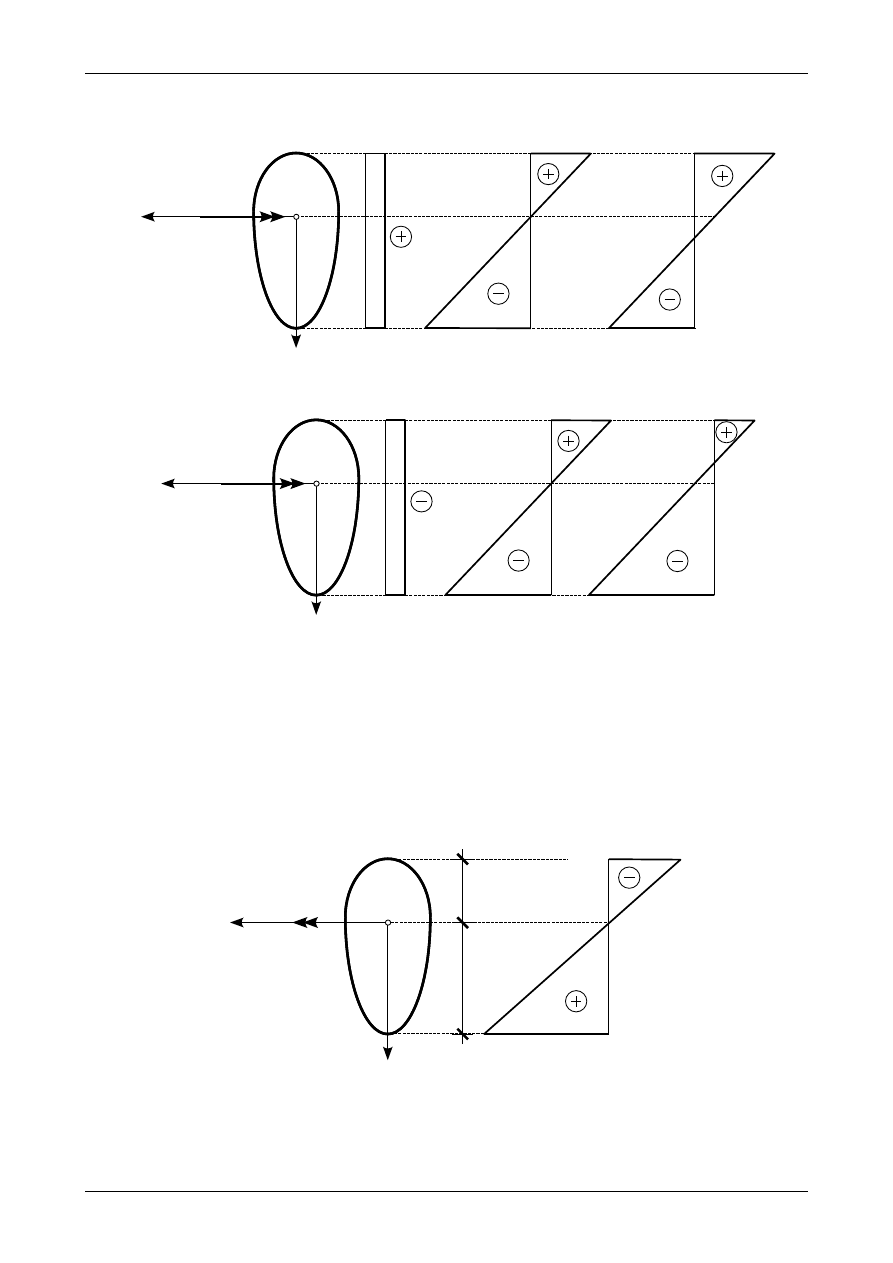
WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

8

działania siły normalnej. Nachylenie wykresu od momentu zginającego i wykresu sumarycznego jest takie
samo.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

N>0

σ

X

sc

σ

X

(N)

σ

X

(M)

Rys. 7.14. Wykres naprężenia normalnego od dodatniej siły normalnej i ujemnego momentu zginającego

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

N<0

σ

X

sc

σ

X

(N)

σ

X

(M)

Rys. 7.15. Wykres naprężenia normalnego od ujemnej siły normalnej i ujemnego momentu zginającego

7.6. Projektowanie przekroju pręta

Projektowanie przekroju pręta ograniczymy tylko do przypadku działania momentu zginającego,

ponieważ naprężenie normalne

σ

X

od działania siły normalnej jest z reguły dużo mniejsze niż naprężenie

normalne

σ

X

od działania momentu zginającego. Rysunek 7.16 przedstawia wykres naprężeń normalnych od

działania tylko momentu zginającego.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

M=M

Y

z

d

0

N=0

z

g

σ

X

σ

X

(d)

σ

X

(g)

sc

Rys. 7.16. Wykres naprężenia normalnego

σ

X

od działania tylko momentu zginającego

Na długości pręta naprężenia normalne

σ

X

będą największe w tym przekroju pręta, w którym moment

zginający M(x) osiąga wartość ekstremalną czyli

Dr inż. Janusz Dębiński

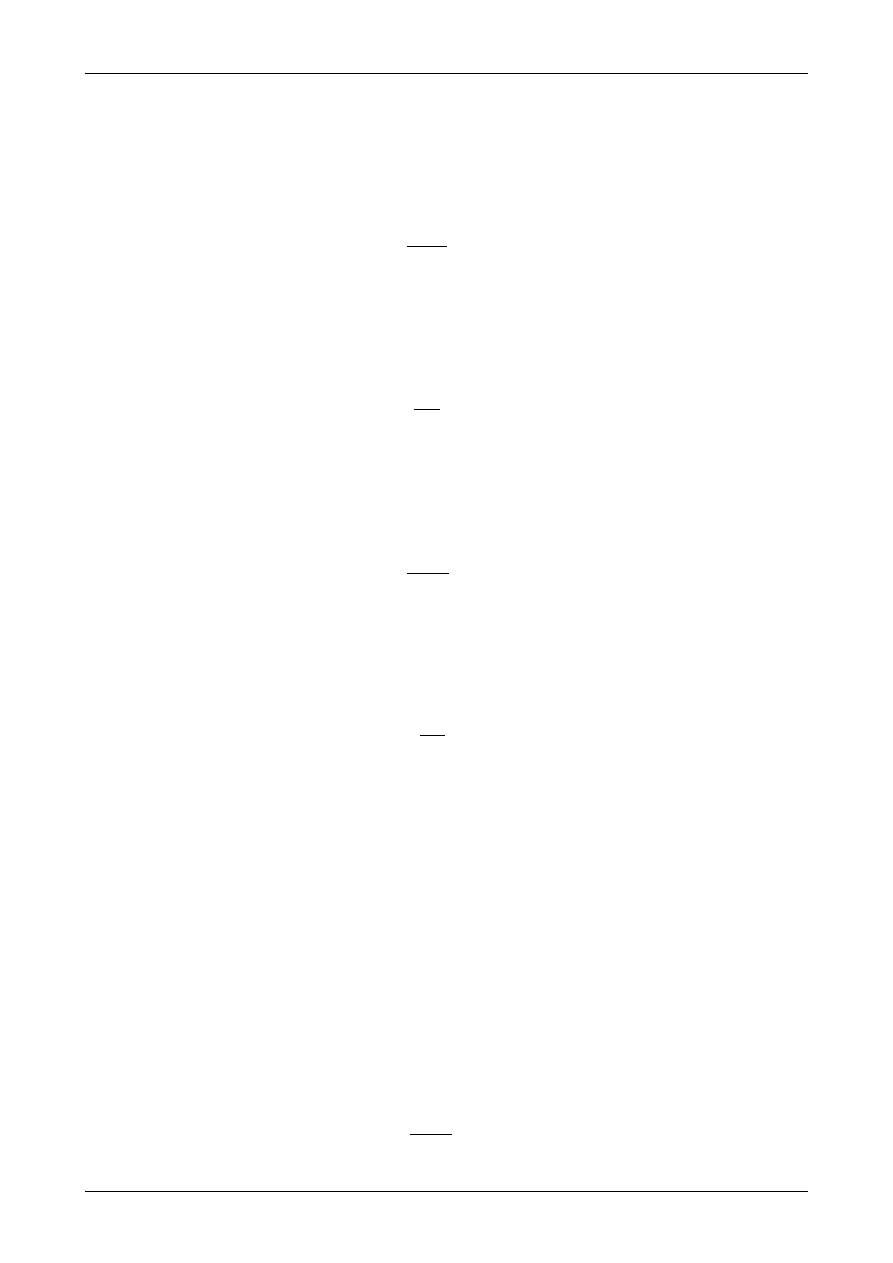
WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

9

M

Y

EXT

=

max

∣

M  x

∣

.

(7.11)

Wartość bezwzględną największego naprężenia normalnego

σ

X

na krawędzi dolnej przekroju pręta wyzna-

czymy ze wzoru

∣



X



d 

∣

=

M

Y

EXT

W

Y



d 

.

(7.12)

We wzorze (7.12) wielkość w mianowniku nazywa się wskaźnikiem wytrzymałości na zginanie dla kra-
wędzi dolnej. Wyznacza się go ze wzoru

W

Y



d 

=

J

Y

z



d 

(7.13)

Wartość bezwzględną największego naprężenia normalnego

σ

X

na krawędzi górnej przekroju pręta wyzna-

czymy ze wzoru

∣



X



g 

∣

=

M

Y

EXT

W

Y



g 

.

(7.14)

We wzorze (7.14) wielkość w mianowniku nazywa się wskaźnikiem wytrzymałości na zginanie dla kra-
wędzi górnej. Wyznacza się go ze wzoru

W

Y



g 

=−

J

Y

z



g 

.

(7.15)

Znak minus wynika z tego, że współrzędna krawędzi górnej jest ujemna natomiast wskaźnik wytrzymałości
na zginanie jest dodatni.

Największą wartość naprężenie normalne osiąga na tej krawędzi, dla której wskaźnik wytrzymałości

jest mniejszy. Możemy w ten sposób określić wskaźnik wytrzymałości dla całego przekroju jako

W

Y

=

min

{

W

Y



d 

W

Y



g 

.

(7.16)

Dla przekrojów, w których oś Y=Y

gl

jest osią symetrii wskaźniki wytrzymałości na zginie dla krawędzi

dolnej i górnej są takie same. Przykładem takich przekrojów są: przekrój dwuteowy i skrzynkowy. Wartość
bezwzględną największych naprężeń normalnych obliczymy ze wzoru

∣



X

EXT

∣

=

M

Y

EXT

W

Y

.

(7.17)

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

10

Naprężenie (7.17) powinno być mniejsze lub równe wytrzymałości materiału R czyli

∣



X

EXT

∣

=

M

Y

EXT

W

Y

≤

R

.

(7.18)

Czyli wskaźnik wytrzymałości przekroju na zginanie powinien wynosić

W

Y

≥

M

Y

EXT

R

.

(7.19)

Procedura projektowania przekrojów prętów zostanie pokazana na załączonych do niniejszego opracowania
przykładach.

Projektując przekroje wykonane z kształtowników walcowanych możemy z tablic do projektowania

konstrukcji metalowych odczytać odpowiednie wartości wskaźników wytrzymałości i tak dobrać przekrój
belki lub ramy aby spełniał on warunek (7.19). Należy pamiętać, że podany w tablicach do projektowania
konstrukcji stalowych wskaźnik jest wskaźnikiem minimalnym. Należy także zwrócić uwagę na oznaczenia
osi zastosowane w tablicach. Najczęściej należy przyjmować wskaźniki wytrzymałości oznaczone w tab-
licach jako W

X

, ponieważ oś X w tablicach pokrywa się z naszą osią główną Y=Y

gl

.

7.7. Działanie siły poprzecznej

Jeżeli w przekroju pręta działa siła poprzeczna T=T

Z

to w dowolnym punkcie działać będzie tylko

składowa styczna wektora naprężenia czyli naprężenie styczne

τ

. Jak wiadomo naprężenie to ma dwie

składowe

τ

XY

oraz

τ

XZ

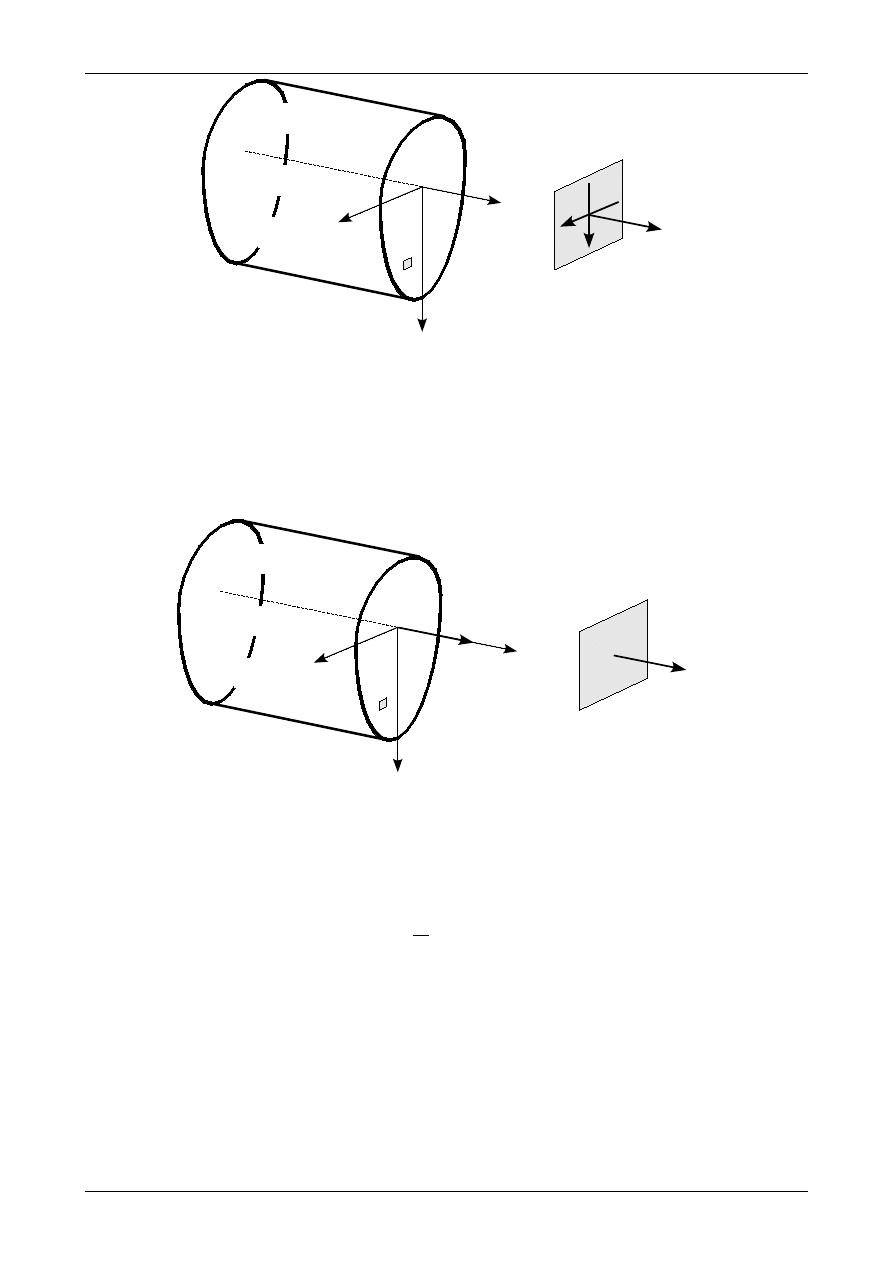
. Przedstawia je rysunek 7.17.

X

dA

dA

τ

XZ

τ

XY

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

Rys. 7.17. Siła poprzeczna w przekroju pręta

Przyjmuje się, że od działania siły poprzecznej T=T

Z

powstają przede wszystkim naprężenia

τ

XZ

, które

w punktach o jednakowej współrzędnej z są stałe. Przedstawia je rysunek 7.18. Wartość bezwzględną naprę-
żenia stycznego

τ

XZ

w punktach o jednakowej współrzędnej z wyznacza się ze wzoru

∣



XZ

∣

=

∣

T

Z

∣

⋅

∣

S

Y



z 

∣

b  z ⋅J

Y

,

(7.20)

Dr inż. Janusz Dębiński

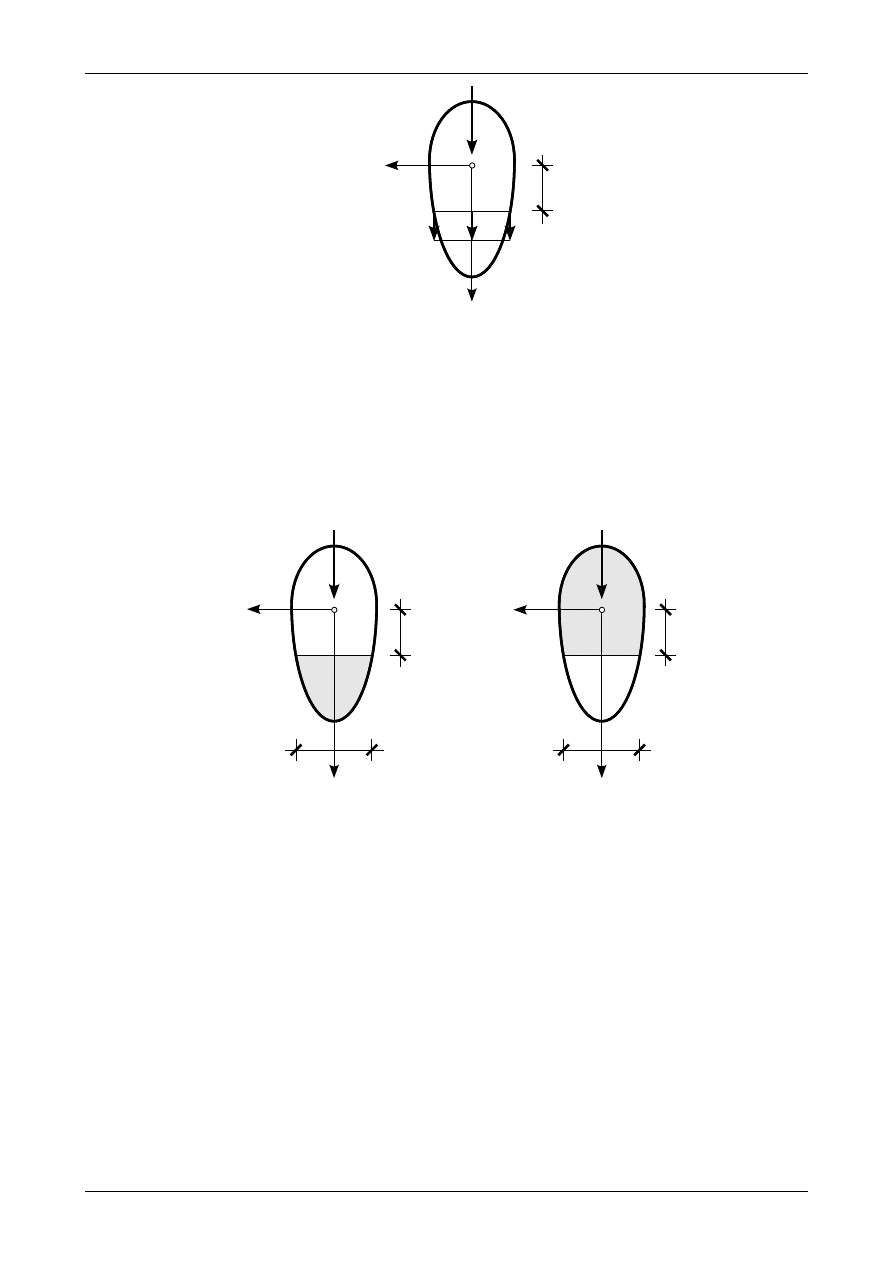
WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

11

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

z

τ

XZ

(z)

sc

Rys. 7.18. Przekrój obciążony siłą poprzeczną

w którym S

Y

(z) jest momentem statycznym względem głównej osi bezwładności Y=Y

gl

części przekroju

pręta leżącej poniżej lub powyżej punktu, w którym wyznaczamy naprężenia styczne

τ

XZ

natomiast b(z) jest

szerokością przekroju w miejscu, w którym wyznaczmy naprężenia styczne

τ

XZ

. Wielkości te przedstawia

rysunek 7.19.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

z

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

z

b(z)

b(z)

S

Y

(z)

(d)

S

Y

(z)

(g)

a)

b)

sc

sc

Rys. 7.19. Wielkości wykorzystywane do wyznaczenia naprężenia stycznego

Moment statyczny części przekroju zaznaczonej na rysunku 7.19 a) jest dodatni natomiast moment

statyczny części zaznaczonej na rysunku 7.19 b) jest ujemny. Ich suma wynosi

S

Y



z





d 



S

Y



z





g 

=

S

Y0

=

0

,

(7.21)

ponieważ oś Y=Y

gl

jest osią środkową przekroju. Możemy więc napisać, że

S

Y



z





d



=−

S

Y



z





g



.

(7.22)

Dlatego więc we wzorze (7.20) nie ma znaczenia czy wykorzystamy część przekroju znajdującą się powyżej
czy poniżej punktu, w którym wyznaczamy naprężenia styczne

τ

XZ

. Ich wartości bezwzględne są jak widać

jednakowe.

Dr inż. Janusz Dębiński

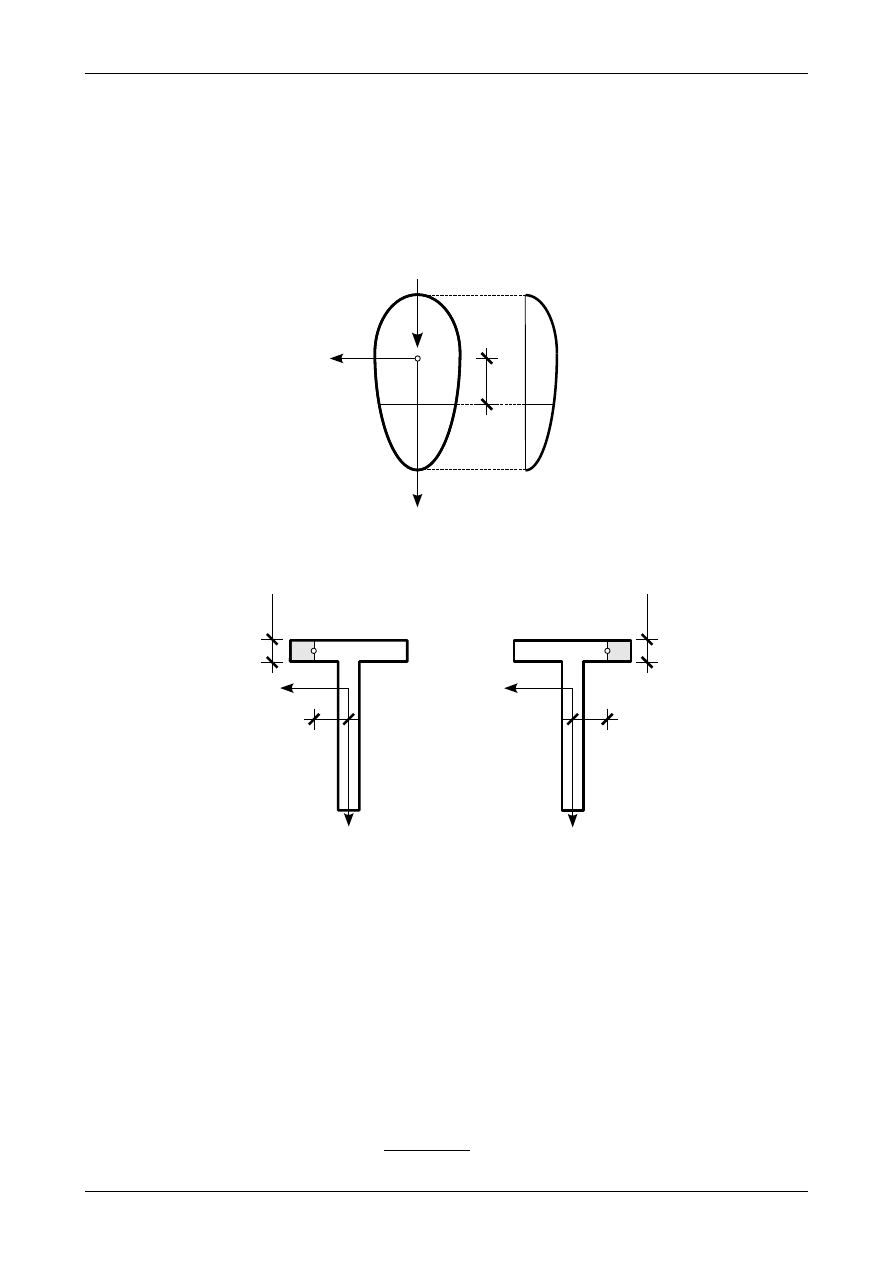
WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

12

Wzór (7.20) jest wzorem ścisłym tylko dla przekroju prostokątnego lub kwadratowego. Dla pozosta-

łych przekrojów jest to wzór przybliżony. Jednak przybliżenie to w przypadkach tu rozpatrywanych jest
zadowalające.

Naprężenie styczne

τ

XZ

ma zawsze ten sam zwrot co siła poprzeczna. Jeżeli siła poprzeczna

działa w dół to naprężenie styczne

τ

XZ

działa w dół zgodnie ze zwrotem osi Z=

Zgl

czyli jest dodatnie.

Jeżeli siła poprzeczna działa do góry to i naprężenie styczne

τ

XZ

działa do góry przeciwnie do zwrotu

osi Z=Z

gl

czyli jest ujemne.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

sc

z

τ

XZ

(z)

τ

XZ

Rys. 7.20. Wykres naprężenia stycznego

τ

XZ

w przekroju pręta

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

y

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

y

A

A

h(y

)

h(

y)

Rys. 7.21. Część półki w przekroju teowym

Największą wartość naprężenia styczne

τ

XZ

osiągną w punktach znajdujących się na wysokości środka

ciężkości przekroju pręta. Natomiast w punktach znajdujących się na krawędzi dolnej i górnej przekroju
pręta naprężenia styczne

τ

XZ

osiągną wartość zero. Rysunek 7.20 przedstawia wykres naprężeń stycznych

τ

XZ

na wysokości przekroju pręta. Dla przekroju, w którym oś Y=Y

gl

jest osią symetrii wykres naprężeń

stycznych

τ

XZ

będzie względem niej symetryczny.

W przekrojach blachownicowych dwuteowych, teowych i skrzynkowych naprężenia styczne

τ

XZ

występują w środnikach tych przekrojów. Natomiast w półkach tych blachownic występują naprężenia
styczne

τ

XY

. Wartość bezwzględną naprężenia stycznego

τ

XY

wyznaczać będziemy ze wzoru

∣



XY

∣

=

∣

T

Z

∣

⋅

∣

S

Y



y

∣

h y ⋅J

Y

,

(7.23)

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

13

w którym h(y) oznacza grubość półki. S

Y

(y) oznacza część przekroju półki. W przypadku przekroju

dwuteowego i teowego część półki mierzymy od krawędzi półki do punktu, w których wyznaczamy
naprężenia styczne

τ

XY

. W przypadku przekroju skrzynkowego część półki mierzymy od osi Z=Z

gl

do

punktu, w których wyznaczamy naprężenia styczne

τ

XY

Rysunki 7.21, 7.22 i 7.23 przedstawiają części

półki, których momenty statyczne uwzględniamy we wzorze (7.23).

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

y

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

y

A

A

h(y

)

h(y

)

Rys. 7.22. Część półki w przekroju dwuteowym

y

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

y

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

A

A

h(

y)

h(y

)

Rys. 7.23. Część półki w przekroju skrzynkowym

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

Rys. 7.24. Analogia wodna do ustalenia zwrotów naprężeń stycznych

τ

XY

w przekroju dwuteowym

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

14

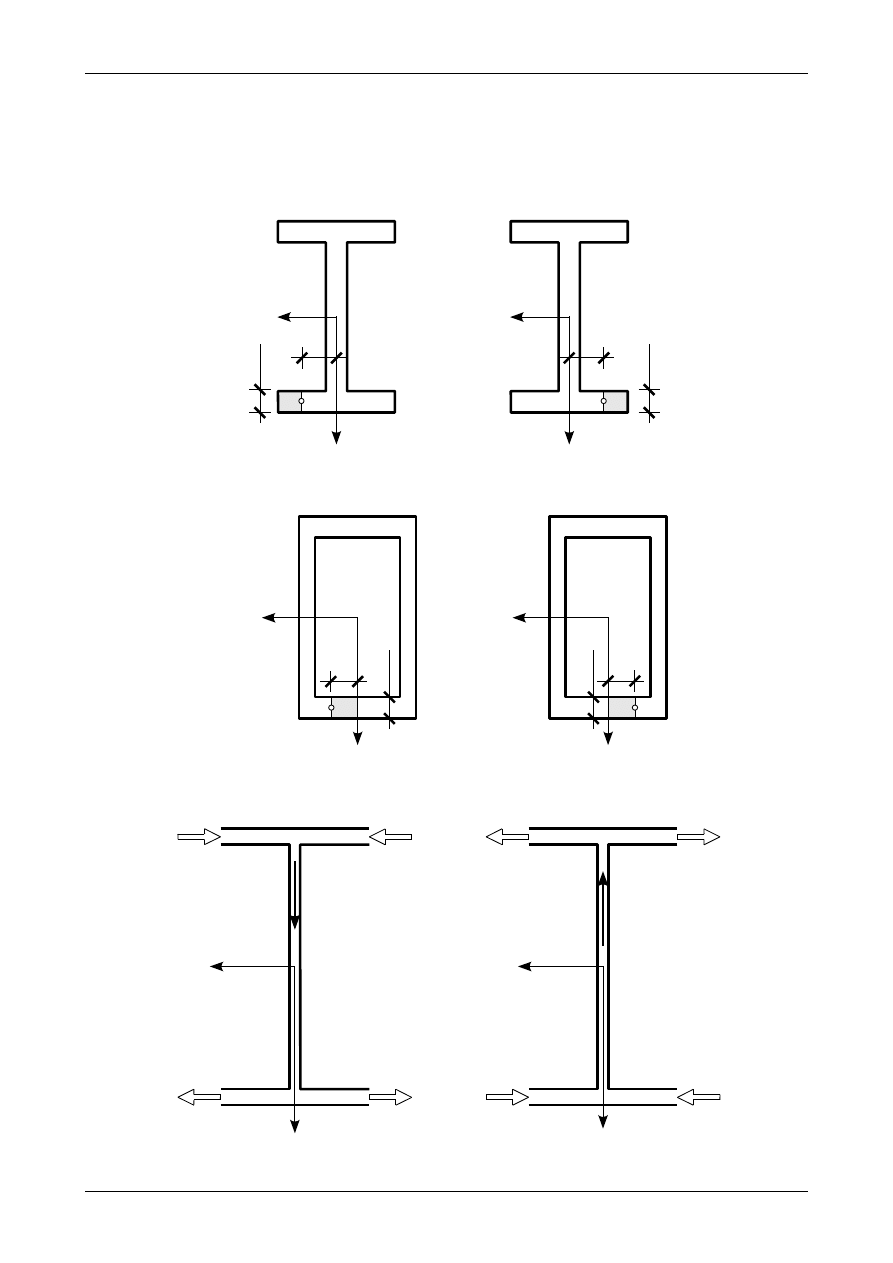
Ze wzoru (7.23) możemy wyznaczyć tylko wartość bezwzględną naprężenia stycznego

τ

XY

. Chcąc

wyznaczyć znak tego naprężenia możemy się posłużyć modelem systemu rurek, w których płynie woda. Dla
przekrojów dwuteowego oraz teowego usuwamy najkrótsze krawędzie w pólkach, którymi woda będzie
wpływać i wypływać. Kierunek przepływu musi być taki, żeby w środniku woda płynęła zgodnie ze
zwrotem naprężeń stycznych

τ

XZ

. Dla przekroju skrzynkowego robimy małą dziurkę w miejscu, w którym

półka przecina oś Z=Z

gl

. Kierunek przepływu wody w półce jest zgodny z kierunkiem naprężenia stycznego

τ

XY

. Naprężenie styczne

τ

XY

będzie dodatnie, jeżeli będzie miało taki sam zwrot jak Y=Y

gl

. Będzie

natomiast ujemne, jeżeli jego zwrot będzie przeciwny do zwrotu osi Y=Y

gl

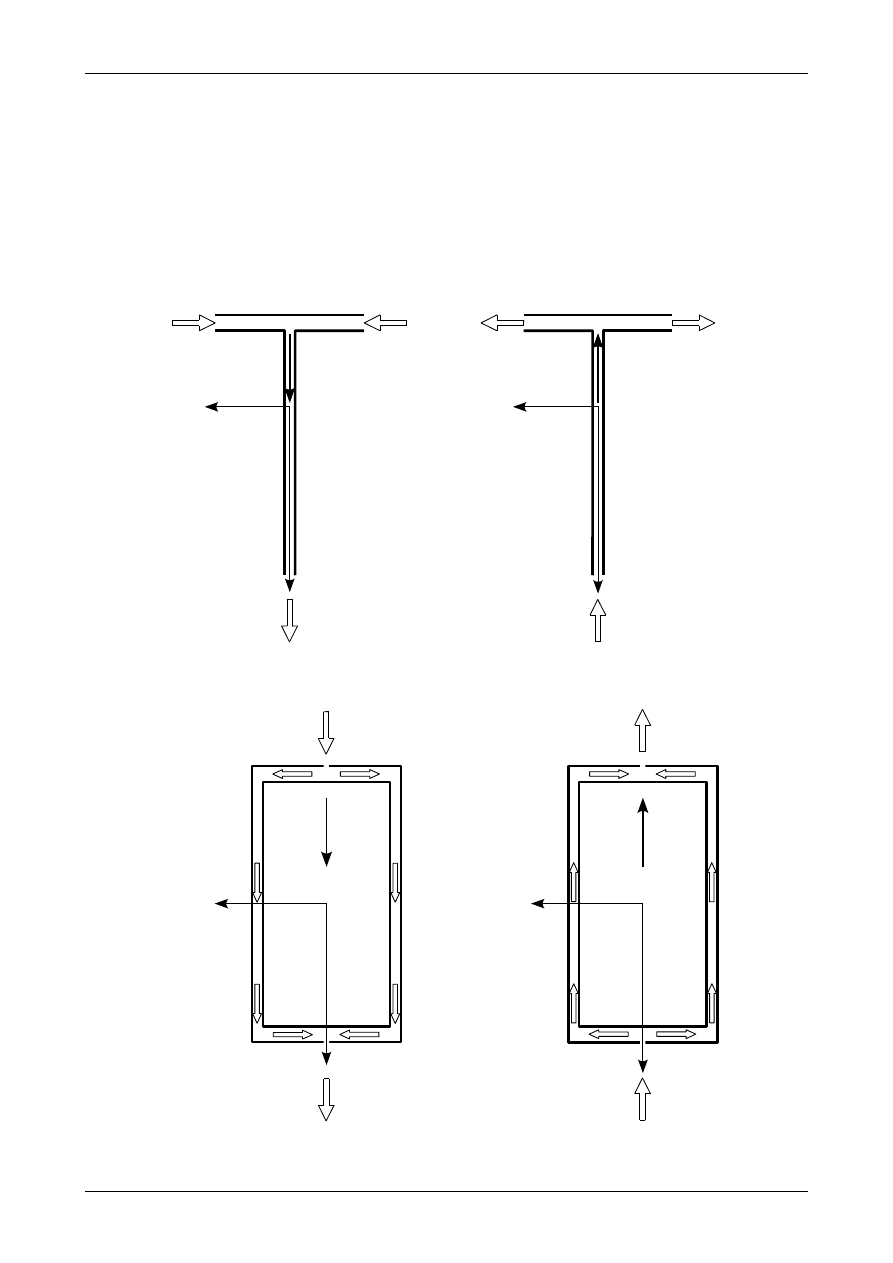
. Rysunki 7.24, 7.25 oraz 7.26

przedstawiają kierunki przepływu wody w systemie rurek w kształcie teownika, dwuteownika i przekroju
skrzynkowego. Strzałki pokazują kierunek przepływu wody.

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

T=T

Z

Rys. 7.25. Analogia wodna do ustalenia zwrotów naprężeń stycznych

τ

XY

w przekroju teowym

T=T

Z

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

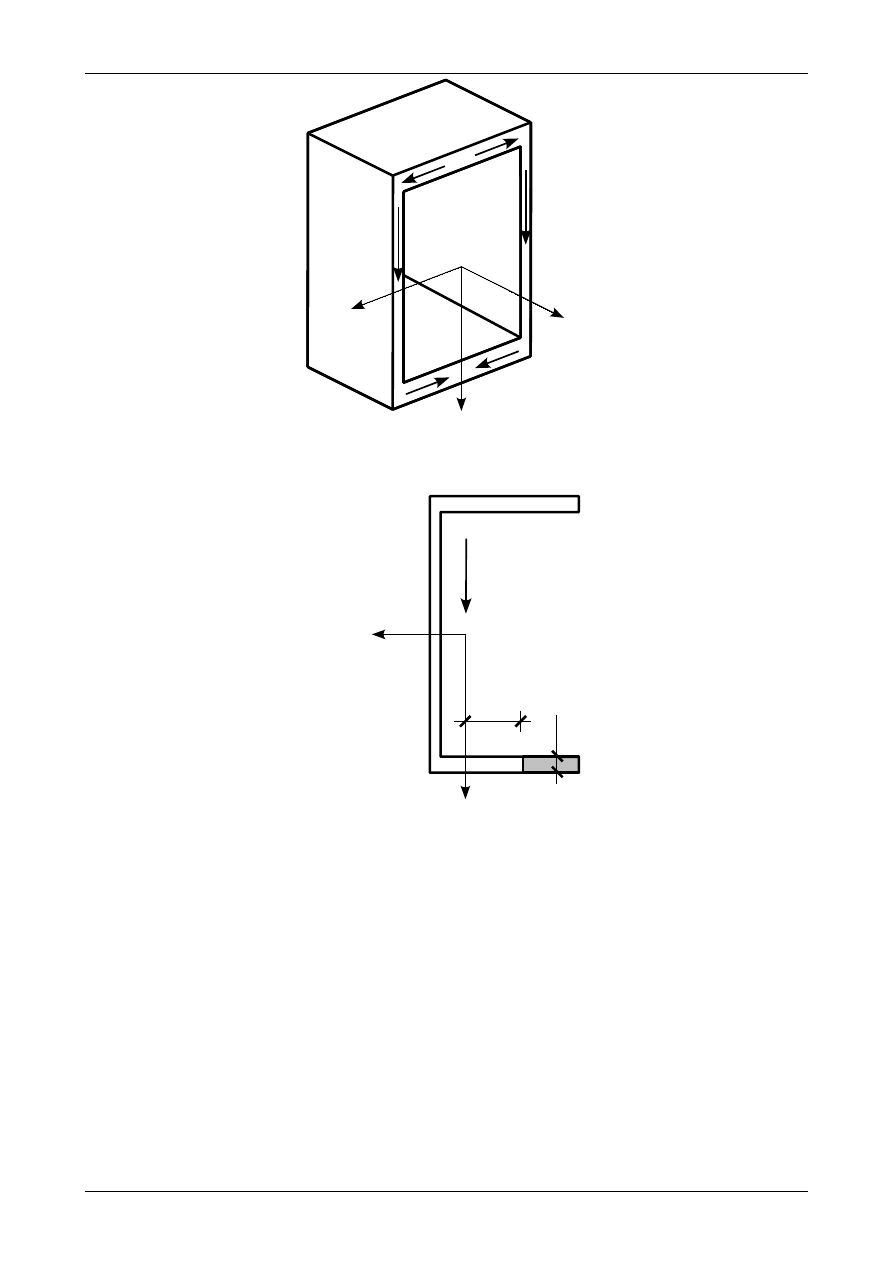
Rys. 7.26. Analogia wodna do ustalenia zwrotów naprężeń stycznych

τ

XY

w przekroju skrzynkowym

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

15

7.8. Środek ścinania

Przekrój dwuteowy, skrzynkowy oraz teowy są symetryczne względem osi Z=Z

gl

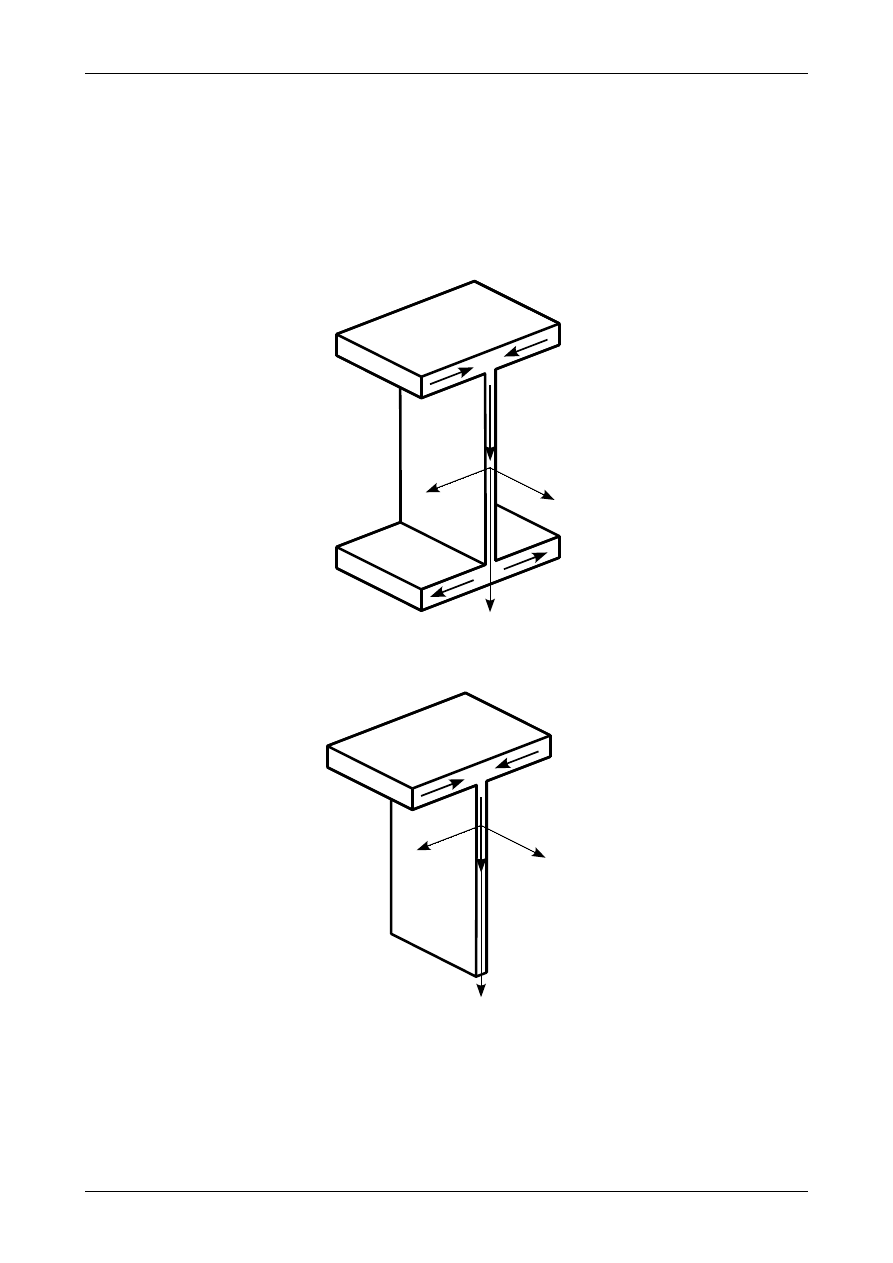
. Rysunki 7.27, 7.28

i 7.29 przedstawiają siły wypadkowe z odpowiednich naprężeń stycznych. Wypadkowa naprężeń stycznych

τ

XZ

Q równa się w przybliżeniu sile poprzecznej T

Z

. Wypadkowa ta w dwuteowniku i teowniku przechodzi

przez środek ciężkości tych przekrojów. W przypadku przekroju skrzynkowego w każdym ze środników
działają siły Q

1

równe w przybliżeniu połowie siły poprzecznej. Wypadkowe naprężeń

τ

XY

w każdej z półek

będą sobie równe co wartości, różnić się będą tylko zwrotem. Wypadkowe te zostały także pokazane na
rysunkach 7.27, 7.28 i 7.29.

Q

H

X

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

H

H

H

Rys. 7.27. Siły wypadkowe z naprężeń stycznych w dwuteowniku

Q

H

H

X

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

Rys. 7.28. Siły wypadkowe z naprężeń stycznych w teowniku

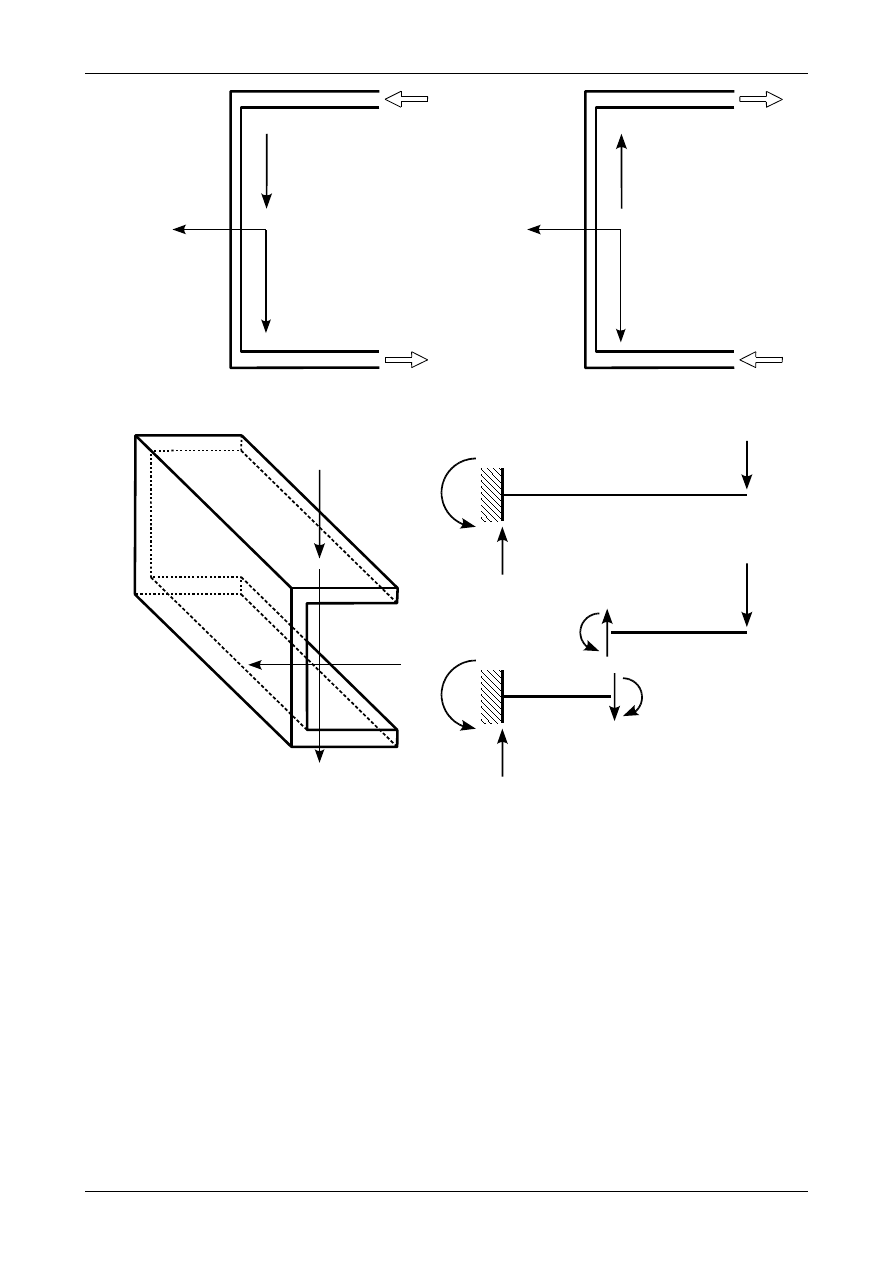
Zupełnie inaczej jest w przekroju ceowym. Naprężenia styczne

τ

XZ

w środniku wyznaczamy ze wzoru

(7.20), naprężenia styczne

τ

XY

w półce wyznaczamy ze wzoru (7.23). Rysunek 7.30 przedstawia część półki,

której moment statyczny podstawiamy do tego wzoru. Jak widać jest ona mierzona od krawędzi półki do
punktu, w którym chcemy wyznaczyć wartość naprężenia stycznego

τ

XY

. Rysunek 7.31 przedstawia zasadę

znakowania naprężeń stycznych

τ

XY

, która jest taka sama, jak zasada dla dwuteownika oraz teownika.

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

16

Q

1

H

Q

1

X

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

H

H

H

Rys. 7.29. Siły wypadkowe z naprężeń stycznych w przekroju skrzynkowym

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

y

h(y

)

Rys. 7.30. Część półki

Rozpatrzymy wspornikowy pręt obciążony na końcu siłą P. Siła ta działa w płaszczyźnie pokrywa-

jącej się z osią główną Z=Z

gl

. Pręt taki przedstawia rysunek 7.32. W dowolnym przekroju tego pręta działają

tylko: siła poprzeczna oraz moment zginający. Rysunek 7.33 a) przedstawia siły wypadkowe z naprężeń
stycznych

τ

XZ

w środniku oraz

τ

XY

w półkach. W przekroju powstanie niezrównoważony moment względem

środka ciężkości przekroju teowego. Kręci się on jak wykręcająca się śruba prawoskrętna. Musi on zostać
zrównoważony momentem o takiej samej wartości ale przeciwnie skierowanym. Ten dodatkowy moment
będzie więc się wkręcał w pręt. Przedstawia go rysunek 7.33 b). Moment ten spowoduje skręcenie się pręta.
Tak skręcony pręt przedstawia rysunek 7.34.

Aby zrównoważyć to skręcanie należy wymusić skręcanie pręta poprzez przesunięcie siły P. Siłę tą

przesuwamy poziomo do punktu, który nazywa się środkiem ścinania lub środkiem skręcania S. Poło-
żenie tego punktu w przekroju ceowym przedstawia rysunek 7.35. Rysunek 7.36 przedstawia położenie
środka ścinania w kilku przykładowych przekrojach prętów. Lina przerywana oznacza płaszczyznę, w której
działa pionowa siła P na końcu wspornika.

Aby uniknąć skręcania należy więc tak projektować przekrój pręta aby był on symetryczny

względem osi, która pokrywa się z płaszczyzną działania sił czynnych i reakcji.

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

17

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

T=T

Z

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

a)

b)

Rys. 7.31. Zasada znakowania naprężeń stycznych w półkach ceownika

P

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

P

P

M

P

P

M

P

P

M(x)

M(x)

Rys. 7.32. Wspornikowy pręt obciążony siłą P na końcu

7.9. Połączenie środnika z półką

W przypadku blachownic o przekroju dwuteowym, teowym lub skrzynkowym należy w jakiś sposób

połączyć środnik i półki. W przeciwnym wypadku każda blacha (środnik i półki) będzie pracowała osobno.
Najczęściej stosowaną metodą jest spawanie. W trakcie spawania poszczególne części łączy się za pomocą
spoin. Spoiną nazywamy tę część złącza, która składa się z metalu stopionego podczas spawania. Może ona
powstać wyłącznie z materiału rodzimego albo z udziałem materiału doprowadzonego z zewnątrz, nazywa-
nego spoiwem. Podstawowy podział spawania jest następujący:

•

spawanie łukiem elektrycznym z elektrodą topliwą lub nietopliwą

•

spawanie gazowe.

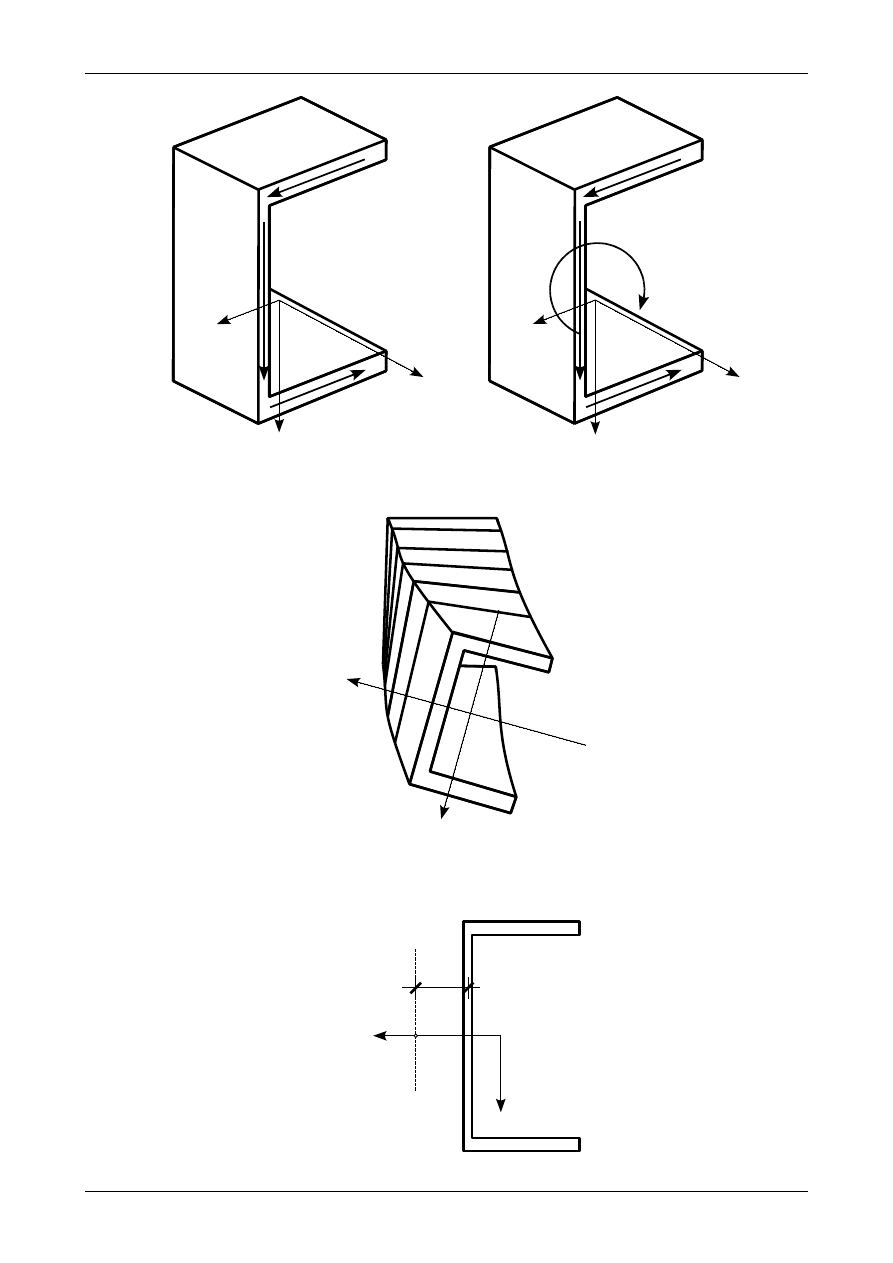
Podstawowym i najbardziej rozpowszechnionym sposobem spawania elektrodą topliwą jest spawanie

elektrodą otuloną, potocznie nazywane ręcznym spawaniem łukowym. Źródłem ciepła jest łuk elektryczny
jarzący się między dwoma elektrodami. Jedną z elektrod może być spawany przedmiot natomiast druga
elektroda może służyć jako spoiwo (elektroda topliwa) lub może tylko służyć do utrzymania łuku (elektroda
nietopliwa), a spoina powstaje wyłącznie ze stopionego materiału rodzimego. Schemat technologii spawania
tą metodą pokazuje schematycznie rysunek 7.37.

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

18

X

Q

H

H

M

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

X

Q

H

H

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

a)

b)

Rys. 7.33. Siły wypadkowe z naprężeń stycznych w przekroju ceowym

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

Rys. 7.34. Deformacja pręta wspornikowego o przekroju ceowym

a

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

S

Rys. 7.35. Środek ścinania w przekroju ceowym

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

19

R

S

S

R

S

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

S

Rys. 7.36. Położenie środka ścinania w różnych przekrojach pręta

Rys. 7.37. Schemat ręcznego spawania łukowego

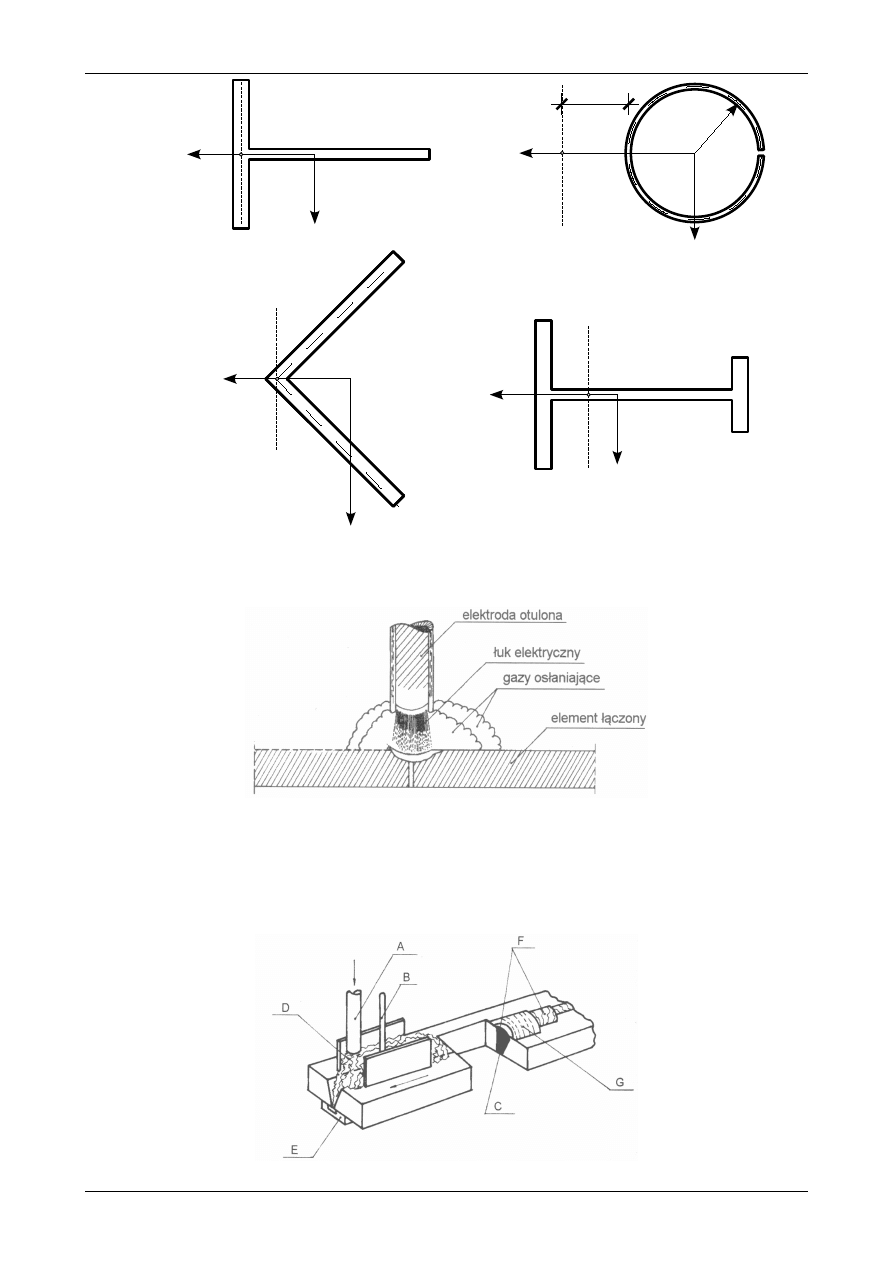
Drugą metodą spawania elektrodą topliwą jest spawanie łukiem krytym. Schemat tej metody został

pokazany na rysunku 7.38.

Rys. 7.38 Schemat spawania łukiem krytym

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

20

Zamiast otuliny stosuje się topnik w postaci proszku, pod którego warstwą jarzy się łuk między

elektrodą topliwą a przedmiotem spawania. Spawanie łukiem krytym odbywa się tylko automatycznie lub
półautomatycznie. Łuk jarzy się niewidocznie pod warstwą topnika (D) zsypywanego z leja (A). Elektroda
w postaci drutu (B) jest podawana samoczynnie z bębna. Na spoinie (C) krzepnie żużel (F). Nadmiar
topnika (G) pozostały na spoinie jest zasysany z powrotem do leja zasypowego. Podkładka (E) jest
stosowana w pewnych przypadkach aby zapobiec wyciekaniu metalu. Proces ten charakteryzuje się bardzo
wysoką wydajnością.

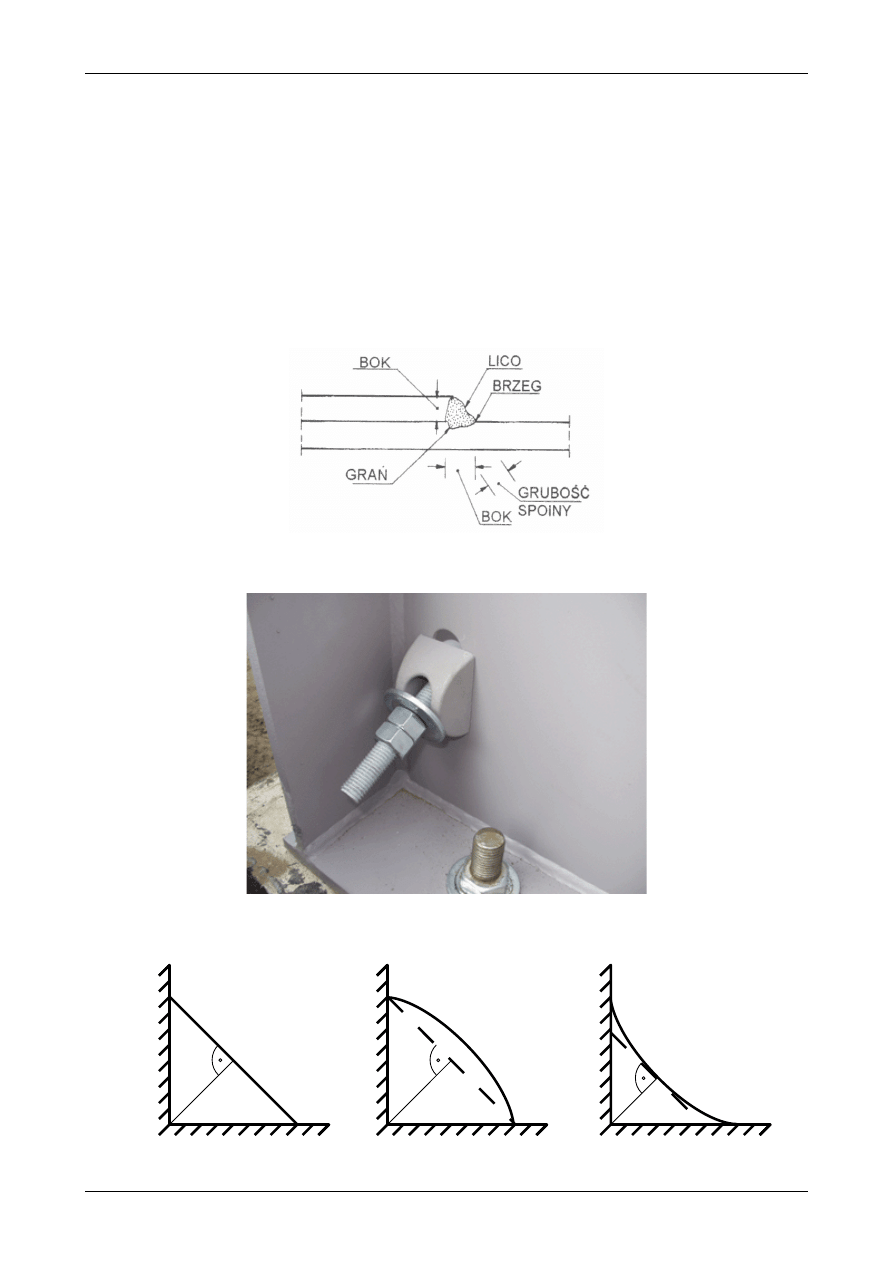
Do łączenia środnika z półką w przekroju dwuteowym i teowym stosuje się spoinę pachwinową.

Nazwy części spoiny pachwinowej pokazane są na rysunku 7.39 natomiast na rysunek 7.40 przedstawia
widok takiej spoiny. Na rysunku 7.41 pokazano przekrój przez spoinę pachwinową. Rysunek 7.41 a)
przedstawia spoinę płaską, rysunek 7.41 b) wypukłą natomiast rysunek 7.41 c) wklęsłą. Grubością spoiny
pachwinowej a określa się wysokość trójkąta wpisanego w spoinę. Przedstawia to także rysunek 7.41.

Rys. 7.39. Podstawowe elementy spoiny pachwinowej

Rys. 7.40. Widok spoiny pachwinowej

a)

a

a

a

b)

c)

Rys/ 7.41. Przekrój przez spoinę pachwinową

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

21

a

a

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

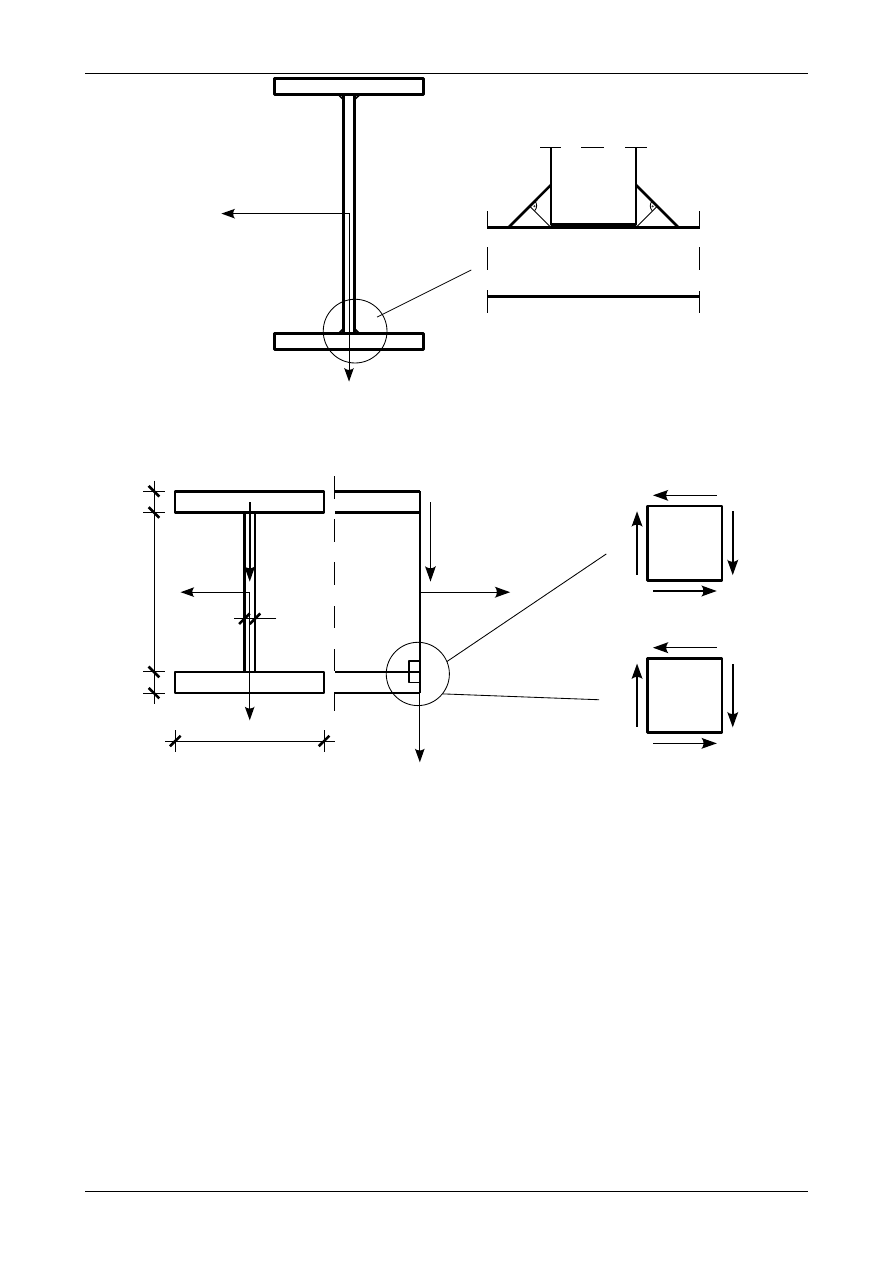
Rys. 7.42. Przekrój przez spoinę pachwinową łączącą środnik z półką

Z=Z

gl

T=T

Z

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

h

S

s

g

T=T

Z

t

t

Y=Y

0

=Y

gl

τ

XZ

τ

XZ

τ

XZ

τ

XZ

τ

XZ

τ

XZ

τ

XZ

τ

XZ

X

Rys. 7.43. Elementarne kostki naprężeń w środniku i półce dolnej

Przekrój spoiny pachwinowej łączącej środnik z półką przedstawiony jest na rysunku 7.42. Rysunek

7.43 przedstawia elementarne kostki naprężeń z zaznaczonymi naprężeniami stycznymi

τ

XZ

od siły poprzecz-

nej T

Z

. Naprężenia te zostały obliczone z wzoru (7.20) podstawiając do niego moment statyczny półki dolnej

względem osi Y=Y

0

=Y

gl

oraz dla górnej kostki jako b(z) grubość środnika g. Dla dolnej kostki należałoby do

wzoru (7.20) wstawić jako b(z) szerokość półki, jednak ze względów praktycznych przyjmuje się szerokość
środnika czyli tak samo jak dla kostki górnej. Sytuacja przedstawiona na rysunku 7.43 dotyczy przypadku,
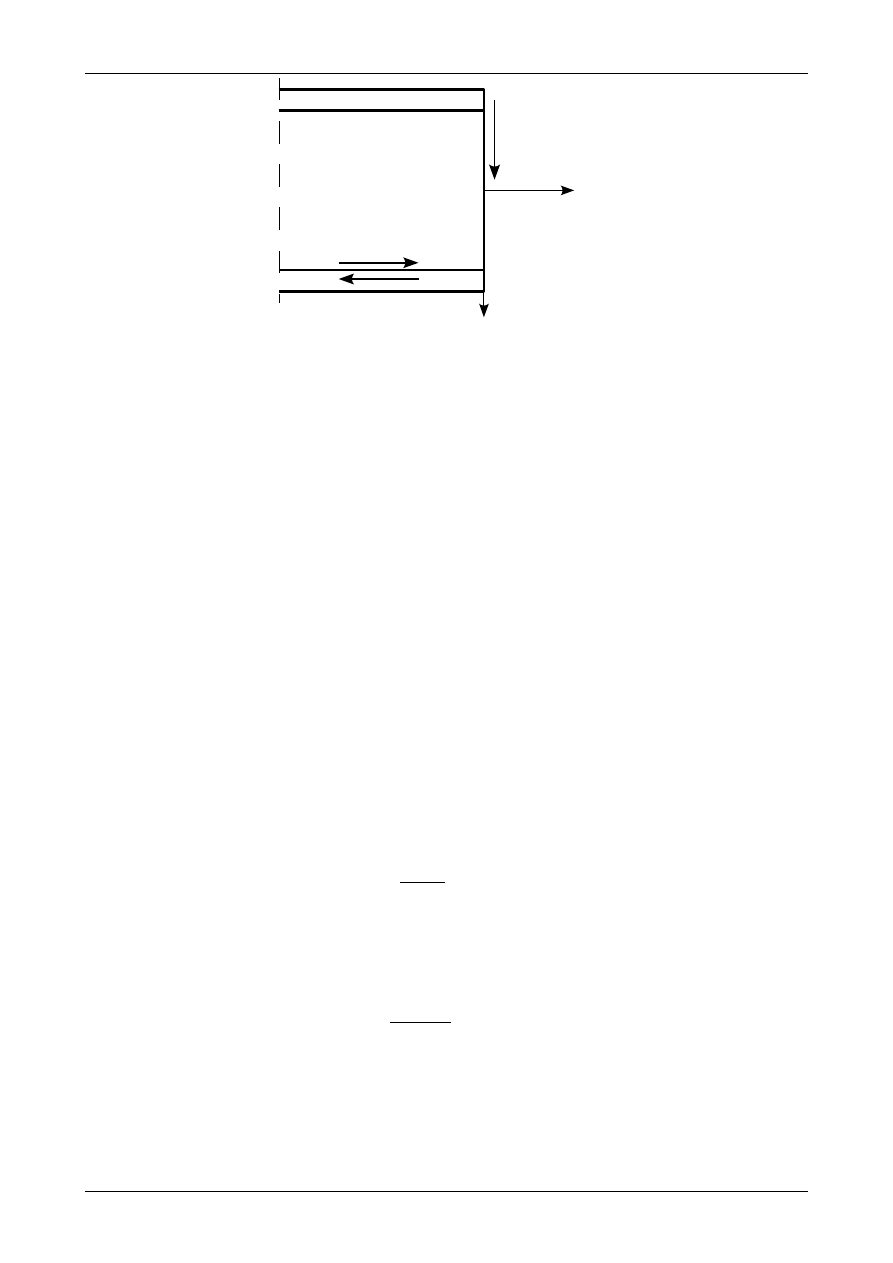
gdy pręt jest wykonany z jednego kawałka metalu. Na styku środnik-półka powstanie siła, którą nazywamy
siłą rozwarstwiającą R przedstawioną na rysunku 7.44. W przypadku blachownicy pręt jest wykonany
z trzech blach, które są połączone za pomocą spoin pachwinowych przedstawionych na rysunku 7.42.
Naprężenia styczne na obu kostkach występujące w pręcie wykonanym z jednego kawałka metalu zostaną
przeniesione przez te spoiny. Siła rozwarstwiająca próbuje przesunąć środnik względem półki. Jednak na
przeszkodzie temu stoją spoiny pachwinowe łączące środnik z półką.

Ze względu na to, że siła poprzeczna T

Z

zmienia się na długości pręta siła rozwarstwiająca także

zmienia swoją wartość. Powoduje to, że spoiny pachwinowe łączące środnik z półką powinny mieć na
długości pręta różną grubość. Ze względów technologicznych jest to nieopłacalne. W praktyce wystarczy
znaleźć ekstremalną siłę poprzeczną na długości pręta i dla tej siły zaprojektować spoiny pachwinowe
o stałej grubości na całej długości pręta.

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

22

X

R

R

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

T=T

Z

Rys. 7.44. Siła rozwarstwiająca

Spoina pachwinowa może być spoiną ciągłą lub przerywaną i wtedy nazywa się szwem spawanym.

Jeżeli stosujemy szew spawany to poszczególne spoiny szwu mogą leżeć po obu stronach naprzeciw siebie,
albo przestawnie wtedy, gdy poszczególne spoiny są układane po obu stronach na przemian. W niniejszym
kursie będziemy rozpatrywać tylko spoinę przerywaną symetryczną.

Na początek zajmiemy się spoiną ciągłą. Siła rozwarstwiająca jak istniałaby pomiędzy środnikiem

i półką wynosi

R=

XZ

⋅

g⋅L

,

(7.24)

w którym

τ

XZ

oznacza naprężenie styczne na styku środnik-półka, g oznacza grubość środnika, L oznacza

długość pręta. Siła rozwarstwiająca przypadająca na parę spoin pachwinowych wynosi

R=

sp

⋅

2⋅a⋅L

,

(7.25)

w którym

τ

sp

oznacza naprężenia styczne w spoinie pachwinowej, natomiast a oznacza grubość spoiny

pachwinowej. Przyrównując do siebie siły rozwarstwiające (7.24) i (7.25) otrzymamy wzór na obliczenie
naprężeń stycznych w spoinie

τ

sp

w postaci



sp

=



XZ

⋅

g

2⋅a

(7.26)

Korzystając ze wzoru (7.20) naprężenia styczne w spoinie pachwinowej wynoszą



sp

=

∣

T

Z

∣⋅∣

S

Y

p

∣

2⋅a⋅J

Y

,

(7.27)

w którym S

Y

P

oznacza moment statyczny półki względem osi Y=Y

gl

.

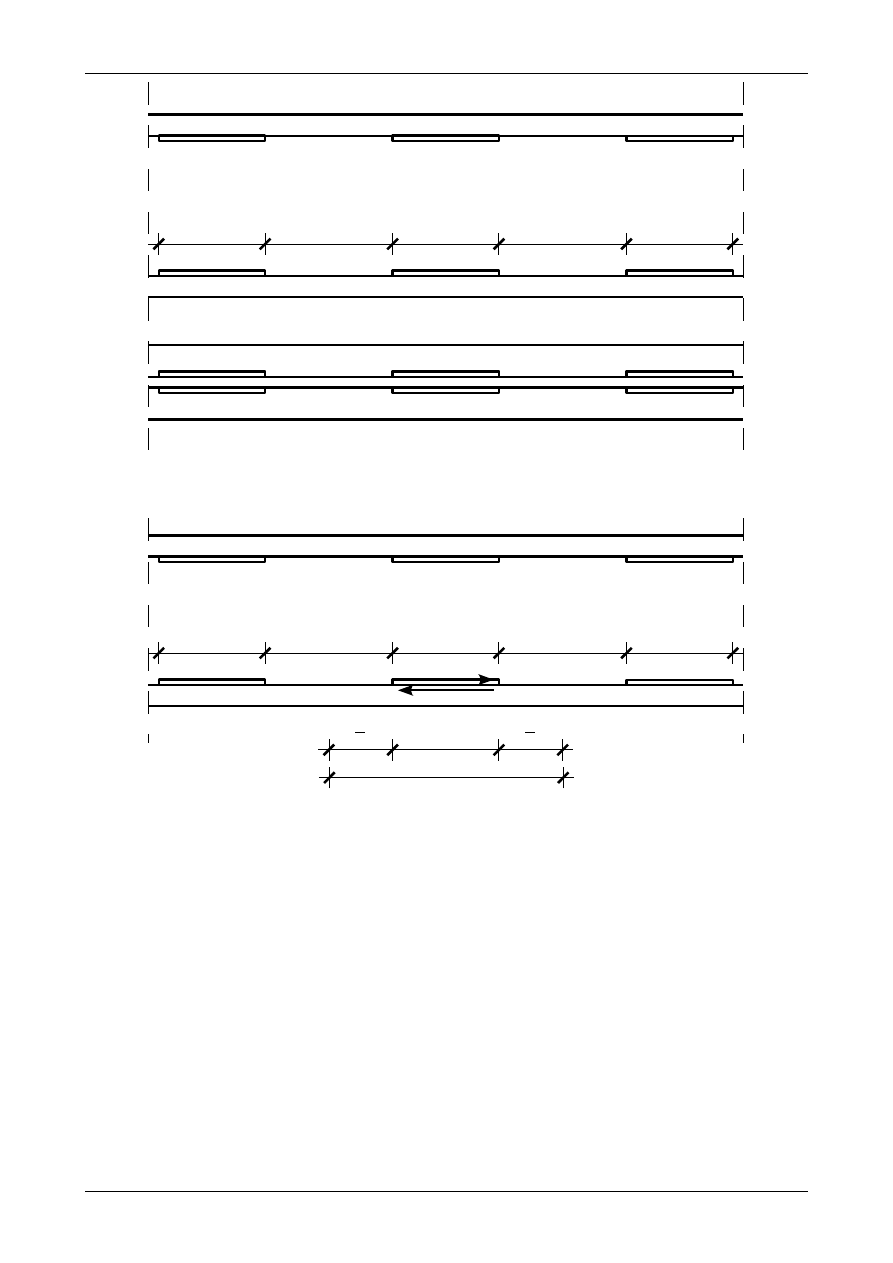
Rysunek 7.45 przedstawia widok z boku i z góry przekroju dwuteowego na spoinę przerywaną,

będącą symetryczną względem środnika. Jak widać składa się ona z odcinków o długości l, które są odda-
lone od siebie o odcinek e.

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

23

l

e

l

e

l

Widok z boku

Widok z góry

Rys. 7.45. Spoina przerywana

l

e

l

e

l

l

R

R

x

e
2

e
2

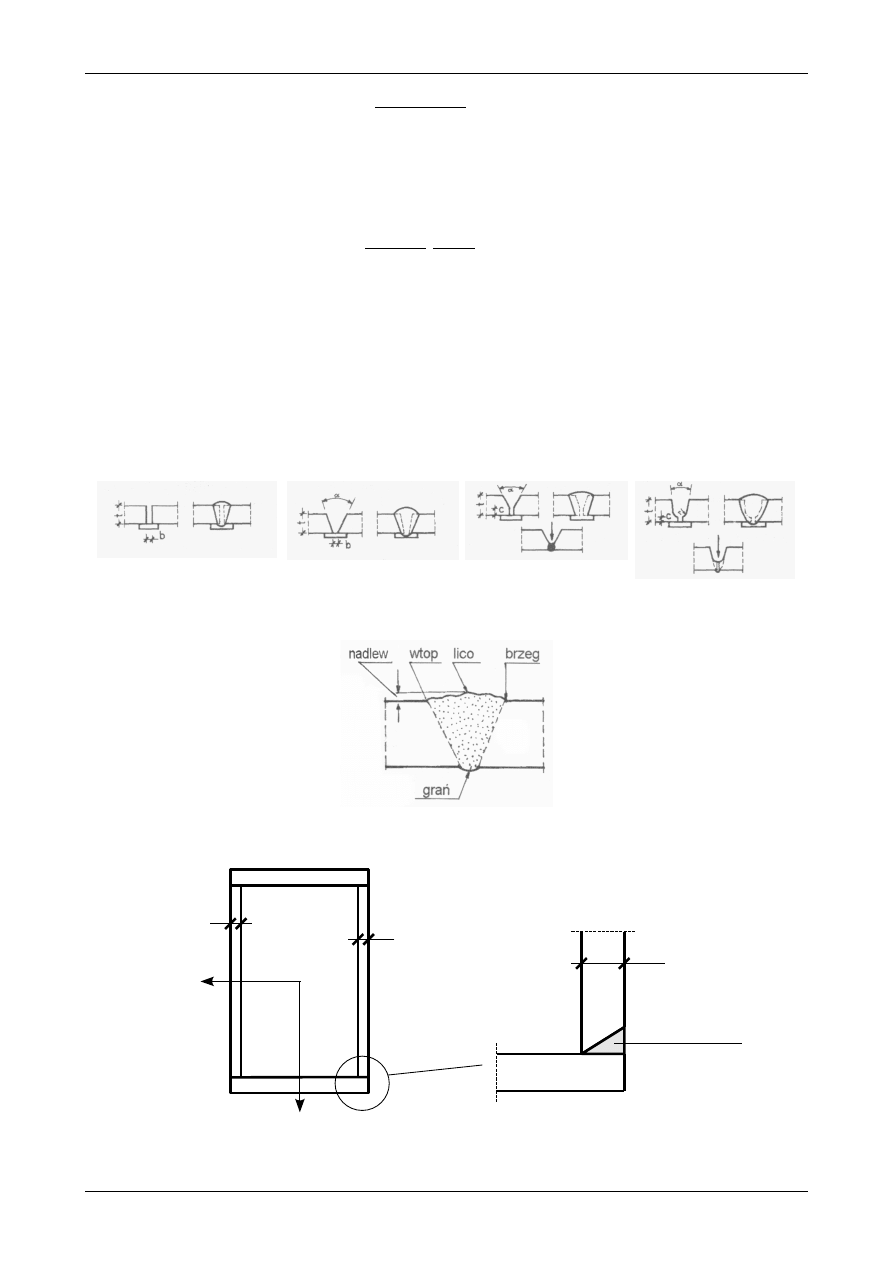
Rys. 7.46. Spoina przerywana

Rysunek 7.46 przedstawia podstawowe wymiary spoiny przerywanej. Siła rozwarstwiająca przypada-

jąca na jedną spoinę będzie wypadkową z naprężeń stycznych

τ

XZ

z długości x przedstawionej na rysunku

7.46. Siła rozwarstwiająca R jaka działałaby na odcinku o długości x pełnego przekroju dwuteowego wynosi

R=

XZ

⋅

g⋅x=

XZ

⋅

g⋅



le



,

(7.28)

w którym g jest grubością środnika. Siła rozwarstwiająca przypadająca na parę spoin pachwinowych prze-
rywanych wynosi

R=

sp

⋅

2⋅a⋅l

.

(7.29)

w którym a oznacza grubość spoiny pachwinowej. Przyrównując do siebie wzory (7.28) oraz (7.29)
otrzymamy wzór na obliczenie naprężeń stycznych w pojedynczej spoinie pachwinowej w postaci

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

24



sp

=



XZ

⋅

g⋅



le



2⋅a⋅l

.

(7.30)

Podstawiając wzór (7.20) otrzymamy ostatecznie



sp

=

∣

T

Z

∣⋅∣

S

Y

p

∣

2⋅a⋅J

Y

⋅



le



l

,

(7.31)

w którym S

Y

P

oznacza moment statyczny półki względem osi Y=Y

gl

.

Drugim rodzajem połączenia spawanego jest spoina czołowa. Połączenie dwóch elementów spoiną

czołową następuje przez całkowite przetopienie ich brzegów na całej grubości łączonych blach. Rysunek
7.47 przedstawia wygląd kilku podstawowych typów spoin czołowych. Jak widać większość typów spoin
czołowych wymaga tak zwanego ukosowania brzegów. Spowodowane jest to wymogiem, aby spoina czoło-
wa znalazła się na całej grubości połączenia. Na rysunku 7.48 przedstawione są elementy przykładowej
spoiny czołowej typu V.

Rys. 7.47. Różne rodzaje spoin czołowych

Rys. 7.48. Podstawowe elementy spoiny czołowej

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

g

g

spoina czołowa

g=a

Rys. 7.49. Spoina czołowa łącząca środnik i półkę przekroju skrzynkowego

Dr inż. Janusz Dębiński

WM

7. NAPRĘŻENIA W BELKACH I RAMACH PŁASKICH

25

Rysunek 7.49 przedstawia spoinę czołową łączącą środnik i półkę w przekroju skrzynkowym. Jak

widać grubość takiej spoiny równa się grubości środnika. Naprężenia styczne w spoinie czołowej
wyznaczymy więc tak samo jak naprężenia w środniku ze wzoru



sp

=

∣

T

Z

∣⋅∣

S

Y

P

∣

2⋅g⋅J

Y

=

∣

T

Z

∣⋅∣

S

Y

P

∣

2⋅a⋅J

Y

,

(7.32)

w którym S

Y

P

oznacza moment statyczny półki względem osi Y=Y

gl

.

Dr inż. Janusz Dębiński