
Politechnika Warszawska
Instytut Automatyki i Robotyki
Prof. dr hab. inż. Jan Maciej Kościelny
PODSTAWY AUTOMATYKI
PODSTAWY AUTOMATYKI
część 2
Opis matematyczny układów liniowych
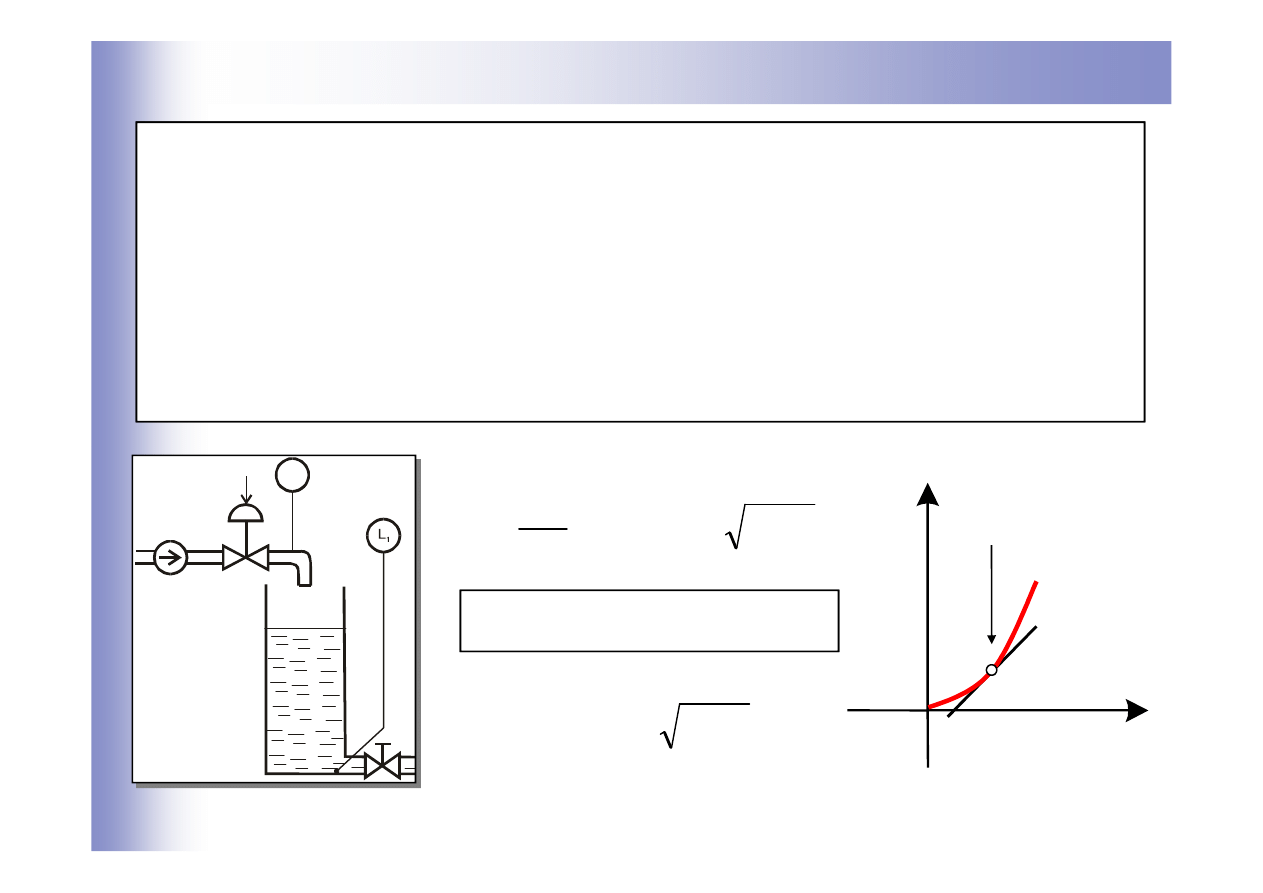
Linearyzacja układów nieliniowych
Rzeczywiste układy regulacji zazwyczaj są układami nieliniowymi.
Dla uproszczenia opisu matematycznego przeprowadza się ich
linearyzację, co pozwala na sformułowanie przybliżonego opisu
liniowego, ważnego w otoczeniu wybranego
punktu pracy na
charakterystyce statycznej (punkt ten odpowiada najczęściej
nominalnym lub uśrednionym warunkom pracy układu).
1
12
12
1
1
2gL
S
F
dt
dL
A
α
−
=
U
F
Charakterystyka statyczna
1
12
12
2gL
S
F
α
=
L
1
punkt pracy
F
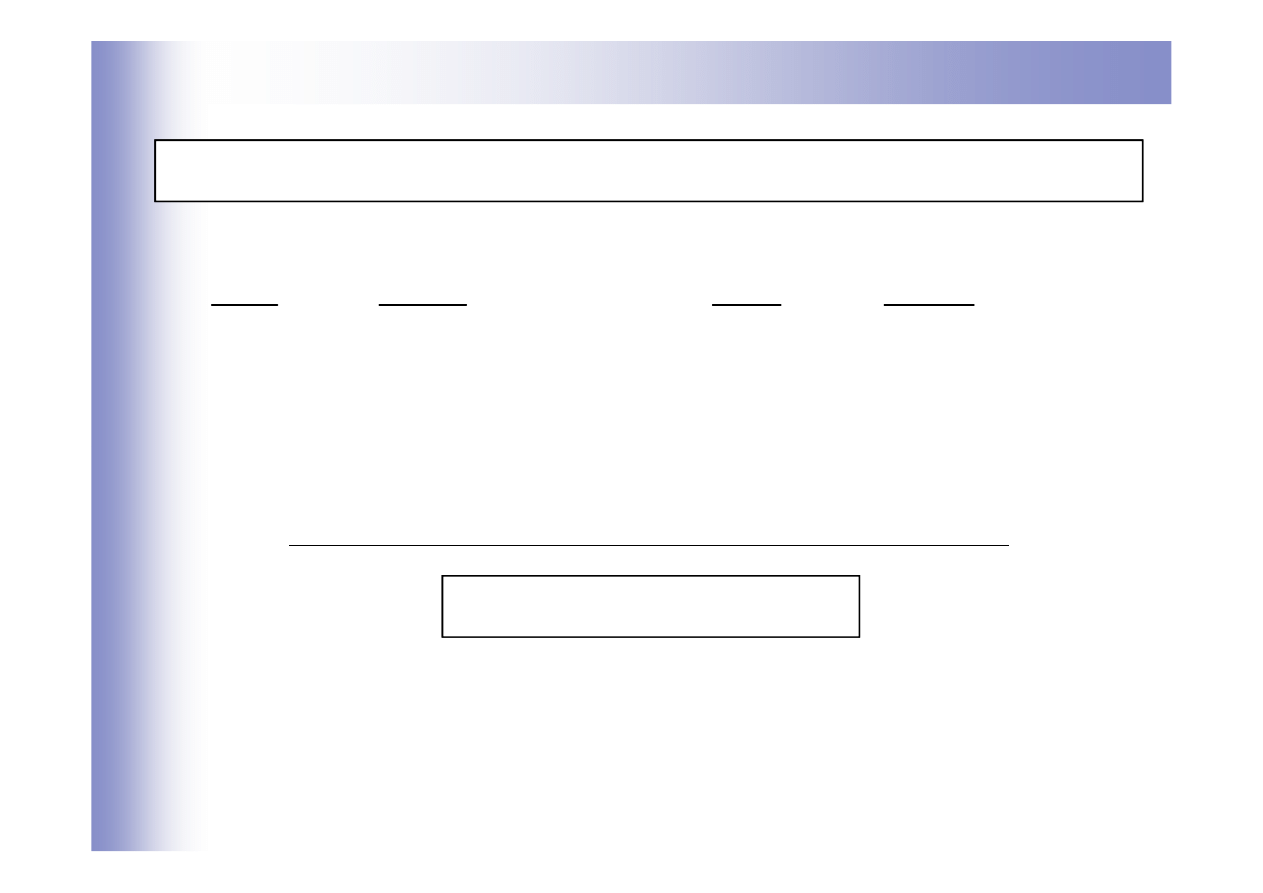
Opis matematyczny układów liniowych
Ogólna postać równania różniczkowego układu liniowego:
gdzie: y- sygnał wyjściowy, u-sygnał wejściowy, a
i
, b
i
- współczynniki stałe
u
b
dt
u
d
b
dt
u
d
b
y
a
dt
y
d
a
dt
y
d
a
m
m
m
m
m
m
n
n
n
n
n
n
0
1
1
1
0
1
1
1
+
+
+
=
+
+
+
−
−
−
−
−
−
K
K
i
i
y, u – są odchyłkami od punktu pracy
ZASADA SUPERPOZYCJI
y(u
1
+u
2
)=y(u
1
)+y(u
2
)
gdzie: y(u
i
) oznacza odpowiedź układu y na wymuszenie u
i
;
oraz y(0)=0

Układy liniowe
Układ liniowy – układ, w którym zachowana jest zasada superpozycji.
Modele matematyczne układów liniowych są opisywane liniowymi
równaniami algebraicznymi lub liniowymi równaniami
różniczkowymi, np.:
u
u
,
y
y
y
2
5
0
2
2
+
=
+
+
&
&
&
&
&
Układ nieliniowy – układy w których nie jest zachowana zasada
superpozycji.
y(u
1
+u
2
)=y(u
1
)+y(u
2
)
Układ, w którym y(0)≠0 nie spełnia zasady superpozycji
np. układ opisanym równaniem algebraicznym y=u+1.
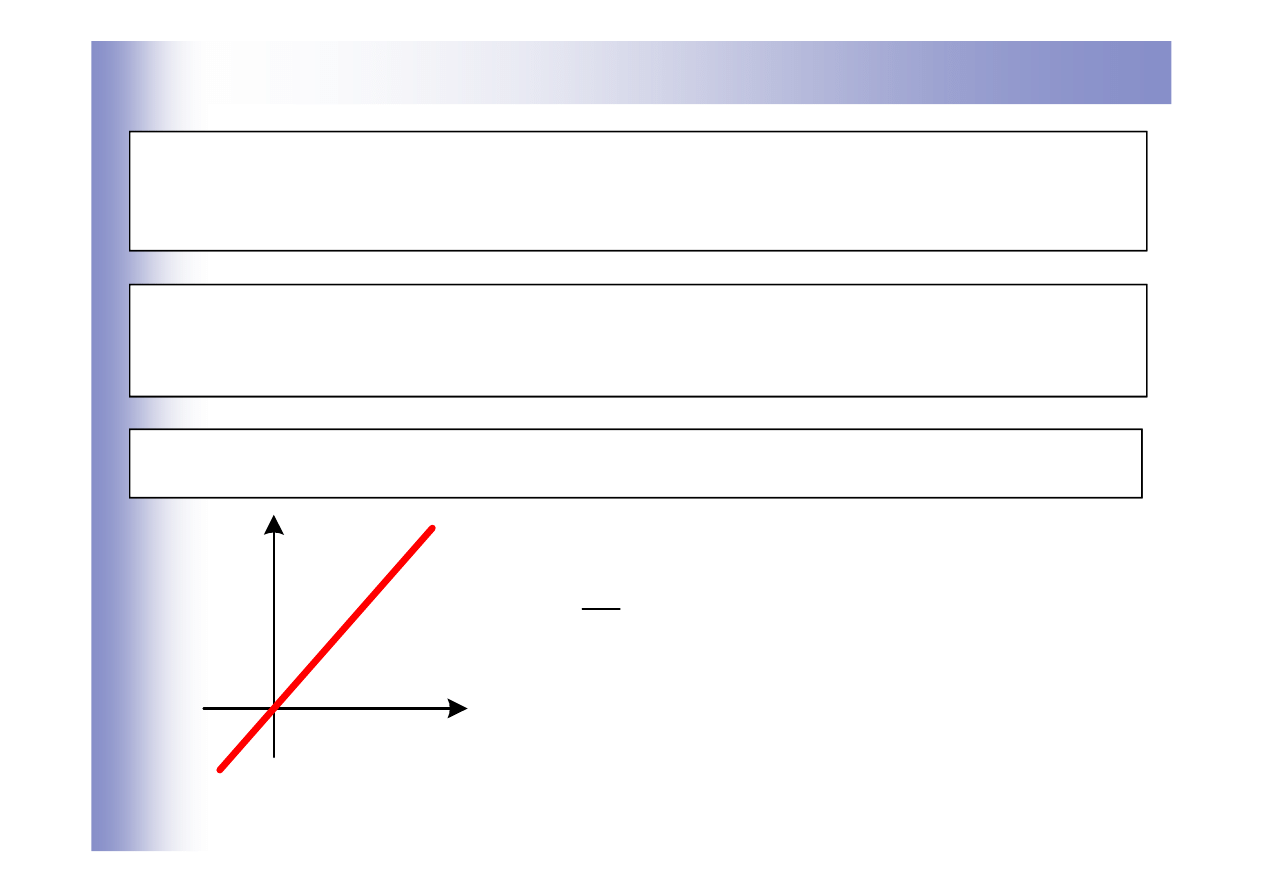
Charakterystyka statyczna
Charakterystyka statyczna układu – przedstawia zależność sygnału
wyjściowego układu od sygnału wejściowego w stanie ustalonym
Stan ustalony układu – wszystkie pochodne sygnału wejściowego
i sygnału wyjściowego są równe zero
u
y
Postać charakterystyki statycznej układów liniowych i zlinearyzowanych:
gdzie: u,y – wejście, wyjście z układu
u
a
b
y
0
0
=

Przekształcenie Laplace’a
Zastąpienie równania różniczkowego transmitancją operatorową,
przejście z dziedziny czasu rzeczywistego na zmienną zespoloną
)
(
)
(
s
f
t
f
⇔
ω
j
c
s
+
=
)]
(
[
)
(
t
f
L
s
f
=
∫
∞
−
=
0
)
(
)
(
dt
e
t
f
s
f
st
)]
(
[
)
(
t
f
L
s
f
=
)]
(
[
)
(
1
s
f
L
t
f
−
=
∫
+
−
=
jω
c
jω
c
st
ds
e
s
F
πj
f(t)
)
(
2
1
przekształcenie
Laplace’a
odwrotne
przekształcenie
Laplace’a

Opis matematyczny układów liniowych
Zastąpienie równania różniczkowego transmitancją operatorową:
u
b
dt
u
d
b
dt
u
d
b
y
a
dt
y
d
a
dt
y
d
a
m
m
m
m
m
m
n
n
n
n
n
n
0
1
1
1
0
1
1
1
+
+
+
=
+
+
+
−
−
−
−
−
−
K
K
)
0
(
)
0
(
)
(
1
1
+
−
+
−
−
−
−
=
n
n
n
n
y
y
s
s
y
s
y
d
L
K
)
(
)
(
)
(
)
(
0
1
1
0
1
1
b
s
b
s
b
s
u
a
s
a
s
a
s
y
m
m
m
m
n
n
n
n
+
+
+
⋅
=
+
+
+
⋅
−
−
−
−
K
K
)
0
(
)
0
(
)
(
1
1
+
−
+
−
−
−
−
=
n
n
n
n
y
y
s
s
y
s
dt
y
d
L
K
)
(s
y
s
dt
y
d
L
n
n
n
=
przy zerowych warunkach
początkowych

Transmitancja operatorowa
Transmitancja operatorowa: stosunek transformaty sygnału
wyjściowego do transformaty sygnału wejściowego
przy zerowych warunkach początkowych
)
(
)
(
)
(
)
(
0
1
1
0
1
1
b
s
b
s
b
s
u
a
s
a
s
a
s
y
m
m
m
m
n
n
n
n
+
+
+
⋅
=
+
+
+
⋅
−
−
−
−
K
K
m
n
a
s
a
s
a
b
s
b
s
b
s
u
s
y
s
G
n
n
n
n
m
m
m
m
≥
+
+
+
+
+
+
=
=
−
−
−
−
,
)
(
)
(
)
(
0
1
1
0
1
1
K
K
)
(
)
(
)
(
s
N
s
M
s
G
=
0
1
1
0
1
1
)
(
)
(
a
s
a
s
a
s
N
b
s
b
s
b
s
M
n
n
n
n
m
m
m
m
+
+
+
=
+
+
+
=
−
−
−
−
K
K

Wyznaczanie transmitancji operatorowej
Przykład 1: Wyznaczyć transmitancję operatorową układu
opisanego równaniem różniczkowym:
Wykorzystując operator różniczkowania s można
powyższe równanie zapisać w postaci
u
y
dt
dy
3
2
=
+
1
2
3
)
(
)
(
)
(
)
(
3
)
(
)
1
2
(
)
(
3
)
(
)
(
2
+
=
=
=
+
=
+
s
s
u
s
y
s
G
s
u
s
y
s
s
u
s
y
s
sy
c
c
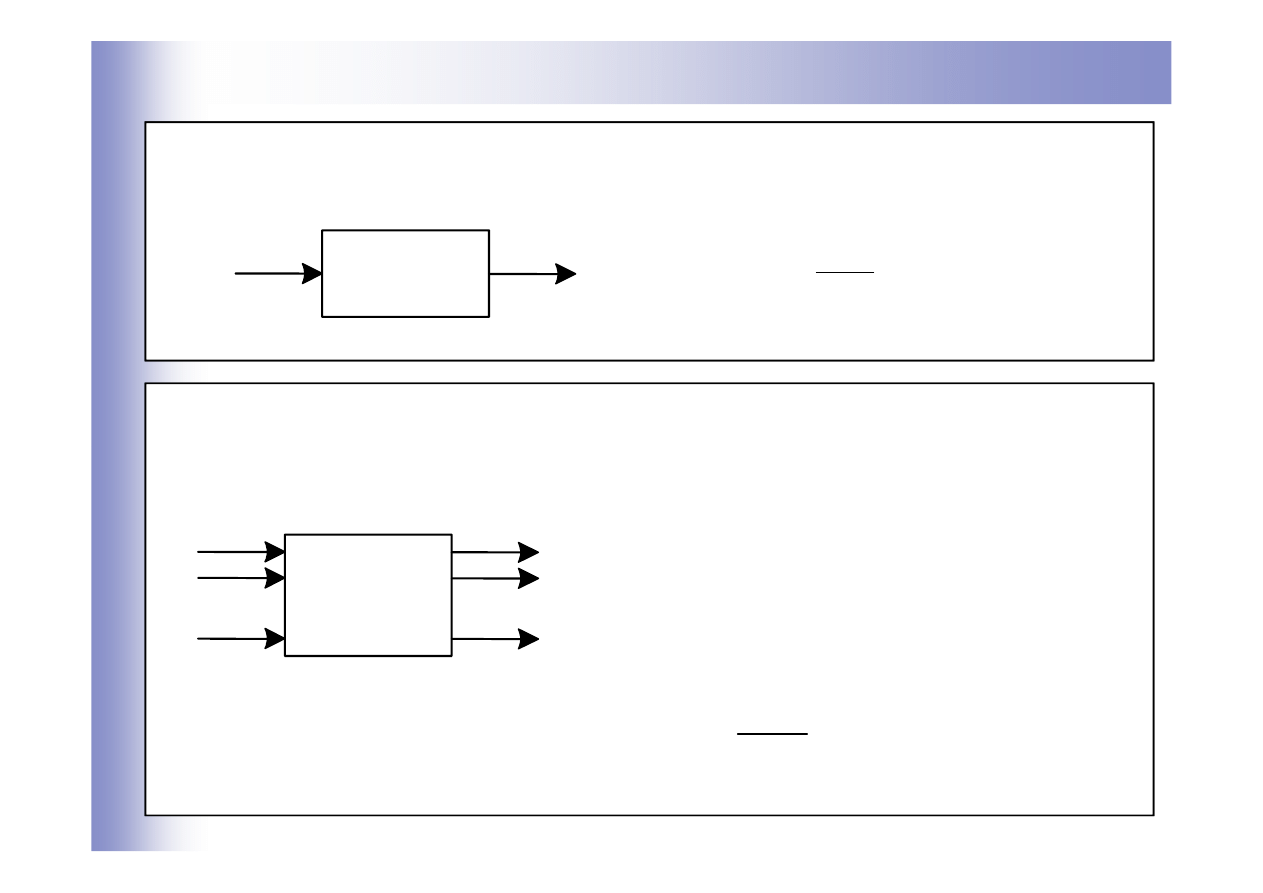
Opis elementów na schematach blokowych
Obiekty o jednym wejściu i jednym wyjściu:
u
y
G(s)
)
(
)
(
)
(
s
u
s
y
s
G
=
Obiekty wielowymiarowe:
..
.
..
.
u
1
u
2
u
m
y
1
y
2
y
n
MG(s)
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
22
21
1
12
11
s
G
s
G
s
G
s
G
s
G
s
G
s
G
s
G
s
G
s
MG
nm
n
n
m
m
K
M
M
M
M
K
K
m
k
n
i
s
u
s
y
s
G
k
i
ik
K
K
1
,
1
,
)
(
)
(
)
(
=
=
=

Wyznaczenie charakterystyki statycznej
z transmitancji operatorowej
)
(
)
(
lim
)
(
lim
)
(
lim
0
0
0
s
u
s
sG
s
sy
t
y
y
s
s
t
→
→
∞
→
=
=
=
),
(
lim
),
(
lim
0
0
t
y
y
t
u
u
t
t
∞
→
∞
→
=
=
Na podstawie twierdzenia o wartości końcowej:
1
)
(
u
s
u
const
u
=
⇒
=
)
(
lim
0
0
0
s
G
u
y
s→
=
Końcowe równanie charakterystyki statycznej:
0
0
0
0
u
a
b
y =
0
0
1
)
(
u
s
s
u
const
u
=
⇒
=

Własności układów
Właściwości dynamiczne – prezentacja przebiegu wielkości wyjściowej
y(t) po wprowadzeniu do układu wymuszenia u(t)
Postać charakterystyki w typowym układzie współrzędnych:
Gdzie: u - sygnał wejściowy
y - sygnał wyjściowy
t - czas [s]

Metody wyznaczania odpowiedzi układu y(t)
Klasyczna:
• Założyć warunki początkowe
• Rozwiązać równanie różniczkowe
u
b
dt
u
d
b
dt
u
d
b
y
a
dt
y
d
a
dt
y
d
a
m
m
m
m
m
m
n
n
n
n
n
n
0
1
1
1
0
1
1
1
+
+
+
=
+
+
+
−
−
−
−
−
−
K
K
Operatorowa:
)]
(
)
(
[
)
(
)]
(
[
)
(
1
1
s
u
s
G
L
t
f
s
y
L
t
f
−
−
=
=
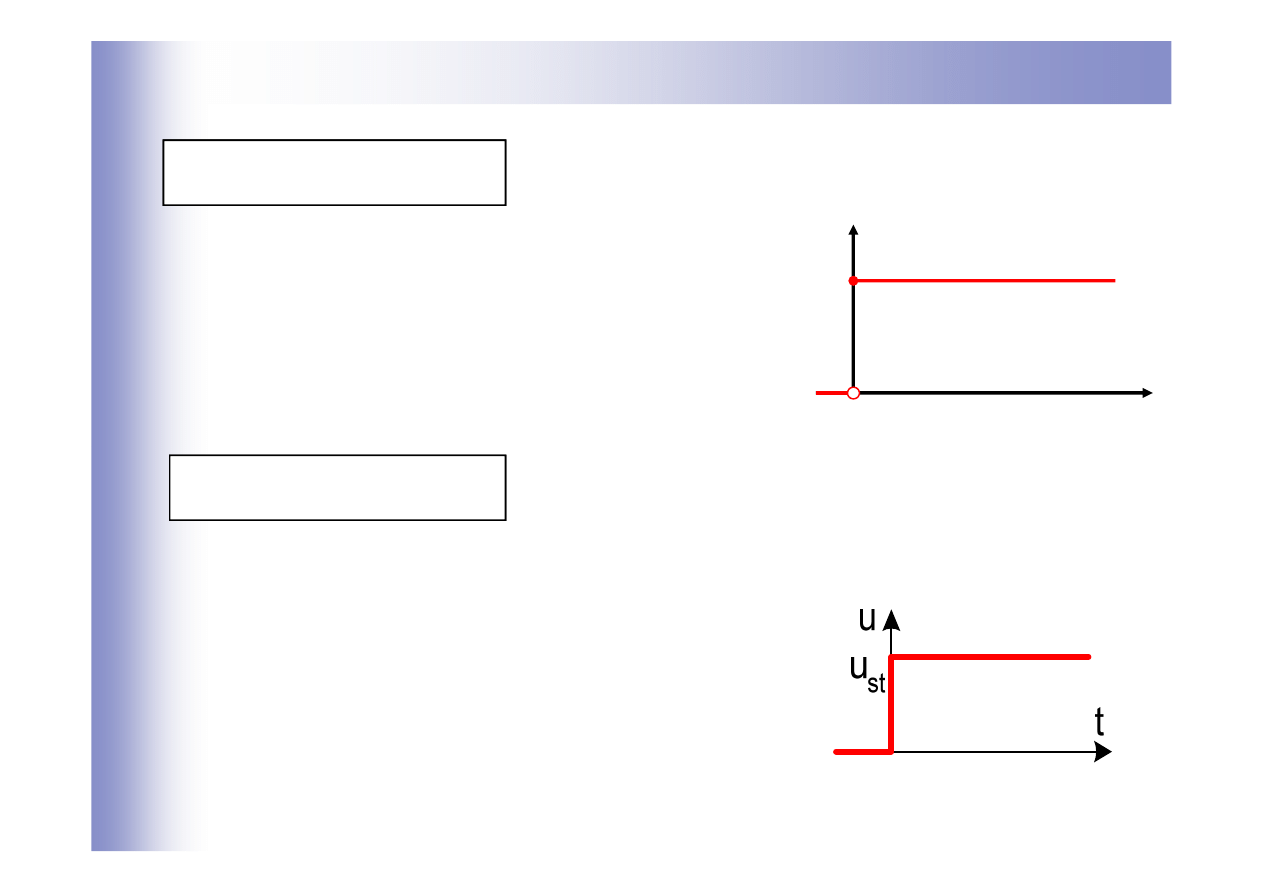
Typowe wymuszenia
Skok jednostkowy
t
u
1(t)
=
0
)
(
1
)
(
t
t
u
dla t ≥ 0
dla t < 0
=
⋅
0
)
(
1
)
(
t
u
t
u
st
dla t ≥ 0
dla t < 0
Skok o wartość stałą
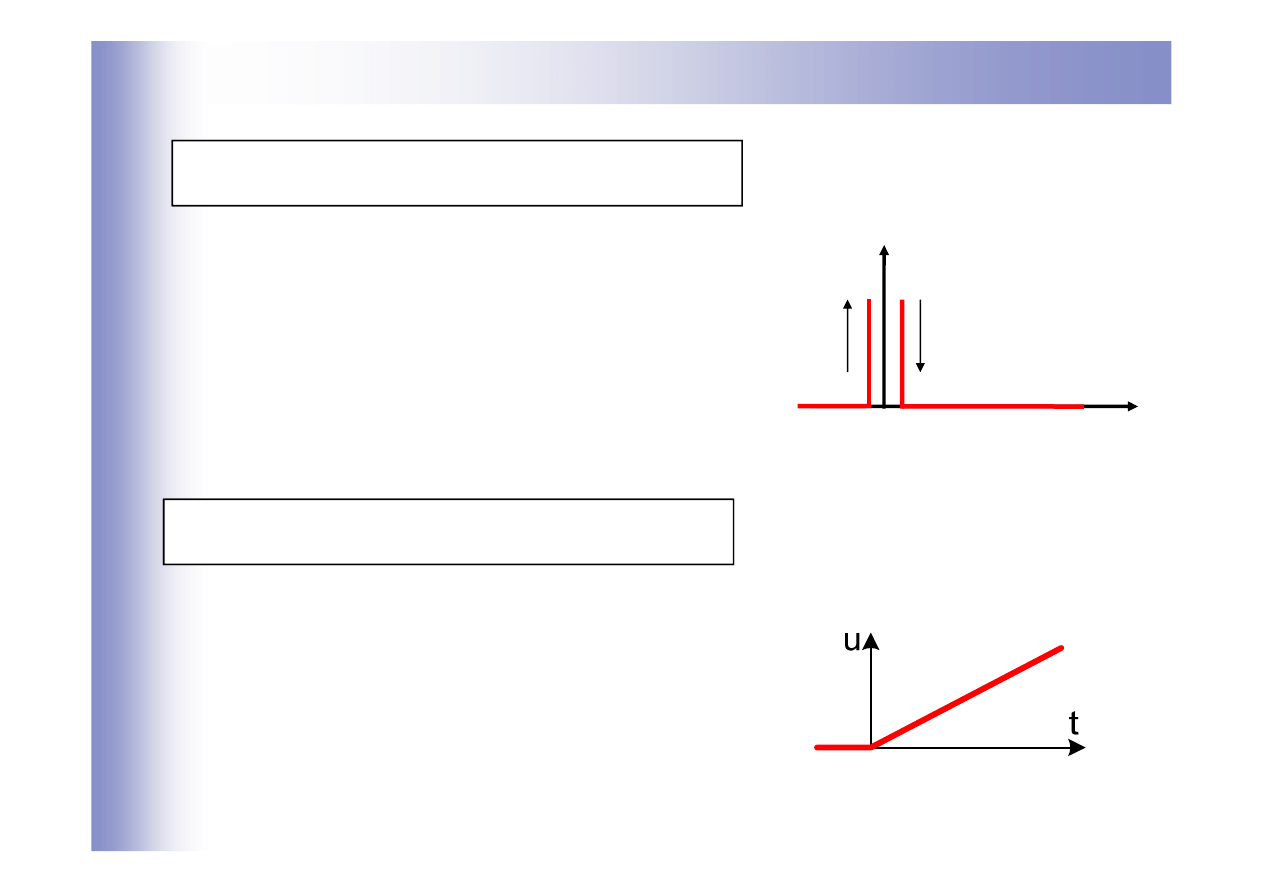
Typowe wymuszenia
Impuls jednostkowy – Delta Diraca
t
u
0
∞
∞
=
=
0
)
(
)
(
t
δ
t
u
dla t ≠ 0
dla t = 0
Wymuszenie liniowo narastające
at
t
u
=
)
(
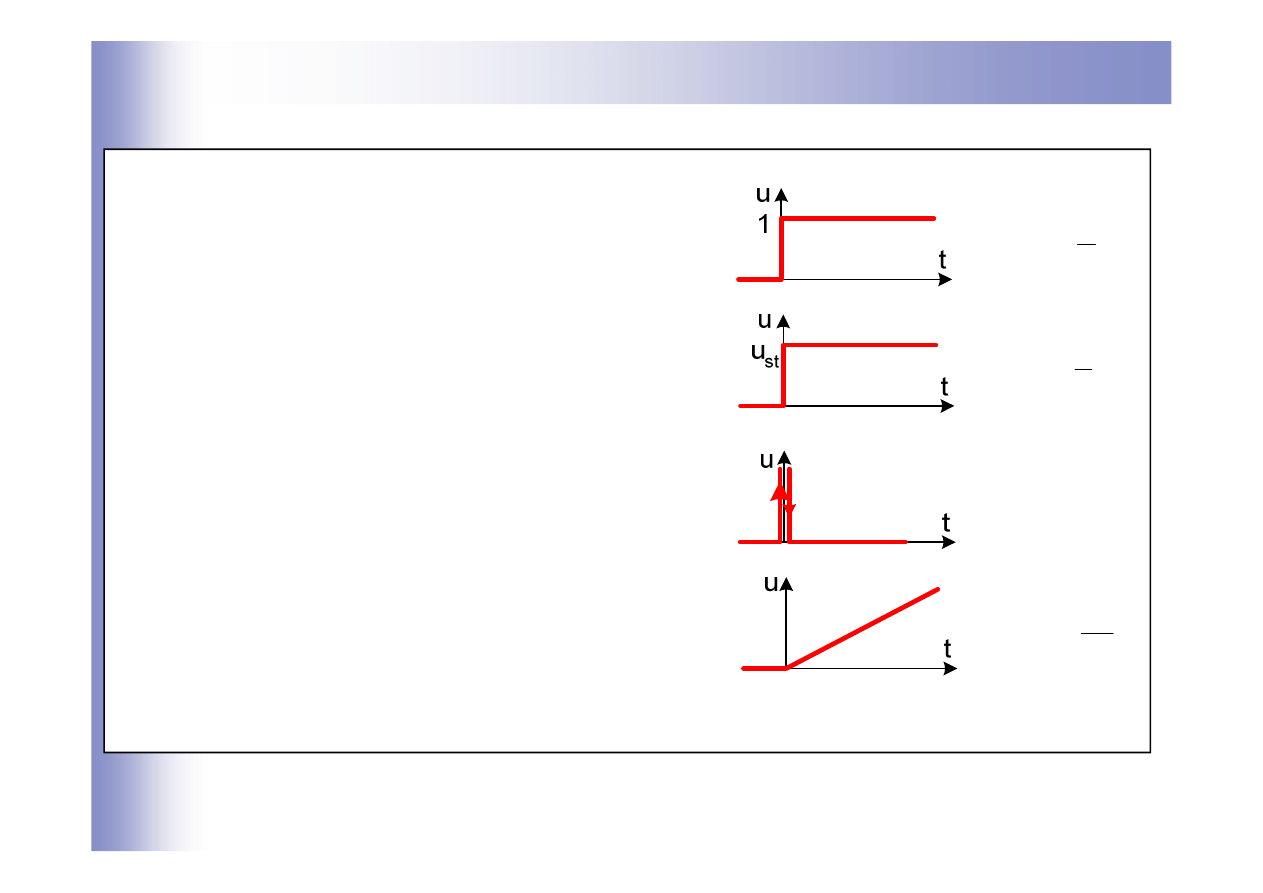
Typowe wymuszenia
•
Wymuszenie skokowe jednostkowe
u(t)=1(t)
•
Wymuszenie skokowe o wartość stałą
u(t)=u
st
·1(t)
s
s
u
1
)
(
=
st
u
s
s
u
1
)
(
=
•
Wymuszenie w postaci impulsu
u(t)=δ(t) Delta Diraca
•
Wymuszenie liniowo narastające
u(t)= a·t
1
)
(
=
s
u
2
)
(
s
a
s
u
=
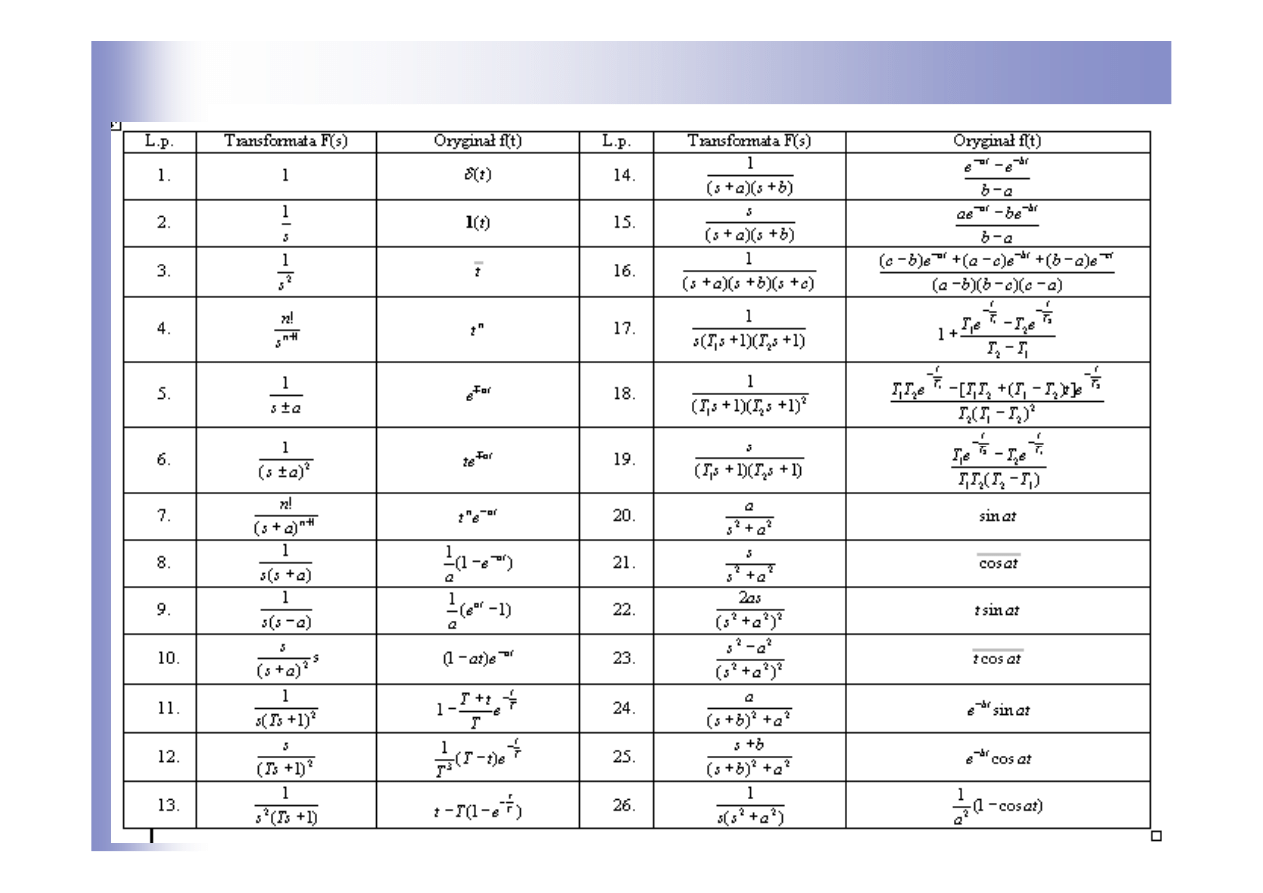
Tablica transformat
Opis układów z użyciem współrzędnych stanu
=
)
(
)
(
)
(
)
(
2
1
t
u
t
u
t
u
t
U
p
M
)
(
1
t
x
wektor wejść
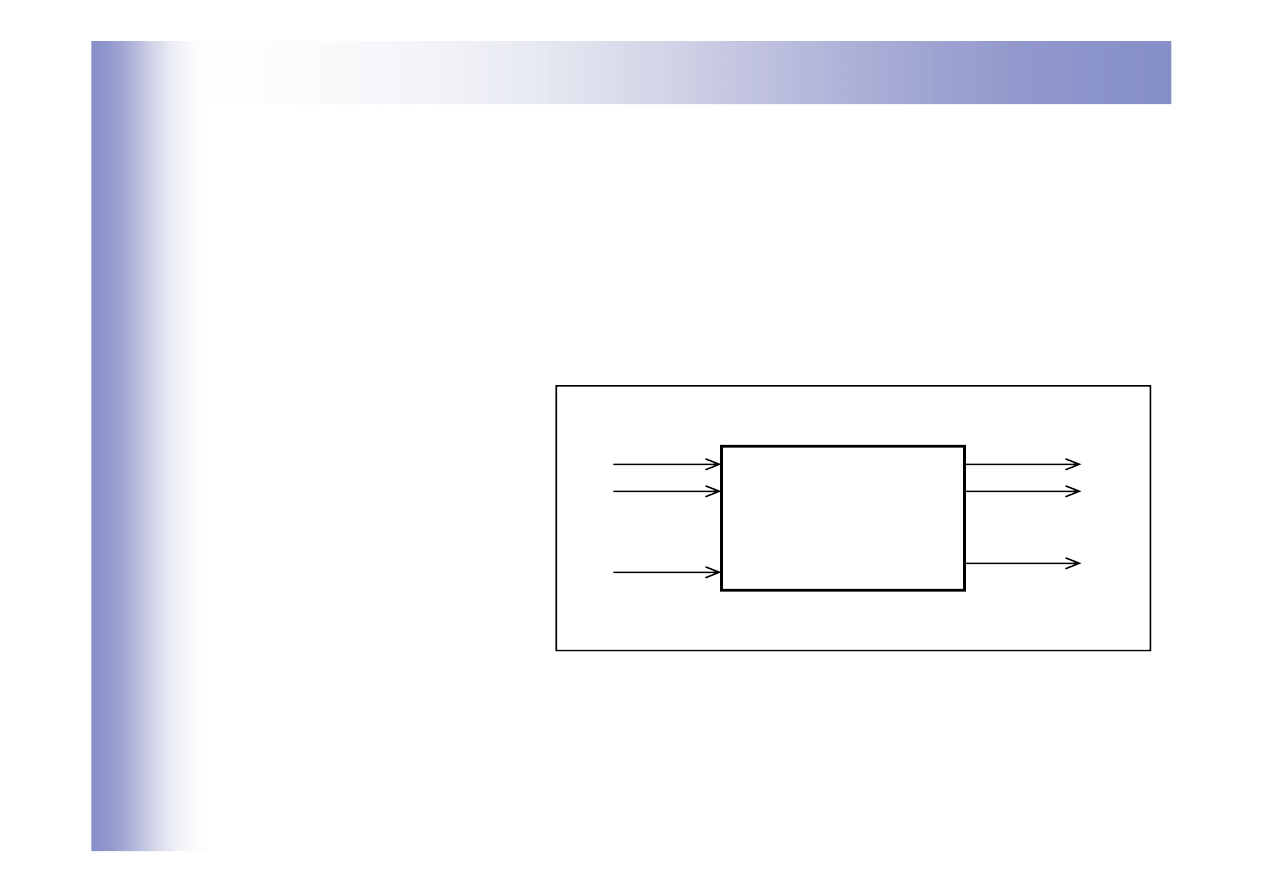
W ogólnym opisie układów wielowymiarowych poszczególne wielkości
określone są w postaci wektorów i oznaczają:
y
Schemat obiektu
=
)
(
)
(
)
(
)
(
2
1
t
x
t
x
t
x
t
X
n
M
=
)
(
)
(
)
(
)
(
2
1
t
y
t
y
t
y
t
Y
q
M
wektor stanu
wektor wyjść
Obiekt
u
1
u
2
u
p
y
1
y
2
y
q
x
n
x
2
x
1
...

Współrzędne stanu
Współrzędne stanu – wielkości charakteryzujące zachowanie się układu
dynamicznego
Wektor stanu układu dynamicznego – minimalny zbiór współrzędnych
stanu wystarczający łącznie ze znajomością wielkości
wejściowych do określenia zachowania się układu w przyszłości.
Liczba współrzędnych stanu jest równa rzędowi równania różniczkowego
opisującego obiekt
opisującego obiekt
Opis układów we współrzędnych stanu jest trudniejszy do interpretacji
fizycznej niż opis w postaci transmitancji i niemożliwy do bezpośredniego
określenia na drodze pomiarowej, ale wygodniejszy do celów modelowania
analogowego oraz projektowania układów wielowymiarowych.
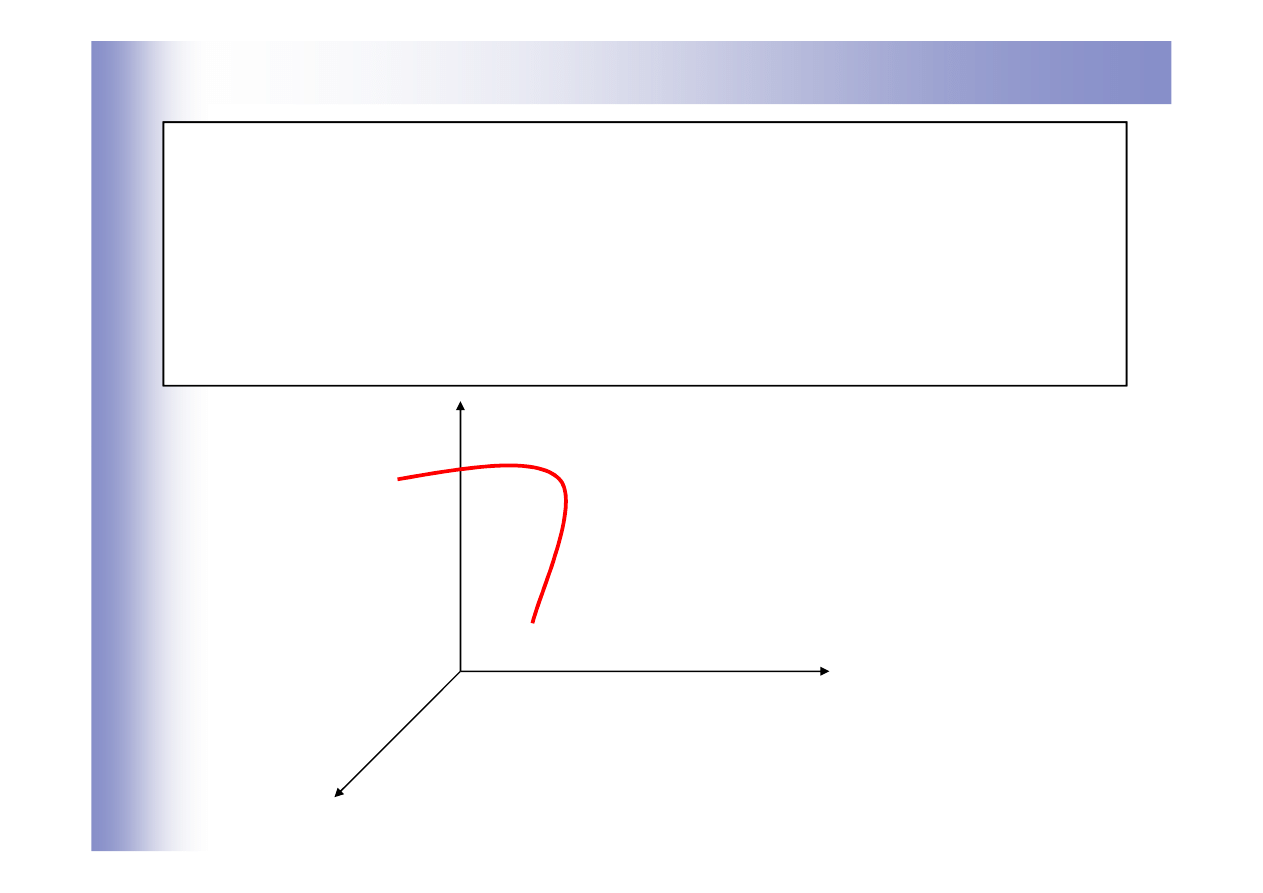
Przestrzeń stanów
Zbiór wszystkich możliwych wartości wektora stanu X(t) w chwilach t
tworzy
przestrzeń stanów układu (przestrzeń fazową).
Zbiór wartości wektora stanu układu w kolejnych chwilach czasu
tworzy w tej przestrzeni krzywą, zwaną
trajektorią stanu układu
(
trajektorią fazową).
x
2
x
3
x
2
x
1

Równania stanu i wyjść
Ogólna postać równania stanu:
z n warunkami początkowymi:
=
=
10
0
1
2
1
2
1
1
1
)
(
)
(
);
;
,
,
,
;
,
,
,
(
)
(
p
n
t
dx
x
t
x
t
u
u
u
x
x
x
f
dt
t
dx
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
K
K
=
=
0
0
2
1
2
1
)
(
);
;
,
,
,
;
,
,
,
(
)
(
n
n
p
n
n
n
x
t
x
t
u
u
u
x
x
x
f
dt
t
dx
K
K
Ogólna postać równania wyjść:
=
=
)
;
,
,
,
;
,
,
,
(
)
(
)
;
,
,
,
;
,
,
,
(
)
(
2
1
2
1
2
1
2
1
1
1
t
u
u
u
x
x
x
g
t
y
t
u
u
u
x
x
x
g
t
y
p
n
q
q
k
n
K
K
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
L
K
K
Zlinearyzowane równania stanu
Po linearyzacji w otoczeniu wybranego stanu ustalonego (nominalnego
punktu pracy), równania przyjmują wówczas postać:
t
t
f
u
u
f
u
u
f
u
u
f
x
x
f
x
x
f
x
x
f
dt
t
dx
p
p
n
n
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
=
1
1
2
2
1
1
1
1
1
2
2
1
1
1
1
1
)
(
K
K
t
t
g
u
u
g
u
u
g
u
u
g
x
x
g
x
x
g
x
x
g
y
p
p
n
n
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
=
1
1
2
2
1
1
1
1
1
2
2
1
1
1
1
1
K
K
...
t
u
u
u
x
x
x
p
n
∂
∂
∂
∂
∂
∂
∂
2
1
2
1
...
przy czym:
A(t) – macierz układu stopnia n×n
B(t) – macierz wejść stopnia n×p
C(t) – macierz wyjść stopnia q×n
D(t) – macierz transmisyjna układu stopnia q×p
Układ niestacjonarny
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
t
U
t
D
t
X
t
C
t
Y
t
U
t
B
t
X
t
A
t
X
+
=
+
=
&
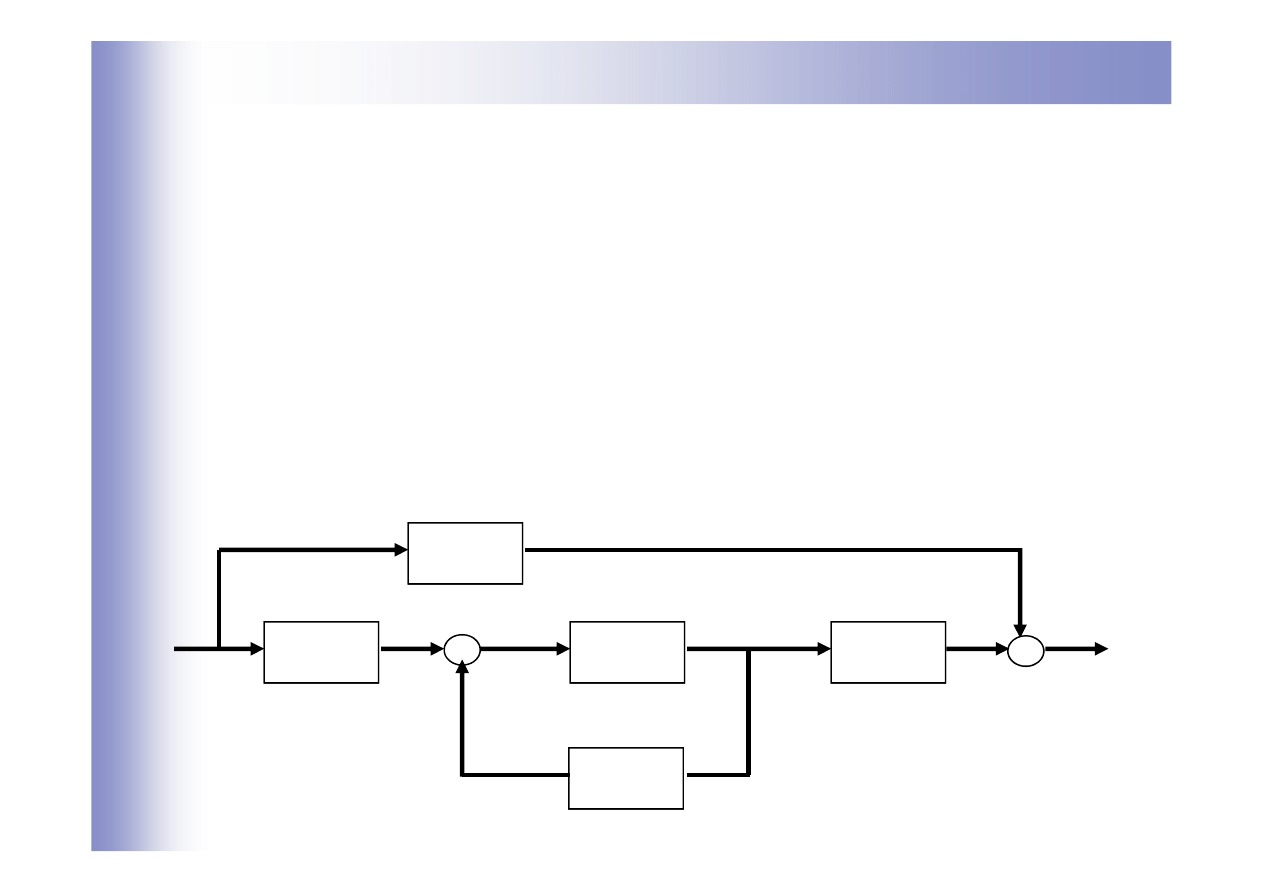
Równania stanu układów liniowych stacjonarnych
Układ stacjonarny - o parametrach niezależnych od czasu
W przypadku szczególnym, gdy układ jest liniowy stacjonarny,
pochodne cząstkowe względem zmiennych x
1
,…,x
n
,…,u
1
,…,u
k
nie
zawierają czasu i pochodne cząstkowe względem czasu są równe
zeru - elementy macierzy są wówczas stałe i równania stanu można
zapisać w postaci:
)
(
)
(
)
(
)
(
)
(
)
(
t
DU
t
CX
t
Y
t
BU
t
AX
t
X
+
=
+
=
&
D
B
A
C
∫∫∫∫
)
(t
U
)
(t
Y
)
(t
X
•
)
(t
X
)
(
)
(
)
(
t
DU
t
CX
t
Y
+
=
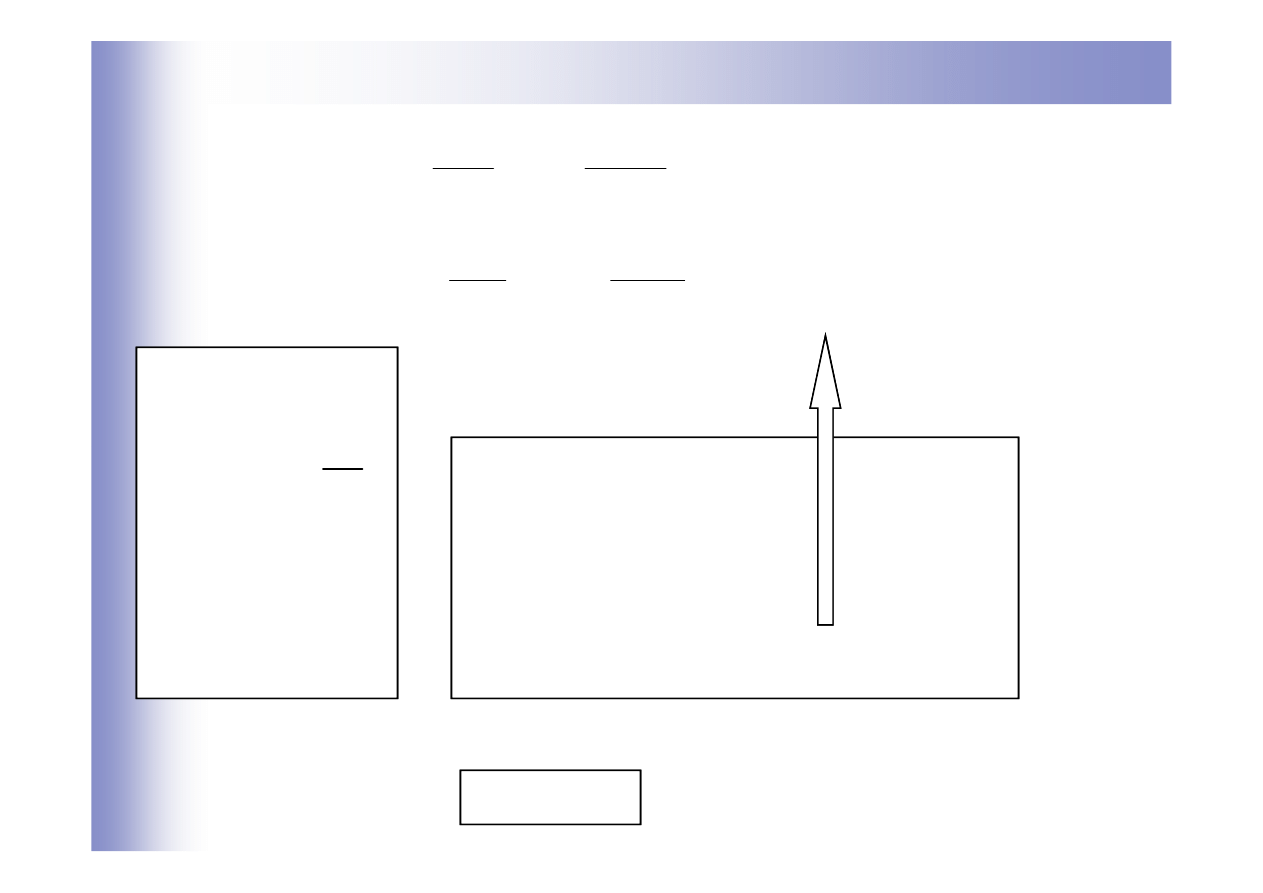
Przykład wyznaczania równań stanu
u
b
y
a
dt
y
d
a
dt
y
d
n
n
n
n
n
0
0
1
1
1
=
+
+
+
−
−
−
K
u
b
y
a
dt
y
d
a
dt
y
d
n
n
n
n
n
0
0
1
1
1
+
−
−
−
=
−
−
−
K
1
=
=
=
dy
x
x
y
x
Współrzędne stanu
Równania stanu
1
2
3
1
2
...
−
=
=
=
=
n
n
x
x
x
x
dt
dy
x
x
&
&
&
u
b
x
a
x
a
x
x
x
x
x
n
n
n
0
1
0
1
3
2
2
1
...
+
−
−
−
=
=
=
−
K
&
&
&
1
x
y =
Równanie wyjść
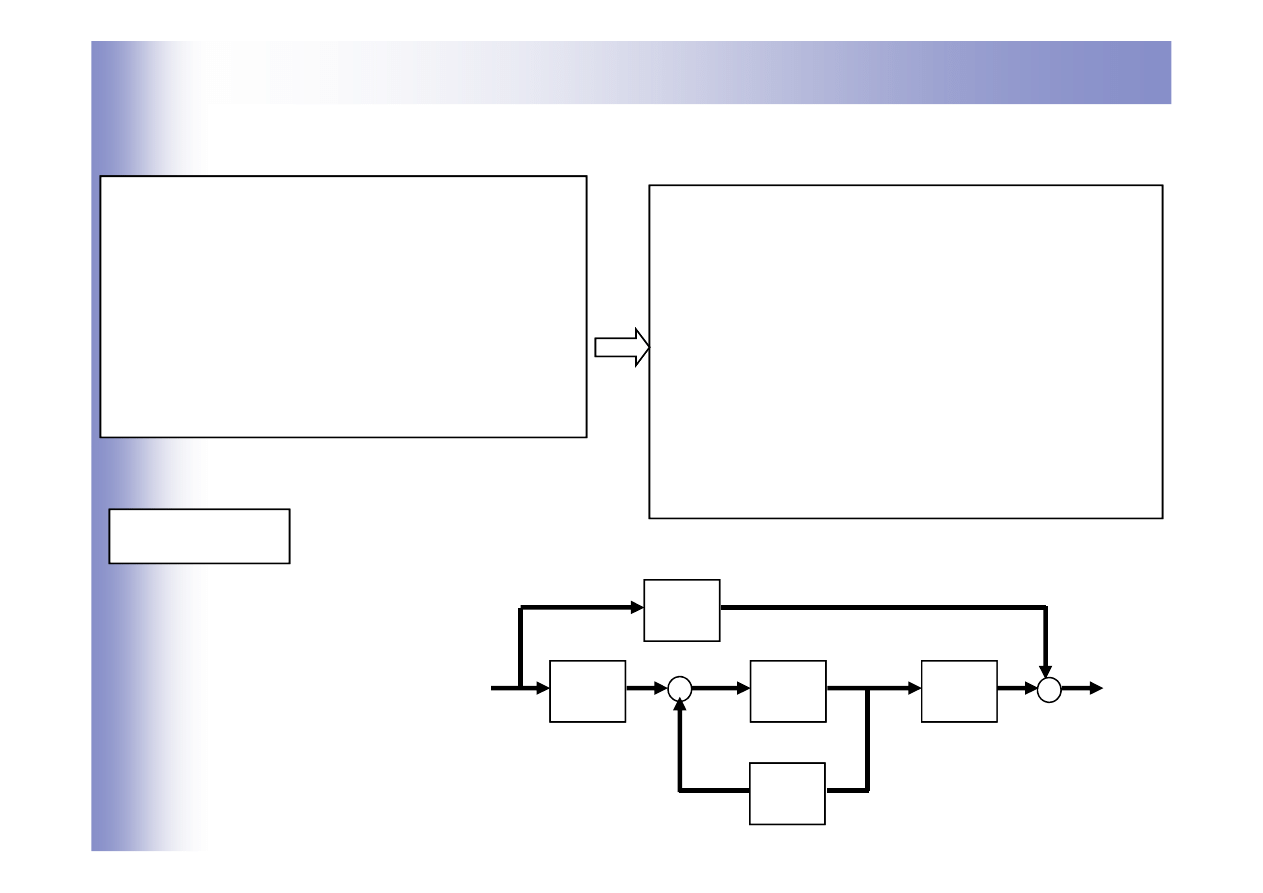
Przykład wyznaczania równań stanu
u
b
x
a
x
a
x
x
x
x
x
n
n
n
0
1
0
1
3
2
2
1
...
+
−
−
−
=
=
=
−
K
&
&
&
Równania stanu
−
−
−
−
=
−1
2
1
0
...
1
...
0
0
0
...
...
...
...
...
0
...
1
0
0
0
...
0
1
0
n
a
a
a
a
A
=
o
b
B
0
...
0
0
1
x
y =
Równanie wyjść
[
]
0
...
0
0
1
=
C
[ ]
0
=
D
D
B
A
C
∫∫∫∫
)
(t
U
)
(t
Y
)
(t
X
)
(t
X&

Wyznaczanie równań stanu z transmitancji
Metoda bezpośrednia
n
n
n
n
n
m
m
m
m
s
s
a
s
a
s
a
s
b
s
b
s
b
s
b
s
u
s
y
s
G
−
−
−
−
−
−
⋅
+
+
+
+
+
+
+
+
=
=
)
(
)
(
)
(
0
1
1
1
0
1
1
1
K
K
1
)
(
)
(
)
(
0
1
1
1
1
0
1
1
1
1
n
n
n
n
n
n
m
m
n
m
m
s
a
s
a
s
a
s
b
s
b
s
b
s
b
s
u
s
y
s
G
−
−
−
−
−
−
−
−
−
−
+
+
+
+
+
+
+
+
=
=
K
K
)
(
)
(
0
1
1
1
1
s
u
s
b
s
b
s
b
s
b
s
y
n
n
n
m
m
n
m
m
−
−
−
−
−
−
+
+
+
+
=
K
1
)
(
)
(
0
1
1
1
1
n
n
n
s
a
s
a
s
a
s
u
s
E
−
−
−
−
+
+
+
+
=
K
)
(
]
[
)
(
0
1
1
1
1
s
E
s
b
s
b
s
b
s
b
s
y
n
n
n
m
m
n
m
m
−
−
−
−
−
−
+
+
+
+
=
K
)
(
1
)
(
0
1
1
1
1
0
1
1
s
u
s
a
s
a
s
a
s
b
s
b
s
b
s
b
s
y
n
n
n
m
m
−
−
−
−
−
+
+
+
+
+
+
+
+
=
K
K
)
(
]
[
)
(
)
(
0
1
1
1
1
s
E
s
a
s
a
s
a
s
u
s
E
n
n
n
−
−
−
−
+
+
+
−
=
K
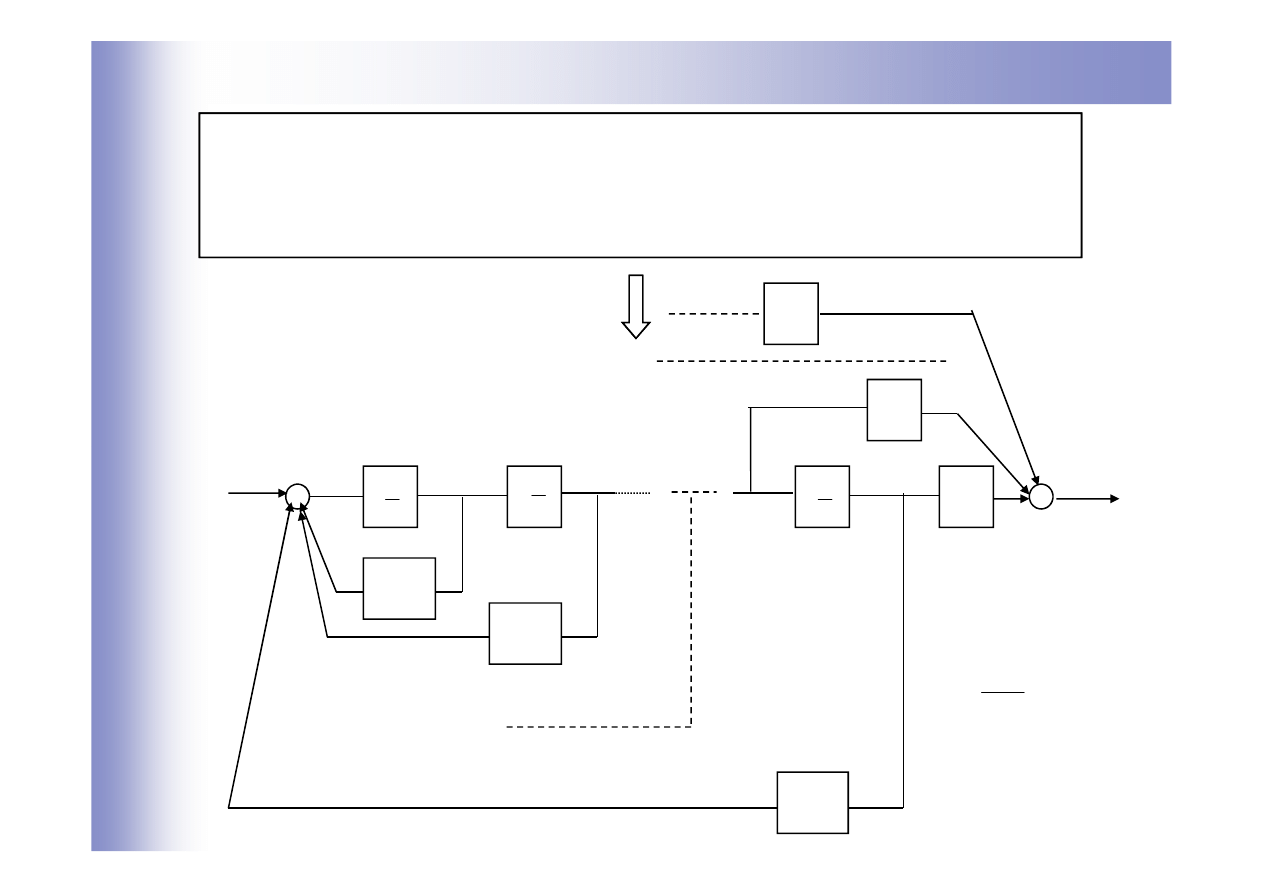
Wyznaczanie równań stanu z transmitancji
)
(
]
[
)
(
0
1
1
1
1
s
E
s
b
s
b
s
b
s
b
s
y
n
n
n
m
m
n
m
m
−
−
−
−
−
−
+
+
+
+
=
K
)
(
]
[
)
(
)
(
0
1
1
1
1
s
E
s
a
s
a
s
a
s
u
s
E
n
n
n
−
−
−
−
+
+
+
−
=
K
)
(s
E
m
b
1
b
)
(s
u
)
(s
y
)
(s
E
+
s
1
s
1
s
1
1
−
−
n
a
2
−
−
n
a
)
(
1
s
E
s
−
)
(
2
s
E
s
−
0
a
−
0
b
+
+
+
+
)
(s
E
s
n
−
)
(s
y
s
dt
y
d
L
n
n
n
=
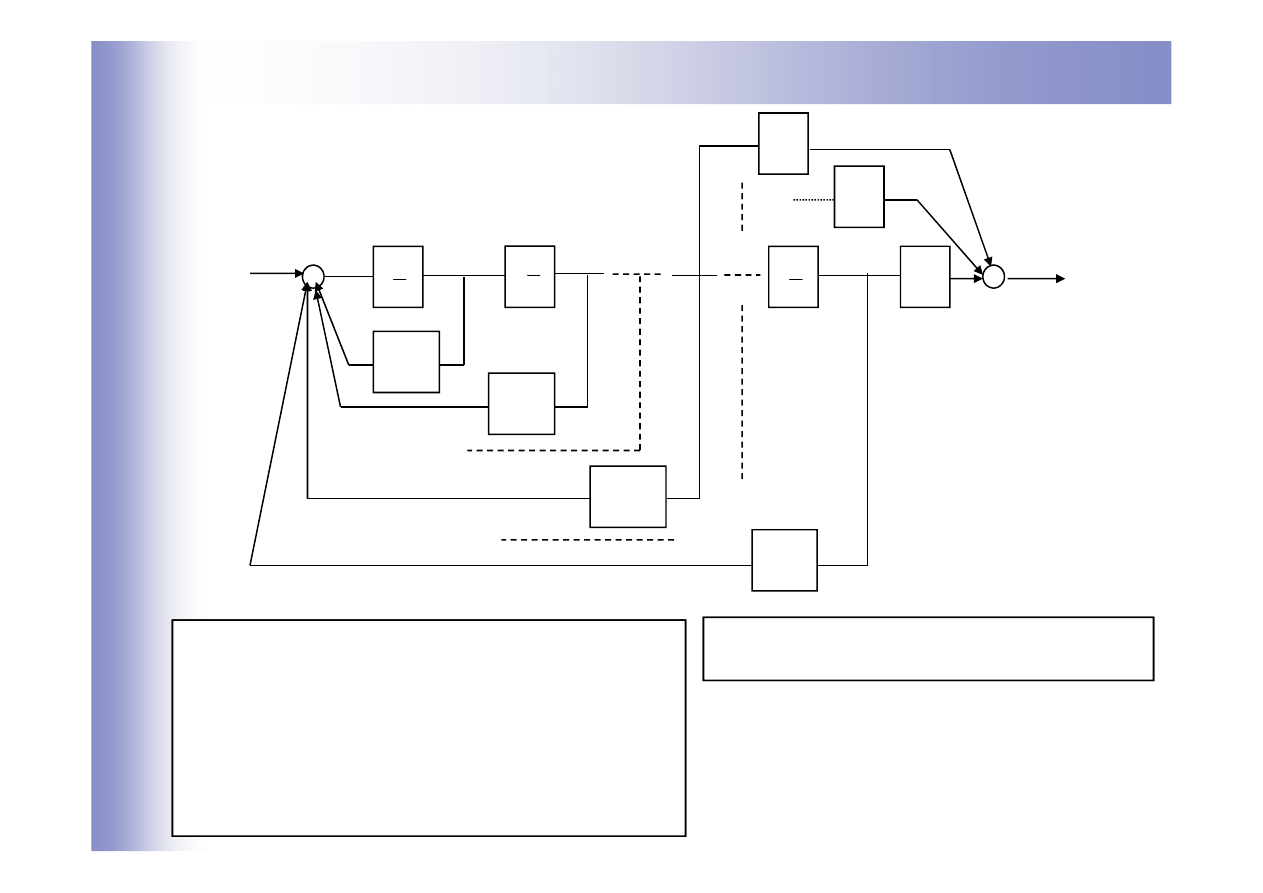
Wyznaczanie równań stanu z transmitancji
)
(s
u
)
(s
y
)
(s
E
+
s
1
s
1
s
1
1
−
−
n
a
2
−
−
n
a
)
(
1
s
E
s
−
)
(
2
s
E
s
−
0
b
m
b
1
b
+
+
+
+
+
)
(s
E
s
n
−
)
(s
E
s
n
m
−
1
x
2
x
n
x
u
x
a
x
a
x
a
x
x
x
x
x
n
n
n
+
−
−
−
−
=
=
=
−1
2
1
1
0
3
2
2
1
...
...
&
&
&
1
2
1
1
0
...
+
+
+
+
=
m
m
x
b
x
b
x
b
y
m
n
a
−
−
0
a
−

Przykład
2
2
2
6
5
2
2
)
3
)(
2
(
)
1
(
2
)
(
)
(
)
(
−
−
⋅
+
+
+
=
+
+
+
=
=
s
s
s
s
s
s
s
s
s
u
s
y
s
G
6
5
1
2
2
)
(
)
(
2
1
2
1
−
−
−
−
+
+
+
=
s
s
s
s
s
u
s
y
)
6
5
1
)
(
)(
2
2
(
)
(
2
1
2
1
−
−
−
−
+
+
+
=
s
s
s
u
s
s
s
y
)
(s
u
6
5
1
)
(
)
(
2
1
−
−
+
+
=
s
s
s
u
s
E
)
(
)
6
5
1
)(
(
2
1
s
u
s
s
s
E
=
+
+
−
−
)
(
)
6
5
)(
(
)
(
2
1
s
u
s
s
s
E
s
E
=
+
+
−
−
)
(
)
6
5
(
)
(
)
(
2
1
s
E
s
s
s
u
s
E
−
−
+
−
=
)
(
)
2
2
(
)
(
2
1
s
E
s
s
s
y
−
−
+
=
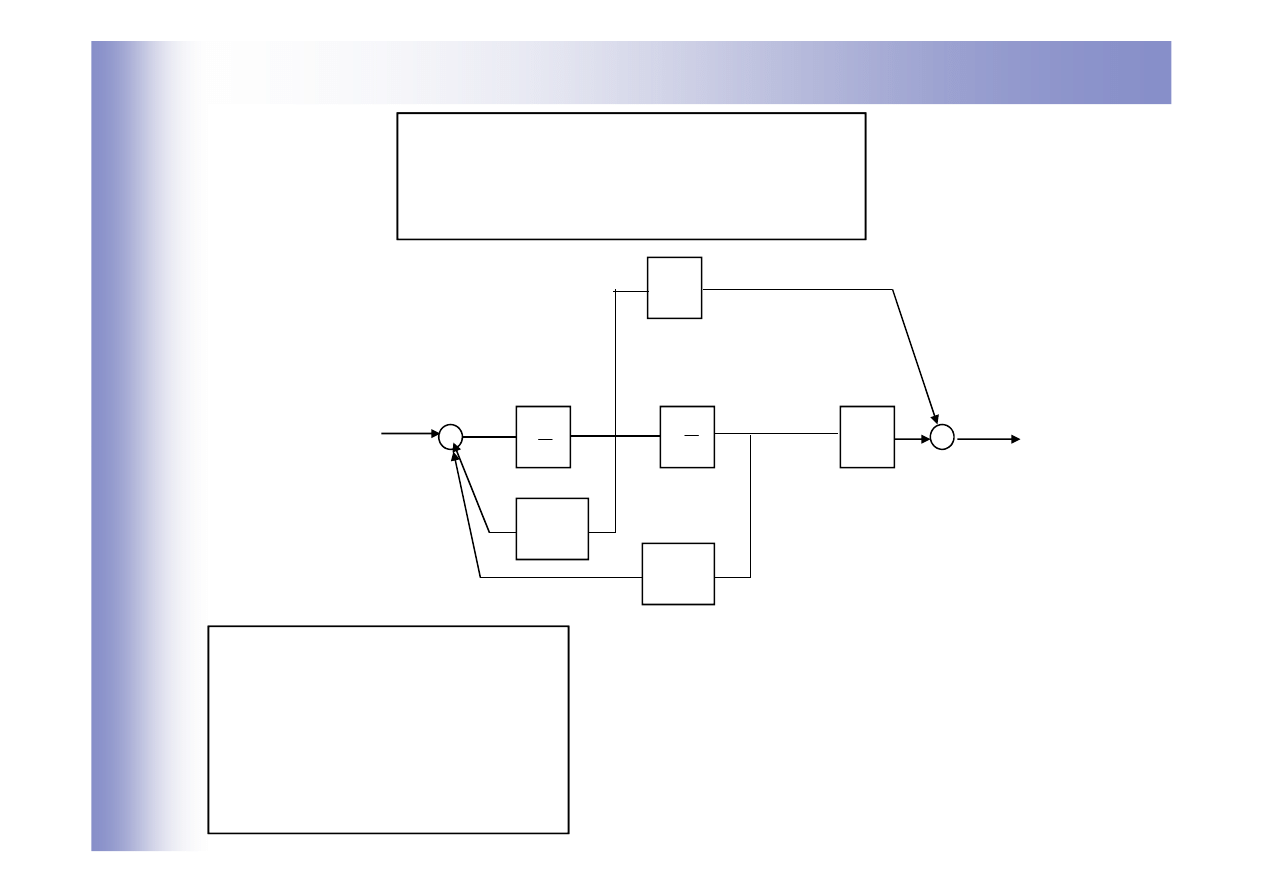
Przykład
)
(
)
6
5
(
)
(
)
(
2
1
s
E
s
s
s
u
s
E
−
−
+
−
=
)
(
)
2
2
(
)
(
2
1
s
E
s
s
s
y
−
−
+
=
)
(s
u
)
(s
y
)
(s
E
+
s
1
s
1
2
2
+
)
(s
u
s
s
5
−
6
−
2
+
+
+
+
1
x
2
x
u
x
x
x
x
x
+
−
−
=
=
2
1
2
2
1
5
6
&
&
2
1
2
2
x
x
y
+
=
−
−
=
5
6
1
0
A
=
1
0
B
[
]
2
2
=
C
[ ]
0
=
D
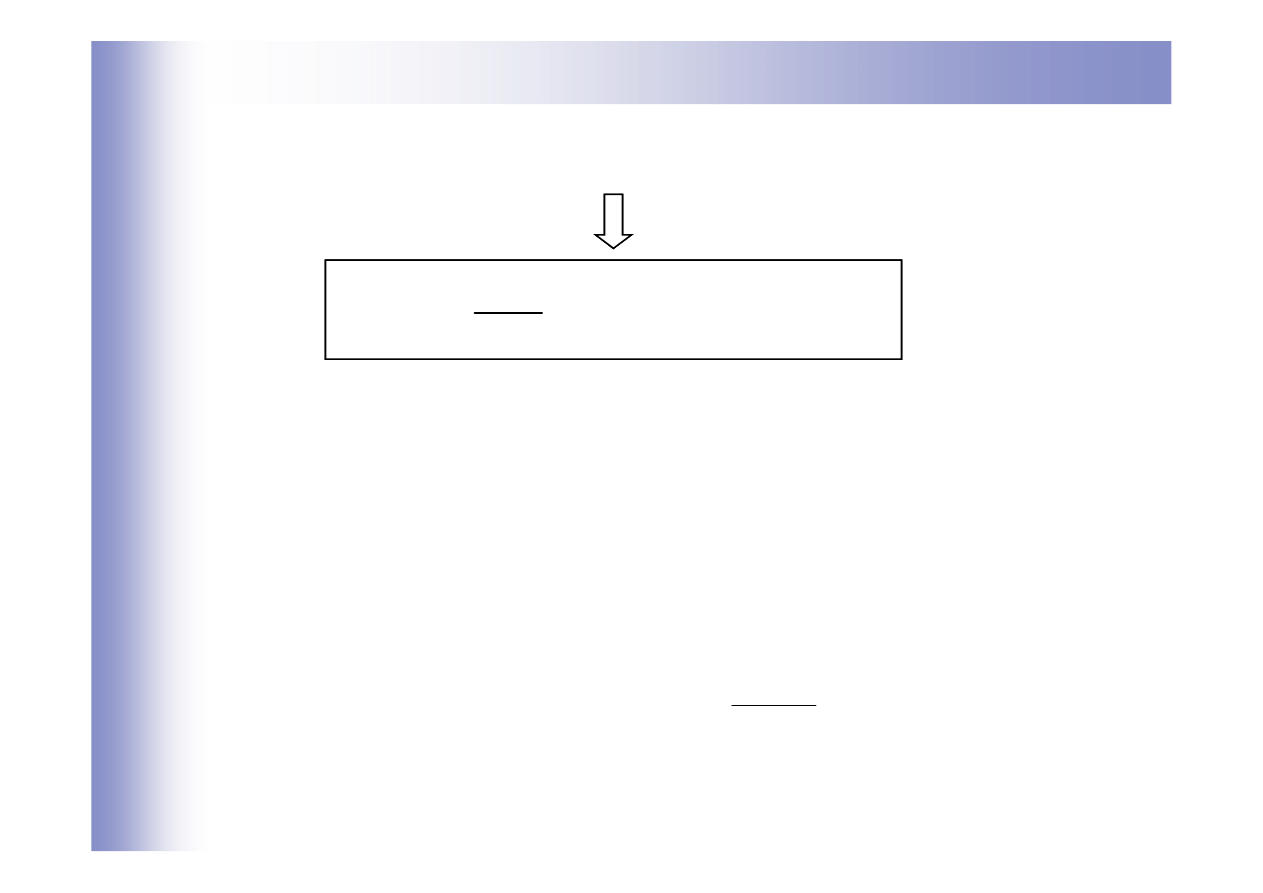
Transmitancja na podstawie równań stanu
)
(
]
)
(
[
)
(
1
s
u
D
B
A
Is
C
s
y
+
−
=
−
D
B
A
Is
C
s
u
s
y
s
G
+
−
=
=
−1
)
(
)
(
)
(
)
(
Przykład
=
1
0
2
1
A
=
1
0
B
[
]
0
1
=
C
[ ]
0
=
D
Przykład
[
]
2
1
)
1
(
2
1
0
1
0
2
1
0
0
0
1
)
(
−
=
−
=
−
s
s
s
s
G
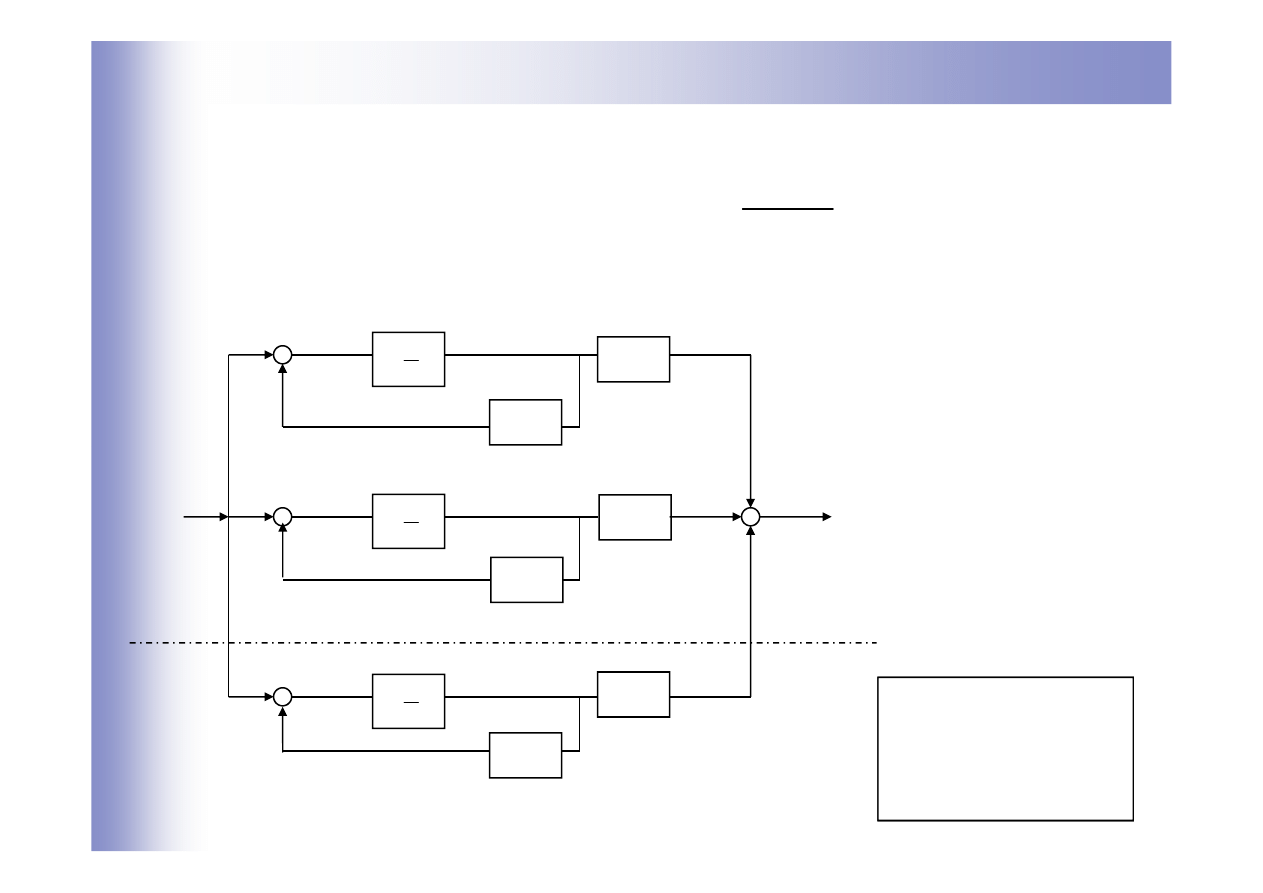
Wyznaczanie równań stanu z transmitancji
Metoda równoległa
)
(
)
(
1
1
∑
∑
+
=
=
n
i
i
n
i
c
s
k
s
G
s
G
1
s
1
k
1
c
−
1
x
+
+
1
s
1
s
2
k
n
k
2
c
−
n
c
−
)
(s
u
2
x
n
x
)
(s
y
+
+
+
+
+
+
+
∑
=
+
−
=
i
i
i
i
i
i
x
k
y
u
x
c
x&
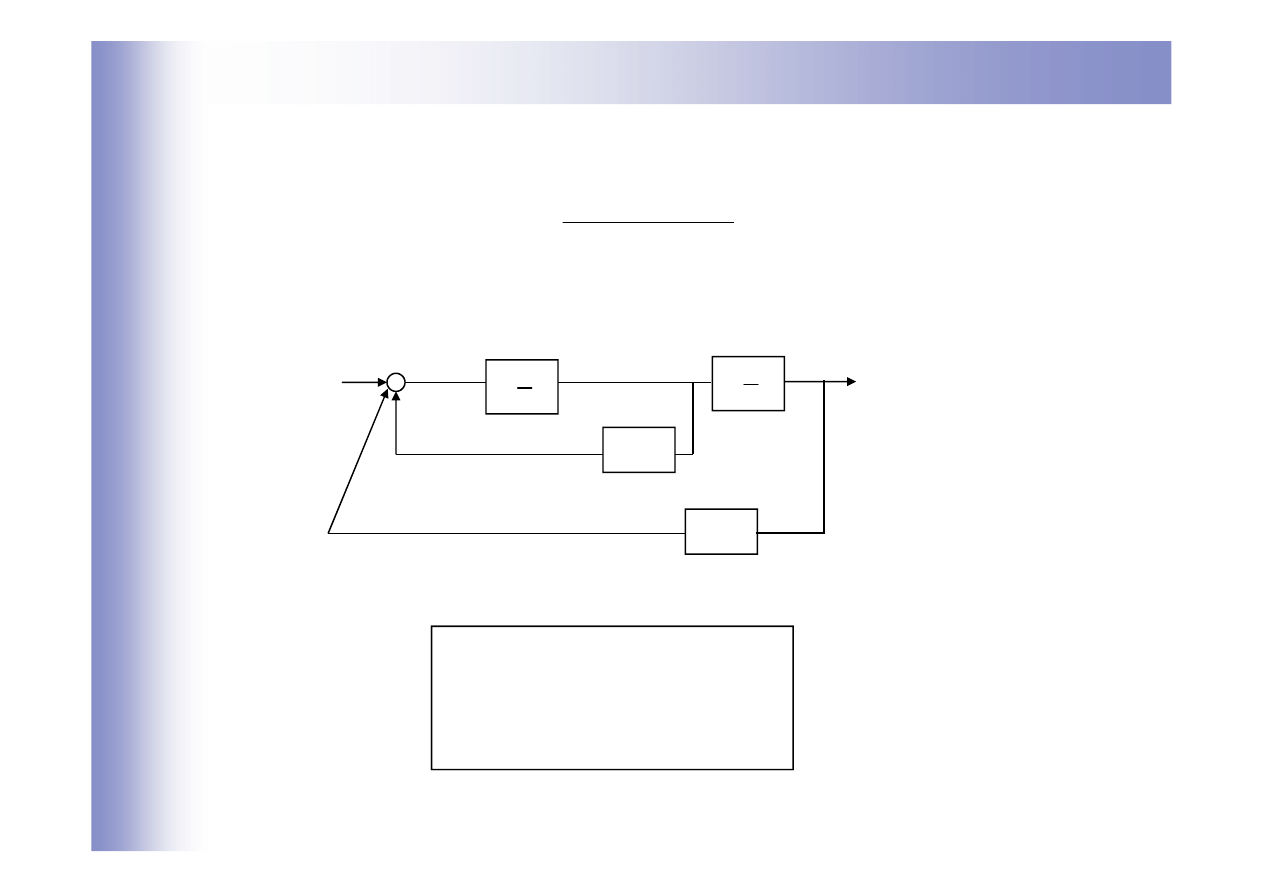
Wyznaczanie równań stanu z transmitancji
Metoda równoległa – bieguny urojone
)
(
2
i
i
i
i
d
s
c
s
k
s
G
+
+
=
1
s
c
−
)
(s
u
i
x
1
i+
x
)
(s
y
+
+
+
1
s
i
d
−
i
c
−
i
i
i
i
i
i
i
x
x
u
x
d
x
c
x
=
+
−
−
=
+
+
1
1
&
&
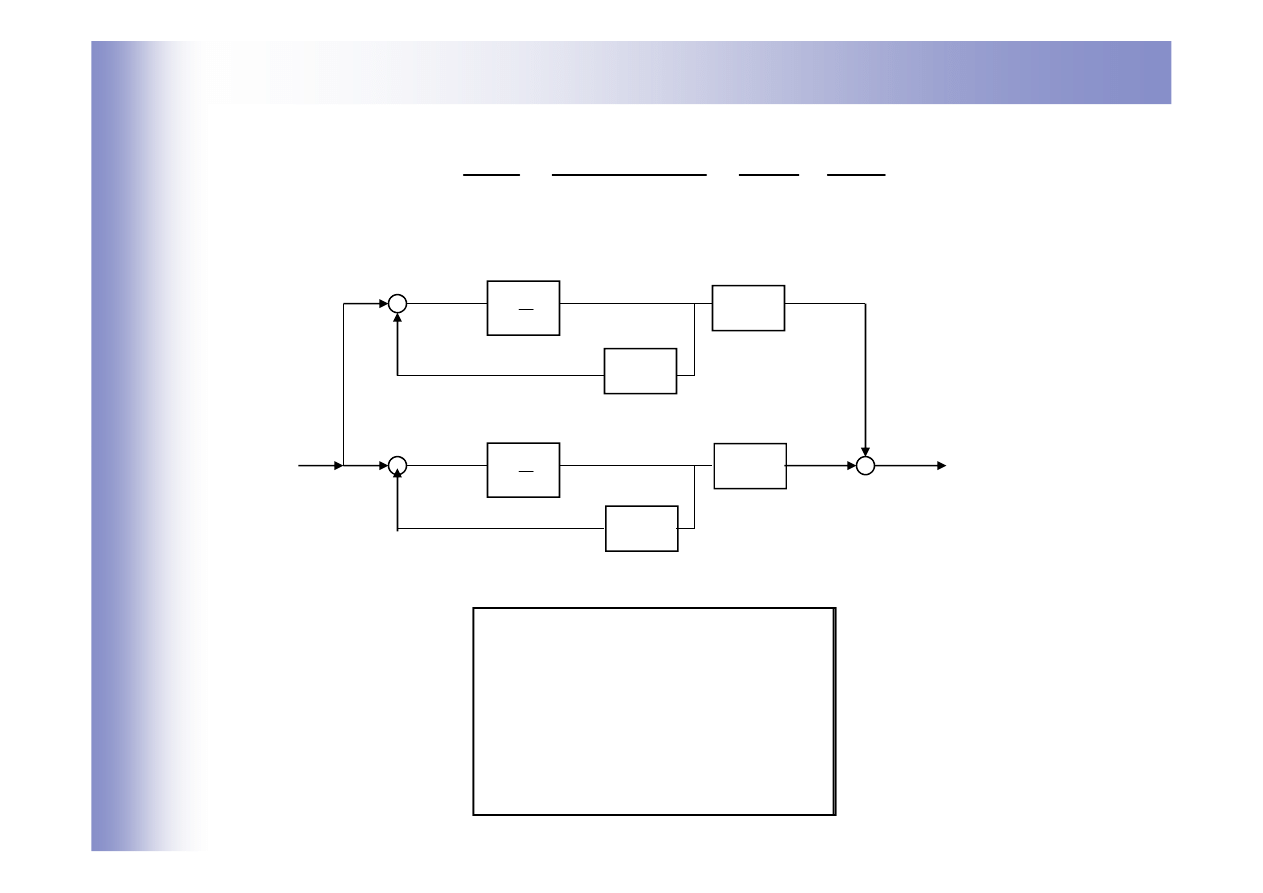
1
s
1
2
−
2
−
1
x
2
x
+
+
+
+
3
4
2
2
)
3
)(
2
(
)
1
(
2
)
(
)
(
)
(
+
+
+
−
=
+
+
+
=
=
s
s
s
s
s
s
u
s
y
s
G
Przykład
1
s
4
3
−
)
(s
u
2
x
)
(s
y
+
+
+
u
x
x
u
x
x
+
−
=
+
−
=
2
2
1
1
3
2
&
&
2
1
4
2
x
x
y
+
−
=
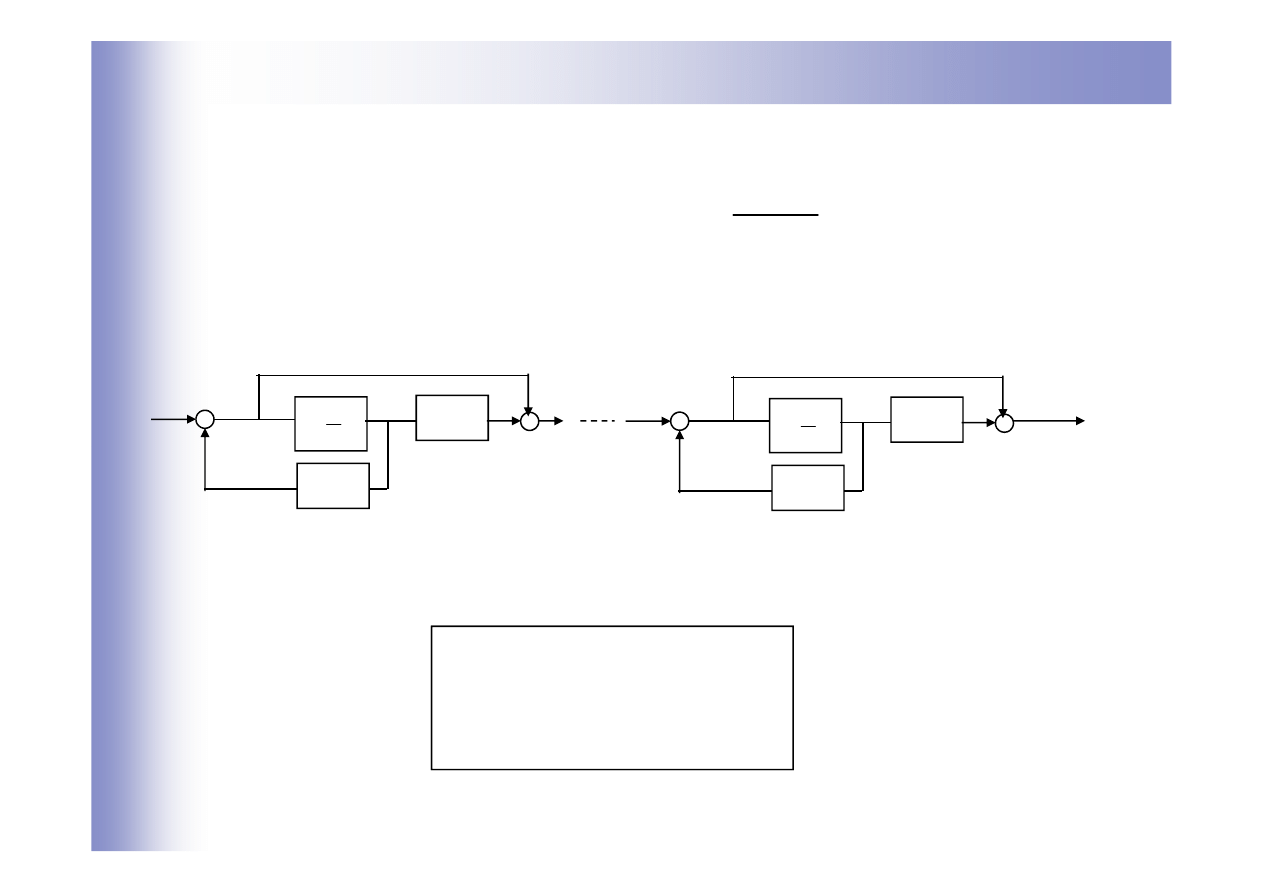
Wyznaczanie równań stanu z transmitancji
Metoda iteracyjna
∏
∏
=
=
+
+
=
=
n
i
i
i
n
i
i
c
s
b
s
s
G
s
G
1
1
)
(
)
(
)
(s
u
)
(s
y
1
s
1
b
1
x
+
+
1
s
n
b
n
x
+
+
)
(s
u
s
1
c
−
+
s
n
c
−
+
i
i
i
i
i
i
i
i
x
b
x
y
u
x
c
x
+
=
+
−
=
&
&
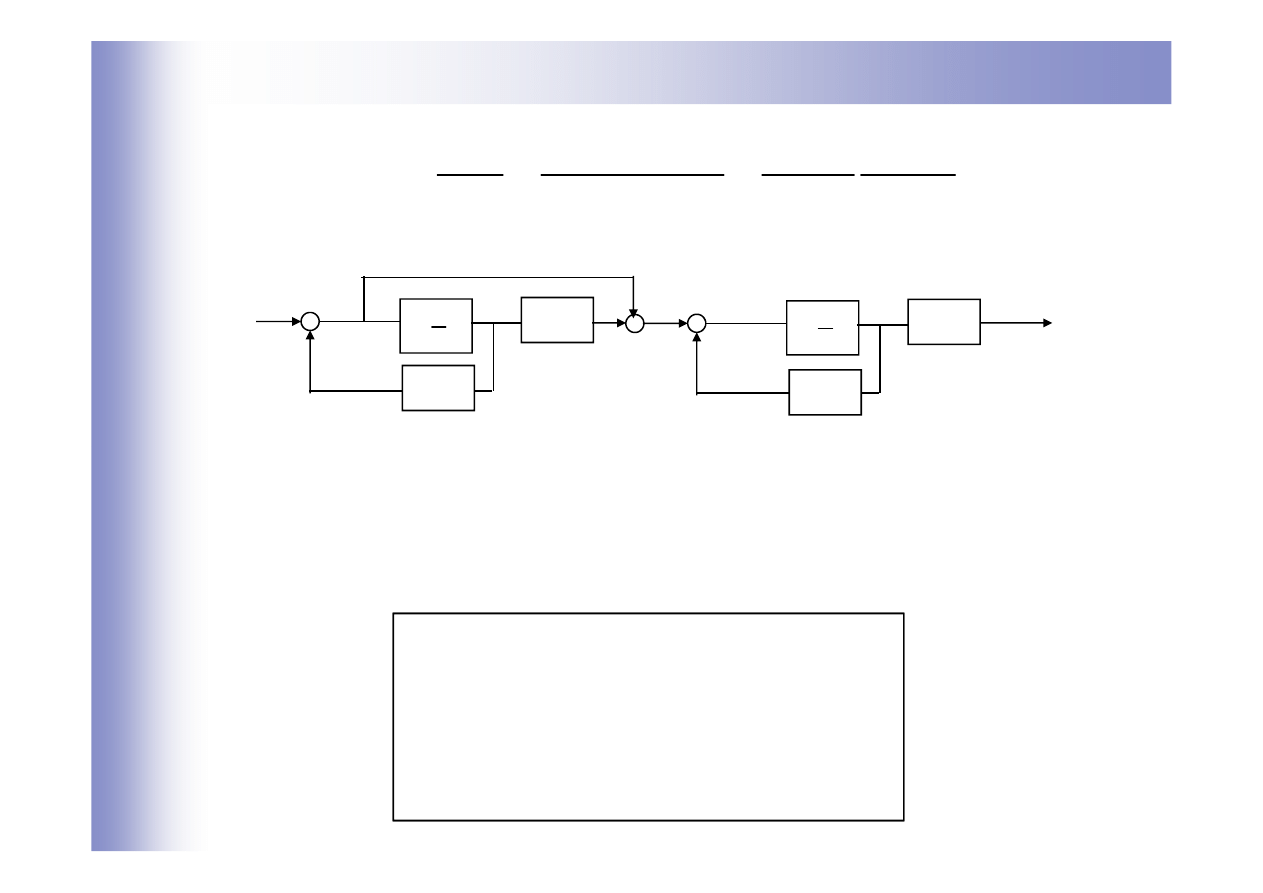
)
2
(
2
)
3
(
1
)
3
)(
2
(
)
1
(
2
)
(
)
(
)
(
+
+
+
=
+
+
+
=
=
s
s
s
s
s
s
s
u
s
y
s
G
Przykład
)
(s
u
)
(s
y
1
s
1
3
−
1
x
+
+
1
s
2
2
-
2
x
+
+
1
y
u
x
x
x
u
x
x
+
−
−
=
+
−
=
2
1
2
1
1
2
4
3
&
&
2
2x
y =
1
1
1
1
1
3
x
x
y
u
x
x
+
=
+
−
=
&
&
2
1
2
2
2
2
x
y
y
x
x
=
+
−
=
&
Wyszukiwarka
Podobne podstrony:
02 Opis matematyczny układów liniowych
02 Modelowanie matematyczne układów dynamicznych
02 Modelowanie matematyczne układów dynamicznych
PA2 opis matematyczny [tryb zgodności]
02 Statystyka Matematyczna Zmienna Losowa Ciągłaid 3789
Modele matematyczne ukladow reg Nieznany
DYSKRETYZACJA CIĄGŁYCH UKŁADÓW LINIOWYCH
02 opis metoda Lehmanna[1]id 3914
12 02 S1 W Matematyka
02 opis metoda Lehmanna(1)
2077 02.,Opis,techniczny Budownictwo,komunikacyjne
w 3 dynamika ukladów liniowych
calkowanie 1 opis matematyczny Nieznany
04 Własności dynamiczne układów liniowych
Modele matematyczne układów elementarnych mod mat
IV.13.14.15 Metody numeryczne rozwiązywania układów liniowyc, IV
Scilab rozwiazywanie ukladow liniowych
zadania pochodne2 (dr R. Lizak), 2 Semestr, Analiza matematyczna i algebra liniowa, zad mat
więcej podobnych podstron