
Katarzyna Siejka, gr 5
Praca projektowa nr 2, temat 58
P
40kN
:=
q
10
kN
m
:=
l
6m
:=
v
0.3
:=
E
210000MPa
:=
odl
8
11
l
⋅
4.364 m
=
:=
A
0.7cm
2
2 10
⋅
30
+
(
)
⋅
0.9 15
⋅
cm
2
+
0.8cm
2
30
2 15
⋅
+
(
)
⋅
+
96.5 cm
2
⋅
=
:=
Sy1
2
1
2
⋅
10
−
(
)
⋅
10
⋅
0.7
⋅
1
2
15
2
⋅
0.9
⋅
+
15 30
⋅
0.8
⋅
+
2 0.5
30
15
+
(
)
⋅
15
⋅
[
] 0.8
⋅
+
931.25
=
:=
Sy1
931.25cm
2
:=
z0
Sy1
A
9.65
=
:=
część o grubości 0.7
Jy1
0.7cm
4
30
9.65
−
(
)
2
⋅
2 10
⋅
9.65
−
(
)
2
⋅
+
2 0.5
⋅
10
−
(
)
2
⋅
2
3
⋅
10
⋅
+
⋅
3725.954 cm
4
⋅
=
:=
Jz1
0.7cm
4
2 15
⋅
10
⋅
15
⋅
0.5 15
⋅
15
⋅
2
3
⋅
15
⋅
+
0.5 15
⋅
15
⋅
2
3
⋅
15
−
⋅
−
⋅
4725 cm
4
⋅
=
:=
część o grubości 0.9
Jy2
0.9cm
4
0.5
9.65
−
⋅
15
⋅
2
3
9.65
−
⋅
1
3
5.35
⋅
+
⋅
0.5 5.35
⋅
15
⋅
2
3
5.35
⋅
1
3
9.65
⋅
−
⋅
+
⋅
315.529 cm
4
⋅
=
:=
Jz2
0cm
4
:=
część o grubości 0.8
Jy3
0.8cm
4
5.35
2
30
⋅
2
5.35
2
15
⋅
0.5 15
2
⋅
2
3
⋅
15
⋅
+
⋅
+
⋅
3173.88 cm
4
⋅
=
:=
Jz3
0.8cm
4
2 15
⋅
15
⋅
15
⋅
0.5 15
⋅
15
⋅
2
3
⋅
15
⋅
+
0.5 15
⋅
15
⋅
2
3
⋅
15
−
⋅
−
⋅
7200 cm
4
⋅
=
:=
Jy
Jy1
Jy2
+
Jy3
+
7215.363 cm
4
⋅
=
:=
Jz
Jz1
Jz2
+
Jz3
+
0 m
4
=
:=
y
B
0cm
:=
z
B
9.65
−
cm
:=
ω5
1
15
− cm 15
⋅
cm
225
−
cm
2
⋅
=
:=
ω2
1
10
− cm 15
⋅
cm
150
−
cm
2
⋅
=
:=
ω4
1
ω5
1
15cm 15
⋅
cm
+
0 m
2
=
:=
Jω
1.y
0.7cm
10cm ω2
1
⋅
15
⋅
cm
(
)
⋅
0.8cm
ω5
1
15
⋅
cm 15
⋅
cm
ω5
1
15
⋅
cm
2
3
⋅
15
⋅
cm
+
⋅
+
832.5
−
m cm
4
⋅
=
:=
z
A
z
B
Jω
1.y
Jz
−
2.669
−
cm
⋅
=
:=
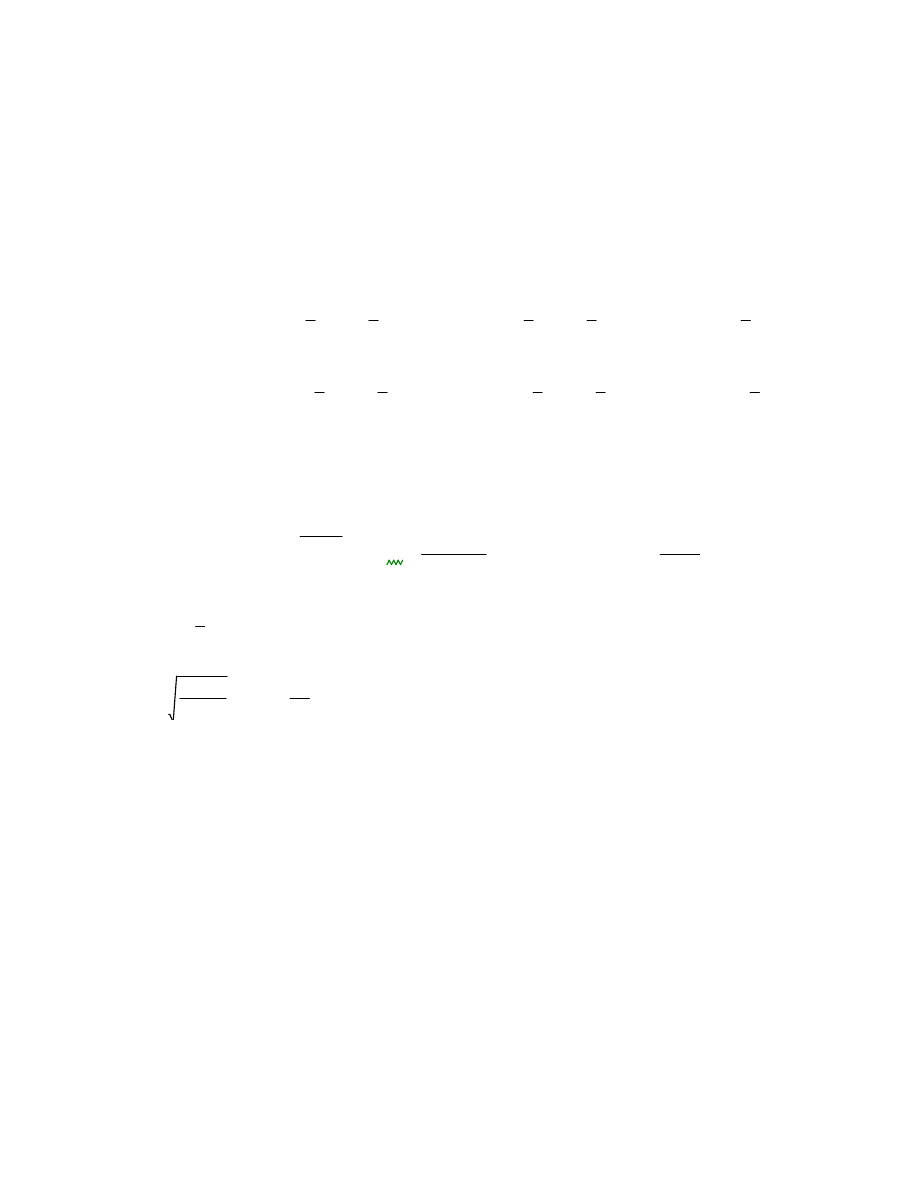
ω1
15cm
9.65cm
z
A
+
(
)
⋅
104.717 cm
2
⋅
=
:=
ω2
ω1
10cm 15
⋅
cm
−
45.283
−
cm
2
⋅
=
:=
ω5
15
− cm
5.35cm
z
A
−
(
)
⋅
120.283
−
cm
2
⋅
=
:=
ω4
ω5
15cm 15
⋅
cm
+
104.717 cm
2
⋅
=
:=
cześć o grubości 0.7
Jω1
0.7cm
ω2 10
⋅
cm
2
3
ω2
⋅
1
3
ω1
⋅
+
⋅
ω1 10
⋅
cm
2
3
ω1
⋅
1
3
ω2
⋅
+
⋅
+
ω1
2
15
⋅
cm
2
3
⋅
+
⋅
:=
część o grubości 0.8
Jω3
0.8cm
ω5 15
⋅
cm
2
3
ω5
⋅
1
3
ω4
⋅
+
⋅
ω4 15
⋅
cm
2
3
ω4
⋅
1
3
ω5
⋅
+
⋅
+
ω5
2
15
⋅
cm
2
3
⋅
+
⋅
:=
Jω
Jω1
Jω3
+
333820.755 cm
6
⋅
=
:=
m
x
q 6.98
⋅
cm
0.698
kN m
⋅
m
⋅
=
:=
G
E
2
1
v
+
(
)
⋅
80.769 GPa
⋅
=
:=
E
1
E
1
v
2
−
230.769 GPa
⋅
=
:=
M
P 10
⋅
cm
4 kN m
⋅
⋅
=
:=
K
S
1
1
3
⋅
0.7cm
(
)
3
50
⋅
cm
0.9cm
(
)
3
15
⋅
cm
+
0.8cm
(
)
3
60
⋅
cm
+
⋅
19.602 cm
4
⋅
=
:=
α
G K
S
⋅
E
1
Jω
⋅
0.005
1
cm
⋅
=
:=


1
Y1 ζ
( )
cosh ζ
( )
:=
Y2 ζ
( )
sinh ζ
( )
:=
Y3 ζ
( )
1
cosh ζ
( )
−
:=
Y4 ζ
( )
ζ
sinh ζ
( )
−
:=
l
6 m
=
Y5 ζ
( )
1
2
ζ
2
⋅
cosh ζ
( )
−
:=
a2
8
11
l
⋅
4.364 m
=
:=
ξ
α l
⋅
:=
a3
0
:=
a4
a2
:=
Given
B0
0kN cm
2
⋅
:=
Mx0
0kN
:=
B0
1
G K
S
⋅
⋅
Y3 ξ
( )
⋅
Mx0
1
G K
S
⋅
α
⋅
⋅
Y4 ξ
( )
⋅
+
M
G K
S
⋅
α
⋅
Y4 ξ
a2 α
⋅
−
(
)
⋅
−
m
x
G K
S
⋅
α
2
⋅
Y5 ξ
α a4
⋅
−
(
)
Y5 ξ
a3 α
⋅
−
(
)
−
(
)
⋅
+
...
0
=
B0 Y1 ξ
( )
⋅
Mx0
1
α
⋅
Y2 ξ
( )
⋅
+
M
α
Y2 ξ
α a2
⋅
−
(
)
⋅
−
m
x
α
2
Y3 ξ
α a4
⋅
−
(
)
Y3 ξ
a3 α
⋅
−
(
)
−
(
)
−
0
=
Find B0 Mx0
,
(
)
2228.1260643808650121 N
⋅
m
2
⋅
−
2275.3170839183874378 J
⋅
m
⋅
−
1470.1286048954912396 J
⋅
2309.6022779477743304 N
⋅
m
⋅
+
→
B0
2228.1260643808650121
−
N m
2
⋅
2275.3170839183874378
−
J m
⋅
+
45034.431
−
kN cm
2
⋅
⋅
=
:=
Mx0
1470.1286048954912396 J
⋅
2309.6022779477743304N m
⋅
+
377.973 kN cm
⋅
⋅
=
:=
B0 Y1 ξ
( )
⋅
Mx0
1
α
⋅
Y2 ξ
( )
⋅
+
M
α
Y2 ξ
α a2
⋅
−
(
)
⋅
−
m
x
α
2
Y3 ξ
α a4
⋅
−
(
)
Y3 ξ
a3 α
⋅
−
(
)
−
(
)
−
0 kN cm
2
⋅
⋅
=
x
0
1
100
l
⋅
,
odl
..
:=
x1
odl odl
1
100
odl
⋅
+
,
l
..
:=
θ x
( )
B0
1
G K
S
⋅
⋅
Y3 x α
⋅
(
)
⋅
Mx0
1
G K
S
⋅
α
⋅
⋅
Y4 x α
⋅
(
)
⋅
+
m
x
G K
S
⋅
α
2
⋅
Y5 x α
⋅
x α
⋅
−
(
)
Y5 x α
⋅
a3 α
⋅
−
(
)
−
(
)
⋅
+
...
:=
θ1 x1
(
)
B0
1
G K
S
⋅
⋅
Y3 x1 α
⋅
(
)
⋅
Mx0
1
G K
S
⋅
α
⋅
⋅
Y4 x1 α
⋅
(
)
⋅
+
M
G K
S
⋅
α
⋅
Y4 x1 α
⋅
a2 α
⋅
−
(
)
⋅
−
m
x
G K
S
⋅
α
2
⋅
Y5 x1 α
⋅
a4 α
⋅
−
(
)
Y5 x1 α
⋅
a3 α
⋅
−
(
)
−
(
)
⋅
+
...
:=
0
2
4
6
0.05
0.1
0.15
0.2
θ x
( )
θ1 x1
(
)
x x1
,
B x
( )
B0 Y1 x α
⋅
(
)
⋅
Mx0
1
α
⋅
Y2 x α
⋅
(
)
⋅
+
m
x
α
2
Y3 x α
⋅
x α
⋅
−
(
)
Y3 x α
⋅
a3 α
⋅
−
(
)
−
(
)
−
:=
B1 x1
(
)
B0 Y1 x1 α
⋅
(
)
⋅
Mx0
1
α
⋅
Y2 x1 α
⋅
(
)
⋅
M
α
Y2 x1 α
⋅
a2 α
⋅
−
(
)
⋅
−
m
x
α
2
Y3 x1 α
⋅
a4 α
⋅
−
(
)
Y3 x1 α
⋅
a3 α
⋅
−
(
)
−
(
)
−
+
...
:=
0
2
4
6
6
−
10
3
×
4
−
10
3
×
2
−
10
3
×
2 10
3
×
4 10
3
×
B x
( )
B1 x1
(
)
x x1
,
MX x
( )
Mx0
m
x
x
a3
−
(
)
⋅
−
:=
MX1 x1
(
)
Mx0
M
−
m
x
a4
a3
−
(
)
⋅
−
:=
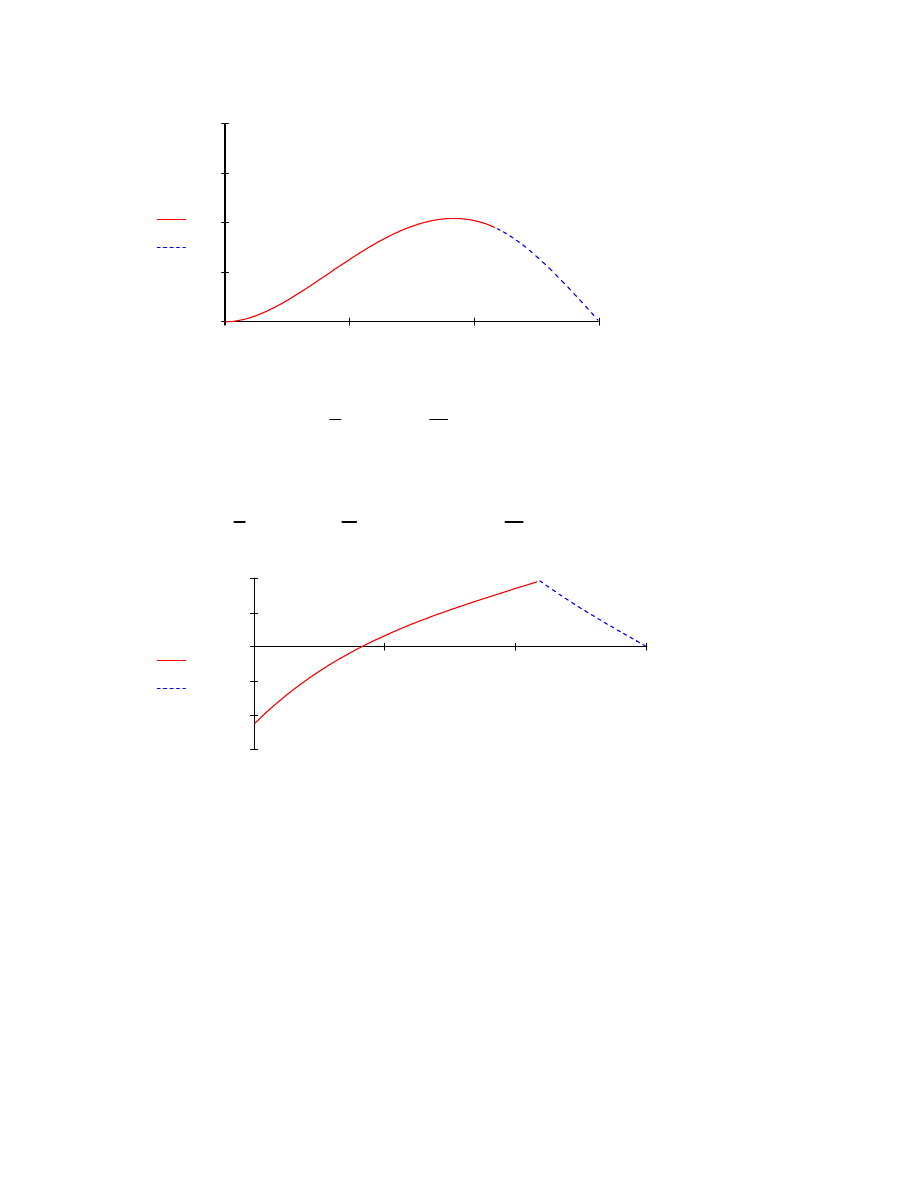
0
2
4
6
4
−
10
3
×
2
−
10
3
×
2 10
3
×
4 10
3
×
MX x
( )
MX1 x1
(
)
x x1
,
Ms x
( )
B0
−
α
⋅
Y2 x α
⋅
(
)
⋅
Mx0 Y3 x α
⋅
(
)
⋅
+
m
x
α
Y4 x α
⋅
x α
⋅
−
(
)
Y4 x α
⋅
α a3
⋅
−
(
)
−
(
)
⋅
+
:=
Ms1 x1
(
)
B0
−
α
⋅
Y2 x1 α
⋅
(
)
⋅
Mx0 Y3 x1 α
⋅
(
)
⋅
+
M Y3 x1 α
⋅
α a2
⋅
−
(
)
⋅
−
m
x
α
Y4 x1 α
⋅
α a4
⋅
−
(
)
Y4 x1 α
⋅
α a3
⋅
−
(
)
−
(
)
⋅
+
...
:=
0
2
4
6
1
−
10
3
×
500
−
500
Ms x
( )
Ms1 x1
(
)
x x1
,
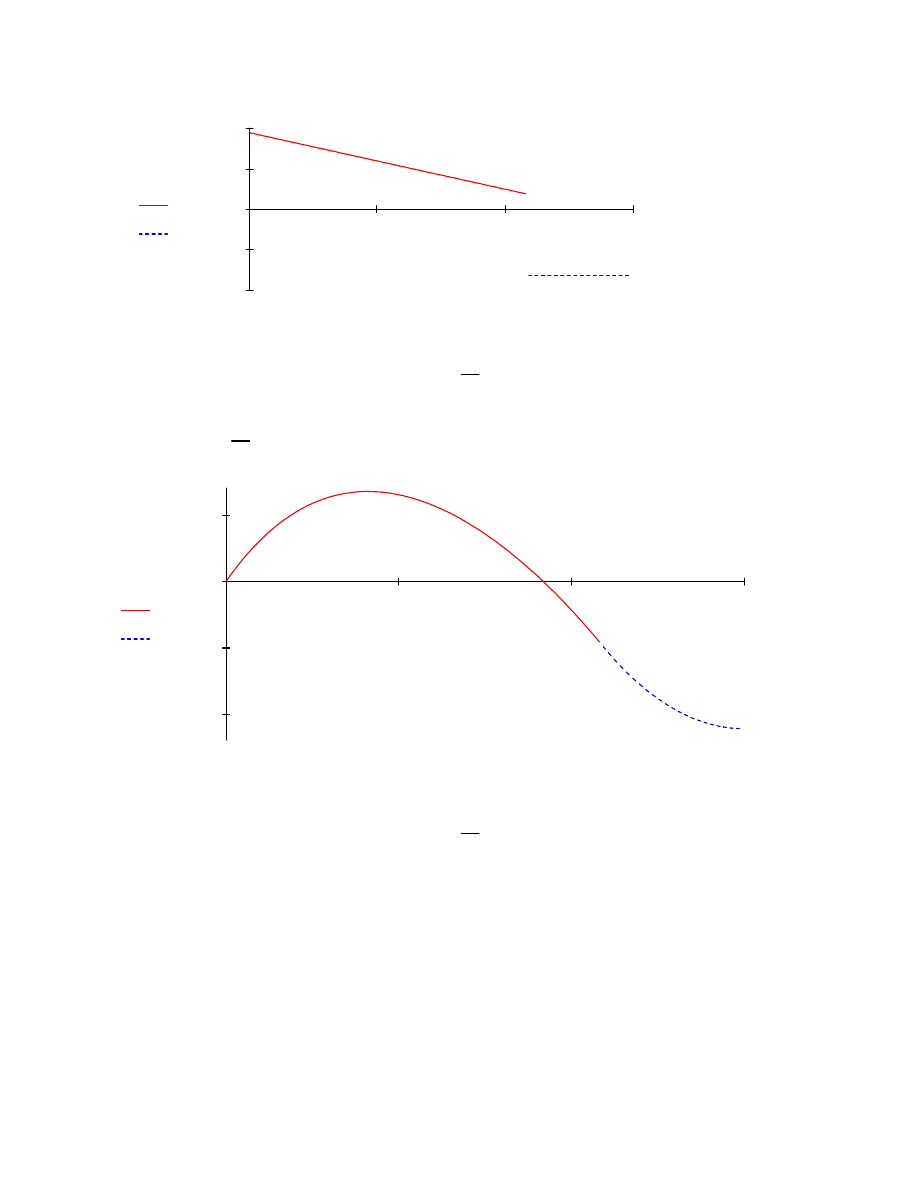
Mω x
( )
B0 α
⋅
Y2 α x
⋅
(
)
⋅
Mx0 Y1 x α
⋅
(
)
⋅
+
m
x
α
Y2 x α
⋅
x α
⋅
−
(
)
Y2 x α
⋅
α a3
⋅
−
(
)
−
(
)
⋅
+
:=
ω
α
α
α
α
α
Mω1 x1
(
)
B0 α
⋅
Y2 x1 α
⋅
(
)
⋅
Mx0 Y1 x1 α
⋅
(
)
⋅
+
M Y1 x1 α
⋅
α a2
⋅
−
(
)
⋅
−
m
x
α
Y2 x1 α
⋅
α a4
⋅
−
(
)
Y2 x1 α
⋅
α a3
⋅
−
(
)
−
(
)
⋅
+
...
:=
0
2
4
6
6
−
10
3
×
4
−
10
3
×
2
−
10
3
×
2 10
3
×
Mω x
( )
Mω1 x1
(
)
x x1
,
0
2
4
6
6
−
10
3
×
4
−
10
3
×
2
−
10
3
×
2 10
3
×
4 10
3
×
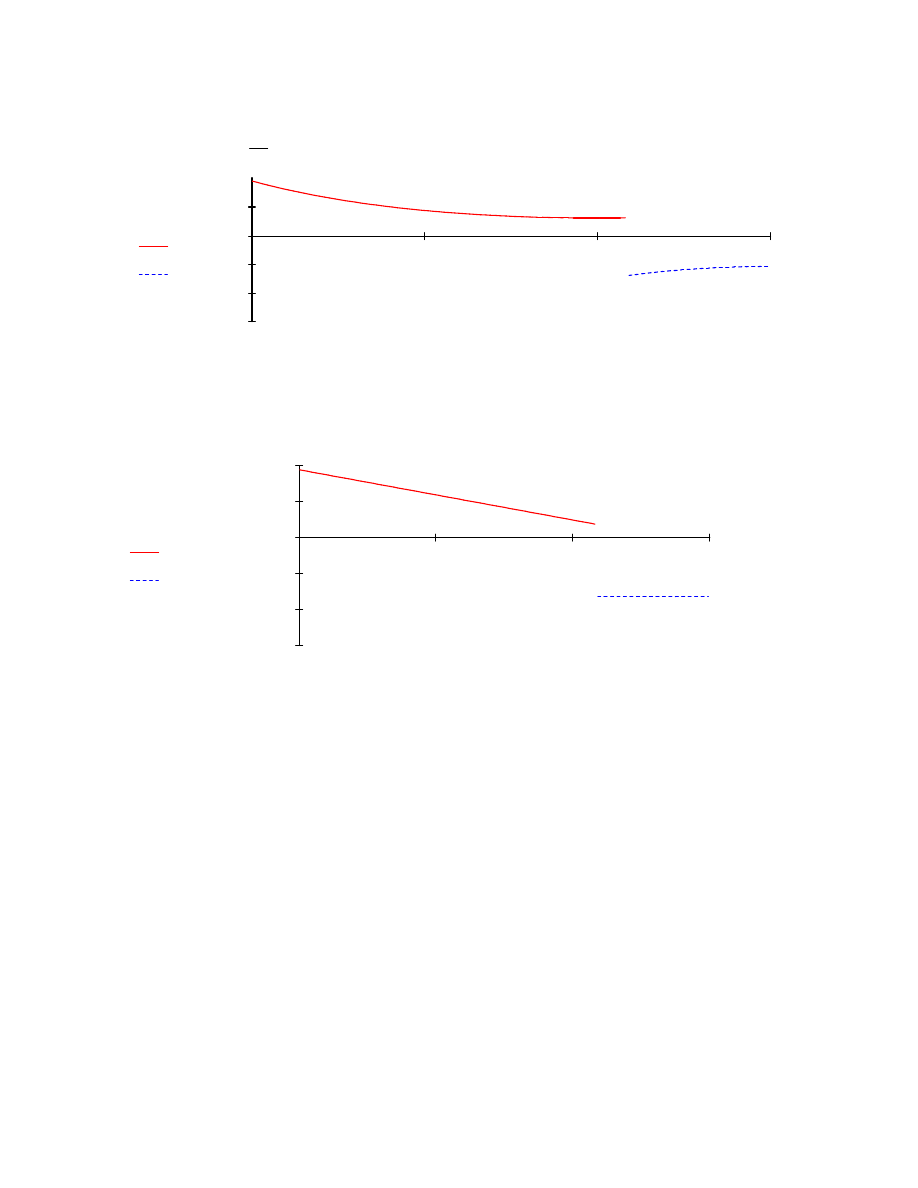
Ms x
( ) Mω x
( )
+
Ms1 x1
(
) Mω1 x1
(
)
+
x x1
,
q
10000 kg s
2
−
⋅
=

zad 2
przekrój 10
odl
4.364 m
=
ten
10
11
l
⋅
5.455 m
=
:=
Tz
24
− kN
:=
Ty x
( )
34.18kN
q odl
⋅
−
:=
Ty ten
(
)
9.456
−
kN
⋅
=
Ty
9.456
−
kN
:=
My x
( )
30.35
−
kN m
⋅
16kN x
⋅
+
P
x
odl
−
(
)
⋅
−
:=
My ten
(
)
1328.636 kN cm
⋅
⋅
=
My
1328.636kN cm
⋅
:=
Mz x
( )
38.53kN m
⋅
34.18kN x
⋅
−
q odl
⋅
x
odl
2
−
⋅
+
:=
Mz ten
(
)
509.645
−
kN cm
⋅
⋅
=
Mz
509.645
−
kN cm
⋅
:=
B ten
(
)
53063.873 kN cm
2
⋅
⋅
=
B
53063.873kN cm
2
⋅
:=
σMy z
( )
My
Jz
z
⋅
1.114160167714884696e7 cm
⋅
kN
⋅
z
⋅
m
4
→
:=
σMz y
( )
Mz
Jy
y
⋅
7.0633314759923974425e6 cm
⋅
kN
⋅
y
⋅
m
4
−
→
:=
σB ω
(
)
B
Jω
ω
⋅
158959.17869153602446 ω
⋅
cm
2
⋅
kN
⋅
L
2
→
:=
p1
9.65
−
15 104.717
(
)
:=
p2
19.65
−
15
45.283
−
(
)
:=
p3
9.65
−
0 0
(
)
:=
p4
20.35 15 104.714
(
)
:=
p5
5.35 15
120.283
−
(
)
:=
pK
14.65
−
15 29.717
(
)
:=
pL
15.35
15
−
17.717
−
(
)
:=
σMy 5.35cm
(
)
0.596
kN
cm
2
⋅
=
σMy 9.65
−
cm
(
)
1.075
−
kN
cm
2
⋅
=
σMy 20.35cm
(
)
2.267
kN
cm
2
⋅
=
σMy 19.65
−
cm
(
)
2.189
−
kN
cm
2
⋅
=
σMz 15cm
(
)
1.059
−
kN
cm
2
⋅
=
σMz 15
− cm
(
)
1.059
kN
cm
2
⋅
=
σB 45.283
−
cm
2
(
)
7.198
−
kN
cm
2
⋅
=
σB 104.717cm
2
(
)
16.646
kN
cm
2
⋅
=
σB 45.283cm
2
(
)
7.198
kN
cm
2
⋅
=
σB 104.717
−
cm
2
(
)
16.646
−
kN
cm
2
⋅
=
(
)
(
)
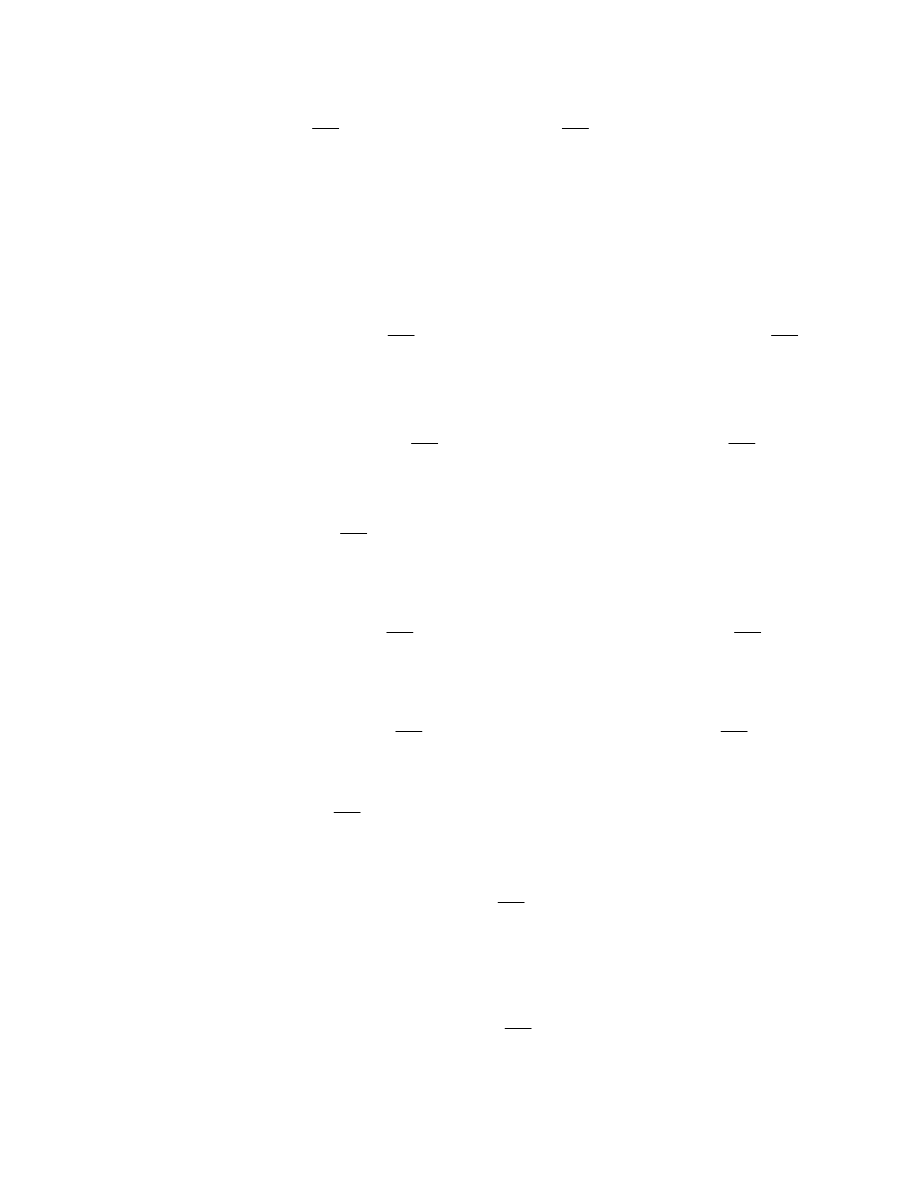
σB 120.283cm
2
(
)
19.12
kN
cm
2
⋅
=
σB 120.283
−
cm
2
(
)
19.12
−
kN
cm
2
⋅
=
σx z y
, ω
,
(
)
σMy z
( )
σMz y
( )
+
σB ω
(
)
+
:=
p1
9.65
−
15 104.717
(
)
:=
p1
1
9.65
−
15
−
104.717
−
(
)
:=
σx 9.65
−
cm 15cm
,
104.717cm
2
,
(
)
14.511
kN
cm
2
⋅
=
σx 9.65
−
cm
15
− cm
,
104.717
−
cm
2
,
(
)
16.661
−
kN
cm
2
⋅
=
p2
19.65
−
15
45.283
−
(
)
:=
p2
1
19.65
−
15
−
45.283
(
)
:=
σx 19.65
−
cm 15cm
,
45.283
−
cm
2
,
(
)
10.447
−
kN
cm
2
⋅
=
σx 19.65
−
cm
15
− cm
,
45.283cm
2
,
(
)
6.068
kN
cm
2
⋅
=
p3
9.65
−
0 0
(
)
:=
σx 9.65
−
cm 0cm
,
0cm
2
,
(
)
1.075
−
kN
cm
2
⋅
=
p4
20.35 15 104.714
(
)
:=
p4
1
20.35
15
−
104.714
−
(
)
:=
σx 20.35cm 15cm
,
104.714cm
2
,
(
)
17.853
kN
cm
2
⋅
=
σx 20.35cm
15
− cm
,
104.714
−
cm
2
,
(
)
13.318
−
kN
cm
2
⋅
=
p5
5.35 15
120.283
−
(
)
:=
p5
1
5.35
15
−
120.283
(
)
:=
σx 5.35cm 15cm
,
120.283
−
cm
2
,
(
)
19.584
−
kN
cm
2
⋅
=
σx 5.35cm
15
− cm
,
120.283cm
2
,
(
)
20.776
kN
cm
2
⋅
=
pkt6
5.35 0 0
(
)
:=
σx 5.35cm 0cm
,
0cm
2
,
(
)
0.596
kN
cm
2
⋅
=
l
pK
14.65
−
15 29.717
(
)
:=
σK
σx 14.65
−
cm 15cm
,
29.717cm
2
,
(
)
:=
σK
2.032
kN
cm
2
⋅
=
pL
15.35
15
−
17.717
−
(
)
:=
σL
σx 15.35cm
15
− cm
,
17.717
−
cm
2
,
(
)
:=
σL
0.047
−
kN
cm
2
⋅
=

momenty statyczne Sz (wykres symetryczny względem osi z)
odcinek
punkt
.4-5
4
.4-5
5
.5-6
6
.1-2
1
.1-2
2
.2-3
3
Sz4
0cm
3
:=
Sz5
0.8cm 15
⋅
cm 15
⋅
cm
180 cm
3
⋅
=
:=
Sz56
Sz5
0.8cm 0.5
⋅
15
⋅
cm 15
⋅
cm
+
270 cm
3
⋅
=
:=
Sz1
0.7cm 15
⋅
cm 10
⋅
cm
105 cm
3
⋅
=
:=
Sz2
0cm
3
:=
Sz13
Sz1
0.7cm 15
⋅
cm 0.5
⋅
15
⋅
cm
+
183.75 cm
3
⋅
=
:=
SzK
0.7cm 15
⋅
cm 5
⋅ cm
52.5 cm
3
⋅
=
:=
SzL
0.8cm 15
⋅
cm 5
⋅ cm
60 cm
3
⋅
=
:=
momenty statyczne Sy
odcinek
punkt
.4-5
4
.4-5
5
.5-6
6
.1-2
1
.1-2
2
.2-3
3
.3-6
3
.3-6
oś
.3-6
6
Sy4
0cm
3
:=
Sy5
20.35cm
5.35cm
+
(
) 0.8
⋅
cm 0.5
⋅
15
⋅
cm
154.2 cm
3
⋅
=
:=
Sy56
Sy5
0.8cm 5.35
⋅
cm 15
⋅
cm
+
218.4 cm
3
⋅
=
:=
Sy1
0.7
−
cm
19.65cm
9.65cm
+
(
)
⋅
10
⋅
cm 0.5
⋅
102.55
−
cm
3
⋅
=
:=
Sy2
0cm
3
:=
l
Sy13
Sy1
0.7cm 9.65
⋅
cm 15
⋅
cm
−
203.875
−
cm
3
⋅
=
:=
Sy36
2 Sy13
⋅
407.75
−
cm
3
⋅
=
:=
Syoś
Sy36
9.65cm 0.5
⋅
0.9
⋅
cm 9.65
⋅
cm
−
449.655
−
cm
3
⋅
=
:=
spr
Sy6
Syoś
0.9cm 5.35
⋅
cm 0.5
⋅
5.35
⋅
cm
+
436.775
−
cm
3
⋅
=
:=
SyK
0.7
−
cm 5
⋅ cm 0.5
⋅
19.65cm
14.65cm
+
(
)
⋅
60.025
−
cm
3
⋅
=
:=
SyL
0.8
−
cm 5
⋅ cm 0.5
⋅
20.35cm
15.35cm
+
(
)
⋅
71.4
−
cm
3
⋅
=
:=
momenty statyczne Sω
Sω4
0cm
4
:=
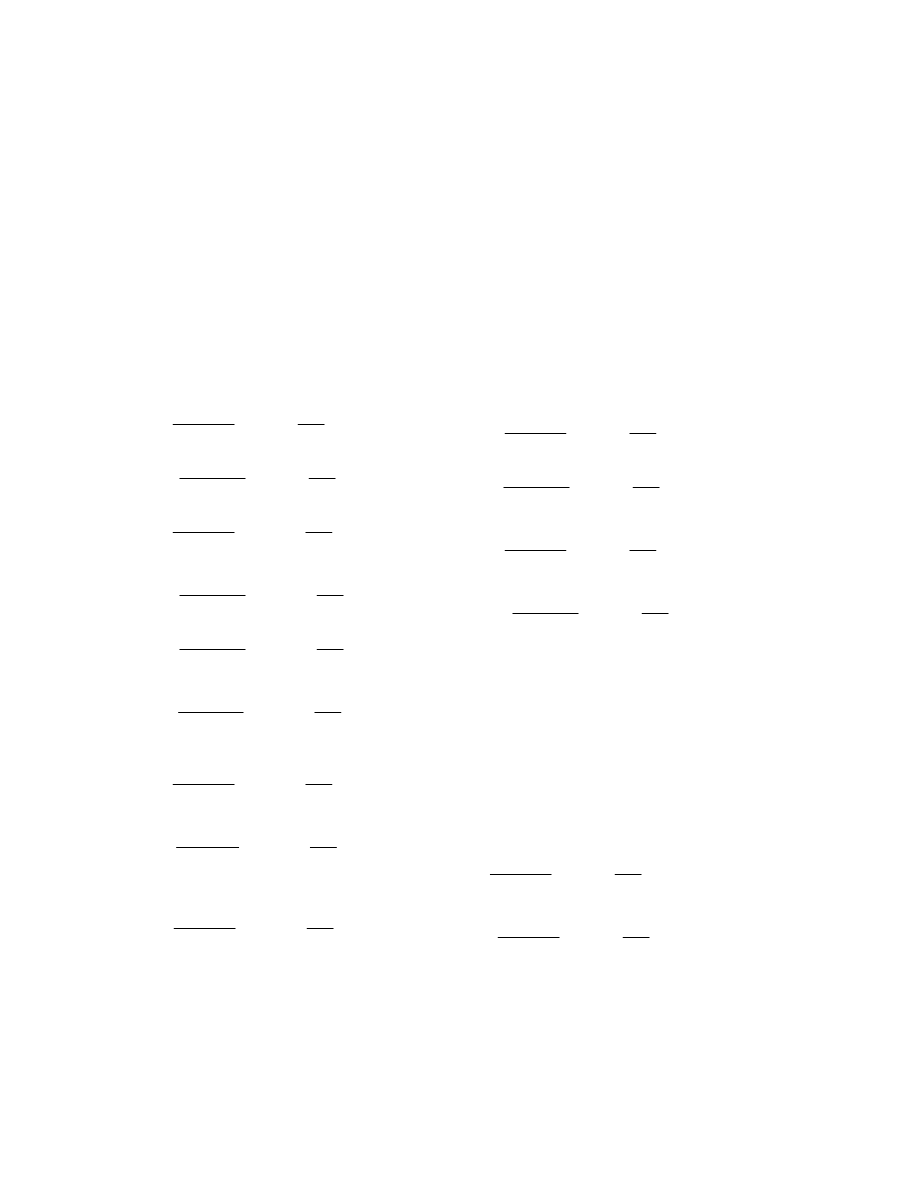
Sω5
0.8cm 0.5
⋅
15
⋅
cm
ω4
ω5
+
(
)
⋅
93.396
−
cm
4
⋅
=
:=
Sω56
Sω5
0.8cm 15
⋅
cm 0.5
⋅
ω5
⋅
+
815.094
−
cm
4
⋅
=
:=
Sω2
0cm
4
:=
Sω1
0.7cm 0.5
⋅
10
⋅
cm
ω2
ω1
+
(
)
⋅
208.019 cm
4
⋅
=
:=
Sω13
Sω1
0.5 0.7
⋅
cm ω1
⋅
15
⋅
cm
+
757.783 cm
4
⋅
=
:=
SωK
0.7cm 0.5
⋅
5
⋅ cm
29.719cm
2
ω2
+
(
)
⋅
27.237
−
cm
4
⋅
=
:=
SωL
0.8cm 0.5
⋅
5
⋅ cm
ω4
5.183cm
2
+
(
)
⋅
219.8 cm
4
⋅
=
:=
naprężenia styczne
Mω ten
(
)
148.682 kN cm
⋅
⋅
=
Mω
148.682kN cm
⋅
:=
τy5
Tz
−
Sy5
⋅
Jy 0.8
⋅
cm
0.641
kN
cm
2
⋅
=
:=
τz5
Ty
−
Sz5
⋅
Jz 0.8
⋅
cm
0.178
kN
cm
2
⋅
=
:=
τy56
Tz
−
Sy56
⋅
Jy 0.8
⋅
cm
0.908
kN
cm
2
⋅
=
:=
τz56
Ty
−
Sz56
⋅
Jz 0.8
⋅
cm
0.268
kN
cm
2
⋅
=
:=
τy1
Tz
−
Sy1
⋅
Jy 0.7
⋅
cm
0.487
−
kN
cm
2
⋅
=
:=
τz1
Ty
−
Sz1
⋅
Jz 0.7
⋅
cm
0.119
kN
cm
2
⋅
=
:=
τy13
Tz
−
Sy13
⋅
Jy 0.7
⋅
cm
0.969
−
kN
cm
2
⋅
=
:=
τz13
Ty
−
Sz13
⋅
Jz 0.7
⋅
cm
0.208
kN
cm
2
⋅
=
:=
τy36
Tz
−
Sy36
⋅
Jy 0.9
⋅
cm
1.507
−
kN
cm
2
⋅
=
:=
τyoś
Tz
−
Syoś
⋅
Jy 0.9
⋅
cm
1.662
−
kN
cm
2
⋅
=
:=
τy6
Tz
−
Sy6
⋅
Jy 0.9
⋅
cm
1.614
−
kN
cm
2
⋅
=
:=
τyK
Tz
−
SyK
⋅
Jy 0.7
⋅
cm
0.285
−
kN
cm
2
⋅
=
:=
τzK
Ty
−
SzK
⋅
Jz 0.7
⋅
cm
0.059
kN
cm
2
⋅
=
:=
τyL
Tz
−
SyL
⋅
Jy 0.8
⋅
cm
0.297
−
kN
cm
2
⋅
=
:=
τzL
Ty
−
SzL
⋅
Jz 0.8
⋅
cm
0.059
kN
cm
2
⋅
=
:=
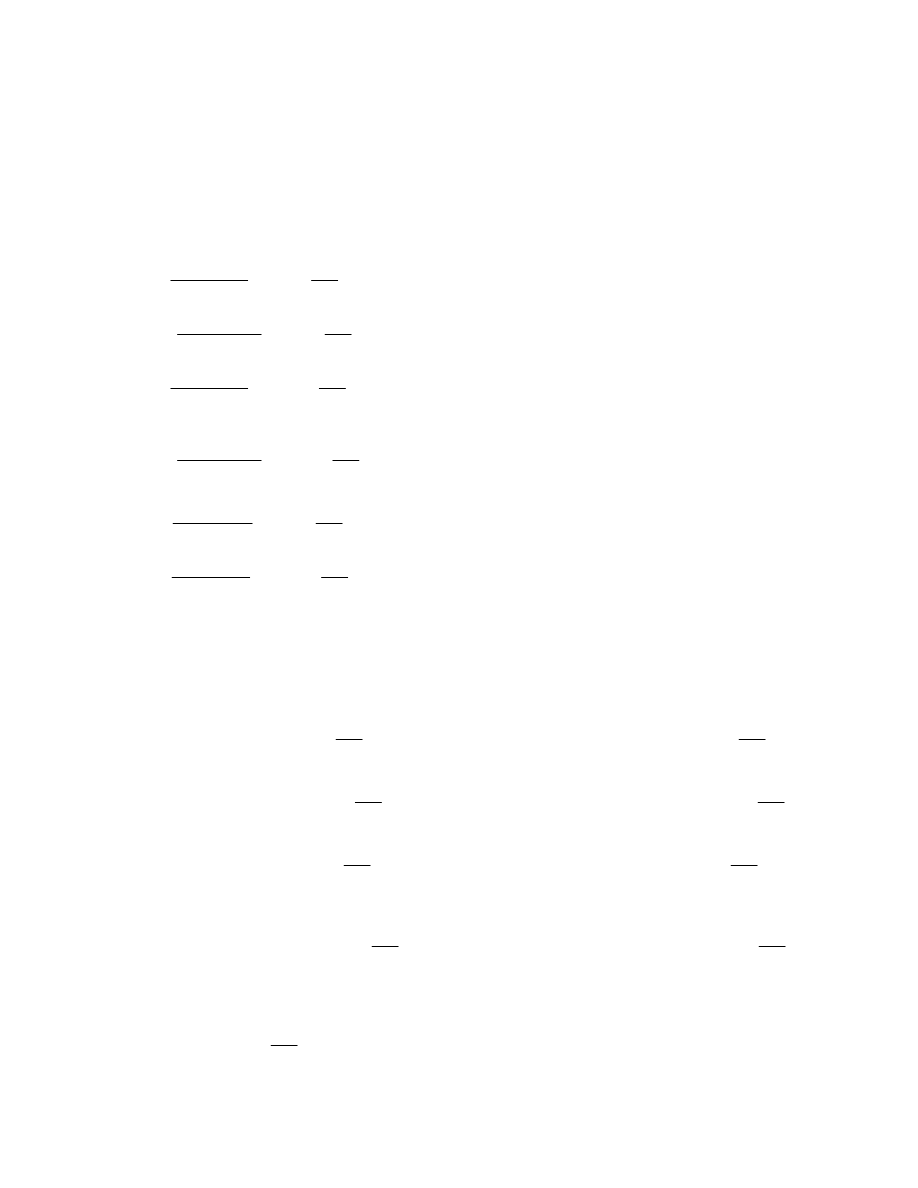
τω5
Mω
−
Sω5
⋅
Jω 0.8
⋅
cm
0.052
kN
cm
2
⋅
=
:=
τω56
Mω
−
Sω56
⋅
Jω 0.8
⋅
cm
0.454
kN
cm
2
⋅
=
:=
τω1
Mω
−
Sω1
⋅
Jω 0.7
⋅
cm
0.132
−
kN
cm
2
⋅
=
:=
τω13
Mω
−
Sω13
⋅
Jω 0.7
⋅
cm
0.482
−
kN
cm
2
⋅
=
:=
τωK
Mω
−
SωK
⋅
Jω 0.7
⋅
cm
0.017
kN
cm
2
⋅
=
:=
τωL
Mω
−
SωL
⋅
Jω 0.8
⋅
cm
0.122
−
kN
cm
2
⋅
=
:=
Lewa strona
Prawa strona
τ5
τy5
τz5
+
τω5
+
0.872
kN
cm
2
⋅
=
:=
τ5
τy5
−
τz5
+
τω5
+
0.411
−
kN
cm
2
⋅
=
:=
τ56
τy56
τz56
+
τω56
+
1.629
kN
cm
2
⋅
=
:=
τ56
τy56
−
τz56
+
τω56
+
0.187
−
kN
cm
2
⋅
=
:=
τ1
τy1
τz1
+
τω1
+
0.501
−
kN
cm
2
⋅
=
:=
τ1
τy1
−
τz1
+
τω1
+
0.474
kN
cm
2
⋅
=
:=
τ13
τy13
τz13
+
τω13
+
1.243
−
kN
cm
2
⋅
=
:=
τ13
τy13
−
τz13
+
τω13
+
0.695
kN
cm
2
⋅
=
:=
τ36
τy36
1.507
−
kN
cm
2
⋅
=
:=
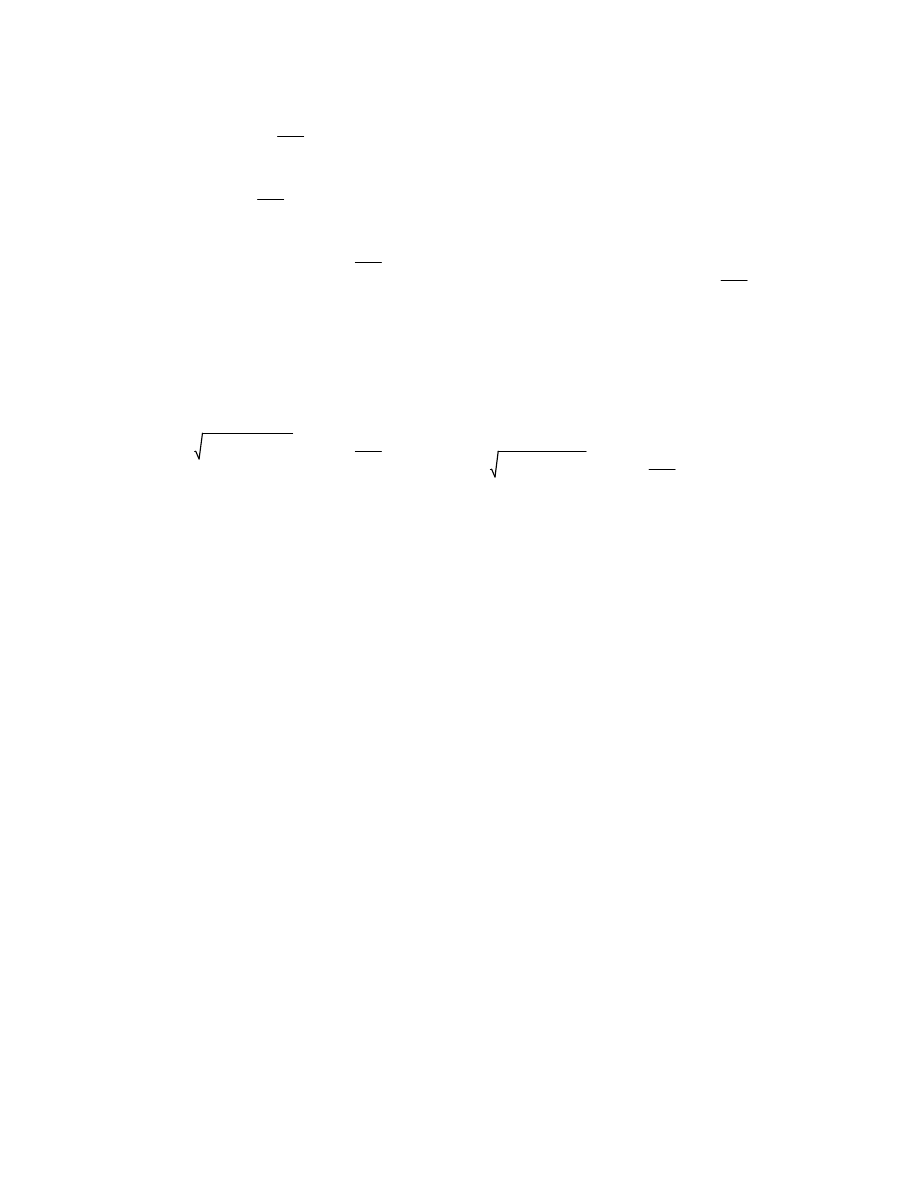
τoś
τyoś
1.662
−
kN
cm
2
⋅
=
:=
τ6
τy6
1.614
−
kN
cm
2
⋅
=
:=
τK
τyK
τzK
+
τωK
+
0.208
−
kN
cm
2
⋅
=
:=
τL
τyL
τzL
+
τωL
+
0.36
−
kN
cm
2
⋅
=
:=
naprężęnia zastępcze
σzK
σK
2
4 τK
2
⋅
+
2.074
kN
cm
2
⋅
=
:=
σzL
σL
2
4 τL
2
⋅
+
0.721
kN
cm
2
⋅
=
:=
Wyszukiwarka
Podobne podstrony:
Mathcad Projekt 10 3 xmcd
Mathcad Projekt 10 2 xmcd
Mathcad, Projekt 10 3.xmcd
Mathcad Projekt 10 xmcd(1)
Mathcad Projekt metal
Mathcad projekt
Mathcad Projekt belki kablobetonowej
Pomoc MathCad, Mathcad W2 1 xmcd
Mathcad Projekt wytrzymałość II cz 3
Mathcad projekt fund
Mathcad projekt 13
Mathcad, projekt nr 1c
Mathcad PROJEKT drewno 2
Mathcad projekt 3
(Mathcad Projekt końcowy ppi
Mathcad Projekt mostu sprężanego
więcej podobnych podstron