
K. Firląg
/
2007/
-1-
POLITECHNIKA WARSZAWSKA
Wydział Transportu
Ć
wiczenia z techniki cyfrowej II
Semestr VII
Synteza sekwencyjnych automatów
synchronicznych
Krzysztof Firl
ą
g
K. Firląg
/
2007/
-2-
1
2
3
4
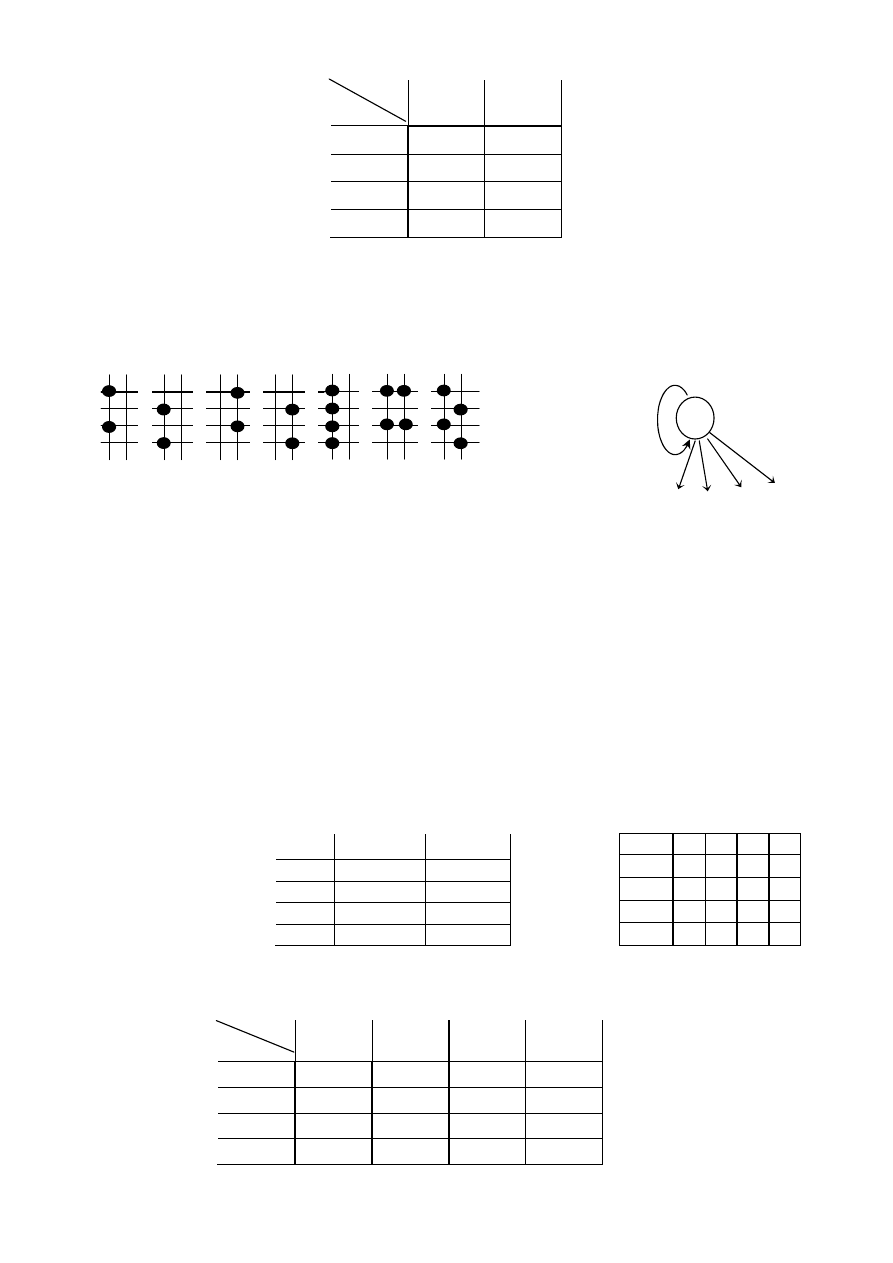
P1s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Mealy’ego
X
S
x
2
x
1
1
1/0
3/1
2
2/1
4/0
3
1/0
3/1
4
2/1
4/0
Podziały zewn
ę
trzne:
π
x2
(y) =
τ
13
π
x1
(y) =
τ
13
π
(y) =
π
x2
(y)*
π
x1
(y) =
τ
13
Struktura kratowa:
Graf podziałów:
τ
1
τ
2
τ
3
τ
4
τ
12
τ
13
τ
14
1
→
→
→
→
ττττ
12
ττττ
13
→
→
→
→
ττττ
14
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
τ
13
τ
13
τ
13
τ
13
1
τ
13
τ
13
ττττ
1
ττττ
2
ττττ
3
ττττ
4
Rodziny ko
ń
cowe:
(sprawdzi
ć
iloczyn)
T
k1
= (
τ
12
,
τ
13
),
T
k2
= (
τ
12
,
τ
14
),
T
k3
= (
τ
13
,
τ
14
).
Ceny:
T
k1
= (
ττττ
12
,
ττττ
13
),
T
k2
= (
τ
12
,
τ
14
),
T
k3
= (
τ
13
,
τ
14
).
C(
τ
12
) = 1+0-1 = 0
C(
τ
12
) = 1+0-1 = 0
C(
τ
13
) = 1+1-1 = 1
C(
τ
13
) = 1+1-1 = 1
C(
τ
14
) = 1+2-1 = 2
C(
τ
14
) = 1+1-1 = 1
C(Y) = 1+1-1 = 1
C(Y) = 1+2-1 = 2
C(Y) = 1+1-1 = 1
∑
∑
∑
∑
C = 2
∑
C = 4
∑
C = 3
s
τ
12
(Q
2
)
τ
13
(Q
1
)
1
0
1
2
0
0
3
1
1
4
1
0
Zakodowana tablica przej
ść
-wyj
ść
:
x
Q
2
Q
1
(x
2
)
0
(x
1
)
1
(x
2
)
0
(x
1
)
1
(2)
00
00
10
1
0
(1)
01
01
11
0
1
(3)
11
01
11
0
1
(4)
10
00
10
1
0
D
2
= x
D
1
= Q
1
(l=0, C=0)
(l=1, C=1)
y = nQ
1
nx+ Q
1
x
Y
T
kopt
= (
ττττ
12
,
ττττ
13
)
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
S’/Y
K. Firląg
/
2007/
-3-
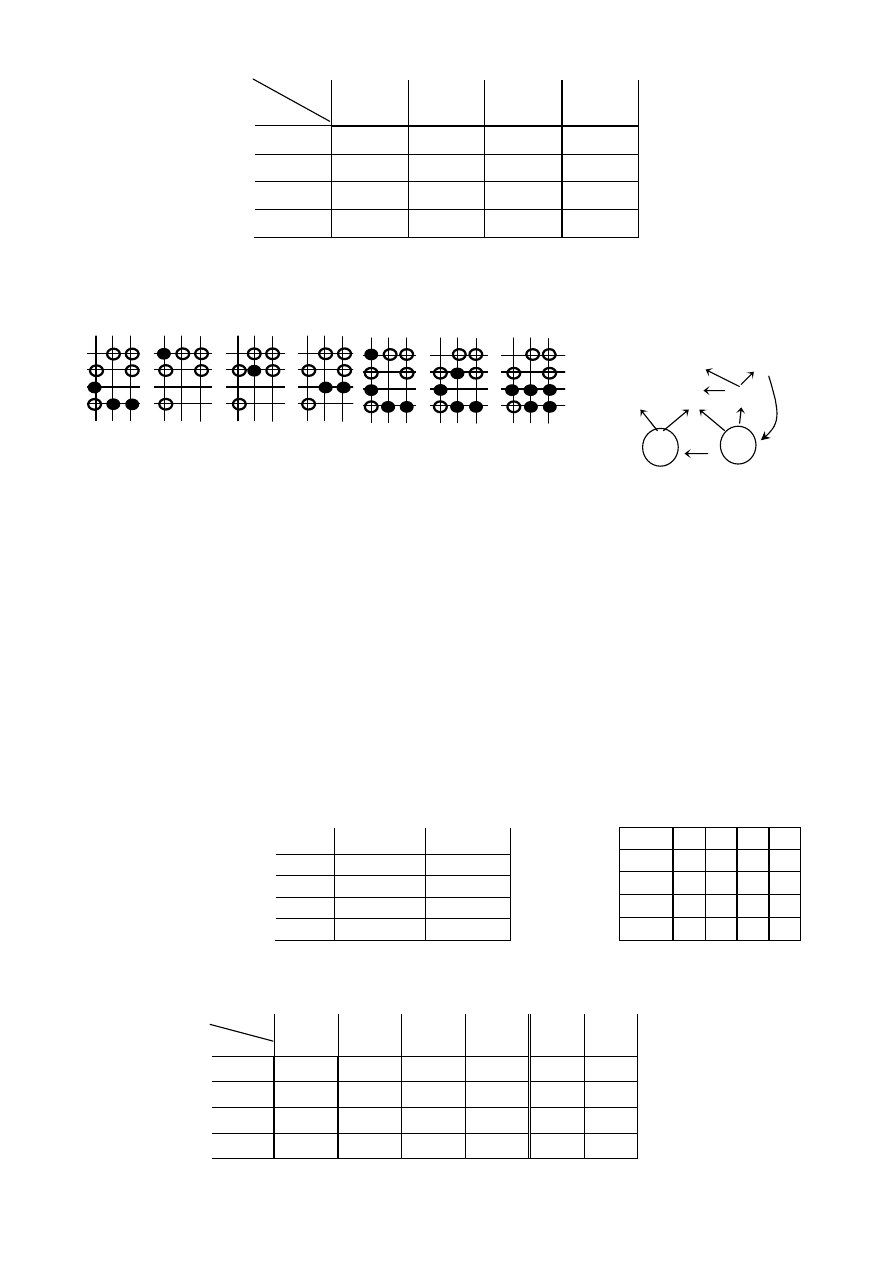
P2s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Moore’a
X
S
x
3
x
2
x
1
Y
1
2
-
-
Y
0
2
-
3
-
Y
1
3
1
4
4
Y
2
4
-
1
1
Y
3
Struktura kratowa: (
Podziały zewn.
π
(y
2
) =
τ
12,
π
(y
1
) =
τ
14
)
Graf podziałów:
τ
1
τ
2
τ
3
τ
4
τ
12
τ
13
τ
14
ττττ
13
→
→
→
→
ττττ
4
ττττ
1
→
→
→
→
ττττ
2
→
→
→
→
ττττ
3
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
ττττ
14
→
→
→
→
ττττ
12
τ
14
τ
1
,
τ
12
,
τ
14,
τ
3
τ
2
,
τ
12
τ
3
,
τ
13
τ
14,
τ
4
τ
3
τ
12
Rodziny ko
ń
cowe:
(sprawdzi
ć
iloczyn)
T
k1
= (
τ
12
,
τ
14
),
T
k2
= (
τ
12
,
τ
13
),
T
k3
= (
τ
13
,
τ
14
).
Ceny:
T
k1
= (
ττττ
12
,
ττττ
14
),
T
k2
= (
τ
12
,
τ
13
),
T
k3
= (
τ
13
,
τ
14
).
C(
τ
12
) = 2+1-1 = 2
C(
τ
12
) = 2+2-1 = 3
C(
τ
13
) = 2+2-1 = 3
C(
τ
14
) = 2+1-1 = 2
C(
τ
13
) = 2+2-1 = 3
C(
τ
14
) = 2+2-1 = 3
C(Y
2
) = 1-1 = 0
C(Y
2
) = 1-1 = 0
C(Y
2
) = 2-1 = 1
C(Y
1
) = 1-1 = 0
C(Y
1
) = 2-1 = 1
C(Y
1
) = 1-1 = 0
∑
∑
∑
∑
C = 4
∑
C = 7
∑
C = 7
s
τ
12
(Q
2
)
τ
14
(Q
1
)
1
1
0
2
1
1
3
0
1
4
0
0
Zakodowana tablica przej
ść
-wyj
ść
:
x
2
x
1
Q
2
Q
1
(x
3
)
00
(x
2
)
01
(x
1
)
11
10
y
2
y
1
(4)
00
-
10
10
-
1
0
(3)
01
10
00
00
-
1
1
(2)
11
-
01
-
-
0
1
(1)
10
11
-
-
-
0
0
D
2
= nx
1
+nQ
1
D
1
= Q
2
(l=1, C=2)
(l=1, C=2)
Y
T
kopt
= (
ττττ
12
,
ττττ
14
)
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
Kodowanie wyjść
Y
0
= 0 0
Y
1
= 0 1
Y
2
= 1 1
Y
3
= 1 0
y
2
y
1
y
2
= nQ
2
y
1
= Q
1
S’ Y
1
2
3
4
K. Firląg
/
2007/
-4-
X=00
S=10
reset
clk
S=11
X=11
clk
S=01
X=00
clk
S=10
clk
S=11
X=01
clk
S=01
X=11
clk
K. Firląg
/
2007/
-5-
1
2
3
4
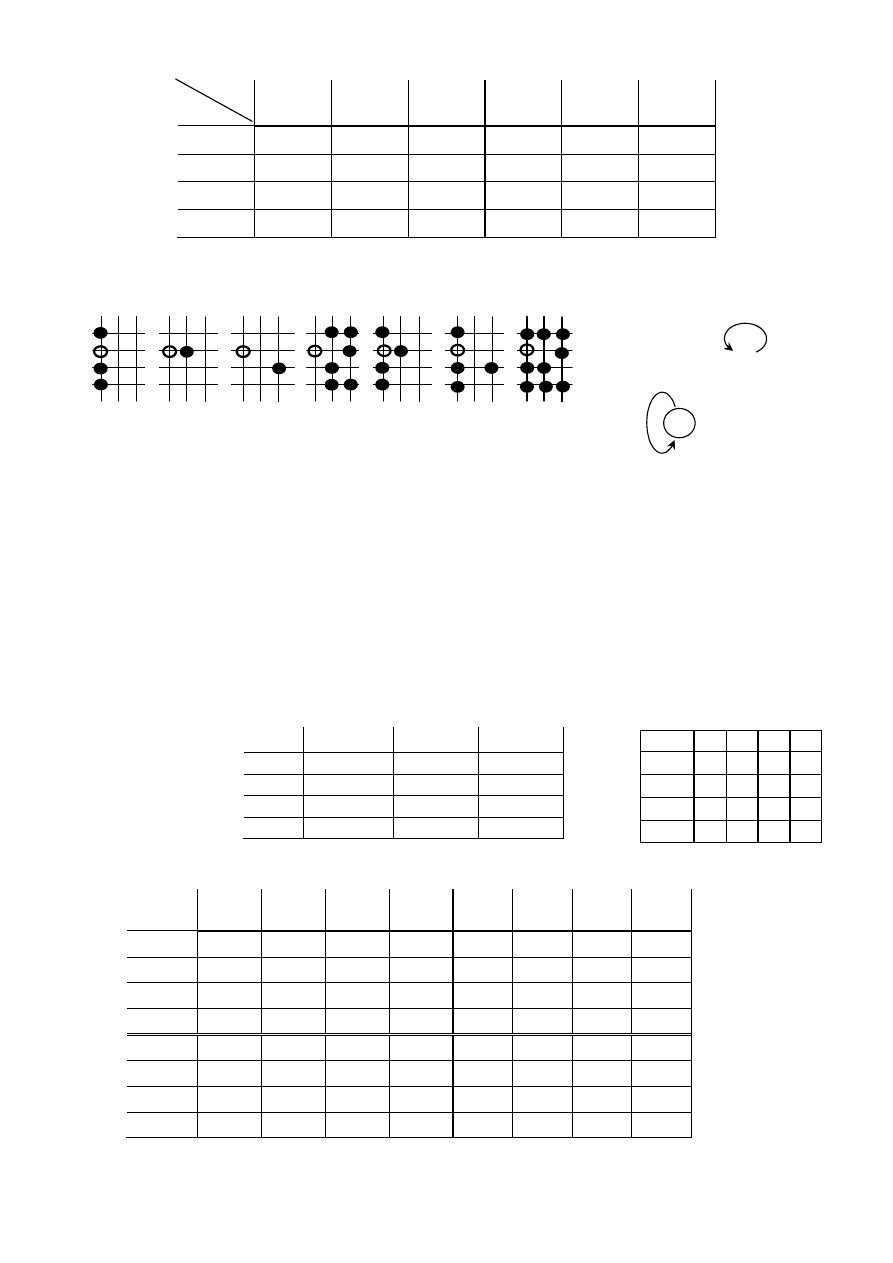
P3s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Mealy’ego
X
S
x
3
x
2
x
1
x
3
x
2
x
1
1
1
4
4
1
0
0
2
-
2
4
-
0
0
3
1
4
3
1
1
0
4
1
4
4
1
0
0
Struktura kratowa:
Graf podziałów:
τ
1
τ
2
τ
3
τ
4
τ
12
τ
13
τ
14
1
→
→
→
→
ττττ
1
←
←
←
←
ττττ
2
→
→
→
→
ττττ
12
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
ττττ
3
→
→
→
→
ττττ
13
1
,
τ
2
τ
2
τ
3
π
τ
2
τ
3
π
Podziały zewn
ę
trzne:
π
x3
(y) = 1
π
x2
(y) =
τ
3
π
x1
(y) = 1
⇒
π
(y) =
ττττ
3
Rodziny ko
ń
cowe:
(sprawdzi
ć
iloczyn)
T
k1
= (
ττττ
1
,
ττττ
2
,
ττττ
3
),
T
k2
= (
τ
12
,
τ
13
),
T
k3
= (
τ
12
,
τ
14
),
T
k4
= (
τ
13
,
τ
14
).
C(
τ
1
)= 2+0-1 =1
C(
τ
12
)= 2+2-1 =3 C(
τ
12
)= 2+2-1 =3 C(
τ
13
)= 2+2-1 =3
C(
τ
2
)= 2+1-1 =2
C(
τ
13
)= 2+2-1 =3 C(
τ
14
)= 2+2-1 =3 C(
τ
14
)= 2+2-1 =3
C(
τ
3
)= 2+1-1 =2
C(Y) = 2+2-1 =3 C(Y) = 2+2-1 =3 C(Y) = 2+2-1 =3
C(Y) = 2+1-1 =2
∑
C = 9
∑
C = 9
∑
C = 9
∑
∑
∑
∑
C = 7
s
τ
1
(Q
3
)
τ
2
(Q
2
)
τ
3
(Q
1
)
1
1
0
1
2
0
1
1
3
0
0
0
4
0
0
1
Zakodowana tablica przej
ść
-wyj
ść
:
x
2
x
1
Q
3
Q
2
Q
1
(x
3
)
00
(x
2
)
01
(x
1
)
11
10
(x
3
)
00
(x
2
)
01
(x
1
)
11
10
(3)
000
101
001
000
-
1
1
0
-
(4)
001
101
001
001
-
1
0
0
-
(2)
011
-
011
001
-
-
0
0
-
010
-
-
-
-
-
-
-
-
110
-
-
-
-
-
-
-
-
111
-
-
-
-
-
-
-
-
(1)
101
101
001
001
-
1
0
0
-
100
-
-
-
-
-
-
-
-
Funkcje wzbudze
ń
:
D
3
= nx
1
D
2
= nx
2
Q
2
D
1
= n
x
2
+ Q
1
(l=0, C=1)
(l=1, C=2)
(l=1, C=2)
T
kopt
= (
ττττ
1
,
ττττ
2,
ττττ
3
)
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
y=nx
1
+ nx
2
nQ
1
(l=1, C=2)
S’ Y
K. Firląg
/
2007/
-6-
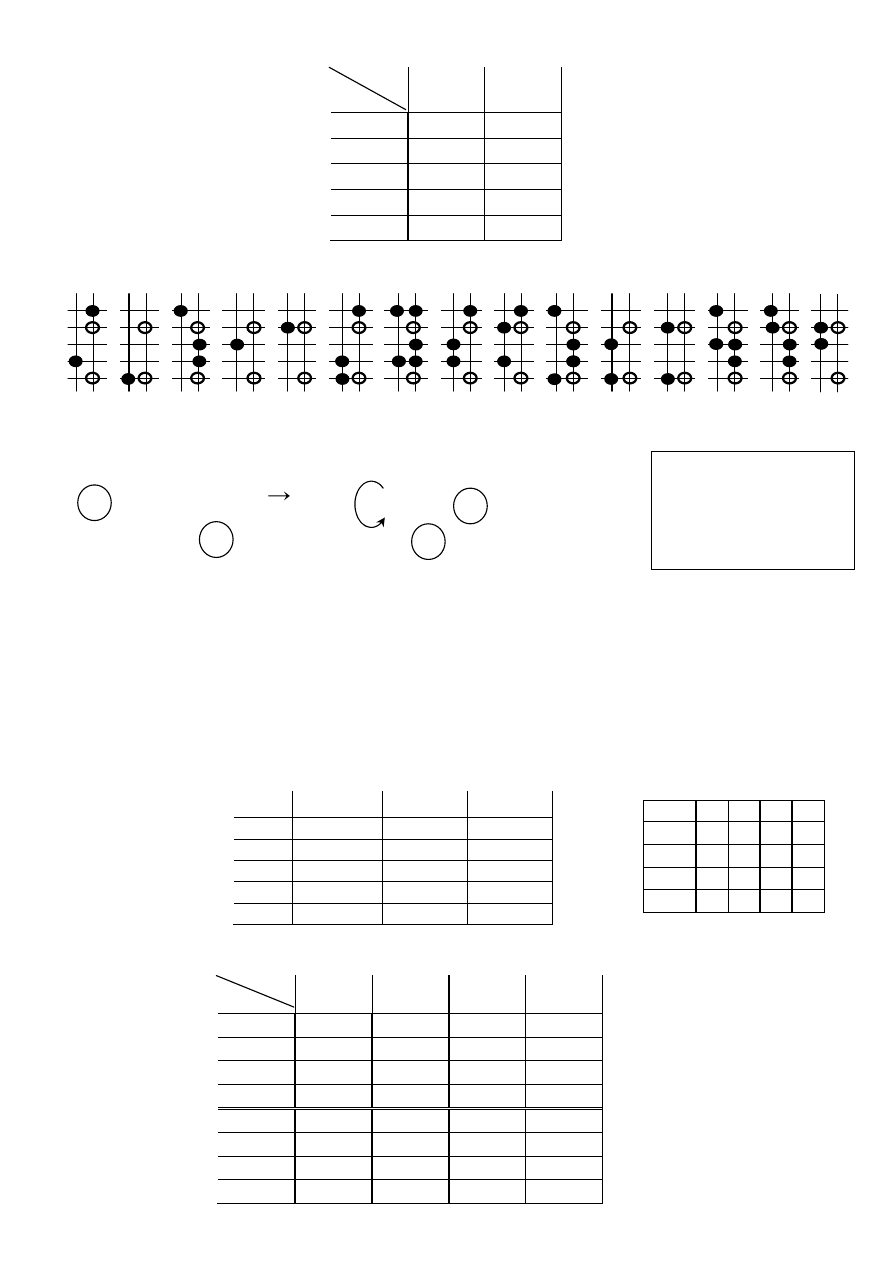
P4s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Mealy’ego
X
S
X
2
X
1
1
3/0
1/0
2
5/0
-
3
4/0
3/0
4
1/0
3/1
5
2/0
-
Struktura kratowa:
τ
1
τ
2
τ
3
τ
4
τ
5
τ
12
τ
13
τ
14
τ
15
τ
23
τ
24
τ
25
τ
34
τ
35
τ
45
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
π
τ
5
τ
1
τ
3
τ
2
π
τ
14
τ
34
π
τ
15
τ
35
τ
25
π
τ
12
τ
23
Graf podziałów:
ττττ
4
←
←
←
←
ττττ
3
←
←
←
←
ττττ
1
ττττ
2
←
←
←
←
ττττ
5
ττττ
25
ττττ
13
←
←
←
←
ττττ
14
←
←
←
←
ττττ
34
ττττ
45
←
←
←
←
ττττ
23
←
←
←
←
ττττ
15
ττττ
24
←
←
←
←
ττττ
35
←
←
←
←
ττττ
12
Rodziny ko
ń
cowe:
(sprawdzi
ć
iloczyn)
T
k1
= (
ττττ
25
,
ττττ
23
,
ττττ
45
),
T
k2
= (
τ
25
,
τ
23
,
τ
15
), T
k3
= (
τ
25
,
τ
35
,
τ
24
), T
k4
= (
τ
25
,
τ
35
,
τ
12
).
C(
τ
25
)= 1+1-1 =1
C(
τ
25
)= 1+1-1 =1 C(
τ
25
)= 1+1-1 =1 C(
τ
25
)= 1+1-1 =1
C(
τ
23
)= 1+3-1 =3
C(
τ
23
)= 1+1-1 =1 C(
τ
35
)= 1+3-1 =3 C(
τ
35
)= 1+1-1 =1
C(
τ
45
)= 1+1-1 =1
C(
τ
1
)= 1+3-1 =3
C(
τ
24
)= 1+1-1 =1 C(
τ
12
)= 1+3-1 =3
C(Y) = 1+1-1 =1
C(Y) = 1+2-1 =2 C(Y) = 1+1-1 =1 C(Y) = 1+2-1 =2
∑
∑
∑
∑
C = 6
∑
C = 7
∑
C = 6
∑
C = 7
s
τ
25
(Q
3
)
τ
23
(Q
2
)
τ
45
(Q
1
)
1
0
1
0
2
1
0
0
3
0
0
0
4
0
1
1
5
1
1
1
Zakodowana tablica przej
ść
-wyj
ść
:
x
Q
3
Q
2
Q
1
(x
2
)
0
(x
1
)
1
(x
2
)
0
(x
1
)
1
(3)
000
011
000
0
0
001
-
-
-
-
(4)
011
010
000
0
1
(1)
010
000
010
0
0
110
-
-
-
-
(5)
111
100
-
0
-
101
-
-
-
-
(2)
100
111
-
0
-
y = Q
1
x
Y
Podziały zewnętrzne:
π
x2
(y) =
1
π
x1
(y) = {4,13,(25)}
π
(y) =
τ
13
,
τ
24
,
τ
45
,
τ
4
T
kopt
= (
ττττ
25
,
ττττ
23
,
ττττ
45
)
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
S’/Y
1
2
3
4
5
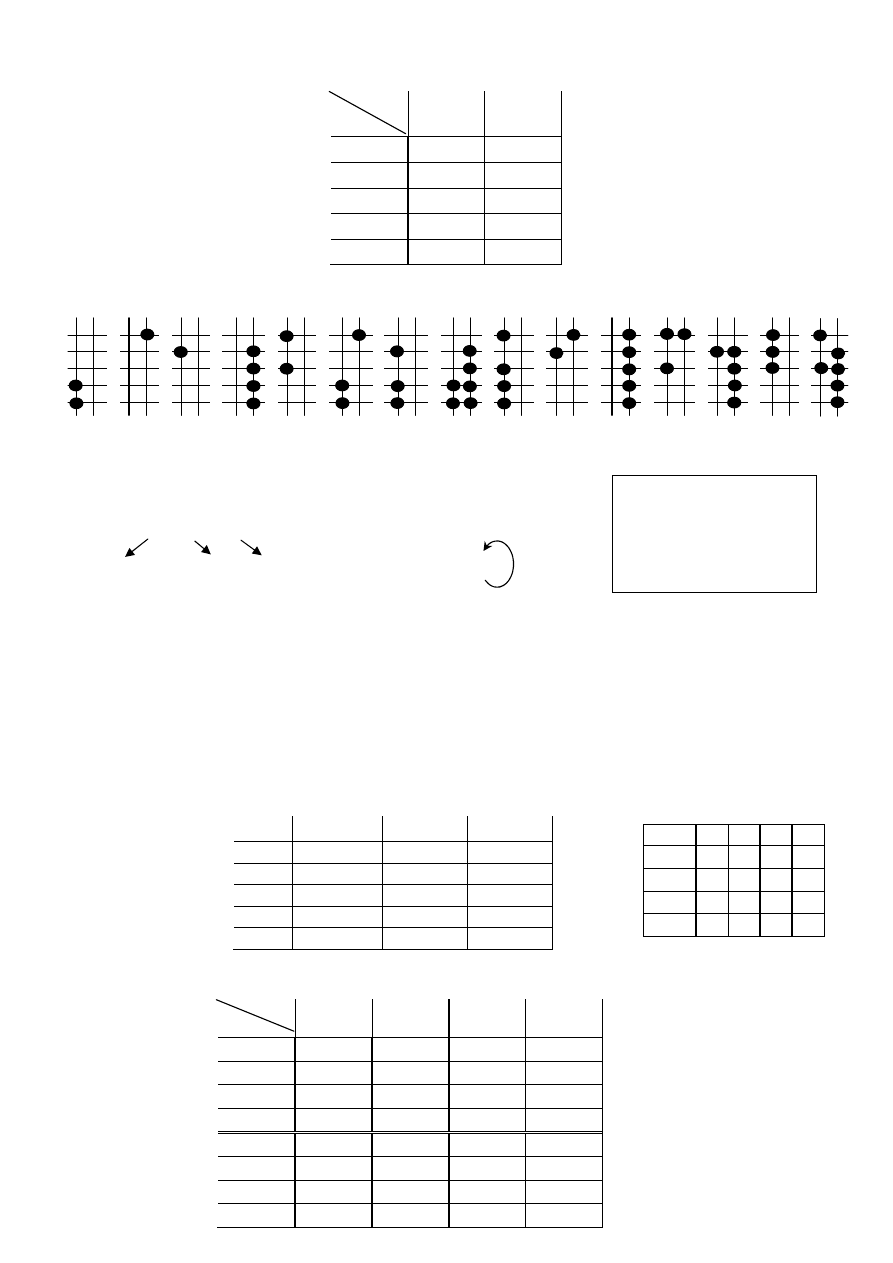
K. Firląg
/
2007/
-7-
D
3
= Q
3
D
2
= nQ
2
nx
+ nQ
3
Q
1
nx + Q
2
nQ
1
x
D
1
= nQ
2
nx
P4_1s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Mealy’ego
X
S
X
2
X
1
1
5/0
2/0
2
3/1
4/1
3
5/1
4/0
4
1/1
4/0
5
1/1
4/1
Struktura kratowa:
τ
1
τ
2
τ
3
τ
4
τ
5
τ
12
τ
13
τ
14
τ
15
τ
23
τ
24
τ
25
τ
34
τ
35
τ
45
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
τ
45
τ
1
τ
2
τ
1
τ
13
π
τ
13
π
τ
2
π
1
π
π
τ
45
π
Graf podziałów:
ττττ
3
←
←
←
←
ττττ
2
←
←
←
←
ττττ
1
←
←
←
←
ττττ
45
ττττ
24
←
←
←
←
1
ττττ
15
ττττ
4
ττττ
35
ττττ
5
←
←
←
←
ττττ
13
Rodziny ko
ń
cowe:
(sprawdzi
ć
iloczyn)
T
k1
= (
τ
24
,
τ
13
,
τ
12
),
T
k2
= (
τ
24
,
τ
13
,
τ
14
), T
k3
= (
τ
24
,
τ
13
,
τ
23
), T
k4
= (
τ
24
,
τ
13
,
τ
34
).
C(
τ
24
)= 1+0-1 =0
C(
τ
24
)= 1+0-1 =0 C(
τ
24
)= 1+0-1 =0 C(
τ
24
)= 1+0-1 =0
C(
τ
13
)= 1+1-1 =1
C(
τ
13
)= 1+1-1 =1 C(
τ
13
)= 1+1-1 =1 C(
τ
13
)= 1+1-1 =1
C(
τ
12
)= 1+2-1 =2
C(
τ
14
)= 1+3-1 =3 C(
τ
23
)= 1+2-1 =2 C(
τ
34
)= 1+3-1 =3
C(Y) = 1+3-1 =3
C(Y) = 1+2-1 =2 C(Y) = 1+3-1 =3 C(Y) = 1+2-1 =2
∑
C = 6
∑
C = 6
∑
C = 6
∑
C = 6
s
τ
24
(Q
3
)
τ
13
(Q
2
)
τ
12
(Q
1
)
1
0
1
0
2
1
0
0
3
0
1
1
4
1
0
1
5
0
0
1
Zakodowana tablica przej
ść
-wyj
ść
:
x
Q
3
Q
2
Q
1
(x
2
)
0
(x
1
)
1
(x
2
)
0
(x
1
)
1
000
-
-
-
-
(5)
001
010
101
1
1
(3)
011
001
101
1
0
(1)
010
001
100
0
0
110
-
-
-
-
111
-
-
-
-
(4)
101
010
101
1
0
(2)
100
011
101
1
1
y = nQ
2
nQ
1
+ Q
1
nx +
+ nQ
3
nQ
2
Y
Podziały zewnętrzne:
π
x2
(y) =
τ
1
π
x1
(y) =
τ
25
π
(y) =
π
= {1,25,34}
T
kopt
= (
ττττ
24
,
ττττ
13
,
ττττ
12
)
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
S’/Y
1
2
3
4
5
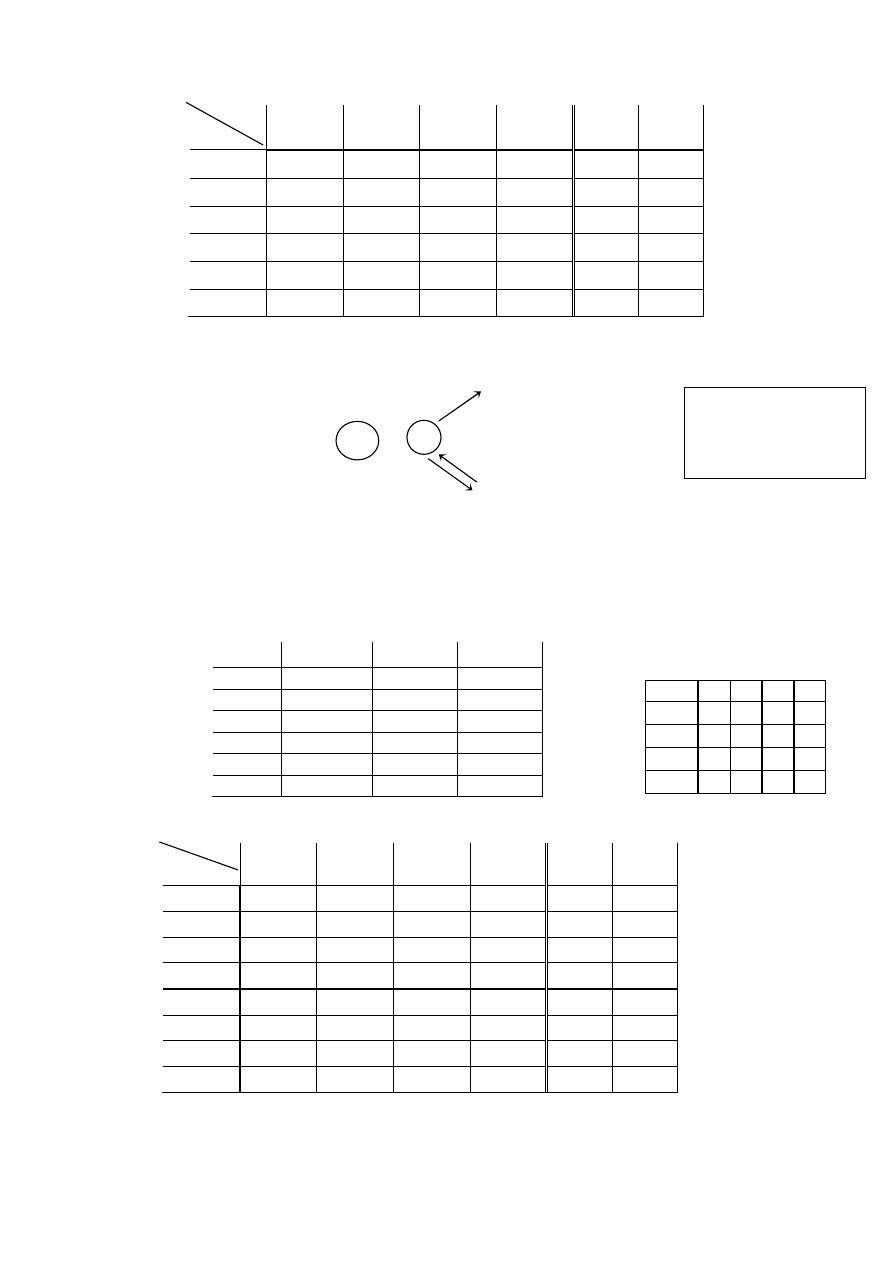
K. Firląg
/
2007/
-8-
D
3
= x
D
2
= nQ
2
n
x
D
1
= nQ
2
nQ
1
+ Q
2
nx + Q
1
x
P5s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Moore’a
X
S
X
4
X
3
X
2
X
1
y
2
y
1
1
-
2
6
-
0
0
2
1
2
6
-
1
0
3
-
2
6
-
1
0
4
2
1
3
6
1
1
5
-
1
4
5
0
1
6
1
2
5
5
0
0
Graf podziałów:
ττττ
34
1
→
→
→
→
ττττ
12
ττττ
123
←
←
←
←
ττττ
4
ττττ
156
←
←
←
←
ττττ
45
→
→
→
→
ττττ
134
ττττ
124
←
←
←
←
ττττ
5
ττττ
56
→
→
→
→
ττττ
36
Ceny podziałów: C(
ττττ
i
) = n + l - 1
Ceny wyj
ść
: C
π
(y
i
) = l - 1
Rodzina ko
ń
cowa optymalna T
kopt
= (
ττττ
12
,
ττττ
45,
ττττ
156
),
(sprawdzi
ć
iloczyn)
s
τ
12
(Q
3
)
τ
45
(Q
2
)
τ
156
(Q
1
)
1
0
0
1
2
0
0
0
3
1
0
0
4
1
1
0
5
1
1
1
6
1
0
1
Zakodowana tablica przej
ść
-wyj
ść
:
x
2
x
1
Q
3
Q
2
Q
1
(x
4
)
00
(x
3
)
01
(x
2
)
11
(x
1
)
10
y
2
y
1
(2)
000
001
000
101
-
1
0
(1)
001
-
000
101
-
0
0
011
-
-
-
-
-
-
010
-
-
-
-
-
-
(4)
110
000
001
100
101
1
1
(5)
111
-
001
110
111
0
1
(6)
101
001
000
111
111
0
0
(3)
100
-
000
101
-
1
0
Funkcje wzbudze
ń
:
D
3
= x
2
D
2
= Q
3
Q
1
x
2
D
1
= nQ
2
x
2
+ nQ
2
nx
1
+ x
2
nx
1
+ Q
2
nx
2
x
1
Podziały zewnętrzne:
π
(y
2
) =
τ
156
π
(y
1
) =
τ
45
y
2
= nQ
1
y
1
= Q
2
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
S’ Y
K. Firląg
/
2007/
-9-
(l=0, C=1)
(l=2, C=3)
(l=1, C=2)
X
S
X
4
X
3
X
2
X
1
y
2
y
1
1
-
2
6
-
0
0
2
1
2
6
-
1
0
3
-
2
6
-
1
0
4
2
1
3
6
1
1
5
-
1
4
5
0
1
6
1
2
5
5
0
0
Struktura kratowa:
τ
12
τ
13
τ
14
τ
15
τ
16
τ
23
τ
24
τ
25
τ
26
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
1
π
π
π
π
π
π
π
π
τ
34
τ
35
τ
36
τ
45
τ
46
τ
56
τ
123
τ
124
τ
125
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
τ
45
π
τ
56
τ
56
π
τ
45
τ
4
τ
5
π
τ
126
τ
134
τ
135
τ
136
τ
145
τ
146
τ
156
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
π
τ
45
π
π
π
π
τ
45
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
S’ Y
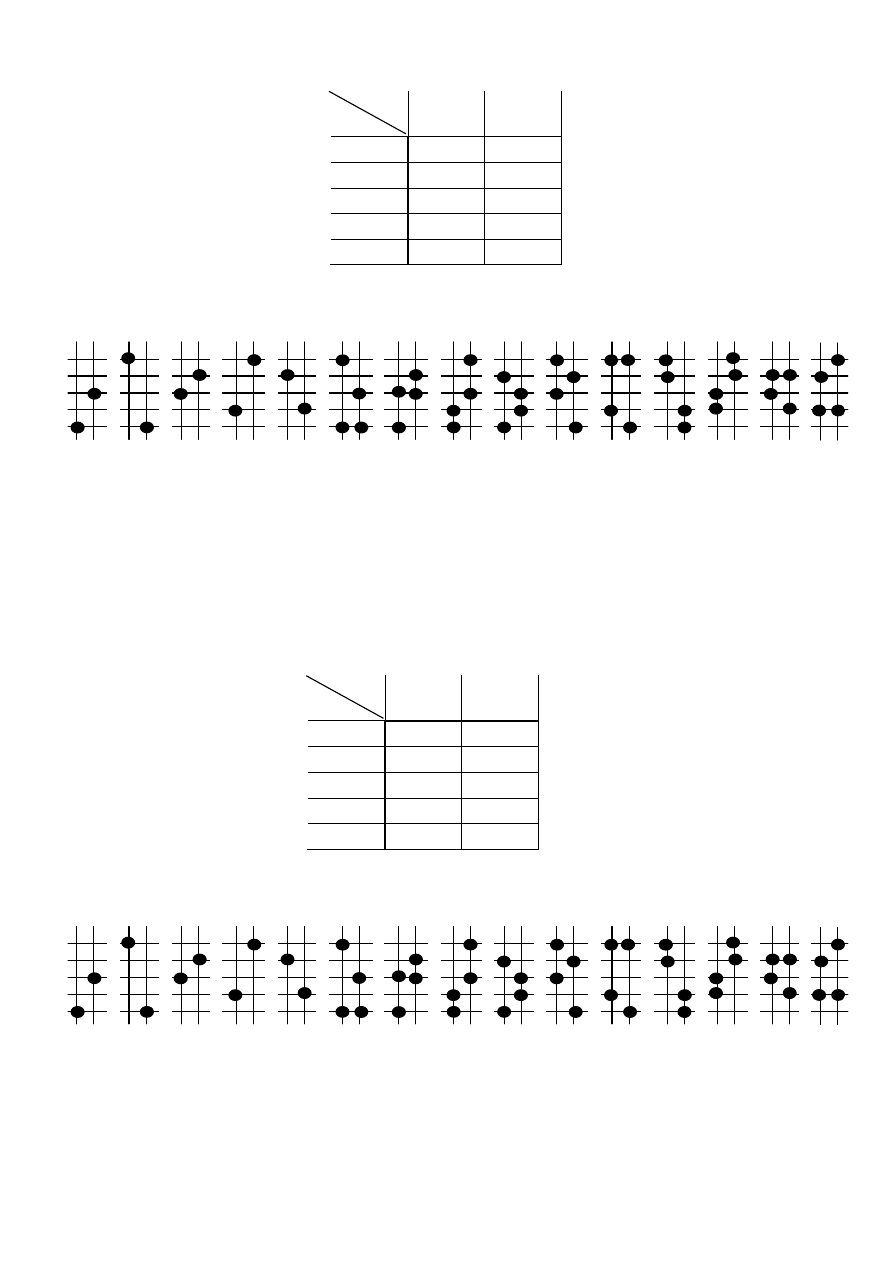
K. Firląg
/
2007/
-10-
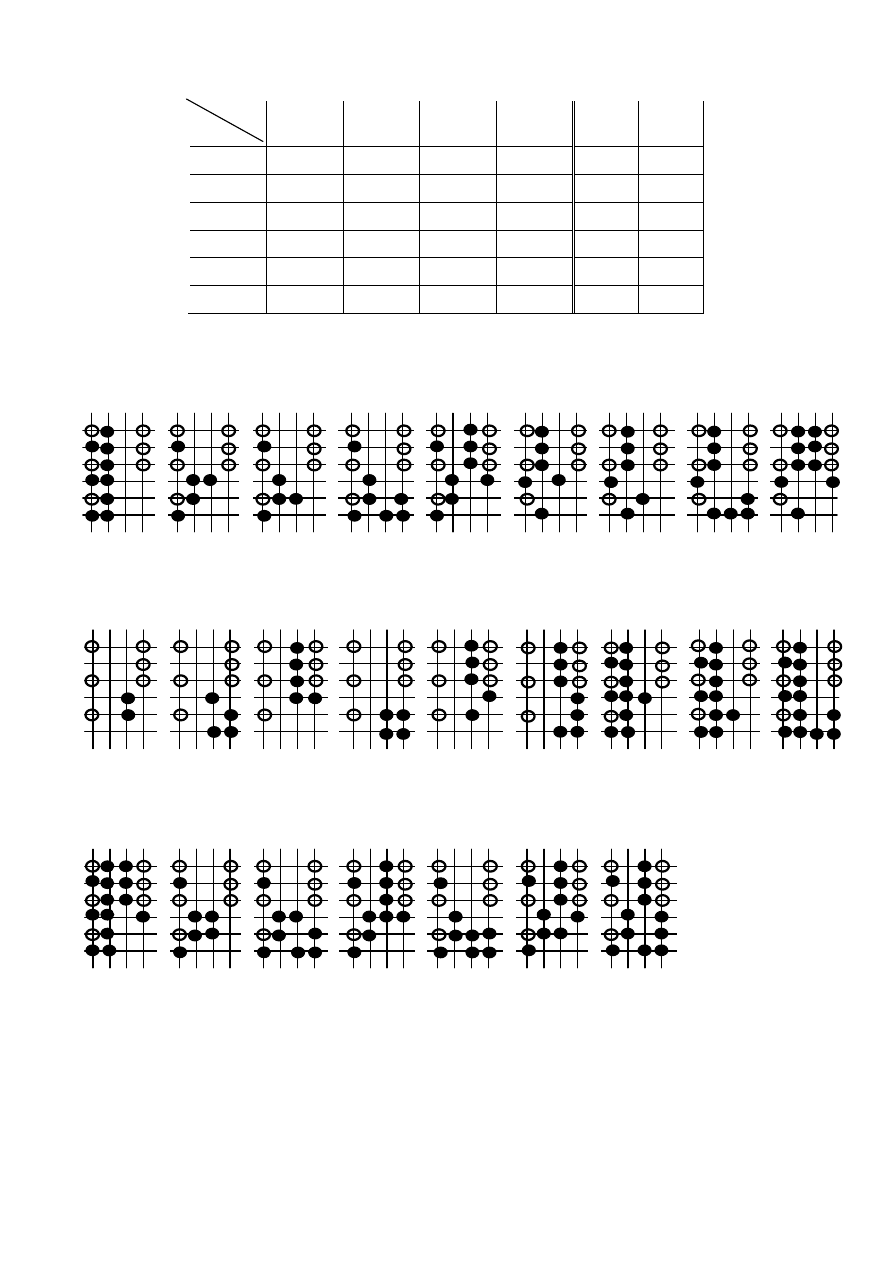
P6s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Mealy’ego
X
S
X
2
X
1
1
2/0
4/0
2
5/0
3/0
3
3/0
1/1
4
4/1
5/1
5
1/1
2/0
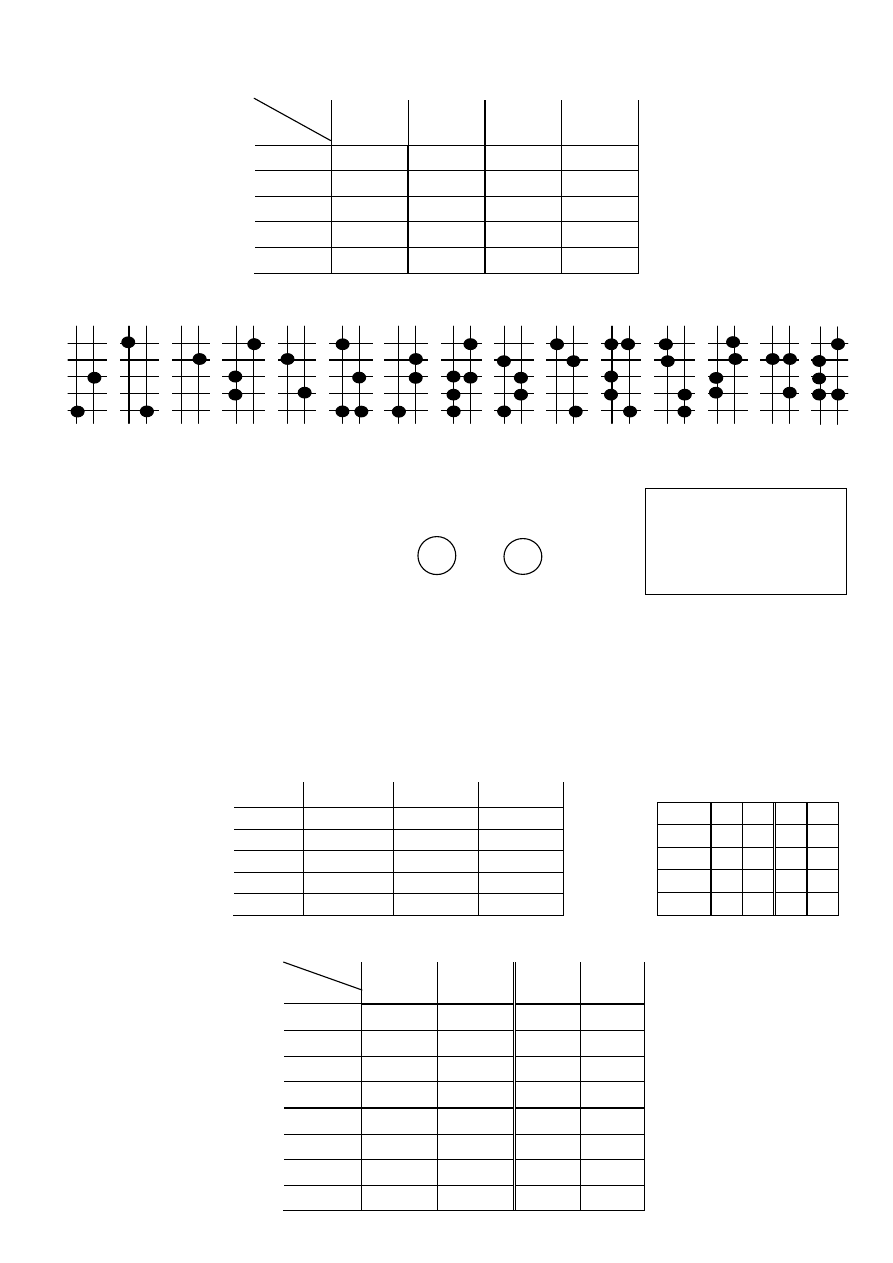
Struktura kratowa:
τ
1
τ
2
τ
3
τ
4
τ
5
τ
12
τ
13
τ
14
τ
15
τ
23
τ
24
τ
25
τ
34
τ
35
τ
45
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
Podziały zewnętrzne:
π
x2
(y) =
τ
45
π
x1
(y) =
τ
34
π
(y) =
τ
45
*
τ
34
=
{4,5,3,12}
P7s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Mealy’ego
X
S
X
2
X
1
1
2/ Y
4
1/ Y
2
2
5/ Y
1
4/ Y
3
3
1/ Y
3
3/ Y
3
4
3/ Y
1
5/ Y
4
5
4/ Y
1
2/ Y
2
Struktura kratowa:
τ
1
τ
2
τ
3
τ
4
τ
5
τ
12
τ
13
τ
14
τ
15
τ
23
τ
24
τ
25
τ
34
τ
35
τ
45
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
Podziały zewnętrzne:
π
x2
(y
2
) =
τ
13
π
x1
(y
2
) =
τ
15
π
(y
2
) =
τ
13
*
τ
15
=
{1,24,3,5}
π
x2
(y
1
) =
τ
3
π
x1
(y
1
) =
τ
4
1
2
3
4
5
1
2
3
4
5
Kodowanie wyjść
Y
1
= 0 0
Y
2
= 0 1
Y
3
= 1 1
Y
4
= 1 0
y
2
y
1
S’/Y
S’/Y
K. Firląg
/
2007/
-11-
π
(y
1
) =
τ
3
*
τ
4
=
{125,3,4}
P8s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Moore’a
X
S
X
2
X
1
y
2
y
1
1
2
4
0
0
2
5
3
1
0
3
4
1
1
0
4
4
5
0
1
5
1
2
1
1
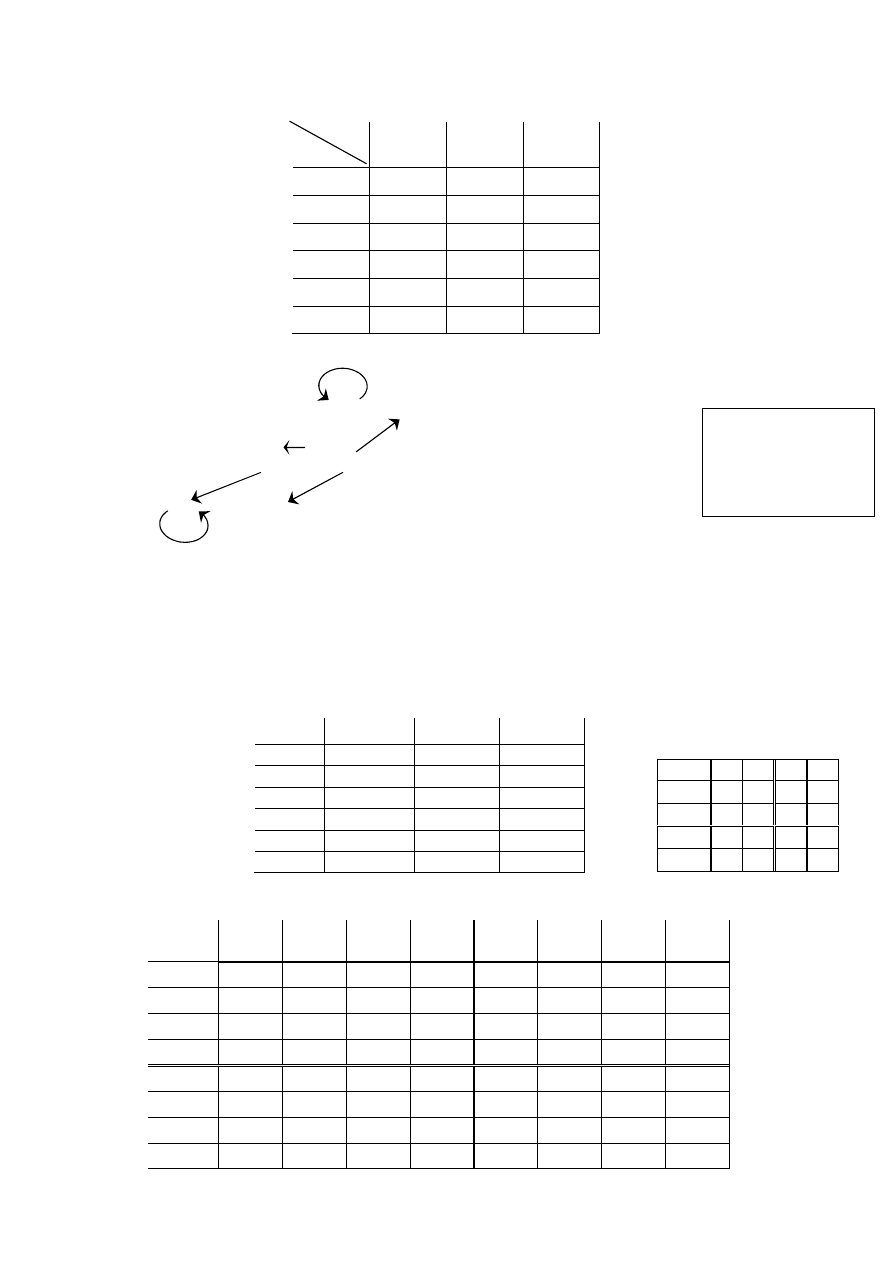
Struktura kratowa:
τ
1
τ
2
τ
3
τ
4
τ
5
τ
12
τ
13
τ
14
τ
15
τ
23
τ
24
τ
25
τ
34
τ
35
τ
45
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
π
π
τ
2
π
π
π
π
π
π
π
π
π
π
π
π
Graf podziałów:
ττττ
3
←
←
←
←
ττττ
2
ττττ
14
ττττ
45
Rodziny ko
ń
cowe:
(sprawdzi
ć
iloczyn)
T
k1
= (
τ
14
,
τ
45
,
τ
3
),
T
k2
= (
ττττ
14
,
ττττ
45
,
ττττ
2
).
C(
τ
14
)= 1+3-1 =3
C(
τ
14
)= 1+3-1 =3
C(
τ
45
)= 1+2-1 =2 C(Y
2
) = 1-1 =0
C(
τ
45
)= 1+2-1 =2 C(Y
2
) = 1-1 =0
C(
τ
3
) = 1+3-1 =3 C(Y
1
) = 1-1 =0
C(
τ
2
) = 1+2-1 =2 C(Y
1
) = 1-1 =0
∑
C = 8
∑
∑
∑
∑
C = 7
s
τ
14
(Q
3
)
τ
45
(Q
2
)
τ
2
(Q
1
)
1
0
0
0
2
1
0
1
3
1
0
0
4
0
1
0
5
1
1
0
Zakodowana tablica przej
ść
-wyj
ść
:
X
Q
3
Q
2
Q
1
(x
2
)
0
(x
1
)
1
y
2
y
1
(1)
000
101
010
0
0
001
-
-
-
-
011
-
-
-
-
(4)
010
010
110
0
1
(5)
110
000
101
1
1
111
-
-
-
-
(2)
101
110
100
1
0
(3)
100
010
000
1
0
1
2
3
4
5
Podziały zewnętrzne:
π
(y
2
) =
τ
14
π
(y
1
) =
τ
45
T
kopt
= (
ττττ
14
,
ττττ
45
,
ττττ
2
)
y
2
= Q
3
(l=1, C=0)
y
1
= Q
2
(l=1, C=0)
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
S’ Y
K. Firląg
/
2007/
-12-
D
3
=Q
1
+Q
2
x+nQ
3
nQ
2
nx
D
2
=nQ
3
x+nQ
3
Q
2
+Q
3
nQ
2
nx
D
1
=Q
3
Q
2
x+nQ
3
nQ
2
nx
(l=3, C=3)
(l=2, C=2)
(l=2, C=2)
P9s. Tablica przej
ść
-wyj
ść
synchronicznego automatu Mealy’ego
X
S
X
3
X
2
X
1
1
6/0
-/0
6/0
2
6/0
2/1
4/1
3
5/0
3/1
-/0
4
6/1
2/0
4/0
5
5/1
3/1
6/1
6
-/1
1/1
-/0
Graf podziałów:
ττττ
156
ττττ
12
←
←
←
←
ττττ
35
→
→
→
→
ττττ
46
ττττ
34
←
←
←
←
ττττ
45
ττττ
125
←
←
←
←
ττττ
35
↓↓↓↓
↑↑↑↑
ττττ
15
→
→
→
→
ττττ
56
←
←
←
←
ττττ
135
→
→
→
→
ττττ
124
→
→
→
→
ττττ
25
ττττ
134
←
←
←
←
ττττ
24
ττττ
23
←
←
←
←
ττττ
16
↑↑↑↑
↑↑↑↑
ττττ
24
→
→
→
→
ττττ
13
ττττ
123
←
←
←
←
1
ττττ
6
Rodziny ko
ń
cowe:
(sprawdzi
ć
iloczyn)
T
k1
= (
ττττ
123
,
ττττ
135
,
ττττ
124
),
T
k2
= (
τ
123
,
τ
24
,
τ
35
).
C(
τ
123
)= 2+0-1 =1
C(
τ
123
)= 2+0-1 =1
C(
τ
135
)= 2+1-1 =2 C(Y) = 2+3-1 =4
C(
τ
24
) = 2+1-1 =2 C(Y) = 2+3-1 =4
C(
τ
124
)= 2+1-1 =2
∑
C = 9
C(
τ
35
) = 2+1-1 =2
∑
C = 9
s
τ
123
(Q
3
)
τ
135
(Q
2
)
τ
124
(Q
1
)
1
1
1
0
2
1
0
0
3
1
1
1
4
0
0
0
5
0
1
1
6
0
0
1
Zakodowana tablica przej
ść
-wyj
ść
:
x
2
x
1
Q
3
Q
2
Q
1
(x
3
)
00
(x
2
)
01
(x
1
)
11
10
(x
3
)
00
(x
2
)
01
(x
1
)
11
10
(4)
000
001
100
000
-
1
0
0
-
(6)
001
-
110
-
-
1
1
0
-
(5)
011
011
111
001
-
1
1
1
-
010
-
-
-
-
-
-
-
-
(1)
110
001
-
001
-
0
0
0
-
(3)
111
011
111
-
-
0
1
0
-
101
-
-
-
-
-
-
-
-
(2)
100
001
100
000
-
0
1
1
-
Funkcje wzbudze
ń
:
Podziały zewnętrzne:
π
x3
(y) =
τ
123
π
x2
(y) =
τ
14
π
x1
(y) =
τ
25
π
(y)={1,2,3,4,5,6}=0
T
kopt
= (
ττττ
123
,
ττττ
135
,
ττττ
124
)
y = ?
(l=3, C=4)
Q
→
Q’
J
K D T
0
→
0 0
-
0
0
0
→
1 1
-
1
1
1
→
0
-
1
0
1
1
→
1
-
0
1
0
S’/Y
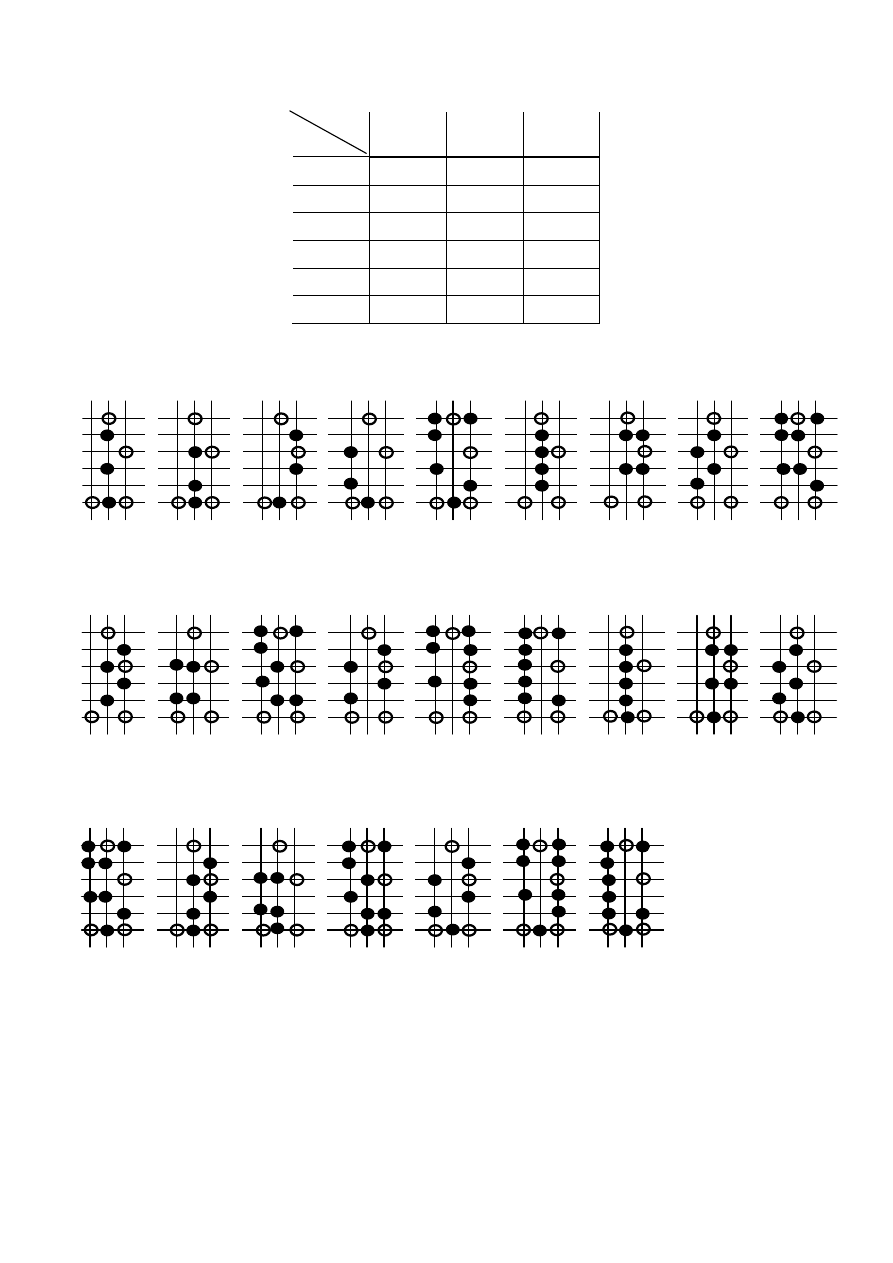
K. Firląg
/
2007/
-13-
D
3
= nx
2
x
1
D
2
= Q
1
nx
2
D
1
= n
x
1
+ Q
2
(l=0, C=1)
(l=1, C=2)
(l=1, C=2)
X
S
X
3
X
2
X
1
1
6/0
-/0
6/0
2
6/0
2/1
4/1
3
5/0
3/1
-/0
4
6/1
2/0
4/0
5
5/1
3/1
6/1
6
-/1
1/1
-/0
Struktura kratowa:
τ
12
τ
13
τ
14
τ
15
τ
16
τ
23
τ
24
τ
25
τ
26
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
τ
135,
τ
35
τ
124
,
τ
24
π
π
π
τ
16
,
τ
6
τ
24
τ
24
π
τ
34
τ
35
τ
36
τ
45
τ
46
τ
56
τ
123
τ
124
τ
125
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
τ
45
τ
35
π
π
τ
35
,
τ
356
τ
15
,
τ
135
,
τ
24
,
τ
156
1
τ
135
τ
35
τ
126
τ
134
τ
135
τ
136
τ
145
τ
146
τ
156
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
↑↑↑↑
π
τ
24
τ
124
π
π
π
π
1
2
3
4
5
6
1
2
3
4
5
6
1
2
3
4
5
6
S’/Y
Wyszukiwarka
Podobne podstrony:
Cwiczenia nr 10 (z 14) id 98678 Nieznany
Cwiczenia nr 13 RPiS id 124686 Nieznany
Cwiczenia nr 13 (z 14) id 98681 Nieznany
Cwiczenia II asynch KFR
F II wyklad 11 id 167234 Nieznany
Cwiczenia nr 10 RPiS id 124684 Nieznany
Fizyka II instr 3 Wsp U id 1767 Nieznany
II Sztuka archaiczna id 210032 Nieznany
cwiczenie9b am 13 14 id 125935 Nieznany
Cwiczenia nr 12 (z 14) id 98680 Nieznany
cwiczenie10a am 13 14 id 125803 Nieznany
AIR II projekt 1 WM id 53378 Nieznany
Cwiczenia nr 11 (z 14) id 98679 Nieznany
II rzad zadania id 209979 Nieznany
ca6 ii pl 0509 id 107558 Nieznany
cwiczenie8a am 13 14 id 125925 Nieznany
Cwiczenie P14 cw P14 id 649717 Nieznany
II Sytem produkcyjny id 210031 Nieznany
cwiczenie lab nr 4 FMEA id 1256 Nieznany
więcej podobnych podstron