Przykładowe badanie funkcji
2
1)
(
)
(
++++
====
x
e
x
f
x
1.
Dziedzina
0
1
≠≠≠≠
++++
x
1
−−−−
≠≠≠≠
⇔
⇔
⇔
⇔
x
)
;
(
)
;
(
}
{
\
+∞
+∞
+∞
+∞
−−−−
∪
∪
∪
∪
−−−−
−∞
−∞
−∞
−∞
====
−−−−
====
1
1
1
R
D
2.
Granice na krańcach przedziałów określoności i asymptoty
a.
Asymptota pionowa
⇒
⇒
⇒
⇒
+∞
+∞
+∞
+∞
====
====
++++
====
+∞
+∞
+∞
+∞
====
====
++++
====
−−−−
−−−−
−−−−
−−−−
−−−−
→
→
→
→
−−−−
→
→
→
→
−−−−
→
→
→
→
−−−−
→
→
→
→
...
)
(
lim
)
(
lim
...
)
(
lim
)
(
lim
2
1
1
2
1
1
1
1
x
e
x
f
x
e
x
f
x
x
x
x
x
x
b.
Asymptota pozioma
0
0
1
2
====
∞
∞
∞
∞
====
++++
====
∞
∞
∞
∞
−−−−
→
→
→
→
∞
∞
∞
∞
−−−−
→
→
→
→
)
(
lim
)
(
lim
x
e
x
f
x
x
x
⇒
⇒
⇒
⇒
prosta
0
====
y
- asymptota pozioma w
∞
∞
∞
∞
−−−−
+∞
+∞
+∞
+∞
====
====
++++
====
∞
∞
∞
∞
++++
→
→
→
→
∞
∞
∞
∞
++++
→
→
→
→
...
)
(
lim
)
(
lim
2
1
x
e
x
f
x
x
x
⇒
⇒
⇒
⇒
brak asymptoty poziomej w
∞
∞
∞
∞
++++
c.
Asymptota ukośna
Istnieje asymptota pozioma w
∞
∞
∞
∞
−−−−
, zatem brak asymptoty ukośnej w
∞
∞
∞
∞
−−−−
Badamy istnienie asymptoty ukośnej w
∞
∞
∞
∞
++++
+∞
+∞
+∞
+∞
====
====
++++
====
∞
∞
∞
∞
++++
→
→
→
→
∞
∞
∞
∞
++++
→
→
→
→
...
)
(
lim
)
(
lim
2
1
x
x
e
x
x
f
x
x
x
⇒
⇒
⇒
⇒
brak asymptoty ukośnej w
∞
∞
∞
∞
++++
.
3.
Punkty przecięcia wykresu z osiami układu współrzędnych
OX:
0
====
)
(x
f
0
1
2
====
++++
⇔
⇔
⇔
⇔
)
(x
e
x
∅
∅
∅
∅
∈
∈
∈
∈
⇔
⇔
⇔
⇔
x
⇒
⇒
⇒
⇒
brak miejsc zerowych
OY:
1
1
0
0
2
0
====
++++
====
)
(
)
(
e
f
4.
Przedziały monotoniczności i ekstrema lokalne
3
)
1
(
)
1
(
...
)
1
(
)
(
2
+
−
=
=
′
+
=
′
x
e
x
x
e
x
f
x
x
1
0
)
1
(
0
)
1
(
)
1
(
0
)
(
3
=
⇔
=
−
⇔
=
+
−
⇔
=
′
x
e
x
x
e
x
x
f
x
x
– punkt stacjonarny
0
)
1
(
)
1
(
0
)
1
(
)
1
(
0
)
(
3
0
3
<
+
−
⇒
<
+
−
⇔
<
′
>
x
x
x
e
x
x
f
x
e
x
Prosta
1
−−−−
====
x
- asymptota pionowa
obustronna
Znak pochodnej
)
1
;
1
(
0
)
(
−
∈
⇔
<
′
x
x
f
)
;
1
(
)
1
;
(
0
)
(
∞
+
∪
−
−∞
∈
⇔
>
′
x
x
f
x
)
1
;
(
−
−∞
1
−
)
1
;
1
(
−
1
)
;
1
(
∞
+
)
(x
f
′
+
X
–
0
+
)
(
x
f
X
min. lok.
4
e
4
)
1
1
(
)
1
(
2
1
min_lok
e
e
f
f
=
+
=
=
5.
Przedziały wypukłości/wklęsłości i punkty przegięcia
4
x
2
1)
+
(x
e
3)
+
2x
-
(x
...
)
1
(
)
1
(
)
(
3
=
=
′
+
−
=
′′
x
e
x
x
f
x
∅
∈
⇔
=
⇔
=
′′
x
x
f
0
1)
+
(x
e
3)
+
2x
-
(x
0
)
(
4
x
2
⇒
⇒
⇒
⇒
brak punktów „podejrzanych o przegięcie”
∅
∈
⇒
∀
>
∀
>
∀
>
⇒
<
⇔
<
′′
∈
∈
∈
x
e
x
f
D
x
R
x
R
x
x
0
1)
+
(x
0
3
+
2x
-
x
0
0
1)
+
(x
e
3)
+
2x
-
(x
0
)
(
4
2
4
x
2
)
;
1
(
)
1
;
(
0
)
(
∞
+
−
∪
−
−∞
∈
⇔
∈
⇔
>
′′
x
D
x
x
f
x
)
1
;
(
−
−∞
1
−
)
;
1
(
∞
+
−
)
(
x
f
′′
+
X
+
)
(
x
f
X
6.
Tabela
x
)
1
;
(
−
−∞
1
−
)
0
;
1
(
−
0
)
1
;
0
(
1
)
;
1
(
∞
+
)
(
x
f
′′
+
X
+
+
+
+
+
)
(
x
f
′
+
X
–
–
–
0
+
)
(
x
f
X
1
min. lok.
4
e
7.
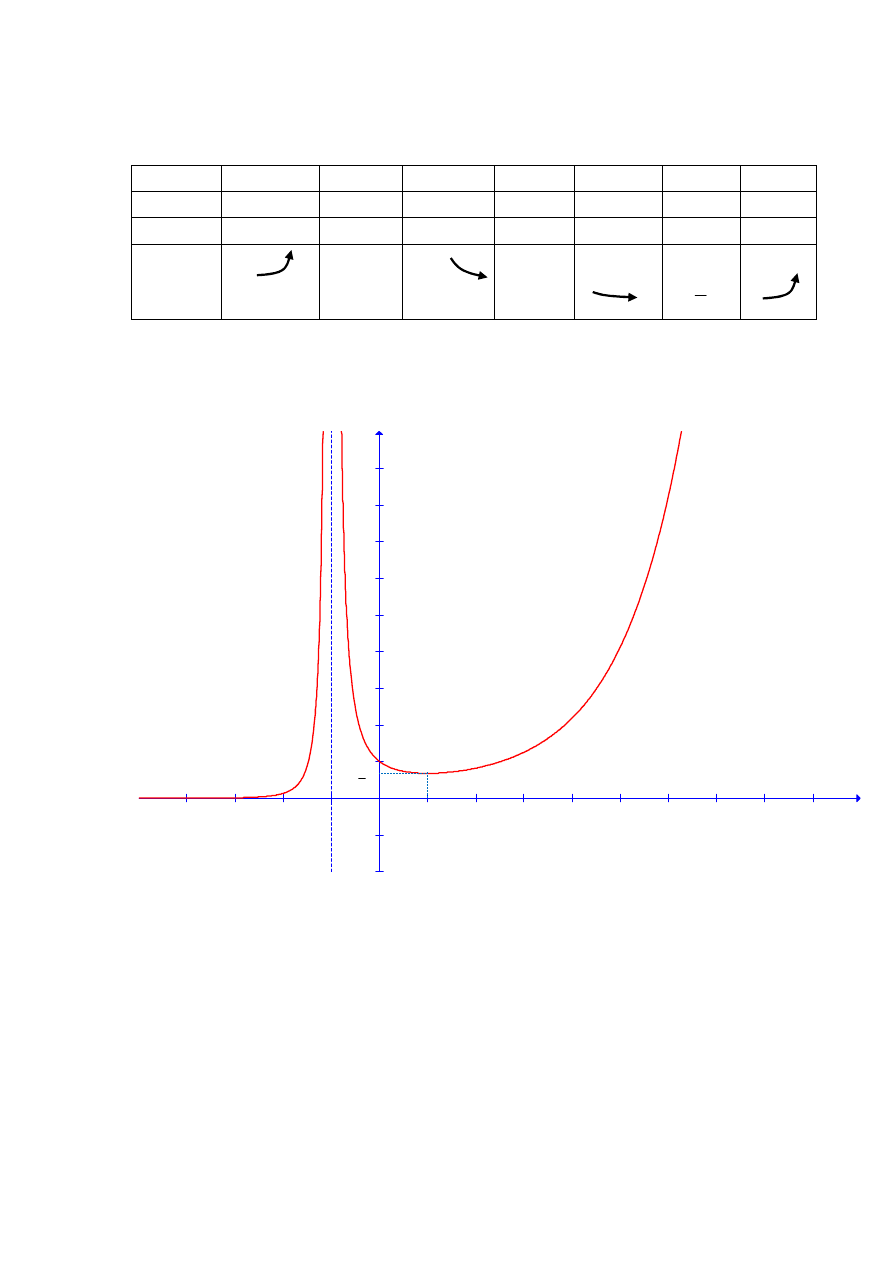
Wykres funkcji
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
-1
1
2
3
4
5
6
7
8
9
x
y
∞
∞
∞
∞
++++
∞
∞
∞
∞
++++
∞
∞
∞
∞
++++
0
4
e
Wyszukiwarka
Podobne podstrony:
am przyklady badanie funkcji lista6
Testowanie, TEST Badania funkcjonalne
3 5 Badanie funkcji 2
Badanie funkcjonalne narzÄ…du ruchu
a6 badanie funkcji Nieznany (2)
060 Tw de L'Hospitala, badanie funkcji
5 Badanie funkcji id 39644 Nieznany (2)
Badanie Funkcji Logicznych
Badanie funkcji
Badanie funkcji
Badanie funkcji2c
arkusz BADANIE FUNKCJI
3 4 Badanie funkcji 1
matematyka badanie funkcji, WSEI, SEMESTR 2, Matematyka
20. Charakterystyka badania przekrojowego-przykłady badań przekrojowych, licencjat(1)
badanie funkcji
08 Badanie funkcji organizmu zdrowego człowieka
więcej podobnych podstron