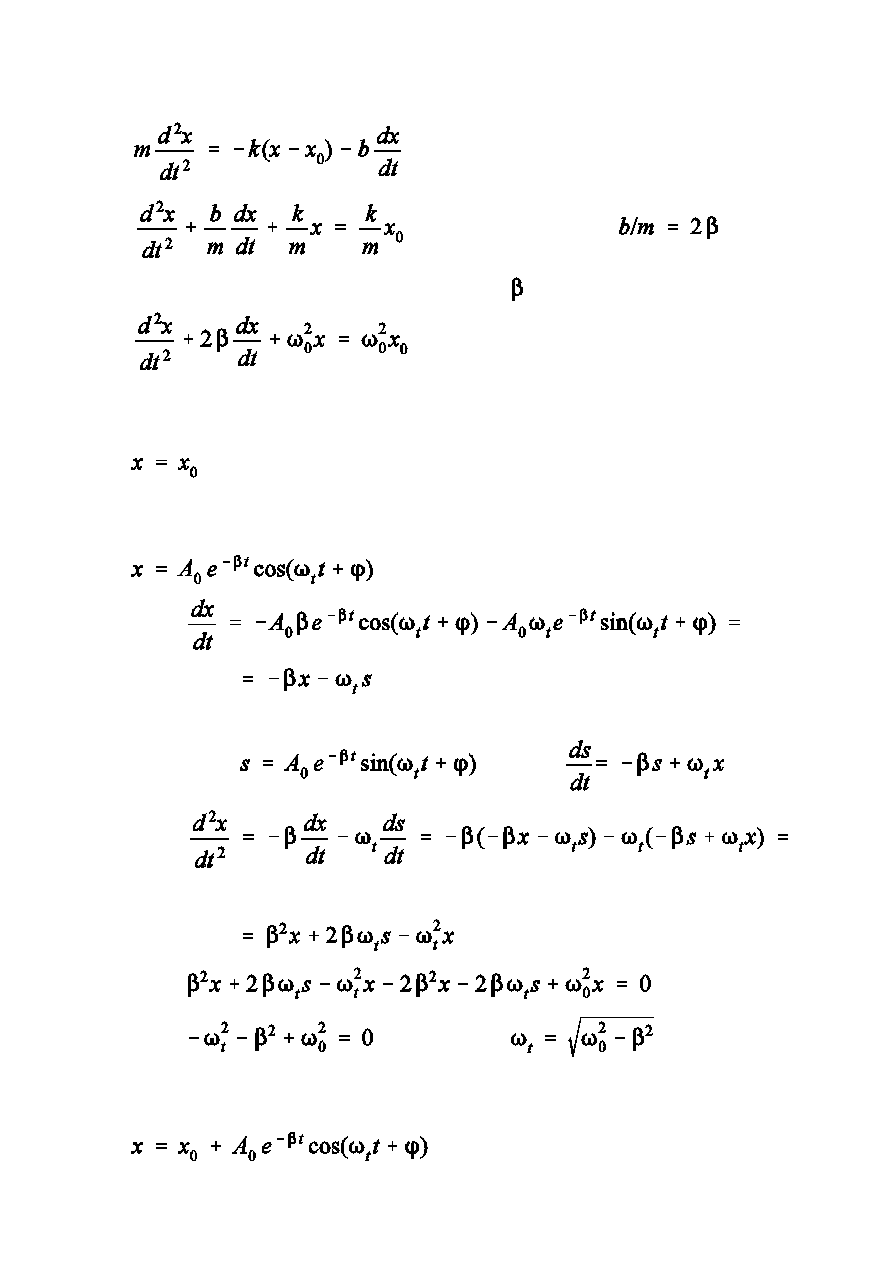
Drgania 12

DRGANIA TºUMIONE

b - wspó»czynnik oporu oÑrodka

 - wspó»czynnik t»umienia

Rozwizanie szczególne równania niejednorodnego

Rozwizanie ogólne równania jednorodnego

Rozwizanie ogólne równania niejednorodnego 

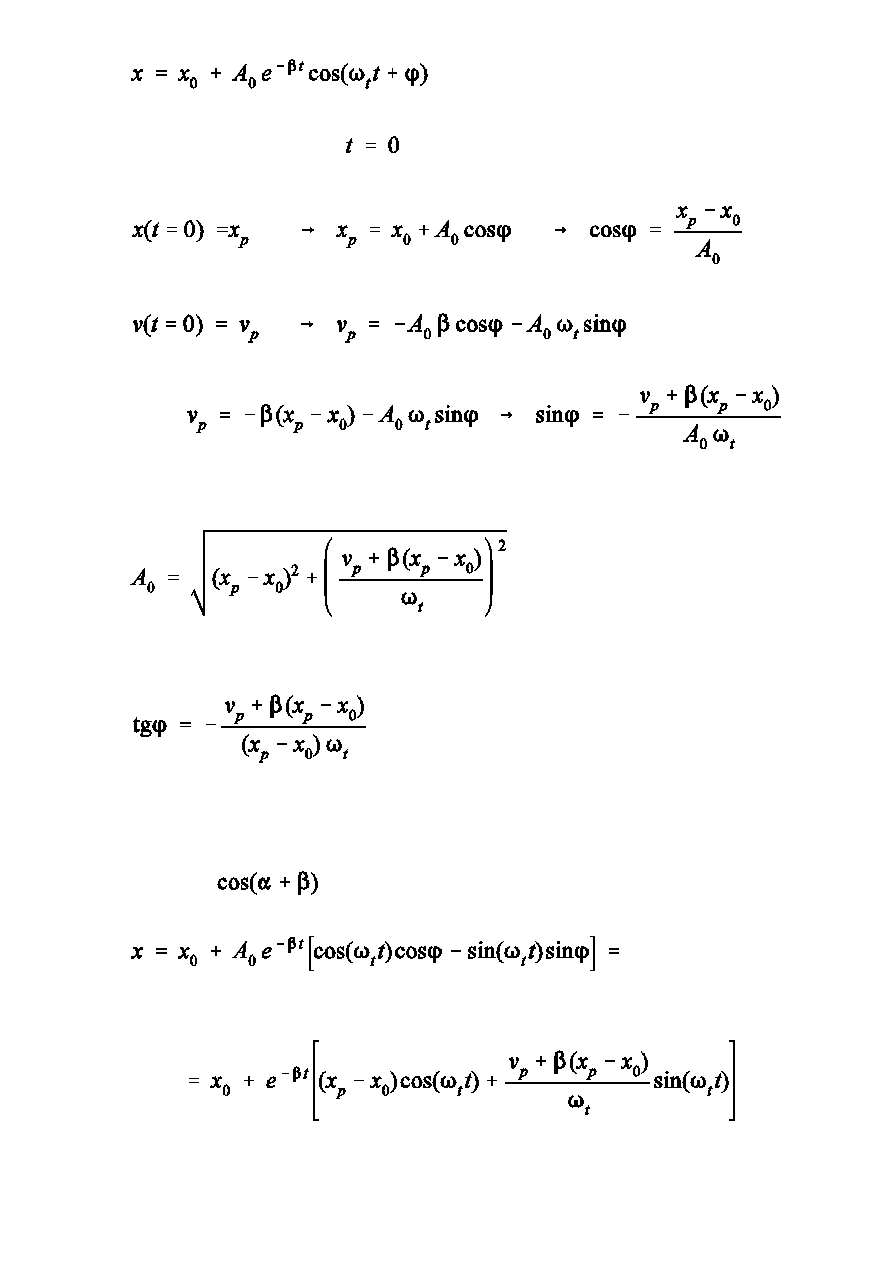
Drgania 13

Warunki pocztkowe (dla   

)

  

Z rozwini“cia 

Drgania 14

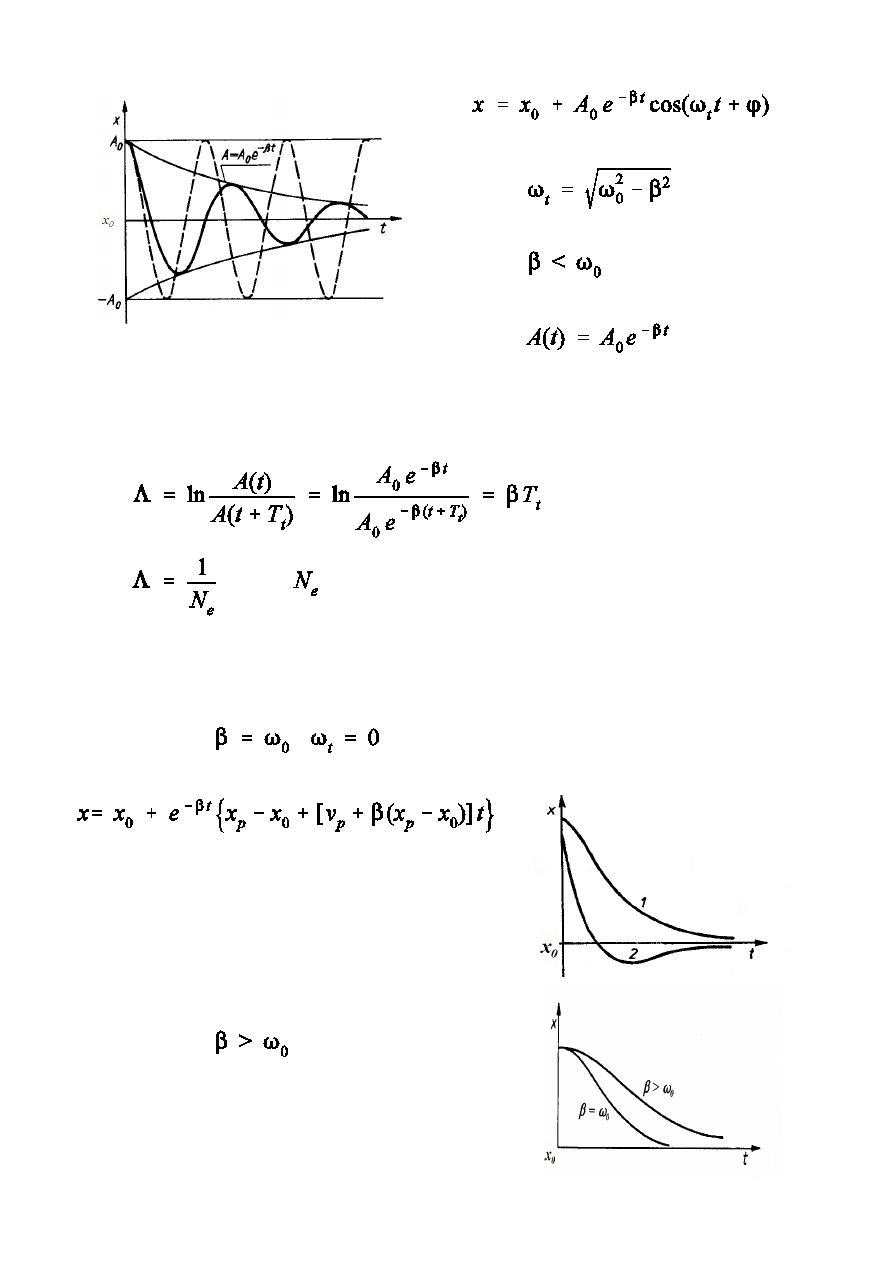
Logarytmiczny dekrement t»umienia

 - liczba drga½ w czasie, w którym amplituda maleje

e razy.

W przypadku 

  

Ruch jest aperiodyczny.
Ruch pe»zajcy krytyczny

W przypadku 

Ruch jest aperiodyczny.
Ruch pe»zajcy.

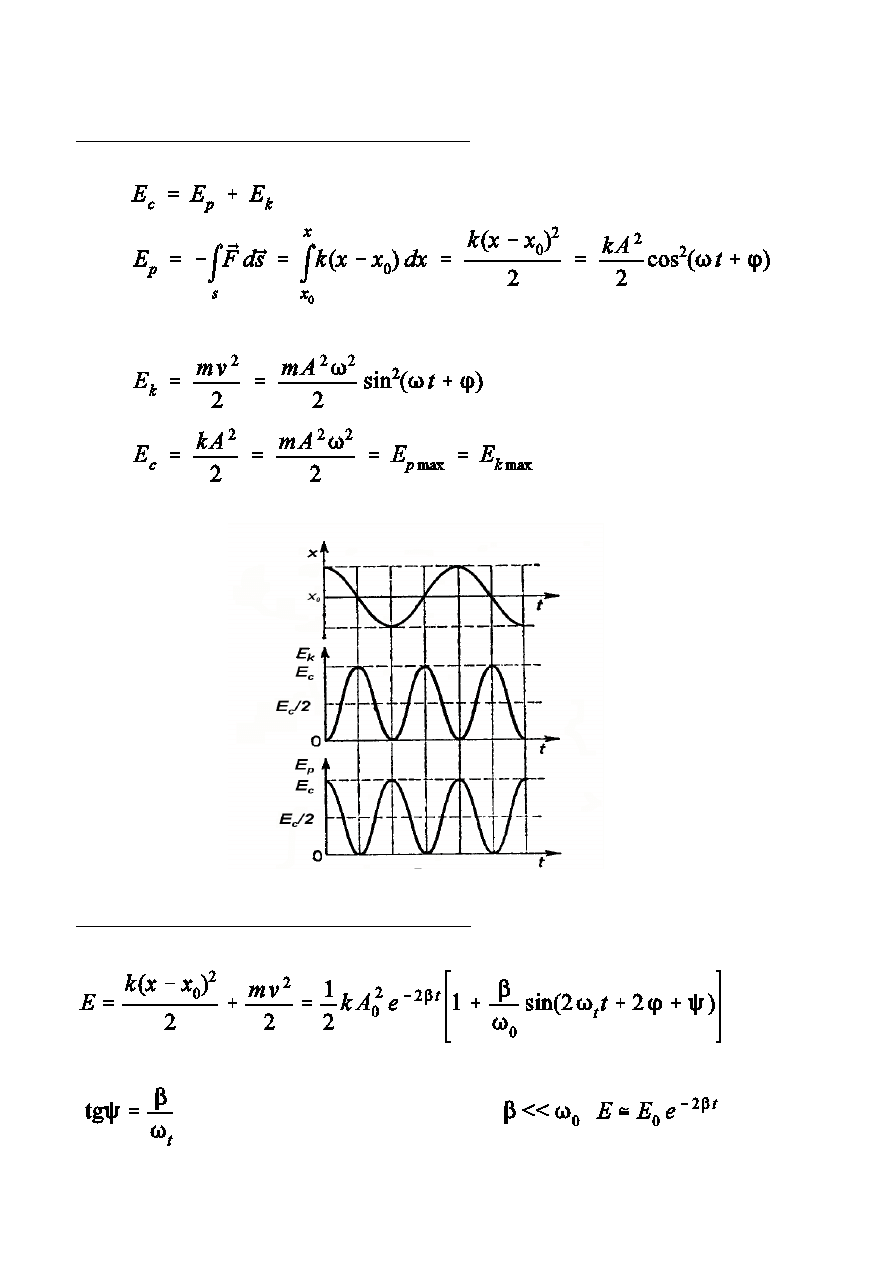
Drgania 15

ENERGIA OSCYLATORA

Energia w ruchu harmonicznym prostym

Energia ca»kowita oscylatora t»umionego           

,

 

    

Dla  

  

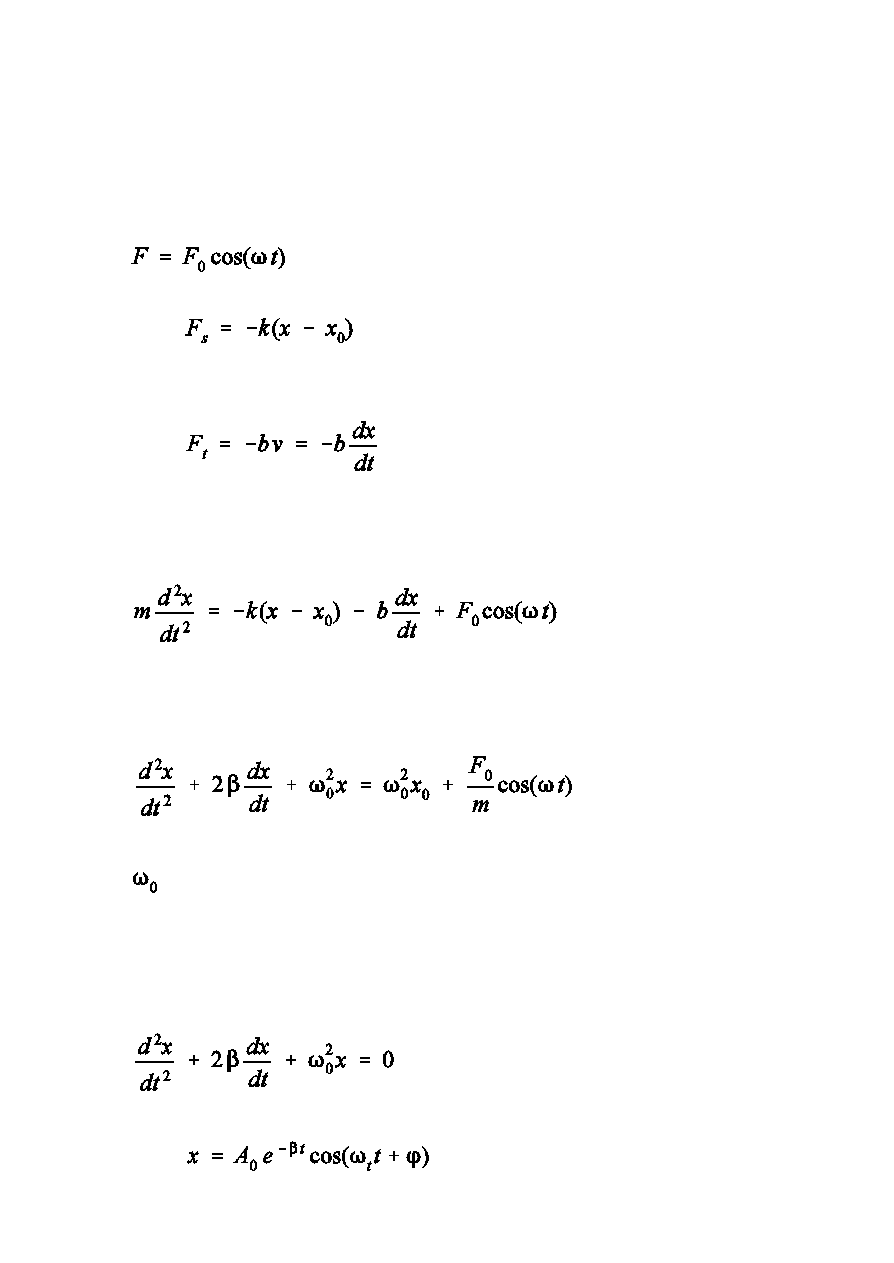
Drgania 16

DRGANIA WYMUSZONE

Drgania swobodne i t»umione to drgania naturalne oscylatora.  Stosunkowo
rzadziej w przyrodzie spotykamy si“ z drganiami wymuszonymi -
zachodzcymi pod wp»ywem okresowo zmiennej si»y.
Przyjmiemy, óe taka si»a ma postaƒ

Oprócz tej si»y na mas“ m. dzia»a jeszcze si»a kwazispr“óysta

oraz si»a t»umica drgania

Równanie ruchu masy m. przyjmuje wi“c postaƒ

lub po uporzdkowaniu

 - cz“stoу drga½ oscylatora w nieobecnoÑci t»umienia i si»y

wymuszajcej

Rozwizanie ogólne  równania jednorodnego 

ma postaƒ  

   i gaÑnie z czasem.

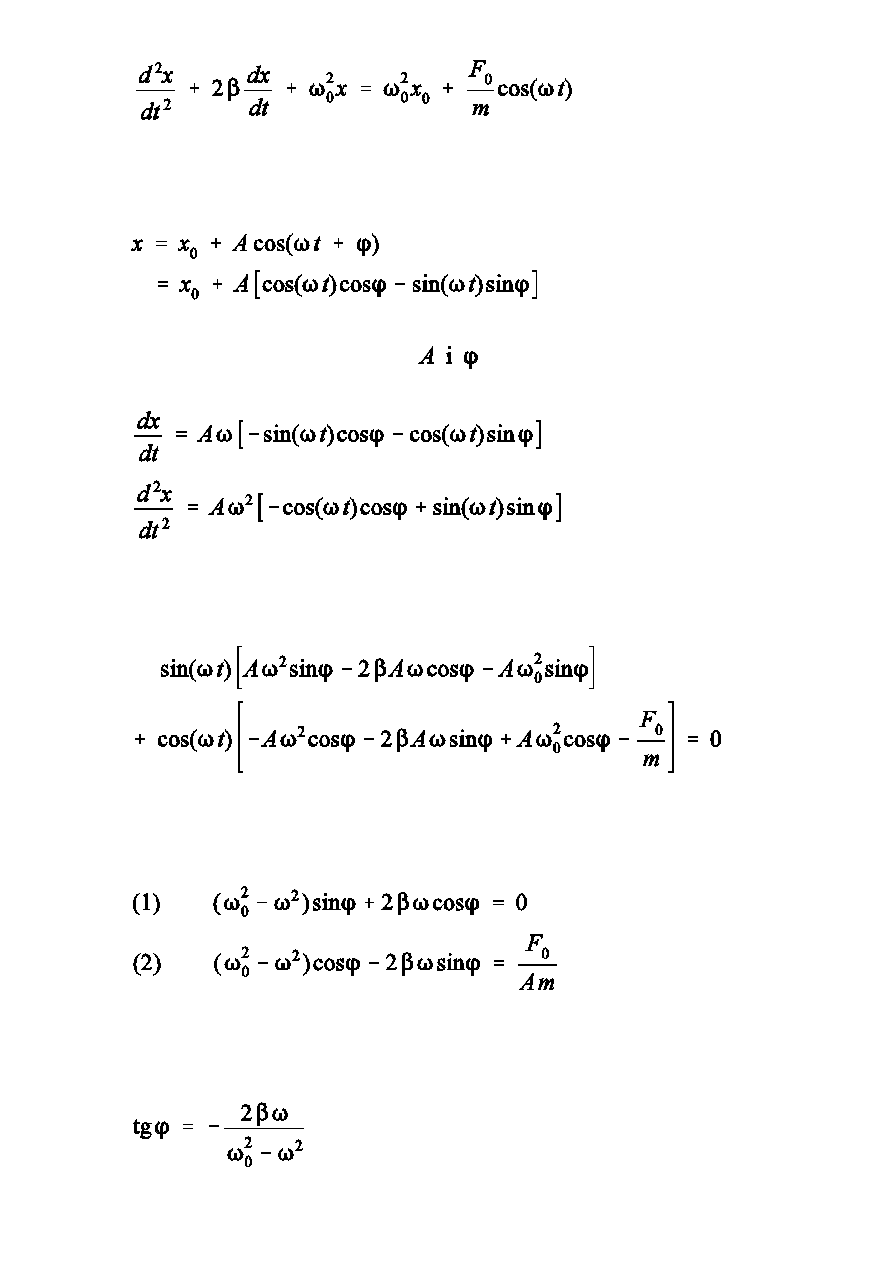
Drgania 17

W stanie  ustalonym (dla duóych t) drgania wymuszone s opisane przez
rozwizanie szczególne równania niejednorodnego majce postaƒ

  

Znajdziemy znaczenie parametrów 

Mamy wi“c

dla dowolnego t, czyli

Na podstawie (1)

Drgania 18

Podnoszc (1) i (2) do kwadratu i dodajc stronami otrzymujemy

lub

Drgania wymuszone w stanie ustalonym opisane s równaniem

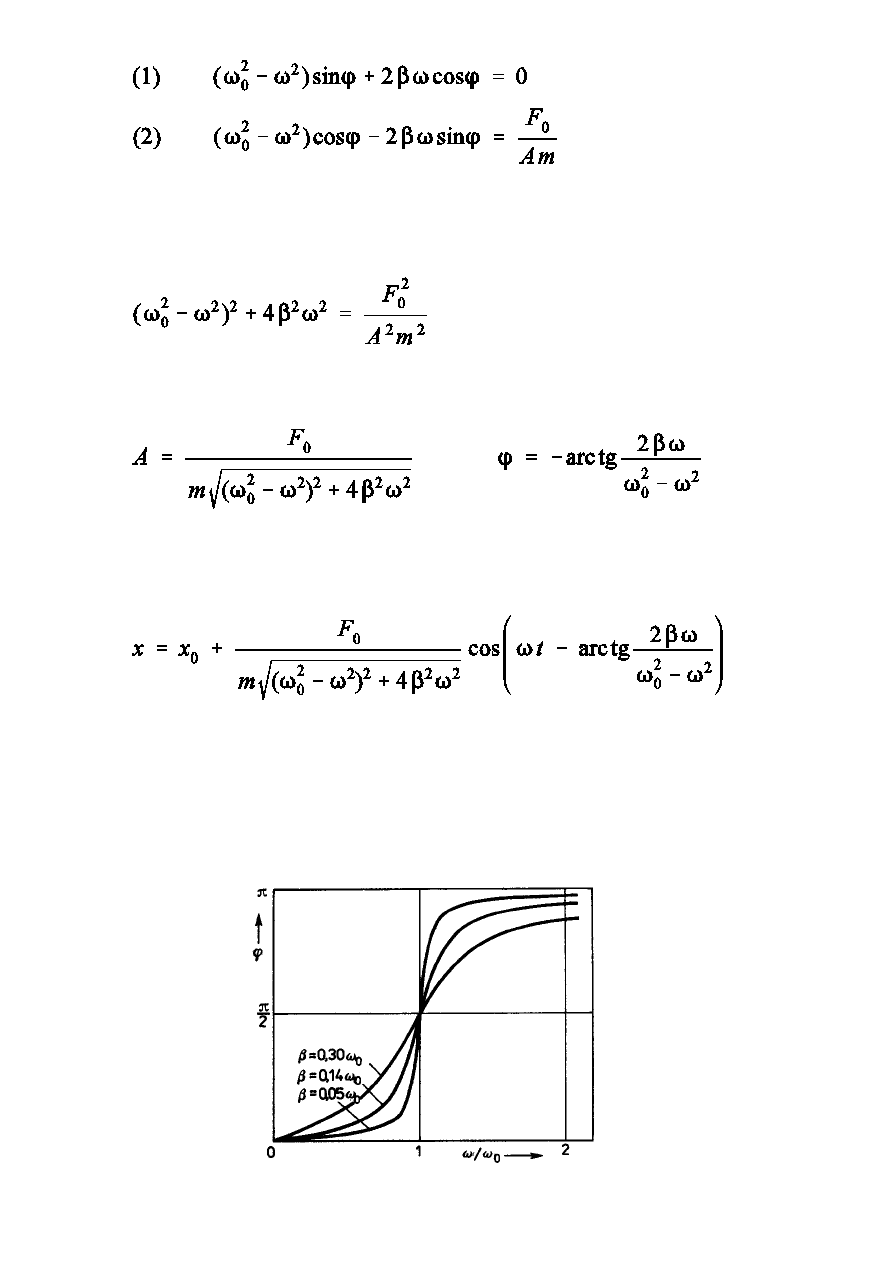
Wnioski:
a)

drgania wymuszone maj cz“stoу si»y wymuszajcej, ale s przesuni“te
w fazie

Drgania 19

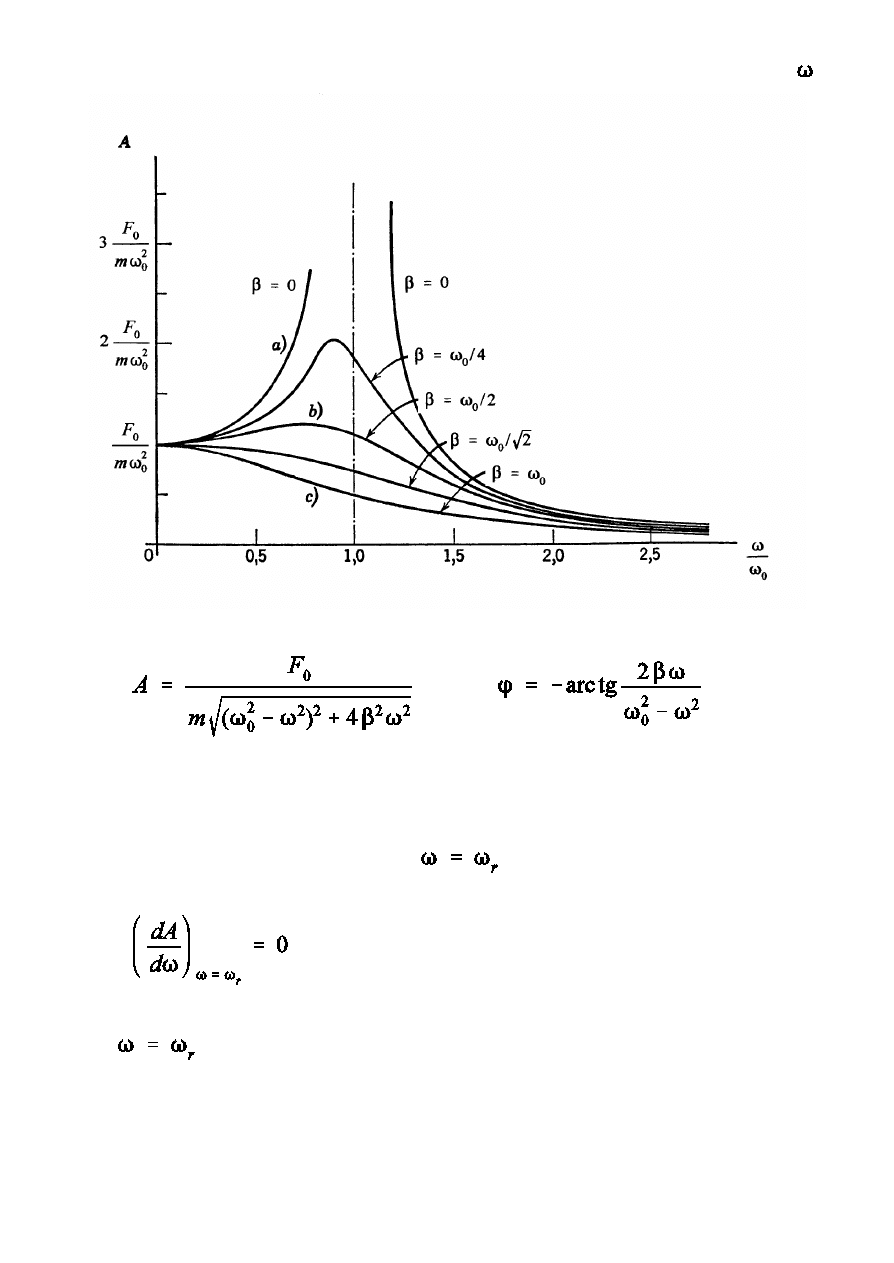
a)

amplituda drga½ wymuszonych jest funkcj cz“stoÑci si»y wymuszajcej 

c)

amplituda ma maksimum dla 

. 

Dla 

 pochodna pierwiastka w mianowniku amplitudy musi byƒ równa

zeru

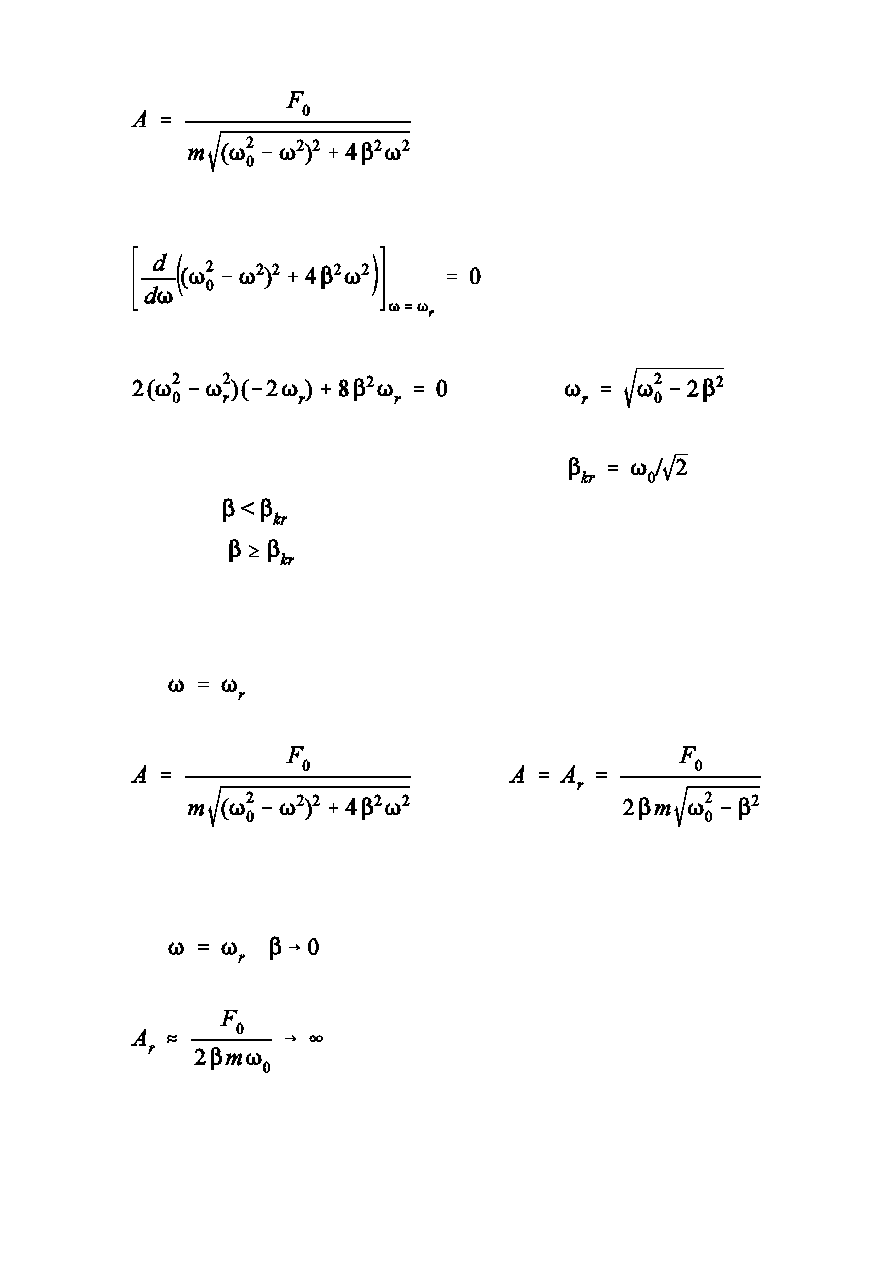
Drgania 20

wartoу krytyczna wspó»czynnika t»umienia  

dla 

jest maksimum na krzywej rezonansowej

dla  

brak maksimum na krzywej rezonansowej

d)

dla 

 

6

e)

dla 

 i 

(niebezpiecze½stwo katastrofy rezonansowej dla ma»ych wspó»czynników
t»umienia)

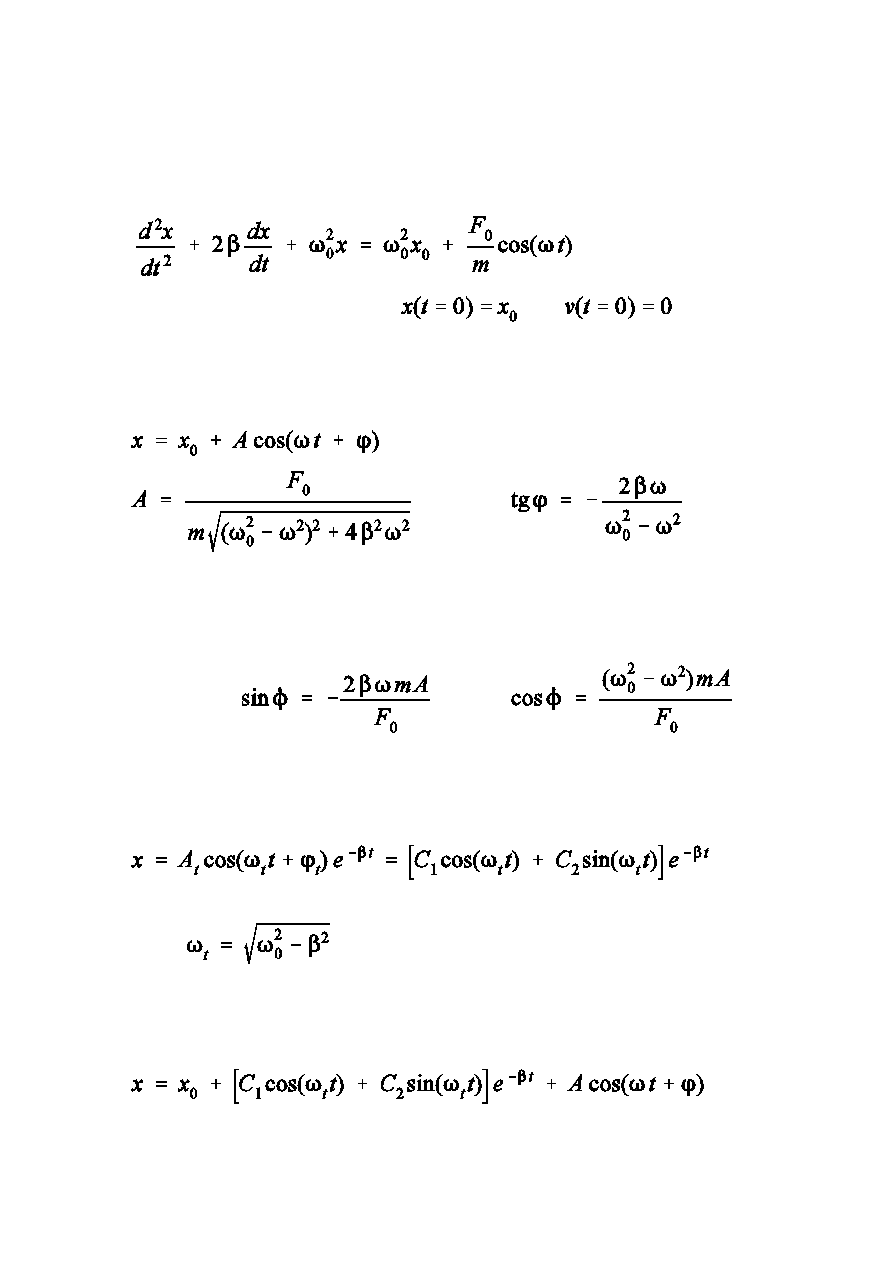
Drgania 21

STANY NIEUSTALONE UKºADÓW DRGAJ€CYCH

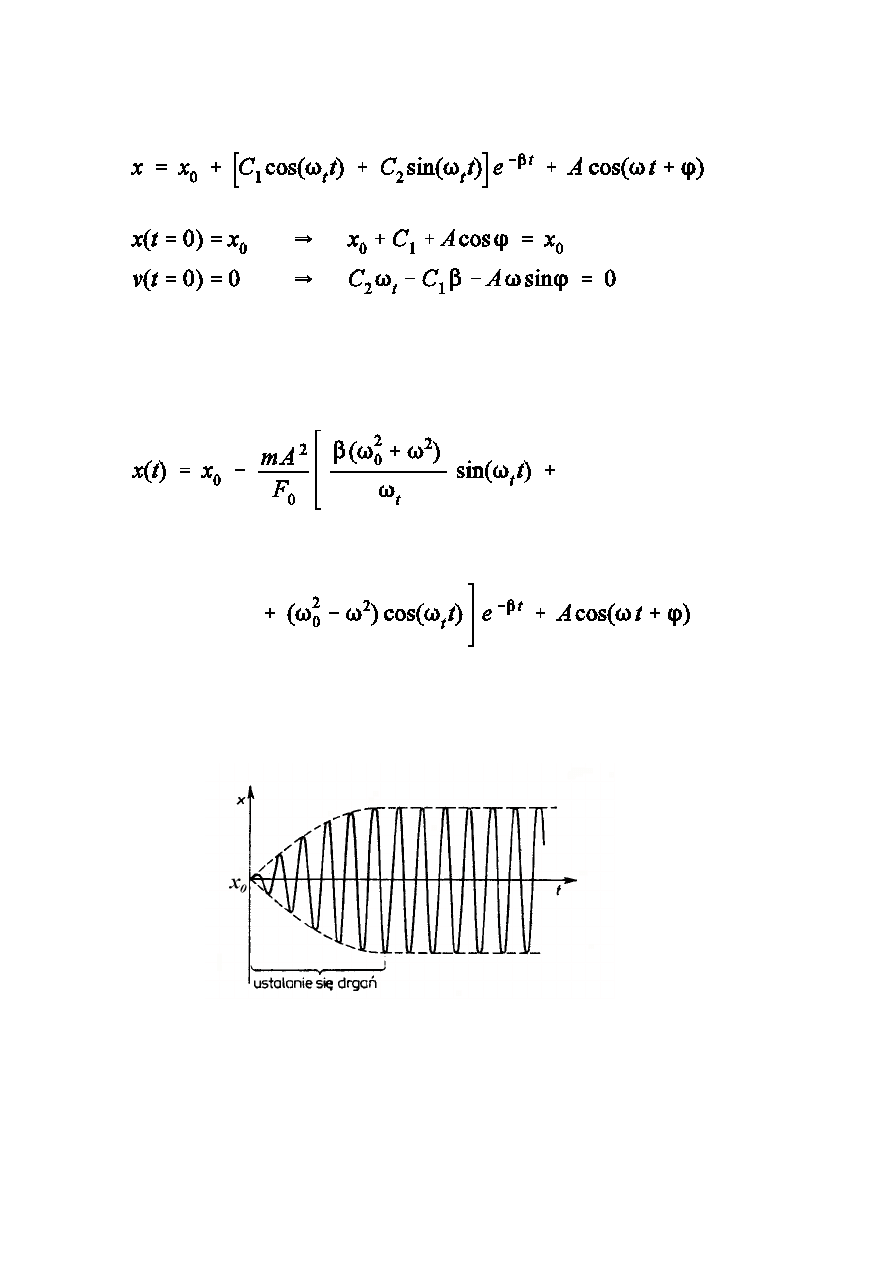
Przyk»ad pe»nego rozwizania równania ruchu dla przypadku drga½
wymuszonych podlegajcych t»umieniu

Warunki pocztkowe: 

,

Rozwizanie szczególne  równania niejednorodnego

Moóna równieó pokazaƒ, óe

Rozwizanie ogólne równania jednorodnego

Pe»ne rozwizanie

sta»e C

1

 i C

2

 moóna wyznaczyƒ korzystajc z warunków pocztkowych

Drgania 22

OkreÑlenie sta»ych C

1

 i C

2