M. Nowak, Materia ly do wyk ladu z logiki na kierunkach humanistycznych

Poj¸

ecie znaku

Definicja znaku Ch. S. Peirce’a:

Znak jest to co´

s, co komu´

s zast¸

epuje co´

s innego pod pewnym wzgl¸

edem lub

w pewien spos´

ob.

Owo “co´

s innego”, czyli to, co jest zast¸

epowane przez znak, nazywane jest

przedmiotem odniesienia dla tego znaku lub przedmiotem, do kt´

orego znak si¸

e

odnosi.

Znaki dzieli si¸

e m.in.

na naturalne i konwencjonalne.

Wed lug jednego

z kryteri´

ow podzia lu, znaki naturalne to te, kt´

ore nie s¸

a wytworem ludzkiej

cywilizacji; konwencjonalne znaki – to te, kt´

ore nie s¸

a naturalne.

Wed lug

drugiego kryterium podzia lu, znak naturalny to taki znak, i˙z mi¸

edzy nim a

jego przedmiotem odniesienia wyst¸

epuje naturalny zwi¸

azek, tzn. nie ustalony

na mocy konwencji. Znak konwencjonalny to znak, kt´

orego zwi¸

azek z przed-

miotem odniesienia ustalony jest na podstawie jakiej´

s umowy (niekoniecznie

spisanej czy u´

swiadamianej). Na przyk lad, b´

ol po prawej dolnej stronie brzucha

jest, wed lug pierwszego jak i drugiego kryterium znakiem naturalnym (objawem,
symptomem) zapalenia wyrostka robaczkowego. Wyra˙zenie “kot” jest wed lug
obu kryteri´

ow znakiem konwencjonalnym.

Znaki konwencjonalne zwane s¸

a symbolami.

Definicja znaczenia znaku K. Ajdukiewicza.

Znaczenie znaku to, wed lug K. Ajdukiewicza, spos´

ob rozumienia znaku,

zale˙zny od m.in. nast¸

epuj¸

acych czynnik´

ow:

(1) typu przedmiot´

ow odniesienia dla znaku,

(2) sposobu kojarzenia przedmiot´

ow odniesienia ze znakiem,

(3) nastawienia uczuciowego do przedmiot´

ow odniesienia.

Dysponuj¸

ac poj¸

eciem znaku mo˙zna definiowa´

c specjalne systemy znak´

ow

jakimi s¸

a j¸

ezyki.

Poj¸

ecie j¸

ezyka

J¸

ezyk wed lug lingwistyki matematycznej:

Przez j¸

ezyk o s lowniku Σ rozumiemy dowolny niepusty zbi´

or sko´

nczonych

ci¸

ag´

ow symboli z Σ. Dowolny ci¸

ag symboli nale˙z¸

acy do j¸

ezyka nazywamy wyra-

˙zeniem tego j¸

ezyka.

S lownik jest to dowolny niepusty zbi´

or symboli.

J¸

ezyk polski jest pewnym zbiorem sko´

nczonych ci¸

ag´

ow symboli. Symbolem

jest tu pojedy´

nczy wyraz lub znak interpunkcyjny, za´

s s lownikiem – zbi´

or wszys-

tkich wyraz´

ow oraz znak´

ow interpunkcyjnych.

1

Kategorie syntaktyczne w j¸

ezyku naturalnym (etnicznym)

W literaturze istnieje precyzyjna, lecz ”nieoperacyjna” (tzn. niestosowalna

w pewnych przypadkach) definicja kategorii (typu syntaktycznego) wedug K.
Ajdukiewicza:

Definicja kategorii syntaktycznej

M´

owimy, ˙ze wyra˙zenia A i B danego j¸

ezyka nale˙z¸

a do tej samej kategorii syn-

taktycznej (lub s¸

a tego samego typu syntaktycznego), gdy z dowolnego wyra˙zenia

W (A), kt´

orego w la´

sciwym sk ladnikiem jest A, po zamianie wyra˙zenia A na

wyra˙zenie B, otrzymujemy ci¸

ag symboli W (B) b¸

ed¸

acy wyra˙zeniem tego j¸

ezyka.

Przyk lad. Wyra˙zenia j¸

ezyka polskiego: “lub”, “cz lowiek” nie s¸

a tego samego

typu. Np. wyra˙zenie W (cz lowiek) postaci: “Jan Kowalski jest cz lowiekiem”
staje si¸

e po zamianie wyra˙zenia “cz lowiek” na wyra˙zenie “lub” ci¸

agiem W (lub):

“Jan Kowalski jest lub”, kt´

ory nie jest wyra˙zeniem j¸

ezyka polskiego.

Definicja kategorii syntaktycznej pozwala, jak wida´

c, na ustalenie, ˙ze dane

dwa wyra˙zenia nie nale˙z¸

a do tej samej kategorii. Nie pozwala jednak na ustale-

nie, czy dwa wyra˙zenia nale˙z¸

a do tej sanej kategorii, w przypadku gdy pos luguj¸

ac

si¸

e wielokrotnie t¸

a definicj¸

a, nie wykazujemy, ˙ze nie nale˙z¸

a do tej samej kategorii.

W j¸

ezyku etnicznym wyr´

o˙znia si¸

e dwie podstawowe kategorie syntaktyczne:

nazwy i zdania oraz kategorie pochodne: funktorowe i operatorowe.

Nazwy

Z powodu nieoperacyjno´

sci definicji typu syntaktycznego wprowadza si¸

e,

niezale˙znie od niej, definicj¸

e typu wyra˙ze´

n zwanych nazwami.

Definicje nazwy, desygnatu nazwy, jej zakresu i tre´

sci

Nazwa jest w to wyra˙zenie mog¸

ace pe lni´

c funkcj¸

e podmiotu lub orzecznika

w zdaniu podmiotowo-orzecznikowym.

Desygnat nazwy jest to przedmiot, do kt´

orego nazwa ta si¸

e odnosi lub inaczej

– przedmiot oznaczany przez nazw¸

e.

Zakres nazwy to zbi´

or wszystkich jej desygnat´

ow.

Tre´

s´

c nazwy to jakikolwiek zbi´

or cech desygnat´

ow tej nazwy taki, ˙ze wszys-

tkie cechy z tego zbioru przys luguj¸

a ka˙zdemu desygnatowi nazwy oraz je˙zeli

wszystkie cechy z tego zbioru przys luguj¸

a jakiemu´

s obiektowi, to obiekt ten jest

desygnatem tej nazwy.

Wielko´

s´

c zakresu nazwy jest odwrotnie proporcjonalna do wielko´

sci tre´

sci

nazwy, w takim oto sensie: je˙zeli tre´

s´

c jednej nazwy jest podzbiorem tre´

sci

drugiej, to zakres drugiej nazwy jest podzbiorem zakresu tej pierwszej.

Bowiem, przy za lo˙zeniu inkluzji tre´

sci pierwszej nazwy w tre´

sci drugiej nazwy,

dowolnemu desygnatowi drugiej nazwy przys luguj¸

a wszystkie cechy nale˙z¸

ace do

tre´

sci pierwszej nazwy, zatem z definicji poj¸

ecia tre´

sci, musi on by´

c desygnatem

pierwszej nazwy; dowodzi to inkluzji zakresu drugiej nazwy w zakresie pierwszej.

2

Ze wzgl¸

edu na ilo´

s´

c desygnat´

ow, nazwy dzielimy na og´

olne, jednostkowe,

puste. Nazwa maj¸

aca wi¸

ecej ni˙z jeden desygnat nazywana jest og´

oln¸

a, ta, kt´

ora

ma dok ladnie jeden desygnat nazywana jest jednostkow¸

a, wreszcie ta, kt´

ora nie

ma desygnat´

ow – nazywana jest pust¸

a.

Ze wzgl¸

edu na wielko´

s´

c tre´

sci, nazwy dzielimy na indywidualne – maj¸

ace

tre´

s´

c pust¸

a, oraz generalne – kt´

orych tre´

s´

c jest niepustym zbiorem. Np. nazwa

“Wis la” jest w ka˙zdym ze swoich znacze´

n nazw¸

a indywidualn¸

a, tymczasem

nazwa “najd lu˙zsza rzeka w Polsce” jest generalna, cho´

c r´

ownie˙z jak “Wis la”

– jednostkowa.

Logika nazw

S lownik j¸

ezyka logiki nazw zawiera nast¸

epuj¸

ace symbole:

S, M, P, S

1

, M

1

, P

1

, S

2

, M

2

, P

2

, . . . - zmienne nazwowe

a, e, i, o - funktory zdaniotw´

orcze od dw´

och argument´

ow nazwowych

J¸

ezyk:

Ka˙zdy ci¸

ag symboli ze s lownika postaci: XuY , gdzie X, Y s¸

a zmiennymi

nazwowymi, a u jest jednym z czterech funktor´

ow ze s lownika, jest formu l¸

a

j¸

ezyka logiki nazw i tylko takie ci¸

agi s¸

a formu lami tego j¸

ezyka.

Zmienne nazwowe reprezentuj¸

a dowolne nazwy og´

olne z j¸

ezyka etnicznego.

Formu la: SaP , reprezentuje funkcj¸

e zdaniow¸

a: ka˙zde S jest P, b¸

ed¸

ac¸

a sche-

matem tzw. zdania og´

olnotwierdz¸

acego (np. ”ka˙zda ryba jest drapie˙znikiem”)

Formu la: SeP , reprezentuje funkcj¸

e zdaniow¸

a: ˙zadne

S

nie

jest

P,

b¸

ed¸

ac¸

a schematem tzw. zdania og´

olnoprzecz¸

acego (np. ”˙zadna ryba nie jest

drapie˙znikiem”)

Formu la: SiP , reprezentuje funkcj¸

e zdaniow¸

a: niekt´

ore S s¸

a P, b¸

ed¸

ac¸

a

schematem tzw. zdania szczeg´

o lowotwierdz¸

acego (np. ”niekt´

ore ryby s¸

a drapie˙z-

nikami”)

Formu la: SoP , reprezentuje funkcj¸

e zdaniow¸

a: niektre

S

nie

s¸

a

P ,

b¸

ed¸

ac¸

a schematem tzw.

zdania szczeg´

o lowoprzecz¸

acego (np.

”niekt´

ore ryby

nie s¸

a drapie˙znikami”).

Semantyka:

Niech V b¸

edzie przyporz¸

adkowaniem ka˙zdej zmiennej nazwowej X dok ladnie

jednego, lecz dowolnego zbioru wi¸

ecej ni˙z 1-elementowego, oznaczanego tu w

postaci V (X). (Domy´

slnie, je´

sli zmienna X reprezentuje dan¸

a nazw¸

e, to V (X)

jest zakresem tej nazwy.) Przyporz¸

adkowanie V nazwiemy warto´

sciowaniem.

Aby okre´

sli´

c spos´

ob przyporz¸

adkowania warto´

sci logicznych prawdy lub fa l-

szu dowolnej formule j¸

ezyka logiki nazw, zdefiniujmy dwa znane stosunki mi¸

edzy

zbiorami:

3

Zbi´

or A jest podzbiorem zbioru B (A ⊆ B), gdy dla dowolnego obiektu b,

je˙zeli b jest elementem zbioru A (b ∈ A), to b jest elementem zbioru B (b ∈ B).

Zbiory A, B s¸

a roz l¸

aczne, gdy nie istnieje obiekt b taki, ˙ze b ∈ A oraz b ∈ B,

czyli, gdy zbiory te nie maj¸

a wsp´

olnego elementu.

Dla dowolnego warto´

sciowania V , dla dowolnych zmiennych nazwowych X, Y ,

powiemy, ˙ze

formu la XaY jest prawdziwa przy warto´

sciowaniu V , gdy V (X) jest pod-

zbiorem zbioru V (Y ),

formu la XeY jest prawdziwa przy warto´

sciowaniu V , gdy zbiory V (X), V (Y )

s¸

a roz l¸

aczne,

formu la XiY jest prawdziwa przy warto´

sciowaniu V , gdy zbiory V (X), V (Y )

nie s¸

a roz l¸

aczne,

formu la XoY jest prawdziwa przy warto´

sciowaniu V , gdy V (X) nie jest

podzbiorem zbioru V (Y ).

Zauwa˙zmy, ˙ze zachodzi prosty zwi¸

azek:

dla dowolnego warto´

sciowania V , XaY jest prawdziwa przy V

wtw XoY

jest fa lszywa (tzn. nie jest prawdziwa) przy V ,

XeY jest prawdziwa przy V

wtw XiY jest fa lszywa przy V .

Centralnym poj¸

eciem jest wynikanie logiczne:

Definicja wynikania logicznego

M´

owimy, ˙ze ze zbioru formu l Z wynika logicznie formu la α (Z |= α), gdy dla

ka˙zdego warto´

sciowania V , przy kt´

orym wszystkie formu ly z Z s¸

a prawdziwe, α

jest r´

ownie˙z prawdziwa.

Przyk lady. (1) Formu la SaP wynika logicznie ze zbioru formu l {SaM, M aP }.
Aby tego dowie´

s´

c, zak ladamy, ˙ze przy jakim´

s, dowolnie wybranym warto´

sciowa-

niu V prawdziwe s¸

a formu ly SaM, M aP , co zapisujemy w postaci pierwszych

wyra˙ze´

n dowodu:

rozwa˙zmy dowolne warto´

sciowanie V ,

(1) SaM jest prawdziwa przy V (za lo˙zenie),
(2) M aP jest prawdziwa przy V (za lo˙zenie).

Po tych za lo˙zeniach celem dowodu jest wykazanie, i˙z
(cel1) formu la SaP jest prawdziwa przy warto´

sciowaniu V .

Korzystaj¸

ac z warunku prawdziwo´

sci dla formu ly og´

olnotwierdz¸

acej specy-

fikujemy ´

ow cel w postaci:

(cel2) V (S) ⊆ V (P ).
Aby go osi¸

agn¸

a´

c stosujemy definicj¸

e stosunku bycia podzbiorem, zatem wyka-

zujemy, ˙ze

(cel3) dla dowolnego obiektu b, je˙zeli b ∈ V (S), to b ∈ V (P ).

4

Aby go zrealizowa´

c za l´

o˙zmy, ˙ze dowolnie wybrany obiekt b jest elementem

zbioru V (S):

rozwa˙zmy dowolny obiekt b,
(3) b ∈ V (S) (za lo˙zenie).

Teraz celem dowodu staje si¸

e wykazanie, ˙ze

(cel4) b ∈ V (P ).
Dalsza specyfikacja celw dowodu nie nast¸

api, bowiem bycie elementem (∈)

zbioru jest terminem pierwotnym, tzn. nie istnieje jego definicja wyra´

zna, z

kt´

orej mo˙zna by korzysta´

c, aby specyfikowa´

c dalej cel. Dlatego aby osi¸

agn¸

a´

c

(cel4) korzystamy z informacji (1), (2), (3) w spos´

ob nast¸

epuj¸

acy. Na podstawie

warunku prawdziwo´

sci dla formu ly og´

olnotwierdz¸

acej, V (S) jest podzbiorem

V (M ) oraz V (M ) jest podzbiorem zbioru V (P ):

(4) V (S) ⊆ V (M ) z (1),
(5) V (M ) ⊆ V (P ) z (2)

Korzystaj¸

ac z definicji bycia podzbiorem, wyra˙zenia (4), (5) zamieniamy na

(6) dla dowolnego obiektu x, je˙zeli x ∈ V (S), to x ∈ V (M ) z (4),
(7) dla dowolnego obiektu x, je˙zeli x ∈ V (M ), to x ∈ V (P ) z (5).

Ostatecznie otrzymujemy:

(8) b ∈ V (M ) z (3), (6),
(9) b ∈ V (P ) z (8), (7),

co ko´

nczy dow´

od.

(2) Wyka˙zemy, ˙ze {M aP, M aS} |= SiP .

rozwa˙zmy dowolne warto´

sciowanie V ,

(1) M aP jest prawdziwa przy V (za lo˙zenie),
(2) M aS jest prawdziwa przy V (za lo˙zenie),
(3) V (M ) ⊆ V (P ) z (1),
(4) V (M ) ⊆ V (S) z (2),
(5) V (M ) jest niepustym zbiorem - z warunku semantycznego, wed lug kt´

orego

zbi´

or V (X) jest wi¸

ecej ni˙z 1-elementowy,

istnieje obiekt b taki, ˙ze
(6) b ∈ V (M ) z (5),
(7) b ∈ V (P ) z (3), (6),
(8) b ∈ V (S) z (4), (6),
(9) zbiory V (S), V (P ) nie s¸

a roz l¸

aczne - z (8),

SiP jest prawdziwa przy V - z (9).

(3) Wykazujemy, ˙ze formu la SeP wynika logicznie ze zbioru formu l {SaM, M eP },
metod¸

a nie wprost.

5

Dowie´

s´

c danego zdania (twierdzenia) nie wprost, to za lo˙zy´

c, ˙ze jest ono

fa lszywe, czyli za lo˙zy´

c, ˙ze zaprzeczenie tego zdania jest prawdziwe i na tej

podstawie, stosuj¸

ac definicje wyra˙ze´

n wyst¸

epuj¸

acych w zdaniu, jak r´

ownie˙z

by´

c mo˙ze znane twierdzenia, doj´

s´

c do absurdu. Polega on na wyprowadzeniu

(wywnioskowaniu) dowolnej pary zda´

n, w kt´

orej jedno zdanie jest zaprzeczeniem

drugiego.

(1) {SaM, M eP } 6|= SeP (za lo˙zenie)
istnieje warto´

sciowanie V takie, ˙ze

(2) SaM jest prawdziwa przy V z (1),
(3) M eP jest prawdziwa przy V z (1),
(4) SeP jest fa lszywa przy V z (1),
(5) V (S) ⊆ V (M ) z (2),
(6) V (M ), V (P ) s¸

a roz l¸

aczne - z (3),

(7) zbiory V (S), V (P ) nie s¸

a roz l¸

aczne - z (4),

istnieje obiekt b taki, ˙ze
(8) b ∈ V (S) z (7),
(9) b ∈ V (P ) z (7),
(10) b ∈ V (M ) z (8), (5),
(11) zbiory V (M ), V (P ) nie s¸

a roz l¸

aczne z (9), (10),

absurd (6), (11).

(4) Aby wykaza´

c, ˙ze {M aP, SoM } 6|= SoP nale˙zy wskaza´

c takie warto´

sciowanie

V , przy ktrym formu ly M aP, SoM s¸

a prawdziwe, za´

s formu la SoP jest fa lszywa.

Na przyk lad, V (S) = zbi´

or miast zamieszka lych przez co najmniej 1 mln miesz-

ka´

nc´

ow, V (M ) = zbi´

or stolic kraj´

ow, V (P ) = zbi´

or miast.

Definicja prawa logicznego (logicznej prawdziwo´

sci lub tautologii)

Formu la α jest prawem logicznym (jest logicznie prawdziwa lub jest tau-

tologi¸

a) logiki nazw, gdy α jest prawdziwa przy ka˙zdym warto´

sciowaniu V .

Przyk lad. Formu ly SaS, SiS s¸

a logicznie prawdziwe. Dow´

od pierwszego faktu

przebiega nast¸

epuj¸

aco:

rozwa˙zmy dwolne warto´

sciowanie V ,

(1) V (S) ⊆ V (S) (na podstawie latwo dowodliwego z definicji bycia podzbio-

rem, twierdzenia: A ⊆ A),

(2) SaS jest prawdziwa przy V z (1).

Definicja sprzecznego zbioru formu l

Zbi´

or formu l Z nazywamy niesprzecznym wed lug logiki nazw, gdy istnieje

warto´

sciowanie V , przy kt´

orym ka˙zda formu la ze zbioru Z jest prawdziwa. Zbi´

or

formu l jest sprzeczny, gdy nie jest niesprzeczny.

Przyk lady (1) Zbiory formu l {SaP, SoP }, {SeP, SiP }, {SoS} s¸

a sprzeczne.

Dow´

od nie wprost pierwszego faktu przebiega nast¸

epuj¸

aco:

(1) zbi´

or formu l {SaP, SoP } jest niesprzeczny (za lo˙zenie),

istnieje warto´

sciowanie V takie, ˙ze

(2) formu la SaP jest prawdziwa przy V z (1),

6

(3) formu la SoP jest prawdziwa przy V z (1),
(4) V (S) ⊆ V (P ) z (2),
(5) V (S) 6⊆ V (P ) z (3),
absurd (4),(5).

(2) Aby wykaza´

c, ˙ze zbi´

or formu l {SeM, M aP, SiP } jest niesprzeczny, nale˙zy

wskaza´

c takie warto´

sciowanie V , przy kt´

orym wszystkie formu ly z tego zbioru s¸

a

prawdziwe, np. V (S) = zbi´

or kr´

ow, V (M ) = zbi´

or koni, V (P ) = zbi´

or zwierz¸

at

ro´

slino˙zernych.

Zdania

Nie ka˙zde zdanie z j¸

ezyka etnicznego zaliczane jest do kategorii zda´

n. Nale˙z¸

a

do niej wy l¸

acznie zdania oznajmuj¸

ace, prawdziwe b¸

ad´

z fa lszywe. Kategori¸

e zda´

n

dzielimy na zdania proste i z lo˙zone, lecz kryterium tego podzia lu nie jest liczba
wyst¸

epuj¸

acych w zdaniu orzecze´

n (jak w gramatyce), ale wyst¸

epowanie tzw.

sp´

ojnika (funktora zdaniotw´

orczego od argument´

ow zdaniowych). Zdanie, w

kt´

orym nie wyst¸

epuje sp´

ojnik nazywamy prostym, zdanie, kt´

ore nie jest proste,

nazywamy z lo˙zonym.

Najwa˙zniejszy typ zda´

n prostych stanowi¸

a zdania podmiotowo-orzecznikowe,

tzn. zdania postaci: a jest P , gdzie a jest podmiotem, za´

s P – orzecznikiem,

np. “Jan Kowalski jest studentem”.

Wsr´

od zda´

n z lo˙zonych wyr´

o˙znia si¸

e m.in.

• zdania negacyjne, postaci: nieprawda, ˙ze A,
• koniunkcyjne: A i B,
• alternatywne: A lub B,
• implikacyjne: je˙zeli A, to B,
• r´

ownowa˙zno´

sciowe: A wtedy i tylko wtedy, gdy B,

gdzie A, B s¸

a dowolnymi zdaniami.

Funktory

Mamy nie jedn¸

a, lecz wiele tzw. kategorii funktorowych, do ktrych nale˙z¸

a

funktory

Definicja funktora

Funktor jest to wyra˙zenie s lu˙z¸

ace do tworzenia wyra˙ze´

n z lo˙zonych z mniej

z lo˙zonych.

Wyra˙zenie z lo˙zone uzyskujemy z wyra˙ze´

n mniej z lo˙zonych przez do l¸

aczenie

do nich funktora.

Wyra˙zenia, kt´

ore do l¸

aczamy do funktora nazywamy jego

argumentami.

Aby wygodnie przedstawi´

c kategorie syntaktyczne funktorowe, przyporz¸

ad-

kowuje si¸

e ka˙zdej kategorii syntaktycznej odpowiedni wska´

znik. Kategorii nazw

przyporz¸

adkowujemy wska´

znik: n, za´

s kategorii zda´

n – z.

W´

owczas ka˙zdej kategorii funktorowej przyporz¸

adkowany jest wska´

znik pos-

taci u lamka, w liczniku kt´

orego wyst¸

epuje wska´

znik kategorii wyra˙zenia z lo˙zo-

7

nego powsta lego przez do l¸

aczenie do funktora argument´

ow, za´

s w mianowni-

ku wyst¸

epuj¸

a wska´

zniki (odzielone przecinkami) kategorii, do kt´

orych nale˙z¸

a

argumenty.

Najwa˙zniejsze kategorie funktorowe:

n
n

– funktory nazwotw´

orcze od jednego argumentu nazwowego, czyli wy-

ra˙zenia, kt´

ore do l¸

aczone do jednej nazwy tworz¸

a now¸

a nazw¸

e, np. “wysoki”,

“ ladny”, “−”,

n

n,n

– funktory nazwotw´

orcze od dw´

och argument´

ow nazwowych, czyli wy-

ra˙zenia, kt´

ore do l¸

aczone do dw´

och nazw tworz¸

a now¸

a nazw¸

e, np. “nad”, “pod”,

“+”,

z

n

– funktory zdaniotw´

orcze od jednego argumentu nazwowego, czyli wy-

ra˙zenia, kt´

ore do l¸

aczone do jednej nazwy tworz¸

a zdanie, np. “´

swieci”, “jest

cz lowiekiem”,

z

n,n

– funktory zdaniotw´

orcze od dw´

och argument´

ow nazwowych, czyli wy-

ra˙zenia, kt´

ore do l¸

aczone do dw´

och nazw tworz¸

a zdanie, np. “kocha”, “lubi”

“≤”,

z
z

– funktory zdaniotw´

orcze od jednego argumentu zdaniowego, czyli wyra-

˙zenia, kt´

ore do l¸

aczone do jednego zdania tworz¸

a nowe zdanie, np. “nieprawda,

˙ze”, “jest konieczne, ˙ze”,

z

z,z

– funktory zdaniotw´

orcze od dw´

och argument´

ow zdaniowych, czyli wy-

ra˙zenia, kt´

ore do l¸

aczone do dw´

och zda´

n tworz¸

a nowe zdanie, np. “i”, “lub”,

“je˙zeli,to”, “wtedy i tylko wtedy, gdy”.

Definicje predykatu i sp´

ojnika

Funktory zdaniotw´

orcze od jednego lub wi¸

ekszej ilo´

sci argument´

ow naz-

wowych nazywamy predykatami.

Funktory zdaniotw´

orcze od jednego lub wi¸

ekszej ilo´

sci argument´

ow zda-

niowych nazywamy sp´

ojnikami.

Istotn¸

a rol¸

e w logice klasycznej odgrywaj¸

a tzw.

sp´

ojniki ekstensjonalne

(prawdziwo´

sciowe). Aby je przedstawi´

c, dobrze jest wystartowa´

c od koncepcji

znaczenia wyra˙zenia autorstwa Gottloba Fregego.

Znaczenie wyra ˙zenia wed lug Gottloba Fregego

G. Frege (1848-1925) - niemiecki matematyk i filozof, odkrywca aksjomaty-

cznej wersji klasycznej logiki zdaniowej; autor semantycznych rozstrzygni¸

e´

c usta-

laj¸

ach typy odniesie´

n i sens´

ow dla wyra˙ze´

n nasyconych, czyli nazw i zda´

n oraz

nienasyconych, czyli funktor´

ow; tw´

orca koncepcji znaczenia kwantyfikator´

ow

jako specjalnych w lasno´

sci przys luguj¸

acych innym w lasno´

sciom; zwr´

oci l uwag¸

e

na pewne zjawisko j¸

ezykowe, zwane p´

o´

zniej intensjonalno´

sci¸

a; tw´

orca tzw. logi-

cyzmu, czyli pogl¸

adu, wed lug kt´

orego poj¸

ecia matematyczne s¸

a sprowadzalne do

(definiowalne przez) poj¸

e´

c logiki, a w rezultacie, i˙z twierdzenia matematyczne

8

s¸

a wyprowadzalne z zasad logiki.

Definicja znaczenia, denotacji i sensu wyra˙zenia wed lug G. Fregego

Znaczenie dowolnego wyra˙zenia A jest okre´

slone przez dwa komponenty:

denotacj¸

e tego wyra˙zenia: D(A) oraz sens tego wyra˙zenia: S(A).

D(A) jest obiektem, do kt´

orego wyra˙zenie A si¸

e odnosi, tzn. jest tym bytem,

dla kt´

orego A jest znakiem.

S(A) jest sposobem, w jaki denotacja wyra˙zenia A jest ustalana. Znajomo´

s´

c

sensu wyra˙zenia jest niezb¸

ednym, cho´

c na og´

o l niewystarczaj¸

acym warunkiem

ustalenia denotacji tego wyra˙zenia.

Gdy wyra˙zenie A jest nazw¸

a, denotacja D(A) jest jej desygnatem b¸

ad´

z za-

kresem. (Frege przez nazw¸

e rozumia l takie wyra˙zenie, kt´

ore we wsp´

o lczesnej

literaturze polskiej nazywane jest ”nazw¸

a jednostkow¸

a” lub ”nazw¸

a pust¸

a o in-

tencji jednostkowej”.) Sens S(A) zazwyczaj jest uto˙zsamiany z tre´

sci¸

a nazwy

A.

Gdy wyra˙zenie A jest zdaniem, denotacja D(A) jest warto´

sci¸

a logiczn¸

a tego

zdania, czyli Prawd¸

a (1), b¸

ad´

z Fa lszem (0). Wed lug Fregego zdania oznajmuj¸

ace

odnosz¸

a si¸

e do Prawdy b¸

ad´

z Fa lszu. Sens S(A) zdania A jest my´

sl¸

a w zdaniu

A wyra˙zon¸

a, zwan¸

a inaczej s¸

adem w sensie logicznym.

Zasada kompozycyjno´

sci denotacji G. Fregego

Denotacja wyra˙zenia z lo˙zonego jest jednoznacznie okre´

slona przez denotacje

wyra˙ze´

n sk ladowych tego wyra˙zenia.

Innymi s lowy, je˙zeli W (A) jest wyra˙zeniem z lo˙zonym, w kt´

orym wyra˙zenie A

jest sk ladnikiem oraz B jest wyra˙zeniem o tej samej denotacji co wyra˙zenie A, to
wyra˙zenie W (B), powsta le przez zast¸

apienie wyra˙zenia A w W (A) wyra˙zeniem

B, ma t¸

e sam¸

a denotacj¸

e co wyra˙zenie W (A).

Przyk lady (1) W (A) := Warszawa jest stolic¸

a Polski

D(W (A)) = 1
A := Warszawa
B := najwi¸

eksze miasto w Polsce

D(A) = D(B)
W (B) := Najwi¸

eksze miasto w Polsce jest stolic¸

a Polski,

D(W (B)) = 1
D(W

1

(A

1

)) = D(W

1

(B

1

)).

(2) W

1

(A

1

) := Jest konieczne, ˙ze Warszawa jest stolic¸

a Polski

D(W

1

(A

1

)) = 0

A

1

:= Warszawa jest stolic¸

a Polski

B

1

:= Ka˙zdy kwadrat jest prostok¸

atem

D(A

1

) = D(B

1

) = 1

W

1

(B

1

) := Jest konieczne, ˙ze ka˙zdy kwadrat jest prostok¸

atem

D(W

1

(B

1

)) = 1

D(W

1

(A

1

)) 6= D(W

1

(B

1

))

9

Definicja funktora ekstensjonalnego i intensjonalnego

Funktor n-argumentowy F nazywamy ekstensjonalnym, gdy dla dowolnych

jego argument´

ow A

1

, A

2

, . . . , A

n

, denotacja D(F (A

1

, A

2

, . . . , A

n

)) wyra˙zenia

z lo˙zonego F (A

1

, A

2

, . . . , A

n

), powsta lego przez do l¸

aczenie funktora F do ar-

gument´

ow A

1

, A

2

, . . . , A

n

, jest jednoznacznie okre´

slona przez denotacje D(A

1

),

D(A

2

), . . . , D(A

n

) tych argument´

ow.

Funktor nazywamy intensjonalnym, gdy nie jest on ekstensjonalny.

Zatem funktor n-argumentowy F jest intensjonalny, gdy istniej¸

a jego argu-

menty A

1

, A

2

, . . . , A

n

oraz argument B tego samego typu co argument A

i

dla

pewnego i = 1, 2, . . . , n takie, ˙ze D(B) = D(A

i

) oraz D(F (A

1

, A

2

, . . . , A

i

, . . . ,

A

n

)) 6= D(F (A

1

, A

2

, . . . , B, . . . , A

n

))

Przyk lady. Funktor “dawny” typu

n
n

jest intensjonalny:

F := dawny
A := senator Rzeczypospolitej
F (A) := dawny senator Rzeczypospolitej
B := kolega marsza lka Bogdana Borusewicza, przy czym D(A) = D(B)
F (B) := dawny kolega marsza lka Bogdana Borusewicza
D(F (A)) 6= D(F (B))

Funktor “jest konieczne, ˙ze” typu

z
z

jest intensjonalny:

F := jest konieczne, ˙ze
A := Warszawa jest stolic¸

a Polski

F (A) := Jest konieczne, ˙ze Warszawa jest stolic¸

a Polski

B := Ka˙zdy kwadrat jest prostok¸

atem

D(A) = D(B) = 1
F (B) := Jest konieczne, ˙ze ka˙zdy kwadrat jest prostok¸

atem

D(F (A)) 6= D(F (B)).

Z og´

olnej definicji funktora ekstensjonalnego otrzymujemy:

Definicj¸

e sp´

ojnika ekstensjonalnego

Sp´

ojnik n-argumentowy F jest ekstensjonalny, gdy dla dowolnych jego argu-

ment´

ow A

1

, A

2

, . . . , A

n

, warto´

s´

c logiczna zdania F (A

1

, A

2

, . . . , A

n

) jest jednoz-

nacznie okre´

slona przez warto´

sci logiczne argument´

ow A

1

, A

2

, . . . , A

n

.

Najwa˙zniejsze sp´

ojniki ekstensjonalne:

negacja: nieprawda, ˙ze . . . (∼),

koniunkcja: . . . i . . . (∧),

alternatywa: . . . lub . . . (co najmniej jedno z dwojga . . . , . . .) (∨)

implikacja: je˙zeli . . ., to . . . (→)

r´

ownowa˙zno´

s´

c: . . . wtedy i tylko wtedy, gdy . . . (↔)

alternatywa roz l¸

aczna: . . . albo . . . (dok ladnie jedno z dwojga . . . , . . .) (÷)

10

alternatywa Sheffera: co najwy˙zej jedno z dwojga . . . , . . . (/)

binegacja: ani nie . . . , ani nie . . . (\)

Sposoby jednoznacznego wyznaczania warto´

sci logicznej zda´

n, w kt´

orych

funktorami g l´

ownymi s¸

a niekt´

ore wymienione sp´

ojniki, w zale˙zno´

sci od warto´

sci

logicznych argument´

ow tych funktor´

ow, podane s¸

a w postaci nast¸

epuj¸

acych

tabelek:

A

∼ A

0

1

1

0

A

B

A ∧ B

0

0

0

0

1

0

1

0

0

1

1

1

A

B

A ∨ B

0

0

0

0

1

1

1

0

1

1

1

1

A

B

A → B

0

0

1

0

1

1

1

0

0

1

1

1

A

B

A ↔ B

0

0

1

0

1

0

1

0

0

1

1

1

A

B

A/B

0

0

1

0

1

1

1

0

1

1

1

0

A

B

A\B

0

0

1

0

1

0

1

0

0

1

1

0

W dalszym ci¸

agu, warto´

sci logiczne b¸

edziemy przyporz¸

adkowywa´

c formu lom

standardowego j¸

ezyka zdaniowego.

J¸

ezyk klasycznej logiki zdaniowej (standardowy j¸

ezyk zdaniowy)

S lownik jest tu zbiorem nast¸

epuj¸

acych symboli:

zmiennych zdaniowych: p

0

, p

1

, p

2

, . . .,

sp´

ojnik´

ow: ∼, ∧, ∨, →, ↔,

nawias´

ow: (, ) .

Definicja standardowego j¸

ezyka zdaniowego podaje, jakie sko´

nczone ci¸

agi

symboli ze s lownika s¸

a wyra˙zeniami tego j¸

ezyka; wyra˙zenie tego j¸

ezyka nazywane

jest formu l¸

a:

(1) ka˙zda zmienna zdaniowa (traktowana jako 1-wyrazowy ci¸

ag) jest formu l¸

a,

(2) je˙zeli sko´

nczony ci¸

ag symboli α jest formu l¸

a, to ci¸

ag postaci: ∼ α, r´

ownie˙z

jest formu l¸

a,

(3) je˙zeli ci¸

agi α, β s¸

a formu lami, to ci¸

agi postaci: (α ∧ β), (α ∨ β), (α →

β), (α ↔ β), r´

ownie˙z s¸

a formu lami,

11

(4) je˙zeli ci¸

ag α jest formu l¸

a, to α jest b¸

ad´

z zmienn¸

a zdaniow¸

a, b¸

ad´

z ci¸

agiem

symboli uzyskanym z prostszych formu l na postawie zastosowania przynajmniej
jednej z regu l (2), (3).

Przyk lad.

Nast¸

epuj¸

ace ci¸

agi symboli s¸

a formu lami: (((p

0

→ p

2

) ∧ p

0

) →

p

2

), ((p

0

→ (p

2

∧ p

0

)) → p

2

). Zazwyczaj nawiasy zewn¸

etrzne pomijamy. Zatem

powy˙zsze dwie formu ly zapisujemy w postaci: ((p

0

→ p

2

) ∧ p

0

) → p

2

, (p

0

→

(p

2

∧ p

0

)) → p

2

.

Klasyczna logika zdaniowa

Centralnymi poj¸

eciami s¸

a tu wynikanie logiczne, tautologia (prawo logiczne),

sprzeczny zbi´

or formu l .

Definicja warto´

sciowania logicznego

Dowolne przyporz¸

adkowanie ka˙zdej zmiennej zdaniowej p dok ladnie jednej z

dwu warto´

sci logicznych: 0, 1, nazywamy warto´

sciowaniem logicznym.

Dane warto´

sciowanie mo˙zna rozszerzy´

c do przyporz¸

adkowania dok ladnie jed-

nej z dwu warto´

sci logicznych ka˙zdej formule j¸

ezyka zdaniowego, w zale˙zno´

sci od

kszta ltu tej formu ly, post¸

epuj¸

ac wed lug tabelek okre´

slaj¸

acych warto´

s´

c logiczn¸

a

formu ly z lo˙zonej w zale˙zno´

sci od warto´

sci logicznych jej podformu l.

Tak wi¸

ec, formule negacyjnej ∼ α dowolne warto´

sciowanie przyporz¸

adkowuje

warto´

s´

c 1 dok ladnie w´

owczas, gdy przyporz¸

adkowuje ono formule α warto´

s´

c 0.

Formule koniunkcyjnej α ∧ β ka˙zde warto´

sciowanie przyporz¸

adkowuje war-

to´

s´

c 1 dok ladnie w´

owczas, gdy obu formu lom α, β warto´

sciowanie to przyporz¸

ad-

kowuje warto´

s´

c 1.

Formule postaci α ∨ β dowolne warto´

sciowanie przyporz¸

adkowuje warto´

s´

c 0

dok ladnie wtedy, gdy obu formu lom α, β przyporz¸

adkowuje ono warto´

s´

c 0.

Formule implikacyjnej α → β dowolne warto´

sciowanie przyporz¸

adkowuje

warto´

s´

c 0 dok ladnie wtedy, gdy formule α warto´

sciowanie to przyporz¸

adkowuje

warto´

s´

c 1 oraz formule β warto´

s´

c 0.

Formule r´

ownowa˙zno´

sciowej α ↔ β ka˙zde warto´

sciowanie przyporz¸

adkowuje

warto´

s´

c 1 dok ladnie w´

owczas, gdy przyporz¸

adkowuje ono obu formu lom α, β t¸

e

sam¸

a warto´

s´

c logiczn¸

a.

W´

owczas, gdy dane warto´

sciowanie przyporz¸

adkowuje danej formule warto´

s´

c

1 (0) m´

owimy, ˙ze jest ona prawdziwa (fa lszywa) przy tym warto´

sciowaniu.

Definicje wynikania logicznego, tautologii oraz sprzecznego zbioru formu l

M´

owimy, ˙ze formu la α wynika logicznie ze zbioru formu l Z (Z |= α), gdy α

jest prawdziwa przy ka˙zdym warto´

sciowaniu, przy kt´

orym prawdziwe s¸

a wszys-

tkie formu ly ze zbioru Z.

M´

owimy, ˙ze formu la α jest tautologi¸

a (jest prawem logicznym lub jest lo-

gicznie oprawdziwa), gdy ka˙zde warto´

sciowanie przyporz¸

adkowuje jej warto´

s´

c

12

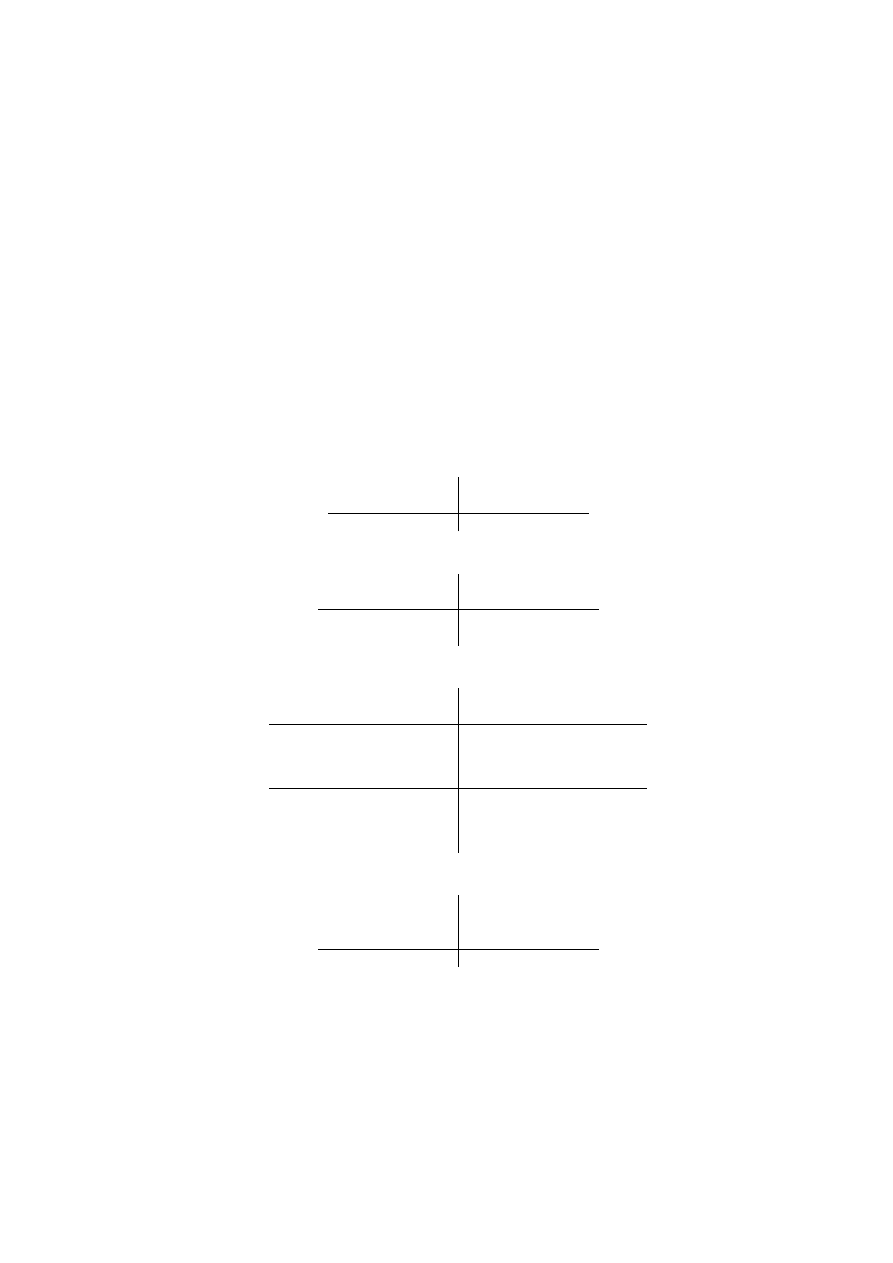
1.

Zbi´

or formu l nazywamy niesprzecznym, gdy istnieje warto´

sciowanie, kt´

ore

ka˙zdej formule z tego zbioru przyporz¸

adkowuje warto´

s´

c 1. Zbi´

or formu l, kt´

ory

nie jest niesprzeczny nazywamy sprzecznym.

Przy sprawdzaniu wynikania logicznego, logicznej prawdziwo´

sci lub sprzecz-

no´

sci zbioru formu l wykonujemy czynno´

sci dw´

och typ´

ow: korzystamy z informa-

cji o warto´

sci logicznej formu ly przy danym warto´

sciowaniu, b¸

ad´

z wykazujemy,

˙ze formu la jest prawdziwa lub fa lszywa przy danym warto´

sciowaniu. Zgodnie

z warunkami prawdziwo´

sci formu l przy danym warto´

sciowaniu (czyli zgodnie z

tabelkami okre´

slaj¸

acymi znaczenia standardowych sp´

ojnik´

ow) wyr´

o˙zni´

c mo˙zna

nast¸

epuj¸

ace sposoby (regu ly) korzystania z prawdziwo´

sci (K1) lub fa lszywo´

sci

(K0) formu l przy danym warto´

sciowaniu (nad poziom¸

a lini¸

a podawana jest

dana informacja, z kt´

orej si¸

e korzysta, pod t¸

a lini¸

a wyst¸

epuje wyra˙zenie (lub

wyra˙zenia), kt´

ore dzi¸

eki tej informacji mo˙zna do dowodu wpisa´

c):

(K1 ∼)

(K0 ∼)

∼ α jest 1 przy v

∼ α jest 0 przy v

α jest 0 przy v

α jest 1 przy v

(K1∧)

(K0∨)

α ∧ β jest 1 przy v

α ∨ β jest 0 przy v

α jest 1 przy v

α jest 0 przy v

β jest 1 przy v

β jest 0 przy v

(K0 ∧ (a))

(K1 ∨ (a))

α ∧ β jest 0 przy v

α ∨ β jest 1 przy v

α jest 0 przy v (za lo˙zenie)

α jest 1 przy v (za lo˙zenie)

..

.

..

.

cel

cel

β jest 0 przy v (za lo˙zenie)

β jest 1 przy v (za lo˙zenie)

..

.

..

.

cel

cel

(K0 ∧ (b))

(K1 ∨ (b))

α ∧ β jest 0 przy v

α ∨ β jest 1 przy v

α jest 1 przy v

α jest 0 przy v

β jest 0 przy v

β jest 1 przy v

13

(K0 ∧ (c))

(K1 ∨ (c))

α ∧ β jest 0 przy v

α ∨ β jest 1 przy v

β jest 1 przy v

β jest 0 przy v

α jest 0 przy v

α jest 1 przy v

(K1 → (a))

α → β jest 1 przy v

α jest 1 przy v
β jest 1 przy v

(K1 → (b))

α → β jest 1 przy v

β jest 0 przy v
α jest 0 przy v

(K1 → (c))

α → β jest 1 przy v

∼ α ∨ β jest 1 przy v

(K0 →)

α → β jest 0 przy v

α jest 1 przy v
β jest 0 przy v

(K1 ↔)

α ↔ β jest 1 przy v
α → β jest 1 przy v
β → α jest 1 przy v

(K0 ↔)

α ↔ β jest 0 przy v

(α → β) ∧ (β → α) jest 0 przy v

Z kolei wyr´

o˙zniamy nast¸

epuj¸

ace sposoby wykazywania prawdziwo´

sci (W 1)

lub fa lszywo´

sci (W 0) formu l przy danym warto´

sciowaniu:

(W 1 ∼)

(W 0 ∼)

wyka˙z: α jest 0 przy v

wyka˙z: α jest 1 przy v

cel: ∼ α jest 1 przy v

cel: ∼ α jest 0 przy v

14

(W 1∧)

(W 0∨)

wyka˙z: α jest 1 przy v

wyka˙z: α jest 0 przy v

wyka˙z: β jest 1 przy v

wyka˙z: β jest 0 przy v

cel: α ∧ β jest 1 przy v

cel: α ∨ β jest 0 przy v

(W 0 ∧ (a))

(W 1∨)(a)

wyka˙z: α jest 0 przy v

wyka˙z: α jest 1 przy v

cel: α ∧ β jest 0 przy v

cel: α ∨ β jest 1 przy v

(W 0 ∧ (b))

(W 1∨)(b)

wyka˙z: β jest 0 przy v

wyka˙z: β jest 1 przy v

cel: α ∧ β jest 0 przy v

cel: α ∨ β jest 1 przy v

(W 0 ∧ (c))

(W 1∨)(c)

wyka˙z: α → ∼ β jest 1 przy v

wyka˙z: ∼ α → β jest 1 przy v

cel: α ∧ β jest 0 przy v

cel: α ∨ β jest 1 przy v

(W 1 → (a))

za l´

o˙z: α jest 1 przy v

i wyka˙z: β jest 1 przy v

cel: α → β jest 1 przy v

(W 1 → (b))

za l´

o˙z: β jest 0 przy v

i wyka˙z: α jest 0 przy v

cel: α → β jest 1 przy v

(W 1 → (c))

wyka˙z: ∼ α ∨ β jest 1 przy v

cel: α → β jest 1 przy v

(W 0 →)

wyka˙z: α jest 1 przy v
wyka˙z: β jest 0 przy v

cel: α → β jest 0 przy v

15

(W 1 ↔)

wyka˙z: α → β jest 1 przy v
wyka˙z: β → α jest 1 przy v

cel: α ↔ β jest 1 przy v

(W 0 ↔)

wyka˙z: (α → β) ∧ (β → α) jest 0 przy v

cel: α ↔ β jest 0 przy v

Przyk lady (1) Wykazujemy, ˙ze {∼ (p ∧ q)} |= ∼ p ∨ ∼ q:

rozwa˙zmy dowolne warto´

sciowanie v,

(1) ∼ (p ∧ q) jest 1 przy v (za lo˙zenie),
(2) p ∧ q jest 0 przy v z (1), (K1 ∼),

teraz stosujemy (K0 ∧ (a)):

(3) p jest 0 przy v (za lo˙zenie)
(4) ∼ p jest 1 przy v z (3), (W 1 ∼),
(5) ∼ p ∨ ∼ q jest 1 przy v, (W 1 ∨ (a))
(6) q jest 0 przy v (za lo˙zenie)
(7) ∼ q jest 1 przy v z (6), (W 1 ∼)
(8) ∼ p ∨ ∼ q jest 1 przy v z (7), (W 1 ∨ (b))

(2) Wykazujemy nie wprost, ˙ze {∼ p ∨ ∼ q} |= ∼ (p ∧ q):

(1) {∼ p ∨ ∼ q} 6|= ∼ (p ∧ q) (za lo˙zenie),
istnieje warto´

sciowanie v takie, ˙ze

(2) ∼ p ∨ ∼ q jest 1 przy v z (1),
(3) ∼ (p ∧ q) jest 0 przy v z (1),
(4) p ∧ q jest 1 przy v z (3), (K0 ∼),
(5) p jest 1 przy v z (4), (K1∧),
(6) q jest 1 przy v z (4), (K1∧),
(7) ∼ p jest 0 przy v z (5), (W 0 ∼),
(8) ∼ q jest 1 przy v z (2), (7), (K1 ∨ (b)),
(9) q jest 0 przy v z (8), (K1 ∼),
absurd (6), (9).

(3) Wykazujemy, ˙ze {p → q, ∼ q} 6|= p w taki spos´

ob, jak chcieliby´

smy dowie´

s´

c

nie wprost, i˙z {p → q, ∼ q} |= p.

Naszym celem jest wskazanie takiego

warto´

sciowania v, przy kt´

orym formu ly p → q, ∼ q s¸

a prawdziwe, za´

s formu la p

jest fa lszywa.

(1) {p → q, ∼ q} 6|= p (za lo˙zenie)
istnieje warto´

sciowanie v takie, ˙ze

(2) p → q jest 1 przy v z (1),
(3) ∼ q jest 1 przy v z (1),

16

(4) p jest 0 przy v z (1),
(5) q jest 0 przy v z (3), (K1 ∼).

W ten spos´

ob wykazali´

smy, i˙z je˙zeli wynikania tu nie ma, tzn. je˙zeli dla

pewnego warto´

sciowania v wszystkie formu ly w naszym zbiorze s¸

a prawdziwe,

za´

s formu la, kt´

ora nie wynika logicznie jest przy v fa lszywa, to warto´

sciowanie

to ma posta´

c: v(p) = 0, v(q) = 0. Latwo sprawdzi´

c (przy u˙zyciu tabelek), i˙z

na odwr´

ot, przy tak okre´

slonym warto´

sciowaniu v, obie formu ly w zbiorze s¸

a

prawdziwe, za´

s formu la nie wynikaj¸

aca jest fa lszywa.

(4) Formu la ((p → r) ∨ (q → r)) → ((p ∧ q) → r) jest tautologi¸

a:

rozwa˙zmy dowolne warto´

sciowanie v,

aby wykaza´

c prawdziwo´

s´

c tej formu ly przy warto´

sciowaniu v stosujemy dwukrot-

nie (W 1 → (a)):

(1) (p → r) ∨ (q → r) jest 1 przy v (za lo˙zenie),

obecnie celem dowodu jest wykazanie, i˙z formu la (p ∧ q) → r jest prawdziwa

przy v. Stosujemy wi¸ec drugi raz (W 1 → (a)):

(2) p ∧ q jest 1 przy v (za lo˙zenie),

teraz celem dowodu jest wykazanie prawdziwo´

sci r przy v:

(3) p jest 1 przy v z (2), (K1∧)
(4) q jest 1 przy v z (2), (K1∧),

stosujemy (K1 ∨ (a)):

(5) p → r jest 1 przy v (za lo˙zenie)
(6) r jest 1 przy v z (5), (3), (K1 → (a)),
(7) q → r jest 1 przy v (za lo˙zenie)
(8) r jest 1 przy v z (7), (4), (K1 → (a)).

(5) Wykazujemy niewprost, ˙ze formu la ((p ∧ q) → r) → ((p → r) ∨ (q → r))
jest tautologi¸

a:

(1) ((p ∧ q) → r) → ((p → r) ∨ (q → r)) nie jest tautologi¸

a (za lo˙zenie)

istnieje warto´

sciowanie v takie, ˙ze

(2) ((p ∧ q) → r) → ((p → r) ∨ (q → r)) jest 0 przy v z (1)
(3) (p ∧ q) → r jest (1) przy v z (2), (K0 →)
(4) (p → r) ∨ (q → r) jest 0 przy v z (2) (K0 →)
(5) p → r jest 0 przy v z (4), (K0∨),
(6) q → r jest 0 przy v z (4), (K0∨),
(7) p jest 1 przy v z (5), (K0 →),
(8) r jest 0 przy v z (5), (K0 →),
(9) q jest 1 przy v z(6), (K0 →),
(10) p ∧ q jest 1 przy v z (7),(9), (W 1∧),

17

(11) r jest 1 przy v z (3),(10), (K1 → (a)),
absurd (8), (11).

(6) Wykazujemy, ˙ze formu la ((p → r) ∨ (q → r)) → ((p ∧ q) → ∼ r) nie
jest tautologi¸

a w taki spos´

ob, jak chcieliby´

smy dowie´

s´

c nie wprost, i˙z jest ona

tautologi¸

a. Naszym celem jest wskazanie takiego warto´

sciowania v, przy kt´

orym

formu la jest fa lszywa.

(1) ((p → r) ∨ (q → r)) → ((p ∧ q) → ∼ r) nie jest tautologi¸

a (za lo˙zenie)

istnieje warto´

sciowanie v takie, ˙ze

(2) ((p → r) ∨ (q → r)) → ((p ∧ q) → ∼ r) jest 0 przy v z (1),
(3) (p → r) ∨ (q → r) jest 1 przy v z (2), (K0 →),
(4) (p ∧ q) → ∼ r jest 0 przy v z (2), (K0 →),
(5) p ∧ q jest 1 przy v z (4), (K0 →),
(6) ∼ r jest 0 przy v z (4), (K0 →),
(7) r jest 1 przy v z (6), (K0 ∼),
(8) p jest 1 przy v z (5), (K1∧),
(9) q jest 1 przy v z (5), (K1∧),

W ten spos´

ob wykazali´

smy, ˙ze je˙zeli formu la nie jest tautologi¸

a, tzn. przy

pewnym warto´

sciowaniu v jest fa lszywa, to warto´

sciowanie to ma posta´

c: v(p) =

v(q) = v(r) = 1. Latwo sprawdzi´

c (przy u˙zyciu tabelek), i˙z na odwr´

ot, przy tak

okre´

slonym warto´

sciowaniu v, formu la jest fa lszywa.

(7) Wykazujemy nie wprost, ˙ze zbi´

or formu l {p ∨ ∼ q, r → q, ∼ (s ∧ ∼ r), s ∧ ∼

p} jest sprzeczny.

(1) zbi´

or {p ∨ ∼ q, r → q, ∼ (s ∧ ∼ r), s ∧ ∼ p} jest niesprzeczny (za lo˙zenie),

istnieje warto´

sciowanie v takie, ˙ze

(2) p ∨ ∼ q jest 1 przy v z (1),
(3) r → q jest 1 przy v z (1),
(4) ∼ (s ∧ ∼ r) jest 1 przy v z (1),
(5) s ∧ ∼ p jest 1 przy v z (1),
(6) s ∧ ∼ r jest 0 przy v z (4) (K1 ∼),
(7) s jest 1 przy v z (5), (K1∧),
(8) ∼ p jest 1 przy v z (5), (K1∧),
(9) p jest 0 przy v z (8), (K1 ∼),
(10) ∼ q jest 1 przy v z (2),(9), (K1 ∨ (b)),
(11) q jest 0 przy v z (10), (K1 ∼),
(12) r jest 0 przy v z (3),(11), (K1 → (b)),
(13) ∼ r jest 0 przy v z (6),(7), (K0 ∧ (b)),
(14) r jest 1 przy v z (13), (K0 ∼),
absurd (12), (14).

(8) Wykazujemy, ˙ze zbi´

or formu l {p → q, r → p, r → ∼ q} jest niesprzeczny w

taki spos´

ob, jak chcieliby´

smy dowie´

s´

c nie wprost, ˙ze jest on sprzeczny. Naszym

celem jest wskazanie takiego warto´

sciowania v, przy kt´

orym ka˙zda formu la z

tego zbioru jest prawdziwa.

18

(1) {p → q, r → p, r → ∼ q} jest niesprzeczny (za lo˙zenie),
istnieje warto´

sciowanie v takie, ˙ze

(2) p → q jest 1 przy v z (1),
(3) r → p jest 1 przy v z (1),
(4) r → ∼ q jest 1 przy v z (1),
(5) ∼ p ∨ q jest 1 przy v z (2), (K1 → (c)),
(6) ∼ p jest 1 przy v (za lo˙zenie)
(7) p jest 0 przy v z (6), (K1 ∼),
(8) r jest 0 przy v z (3),(7), (K1 → (b)),

W ten spos´

ob wykazali´

smy, ˙ze je˙zeli zbi´

or formu l jest niesprzeczny, tzn.

przy pewnym warto´

sciowaniu v ka˙zda formu la z tego zbioru jest prawdziwa, a

ponadto spe lnione jest za lo˙zenie (6), to warto´

sciowanie to ma posta´

c: v(p) =

v(r) = 0, pozosta lym zmiennym v przyporz¸

adkowuje dowolne warto´

sci ze zbioru

{0, 1}. Latwo sprawdzi´c, i˙z na odwr´

ot, przy tak okre´

slonym warto´

sciowaniu v,

wszystkie formu ly ze zbioru s¸

a prawdziwe.

Operatory

Poza zdaniami, nazwami i funktorami, wyr´

o˙znia si¸

e jeszcze kategorie opera-

torowe. Aby zdefiniowa´

c poj¸

ecie operatora zacznijmy od nast¸

epuj¸

acych definicji:

Definicje funkcji zdaniowej i nazwowej

Funkcja zdaniowa [nazwowa] dla j¸

ezyka naturalnego, to wyra˙zenie zawie-

raj¸

ace zmienne okre´

slonych typ´

ow (np. zmienne przebiegaj¸

ace zdania, b¸

ad´

z

zmienne dla nazw indywidualnych, b¸

ad´

z zmienne dla nazw generalnych), kt´

ore

w rezultacie podstawienia w nim w miejsce zmiennych wyra˙ze´

n z j¸

ezyka natural-

nego odpowiednio tych samych typ´

ow co typy tych zmiennych, staje si¸

e zdaniem

(prawdziwym lub fa lszywym) [nazw¸

a].

Na przyk lad wyra˙zenie ”x jest cz lowiekiem”, jest funkcj¸

a zdaniow¸

a, w kt´

orej

wyst¸

epuje zmienna x dla nazw indywidualnych; wyra˙zenie ”x + x” jest funkcj¸

a

nazwow¸

a, w kt´

orej wyst¸

epuje zmienna dla nazw indywidualnych; wyra˙zenie

”ka˙zde S jest M ” jest funkcj¸

a zdaniow¸

a, w kt´

orej S, M s¸

a zmiennymi dla nazw

generalnych; wyra˙zenie ”A i B” jest funkcj¸

a zdaniow¸

a, w kt´

orej A, B s¸

a zmien-

nymi dla zda´

n.

Wyra˙zenie: ”dla ka˙zdego x, je˙zeli x jest cz lowiekiem, to x jest ´

smiertelny”,

nie jest funkcj¸

a zdaniow¸

a, je´

sli x jest zmienn¸

a dla nazw indywidualnych. Jest

ono zdaniem. Wyra˙zenie: ”{x : x jest liczb¸

a rzeczywist¸

a i x + 2 > 4}”, mimo, ˙ze

wyst¸

epuje w nim zmienna (dla nazw indywidualnych) nie jest funkcj¸

a nazwow¸

a,

lecz jest nazw¸

a (zbioru). Podobnie wyra˙zenie ”

R xdx” nie jest funkcj¸a nazwow¸a,

lecz jest nazw¸

a (funkcji).

Wyra˙zenia takie jak: ”dla ka˙zdego x”, ”{x : }”, ”

R

dx” r´

ownie˙z nie s¸

a ani

funkcjami zdaniowymi, ani nazwowymi, cho´

c wyst¸

epuj¸

a w nich zmienne. Wy-

ra˙zenia te nie s¸

a jednak ani zdaniami, ani nazwami, ani funktorami. Nazywane

s¸

a operatorami.

19

Definicja operatora

Operator jest to wyra˙zenie zawieraj¸

ace zmienn¸

a, kt´

ore po do l¸

aczeniu do

funkcji zdaniowej b¸

ad´

z nazwowej, w kt´

orej ta zmienna wyst¸

epuje, tworzy wraz

z ni¸

a zdanie b¸

ad´

z nazw¸

e.

Niekt´

ore typy syntaktyczne operator´

ow:

z

|z

jest wska´

znikiem kategorii operator´

ow zdaniotw´

orczych, kt´

orych argu-

mentem jest funkcja zdaniowa,

n

|n

jest wska´

znikiem kategorii operator´

ow nazwotw´

orczych, kt´

orych argu-

mentem jest funkcja nazwowa,

n

|z

jest wska´

znikiem kategorii operator´

ow nazwotw´

orczych, kt´

orych argu-

mentem jest funkcja zdaniowa.

Przyk lady.

dla ka˙zdego x, dla pewnego x:

z

|z

,

R

dx:

n

|n

,

{x : }:

n

|z

.

J¸

ezyk logiki kwantyfikator´

ow

S lownik:
zmienne nazwowe: x

1

, x

2

, . . .,

sp´

ojniki: ∼, ∧, ∨, →, ↔,

kwantyfikatory:
du˙zy, og´

olny lub uniwersalny: ∀ (dla ka˙zdego),

ma ly, szczeg´

o lowy lub egzystencjalny: ∃ (dla pewnego)

predykat identyczno´

sci: =, (2-argumentowy)

sta le nazwowe: c

1

, c

2

, . . . , c

k

, k ≥ 0

predykaty: P

1

, P

2

, . . . , P

n

, n ≥ 0 (1- i 2-argumentowe)

nawiasy i przecinek: (,) , .

Definicja termu nazwowego

Dowoln¸

a zmienn¸

a lub sta l¸

a nazwow¸

a nazywamy termem (nazwowym).

Dysponuj¸

ac definicj¸

a termu mo˙zna sformu lowa´

c

Definicj¸

e zbioru formu l

(1) Je˙zeli t, s s¸

a termami, to ci¸

ag symboli: t = s jest formu l¸

a.

(2) Je˙zeli t jest termem oraz P jest 1-argumentowym predykatem, to ci¸

ag

P (t) jest formu l¸

a.

(3) Je˙zeli t, s s¸

a termami oraz P jest 2-argumentowym predykatem, to ci¸

ag:

P (t, s) jest formu l¸

a.

(4) Je˙zeli α jest formu l¸

a, to ∼ α jest formu l¸

a.

20

(5) Je˙zeli α, β s¸

a formu lami, to ci¸

agi: (α ∧ β), (α ∨ β), (α → β), (α ↔ β) s¸

a

formu lami.

(6) Je˙zeli x jest zmienn¸

a nazwow¸

a oraz α jest formu l¸

a, to ci¸

agi: ∀xα, ∃xα

s¸

a formu lami.

(7) Je˙zeli ci¸

ag symboli α jest formu l¸

a, to α jest jednej z postaci podanych w

warunkach (1) - (6).

Formu ly, kt´

orych postacie zosta ly wymienione w (1), (2), (3) nazywane s¸

a

formu lami atomowymi.

Definicje

M´

owimy, ˙ze w formule ∀xα kwantyfikator ∀ wi¸

a˙ze zmienn¸

a x, za´

s formu l¸

e α

nazywamy zasi¸

egiem tego kwantyfikatora. Analogicznie dla formu ly ∃xα.

Ka˙zde pojawienie si¸

e nie bezpo´

srednio po kwantyfikatorze danej zmiennej x

w danej formule α nazywamy wyst¸

epowaniem zmiennej x w α.

Wyst¸

epowanie zmiennej x w formule β nazywamy wolnym, gdy nie jest ono

w zasi¸

egu ˙zadnego kwantyfikatora wi¸

a˙z¸

acego t¸

e zmienn¸

a.

M´

owimy, ˙ze zmienna x jest wolna w formule β, gdy zmienna ta ma w tej

formule przynajmniej jedno wolne wyst¸

epowanie.

Formu l¸

e nazywamy domkni¸

et¸

a (lub zdaniem), gdy nie wyst¸

epuje w niej

zmienna wolna.

Przyk lad. W formule: ∀xP

1

(x, y)∧P

2

(x), zmienne x, y s¸

a wolne, natomiast

w formule ∀xP

1

(x, y) tylko zmienna y jest wolna. Formu la ∃y∀xP

1

(x, y) jest

zdaniem.

Zasady zapisu schemat´

ow w j¸

ezyku logiki kwantyfikator´

ow dla zda´

n

z j¸

ezyka naturalnego

Niech A b¸

edzie dowolnym zdaniem oznajmuj¸

acym z j¸

ezyka polskiego. Na-

szym celem jest zapisanie formu ly domkni¸

etej w j¸

ezyku logiki kwantyfikator´

ow,

ukazuj¸

acej “struktur¸

e logiczn¸

a” zdania A, nazywanej z tego powodu, schematem

zdania A.

1) Ka˙zdej nazwie indywidualnej wyst¸

epuj¸

acej w zdaniu A odpowiada w jego

schemacie sta la nazwowa (r´

o˙znym nazwom odpowiadaj¸

a r´

o˙zne sta le).

2) ˙

Zadna nazwa generalna S wyst¸

epuj¸

aca w zdaniu A nie ma odpowiednika w

jego schemacie, lecz 1-argumentowemu predykatowi postaci jest S, powsta lemu
przez do l¸

aczenie do nazwy S wyra˙zenia jest, odpowiada w schemacie zdania A

1-argumentowy predykat ze s lownika j¸

ezyka logiki kwantyfikator´

ow.

3) Ka˙zdemu 1- i 2-argumentowemu predykatowi wyst¸

epuj¸

acemu w zdaniu

A odpowiada w schemacie tego zdania odpowiednio 1- b¸

ad´

z 2-argumentowy

predykat ze s lownika (r´

o˙znym predykatom z j¸

ezyka polskiego odpowiadaj¸

a r´

o˙zne

predykaty ze s lownika)

21

4) Je˙zeli w A wyst¸

epuj¸

a kwantyfikatory (ka˙zdy, ˙zaden, wszystkie, pewne,

niekt´

ore, to dokonujemy jego rozk ladu na g l´

owny kwantyfikator i funkcj¸

e zda-

niow¸

a, kt´

ora jest jego argumentem, nast¸

epnie rozk ladamy t¸

e funkcj¸

e zdaniow¸

a

na jej g l´

owny kwantyfikator i jego argument itd., a˙z oznaczymy wszystkie funkcje

zdaniowe, w kt´

orych ju˙z nie wyst¸

epuje kwantyfikator.

5) Funkcjom zdaniowym, w kt´

orych nie wyst¸

epuj¸

a kwantyfikatory, otrzy-

manym wed lug zasady 4), odpowiadaj¸

a w schemacie zdania A, formu ly ato-

mowe.

Przyk lady. Schematami zda´

n: Ja´

s kocha Ma lgosi¸

e, Ma lgosia kocha Jasia s¸

a

odpowiednio formu ly atomowe: K(j, m), K(m, j), gdzie K jest predykatem ze
s lownika odpowiadaj¸

acym predykatowi kocha oraz j, m s¸

a sta lymi nazwowymi

odpowiadaj¸

acymi odpowiednio nazwom indywidualnym Ja´

s, Ma lgosia.

Schematami zda´

n Ja´

s kocha wszystkich ludzi, Ja´

s kogo´

s kocha, s¸

a odpowied-

nio formu ly: ∀x(C(x) → K(j, x)), ∃x(C(x) ∧ K(j, x)), gdzie C jest predykatem
ze s lownika odpowiadaj¸

acym predykatowi: jest cz lowiekiem.

Semantyka dla j¸

ezyka I rz¸

edu (kwantyfikatorowego

Naszym celem jest obecnie zdefiniowanie dw´

och poj¸

e´

c: interpretacji j¸

ezyka

kwantyfikatorowego oraz prawdziwo´

sci, wzgl¸

ednie fa lszywo´

sci zdania w danej

interpretacji. Dysponuj¸

ac poj¸

eciem prawdziwo´

sci zdania w danej interpretacji

mo˙zna b¸

edzie wprowadzi´

c centralne poj¸

ecie wynikania logicznego, a nast¸

epnie

tautologii oraz sprzecznego zbioru zda´

n.

Definicje

Niech D b¸

edzie dowolnym niepustym zbiorem (klas¸

a, mnogo´

sci¸

a) obiekt´

ow.

Przypominany, ˙ze dowolny zbi´

or, kt´

orego ka˙zdy element nale˙zy do zbioru D

nazywamy podzbiorem zbioru D.

Dowolny zbi´

or dwuwyrazowych ci¸

ag´

ow element´

ow zbioru D nazywamy re-

lacj¸

a binarn¸

a na zbiorze D.

Na formaln¸

a semantyk¸

e dla j¸

ezyka kwantyfikatorowego sk ladaj¸

a si¸

e jego in-

terpretacje:

Definicja interpretacji

Przez interpretacj¸

e j¸

ezyka I rz¸

edu wyznaczonego przez sta le nazwowe: c

1

, . . . ,

c

k

, oraz predykaty P

1

, . . . , P

n

, rozumiemy nast¸

epuj¸

acy uk lad:

I = (D, c

∗

1

, . . . , c

∗
k

, P

∗

1

, . . . , P

∗

n

), gdzie

(1) D jest dowolnym niepustym zbiorem, zwanym dziedzin¸

a interpretacji,

(2) dla ka˙zdego j = 1, . . . , k : c

∗
j

∈ D jest wyr´

o˙znionym elementem zbioru

D (kt´

orego nazw¸

a w definiowanej interpretacji jest sta la c

j

),

(3)

dla ka˙zdego j = 1, . . . , n :

P

∗

j

jest albo podzbiorem zbioru D, gdy

nazywaj¸

acy go predykat P

j

jest 1-argumentowy, albo jest relacj¸

a binarn¸

a na

zbiorze D, gdy P

j

jest 2-argumentowy.

22

Aby zdefiniowa´

c poj¸

ecie prawdziwo´

sci formu ly domkni¸

etej w interpretacji I

rozszerzamy przy ustalonej interpretacji I zbi´

or sta lych nazwowych {c

1

, . . . , c

k

}

o nowe sta le a

d

, d ∈ D. W ten spos´

ob dla danej interpretacji I ulega rozszerzeniu

zbi´

or formu l tego j¸

ezyka I rz¸

edu, kt´

orego I jest interpretacj¸

a, w szczeg´

olno´

sci

jego zbi´

or zda´

n. B¸

edziemy definiowa´

c prawdziwo´

s´

c w interpretacji I dla zda´

n z

tego szerszego zbioru.

Ka˙zda interpretacja wyznacza tzw.

waluacj¸

e term´

ow domkni¸

etych, czyli

przyporz¸

adkowanie ka˙zdemu termowi domkni¸

etemu pewnego elementu z dzie-

dziny tej interpretacji (nieformalnie: elementu nazywanego tym termem w tej
interpretacji), jak nast¸

epuje:

(a) |c

j

| = c

∗
j

, j = 1, . . . , k,

(b) |a

d

| = d, d ∈ D.

Definicja prawdziwo´

sci formu ly domkni¸

etej w interpretacji I

Dla dowolnych sta lych a, b rozszerzonego j¸

ezyka oraz dowolnych 1-argumen-

towego predykatu P i 2-argumentowego predykatu Q:

(1) a = b jest prawdziwa w I wtw |a|, |b| s¸

a jednym i tym samym obiektem,

(2) P (a) jest prawdziwa w I wtw |a| ∈ P

∗

,

(3) Q(a, b) jest prawdziwa w I wtw (|a|, |b|) ∈ Q

∗

,

dla dowolnych formu l domkni¸

etych α, β:

(4) ∼ α jest prawdziwa w I wtw α nie jest prawdziwa w I,

(5) α ∧ β jest prawdziwa w I wtw obie formu ly: α, β, s¸

a prawdziwe w I,

(6) α ∨ β jest prawdziwa w I wtw przynajmniej jedna z formu l: α, β, jest

prawdziwa w I,

(7) α → β jest prawdziwa w I wtw α nie jest prawdziwa w I lub β jest

prawdziwa w I,

(8) α ↔ β jest prawdziwa w I wtw obie formu ly: α, β, s¸

a prawdziwe w I,

b¸

ad´

z obie te formu ly nie s¸

a prawdziwe w I

dla dowolnej formu ly α z co najwy˙zej jedn¸

a zmienn¸

a woln¸

a, kt´

or¸

a jest

zmienna x:

(9) ∀xα jest prawdziwa w I wtw dla ka˙zdego elementu d ∈ D:

formu la

α[x/a

d

] jest prawdziwa w I,

(10) ∃xα jest prawdziwa w I wtw dla pewnego elementu d ∈ D: formu la

α[x/a

d

] jest prawdziwa w I,

gdzie α[x/a

d

] jest formu l¸

a uzyskan¸

a z formu ly α przez zast¸

apienie w niej

ka˙zdego wolnego wyst¸

epowania zmiennej x sta l¸

a a

d

.

Na podstawie definicji prawdziwo´

sci formu l og´

olnych i szczeg´

o lowych w danej

23

interpretacji, mo˙zna sformu lowa´

c nast¸

epuj¸

ace regu ly (sposoby) korzystania z

informacji o prawdziwo´

sci lub fa lszywo´

sci w danej interpretacji tych formu l:

(K1∀)

(K0∃)

∀xα jest 1 w I

∃xα jest 0 w I

α[x/a] jest 1 w I

α[x/a] jest 0 w I

gdzie a jest dowoln¸

a sta l¸

a nazwow¸

a spo´

sr´

od c

1

, . . . , c

k

, b¸

ad´

z sta lych a

d

, d ∈ D

(K0∀)

(K1∃)

∀xα jest 0 w I

∃xα jest 1 w I

α[x/a] jest 0 w I dla pewnego a

α[x/a] jest 1 w I dla pewnego a

a jest tu niewyspecyfikowan¸

a sta l¸

a nazwow¸

a spo´

sr´

od sta lych a

d

, d ∈ D i tak¸

a,

kt´

ora wcze´

sniej w dowodzie nie pojawi la si¸

e

Sposoby wykazywania prawdziwo´

sci lub fa lszywo´

sci w danej interpretacji

formu l og´

olnych i szczeg´

o lowych:

(W 1∀)

(W 0∃)

rozwa˙zmy dowolne a

rozwa˙zmy dowolne a

wyka˙z: α[x/a] jest 1 w I

wyka˙z: α[x/a] jest 0 w I

cel: ∀xα jest 1 w I

cel: ∃xα jest 0 w I

a jest tu dowoln¸

a niewyspecyfikowan¸

a sta l¸

a nazwow¸

a (tzn. nie wiemy jaki

obiekt z dziedziny interpretacji I jest przez ni¸

a nazywany) spo´

sr´

od sta lych

a

d

, d ∈ D

(W 0∀)

(W 1∃)

wyka˙z: α[x/a] jest 0 w I

wyka˙z: α[x/a] jest 1 w I

cel: ∀xα jest 0 w I

cel: ∃xα jest 1 w I

a jest tu jak¸

akolwiek sta l¸

a nazwow¸

a spo´

sr´

od c

1

, . . . , c

k

, b¸

ad´

z sta lych a

d

, d ∈ D

Wynikanie loguiczne, tautologia, sprzeczny zbi´

or zda´

n w logice

kwantyfikator´

ow

Centralnym poj¸

eciem semantycznym jest tu wynikanie logiczne lub inaczej

relacja konsekwencji logicznej.

Definicja wynikania logicznego

M´

owimy, ˙ze zdanie α wynika logicznie ze zbioru zda´

n Z ustalonego j¸

ezyka

kwantyfikatorowego (Z |= α), gdy α jest prawdziwe w ka˙zdej interpretacji, w
kt´

orej prawdziwe jest ka˙zde zdanie ze zbioru Z.

Przyk lady (1) Zdanie ∃xQ(x, c) wynika logicznie ze zbioru zda´

n:

{∃x∀y(P (y, x) → Q(x, y)), ∀xP (c, x)}.

24

Rozwa˙zmy bowiem dowoln¸

a interpretacj¸

e I = (D, c

∗

, P

∗

, Q

∗

) i za l´

o˙zmy, ˙ze

(1) ∃x∀y(P (y, x) → Q(x, y)) jest 1 w I,
(2) ∀xP (c, x) jest 1 w I,

W´

owczas:

(3) ∀y(P (y, a) → Q(a, y)) jest 1 w I dla pewnej sta lej a z (1), (K1∃),
(4) P (c, a) → Q(a, c) jest 1 w I z (3), (K1∀),
(5) P (c, a) jest 1 w I z (2), (K1∀),
(6) Q(a, c) jest 1 w I z (4),(5), (K1 →)(a),
∃xQ(x, c) jest 1 w I z (6), (W 1∃).

(2) Zdanie (1) ∃x(P

1

(x)∧ ∼ Q(x, x)) nie wynika logicznie ze zbioru zda´

n:

{(2) ∃x(P

2

(x) ∧ ∀y(P

1

(y) → ∼ Q(x, y))), (3) ∀x(P

1

(x) → P

2

(x))}.

Aby to wykaza´

c, nale˙zy wskaza´

c tak¸

a interpretacj¸

e I = (D, P

∗

1

, P

∗

2

, Q

∗

), w

kt´

orej zdania (2), (3) s¸

a prawdziwe, natomiast zdanie (1) jest fa lszywe. Po l´

o˙zmy:

D = zbi´

or liczb naturalnych N ,

P

∗

1

= zbi´

or liczb naturalnych parzystych,

P

∗

2

= N, Q

∗

= {(i, i) : i ∈ N } (relacja identyczno´

sci na N ).

W I zdanie (1) jest fa lszywe: nie istnieje liczba naturalna, kt´

ora jest parzysta

i r´

o˙zna od siebie samej. Poniewa˙z np. liczba 1 jest naturalna i ka˙zda liczba

parzysta naturalna jest od niej r´

o˙zna, wi¸

ec prawdziwe w I jest zdanie (2).

Oczywi´

scie ka˙zda liczba naturalna parzysta jest liczb¸

a naturaln¸

a, dlatego praw-

dziwe w I jest zdanie (3).

Definicja tautologii

Zdanie α danego j¸

ezyka I rz¸

edu nazywamy tautologi¸

a, gdy α jest prawdziwe

w ka˙zdej interpretacji dla tego j¸

ezyka.

Przyk lady (1) Zdanie: ∃x∀yQ(x, y) → ∀y∃xQ(x, y), jest tautologi¸

a.

Rozwa˙zmy bowiem dowoln¸

a interpretacj¸

e I = (D, Q

∗

). Naszym celem jest

wykazanie prawdziwo´

sci tego zdania w I. Na podstawie (W 1 →)(a) za l´

o˙zmy,

˙ze

(1) ∃x∀yQ(x, y) jest 1 w I.

Na mocy (W 1∀) niech a b¸

edzie sta l¸

a nazywaj¸

ac¸

a dowolnie wybrany obiekt

z dziedziny D. W´

owczas:

(2) ∀yQ(b, y) jest prawdziwa w I dla pewnej sta lej b z (1), (K1∃),
(3) Q(b, a) jest 1 w I z (2) (K1∀),
∃xQ(x, a) jest 1 w I z (3), (W 1∃),

co, na mocy (W 1∀), dowodzi prawdziwo´

sci zdania: ∀y∃xQ(x, y). Zatem,

wed lug (W 1 → (a)), nasze zdanie jest prawdziwe w I.

(2) Implikacja: ∀y∃xQ(x, y) → ∃x∀yQ(x, y) nie jest tautologi¸

a.

25

Aby to wykaza´

c, nale˙zy wskaza´

c tak¸

a interpretacj¸

e I = (D, Q

∗

), w kt´

orej

zdanie to jest fa lszywe. Niech wi¸

ec np.

D = N oraz
Q

∗

= {(i, j) : i, j ∈ N : i ≥ j}.

W tej interpretacji poprzednik: ∀y∃xQ(x, y) jest prawdziwy, lecz nast¸

epnik:

∃x∀yQ(x, y) jest fa lszywy.

Zatem nasza implikacja jest w tej interpretacji

fa lszywa.

Definicja sprzecznego zbioru zda´

n

Zbi´

or zda´

n X nazywamy niesprzecznym, gdy istnieje interpretacja, w kt´

orej

ka˙zde zdanie z X jest prawdziwe. Zbi´

or zda´

n jest sprzeczny, gdy nie jest on

niesprzeczny.

Przyk lady (1) Zbi´

or zda´

n:

{∀x∀y((P

1

(x)∧P

2

(y)) → Q(x, y)), ∃x(P

1

(x)∧P

2

(x)), ∀x(P

1

(x) → ∼ Q(x, x))},

jest sprzeczny.

Aby tego dowie´

s´

c, za l´

o˙zmy nie wprost, ˙ze jest niesprzeczny. W´

owczas istnieje

interpretacja I = (D, P

∗

1

, P

∗

2

, Q

∗

), w kt´

orej prawdziwe s¸

a formu ly:

(1) ∀x∀y((P

1

(x) ∧ P

2

(y)) → Q(x, y)),

(2) ∃x(P

1

(x) ∧ P

2

(x)),

(3) ∀x(P

1

(x) → ∼ Q(x, x)).

Zatem

(4) P

1

(a) ∧ P

2

(a) jest 1 w I dla pewnego a z (2), (K1∃),

(5) ∀y((P

1

(a) ∧ P

2

(y)) → Q(a, y)) jest 1 w I z (1), (K1∀),

(6) (P

1

(a) ∧ P

2

(a)) → Q(a, a) jest 1 w I z (5), (K1∀),

(7) Q(a, a) jest 1 w I z (6), (4), (K1 →)(a),
(8) P

1

(a) jest 1 w I z (4), (K1∧),

(9) P

1

(a) → ∼ Q(a, a) jest 1 w I z (3), (K1∀),

(10) ∼ Q(a, a) jest 1 w I z (9), (8), (K1 → (a)),
(11) Q(a, a) jest 0 w I z (10), (K1 ∼),
absurd (11), (7).

(2) Zbi´

or zda´

n: {∀x(Q(c, x) → Q(x, c)), ∼ Q(c, c)} jest niesprzeczny.

Aby to wykaza´

c, wystarcza wskaza´

c jak¸

akolwiek interpretacj¸

e, w kt´

orej ka˙zda

formu la z tego zbioru jest prawdziwa. Np. niech dziedzin¸

a interpretacji b¸

edzie

jakikolwiek niepusty zbi´

or D oraz niech

Q

∗

= {(u, v) : u, v ∈ D, u 6= v}.

Poj¸

ecie klasyfikacji

Przypominamy, i˙z przez relacj¸

e binarn¸

a okre´

slon¸

a na danym zbiorze A rozu-

miemy dowolny (w tym r´

ownie˙z pusty) zbi´

or 2-wyrazowych ci¸

ag´

ow element´

ow

zbioru A. Zbi´

or wszystkich 2-wyrazowych ci¸

ag´

ow element´

ow zbioru A nazy-

wamy relacj¸

a pe ln¸

a na A i oznaczamy A

2

.

26

Niech R b¸

edzie dowoln¸

a relacj¸

a binarn¸

a okre´

slon¸

a na ustalonym zbiorze

A. Zamiast pisa´

c: ”ci¸

ag (x, y) element´

ow zbioru A jest elementem relacji R”

piszemy: ”xRy”.

Definicja najwa˙zniejszych formalnych w lasno´

sci relacji binarnych okre´

slonych

na danym zbiorze

M´

owimy, ˙ze

R jest zwrotna na A wtw dla dowolnego elementu x zbioru A zachodzi

xRx,

R jest przeciwzwrotna na A wtw dla ˙zadnego elementu x zbioru A nie

zachodzi: xRx,

R jest symetryczna na A wtw dla dowolnych element´

ow x, y zbioru A

(niekoniecznie r´

o˙znych), je˙zeli xRy, to yRx,

R jest przeciwsymetryczna na A wtw dla dowolnych element´

ow x, y zbioru

A, je˙zeli xRy, to nie zachodzi yRx,

R jest antysymetryczna na A wtw dla dowolnych element´

ow x, y zbioru

A, je˙zeli xRy oraz yRx, to x = y,

R jest przechodnia na A wtw dla dowolnych element´

ow x, y, z zbioru A,

je˙zeli xRy oraz yRz, to xRz,

R jest sp´

ojna na A

wtw

dla dowolnych element´

ow x, y zbioru A, je˙zeli

x 6= y, to xRy lub yRx.

Jeden z najwa˙zniejszych typ´

ow relacji binarnych okre´

slonych na danym zbiorze

stanowi¸

a relacje r´

ownowa˙zno´

sciowe.

Definicja relacji r´

ownowa˙zno´

sci

M´

owimy, ˙ze R jest r´

ownowa˙zno´

sciowa lub ˙ze jest relacj¸

a r´

ownowa˙zno´

sci na

zbiorze A, gdy R jest zwrotna, symetryczna i przechodnia na A.

Przyk lady (1) Relacja pe lna A

2

oraz tzw. relacja identyczno´

sciowa id(A)

okre´

slona na A nast¸

epuj¸

aco: dla dowolnych element´

ow x, y zbioru A,

x(id(A))y wtw x = y,

s¸

a relacjami r´

ownowa˙zno´

sci na zbiorze A.

(2) Na zbiorze tr´

ojelementowym A = {a, b, c} mamy pi¸

e´

c relacji r´

ownowa˙zno´

sci:

id(A) = {(a, a), (b, b), (c, c)},

R

1

= {(a, a), (b, b), (c, c), (a, b), (b, a)},

R

2

= {(a, a), (b, b), (c, c), (a, c), (c, a)},

R

3

= {(a, a), (b, b), (c, c), (b, c), (c, b)},

27

A

2

= {(a, a), (b, b), (c, c), (a, b), (b, a), (a, c), (c, a), (b, c), (c, b)}.

Definicja klasy abstrakcji wzgl¸

edem danej relacji r´

ownowa˙zno´

sci

Dla dowolnej relacji r´

ownowa˙zno´

sci R okre´

slonej na danym zbiorze A oraz

dowolnego elementu a zbioru A, zbi´

or wszystkich element´

ow x zbioru A ta-

kich, ˙ze aRx nazywamy klas¸

a abstrakcji b¸

ad´

z reprezentacji elementu a wzgl¸

edem

relacji R i oznaczamy w postaci: [a]

R

.

Przyk lady

(1) Dla dowolnego elementu a danego zbioru A, [a]

id(A)

= {a}

oraz [a]

A

2

= A,

(2) Dla relacji r´

ownowa˙zno´

sci R

1

, R

2

, R

3

z poprzedniego przyk ladu, okre´

slonych

na zbiorze {a, b, c} mamy:

[a]

R

1

= {a, b}, [b]

R

1

= {a, b} = [a]

R

1

, [c]

R

1

= {c},

[a]

R

2

= {a, c}, [b]

R

2

= {b}, [c]

R

2

= {a, c} = [a]

R

2

,

[a]

R

3

= {a}, [b]

R

3

= {b, c}, [c]

R

3

= {b, c} = [b]

R

3

.

Niech R b¸edzie relacj¸

a r´

ownowa˙zno´

sci na A. Poniewa˙z dla dowolnego ele-

mentu a zbioru A zachodzi: aRa, wi¸

ec a jest elementem swojej klasy abstrakcji,

zatem

dowolna klasa abstrakcji jest niepustym zbiorem.

Interesuj¸

ace dla zastosowa´

n s¸

a kolejne dwie w lasno´

sci klas abstrakcji:

Druga istotna w lasno´

s´

c klas abstrakcji ma posta´

c:

dla dowolnych element´

ow x, y zbioru A : xRy wtw [x] = [y].

Dow´

od: (⇒): Za l´

o˙zmy, ˙ze xRy. Aby wykaza´

c r´

owno´

s´

c zbior´

ow dowodzimy,

i˙z maj¸

a one te same elementy. Niech wi¸

ec a b¸

edzie elementem klasy abstrakcji

[x]. Zatem xRa. Poniewa˙z z za lo˙zenia na mocy symetrii relacji R mamy: yRx,
wi¸

ec w konsekwencji na podstawie przechodnio´

sci R otrzymujemy: yRa, co oz-

nacza, i˙z a jest elementem zbioru [y]. W ten spos´

ob wykazali´

smy, ˙ze ka˙zdy

element zbioru [x] jest elementem zbioru [y]. Na odwr´

ot przypu´

s´

cmy, i˙z a jest

elementem klasy abstrakcji [y]. Zatem yRa. St¸

ad na mocy za lo˙zenia i przechod-

nio´

sci relacji R mamy: xRa, dlatego a jest elementem zbioru [x].

(⇐): Za l´

o˙zmy, ˙ze [x] = [y]. Poniewa˙z y jest elementem klasy abstrakcji [y],

wi¸

ec na mocy za lo˙zenia otrzymujemy: y jest elementem zbioru [x], zatem xRy.

Trzecia w lasno´

s´

c klas abstrakcji:

dla dowolnych element´

ow x, y zbioru A: je˙zeli klasy abstrakcji [x], [y] nie s¸

a

roz l¸

aczne, to s¸

a r´

owne.

Dow´

od: Za l´

o˙zmy, ˙ze a jest elementem obu klas abstrakcji [x], [y]. W´

owczas

xRa oraz yRa. Zatem z symetrii relacji R mamy: aRy, co z przechodnio´

sci

relacji R implikuje: xRy i w konsekwencji na mocy drugiej w lasno´

sci klas ab-

strakcji otrzymujemy: [x] = [y].

28

Definicja podzia lu danego zbioru

Przez podzia l

danego zbioru A rozumiemy dowolny zbi´

or Π niepustych

podzbior´

ow zbioru A spe lniaj¸

acy nast¸

epuj¸

ace dwa warunki:

(1) dowolne dwa r´

o˙zne elementy zbioru Π s¸

a roz l¸

aczne,

(2) dla ka˙zdego elementu a zbioru A istnieje element X zbioru Π taki ˙ze a

nale˙zy do X.

Przyk lady (1) Zbi´

or 1-elementowy {A} jest podzia lem zbioru A.

(2) Zbi´

or z lo˙zony ze wszystkich jednoelementowych podzbior´

ow {a} dowolnego

zbioru A jest podzia lem zbioru A.

(3) Istnieje pi¸e´

c podzia l´

ow tr´

ojelementowego zbioru A = {a, b, c}:

{{a}, {b}, {c}},

{{a, b}, {c}},

{{a, c}, {b}},

{{b, c}, {a}},

{{a, b, c}}.

Jednym z podstawowych twierdze´

n dotycz¸

acych podzia l´

ow jest

Zasada abstrakcji

Dla dowolnej relacji r´

ownowa˙zno´

sci R okre´

slonej na zbiorze A zbi´

or wszyst-

kich klas abstrakcji element´

ow zbioru A wzgl¸

edem relacji R jest podzia lem tego

zbioru.

Dow´

od: Zauwa˙zmy najpierw, i˙z dowolna klasa abstrakcji [x] wzgl¸

edem R

jest niepustym podzbiorem zbioru A (pierwsza w lasno´

s´

c klas abstrakcji). Po

drugie, na mocy trzeciej w lasno´

sci klas abstrakcji zachodzi warunek (1) definicji

podzia lu dla zbioru wszystkich klas abstrakcji wzgl¸

edem R. Warunek (2) tej

definicji jest spe lniony, bo dowolny element a zbioru A jest elementem klasy
abstrakcji [a].

Twierdzenie 1. Dla dowolnego podzia lu Π zbioru A relacja R okre´

slona na

A nast¸

epuj¸

aco: dla dowolnych element´

ow x, y zbioru A : xRy

wtw istnieje

element X podzia lu Π taki, ˙ze x, y s¸

a elementami X, jest relacj¸

a r´

ownowa˙zno´

sci

na zbiorze A.

Dow´

od: Zwrotno´

s´

c relacji R wynika z warunku (2) definicji podzia lu, syme-

tria wprost z okre´

slenia relacji R, natomiast jej przechodnio´

s´

c jest konsekwencj¸

a

warunku (1) definicji podzia lu: przypu´

s´

cmy bowiem, ˙ze xRy oraz yRz. Zatem

x, y s¸

a elementami pewnego zbioru X nale˙z¸

acego do Π oraz y, z s¸

a elementami

pewnego zbioru Y nale˙z¸

acego do podzia lu Π. St¸

ad X, Y nie s¸

a roz l¸

aczne. Zatem,

wed lug warunku (1) definicji podzia lu: X = Y . Dlatego x, z s¸

a elementami tej

samej cz¸

e´

sci podzia lu Π. Na mocy definicji relacji R otrzymujemy ostatecznie:

xRz.

29

Na mocy zasady abstrakcji, ka˙zda relacja r´

ownowa˙zno´

sci okre´

slona na danym

zbiorze wyznacza podzia l tego zbioru.

Natomiast zgodnie z Tw.1, dowolny

podzia l danego zbioru wyznacza relacj¸

e r´

ownowa˙zno´

sci okre´

slon¸

a na tym zbiorze.

Mo˙zna wykaza´

c nieco wi¸

ecej: relacja r´

ownowa˙zno´

sci wyznaczona przez podzia l,

kt´

ory sam wyznaczony jest przez dan¸

a relacj¸

e r´

ownowa˙zno´

sci, jest to˙zsama z t¸

a

dan¸

a relacj¸

a. Ponadto, podzia l wyznaczony przez relacj¸

e r´

ownowa˙zno´

sci, kt´

ora

sama jest wyznaczona przez dany podzia l, jest to˙zsamy z tym danym podzia lem.

Przyk lad. Przyporz¸

adkowanie: relacja r´

ownowa˙zno´

sci ←→ podzia l, dla zbioru

A = {a, b, c} przedstawia si¸

e nast¸

epuj¸

aco:

{(a, a), (b, b), (c, c)} ←→ {{a}, {b}, {c}} ,

{(a, a), (b, b), (c, c), (a, b), (b, a)} ←→ {{a, b}, {c}},

{(a, a), (b, b), (c, c), (a, c), (c, a)} ←→ {{a, c}, {b}},

{(a, a), (b, b), (c, c), (b, c), (c, b)} ←→ {{b, c}, {a}},

{(a, a), (b, b), (c, c), (a, b), (b, a), (a, c), (c, a), (b, c), (c, b)} ←→ {{a, b, c}}.

Definicja relacji bycia drobniejszym

Niech Π, Σ b¸

ed¸

a dowolnymi podzia lami danego zbioru A. M´

owimy, ˙ze podzia l

Π jest drobniejszy ni˙z podzia l Σ, gdy dla ka˙zdego elementu X podzia lu Π istnieje
element Y podzia lu Σ taki, ˙ze X jest podzbiorem zbioru Y .

W lasno´

sci formalne relacji bycia drobniejszym podaje nast¸

epuj¸

ace

Twierdzenie 2. Relacja bycia drobniejszym, tzn relacja dr okre´

slona na zbiorze

wszystkich podzia l´

ow zbioru A nast¸

epuj¸

aco:

ΠdrΣ wtw Π jest drobniejszy ni˙z

Σ, jest relacj¸

a zwrotn¸

a, antysymetryczn¸

a i przechodni¸

a.

Dow´

od: Oczywi´

scie dla dowolnego podzia lu Π danego zbioru A :

ΠdrΠ,

bowiem dla ka˙zdego elementu X podzia lu Π : X jest podzbiorem X.

W celu wykazania przechodnio´

sci przypu´

s´

cmy, ˙ze (1) ΠdrΣ oraz (2) ΣdrΘ

dla jakich´

s podzia l´

ow Π, Σ, Θ zbioru A. Aby wykaza´

c, ˙ze ΠdrΘ za l´

o˙zmy, ˙ze X

jest elementem podzia lu Π. W´

owczas z za lo˙zenia (1) istnieje taki element Y

podzia lu Σ, ˙ze X jest jego podzbiorem. Analogicznie, na mocy za lo˙zenia (2)
istnieje element Z podzia lu Θ taki, ˙ze Y jest podzbiorem Z. Zatem X jest
podzbiorem Z (bo relacja bycia podzbiorem jest przechodnia), co dowodzi, i˙z
ΠdrΘ. Aby dowie´

s´

c antysymetrii relacji dr za l´

o˙zmy, ˙ze (3) ΠdrΣ oraz (4) ΣdrΠ.

Celem jest wykazanie r´

owno´

sci: Π = Σ, tzn. tego, ˙ze podzia ly Π, Σ maj¸

a te same

elementy. Niech wi¸

ec X b¸

edzie elementem podzia lu Π. W´

owczas z za lo˙zenia (3)

istnieje element Y podzia lu Σ taki, ˙ze (5) X jest podzbiorem Y . Z za lo˙zenia
(4) istnieje element Z podzia lu Π taki, ˙ze (6) Y jest podzbiorem Z. Wobec
tego z (5) i (6) mamy: X jest podzbiorem Z, a poniewa˙z X jest niepusty, wi¸

ec

elementy X, Z podzia lu Π nie s¸

a roz l¸

aczne. Zatem X = Z na mocy warunku

(1) definicji podzia lu. Oznacza to wraz z (6), ˙ze Y jest podzbiorem X. St¸

ad i

z (5) wnosimy, ˙ze zbiory X, Y maj¸

a te same elementy, tzn. , ˙ze X = Y . Lecz

30

Y to element podzia lu Σ, Zatem X jest elementem podzia lu Σ. W ten spos´

ob

wykazano, ˙ze ka˙zdy element podzia lu Π jest elementem podzia lu Σ. Nale˙zy
jeszcze dowie´

s´

c, ˙ze ka˙zdy element podzia lu Σ jest elementem podzia lu Π, co

czyni si¸e analogicznie.

Definicja klasyfikacji

Przez klasyfikacj¸

e zbioru A rozumie si¸

e dowolny niepusty zbi´

or podzia l´

ow

zbioru A taki, ˙ze dla dowolnych podzia l´

ow Π, Σ z tego zbioru, Π jest drobniejszy

ni˙z Σ lub Σ jest drobniejszy ni˙z Π.

Przyk lad. Zbi´

or podzia l´

ow: {{a, b, c}}, {{a, b}, {c}}, {{a}, {b}, {c}} zbioru

A = {a, b, c} jest klasyfikacj¸

a tego zbioru.

31