1

PRZETWARZANIE SYGNAŁÓW

PYTANIA EGZAMINACYJNE

1. Uogólniony szereg Fouriera

2. Rozwini

ę

cie sygnałów w szereg wykładniczy.

3. Rozwini

ę

cie sygnałów w szereg trygonometryczny.

4. Całkowe przekształcenie Fouriera sygnałów nieokresowych.

5. Podstawowe wła

ś

ciwo

ś

ci przekształcenia Fouriera.

6. Analiza korelacyjna sygnałów o ograniczonej energii.

7. Analiza korelacyjna sygnałów o ograniczonej mocy.

8. Sygnał w

ą

skopasmowy.

9. Sygnał analityczny, widmo sygnału analitycznego.

10. Przekształcenie Hilberta

11. Układy liniowe ci

ą

głe.

12. Konwersja analogowo-cyfrowa.

13. Twierdzenie o próbkowaniu.

14. Próbkowanie idealne, naturalne i z pami

ę

ci

ą

.

15. Konwersja cyfrowo-analogowa.

16. Przekształcenie Fouriera sygnałów dyskretnych.

17. Dyskretne przekształcenie Fouriera.

18. Analiza korelacyjna dyskretnych sygnałów o ograniczonej energii.

19. Analiza korelacyjna dyskretnych sygnałów o ograniczonej mocy.

20. Splot dyskretny.

21. Przekształcenie Z.

22. Wst

ę

p do dyskretnych układów liniowych.

23. Układy liniowe dyskretne.

24. Elementy filtrów cyfrowych.

1. Uogólniony szereg Fouriera.

(do czego słu

ż

y, czym jest, podstawowe poj

ę

cia pozwalaj

ą

ce zdefiniowa

ć

uogólniony szereg Fouriera, etapy rozwijania w szereg, dla

sygnału rzeczywistego i zespolonego)

- jest to analityczna reprezentacja sygnału, która prowadzi do uproszczenia oblicze

ń

i umo

ż

liwia gł

ę

bsz

ą

interpretacje jego cech fizycznych

- reprezentacja dyskretna sygnału umo

ż

liwia zast

ą

pienia badania funkcyjnej zale

ż

no

ś

ci w nieprzeliczalnym zbiorze

punktów badaniem przeliczalnego, ale w ogólnym przypadku niesko

ń

czonego, zbioru współczynników (liczb

rzeczywistych lub zespolonych)

- jest to zagadnienie dyskretnej reprezentacji sygnału, które sprowadza si

ę

do zagadnienia aproksymacji, czyli

przybli

ż

enia sygnału x(t) szeregiem typu:

∑

=

n

i

i

i

t

u

a

0

)

(

Gdzie:

a

i

– współczynniki szeregu

u

i

(t) – ustalone funkcje czasu

fazy rozwijania w szereg:

- wybranie zbioru funkcji u

i

(t) o okre

ś

lonych wła

ś

ciwo

ś

ciach

- wyznaczenie liczby a

i

tak aby bł

ą

d aproksymacji był najmniejszy w sensie pewnego ustalonego

kryterium miary bł

ę

du (funkcje u

i

(t) s

ą

dobierane tak aby wraz ze wzrostem ich liczby bł

ą

d aproksymacji malał,

mówimy wówczas

ż

e ci

ą

g funkcji jest zbie

ż

ny w sensie ustalonego kryterium zbie

ż

no

ś

ci do sygnału x(t))

- szereg

Edited by Foxit Reader
Copyright(C) by Foxit Software Company,2005-2007
For Evaluation Only.

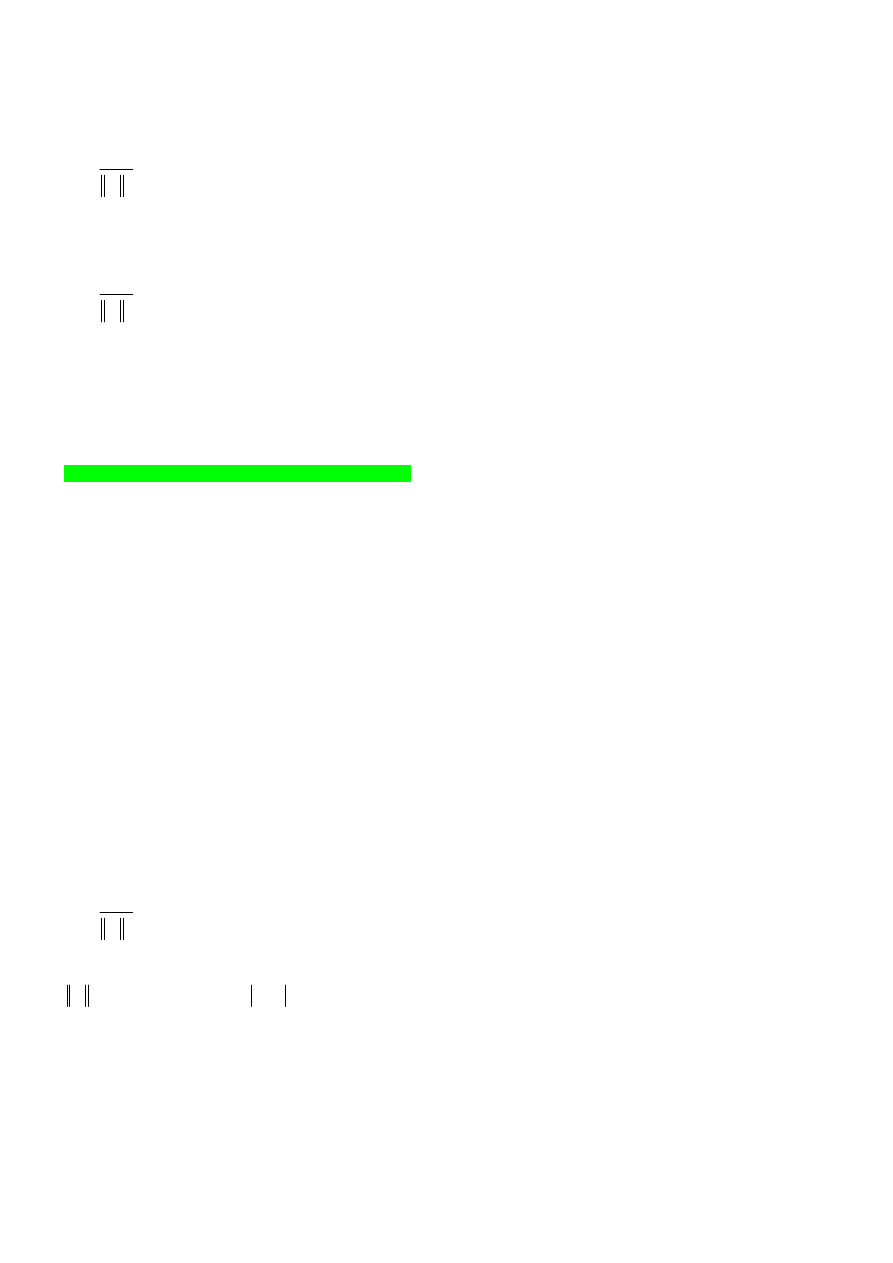
2

∑

=

=

n

i

i

i

t

u

a

t

x

0

)

(

)

(

Dla którego współczynniki a

i

okre

ś

lone s

ą

zale

ż

no

ś

ci

ą

∫

=

2

1

)

(

)

(

1

2

t

t

i

i

i

dt

t

u

t

x

u

a

nosi nazw

ę

uogólnionego szeregu Fouriera.

- współczynnik uogólnionego szeregu Fouriera dla układu ortogonalnych funkcji zespolonych wyznacza si

ę

z

nast

ę

puj

ą

cego wzoru

∫

∗

=

2

1

)

(

)

(

1

2

t

t

i

i

i

dt

t

u

t

x

u

a

Uogólniony szereg F. zapewnia najlepsz

ą

aproksymacj

ę

w sensie minimum bł

ę

du

ś

redniokwadratowego. Ma

bardzo istotne znaczenie praktyczne, zamiast bada

ć

zale

ż

no

ść

w nieprzeliczalnym zbiorze punktów, mo

ż

emy

charakteryzowa

ć

go przeliczalnym zbiorem współczynników. Do celów analizy wybiera si

ę

takie funkcje, które

zapewniaj

ą

najszybsz

ą

zbie

ż

no

ść

szeregu tzn. wymagaj

ą

cych najmniejszej liczby wyrazów szeregu, przy zadanej

dokładno

ś

ci przybli

ż

enia.

2. Rozwini

ę

cie sygnałów w szereg wykładniczy.

(rozpocz

ąć

od definicji uogólnionego szeregu Fouriera, wykaza

ć

,

ż

e zbiór funkcji wykładniczych spełnia warunki nakładane na zbiór funkcji

bazowych, przypadki rozwijania sygnału dowolnego oraz sygnału okresowego)

- jest to analityczna reprezentacja sygnału, która prowadzi do uproszczenia oblicze

ń

i umo

ż

liwia gł

ę

bsz

ą

interpretacje jego cech fizycznych

- reprezentacja dyskretna sygnału umo

ż

liwia zast

ą

pienia badania funkcyjnej zale

ż

no

ś

ci w nieprzeliczalnym zbiorze

punktów badaniem przeliczalnego, ale w ogólnym przypadku niesko

ń

czonego, zbioru współczynników (liczb

rzeczywistych lub zespolonych)

- jest to zagadnienie dyskretnej reprezentacji sygnału, które sprowadza si

ę

do zagadnienia aproksymacji, czyli

przybli

ż

enia sygnału x(t) szeregiem typu:

∑

=

n

i

i

i

t

u

a

0

)

(

Gdzie:

a

i

– współczynniki szeregu

u

i

(t) – ustalone funkcje czasu

- dowolny sygnał mo

ż

na rozwin

ąć

w przedziale (t

0

,t

0

+T) w szereg wykładniczy

∑

∞

−∞

=

=

i

t

ji

i

o

e

a

t

x

ω

)

(

- współczynniki uogólnionego szeregu F. dla układu funkcji zespolonych wyznacza si

ę

z nast

ę

puj

ą

cych wzorów:

∫

+

∗

=

T

t

t

i

i

i

dt

t

u

t

x

u

a

0

0

)

(

)

(

1

2

gdzie:

∫

∫

+

=

=

T

t

t

i

i

i

i

dt

t

u

dt

t

u

t

u

u

0

0

2

*

2

)

(

)

(

)

(

- zatem układ funkcji wykładniczych

3

∫

∫

+

−

+

−

=

=

=

T

t

t

t

ji

i

T

t

t

t

ji

t

ji

i

dt

e

t

x

T

a

oraz

T

dt

e

e

u

0

0

0

0

0

0

0

)

(

1

2

ω

ω

ω

Podsumowuj

ą

c:

Przedstawienie dowolnego sygnału x(t) za pomoc

ą

szeregu wykładniczego

∑

∞

−∞

=

=

i

t

ji

i

o

e

a

t

x

ω

)

(

Gdzie

∫

+

−

=

T

t

t

t

ji

i

dt

e

t

x

T

a

0

0

0

)

(

1

ω

nazywamy rozwini

ę

ciem sygnału w szereg wykładniczy Fouriera w przedziale (t

0

,t

0

+T).

- je

ż

eli sygnał x(t) jest okresowy z okresem T to równo

ść

jest zachowana w przediale niesko

ń

czonym, czyli

przedstawienie sygnału okresowego x(t), o okresie T, za pomoc

ą

szeregu wykładniczego

∑

∞

−∞

=

=

i

t

ji

i

e

a

t

x

0

)

(

ω

gdzie:

∫

+

−

=

T

t

t

t

ji

i

dt

e

t

x

T

a

0

0

0

)

(

1

ω

nazywamy rozwini

ę

ciem sygnału okresowego w szereg wykładniczy Fouriera w przedziale niesko

ń

czonym.

Współczynniki a

i

w ogólnym przypadku s

ą

wielko

ś

ciami zespolonymi uwzgl

ę

dniaj

ą

c,

ż

e

)

sin(

)

cos(

0

0

0

t

i

j

t

i

e

t

ji

ω

ω

ω

−

=

−

Otrzymamy:

is

ic

T

t

t

T

t

t

i

ja

a

tdt

i

t

x

T

j

tdt

i

t

x

T

a

−

=

−

=

∫

∫

+

+

0

0

0

0

0

0

sin

)

(

1

cos

)

(

1

ω

ω

gdzie:
a

is

– składowa urojona współczynnika a

i

a

ic

– składowa rzeczywista współczynnika a

i

- współczynniki a

i

mo

ż

na równie

ż

przedstawi

ć

w postaci wykładniczej

3. Rozwini

ę

cie sygnałów w szereg trygonometryczny.

(rozpocz

ąć

od definicji uogólnionego szeregu Fouriera, nie wykazywa

ć

,

ż

e zbiór funkcji trygonometrycznych spełnia warunki nakładane na

zbiór funkcji bazowych, przypadki rozwijania sygnału dowolnego oraz sygnału okresowego)

- jest to analityczna reprezentacja sygnału, która prowadzi do uproszczenia oblicze

ń

i umo

ż

liwia gł

ę

bsz

ą

interpretacje jego cech fizycznych

- reprezentacja dyskretna sygnału umo

ż

liwia zast

ą

pienia badania funkcyjnej zale

ż

no

ś

ci w nieprzeliczalnym zbiorze

punktów badaniem przeliczalnego, ale w ogólnym przypadku niesko

ń

czonego, zbioru współczynników (liczb

rzeczywistych lub zespolonych)

- jest to zagadnienie dyskretnej reprezentacji sygnału, które sprowadza si

ę

do zagadnienia aproksymacji, czyli

przybli

ż

enia sygnału x(t) szeregiem typu:

∑

=

n

i

i

i

t

u

a

0

)

(

Gdzie:

a

i

– współczynniki szeregu

u

i

(t) – ustalone funkcje czasu

Dla którego współczynniki a

i

okre

ś

lone s

ą

zale

ż

no

ś

ci

ą

4

∫

=

2

1

)

(

)

(

1

2

t

t

i

i

i

dt

t

u

t

x

u

a

- dowolny sygnał mo

ż

na rozwin

ąć

w przedziale (t

0

,t

0

+T) w szereg postaci

∑

∑

∞

=

∞

=

+

+

=

+

=

1

0

0

0

0

0

0

)

sin

cos

(

)

sin

cos

(

)

(

i

i

i

i

i

i

t

i

b

t

i

a

a

t

i

b

t

i

a

t

x

ω

ω

ω

ω

gdzie:

∫

∫

+

+

=

=

T

t

t

i

T

t

t

i

tdt

i

t

x

T

b

tdt

i

t

x

T

a

0

0

0

0

0

0

sin

)

(

2

cos

)

(

2

ω

ω

Podsumowuj

ą

c dowolny sygnał x(t) mo

ż

na rozwin

ąć

w szereg trygonometryczny w przedziale (t

0

,t

0

+T)

∑

∑

∞

=

∞

=

+

+

=

+

=

1

0

0

0

0

0

0

)

sin

cos

(

)

sin

cos

(

)

(

i

i

i

i

i

i

t

i

b

t

i

a

a

t

i

b

t

i

a

t

x

ω

ω

ω

ω

Gdzie:

∫

∫

∫

=

=

=

+

+

T

t

t

T

t

t

i

T

t

t

i

dt

t

x

T

a

tdt

i

t

x

T

b

tdt

i

t

x

T

a

0

0

0

0

0

0

)

(

1

sin

)

(

2

cos

)

(

2

0

0

0

ω

ω

A sygnał okresowy o okresie T mo

ż

na rozwin

ąć

w szereg trygonometryczny w przedziale niesko

ń

czonym (wzory

takie same jak wy

ż

ej).

4. Całkowe przekształcenie Fouriera sygnałów nieokresowych.

(uzasadni

ć

potrzeb

ę

poszukiwania innych narz

ę

dzi (innej reprezentacji) ni

ż

rozwijanie w szereg, koncepcja okresowego powielania sygnału

nieokresowego, widmo amplitudowe, widmo fazowe, warunki Dirichleta)

Aby sygnał x(t) mo

ż

na było rozwin

ąć

w szereg F. musi spełnia

ć

tzw. Warunki Dirichleta

1. sygnał x(t) musi by

ć

bezwzgl

ę

dnie całkowalny

∫

+

∞

<

T

t

t

dt

t

x

0

0

)

(

2. dla dowolnego przedziału czasu o długo

ś

ci T sygnał x(t) posiada sko

ń

czon

ą

liczb

ę

ekstremów

3. dla dowolnego przedziału czasu o długo

ś

ci T sygnał x(t0 posiada sko

ń

czon

ą

liczb

ę

punktów nieci

ą

gło

ś

ci

Ka

ż

dy przebieg okresowy, który mo

ż

na wytworzy

ć

w warunkach eksperymentalnych spełnia warunki Dirichleta.

Sygnał okresowy x(t, o okresie T mo

ż

na rozwin

ąć

w przedziale niesko

ń

czonym szereg trygonometryczny lub

wykładniczy, w rzeczywisto

ś

ci analizie poddawane s

ą

sygnały ograniczone w czasie oraz na ogół nieokresowe,

nastała potrzeba stworzenia narz

ę

dzi analitycznych do badania dowolnych sygnałów, w tym nieokresowych, o

dowolnym czasie trwania.

∫

∫

−

∞

∞

−

=

=

dt

e

t

x

X

d

e

X

t

x

t

j

t

j

ω

ω

ω

ω

ω

π

)

(

)

(

)

(

2

1

)

(

Wyra

ż

enia te stanowi

ą

par

ę

całkowych przekształce

ń

Fouriera.

Przekształcenie całkowe F. przedstawia sygnał impulsowy w postacie niesko

ń

czonej sumy małych składowych

harmonicznych okre

ś

lonych na całej osi pulsacji. Widmo X(w) jest zespolon

ą

funkcj

ą

pulsacji, nios

ą

c

ą

zarówno

informacje o amplitudzie jak i fazie elementarnych składowych harmonicznych.

5

Charakterystyk

ę

widmow

ą

sygnału x(t) mo

ż

na przedstawi

ć

w postaci trygonometrycznej oraz wykładniczej

gdzie:

Moduł charakterystyki widmowej sygnału nazywa si

ę

charakterystyk

ą

amplitudowo-cz

ę

stotliwo

ś

ciow

ą

(widmo

amplitudowe), a argument – charakterystyk

ą

azowo-cz

ę

stotliwo

ś

ciow

ą

(widmo fazowe).

Warunki istnienia transformaty Fouriera. Przekształcenie F. nie zawsze mo

ż

e by

ć

wyznaczone dla wszystkich

sygnałów x(t). musi spełnia

ć

warunki Dirichleta. W celu rozszerzenia zakresu stosowalno

ś

ci analizy

cz

ę

stotliwo

ś

ciowej na sygnały nie posiadaj

ą

ce F – transformaty w sensie zwykłym wprowadzane s

ą

uogólnienia, np. przekształcenie Fouriera w sensie granicznym.

5. Podstawowe wła

ś

ciwo

ś

ci przekształcenia Fouriera.

(nie wystarczy ich wymienienie - konieczna dyskusja kolejnych wła

ś

ciwo

ś

ci)

Dane s

ą

pary transformat:

Własno

ś

ci:

Twierdzenie o liniowo

ś

ci:

Twierdzenie o symetrii:

Je

ś

li sygnał o kształcie x(t) ma widmo X(w), to sygnał X(t) o kształcie tego widma ma widmo o kształcie sygnału

pierwotnego odbitego wzgl

ę

dem osi rz

ę

dnych przeskalowane o 2pi.

Twierdzenieo przesuni

ę

ciu w dziedzinie czasu:

Twierdzenie o przesuni

ę

ciu w dziedzinie cz

ę

stotliwo

ś

ci (o modulacji):

Twierdzenie o podobie

ń

stwie (o zamianie skali):

Twierdzenie o splocie w dziedzinie czasu

Twierdzenie o splocie w dziedzinie cz

ę

stotliwo

ś

ci:

Uogólnione twierdzenie Rayleigh:

Iloczyn skalarny jest proporcjonalny do iloczynu skalarnego ich widm

Twierdzenie o energii (Parsevala):

6

Twierdzenie o ró

ż

niczkowaniu w dziedzinie czasu:

Twierdzenie o funkcji korelacji wzajemnej:

6. Analiza korelacyjna sygnałów o ograniczonej energii.

(poj

ę

cie sygnału o ograniczonej energii, funkcja autokorelacji i jej wła

ś

ciwo

ś

ci, jej zwi

ą

zek z widmem energii, funkcja korelacji wzajemnej i

jej wła

ś

ciwo

ś

ci, zwi

ą

zek z widmem energii wzajemnej)

Funkcje korelacji – miary podobie

ń

stwa sygnałów. Porównanie analizowanego sygnału z innym w szczególnym

przypadku ze swoja własn

ą

, przesuni

ę

t

ą

w czasie kopia, potrzeba okre

ś

lenia ilo

ś

ciowego stopnia ich

podobie

ń

stwa. Miar

ą

tego podobie

ń

stwa jest funkcja autokorelacji okre

ś

lonej w oparciu o definicj

ę

iloczynu

skalarnego sygnałów.

Iloczyn skalarny zespolonego sygnału x(t) oraz jego przesuni

ę

ty o tał kopii

Funkcj

ą

autokorelacji sygnału x(t) o ograniczonej energii nazywamy zale

ż

no

ść

iloczynu skalarnego od przesuni

ę

cia

tał

Funkcja autokorelacji sygnału zespolonego jest zespolona, rzeczywistego – rzeczywista.

Własno

ś

ci funkcji autokorelacji:

- warto

ść

funkcji autokorelacji przy tał = 0 jest rzeczywista i równa energii sygnału

- funkcja autokorelacji sygnału jest funkcj

ą

hermitowsk

ą

(dla sygnałów rzeczywistych jest funkcj

ą

rzeczywist

ą

i

parzyst

ą

)

- dla ka

ż

dej warto

ś

ci przesuni

ę

cia tał moduł funkcji autokorelacji nie przekracza co do modułu warto

ś

ci energii

sygnału (funkcja autokorelacji ma zawsze dla tał = 0 dodatnie maksimum)

- je

ś

li dla pewnego przesuni

ę

cia tał0 funkcja autokorelacji

to sygnał x(t) i

s

ą

ortogonalne

- funkcja autokorelacji jest niezmiennicza wzgl

ę

dem przesuni

ę

cia, tzn. funkcja autokorelacji sygnału x(t) równa jest

funkcji autokorelacji sygnału

dla dowolnej warto

ś

ci przesuni

ę

cia t.

- funkcja autokorelacji sygnału o ograniczonej energii jest funkcj

ą

o ograniczonej energii (F-transormowaln

ą

)

Zwi

ą

zek funkcji autokorelacji z widmem energii sygnału

Para transformat Fouriera:

Zakładaj

ą

c w wyra

ż

eniu na odwrotn

ą

transformat

ę

Fouriera tał =0 otrzymamy

7

Podsumowuj

ą

c, energi

ę

sygnału mo

ż

na wyznaczy

ć

na trzy sposoby:

- w dziedzinie czasu

- w dziedzinie korelacyjnej

- w dziedzinie cz

ę

stotliwo

ś

ci

Widmo energii jest nieujemn

ą

, rzeczywist

ą

funkcj

ą

pulsacji. Funkcja autokorelacji sygnału rzeczywistego jest

funkcj

ą

rzeczywist

ą

i parzyst

ą

, zatem widmo energii sygnału te

ż

jest funkcj

ą

parzyst

ą

.

Charakterystyczn

ą

cech

ą

widmowej reprezentacji sygnału jest to,

ż

e energie odpowiadaj

ą

ce ró

ż

nym przedziałom

pulsacji sumuj

ą

si

ę

jako liczby rzeczywiste, podczas gdy opis widmowy za pomoc

ą

transformaty Fouriera

sygnału polega na sumowaniu amplitud zespolonych, opisuj

ą

cych wkłady poszczególnych małych przedziałów

pulsacji; amplitudy sumuj

ą

si

ę

jako liczby zespolone. Opis sygnału w funkcji autokorelacji (widma energii)

powoduj

ę

utrat

ę

informacji zawartej w fazowych charakterystykach sygnału. Na podstawie znajomo

ś

ci funkcji

autokorelacji nie mo

ż

na odtworzy

ć

czasowej postaci sygnału. Wszystkie sygnały o jednakowym kształcie,

ró

ż

ni

ą

ce si

ę

jedynie poło

ż

eniem na osi czasu, s

ą

w uj

ę

ciu energetycznym uto

ż

samione i tym samym

nierozró

ż

nialne.

Funkcja korelacji wzajemnej sygnałów:

Funkcja korelacji wzajemnej okre

ś

la zwi

ą

zki pomi

ę

dzy dwoma ró

ż

nymi sygnałami. Dla sygnałów o ograniczonej

energii x(t) oraz y(t) funkcja korelacji wzajemnej mi

ę

dzy sygnałem x(t) a y(t) okre

ś

lona jest wyra

ż

eniem

Podobnie funkcja korelacji wzajemnej mi

ę

dzy sygnałem y(t) a x(t)

Analogicznie do funkcji autokorelacji warto

ś

c funkcji korelacji wzajemnej dla tał=0 nazywana jest energi

ą

wzajemn

ą

:

Własno

ś

ci funkcji korelacji wzajemnej:

Funkcje korelacji wzajemnej sygnałów rzeczywistych nie s

ą

funkcjami parzystymi zmiennej tał oraz nie musz

ą

przybiera

ć

warto

ś

ci maksymalnych dla tał=0. warto

ść

funkcji korelacji wzajemnej nie przekraczaj

ą

co do

modułu pierwiastka z iloczynu energii obydwu sygnałów. Funkcje korelacji wzajemnej sygnałów o ograniczonej
energii s

ą

całkowalne w kwadracie, a wi

ę

c F-transformowalne.

Widma energii wzajemnej sygnałów:

Wielko

ść

nazywana jest widmem energii wzajemnej mi

ę

dzy sygnałem x(t) a y(t).

W przeciwie

ń

stwie do widma energii widma energii wzajemnej posiadaj

ą

cz

ęś

ciow

ą

informacj

ę

o fazach sygnałów.

7. Analiza korelacyjna sygnałów o ograniczonej mocy.

(poj

ę

cie sygnału o ograniczonej mocy, funkcja autokorelacji i jej wła

ś

ciwo

ś

ci, jej zwi

ą

zek z widmem mocy, funkcja korelacji wzajemnej i jej

wła

ś

ciwo

ś

ci, zwi

ą

zek z widmem mocy wzajemnej)

Sygnały analogowe o ograniczonej mocy

ś

redniej:

Dla sygnałów o ograniczonej mocy

ś

redniej całka definiuj

ą

ca autokorelacji jest rozbie

ż

na i definicja funkcji

autokorelacji dla tej klasy sygnałów jest inna.

Funkcj

ą

autokorelacji

ψ

x

(τ) sygnału x(t) o ograniczonej mocy średniej nazywamy wielkość graniczną:

8

Dla sygnałów okresowych:

Gdzie t

0

warto

ść

dowolna.

Własno

ś

ci funkcji autokorelacji:

- warto

ść

autokorelacji

ψ

x

(τ) przy tał = 0 jest rzeczywista i równa mocy sygnału

- funkcja autokorelacji sygnału jest funkcją hermitowską

- dla ka

ż

dej warto

ś

ci przsuni

ę

cia tał moduł funkcji autokorelacji

ψ

x

(τ) nie przekracza co do modułu wartości mocy

sygnału

Jeśli dla pewnego przesunięcia tał0 funkcja autokorelacji ψ

x

(τ)=0 to sygnały x(t) i x(t-tał0) są ortogonalne

Funkcja autokorelacji ψ

x

(τ)jest niezmiennicza względem przesunięcia, tzn funkcja autokorelacji sygnału x(t) równa jest funkcji

autokorelacji sygnału x(t-t

0

) dla dowolnej wartości przesunięcia t

0

- funkcja autokorelacji ψ

x

(τ) sygnału o ograniczonejmocy średniej jest F-transformowalna w sensie granicznym

- funkcja autokorelacji ψ

x

(τ) sygnału okresowego o okresie T

0

jest również funkcją okresową T

0

Związek funkcji autokorelacji z widmem mocy sygnału:
Własności energetyczne sygnałów o ograniczonej energii opisuje dziedzinie pulsacji widmo energii. Właściwości energetyczne

sygnałów o ograniczonej mocy średniej opisuje w dziedzinie pulsacji widmo mocy.

- widmem mocy sygnału o ograniczonej mocy średniej x(t) nazywamy granicę:

- widmo mocy równie

ż

nie zawiera informacji o strukturze sygnału

- je

ś

li x(t) jest rzeczywiste, to widmo moy jest funkcj

ą

rzeczywist

ą

i parzysta i prawdziwa jest zale

ż

no

ść

Funkcje korelacji wzajemnej sygnałów x(t) i y(t) o ograniczonej mocy

ś

redniej

- dla sygnałów okresowych

Własno

ś

ci funkcji korelacji wzajemnej sygnałów o ograniczonej mocy

ś

redniej s

ą

analogiczne do własno

ś

ci funkcji

korelacji wzajemnej sygnałów o ograniczonej energii.

Widma mocy wzajemnej sygnałów:
Funkcje korelacji wzajemnej i wima mocy wzajemnej sygnałów x(t) i y(t) o ograniczonej mocy

ś

redniej stanowi

ą

odpowiednio pary transformat Fouriera (w sensie granicznym).

8. Sygnał w

ą

skopasmowy.

(definicja, modele matematyczne)

Sygnały, których widma są różne od zera jedynie w pewnym przedziale o skończonej długości nazywamy sygnałami o
ograniczonym paśmie.
Sygnał wąskopasmowy jest szczególną klasą sygnałów o ograniczonym paśmie, jest to sygnał o widmie skupionym w
przedziale pulsacji o szerokości B w otoczeniu wartości środkowych

9

,

Matematyczne modele sygnałów wąskopasmowych:

Model (III)

Model (IV)

Sygnał wąskopasmowy jest złożonym drganiem powstałym przez jednoczesną modulację amplitudy i kąta harmonicznej fali
nośnej. Pulsacja chwilowa sygnału wąskopasmowego:

A jego obwiednia rzeczywista:

9. Sygnał analityczny, widmo sygnału analitycznego.

Funkcję:

nazywamy sygnałem analitycznym stowarzyszonym z sygnałem rzeczywistym x(t),

X(w)-widmo sygnału

Część urojona sygnału analitycznego:

nazywa się sygnałem skojarzonym z x(t)

Sygnał analityczny

można przedstawić jako wektor na płaszczyźnie zespolonej, rzut tego wektora na

oś rzeczywistą jest wartość sygnału x(t) w danej chwili czasu

Jeśli sygnał analityczny posiada widmo, to:

i

10

Z liniowości przekształcenia Fouriera wynika, że widmo sygnału analitycznego:

10. Przekształcenie Hilberta.

(definicja, zwi

ą

zek z definicj

ą

sygnału analitycznego, filtr kwadraturowy)

Wyra

ż

enia:

i

stanowi

ą

proste i odwrotne przekształcenie Hilberta.

Sygnał analityczny mo

ż

na zapisa

ć

:

Filtr kwadraturowy realizuje przesuni

ę

cie wszystkich składowych o -90

o

w zakresie dodatnich pulsacji i 90

o

dla

ujemnych bez zmiany ich amplitud, nazywany jest filtrem Hilberta. Własno

ś

ci przekształcenia Hilberta to liniowo

ść

oraz transformata od stałej równa jest 0. Sygnały

11. Układy liniowe ci

ą

głe.

(poj

ę

cie układu, klasyfikacja, opis układu w dziedzinie czasu i cz

ę

stotliwo

ś

ci)

Matematycznym modelem układu jest przekształcenie sygnału wej

ś

ciowego na sygnał wyj

ś

ciowy, układ mo

żę

by

ć

wielowej

ś

ciowy i wielowyj

ś

ciowy. Je

ś

li dziedzina i przeciwdziedzina s

ą

sygnałami ci

ą

głymi w czasie to układ

nazywamy analogowym.
Klasyfikacja układów:
- stacjonarny, je

ś

li jest opisany operatorem stacjonarnym, czyli je

ś

li dla ka

ż

dych x(t) i t

0

zachodzi zale

ż

no

ść

: Je

ś

li

nie jest ona spełniona to układ jest niestacjonarny.

Operatory stacjonarne to:ró

ż

niczkowanie, całkowanie,opó

ź

nienie w czasie, podnoszenie do kwadratu,

pierwiastkowanie i logarytmowanie do niestacjonarnych nale

ż

y np.

-układ liniowy, jesli spełnia zasad

ę

superpozycji, czyli odpowied

ź

układu na sum

ę

sygnałów wej

ś

ciowych równa

jest sumie odpowiedzi na ka

ż

dy z sygnałów, w przeciwnm wypadku układ jest nieliniowy

-układ nazywamy przyczynowym, je

ś

li warto

ść

sygnału na wyj

ś

ciu w dowolnej chwili t zale

ż

y od bie

żą

cej i

poprzednich warto

ś

ci sygnału wej

ś

ciowegoi nie zale

ż

y od warto

ś

ci przyszłych sygnału wej

ś

ciowego, w przeciwnym

wypadku układ jest nieprzyczynowy. Dla układu przyczynowego odpowied

ź

nie mo

ż

e wyprzedza

ć

wymuszenia.

Opisuj

ą

c układ w dziedzinie czasu posługujemy si

ę

:

-odpowiedzi

ą

impulsow

ą

h(t) – odpowiedzi

ą

układu na impuls Diracka

-odpowiedzi

ą

jednostkow

ą

r(t) – b

ę

d

ą

c

ą

reakcj

ą

na skok jednostkowy

Znajomo

ść

jednej z tych odpowiedzi pozwala znale

ść

odpowied

ź

układu na dowolne wymuszenie. W zwi

ą

zku z

tym,

ż

e nie mo

ż

na wygenerowa

ć

impulsu Diracka to odpowie

ź

impulsowa stanowi opis teoretyczny układu,

natomiast skok jednostkowy mo

ż

na w sposób przybli

ż

ony wytworzy

ć

, wi

ę

c odpowied

ź

r(t) stanowi narz

ę

dzie do

badania układów fizycznych

Je

ś

li T jest operatorem przekształcenia, to

wynika z tego zwi

ą

zek mi

ę

dzy

odpowiedziami czasowymi układu:

, oraz

Znaj

ą

c charakterystyki czasowe układu zwi

ą

zek pomi

ę

dzy wymuszeniem i odpowiedzi

ą

mo

ż

na wyznaczy

ć

wykorzystuj

ą

c operacje splotu:

oraz ze wzgl

ę

du na przemienno

ść

splotu:

Stacjonarne ukłay liniowe w dziedzinie cz

ę

stotliwo

ś

ci opisywane s

ą

charakterystykami amplitudowo-fazowymi:

, zale

ż

no

ść

charakterystyki od

wynika ze zwi

ą

zku z transformat

ą

Laplace’a

11

Zwi

ą

zek pomi

ę

dzy widmami sygnałów na wej

ś

ciu i wyj

ś

ciu okre

ś

la równanie transmisyjne układu:

12. Konwersja analogowo-cyfrowa.

(wprowadzenie-etapy, rozwijanie sygnałów w szereg Kotielnikowa-Shannona)

Operacja próbkowania dostarcza informacji o warto

ś

ci chwilowej sygnału w momentch próbkowania, jednak

znajomo

ść

próbek nie wystarcza do odtworzenia postaci analogowej. Próbkowaniu bez strat mog

ą

by

ć

poddawane jedynie sygnały nale

żą

ce do klasy sygnałów o ograniczonym pa

ś

mie.

Dowolny sygnał x(t) mo

ż

na rozwin

ąć

w szereg Fouriera. Mo

ż

na wykaza

ć

,

ż

e zbiór funkcji próbkuj

ą

cych Sa :

tworzy w przestrzeni sygnałów o ograniczonej energii i

ograniczonym pa

ś

mie układ ortogonalny w przedziale

Dowolny sygnał mo

ż

na rozwin

ąć

w przedziale

w szereg wzgl

ę

dem funkcji próbkuj

ą

cych Sa (szereg

Kotielnikowa-Shannona) o postaci:

, którego współczynniki wyznacza si

ę

ze wzorów:

, mo

ż

na wykaza

ć

,

ż

e współczynniki rozwini

ę

cia ai równe s

ą

warto

ś

ciom sygnału x(t) w chwilach i Ts, zatem:

13. Twierdzenie o próbkowaniu.

(twierdzenie, filozofia dowodu, ilustracja-z komentarzem-na przebiegach w dziedzinie czasu i cz

ę

stotliwo

ś

ci, zjawisko „aliasingu”)

Je

ż

eli sygnał x(t) jest sygnałem o widmie sko

ń

czonym w pa

ś

mie podstawowym w przedziale

gdzie

stała

jest najwy

ż

sz

ą

niezerow

ą

składow

ą

cz

ę

stotliwo

ś

ciow

ą

sygnału x(t) wówczas sygnał ten jest

równowa

ż

ny zbiorwi swoich próbek odległych od siebie o stały przedział (okres):

Sygnał wyj

ś

ciowy mo

ż

na odtworzy

ć

z ci

ą

gu próbek stosuj

ą

c idealny filtr dolnoprzepustowy o pa

ś

mie

i

wzmocnieniu 1. operacja filtracji pojedynczego okresu widma sygnału spróbkowanego:

, poniewa

ż

12

, to wykorzystuj

ą

c transformat

ę

Fouriera otrzymamy:

, wi

ę

c

Wykonuj

ą

c odwrotne przekształcenie Fouriera otrzymamy:

, nast

ę

pnie wykorzystanie wła

ś

ciwo

ś

ci okresowego

próbkowania dystrybucji sza oraz podstawiaj

ą

c

otrzymamy zale

ż

no

ść

:

, co dowodzi twierdzenie o próbkowaniu.

Gdy przedział próbkowania odbiega od jego warto

ś

ci granicznej

wówczas w zale

ż

no

ś

ci relacji

widmo sygnału przyjmie posta

ć

jak na rysunku:

gdy

powoduje nakładanie si

ę

s

ą

siednich kopii

widma nazywamy aliasingiem

14. Próbkowanie idealne, naturalne i z pami

ę

ci

ą

.

(dla ka

ż

dego z nich: idea na schemacie funkcjonalnym, analityczna posta

ć

widma sygnału wyj

ś

ciowego, przebiegi w dziedzinie czasu i

cz

ę

stotliwo

ś

ci sygnału po operacji próbkowania, komentarz)

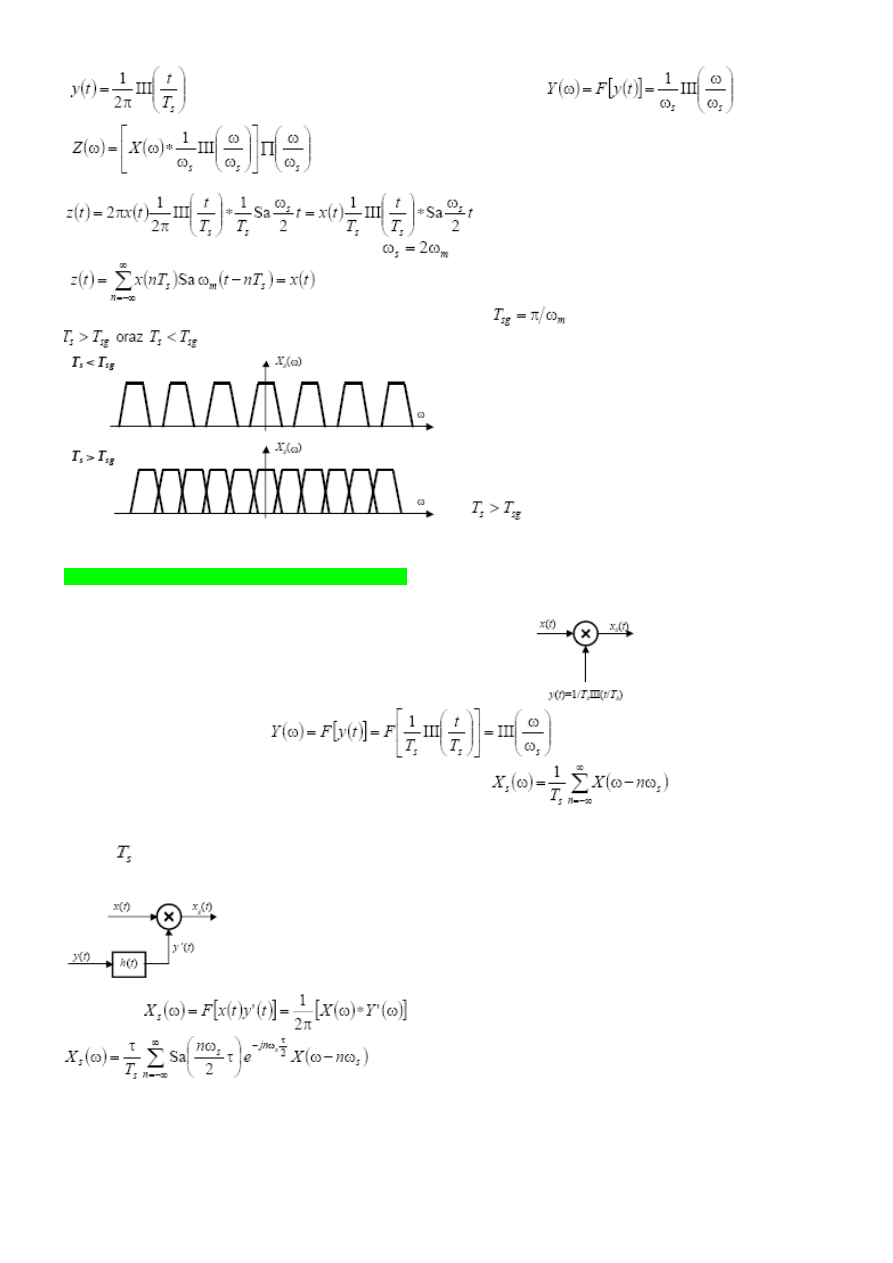
Próbkowanie idealne przebiega w układzie modulatora iloczynowego:

widmo sygnału próbkuj

ą

cego:

wykorzystuj

ą

c okresowe powielanie dystrybucji sza otrzymamy:

Operacja próbkowania idealnego wymaga wygenerowania ci

ą

gu impulsów Diracka, jest zatem nierealizowalna w

praktyce, sygnał ten mo

ż

na przybli

ż

y

ć

za pomoc

ą

ci

ą

gu impulsów prostok

ą

tnych o sko

ń

czonym czasie trwania i

okresie

. Taki sygnał mo

ż

na otrzyma

ć

jako odpowied

ź

filtru o odpowiedzi ipulsowej w postaci impulsu

prostok

ą

tnego o parametrach impulsów próbkuj

ą

cych na wymuszenie w postaci dystrybucji sza. Próbkowanie

naturalne mo

ż

na zrealizowa

ć

w układzie modulatora iloczynowego:

widmo sygnału na wyj

ś

ciu:

ostatecznie:

Przebiegi sygnałów i ich widma:

13

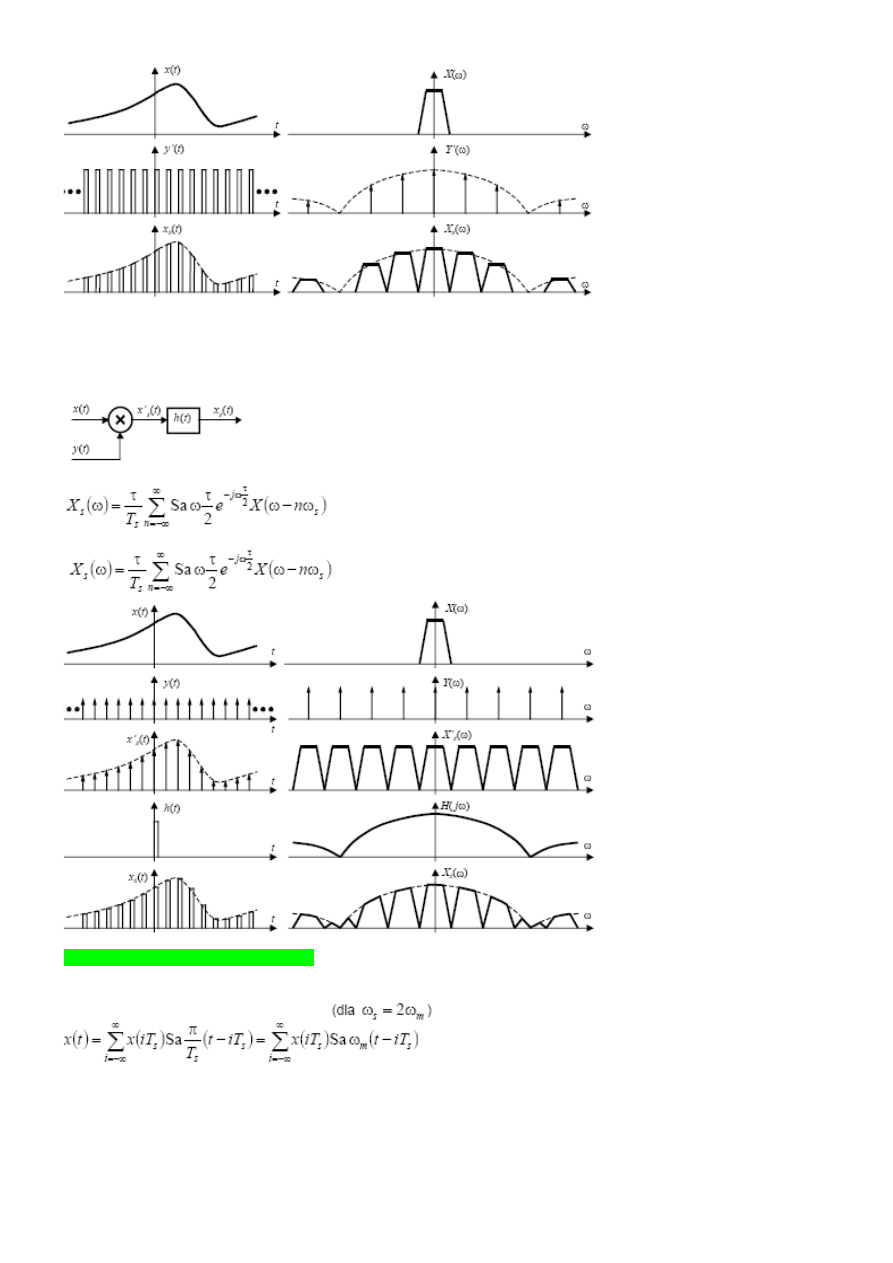
Próbkowanie chwilowe (z pami

ę

ci

ą

) mo

ż

na zrealizowa

ć

w idealnym modulatorze iloczynowym, którego próbki

wyj

ś

ciowe zostaj

ą

splecione w filtrze z jego odpowiedzi

ą

impulsw

ą

w postaci jednostkowego impulsu

prostok

ą

tnego. W tym próbkowaniu na impulsy prostok

ą

tne próbkuj

ą

ce nakładaj

ą

si

ę

jedynie chwilowe warto

ś

ci

sygnału próbkowanego, ale przy spełnionym kryterium Nyquista zawiera to pełn

ą

informacj

ę

o sygnale

próbkowanym.

Widmo sygnału na wyj

ś

ciu:

Ostatecznie:

15. Konwersja cyfrowo-analogowa.

(wprowadzenie, schodkowa metoda odtwarzania sygnału z próbek, wyj

ś

ciowy filtr korekcyjny)

Teoretycznie odtwarzanie sygnału analogowego z ci

ą

gu próbek z okresemTs

Okre

ś

la szereg Kotielnikowa-Shannona

:

, znajomo

ść

funkcji Sa pozwala wyznaczy

ć

warto

ść

sygnału

w dowolnej chwili t, niekso

ń

czona liczba sumowa

ń

wyklucza zastosowanie praktyczne, w praktyce stosuje si

ę

przetwornik C/A plus filtr dolnoprzepustowy, najprostsza jest metoda schodkowa:

14

, bł

ą

d tej metody powoduje zniekształcenia widma. Sygnał schodkowy stanowi

sum

ę

przesuni

ę

tych impulsów prostok

ą

tnych:

Zatem sygnał schodkowy:

Sygnał schodkowy mo

ż

emy wyrazi

ć

jako splot:

A widmo sygnału schodkowego:

Z wyra

ż

enia tego wynika,

ż

e widmo tego sygnału jest zniekształcone obwiedni

ą

funkcji Sa, zniekształcenia te

zmniejsza si

ę

stosuj

ą

c wi

ę

ksz

ą

cz

ę

stotliwo

ść

próbkowania lub stosuj

ą

c dolnoprzepustowy filtr korekcyjny

16. Przekształcenie Fouriera sygnałów dyskretnych.

(proste i odwrotne przekształcenie Fouriera sygnałów dyskretnych, wła

ś

ciwo

ś

ci przekształcenia Fouriera sygnałów dyskretnych)

Transformata Fouriera w zwykłym sensie:

Poniewa

ż

:

To wyra

ż

enie na prost

ą

transformat

ę

Fouriera przyjmie posta

ć

:

sygnałowi dyskretnemu

zostaje przyporz

ą

dkowana zespolona

funkcja o zmiennej rzeczywistej

Poniewa

ż

funkcja

jest funkcj

ą

okresow

ą

mo

ż

na j

ą

rozwin

ąć

w wykładniczy szereg Fouriera

Poszukiwanie sygnału w dziedzinie dyskretnej czasu opiera si

ę

na zale

ż

no

ś

ci:

Para transformat Fouriera dla nienormowanych zmiennych niezale

ż

nych:

15

, a dla zmiennych normowanych niezale

ż

nych:

Wła

ś

ciwo

ść

i przekształcenia Fouriera dla sygnałów dyskretnych:

-liniowo

ść

:

-przesuni

ę

cie w dziedzinie czasu:

-przesuni

ę

cie w dziedzinie cz

ę

stotliwo

ś

ci:

-splot w dziedzinie czasu:

-splot w dziedzinie cz

ę

stotliwo

ś

ci:

-uogólnione twierdzenie Rayleigha:

, iloczyn skalarny sygnałów jest

proporcjonalny do iloczynu skalarnego ich widm

-twierdzenie o energii Parsevala:

17. Dyskretne przekształcenie Fouriera.

(wprowadzenie, definicje prostego i odwrotnego dyskretnego przekształcenia Fouriera, dyskretne widmo amplitudowe i fazowe,
wła

ś

ciwo

ś

ci dyskretnego przekształcenia Fouriera)

Ze wzgl

ę

du na zło

ż

ono

ść

sygnałów współczesna analiza dokonuwana jest metodami numerycznymi.

Sygnał podlega obserwacji w sko

ń

czonej dziedzinie czasu i ma sko

ń

czon

ą

liczb

ę

próbek N=T/Ts.

Sygnał dyskretny posiada widmo okre

ś

lone wyra

ż

eniem:

Metody numeryczne polegaj

ą

na wyznaczeniu warto

ś

ci widma w sko

ń

czonej liczbie równoodległych punktów.

Najmniejsza liczba punktów wynosi N, gdy

ż

wtedy otrzymujemy N równa

ń

z N niewiadomymi. Dyskretna

transformata Fouriera (DTF) okre

ś

lona jest zale

ż

no

ś

ci

ą

:

, sygnałowi zostaje przyporz

ą

dkowana funkcja zmiennej k o okresie N. W skrócie

oznaczamy j

ą

X[k] i nazywamy N-punktow

ą

DTF. Funkcje:

Wprowadzana jest wielko

ść

:

, wykorzystuj

ą

c j

ą

DTF przyjmuje posta

ć

:

Odwrotna dyskretna transformata Fouriera (ODTF) okre

ś

lona jest wyra

ż

eniem:

Własmo

ś

ci DTF:

-liniowo

ść

16

-warto

ść

w k=0,

-wła

ś

ciwo

ść

symetrii: dla sygnału x[n] rzeczywistego i parzystego próbki widma symetryczne wzgl

ę

dem N/2 s

ą

parami sprz

ęż

one

-twierdzenie o przesuni

ę

ciu w dziedzinie czasu

-twierdzenie o przesuni

ę

ciu w dziedzinie cz

ę

stotliwo

ś

ci:

-twierdzenie Parsevala:

18. Analiza korelacyjna dyskretnych sygnałów o ograniczonej energii.

(poj

ę

cie dyskretnego sygnału o ograniczonej energii, funkcja autokorelacji i jej wła

ś

ciwo

ś

ci, jej zwi

ą

zek z widmem energii, funkcja korelacji

wzajemnej, zwi

ą

zek z widmem energii wzajemnej)

Sygnały dyskretne o ograniczonej energii:

Definicja funkcji autokorelacji:

jako iloczyn skalarny

Funkcj

ą

autokorelacji sygnału dyskretnego o ograniczonej energii nazywamy zale

ż

no

ść

iloczynu skalarnego od

przesuni

ę

cia m:

własno

ś

ci funkcji autokorelacji:

-jest funkcj

ą

hermitowsk

ą

:

-warto

ść

przy m=0 jest rzeczywista i równa energii sygnału:

-dla ka

ż

dej warto

ś

ci m moduł funkcji nie przekracza energii sygnału:

-jest niezmiennicza wzgl

ę

dem przesuni

ę

cia to znaczy,

ż

e x(n)=x(n-n

0

-funkcja autokorelacji sygnału o ograniczonej energii jest funkcj

ą

o ograniczonej energii

Zwi

ą

zek z widmem energii: w oparciu o tw. Rayleigha funkcja autokorelacji sygnału i jego widmo energii stanowi

ą

par

ę

transformat Fouriera:

, podstawiaj

ą

c w odwrotnej transformacie m=0 uzyskamy:

jest to pole pod krzyw

ą

widma energii u

ś

rednione za okres

Funkcja korelacji wzajemnej okre

ś

la zwi

ą

zki pomi

ę

dzy dwoma ró

ż

nymi sygnałami dyskretnymi. Dla sygnałów x(n) i

y(n) o ograniczonej energi funkcja korelacji mi

ę

dzy x a y okre

ś

la si

ę

:

a mi

ę

dzy y a x:

Warto

ść

funkcji korelacji dla m=0 nazywana jest energi

ą

wzajemn

ą

:

Wła

ś

ciwo

ś

ci:

-symetria przesuni

ę

cia dla sygnałów rzeczywistych

-warto

ś

ci funkcji nie przekraczaj

ą

co do modułu pierwiastka z iloczynu energii obu sygnałów

-je

ś

li warto

ść

jest 0 to sygnały x(n) oraz y(n-m) s

ą

ortogonalne

Widmo energii wzajemnej sygnałów dyskretnych x(n) i y(n) okre

ś

lone jest wyra

ż

eniem:

, a

mi

ę

dzy y(n) a x(n):

i wieldko

ść

i te tworz

ą

pary transformat Fouriera:

17

19. Analiza korelacyjna dyskretnych sygnałów o ograniczonej mocy.

(poj

ę

cie dyskretnego sygnału o ograniczonej mocy, funkcja autokorelacji i jej wła

ś

ciwo

ś

ci, sygnały N-okresowe, zwi

ą

zek z widmem mocy,

funkcja korelacji wzajemnej)

- sygnały

N

–okresowe

próbkowanie analogowego sygnału okresowego nie zawsze daje w wyniku sygnał okresowy;
je

ś

li analogowy sygnał okresowy

x

(

t

)

o okresie

T

jest próbkowany z okresem

T

s

takim,

ż

e

NT

s

=

T

, to otrzymany sygnał dyskretny jest okresowy z okresem

N

(dla unormowanego czasu)

nazywany inaczej sygnałem

N

–

okresowym

18

- zwi

ą

zek funkcji autokorelacji z widmem mocy sygnału

Wła

ś

ciwo

ś

ci energetyczne sygnałów o ograniczonej energii opisuje w dziedzinie pulsacji widmo

energii wła

ś

ciwo

ś

ci energetyczne sygnałów o ograniczonej mocy

ś

redniej opisuje w dziedzinie

pulsacji widmo mocy.

20. Splot dyskretny.

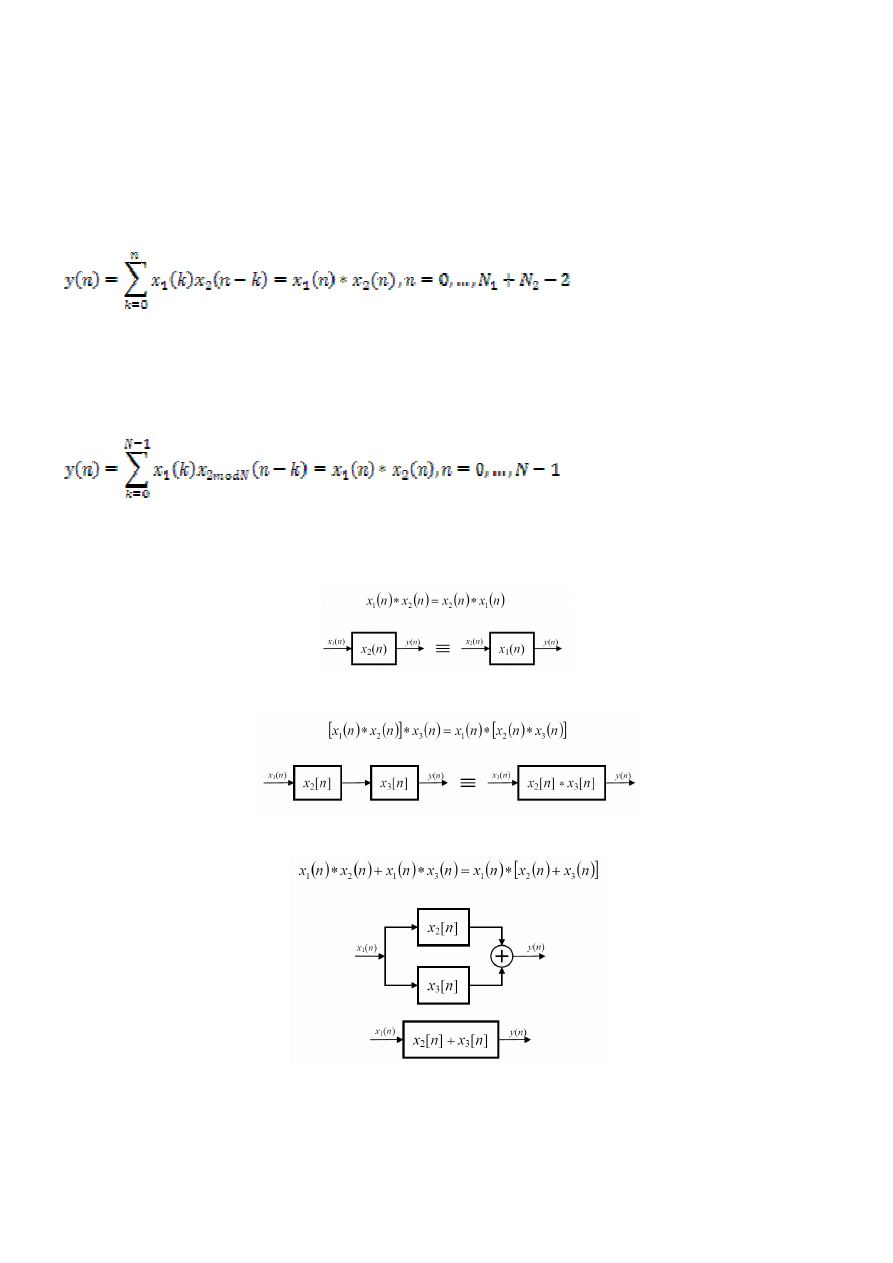
19

(definicja splotu liniowego i kołowego, wła

ś

ciwo

ś

ci splotu, wyznaczanie splotu przy pomocy DFT)

Splot dyskretny w systemach liniowych jest podstawowym narzędziem do opisu
wzajemnej zależności pomiędzy trzema sygnałami – sygnałem wejściowym,
odpowiedzią impulsowa i sygnałem wyjściowym. W systemach cyfrowych stanowi
matematyczną podstawę ich opisu.

1.

Splot liniowy

Splotem liniowym dwustronnym y[n] dwóch sygnałów czasu dyskretnego x

1

[n] i x

2

[n]

nazywamy sumę:

2.

Splot kołowy (splot cykliczny, splot okresowy (dla ciągów o długości N

1

= N

2

= N )

W splocie kołowym (cyklicznym) zamiast odwrócenia i przesunięcia sygnałów
stosujemy odpowiednio obrót cykliczny i opóźnienie cykliczne splatanych sygnałów.
Dla dwóch ciągów x[n] i h[n] o identycznej długości N splot kołowy definiujemy jako:

3.

Właściwości splotu dyskretnego.

- właściwość przemienności

- właściwości łączności

- właściwość rozdzielności względem dodawania

4. wyznaczanie splotu przy pomocy DFT

20

21.

Przekształcenie Z.

(proste i odwrotne przekształcenie Z, obszar zbie

ż

no

ś

ci, wła

ś

ciwo

ś

ci, zwi

ą

zek z przekształceniem Fouriera sygnału dyskretnego)

1.

Przekształcenie Z jest efektywnym narzędziem do analizy i syntezy sygnałów i

układów

czasu dyskretnego i jest odpowiednikiem przekształcenia Laplace’a dla układów czasu
ciągłego.
Transformata Z ciągu (funkcji argumentu całkowitego) {x(n)} jest funkcja zespolona
zmiennej zespolonej z zdefiniowana równaniem:

Jest to transformata dwustronna. Transformata Z jednostronna określona jest
wyrażeniem:

gdzie operacja całkowania odbywa sie po konturze zamkniętym, obejmującym
początek płaszczyzny zespolonej, leżącym całkowicie wewnątrz obszaru zbieżności
funkcji X (z) ze względu na trudności w całkowaniu zazwyczaj korzysta sie z
twierdzenia Cauchy’ego o residuach.



Obszar zbieżności:

określenie obszaru zbieżności jest bardzo istotne; istnieją funkcje posiadające
identyczne
transformaty Z , różniące sie jedynie obszarem zbieżności; zatem transformata Z jest
wzajemnie jednoznaczna po uwzględnieniu obszaru zbieżności

21

Właściwości przekształcenia Z:
- obszar zbieżności wymiernej transformaty Z nie może zawierać żadnych biegunów,
jest on zatem ograniczony przez bieguny, przez zero, lub nieskończoność (transformata
Z nie jest zbieżna w biegunie)
- twierdzenia graniczne: suma wszystkich próbek sygnału równa jest transformacie Z
tego sygnału dla z = 1

22

22.

Wst

ę

p do dyskretnych układów liniowych.

(poj

ę

cie układu dyskretnego, klasyfikacja, opis układu w dziedzinie czasu: odpowied

ź

impulsowa, równanie ró

ż

nicowe, schemat

strukturalny)

UKŁADY DYSKRETNE2
Pojecie układu
• matematyczna definicja (modelem) układu jest jednoznaczne przekształcenie
(operator) odwzorujące sygnał wejściowy x w sygnał wyjściowy y
jest to tzw. ujecie transmisyjne

• w ogólnym przypadku układ może być wielowejściowy i wielowyjściowy
• powyższa definicja układu ma charakter uniwersalny i może odnosić Sie do różnych
klas sygnałów
• jeśli dziedzina X i przeciwdziedzina Y operatora T są zbiorami sygnałów
dyskretnych w czasie, układ nazywamy dyskretnym

23

Klasyfikacja układów
• układ stacjonarny (niezmienny względem przesunięcia, inwariantny w czasie)
- operator przesunięcia w czasie sygnałów dyskretnych

- operator T określony w dziedzinie sygnałów dyskretnych nazywamy stacjonarnym,
Jeśli dla każdych x(n) i 0 n zachodzi przemienność

układ opisany operatorem stacjonarnym nazywamy układem stacjonarnym;
układ opisany operatorem nie spełniającym warunku stacjonarności nazywamy
układem niestacjonarnym

- dla stacjonarnych układów dyskretnych spełniona jest zależność

- operatory: mnożenia skalarnego y(n) = ax(n) oraz opóznienia y(n) = x(n −1)
w dziedzinie sygnałów dyskretnych sa operatorami stacjonarnymi
- operator typu y(n) = n x(n) w dziedzinie sygnałów dyskretnych jest operatorem
niestacjonarnymi
• układ liniowy
-

układ dyskretny nazywamy liniowym jeśli spełnia zasadę superpozycji, tzn.

odpowiedz układu na ważoną sumę sygnałów wejściowych równa jest sumie
ważonych odpowiednio odpowiedzi oddzielnie na każdy z sygnałów, w przeciwnym
przypadku układ nazywamy nieliniowym

• układ przyczynowy
jeżeli układ opisany operatorem T odwzorowuje zbiór sygnałów X w zbiór
sygnałów Y i jeżeli y

1

= T[x

1

] oraz y

2

= T[x

2

] wówczas operator T określony

w zbiorze sygnałów dyskretnych X nazywa się operatorem przyczynowym jeśli dla
każdych x

1

(n),x

2

(n)єX, i każdego n

0

z równości x

1

(n)=x

2

(n) , n < n

0

wynika równość

y

1

(n)=y

2

(n), n < n

układ opisany operatorem przyczynowym nazywamy układem przyczynowym; w
przeciwnym wypadku układ nazywamy układem nieprzyczynowym

z powyższych definicji wynika, że dla układu przyczynowego z równości

0

)

(

≡

n

x

dla n<n

0

, wynika równość

0

)

(

≡

n

y

n < n - zatem

odpowiedz układu

przyczynowego nie może poprzedzać wymuszenia

inaczej układ dyskretny nazywamy przyczynowym jeśli wartość sygnału na jego
wyjściu y(n) w dowolnym momencie czasu n zależy jedynie od bieżącej
i poprzednich wartości sygnały wejściowego i nie zależy od przyszłych wartości sygnału
wejściowego w przeciwnym przypadku układ nazywamy nieprzyczynowym.

* odpowiedz układu na pobudzenie testowe (przy zało*eniu zerowych warunków

24

poczatkowych) jest jego charakterystyka opisujaca w dziedzinie czasu relacje
„wejscie -wyjscie”



• odpowiedz impulsowa h(n) układu nazywamy jego reakcje (sygnał wyjściowy) na
pobudzenie w postaci impulsu Kroneckera (n) przy zerowych warunkach
początkowych

znajomość odpowiedzi impulsowej pozwala wyznaczyć reakcje układu na dowolne
pobudzenie

25

Do opisu przyczynowych układów liniowych, niezmiennych względem przesunięcia
wykorzystuje się równania różnicowe, wiążące z sobą pobudzenie układu x(n) z jego
odpowiedzią y(n); są t równania różnicowe M-tego rzędu o stałych współczynnikach
postaci

23. Układy liniowe dyskretne.

(równanie ró

ż

nicowe, transmitancja układu, charakterystyka cz

ę

stotliwo

ś

ciowa, klasyfikacja układów dyskretnych)

• do opisu przyczynowych układów liniowych, niezmiennych względem przesunięcia
,wykorzystuje się równania różnicowe, wiążące z sobą pobudzenie układu x(n) z jego
odpowiedzią y(n) ; są to równania różnicowe M -tego rzędu o stałych
współczynnikach postaci

gdzie {a

k

} oraz {b

k

} stałe współczynniki opisujące właściwości układu, niezależne od

x(n) oraz y(n).
Równania różnicowe są dyskretnym odpowiednikiem równań różniczkowych,
opisujących układy analogowe

26

• funkcje

nazywamy transmitancją (inaczej funkcją przenoszenia, przy założeniu zerowych
warunków początkowych) dyskretnego, przyczynowego układu liniowego,
niezmiennego względem przesunięcia; transmitancja układu H(z) jest transformatą Z
jego odpowiedzi impulsowej h(n)
• wyznaczając transformatę Z równania różnicowego określamy transmitancję układu

- charakterystyka częstotliwościowa układu dyskretnego

24. Elementy filtrów cyfrowych.

(rodzaje struktur filtrów FIR oraz IIR, porównanie wła

ś

ciwo

ś

ci filtrów FIR oraz IIR )

• stacjonarny układ (filtr) liniowy dyskretny opisuje jest równanie różnicowe
( a

0

= 0 )

(współczynniki a

k

i b

k

decydują o właściwościach układu, max(M,N) - rząd filtru)

Klasyfikacja:

• struktura filtru IIR opisana powyższym równaniem przedstawiona jest na schemacie
(1 forma bezpośrednia niekanoniczna)

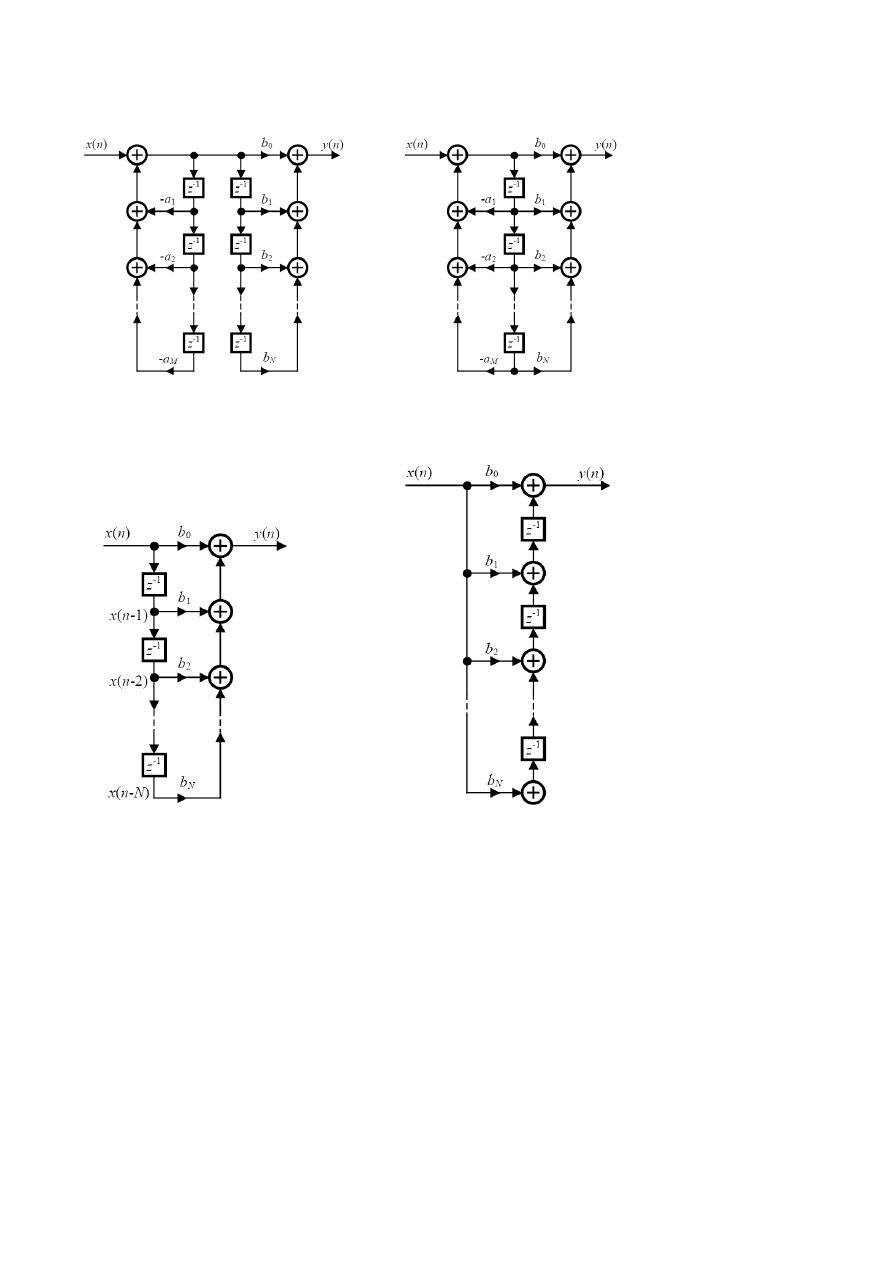
27

• 2 forma bezpośrednia niekanoniczna oraz 2 forma bezpośrednia kanoniczna

• odwrócona bezpośrednia forma kanoniczna filtrów FIR

• jeśli h(n) układu FIR spełnia warunek symetrii

>

∈<

−

=

N

n

dla

n

N

h

n

h

,

0

)

(

)

(

to układ posiada liniową charakterystykę fazową

• uproszczona struktura filtru FIR o liniowej charakterystyce fazowej dla parzystej
liczby ogniw filtru ( N nieparzyste)

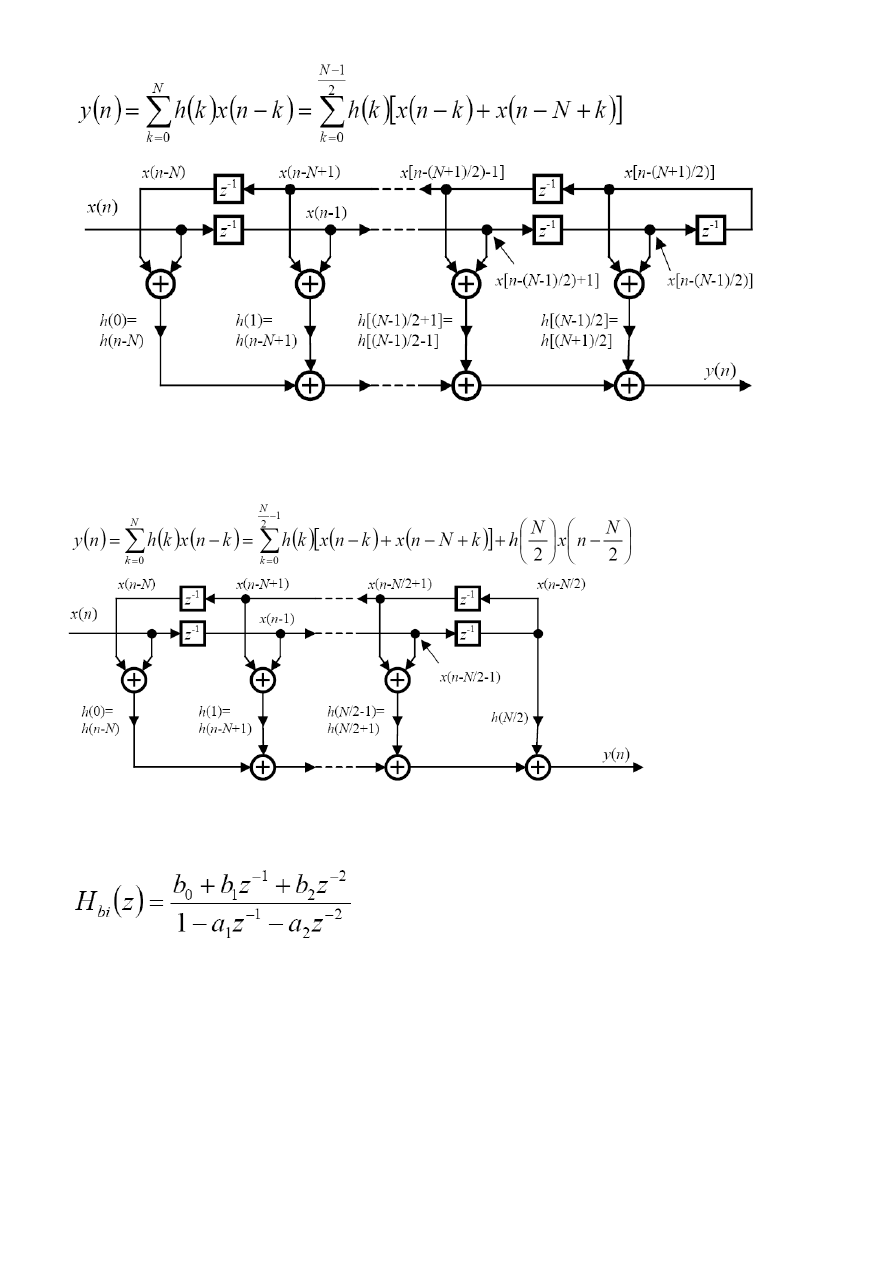
28

• uproszczona struktura filtru FIR o liniowej charakterystyce fazowej

)

(

)

(

n

N

h

n

h

−

=

dla

nieparzystej liczby ogniw filtru ( N parzyste)

• przedstawione realizacje nie mają znaczenia praktycznego, zwłaszcza gdy rząd filtru
przekracza wartość 3-5; dla realizacji filtrów wyższych rzędów, dla zmniejszenia ich
wrażliwości na zmiany wartości współczynników stosuje się kaskadowe lub równoległe
połączenia sekcji drugiego rzędu, tzw. sekcji bikwadratowych o transmitancji postaci

29