Budownictwo przemysłowe – słup skrajny.

2.3.2. Słup skrajny.
Wstępne przyjęcie wymiarów słupa.

•

wysokość

h

s

= H

p

0,96­h

I550PE

0,300,10=5,180,96­0,550,300,10=5,99 m≈6,0 m

•

wymiary przekroju:

○

h = 0,80 m

○

b = 0,50 m

2.3.2.1. Przedstawienie schematów obciążeń działających na słup w płaszczyźnie prostopadlej do toru.
Schematy obciążeń słupa w płaszczyźnie prostopadłej do toru:

•

obciążenie stałe:

○

ciężar belki

Q

b

=

f

m

b

g l=1,1⋅148,37

kg

m

⋅9,81 m

s

2

⋅7 m=11,21 kN

○

ciężar własny słupa

Q

p

=

f



s

l b h=1,1⋅25

kN

m

3

⋅5,59 m⋅0,5 m⋅0,8 m=61,49 kN

•

obciążenie od suwnic:

○

położenie A suwnicy

◊

maksymalna siła pozioma przy położeniu A suwnicy:

H

⊥ max

=H '

max

i



i

=81,23⋅1,004544,27⋅0,0345=83,123 kN

◊

maksymalna siła pionowa przy położeniu A suwnicy

R

max

=N

max

∑

i=1

4



i

=369,05⋅1,00450,17770,0345­0,0115=444,521 kN

R

max

=444,521 kN

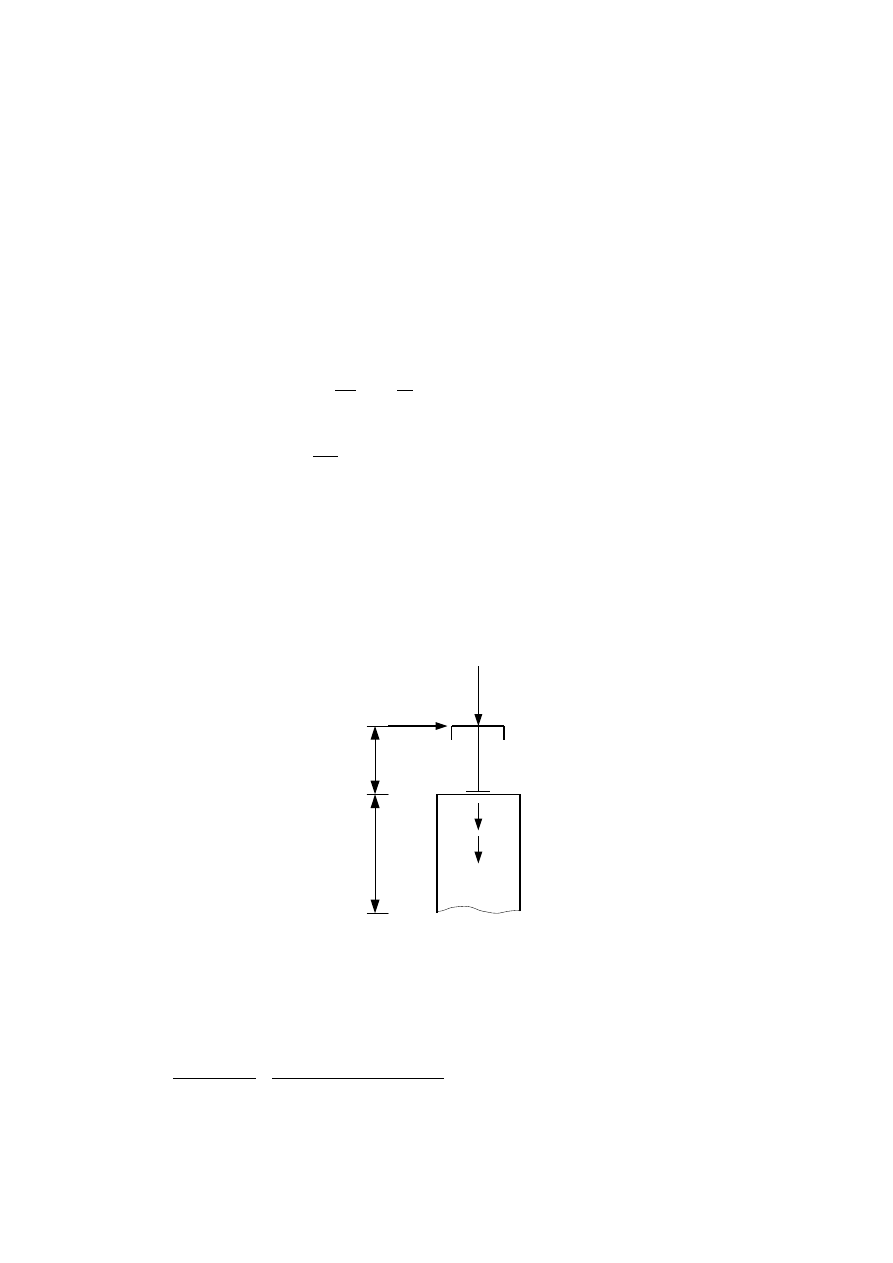
Q

b

=11,21 kN

Q

s

=61,49 kN

0,55 m

5,59 m

H

⊥ max

=83,123 kN

Schemat IA

Wyznaczenie sił przekrojowych:

M

Sd

A

= H

⊥

⋅ h

s

h

I550

=83,123⋅6,00,55=544,46 kNm

N

Sd

IA

=RQ

b

Q

s

=444,52111,2161,49=517,22 kNm

Wyznaczenie mimośrodu:

e

e

=

M

Sd

A

RQ

b

Q

s

=

544,46

444,52111,2161,49

=1,05 m

◊

minimalna siła pionowa przy położeniu A suwnicy

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

R

min

= N

min

∑

i=1

4



i

=114,95⋅1,00450,17770,0345­0,0115=139,86 kN

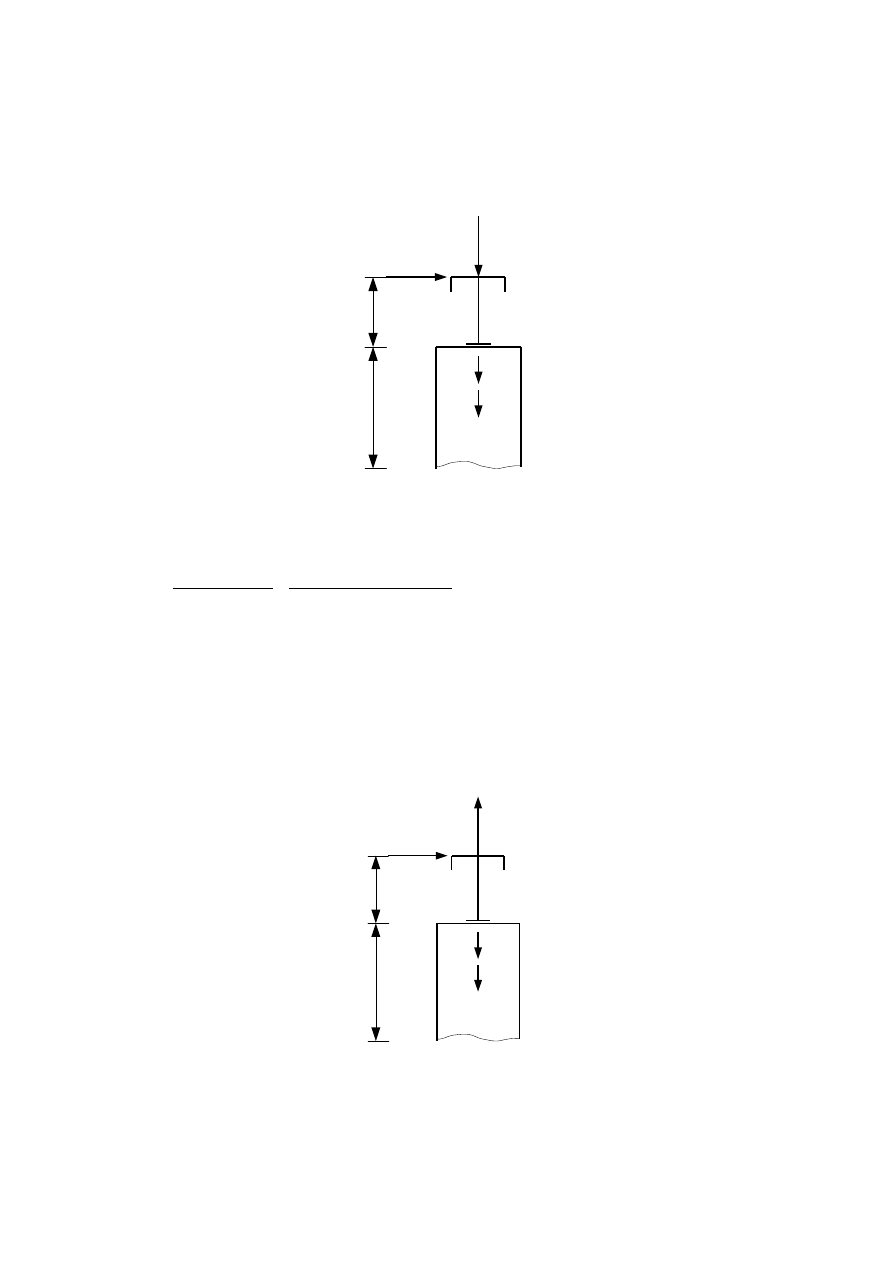
Q

b

=11,21 kN

Q

s

=61,49 kN

0,55 m

5,59 m

H

⊥ max

=83,123 kN

R

min

=139,86 kN

Schemat IIA

N

Sd

IIA

= RQ

b

Q

s

=139,8611,2161,49=212,56 kNm

Wyznaczenie mimośrodu:

e

e

=

M

Sd

A

R

min

Q

b

Q

s

=

544,46

139,8611,2161,49

=2,56 m

○

położenie B suwnicy

◊

maksymalna siła pozioma przy położeniu B suwnicy:

H

⊥ max

=H '

max

i



i

=81,23⋅0,126844,27⋅0,0115=10,81 kN

◊

maksymalna siła pionowa przy położeniu B suwnicy

R

max

=V

max

∑

i=1

4



i

=114,95⋅­0,12680,0335369,05 0,0323­0,0115=­3,05 kN

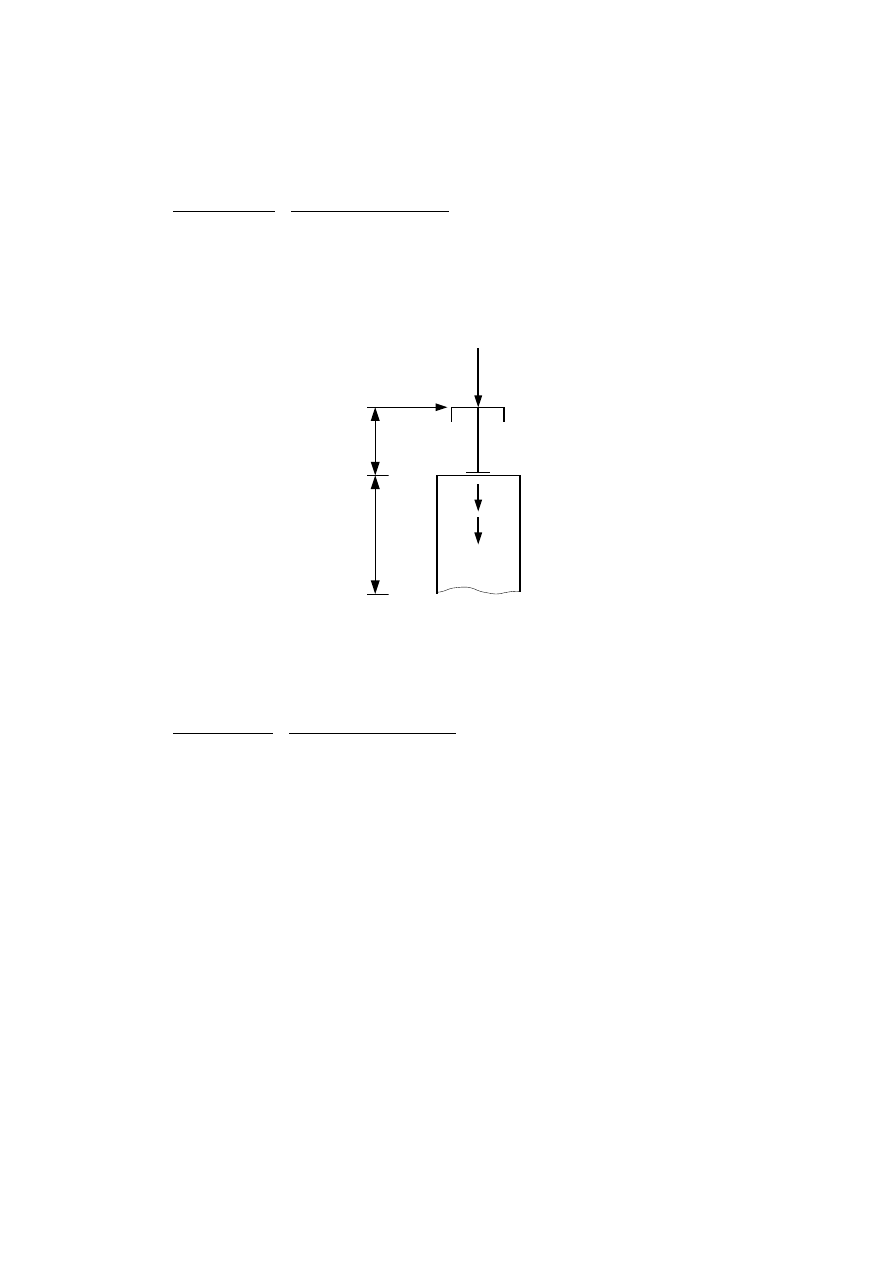
Q

b

=11,21 kN

Q

s

=61,49 kN

0,55 m

5,59 m

R

max

=­3,05 kN

H

⊥ max

=10,81 kN

Schemat IB

Wyznaczenie sił przekrojowych:

M

Sd

A

= H

⊥ max

⋅h

s

h

I550

=10,81⋅6,00,55=70,81 kNm

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

N

Sd

IB

=RQ

b

Q

s

=­3,0511,2161,49=69,65 kNm

Wyznaczenie mimośrodu:

e

e

=

M

Sd

A

R

max

Q

b

Q

s

=

70,81

­3,0511,2161,49

=1,02 m

◊

minimalna siła pionowa przy położeniu B suwnicy

R

min

=369,05⋅­0,12680,335114,95 0,0323­0,0115=­32,04 kN

Q

b

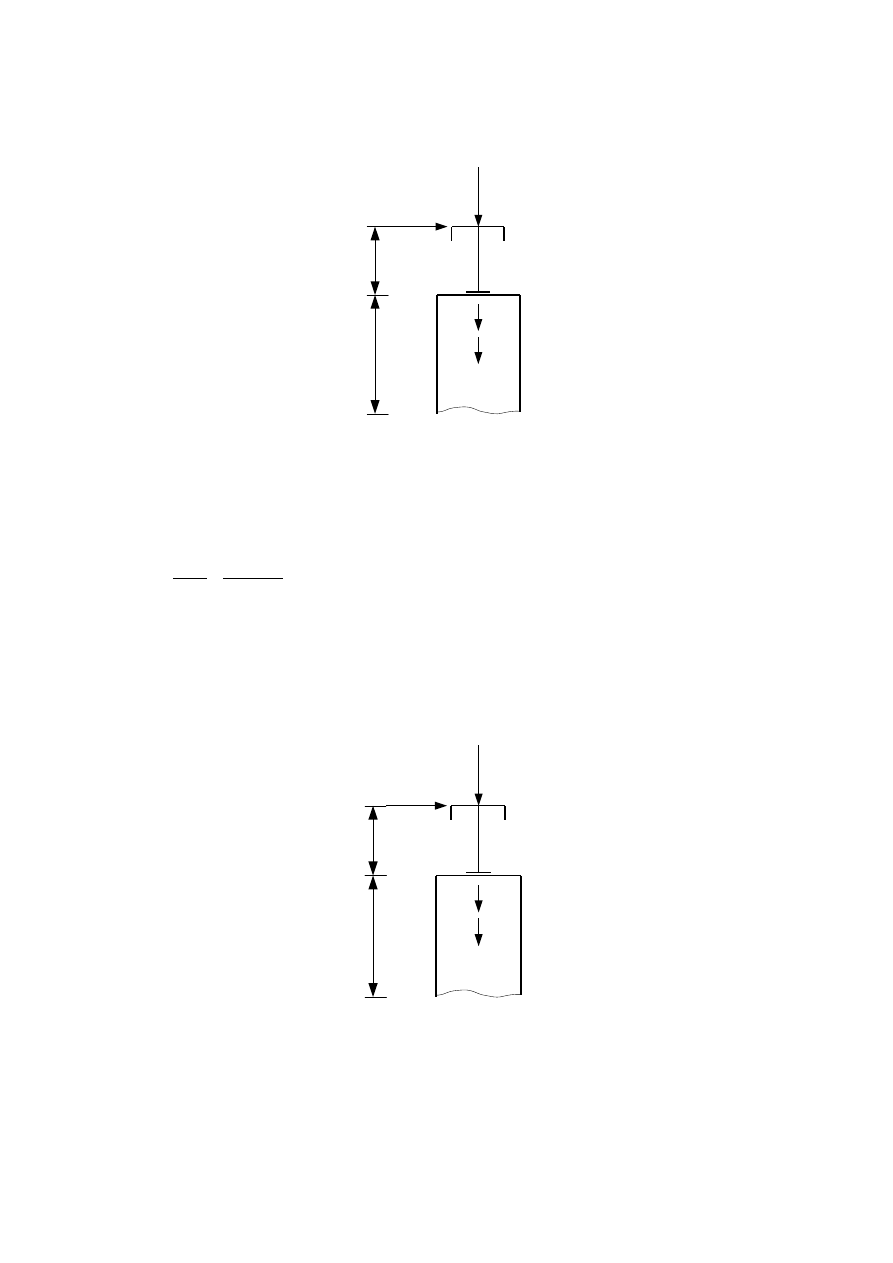
=11,21 kN

Q

s

=61,49 kN

0,55 m

5,59 m

H

⊥ max

=10,81 kN

R

min

=­32,04 kN

Schemat IIB

N

Sd

IIB

=RQ

b

Q

s

=­32,0411,2161,49=40,66 kNm

Wyznaczenie mimośrodu:

e

e

=

M

Sd

A

R

min

Q

b

Q

s

=

70,81

­32,0411,2161,49

=1,74 m

○

położenie C suwnicy

◊

maksymalna siła pozioma przy położeniu C suwnicy:

H

⊥ max

=H '

max

i



i

=81,23⋅0,984544,27⋅0,9795=123,33 kN

◊

maksymalna siła pionowa przy położeniu C suwnicy

R

max

=N

max

∑

i=1

4



i

=369,05⋅­0,00620,98450,97950,0011=722,932 kN

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

Q

b

=11,21 kN

Q

s

=61,49 kN

0,55 m

5,59 m

R

max

=722,932 kN

H

⊥ max

=123,33 kN

Schemat IC

Wyznaczenie sił przekrojowych:

M

Sd

A

= H

⊥

⋅ h

s

h

I550

=123,33⋅6,00,55=805,65 kNm

N

Sd

A

=RQ

b

Q

s

=722,93211,2161,49=795,632 m

Wyznaczenie mimośrodu:

e

e

=

M

Sd

A

N

Sd

A

= 805,65

795,632

=1,012 m

◊

minimalna siła pionowa przy położeniu C suwnicy

R

min

= N

min

∑

i=1

4



i

=114,95⋅­0,00620,98450,97950,0011=225,17 kN

Q

b

=11,21 kN

Q

s

=61,49 kN

0,55 m

5,59 m

R

min

=225,17 kN

H

⊥ max

=123,33 kN

Schemat IIC

Wyznaczenie sił przekrojowych:

M

Sd

A

= H

⊥

⋅ h

s

h

I550

=123,33⋅6,00,55=805,65 kNm

N

Sd

A

=RQ

b

Q

s

=225,1711,2161,49=297,87 m

Wyznaczenie mimośrodu:

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

e

e

=

M

Sd

A

N

Sd

A

=805,65

297,87

=2,70 m

Najbardziej niekorzystnym przepadkeim obciążenia słupa skrajnego jest jego obciążenie zgodnie ze

schematem IIC i obliczenie zbrojenie przeprowadzimy dla tego przypadku.

2.3.2.2. Obliczenie wymaganej ilości zbrojenia w słupie ze względu na obciążenia działające w

płaszczyźnie prostopadłej do toru.

Dla celów projektowych zakładam:

•

klasa ekspozycji XC4 (wnętrza budynku o umiarkowanej wilgotności)

•

beton klasy C25/30 (B30) dla całej konstrukcji:

○

wytrzymałość charakterystyczna

f

ck

= 25 MPa

○

wytrzymałość obliczeniowa

f

cd

=16,7 MPa

○

średnia wytrzymałość na rozciąganie

f

ctm

= 2,6 MPa

○

wytrzym. obl. na rozc. w żelbet. i spręż.

f

ctd

= 1,2 MPa

○

moduł sprężystości

E

cm

= 31Gpa

•

stal zbrojeniowa klasy A-III, 34GS:

○

charakterystyczna granica plastyczności

f

yk

= 410 MPa

○

obliczeniowa granica plastyczności

f

yd

= 350 MPa

○

moduł sprężystości dla wszystkich klas stali

E

s

=200 Gpa

•

początkowa średnica zbrojenia Φ = 20 mm

Określenie grubości otulenia prętów zbrojenia:

c

min

≥max

{

=20 mm

d

g

≤32 mm

d

g

5=165=21 mm

25 mm

c

nom

=c

min

 c=255=30[mm ]

a

1

=c

nom



strz





2

=308 20

2

=48[mm ]

Przyjmuję grubość otulenia a

1

= 50 mm.

Wymiary przekroju:

b=0,5 m
h=0,8 m

d =h­a

1

=0,8­0,05=0,75 m

Długość słupa:

l

col

=6,0 m

Długośc wyboczeniwa słupa:

l

0

=⋅l

col

=2,0⋅6,0 m=12,0 m

Wyznaczenie zbrojenia minimalnego(wyznaczam ze względu na maksymalną siłę normalną tj. siłę ze
schematu A):

A

s min

=max

{

0,15

N

Sd

f

yd

=0,15

722,932

350000

=0,00030983 m

2

=2,22 cm

2

0,003 b d =0,003⋅0,50⋅0,75=0,001125 m

2

=11,25 cm

2

Mimośród działania siły (schemat IIC).

Krzysztof Wieczorek

KBI2 2006 /2007

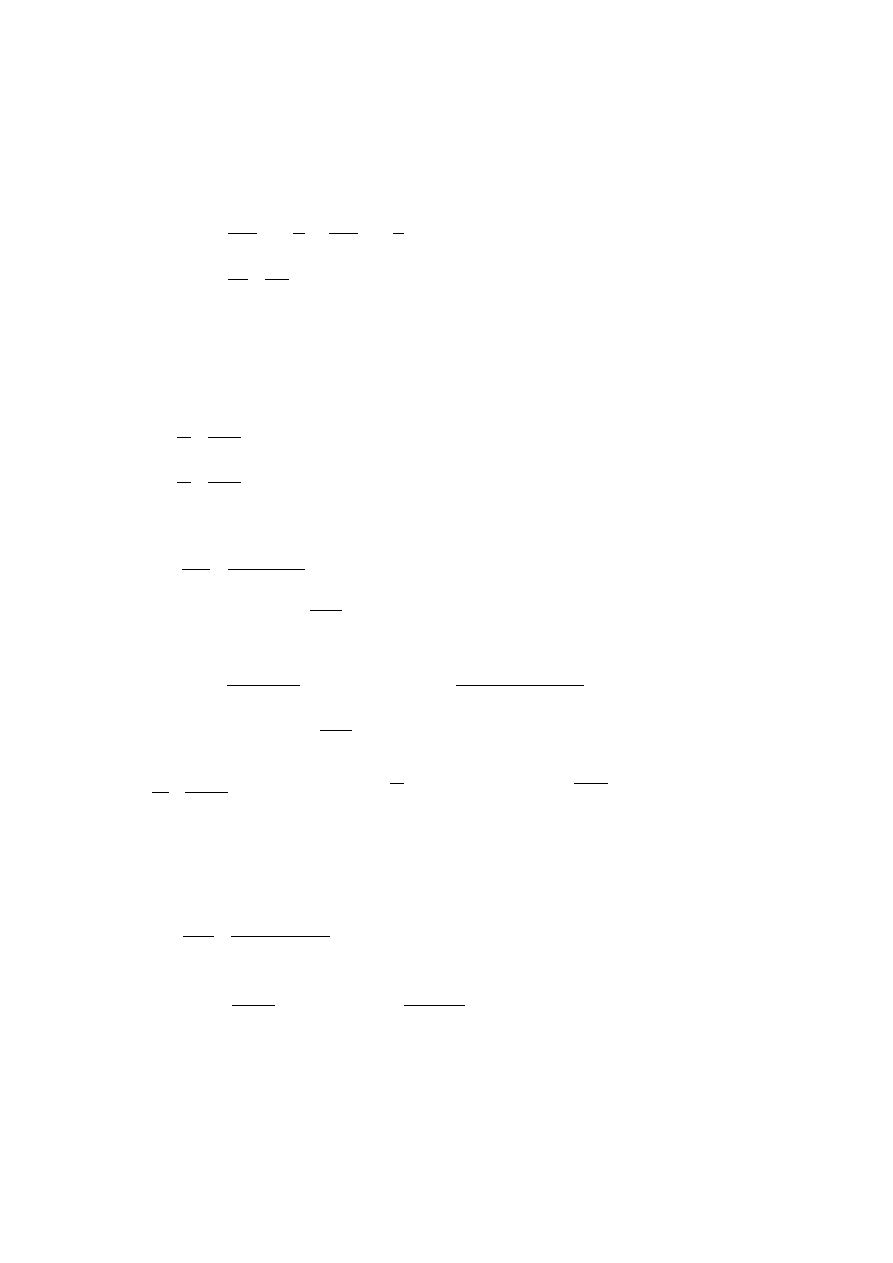
Budownictwo przemysłowe – słup skrajny.

e

e

=2,70 m

Wyznaczenie maksymalnego mimośrodu niezamierzonego (n – pierwsza kondygnacja licząc od góry).

e

a

=max

{

l

col

600



1

1
n



= 6,0

600



1

1
1



=0,020 m

h

30

=0,8

30

=0,027 m ⇐ e

a

=0,027 m

0,001

Obliczenie mimośrodu początkowego względem środka ciężkości przkroju betonu:

e

0

=e

a

e

e

=0,0272,70=2,731 m

Smukłość:

=

l

0

i

=12,0

0,23

=51,9625

=

l

0

h

=12,0

0,80

=15,007

Należy uwzględnić wpływ wyboczenia.

Obliczenie zwiększonego mimorodu początkowego:

I

c

= b h

3

12

= 0,50

⋅0,80

3

12

=0,021 m

4

E

cm

=31GPa=31000 MN

m

2

=1,5%=0,015

I

s

=b d



h­a

1

­a

2

2



2

=0,015⋅0,50⋅0,75



0,80­0,05­0,05

2



2

=0,000689 m

4

E

s

=200 GPa=200000 MN

m

2

e

0

h

=2,731

0,80

=3,414

{

0,50­0,01

l

0

h

­0,01 f

cd

=0,50­0,01 12,0

0,80

­0,01⋅16,7=0,183

0,05

Wilgotność względna powierza RH = 50%
Miarodajny przekrój elementu wynosi:

h

0

=

2 A

c

u

= 2

⋅800⋅500

2⋅800500

=307,692 mm ⇒ ∞ ,t

0

=2,625

N

Sd ,lt

=268,083 kN

k

lt

=10,5

N

Sd , lt

N

Sd

∞ , t

0

=10,5 268,083

297,87

2,625=2,181

Krzysztof Wieczorek

KBI2 2006 /2007

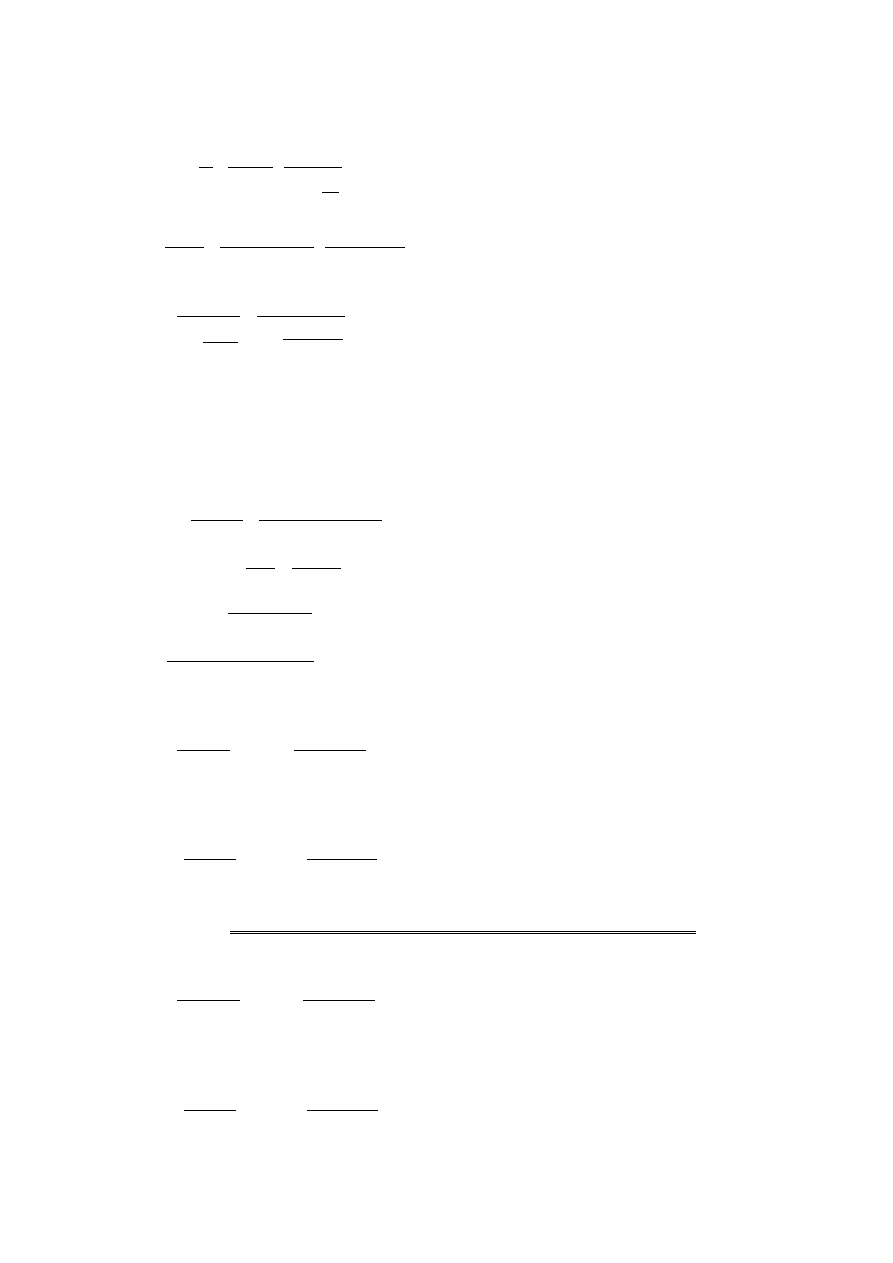
Budownictwo przemysłowe – słup skrajny.

N

crit

=9

l

0

2

⋅

[

E

cm

I

c

2 k

lt



0,11

0,1

e

0

h

0,1



E

s

I

s

]

=

=

9

12,0

2

⋅

[

31000⋅0,021

2⋅2,181



0,11

0,12,588

0,1



200000⋅0,000689

]

=9,857 MN =9 857,38 kN

N

Sd

=297,87 kN ≤0,9 N

crit

=0,9⋅9 857,38=8871,639 kN

=

1

1­

N

Sd

N

cdit

=

1

1­

297,87

9857,38

=1,031

e

tot

= e

0

=1,031⋅2,731=2,816 m

Obliczanie mimośrodu względem środka ciężkości zbrojenia rozciąganego:

e

s1

=e

tot

0,5 h­a

1

=2,8160,5⋅0,80­0,05=3,17 m

e

s2

=e

tot

­0,5 ha

2

=2,816­0,5⋅0,800,05=2,47 m

Obliczenie powierzchni zbrojenia ściskanego:



eff

=

N

Sd

b d f

cd

=

297,87

0,50⋅0,75⋅16700

=0,048≤

eff ,lim

=0,53 - duży mimosród.



eff

=0,048

2 a

2

d

= 2

⋅0,05
0,75

=0,1333

A

s1

=A

s2

=

N

Sd

e

s2



d ­a

2



f

yd

=

=

297,87⋅2,47



0,75­0,05



350000

=0,002999 m

2

=29,99 cm

2

Obliczenie stopnia zbrojenia:

=

2⋅A

s min

b h

100 %=

2⋅29,99

0,50⋅0,80

100 %=1,57 %

Obliczenie procentowej różnicy względnej między stopniem zbrojenia obliczonego a stopniem zbrojenia
założonym:

=

∣

­

zał



zał

∣

100 %=

∣

1,5­1,57

1,50

∣

100 %=4,67 %

dop

=10 %

Przyjmujemy zbrojenie 2 20 i 5 25

A

s1

= A

s2

=30,83 cm

2

.

Obliczenie stopnia zbrojenia:

=

A

s1

 A

s2

b h

100 %=

2⋅30,83

0,50⋅0,80

100 %=1,5%

Obliczenie procentowej różnicy względnej między stopniem zbrojenia obliczonego a stopniem zbrojenia
założonym:

=

∣

­

zał



zał

∣

100 %=

∣

1,50­1,5

1,5

∣

100 %=0,0 %

dop

=10 %

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

Sprawdzenie nośności przekroju słupa prostokątnego, mimośrodowo ściskanego:



eff , lim

=0,53

e

s1

=3,17d ­a

2

=0,75­0,05=0,7 m

B=1­

e

s1

d

=1­ 3,17

0,75

=­3,2220



s1

=

A

s1

e

s1

b d

2

f

yd

f

cd

=0,003083

⋅3,17

0,50⋅0,75

2

350

16,7

=0,7409



s2

=

A

s2

e

s2

b d

2

f

yd

f

cd

= 0,003083

⋅2,47

0,50⋅0,75

2

350

16,7

=0,5771



eff

=B



B

2

2





s1

­

s2



=­3,222



­3,222

2

2



0,7409­0,5771



=0,0504



eff

=0,0504≤

eff ,lim

=0,53



eff

=0,0504

2 a

2

d

= 2

⋅0,05
0,75

=0,1333

N

Rd

=

A

s1

f

yd



d ­a

2



e

s2

=0,003083

⋅3500000,75­0,05

2,47

=311,902 kN N

sd

=722,932

Warunek został spełniony.

Sprawdzenie nośności słupa dla schematu IC

e

e

=1,14 m

Wyznaczenie maksymalnego mimośrodu niezamierzonego.

e

a

=max

{

l

col

600



1

1
n



= 6,0

600



1

1
1



=0,020 m

h

30

=0,8

30

=0,027 m ⇐ e

a

=0,027 m

0,001

Obliczenie mimośrodu początkowego względem środka ciężkości przkroju betonu:

e

0

=e

a

e

e

=0,0271,14=1,168 m

Obliczenie zwiększonego mimorodu początkowego:

I

c

= b h

3

12

= 0,50

⋅0,80

3

12

=0,021 m

4

E

cm

=31GPa=31000 MN

m

2

=1,5%=0,015

I

s

=b d



h­a

1

­a

2

2



2

=0,015⋅0,50⋅0,75



0,80­0,05­0,05

2



2

=0,000689 m

4

E

s

=200 GPa=200000 MN

m

2

Krzysztof Wieczorek

KBI2 2006 /2007

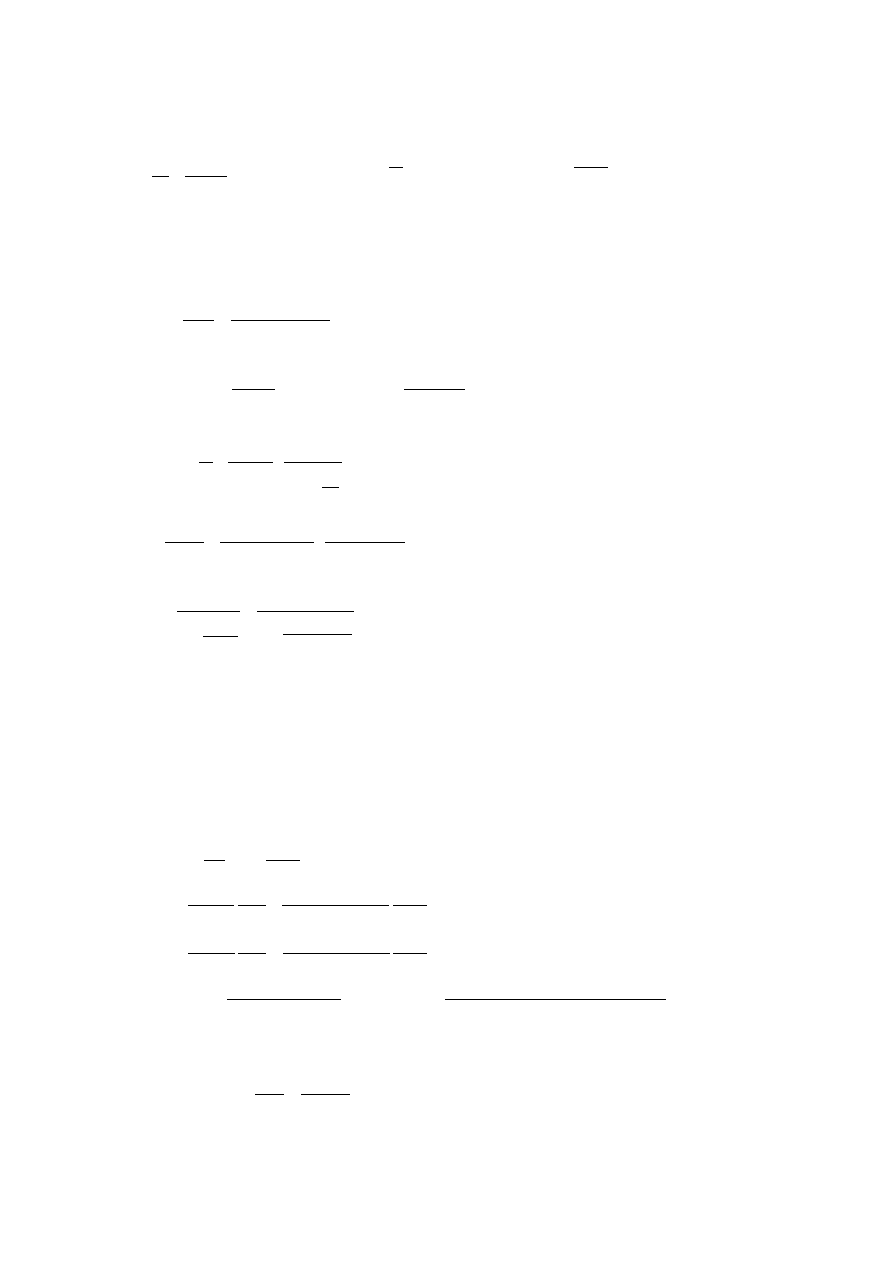
Budownictwo przemysłowe – słup skrajny.

e

0

h

=1,168

0,80

=1,460

{

0,50­0,01

l

0

h

­0,01 f

cd

=0,50­0,01 12,0

0,80

­0,01⋅16,7=0,183

0,05

Wilgotność względna powierza RH = 50%
Miarodajny przekrój elementu wynosi:

h

0

=

2 A

c

u

= 2

⋅800⋅500

2⋅800500

=307,692 mm ⇒ ∞ ,t

0

=2,625

N

Sd ,lt

=650,639 kN

k

lt

=10,5

N

Sd , lt

N

Sd

∞ , t

0

=10,5 650,639

825,038

2,625=2,181

N

crit

=9

l

0

2

⋅

[

E

cm

I

c

2 k

lt



0,11

0,1

e

0

h

0,1



E

s

I

s

]

=

=

9

12,0

2

⋅

[

31000⋅0,021

2⋅2,181



0,11

0,11,460

0,1



200000⋅0,000689

]

=10,229 MN =10 228,96 kN

N

Sd

=722,932 kN ≤0,9 N

crit

=0,9⋅10228,96=9206,063 kN

=

1

1­

N

Sd

N

cdit

=

1

1­

722,932

10228,96

=1,076

e

tot

= e

0

=1,076⋅1,168=1,257 m

Obliczanie mimośrodu względem środka ciężkości zbrojenia rozciąganego:

e

s1

=e

tot

0,5 h­a

1

=1,2570,5⋅0,80­0,05=1,61 m

e

s2

=e

tot

­0,5 ha

2

=1,257­0,5⋅0,800,05=0,91 m

Sprawdzenie nośności przekroju słupa prostokątnego, mimośrodowo ściskanego:



eff , lim

=0,53

e

s1

=1,61d ­a

2

=0,75­0,05=0,7 m

B=1­

e

s1

d

=1­ 1,61

0,75

=­1,1423



s1

=

A

s1

e

s1

b d

2

f

yd

f

cd

=0,003083

⋅1,61

0,50⋅0,75

2

350

16,7

=0,3760



s2

=

A

s2

e

s2

b d

2

f

yd

f

cd

= 0,003083

⋅0,91

0,50⋅0,75

2

350

16,7

=0,2122



eff

=B



B

2

2





s1

­

s2



=­1,1423



­1,1423

2

2



0,3760­0,2122



=0,1354



eff

=0,1354≤

eff ,lim

=0,53



eff

=0,1354

2 a

2

d

= 2

⋅0,05
0,75

=0,1333

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

N

Rd

=



eff



1­0,5

eff



d

2

f

cd

 A

s2

f

yd



d ­a

2



e

s1

=

= 0,1354



1­0,5⋅0,1354



0,75

2

⋅167000,003083⋅3500000,75­0,05

1,61

=847,726 kN N

sd

=722,932

Warunek został spełniony.

2.3.2.2.2 Obliczenie podstawowej długości zakotwienia pętów (dla dobrych warunków przyczepności
prętów do betonu):



a

=1,0

l

b

=



4

f

yd

f

bd

= 0,025

4

350

2,7

=0,65 m

Obliczenie minimalnej długości zakotwienia prętów rozciąganych:

l

b , min

=0,3 l

b

=0,3⋅0,65=0,19 m≥

{

10 =10⋅0,025=0,25 m
100 mm=0,1 m

Obliczenie minimalnego zakotwienia prętów ściskanych:

l

b , min

=0,6 l

b

=0,6⋅0,65=0,39 m≥

{

10 =10⋅0,025=0,25 m
100 mm=0,1 m

Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego:

A

s , reg

=29,9929,99=59,98 cm

2

A

s , prov

=30,8330,83=61,66 cm

2

l

bd

=

a

l

b

A

s , reg

A

s , prov

=1,0⋅0,65 59,98

61,66

=0,59 cm

2.3.2.2.3 Obliczenie obliczeniowej wymaganej długości zakładu:

•

strefa ściskana

l

s ,min

≥0,3 

a



1

l

b

A

s , reg

A

s , prov

=0,3⋅1,0⋅1,0⋅0,65 59,98

61,66

=0,18 cm

l

s

=

1

l

bd

=1,0⋅0,65=0,65 cm

•

strefa rozciągana

l

s ,min

≥0,3 

a



1

l

b

A

s , reg

A

s , prov

=0,3⋅1,0⋅2,0⋅0,65 59,98

61,66

=0,36 cm

l

s

=

1

l

bd

=2,0⋅0,65=1,30 cm

2.3.2.2.4 Redukcja zbrojenia w słupie skrajnym.
Warunek równowagi:

N

Rd

= A

S2

f

yd

 f

cd

⋅b⋅d⋅

eff

­ A

s1

⋅ f

yd

⋅

[

2 1­

eff



1­

eff ,lim

­1

]

Po przekztałceniach otrzymujemy:

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.



eff

=

 N

Sd

A

s2

⋅ f

yd

⋅1­

eff , lim

A

s1

⋅ f

yd

⋅1

eff ,lim



f

cd

⋅b⋅d 1­

eff , lim

2 A

s1

⋅ f

yd

2.3.2.2.4.1 Redukujemy zbrojenie z 2  20 i 5  25 do 25

A

s1

= A

s2

=24,55 cm

2

Obliczenia dla schematu IA.



eff

=

517,220,002455⋅350000⋅1­0,530,002455⋅350000⋅10,53

16700⋅0,5⋅0,751­0,532⋅0,002455⋅350000

=0,0196

Obliczamy 

s

:



s

=

21­

eff



1­

eff , lim

­1=

21­0,0196

1­0,53

­1=3,1719

- ponieważ 

s

=3,17191­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:

N

Rd

= A

S2

f

yd

 f

cd

⋅b⋅d⋅

eff

­ A

s1

⋅ f

yd

⇒



eff

=

N

Rd

­ A

S2

f

yd

 A

s1

⋅f

yd

f

cd

⋅b⋅d

Po podstawieniu otrzymujemy:



eff

=

N

Rd

­A

S2

f

yd

 A

s1

⋅f

yd

f

cd

⋅b⋅d

= 517,22

­0,002455⋅3500000,002455⋅350000

16700⋅0,50⋅0,75

=0,0826

Sprawdzamy warunek: 

eff

2

a

2

d



eff

=0,08262

a

2

d

=2 0,005

0,75

=0,1333 - warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Korzystamy z warunku równowagi momentów względem środka ciężkośći zbrojenia ściskanego:

M

Rd

­N

sd

0,5⋅h­a

2

=A

s1

⋅ f

yd

d ­a

2



Obliczamy M

rd

:

M

Rd

=A

s1

⋅ f

yd

d ­a

2

 N

sd

0,5⋅h­a

2

=

=0,002455⋅3500000,75­0,05517,220,5⋅0,8­0,05=498,03 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do 5 25 :

x=

M

Rd

H

⊥

= 498,03

83,123

=5,99

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­5,99=0,56 m

Postępując analogicznie jak w powyższym przykładzie obliczam h

zred

dla pozostałych schematów

obciążenie

Obliczenia dla schematu IIA.



eff

=

N

Rd

­A

S2

f

yd

 A

s1

⋅f

yd

f

cd

⋅b⋅d

= 212,56

­0,002455⋅3500000,002455⋅350000

16700⋅0,50⋅0,75

=0,0182

Obliczamy 

s

:



s

=

21­

eff



1­

eff , lim

­1=

21­0,0182

1­0,53

­1=3,1780 - ponieważ 

s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:

Krzysztof Wieczorek

KBI2 2006 /2007

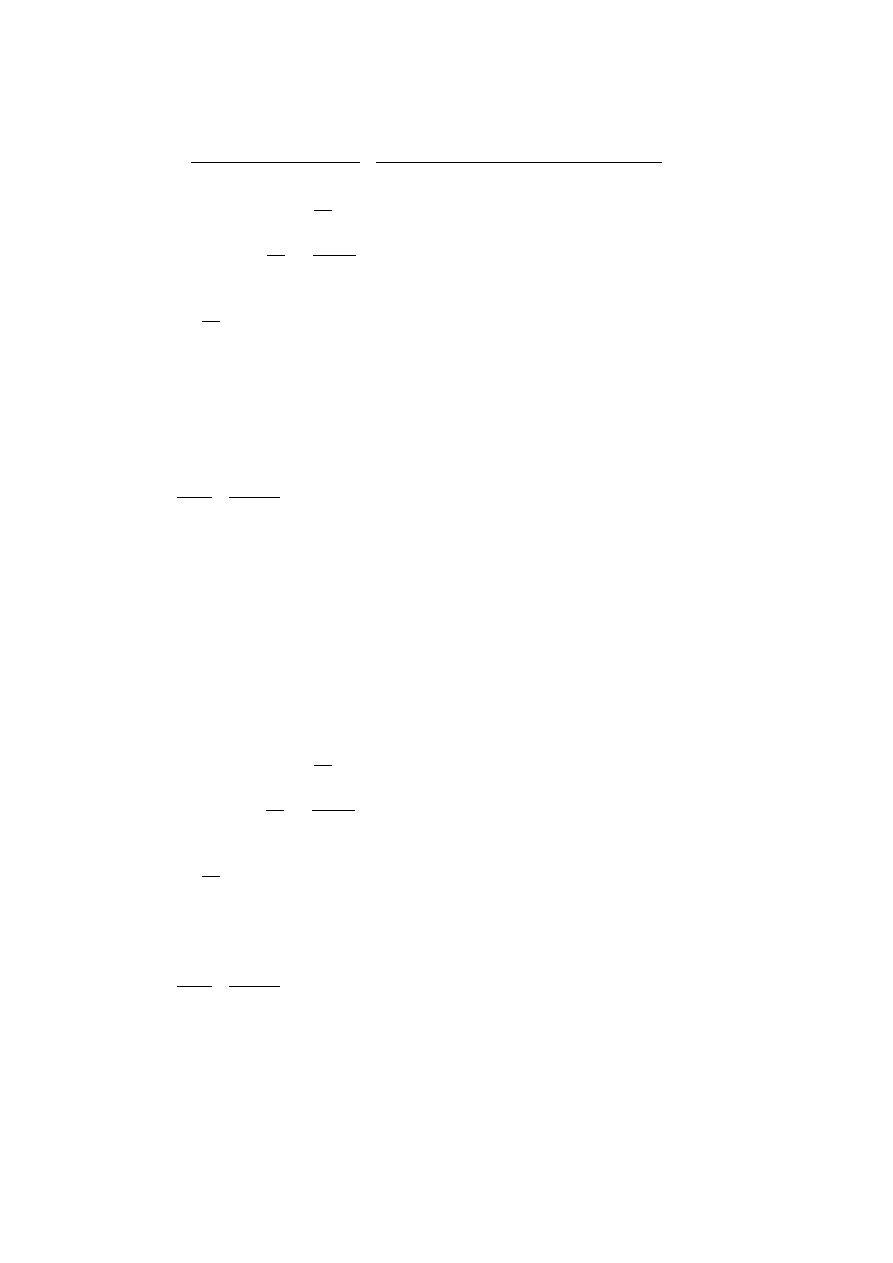
Budownictwo przemysłowe – słup skrajny.



eff

=

N

Rd

­A

S2

f

yd

 A

s1

⋅f

yd

f

cd

⋅b⋅d

=

­0,002455⋅3500000,002455⋅350000

16700⋅0,50⋅0,75

=0,0339

Sprawdzamy warunek: 

eff

2

a

2

d



eff

=0,03392

a

2

d

=2 0,005

0,75

=0,1333 - warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Korzystamy z warunku równowagi momentów względem środka ciężkośći zbrojenia ściskanego:

M

Rd

­N

sd

0,5⋅h­a

2

=A

s1

⋅ f

yd

d ­a

2



Obliczamy M

rd

:

M

Rd

=A

s1

⋅ f

yd

d ­a

2

 N

sd

0,5⋅h­a

2

=

=0,002455⋅3500000,75­0,05212,56 0,5⋅0,8­0,05=558,96 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do 5 25 :

x=

M

Rd

H

⊥

= 558,96

83,123

=6,72

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­6,72=­0,17 m

Obliczenia dla schematu IB.



eff

=0,0175

Obliczamy 

s

:



s

=3,1808 - ponieważ 

s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:



eff

=0,0111

Sprawdzamy warunek:



eff

2

a

2

d



eff

=0,01112

a

2

d

=2 0,005

0,75

=0,1333 - warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Obliczamy M

rd

:

M

Rd

=587,55 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do

5 25

:

x=

M

Rd

H

⊥

= 587,55

10,81

=54,35

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­54,35=­47,80 m

Obliczenia dla schematu IC.



eff

=0,0209

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

Obliczamy 

s

:



s

=3,1663

- ponieważ



s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:



eff

=0,1270

Sprawdzamy warunek: 

eff

2

a

2

d



eff

=0,12702

a

2

d

=2 0,005

0,75

=0,1333

- warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Obliczamy M

rd

:

M

Rd

=442,35 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do 5 25 :

x=

M

Rd

H

⊥

= 442,35

123,33

=3,59 m - najmnijejsza wartość

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­3,59=2,96 m - największa wysokosć.

Obliczenia dla schematu IIC.



eff

=0,0186

Obliczamy 

s

:



s

=3,1763 - ponieważ 

s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:



eff

=0,0476

Sprawdzamy warunek: 

eff

2

a

2

d



eff

=0,04762

a

2

d

=2 0,005

0,75

=0,1333 - warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Obliczamy M

rd

:

M

Rd

=541,90 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do 5 25 :

x=

M

Rd

H

⊥

= 541,90

123,33

=4,39 m

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­4,39=2,16 m

Zbrojenie 5  25 możemy zastosować na wsyokości

h

zred

=2,16 m

słupa

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

2.3.2.2.4.2 Redukujemy zbrojenie z 5  25 do 3  25 A

s1

= A

s2

=14,73 cm

2

Obliczenia dla schematu IA.



eff

=

517,220,001473⋅350000⋅1­0,530,001473⋅350000⋅10,53

16700⋅0,5⋅0,751­0,532⋅0,001473⋅350000

=0,0128

Obliczamy 

s

:



s

=

21­

eff



1­

eff , lim

­1=

21­0,0128

1­0,53

­1=3,2007 - ponieważ 

s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość



eff

:

N

Rd

= A

S2

f

yd

 f

cd

⋅b⋅d⋅

eff

­ A

s1

⋅ f

yd

⇒



eff

=

N

Rd

­ A

S2

f

yd

 A

s1

⋅f

yd

f

cd

⋅b⋅d

Po podstawieniu otrzymujemy:



eff

=

N

Rd

­A

S2

f

yd

 A

s1

⋅f

yd

f

cd

⋅b⋅d

= 517,22

­0,001473⋅3500000,002455⋅350000

16700⋅0,50⋅0,75

=0,0826

Sprawdzamy warunek:



eff

2

a

2

d



eff

=0,08262

a

2

d

=2 0,005

0,75

=0,1333 - warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Korzystamy z warunku równowagi momentów względem środka ciężkośći zbrojenia ściskanego:

M

Rd

­N

sd

0,5⋅h­a

2

=A

s1

⋅ f

yd

d ­a

2



Obliczamy M

rd

:

M

Rd

=A

s1

⋅ f

yd

d ­a

2

 N

sd

0,5⋅h­a

2

=

=0,001473⋅3500000,75­0,05517,220,5⋅0,8­0,05=257,44 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do

5 25

:

x=

M

Rd

H

⊥

= 257,44

83,123

=3,10

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­257,44=3,45 m

Postępując analogicznie jak w powyższym przykładzie obliczam h

zred

dla pozostałych schematów

obciążenia

Obliczenia dla schematu IIA.



eff

=0,0114

Obliczamy 

s

:



s

=3,2069

- ponieważ



s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:



eff

=0,0339

Sprawdzamy warunek: 

eff

2

a

2

d



eff

=0,03392

a

2

d

=2 0,005

0,75

=0,1333

- warunek nie został spełniony,

Przyjmujemy:

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.



eff

=2

a

2

d

=0,1333

Obliczamy M

rd

:

M

Rd

=318,37 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do 5 25 :

x=

M

Rd

H

⊥

= 318,37

8,123

=3,83 m

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­3,83=2,72 m

Obliczenia dla schematu IB.



eff

=0,0107

Obliczamy 

s

:



s

=3,2097 - ponieważ 

s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:



eff

=0,0111

Sprawdzamy warunek:



eff

2

a

2

d



eff

=0,01112

a

2

d

=2 0,005

0,75

=0,1333 - warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Obliczamy M

rd

:

M

Rd

=346,96 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do

3 25

:

x=

M

Rd

H

⊥

= 346,96

10,81

=32,10

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­32,10=­25,55 m

Obliczenia dla schematu IC.



eff

=0,0141

Obliczamy 

s

:



s

=3,1951

- ponieważ



s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:



eff

=0,1270

Sprawdzamy warunek: 

eff

2

a

2

d



eff

=0,12702

a

2

d

=2 0,005

0,75

=0,1333

- warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

Obliczamy M

rd

:

M

Rd

=201,76 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do

5 25

:

x=

M

Rd

H

⊥

= 201,76

123,33

=1,64 m - najmniejsza wartość

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­1,64=4,91 m - największa wysokosć.

Obliczenia dla schematu IIC.



eff

=0,0118

Obliczamy 

s

:



s

=3,2052

- ponieważ



s

1­ przyjmujemy 

s

=1,0

Obliczamy nową wartość 

eff

:



eff

=0,0476

Sprawdzamy warunek: 

eff

2

a

2

d



eff

=0,04762

a

2

d

=2

0,005

0,75

=0,1333

- warunek nie został spełniony,

Przyjmujemy:



eff

=2

a

2

d

=0,1333

Obliczamy M

rd

:

M

Rd

=301,31 kNm

Oblicenie wysokości x, na której można zredukować zbrojenie do 5 25 :

x=

M

Rd

H

⊥

= 301,31

123,33

=2,44 m

Obliczamy na jakiej (licząc od spodu słupa) można zredukowac zbrojenie:

h

zred

=h

s

h

I550PE

­x=6,00,55­2,44=4,11 m

Zbrojenie 5 25 możemy zastosować na wsyokości h

zred

=4,91 m słupa

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

2.3.2.3 Przedstawienie schematów obciążeń działających w płaszczyźnie równoległej do toru.

Obciążenie równeległe do toru:

H

∥

=

2⋅H '

∥

5

= 2

⋅66,50 kN

5

=26,6

R

min

=­32,04 kN

Wyznaczenie sił przekrojowych:

0,5 m

0,55 m

5,59 m

Q

b

=11,21 kN

Q

s

=61,49 kN

H

∥

=26,6 kN

R

min

=­32,04 kN

Schemat IIBr

M

Sd

= H

∥

⋅h

s

h

I550

=26,6⋅6,00,55=174,23 kNm

N

Sd

=R

A min

Q

b

Q

s

=­32,0411,2161,49=40,66 kN

Wyznaczenie mimośrodu:

e

e

=

M

Sd

N

Sd

=174,23

40,66

=4,29 m

2.3.2.4 Obliczenie wymaganej ilości zbrojenia w słupie ze względu na obciążenia działające w

płaszczyźnie równoległej do toru.

Wymiary przekroju:

b=0,8 m
h=0,5 m

Przyjmuję grubość otulenia a

1

= 50 mm.

d =h­a

1

=0,5­0,05=0,45 m

Długość słupa:

l

col

=6,0 m

Długośc wyboczeniwa słupa:

l

0

=⋅l

col

=1,8⋅6,0 m=10,8 m

Wyznaczenie zbrojenia minimalnego(wyznaczam ze względu na maksymalną siłę normalną tj. siłę ze
schematu A):

A

s min

=max

{

0,15

N

Sd

f

yd

=0,15

517,221

350000

=0,00022167 m

2

=2,22 cm

2

0,003 b d =0,003⋅0,50⋅0,75=0,001125 m

2

=11,25 cm

2

Mimośród działania siły (schemat 1).

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

e

e

=4,29 m

Wyznaczenie maksymalnego mimośrodu niezamierzonego.

e

a

=max

{

l

col

600



1

1
n



= 6,0

600



1

1
1



=0,020 m ⇐ e

a

=0,020

h

30

=0,5

30

=0,017 m m

0,001

Obliczenie mimośrodu początkowego względem środka ciężkości przkroju betonu:

e

0

=e

a

e

e

=0,0204,29=4,305 m

Smukłość:

=

l

0

i

=10,8

0,14

=74,8225

=

l

0

h

=10,8

0,50

=21,607

Należy uwzględnić wpływ wyboczenia.

Obliczenie zwiększonego mimorodu początkowego:

I

c

= b h

3

12

= 0,50

3

⋅0,80

12

=0,0083 m

4

E

cm

=31GPa=31000 MN

m

2

=0,6 %=0,006

I

s

=b d



h­a

1

­a

2

2



2

=0,006⋅0,80⋅0,45



0,50­0,05­0,05

2



2

=0,000086 m

4

E

s

=200 GPa=200000 MN

m

2

e

0

h

=4,305

0,80

=3,235

{

0,50­0,01

l

0

h

­0,01 f

cd

=0,50­0,0110,8

0,50

­0,01⋅16,7=0,117

0,05

Wilgotność względna powierza RH = 50%
Miarodajny przekrój elementu wynosi:

h

0

=

2 A

c

u

= 2

⋅800⋅500

2⋅800500

=307,692 mm ⇒ ∞ ,t

0

=2,625

N

Sd ,lt

=36,594 kN

k

lt

=10,5

N

Sd , lt

N

Sd

∞ , t

0

=10,5 36,594

40,66

2,625=2,181

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

N

crit

=9

l

0

2

⋅

[

E

cm

I

c

2 k

lt



0,11

0,1

e

0

h

0,1



E

s

I

s

]

=

=

9

10,80

2

⋅

[

31000⋅0,0083

2⋅2,181



0,11

0,18,610

0,1



200000⋅0,000086

]

=1,848 MN =1 847,98 kN

N

Sd

=40,66 kN ≤0,9 N

crit

=0,9⋅1847,98=1663,182 kN

=

1

1­

N

Sd

N

cdit

=

1

1­

40,66

1847,98

=1,022

e

tot

= e

0

=1,022⋅4,305=4,402 m

Obliczanie mimośrodu względem środka ciężkości zbrojenia rozciąganego:

e

s1

=e

tot

0,5 h­a

1

=4,4020,5⋅0,50­0,05=4,60 m

e

s2

=e

tot

­0,5 ha

2

=4,402­0,5⋅0,500,05=4,20 m

Obliczenie powierzchni zbrojenia ściskanego:



eff

=

N

Sd

b d f

cd

=

40,66

0,80⋅0,45⋅16700

=0,007≤

eff ,lim

=0,53 - duży mimosród.



eff

=0,007

2 a

2

d

= 2

⋅0,05
0,45

=0,2222

A

s1

=A

s2

=

N

Sd

e

s2



d ­a

2



f

yd

=

40,66⋅4,20



0,45­0,05



350000

=0,0012 m

2

=12,20 cm

2

Obliczenie stopnia zbrojenia:

=

2⋅A

s min

b h

100 %=

2⋅12,20

0,50⋅0,80

100 %=0,61 %

Obliczenie procentowej różnicy względnej między stopniem zbrojenia obliczonego a stopniem zbrojenia
założonym:

=

∣

­

zał



zał

∣

100 %=

∣

0,61­0,6

0,6

∣

100 %=1,70 %

dop

=10 %

Przyjmujemy zbrojenie 1  20 i 2  25 A

s1

= A

s2

=12,96 cm

2

.

Obliczenie stopnia zbrojenia:

=

A

s1

 A

s2

b h

100 %=

2⋅12,96

0,50⋅0,80

100 %=0,63 %

Obliczenie procentowej różnicy względnej między stopniem zbrojenia obliczonego a stopniem zbrojenia
założonym:

=

∣

­

zał



zał

∣

100 %=

∣

0,63­0,6

0,6

∣

100 %=4,67 %

dop

=10 %

Sprawdzenie nośności przekroju słupa prostokątnego, mimośrodowo ściskanego:

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.



eff , lim

=0,53

B=1­

e

s1

d

=1­ 4,60

0,45

=­9,2264



s1

=

A

s1

e

s1

b d

2

f

yd

f

cd

=0,001256

⋅4,60

0,80⋅0,45

2

350

16,7

=0,7478



s2

=

A

s2

e

s2

b d

2

f

yd

f

cd

= 0,001256

⋅4,20

0,80⋅0,45

2

350

16,7

=0,6828

e

s1

=4,60d ­a

2

=0,45­0,05=0,4 m



eff

=B



B

2

2





s1

­

s2



=­9,2264



­9,2264

2

2



0,7478­0,6828



=0,0070



eff

=0,0070≤

eff ,lim

=0,53



eff

=0,0070

2 a

2

d

= 2

⋅0,05
0,45

=0,2222

N

Rd

=

A

s1

f

yd



d ­a

2



e

s2

=0,001296

⋅350000 0,45­0,05

4,20

=41,848 kN  N

Sd

=40,66 kN

Warunek został spełniony.

Nie przeprowadzamy obliczen dla maksymalnej siły normalnej, ponieważ obliczenia te zostały wykonane

dla sił działających prostopadle do belki podsuwnicowej.

2.3.2.4.1. Redukcja zbrojenia
Zbrojenia dla obciążenia równoległego do toru nie redukujem ze względu na warunek z PN-B-
03264:2002: pręty rozmieszcza się na obwodzie w odległościach nie przekraczających 400 mm.
Przyjęto

1 20 i 2 25

, a bok słupa na którym zostały rozmieszczone ma wymiar 800 mm, dlatego

aby warunek został spełniony, przez całą długość słupa na tym boku muszą znajdować się 3 pręty.
Można jedynie zmienić średnicę prętów, ale ze względu ułatwienia wykonania słupa, zalecamy
pozostawienie 1 20 i 2 25 .

2.3.2.4.2. Obliczenie podstawowej długości zakotwienia prętów (dla dobrych warunków

przyczepności prętów do betonu):



a

=1,0

l

b

=



4

f

yd

f

bd

= 0,02

4

350

2,7

=0,65 m

Obliczenie minimalnej długości zakotwienia prętów rozciąganych:

l

b , min

=0,3 l

b

=0,3⋅0,65=0,19 m≥

{

10 =10⋅0,02=0,20 m
100 mm=0,1 m

Obliczenie minimalnego zakotwienia prętów ściskanych:

l

b , min

=0,6 l

b

=0,6⋅0,65=0,39 m≥

{

10 =10⋅0,020=0,20 m
100 mm=0,1 m

Obliczenie obliczeniowej wymaganej długości zakotwienia prętów zbrojenia głównego:

A

s , reg

=12,2012,20=24,4 cm

2

A

s , prov

=12,5612,56=25,12 cm

2

Krzysztof Wieczorek

KBI2 2006 /2007

Budownictwo przemysłowe – słup skrajny.

l

bd

=

a

l

b

A

s , reg

A

s , prov

=1,0⋅0,65 24,4

25,12

=0,63 cm

2.3.2.4.3. Obliczenie obliczeniowej wymaganej długości zakładu:

•

strefa ściskana

l

s ,min

≥0,3 

a



1

l

b

A

s , reg

A

s , prov

=0,3⋅1,0⋅1,0⋅0,65 24,4

25,12

=0,19 cm

l

s

=

1

l

bd

=1,0⋅0,65=0,65 cm

•

strefa rozciągana

l

s ,min

≥0,3 

a



1

l

b

A

s , reg

A

s , prov

=0,3⋅1,0⋅2,0⋅0,65 24,4

25,12

=0,38 cm

l

s

=

1

l

bd

=2,0⋅0,65=1,30 cm

2.3.2.4.3. Strzemiona.
Przyjęcie średnicy strzemion:



s

≥max

{

0,25 =0,25⋅25 mm=5 mm
6,0 mm

Wyznaczenie rozstwu strzemion:



s

≥min

{

15=15⋅25 mm=300 mm=30 cm ⇐ 

L

≤3 %

b

sł

=500 mm=50 cm

400mm=40 cm

Przyjęto strzemiona czterocięte w rozstawie 30 cm.

Krzysztof Wieczorek

KBI2 2006 /2007