PERWAPORACJA I SEPARACJA PAR – ROZDZIELANIE 

MIESZANIN CIEKŁYCH Z WYKORZYSTANIEM MEMBRAN 

 
 

Wojciech

 

KUJAWSKI

 

 

Uniwersytet Mikołaja Kopernika, Wydział Chemii, 

Katedra Chemii Fizycznej i Fizykochemii Polimerów, 

ul. Gagarina 7, 87-100 Toruń 

e-mail: kujawski@chem.umk.pl 

 
 

1.  WPROWADZENIE 

 
Metodą powszechnie stosowaną w przemyśle do rozdzielania mieszanin 
substancji ciekłych na składniki jest destylacja. Jest to jednak metoda ener-
gochłonna, a w przypadku rozdziału azeotropów, składników blisko wrzą-
cych czy substancji nietrwałych termicznie wymaga stosowania wielostop-
niowych, złożonych rozwiązań. 
 

Rozdzielcze techniki membranowe, szczególnie w połączeniu z kon-

wencjonalnymi metodami rozdziału, stwarzają warunki do uzyskania dużo 
lepszych efektów końcowych zarówno pod względem jakościowym jak  
i ekonomicznym.  

Ogólnie rzecz ujmując, rozdzielanie składników mieszaniny w pro-

cesie membranowym polega na doprowadzeniu tej mieszaniny do kontaktu 
z powierzchnią półprzepuszczalnej membrany, przez którą pewne składniki 
przenikają preferencyjnie pod działaniem określonej siły napędowej oraz 
dzięki specyficznym właściwościom membrany [1, 2]. Jednocześnie, mem-
brana stanowi zasadniczy element układu membranowego i powinna cha-
rakteryzować się następującymi właściwościami [3]: 

•  wysoką selektywnością w stosunku do wybranych składników roz-

dzielanej mieszaniny, 

•  dobrą przepuszczalnością, 

•  dobrą wytrzymałością mechaniczną i odpornością chemiczną, 

•  niskim kosztem wytwarzania. 

 

2.  CHARAKTERYSTYKA OGÓLNA PERWAPORACJI 

MEMBRANY 

TEORIA I PRAKTYKA 

ZESZYT III 

 

WYKŁADY 

MONOGRAFICZNE  

I SPECJALISTYCZNE  

TORUŃ 2009 

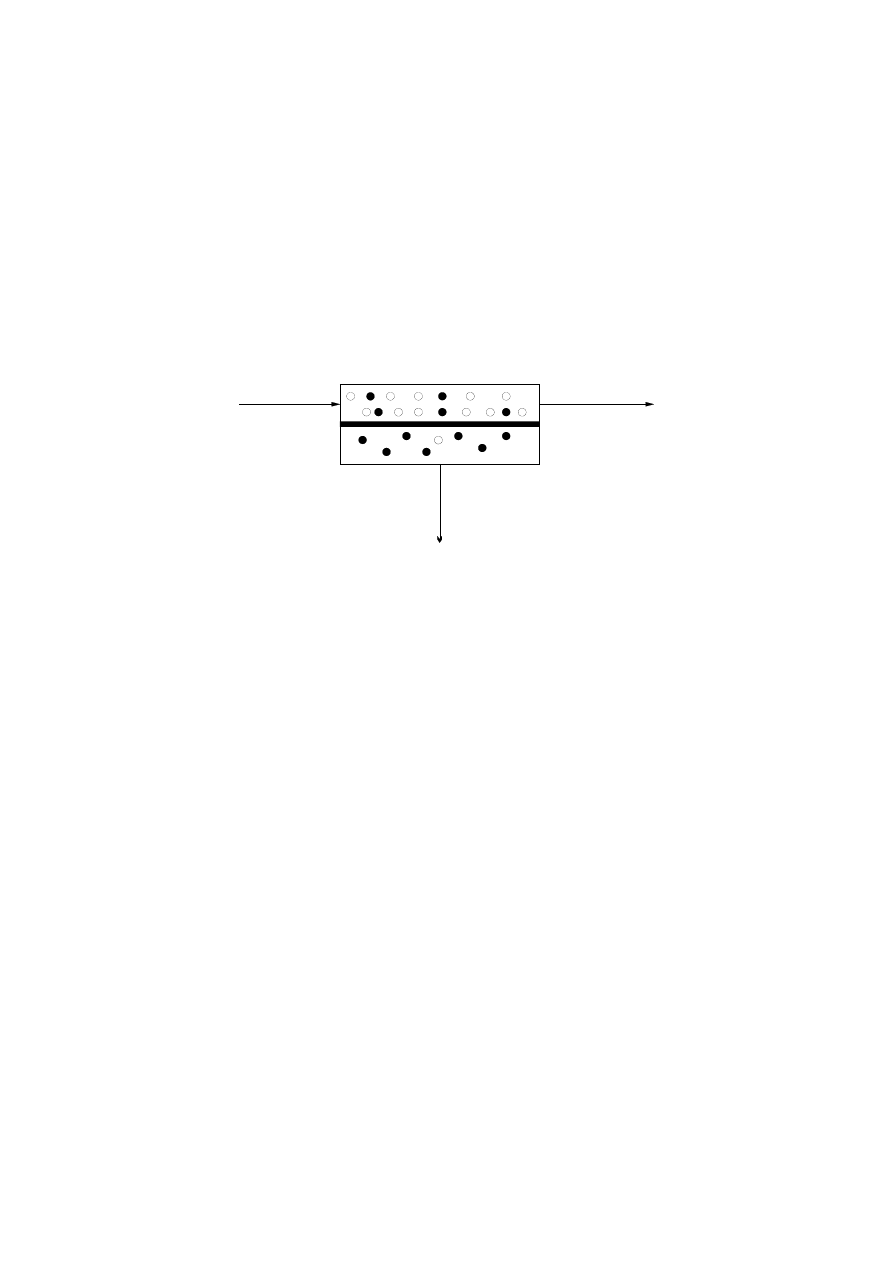
                                             Perwaporacja i separacja… 

 

111 

I PERMEACJI PAR 

 

Technikami membranowymi, które stosuje się do rozdzielania mieszanin 
ciekłych na skalę przemysłową, są perwaporacja oraz permeacja par. 
W perwaporacji składniki roztworu zasilającego znajdują się w fazie ciekłej, 
natomiast w przypadku permeacji par nadawa jest w fazie parowej. W obu 
tych technikach strumień zasilający znajduje się w bezpośrednim kontakcie 
z powierzchnią membrany, a określony składnik mieszaniny jest preferen-
cyjnie transportowany na drugą stronę membrany (rys. 1) [1

−5].  

 

nadawa

retentat

MEMBRANA

permeat

 

Rys. 1. Zasada rozdziału w perwaporacji i permeacji par 

 
 

 

W wyniku procesu rozdzielenia strumień zasilający dzieli się na stru-

mień permeatu oraz strumień retentatu (rys. 1). Permeat wzbogacony jest  
o składnik przenoszony preferencyjnie przez membranę, natomiast retentat 

− 

o składnik, który jest zatrzymywany na membranie. Selektywność rozdziału 
w procesie perwaporacji i permeacji par wynika z różnic w przepuszczal-
ności składników rozdzielanej mieszaniny przez membranę polimerową. 
Należy podkreślić, że rozdział w perwaporacji i permeacji par nie zależy od 
równowagi ciecz

−para, w związku z czym, można te procesy efektywnie 

stosować m.in. do rozdziału azeotropów i cieczy bliskowrzących. 
 

Pierwsze informacje w literaturze dotyczące perwaporacji datują się 

na początek XX wieku. W roku 1906 Kahlenberg opisał rozdział miesza-
niny węglowodorów i alkoholi przez błonę kauczukową, a w roku 1917 
Kober wprowadził termin „perwaporacja” [6]. Dopiero jednak od lat 60. 
ubiegłego stulecia liczyć należy współczesny etap badań nad tą techniką, 
gdy Binning i współpracownicy podjęli próby komercjalizacji tego procesu 
[7]. Na ten okres przypada także początek badań prowadzonych przez 
Nèela. Szybki rozwój perwaporacji nastąpił jednak dopiero na początku lat 
80. XX wieku, z chwilą opracowania hydrofilowych membran kompozyto-
wych z warstwą selektywną z polialkoholu winylowego, przeznaczonych do 
odwadniania alkoholu etylowego [3, 8]. Dalszy szybki rozwój zastosowań 
przemysłowych perwaporacji nastąpił na początku XXI wieku, z chwilą 
opracowania membran ceramicznych do perwaporacji i permeacji par [9]. 

W. Kujawski                                                                       

 

112

 

Permeacja par jest jedną z nowszych technik separacyjnych stosowa-

nych do rozdziału mieszanin ciekłych. W porównaniu z perwaporacją tech-
nika ta ma tę zaletę, że w czasie przebiegu procesu nie zachodzi przemiana 
fazowa, w związku z czym nie ma problemu z dostarczeniem energii po-
trzebnej na zrównoważenie strat cieplnych w układzie [10]. 

Charakterystyka efektywności rozdzielenia mieszanin techniką per-

waporacji i permeacji par odnoszona jest zawsze do tego składnika, który 
jest przenoszony preferencyjnie przez membranę. Podstawą oceny efektyw-
ności rozdziału są następujące wielkości: współczynnik rozdzielenia 

α

, 

współczynnik wzbogacenia 

β

, strumień permeatu J, indeks separacji perwa-

poracyjnej (parametr Ψ) oraz diagram selektywności McCabe-Thielego [3, 
5, 11]. 

Współczynniki rozdzielenia 

α

 i wzbogacenia 

β

 zdefiniowane są 

równaniami (1) i (2): 

B

A

B

A

B

A

B

A

B

A

X

X

J

J

X

X

Y

Y

/

/

/

/

/

=

=

α

, 

   (1) 

A

A

B

A

X

Y

=

/

β

. 

      (2) 

W wyrażeniach (1) i (2) X

i

 oraz Y

i

 oznaczają  ułamek (molowy lub 

masowy) składnika i, odpowiednio w nadawie oraz w permeacie, J

i

 

− stru-

mień cząstkowy składnika  i, natomiast indeksy dolne A i B 

− oznaczają 

składniki rozdzielanej mieszaniny, przy czym

 

A odnosi się do składnika 

przenoszonego preferencyjnie przez membranę. 

Współczynniki 

α

 i 

β

 powiązane są następującymi zależnościami: 

β

β

α

A

A

B

A

X

X

−

−

=

1

1

/

, 

     (3) 

A

B

A

X

)

1

(

1

/

−

+

=

α

α

β

. 

    (4) 

Strumień permeatu  J określa ilość permeatu, jaka przeniknęła przez 

jednostkową powierzchnię membrany w jednostce czasu i w przypadku 
perwaporacji oraz permeacji par wyrażany jest najczęściej w [g m

-2

 h

-1

] lub 

[mol m

-2

  h

-1

]. Strumień wywołany jest działaniem określonej siły 

napędowej, co w przypadku omawianych procesów może być zapisane 
następującym równaniem [2]: 

l

)

p

p

(

P

J

P

i

N

i

i

i

,

,

−

=

,     (5) 

gdzie:  J

i

 – strumień składnika  i,  P

i

 

− współczynnik przepuszczalności 

składnika i, l – grubość membrany, p

i,  N

 – cząstkowa prężność pary skład-

nika i po stronie nadawy, p

i, P

 – cząstkowa prężność pary składnika i po stro-

nie permeatu. W procesie perwaporacji i permeacji par po stronie permeatu 
ciśnienie parcjalne składnika i jest bliskie zeru (p

i, P

 ≈ 0), można więc przy-

                                             Perwaporacja i separacja… 

 

113 

jąć,  że strumień permeatu jest proporcjonalny do ciśnienia cząstkowego 
składnika i w nadawie: 

l

p

P

J

N

i

i

i

,

=

. 

     (6) 

Ponieważ membrany mają różną grubość, wprowadzono pojęcie 

strumienia znormalizowanego składnika  i przez membranę  J

Ni

, wyrażające 

iloczyn strumienia rzeczywistego oraz grubości membrany. Taka procedura 
umożliwia porównywanie właściwości transportowych membran o różnej 
grubości: 

l

J

J

i

Ni

=

. 

     (7) 

Strumień całkowity permeatu, J, jest równy sumie strumieni cząstko-

wych: 

.

∑

=

i

i

J

J

 

     (8) 

Strumień cząstkowy składnika i można obliczyć na podstawie znajo-

mości składu permeatu i strumienia całkowitego: 

i

i

Y

J

J

=

. 

     (9) 

Parametr  Ψ, tzw. indeks separacji perwaporacyjnej (Pervaporation 

Separation Index), zdefiniowany jest równaniem (10) [12, 13]: 

)

(

1

−

α

= J

Ψ

.     (10) 

Parametr  Ψ umożliwia porównanie efektywności rozdziału danej 

mieszaniny ciekłej, z 

wykorzystaniem różnych rodzajów membran. 

Z dwóch membran, różniących się selektywnością oraz wielkością 
strumienia permeatu, bardziej efektywna będzie ta membrana, dla której 
parametr Ψ przyjmuje większą wartość. 

Należy podkreślić,  że parametry efektywności membrany zależą od 

składu nadawy, dlatego też pełna charakterystyka wymaga określenia war-
tości tych parametrów w takim zakresie składu nadawy, w jakim będzie 
stosowana membrana. W celu zobrazowania selektywności membrany 
w omawianych procesach stosuje się także diagram separacyjny McCabe- 
-Thielego będący wykresem zawartości składnika i w permeacie, w funkcji 
zawartości tego składnika w nadawie [5, 11].  

 

3.  OPIS TRANSPORTU I SEPARACJI MASY W UJĘCIU MODELU 

ROZPUSZCZANIA-DYFUZJI 

 

Proces transportu przez nieporowate membrany polimerowe opisuje teoria 
rozpuszczania-dyfuzji. Zgodnie z tą teorią transport i separacja masy w per-
waporacji i permeacji par odbywa się w trzech następujących po sobie, eta-
pach [4, 5, 11, 14]:  

1. Sorpcja do spęczniałej części membrany. 
  Etap ten determinuje stężenie każdego składnika w tej części membrany 

− jest to punkt początkowy profilu stężenia składnika w membranie. 
Wielkość sorpcji do membrany będzie zależała zarówno od właściwości 

W. Kujawski                                                                       

 

114

składników rozdzielanej mieszaniny, znajdującej się w kontakcie  
z membraną, jak i od rodzaju użytej membrany. W wyniku sorpcji do 
membrany polimerowej następuje zmiana oddziaływań pomiędzy  łań-
cuchami polimerowymi, powodując pęcznienie membrany. 

2. Dyfuzja molekuł penetranta przez membranę.  
 Dyfundujący poprzez membranę składnik rozdzielanej mieszaniny 

plastyfikuje amorficzne części membrany, zwiększając tym samym 
odległości pomiędzy  łańcuchami polimerowymi i ułatwiając przeni-
kanie. Stężenie penetranta na drodze dyfuzji spada, w wyniku czego 
również zmniejsza się efekt plastyfikujący oraz szybkość dyfuzji. Etap 
dyfuzji wraz z etapem sorpcji decydują o selektywności całego pro-
cesu. 

3. Desorpcja permeatu.  
  Etap ten, z uwagi na panujące obniżone ciśnienie po stronie permeatu, 

jest etapem bardzo szybkim. Dlatego zakłada się, że nie wpływa on na 
całkowitą selektywność procesu permeacji. 

 

 

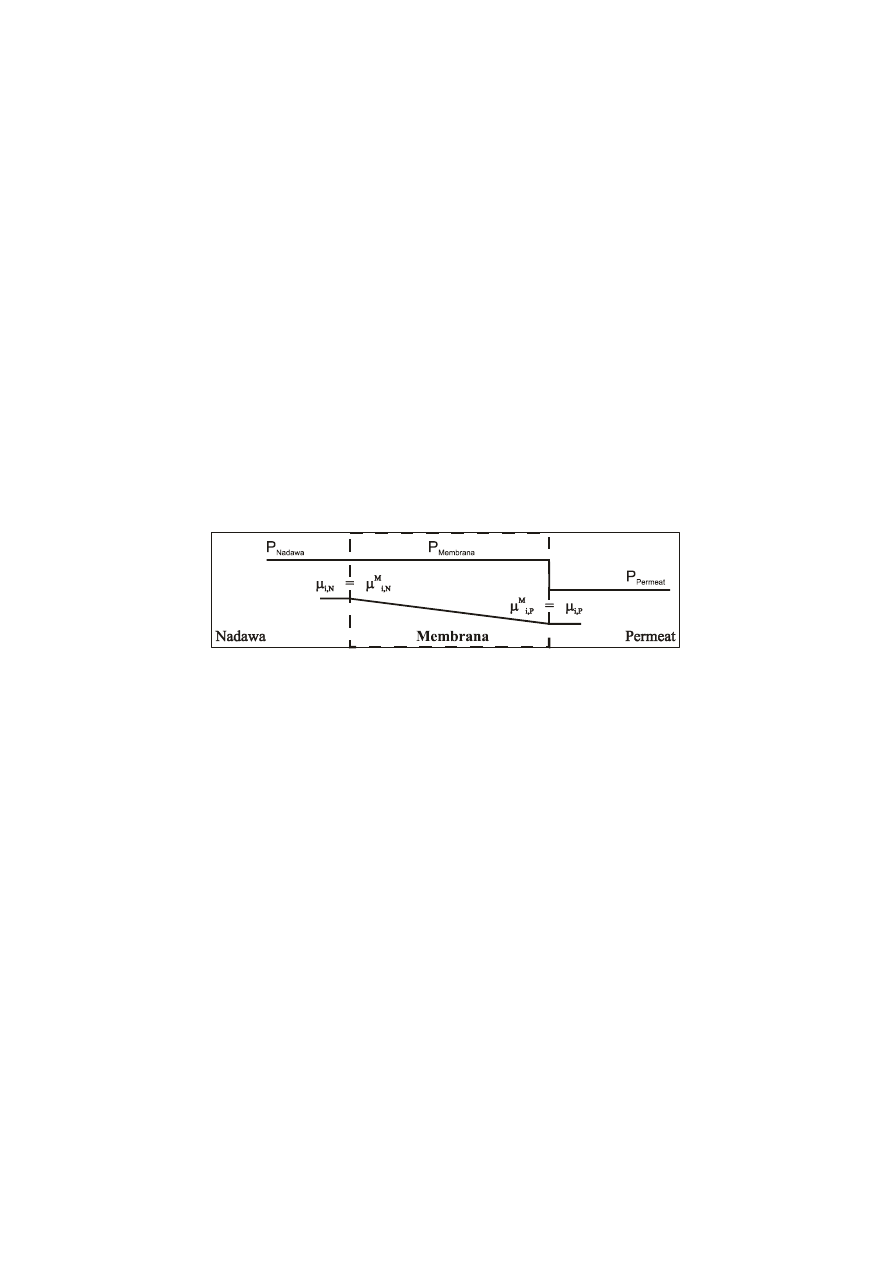
Rys. 2. Schemat równowag w układzie: nadawa

−membrana nieporowata − permeat, 

w ujęciu modelu rozpuszczania-dyfuzji 

 
 

 

Matematyczny opis zjawisk transportowych w ujęciu modelu roz-

puszczania-dyfuzji wyprowadzony jest w oparciu o następujące założenia 
(rys. 2) [15]: 

• membrana traktowana jest jako faza ciągła, 

• na granicach faz pomiędzy powierzchnią membrany a fazą nadawy 

lub fazą permeatu panuje równowaga chemiczna odnośnie do 
składników pojedynczych, 

• ciśnienie wewnątrz membrany jest równe ciśnieniu po stronie 

nadawy, 

• pomija się oddziaływania pomiędzy strumieniami cząstkowymi per-

meujących składników, 

• wzdłuż drogi dyfuzji składnika przez membranę istnieje ciągły gra-

dient potencjału chemicznego, 

• strumień składnika przez membranę jest proporcjonalny do siły 

napędowej, która jest wyrażana przez potencjał chemiczny skład-
nika i (

µ

i

): 

                                             Perwaporacja i separacja… 

 

115 

dx

d

L

J

i

i

i

µ

−

=

, 

 

 

 

 

 

(11) 

,

)

(

dp

υ

c

γ

ln

RTd

µ

d

i

i

i

i

+

=

 

   (12) 

J

i

 

− strumień składnika i, 

L

i

 

− fenomenologiczny współczynnik przewodnictwa, 

µ

i

 

− potencjał chemiczny składnika i, 

c

i

 – stężenie, 

γ

i

 

− współczynnik aktywności, 

υ

i

 

− objętość molowa składnika i. 

 

W przypadku faz nieściśliwych (faza ciekła, membrana) objętość nie 

zmienia się wraz ze zmianą ciśnienia, a scałkowanie równania (12) po stę-
żeniu i ciśnieniu daje następujące wyrażenie na potencjał chemiczny skład-
nika i: 

)

(

)

(

o

i

i

i

i

o

i

i

p

p

υ

c

γ

ln

RT

µ

µ

−

+

+

=

.     (13) 

Natomiast w przypadku fazy gazowej objętość molowa zmienia się  

z ciśnieniem i scałkowanie równania (12) prowadzi do następującego wyra-
żenia na potencjał chemiczny składnika i: 

( )

o

i

i

i

o

i

i

p

p

ln

RT

c

ln

RT

µ

µ

+

γ

+

=

. 

   (14) 

Standardowy potencjał chemiczny składnika  i  (

µ

i

o

) powinien być 

identyczny w równaniu (13) i (14). W tym celu jako ciśnienie odniesienia 
wybrane zostało ciśnienie pary nasyconej tego składnika (p

i, sat

). W takim 

przypadku równania (13) i (14), opisujące potencjał chemiczny składnika i, 
przyjmą następującą postać: 

)

(

)

(

sat

,

i

i

i

i

o

i

i

p

p

υ

c

γ

ln

RT

µ

µ

−

+

+

=

,     (15) 

( )

sat

,

i

i

i

o

i

i

p

p

ln

RT

c

γ

ln

RT

µ

µ

+

+

=

. 

   (16) 

Zgodnie z założeniem modelu rozpuszczania-dyfuzji ciśnienie we-

wnątrz membrany jest stałe i równe ciśnieniu po stronie nadawy, a gradient 
potencjału chemicznego przez membranę wyrażony jest przez gradient ak-
tywności składnika i. Strumień tego składnika wyraża równanie (11), które 
wobec stałości ciśnienia może być zapisane następująco: 

dx

dc

c

RTL

J

i

i

i

i

−

=

,  

 

 

 

 

(17) 

a więc analogicznie do równania Ficka: 

dx

dc

D

J

i

i

i

−

=

. 

 

 

 

 

 

(18) 

Scałkowanie tego ostatniego równania po grubości membrany daje 

następujące wyrażenie na transport składnika przez membranę: 

W. Kujawski                                                                       

 

116

l

c

c

D

J

M

P

i

M

N

i

i

i

)

(

,

,

−

=

, 

    (19) 

gdzie: 

M

N

i

c

,

 

− oznacza stężenie składnika i w membranie, na granicy faz nadawa-

membrana, 

M

P

i

c

,

 

− oznacza stężenie składnika i w membranie, na granicy faz mem-

brana-permeat. 

Równanie (19) jest fundamentalnym równaniem modelu rozpuszcza-

nia-dyfuzji [19]. W celu wykorzystania tego równania do opisu zjawisk 
transportowych należy je przekształcić przez wyprowadzenie dodatkowych 
zależności opisujących stężenia składników w membranie (

M

N

i

c

,

 oraz 

M

P

i

c

,

) 

w funkcji parametrów roztworów przymembranowych. 

 

3.1.  SEPARACJA PAR I GAZÓW 

 

W procesie separacji gazów lub par nadawę stanowi mieszanina gazowa 
o ciśnieniu  p

N

, natomiast gazowy permeat odbierany jest po stronie ni-

skociśnieniowej (p

P

) membrany. 

Wyprowadzenie odpowiednich równań transportowych rozpoczyna 

się od przyrównania potencjałów chemicznych składników na granicy faz 
nadawa/membrana i membrana/permeat. W procesie separacji gazów/par, 
do fazy nadawy i permeatu musimy zastosować równania opisujące poten-
cjał chemiczny dla fazy ściśliwej (równanie (14)), natomiast potencjał che-
miczny składnika w membranie opisuje równanie dla fazy nieściśliwej (13). 

Tak więc w procesie separacji gazów/par dla granicy faz gazowa 

nadawa/membrana otrzymujemy dla stanu stacjonarnego: 

)

(

)

(

)

(

,

,

,

,

,

sat

i

N

i

M

N

i

M

N

i

o

i

sat

,

i

N

N

i

N

i

o

i

p

p

υ

c

γ

ln

RT

µ

p

p

ln

RT

c

γ

ln

RT

µ

−

+

+

=

+

+

, 

  (20) 

a w wyniku odpowiednich przekształceń: 

)

)

(

(

,

,

,

RT

p

p

υ

exp

c

p

p

γ

γ

c

sat

i

N

i

N

,

i

sat

i

N

M

N

i

i

M

N

,

i

−

−

=

.  

(21) 

Ponieważ wyraz eksponencjalny w równaniu (21) jest bliski jedności, 

to równanie to można przekształcić do postaci: 

sat

i

N

M

N

i

N

i

i

M

N

i

p

p

γ

c

γ

c

,

,

,

,

=

.     (22) 

Wyraz c

i,  N 

p

N

 jest ciśnieniem parcjalnym składnika w nadawie, więc 

równanie powyższe upraszcza się do postaci: 

sat

i

N

i

M

N

,

i

i

M

N

i

p

p

γ

γ

c

,

,

,

=

.  

 

 

 

 

(23) 

                                             Perwaporacja i separacja… 

 

117 

Wyraz 

γ

i, N

/(p

i, sat

M

N

i

γ

,

) jest określony mianem współczynnika sorpcji 

,

G

i

K

 więc ostatecznie, wyrażenie na stężenie składnika i w membranie na 

granicy faz nadawa/membrana przyjmuje postać: 

N

i

G

i

M

N

i

p

K

c

,

,

=

.   

 

 

 

 

(24) 

Analogiczną postać ma równanie na stężenie składnika i w membra-

nie na granicy faz membrana/permeat: 

P

i

G

i

M

P

i

p

K

c

,

,

=

. 

 

 

 

 

 

(25) 

Podstawiając zależności (24) i (25) do równania (19), otrzymujemy 

równanie opisujące transport składnika w procesie separacji par i gazów: 

)

(

,

,

P

i

N

i

G

i

i

i

p

p

l

K

D

J

−

=

 

    (26) 

lub 

)

(

,

,

P

i

N

i

G

i

i

p

p

l

P

J

−

=

. 

    (27) 

Równanie (27) można wykorzystać do oceny właściwości selektyw-

nych membrany w separacji mieszaniny par lub gazów. Wykorzystuje się 
do tego celu współczynnik przepuszczalności ,

G

i

P  przekształcony do po-

staci [15]: 

sat

i

M

i

i

i

G

i

p

D

P

,

γ

γ

=

. 

 

 

 

 

 

(28) 

Równanie powyższe było podstawą interpretacji zależności współ-

czynnika przepuszczalności membran w kontakcie z węglowodorami o ro-
snącej długości łańcucha węglowodorowego [15]. 

 

3.2.  PERWAPORACJA 

 

Perwaporacja jest procesem membranowym, w którym dwuskładnikowa 
mieszanina ciekła jest transportowana przez selektywną membranę. Po stro-
nie permeatu panuje obniżone ciśnienie, więc separowane składniki odbie-
rane są w fazie gazowej. 
 

Na granicy faz ciekła nadawa/membrana równość potencjałów che-

micznych składnika zapisujemy następująco: 

)

(

)

(

)

(

)

(

,

,

,

,

,

,

sat

i

N

i

M

N

i

M

N

i

o

i

sat

i

N

i

N

i

N

i

o

i

p

p

υ

c

γ

ln

RT

µ

p

p

υ

c

γ

ln

RT

µ

−

+

+

=

=

−

+

+

 

 

 

 

co prowadzi, po prostych przekształceniach matematycznych, do wyrażenia 
na stężenie składnika w membranie na granicy faz nadawa/membrana: 

N

i

i

M

N

i

N

i

i

M

N

i

c

K

γ

c

γ

c

,

,

,

,

=

=

. 

    (30) 

,                   (29)

 

W. Kujawski                                                                       

 

118

 

Na granicy faz membrana/permeat ciśnienie spada od wartości  p

0

  

w membranie do wartości p

P

 w permeacie, a wyrażenie opisujące równość 

potencjałów chemicznych jest następujące: 

)

(

)

(

)

(

,

,

,

,

,

,

sat

i

P

i

M

P

i

M

P

i

o

i

sat

i

P

P

i

P

i

o

i

p

p

υ

c

γ

ln

RT

µ

p

p

ln

RT

c

γ

ln

RT

µ

−

+

+

=

=

+

+

   

 

 

 

Natomiast stężenie składnika w membranie otrzymane po przekształ-

ceniu powyższej zależności, przedstawia równanie (32): 

)

)

(

(

,

,

,

,

,

,

RT

p

p

υ

exp

c

p

p

c

sat

i

P

i

P

i

sat

i

P

M

P

i

P

i

M

P

i

−

−

γ

γ

=

.     (32) 

 

Podobnie jak w poprzednim przypadku, wyraz eksponencjalny jest 

bliski jedności, więc stężenie składnika w membranie na granicy faz mem-
brana/permeat wyraża równanie: 

P

i

G

i

sat

i

P

i

M

P

i

P

i

M

P

i

p

K

p

p

c

,

,

,

,

,

,

=

γ

γ

=

. 

   (33) 

 

Równania na stężenia składnika wewnątrz membrany (30) i (33) 

mogą być podstawione do równania Fick’a (19) na strumień. Należy za-
uważyć,  że współczynniki sorpcji w równaniu (30) i (33) odnoszą się do 
innych faz, konieczne jest więc wyprowadzenie zależności na interkonwer-
sję tych współczynników. Dokonuje się tego w oparciu o równowagę po-
między cieczą a parą, opisaną równaniem (34) [12]: 

sat

i

N

G

N

i

G

N

i

o

i

sat

i

N

i

L

N

i

L

N

i

o

i

p

p

ln

RT

c

γ

ln

RT

µ

p

p

υ

c

γ

ln

RT

µ

,

,

,

,

,

,

)

(

)

(

)

(

+

+

=

=

−

+

+

 

 

 

 

W równaniu (34) indeks górny L odnosi się do fazy ciekłej, a G 

− do 

fazy parowej. 

Postępując podobnie jak przy wyprowadzaniu zależności (33), mo-

żemy zapisać: 

sat

i

N

i

L

N

i

G

N

i

N

i

p

p

c

,

,

,

,

,

γ

γ

=

,   

 

 

 

 

(35) 

gdzie p

i, N

 jest parcjalnym ciśnieniem składnika i w równowadze z fazą cie-

kłą. Wyraz 

L

N

i

γ

,

p

i, sat

/

G

N

i

γ

,

 jest określany jako stała Henry’ego. Podstawienie 

równania (35) do równania (30) prowadzi do następującej zależności na 
stężenie: 

N

i

G

i

sat

i

N

i

L

N

i

G

N

i

N

i

p

K

p

p

c

,

,

,

,

,

,

=

γ

γ

=

. 

   (36) 

 
 
 

.                         (31)

 

.                       (34)

 

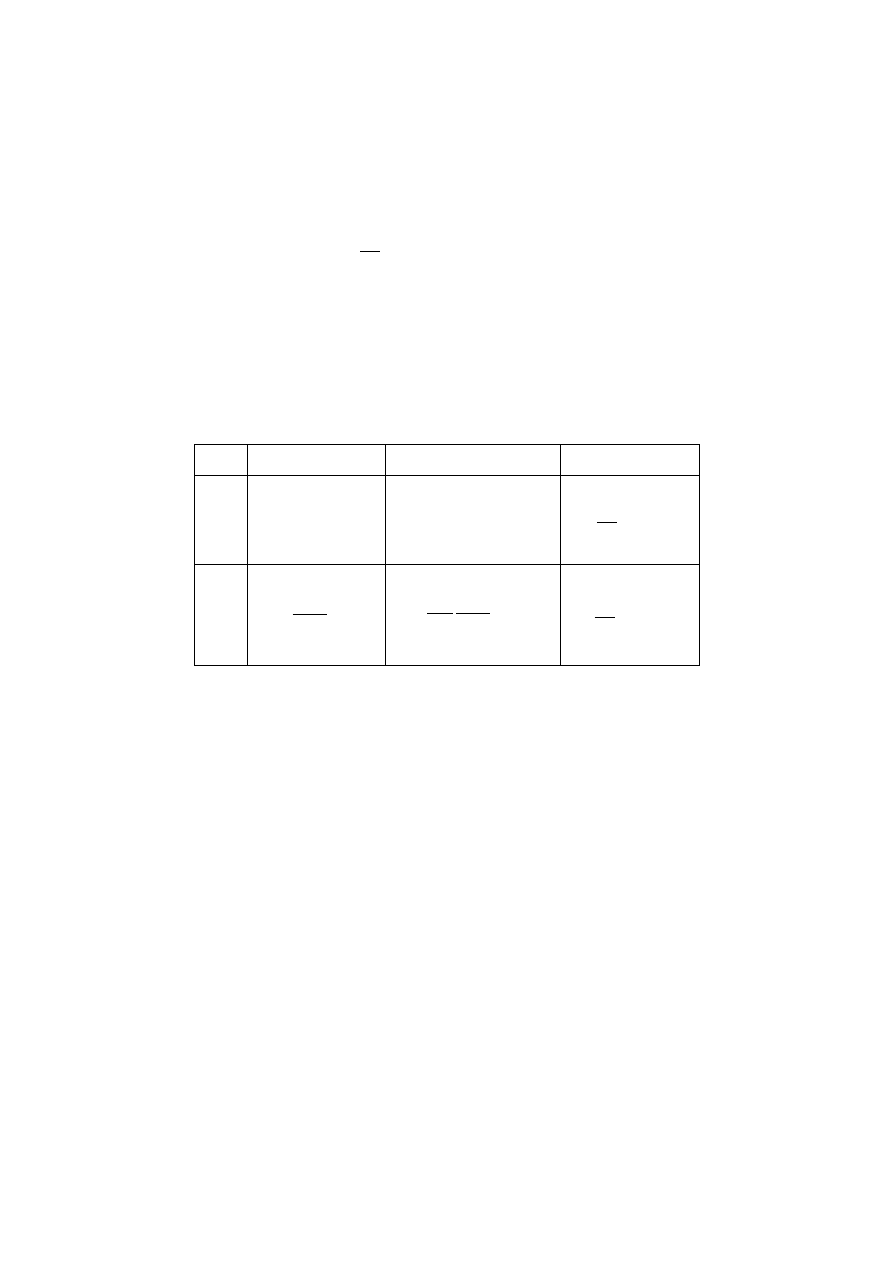
                                             Perwaporacja i separacja… 

 

119 

W takim przypadku równanie transportowe na strumień składnika przyj-
muje postać: 

)

(

,

,

P

i

N

i

G

i

i

p

p

l

P

J

−

=

.     (37) 

Równanie (37) wyraża siłę napędową w perwaporacji przez ciśnienie 

pary. 

W tab. 1 zestawiono wyprowadzone wyżej zależności na stężenia 

składników transportowanych w membranie 

M

N

i

c

,

 oraz 

M

P

i

c

,

, w funkcji wła-

ściwości przymembranowych roztworów zewnętrznych. 
 

Tabela 1. Zależności na stężenia składników w membranie oraz strumień permeatu 

w ujęciu modelu rozpuszczania-dyfuzji [15] 

 
 

W praktyce laboratoryjnej proces perwaporacji jest realizowany róż-

nymi metodami. Niezależnie jednak od przyjętego rozwiązania ciekła 
nadawa zawsze pozostaje w bezpośrednim kontakcie z jedną stroną mem-
brany, a siłą napędową jest gradient ciśnień parcjalnych składników po obu 
stronach membrany. Metody realizacji perwaporacji różnią się sposobem 
odbioru permeatu. 
 

4.  ZASTOSOWANIE PROCESU PERWAPORACJI 

W PERWAPORACJI I PERMEACJI PAR 

 
W procesie perwaporacji i permeacji par używa się gęstych nieporowatych 
membran liofilowych, wśród których można wyróżnić [4, 11, 16

−18]: 

•  membrany obojętne o charakterze hydrofilowym (np. z poliakryloni-

trylu, poli(alkoholu winylowego), poliakryloamidu, octanu celulozy), 

•  membrany obojętne o charakterze hydrofobowym (np. z polistyrenu, 

poli(chlorku winylu), polietylenu, polipropylenu, polidimetylo-silok-
sanu), 

•  membrany jonowymienne mające charakter hydrofilowy, 

Proces 

M

N

i

c

,

 

M

P

i

c

,

 

J 

Permeacja 

gazów i 

pa

r 

N

i

G

i

M

N

i

p

K

c

,

,

=

 

P

i

G

i

M

P

i

p

K

c

,

,

=

 

)

(

,

,

P

i

N

i

G

i

i

p

p

l

P

J

−

=

 

Perwaporacja 

N

i

i

M

N

i

N

i

i

M

N

i

c

K

c

c

,

,

,

,

=

γ

γ

=

P

i

G

i

sat

i

P

i

M

P

i

P

i

M

P

i

p

K

p

p

c

,

,

,

,

,

,

=

γ

γ

=

)

(

,

,

P

i

N

i

G

i

i

p

p

l

P

J

−

=

 

W. Kujawski                                                                       

 

120

•  membrany z polimerów przewodzących. 

Membrany do perwaporacji formowane są także z materiałów 

ceramicznych, jak modyfikowana krzemionka czy zeolity [19

−22]. 

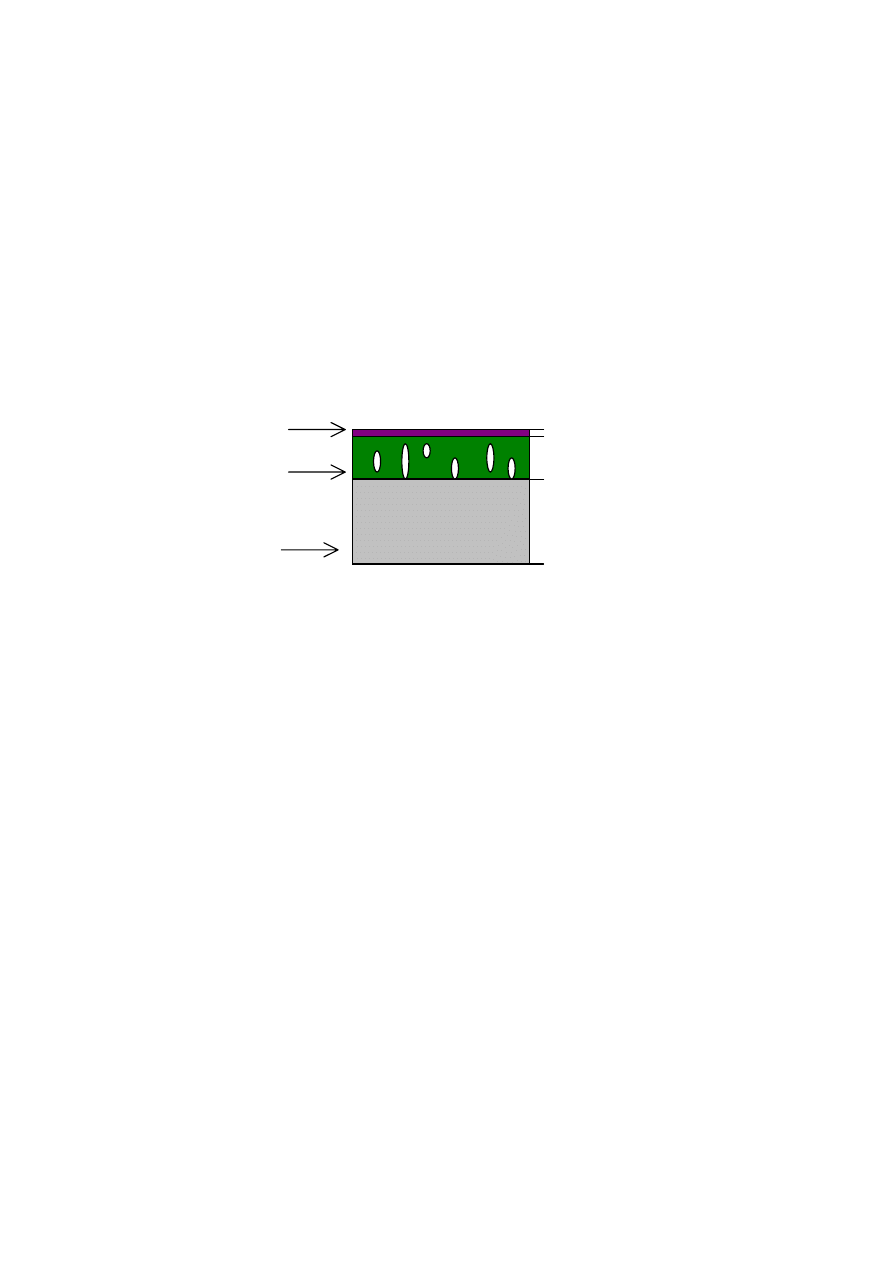
Polimerowe membrany obojętne formuje się jako kompozytowe 

membrany asymetryczne, które składają się z warstwy podłoża (włóknina 
polimerowa), porowatej warstwy wzmacniającej oraz z cienkiej, gęstej war-
stwy naskórkowej. Warstwa naskórkowa decyduje o właściwościach trans-
portowych i selektywnych membrany. Schematyczna budowa membrany 
kompozytowej przedstawiona jest na rys. 3. 
 
 

naskórek

porowata

warstwa

podłoże

2*10

6

- m

50*10

6

- m

150-200*10

-

-6

m

 

 

Rys. 3. Schemat budowy membrany laminowanej 

 
 

 Szybki 

postęp badań nad zastosowaniem procesu perwaporacji  

w przemyśle nastąpił na początku lat 80. XX wieku, gdy niemiecka firma 
Deutsche Carbone AG, GFT (obecnie Sulzer) opracowała kompozytowe 
membrany hydrofilowe z naskórkiem z polialkoholu winylowego. Mem-
brany te, o handlowej nazwie PERVAP-1000, zostały zastosowana  
w pierwszych przemysłowych instalacjach przeznaczonych do odwadniania 
etanolu. Pod koniec XX wieku rozpoczęto także, zakończone sukcesem, 
próby zastosowania w instalacjach przemysłowych membran ceramicznych 
[22]. W chwili obecnej na świecie pracuje ponad 100 przemysłowych in-
stalacji do perwaporacji, o różnym przeznaczeniu i wydajnościach od 100 
do 150 000 l/dzień. Aktualnie, proces perwaporacji jest wykorzystywany 
głównie jako tania i efektywna metoda odwadniania różnych rozpuszczalni-
ków [8, 10, 22

−26]. 

 

Ogólnie do najważniejszych kierunków zastosowania procesu per-

waporacji należy zaliczyć [4, 8, 10, 17

−36]: 

1. odwadnianie ciekłych mieszanin wodno-organicznych, szczególnie zaś: 

•  usuwanie wody z mieszanin azeotropowych typu woda/EtOH, 

woda/i-propanol, woda/pirydyna, 

•  odwadnianie rozpuszczalników organicznych, np. alkoholi, es-

trów, ketonów, eterów, kwasów karboksylowych, chlorowcopo-
chodnych węglowodorów; 

                                             Perwaporacja i separacja… 

 

121 

2. usuwanie ciekłych związków organicznych z wody, m.in.: 

•  usuwanie węglowodorów i ich chlorowcopochodnych z wód 

gruntowych i powierzchniowych, 

•  zatężanie substancji zapachowych, np. aromatów dla przemysłu 

spożywczego, 

•  usuwanie produktów organicznych w procesie ciągłej fermentacji 

(etanol, butanol); 

3. rozdział mieszanin dwóch lub więcej ciekłych związków organicznych, 

w tym:  

•  rozdział izomerów (np. o-, m-, p-ksylenów), 

•  rozdział azeotropów (np. metanol-eter metylowo t-butylowy 

/MTBE/, metanol-dwumetylowęglan /DMC/, etanol-cyklohek-
san). 

 

7. LITERATURA 

 

[1]  Membrany i membranowe techniki rozdziału, A. Narębska (red.), Wydawnictwo 

Uniwersytetu Mikołaja Kopernika, Toruń 1997. 

[2]  M. Mulder, Basic Principles of Membrane Technology (Second Edition), Kluwer 

Academic Publisher, Dordrecht, Boston, London 2003. 

[3]  A. Narębska, E. Buczyło, M. Bodzek, N. Chlubek, Membrany i techniki membranowe 

− nazewnictwo polskie, Polimery, 36 (1991) 158. 

[4]  J. Neel, Introduction to pervaporation, w: R.Y.M. Huang (Ed.), Pervaporation 

Separation Processes, Elsevier, Amsterdam 1991, s. 1–109. 

[5]  K.W. Boddeker, Terminology in pervaporation, J. Membr. Sci., 51 (1990) 259. 
[6]  P.A. Kober, Pervaporation, perstillation and percrystallization, J. Am. Chem. Soc., 39 

(1917), s. 944–948; J. Membr. Sci., 100 (1995), s. 61–64. 

[7]  R.C. Binning, R.J. Lee, J.F. Jennings, E.C. Martin, Separation of liquid mixtures by 

permeation, Ind. Engn. Chem., 53 (1961), s. 45–50. 

[8]  J.L. Rapin, The Betheniville pervaporation unit 

− the first large-scale production plant 

for the dehydration of ethanol, R. Bakish (Ed.), Proc. 3

rd

 Int. Conf. on Pervaporation 

Processes in Chemical Industry, Bakish Materials Corp., Englewood 1989, s. 364–378. 

[9]  J. Caro, M. Noack, P. Koelsch, Zeolite membranes: from the laboratory scale to 

technical applications, Adsorption 11 (2005), s. 215–227. 

[10]  U. Sander, H. Janssen, Industrial application of vapor permeation, J. Membr. Sci., 61 

(1991), s. 113–129. 

[11]  W. Kujawski, Pervaporation, w: A. Noworyta, A. Trusek-Hołownia (Eds.), Membrane 

Separation, Agencja Wydawnicza „ARGIS”, Wrocław 2001, s. 121–145. 

[12]  R.Y.M. Huang, J.W. Rhim, Separation characteristics of pervaporation membrane 

separation processes, w: R.Y.M. Huang (Ed.), Membrane Science and Technology 
Series, 1. Pervaporation Membrane Separation Processes, Elsevier, Amsterdam 1991, 
s. 111–180. 

[13]  X. Feng, R.Y.M. Huang, Pervaporation with chitosan membranes. I. Separation of 

water from ethylene glycol by a chitosan/polysulfone composite membranes, 
J. Membrane Sci. 116 (1996), s. 67–76. 

[14]  W.Kujawski, Membrane selectivity in pervaporation, Sep. Sci. Technol. 31 (1996),  

s. 1555–1571. 

[15]  J.G. Wijmans, R.W. Baker, The solution-diffusion model: a review, J. Membr. Sci., 

107 (1995), s. 1–21. 

W. Kujawski                                                                       

 

122

[16]  G.H. Koops, C.A. Smolders, Estimation and evaluation of polymeric materials for 

pervaporation membranes, R.Y.M. Huang (Ed.), Pervaporation Separation Processes, 
Elsevier, Amsterdam 1991, s. 253–278. 

[17]  W. Kujawski, M. Waczyński, Perwaporacja-membranowa technika separacyjna, 

Przemysł Chemiczny, 75 (1996), s. 326–328. 

[18]  W. Kujawski, Pervaporation and vapor permeation – separation through nonporous 

membranes, Polish J. Chem. Technol., 5 (2003), s. 1–7. 

[19]  A.W. Verkerk, P. van Male, M.A.G. Vorstman, J.T.F. Keurentjes, Properties of high 

flux ceramic pervaporation membranes for dehydration of alcohol:water mixtures, Sep. 
Purif. Technol., 22–23 (2001), s. 689–695. 

[20]  A. Urtiaga, E.D. Gorri, C. Casado, I. Ortiz, Pervaporative dehydration of industrial 

solvents using a zeolite NaA commercial membrane, Sep. Purif. Technol., 32 (2003),  
s. 207–213. 

[21]  H. Verweij, Ceramic membranes: Morphology and transport, J. Materials Sci., 38 

(2003), s. 4677–4695. 

[22]  M. Kondo, M. Komori, H. Kita, K. Okamoto, Tubular-type pervaporation module with 

zeolite NaA membrane, J. Membr. Sci., 133 (1997), s. 133–141. 

[23]  H. Bruschke, Industrial applications of membrane separation processes, Pure Appl. 

Chem., 67 (1995), s. 993–1002. 

[24]  U. Sander, P.B. Soukup, Practical experience with pervaporation systems for liquid and 

vapour separation, J. Membr. Sci., 62 (1991), s. 67–89. 

[25]  K. Scott (Ed.), Handbook of Industrial Membranes, Elsevier, Oxford 1995. 
[26]  A. Jonquières, R. Clément, P. Lochon, J. Néel, M. Dresch, B. Chrétien, Industrial state- 

-of-the art of pervaporation and vapour permeation in the western countries, J. Membr. 
Sci., 206 (2002), s. 87–117. 

[27]  D.J. O’Brien, L.H. Roth, A.J. McAloon, Ethanol production by continuous 

ferementation-pervaporation: a preliminary economic analysis, J. Membr. Sci., 166 
(2000), s. 105–111. 

[28]  W. Kujawski, W. Capała, M. Palczewska-Tulińska, W. Ratajczak, D. Linkiewicz, 

B. Michalak, Application of membrane pervaporation process to the enhanced 
separation of fusel oils, Chem. Pap., 56 (2002), s. 3–6. 

[29]  H.L. Fleming, C.S. Slater, Pervaporation, w: W.S. Winston HO, K.K. Sirkon (Eds.), 

Membrane Handbook, Van Nostrand Reinhold, New York 1992, III, s. 103–160. 

[30]  W. Kujawski, Pervaporative removal of organics from water using hydrophobic 

membranes. Binary mixtures, Sep. Sci. Technol., 35 (2000), s. 89–108. 

[31]  U. Hommerich, R. Rautenbach, Design and optimization of combined 

pervaporation/distillation processes for the production of MTBE, J. Membr. Sci., 146 
(1998), s. 53–64. 

[32]  G.S. Luo, M. Niang, P. Schaetzel, Separation of ethyl tert-butyl ether-ethanol by 

combined pervaporation and distillation, Chem. Eng. J., 68 (1997), s. 139–143. 

[33]  T. Sano, M. Hasegawa, Y. Kawakami, H. Yanagishita, Separation of methanol/methyl-

-tert-butyl ether mixture by pervaporation using silicalite membrane, J. Membr. Sci., 
107 (1995), s. 193–196. 

[34]  F. Lipnizki, R.W. Field, P.-K. Ten, Pervaporation-based hybrid process: a review of 

process design, applications and economics. J. Membr. Sci., 153 (1999), s. 183

−210. 

[35]  S. Takizawa, T. Win, Removal of trichloroethylene and trichloromethane using a novel 

hollow-fibre gas-permeable membrane, Water Sci. Technol.: Water Supply, 3 (2003),  
s. 67–72. 

[36]  V. Van Hoof, L. Van den Abeele, A. Buekenhoudt, C. Dotremont, R. Leysen, 

Economic comparison between azeotropic distillation and different hybrid systems 
combining distillation with pervaporation for the dehydration of isopropanol, Sep. 
Purif. Technol., 37 (2004), s. 33–49.