Przedmiot:

Logika

Wykładowca:

Bartosz Orlewicz

Liczba godzin:

Literatura:

1. B. Stanosz "Wprowadzenie do logiki formalnej"

2. B. Stanosz "Ćwiczenia z logiki"

3. M. Tokarz "Metdyka, perswazja" ( zwłaszcza rozdział V i VI – sztuka argumentacji i sztuka dyskutowania)

Zaliczenie:

egzaqmin pisemny: 2-3 pytania teoretyczne + 2-3 zadania praktyczne (z tym, że naistotniejsze jest

ostatnie zadanie, np. "Sprawdź czy wniosek wynika logicznie z przesłanek". Jeśli ktoś nie będzie

potrafił opanować teorii, nie zrobi ostatniego zdania). Będzie można mieć ściągę w postaci tabelki

prawdowościowej). Jeśli ktoś nie może stawić się w wyznaczonym terminie zaliczenie może o

dbyć się na dyżurze lub na innym wykładzie. Wpoisy do indeksów odbywają się poprzez

starostów. Pracę oddajemy grupami. Praca musi zawierać: datę, specjalizację, imię i nazwisko –

DRUKOWANYMI LITERAMI!!!

Cel wykładów:

nauka budowy argumentu. Język logiki służy wyrabianiu umiejętności budowania poprawnych

argumentów.

16 października 2010r.

LOGIKA FORMALNA

RACHUNEK

ZDAŃ

RACHUNEK KWANTYFIKATORÓW

dotyczy zdań jako całości bez względu na ich treść

w tym przypadku ważna jest wewnętrzna

budowa zdania

I.

RACHUNEK ZDAŃ – ma swój język (reguły łaczenia tego języka).

Używane symbole:

Symbol

Nazwa

Co oznacza

p, q, r, s, t, v

zmienna zdaniowa

coś za co można wstawić dowolne zdanie lub stwierdzenie. Jeśli

przyporządkujemy daną literę jakiemuś zdaniu lub stwierdzeniu, to gdy

następnym razem ono się pojawi, zamiast pisać je powtórnie –

używamy danej litery.

∩ (i)

ale, lecz, a

koniunkcja

v

lub

alternatywa

V

albo

alternatywa względna

┴

Ani...., ani....

binegacja!!!

→

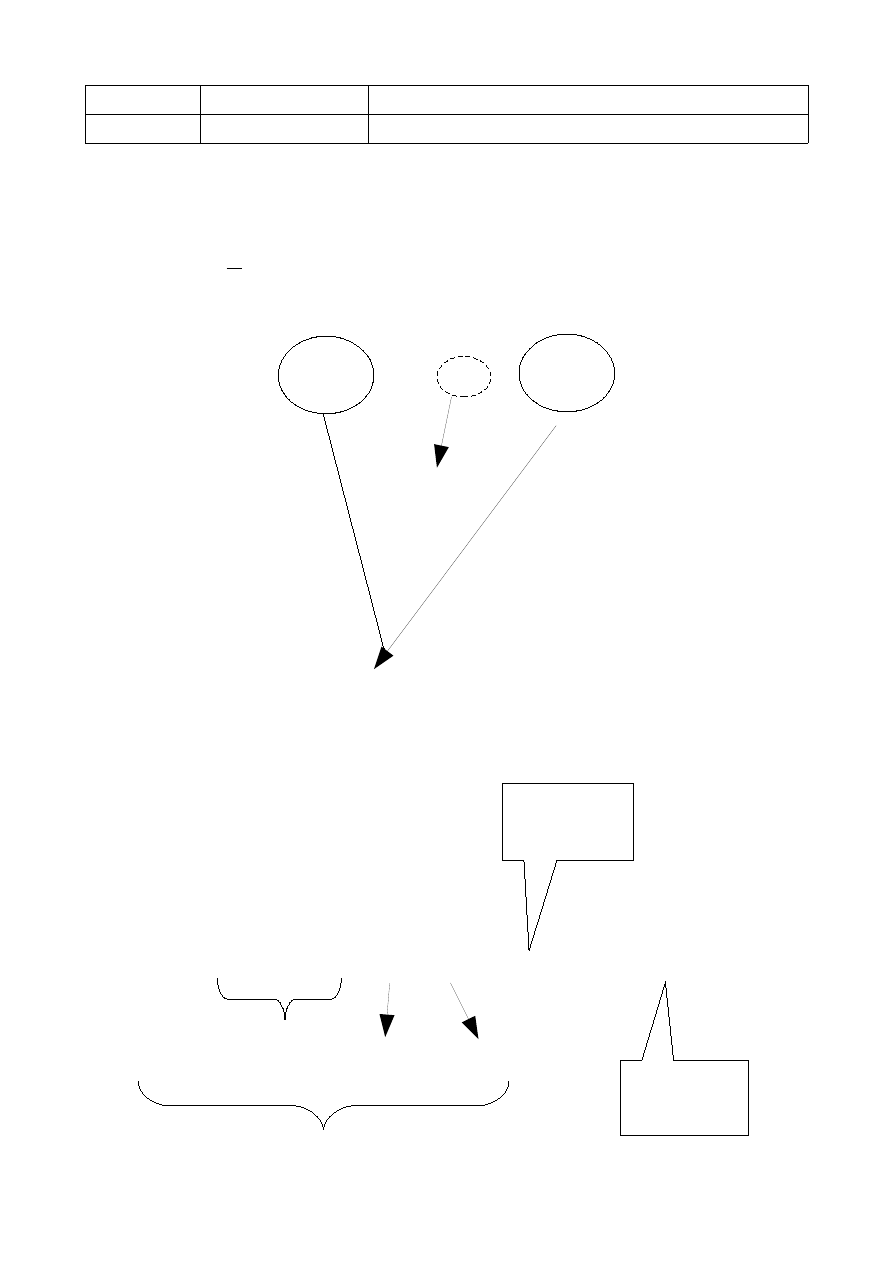
Jeśli....., to.........

implikacja materialna

↔

wtedy

równoważność

Formuły zdaniowe:

p v q

(czyt: p albo q, lub alternatywa p i q)

p ∩ q

(czyt: p i q, lub koniunkcja p i q)

p V q

(czyt: p albo q)

p → q

(czyt: jeśli p, to q, lub p implikuje q)

(p v q) → (r ∩ t)

SPÓJNIK FORMUŁY

FORMUŁY ZDANIOWE

nawiasy sprawiają, że te dwie formuły tworzą osobne formuły zdaniowe, nawet jeśli są

zbudowane z tej samej formuły i tych samych spójników. Umozliwiają ponadto znalezienie spójnika głównego

formuły, który znajduje się między nawiasami lub przed nawiasem.

[ (p ↔ q) → r] → (s v t)

IMPLIKACJA
(spójnik główny)

NASTĘPNIK
IMPLIKACJI

POPRZEDNIK IMPLIKACJI

POPRZEDNIK
IMPLIKACJI IMPLIKACJA NASTĘPNIK

IMPLIKACJI

Inne symbole:

1 – prawda

0 – fałsz.

~ - nie prawda, że (napisany przed pojedynczą literą odnosi się tylko do niej, stawiany przed

nawiasem dotyczy całego nawiasu)

tautologia –

to formuła logicznie prawdziwa dla każdego wartościowania jej zmiennych.

Tautologia rachunku

zdań

to formuła logiczna tego rachunku, która jest prawdziwa dla każdego wartościowania jej zmiennych

zdaniowych.

Tabela prawdziwościowa

p

q

p ∩ q

p v q

P V q

P ┴ q

P → q

p ↔ q

1

1

1

1

0

0

1

1

1

0

0

1

1

0

0

0

0

1

0

1

1

0

1

0

0

0

0

0

0

1

1

1

Wartość logiczna całej formuły zależy od ( i jest wyznaczona przez) wartości logicznych jej

części składowych, którymi mogą być inne formuły (np. (p v q), (p ∩ q) itp.) lub zmienne (najmniejsza możliwa

formuła np. p, q, r utd.)

Nazwa

Cecha charakterystyczna

KONIUNKCJA

jest prawdziwa tylko w jednym przypadku – kiedy wszystkie jej części
składowe są prawdziwe (pozostałe jej części są fałszywe).

ALTERNATYWA

Jest prawdziwa w trzech przypadkach. Fałszywa jest tylko wtedy, gdy wszystkie
jej części składowe są fałszywe.

ALTERNATYWA

ROZŁĄCZNA

Jest zbudowana za pomocą spójnika "albo".Jest prawdziwa tylko wtedy, gdy
jedna z jej części składowych jest prawdziwa.

BINEGACJA

"Ani nie ma Boga, ani nie ma Szatana" – oba zdania są prawdziwe, więc
binegacja jest prawdziwa tylko wtedy, gdy jej elementy składowe są fałszywe.

IMPLIKACJA

MATERIALNA

Fałszywa jest tylko w jednym przypadku – kiedy poprzednik jest prawdziwy, a
nastepnik fałszywy.
prawda → prawda
fałsz → prawdę
fałsz → fałsz

RÓWNOWAŻNOŚĆ

Jest prawdziwa tylko wtedy, gdy wszystkie elementy składowe mają tę samą
wartość logiczną (albo obie są prawdą, albo obie są fałszem)

Przykładowe zadanie egzaminacyjne dla 3 zmiennych !!!!

Jaką wartość logiczną posiada zdanie oznaczone literą "p", jeśli:

➢

prawdą jest, że "p" tworzy fałszywą koniunkcję z dowolnym zdaniem,

➢

p tworzy fałszywą alternatywę z niektórymi zdaniami,

➢

implikacja, której poprzednikiem jest "p" jest zawsze prawdziwa,

➢

implikacja, której poprzednikiem jest "p" jest niekiedy fałszywa.

Określanie wartości logiczne:

1)

( p v q ) → r

(1) v (1) → (0)

poprzednik (1) następnik (0)

wartość logiczna zdania = 0

2) ( p <-> q ) ┴ ( s ∩ t )

(1) (0) (1) (0)

(0)

(0)

(1)

p

→ p - takie zdanie nazywamy autologią, tzw. prawo tożsamości. Każde zdanie implikuje samo siebie.

(1) (1) = 1

(0) (0) = 1

E!!! Sprawdź czy podana formuła jest autonomią: [(p → q)

∩ p]

→ q

p

q

(p → q)

(p → q)

∩ p

[(p → q)

∩ p]

→ q

1

1

1

1

1

1

0

0

0

1

0

1

1

0

1

0

0

1

0

1

Przy rozwiązywaniu tego zadania należy posiłkować się tabelą prawdziwościową.

Odp. Podana formuła jest autologią.

1.

(pzresłanka) p

→ q

2. (przesłanka) p

3. (przesłanka) q

Schemat rozumowania niezawodnego – jest nią każda autologia. Rozumoanie niezawodne (oparte na schemacie

autologii), to takie, które o ile jego rzesłanki są prawdziwe, zawsze prowadzą do prawdziwego wniosku.

Zadanie. P. Maria jest podejrzana o zabójstwo swojego partnera. Załóżmy, ze po 10 godz. się przyznała.

Stwierdziła. Że udusiła konkubenta gołymi rękoma. Ale policjant ma wątpliwości. Jesli udusiła konkubenta

gołymi rękoma, to na jego szy powinny być odciski palców.

p – p. Maria zadusiła konkubenta rękoma

q – na szy konkubenta są odciski

Takie twierdzenie przedstawimy w następujący sposób:

[(p → q)

∩ p]

→ q

1. p → q

2. p

3. q

Zostały przeprowadzone badania, podczas których nie znaleziono odcisków kobiety, zatem:

1.

p → q

2. ~ q

3. ~ p

Jest to tylko schemat, ale w praktyce moży być on bardzo skomplikowany.

Zadanie. Sprawdź czy podana formuła jest autologią: ~[(p v q) → r ]

p

q

r

p v q

[(p v q) → r ]

~ [ (p v q) → r ]

1

1

1

1

1

0

1

1

0

1

0

1

1

0

0

1

0

1

0

0

0

0

1

0

0

0

1

0

1

0

0

1

1

1

1

0

1

1

1

1

1

0

0

1

0

1

0

1

Odp.: Ta formuła nie jest autologią.

jest to autologia,

modus ponendo ponens – MPP

Tautologia rachunku zdań mówi, że jeśli
uznajemy

prawdziwość

poprzednika

prawdziwej

implikacji

, to musimy uznać też

prawdziwość jej

następnika

jest to autologia,

modes tollendo tollens (MTT)

wnioskowanie

logiczne, reguła

logiki

mówiąca, że jeśli zaakceptujemy, że z p
wynika q oraz że q jest fałszywe, to musimy
zaakceptować też fałszywość p.

Zadanie. Sprawdź, czy podana formuła jest autologią: ~ (p

∩

q) ↔ (~p v ~ q)

p

q

p

∩

q

~ (p

∩

q)

~p

~ q

(~p v ~ q)

~ (p

∩

q) ↔ (~p v ~ q)

1

1

1

0

0

0

0

1

1

0

0

1

0

1

1

1

0

1

0

1

1

0

1

1

0

0

0

1

1

1

1

1

Odp.: ta formula jest utologią.

~ (p

∩

q) ↔ (~p v ~ q)– tzw. Prawo negowania koniunkcji – negacja koniunkcji jest równoważna alternatywie

negacji.

Przykłady tożsamych zdań:

~ (p

∩

q

∩

r

∩

s) ↔ (~p

∩

~ q

∩

~ r

∩

~s)

=

(p

∩

q

∩

r

∩

s) → t

~ t

~ (p

∩

q

∩

r

∩

s)

Zadanie. Sprawdź, czy podana formuła jest autologią: [(p → q)

∩

(q → r)] → (p → r)

p

q

r

(p → q) (q → r) (p → r) (p → q)

∩

(q → r) [(p → q)

∩

(q → r)] → (p → r)

1

1

1

1

1

1

1

1

1

1

0

1

0

0

0

1

1

0

0

0

1

0

0

1

0

0

0

1

1

1

1

1

0

0

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

1

0

1

0

0

0

1

Odp. Ta formuła jest autologią.

Skrócona metoda rozwiązywania tego problemu !!!

Autologiczne zdanie to takie, którego wnisek zawsze jest prawdą (niezależnie czy jego części

składowe są prawdziwe czy fałszywe).

Krok 1. "Ufałszywiamy wniosek" tj. Podstawiamy do jego zmiennych takie wartości, aby wyszedł nam fałsz. W

przypadku implikacji materialnej fałsz następuje wtedy, kiedy poprzednik jest prawdziwy, a następnik fałszywy,

zatem:

[(p → q)

∩

(q → r)] → (p → r)

(1) (0)

Krok 2. Wiadomo już, że "p" musi mieć wartość (1), a "r" 0. Podstawiamy do reszty wzoru wartości "p" i "r"

[(p → q)

∩

(q → r)] → (p → r)

(1) (0) (1) (0)

Krok 3. Aby nasze zdanie nie było autologią, i skoro następnik jest fałszywy, to muzimy sprawić, aby poprzednik

był prawdziwy. Dlatego proponuję nadać zmiennej "q" wartość dodatnią.

[(p → q)

∩

(q → r)] → (p → r)

(1) (1) (1) (0) (1) (0)

(1)

(0) (0)

(0) ..

(1)

Jeśli ta implikacja jest autolgią, to nie ma takiego wartościowania, dla którego poprzednik tej implikacji

byłby prawdziwy, a następnik fałszywy. Autologia to formuła zawsze prawdziwa. Nieisana zasada mówi o tym,

że przy tego typu zadaniach ufałszywiamy następnik a uprawdziwamy poprzednik.

30 października 2010r.

Zadanie. Zbadaj, które z podanych niżej wnioskoań są dedukcyjne.

Aby móc rozwiązać to polecenie należy wiedzieć co to jest WNIOSKWANIE DEDUKCYJNE.

W tym zaś celu nalezy wiedzieć, czym jest WYNIKANIE LOGICZNE.

WYNIKANIE LOGICZNE:

(Z

1

→ Z

2

)

Zdanie Z2 wynika logicznie ze zdania Z1 wtedy, i tylko wtedy gdy całe zdanie (Z1 → Z2) jest

tautologią.

1.

p → q

2.

p

3.

q

Mając na uwadze te trzy przesłanki sprawdź czy z dwóch pierwszych przesłanek wynika "q".

Zapiszemy to tak:

[(p → q) ∩ p] → q

pierwsza przesłanka zdania łaczące poprzednik druga przesłanka wniosek

łaczymy za pomocą koniunkcji

Ćwiczenie 1. Jeśli Jan uczy się Pilnie, to otrzymuje dobre stopnie, a jeśli nie otrzymuje dobrych stopni, to traci

humor. Jan nie taci humoru, zatem Jan uczy się pilnie.

p – Jan uczy się pilnie,

q – Jan otrzymuje dobre stopnie

~q – Jan nie otrzymuje dobrych stopni

r – Jan traci humor

1.

p→q

2.

~q → r

3.

~ r

4.

p

X

[(p → q) ∩ (~q → r) ∩ ~r] → p

(0) (1) (0) (0) (1) (0)

(0) (0) (1) (1) (0)

(1) (1)

(1)

(1)

(0)

(1) lub (0) ta formuła nie jest tautologią.

Ćwiczenie 2. Jeżeli Jan jest zdolniejszy od Pitra, a Piotr ma lepsze wyniki w nauce, to Jan mógłby się uczyć

pilniej. Niestety Jan nie mógł się uczyć pilniej, a piotr ma lepsze wyniki w nauce, zatem Jan nie jest zdolniejszy

od Piotra.

p – Jan jest zdolniejszy od Piotra

1. (p

∩ q) → r

2.

~ r ∩ q

q – a Piotr ma lepsze wyniki w nauce

r – Jan mógłby się uczyć lepiej

3.

~ p

[(

p

∩

q

)

→ r]

∩

(

~ r ∩

q)] → ~ p

1

1

0

1

1

0

1

1

0

0

1

Ćwiczenie 3. Jęsli Jan nie lubi logiki, to twierdzi, że ma zainteresowania humanistyczne i uważa, że znajomość

logiki jest humanistom niepotrzebna. Zatem jeśli Jan twierdzi, że ma zainteresowania humanistyczne, to uważa,

że znajomość logiki jest humanistom niepotrzebna.

p – Jan nie lubi logiki

1. p

→ (q∩r)

q – to uważa, że ma zainteresowania humanistyczne

r – uważa, ze logika jest niepotrzebna

2. q

→ r

[p

→

(q

∩

r)]

→

(q

→

r)

0

1

0

1

0

0

0

1

0

Ćwiczenie 4. Jesli Jan nie będzie schlebiał Piotrowi, to straci posadę. Jeśli Jan straci posadę, to rzuci go

kochanka. Jeżeli Jan będzie schlebiał Piotrowi, to straci dobrą opinię. Zatem Jan straci kochankę lub straci dobrą

opinię.

p - schlebianie

1. ~ p → q
2. p → r
3. p → s

q - posada
r - kochanka
s – dobra opinia

4. r v s

[(

~p → q)

∩

(p

→ r)

∩

(p

→ s)] → r

v

s

1

0

0

0

0

0

0

0

0

1

1

0

1

0

0

1