1.
Układy doświadczalne krzyżowe i hierarchiczne
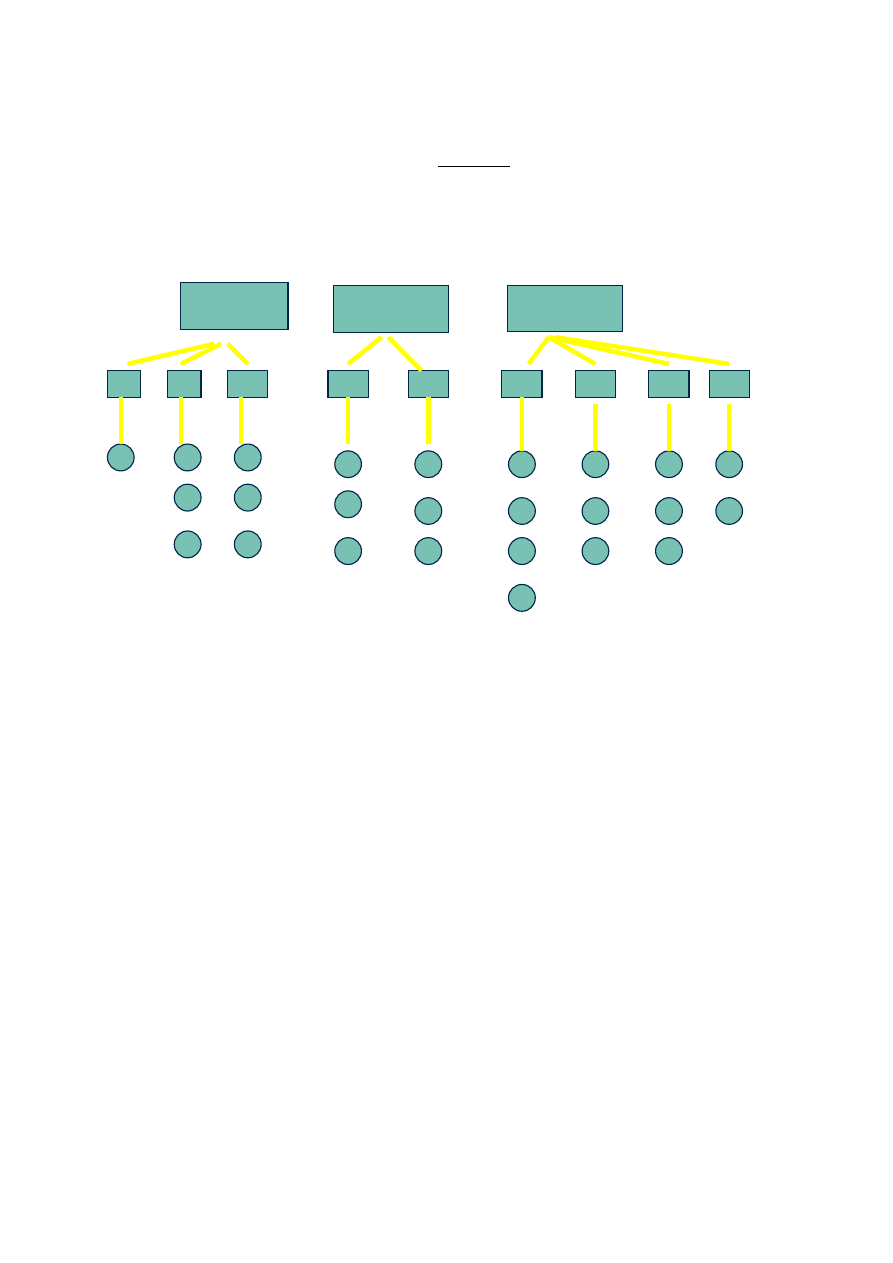
Z układem hierarchicznym doświadczenia mamy do czynienia wówczas, gdy badamy wpływ
poziomów jednego czynnika (tzw. podgrupy) w obrębie poziomów czynnika nadrzędnego
(tzw. grupy), przy czym oba czynniki traktujemy jako efekty losowe. Taki układ
doświadczenia często występuje w badaniach genetycznych (grupa=ojciec, podgrupa=matka).
Klasyfikacja krzyżowa
Gdy w populacji działają co najmniej 2 równorzędne typy czynników jej strukturę opisuje
klasyfikacja krzyżowa; dla dwóch typów czynników, A i B, działających niezależnie od
siebie, otrzymujemy klasyfikację krzyżową dwukierunkową, którą oznacza się symbolem A x
B, a opisuje ją model:opisuje ją model:
[2]
x
ijk
=
µ
+ a
i
+ b
j
+ e
ijk
,
W modelu tym x,
µ
oraz e mają znaczenie jak poprzednio, natomiast a
i
oznacza efekt i-tego
czynnika typu A, zaś b
j
– efekt j-tego czynnika typu B.
Strukturę krzyżową dwukierunkową ma np. grupa zwierząt użytych w doświadczeniu
mającym wykazać, jak reagują zwierzęta w różnym wieku (czynnik typu A) na różne stężenia
podawanego specyfiku (czynnik typu B). Do grupy tej wybierze się pewną liczbę zwierząt w
wieku w
1
, w wieku w
2
itd., każdą z grup wiekowych podzieli się na pewną liczbę podgrup, w
których zwierzętom zaaplikuje się specyfik w stężeniu s
1
, w stężeniu s
2
itd.
Ilustracją klasyfikacji dwukierunkowej jest tablica prostokątna, w której wiersze traktujemy
jako grupy typu A (np. grupy wiekowe), a kolumny jako grupy typu B (stężenie specyfiku).
GRUPA
1
GRUPA 2
GRUPA 3
Na przecięciu i-tego wiersza i j-tej kolumny występuje podgrupa (i,j) złożona z osobników w
wieku w
i
, którym zaaplikowano specyfik w stężeniu s
j
.
Niekiedy działanie czynników typu A i B nie jest niezależne, a więc istnieją takie poziomy
czynnika A i czynnika B, których łączne działanie jest inne niż to wynika z sumy
odpowiednich efektów. Mówimy wtedy, że nastąpiła interakcja efektów. Z pewnych
powodów wskazane jest, aby składniki modelu były niezależne od siebie. Aby ten wymóg
spełnić, w przypadku, gdy występuje interakcja, jej efekt można wydzielić i uwzględnić w
modelu jako osobny składnik:
x
ijk
=
µ
+ a
i
+ b
j
+ (ab)
ij
+ e
ijk
.
W modelu tym (ab)
ij
oznacza efekt interakcji czynników A i B w podgrupie (i,j), czyli wynik
współdziałania efektu a
i
oraz b
j
. Istotę interakcji wyjaśnia poniższy przykład.
Przykład
W pewnej hipotetycznej populacji bydła o średniej wydajności
µ
= 5000 kg mleka występuje
potomstwo 3 ojców rozmieszczone w 3 stadach. Warunki istniejące w stadzie A
1
przyczyniają się do
wzrostu wydajności o 500 kg, a w stadzie A
3
do spadku o 500 kg – w stosunku do stada A
2
.
Analogicznie, wartość hodowlana buhaja B
1
warunkuje uzyskanie przez jeg
o córki wydajności o
100 kg wyższej, a buhaja B
3
o 100 kg niższej w stosunku do córek buhaja B
2
. Możemy zatem przyjąć,
ż
e:
a
1
= 500, a
2
= 0, a
3
= –500,
b
1
= 100, b
2
= 0, b
3
= –100,
W poniższej tabeli przedstawiono średnie wydajności krów w poszczególnych podgrupach stado–
ojciec. Interakcja danego stada z określonym buhajem powoduje że wydajność w odpowiadającej im
podgrupie różni się od sumy efektów tego stada i ojca (i wartości średniej). Na przykład, dla podgrupy
(1,1) suma efektów wynosi:
µ
+ a
1
+ b
1
= 5000 + 500 + 100 = 5600,
natomiast faktyczna średnia wydajność podgrupy wynosiła 5650. Różnica 5650 – 5600 = 50 kg jest
wynikiem interakcji efektów a
1
i b
1
.
Wynik interakcji przedstawiono w nawiasach.
Ojciec (j)
Stado b
j
(i) a
i
1
100
2
0
3
–100
1 500
2 0
3 -500
5650(+50)
5080(–20)
4570(30)
5510(+10)
5000 (0)
4510(+10)
5310(–60)
4920(+20)
4420(+20)
Gdy w populacji wyróżnia się 3 typy równorzędnych czynników (A, B, C), otrzymujemy
klasyfikację krzyżową trójkierunkową AxBxC:
x
ijkl
=
µ
+ a
i
+ b
j
+ c
k
+(ab)
ij
+(ac)
ik
+(bc)
jk
+(abc)
ijk
+ e
ijkl
.
Symbole z nawiasami oznaczają odpowiednie interakcje, np. (bc)
ik
to interakcja efektów b
j
oraz c
k
, natomiast (abc)
ijk
oznacza inerakcję trzech efektów: a
i
, b
j
oraz c
k
.
2.
Liczba zwierząt w doświadczeniu, 3. Podaj sposób obliczania współczynnika
zmienności i omów krótko informacje jakie uzyskasz po jego obliczeniu
4. Co to jest i do czego służy szereg rozdzielczy?
Szereg rozdzielczy (ang. stem-and-leaf lub stemplot) jest statystycznym sposobem prezentacji
rozkładu empirycznego. Uzyskuje się go dzieląc dane statystyczne na pewne kategorie i
podając liczebność lub częstość zbiorów danych przypadających na każdą z tych kategorii.
Szeregi rozdzielcze:
•
strukturalny (cecha jakościowa, grupowanie typologiczne)
•
punktowy (cecha ilościowa, skokowa)
•
przedziałowy (cecha ilościowa, ciagła)
•
punktowy plus przedziałowy (grupowanie wariancyjne)
Kolejne kroki podczas wykonywania szeregu rozdzielczego:
•
porządkujemy (jeśli to możliwe rosnąco) wartości cechy
•
zliczamy ilość wystąpień danej cechy w próbie
•
obliczamy częstości występowania dla każdej wartości cechy
•
prezentujemy wynik w formie tabeli
Jeśli cecha ma charakter ciągły, wtedy przedział wartości cechy dzieli się na przedziały
klasowe. Liczba i rozpiętości przedziałów powinny być tak dobrane, aby dawały przejrzysty
obraz rozkładu. Na ogół przyjmuje się, że liczba przedziałów powinna być większa od 5 i
mniejsza od 20.
Jeśli cecha ma charakter skokowy, ale liczba możliwych wartości jest bardzo duża, wtedy
można postąpić podobnie jak w przypadku cechy o charakterze ciągłym.
Szereg rozdzielczy tworzy się przez uszeregowanie danych według wzrastającej lub malejącej
wartości i podzielenie powstałego szeregu na rozłączne podzbiory zwane grupami.
W wyniku takiego podziału otrzymujemy bardziej jednorodne grupy. Obliczając częstości
wystąpień w danej grupie otrzymujemy szereg rozdzielczy. Każdy szereg rozdzielczy
charakteryzują przedziały klasowe grup i ilości przypadków występujących w kolejnych
grupach. Szereg rozdzielczy reprezentuje postać rozkładu danych populacji próby.
5. Co to jest hipoteza zerowa i do czego służy?
Hipoteza zerowa (H
0
) - Jest to hipoteza poddana procedurze weryfikacyjnej, w której
zakładamy, że różnica między analizowanymi parametrami lub rozkładami wynosi zero.
Przykładowo wnioskując o parametrach hipotezę zerową zapiszemy jako:
6. Co to jest hipoteza alternatywna i do czego służy?
Hipoteza alternatywna (H
1
) - hipoteza przeciwstawna do weryfikowanej. Możemy ją zapisać
na trzy sposoby w zależności od sformułowania badanego problemu:
7. Co to jest obiekt doświadczalny i materiał doświadczalny?
Obiekt doświadczalny – grupa zwierząt (rasa, stado, grupa kontrolna, grupy
doświadczalne), skupiska roślin (stanowisko, pole, poletko)
Materiał doświadczalny – zwierzęta, rośliny biorące udział w doświadczeniu
8. Co to jest układ ortogonalny i nieortogonalny?
Model klasyfikacyjny określa strukturę populacji, a w szczególności wyróżnia czynniki
istotnie oddziałujące na tę strukturę. Wnioskowanie statystyczne dotyczące tych czynników
będzie się odbywać na podstawie próby losowej wybranej z populacji; próba ta powinna mieć
strukturę podobną do struktury populacji. To ostatnie stwierdzenie odnosi się do sytuacji, gdy
interesują nas, na przykład, różnice między grupami czy podgrupami realnie istniejącej
populacji (np. między rasami, stadami czy ojcami).
W doświadczalnictwie często mamy sytuację odmienną. Jeżeli chcemy np. sprawdzić jakość
różnych pasz, wykonujemy doświadczenie, tzn. kompletujemy kilka grup zwierząt i każdą z
nich żywimy inną paszą, a wskaźnikiem jakości paszy jest wartość określonej cechy w grupie,
np. przyrostu masy ciała. Różnice między grupami będą świadczyć o różnicach w jakości
pasz. Badanie istotności tych różnic sprowadza się do testowania hipotezy o równości
wartości średnich grup w populacji, lecz populacja ta realnie nie istnieje, gdyż nie ma
populacji żywionej badanymi w doświadczeniu paszami. W tej sytuacji warunek losowości
próby dotyczy kompletowania grup doświadczalnych (losowy dobór zwierząt do grup),
losowość nie dotyczy zaś struktury liczbowej próby. Okazuje się, że wnioskowanie
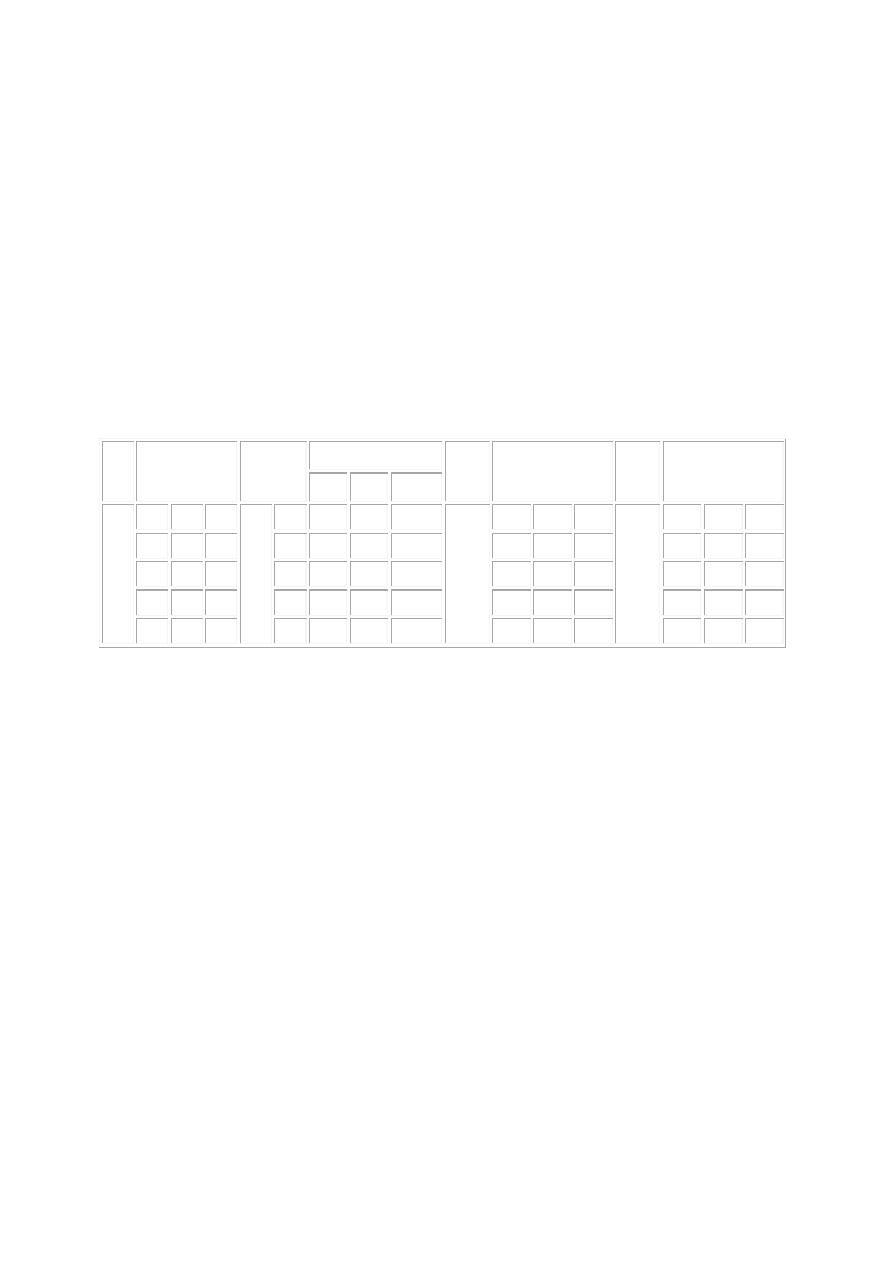
statystyczne jest najefektywniejsze, jeżeli próba ma tzw. układ ortogonalny. W klasyfikacji
krzyżowej układ jest ortogonalny, jeżeli liczebności podgrup są jednakowe lub
proporcjonalne. Wyjaśniają to rysunki a) i b), zawierające przykłady układów ortogonalnych
dla klasyfikacji krzyżowej dwukierunkowej AxB. W kratkach podane są liczebności podgrup;
na rysunku a) liczebności podgrup są jednakowe i przypadek ten nie wymaga wyjaśnień,
natomiast na rysunku b) przedstawiono liczebności proporcjonalne. Liczebności w pierwszym
wierszu (i pierwszej kolumnie) są dowolne, natomiast w pozostałych wierszach (i kolumnach)
są one równe liczebnościom z wyróżnionego wiersza (wyróżnionej kolumny) pomnożonych
przez odpowiednie współczynniki proporcjonalności; współczynniki te są zapisane w
nawiasach.
B
a)
B
b)
(2)
(2,5)
c)
B
d)
B
2
2
2
2
4
5
2
4
5
2
4
5
2
2
2
(4)
8
16
20
8
3
1
8
16
20
2
2
2
(2)
4
8
10
4
5
6
4
8
0
2
2
2
(1)
2
4
5
2
12
7
2
4
5
A
2
2
2
A
(3)
6
12
15
A
6
8
2
A
6
0
12
Układ nie spełniający warunku proporcjonalności nazywamy układem nieortogonalnym. W
szczególności, układ jest nieortogonalny, jeżeli przynajmniej jedna podgrupa jest pusta
(liczebność zerowa). Przykłady układów nieortogonalnych przedstawione są na rysunkach c) i
d).
W przypadku klasyfikacji hierarchicznej układ jest ortogonalny, jeżeli równocześnie
spełnione są dwa warunki: 1) wewnątrz każdej grupy klasyfikacji zewnętrznej występuje ta
sama liczba podgrup klasyfikacji wewnętrznej; 2) w każdej podgrupie występuje ta sama
liczba obserwacji.
9. Typy doświadczeń zootechnicznych
10. Co to jest błąd doświadczenia?
