11.06.2012 r.

Politechnika Rzeszowska

Ignacego Łukasiewicza

Wydział Budowy Maszyn i Lotnictwa

Katedra Samolotów i Silników Lotniczych

Metody numeryczne w budowie i eksploatacji konstrukcji lotniczych

Metoda Jacobiego i Gaussa-Seidla

Jacek Kaczmarek

Katarzyna Kozendra

Łukasz Krawczyk

Tomasz Miziniak

Kamil Piotrowski

Łukasz Rupar

I MDLiK-B

1. Wstęp teoretyczny

Zarówno metoda Jacobiego, jak i metoda Gaussa-Seidla są metodami iteracyjnymi pozwalającymi

obliczyć układ n równań z n niewiadomymi Ax = b. Wektor x

0

będący początkowym przybliżeniem

rozwiązania układu będzie dany (zwykle przyjmuje się go jako wektor złożony z samych zer). By

zastosować tą metodę należy najpierw tak zamienić kolejność równań układu, aby na głównej

przekątnej były elementy różne od zera.

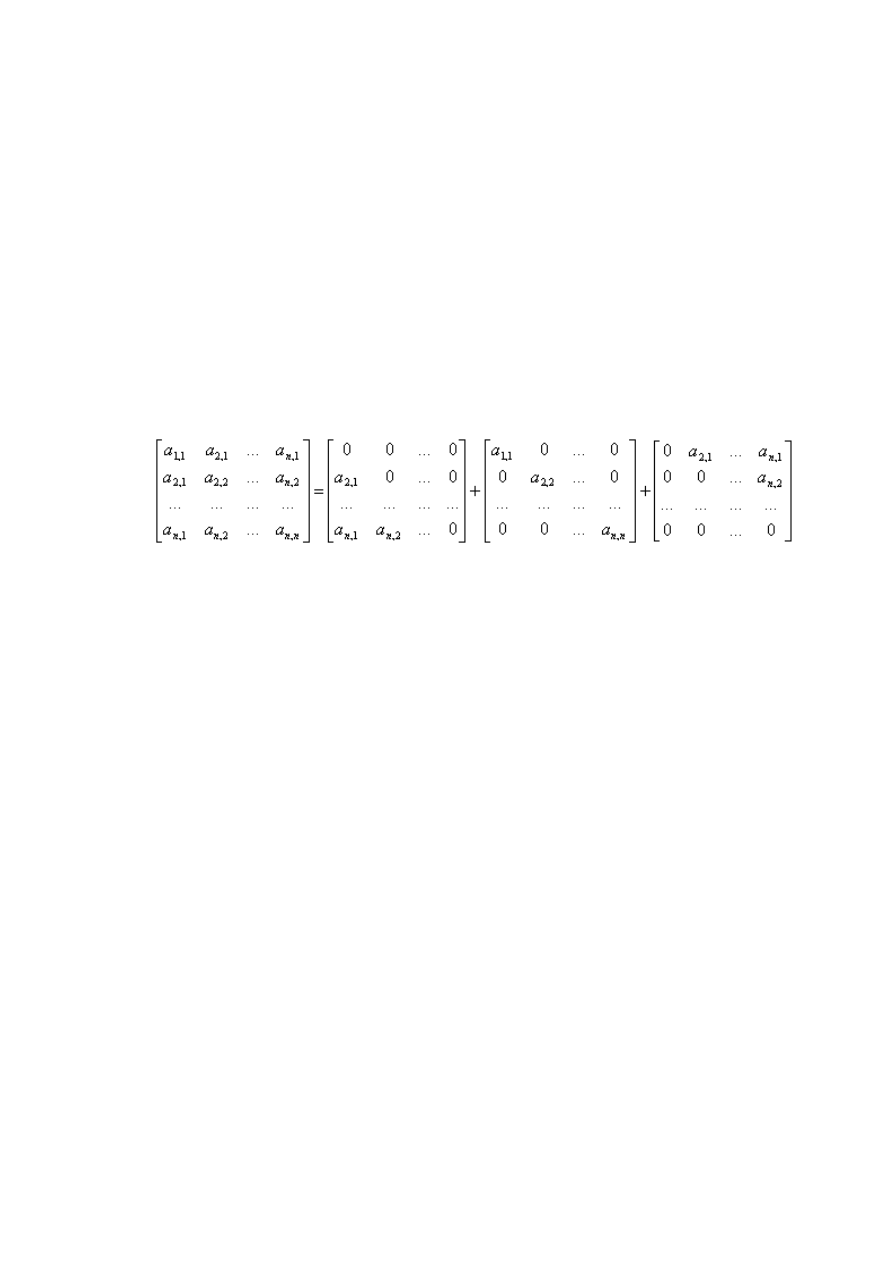
Na początku macierz współczynników A rozłożymy na sumę trzech macierzy A = L + D + U, gdzie

L jest macierzą w której znajdują się elementy których numer wiersza jest większy od numeru

kolumny, D to macierz diagonalna z elementami tylko na głównej przekątnej, a U to macierz, w

której znajdują się elementy których numery wiersza są mniejsze od numerów kolumny. Można to

zapisać następująco:

A = L + D + U

Różnice między metodami:

Głowna różnica pomiędzy tymi metodami polega na zastosowaniu innego wzoru służącego do

obliczania kolejnych przybliżeń:



metoda Jacobiego- kolejne przybliżenia oblicza się z następującego wzoru:

gdzie:

M = I – NA

N - pewna macierz kwadratowa

I - macierz jednostkowa

W metodzie Jacobiego przyjmujemy, że N=D

-1

, to wówczas M = -D

-1

(L+U). By zastosować tą

metodę należy najpierw tak zamienić kolejność równań układu, aby na głównej przekątnej były

elementy różne od zera. Macierz D

-1

otrzymamy po podniesieniu do potęgi „-1” wszystkich

wartości na głównej przekątnej macierzy D. Metoda ta jest zbieżna dla dowolnego przybliżenia

początkowego rozwiązania x

0

, jeśli promil spektralny –D

-1

(L+U) jest mniejszy od jeden (promień

spektralny to największa wartość bezwzględna z wartości własnej macierzy). W przeciwnym

wypadku nie dla każdego przybliżenia początkowego otrzymamy rozwiązanie uk ładu.



metoda Gaussa-Seidla- kolejne przybliżenia oblicza się z następującego wzoru:

Metoda Gaussa-Seidla bazuje na metodzie Jacobiego, w której krok iteracyjny zmieniono w ten

sposób, by każda modyfikacja rozwiązania próbnego korzystała ze wszystkich aktualnie

dostępnych przybliżonych składowych rozwiązania. Pozwala to zaoszczędzić połowę pamięci

operacyjnej i w większości zastosowań praktycznych zmniejsza ok. dwukrotnie liczbę obliczeń

niezbędnych do osiągnięcia zadanej dokładności rozwiązania.

Przykład:

Obliczymy następujący układ równań:

Zapiszmy go teraz w postaci

:

Podzielmy teraz macierz

na sumę macierzy :

Obliczmy teraz macierz

:

Do tego momentu obie metody się nie różnią.



Metoda Gaussa-Seidla:

Wyznaczamy kolejno

:

Rozpoczynamy od zerowego przybliżenia czyli:

Obliczmy pierwszą iterację metody, według przytoczonego na początku wzoru:

Kolejna iteracja:

Można teraz obliczyć kolejną iterację. Każda z nich przybliża nas do dokładnego wyniku.



Metoda Jacobiego:

Wyznaczamy kolejno

:

Rozpoczynamy od zerowego przybliżenia czyli:

Obliczmy pierwszą iterację metody, według przytoczonego na początku wzoru:

Kolejna iteracja:

Można teraz obliczyć kolejną iterację. Każda z nich przybliża nas do dokładnego wyniku.

2. Kod źródłowy programów w których zaimplementowano powyższe iteracje

METODA JACOB IEGO

function

[x, it, blad] = jacobi(A, b, max_it, tol)

% [x, it, blad] = jacobi(A, b, max_it, tol)

%

% Układ służy do rozwiązywania liniowych układów równań metoda Jacobiego

% typu Ax=b

%

% wejscie A macierz wspolczynnikow po lewej stronie rownania

% b macierz wyrazow wolnych

% max_it maksymalna liczba iteracji

% tol tolerancja z jaką przybliżamy

%

% wyjscie x macierz rozwiazan ukladu

% it liczba wykonanych iteracji

% blad maksymalna roznica miedzy kolejnymi iteracjami

%

it=0;

[m,n]=size(A);

[p,r]=size(b);

if

m~=n

disp(

'Macierz A nie jest kwadratowa. Obliczenia nie beda dalej prowadzone.'

)

else

if

m~=p

disp(

'Liczba wierszy macierzy b nie jest zgodna z liczbą wierszy macierzy A.

Obliczenia nie beda dalej prowadzone.'

)

else

for

i=1:m;

% procedura dostosowywania macierzy A

z=norm(A(i,:));

if

z==0

% sprawdzanie czy sa zerowe wiersze

disp(

'Przynajmniej jeden z wierszy jest zerowy. Obliczenia nie beda dalej

prowadzone.'

)

else

;

while

A(i,i)==0;

% zamiana kolejnosci rownan aby nie

bylo zer na glownej przekatnej

for

j=1:n-1;

bufor=A(j,:);

A(j,:)=A(j+1,:);

A(j+1,:)=bufor;

bufor=A(j+1,:);

A(j+1,:)=A(n-j,:);

A(n-j,:)=bufor;

buforb=b(j,:);

b(j,:)=b(j+1,:);

b(j+1,:)=buforb;

buforb=b(j+1,:);

b(j+1,:)=b(n-j,:);

b(n-j,:)=buforb;

end

end

end

end

L=zeros(m,n);

D=L;

U=L;

for

i=1:m-1;

for

j=1:i;

L(i+1,j)=A(i+1,j);

end

end

for

i=1:m;

D(i,i)=A(i,i);

end

for

i=1:m-1;

for

j=i:n-1;

U(i,j+1)=A(i,j+1);

end

end

N=D^-1;

M=zeros(m,n);

M=-1*N*(L+U);

x=zeros(p,r);

blad=max(abs(b));

while

(it<max_it & abs(blad)>tol);

x1=M*x+N*b;

blad=max(abs(x-x1));

x=x1;

it=it+1;

end

if

it>=max_it;

disp(

'Osiagnieto maksymalna liczbe iteracji.'

)

else

disp(

'Osiagnieto wymagana dokladnosc.'

)

end

end

end

end

METODA GAUSSA-SEIDLA

function

[x, it, blad] = gauseidl(A, b, max_it, tol)

% [x, it, blad] = gauseidl(A, b, max_it, tol)

%

% Układ służy do rozwiązywania liniowych układów równań metoda

% Gaussa- Seidla typu Ax=b

%

% wejscie A macierz wspolczynnikow po lewej stronie rownania

% b macierz wyrazow wolnych

% max_it maksymalna liczba iteracji

% tol tolerancja z jaką przybliżamy

%

% wyjscie x macierz rozwiazan ukladu

% it liczba wykonanych iteracji

% blad maksymalna roznica miedzy kolejnymi iteracjami

%

it=0;

[m,n]=size(A);

[p,r]=size(b);

if

m~=n

disp(

'Macierz A nie jest kwadratowa. Obliczenia nie beda dalej prowadzone.'

)

else

if

m~=p

disp(

'Liczba wierszy macierzy b nie jest zgodna z liczbą wierszy macierzy A.

Obliczenia nie beda dalej prowadzone.'

)

else

for

i=1:m;

% procedura dostosowywania macierzy A

z=norm(A(i,:));

if

z==0

% sprawdzanie czy sa zerowe wiersze

disp(

'Przynajmniej jeden z wierszy jest zerowy. Obliczenia nie beda dalej

prowadzone.'

)

else

;

while

A(i,i)==0;

% zamiana kolejnosci rownan aby nie

bylo zer na glownej przekatnej

for

j=1:n-1;

bufor=A(j,:);

A(j,:)=A(j+1,:);

A(j+1,:)=bufor;

bufor=A(j+1,:);

A(j+1,:)=A(n-j,:);

A(n-j,:)=bufor;

buforb=b(j,:);

b(j,:)=b(j+1,:);

b(j+1,:)=buforb;

buforb=b(j+1,:);

b(j+1,:)=b(n-j,:);

b(n-j,:)=buforb;

end

end

end

end

L=zeros(m,n);

D=L;

U=L;

for

i=1:m-1;

for

j=1:i;

L(i+1,j)=A(i+1,j);

end

end

for

i=1:m;

D(i,i)=A(i,i);

end

for

i=1:m-1;

for

j=i:n-1;

U(i,j+1)=A(i,j+1);

end

end

M=zeros(m,n);

M=(L+D)^-1;

x=zeros(p,r);

blad=max(abs(b));

while

(it<max_it & abs(blad)>tol);

x1=-1*M*U*x+M*b;

blad=max(abs(x-x1));

x=x1;

it=it+1;

end

if

it>=max_it;

disp(

'Osiagnieto maksymalna liczbe iteracji.'

)

else

disp(

'Osiagnieto wymagana dokladnosc.'

)

end

end

end

end

3. Porównanie wydajności metod

Dokonano również porównania w wydajności obydwóch metod iteracyjnych.



>> A=[4 -1 -0.2 2; -1 5 0 -2; 0.2 1 10 -1; 0 -2 -1 4]

A =

4.0000 -1.0000 -0.2000 2.0000

-1.0000 5.0000 0 -2.0000

0.2000 1.0000 10.0000 -1.0000
0 -2.0000 -1.0000 4.0000



>> b=[30;0;10;5]

b =

30
0
10
5



>> [x, it, blad] = gauseidl(A, b, 200, 0.00000001)
Osiągnięto wymagana dokładność.

x =

6.8083
2.4382
0.8892
2.6914

it =

%liczba iteracji

14

blad =

6.5911e-009

>> g=A*x

%sprawdzenie

g =

30.0000
-0.0000
10.0000
5.0000



>> [x, it, blad] = jacobi(A, b, 200, 0.00000001)
Osiągnięto wymaganą dokładność.

x =

6.8083
2.4382
0.8892
2.6914

it =

%liczba iteracji

40

blad =

7.1697e-009

>> h=A*x

%sprawdzenie

h =

30.0000
-0.0000
10.0000
5.0000

4. Podsumowanie

Obie metody są bardzo do siebie podobne pod względem głównych założeń. Różnią się jedynie
sposobem obliczania kolejnego przybliżenia. Metoda Gaussa-Seidla jest rozwinięciem metody
Jacobiego mającym na celu poprawę szybkości wykonywania obliczeń. Jak widać na przykładzie
jest to prawdą- w metodzie Jacobiego potrzebne było, aż 40 iteracji, żeby uzyskać założoną
dokładność obliczeń. Natomiast w metodzie Gaussa-Seidla wystarczyło do tego celu tylko 14
iteracji. Jest, to prawie trzy krotny wzrost prędkości wykonywania obliczeń.