Instytut Metrologii i InŜynierii Biomedycznej
PODSTAWY METROLOGII 2
PODSTAWY METROLOGII 2
Analiza wymiarowa
Analiza wymiarowa
S. śebrowska-Łucyk
Wydział Mechatroniki, pok. 218
szl@mchtr.pw.edu.pl
Instytut Metrologii i InŜynierii Biomedycznej
PODSTAWY METROLOGII 2
PODSTAWY METROLOGII 2
Analiza wymiarowa
Analiza wymiarowa
S. śebrowska-Łucyk
Wydział Mechatroniki, pok. 218
szl@mchtr.pw.edu.pl
Łańcuchy wymiarowe technologiczne
Łańcuchy montaŜowe
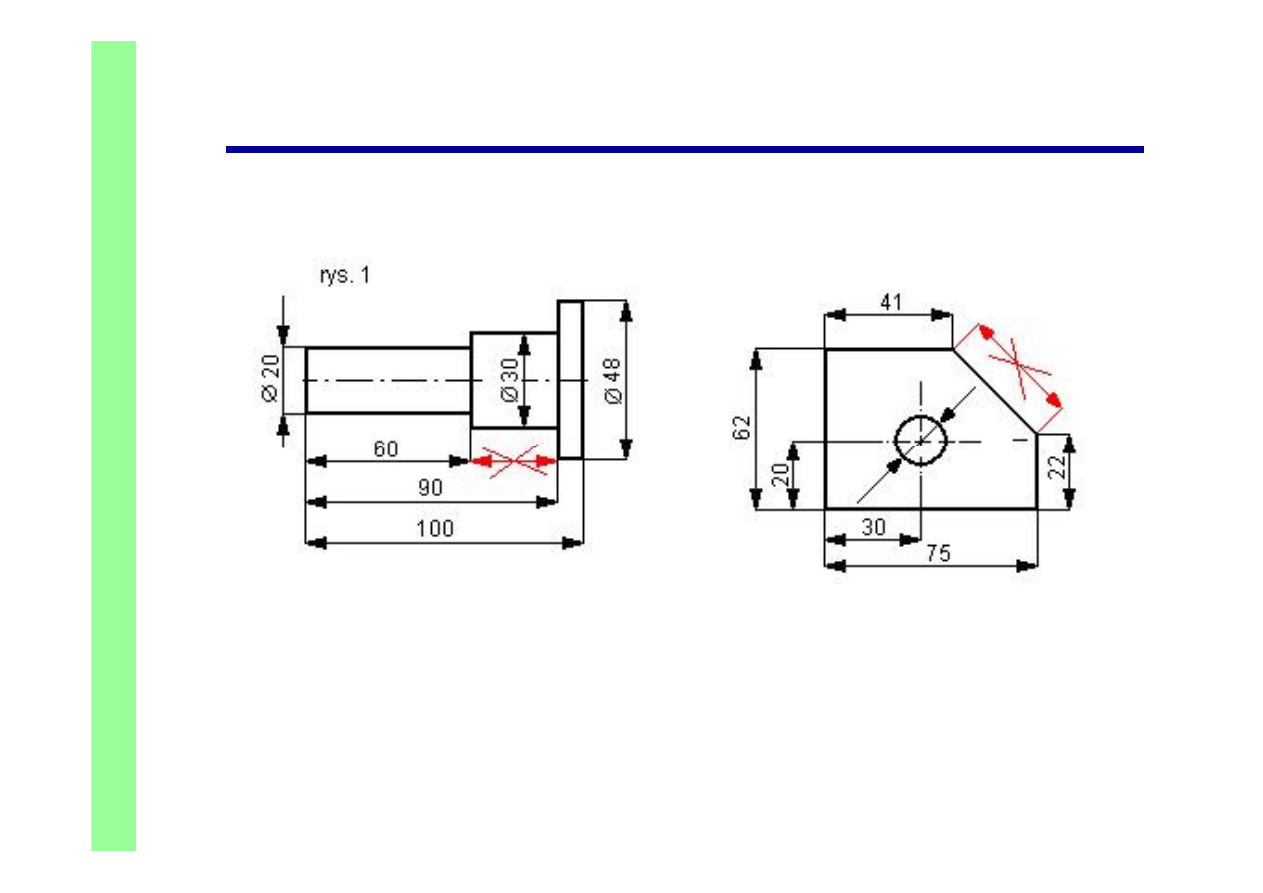
Wymiarowanie - zasada niezamykania łańcucha
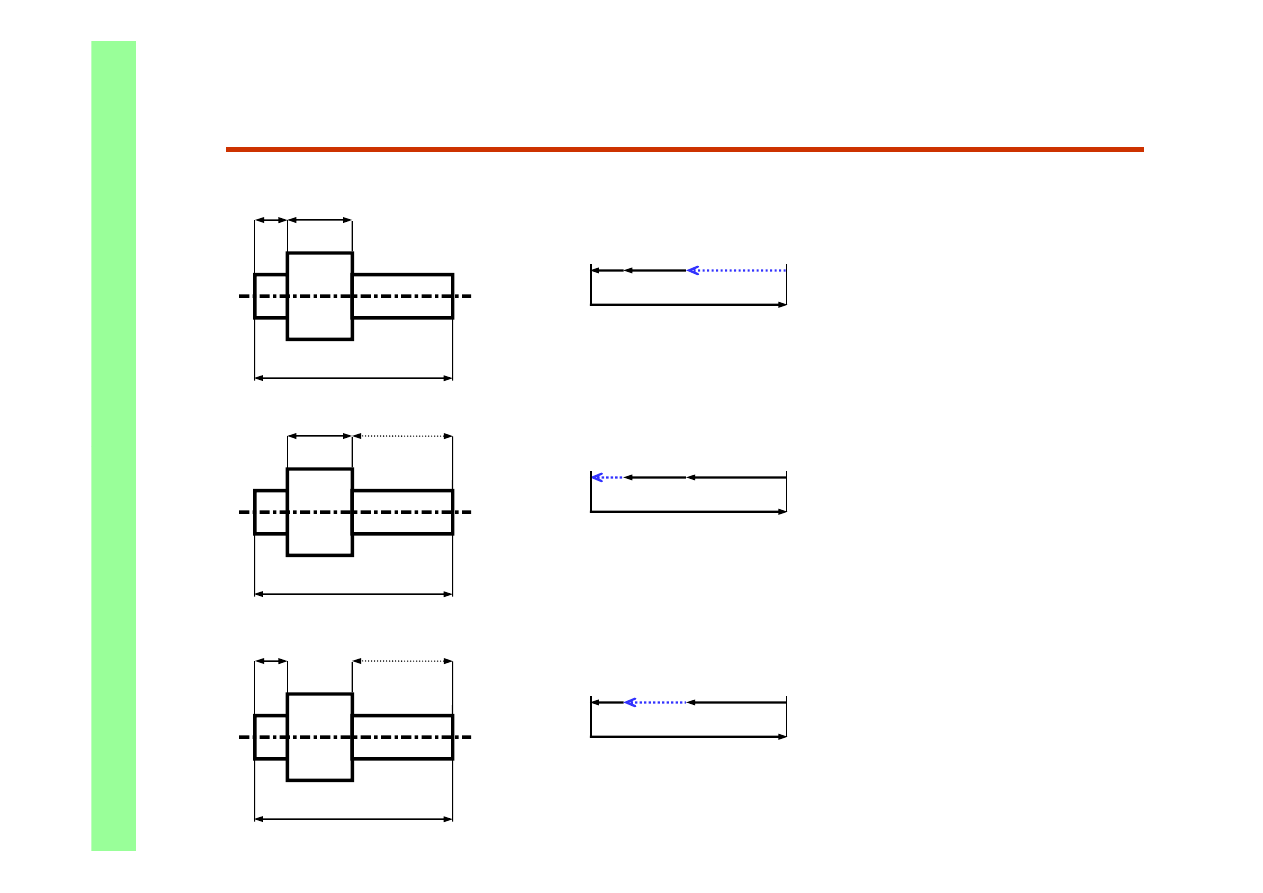
Łańcuchy technologiczne. Przykłady wymiarowania
A
(X)
(X)
B
D
B
C
(
C
)
2
1
2
1
2
1
2
1
b
b
a
a
d
d
c
c
B
A
D
C
−
−
=
(
A
)
B
A
D
C
T
T
T
T
+
+
=
(X)
D
A
C
D
X
X
2
1
2
1
2
1
2
1
c
c
b
b
d
d
a
a
C
B
D
A
−
−
=
2
1
2
1
2
1
2
1
c
c
a
a
d
d
b
b
C
A
D
B
−
−
=
(
A
)
(
B
)
C
B
D
A
T
T
T
T
+
+
=
C
A
D
B
T
T
T
T
+
+
=
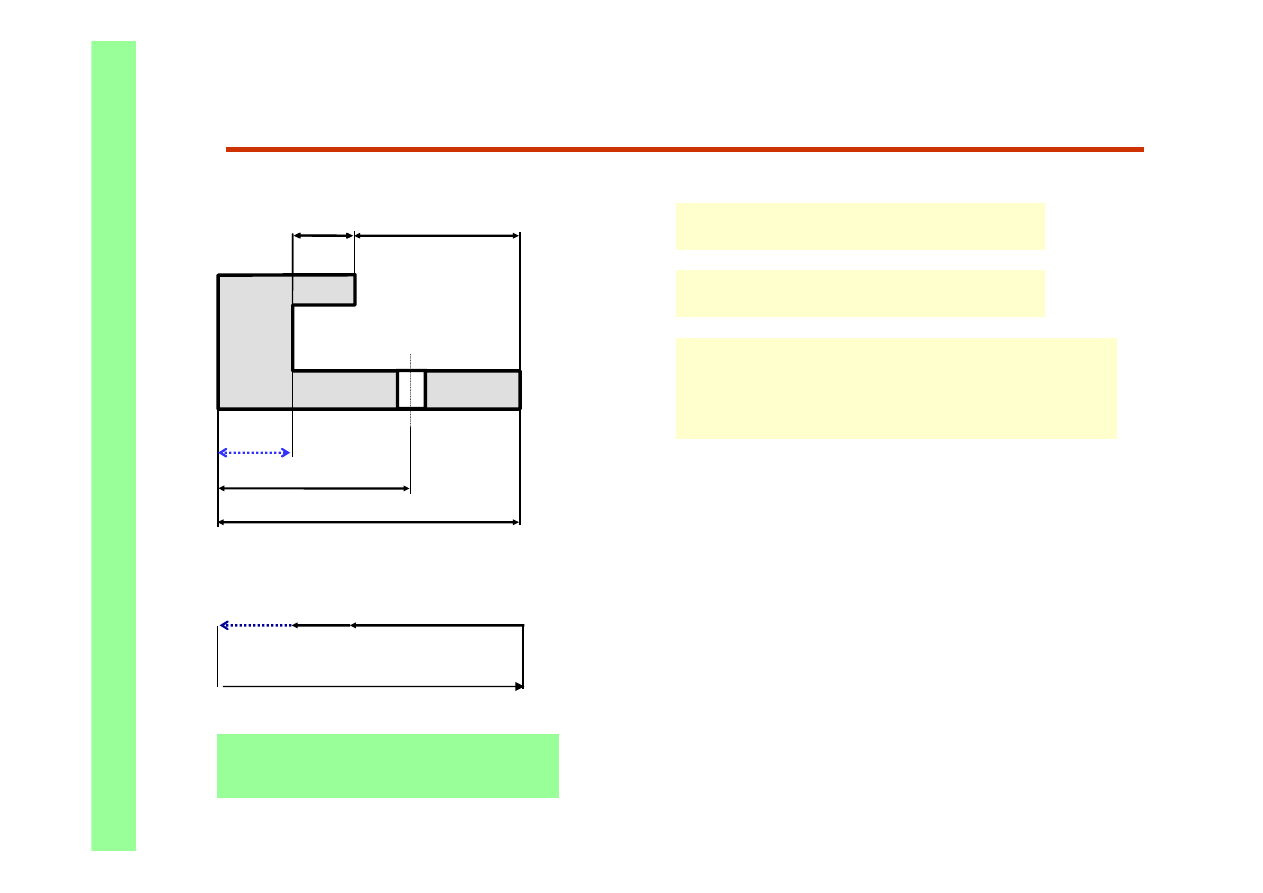
Łańcuchy technologiczne - przykład obliczeń
C
D
X
X
max
= A
max
- D
min
- C
min
X
min
= A
min
- D
max
- C
max
X+x
2
= (A+a
2
) - (D+d
1
) - (C+c
1
)
X+x
1
= (A+a
1
) - (D+d
2
) - (C+c
2
)
X
A
B
X
A
C
D
X = A - D - C
x
2
= a
2
- d
1
- c
1
x
1
= a
1
- d
2
- c
2
x
2
-x
1
= (a
2
- a
1
)+ (d
2
- d
1
)+(c
2
-c
1
)
T
X
= T
A
+T
D
+T
C
2
1
2
1
2
1
2
1
d
d
c
c
a
a
x
x
D
C
A
X
−
−
=
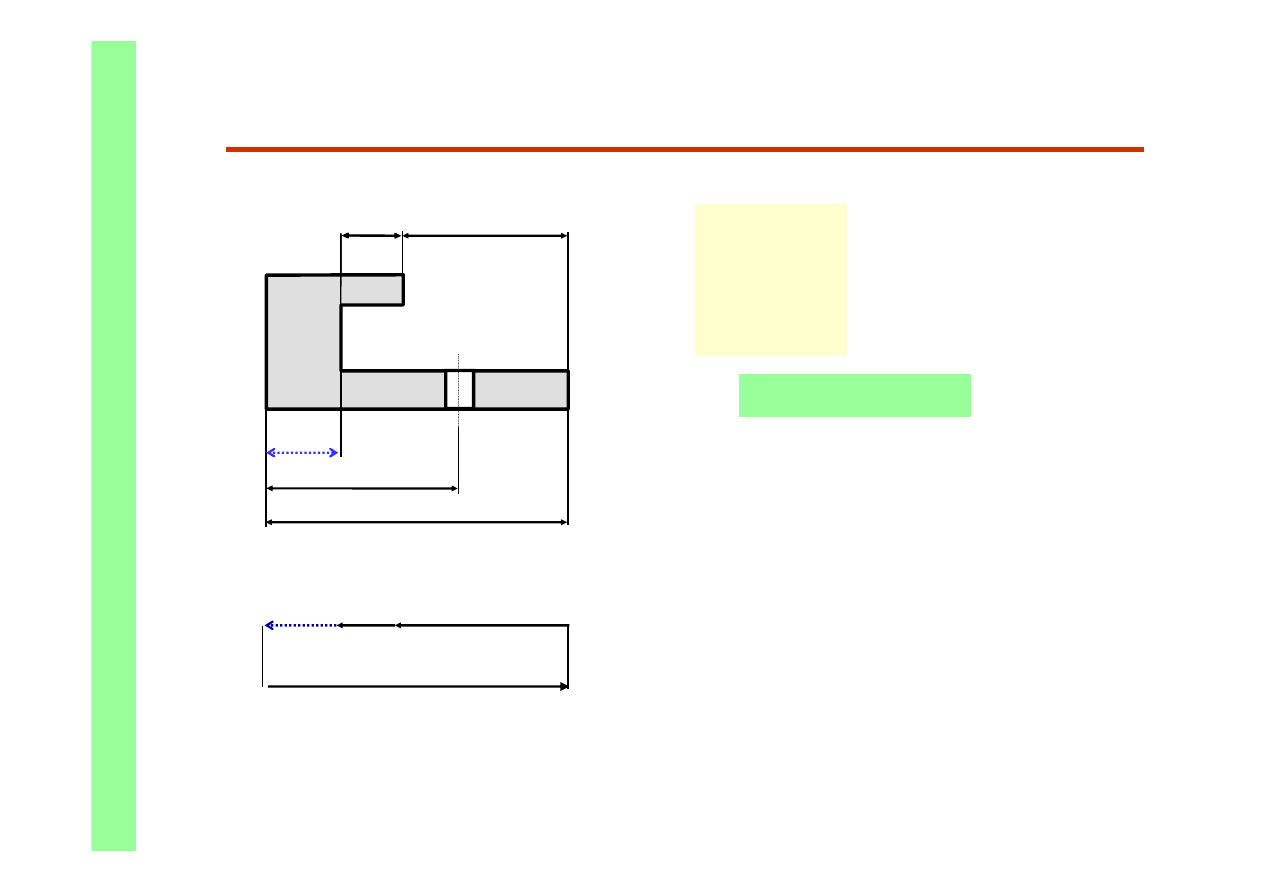
Łańcuchy technologiczne - przykład obliczeń cd
C
D
X
T
A
= 0,2 mm
T
D
= 0,3 mm
T
C
= 0,4 mm
0
2
,
0
90
−
=
A
2
,
0
5
,
0
20
−
−
=
D
2
,
0
2
,
0
45
+
−
=
C
T = T + T + T = 0,9 mm
2
1
2
1
2
1
2
1
d
d
c
c
a
a
x
x
D
C
A
X
−
−
=
X
A
B
X
A
C
D
x
2
= 0 + 0,2 + 0,5 = 0,7 mm
x
1
= - 0,2 - 0,2 + 0,2 = - 0,2 mm
Spr.: x
2
- x
1
= 0,9 mm
T
X
= T
A
+ T
C
+ T
D
= 0,9 mm
x
2
= a
2
- c
1
- d
1
x
1
= a
1
- c
2
- d
2
D
C
A
X
−
−
=
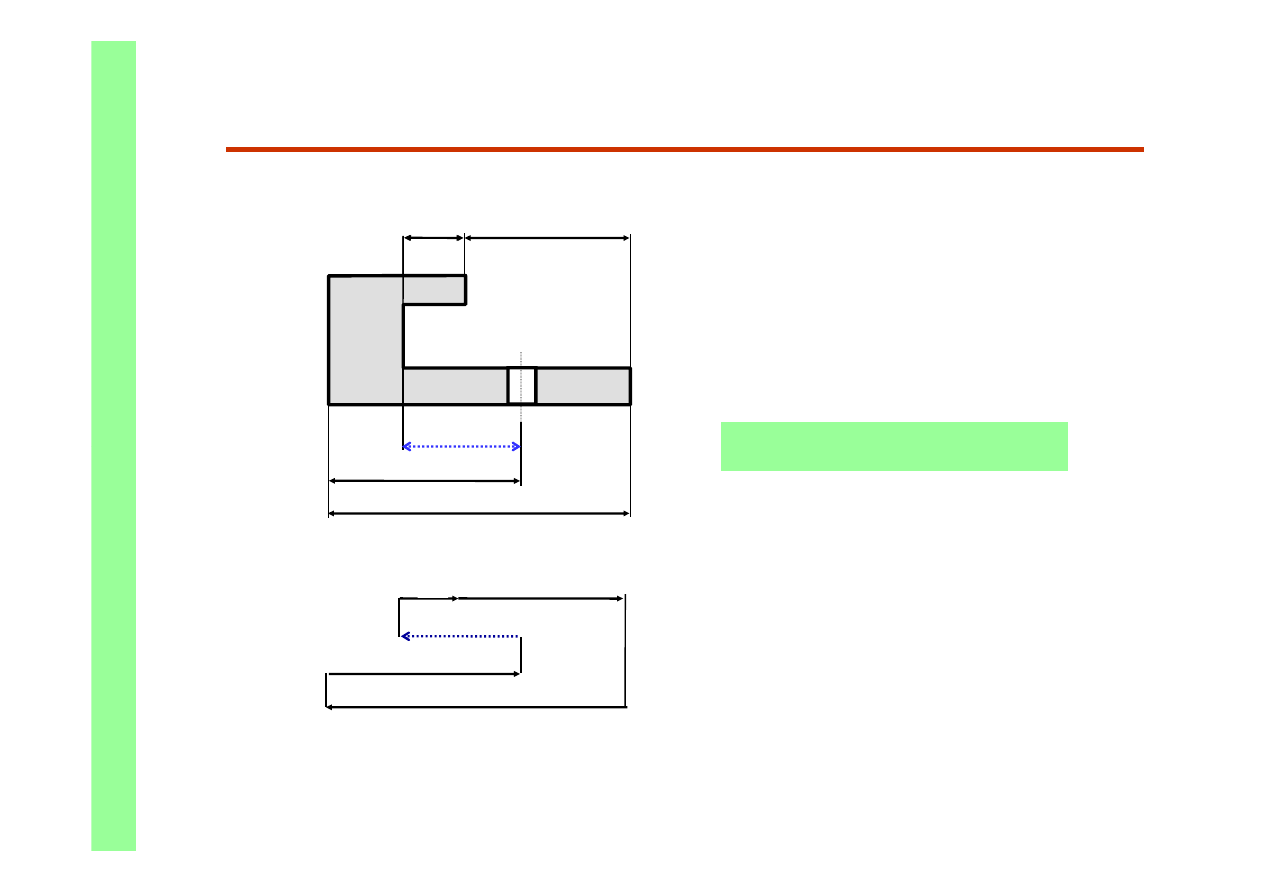
Łańcuchy technologiczne
C
Y
D
Y
A
B
D
C
y1
y2
a1
a2
b1
b2
d1
d2
c1
c2
= −
+
+
+
A
B
A
C
D
Y
B
Y
A
B
D
C
y1
a1
b1
d1
c1
= −
+
+
+
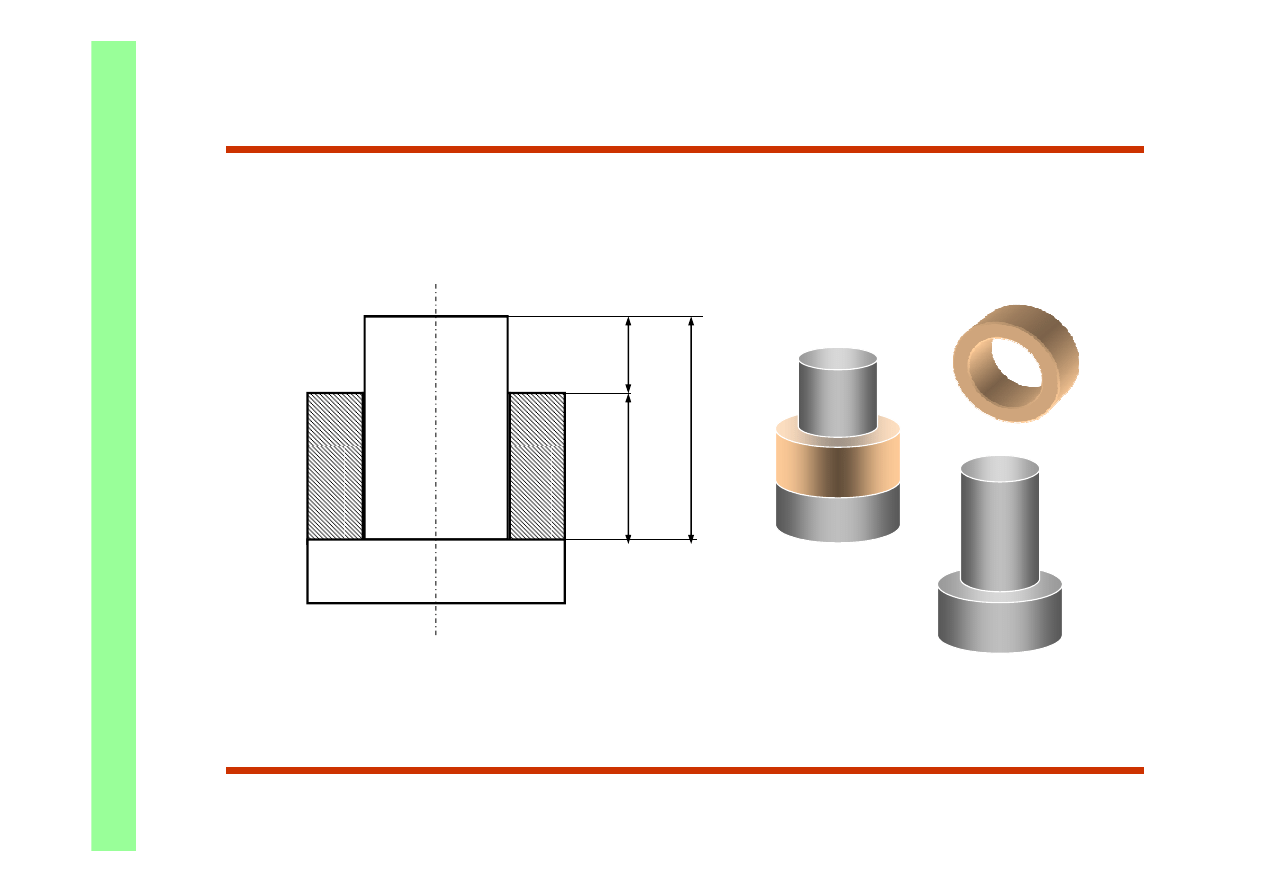
Łańcuchy montaŜowe
X
B
A
Przykład łańcuch montaŜowego
X
A
B
9
0
±
0
,0
3
1
6
-0
,0
2
0
5
0
-0
,0
5
0
2
1
2
1
2
1
a
a
b
b
x
x
A
B
X
−
=
0
02
,
0
03
,
0
03
,
0
2
1
16
90
b
b
B
−
+
−
−
=
05
,
0
03
,
0
2
1
74
+
−
=
b
b
B
0
05
,
0
2
1
50
−
=
a
a
A
10
,
0
03
,
0
2
1
24
+
−
=
x
x
X
mm
x
x
T
X
13
,
0
)
03
,
0
(
10
,
0
1
2
=
−
−
=
−
=
mm
T
T
T
A
B
x
13
,
0
08
,
0
05
,
0
=
+
=
+
=
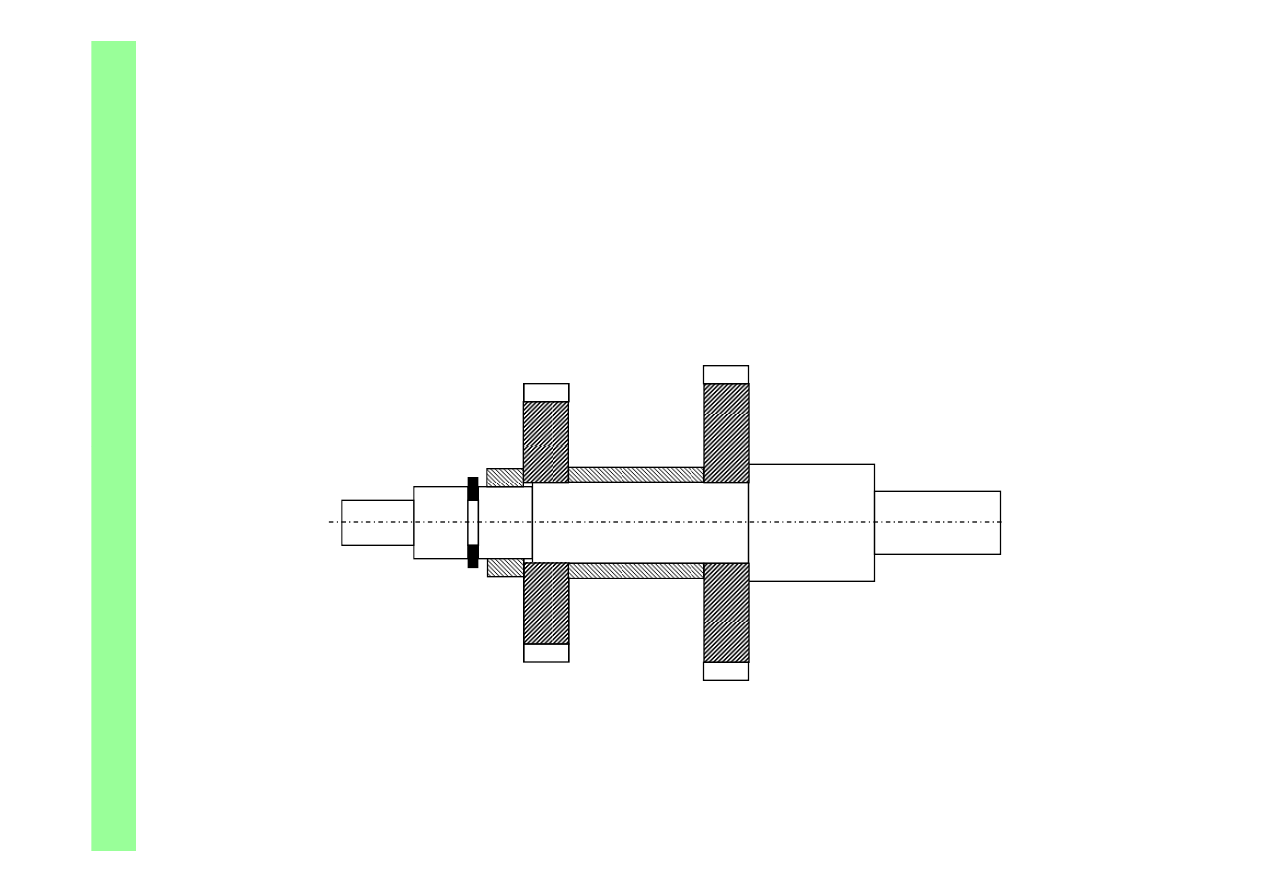
Przykład zmontowanego zespołu
`
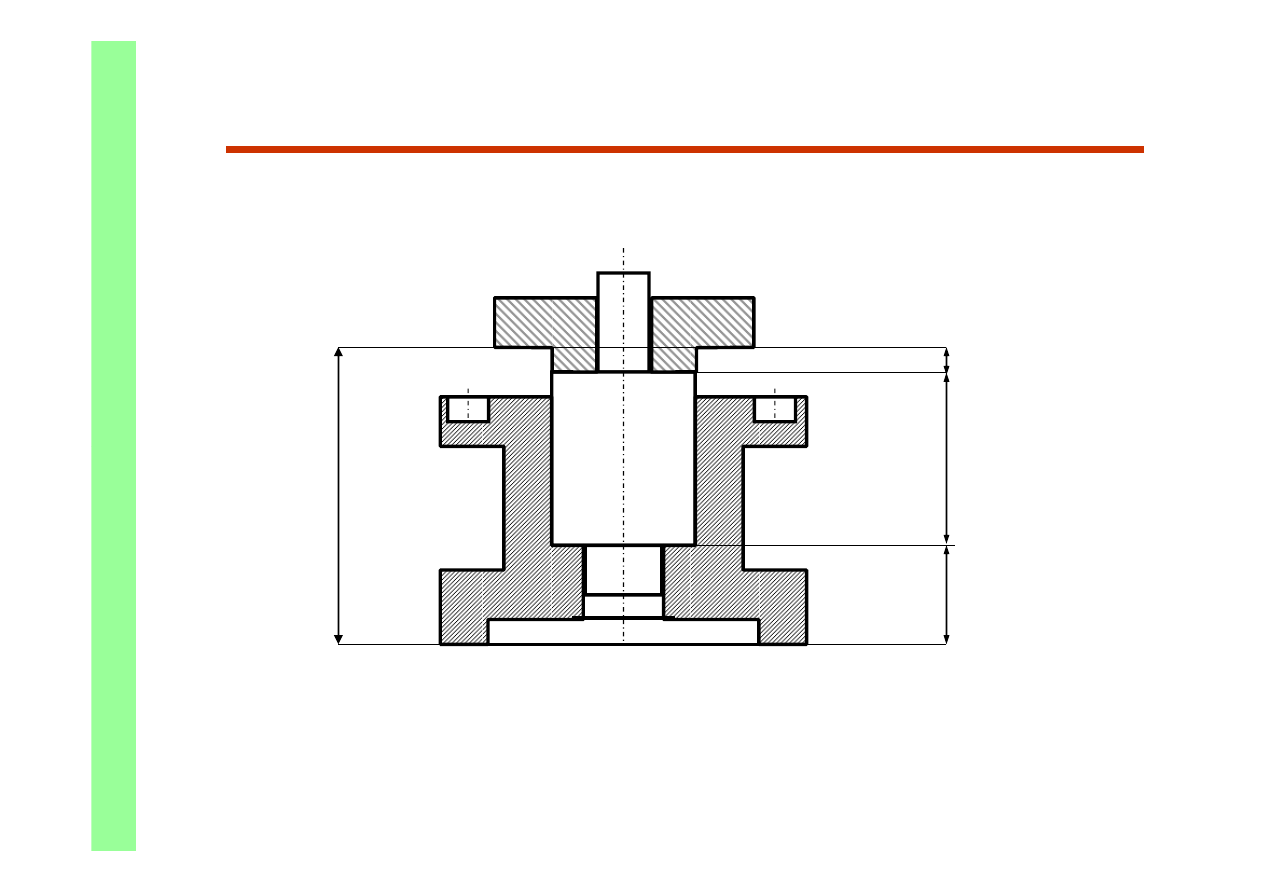
Łańcuchy montaŜowe
A
B
Y
B
C
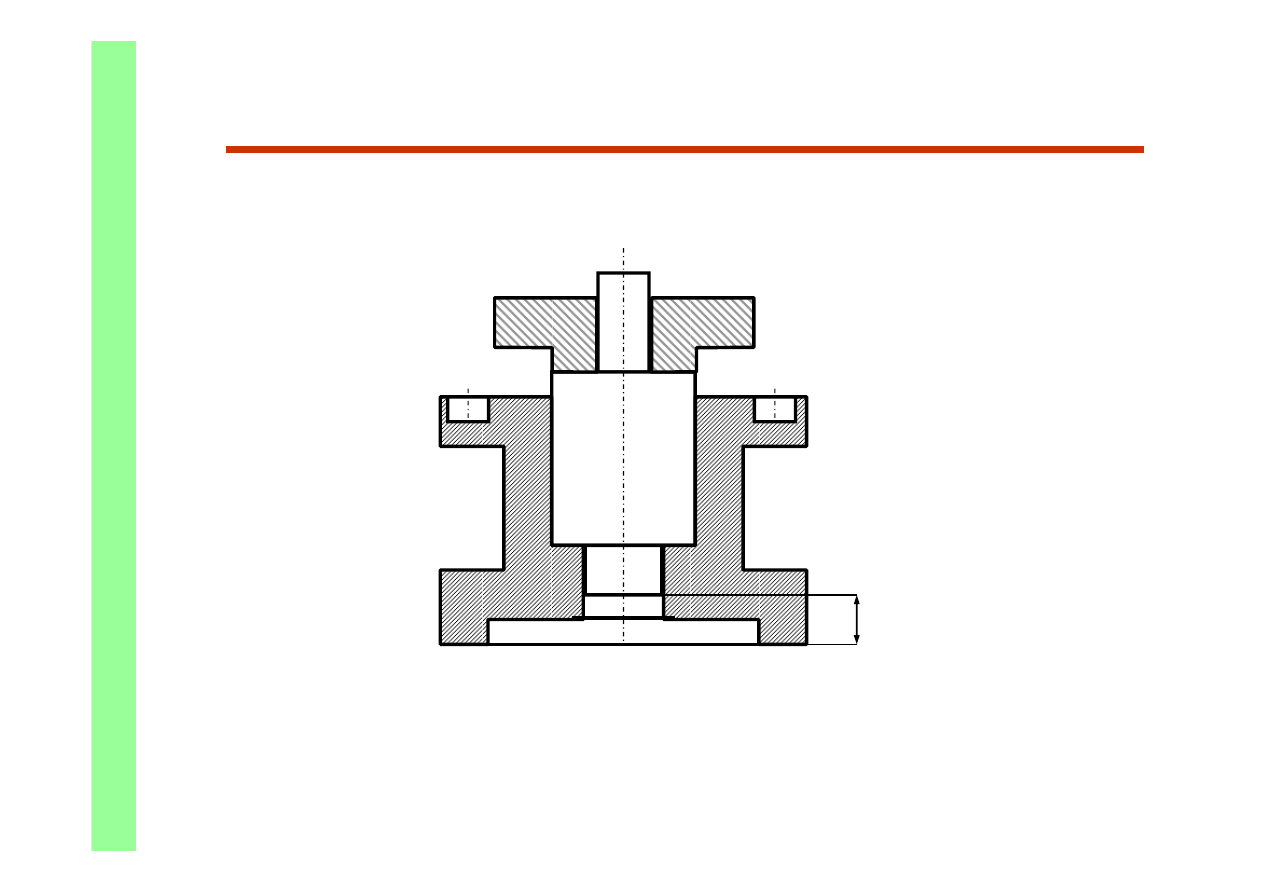
Przykład zmontowanego zespołu
U
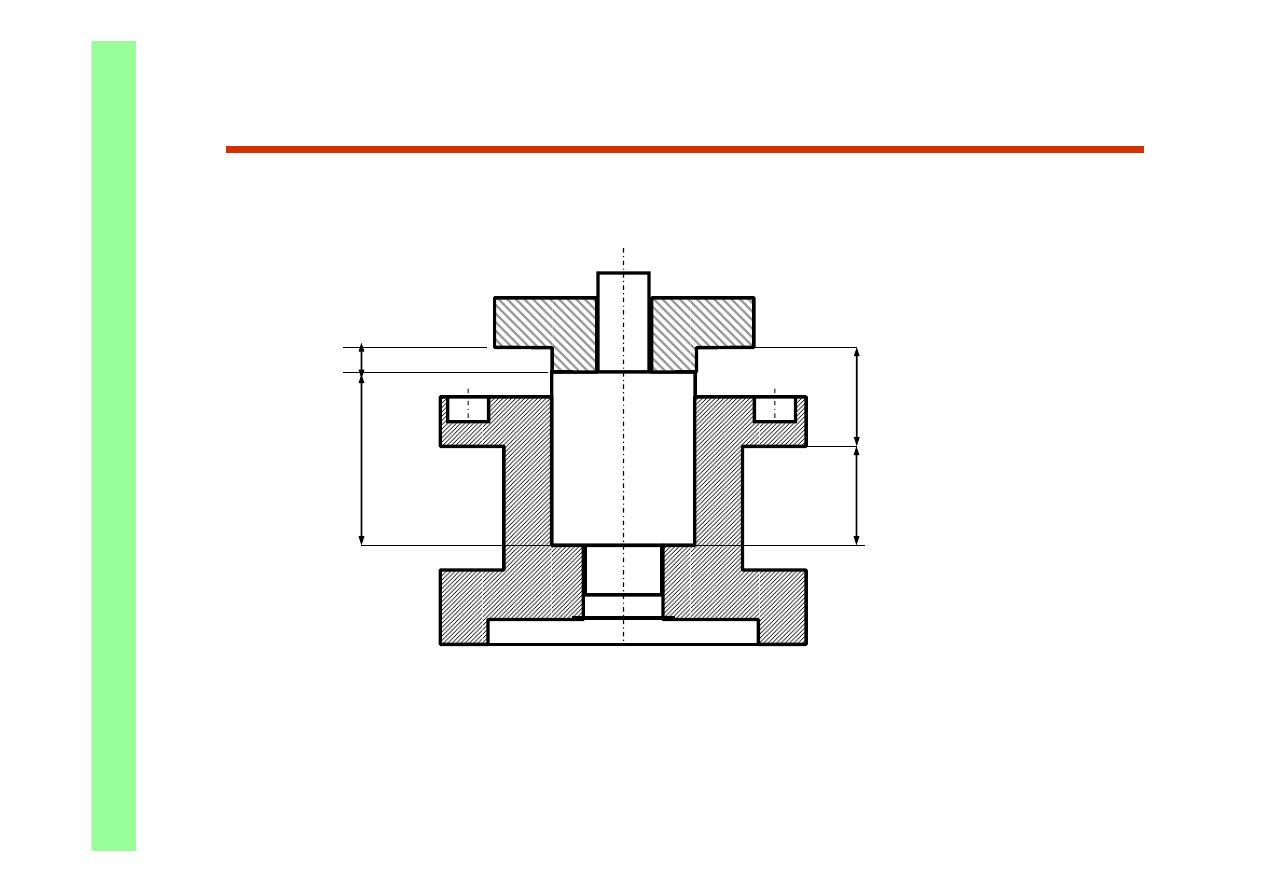
Łańcuchy montaŜowe
T
F
A
G
F
Tolerancje wynikowe – dwa podejścia
K
+
+
=
B
A
X
T
T
T
K
+
+
=
2
2
2
2
T
k
T
k
T
podejście probabilistyczne
podejście deterministyczne
(uwzględnienie wartości granicznych)
K
+
+
=
2
2
2
2
B
B
A
A
X
T
k
T
k
T
podejście probabilistyczne
1
...
=
=
=
B
A
k
k
Zwykle
K
+
+
=
2
2
B
A
X
T
T
T
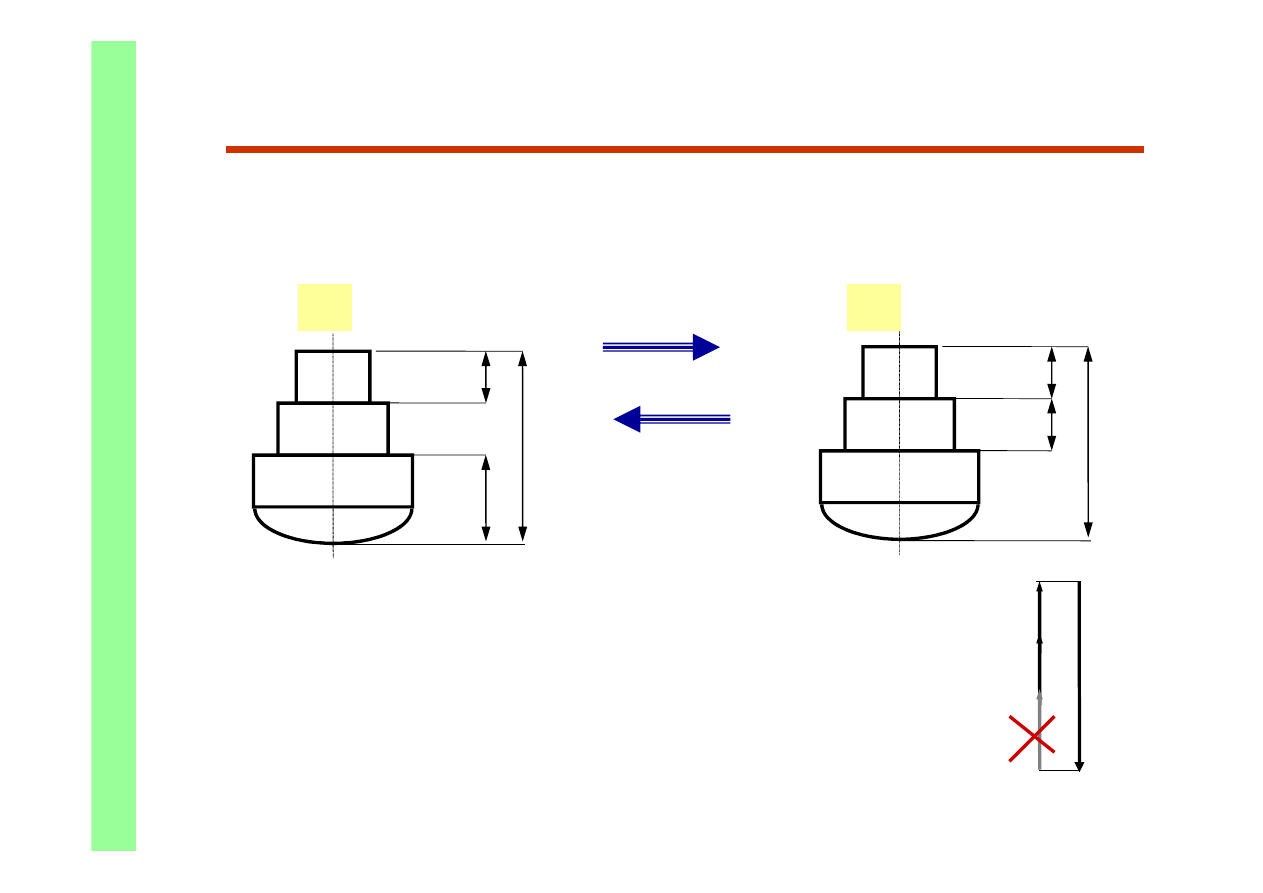
Zmiana sposobu wymiarowania
B
C
X
B
B
C
X
B
D
1
2
Zmieni
ć
wymiarowanie z podanego na rys. 1 na pokazane na rys. 2.
Wymiar A uzyskany w gotowych elementach po zmianie wymiarowania
powinien pozosta
ć
taki sam jak podany na rysunku 1.
C
A
A
C
C
A
C
2
1
2
1
2
1
2
1
d
d
b
b
c
c
a
a
D
B
C
A
−
−
=
D
c
B
A
T
T
T
T
+
+
=
Sprawdzi
ć
czy T
A
> T
B
+ T
c
Je
ś
li nie, to zmniejszy
ć
T
B
lub T
C
(b
ą
d
ź
T
B
oraz T
C
)
B
C
X
A
B
D
C
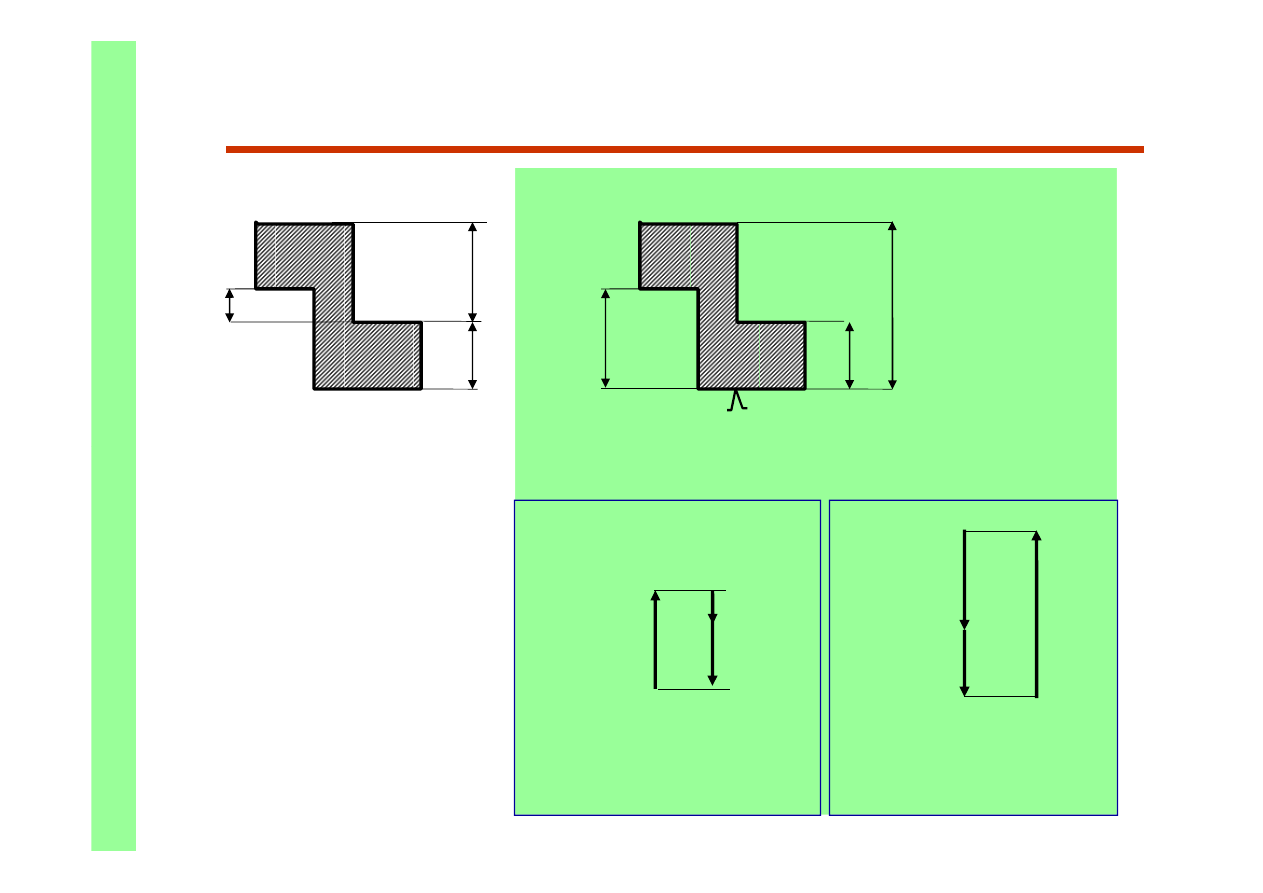
Zmiana bazy wymiarowej
A
C
B
B
E
D
2
1
2
1
2
1
b
b
e
e
c
c
B
E
C
−
=
E
C
B
B
A
D
2
1
2
1
2
1
b
b
d
d
a
a
B
D
A
−
=
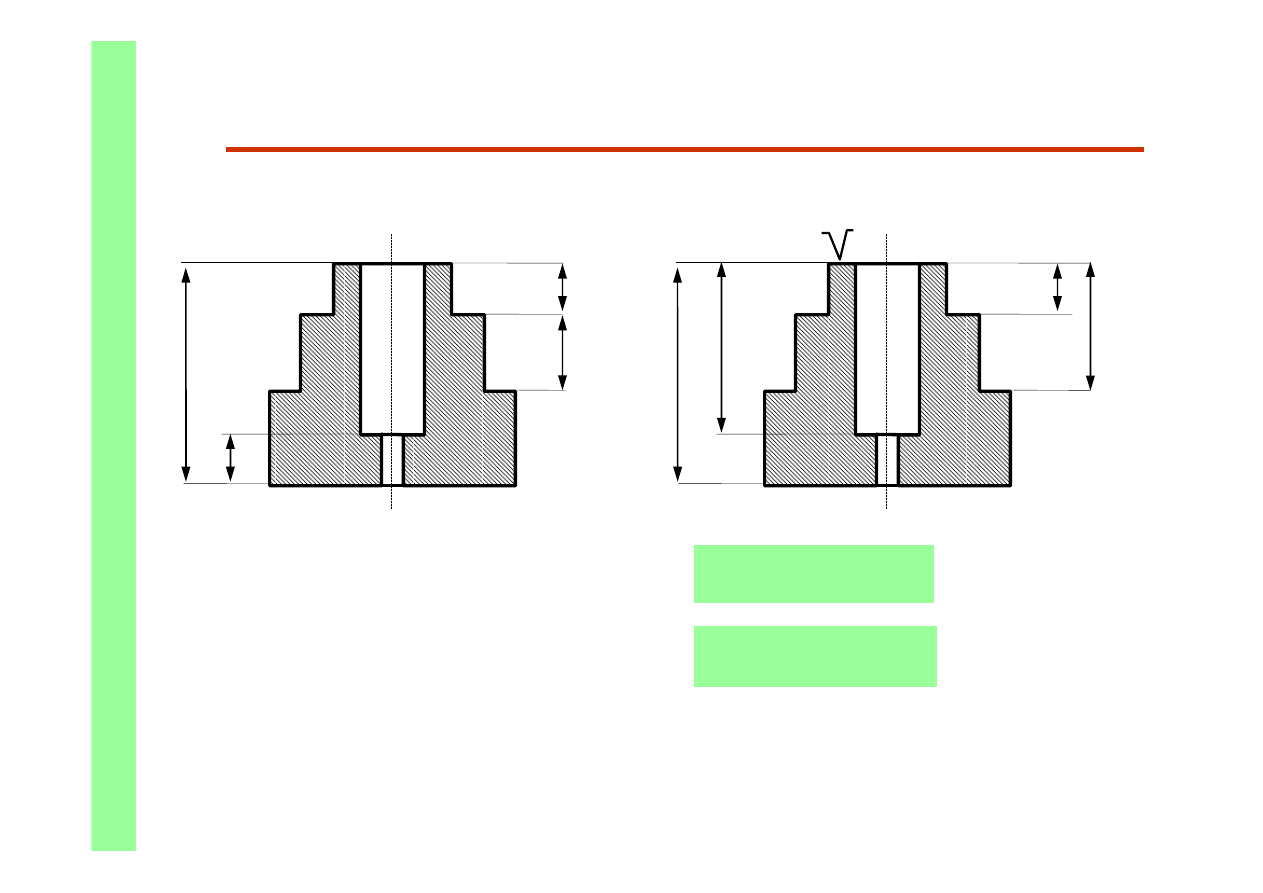
Zmiana bazy wymiarowej
B
D
C
A
F
E
C
A
D
2
1
2
1
2
1
e
e
a
a
d
d
E
A
D
−
=
2
1
2
1
2
1
c
c
f
f
b
b
C
F
B
−
=